Moving Colorable Graphs: A Mobility-Aware Traffic Steering Framework for Congested Terrestrial–Sea–UAV Networks
Abstract
1. Introduction
1.1. Challenges in Dense Maritime Communication Networks
1.2. Limitations of Existing Frequency Allocation Methods
1.3. Objectives and Contributions
- Moving colorable graphs are introduced as a general modeling framework for dynamic spectrum allocation in dense and heterogeneous maritime communication networks, including terrestrial, aerial and sea transmitters. The concept bridges the gap between static interference graphs and time-varying real-world deployments, capturing the joint effects of mobility, congestion, and multi-tier heterogeneity in port environments.
- We design and analyze a family of MCG-based frequency allocation algorithms that incrementally update spectrum assignments over time, balancing the trade-off between allocation optimality and re-coloring overhead. The proposed variants, including the unweighted (UW-MCG), priority-based (PR-MCG), and selective-reuse (SR-MCG), enable different levels of adaptivity and service differentiation.
- A selective reuse (SR-MCG) mechanism is introduced to further enhance spectrum utilization by allowing controlled PRB reuse between non-conflicting users when interference remains within acceptable SINR margins. This relaxation mechanism significantly reduces uncolored users under heavy congestion while preserving service guarantees for prioritized traffic.
- We implement and evaluate the proposed framework in a realistic dense-port scenario involving multiple heterogeneous transmitters (CBS, ABS, SBS) and mixed traffic profiles (Voice and Mobile broadband services). Simulation results demonstrate the superior throughput and demand satisfaction achieved by MCG-based methods compared to classical baselines.
2. Background and Graph Coloring
2.1. Spectrum Management in Maritime Communication Networks
2.2. Graph Coloring in Wireless Communications
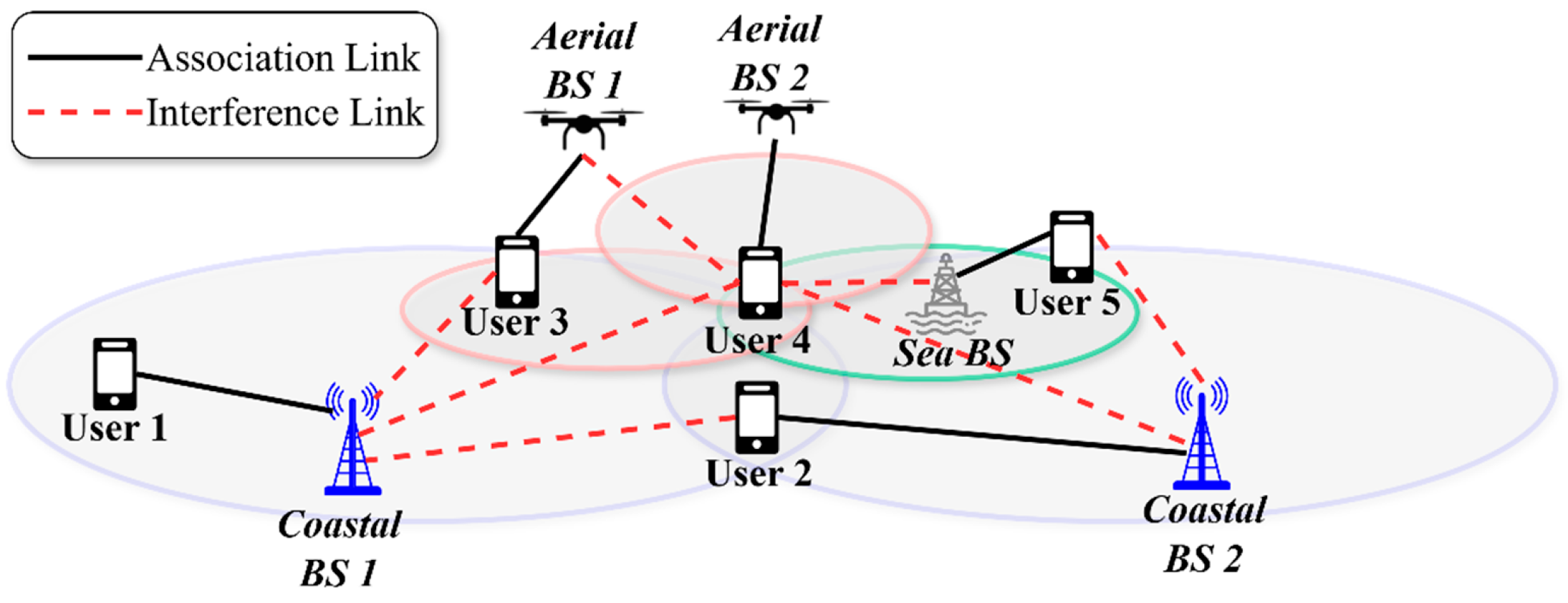
3. System Model
3.1. Dense and Heterogeneous MCN Architecture
3.2. Channel and Interference Models
3.3. Mobility and Congestion Models
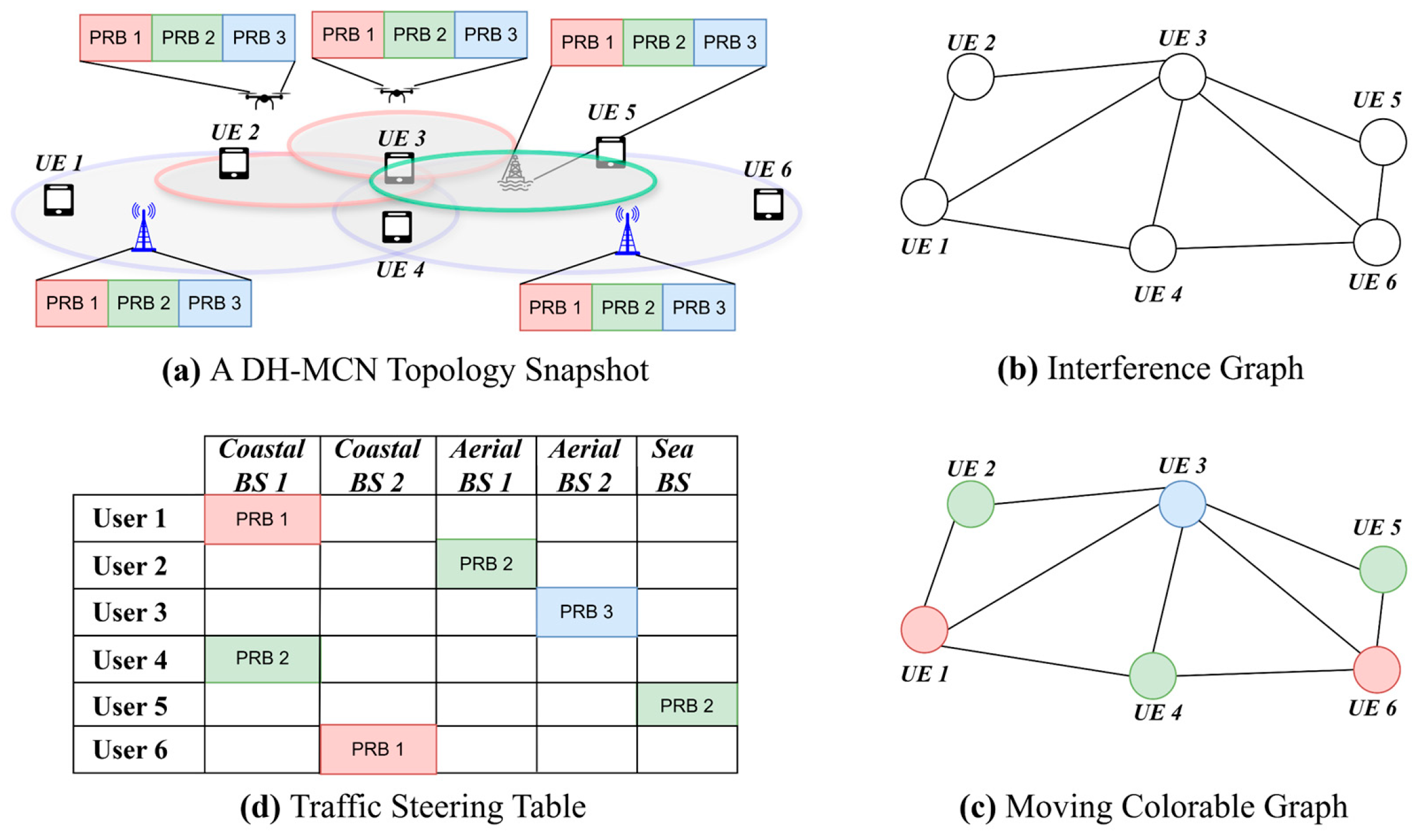
4. Moving Colorable Graphs: Concept and Optimization
4.1. Definition of MCGs and Optimization Problem
4.2. Tutorial Perspective
4.3. Handling Non–Fully Colored Graphs
- Priority-Based Partial Coloring [50]: Each user is assigned a weight proportional to its service class or demand urgency. Voice services correspond to low-throughput and delay-sensitive traffic (e.g., VoIP, safety signaling). Typical throughput requirements range between 64–256 kbps, but they demand high reliability and priority. MBB services, on the other hand, represent high-throughput, delay-tolerant applications (e.g., video streaming, data upload/download, IoT data aggregation). Their throughput demands typically range between 2–5 Mbps depending on the service tier, but they can tolerate moderate delay and controlled interference fluctuations. Weights reflect the urgency or criticality of the service and influence the order in which vertices are colored during the MCG-based allocation. Hence, we consider the following formulation:where are the weight of Voice and MBB users. The coloring algorithm then prioritizes vertices with higher weights, ensuring that critical services such as voice or safety-related links are preserved, while low-priority MBB users may be temporarily deferred. Based on (9), the objective thus becomes to maximize the weighted satisfaction ratio:
5. Proposed Graph-Based Algorithm
5.1. Workflow
- Step 1 (Topology and Channel Update): User and BS positions are updated according to the corresponding mobility models (see Section 3.3). The path-loss and small-scale fading parameters are recalculated, and new SINR values are estimated based on (2).
- Step 2 (Interference Graph Construction): Using the updated SINR values and user demands , the conflict graph is built by connecting each user’s pair according to (8). Each vertex carries an associated weight to indicate its service priority.
- Step 3 (Graph Coloring/PRB Assignment): The graph-coloring stage constitutes the core of the proposed MCG-based allocation mechanism and is presented in detail in Algorithm 1 of Section 5.2. The outcome is the final allocation of PRBs to users in the form of a traffic steering table (see Figure 3d).
- Step 4 (Performance Evaluation and Re-coloring Check): After the coloring step, the achieved rates are evaluated. Users not satisfying their demand are recorded, and the overall Demand Satisfaction Ratio (DSR) is updated as:
- Step 5 (MCG Update): The resulting colored graph is appended to the sequence , forming the Moving Colorable Graph representation of the network evolution.
5.2. Graph Coloring Algorithm
| Algorithm 1. Weighted MCG-Based Graph Coloring Procedure |
| Inputs: Conflict graph ; PRB set ; Demands , SINR values ; service type , selective_reuse ∈ {TRUE, FALSE} %optional flag |
| % ------Initial Unweighted Coloring------ |
| 1: Initialize all users as uncolored: |
| 2: Sort vertices by descending degree in (t) |
| 3: for each user u in sorted order do |
| 4: for each PRB k ∈ do |
| 5: if k is not used by any neighbor then |
| 6: Assign PRB k to user u: |
| 7: break |
| 8: end_if |
| 9: end_for |
| 10: end_for |
| 11: Identify uncolored users |
| % ------Priority-Based Recoloring (if needed)------ |
| 12: if then |
| 13: Assign weights for voice users, for MBB users |
| 14: Reconstruct (t) with weighted vertices |
| 15: Sort vertices in descending |
| 16: for each user u in sorted order do |
| 17: for each PRB k ∈ do |
| 18: if k is not used by any higher-priority neighbor then |
| 19: Assign PRB k to user u: |
| 20: break |
| 21: end_if |
| 22: end_for |
| 24: Identify remaining uncolored users |
| % ------Optional Selective Reuse------ |
| 25: if selective_reuse = TRUE and |_un2(t)| > 0 then |
| 26: for each uncolored user do |
| 27: for each PRB k ∈ do |
| 28: if (k unused in ) and (∀ using k then |
| 29: Assign PRB k to user u: |
| 30: mark u as “partially satisfied” |
| 31: break |
| 32: end_if |
| 33: end_for |
| 34: end_for |
| 35: end_if |
| 36: end_if |
| 37: Compute using (12) |
| 38: return coloring vector , , |
5.3. Complexity Insights
6. Numerical Results
6.1. Simulation Setup
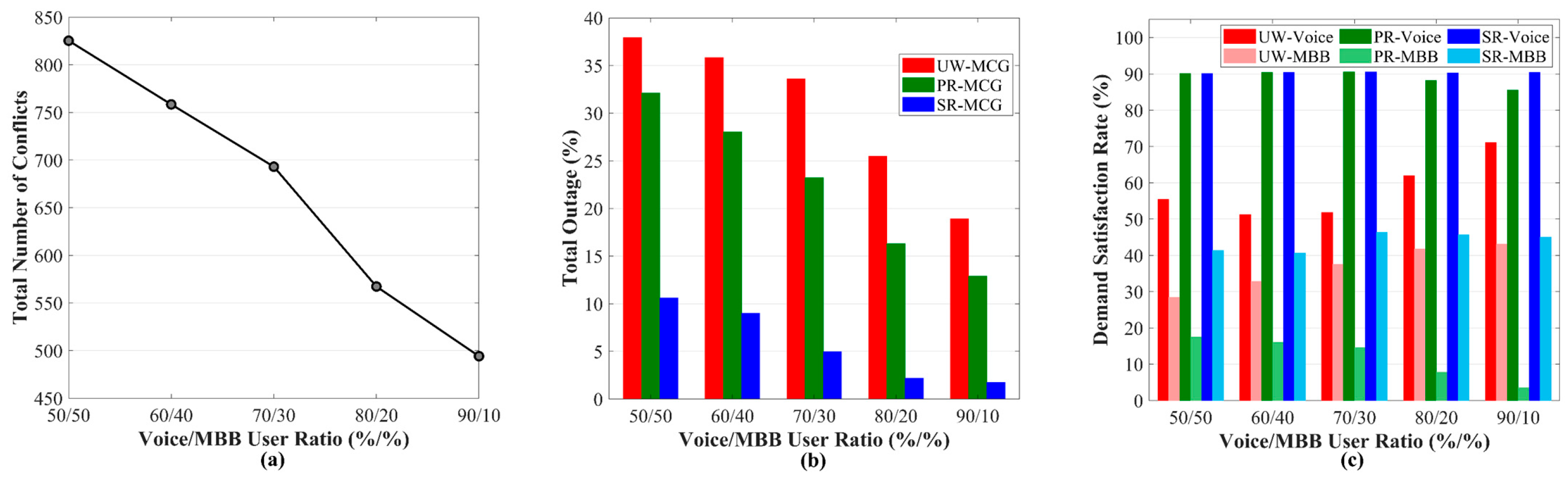
6.2. Performance Under Varying Demand and Conflict Intensity
- Unweighted Coloring-based MCG (UW-MCG): corresponds to lines 1–11 of Algorithm 1. All users are treated equally, and PRB allocation follows a degree-based greedy procedure without considering service heterogeneity. This baseline seeks to maximize coverage without QoS awareness.
- Priority-Based Recoloring MCG (PR-MCG): includes the weighted recoloring phase (lines 12–24 of Algorithm 1). Higher weights are assigned to Voice users so that the algorithm prioritizes their allocation when spectrum contention arises (i.e., uncolored users exist), ensuring service continuity under congestion.
- Selective Reuse-enabled MCG (SR-MCG): extends PR-MCG by activating the selective-reuse option (lines 25–35 of Algorithm 1). Uncolored users may reuse PRBs already assigned to other BSs, provided this reuse does not degrade the originally satisfied users. This variant increases spectral efficiency by exploiting interference-tolerant reuse.
6.3. Impact of Transmitting Power and PRB Bandwidth
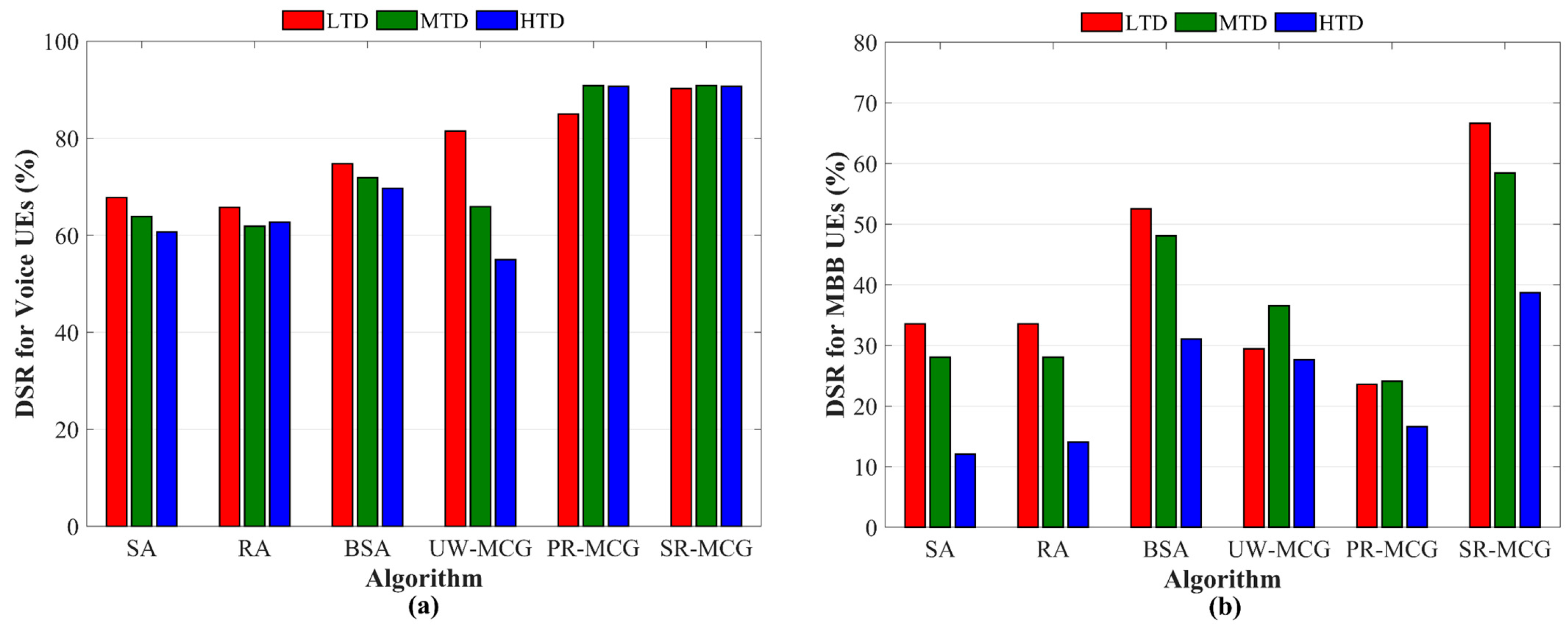
6.4. Benchmarking Against Baselines
- Low Traffic Demand (LTD): 90% Voice/10% MBB, Demand for MBB Mbps.
- Moderate Traffic Demand (MTD): 70% Voice/30% MBB, Mbps.
- High Traffic Demand (HTD): 50% Voice/50% MBB, Mbps.
- Static PRB Allocation (SA): Each BS assigns PRBs sequentially (user 1 occupies PRB 1, user 2 occupies PRB 2, and so on), without interference awareness.
- Random PRB Allocation (RA): Each BS randomly assigns available PRBs among its associated users, avoiding intra-cell reuse.
- Best Signal-based PRB Allocation (BSA): Users are sorted by received signal strength and allocated PRBs greedily, favoring high-SNR links.
6.5. Theoretical Justification of MCG Superiority over Baselines
6.6. Assumptions and Potential Limitations
7. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABS | Aerial Base Station |
| BS | Base Station |
| BSA | Best Signal-based PRB Allocation |
| BW | Bandwidth |
| CBS | Coastal Base Station |
| DH-MCN | Dense Heterogeneous Maritime Communication Network |
| DRL | Deep Reinforcement Learning |
| DSA | Dynamic Spectrum Access |
| DSR | Demand Satisfaction Rate |
| MCG | Moving Colorable Graph |
| MCN | Maritime Communication Network |
| ML | Machine Learning |
| PR-MCG | Priority-based Recoloring for Moving Colorable Graph |
| PRB | Physical Resource Block |
| QoS | Quality of Service |
| RA | Random PRB Allocation |
| SA | Static PRB Allocation |
| SBS | Sea Base Station |
| SINR | Signal-to-Interference-plus-Noise Ratio |
| SR-MCG | Selective Reuse-enabled Coloring for Moving Colorable Graph |
| UAV | Unmanned Aerial Vehicles |
| UE | User Equipment |
| UW-MCG | Unweighted Coloring for Moving Colorable Graph |
References
- Kapidani, N.; Bauk, S.; Davidson, I.E. Digitalization in developing maritime business environments towards ensuring sustainability. Sustainability 2020, 12, 9235. [Google Scholar] [CrossRef]
- Xylouris, G.; Nomikos, N.; Kalafatelis, A.; Giannopoulos, A.; Spantideas, S.; Trakadas, P. Sailing into the future: Technologies, challenges, and opportunities for maritime communication networks in the 6G era. Front. Commun. Netw. 2024, 5, 1439529. [Google Scholar] [CrossRef]
- Giannopoulos, A.; Gkonis, P.; Kalafatelis, A.; Nomikos, N.; Spantideas, S.; Trakadas, P.; Syriopoulos, T. From 6G to SeaX-G: Integrated 6G TN/NTN for AI-Assisted Maritime Communications—Architecture, Enablers, and Optimization Problems. J. Mar. Sci. Eng. 2025, 13, 1103. [Google Scholar] [CrossRef]
- Alqurashi, F.S.; Trichili, A.; Saeed, N.; Ooi, B.S.; Alouini, M.S. Maritime communications: A survey on enabling technologies, opportunities, and challenges. IEEE Internet Things J. 2022, 10, 3525–3547. [Google Scholar] [CrossRef]
- Wei, T.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N.; Lu, J. Hybrid satellite–terrestrial communication networks for the maritime Internet of Things: Key technologies, opportunities, and challenges. IEEE Internet Things J. 2021, 8, 8910–8934. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.M.; Xia, T.; Wang, L. Maritime IoT: An architectural and radio spectrum perspective. IEEE Access 2020, 8, 93109–93122. [Google Scholar] [CrossRef]
- Li, X.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N. Maritime coverage enhancement using UAVs coordinated with hybrid satellite–terrestrial networks. IEEE Trans. Commun. 2020, 68, 2355–2369. [Google Scholar] [CrossRef]
- Li, X.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N. UAV-enabled accompanying coverage for hybrid satellite–UAV–terrestrial maritime communications. In Proceedings of the 2019 28th Wireless and Optical Communications Conference (WOCC), Beijing, China, 9–10 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Fahim, P.; Rezaei, J.; Jayaraman, R.; Poulin, M.; Montreuil, B.; Tavasszy, L. The physical Internet and maritime ports: Ready for the future? IEEE Eng. Manag. Rev. 2021, 49, 136–149. [Google Scholar] [CrossRef]
- Yau, K.L.A.; Peng, S.; Qadir, J.; Low, Y.C.; Ling, M.H. Towards smart port infrastructures: Enhancing port activities using information and communications technology. IEEE Access 2020, 8, 83387–83404. [Google Scholar] [CrossRef]
- Haidine, A.; Aqqal, A.; Dahbi, A. Communications backbone for environment monitoring applications in smart maritime ports—Case study of a Moroccan port. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Geoscience, Electronics and Remote Sensing Technology (AGERS), Casablanca, Morocco, 22–24 September 2021; pp. 136–140. [Google Scholar] [CrossRef]
- Armitage, S.; Awty-Carroll, K.; Clewley, D.; Martinez-Vicente, V. Detection and classification of floating plastic litter using a vessel-mounted video camera and deep learning. Remote Sens. 2022, 14, 3425. [Google Scholar] [CrossRef]
- Abdel-Malek, M.A.; Azab, M. UAV-fleet management for extended NextG emergency support infrastructure with QoS and cost aware. Internet Things 2024, 25, 101043. [Google Scholar] [CrossRef]
- Shivkumar, S.; Supriya, M. A framework for fleet management using IoT and predictive analytics. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kanpur, India, 3–5 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Kalafatelis, A.S.; Nomikos, N.; Giannopoulos, A.; Alexandridis, G.; Karditsa, A.; Trakadas, P. Towards predictive maintenance in the maritime industry: A component-based overview. J. Mar. Sci. Eng. 2025, 13, 425. [Google Scholar] [CrossRef]
- Tan, L.; Feng, Z.; Li, W.; Jing, Z.; Gulliver, T.A. Graph coloring-based spectrum allocation for femtocell downlink interference mitigation. In Proceedings of the 2011 IEEE Wireless Communications and Networking Conference (WCNC), Cancun, Mexico, 28–31 March 2011; pp. 1248–1252. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Zhang, Y.; Zhang, S. A dynamic spectrum allocation algorithm for a maritime cognitive radio communication system based on a queuing model. Information 2017, 8, 119. [Google Scholar] [CrossRef]
- Wu, R.; Li, Z.; Xie, Z.; Liang, X. Intelligent spectrum sharing strategy for integrated satellite–maritime heterogeneous mobile networks. IEEE Trans. Veh. Technol. 2023, 73, 6780–6794. [Google Scholar] [CrossRef]
- Giannopoulos, A.; Spantideas, S.; Trakadas, P. Spatiotemporal graph coloring for frequency assignment in spectrum-constrained ground–air–sea networks. Authorea Prepr. 2025. [Google Scholar] [CrossRef]
- Falk, J.; Zebelein, C.; Haubelt, C.; Teich, J. A rule-based quasi-static scheduling approach for static islands in dynamic dataflow graphs. ACM Trans. Embed. Comput. Syst. 2013, 12, 74. [Google Scholar] [CrossRef]
- Hasan, M.K.; Ismail, A.F.; Islam, S.; Hashim, W.; Pandey, B. Dynamic spectrum allocation scheme for heterogeneous network. Wirel. Pers. Commun. 2017, 95, 299–315. [Google Scholar] [CrossRef]
- Hao, D.D.; Zou, S.H.; Cheng, S.D. Heuristic algorithms for dynamic spectrum assignment in open spectrum system. J. Softw. 2008, 19, 479–491. [Google Scholar] [CrossRef]
- Kaur, A.; Kumar, K. A comprehensive survey on machine learning approaches for dynamic spectrum access in cognitive radio networks. J. Exp. Theor. Artif. Intell. 2022, 34, 1–40. [Google Scholar] [CrossRef]
- Li, F.; Shen, B.; Guo, J.; Lam, K.Y.; Wei, G.; Wang, L. Dynamic spectrum access for Internet of Things based on federated deep reinforcement learning. IEEE Trans. Veh. Technol. 2022, 71, 7952–7956. [Google Scholar] [CrossRef]
- Giannopoulos, A.E.; Spantideas, S.T.; Zetas, M.; Nomikos, N.; Trakadas, P. FedShip: Federated over-the-air learning for communication-efficient and privacy-aware smart shipping in 6G communications. IEEE Trans. Intell. Transp. Syst. 2024, 25, 19873–19888. [Google Scholar] [CrossRef]
- Xi, Y.; Yeh, E.M. Distributed algorithms for spectrum allocation, power control, routing, and congestion control in wireless networks. In Proceedings of the 8th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc 2007), Montréal, QC, Canada, 9–14 September 2007; pp. 180–189. [Google Scholar] [CrossRef]
- Welsh, D.J.; Powell, M.B. An upper bound for the chromatic number of a graph and its application to timetabling problems. Comput. J. 1967, 10, 85–86. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, Z.; Du, H.; Sang, L.; Yang, D. A spectrum allocation algorithm based on bandwidth matching and interference avoidance in cognitive radio networks. In Proceedings of the 2012 IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Sydney, Australia, 9–12 September 2012; pp. 950–955. [Google Scholar] [CrossRef]
- He, Q. A new model of spectrum allocation based on the graph theory. In Recent Advances in Computer Science and Information Engineering; Qian, Z., Cao, L., Su, W., Wang, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 4, pp. 675–681. [Google Scholar] [CrossRef]
- Salani, W.; Mfupe, L.; Oyerinde, O.O. Dynamic spectrum allocation in the C-band: An overview. Appl. Sci. 2025, 15, 9762. [Google Scholar] [CrossRef]
- Jo, S.W.; Shim, W.S. LTE-maritime: High-speed maritime wireless communication based on LTE technology. IEEE Access 2019, 7, 53172–53181. [Google Scholar] [CrossRef]
- Villegas, E.G.; Ferré, R.V.; Paradells, J. Frequency assignments in IEEE 802.11 WLANs with efficient spectrum sharing. Wirel. Commun. Mob. Comput. 2009, 9, 1125–1140. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Chen, Z.; Wang, Y.; Eljailany, H.A.; Ipaye, A.A. Optimizing V2X communication: Spectrum resource allocation and power control strategies for next-generation wireless technologies. Appl. Sci. 2024, 14, 531. [Google Scholar] [CrossRef]
- Giral, D.; Hernández, C.; Rodríguez-Colina, E. Spectrum decision-making in collaborative cognitive radio networks. Appl. Sci. 2020, 10, 6786. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y.; He, M. Deep reinforcement learning-based spectrum allocation algorithm in Internet of Vehicles discriminating services. Appl. Sci. 2022, 12, 1764. [Google Scholar] [CrossRef]
- Basloom, S.; Nazar, A.; Aldabbagh, G.; Abdullah, M.; Dimitriou, N. Resource allocation using graph coloring for dense cellular networks. In Proceedings of the 2016 International Conference on Computing, Networking and Communications (ICNC), Kauai, HI, USA, 15–18 February 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Yuan, L.; Qin, L.; Lin, X.; Chang, L.; Zhang, W. Effective and efficient dynamic graph coloring. Proc. VLDB Endow. 2017, 11, 338–351. [Google Scholar] [CrossRef]
- Lien, S.Y.; Shieh, S.L.; Huang, Y.; Su, B.; Hsu, Y.L.; Wei, H.Y. 5G new radio: Waveform, frame structure, multiple access, and initial access. IEEE Commun. Mag. 2017, 55, 64–71. [Google Scholar] [CrossRef]
- Lin, X.; Li, J.; Baldemair, R.; Cheng, J.F.T.; Parkvall, S.; Larsson, D.C.; Werner, K. 5G new radio: Unveiling the essentials of the next generation wireless access technology. IEEE Commun. Stand. Mag. 2019, 3, 30–37. [Google Scholar] [CrossRef]
- Al Kassir, H.; Giannopoulos, A.; Spantideas, S.; Trakadas, P.; Xylouris, G.; Kourtis, M.A.; Zaharis, Z.D. Automated end-to-end AI/ML lifecycles for radio management in 6G networks. In Proceedings of the 2024 IEEE Future Networks World Forum (FNWF), Montreal, QC, Canada, 9–11 October 2024; pp. 365–371. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, H.; Li, Y.; Sun, Q.; Wu, Y.; Jin, S.; Xu, C. Wireless channel models for maritime communications. IEEE Access 2018, 6, 68070–68088. [Google Scholar] [CrossRef]
- Kurt, S.; Tavli, B. Path-loss modeling for wireless sensor networks: A review of models and comparative evaluations. IEEE Antennas Propag. Mag. 2017, 59, 18–37. [Google Scholar] [CrossRef]
- Tan, C.C.; Beaulieu, N.C. On first-order Markov modeling for the Rayleigh fading channel. IEEE Trans. Commun. 2000, 48, 2032–2040. [Google Scholar] [CrossRef]
- Wang, L.C.; Liu, W.C.; Cheng, Y.H. Statistical analysis of a mobile-to-mobile Rician fading channel model. IEEE Trans. Veh. Technol. 2008, 58, 32–38. [Google Scholar] [CrossRef]
- Lee, S.; Park, S. Mobility-assisted digital twin network optimization over industrial Internet of Things. Appl. Sci. 2024, 14, 9090. [Google Scholar] [CrossRef]
- Alam, M.M.; Spadon, G.; Etemad, M.; Torgo, L.; Milios, E. Enhancing short-term vessel trajectory prediction with clustering for heterogeneous and multi-modal movement patterns. Ocean Eng. 2024, 308, 118303. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R.; Lim, T.J. Placement optimization of UAV-mounted mobile base stations. IEEE Commun. Lett. 2016, 21, 604–607. [Google Scholar] [CrossRef]
- Tadokoro, K.; Kinugasa, N.; Kato, T.; Terada, Y.; Matsuhiro, K. A marine-buoy-mounted system for continuous and real-time measurement of seafloor crustal deformation. Front. Earth Sci. 2020, 8, 123. [Google Scholar] [CrossRef]
- Xiong, H.; Yao, L.; Tan, H.; Wang, W. Pedestrian walking behavior revealed through a random walk model. Discret. Dyn. Nat. Soc. 2012, 2012, 405907. [Google Scholar] [CrossRef]
- Chow, F.; Hennessy, J. Register allocation by priority-based coloring. In Proceedings of the 1984 SIGPLAN Symposium on Compiler Construction, Montreal, QC, Canada, 17–22 June 1984; pp. 222–232. [Google Scholar] [CrossRef]
- Sroka, P.; Kułacz, Ł.; Janji, S.; Dryjański, M.; Kliks, A. Policy-based traffic steering and load balancing in O-RAN-based vehicle-to-network communications. IEEE Trans. Veh. Technol. 2024, 73, 9356–9369. [Google Scholar] [CrossRef]
- Che, Y.; Zhao, Z.; Luo, S.; Wu, K.; Duan, L.; Leung, V.C.M. UAV-Aided Wireless Energy Transfer for Sustaining Internet of Everything in 6G. Drones 2023, 7, 628. [Google Scholar] [CrossRef]
- Williams, Z.; Soto Calvo, M.; Lee, H.S.; Aljber, M.; Jeong, J.-S. A Low-Cost Autonomous Multi-Functional Buoy for Ocean Currents and Seawater Parameter Monitoring, and Particle Tracking. J. Mar. Sci. Eng. 2025, 13, 1629. [Google Scholar] [CrossRef]



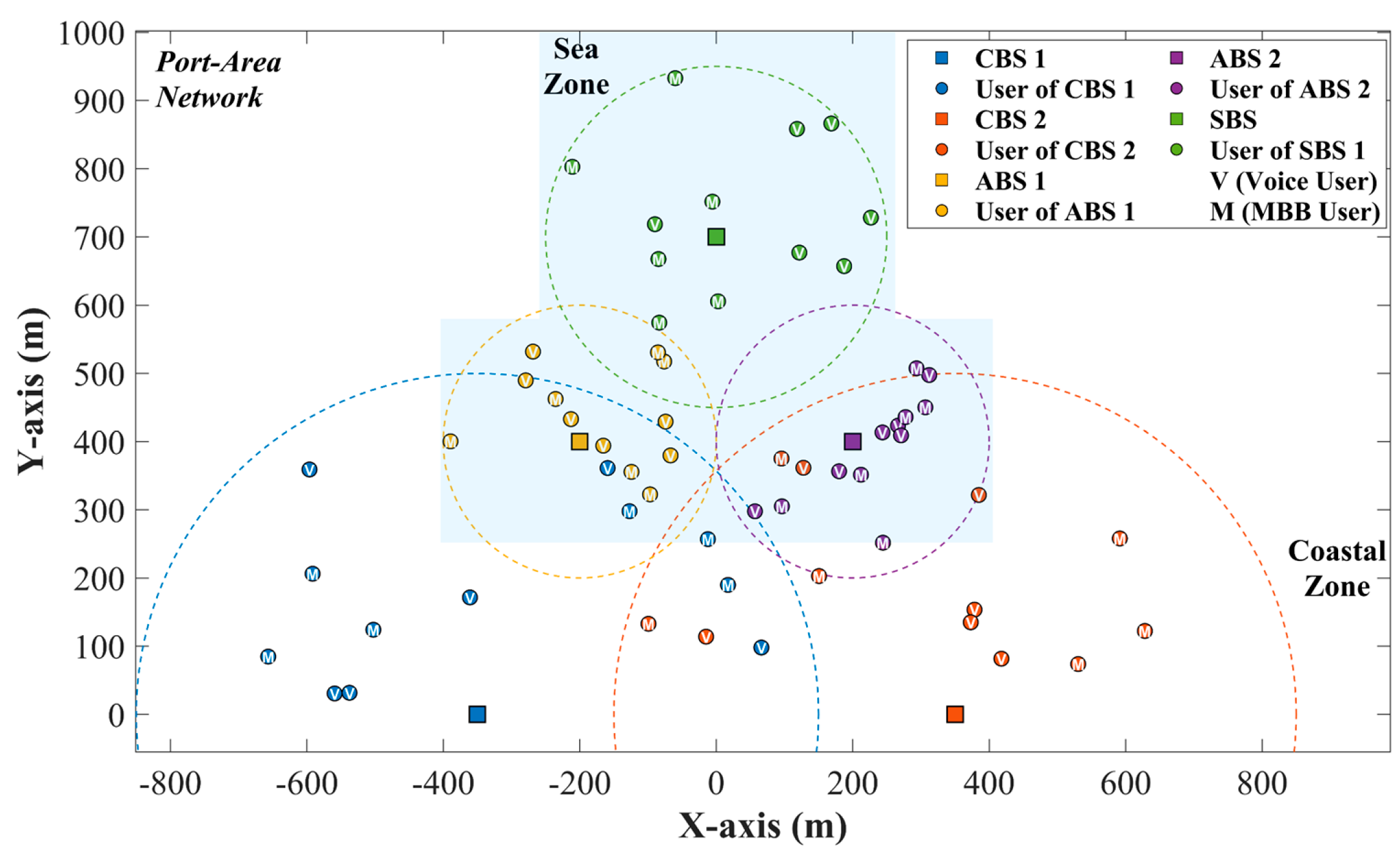

| Parameter | Symbol | Value | Parameter | Symbol | Value |
|---|---|---|---|---|---|
| Number of BS | 5 | CBS 1,2 positions | - | (−350, 0) m, (350, 0) m | |
| CBSs, ABSs, SBS | ( | (2, 2, 1) | ABS 1, 2 positions | - | Dynamic [47] |
| Number of Episodes | 100 | SBS position | - | (0, 700) m (small drifts) | |
| Time slots | 100 | CBS radius | 500 m | ||
| Total Bandwidth | 5 MHz | ABS radius | 200 m | ||
| Numerology | 1 | SBS radius | 250 m | ||
| Guard band | 0.25 MHz | CBS transmit power | 1 W | ||
| PRBs per BS | 12 | ABS transmit power | 0.1 W | ||
| Number of users | 60 | SBS transmit power | 0.1 W | ||
| Voice/MBB user ratio | - | 50%/50% | Noise power | −104 dBm | |
| Voice demand | 256 kbps | Path-loss exponents | (2.7, 2.2, 2.5) | ||
| MBB demand | 3 Mbps | Rician K-factors | (8 dB, 6 dB) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giannopoulos, A.; Spantideas, S. Moving Colorable Graphs: A Mobility-Aware Traffic Steering Framework for Congested Terrestrial–Sea–UAV Networks. Appl. Sci. 2025, 15, 11560. https://doi.org/10.3390/app152111560
Giannopoulos A, Spantideas S. Moving Colorable Graphs: A Mobility-Aware Traffic Steering Framework for Congested Terrestrial–Sea–UAV Networks. Applied Sciences. 2025; 15(21):11560. https://doi.org/10.3390/app152111560
Chicago/Turabian StyleGiannopoulos, Anastasios, and Sotirios Spantideas. 2025. "Moving Colorable Graphs: A Mobility-Aware Traffic Steering Framework for Congested Terrestrial–Sea–UAV Networks" Applied Sciences 15, no. 21: 11560. https://doi.org/10.3390/app152111560
APA StyleGiannopoulos, A., & Spantideas, S. (2025). Moving Colorable Graphs: A Mobility-Aware Traffic Steering Framework for Congested Terrestrial–Sea–UAV Networks. Applied Sciences, 15(21), 11560. https://doi.org/10.3390/app152111560







