An Area-Efficient and Low-Error FPGA-Based Sigmoid Function Approximation

Abstract

Neuromorphic hardware systems allow efficient implementation of artificial neural networks (ANNs) across various applications that demand high data throughput, reduced physical size, and low energy consumption. Field-Programmable Gate Arrays (FPGAs) possess inherent features that can be aligned with these requirements. However, implementing ANNs on FPGAs also presents challenges, including the computation of the neuron activation functions, due to the balance between resource constraints and numerical precision. This paper proposes a resource-efficient hardware approximation method for the sigmoid function, utilizing a combination of first- and second-degree polynomial functions. The method aims mainly to minimize the approximation error. This paper also evaluates the obtained results against existing techniques and discusses their significance. The experimental results showed that, although the proposed method mainly aimed to minimize the approximation error, it also had lower hardware resource usage than several of the most closely related works. Using 16-bit fixed-point number representation, the absolute mean error was $1.66\times {10}^{-3}$ by using 0.04% of the logic blocks and 3.21% of the DSP blocks in a Ciclone V 5CGXFC7C7F23C8 FPGA Device.

1. Introduction

The field of neuroengineering is experiencing significant growth, with its activities characterized by several challenging tasks. One important area of focus within this field is the creation of neuromorphic hardware systems. These systems are composed of electronic circuits specifically designed to directly implement artificial neural networks (ANNs). The primary aim of developing such systems is to facilitate the application of neural computing models across a broad range of scenarios, each with its unique set of requirements. One critical need addressed by neuromorphic hardware is the acceleration of processing speed in ANN. For instance, many applications require the ability to achieve high data throughput to support fast training and/or recall cycles, such as video processing [1]. Furthermore, some applications require real-time responses from ANN, such as in cryptography/encryption processing [2] and in Internet of Things (IoT) environments, where it is essential to handle data from sensor networks instantly [3]. In addition to processing speed, neuromorphic systems also meet the requirements of mobile applications. For example, robotic platforms can benefit greatly from the reduced physical size and energy consumption of these systems [4]. Additionally, telecommunications is another example of a subject area where minimizing both hardware size and power requirements is important [5]. In this context, neuromorphic systems generally make it feasible to deploy neural network capabilities in compact and energy-efficient devices.

ASIC (Application-Specific Integrated Circuit) and FPGA (Field-Programmable Gate Array) technologies allow the creation of highly parallel computing architectures when implementing ANNs, which can achieve greater processing speeds than traditional Central Processing Units (CPUs) [3]. In addition, the low energy consumption of ASIC and FPGA circuits makes them well-suited for developing embedded neuromorphic systems, offering an advantage over Graphics Processing Units (GPUs) and CPUs in this regard [6]. While ASIC chips are ideal for ultra-low power applications like brain–computer interfaces, FPGA technology is beneficial due to its shorter development cycles and lower costs for small- and medium-scale production [7]. FPGAs can thus achieve high data throughput while minimizing space and energy use, making them a suitable choice for the types of ANN applications described above.

However, implementing ANNs directly on hardware, particularly on FPGA, also presents several challenges. These difficulties arise from the inherent complexity of neural computations and the constraints of hardware resources. Some of these difficulties include the limited capacity of the chips and the numerical precision of calculations. The challenge of limited hardware resources is related to FPGAs having a finite number of logic blocks (commonly implemented as Look-Up Tables (LUTs) ), memory, and Digital Signal Processing units (DSPs), which can restrict the size and complexity of the networks that can be implemented [8]. The second challenge involves numerical precision, as implementing ANNs on hardware often uses fixed-point arithmetic instead of floating-point [9]. While this strategy saves resources, it can lead to precision loss. Therefore, numerical precision should be monitored in ANN hardware implementations to ensure it does not affect model accuracy. One specific computation in which chip resources and precision issues can arise is in the implementation of neural activation functions like the sigmoid function [10]. The sigmoid function, $\sigma \left(x\right)$, is defined as follows:

$$y=\sigma \left(x\right)={\displaystyle \frac{1}{1+e^{-\lambda (x-\rho )}}}$$

(1)

where $\lambda$ represents the slope of the curve and $\rho$ represents the horizontal translation that adjusts the location of the curve’s inflection point. As a neural activation function, the sigmoid function is often used with $\lambda =1$ and $\rho =0$ [11].

Directly implementing the sigmoid function in hardware is impractical due to the extensive operations involved, such as exponentiation and division. In this way, the present work focuses on developing a hardware-based approximation of the sigmoid function using a combination of first- and second-degree polynomial functions, depending on the region in the function domain. Based on the outlined motivation, the proposal is intended to be resource-efficient to conserve chip area and maintain numerical precision comparable to previous publications.

The function approximation by low-degree polynomials, in this work, will be performed at the software level, using a hardware description language. Then, it will be up to the FPGA vendor’s hardware synthesis software, based on that description, to find the corresponding hardware implementation compatible with the characteristics of each specific chip model.

Some related works ([12,13,14,15,16]) restricted the values of operands or boundaries between approximation regions to be powers of two, hoping this would save hardware resources. However, this restriction may result in a loss of accuracy. Previous works, as [16,17], have also adopted the strategy of approximating regions of the function domain using low-degree polynomials. However, they adopted arbitrary values for the boundaries between those regions. In the present work, instead, it was decided to carry out a systematic search for the best values of those boundaries, hoping that this would better identify which regions of the function would be more suitable for approximations by polynomials of which degrees.

A methodological challenge encountered in works related to FPGA algorithm implementations is the wide variety of devices, with different types of internal hardware modules available, produced by different companies, each with its own synthesis software. For instance, experimental results in [17] were obtained for Xilinx FPGA XC7V2000 with Vivado design suit, while in [14] the authors used Quartus II for FPGA device EP3C16F484C6 from Cyclone III family. This often makes direct comparisons between published results produced in different studies impractical. The representation of operands and coefficients used in calculations also varies from study to study, in terms of the total number of bits, the number of bits in the integer part, and the number of bits in the fractional part (when using fixed point representation), potentially rendering comparisons meaningless.

The main contributions of this work are as follows:

• In the sigmoid approximation, it systematically searches for the best boundaries between approximation regions in its domain, rather than establishing them arbitrarily. The use of this strategy provided a low mean absolute approximation error value ($1.66\times {10}^{-3}$) when compared to related works.
• It relaxes the common restriction on using operands that are powers of two, allowing them to assume values freely. Experimental results showed that this had no systematic negative impact on hardware resource usage and probably contributed to the quality of the results.
• As a methodological contribution, the results are validated for multiple chip models, from two large companies, making the comparisons with other works fair and more general. Furthermore, all related works considered here were implemented in VHDL language according to the details provided in the original articles and their codes were made publicly available for reproduction by the scientific community and for the continuation of this research.
• Also seeking fairness and a methodologically correct procedure, we advocate that the comparison with the results of related works be made by standardizing the number of bits of the operands, the FPGA synthesis programs, and the chip models for implementation.

The remainder of the paper is organized as follows: The next section presents the justification for this study and a review of the literature. Section 3 details the proposed method, and the final two sections present the results, discussion, comparisons to published works, and conclusions.

2. Justification and Related Works

In the field of machine learning, the sigmoid function is a widely used nonlinear component, commonly serving as a neural activation function. It is frequently employed in shallow networks, such as Multilayer Perceptrons (MLPs), both during the operation phase (inference) and the training phase, in the derivative for error backpropagation and weight adjustment [11]. However, the sigmoid function is also essential in various other neural computing models beyond MLP. For example, it regulates the retention, forgetting, and passing of information in recurrent neural networks, acting as the activation function for different gates in Long Short-Term Memory (LSTM) networks [18], and in Gated Recurrent Units (GRUs) [19,20]. While the Rectified Linear Unit (ReLU) and its variants, collectively known as the ReLU family, have gained popularity as activation functions in deep learning networks [21], the sigmoid function remains in use within deep models as well. Examples of its use can be found for modulating the flow of information in Structured Attention Networks (SANs), which incorporate structured attention mechanisms to focus on specific parts of the input data [22]. The sigmoid function is also employed to map internal values to a range between 0 and 1 in deep models, particularly for binary decisions or probabilistic outputs, as seen in convolutional neural networks, like LeNet [23], and in Autoencoders [24].

The continued interest in researching the sigmoid function is also reflected in the numerous studies published on its hardware implementation. Common approaches to implementing the sigmoid function include piecewise approximation with linear or nonlinear segments, LUTs for direct storage of output values, Taylor series expansion, and Coordinate Rotation Digital Computer (CORDIC) methods. The work [25] aims to achieve low maximum approximation error using CORDIC-based techniques to iteratively calculate trigonometric and hyperbolic functions. However, this approach demands significant chip resources. Similarly, the authors in [26] employed Taylor’s theorem and the Lagrange form for approximation. The work also proposes incorporating the reutilization of neuron circuitry into the approximation calculation to enhance chip area efficiency.

For piecewise approximation of the sigmoid curve, the authors in [27] utilized exponential function approximation, which involves complex division operations. A number of studies propose multiple approximation schemes. For instance, the authors in [13] introduced an approach using three independent modules—Piecewise Linear Function (PWL), Taylor series, and the Newton–Raphson method—that can be combined to achieve the desired balance between accuracy and resource efficiency. The study in  [28] presents two methods for approximation: one centralized and the other distributed, using reconfigurable computing environments to optimize implementation.

Meanwhile, the authors in [16] proposed different schemes for sigmoid approximation, utilizing first- or second-order polynomial functions depending on the required accuracy and resource usage. Nevertheless, most works focus on different PWL approximation strategies. Reference [17] uses curvature analysis to segment the sigmoid function for PWL approximation, adjusting each segment based on maximum and average error metrics to balance precision and resource consumption. In another approach, the authors in [29] employed a first-order Taylor series expansion to define the intersection points of the PWL segments, while [30] leveraged statistical probability distribution to determine the number of segments, fragmenting the function into unequal spaces to minimize approximation error. Other approaches aim to reduce computational complexity. For example, the authors in [31] explored a technique that combines base-2 logarithmic functions with bit-shift operations for approximation, resulting in reduced chip area.

The use of LUTs for direct storage of sigmoid output values is explored in [32], providing a straightforward method for FPGA implementation. On the other hand, the authors in [33] achieved high precision by using floating-point arithmetic, directly computing the sigmoid function with exponent function interpolation via the McLaurin series and Padé polynomials. However, this implementation requires a large chip area.

A restriction adopted in several related works ([12,13,14,15,16]) was to only use multiplications by powers of 2 or operations with base-2 logarithm instead of using coefficients with generic values, in order to use shifts replacing normal multiplications, to save hardware resources. However, this risks sacrificing accuracy.

3. Materials and Methods

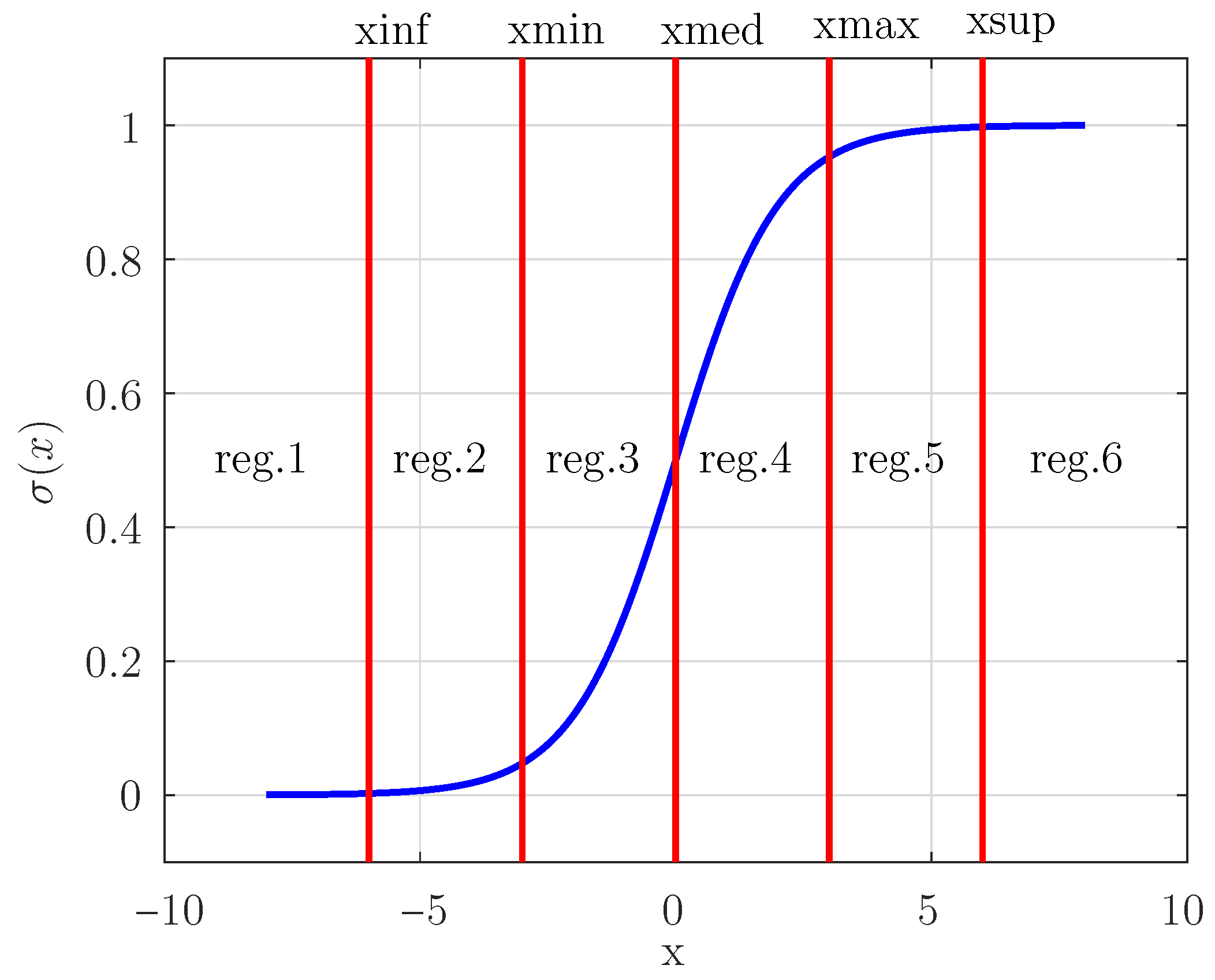
As in some of the related works, the scheme proposed here consists in splitting the sigmoid function domain into a small number of subdomains (Figure 1) and in approximating the function in each subdomain by a low-degree polynomial, expecting in this way a low hardware resource usage. The polynomial degrees are chosen based in the function graph form in each subdomain. For x in the function domain, if $x<\mathit{xinf}$, $\sigma \left(x\right)$ will be approximated as being a constant equal to zero. For $x>\mathit{xsup}$, $\sigma \left(x\right)$ will be approximated as being the constant one. For $\mathit{xinf}<x<\mathit{xmin}$ and for $\mathit{xmax}<x<\mathit{xsup}$, $\sigma \left(x\right)$ will be approximated by first degree polynomials. For $\mathit{xmin}<x<\mathit{xmed}$ and for $\mathit{xmed}<x<\mathit{xmax}$, $\sigma \left(x\right)$ will be approximated by second degree polynomials. However, unlike those works, the boundaries between the approximation regions will not be defined arbitrarily, but will be systematically sought, in an approximately continuous way, in order to minimize the average absolute error in the range $-8<x<+8$. This range to be explored was chosen here, as in [17], because outside it, $\sigma \left(x\right)$ is approximately constant, 0 or 1. As an alternative, the structure of the same algorithm will search for the boundaries that minimizes the maximum (the peak) of the absolute error in the same domain.

Algorithm 1 was used to search for the best approximations boundaries. It was implemented in the GNU Octave software [34]. Initially, the search step dx is set to 0.005. Due to the sigmoid function symmetry about the point $(0,0.5)$, xmed is set to 0. Variables minAvgAbsError and minMaxAbsError are used to register the smaller average absolute error and the minimum value for the absolute error peak, respectively, known up to each iteration along the whole domain. Then, two nested for loops generate many combinations of values to xinf and xmin. The particular ranges used in those for loops in Algorithm 1 were chosen after experimentation with wider ranges and with larger steps, in a preliminar coarse experiment. Those ranges are used in a final refinement. In lines 7 and 8, symmetric values about the origin are set for xmax and xsup in relation to xmin and xinf, respectively. Lines from 9 to 14 build sequences of values for x in each of the approximations regions. Lines 15 to 20 build sequences containing the standard values for the sigmoid in each region. In lines from 21 to 24, the Octave function polyfit is applied to the sequences belonging to each of the regions where polynomial approximations are adopted, using the least square error criterion. The third polyfit argument is the degree of the desired polynomial. Variables $p2$, $p3$, $p4$, and $p5$ receive the polynomials coefficients of the corresponding regions. Lines from 25 to 31 calculate and concatenate the errors for each domain value. Line 32 calculates the average absolute error (avgAbsError) and line 33 calculates the maximum absolute error (maxAbsError) for the current $(\mathit{xinf},\mathit{xmin})$ combination. Lines 34 to 42 check if the newly calculated avgAbsError is smaller than the least average absolute error known up to this moment, in which case the corresponding optimal conditions are registered. The same kind of checking is performed for maxAbsError in lines from 43 to 51. So, at the execution end, the best boundaries and the corresponding polynomials coefficients are known for both criteria. There was no concern about optimizing this algorithm in terms of execution time, because it only needs to be executed once. We do not adopt here the restriction or preference for operations involving powers of 2, thus leaving the possibilities of values for the polynomial coefficients and for the boundaries more free.

The application of Algorithm 1 to any other function (for example, the hyperbolic tangent, also a common neural activation function [11]) is straightforward. It will suffice to replace the sigmoid calculation in lines from 15 to 20 by that function. Depending on that function’s characteristics, one may change the number of regions in the domain and the polynomial degrees, but the strategy remains the same.

The results obtained by executing the Algorithm 1 are shown in

Table 1. Results obtained by Algorithm 1.

To obtain the minimal average absolute error:
$\mathit{xinf}(=-\mathit{xsup})$	$-5.440$
$\mathit{xmin}(=-\mathit{xmax})$	$-3.250$
minAvgAbsError	0.0016548
minMaxAbsError	0.0064729
region 2 polynomial	$0.014117x+0.076735$
region 3 polynomial	$0.040384x^2+0.272505x+0.502208$
region 4 polynomial	$-0.040394x^2+0.272543x+0.497762$
region 5 polynomial	$0.014117x+0.923265$
To obtain the minimum value for the error peak:
$\mathit{xinf}(=-\mathit{xsup})$	$-5.190$
$\mathit{xmin}(=-\mathit{xmax})$	$-3.240$
minAvgAbsError	0.0016775
minMaxAbsError	0.0055832
region 2 polynomial	$0.015656x+0.082845$
region 3 polynomial	$0.040434x^2+0.272634x+0.502260$
region 4 polynomial	$-0.040444x^2+0.272674x+0.497709$
region 5 polynomial	$0.015656x+0.917155$

.

Table 1 shows that, as expected, the average absolute error was slightly lower in the first implementation than in the second. The maximum absolute error was slightly lower in the second implementation than in the first.

Algorithm 1 Search for the best boundaries between approximation regions

1: $dx$ = 0.005 2: xmed = 0 3: minAvgAbsError = ∞ 4: minMaxAbsError = ∞ 5: for $xinf$ from $-6$ to $-5$ in 0.01 steps do 6:     for $xmin$ from $-4$ to $-3$ in 0.01 steps do 7:         $xmax=-xmin$                        ▹$xmax$ and $xmin$ symmetrical about the origin 8:         $xsup=-xinf$                              ▹$xsup$ and $xinf$ symmetrical about the origin Build the ranges of x (sigmoid domain): 9:         $xReg1=$ sequence from $-8$ to $xinf$, with increments of $dx$ 10:         $xReg2=$ sequence from $(xinf+dx)$ to $xmin$, with increments of $dx$ 11:         $xReg3=$ sequence from $(xmin+dx)$ to $xmed$, with increments of $dx$ 12:         $xReg4=$ sequence from $(xmed+dx)$ to $(xmax-dx)$, with increments of $dx$ 13:         $xReg5=$ sequence from $xmax$ to $(xsup-dx)$, with increments of $dx$ 14:         $xReg6=$ sequence from $xsup$ to 8, with increments of $dx$ Build y standard per range: 15:         $yReg1=$ sequence built from 1 / ( 1 + exp( $-xReg1$ ) ) 16:         $yReg2=$ sequence built from 1 / ( 1 + exp( $-xReg2$ ) ) 17:         $yReg3=$ sequence built from 1 / ( 1 + exp( $-xReg3$ ) ) 18:         $yReg4=$ sequence built from 1 / ( 1 + exp( $-xReg4$ ) ) 19:         $yReg5=$ sequence built from 1 / ( 1 + exp( $-xReg5$ ) ) 20:         $yReg6=$ sequence built from 1 / ( 1 + exp( $-xReg6$ ) ) Polynomial coefficients calculation per region: 21:         $p2$ = polyfit( $xReg2$, $yReg2$, 1 )                                                   ▹ first degree 22:         $p3$ = polyfit( $xReg3$, $yReg3$, 2 )                                                ▹ second degree 23:         $p4$ = polyfit( $xReg4$, $yReg4$, 2 )                                                ▹ second degree 24:         $p5$ = polyfit( $xReg5$, $yReg5$, 1 )                                                   ▹ first degree Error calculation: 25:         $errorReg1$ = zeros( 1, size( $xReg1$, 2 ) ) − $yReg1$ 26:         $errorReg2$ = polyval( p2, $xReg2$ ) − $yReg2$ 27:         $errorReg3$ = polyval( p3, $xReg3$ ) − $yReg3$ 28:         $errorReg4$ = polyval( p4, $xReg4$ ) − $yReg4$ 29:         $errorReg5$ = polyval( p5, $xReg5$ ) − $yReg5$ 30:         $errorReg6$ = ones( 1, size( $xReg6$, 2 ) ) − $yReg6$ 31:         $errorAllRegions$ = concatenation( $errorReg1,errorReg2,\dots ,errorReg6$ ) 32:         $avgAbsError$ = mean( abs( $errorAllRegions$ ) ) 33:         $maxAbsError$ = max( abs( $errorAllRegions$ ) ) 34:         if $avgAbsError<minAvgAbsError$ then 35:            $bestXinfAvgAbsError=xinf$ 36:            $bestXminAvgAbsError=xmin$ 37:            $minAvgAbsError=avgAbsError$ 38:            $bestP2AvgAbs=p2$ 39:            $bestP3AvgAbs=p3$ 40:            $bestP4AvgAbs=p4$ 41:            $bestP5AvgAbs=p5$ 42:         end if 43:         if $maxAbsError<minMaxAbsError$ then 44:            $bestXinfMaxAbsError=xinf$ 45:            $bestXminMaxAbsError=xmin$ 46:            $minMaxAbsError=maxAbsError$ 47:            $bestP2MaxAbs=p2$ 48:            $bestP3MaxAbs=p3$ 49:            $bestP4MaxAbs=p4$ 50:            $bestP5MaxAbs=p5$ 51:         end if 52:     end for 53: end for

The two sigmoid modules corresponding to Table 1 were implemented in Very High Speed Integrated Circuits Hardware Description Language (VHDL) language [35], in a behavioral way. Each implementation consists of two VHDL files: a package file, called pck_abs_avg_error.vhdl (in Appendix A.1) when containing constants definitions for the first module) and a sigmoid.vhdl file (in Appendix A.2), containing the approximation algorithm. Those constants are the polynomial coefficients and the boundaries values. The package files for the second module are omitted here because only the constant values change between the two implementations. The sigmoid.vhdl file is the same for both.

The input x, the output $y=\sigma \left(x\right)$, the boundaries values, and the polynomial coefficients are all represented as 16 bit numbers, in fixed point, with 4 bits for the integer part and 12 bits for the fractional part, as in [17]. So, the real number 1 is represented as the binary number $0001000000000000$, which corresponds to the decimal number $2^{12}=4096$ (without considering the decimal point position). Thus, each constant in Table 1 appears multiplied by 4096 in the VHDL file pck_abs_avg_error.vhdl. Two’s complement representation was used to allow calculations with negative numbers, by using the type signed from the ieee.numeric_std VHDL package.

The sigmoid implementation in the file sigmoid.vhdl follows directly from Table 1 and from Figure 1. An x value is read at the clock (ck) rise and the output y is then calculated according to the x approximation region. After each multiplication operation is performed, its result contains a number of bits that is the sum of the numbers of bits of its operands: 8 bits to the integer part and 24 bits to the fractional part. So, following this operation, the result is truncated, by discarding the 4 leftmost and the 12 rightmost bits, producing a number respecting again the convention with 16 bits. Due to the multiplication operands particular values used here (Table 1), the resulting 4 leftmost bits are always zeros for positive results and ones for negative results (in two’s complement), allowing them to be discarded. Discarding the 12 least significant bits affects the results very little, because they have very small weights.

The proposed sigmoid calculation is not iterative, but rather a single-pass one. The input argument x is presented, the approximation region is identified, the polynomial corresponding to that region is calculated, and the result is output in a single pass (a single clock cycle), without further iterations.

To compare the hardware resource usage and accuracy of our implementations with those of related works cited in Section 2, we attempted to reimplement them all in a uniform way, not necessarily identical to theirs, but seeking to reproduce as faithfully as possible their algorithms and their sigmoid approximations, by using a uniform fixed-point representation, with the same number of bits (16 bits, being 4 bits for the integer part and 12 bits for the decimal part), on uniform chip models, and using uniform synthesis programs. 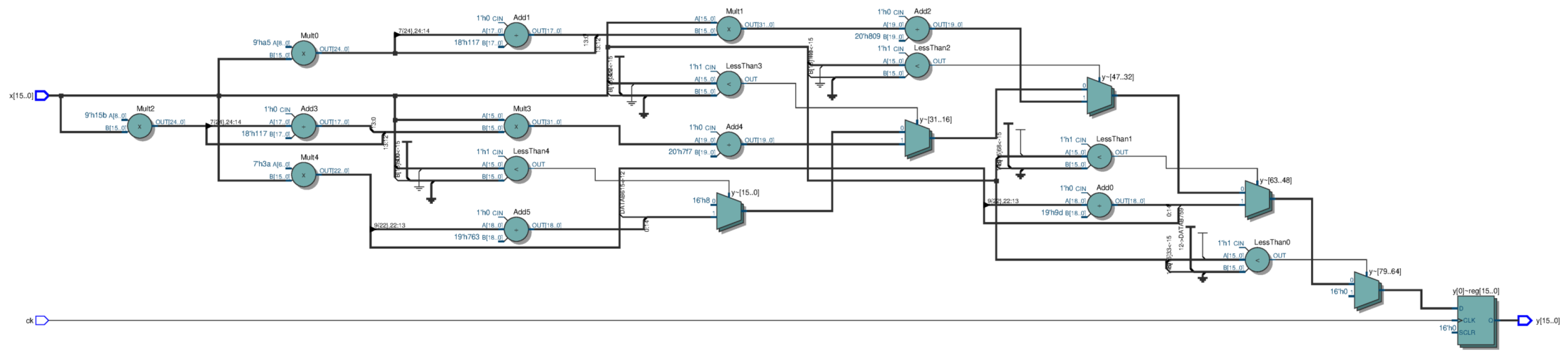This was possible only for some of the related works [12,13,14,15,16,17], because their implementations were described in sufficient detail there. Each proposed sigmoid approximation was described in VHDL. The synthesis programs were Quartus Prime Version 24.1 std, Build 1077 SC Lite Edition, for the FPGA chips Device 5CGXFC7C7F23C8 and Device MAX-10 10M02DCU324A6G, and Vivado v2025.1, for the FPGA chips Virtex-7—Device xc7v585tffg1157-3, Spartan-7—Device xc7s75fgga484-1 and Zinq-7000—Device xc7z045iffg900-2L. So, programs were chosen from companies that are among the leaders in the FPGA field and, for each company, chips of varying levels of complexity were chosen. The block diagram obtained by Quartus is in Figure 2.

Regarding accuracy, the criterion most used in the cited works was the average absolute error of the function over the domain considered, which justifies its adoption here.

Each VHDL description used in the comparisons was simulated using the GHDL program [36], because it is fast to execute and is capable of recording results in text files for later analysis. Each simulation run consisted in calculating and comparing the standard value of the sigmoid function, $\sigma \left(x\right)$ (obtained by the GNU Octave program [34]), with the value generated by the system described in VHDL, for each of the $2^{16}$ = 65,536 possible values in the x domain and obtaining, at the end, the average of the absolute error. In other words, the tests were exhaustive, performed for all representable input values with 16 bits.

4. Results

Table 2. Results on FPGA used resources. Only results that varied between implementations are shown.

Work	[17]	[12]	[13]	[14]	[15]	[16]	Ours Avg.	Ours Max.	Available
Quartus Prime Version 24.1 std. 0 Build 1077 SC Lite Edition
Family Ciclone V-Device 5CGXFC7C7F23C8
Logic Utilization	117	25	91	39	41	176	25	52	56,480
percentage	0.21	0.04	0.16	0.07	0.07	0.31	0.04	0.09	100
DSP Blocks	4	2	6	3	0	8	5	4	156
percentage	2.56	1.28	3.85	1.92	0.00	5.13	3.21	2.56	100
Quartus Prime Version 24.1 std. 0 Build 1077 SC Lite Edition
Device MAX-10 10M02DCU324A6G
Logic Elements	505	95	394	238	79	424	362	310	2304
percentage	21.92	4.12	17.10	10.33	3.43	18.40	15.71	13.45	100
Embed. Multiplier	0	4	6	2	0	16	4	4	32
percentage	0.00	12.50	18.75	6.25	0.00	50.00	12.50	12.50	100
Vivado v2025.1
Family Virtex-7-Device xc7v585tffg1157-3
LUT as Logic	202	66	168	86	114	282	67	80	364,200
percentage	0.06	0.02	0.05	0.02	0.03	0.08	0.02	0.02	100
DSPs	4	2	5	3	0	8	6	4	1260
percentage	0.32	0.16	0.40	0.24	0.00	0.63	0.48	0.32	100
Vivado v2025.1
Family Spartan-7-Device xc7s75fgga484-1
LUT as Logic	202	66	169	86	114	281	67	80	48,000
percentage	0.42	0.14	0.35	0.18	0.24	0.59	0.14	0.17	100
DSPs	4	2	5	3	0	8	6	4	140
percentage	2.86	1.43	3.57	2.14	0.00	5.71	4.29	2.86	100
Vivado v2025.1
Family Zinq-7000-Device xc7z045iffg900-2L
LUT as Logic	202	66	169	86	114	282	67	80	218,600
percentage	0.09	0.03	0.08	0.04	0.05	0.13	0.03	0.04	100
DSPs	4	2	5	3	0	8	6	4	900
percentage	0.44	0.22	0.56	0.33	0.00	0.89	0.67	0.44	100

shows the synthesis results regarding the use of hardware resources in the FPGA, for each sigmoid approximation. There are six approximations from related works and our two approximations: to minimize the error average (“ours avg.”) and to minimize the error peak (“ours max.”). The table has five parts, one for each software–device combination. It shows the FPGA resources used by each implementation as reported by the corresponding synthesis software. The kinds of those resources vary depending on the device type. For instance, only some devices have DSP blocks. The last column shows the total available number of each resource type in each FPGA device. The percentage of usage of each resource type relative to availability is also indicated. Reports from all implementations indicated that 16 registers (due to 16-bit operands) and 33 pins (16 input bits, 16 output bits, and a clock pin) were used. Thus, these results were omitted from Table 2, keeping in it only those relevant for comparison purposes.

Comparing resource usage between implementations is not straightforward because they are of different types and available in different quantities. However, at first glance, one can see in Table 2 that our implementations are neither systematically better nor systematically worse, in general, than the others in terms of resource usage, even though this criterion did not guide the creation of our implementations. Specifically, only the implementation in [12] always matches ours or is advantageous.

Table 3. Average absolute error in the sigmoid implementation, obtained for 65,536 equally spaced values in its domain.

Work	Avg. Abs. Error
[17]	$1.71\times {10}^{-3}$
[12]	$7.70\times {10}^{-3}$
[13]	$1.07\times {10}^{-3}$
[14]	$4.25\times {10}^{-3}$
[15]	$5.90\times {10}^{-3}$
[16]	$2.44\times {10}^{-3}$
ours (min. avg.)	$1.66\times {10}^{-3}$
ours (min. max.)	$1.68\times {10}^{-3}$

shows the average absolute error for all sigmoid implementations, obtained for 65,536 equally spaced values in its domain. It should be noted that, unlike with Table 2, these results do not depend on the chip model on which the implementation was made, but only on the VHDL descriptions.

In Table 3, one can see that only the implementation from [13] managed to achieve a lower error than ours. However, in Table 2, we see that it used more resources of most types compared to our implementations. Another interesting result was that our second implementation, which aimed only to obtain the minimum error peak, surpassed almost all others in the average absolute error criterion. The implementation in [12], which is advantageous compared to ours concerning resource usage, has a much bigger average absolute error.

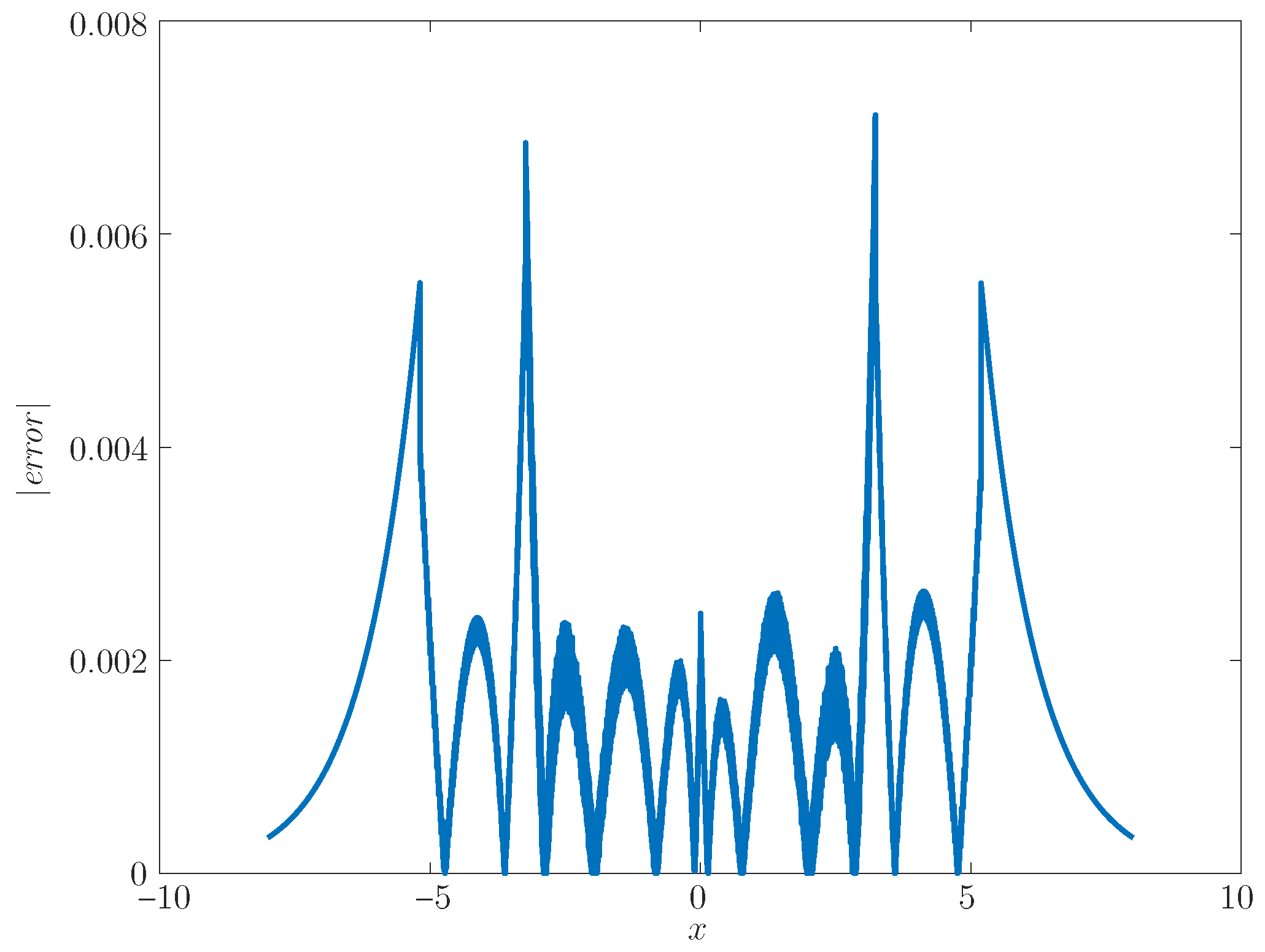
The absolute error for our first implementation is shown in Figure 3 and for the second implementation, in Figure 4 for the function domain.

The maximum absolute errors of our implementations were 0.0068181 for the first and 0.0071184 for the second. They are larger than those before VHDL implementations occur (Table 1), surely due to the use of fixed point representation in 16 bits. Another effect was that now, the maximum error of the first implementation is lower than that of the second implementation. However, in some cases, the second implementation is advantageous in relation to the first in resource utilization (Table 2).

After obtaining these results, new experiments were carried out to observe the effect of the number of bits in the representation of the operands on the average absolute error and on the use of hardware resources.

We then also implemented our approximation using 8-bit and 32-bit fixed-point representation, always keeping 4 bits for the integer part and the rest for the fractional part. We kept 4 bits in the integer part because they were enough to cover the range of values from $-8$ to $+8$ used in the experiments. The average absolute error values for these cases and for the previous case are in

Table 4. The average absolute error values for different numbers of bits in the representation of the operands.

Number of Bits	Avg. Abs. Error
8	$81.0\times {10}^{-3}$
16	$1.66\times {10}^{-3}$
32	$1.66\times {10}^{-3}$

:

It can be seen that the mean absolute error for both the 16-bit and 32-bit fixed-point implementations was equal to that obtained using the low-degree polynomial approximation to the sigmoid on a general-purpose 64-bit floating-point computer, prior to the VHDL description (Table 3). Therefore, for both 16-bit and 32-bit, the mean error value is likely due solely to having approximated the sigmoid by low-degree polynomials, not to the use of those bit numbers or the fixed-point implementation.

The results of hardware resource usage as a function of the number of bits in the operands, for two chip models, are given in

Table 5. Results on FPGA used resources as a function of the number of bits for the operands.

Number of Bits	8	16	32	Available
Quartus Prime Version 24.1 std. 0 Build 1077 SC Lite Edition
Family Ciclone V-Device 5CGXFC7C7F23C8
Logic Utilization	25	25	231	56,480
percentage	0.0443	0.0443	0.409	100
DSP Blocks	2	5	15	156
percentage	1.28	3.20	9.62	100
Quartus Prime Version 24.1 std. 0 Build 1077 SC Lite Edition
Device MAX-10 10M02DCU324A6G
Logic Elements	50	362	1159	2304
percentage	2.17	15.7	50.3	100
Embed. Multiplier	2	4	32	32
percentage	6.25	12.5	100	100

. It can be seen that hardware resource usage grew much more than linearly with the number of bits in the operands. This must be taken into account in a design, especially in a case like this, where the error value saturates beyond a certain number of bits.

Table 6. Results for the data path delay.

Work	[17]	[12]	[13]	[14]	[15]	[16]	Ours Avg.
Vivado v2025.1
Family Virtex-7-Device xc7v585tffg1157-3
delay (ns)	8.16	7.97	21.6	12.5	6.93	9.86	9.38
Vivado v2025.1
Family Spartan-7-Device xc7s75fgga484-1
delay (ns)	13.8	14.5	38.9	21.8	14.0	18.3	16.2
Vivado v2025.1
Family Zinq-7000-Device xc7z045iffg900-2L
delay (ns)	8.89	8.84	23.5	14.0	7.06	10.7	10.5

presents the data path delay results for some chip models, for related works and for our implementation that aimed to minimize the mean absolute error. In it, one can see that the delay in our implementation does not differ much from most others, but that it is much lower than that of proposal [13], which presented the lowest average absolute error.

5. Discussion and Conclusions

The sigmoid approximation for its implementation in FPGA, by dividing its domain into a few subdomains, approximating it, in each subdomain, using a low-degree polynomial, and systematically searching for the best boundaries between the subdomains, allowed us to obtain results with a good compromise between the use of hardware resources and the average absolute approximation error ($1.66\times {10}^{-3}$ for the interval from $-8$ to $+8$ in the function domain). It thus becomes a good alternative to preexisting solutions.

The fact that we did not restrict operands or boundaries between approximation regions to be powers of two did not prevent relatively good results from being obtained not only in error value, but also in resource usage when compared to related works. Therefore, consideration should be given to the use of such restrictions.

The method proposed here aimed to obtain a low value for the average absolute error. In this, the work in [13] obtained better results ($1.07\times {10}^{-3}$, versus ours, $1.66\times {10}^{-3}$), using a more elaborate method, including Newton–Raphson approximation, but requiring greater use of hardware resources in most cases (for instance, in Logic Utilization, 91 versus 25 for Ciclone V - Device 5CGXFC7C7F23C8). Therefore, it may be preferred when the importance of the error is much greater than the importance of the use of resources.

A limitation of this work was that it attempted to reproduce the implementations described in other studies, with the possibility that this reproduction might have had differences from the originals that could have influenced the results. Furthermore, some of those proposals allowed for parameter adjustments, whereas in this reproduction, to minimize the length of the work, we sought to use only a typical version of what was described in each article.

As future work, a complete neural network can be implemented in FPGA using, in each neuron, a sigmoid implementation, as proposed here, comparing its performance with a version implemented in a general-purpose computer.

One can also investigate the implementation of other activation functions, such as the hyperbolic tangent, using the principles used here for the sigmoid.