Featured Application
Building upon existing research, this study refines the structural degree index of loess and derives the structural evolution parameters and structural modification parameters. Based on this foundation, the concept of complex stress state structural parameters for loess is proposed, and their correlation with soil strength indices is systematically investigated. The results demonstrate that the complex stress state structural parameters effectively capture the variation patterns of soil structure and, similar to conventional physical indices such as density and moisture content, reflect the intrinsic properties of soil. Furthermore, by establishing the relationship between complex stress state structural parameters and strength indices, key mechanical properties can be directly predicted from basic soil parameters such as moisture content and dry density. This confirms the scientific validity and practical applicability of the proposed parameters.
Abstract
This paper derives and modifies the structural quantitative indicator of loess—the structural index—based on the theory of limit equilibrium, thereby obtaining structural evolution parameters and structural modification parameters. However, since the structural index is defined for uniaxial stress states, this paper also introduces a structural parameter applicable to complex stress states—the complex stress structural parameter . This parameter is not only applicable to complex stress states, but also enables the study of soils such as soft clay that are difficult to test under uniaxial compression. Additionally, it offers the advantages of requiring less testing effort, featuring simpler expression formulas, and possessing clearer physical meaning. Finally, the relationship between complex stress structure parameters and soil strength indicators was analyzed. We defined a quantitative indicator—the comprehensive structural state parameter —that reflects the combined effects of soil structural factors. By combining comprehensive structural state parameters with the physical properties of undisturbed loess (such as moisture content and dry density), it is possible to determine the strength parameters of loess under a given structural state over a wide range.
1. Introduction
Generally, soil structure is defined as the connection characteristics between particles and the arrangement of particles, which includes all the different features between the soil and its corresponding remolded soil [1,2,3]. In terms of mechanical properties, the structural properties of soil are reflected in its ability to maintain its original structural state without being destroyed. Its essence is the loss of the bonding force between particles in the soil under the impact of external factors, resulting in adjustments to the spatial arrangement of structural units, and changes in pore morphology, size, quantity, and distribution [4,5]. As early as 1948, K. Terzaghi [6], the founder of soil mechanics, pointed out the importance of studying soil structure. With the gradual deepening of research, scholars are increasingly focusing their research on the structure of soil, and they have elevated it to the core position of soil mechanics [7,8,9,10]. The importance of the study of soil structure is ultimately manifested through its relationship to the mechanical and engineering properties of the soil, so the best method for studying soil structure and its application is still soil mechanics. The primary advantage of soil mechanics research methods lies in their ability to directly establish the relationship between soil structure and its engineering properties [11,12,13,14,15,16,17].
Based on lateral compression tests conducted on undisturbed soil, saturated undisturbed soil, and disturbed remolded soil, Xie et al. [12,18,19] proposed the comprehensive structural potential . The structural parameters (comprehensive structural potential) established through soil mechanics methods comprehensively consider the effects of loading and moisture content on loess structural behavior, thereby pioneering a new approach to soil structural research. The comprehensive structural potential offers advantages such as simplicity and practicality, serving as a structural parameter defined by the strain variable. The strain structural parameters are based on compression tests. When the compressive deformation reaches a state of near-stability, the applied pressure can be increased indefinitely without causing strength failure in an engineering sense. Moreover, the relationship between the axial pressure and compression deformation of the sample shows a strain hardening curve, which is significantly different from the shear failure state of soil. In order to solve this problem, many scholars have extended the above methods and proposed structural parameters based on strength. The literature [9,20,21,22,23] proposes structural parameters based on strength, according to the understanding that “strength and deformation of the soil are controlled by the same structural law”. The above structural parameters basically describe the structural change law of soil during the deformation process, and they reflect the change in soil structure during the stress process [24,25,26]. In view of this, references [27,28] proposed the structural parameters based on unconfined compressive strength for undisturbed soil, saturated undisturbed soil, and disturbed remolded soil structural index . It, along with particle size, density, and moisture content, reflects the fundamental properties of the soil. Therefore, the construction index is more reasonable than other definitions. However, for some soils that are not suitable for uniaxial compression testing, such as sandy soils and soft clays, there are obvious shortcomings in the study of their structural properties. In addition, in engineering practice there are very few engineering problems in the uniaxial stress state, and the structural index is not suitable for complex stress states. Therefore, using the above definition to study the structure of the soil does not correspond to the stress state of the actual soil at the engineering site.
The purpose of this paper is to evolve and modify it on the “construction” index and propose a new structural parameter based on strength. This makes the improved structural parameters applicable not only to complex stress states, but also to soils of all properties. Finally, the improved and newly proposed parameters are tested, compared and verified. Based on a large number of experiments conducted on loess under different humidity and density conditions, the author has carried out some research and exploration on the structural properties of loess. The author has proposed soil structural parameters applicable to complex stress conditions in reference [29,30]. This parameter is called the complex stress structural parameter , and the variation laws of loess structure under different influencing factors were analyzed here. The complex stress structural parameters presented in reference [29,30] were defined based on the shear strength of the soil. However, it cannot reflect the relationship between structural parameters and soil strength indicators, nor can it be directly applied to soil strength or stability analysis. This paper initially explores the relationship between structural parameters and strength indicators of loess, as well as the use of structural parameters to obtain strength indicators of loess in different states, in an attempt to establish a connection between loess structural research and practical engineering applications.
2. Modification and Evolution of Structural Parameters of Loess
2.1. Definition Method of Structural Evolution Parameters
Using the unconfined compressive strength of undisturbed, remolded and undisturbed saturated soil samples, also known as the structural index, Sheng-jun Shao [27,28] developed the structural parameter of loess.
represents the structural index. and in Formula (1) stand for the soil structure’s stability and variability, and the unconstrained compressive strengths of undisturbed soil, remolded soil, and undisturbed saturated soil are represented by letters and .
The structural index is calculated based on the uniaxial compressive strength of soil samples, so this definition is applicable to soils with high viscosity such as loess, clay, and silty clay, but not to soils such as sand and soft clay that cannot undergo uniaxial compression tests. In addition, there are not many uniaxial stress state engineering problems in everyday engineering practice. In engineering, the structure of the soil and the stress state of the actual soil cannot be studied using Formula (1). Based on these problems, the evolution expression of the structure parameters is derived, after which the mechanical parameters of the structure index are evolved. The defining expression of the structure parameters is then followed by the evolution expression of the structure index. The soil limit equilibrium theory is used to obtain the mechanical theory from Formula (1), and the strength parameters are then used to derive the soil structure parameters.
When the soil sample is in a state of ultimate equilibrium, the major principal stress and minor principal stress acting on the sample satisfy the following relationship:
In Formula (1), and represent large and small principal stresses, respectively; is the cohesive force, and is the internal friction angle. Since the soil mass must be in an unconfined state for the definition of the structural index to be obtained, when = 0, = , Formula (2) can be rewritten as Formula (3).
The in Formula (3) is the unconfined compressive strength. Substituting Formula (3) into Formula (1) gives the evolution expression of the soil structural parameters.
represents the structural evolution parameter. In Formula (4), and from Formula (1) stand for the soil structure’s stability and variability; , and represent respectively the unconfined compressive strength of undisturbed soil, remolded soil, and undisturbed saturated soil. and are the parameters indicating the strength of undisturbed soil, and are the parameters indicating the strength of remolded soil, and are the parameters indicating the strength of undisturbed saturated soil.
The evolution expression (4) appears to have changed only through making a variable substitution, but its essence is completely different. First, the original definition expression (1) is expressed in terms of uniaxial compressive strength, while the evolution expression (5) is expressed in terms of shear strength indicators (internal friction angle and cohesion force). As is well known, the magnitude of the internal friction angle depends on the frictional resistance and interlocking effects between soil particles, and the internal friction angle reflects the soil’s frictional properties. Cohesion is a characteristic indicator of clayey soils, encompassing both primary cohesion formed by molecular attraction between soil particles and secondary cohesion formed by the bonding of compounds within the soil. Therefore, the structural evolution parameter is a material constant that represents the comprehensive response to the strength of soil materials. This definition is more standardized and has a broader scope of application. Secondly, the original definition can only be measured by uniaxial compression testing, whereas the evolution expression can be measured by conventional triaxial testing, direct shear testing or even in situ testing, and the test method is more flexible. Finally, the original definition is only suitable for soils with strong structure, whereas the expressions can also be used to study the structure of soils that cannot be formed into uniaxial specimens, such as sandy soils and soft clays, and the research problems are more comprehensive.
2.2. Definition Method of Structural Modification Parameters
The evolution expression (4) of the soil structural parameters removes the limitation of the original definition to test conditions and can be applied to complex stress states. However, it is necessary to perform uniaxial, triaxial or direct shear tests on undisturbed soil, remodeled soil and undisturbed saturated soil simultaneously, so the test conditions are very complicated and the test workload very high. Therefore, it is proposed to use the strength parameters of the remodeled saturated soil instead of the strength parameters of the saturated soil and the remodeled soil in order to simultaneously eliminate the stability and variability of the soil structure. The evolution formula has been improved to not only retain the characteristics of the original formula but also reduce the experimental workload. For this reason, the expressions of the soil structural change parameters in this paper are defined as follows:
represents the structural modification parameter. and in Formula (5) represent the unconfined compressive strength of undisturbed soil and remolded saturated soil, respectively. The expression of soil structure modification parameter is given in Formula (5). and are the parameters for undisturbed soil’s strength in Formula (5), while and are the parameters for remolded saturated soil’s strength. The advantage of changing parameter (5) is that the strength parameter of the remodeled saturated soil can simultaneously relieve the stability of the soil structure and variability of the soil structure, reduce the test effort, and have a simpler formula expression with a clearer physical meaning.
Of course, if in practice it becomes necessary to consider the stability of the soil structure and variability of the soil structure independently, we simply use the remodeled soil strength parameter or the undisturbed saturated soil strength parameter as the denominator in Formula (5). The following definitions apply to the stability and variability parameters for loess.
and in Formulas (6) and (7) are referred to as soil structural stability parameters and variability parameters, respectively.
2.3. Comparison of Structural Indicators, Modified Parameters, and Structural Evolution Parameters
2.3.1. Experimental Verification of Structural Evolution Parameters and Modified Parameters
In order to verify the structural evolution parameters and modify the parameter definitions, direct shear experiments and triaxial experiments are designed. The test soil samples were obtained from loess in Weinan, Shaanxi Province. Undisturbed soil samples were collected using the borehole method at a sampling depth of 5 m below ground level. The loess is brownish-yellow, consisting of powdery clay. It contains wormholes, and snail shells are occasionally found. The physical properties of the soil samples were determined in accordance with the Standard for Geotechnical Test Methods (GB/T 50123–2019) [31], and the results are presented in Table 1.

Table 1.
Physical indices of loess.
To validate structural evolution parameters and refine parameter definitions, direct shear tests and triaxial tests were designed. Undisturbed, remolded, undisturbed saturated, and remolded saturated soil samples were prepared in accordance with the Standard for Geotechnical Test Methods (GB/T 50123–2019) [31]. Uniaxial compression tests, direct shear tests, and triaxial shear tests were conducted in compliance with this standard. The relevant strength and structural parameters obtained from direct shear tests are shown in Table 2 and Table 3.

Table 2.
Shear strength parameters obtained from direct shear test.

Table 3.
Contribution of strength parameters to structural parameters in direct shear test.
To obtain the value = 5.06 of the structural parameter evolution expression, the values of and from the direct shear test are substituted into Formula (4) as indicated in Table 3. The structural modification parameter’s value = 7.45 can be obtained by substituting it into Formula (5).
The relevant strength and structural parameters obtained from traditional triaxial tests are shown in Table 4 and Table 5.

Table 4.
Shear strength parameters obtained from direct triaxial test.

Table 5.
Contribution of strength parameters to structural parameters in triaxial test.
In Formula (4), we substitute the and values from traditional triaxial tests to get the structural development parameter = 7.56. The structural modification parameter’s value = 9.01 can be obtained by substituting it into Formula (5).
The conclusions drawn from the above test data are as follows.
- The result of the structural modification parameters is close to the evolution definition, and the modification definition can be used instead of the evolution definition.
- The structural modification parameters and evolution definitions mainly involve strength parameters (c, φ), which are essential properties of soil and can be regarded as material constants. The values of c and φ remain constant under all test conditions, and thus the structural modification parameters and evolution parameters are also fixed values under all test conditions.
2.3.2. Comparison of Structural Evolution Parameters and Modified Parameters with Structural Index
Compared to the structure index, the structural evolution parameter appears to be just a variable substitution, but its essence is completely different and it has the following three advantages.
- The structural index is expressed as uniaxial compressive strength, while the evolution parameter is represented by strength parameters. This indicates that the structural parameter is a material constant, and the defining expression for the structural evolution parameter is more standardized and applicable to a broader range of scenarios.
- The structural index is a structural parameter of the soil that can only be measured by uniaxial compression testing, whereas the evolution parameter can be used for both triaxial and direct shear testing and the test method is more flexible.
- Formula (1) is only applicable to soils with obvious structural characteristics such as loess. Formula (4) can also be used to study soils such as sand and soft clay that cannot be made into uniaxial specimens and do not have obvious structural characteristics, and its research scope is broader.
The aforementioned benefits demonstrate that the structural evolution parameters suggested in this research can be utilized to determine the structural parameters of soil with weak structure in addition to being applicable to uniaxial testing. also denotes that the structural parameter is a material constant that is unaffected by changes in the stress levels and test settings.
The structural modification parameter is an enhancement of the structural evolution parameter and preserves the properties of the original formula. The following three benefits apply to .
- In order to determine , simultaneous triaxial or direct shear tests must be performed on undisturbed soil, remolded soil, and undisturbed saturated soil. This involves extensive test effort as well as the computation of a soil’s strength parameters in three separate states. Workload is significantly reduced because can only be determined by triaxial or direct shear testing on undisturbed soil and saturated remolded soil.
- The strength of remolded saturated soil is the denominator of . The structural failure mechanism of remolded saturated soils compared to undisturbed soils is analogous to the coupled failure of immersion and disturbance, which simultaneously eliminates the stability and variability of soil structure. It provides a new perspective on the coupled failure of soil structure caused by immersion and disturbance.
- Formula (5) can also be used independently to study the stability and variability of soil structure by simply replacing the denominator with the strength of the remolded or undisturbed saturated soil, i.e., Formulas (6) and (7).
The three-strength-parameter calculation method is optimized into a two-strength-parameter calculation method. This method not only considers the coupling effect of immersion and disturbance on soil structure damage, but also can independently study the influence of structural variability or stability on soil structure. It is clear that alters the state of the soil sample used in the test based on . The three-strength-parameter calculation method was originally designed to calculate strength based on three parameters. Therefore has greater practical value than and is more adaptable and succinct.
3. Structural Parameters of Complex Stress State in Loess
3.1. Definition of Structural Parameters for Complex Stress State of Loess
Although the two schemes of structural evolution parameters and modification parameters of loess have improved the two shortcomings of the definition of the structural index, ① the parameters change with the load conditions and ② the parameters can be obtained by a direct shear experiment and triaxial shear experiment. However, the evolutionary and modified parameters still cannot adapt to changes in complex stress states. Therefore, in reference [29,30] to the definition of comprehensive structural potential [9], the author established the definition of complex stress structural parameters of loess through soil mechanics methods. This parameter is called the structural parameter of complex stress in loess. The calculation procedure is detailed in Formula (8).
In Formula (8), is the shear strength of undisturbed soil, and is the shear strength of remolded saturated soil. By defining complex stress structural parameters, it can be concluded that the stronger the bonding between undisturbed soil particles, the greater the strength loss of loess caused by disturbance, and the more unstable the arrangement of soil particles. After waterlogging and disturbance, the loss of strength due to the disruption of soil structure under applied forces becomes more pronounced, and the arrangement of soil particles becomes increasingly unstable. The greater the strength of the undisturbed soil, the larger becomes; the greater the effects of disturbance and immersion, the larger becomes. Changes in and can be sensitively reflected in variations in .
According to Coulomb’s law, the shear strength of soil can be worked out using Formula (9).
In Formula (9), represents cohesion and represents internal friction angle. The normal stress can be worked out by the following formula.
The angle in Equation (10) represents the angle between the shear failure plane and the plane of action of the principal stress, referred to as the failure angle. It can be calculated using Formula (11).
From Formulas (9)–(11) the following equation can be derived using Formula (8).
Formula (12) is the final calculation formula for the complex stress structural parameter after evolution. Through triaxial testing, the values of the major and minor principal stresses ( and ) at specimen failure, as well as the strength parameters and , can be determined. By substituting these values into Formula (12), the values of the complex stress structural parameter can be obtained.
Based on the shear strength of the soil, the newly defined structural parameter of loess under a complex stress state represents the structural strength of soil at its ultimate failure state. It has the following advantages over the current quantitative definition of soil structure.
- The definition of the original structural index involves soil samples in three states: undisturbed sample, remolded sample, and saturated sample. The definition of the new complex stress structural parameter, however, only includes soil samples in two states: undisturbed samples and remolded saturated samples. This simplifies the experimental conditions, reduces the sample size, and decreases the workload.
- The strength ratio concept is easier to understand than the sum of the two previously defined coefficients, which is the second advantage of replacing the coefficient ratio with it.
- The triaxial strength, which is suitable for complex stress situations, replaces the uniaxial strength in the new parameter.
- The stress state is introduced by the new parameter and can be used to directly create the constitutive relationship.
- Structural properties vary at different locations and the change in stress state can be taken into account in engineering applications.
- The sixth advantage is that this parameter can be used with sand and soft clay in addition to loess.
Finally, the new parameter gets to the heart of the matter: strength is the essence of soil structure. Strength parameters can be used to influence aspects of soil structure such as water content, compactness and grain size distribution.
3.2. Testing Method for Structural Parameters of Complex Stress States
The soil used in the experiment is the same as that in Section 2.3.1, which is Weinan loess from Shaanxi Province. The physical property indices of the loess are shown in Table 1.
Moisture content, dry density, and force are the main factors affecting soil structure, so triaxial test schemes are designed for loess soil samples with different confining pressures, moisture contents, and dry densities [5,32,33].
3.2.1. Test Plan Under Different Confining Pressure Conditions
We investigate the pattern of change in undisturbed loess structural parameters under different confining pressures. Using the control variable method, identical undisturbed soil samples were collected to ensure consistent dry density and moisture content. Remodeled soil samples of the same specifications and condition were then prepared. During the triaxial shear test, confining pressures of 100, 200, 300 and 400 kPa were applied under consolidated undrained conditions.
3.2.2. Test Plan Under Different Moisture Contents
The variation patterns of structural parameters in undisturbed loess under different moisture contents were investigated. A consolidated undrained triaxial shear test was conducted, with strict control of experimental variables. All soil specimens were sampled from the same source material and prepared to achieve uniform dry density. Seven groups of loess samples with target moisture contents of 6%, 11%, 16%, 21%, 26%, 31%, and 36% were prepared for testing.
3.2.3. Test Plan Under Different Dry Densities
Investigate the pattern of change in structural parameters in undisturbed loess at different dry densities. The experiment employed a controlled variable method, using identical loess samples to ensure consistent moisture content across all specimens. Take five undisturbed soil samples at different depths to ensure varying initial dry densities of the native loess. Then prepare remolded soil samples with the same moisture content and the same dry density as the undisturbed samples, as shown in Table 6. The natural moisture content of undisturbed loess varies at different depths, so the moisture content of loess samples must be adjusted. Conduct triaxial shear tests on specimens under identical confining pressure to analyze the variation patterns of loess structural parameters at different dry densities.

Table 6.
Dry density value of loess sample.
4. The Relationship Between Structural Parameters and Strength Indicators of Complex Stress States in Loess
4.1. The Relationship Between Structural Parameter Ratio and Structural Influencing Factors
In loess engineering, moisture content is usually regarded as a generalized force, which can weaken the binding of soil particles and dissolve chemical substances in the soil. The increase in moisture content will damage the integrity of the loess structure [23,34]. Loess is water-sensitive; if it is immersed in water or even humidified, the strength of soil decreases and the deformation increases greatly. Collapsibility is a concrete manifestation of water sensitivity in deformation. After water immersion, soil deformation increases rapidly and soil structure collapses rapidly, which will seriously affect its strength and the stability of the superstructure [35].
Soil is composed of loosely packed particles, with the interconnections between soil particles being far weaker than the connections within the particles themselves. Therefore, the strength of soil primarily depends on the interparticle forces [36]. The varying dry densities of the same loess determine its porosity ratio, which in turn determines the forces between particles. From another perspective, dry density also influences the degree of interparticle bonding in soils. Dry density is one of the factors affecting soil structure. An increase in dry density reduces the structural variability of loess and enhances its structural stability, collectively contributing to a structural transformation.
The moisture content and dry density are important factors affecting soil structure [37,38]. Table 7 and Table 8 present the structural parameters of various loess samples under different confining pressures, moisture contents, and dry densities, as determined from triaxial shear tests. The structural parameter ratios in the table are based on the structural parameters of natural moisture content and dry density of undisturbed loess ( = 1.36 g/cm3, w = 11%) as standard values. Then, the structural parameters of soil samples with different moisture contents and different dry densities under different confining pressures are compared with the standard value to obtain the structural parameter ratio of each soil sample. The average parameters in Table 7 and Table 8 represent their average values under various confining pressures. According to Table 7 and Table 8, the curves depicting the variation in the average structural parameter ratio with respect to water content and dry density were obtained, as shown in Figure 1 and Figure 2. Based on this, corresponding relationship equations can also be obtained, namely Equations (13) and (14) (the structural parameter ratio mentioned below refers to the average structural parameter ratio).

Table 7.
Structural parameters of soil samples with different moisture contents and their structural parameter ratios.

Table 8.
Structural parameters of soil samples with different dry densities and their structural parameter ratios.
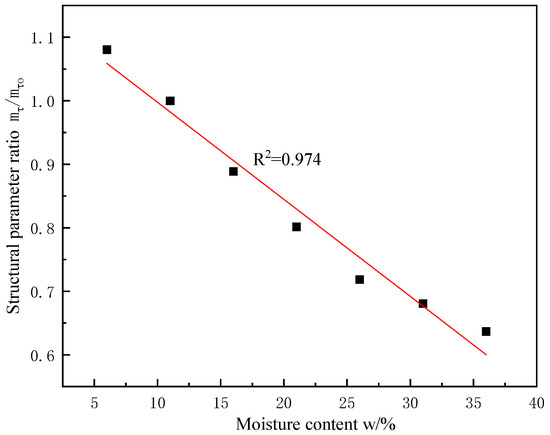
Figure 1.
The relationship between moisture content and structural parameters.

Figure 2.
The relationship between dry density and structural parameters.
From Figure 1 and Figure 2, the relationship equation between moisture content and structural parameters can be obtained as follows:
The relationship equation between dry density and structural parameters is
4.2. The Relationship Between Structural Parameter Ratio and Strength Index
Table 9 and Table 10 show the strength indicators (test values) obtained from triaxial shear tests of undisturbed loess with different moisture contents and dry densities. In addition, based on the strength indicators ( = 31.32 kPa, = 30.15°) of natural moisture content and dry density ( = 1.36, = 11%) of undisturbed loess, the structural parameters and standard values of different moisture contents and dry densities of the original loess were first calculated, and then the ratios of the test values of the strength indicators were obtained. From Table 9 and Table 10, it can be seen that the strength indicators directly obtained from the test not only have reasonable regularity in a statistical sense, but also have their certainty and regularity in practical applications. The relationships between the structural parameter ratios in Table 7 and Table 8 and the two types of strength index ratios in Table 9 and Table 10 are established as shown in Figure 3, Figure 4, Figure 5 and Figure 6, and from this, the relationship expressions (15) to (18) between them are derived.

Table 9.
Experimental results and strength index ratio of soil samples with different moisture contents.

Table 10.
Experimental results and strength index ratio of soil samples with different dry densities.
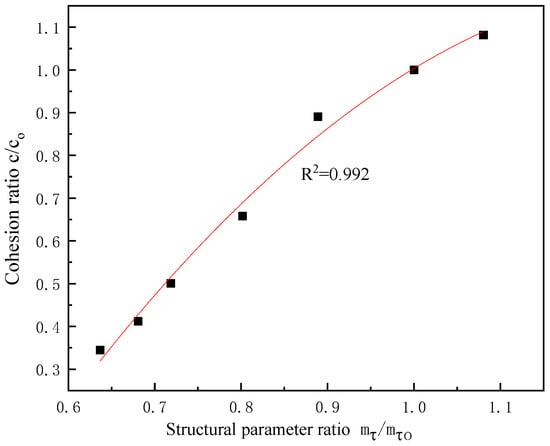
Figure 3.
The relationship between structural parameter ratio and cohesion ratio of soil samples with different moisture contents.
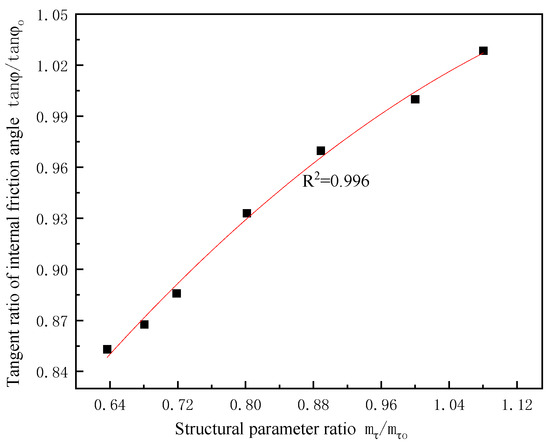
Figure 4.
The relationship between structural parameter ratio and internal friction tangent ratio of soil samples with different moisture contents.
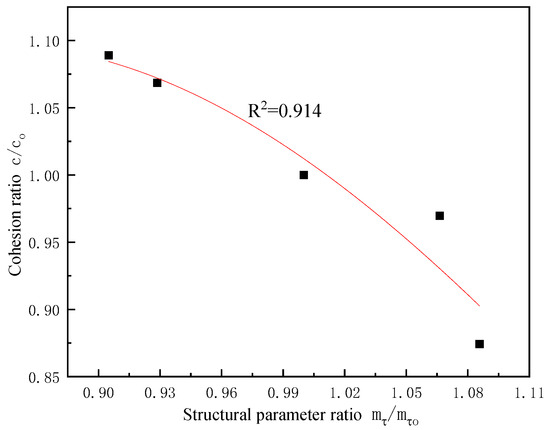
Figure 5.
The relationship between structural parameter ratio and cohesion ratio of soil samples with different dry densities.
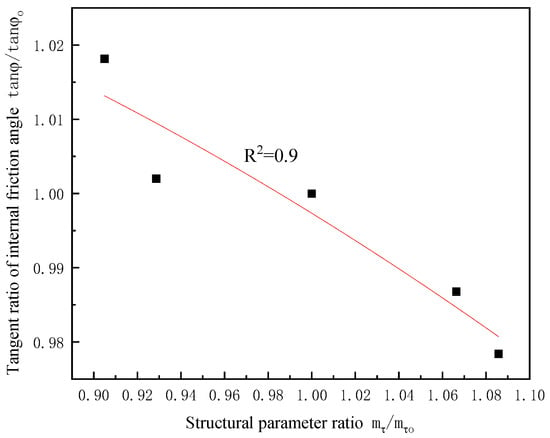
Figure 6.
The relationship between structural parameter ratio and internal friction tangent ratio of soil samples with different dry densities.
The functional relationship between the structural parameter ratio and cohesion ratio of soil samples with different moisture contents can be obtained from Figure 3 and Figure 4:
The functional relationship between the structural parameter ratio and the tangent ratio of the internal friction angle is as follows:
The functional relationship between the structural parameter ratio and cohesion ratio of soil samples with different dry densities can be obtained from Figure 5 and Figure 6:
The functional relationship between the structural parameter ratio and the tangent ratio of the internal friction angle is as follows:
After sorting out the corresponding structural parameter ratios from Equations (13) and (14), substitute them into Equations (15) to (18) to obtain the corresponding strength index ratios. Then, using the strength index under the natural moisture content ( = 1.36 g/cm3, = 11%) of undisturbed loess as the standard, obtain the strength index ( = 31.32 kPa, = 30.15°) of soil samples with different moisture contents and dry densities, as shown in Table 11 and Table 12.

Table 11.
Formula calculation results of strength indicators for soil samples with different moisture contents.

Table 12.
Formula calculation results of strength indicators for soil samples with different dry densities.
Figure 7 and Figure 8 respectively show the contrast between the test values and calculated values of the strength indicators of the undisturbed loess with different moisture contents and different dry densities. By comparing these results, it can be seen that the calculated strength indicators can reflect the authenticity of the test results.
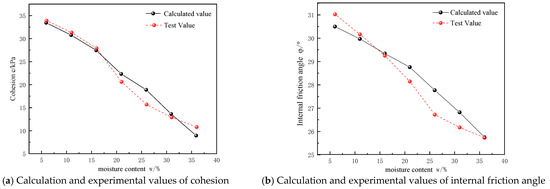
Figure 7.
Experimental and calculated values of strength indicators at different moisture contents.
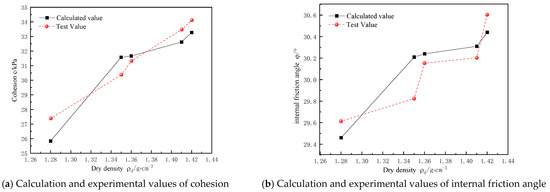
Figure 8.
Experimental and calculated values of strength indicators at different dry densities.
5. The Comprehensive Structural State Variables and Their Applications
Obviously, the formulas obtained in this paper for the ratios of structural parameters are applicable to all structural soils within the test range listed in reference [39] for the structural state, that is, undisturbed loess with moisture content ranging from 6% to 36% and dry density ranging from 1.28 g/cm3 to 1.42 g/cm3. To facilitate a more comprehensive analysis of the relationship between varying structural states of loess and the corresponding structural parameter ratios, assuming that the moisture content and dry density of loess are known, the functional relationship between the structural parameter ratio and these two variables can still be described by Equations (13) and (14), enabling the derivation of a comprehensive structural parameter based on the functional dependence on moisture content and dry density. Finally, the parameters that collectively influence the structural properties are defined as the comprehensive structural state variable of loess, denoted by .
In Formula (19), represents the dry density (g/cm3) and represents the moisture content (%).
By substituting the physical property index values obtained from the triaxial shear tests of the loess soil samples, as presented in Table 7 and Table 8, into Formula (19), the values of the comprehensive structural state variable can be determined. A nonlinear fitting analysis of the functional relationship between the structural parameter ratio and the comprehensive structural state variable was performed using Origin 2022. The fitting yielded a correlation coefficient (R2) of 0.8984, indicating a good fit, as illustrated in Figure 9.
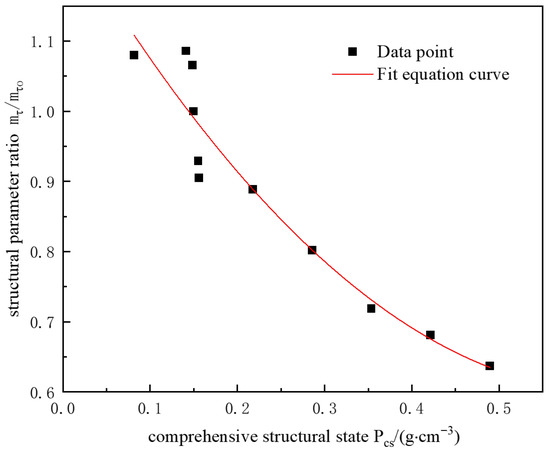
Figure 9.
The relationship between structural parameter ratio and comprehensive structural state .
The functional relationship between the structural parameter ratio of loess and the comprehensive structural state variable is expressed in Formula (20).
By combining Formulas (19) and (20), it can be concluded that the structural parameter ratio of undisturbed loess can be determined from any given dry density and moisture content. By combining Formulas (19) and (20) with the natural moisture content of unsaturated loess and its corresponding triaxial shear strength index value, the shear strength index of unsaturated loess in any given environment with different structural states can be solved [22,40,41].
6. Conclusions
This paper mainly explores the structural parameters based on strength, improves the structural index, and obtains the structural evolution parameters and modified parameters. However, due to the limitations of evolution parameters and modification parameters for complex stress states, the author also proposed the concept of structural parameters for complex stress states in loess. And the internal relationship between the influencing factors of loess structure, structural parameter ratio, and strength index was analyzed and studied. The following conclusions can be drawn.
- (1)
- A mechanical derivation of the formula for the structural degree index is achieved and we obtain the soil structural evolution parameters characterized by strength parameters of undisturbed soil, remolded soil, and saturated soil. Since this parameter requires testing on three soil sample states, it requires a substantial workload and fails to reflect the coupled effects of immersion and disturbance on soil structure. Therefore, the structural modification parameter characterized by the strength parameters of undisturbed soil and saturated remolded soil was proposed.
- (2)
- The structural evolution parameters relieve the limitations of experimental conditions and can be measured through triaxial tests or direct shear tests to determine the structural parameters of soil. For soil samples such as soft clay that cannot be prepared as uniaxial specimens, their structural properties can also be studied. The experimental workload for structural modification parameters is smaller than that for evolution parameters, and it can simultaneously reflect the coupled failure effects of immersion and disturbance on soil structure. Both structural evolution parameters and modified parameters are not applicable to complex stress states and have limitations.
- (3)
- In order to solve the problem that structural evolution parameters and modified parameters cannot adapt to complex stress states, a new solution is proposed—structural parameters for complex stress states in loess. Triaxial shear tests were conducted on soil samples with varying moisture contents and dry densities, and the corresponding complex stress structural parameters and strength indices were obtained under these conditions.
- (4)
- Through fitting analysis of the intrinsic correlations among the factors influencing loess structural properties, the structural parameter ratio , and the strength indicators, it can be concluded that the structural parameter ratio is negatively correlated with both water content and dry density . The structural strength indicator ratios (,) of unsaturated loess satisfy exponential function relationships with their structural parameter ratio values (). By utilizing the derived functional relationship, a formula related to the structural parameters was established, which can comprehensively reflect the factors influencing the structural properties of loess—the comprehensive structural state variable Pcs.
- (5)
- Based on Origin software, nonlinear fitting of the relationship between the structural parameter ratio and the comprehensive structural state variable effectively reflects the combined influence of various structural factors (, ) of loess. Given the comprehensive structural state variable Pcs as a function of and , the structural parameter ratio can be determined, enabling the calculation of the strength index of loess under arbitrary structural conditions.
- (6)
- The newly defined complex stress structural parameters of loess in this article are represented by the shear strength of the soil, which is a material constant. Through comparison, it can also be seen that the complex stress structural parameters of loess proposed in this paper have broader applicability and are not limited to specific experimental conditions. The correctness and rationality of the complex stress structural parameters of loess have been demonstrated by the experimental results in references [27,28].
- (7)
- The next research focus should be on establishing a structural constitutive model for loess based on complex stress structural parameters, and expanding the application space of complex stress structural parameters.
Author Contributions
Methodology, X.-J.W. and F.-N.D.; field investigation, X.-J.W. and J.-Y.L.; experiment, X.-J.W. and J.-Y.L.; data curation, X.-J.W.; writing—original draft preparation, X.-J.W.; writing—review and editing, X.-J.W. and F.-N.D.; supervision, F.-N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by the National Natural Science Foundation of China (No: 51979225), the Shaanxi Key R&D Program Project (No: 2022ZDLSF07-02) and the Key Laboratory Project of Shaanxi Provincial Department of Education (No: 20JS091).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
References
- Li, Y.R.; Zhao, J.G.; Li, B. Loess and Loess Geohazards in China; CRC Press: Boca Raton, FL, USA; Taiyuan University of Technology: Taiyuan, China, 2017. [Google Scholar] [CrossRef]
- Li, Y.R.; Shi, W.H.; Aydin, A.; Beroya-Eitner, M.A.; Gao, G.H. Loess genesis and worldwide distribution. Earth-Sci. Rev. 2020, 201, 102947. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, F.; Ma, F.L.; Wang, M.; Bai, X.H.; Zheng, Y.L.; Yin, H.; Zhang, G.P. Collapsibility, composition, and microstructure of loess in China. Can. Geotech. J. 2015, 53, 673–686. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, Y.L.; Gao, Y.; Yuan, X.Q. Structural characteristics and its influencing factors of typical loess. Bull. Eng. Geol. Environ. 2019, 78, 4893–4905. [Google Scholar] [CrossRef]
- Jiang, M.; Zhang, F.; Hu, H.; Cui, Y.; Peng, J. Structural characterization of natural loess and remolded loess under triaxial tests. Eng. Geol. 2014, 181, 249–260. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck Ralph, B.; Mesri, G. Soil Mechanics in Engineering Practice; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar] [CrossRef]
- Wang, H.; Tian, K.; Ma, B.; Zhang, H.; Zhang, R.; Li, D. Study on the Dynamic Structural Parameters and Dynamic Structural Constitutive Relation of Intact Loess. Soil Mech. Found. Eng. 2021, 58, 100–108. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, S.; Chen, D.; Zhao, D.; Zhang, D. An experimental study of the influence of structural parameters on dynamic characteristics of loess. Soil Dyn. Earthq. Eng. 2020, 132, 106067. [Google Scholar] [CrossRef]
- Luo, Y.S.; Xie, D.Y.; Shao, S.J.; Zhang, A.J. Structural Parameter of Soil Under Complex Stress Conditions. Chin. J. Rock Mech. Eng. 2004, 23, 4248–4251. [Google Scholar]
- Xu, L.; Coop, M.R. Influence of structure on the behavior of a saturated clayey loess. Can. Geotech. J. 2016, 53, 1026–1037. [Google Scholar] [CrossRef]
- Xiong, C.X.; Gong, X.N. An updated elastoplastic damage model for structural soft-clays. Rock Soil Mech. 2006, 27, 395–397. [Google Scholar] [CrossRef]
- Xie, D.Y.; Qi, J.L.; Zhang, Z. A Constitutive Laws Considering Soil Structural Properties. China Civ. Eng. J. 2000, 4, 35–41. [Google Scholar] [CrossRef]
- Shen, Z.J. Masonry model for structural clays. Rock Soil Mech. 2000, 21, 1–4. [Google Scholar] [CrossRef]
- Chen, C.L.; Hu, Z.Q.; Gao, P. Research on relationship between structure and deformation property of intact loess. Rock Soil Mech. 2006, 11, 1891–1896. [Google Scholar] [CrossRef]
- Wang, L.Z.; Zhao, Z.Y.; Li, L.L. Non-linear elastic model considering soil structural damage. J. Hydraul. Eng. 2004, 1, 83–89. [Google Scholar] [CrossRef]
- Qi, J.L.; Xie, D.Y.; Shi, Y. Research methods and current status of soil structure. Northwestern Seismol. J. 2001, 23, 99–103. [Google Scholar]
- Meng, F.; Chen, R.; Kang, X.; Li, C.Z. e-p curve-based structural parameter for assessing clayey soil structure disturbance. Bull. Eng. Geol. Environ. 2020, 79, 4387–4398. [Google Scholar] [CrossRef]
- Xie, D.Y.; Qi, J.L. Soil structure characteristics and new approach in research on its quantitative parameter. Chin. J. Geotech. Eng. 1999, 21, 651–656. [Google Scholar]
- Xie, D.Y.; Qi, J.L.; Zhu, Y. Soil structure parameter and its relations to deformation and strength. J. Hydraul. Eng. 1999, 10, 1–6. [Google Scholar] [CrossRef]
- Luo, Y.S.; Xie, D.Y.; Shao, S.J.; Zhang, A. Variation characteristics of soil structure of unsaturated loess. J. Northwest A F Univ. (Nat. Sci. Ed.) 2004, 32, 114–118. [Google Scholar] [CrossRef]
- Luo, Y.S.; Xie, D.Y. Structural Constitutive Relation of Soils Under Complex Stress Conditions. J. Sichuan Univ. (Eng. Sci. Ed.) 2005, 37, 14–18. [Google Scholar] [CrossRef]
- Luo, Y.S.; Hu, Z.Y.; Zhang, A.J. Regularity of Relation between Structural Parameter and Strength Indexes of Unsaturated Loess. Rock Soil Mech. 2009, 30, 943–948. [Google Scholar] [CrossRef]
- Shao, S.J.; Zheng, W.; Wang, Z.; Wang, S. Structural index of loess and its testing method. Rock Soil Mech. 2010, 31, 15–19+38. [Google Scholar] [CrossRef]
- Xie, D.Y. Exploration of some new tendencies in research of loess soil mechanics. Chin. J. Geotech. Eng. 2001, 23, 3–13. [Google Scholar] [CrossRef]
- Huang, Q. People and Events in Geotechnical Engineering for the 66th Anniversary of the Founding of the People’s Republic of China; China Building Industry Press: Beijing, China, 2015. [Google Scholar]
- Xie, D.Y. Thoughts on Soil Mechanics in the 21st Century. Chin. J. Geotech. Eng. 1997, 19, 111–114. [Google Scholar]
- Shao, S.J.; Zhou, F.F.; Long, J.Y. Structural properties of loess and its quantitative parameter. Chin. J. Geotech. Eng. 2004, 26, 531–536. [Google Scholar]
- Shao, S.J.; Wang, L.Q.; Tao, H.; Wang, Q.; Wang, S. Structural index of loess and its relation with granularity, density and humidity. Chin. J. Geotech. Eng. 2014, 36, 1387–1393. [Google Scholar] [CrossRef]
- Wu, X.J.; Dang, F.N.; Li, J.Y. The Parameter of Soil Structural Properties and Their Relationship to Grain Size, Density, and Moisture Content. Appl. Sci. 2025, 15, 1872. [Google Scholar] [CrossRef]
- Wu, X.J.; Dang, F.N.; Li, J.Y. Research on structural parameters of loess and its experimental determination method. Front. Built Environ. 2025, 11, 1529204. [Google Scholar] [CrossRef]
- GB/T50123-2019; Standard for Geotechnical Test Methods. Ministry of Water Resources of the People’s Republic of China: Beijing, China; China Planning Press: Beijing, China, 2019.
- Hao, Y.Z.; Wang, T.H.; Wang, J.J. Structural properties of unsaturated compacted loess for various sample moisture contents. Arab. J. Geosci. 2019, 12, 258. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, W.W.; Wang, G.H.; Sun, G.P.; Zhang, F.Y. Influence of initial dry density and water content on the soil–water characteristic curve and suction stress of a reconstituted loess soil. Bull. Eng. Geol. Environ. 2017, 76, 1085–1095. [Google Scholar] [CrossRef]
- Chen, C.-L.; Gao, P.; Tang, J. Structural quantitative parameter of intact loess with different water contents under triaxial stress condition. Chin. J. Rock Mech. Eng. 2006, 11, 2313–2319. [Google Scholar]
- Gao, Y. Study on the Influencing Factors of Structural Properties of Loess in Xianyang. Master’s Thesis, Jilin University, Jilin, China, 2016. [Google Scholar]
- Hu, Z.Q.; Xie, D.Y.; Shen, Z.J. Experimental study on stable porous ratio principle of loess. J. Hydrol. 2002, 33, 97–100. [Google Scholar] [CrossRef]
- Kramarenko, V.V.; Nikitenkov, A.N.; Molokov, V.Y.; Matveenko, I.A.; Shramok, A.V. The Relationship of Physical Property Indicators and Clay Soil Structural Strength of Tomsk Oblast Territory. Earth Environ. Sci. 2015, 27, 12030. [Google Scholar] [CrossRef]
- Li, Y.R. A review of shear and tensile strengths of the Malan Loess in China. Eng. Geol. 2018, 236, 4–10. [Google Scholar] [CrossRef]
- Freedlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; China Architecture and Building Press: Beijing, China, 1997. [Google Scholar]
- Zhang, X.D.; Li, Q.W.; Li, G.H.; Su, J. Experimental Research on Relationship of Structural Parameters with Structural Strength Indexes of Intact Unsaturated Aeolian Soil. J. Highw. Transp. Res. Dev. 2009, 30, 41–48+56. [Google Scholar] [CrossRef]
- Luo, Y.S. Variation Characteristics of Soil Structure and Structural Constitutive Relation of Unsaturated Loess Under Static and Dynamic Complex Stress Conditions. Ph.D. Dissertation, Xi’an University of Technology, Xi’an, China, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).