Integrated Attenuation Compensation and Q-Constrained Inversion for High-Resolution Reservoir Characterization in the Ordos Basin
Abstract
1. Introduction
2. Geological Setting
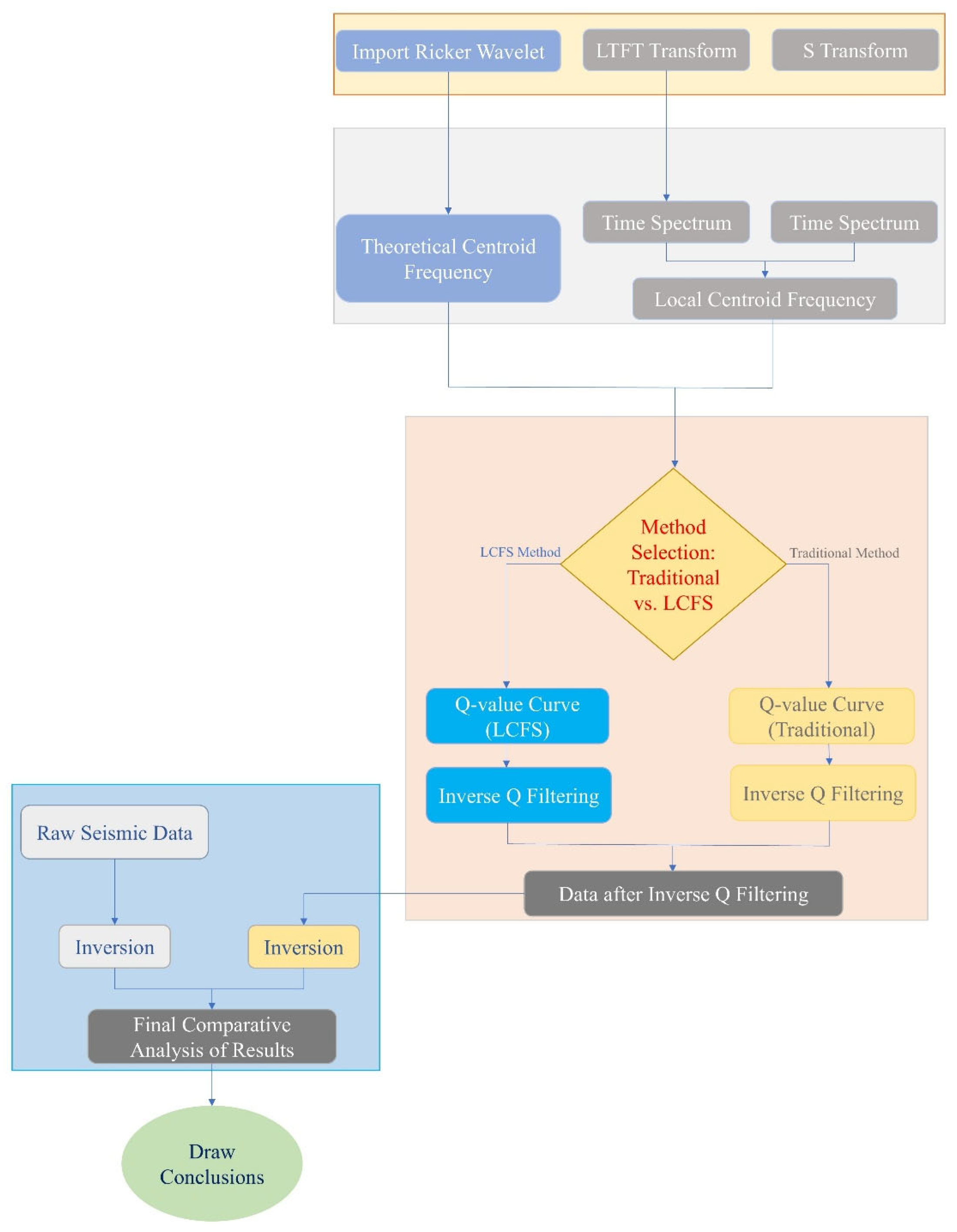
3. Theory and Methodology
3.1. Q-Factor Estimation via the Local Centroid Frequency Shift (LCFS)
3.2. Attenuation Compensation via Stable Inverse Q-Filtering
3.3. Post-Stack Model-Based Acoustic Impedance Inversion for Reservoir Properties
4. Results and Discussion
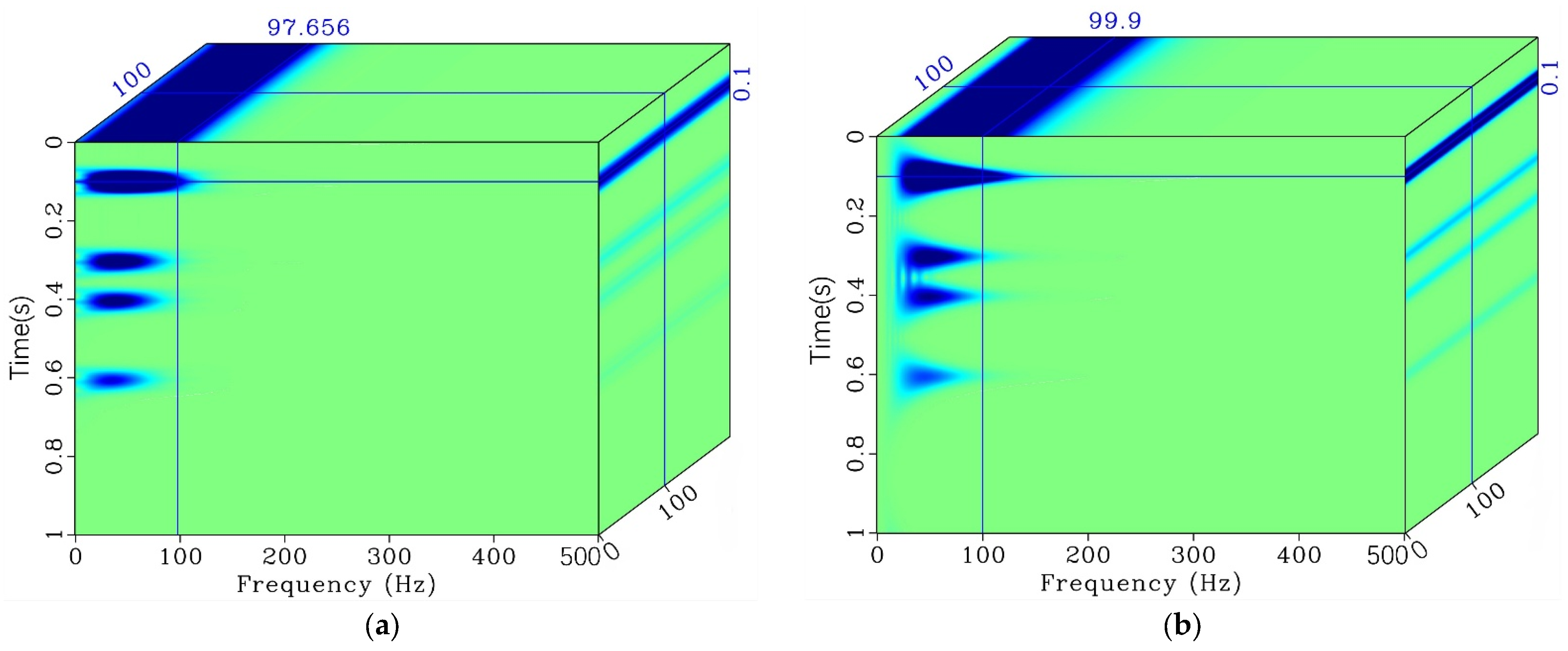
4.1. Synthetic Data Validation
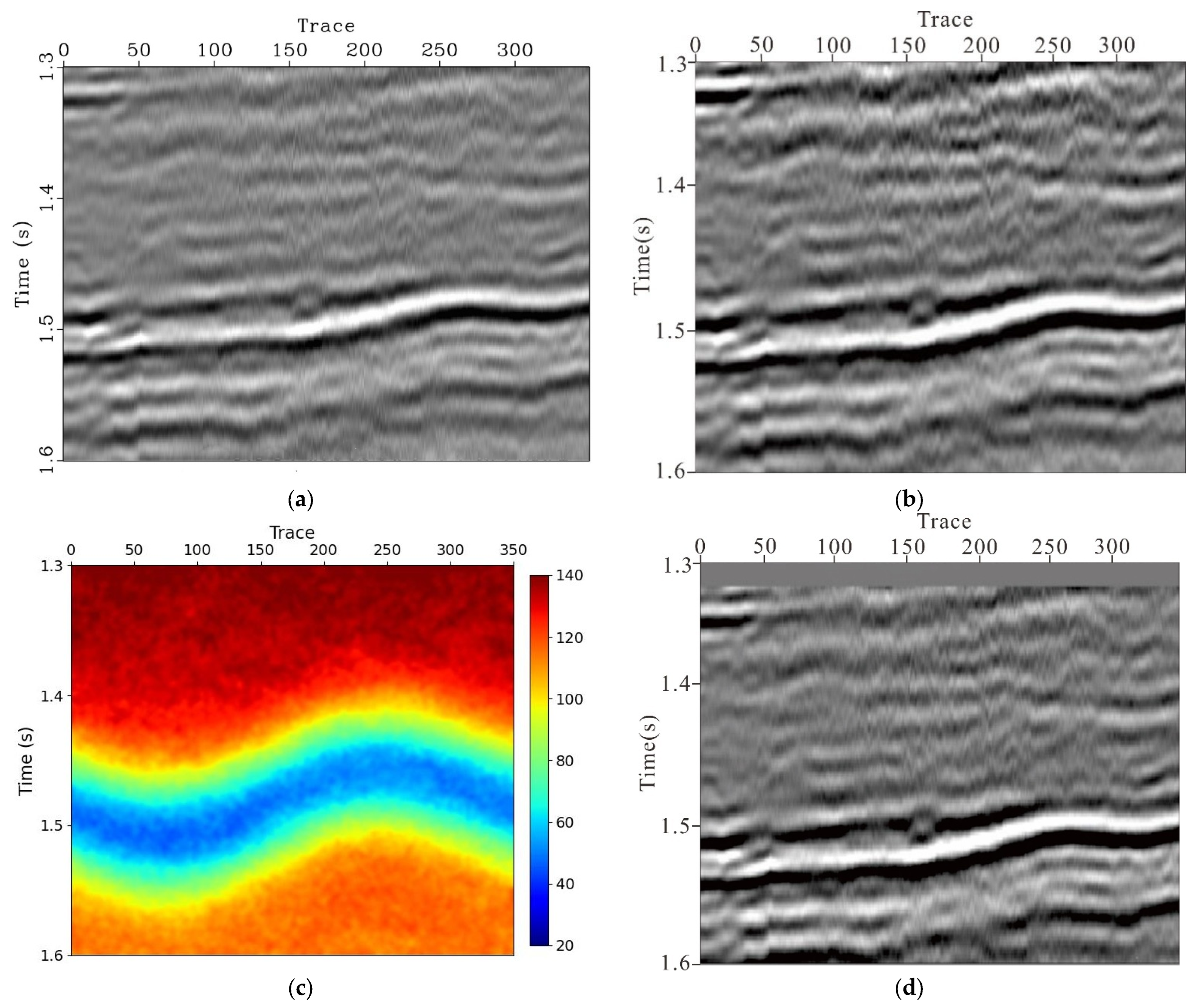
4.2. Field Data Application: Q-Estimation and Attenuation Compensation
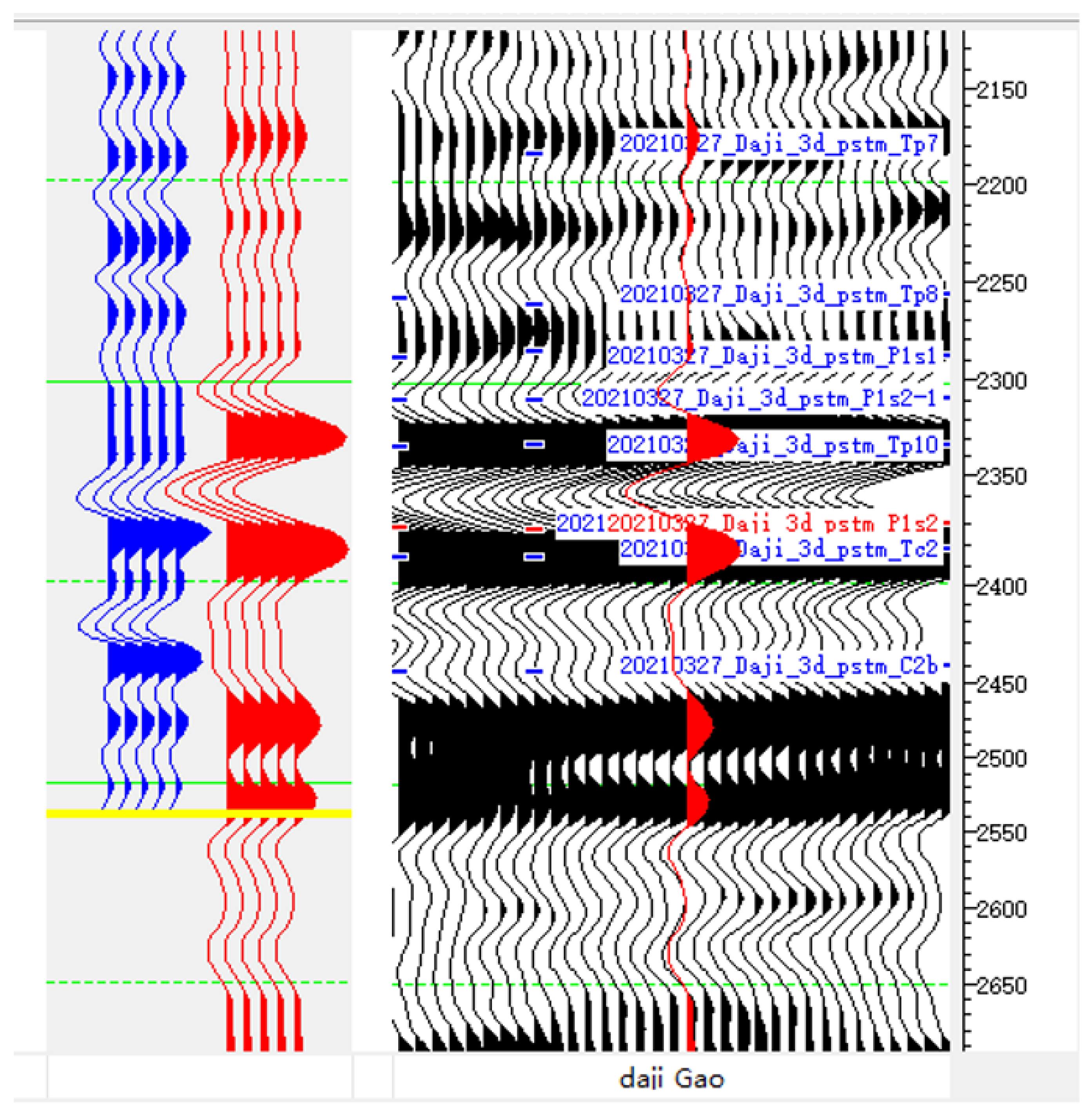
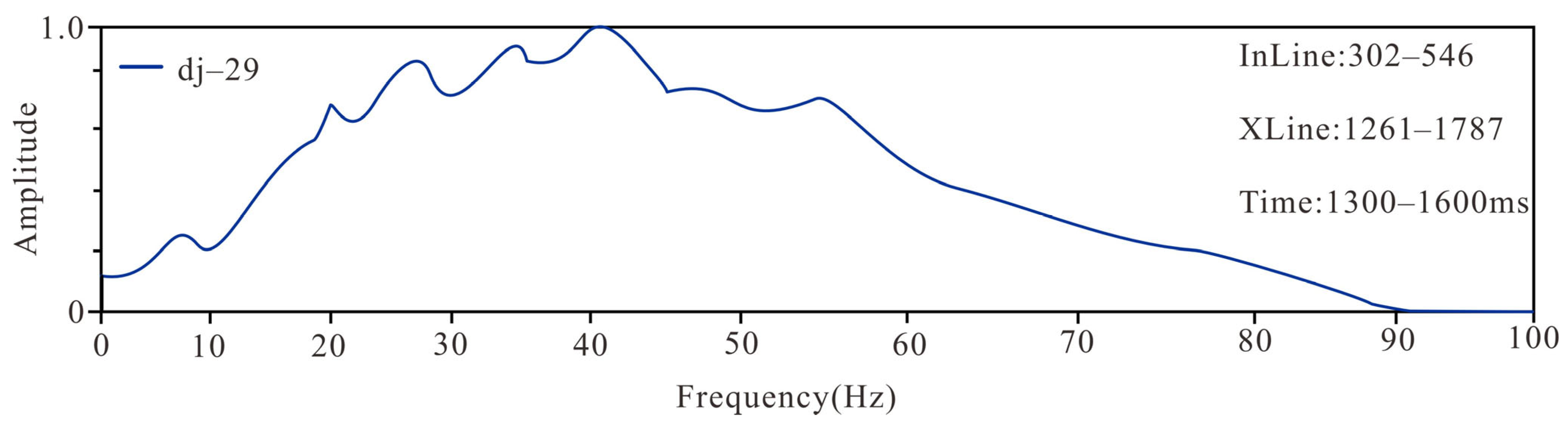
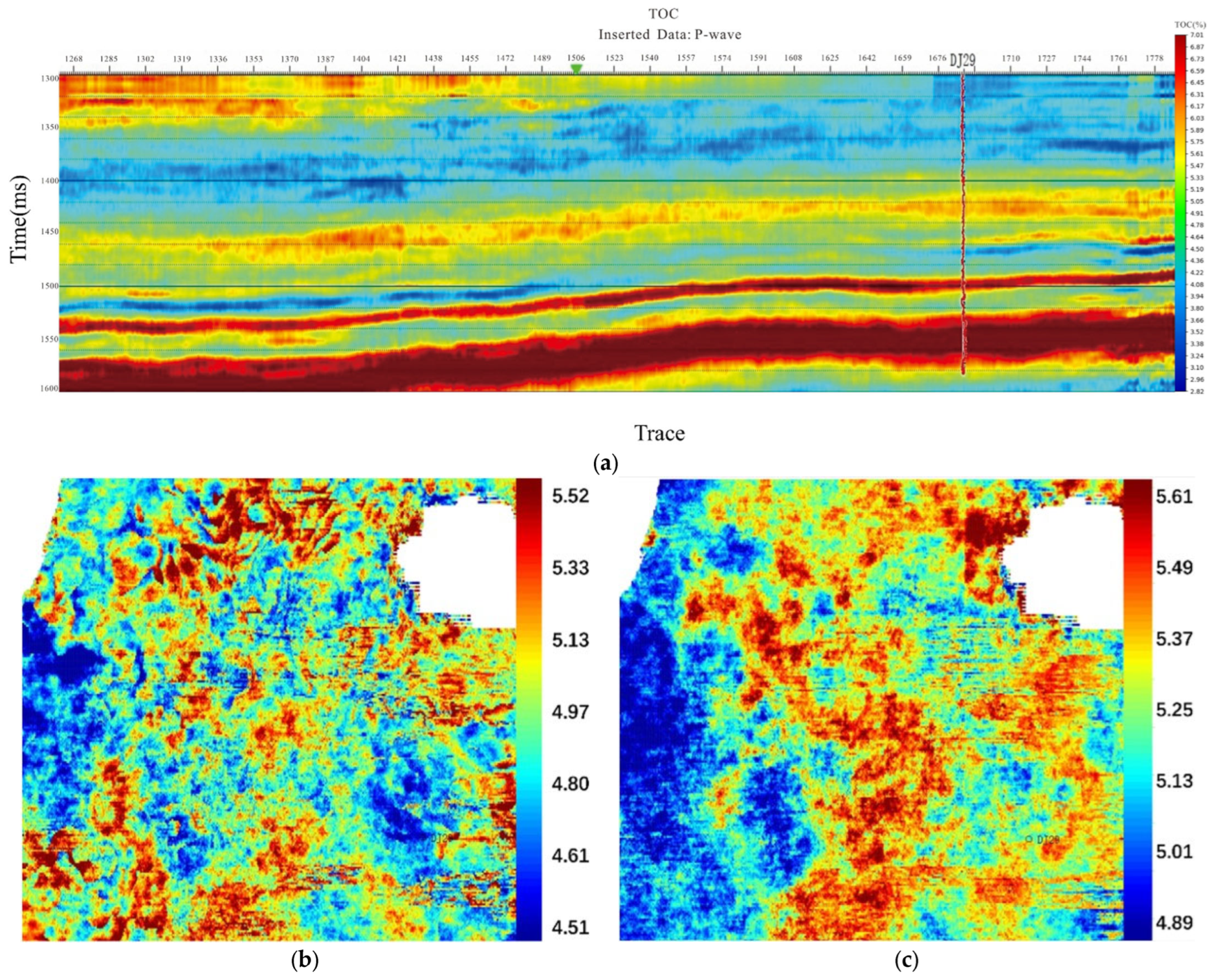
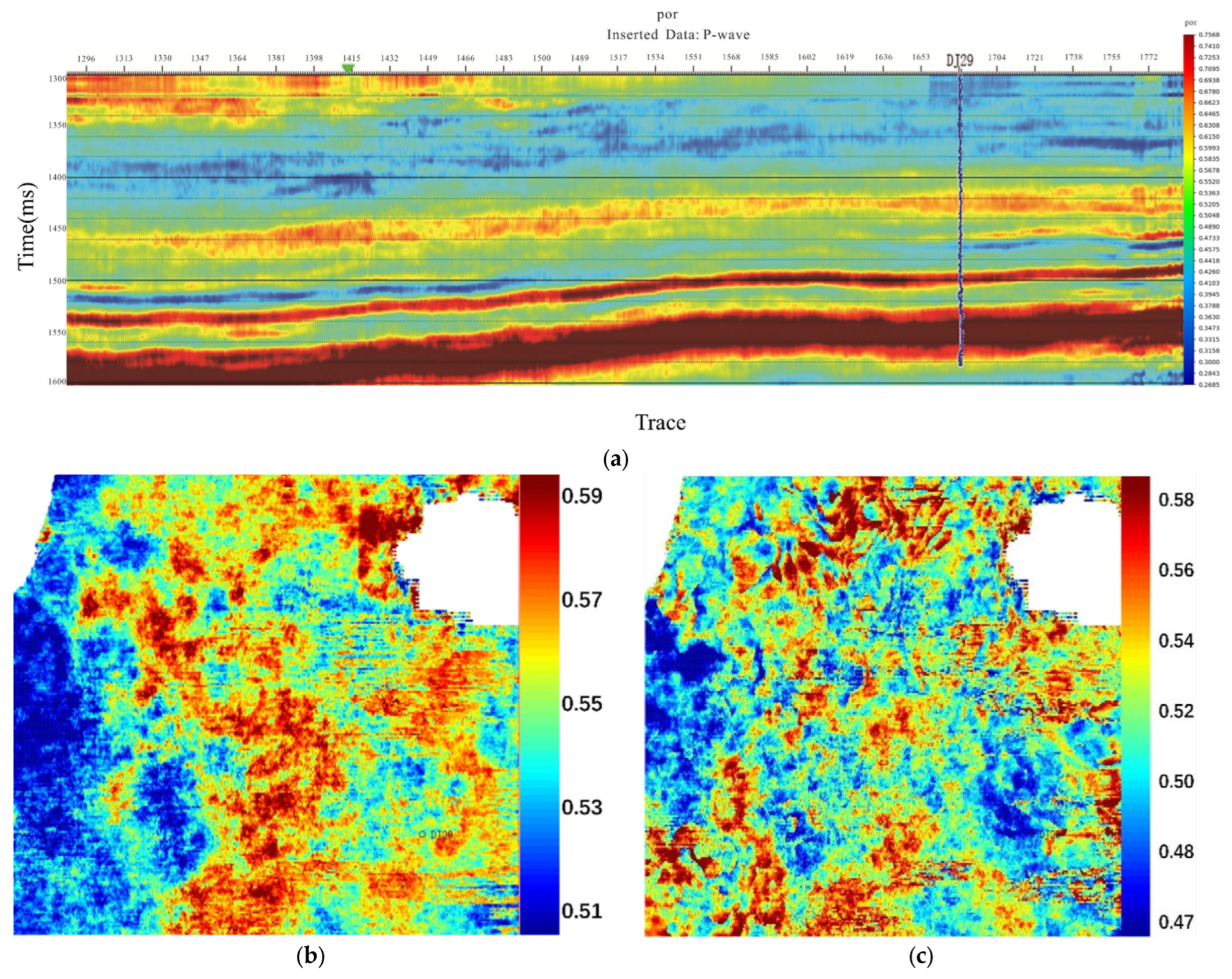
4.3. Quantitative Inversion and Reservoir Characterization
4.3.1. Building a Constrained Inversion Framework
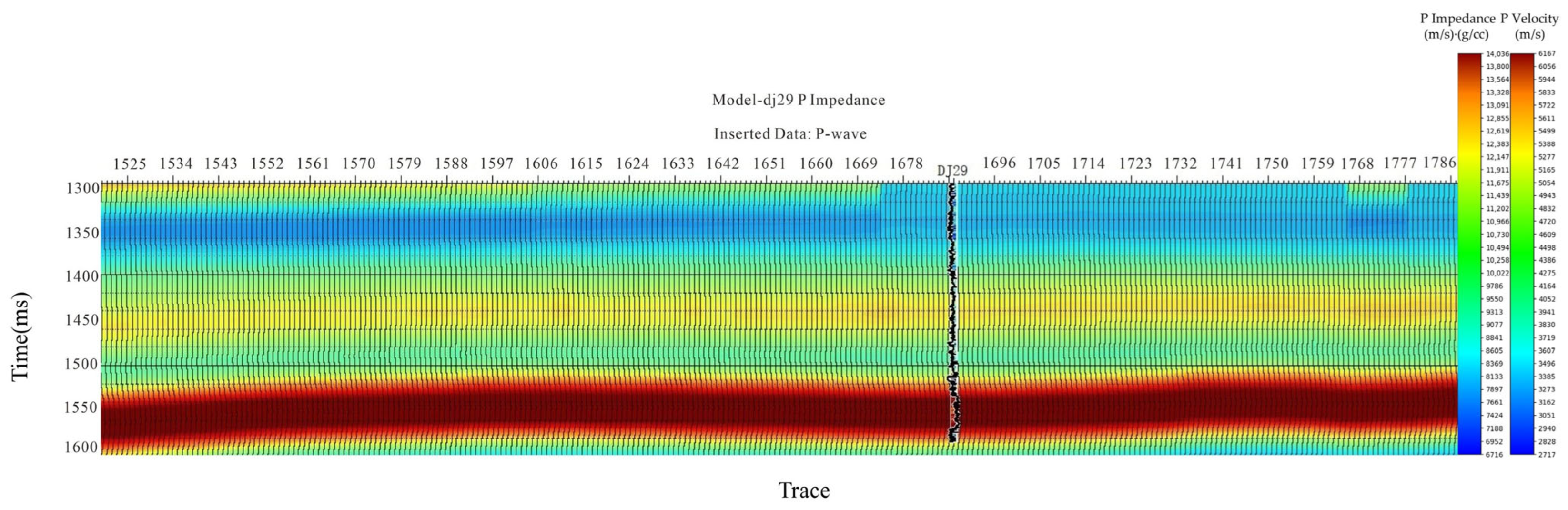
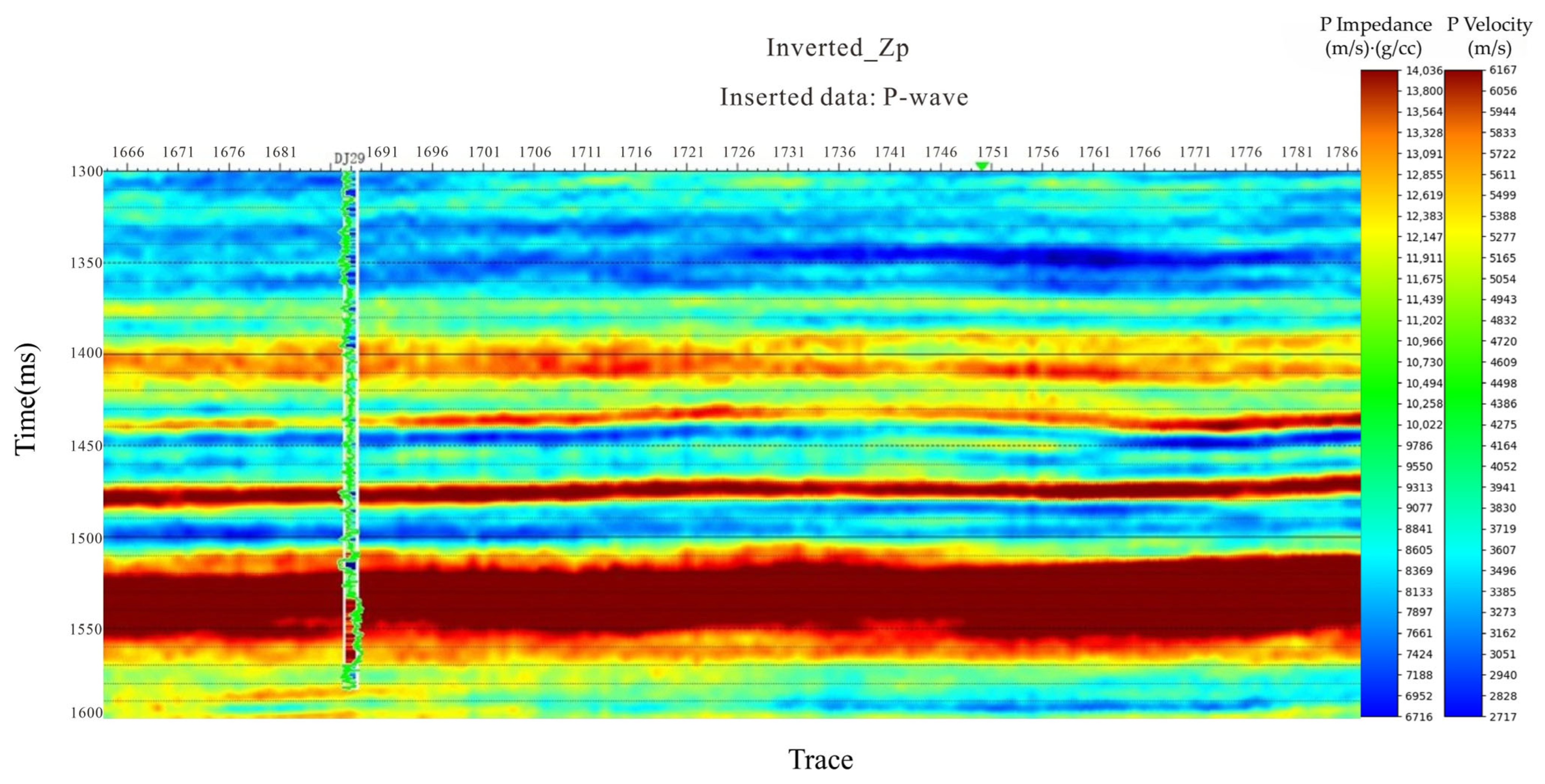
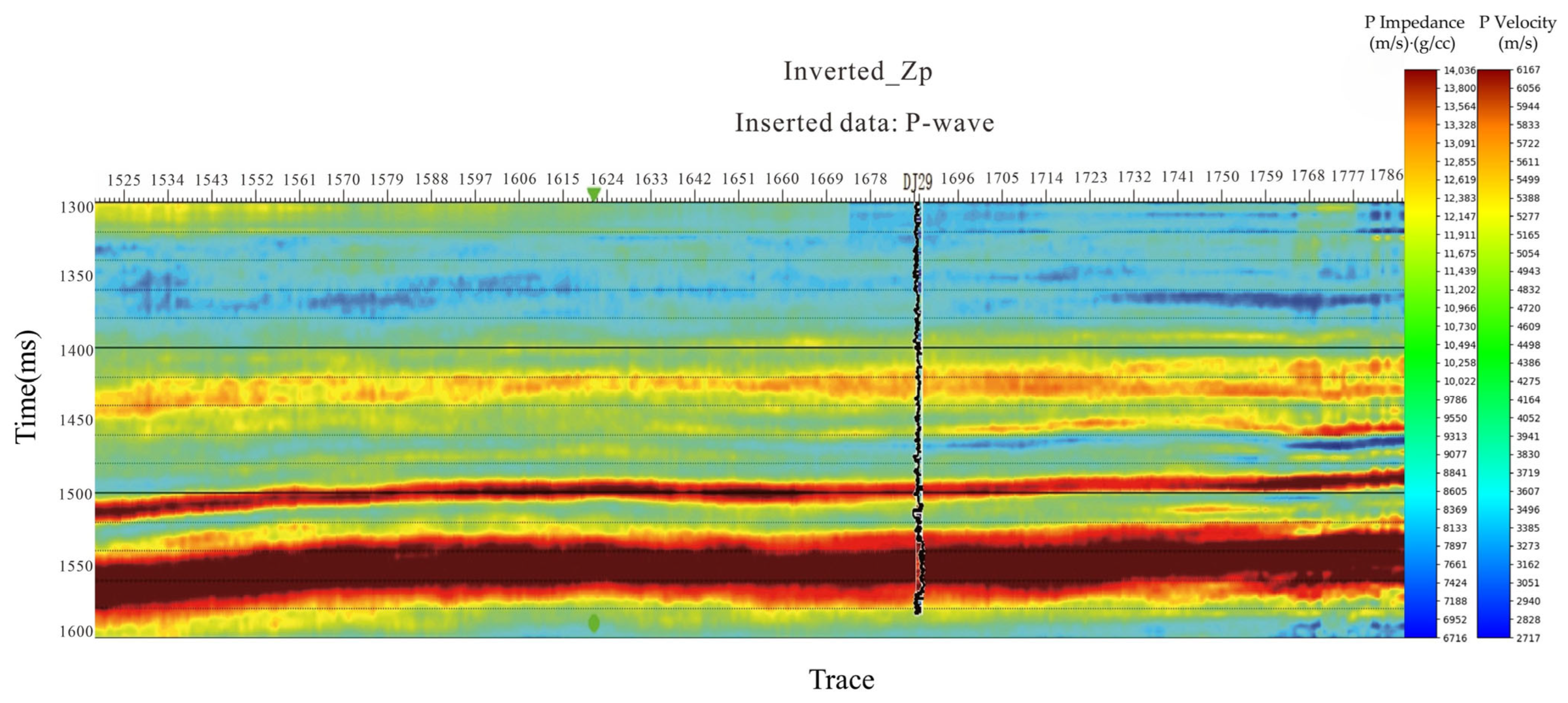
4.3.2. Impact on P-Impedance: The Foundation for Quantitative Interpretation
4.3.3. Unlocking Higher-Fidelity Reservoir Parameter Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Duan, W.; Qin, L.; Zheng, D.; Wang, X.; Liu, L. Adjacent channel attenuation difference estimation and its application in near-surface Q inversion. J. Appl. Geophys. 2023, 215, 105064. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Huang, X.; Qin, H.; Xie, Y.; Chen, K.; Zhang, Z. Seismic Attenuation Parameter Estimation Based on Improved GLCT. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3004605. [Google Scholar] [CrossRef]
- Zhang, Q.; Lv, X.-y.; Lei, Q.; Peng, B.; Li, Y.; Zhang, Y.-w. Seismic multiple attenuation based on improved U-Net. Appl. Geophys. 2024, 21, 680–696. [Google Scholar] [CrossRef]
- Liu, W.; Zhai, Z.; Fang, Z. A multisynchrosqueezing-based S-transform for time-frequency analysis of seismic data. Pure Appl. Geophys. 2025, 182, 1279–1295. [Google Scholar] [CrossRef]
- Yin, Z.; Wei, J.; Di, B. Identification of fracture strike using Q-anisotropy. Pet. Geophys. Prospect. 2011, 46, 429–433. [Google Scholar] [CrossRef]
- Bose, S.; Singh, C.; Sarkar, S.; Dutta, A. Crustal Heterogeneity of the Bhutan Himalaya: Insights from PgQ Tomography. Bull. Seismol. Soc. Am. 2025, 115, 248–259. [Google Scholar] [CrossRef]
- Duan, M.; Zhou, L.; Fu, Y.; An, Y.; Yang, J.; Zhang, X. The 3D QP model of the China Seismic Experimental Site (CSES-Q1.0) and its tectonic implications. Solid Earth 2025, 16, 391–408. [Google Scholar] [CrossRef]
- Peng, Z.; Qu, J.; Chen, C.; Wang, H.; Zhu, D.; Mi, Z.; Xie, E.; Zhang, Z.; Yu, X.; Wang, H. Coal Accumulation in Marine to Continental Transitional Sequence During Late Carboniferous-Early Permian in the Southeastern Ordos Basin, China. Geol. J. 2025; early access. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, K.; Li, Q.; Zheng, X.; Wang, B.; Li, D.; Tang, W. Seismic prediction technology for thin reservoirs of tight gas in coal measure strata: A case study of Block L in the eastern margin of the Ordos Basin. Front. Earth Sci. 2025, 12, 1487487. [Google Scholar] [CrossRef]
- Zhang, K.; Li, S.; Zhong, G.; Feng, P.; Chang, C.; Li, H. Characteristics of in-situ stress field of coalbed methane reservoir in the eastern margin of Ordos basin. Int. J. Coal Geol. 2025, 301, 104715. [Google Scholar] [CrossRef]
- Seelam, N.K.; Kumar, T.; Dhubia, S.; Rao, G.S.; Pal, S.K. Enhancing Thin Coal Seam Detection in Eastern Indian Coalfields Using ICWT-Decon-Based Seismic Attributes and Acoustic Impedance Inversion. Minerals 2024, 14, 920. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.; Wu, Y.; Li, S.; Gu, Y.; Li, X. Factors controlling spatial distribution of complex lithology in transitional shale strata: Implications from logging and 3D seismic data, Shan-2 Lower Sub-member, Eastern Ordos Basin. Front. Earth Sci. 2023, 10, 951524. [Google Scholar] [CrossRef]
- Yu, H.; Wang, H.; Wu, L.; Chen, T. A precise time-depth conversion method for coal seam based on machine learning and seismic velocity inversion. Acta Geophys. 2025, 73, 4059–4073. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, S.; Liu, Q.; Dong, S.; Huang, Y.; Zhang, P. Amplitude variation with offset and azimuth inversion to predict and evaluate coal seam fracture parameters. Front. Earth Sci. 2023, 17, 505–513. [Google Scholar] [CrossRef]
- Veeken, P.; Da Silva, M. Seismic inversion methods and some of their constraints. First Break 2004, 22, 2004. [Google Scholar] [CrossRef]
- Gholami, A. A fast automatic multichannel blind seismic inversion for high-resolution impedance recovery. Geophysics 2016, 81, V357–V364. [Google Scholar] [CrossRef]
- Zhang, B.; Pu, Y.; Dai, R.; Cao, D. Seismic poststack impedance inversion using geophysics-informed deep-learning neural network. Interpretation 2025, 13, T219–T232. [Google Scholar] [CrossRef]
- Zhao, Y.; Wen, X.; Xie, C.; Li, B.; Pan, X.; Zhou, X.; Li, C. Seismic inversion of anisotropic and isotropic fluid indicators and fracture density in the TTI medium. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5911821. [Google Scholar] [CrossRef]
- Arabpour, A.; Hamidzadeh Moghadam, R.; Niri, M.E. Bayesian seismic inversion by residual flow. Geophysics 2025, 90, R345–R362. [Google Scholar] [CrossRef]
- Jing, S.; Dengfa, H. Tectonic characteristics and evolution of the middle segment of the Jinxi flexure fold belt in the eastern margin of the Ordos Basin. Chin. J. Geol. 2024, 59, 723–731. [Google Scholar] [CrossRef]
- Liu, S. The coupling mechanism of basin and orogen in the western Ordos Basin and adjacent regions of China. J. Asian Earth Sci. 1998, 16, 369–383. [Google Scholar] [CrossRef]
- Dengfa, H.; Cheng, X.; Zhang, G.; Wenzhi, Z.; Zhe, Z.; Xinshe, L.; Hongping, B.; Liyong, F.; Song, Z.; Baize, K. Scope, nature, and exploration significance of Ordos Basin during geological historical periods, NW China. Pet. Explor. Dev. 2025, 52, 855–871. [Google Scholar] [CrossRef]
- Liu, J.; Liu, K.; Huang, X. Effect of sedimentary heterogeneities on hydrocarbon accumulations in the Permian Shanxi Formation, Ordos Basin, China: Insight from an integrated stratigraphic forward and petroleum system modelling. Mar. Pet. Geol. 2016, 76, 412–431. [Google Scholar] [CrossRef]
- Liu, S.; Li, J.; Jin, F.; Liu, H.; Wang, M.; Cheng, Y.; Zhong, X.; Lu, H. Genesis of efficient reservoirs in mixed sedimentary setting: A case study of Benxi Formation in the Gaoqiao area, Ordos Basin. Turk. J. Earth Sci. 2024, 33, 118–145. [Google Scholar] [CrossRef]
- Guo, W.; Shen, W.; Zhou, S.; Xue, H.; Liu, D.; Wang, N. Shale favorable area optimization in coal-bearing series: A case study from the Shanxi Formation in Northern Ordos Basin, China. Energy Explor. Exploit. 2018, 36, 1295–1309. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, J.; Guo, M.; Wang, Y.; Wu, H.; Li, J.; Wu, W. Depositional process and its control on the densification of coal-measure tight sandstones: Insights from the Permian Shanxi Formation of the northeastern Ordos Basin, China. Int. J. Earth Sci. 2023, 112, 1871–1890. [Google Scholar] [CrossRef]
- Zhao, W.-B.; Zhang, H.; Shi, Y.-H.; Fu, X.-X.; Hui, J.; Jing, X.-Y. Geological characteristics and exploration potential of the coal measure gas from Shan 2 of the Shanxi formation in the eastern Ordos Basin. Front. Earth Sci. 2023, 11, 1142141. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, S.; Hu, Z.; Shen, B.; Feng, D.; Zhang, J.; Ye, J.; Ma, C.; Dong, Z. Characteristics and controlling factors of coal-measure unconventional reservoirs—A case study of the Carboniferous-Permian in the Ordos Basin. Unconv. Resour. 2025, 6, 100153. [Google Scholar] [CrossRef]
- Tao, H.; Cui, J.; Zhao, F.; Ren, Z.; Qi, K.; Liu, H.; Su, S. Thermal history and hydrocarbon accumulation stages in Majiagou Formation of Ordovician in the East-Central Ordos Basin. Energies 2024, 17, 4435. [Google Scholar] [CrossRef]
- Fang, X.; Qiu, F.; Shu, L.; Huo, Z.; Li, Z.; Cai, Y. Reservoir Properties and Gas Potential of the Carboniferous Deep Coal Seam in the Yulin Area of Ordos Basin, North China. Energies 2025, 18, 3987. [Google Scholar] [CrossRef]
- Zhao, W.; Wen, Z.; Zhang, H.; Wu, C.; Liu, Y.; Song, H.; Zhang, L.; Xi, Y.; Sun, L. Integrated assessment of marine-continental transitional facies shale gas of the carboniferous Benxi Formation in the Eastern Ordos Basin. Energies 2021, 14, 8500. [Google Scholar] [CrossRef]
- Chen, S.; Xu, Y.; Yu, Y.; Feng, J.; Yuan, S. Geologically Guided Sparse Multitrace Reflectivity Inversion for High-Resolution Characterization of Subtle Reservoirs. Appl. Sci. 2025, 15, 5125. [Google Scholar] [CrossRef]
- Qi, Y.; Wu, K.; Wang, B.; Zheng, X.; Li, W.; Li, D. Lithofacies identification of deep coalbed methane reservoir based on high-resolution seismic inversion. Front. Earth Sci. 2024, 12, 1440729. [Google Scholar] [CrossRef]
- Basin, T. Analysis of Seismic Response Characteristics of Coal-Bearing Sandstone Reservoirs in the Middle and Lower Jurassic in the South. In Proceedings of the International Field Exploration and Development Conference 2023: Volume 2, Wuhan, China, 19–21 September; Springer Nature: Berlin/Heidelberg, Germany, 2024; p. 234. [Google Scholar] [CrossRef]
- Lihong, Z.; Yong, L.; Rong, D.; Wei, H.; Yongzhou, L.; Hui, M.; Haijiao, F.; Yi, D.; Zhitong, Z.; Zhuangsen, W. Differential accumulation characteristics and production of coalbed methane/coal-rock gas: A case study of the No. 8 coal seam of the Carboniferous Benxi Formation in the Daji block, Ordos Basin, NW China. Pet. Explor. Dev. 2025, 52, 872–882. [Google Scholar] [CrossRef]
- Liyuan, L.; Yong, L.; Shuxin, L.; Qingbo, H.; Shijia, C.; Xiang, L.; Xingtao, L.; Jungang, L.; Zhenglu, X.; Xiangdong, Y. Controlling factors of Marine and continental transitional shale gas enrichment in Shan2 3 sub-member, Daji area, eastern margin of Ordos Basin. Nat. Gas Geosci. 2025, 36, 554–566. [Google Scholar] [CrossRef]
- Lin, H.; Liu, X.; Xiong, J.; Liang, L.; Ding, Y.; Wu, J.; Li, B. Research on transversely isotropic in-situ stress logging prediction of transitional shale reservoir: A case study of Daji Block, Eastern Ordos Basin, North China. Pet. Sci. Technol. 2024, 42, 1296–1315. [Google Scholar] [CrossRef]
- Yan, T.; He, S.; Zheng, S.; Bai, Y.; Chen, W.; Meng, Y.; Jin, S.; Yao, H.; Jia, X. Critical tectonic events and their geological controls on deep buried coalbed methane accumulation in Daning-Jixian Block, eastern Ordos Basin. Front. Earth Sci. 2023, 17, 197–217. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, D.; Qiu, Z.; Wu, C.; Zhang, Q.; Wang, Y.; Liu, D.; Deng, Z.; Zhou, S.; Pan, S. Sedimentology and geochemistry of Carboniferous-Permian marine-continental transitional shales in the eastern Ordos Basin, North China. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2021, 571, 110389. [Google Scholar] [CrossRef]
- Kuang, L.; Dazhong, D.; Wenyuan, H.; Shengming, W.; Shasha, S.; Shuxin, L.; Zhen, Q.; Xinwei, L.; Yong, L.; Jin, W. Geological characteristics and development potential of transitional shale gas in the east margin of the Ordos Basin, NW China. Pet. Explor. Dev. 2020, 47, 471–482. [Google Scholar] [CrossRef]
- Pan, B.; Wang, K.; Dong, G.; Zhou, X.; Chen, Y.; Zhuang, Y.; Gao, X.; Du, X. Geochemical Characteristics and Paleoenvironmental Significance of No. 5 Coal in Shanxi Formation, Central–Eastern Ordos Basin (China). Minerals 2025, 15, 177. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, H.; Guo, G.; Mo, R.; Pan, Z.; Cai, Y.; Abuduerxiti, A. Gas distribution and its geological factors in the No. 5 coal seam of the Weibei field, Southeastern Ordos Basin, North China. Processes 2022, 10, 659. [Google Scholar] [CrossRef]
- Peng, H.J.; Zhao, J.T.; Qiu, Z.; Zhang, Q.; Liu, W.; Kong, W.L.; Gao, W.L.; Sheng, T.J.; Li, W.Y.; Yang, Y.G. Multi-scale fracture characterization method for transitional shale reservoir based on post-stack multi-attribute ant-tracking fusion and pre-stack wide-azimuth gathers AVAZ analysis. Geomech. Geophys. Geo-Energy Geo-Resour. 2025, 11, 13. [Google Scholar] [CrossRef]
- Wang, D.-X.; Wang, Y.-G.; Zhao, Y.-H.; Tian, R.-F.; Xue, Y.-J. A strong seismic reflection amplitude suppressing method applied in the Ordos Basin. In Proceedings of the SPG/SEG 2016 International Geophysical Conference, Beijing, China, 20–22 April 2016; pp. 389–391. [Google Scholar] [CrossRef]
- Rongtao, G.; Yun, C.; Ziqi, T.; Zhao, L. Data Processing Solutions on Low Signal-to-Noise Data in Loess Plateau Area-A Case Study in Ordos Basin, China. CT Theory Appl. 2025. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, N.; Huang, L.-G.; Li, Q.-Y.; Ge, B.-Y. Seismic Prediction of Laminated-Type Shale Oil Reservoirs and Its Application in Qingcheng Area, Ordos Basin. In Proceedings of the International Field Exploration and Development Conference, Xi’an, China, 12–14 September 2024; Springer: Berlin/Heidelberg, Germany; pp. 917–927. [Google Scholar] [CrossRef]
- Manzoor, U.; Ehsan, M.; Hussain, M.; Bashir, Y. Improved reservoir characterization of thin beds by advanced deep learning approach. Appl. Comput. Geosci. 2024, 23, 100188. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Chen, H.; Duan, Z.; Qiu, Z.; Zhou, X.; Hou, Y. The characteristics of lithofacies and depositional model of fine-grained sedimentary rocks in the Ordos Basin, China. Energies 2023, 16, 2390. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Z.; Zhang, L.; Dai, D.; Zhang, L.; Li, C.; Shi, Y.; Liu, G. Applications of NMR logs to complex lithology interpretation of ordos basin. In Proceedings of the SPWLA Annual Logging Symposium, Austin, TX, USA, 3–6 June 2007; p. SPWLA–2007-JJJ. [Google Scholar]
- Huang, Z.; Zhou, R.; Yang, J.; Wang, M.; Wang, D.; Ma, Z.; Qi, L.; Men, X.; Fang, L. Study on optimization of well pattern and well spacing for CBM development: Taking Daning Block as an example. Coal Sci. Technol. 2023, 51, 121–131. [Google Scholar] [CrossRef]
- Wanghua, S. Catastrophic mechanism of seepage deformation and failure of mining rock mass and its prevention & control I: Water-sand mixture inrush from seam roof. J. Earth Sci. Environ. 2022, 44, 903–921. [Google Scholar] [CrossRef]
- Quan, Y.; Harris, J.M. Seismic attenuation tomography using the frequency shift method. Geophysics 1997, 62, 895–905. [Google Scholar] [CrossRef]
- Fomel, S. Shaping regularization in geophysical-estimation problems. Geophysics 2007, 72, R29–R36. [Google Scholar] [CrossRef]
- Fomel, S. Local seismic attributes. Geophysics 2007, 72, A29–A33. [Google Scholar] [CrossRef]
- Wang, Y. Inverse Q-filter for seismic resolution enhancement. Geophysics 2006, 71, V51–V60. [Google Scholar] [CrossRef]
- Alshangiti, A.; Zhou, H.W. Estimation of seismic attenuation for reservoirs mapping and inverse Q-filtering: An application on land seismic data. Geophys. Prospect. 2023, 71, 682–697. [Google Scholar] [CrossRef]
- Wang, Y. Seismic Inverse Q Filtering; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Maurya, S.; Singh, N.; Singh, K. Post-stack seismic inversion. In Seismic Inversion Methods: A Practical Approach; Springer: Berlin/Heidelberg, Germany, 2020; pp. 39–80. [Google Scholar] [CrossRef]
- Kumar, R.; Das, B.; Chatterjee, R.; Sain, K. A methodology of porosity estimation from inversion of post-stack seismic data. J. Nat. Gas Sci. Eng. 2016, 28, 356–364. [Google Scholar] [CrossRef]
- Sotelo, V.; Almanza, O.; Montes, L. Post-stack seismic inversion through probabilistic neural networks and deep forward neural networks. Earth Sci. Inform. 2024, 17, 1957–1966. [Google Scholar] [CrossRef]
- Shakir, U.; Ali, A.; Hussain, M.; Azeem, T.; Bashir, L. Selection of sensitive post-stack and pre-stack seismic inversion attributes for improved characterization of thin gas-bearing sands. Pure Appl. Geophys. 2022, 179, 169–196. [Google Scholar] [CrossRef]
- Pramudito, D.; Harisandi, A.; Sinaga, R.P.; Nuraeni, F. Enhancing Low-Frequency Model for Post-Stack Inversion using Geostatistics: A Case Study in Imaging Carbonate Structure. J. Geofis. 2021, 19, 69–73. [Google Scholar] [CrossRef]
- Datta Gupta, S.; Sinha, S.K.; Chahal, R. Capture the variation of acoustic impedance property in the Jaisalmer Formation due to structural deformation based on post-stack seismic inversion study: A case study from Jaisalmer sub-basin, India. J. Pet. Explor. Prod. Technol. 2022, 12, 1919–1943. [Google Scholar] [CrossRef]
- Das, B.; Chatterjee, R. Porosity mapping from inversion of post-stack seismic data. Georesursy 2016, 18, 306–313. [Google Scholar] [CrossRef]
- El-Sayed, A.S.; Mabrouk, W.M.; Metwally, A.M. Utilizing post-stack seismic inversion for delineation of gas-bearing sand in a pleistocene reservoir, baltim gas field, nile delta, Egypt. Sci. Rep. 2024, 14, 29596. [Google Scholar] [CrossRef]
- Xue, Y.-J.; Cao, J.-X.; Wang, X.-J.; Du, H.-K. Estimation of seismic quality factor in the time-frequency domain using variational mode decomposition. Geophysics 2020, 85, V329–V343. [Google Scholar] [CrossRef]
- Bouchaala, F.; Ali, M.Y.; Matsushima, J.; Bouzidi, Y.; Jouini, M.S.; Takougang, E.M.; Mohamed, A.A. Estimation of seismic wave attenuation from 3D seismic data: A case study of OBC data acquired in an offshore oilfield. Energies 2022, 15, 534. [Google Scholar] [CrossRef]
- Liu, Y.; Fomel, S. Seismic data analysis using local time-frequency decomposition. Geophys. Prospect. 2013, 61, 516–525. [Google Scholar] [CrossRef]
- Sun, H.; Xu, R.; Zhang, J.; Huang, X.; Han, L. A Modified Unscaled S-Transform for Seismic Time-Frequency Analysis of Road Detection in Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2025; early access. [Google Scholar] [CrossRef]
- Ma, S.; Cao, J. An Efficient Transformer Model Enhanced by S-transform and Transfer Learning for Predicting Gas Distribution in Deeply Buried Reservoirs. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5910414. [Google Scholar] [CrossRef]
- Ba, J.; Ba, X.-Y.; Dong, H.-J.; Cheng, J.-W.; Luo, C.; Yang, Z.-F.; Pang, M.-Q.; Tan, W.-H. Reservoir property estimation of interbedded sandstone and shale layers using segmented 3D rock-physics templates. Appl. Geophys. 2025, 1–17. [Google Scholar] [CrossRef]
- Fawei, M.; Yanxiao, H.; Zhengxin, T.; Shengbo, Y.; Jingyang, N. A seismic reservoir characterization method based on post and pre-stack joint inversion. Pet. Sci. Bull. 2025, 10, 666. [Google Scholar] [CrossRef]
- Samuel, S.A. Integrated Post-Stack Seismic Inversion, Multi-Attribute Analysis, and Machine Learning for Carbon Storage; Oklahoma State University: Stillwater, OK, USA, 2025; Available online: https://hdl.handle.net/20.500.14446/346428 (accessed on 22 October 2025).
- Liu, S.; Zhou, L.; Zhang, B.; Dai, R.; Lu, P.; He, C.; Wu, Y.; Ni, C. Thin-Layer Siliceous Dolomite Prediction Based on Post-Stack Seismic Data Mining and Optimization. Appl. Sci. 2025, 15, 9631. [Google Scholar] [CrossRef]
- Li, M.; Huang, X.; Tang, S.; Chen, K.; Ran, Q. Reservoir-oriented migrated seismic image improvement and poststack seismic inversion using well-seismic mistie. Interpretation 2025, 13, T99–T112. [Google Scholar] [CrossRef]
- Kirkevik, T. Simultaneous Inversion of Post-Stack Seismic Time-Lapse Data. In Proceedings of the 86th EAGE Annual Conference & Exhibition, Toulouse, France, 2–5 June 2025; European Association of Geoscientists & Engineers: Bunnik, The Netherlands, 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Cai, G.; Gu, Y.; Song, D.; Jiang, Y.; Fu, Y.; Liu, Y.; Zhang, F.; Lu, J.; Qiu, Z. Gas occurrence characteristics in marine-continental transitional shale from Shan23 sub-member shale in the Ordos Basin: Implications for shale gas production. Nat. Gas Ind. B 2025, 12, 368–385. [Google Scholar] [CrossRef]
- Chen, M.; Wang, B.; Tian, H.; Sun, J.; Liu, L.; Liang, X.; Chen, B.; Yu, B.; Zhang, Z. Multilayer Gas-Bearing System and Productivity Characteristics in Carboniferous–Permian Tight Sandstones: Taking the Daning–Jixian Block, Eastern Ordos Basin, as an Example. Energies 2025, 18, 2398. [Google Scholar] [CrossRef]
- Zhang, J.; Dang, W.; Zhang, Q.; Wang, X.; Du, G.; Shan, C.; Lei, Y.; Shangguan, L.; Xue, Y.; Zhang, X. Fractal Characterization of Pore Structures in Marine–Continental Transitional Shale Gas Reservoirs: A Case Study of the Shanxi Formation in the Ordos Basin. Energies 2025, 18, 4013. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhao, J.; Sheng, T.; Peng, H.; Zhang, Q.; Qiu, Z. Integrated Attenuation Compensation and Q-Constrained Inversion for High-Resolution Reservoir Characterization in the Ordos Basin. Appl. Sci. 2025, 15, 11504. https://doi.org/10.3390/app152111504
Yang Y, Zhao J, Sheng T, Peng H, Zhang Q, Qiu Z. Integrated Attenuation Compensation and Q-Constrained Inversion for High-Resolution Reservoir Characterization in the Ordos Basin. Applied Sciences. 2025; 15(21):11504. https://doi.org/10.3390/app152111504
Chicago/Turabian StyleYang, Yugang, Jingtao Zhao, Tongjie Sheng, Hongjie Peng, Qin Zhang, and Zhen Qiu. 2025. "Integrated Attenuation Compensation and Q-Constrained Inversion for High-Resolution Reservoir Characterization in the Ordos Basin" Applied Sciences 15, no. 21: 11504. https://doi.org/10.3390/app152111504
APA StyleYang, Y., Zhao, J., Sheng, T., Peng, H., Zhang, Q., & Qiu, Z. (2025). Integrated Attenuation Compensation and Q-Constrained Inversion for High-Resolution Reservoir Characterization in the Ordos Basin. Applied Sciences, 15(21), 11504. https://doi.org/10.3390/app152111504





