Identifying Multi-Omics Interactions for Lung Cancer Drug Targets Discovery Using Kernel Machine Regression
Abstract
1. Introduction
2. Preliminaries
3. Methodology
3.1. Data Sources
3.2. Material and Methods
3.2.1. Differential Expression Study
- n number of paired samples,
- mean of the paired differences,
- standard deviation of the paired differences, and
- expected mean difference (often 0 under the null hypothesis).
- Calculate Differences: For each pair i, calculate the difference
- Handle Zero Differences: Exclude pairs where . The adjusted sample size after exclusions is denoted as .
- Rank Absolute Differences: Compute for all remaining pairs and rank these values from smallest to largest. The smallest non-zero absolute difference receives rank , the next , and so on.
- Assign Signed Ranks: Attach the original sign of to its corresponding rank , producing signed ranks.
- Calculate Test Statistic: The Wilcoxon test statistic W is computed as
3.2.2. Multi-Omics Analysis
3.2.3. Evaluating Marginal Effects
3.2.4. Testing Interaction Effects
3.2.5. Statistical Testing
3.3. Drug Repurposing via Molecular Docking Analysis
3.4. ADMET Analysis
4. Computational Analysis and Results
4.1. KMR-Based Analysis of Lung Cancer Omics Data
4.2. Drug Repurposing
4.3. ADMET Profiling and Pharmacokinetic Evaluation of Selected Compounds
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| KMR | Kernel Machine Regression |
| TCGA | The Cancer Genome Atlas |
| GE | Gene Expression |
| DNA | Deoxyribonucleic Acid |
| miRNA | Micro Ribonucleic Acid |
| DEG | Differential Gene Expression |
| LIMMA | Linear Models for Microarray Data |
| MIRKAT | Microbiome Regression-Based Kernel Association Test |
| CCA | Canonical Correlation Analysis |
| LUSC | Lung Squamous Cell Carcinoma |
| CNV | Copy Number Variation |
| ReML | Restricted Maximum Likelihood |
| PDB | Protein Data Bank |
| PCA | Principal Component Analysis |
| RPKM | Reads Per Kilobase per Million mapped reads |
| SKAT | Sequence Kernel Association Test |
| MCC | Maximal Clique Centrality |
| MNC | Maximum Neighborhood Component |
| EPC | Edge Percolated Component |
| PPI | Protein–Protein Interaction |
References
- Alam, M.A.; Lin, H.Y.; Deng, H.W.; Calhoun, V.D.; Wang, Y.P. A kernel machine method for detecting higher order interactions in multimodal datasets: Application to schizophrenia. J. Neurosci. Methods 2018, 309, 161–174. [Google Scholar] [CrossRef]
- Rappoport, N.; Shamir, R. Multi-omic and multi-view clustering algorithms: Review and cancer benchmark. Nucleic Acids Res. 2018, 46, 10546–10562. [Google Scholar] [CrossRef]
- Goodwin, S.; McPherson, J.D.; McCombie, W.R. Coming of age: Ten years of next-generation sequencing technologies. Nat. Rev. Genet. 2016, 17, 333–351. [Google Scholar] [CrossRef]
- Ozsolak, F.; Milos, P.M. RNA sequencing: Advances, challenges and opportunities. Nat. Rev. Genet. 2011, 12, 87–98. [Google Scholar] [CrossRef]
- Allison, D.; Cui, X.; Page, G.; Sabripour, M. Microarray Data Analysis: From Disarray to Consolidation and Consensus. Nat. Reviews. Genet. 2006, 7, 55–65. [Google Scholar] [CrossRef]
- Yong, W.S.; Hsu, F.M.; Chen, P.Y. Profiling genome-wide DNA methylation. Epigenetics Chromatin 2016, 9, 26. [Google Scholar] [CrossRef]
- Canzler, S.; Schor, J.; Busch, W.; Schubert, K.; Rolle-Kampczyk, U.; Seitz, H.; Kamp, H.; Von Bergen, M.; Buesen, R.; Hackermüller, J. Prospects and challenges of multi-omics data integration in toxicology. Arch. Toxicol. 2020, 94, 371–388. [Google Scholar] [CrossRef]
- Nevedomskaya, E.; Haendler, B. From Omics to Multi-Omics Approaches for In-Depth Analysis of the Molecular Mechanisms of Prostate Cancer. Int. J. Mol. Sci. 2022, 23, 6281. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Zhang, A. Integrate multi-omics data with biological interaction networks using Multi-view Factorization AutoEncoder (MAE). BMC Genom. 2019, 20, 944. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.A.; Qiu, C.; Shen, H.; Wang, Y.P.; deng, H.W. A generalized kernel machine approach to identify higher-order composite effects in multi-view datasets, with application to adolescent brain development and osteoporosis. J. Biomed. Inform. 2021, 120, 103854. [Google Scholar] [CrossRef] [PubMed]
- Duan, R.; Gao, L.; Gao, Y.; Hu, Y.; Xu, H.; Huang, M.; Song, K.; Wang, H.; Dong, Y.; Jiang, C.; et al. Evaluation and comparison of multi-omics data integration methods for cancer subtyping. PLoS Comput. Biol. 2021, 17, e1009224. [Google Scholar] [CrossRef]
- Menyhart, O.; Györffy, B. Multi-omics approaches in cancer research with applications in tumor subtyping, prognosis, and diagnosis. Comput. Struct. Biotechnol. J. 2021, 19, 949–960. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Zhang, C.; Zhou, H.; Ma, J.; Vaishnani, D.K.; Zeng, B.; Yu, J.; Mao, H.; Zheng, J. Multi-Omics and Experimental Validation Reveal Anti-HCC Mechanisms of Tibetan Liuwei Muxiang Pill and Quercetin. Pharmaceuticals 2025, 18, 900. [Google Scholar] [CrossRef]
- Mokou, M.; Lygirou, V.; Angelioudaki, I.; Paschalidis, N.; Stroggilos, R.; Frantzi, M.; Latosinska, A.; Bamias, A.; Hoffmann, M.J.; Mischak, H.; et al. A Novel Pipeline for Drug Repurposing for Bladder Cancer Based on Patients’ Omics Signatures. Cancers 2020, 12, 3519. [Google Scholar] [CrossRef]
- www.cancer.org. American Cancer Society, Key Statistics for Lung Cancer. 2022. Available online: https://www.cancer.org/cancer/lung-cancer/about/key-statistics.html (accessed on 23 September 2025).
- Lemjabbar-Alaoui, H.; Hassan, O.U.; Yang, Y.W.; Buchanan, P. Lung cancer: Biology and treatment options. Biochim. et Biophys. Acta (BBA)-Rev. Cancer 2015, 1856, 189–210. [Google Scholar] [CrossRef] [PubMed]
- Sathyanarayanan, A.; Gupta, R.; Thompson, E.; Nyholt, D.; Bauer, D.; Nagaraj, S. A comparative study of multi-omics integration tools for cancer driver gene identification and tumour subtyping. Briefings Bioinform. 2019, 21, 1920–1936. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, T.; Schölkopf, B.; Smola, A. Kernel methods in machine learning. Ann. Stat. 2007, 36, 1171–1220. [Google Scholar] [CrossRef]
- Baião, A.; Cai, Z.S.; Poulos, R.; Robinson, P.; Reddel, R.; Zhong, Q.; Vinga, S.; Gonçalves, E. A technical review of multi-omics data integration methods: From classical statistical to deep generative approaches. Briefings Bioinform. 2025, 26, bbaf355. [Google Scholar] [CrossRef] [PubMed]
- Briscik, M.; Tazza, G.; Vidacs, L.; Dillies, M.A.; Déjean, S. Supervised multiple kernel learning approaches for multi-omics data integration. BioData Min. 2024, 17, 53. [Google Scholar] [CrossRef] [PubMed]
- Yan, K.K.; Zhao, H.; Pang, H. A comparison of graph- and kernel-based –omics data integration algorithms for classifying complex traits. BMC Bioinform. 2017, 18, 539. [Google Scholar] [CrossRef]
- Yu, S.; Tranchevent, L.C.; De Moor, B.; Moreau, Y. Kernel-Based Data Fusion for Machine Learning-Methods and Applications in Bioinformatics and Text Mining; Springer: Berlin/Heidelberg, Germany, 2011; Volume 345. [Google Scholar] [CrossRef]
- Richfield, O.; Alam, M.A.; Calhoun, V.; Wang, Y.P. Learning Schizophrenia Imaging Genetics Data Via Multiple Kernel Canonical Correlation Analysis. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine, Shenzhen, China, 15–18 December 2016. [Google Scholar] [CrossRef]
- Rupnik, J.; Shawe-Taylor, J. Multi-View Canonical Correlation Analysis. In Proceedings of the Conference on Data Mining and Data Warehouses (SiKDD 2010), Ljubljana, Slovenia, 12 October 2010. [Google Scholar]
- Brandolini, M.; Pétéra, M.; Gaudreau, P.; Comte, B.; Bougeard, S.; Pujos-Guillot, E. Multi-block PLS discriminant analysis for the joint analysis of metabolomic and epidemiological data. Metabolomics 2019, 15, 134. [Google Scholar] [CrossRef]
- Csala, A.; Zwinderman, A.; Hof, M. Multiset sparse partial least squares path modeling for high dimensional omics data analysis. BMC Bioinform. 2020, 21, 9. [Google Scholar] [CrossRef]
- Dugourd, A.; Saez-Rodriguez, J. Footprint-based functional analysis of multiomic data. Curr. Opin. Syst. Biol. 2019, 15, 82–90. [Google Scholar] [CrossRef]
- Liu, D.; Lin, X.; Ghosh, D. Semiparametric Regression of Multidimensional Genetic Pathway Data: Least-Squares Kernel Machines and Linear Mixed Models. Biometrics 2008, 63, 1079–1088. [Google Scholar] [CrossRef]
- Alam, M.A.; Fukumizu, K. Higher-Order Regularized Kernel Canonical Correlation Analysis. Int. J. Pattern Recognit. Artif. Intell. 2015, 29, 150302192043004. [Google Scholar] [CrossRef]
- Cai, Z.S.; Poulos, R.; Liu, J.; Zhong, Q. Machine learning for multi-omics data integration in cancer. iScience 2022, 25, 103798. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.A. Kernel Choice for Unsupervised Kernel Methods. Ph.D. Thesis, The Graduate University of Advanced Studies, Hayama, Japan, 2014. [Google Scholar]
- Kung, S. Kernel Methods and Machine Learning; Cambridge University Press: Singapore, 2014. [Google Scholar] [CrossRef]
- Peng, Q.; Zhao, J.; Fuzhong, X. A gene-based method for detecting gene-gene co-association in a case-control association study. Eur. J. Hum. Genet. 2009, 18, 582–587. [Google Scholar] [CrossRef]
- Alam, M.A.; Komori, O.; deng, H.W.; Calhoun, V.; Wang, Y.P. Robust Kernel Canonical Correlation Analysis to Detect Gene-Gene Co-associations: A Case Study in Genetics. J. Bioinform. Comput. Biol. 2019, 17, 1950028. [Google Scholar] [CrossRef]
- Mariette, J.; Villa-Vialaneix, N. Unsupervised multiple kernel learning for heterogeneous data integration. Bioinformatics 2017, 34, 1009–1015. [Google Scholar] [CrossRef] [PubMed]
- Rattray, N.; Deziel, N.; Wallach, J.; Khan, S.; Vasiliou, V.; Ioannidis, J.; Johnson, C. Beyond genomics: Understanding exposotypes through metabolomics. Hum. Genom. 2018, 12, 4. [Google Scholar] [CrossRef] [PubMed]
- Ge, T.; Nichols, T.E.; Ghosh, D.; Mormino, E.C.; Smoller, J.W.; Sabuncu, M.R. A kernel machine method for detecting effects of interaction between multidimensional variable sets: An imaging genetics application. NeuroImage 2015, 109, 505–514. [Google Scholar] [CrossRef][Green Version]
- Zhao, N.; Zhang, H.; Clark, J.J.; Maity, A.; Wu, M.C. Composite kernel machine regression based on likelihood ratio test for joint testing of genetic and gene-environment interaction effect. Biometrics 2019, 75, 625–637. [Google Scholar] [CrossRef]
- Liu, S.; Bobb, J.; Claus Henn, B.; Gennings, C.; Schnaas, L.; Tellez Rojo Solis, M.M.; Bellinger, D.; Arora, M.; Wright, R.; Coull, B. Bayesian varying coefficient kernel machine regression to assess neurodevelopmental trajectories associated with exposure to complex mixtures. Stat. Med. 2018, 37, 4680–4694. [Google Scholar] [CrossRef]
- Feng, J.; Jiang, L.; Li, S.; Tang, J.; Wen, L. Multi-Omics Data Fusion via a Joint Kernel Learning Model for Cancer Subtype Discovery and Essential Gene Identification. Front. Genet. 2021, 12, 647141. [Google Scholar] [CrossRef] [PubMed]
- TCGA. Multi-Omics Cancer Benchmark TCGA Preprocessed Data. 2021. Available online: http://acgt.cs.tau.ac.il/multi_omic_benchmark/download.html (accessed on 23 September 2025).
- Ritchie, M.; Phipson, B.; Wu, D.; Hu, Y.; Law, C.; Shi, W.; Smyth, G. LIMMA powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015, 43, e47. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Churchill, G. Statistical tests for differential expression in cDNA microarray experiments. Genome Biol. 2003, 4, 210. [Google Scholar] [CrossRef] [PubMed]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. In Breakthroughs in Statistics: Methodology and Distribution; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar] [CrossRef]
- Nazari, H.; Rezaeipanah, A. A Gene Expression Clustering Method to Extraction of Cell-to-Cell Biological Communication. Intel. Artif. 2022, 25, 1–12. [Google Scholar] [CrossRef]
- Hardoon, D.R.; Szedmak, S.; Shawe-Taylor, J. Canonical Correlation Analysis: An Overview with Application to Learning Methods. Neural Comput. 2004, 16, 2639–2664. [Google Scholar] [CrossRef]
- HARVILLE, D.A. Bayesian inference for variance components using only error contrasts. Biometrika 1974, 61, 383–385. [Google Scholar] [CrossRef]
- Wu, M.; Seunggeun, L.; Cai, T.; Li, Y.; Boehnke, M.; Lin, X. Rare-Variant Association Testing for Sequencing Data with the Sequence Kernel Association Test. Am. J. Hum. Genet. 2011, 89, 82–93. [Google Scholar] [CrossRef]
- Berman, H.; Battistuz, T.; Bhat, T.; Bluhm, W.; Bourne, P.; Burkhardt, K.; Feng, Z.; Gilliland, G.; Iype, L.; Jain, S.; et al. The Protein Data Bank. Acta Crystallogr. Sect. D 2002, 58, 899–907. [Google Scholar] [CrossRef]
- Waterhouse, A.; Bertoni, M.; Bienert, S.; Studer, G.; Tauriello, G.; Gumienny, R.; Heer, F.; Beer, T.; Rempfer, C.; Bordoli, L.; et al. SWISS-MODEL: Homology modelling of protein structures and complexes. Nucleic Acids Res. 2018, 46, W296–W303. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem 2019 update: Improved access to chemical data. Nucleic Acids Res. 2018, 47, D1102–D1109. [Google Scholar] [CrossRef] [PubMed]
- Dassault Systèmes. Discovery Studio Visualizer, v21.1.0.20298. 2021. Available online: https://discover.3ds.com/discovery-studio-visualizer-download (accessed on 23 September 2025).
- UCSF Chimera. PDB2PQR Server Documentation. Available online: https://www.cgl.ucsf.edu/chimera/docs/ContributedSoftware/apbs/pdb2pqr.html (accessed on 23 September 2025).
- Hanwell, M.; Curtis, D.; Lonie, D.; Vandermeersch, T.; Zurek, E.; Hutchison, G. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J Chem Inf 4. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Morris, G.; Huey, R.; Lindstrom, W.; Sanner, M.; Belew, R.; Goodsell, D.; Olson, A. AutoDock4 and AutoDockTools4: Automated Docking with Selective Receptor Flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A. Software News and Update AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Reza, M.S.; Qiu, C.; Lin, X.; Su, K.; Liu, A.; Zhang, X.; Gong, Y.; Luo, Z.; Tian, Q.; Nwadiugwu, M.; et al. An Attention-Aware Multi-Task Learning Framework Identifies Candidate Targets for Drug Repurposing in Sarcopenia. J. Cachexia Sarcopenia Muscle 2025, 16, e13661. [Google Scholar] [CrossRef]
- Visualizer, D.S. v4. 0.100. 13345; Accelrys Softw. Inc.: San Diego, CA, USA, 2005. [Google Scholar]
- Pires, D.; Blundell, T.; Ascher, D. pkCSM: Predicting Small-Molecule Pharmacokinetic and Toxicity Properties Using Graph-Based Signatures. J. Med. Chem. 2015, 58, 4066–4072. [Google Scholar] [CrossRef] [PubMed]
- Ashburn, T.; Thor, K. Drug repositioning: Identifying and developing new uses for existing drugs. Nat. Reviews. Drug Discov. 2004, 3, 673–683. [Google Scholar] [CrossRef]
- Afroz, S.; Islam, N.; Habib, M.A.; Reza, M.S.; Alam, M.A. Multi-omics data integration and drug screening of AML cancer using generative adversarial network. Methods 2024, 226, 138–150. [Google Scholar] [CrossRef]
- Rosen, J.; Weiss, J.; Pham, N.A.; Li, Q.; N. Martins-Filho, S.; Wang, Y.; Tsao, M.S.; Moghal, N. Antitumor efficacy of XPO1 inhibitor Selinexor in KRAS-mutant lung adenocarcinoma patient-derived xenografts. Transl. Oncol. 2021, 14, 101179. [Google Scholar] [CrossRef] [PubMed]
- Brazel, D.; Zhang, S.; Nagasaka, M. Spotlight on Tepotinib and Capmatinib for Non-Small Cell Lung Cancer with MET Exon 14 Skipping Mutation. Lung Cancer Targets Ther. 2022, 13, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Alam, M.A.; Calhoun, V.D.; Wang, Y.P. Identifying outliers using multiple kernel canonical correlation analysis with application to imaging genetics. Comput. Stat. Data Anal. 2018, 125, 70–85. [Google Scholar] [CrossRef]
- Alam, M.A.; Fukumizu, K.; Wang, Y.P. Influence function and robust variant of kernel canonical correlation analysis. Neurocomputing 2018, 304, 12–29. [Google Scholar] [CrossRef]

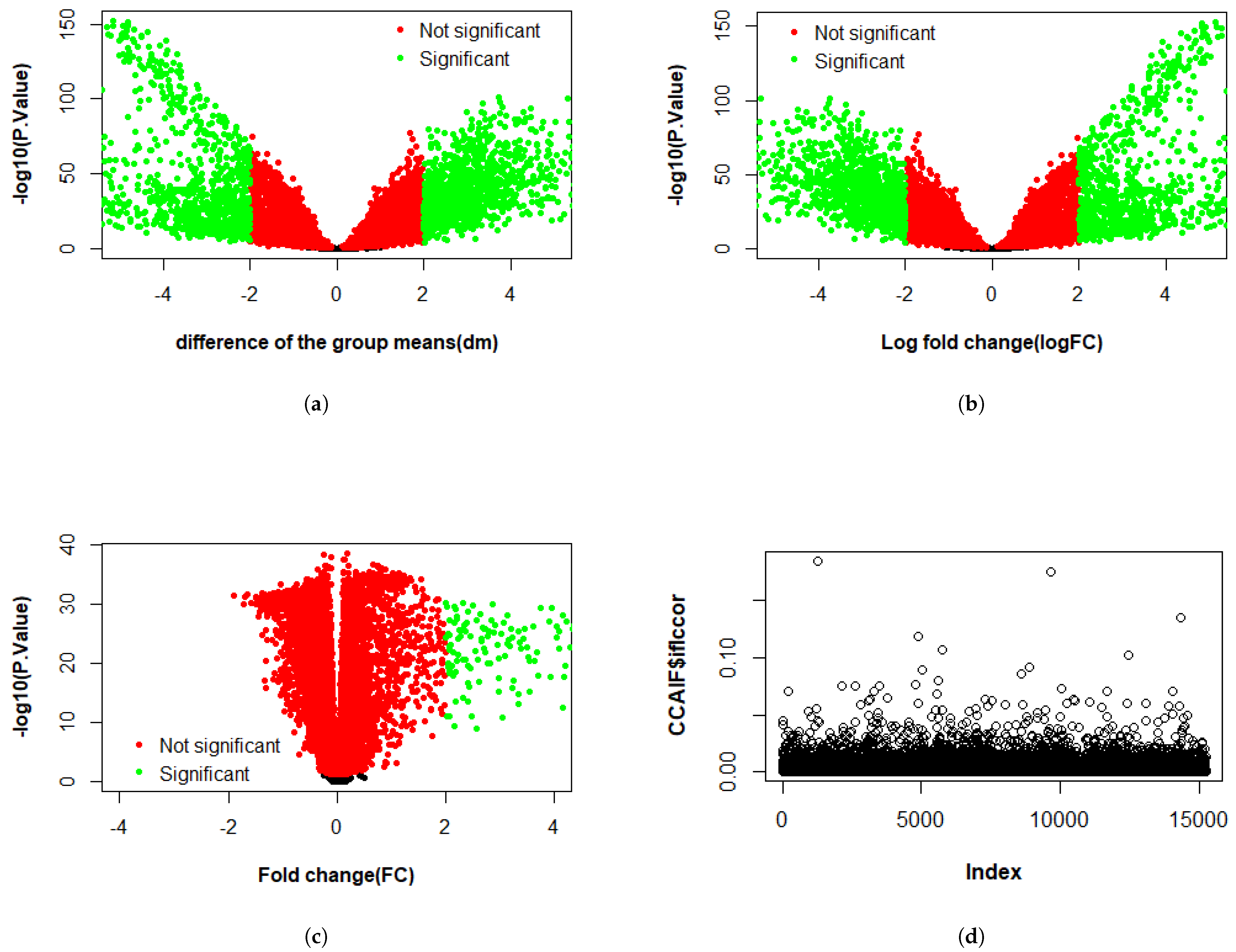
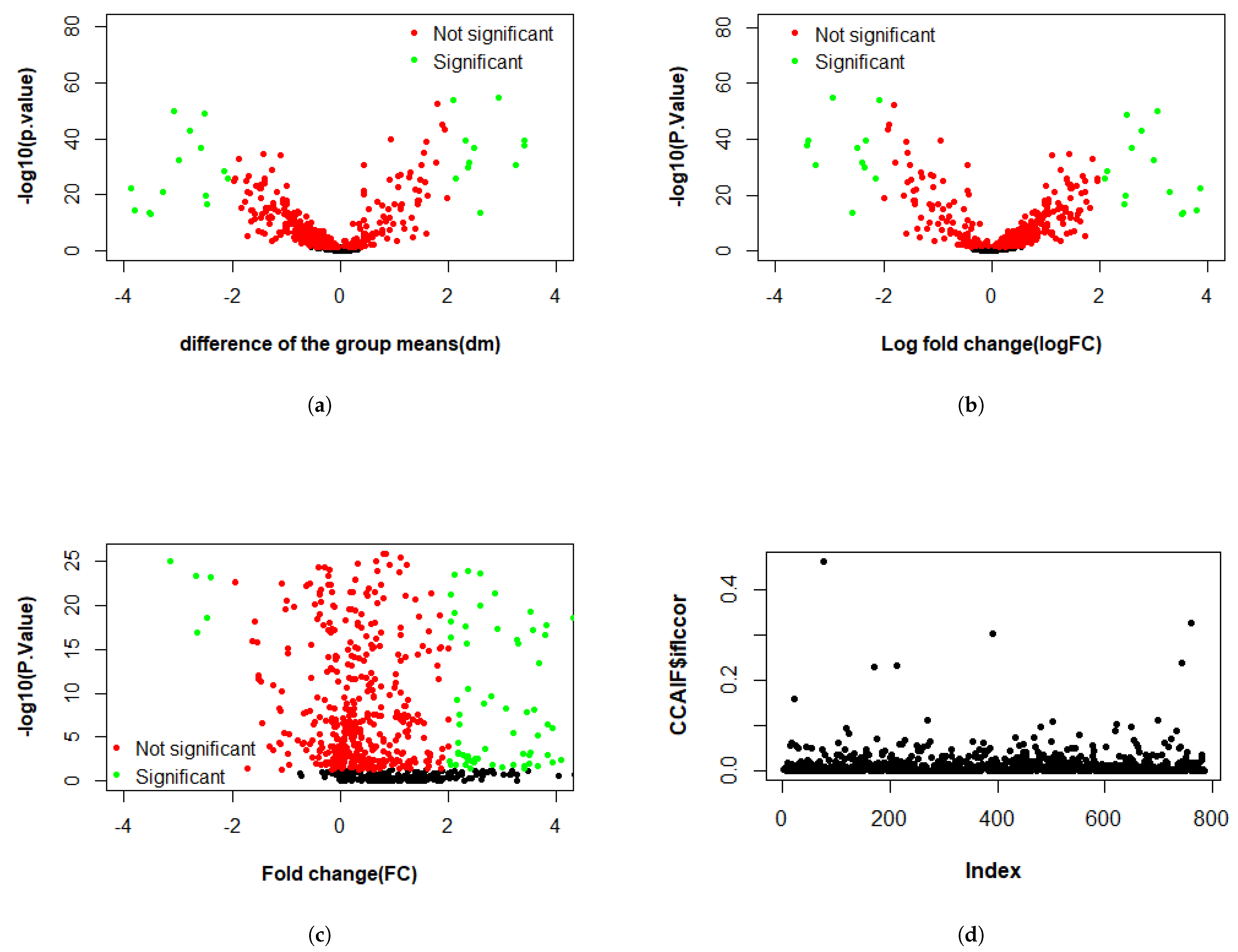
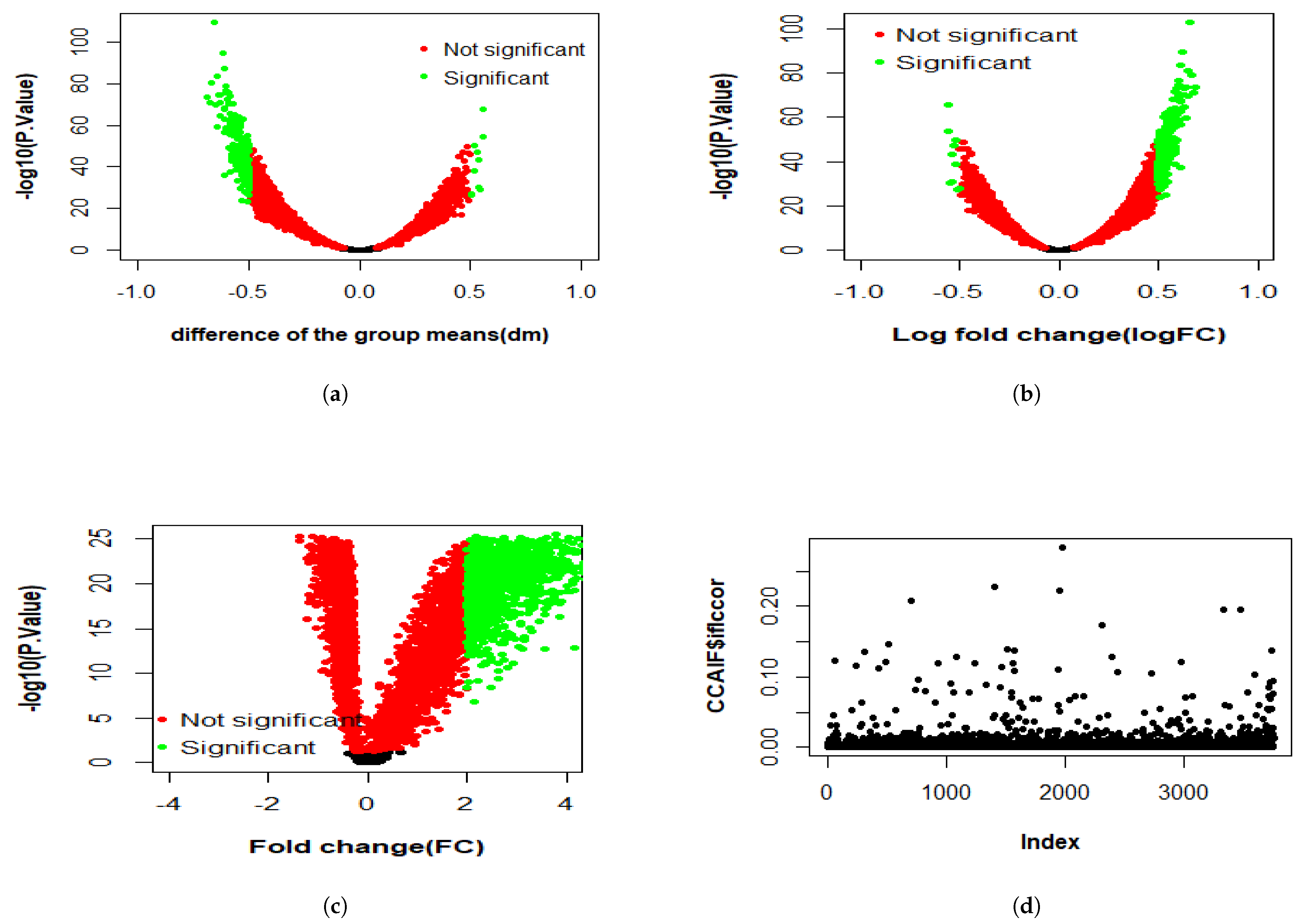

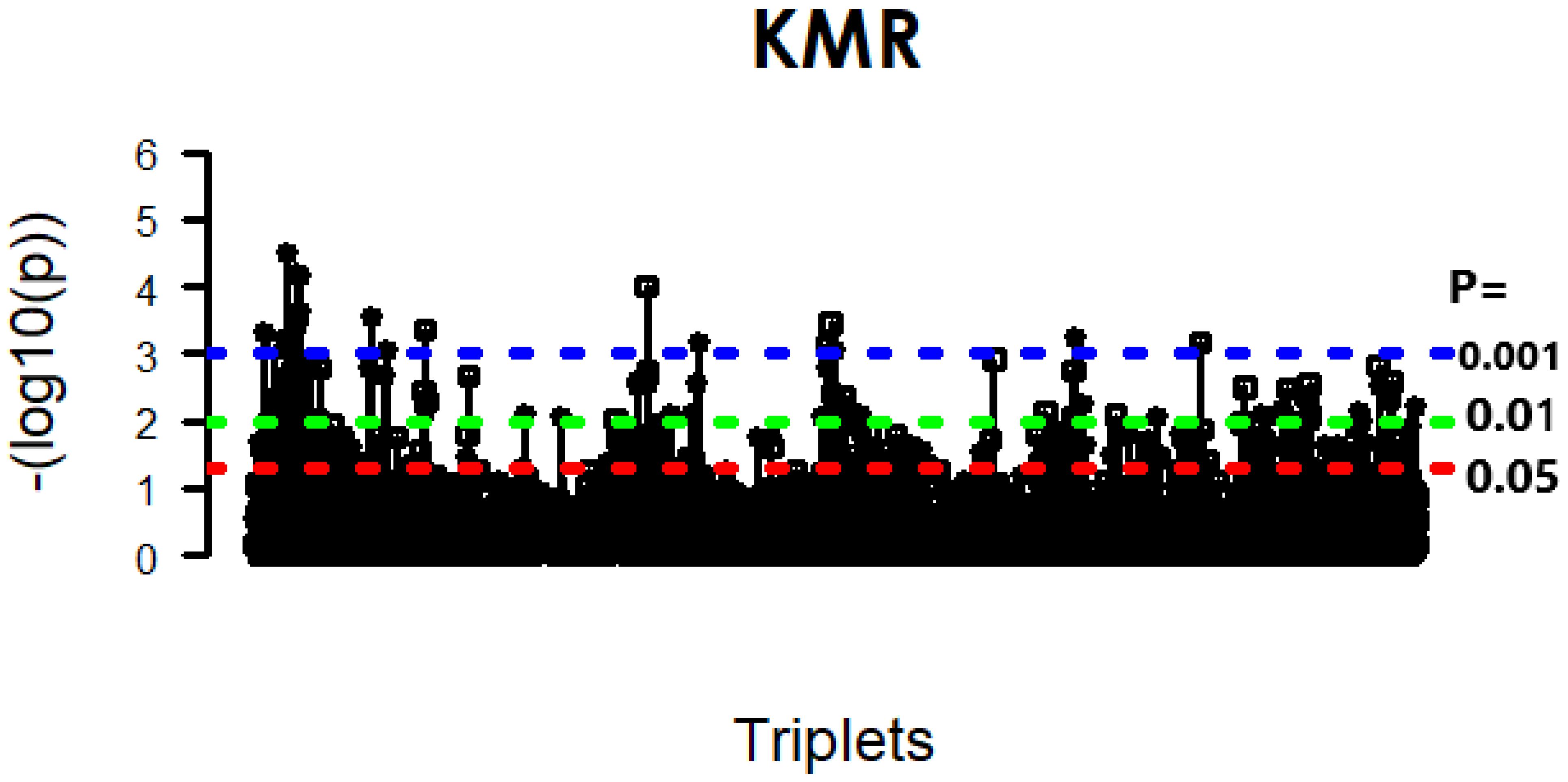
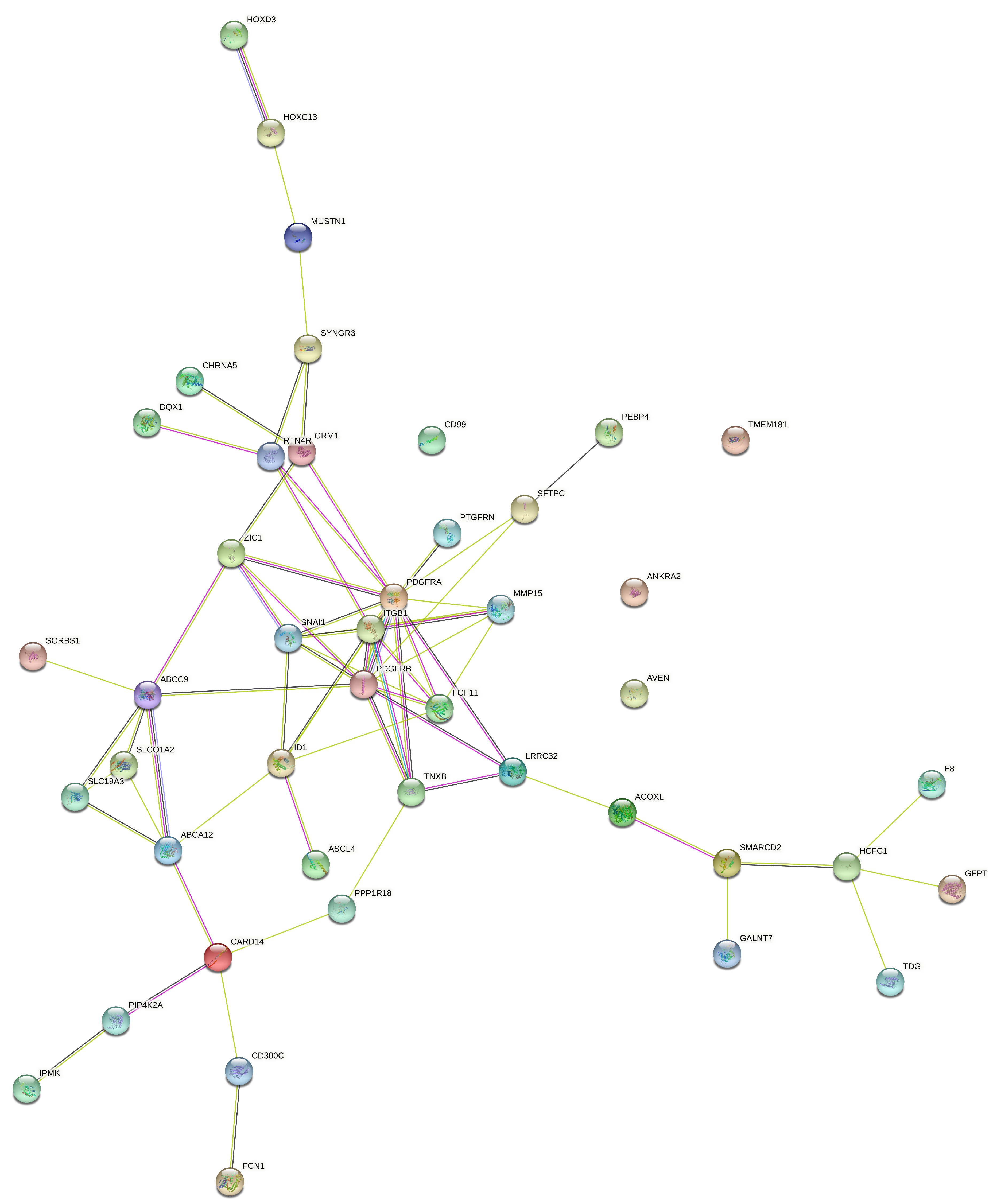


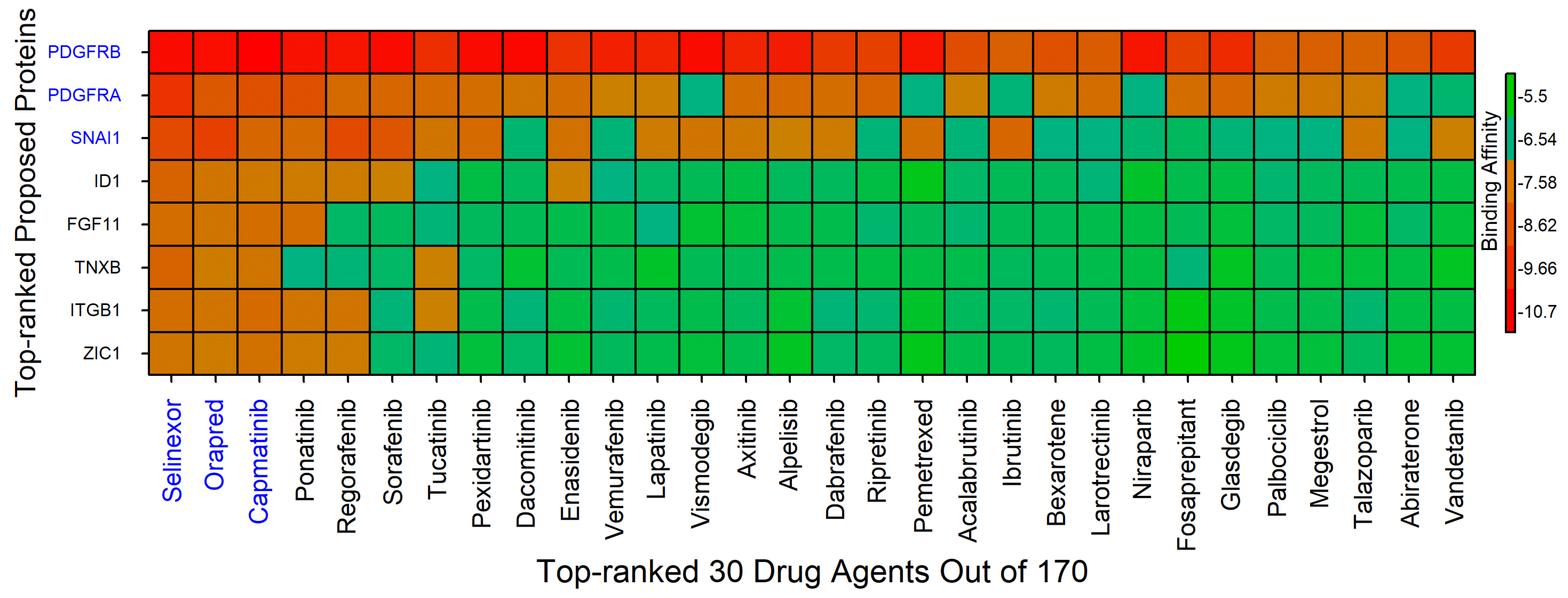
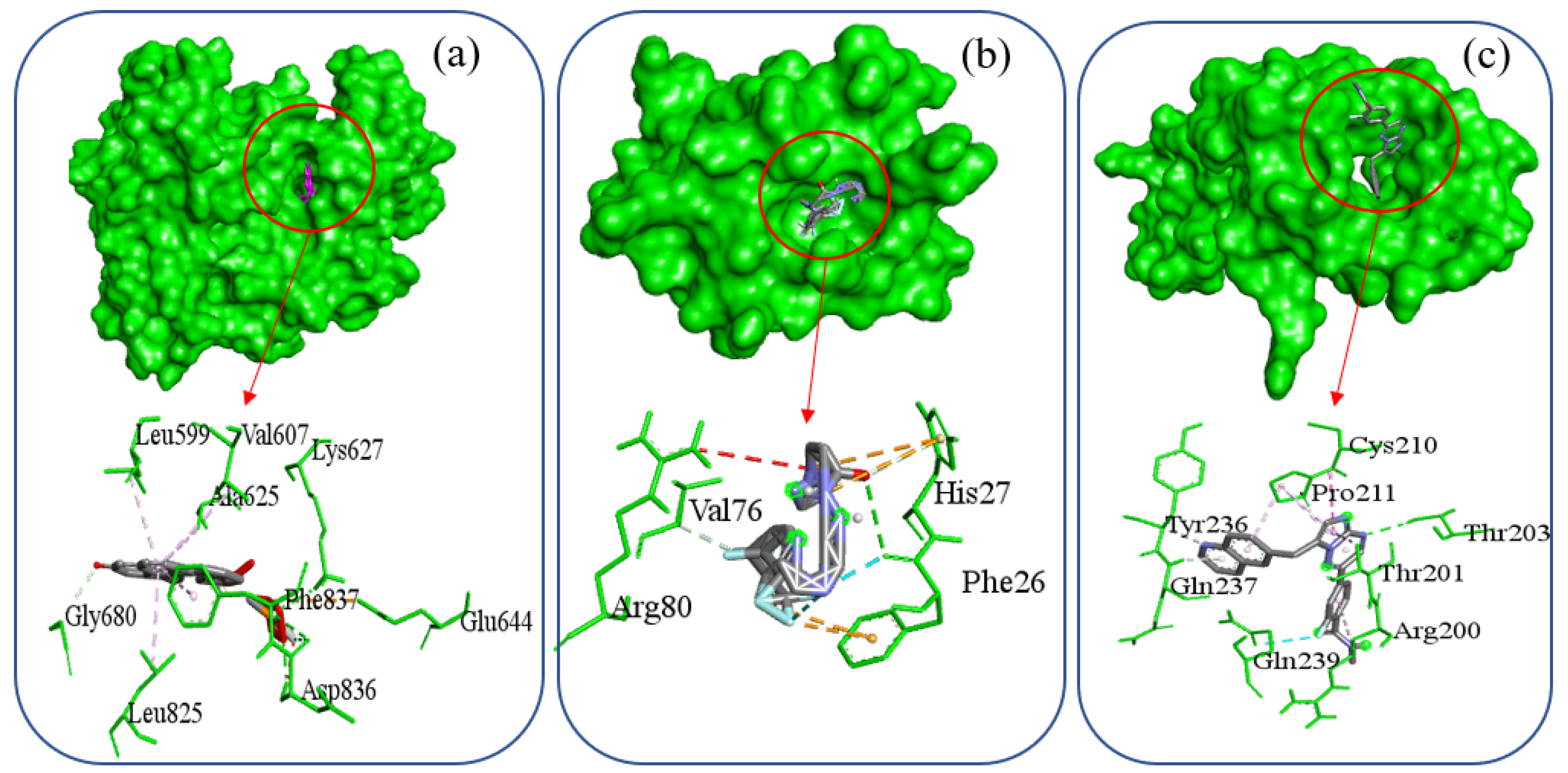
| Error Family | Link Function (g) | Inverse Link Function () | Data Type / Use |
|---|---|---|---|
| Gaussian | Identity, g(y) = y | Normally distributed continuous data, | |
| Gamma | Inverse gamma, g(y) = 1/y | Positive continuous data, | |
| Binomial | logit, g(y) = log | Binary or proportion data, (0 or 1) | |
| Poisson | log, g(y) = log(y) | Exponential, exp(y) | Count data that are equidispersed |
| Gene Expression | miRNA Expression | DNA Methylation | OV | HOC | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ABCA12 | SNAI1 | ABCC9 | 0.9963 | 0.0097 | 1.19 × 10−6 | 0.0071 | 1.28 × 10−7 | 0.0055 | 0.0087 | 0.0100 | 0.4424 | 0.0008 |
| ABCA12 | PDGFRA | ABCC9 | 0.9986 | 0.0100 | 1.01 × 10−6 | 0.0095 | 3.18 × 10−6 | 0.0093 | 0.0101 | 0.0100 | 0.4670 | 0.0047 |
| ABCA12 | PDGFRB | SLCO1A2 | 1.0000 | 0.0100 | 0.0071 | 0.0100 | 3.24 × 10−7 | 0.0100 | 0.0100 | 0.0100 | 0.2948 | 0.0055 |
| F8 | ITGB1 | SLCO1A2 | 1.0000 | 0.0004 | 0.0009 | 0.0012 | 1.66 × 10−8 | 0.0005 | 0.0010 | 0.0100 | 0.1190 | 0.0077 |
| HOXC13 | ITGB1 | ABCC9 | 1.0000 | 6.28 × 10−9 | 3.72 × 10−5 | 0.0009 | 0.0012 | 0.0009 | 0.0008 | 0.0100 | 0.2328 | 0.0057 |
| HOXC13 | MMP15 | SLCO1A2 | 1.0000 | 5.61 × 10−8 | 0.0010 | 0.0010 | 0.0011 | 0.0009 | 0.0010 | 0.0100 | 0.1153 | 0.0068 |
| HOXC13 | SNAI1 | ASCL4 | 1.0000 | 0.0093 | 0.0039 | 1.65 × 10−8 | 0.0102 | 0.0068 | 0.0068 | 0.0100 | 0.3306 | 0.0042 |
| PEBP4 | PTGFRN | SLCO1A2 | 1.0000 | 3.09 × 10−8 | 0.0005 | 0.0009 | 0.0010 | 0.0006 | 0.0010 | 0.0100 | 0.0035 | 0.0084 |
| SFTPC | ID1 | SLCO1A2 | 1.0000 | 0.0001 | 1.59 × 10−6 | 9.31 × 10−5 | 1.07 × 10−6 | 9.85 × 10−5 | 0.0001 | 0.0001 | 0.0671 | 0.0069 |
| p-Value | Gene Expression | miRNA Expression | DNA Methylation |
|---|---|---|---|
| 0.05 | 23 | 28 | 14 |
| 0.01 | 18 | 19 | 10 |
| 0.001 | 9 | 7 | 5 |
| 0.0001 | 2 | 3 | 3 |
| Method | Genome |
|---|---|
| Genes | ABCA12, ACOXL, C18orf56, CARD14, CD300C, CHRNA5, DQX1, F8, FCN1, FGF11, HOXC13, LRRC32, MUSTN1, PEBP4, SFTPC, SLC19A3, SORBS1, TNXB |
| miRNA expression | SNAI1, PDGFRA, PDGFRB, TMEM181, ANKRA2, PPP1R18, CD99, PTGFRN, GALNT7, SYNGR3, SMARCD2, PIP4K2A, ITGB1, AVEN, TDG, MMP15, ID1 |
| DNA methylation | HCFC1, ABCC9, SLCO1A2, ZIC1, PANCR, IPMK, HOXD3, GRM1, ASCL4 |
| Complex Name | Interacting Amino Acid | Hydrogen Bond | Hydrophobic Interaction | Electrostatic Interaction | Halogen Bond |
|---|---|---|---|---|---|
| PDGFRB-Selinexor | Glu644, Lys627, Asp836, Gly680, Leu599, Val607, Ala625, Leu825, Phe837 | Lys627, Asp836, Gly680 | Leu599, Val607, Ala625, Leu825, Phe837 | Glu644 | |
| PDGFRA-Orapred | Phe26, Val76, His27, Arg80 | Phe26, Val76 | His27 | His27, Phe26 | Phe26 |
| SNAI1-Capmatinib | Thr203, Tyr236, Gln239, Gln237, Arg200, Thr201, Cys210, Pro211 | Thr203, Tyr236, Gln237 | Arg200, Thr201, Cys210, Pro211 | Gln239 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.I.; Hossain, M.D.; Rahman, M.M.; Mia, M.S.; Watanobe, Y.; Habib, M.A.; Rashid, M.M.; Reza, M.S.; Alam, M.A. Identifying Multi-Omics Interactions for Lung Cancer Drug Targets Discovery Using Kernel Machine Regression. Appl. Sci. 2025, 15, 11506. https://doi.org/10.3390/app152111506
Ahmed MI, Hossain MD, Rahman MM, Mia MS, Watanobe Y, Habib MA, Rashid MM, Reza MS, Alam MA. Identifying Multi-Omics Interactions for Lung Cancer Drug Targets Discovery Using Kernel Machine Regression. Applied Sciences. 2025; 15(21):11506. https://doi.org/10.3390/app152111506
Chicago/Turabian StyleAhmed, Md. Imtyaz, Md. Delwar Hossain, Md. Mostafizer Rahman, Md. Shahajada Mia, Yutaka Watanobe, Md. Ahsan Habib, Md. Mamunur Rashid, Md. Selim Reza, and Md. Ashad Alam. 2025. "Identifying Multi-Omics Interactions for Lung Cancer Drug Targets Discovery Using Kernel Machine Regression" Applied Sciences 15, no. 21: 11506. https://doi.org/10.3390/app152111506
APA StyleAhmed, M. I., Hossain, M. D., Rahman, M. M., Mia, M. S., Watanobe, Y., Habib, M. A., Rashid, M. M., Reza, M. S., & Alam, M. A. (2025). Identifying Multi-Omics Interactions for Lung Cancer Drug Targets Discovery Using Kernel Machine Regression. Applied Sciences, 15(21), 11506. https://doi.org/10.3390/app152111506






