1. Introduction
During flood season, levees are prone to excessive groundwater seepage pressure, which can result in internal erosion, such as uplifting, heave and piping, weakening the stability of levees, and even causing potential levee failures [
1,
2,
3]. For example, approximately 68% of Yangtze River levees in China suffered from seepage failures during flood seasons ever year [
4]. To prevent the internal erosion of levees, various seepage control measures have been proposed, including seepage walls [
5], relief wells [
6,
7,
8], filter layers, [
9] and upstream clay blankets [
10]. Among these measures, relief wells are an effective seepage control measure to reduce internal water pressure within a levee or dam to prevent seepage damage and structural instability [
11,
12,
13].
Relief wells are strategically constructed near the toe of levee on the downstream side to facilitate the discharge of excessive groundwater through the well system [
14,
15], thereby alleviating internal hydraulic pressures within the levee foundation and protecting the levee from seepage failure. Numerous factors influence the performance of relief wells, such as the well diameter, well spacing, and penetration depth. For example, Li et al. [
16] found that the penetration depth of the well and the permeability of the filter layer have a significant impact on its effectiveness, while the wellhead elevation and the well spacing have certain influences on the performance of relief wells. Salmasi et al. [
17] investigated the effects of well spacing and well diameter on uplift pressure in earthen dams. However, Chen et al. [
18] found that the top elevation of the riser pipes exhibits more influence on well discharge rates than well screen permeability, where the PIVL case study shows that the well discharge rate is 17 times more sensitive to the top elevation of the riser pipe than to the skin factor of the well. Currently, relief well designs mainly focus on conventional parameters such as well depth, well diameter, and well spacing. The design of the wellhead elevation and its impact on the performance of relief wells remain unclear. The wellhead elevation critically affects the maximum achievable reduction in confined hydraulic heads, which should also be considered in the design specifications. Moreover, the design parameters of relief wells are traditionally determined by engineering experience or trial-and-error adjustments. Although the empirical methods are widely used to provide a tangible basis for design in similar conditions for its simplicity, they generally lack rigorous analytical or numerical modeling, which may fail to accurately predict the hydraulic performance of levee and potentially lead to unreasonable designs (i.e., overly conservative or insufficient designs) [
19]. Therefore, determining the design parameters of relief wells by reasonably taking both the levee safety and economic cost into consideration still remains a challenging task.
Recently, Chen et al. [
18] applied non-dominated sorting genetic algorithm-II (NSGA-II) to optimize the pumping operations of relief wells by maximizing the safety factor of levee while minimizing pumping rates and the number of pumping wells. The determination of design parameters of relief wells can also be formulated as a multi-objective optimization problem to find a set of Pareto optimal solutions that can balance the levee safety and economic cost. Among the numerous solution methods, NSGA-II is a powerful decision space exploration engine based on Genetic Algorithm (GA) for solving multi-objective optimization problems [
20,
21,
22]. The core of NSGA-II is to employ the non-dominated sorting, crowding distance, and elitist strategies to find a well-distributed set of Pareto optimal solutions, which has been widely used in the hydrology field [
23,
24]. To address the complex and uncertain multi-objective decision-making problems, the Evolutionary Bayesian Networks (EBNs) are also proposed to explicitly depict the dependencies among decision variables by learning from parent individuals and constructing a probabilistic graph model to generate new high-quality solutions [
25,
26]. However, multi-objective optimization methods have not been reported in the calibration of design parameters of relief wells. Additionally, optimization design of relief wells usually involves extensive computational effort to perform groundwater numerical simulations to derive reliable estimates of hydraulic characteristics (i.e., hydraulic gradient) of levees. As an alternative, Chen et al. [
18] applied the first-order Taylor series expansion to approximately calculate the groundwater head at relief well sites to estimate the seepage safety factor by simplifying the complex nonlinear groundwater flow equation into a linear function with only the first derivative. However, the groundwater seepage is typically complicated with nonlinear implicit functions. Linear simplifications cannot accurately capture the seepage field of the levee foundation, leading to inaccurate calculation of seepage safety factor. In recent years, machine learning has been a data-driven process that can identify the nonlinear relationships between inputs and outputs, enabling them to make accurate predictions or classifications when presented with new data [
27,
28], which has been successfully applied to develop intelligent surrogate models in groundwater simulation [
29,
30], flood forecasting [
31,
32,
33,
34], hydrological modeling [
35,
36,
37], and geotechnical engineering [
38]. For example, artificial neural networks (ANNs), support vector regression (SVR), deep learning (DL), ensemble learning (EN), and hybrid-modeling (HM) are used in groundwater management and hydrology [
36]. Among these machine learning algorithms, ensemble learning methods based on tree models, such as random forest (RF), have the advantages of high accuracy, the ability to handle nonlinear relationships, and lenient requirements for data distribution assumptions, showing good performance in hydrological forecasting [
39,
40] and water quality prediction [
41]. Meanwhile, RF has an inherent capability to quantify the importance of input parameters. The feature importance directly identifies which design parameters (e.g., well diameter, well spacing, and penetration depth) exert the most significant influence on the hydraulic characteristics (i.e., hydraulic gradient) of levees, which is critically valuable for engineers and decision-makers to find the key factors controlling the effectiveness of a relief well system. However, the application of RF in the optimization design of relief wells for levee safety is still relatively limited and requires further exploration.
To this end, this paper proposes a random forest-based multi-objective optimization method for determining the design parameters (i.e., wellhead elevation and number of wells) of relief wells within levees. MODFLOW is used to develop a three-dimensional transient seepage numerical model of levee with relief wells. The design parameters of relief wells are optimized by minimizing the safety factor deficit to a defined threshold and minimizing the economic cost. Then, the non-dominated sorting genetic algorithm-II (NSGA-II) is used to obtain the optimal design of relief wells. To remove the computational burden of repetitive three-dimensional MODFLOW simulations in the multi-objective optimization, RF is used to establish an intelligent surrogate model for evaluating the hydraulic characteristic (i.e., hydraulic gradient) of levees with relief wells instead of numerous numerical simulations. The final optimal design parameters among alternative Pareto solutions are determined by entropy weight and the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS). Finally, the proposed approaches are illustrated using relief wells in Wuhan Yangtze River Levee, China.
2. Seepage Stability Factor of Safety for Levees
Optimization design of relief wells is to ensure that the safety of the levee meets the predefined standards, while minimizing the economic cost. The seepage stability factor of safety is a critical index for evaluating the stability of levees, which is defined as the ratio of the critical hydraulic gradient to the actual hydraulic gradient:
where
icr represents the critical hydraulic gradient;
i is the actual upward hydraulic gradient. Generally, the critical hydraulic gradient
icr can be given as
where
γsat is the saturated unit weight of the soil;
γw is the unit weight of water. The hydraulic gradient
i is a fundamental concept in hydrogeology and fluid mechanics, representing the rate of change in hydraulic head with distance along a specific flow path and the driving force of groundwater movement. Mathematically, it is defined as
where Δ
h is the head difference between the upstream and the downstream along a specific flow path;
L is the length of seepage path. The hydraulic gradient
i can be derived from the MODFLOW in Groundwater Modeling System (GMS) by performing three-dimensional transient flow simulation.
3. Methodology
3.1. RF-Based Surrogate Model for Evaluating the Hydraulic Gradient of Levees with Relief Wells
The numerical simulation to estimate the hydraulic gradient
i usually involves complex numerical calculation of seepage field. To reduce the computational burden of MODFLOW simulations, this study applies RF algorithm to establish an intelligent surrogate model for evaluating the hydraulic characteristic (i.e., hydraulic gradient) of levees with relief wells. Generally, a large number of random samples are needed to perform repeated simulations to establish an intelligent surrogate model. The training samples for developing a valid surrogate model must capture the overall design space of input parameters. In this study, Latin hypercube sampling (LHS) is applied to generate training and testing samples for the construction and validation of a surrogate model [
42], which can generate samples uniformly distributed within the design space, avoiding repeated runs and reducing the number of simulations.
RF algorithm is a robust ensemble learning method extensively used for classification and regression [
43,
44]. It uses the bootstrap aggregation of multiple regression trees to reduce the risk of overfitting, and it combines the predictions from many trees to produce more accurate predictions. In bootstrap aggregation, multiple subsets of the training dataset are generated by random sampling with replacement. Each subset is used to train a different decision tree. Two-thirds of the training samples are used to develop the regression function. The remaining one-third of training samples constitutes the out-of-bag (OOB) sample for performance evaluation [
45]. This built-in validation effectively eliminates the need for additional cross-validation for RF. All the regression trees in the forest are grown without pruning and the growing algorithm is CART regression trees. A comprehensive prediction can be obtained by averaging the predictions of all the trees to produce a final output. Mathematically, for a given input
x, the prediction
y’ is given by:
where
NRF is the number of trees in the forest;
gi(
x) is the prediction from the
i-th tree. This ensemble method reduces variance and improves model predictability by combining the strengths of multiple uncorrelated trees. Within RF algorithm, two primary hyperparameters, namely the number of decision trees and the maximum number of features considered for splitting at each node significantly influence the overall performance and efficiency of RF model, which can be rationally determined by grid search or random search [
46].
To verify the prediction accuracy of the RF surrogate model, two performance metrics, i.e., Root Mean Squared Error (
RMSE) and the coefficient of determination (
R2) are used.
R2 is a statistical metric used to assess the goodness of fit of a predictive model. It reflects the proportion of the variance between the predicted dependent variable and the measured value, which is given by:
where
N is the number of the data;
y represents the calculated hydraulic gradient by the MODFLOW numerical simulation;
y’ is the predicted hydraulic gradient by RF surrogate model; and
is the mean value of the calculated hydraulic gradient by the numerical simulation. A higher
R2 value indicates a better fitness of the model.
RMSE quantifies the average discrepancy between the calculated and the predicted values of hydraulic gradient, which is calculated as
3.2. Optimization Design of Relief Wells Using NSGA-II
To ensure the safety of levee, an economical and effective strategy for relief well design is to meet the required safety factor while minimizing the economic cost. Then, this can be formulated into a two-objective optimization problem. Assuming the threshold of safety factor of the levee is denoted as
FSt, the primary objective is to make the safety factor exceed the specified threshold
FSt. Therefore, the first objective function is to minimize the difference between the levee safety factor and the specified threshold, which can be written as
where
is the deficit of
FS;
FS is the safety factor at the most dangerous location of the levee.
The second objective function is to minimize the economic cost. For simplicity, only the wellhead elevation and the number of wells is taken as the design parameters needed to be determined. Other design parameters of relief wells, such as well diameter and penetration depth, can also be incorporated into the proposed approaches to develop a multi-objective optimization problem. It does not affect the method itself. Assuming that the unit depth-dependent drilling cost of a relief well is 0.2 × 10
4 CNY per meter, and the installation cost for each relief well is 10 × 10
4 CNY, respectively, then, the corresponding second objective function is as follows:
where
c1 = 0.2 × 10
4 CNY/m, representing the unit drilling cost of relief well;
c2 = 10 × 10
4 CNY/well, denoting the construction cost for each relief well;
H0 is the elevation of ground surface at the site of relief wells;
Lr is the length of relief wells;
n is the number of relief wells; and
H is the wellhead elevation. The wellhead elevation and number of relief wells are bounded by their upper bounds and lower bounds, which can be written as
in which
Hmin and
Hmax are the minimum and maximum value of
H, respectively, and
nmin and
nmax are the minimum and maximum value of
n, respectively.
It should be noted that the optimization of relief well design involves FS calculation for a set of given design parameters, i.e., the wellhead elevation H and number of relief wells n. This can be formulated in a groundwater model to obtain the hydraulic gradient i with respect to the given design parameter to calculate the FS by Equation (1). However, the numerical simulation involves a large number of repetitive groundwater three-dimensional transient seepage simulations, resulting in significant computational burden. To bypass this problem, an RF-based surrogate model is applied in this study to approximately estimate the hydraulic gradient for levee seepage stability.
To find the optimal design parameters of relief wells (i.e., the wellhead elevation
H and number of relief wells
n), NSGA-II is employed to find a set of optimal solutions that balance the trade-offs between the two conflicting objectives in Equations (7) and (8). NSGA-II is an evolutionary algorithm that utilizes fast non-dominated sorting to rank solutions and crowding distance to maintain diversity within the Pareto front [
20]. Through iterative selection, crossover, mutation, and elitism, NSGA-II effectively converges towards a set of Pareto optimal solutions that balance competing objectives. Initially, a parent population of
H and
n is randomly generated from their ranges. For each (
H,
n), the hydraulic gradient
i of levee is calculated by the established RF surrogate model. Then, the algorithm evaluates each solution based on its performance across the two objectives, i.e., Equations (7) and (8). Using non-dominated sorting, solutions are ranked into Pareto fronts, with crowding distance ensuring diversity among the solutions. Through repeated iterations of selection, crossover, mutation, and elitism preservation, a child population of (
H,
n) is generated, evolving towards a well-distributed Pareto optimal front. This front provides decision-makers with a range of optimal trade-offs between the minimal
FS deficit and minimal economic cost.
3.3. Selection of the Final Optimal Design Parameters of Relief Wells Using Entropy Weight Method and TOPSIS
The NSGA-II algorithm generates a set of Pareto optimal solutions for relief well design. To objectively determine the final optimal design parameters of relief wells among Pareto solutions, the entropy weight and TOPSIS method is applied. The entropy method is used to objectively determine the weight of each indicator, avoiding biases caused by subjective weighting, while TOPSIS is applied to rank the alternatives, providing more reasonable decision results. The entropy weight method determines the weights of each indicator based on the concept of information entropy [
47,
48]. Indicators with higher entropy values contribute to more information, and should be assigned to greater weights. Conversely, indicators with lower entropy values are assigned to smaller weights. Consider m set of Pareto optimal solutions for the two objective functions, which is denoted as an initial matrix
β of evaluation indicators:
where
βi1 and
βi2 are the original values of the two objective functions in Equations (7) and (8) for alternative
i, respectively;
m is the number of alternative Pareto optimal solutions. Since different indicators may have different units or dimensions, the evaluation indicators are normalized as follows:
where
(
j = 1 and 2) are the normalized values of
βi1 and
βi2, respectively; max(▪) and min(▪) are the maximum and minimum of the evaluation indicators, respectively. Then, the entropy value
Ej (
j = 1 and 2) for each evaluation indicator is given as
where
is a constant;
. The weight for each objective is written as
Once the weights for each objective are determined using entropy weight method, TOPSIS method is subsequently applied to rank the alternative Pareto optimal solutions [
49]. TOPSIS was proposed by Hwang and Yoon [
50] to enable policy-makers to determine the positive ideal solution (
A+) and negative ideal solution (
A−). It is based upon the assumption that the chosen alternative should have the shortest distance from the positive ideal solution and the farthest from the negative ideal solution. Firstly, a weighted normalized decision matrix
vij is constructed by multiplying each element of the normalized matrix
and its corresponding weight:
Then, the positive ideal solution (
A+) and negative ideal solution (
A−) are determined as
The distance to the positive ideal and negative ideal solutions are calculated as
The coefficient of closeness is determined for every alternative:
An alternative is closer to A+ and farther from A− as Bi approaches 1. Based on closeness coefficient Bi, the Pareto solution with the highest value of Bi is finally selected from a set of feasible alternatives as the final optimal solution. Although TOPSIS effectively incorporates decision-maker preferences and demonstrates high practical acceptability, it faces limitations in resolving subjective weighting issues. Therefore, this study integrates TOPSIS with the entropy weight method to determine and identify the optimal design parameters of relief wells.
4. Implementation Procedure
The implementation procedures are divided into three parts: construction of RF intelligent surrogate model for evaluating the hydraulic gradient of levees with relief wells, multi-objective optimization design of relief wells using NSGA-II, and selection of the final optimal design parameters of relief wells using entropy weight method and TOPSIS, which are summarized as follows:
- (1)
Construction of RF intelligent surrogate model for evaluating the hydraulic gradient of levees with relief wells: (I) Generate Ntr training samples and Nte testing samples of design parameters of relief wells (including the wellhead elevation H and the number of wells n) using LHS. (II) Insert Ntr training samples of input parameters into the MODFLOW numerical model to calculate the corresponding values of hydraulic gradient at the most dangerous section of levee with relief wells. (III) Develop the RF model for calculating the hydraulic gradient using Ntr samples of design parameters as inputs and corresponding values of hydraulic gradient as outputs. (IV) Validate the RF model using Nte testing samples.
- (2)
Multi-objective optimization design of relief wells using NSGA-II: (I) Randomly generate a parent population of H and n from their ranges and calculate the hydraulic gradient at the most dangerous section by the established RF surrogate model. (II) Establish the objective functions, i.e., Equations (7) and (8). (III) Rank the solutions into Pareto fronts using non-dominated sorting and crowding distance. (IV) Generate a child population of (H, n) through repeated iterations of selection, crossover, mutation, and elitism preservation to evolve toward a well-distributed Pareto optimal front.
- (3)
Selection of the final optimal design parameters of relief wells using entropy weight method and TOPSIS: (I) Calculate the weights of each indicator (i.e., objective function) based on the concept of information entropy. (II) Rank the alternative Pareto optimal solutions using TOPSIS method. (III) Select the final optimal design parameters with the minimal FS deficit and minimal economic cost.
The aforementioned procedures can be implemented by MATLAB codes. Then, the user functions can be used as a “black box” for hydraulic practitioners to select the cost-effective optimal design scheme of relief wells for levee safety. They need to provide a project-specific geological profile of levee with relief wells, statistic characteristics of geotechnical properties, information about hydraulic boundary condition, candidate design parameters of relief wells, and the ranges of design parameters as input. The user functions return the optimal design scheme of relief wells as output. The proposed method is illustrated through the design of relief wells in the Wuhan Yangtze River levee, China.
5. Illustrative Example
5.1. Study Area
The studied Yangtze River levee is located in the south area of Wuhan, China, which is a key component of Wuhan’s Yangtze River flood control system. The top elevation of the levee ranges between 30.50 m and 31.53 m. Geotechnical investigations indicated that the ground elevations range from 21.40 m to 25.50 m. The foundation of the Wuhan Yangtze River levee mostly consists of binary or multiple-layer structures, with a thin impermeable in the upper layer and a thick permeable in the lower layer. The upper part of the levee foundation in the study area consists mainly of clayed soil, with a permeability coefficient ranging from 5.1 × 10
−7 m/s to 1.0 × 10
−6 m/s, exhibiting slightly to weakly permeable characteristics. The middle section is predominantly sandy soil, with a permeability coefficient ranging from 1.0 × 10
−5 to 6.00 × 10
−4 m/s, showing moderately to strongly permeable properties. The lower part is primarily composed of old clay soil, with a permeability coefficient ranging from 8.5 × 10
−9 to 1.0 × 10
−8 m/s. The permeability coefficients of soil layers are summarized in
Table 1. For simplification, the permeability is assumed as isotropic for each layer. It can be seen that the geological conditions of the levee is a typical dual-layer foundation. During the flood season, when the water level of the Yangtze River rises sharply, the levee is prone to seepage failure under high groundwater pressure, such as piping and sand boiling.
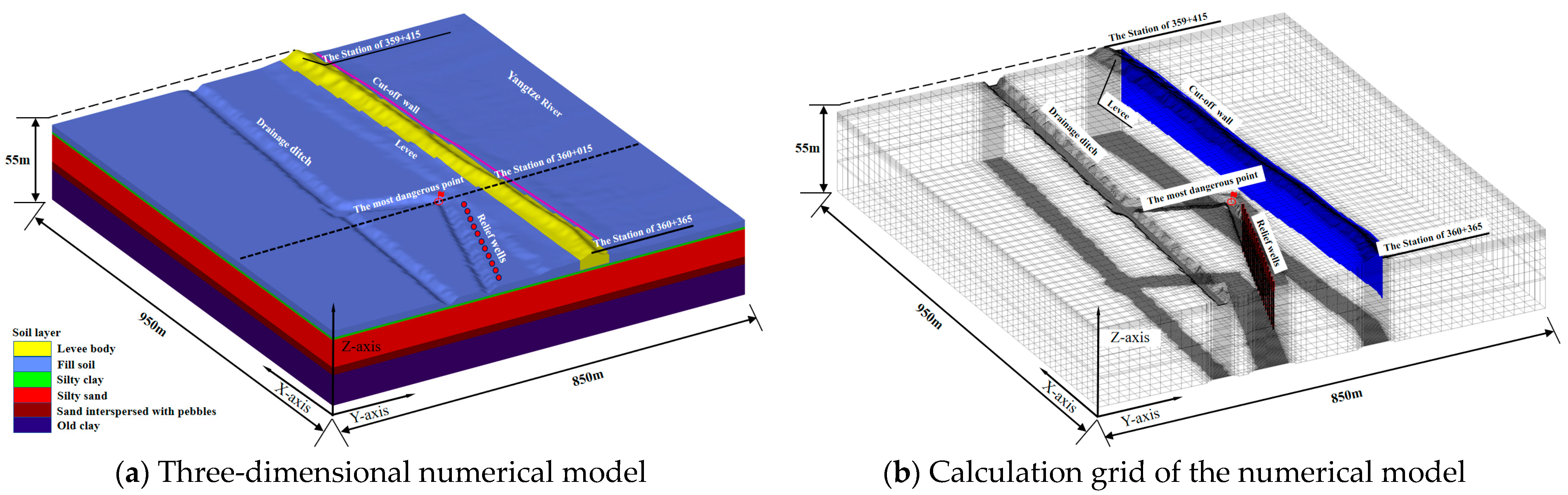
To protect the safety of the levee, a preliminary mitigation measure involves constructing two sections of fully enclosed concrete cut-off walls on the riverside and relief wells between the gap of the cut-off walls on the downstream (see
Figure 1a). The sections of Chainage 358 + 315 to 360 + 315 and Chainage 360 + 515 to 362 + 515 have been designed with fully enclosed concrete cut-off walls, respectively. Each section has a continuous length of 2 km, and the total length of cut-off walls is 4 km. There is a 200 m gap between these two sections of cut-off walls (i.e., Chainage 360 + 315 to 360 + 515). To prevent potential seepage bypassing this discontinuity of walls (i.e., Chainage 360 + 315 to 360 + 515), a complementary seepage control measure is proposed to install relief wells along the drainage ditches of the levee. The design parameters of relief wells, i.e., wellhead elevation and number of wells, are set as 20.5 m and 20, respectively, by the engineering experience. In order to obtain the design parameters objectively and intelligently, the proposed approaches are used to determine the optimal wellhead elevation
H and the number of wells
n. The threshold of safety factor
FSt for the levee is taken as 2.0 in this study.
5.2. Three-Dimensional Seepage Modeling
To evaluate the safety factor of the Wuhan Yangtze River levee in the study area, a three-dimensional transient seepage numerical model is firstly established by MODFLOW [
51,
52] using the geological profiles of levee with relief wells. The simulated area is 950 m × 850 m, as shown in
Figure 1a. The top elevation and the width of the levee is 30 m and 9 m, respectively. The slope ratio of the upstream and downstream sides of the levee is about 1:3.3. The bottom elevation of the model is −25 m. The strata from top to bottom are as follows: fill soil of the levee body with a thickness of approximately 6 m, artificial fill soil with a thickness of 4.5 m; 1.5 m thick silty clay, 18 m thick sand, 5 m thick medium and coarse sand interspersed with pebbles, 20 m thick old clay soil. The cut-off wall is set 5 m away from the toe of the levee on the riverside, with a thickness of 0.6 m and a penetration depth of 1 m into the underlying old clay layer. Relief wells are arranged along the drainage ditch, with a constant well diameter of 0.4 m, and a depth of 30 m. In this paper, only the wellhead elevation
H and the number of wells
n are unknown design parameters which are determined by the proposed approaches. The ranges of the wellhead elevation
H and the number of wells
n are set as [19.0, 22.5] m and [
1,
40], respectively.
The horizontal flow barrier (HFB) in MODFLOW-USG is used to simulate the cut-off walls [
51]. The connected linear network (CLN) and the drainage module (DRN) is employed to simulate the relief wells within the study area [
18]. The numerical model is meshed using a hexahedral partitioning method. Each mesh size was set at 10 m. To ensure the calculation accuracy of the model, the mesh sizes at the toe of the levee and drainage ditches were refined to 3 m and 1 m, respectively. The total number of simulation grids is 1,207,472 (see
Figure 1b). For the hydraulic boundary, a design flood level of 29 m is considered on the riverside, while a constant head of 20.5 m of drainage ditch is applied on the downstream of the levee. The boundary conditions of relief wells are taken as the wellhead elevation.
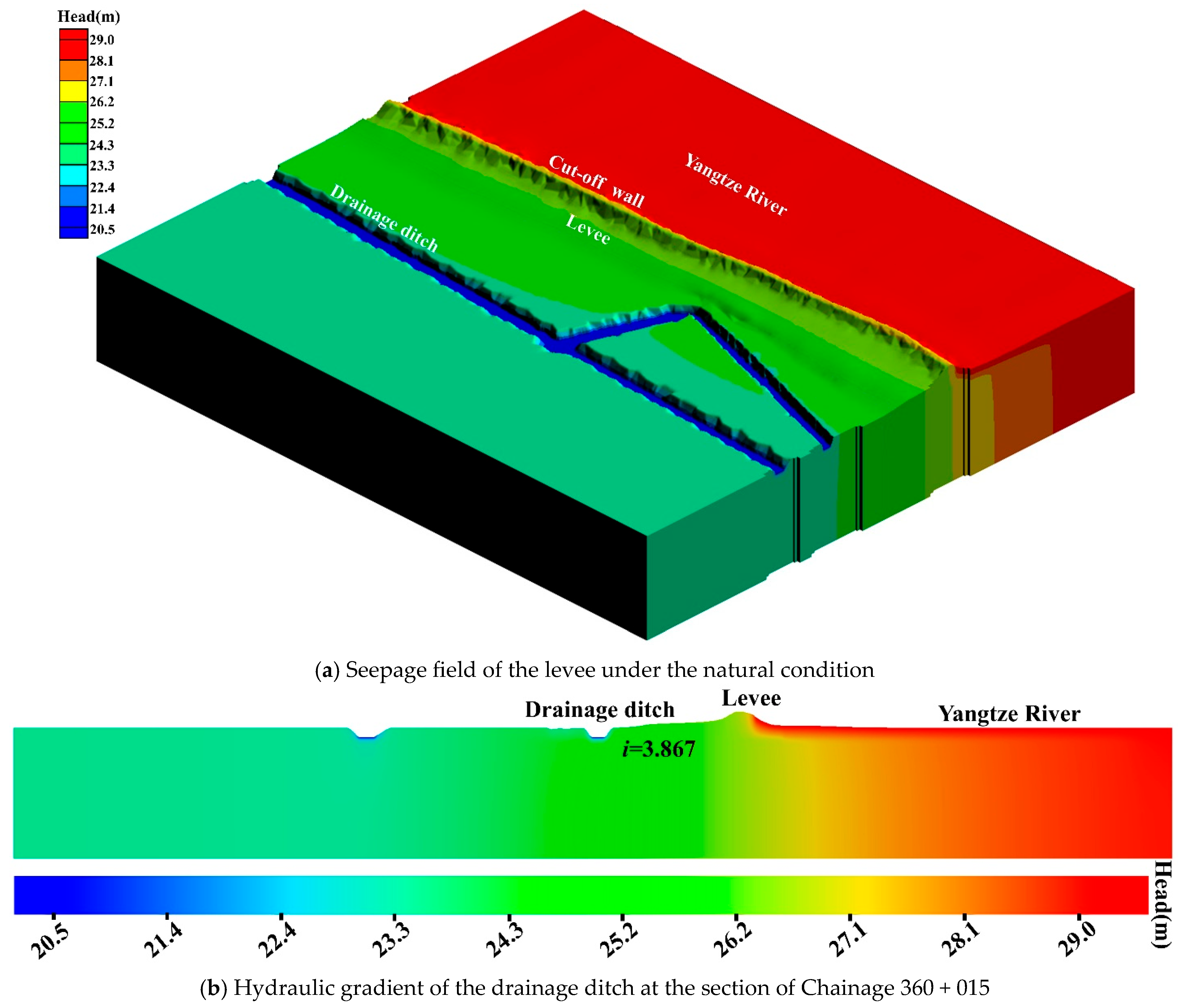
Figure 2a shows the seepage field of the levee under the natural condition. It can be seen that the maximum hydraulic gradient is 3.867 found at the drainage ditch (i.e., Chainage 360 + 015), which is closest to the toe of the levee (see
Figure 2b). Obviously, the hydraulic gradient at the drainage ditch (i.e., Chainage 360 + 015) is larger than the critical hydraulic gradient of fill soil (i.e., 0.3), indicating the potential seepage failure. Thus, this section is considered as the most dangerous point and selected to analyze the safety of the levee.
5.3. Pareto Solutions of Levee Relief Well Pumping Strategy
As indicated by Equations (1)–(3), the hydraulic gradient obtained from three-dimensional numerical simulation are necessary inputs for calculating
FS of the levee. To reduce computational cost, the underlying relationship between the design parameters (i.e., the wellhead elevation and the number of wells) and hydraulic gradient
i is established by the RF algorithm. In this study, LHS is applied to generate 1400 training samples of design parameters within their ranges for developing a training model and 100 independent testing samples for validation.
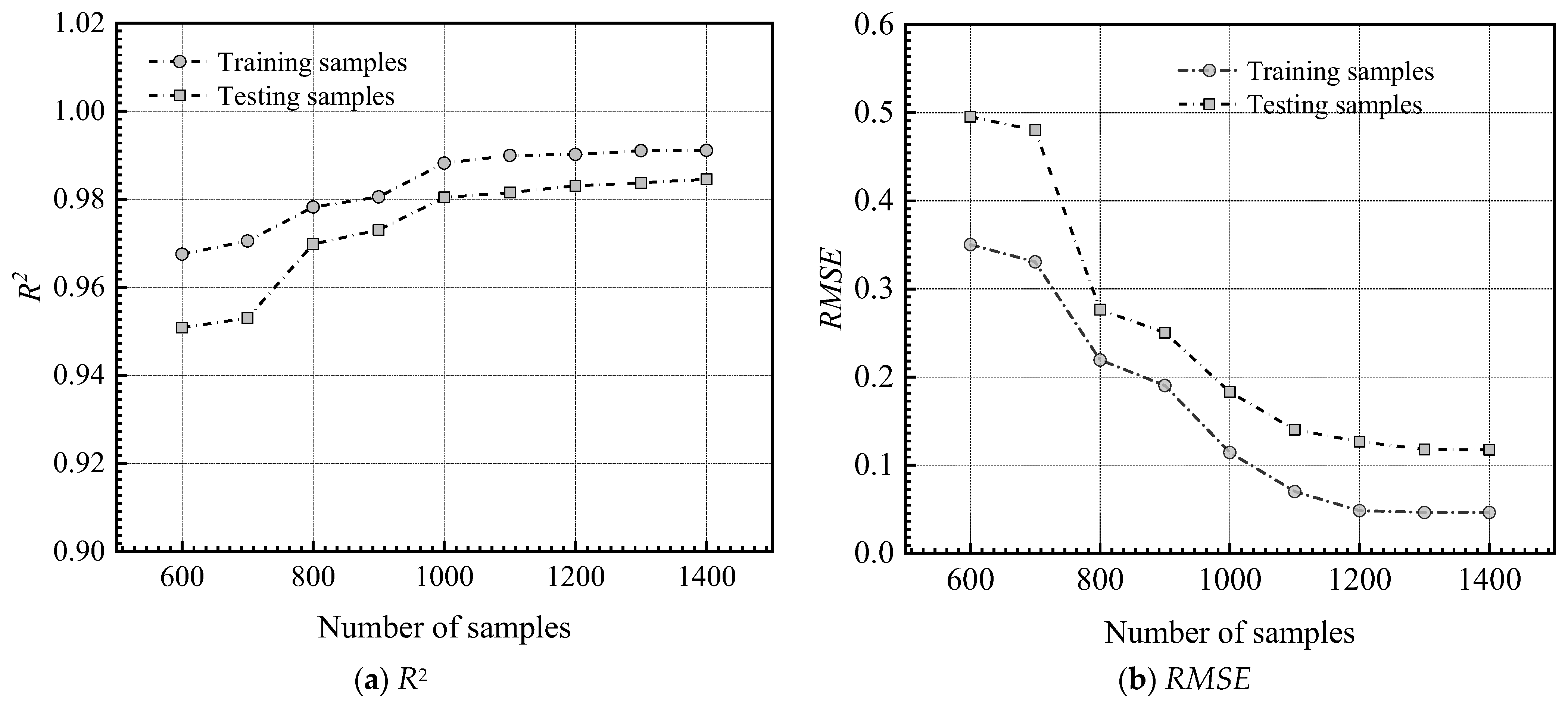
Figure 3 also plots the effects of the number of training samples on the performance metrics of the RF model (i.e.,
R2 and
RMSE). It can be seen that
R2 of the RF surrogate model for training and testing samples increases with the number of training samples.
RMSE of the surrogate model decreases with the number of training samples. When the number of training samples exceeds 1200, the accuracy of the RF surrogate model in predicting the hydraulic gradient does not show obvious improvement. Therefore, a sample size of 1400 for the input parameters is sufficient for training the RF surrogate model, which also satisfies the empirical size proposed by Silvestrini et al. [
53].
Then, these 1400 training samples are put into MODFLOW for repetitive seepage analysis to obtain the hydraulic gradient
i at the most dangerous point of the levee (i.e., Chainage 360 + 015). The RF algorithm is applied to construct a surrogate model between input parameters and the hydraulic gradient
i. For the RF surrogate model, the optimal hyperparameters (i.e., number of trees and maximum depth) are determined using the 1400 training samples via a grid search coupled with five-fold cross-validation. The optimal value of number of trees for each RF model is set at 500, and the maximum depth is taken as 2 for the surrogate model. For validation, 100 testing samples of input parameters are used to illustrate the prediction accuracy of the surrogate model. Two performance metrics, i.e.,
R2 and
RMSE, are adopted to evaluate the performance of the RF surrogate model.
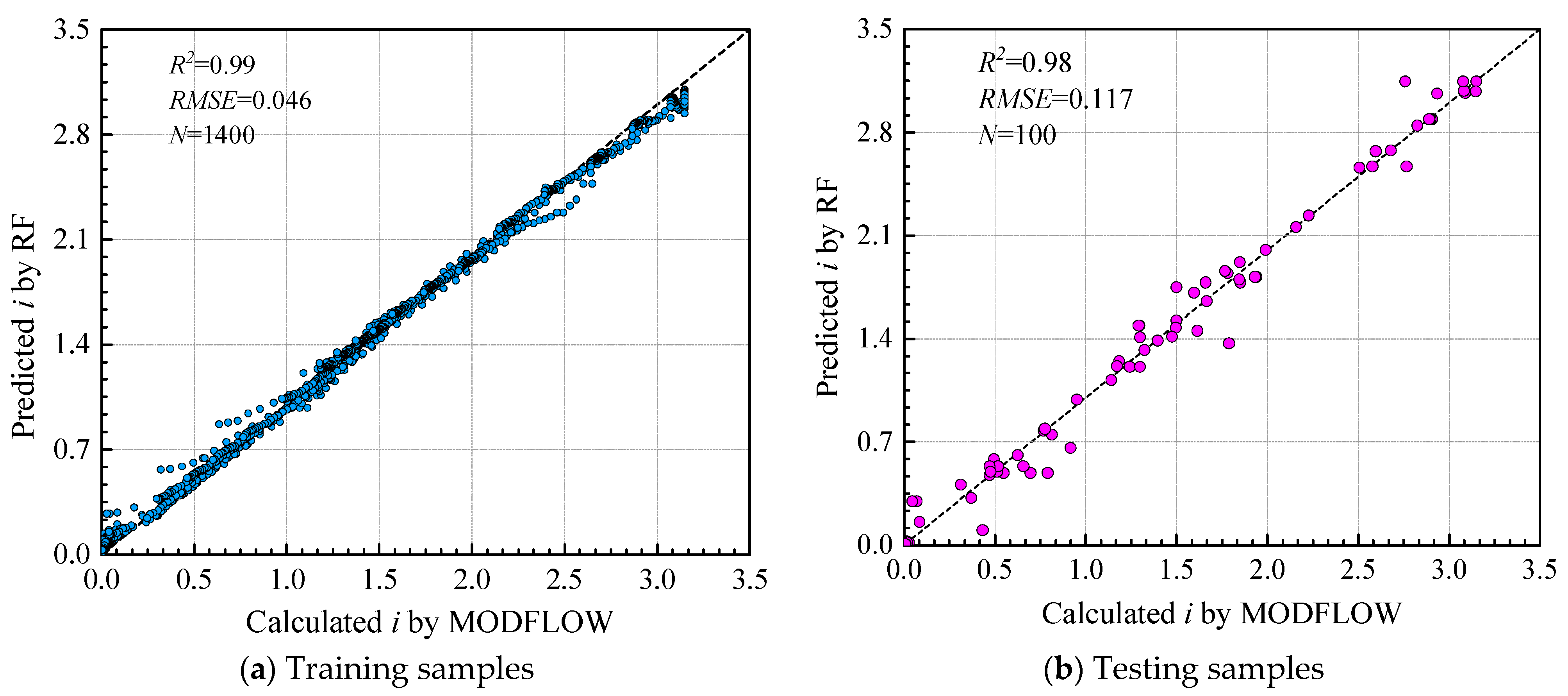
Figure 4 plots the predicted and calculated values of
i at the most dangerous point for the training and testing samples. It can be seen that the predicted
i by the RF surrogate model generally agrees well with that of MODFLOW. The
R2 values for the training and testing samples are all above 0.95, indicating that the developed surrogate model is able to predict the hydraulic gradient
i in the study area with desired accuracy.
The importance of input parameters given by RF algorithm essentially reflects the contribution of each feature to the model’s prediction of hydraulic gradient [
31]. The importance of wellhead elevation
H and the number of wells
n on the hydraulic gradient
i is 86% and 14%, respectively. This shows that the wellhead elevation plays a dominant role in estimating the hydraulic gradient. This also means that a reasonable design of the wellhead elevation is of vital importance for the safety of the levee in the study area.
5.4. Multi-Objective Optimization of Design Parameters of Relief Wells
Multi-objective optimization of NSGA-II is used to determine the optimal design parameters of relief wells in order to obtain an appropriate design scheme that can ensure a balance between the economy and safety of levee. For the NSGA-II algorithm, the population size is set as 100. The maximum number of iterations is 500. The crossover and mutation probability are 0.8 and 0.05, respectively. The constraint conditions for the design parameters are set as:
and
. The convergence is achieved when the average changes in H and
n are less than 0.01. By integrating the RF surrogate model in the previous section into NSGA-II algorithm, a set of 57 Pareto optimal solutions are obtained, as shown in
Figure 5. It is evident that the optimal
values decrease significantly with the increase in the economic cost. It also reveals that if more wells are pumped, the higher
FS of levee is derived. In such a case, although the greater
FS can be obtained, the design scheme is not cost-effective. Therefore, the final optimal design parameters are selected from the 57 sets of Pareto optimal solutions using entropy weight method. The entropy weights for each evaluation indicator across the two objectives (i.e., Equations (7) and (8) are 0.895 and 0.105, respectively. It can be seen that the weights of the two objectives show significant disparity in the study area. Obviously, the levee safety is more important than the economic cost in determining the optimal design parameters of relief wells in the study area.
Table 2 lists the coefficient of closeness of the 57 sets of Pareto optimal solutions. All the optimal schemes are ranked using the TOPSIS method. The maximum coefficient of closeness is considered as the most suitable design scheme of relief wells. It can be seen that the first scheme has the maximum coefficient of closeness with a value of 0.895. The design parameters of the first scheme are 20.5 m for
H and 17 for
n, respectively. Clearly, the number of wells obtained from the proposed approaches are less than that estimated by the engineering experience (i.e.,
n = 20).
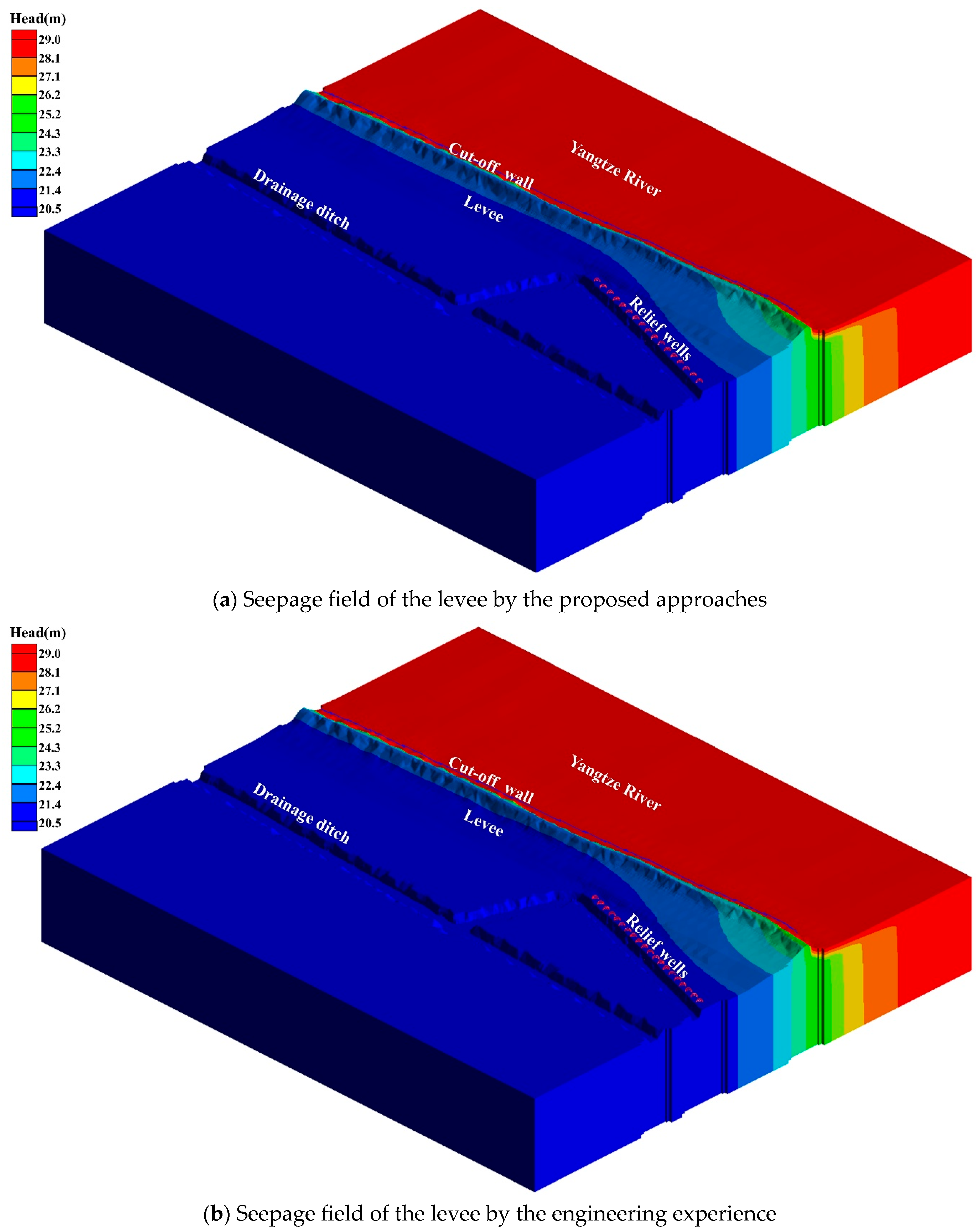
Figure 6a shows the groundwater seepage field using the final optimal design parameters of relief wells. It can be seen that the hydraulic gradient
i at the most dangerous point is 0.298, which is very close to the critical hydraulic gradient of fill soil (i.e., 0.3). The economic cost of the relief wells is about CNY 2.84 million. As for the design scheme by engineering experience, the hydraulic gradient
i at the most dangerous point is 0.088 and the economic cost is about CNY 3.34 million (see
Figure 6b). Obviously, compared to the empirical method, the hydraulic gradient derived from the proposed approaches is increased by 0.210, while the economic cost is decreased by CNY 0.50 million, with a reduction rate of 15%. This proves that the proposed approaches can achieve 15% cost reduction provided that the safety factor is strictly ensured to meet the minimum requirements of the threshold (
FSt ≥ 2). This means that the proposed approaches have achieved refined and quantitative design through objective optimization theories, and significant economic benefits and potential functional advantages while meeting the requirements of levee safety.
It should also be noted that although, for the 1400 training samples, repetitive MODFLOW numerical simulations take about 10 d on a desktop computer with 32 GB RAM and 12 Intel Core i7 CPU clocked at 2.10 GHz, the NSGA-II algorithm actually performs 50,000 times (i.e., 500 generations and 100 populations) of evaluations using the surrogate model within 1 min. Equivalently, 50,000 times of MODFLOW numerical simulations will take about 357 days, which renders the direct simulation approach infeasible for practical engineering applications. It can be seen that the proposed approaches only need a relatively small number of simulations (e.g., 1400 samples generated by LHS) to build the initial RF surrogate models. Then, the computational cost within the NSGA-II optimization of design parameters of relief wells is significantly reduced by the RF model. Furthermore, the proposed approaches are entirely data-driven, determining the optimal design parameters by objectively balancing levee safety and economic cost, thus eliminating the subjective bias inherent in empirical methods. This data-driven framework becomes increasingly advantageous as the dimensionality of the optimization problem grows, a scenario where traditional methods would face an insurmountable computational burden.
5.5. Effects of Wellhead Elevation and Number of Wells on Levee Safety
To further investigate the effects of wellhead elevation and number of wells on the levee safety,
Figure 7 presents the effects of
H and
n on the total discharge of relief wells and the safety of levee.
Results show that when the wellhead elevation
H is designed as 22.5 m, increasing the number of wells does not result in a significant change in the hydraulic gradient at the most dangerous point, which remains nearly a constant around 3.146. Even 40 relief wells are installed with a well spacing of 8.5 m, the relief wells have no effect on decreasing the excessive groundwater pressure. The total discharge of relief wells only increases from 0.55 m
3/d to 12.9 m
3/d. In this case, the hydraulic gradient at the drainage ditch (i.e., Chainage 360 + 015) is 3.146; this is larger than the critical hydraulic gradient of fill soil (i.e., 0.3), indicating that the levee is still unsafe. However, when the wellhead elevation
H decreases to 21.5 m and 20.5 m, respectively, the hydraulic gradient at the most dangerous point generally decreases with the number of wells.
Table 3 summarizes the effects of the wellhead elevation on the levee safety where the number of wells is 20. It is clear that as the wellhead elevation decreases from 22.5 m to 20.5 m, the total discharge of wells increases greatly from 7.34 m
3/d to 909.84 m
3/d. The hydraulic gradient at the most dangerous point decreases sharply from 3.146 to 0.088.
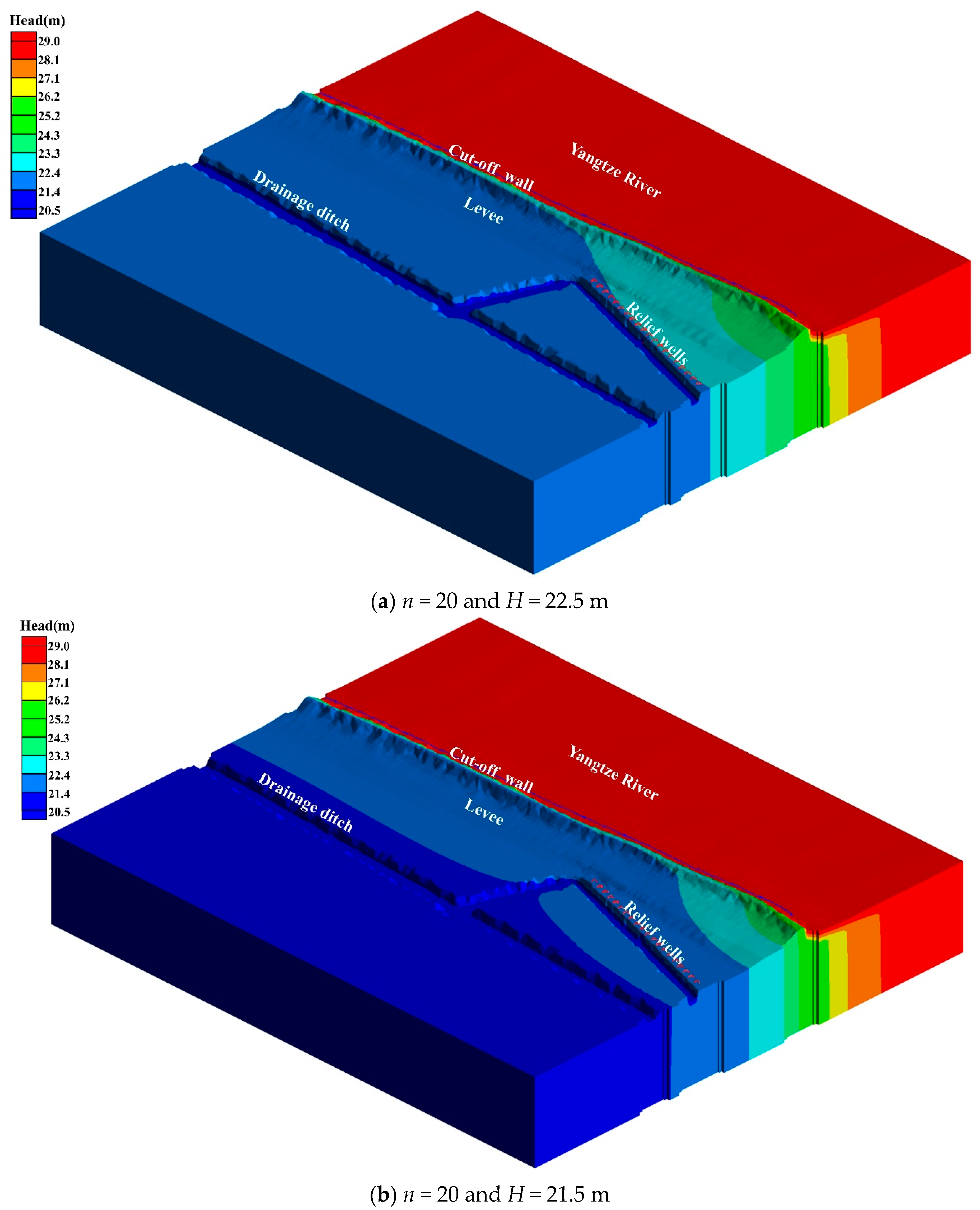
The reason lies in that when the wellhead elevation is designed as 22.5 m, it is larger than the phreatic surface (i.e., an elevation of 21.8 m), making it impossible to drain the excessive groundwater (see
Figure 8a). Therefore, the increase in the number of wells does not contribute to the decrease in the hydraulic gradient. On the contrary, if the wellhead elevation is lower than the phreatic surface, the hydraulic gradient is obviously reduced, e.g., 1.461 for
H = 21.5 m (see
Figure 8b). This indicates that it is important to determine a proper wellhead elevation for the design of relief wells.
Figure 7 also shows that, as for
H = 21.5 m, when
n increases from 1 to 40, the total well discharge rises from 87.51 m
3/d to 486.12 m
3/d. Meanwhile, the hydraulic gradient decreases from 2.717 to 1.373. As for
H = 20.5 m, when
n increases from 1 to 40, the total well discharge rises from 171.78 m
3/d to 1013.99 m
3/d. The hydraulic gradient significantly decreases from 2.363 to 0.015. Generally, when the wellhead elevation is lower than the phreatic surface, the performance of well drainage and the levee safety improve with the increasing well numbers. However, as for
H = 20.5 m, there is no significant increase in the total well discharge and the decrease in
i as the
n increases from 25 to 40. The total well discharge increases from 949.14 m
3/d to 1013.99 m
3/d, with a relative increase of 6.8%. The average decrease in
i is about 0.012. This suggests that when the wellhead elevation is extremely small, excessively increasing the number of wells may not significantly improve the performance of well drainage and the levee safety. On the contrary, it will lead to excessive designs.
6. Discussions
It should be noted that the proposed approaches are illustrated to determine the two design parameters (i.e., wellhead elevation and the number of wells) of relief wells in the Wuhan Yangtze River Levee, China. Other design parameters of relief wells, such as well diameter and penetration depth can also be incorporated into the proposed approaches to develop a multi-objective optimization problem. It does not affect the method itself. The proposed approaches are also be appliable to other specific sites to determine the design parameters for decision-makers. Although the design flood level (i.e., 29 m) is considered in this study to optimize the design parameters of relief wells, the proposed approaches are also be appliable to other hydraulic conditions on the riverside and levees with different geological conditions. In this case, new boundary or geological conditions are considered to develop a new MODFLOW model. A new RF surrogate model should be re-constructed to calculate the hydraulic gradient at the most dangerous point.
Moreover, for simplification, MODFLOW is used to simulate saturated seepage of levee. If sufficient unsaturated parameters are available (e.g., van Genuchten parameters), steady-state saturated-unsaturated seepage analysis can also be performed to optimize the design parameters of relief wells. This capability does not fundamentally alter the methodology itself.
While the integration of RF surrogate models with NSGA-II offers computational efficiency for optimizing relief well design, several limitations persist. Firstly, the developed RF surrogate model for predicting the hydraulic gradient at the most dangerous point is only applicable for the study area. If the actual geological model changes significantly (e.g., in stratum structure, geotechnical parameters, or boundary conditions), the original surrogate model becomes invalid. Consequently, a new RF model should be retrained with the updated geological data. Moreover, the RF model in this study is also only applicable within the ranges of input design parameters. When the design parameters exceed the defined ranges or take values at the boundary, they are unable to accurately predict the hydraulic gradient, which are associated with great uncertainty. The performance of RF hinges on the quality and quantity of training data, which is often costly to generate for complex geological systems. Its performance is highly sensitive to hyperparameter selection (e.g., tree depth, population size). Inappropriate choices can lead to poor convergence, overfitting, or excessive computational cost. The RF model is an approximation of the complex numerical simulations, which inherently contain predictive uncertainty. This uncertainty will propagate into the determination of design parameters. In the future, it is necessary to characterize the uncertainties of the RF surrogate model to improve its accuracy.
This paper applies RF to construct an accurate surrogate model for the MODFLOW simulations. It is important to emphasize that the proposed approaches are not exclusively tied to this specific algorithm. The choice of RF is motivated by its renowned robustness, its ability to handle complex nonlinear relationships without extensive preprocessing, and its inherent resistance to overfitting. These characteristics made it an excellent and reliable choice for this application. However, other powerful machine learning algorithms could also potentially serve as viable alternatives. For instance, Gradient Boosting Machines (e.g., XGBoost and LightGBM), known for their high predictive performance, or Support Vector Regression (SVR), which can be effective in high-dimensional spaces, could be explored. Any machine learning model that can be trained to satisfactorily emulate the numerical model’s outputs with desired accuracy can be seamlessly integrated into the NSGA-II optimization. Future work could involve a comparative analysis of different algorithms to identify the most computationally efficient surrogate for specific types of groundwater models. Secondly, as a heuristic method, NSGA-II provides no mathematical guarantee of convergence to the true Pareto optimal front. Its performance is highly dependent on parameter tuning (e.g., crossover and mutation rates), and it can suffer from premature convergence or get trapped in local optima, particularly in complex, high-dimensional search spaces. The algorithm also requires substantial computational resources for large populations or many generations, and the solutions generated are approximations whose quality cannot be rigorously proven.
7. Summary and Conclusions
This paper proposed an RF-based multi-objective optimization design method of relief wells for levee safety. MODFLOW is used to simulate the seepage field of levee systems with relief wells. The design parameters (e.g., the wellhead elevation and the number of wells) of relief wells are optimized by minimizing the safety factor deficit to a defined threshold and minimizing the economic cost. Then, the optimal design of relief wells was determined by NSGA-II. To remove the computational burden of repetitive MODFLOW simulations in the multi-objective optimization, RF was used to establish a surrogate model for evaluating the hydraulic characteristic of levees with relief wells. The entropy weight method and TOPSIS were integrated to determine the final optimal design parameters among alternative Pareto solutions. Finally, the proposed approaches were illustrated using the relief wells in Wuhan Yangtze River Levee, China.
Results show that the RF-based surrogate model for multi-objective optimization design of relief wells can accurately estimate the hydraulic gradient i at the most dangerous point, achieving an R2 value above 0.95 for both the training and testing samples. Compared with the conventional NSGA-II optimization, the integration of RF and NSGA-II can significantly decrease the computational burden. Meanwhile, the RF algorithm can also provide the relative importance of design parameters. Compared to the engineering experience method, the proposed approaches are entirely data-driven to determine the optimal design parameters of relief wells by objectively balancing levee safety and economic cost, eliminating the subjective bias inherent in empirical methods.
The wellhead elevation of relief wells is of more vital importance than the number of wells for the safety of the levee in the study area. When the wellhead elevation is designed higher than the phreatic surface, the relief wells will not be able to effectively relieve excessive groundwater pressure. Generally, when the wellhead elevation is lower than the phreatic surface, the performance of well drainage and the levee safety improve with the increasing well numbers. When the wellhead elevation is extremely small, excessively increasing the number of wells may not significantly improve the performance of well drainage and the levee safety.
Author Contributions
Conceptualization, M.T. and A.-W.A.; Data curation, A.-W.A.; Formal analysis, A.-W.A. and M.T.; Funding acquisition, A.-W.A. and M.T.; Methodology, A.-W.A., M.T. and W.-Y.W.; Writing—original draft, A.-W.A. and M.T.; Writing—review and editing, M.T., A.-W.A. and W.-Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Foreign Experts Program (Project No. H20250438), Special Fund for National Key Laboratories of China Minmetals Corporation Limited. (Project No. WKZB2412BJ0402105), the Natural Science Foundation of Hubei Province of China (Project No. 2024AFB796), and Outstanding Young and middle-aged Science and Technology Innovation Team Project of colleges and universities of Hubei Province (Project No. T2022010).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data in this study are available from the corresponding author upon reasonable request.
Acknowledgments
Thanks to Shiping Yang, Zhu Yang and Long Teng for their supports. The authors are also grateful to the anonymous reviewers for their helpful comments and advice.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NSGA-II | Nondominated Sorting Genetic Algorithm-II |
| RF | Random Forest |
| LHS | Latin hypercube sampling |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
References
- Turnbull, W.J.; Mansur, C.I. Investigation of underseepage—Mississippi River levees. J. Soil Mech. Found. Div. 1959, 85, 41–93. [Google Scholar] [CrossRef]
- Hird, C.C.; Marsland, A.; Schofield, A.N. The development of centrifugal models to study the influence of uplift pressures on the stability of a flood bank. Géotechnique 1978, 28, 85–106. [Google Scholar] [CrossRef]
- Farzampour, A.; Salmasi, F.; Mansuri, B. Optimum size for clay core of alavian earth dam by numerical simulation. Iran. J. Energy Environ. 2014, 5, 240–246. [Google Scholar] [CrossRef]
- Yi, C.; Wang, B.; Jin, M.; Guo, Z. Two-dimensional simulation of underground seepage in a dangerous piping zone of the Jingjiang great levee, the middle reach of the Yangtze River. Q. J. Eng. Geol. Hydrogeol. 2007, 40, 85–92. (In Chinese) [Google Scholar] [CrossRef]
- Mansuri, B.; Salmasi, F.; Oghati, B. Effect of location and angle of cutoff wall on uplift pressure in diversion dam. Geotech. Geol. Eng. 2014, 32, 1165–1173. [Google Scholar] [CrossRef]
- USACE. Technical Memorandum TM 3-424: Investigation of Underseepage and Its Control, Lower Mississippi River Levees; U.S. Army Corps of Engineers, Waterways Experiment Station, Mississippi River Commission: Vicksburg, MS, USA, 1956. [Google Scholar]
- USACE. Engineer Manual EM 1110-2-1901: Seepage Analysis and Control for Dams; U.S. Army Corps of Engineers: Washington, DC, USA, 1993. [Google Scholar]
- Keffer, A.M.; Guy, E.D.; Chang, E.M. Finite element modeling of partial penetration well uplift factors. In Geo-Congress 2019: Embankments, Dams, and Slopes; Meehan, C.L., Kumar, S., Pando, M.A., Coe, J.T., Eds.; Geotechnical Special Publication 305: Reston, VA, USA, 2019; pp. 57–66. [Google Scholar]
- Jafari, F.; Salmasi, F.; Abraham, J. Numerical investigation of granular filter under the bed of a Canal. Appl. Water Sci. 2019, 9, 137. [Google Scholar] [CrossRef]
- Nourani, B.; Salmasi, F.; Abbaspour, A.; Oghati Bakhshayesh, B. Numerical investigation of the optimum location for vertical drains in gravity dams. Geotech. Geol. Eng. 2017, 35, 799–808. [Google Scholar] [CrossRef]
- Fell, R.; Fry, J.J. Internal Erosion of Dams and Their Foundations: Selected and Reviewed Papers from the Workshop on Internal Erosion and Piping of Dams and Their Foundations, Aussois, France, 25–27 April 2005, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Yao, Q.; Xu, C.; Xu, W.; Kwan, T.H.; Wang, S. Transient antiseepage analysis of the relief well in Beijiang Dike. Math. Probl. Eng. 2020, 9, 7623481. [Google Scholar]
- Keffer, A.M.; Guy, E.D.; Grote, K.R. Finite line relief well system design for dams and levees. In Proceedings of the Geo-Congress 2023, Reston, VA, USA, 12–15 March 2023; American Society of Civil Engineers: Reston, VA, USA, 2023; pp. 31–48. [Google Scholar] [CrossRef]
- Mansur, C.I.; Kaufman, R.I. Dewatering and Control of Groundwater. In Foundation Engineering, 1st ed.; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Mansur, C.I.; Postol, G.; Salley, J.R. Performance of relief well systems along Mississippi River levees. J. Geotech. Geoenviron. Eng. 2000, 126, 727–738. [Google Scholar] [CrossRef]
- Li, J.J.; Yang, Y.; Duan, X.B.; Xie, L.F.; Zhou, X. Numerical analysis on factors affecting the effectiveness of relief-well. J. Chang. River Sci. Res. Inst. 2016, 33, 151. (In Chinese) [Google Scholar]
- Salmasi, F.; Nourani, B.; Abraham, J.; Norouzi, R. Numerical investigation of relief well performance for decreasing uplift pressure under embankment dams. Int. J. Environ. Sci. Technol. 2021, 18, 2819–2830. [Google Scholar] [CrossRef]
- Chen, Y.H.; Tsai, T.C.; Cadigan, J.A.; Jafari, N.H.; Shih, T.H. Relief well evaluation: Three-dimensional modeling and blanket theory. J. Geotech. Geoenviron. Eng. 2021, 147, 04021054. [Google Scholar] [CrossRef]
- USACE. Engineer Manual EM 1110-2-1914: Design, Construction, and Maintenance of Relief Wells; U.S. Army Corps of Engineers: Washington, DC, USA, 1992. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J. Multi-objective evolutionary algorithm for operating parallel reservoir system. J. Hydrol. 2009, 377, 12–20. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Dumedah, G.; Berg, A.A.; Wineberg, M.; Collier, R. Selecting model parameter sets from a trade-off surface generated from the non-dominated sorting genetic algorithm-II. Water Resour. Manag. 2010, 24, 4469–4489. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Zhang, C.; Sun, N. Modeling and combined application of orthogonal chaotic NSGA-II and improved TOPSIS to optimize a conceptual hydrological model. Water Resour. Manag. 2018, 32, 3781–3799. [Google Scholar] [CrossRef]
- Larranaga, P.; Karshenas, H.; Bielza, C.; Santana, R. A review on evolutionary algorithms in Bayesian network learning and inference tasks. Inf. Sci. 2013, 233, 109–125. [Google Scholar] [CrossRef]
- Molina, J.L.; Farmani, R.; Bromley, J. Aquifers management through evolutionary Bayesian networks: The Altiplano case study (SE Spain). Water Resour. Manag. 2011, 25, 3883–3909. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kreuzberger, D.; Kühl, N.; Hirschl, S. Machine learning operations (MLOps): Overview, definition, and architecture. IEEE Access 2023, 11, 31866–31879. [Google Scholar] [CrossRef]
- Haggerty, R.; Sun, J.; Yu, H.; Li, Y. Application of machine learning in groundwater quality modeling: A comprehensive review. Water Res. 2023, 233, 119745. [Google Scholar] [CrossRef]
- Garzón, A.; Kapelan, Z.; Langeveld, J.; Taormina, R. Machine learning-based surrogate modeling for urban water networks: Review and future research directions. Water Resour. Res. 2022, 58, e2021WR031808. [Google Scholar] [CrossRef]
- Nevo, S.; Morin, E.; Rosenthal, A.G.; Metzger, A.; Barshai, C.; Weitzner, D.; Voloshin, D.; Kratzert, F.; Elidan, G.; Dror, G. Flood forecasting with machine learning models in an operational framework. Hydrol. Earth Syst. Sci. 2022, 26, 4013–4032. [Google Scholar] [CrossRef]
- Puttinaovarat, S.; Horkaew, P. Flood forecasting system based on integrated big and crowdsource data by using machine learning techniques. IEEE Access 2020, 8, 5885–5905. [Google Scholar] [CrossRef]
- Hamitouche, M.; Molina, J.L. Event-based Bayesian causal modelling for flood hydrograph prediction, Upper Andarax intermittent stream, Spain. J. Hydrol. Reg. Stud. 2022, 44, 101260. [Google Scholar] [CrossRef]
- Vogel, K.; Weise, L.; Schröter, K.; Thieken, A.H. Identifying driving factors in flood-damaging processes using graphical models. Water Resour. Res. 2018, 54, 8864–8889. [Google Scholar] [CrossRef]
- Tripathy, K.P.; Mishra, A.K. Deep learning in hydrology and water resources disciplines: Concepts, methods, applications, and research directions. J. Hydrol. 2024, 628, 130458. [Google Scholar] [CrossRef]
- Boo, K.B.W.; El-Shafie, A.; Othman, F.; Khan, M.M.H.; Birima, A.H.; Ahmed, A.N. Groundwater level forecasting with machine learning models: A review. Water Res. 2024, 252, 121249. [Google Scholar] [CrossRef] [PubMed]
- Slater, L.J.; Arnal, L.; Boucher, M.A.; Chang, A.Y.Y.; Moulds, S.; Murphy, C.; Zappa, M. Hybrid forecasting: Blending climate predictions with AI models. Hydrol. Earth Syst. Sci. 2023, 27, 1865–1889. [Google Scholar] [CrossRef]
- Pirnia, P.; Duhaime, F.; Manashti, J. Machine Learning Algorithms for Applications in Geotechnical Engineering. In Proceedings of the GeoEdmonton 2018 Conference, Edmonton, AB, Canada, 1–4 October 2018; Canadian Geotechnical Society: Edmonton, AB, Canada, 2018; pp. 1–37. [Google Scholar]
- Solanki, H.; Vegad, U.; Kushwaha, A.; Mishra, V. Improving streamflow prediction using multiple hydrological models and machine learning methods. Water Resour. Res. 2025, 61, e2024WR038192. [Google Scholar] [CrossRef]
- Kumar, V.; Kedam, N.; Sharma, K.V.; Mehta, D.J.; Caloiero, T. Advanced machine learning techniques to improve hydrological prediction: A comparative analysis of streamflow prediction models. Water 2023, 15, 2572. [Google Scholar] [CrossRef]
- Baena-Navarro, R.; Carriazo-Regino, Y.; Torres-Hoyos, F.; Pinedo-López, J. Intelligent prediction and continuous monitoring of water quality in aquaculture: Integration of machine learning and Internet of Things for sustainable management. Water 2025, 17, 82. [Google Scholar] [CrossRef]
- Kang, F.; Han, S.; Salgado, R.; Li, J. System probabilistic stability analysis of soil slopes using gaussian process regression with latin hypercube sampling. Comput. Geotech. 2015, 63, 13–25. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Zhang, W.; Zhang, Y.; Gu, X.; Wu, C.; Han, L. Application of Soft Computing, Machine Learning, Deep Learning and Optimizations in Geoengineering and Geoscience; Springer Nature: Berlin, Germany, 2022. [Google Scholar]
- Li, M.; Sun, H.; Singh, V.P.; Zhou, Y.; Ma, M. Agricultural water resources management using maximum entropy and entropy-weight-based TOPSIS methods. Entropy 2019, 21, 364. [Google Scholar] [CrossRef]
- Li, Z.; Luo, Z.; Wang, Y.; Fan, G.; Zhang, J. Suitability evaluation system for the shallow geothermal energy implementation in region by entropy weight method and TOPSIS method. Renew. Energy 2022, 184, 564–576. [Google Scholar] [CrossRef]
- Hsu, P.F.; Hsu, M.G. Optimizing the information outsourcing practices of primary care medical organizations using entropy and TOPSIS. Qual. Quant. 2008, 42, 181–201. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer-Verlag: Berlin, Germany, 1981. [Google Scholar]
- Lautz, L.K.; Siegel, D.I. Modeling surface and ground water mixing in the hyporheic zone using MODFLOW and MT3D. Adv. Water Resour. 2006, 29, 1618–1633. [Google Scholar] [CrossRef]
- Panday, S.; Langevin, C.D.; Niswonger, R.G.; Ibaraki, M.; Hughes, J.D. MODFLOW–USG Version 1: An Unstructured Grid Version of MODFLOW for Simulating Groundwater Flow and Tightly Coupled Processes Using a Control Volume Finite-Difference Formulation; U.S. Geological Survey: Reston, VA, USA, 2013. [Google Scholar]
- Silvestrini, R.T.; Montgomery, D.C.; Jones, B. Comparing computer experiments for the gaussian process model using integrated prediction variance. Qual. Eng. 2013, 25, 164–174. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).