Performance Evaluation of Conventional and Recycled Ballast Materials: A Coupled FDM-DEM Approach Considering Particle Breakage
Abstract
1. Introduction
| Authors | Research | Principal Findings |
|---|---|---|
| Godson et al. [25] | Large-scale tests were conducted to compare the physical, mechanical, and environmental performance of electric arc furnace slag (EAFS) with conventional material. | The shear strength of EAFS was 15–22% higher than that of granite, with less final vertical deformation and a 20% increase in the load-bearing capacity of the granular layer. In addition, its leaching is within regulatory limits, making it safe for railway use. |
| Nasrollahi et al. [26] | Real-time monitoring of a zone between a ballasted track and a slab track with fiber Bragg grating (FBG) sensors installed in situ. | The FBG system reliably captures short- and long-term deformations/accelerations of the rail and sleeper; useful data for early diagnosis and model calibration. |
| Chen et al. [27] | Diametral compression tests by size, large-scale triaxial tests, and numerical modeling using the Discrete Element Method (DEM), to access micromechanical indicators such as coordination number, contact forces, and anisotropy. | The strength of ballast follows a Weibull distribution, and heterogeneous grading improves its performance, although large particles increase the risk of fracture. |
| Indraratna et al. [14] | Evaluation of recycled material tests: CWRC 1, SEAL 2 (slag + CW + RC), tire cells, and UBM 3 under ballast. | The recycled materials studied increase energy dissipation, reduce degradation, and vibrations. |
| Li et al. [28] | Full-scale track testing on ballasted track: dynamic responses and cumulative settlements. | They recorded vibration speeds, dynamic stresses, and settlement evolution under moving loads. |
| Sayeed and Shahin [29] | A design method for ballasted railway track foundations is proposed, combining improved empirical models and 3D numerical analysis, capable of supporting high-speed trains and heavy loads. | The new design method for railway foundations prevents critical failures using empirical models and 3D analysis, offering a more robust solution that is adaptable to various design conditions and modern railway traffic. |
| Edwards et al. [30] | Laboratory and field tests on concrete sleepers using surface strain gauges to obtain bending moments. | Non-invasive method that quantifies variability between sleepers and provides data for design/service life. |
| Lu and McDowell [31] | The study uses the Discrete Element Method (DEM) to simulate the behavior of ballast under monotonic and cyclic loads, replicating shear strength and volumetric response, validated experimentally. | The model shows that shear strength varies with confining pressure and ballast size, being less sensitive to pressure in small particles. The number of roughness features influences the peak friction angle, but not the residual friction angle. |
| Lim et al. [32] | Compression tests were performed on six types of rock to analyze the strength of the ballast, evaluating the results with the Weibull distribution to explore the relationship between size and strength. | The strengths of the ballast conform to the Weibull distribution, but the relationship between size and strength differs from the theory due to factors such as quarry processing and surface fractures, which limit the applicability of the model. |
| Li and Selig [33] | A design method is proposed to determine the thickness of the granular layer between ballast and subballast, preventing subgrade failure due to repeated loads, using procedures that consider soil strength and railway load. | The method converts traffic conditions into design parameters and defines two criteria to prevent failure and deformation. Validated in the field, it showed good results in tests and real sites. |
| Cundall and Strack [34] | This research presents the Discrete Element Method (DEM) as a numerical tool designed to describe the mechanical behavior of assemblies of particles represented by disks or spheres. | The numerical results showed a high degree of visual similarity with those obtained experimentally, which supported the validity of the DEM for investigating granular behavior. |
2. Database
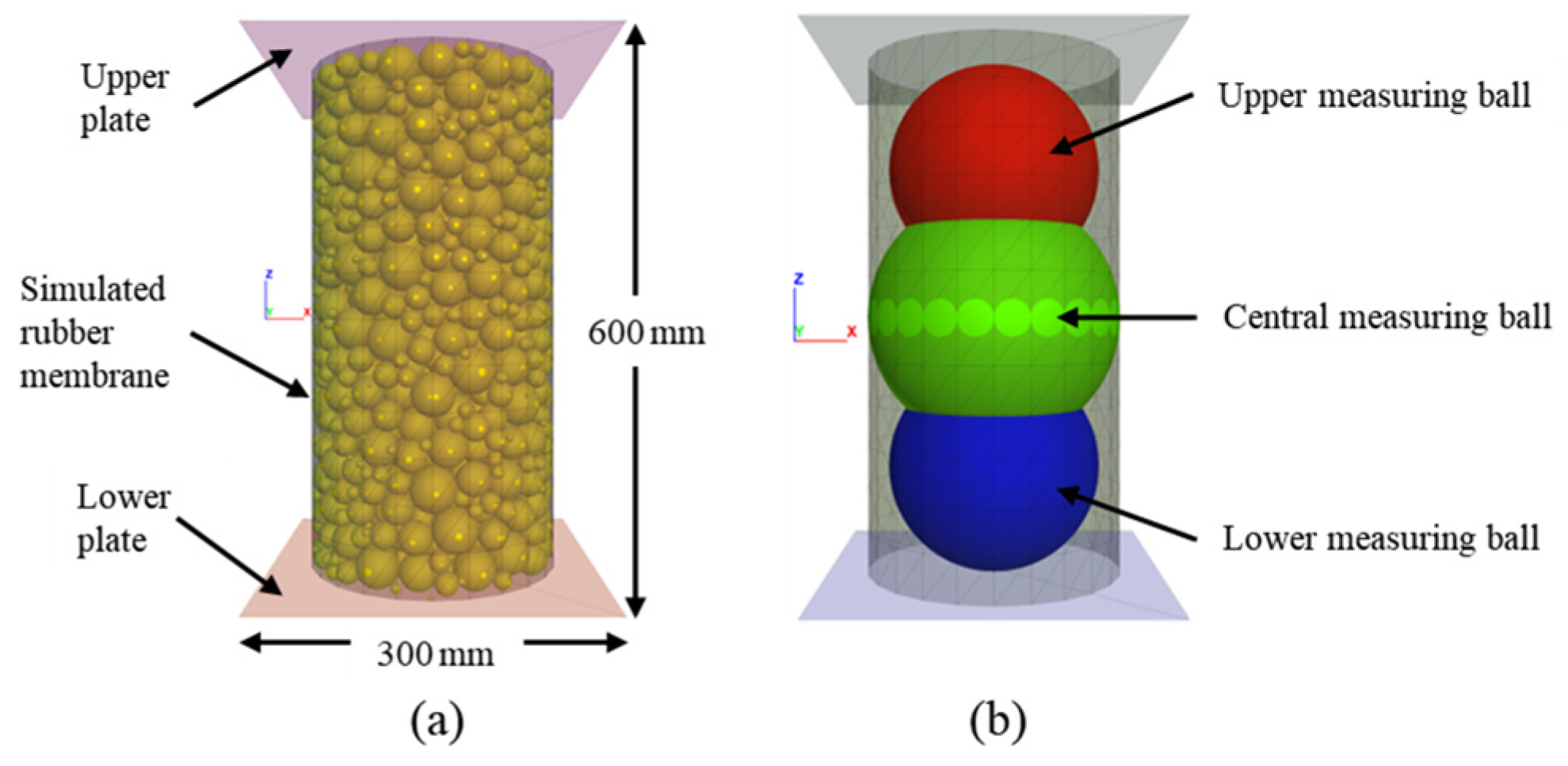
3. Model Description
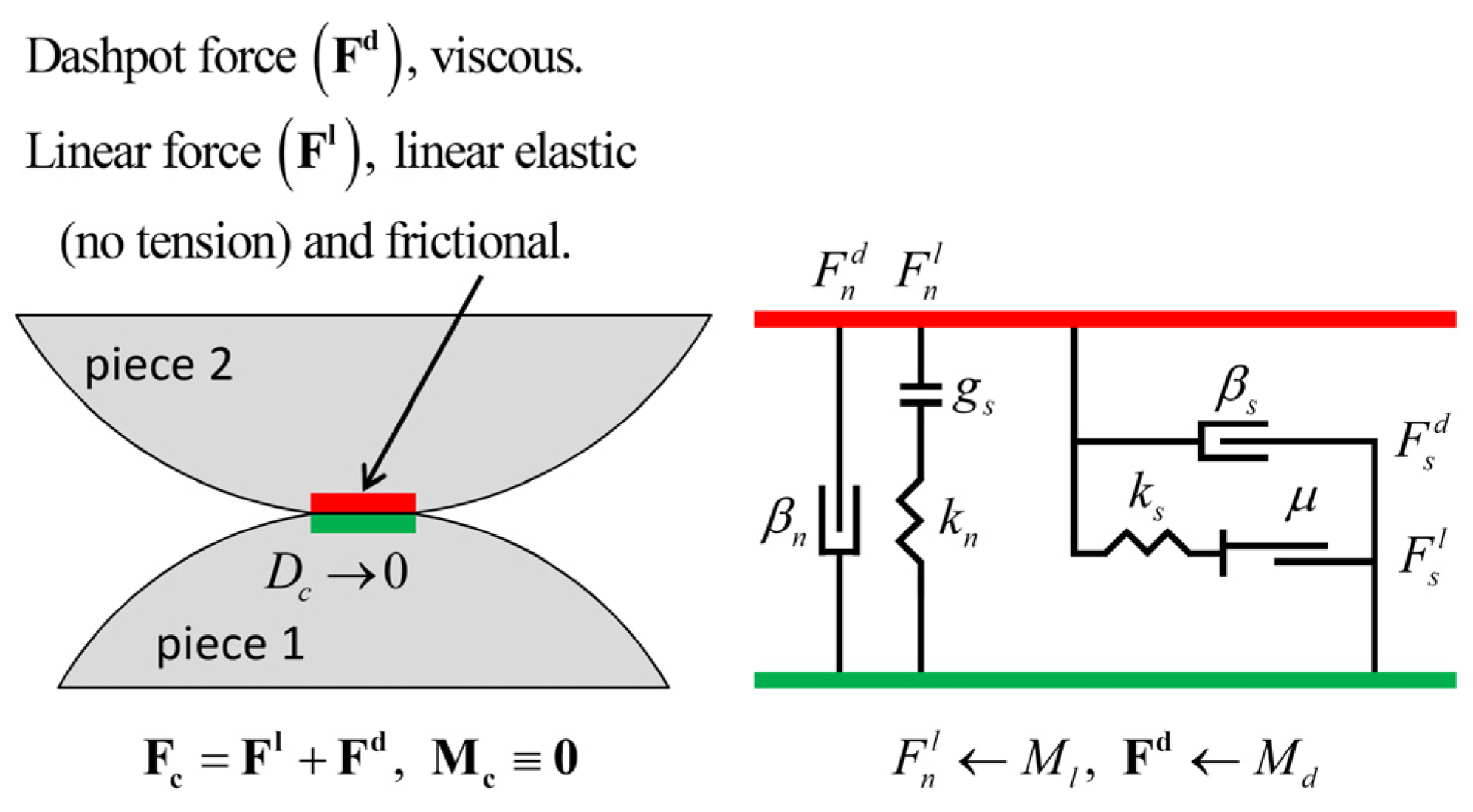
3.1. Rolling Resistance Contact Model
3.2. Lineal Model
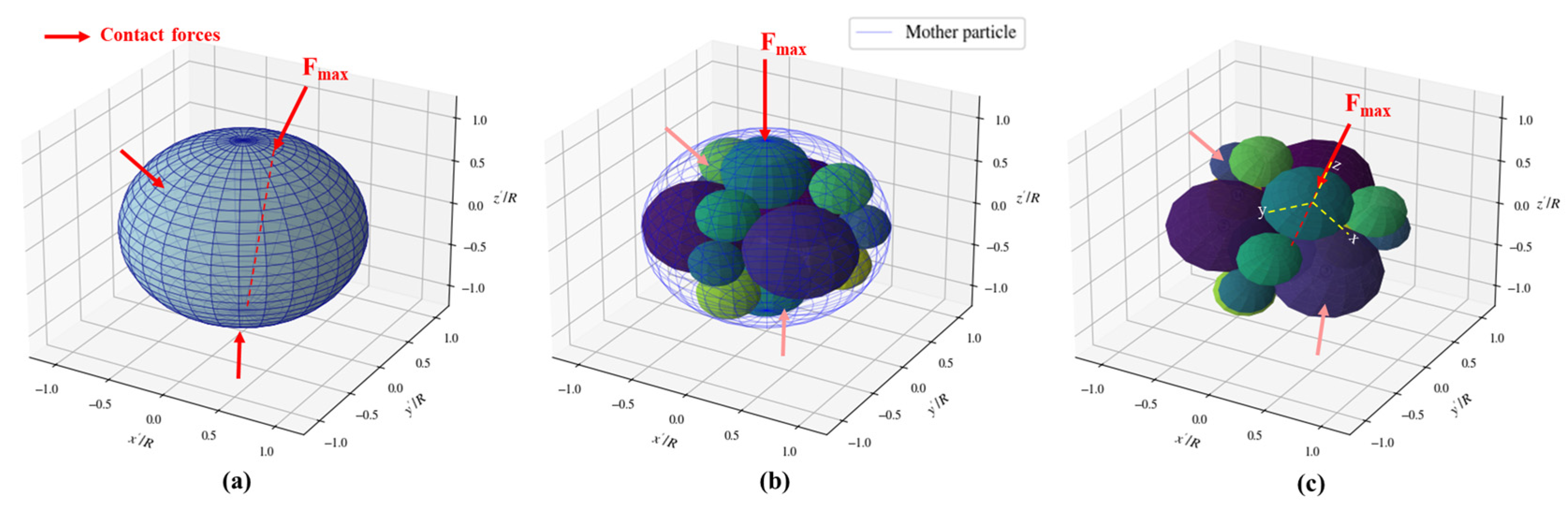
3.3. Breakage Particle
4. Model Calibration
4.1. Parameter Calibration
| Contact Model | Normal Stiffness, kn | Shear Stiffness, ks | Young Modulus, E | Friction Coefficient, μ | Rolling Friction Coefficient, μr | Reference |
|---|---|---|---|---|---|---|
| (N/m) | (N/m) | (Pa) | (-) | (-) | ||
| Linear | 1.5 × 105 | 1.5 × 105 | - | 1.00 | - | Liu et al. [53] |
| Linear | 8.0 × 105 | 8.0 × 105 | - | 0.60 | - | Wang et al. [54] |
| Hertz | - | - | 1.2 × 107 | 1.00 | - | Perez et al. [55,56] |
| RRLM | 1.0 × 103 | 1.0 × 103 | - | 1.50 | - | Gong et al. [57] |
| RRLM | 3.28 × 105 | 2.18 × 105 | - | 1.00 | 0.1 | Guo et al. [58] |
| Hertz | - | - | 5.0 × 107 | 1.00 | - | Wu et al. [59] |
| Linear | 2.0 × 105 | 2.0 × 105 | - | 1.00 | - | Zhang et al. [60] |
| Linear | - | - | 1.57 × 107 | - | - | Ngo et al. [61] |
| Contact Type | Normal Stiffness, kn | Shear Stiffness, ks | Friction Coefficient, μ | Rolling Friction Coefficient, μr |
|---|---|---|---|---|
| (N/m) | (N/m) | - | - | |
| Ballast–ballast | 3.3 × 107 | 3.3 × 107 | 0.45 | 0.80 |
| Rubber–rubber | 4.5 × 103 | 4.5 × 103 | 1.00 | |
| Ballast–rubber | 2.0 × 106 | 2.0 × 106 | 1.00 | 0.50 |
| Particle–wall | 1.7 × 108 | 1.7 × 108 | 0.30 |
4.2. Coupled Numerical Model PFC3D—FLAC3D
5. Results
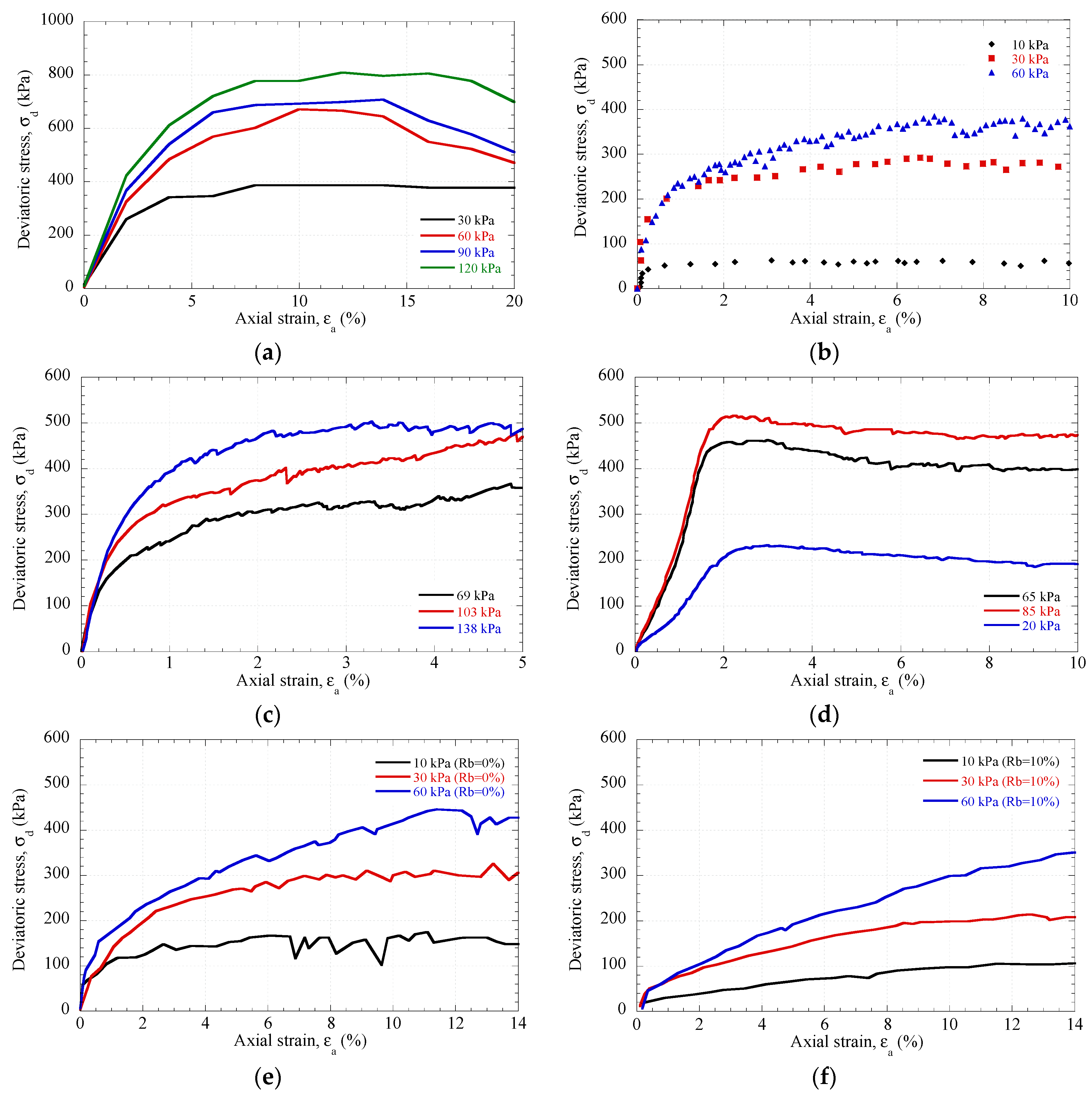
5.1. Monotonic Load
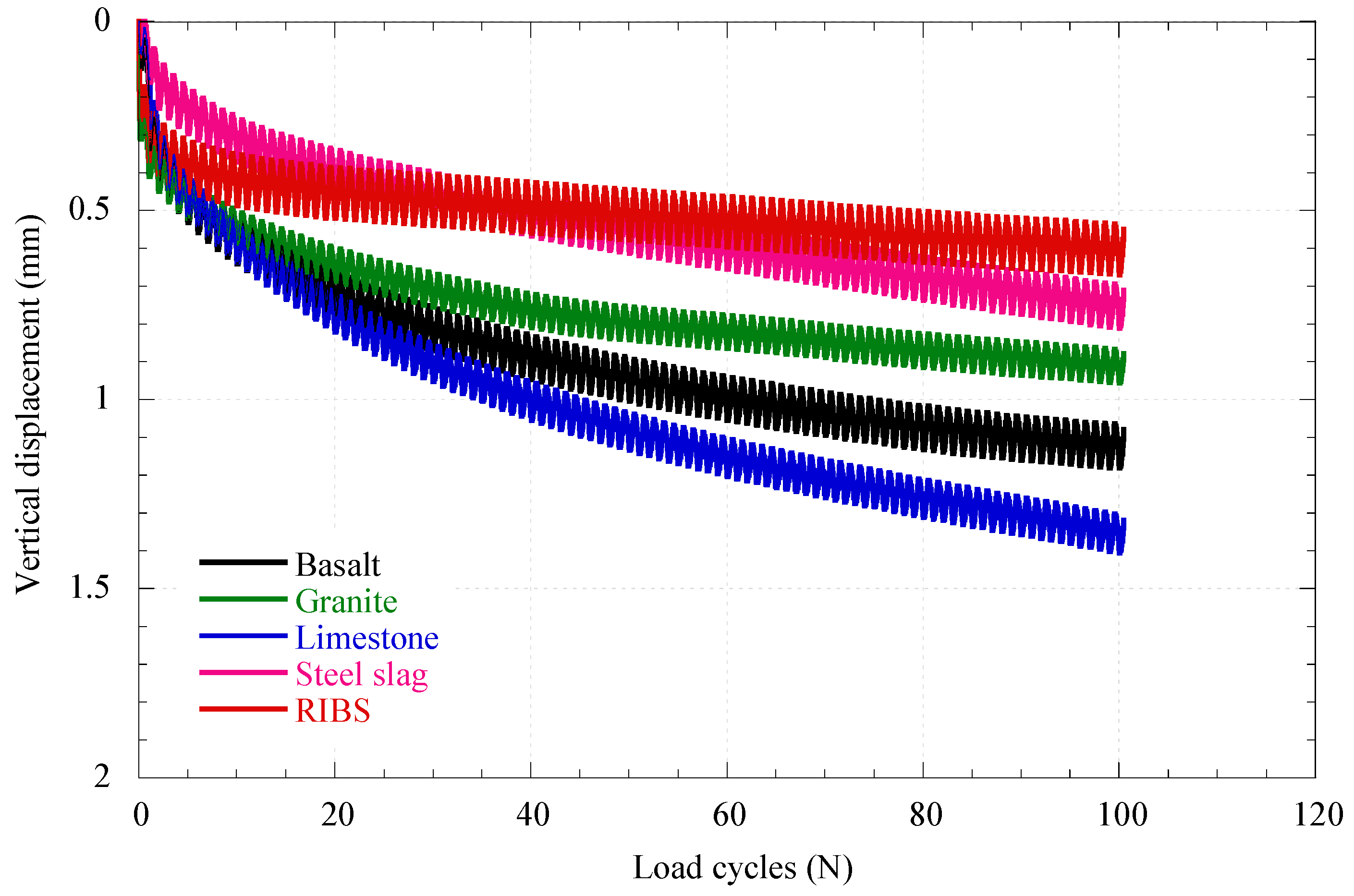
5.2. Cyclic Loading
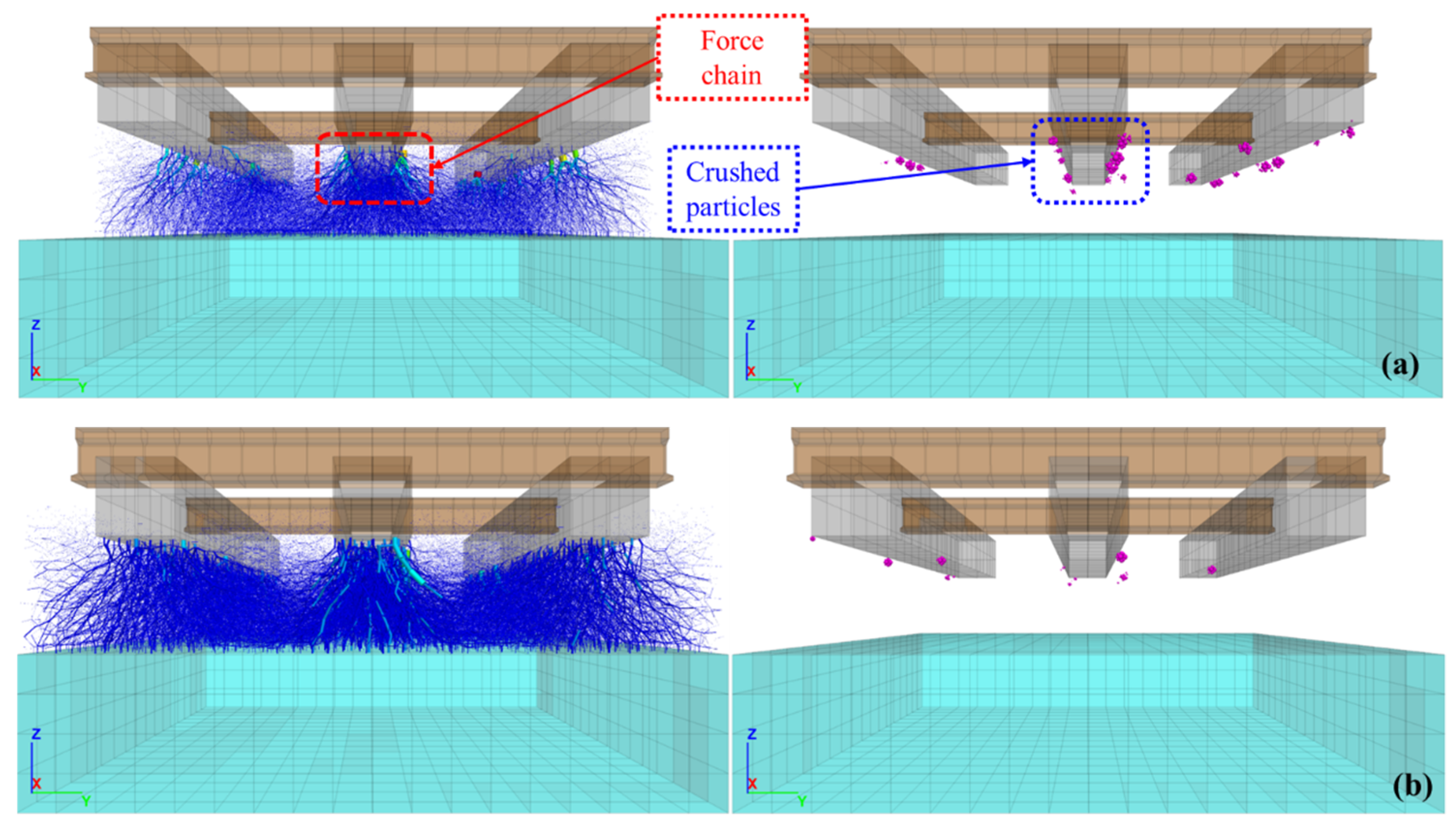
5.3. Ballast Breakage
5.4. Economic Implications
6. Discussion
- Analyze the combined effects of temperature, humidity, and chemical aging on recycled ballast.
- Study the influence of water, saturation, and freeze–thaw cycles through coupled thermo-hydro-mechanical models.
- Evaluate long-term durability with large-scale cyclic triaxial tests (>106 cycles) and DEM simulations that include multigenerational failure.
- Conduct life cycle assessments (LCA) and life cycle cost analyses (LCC) to quantify environmental and economic benefits.
- Develop pilot sections equipped with fiber optic sensors (FBG) and piezometers to validate numerical models and build digital twins that enhance predictive maintenance and performance-based design.
7. Conclusions
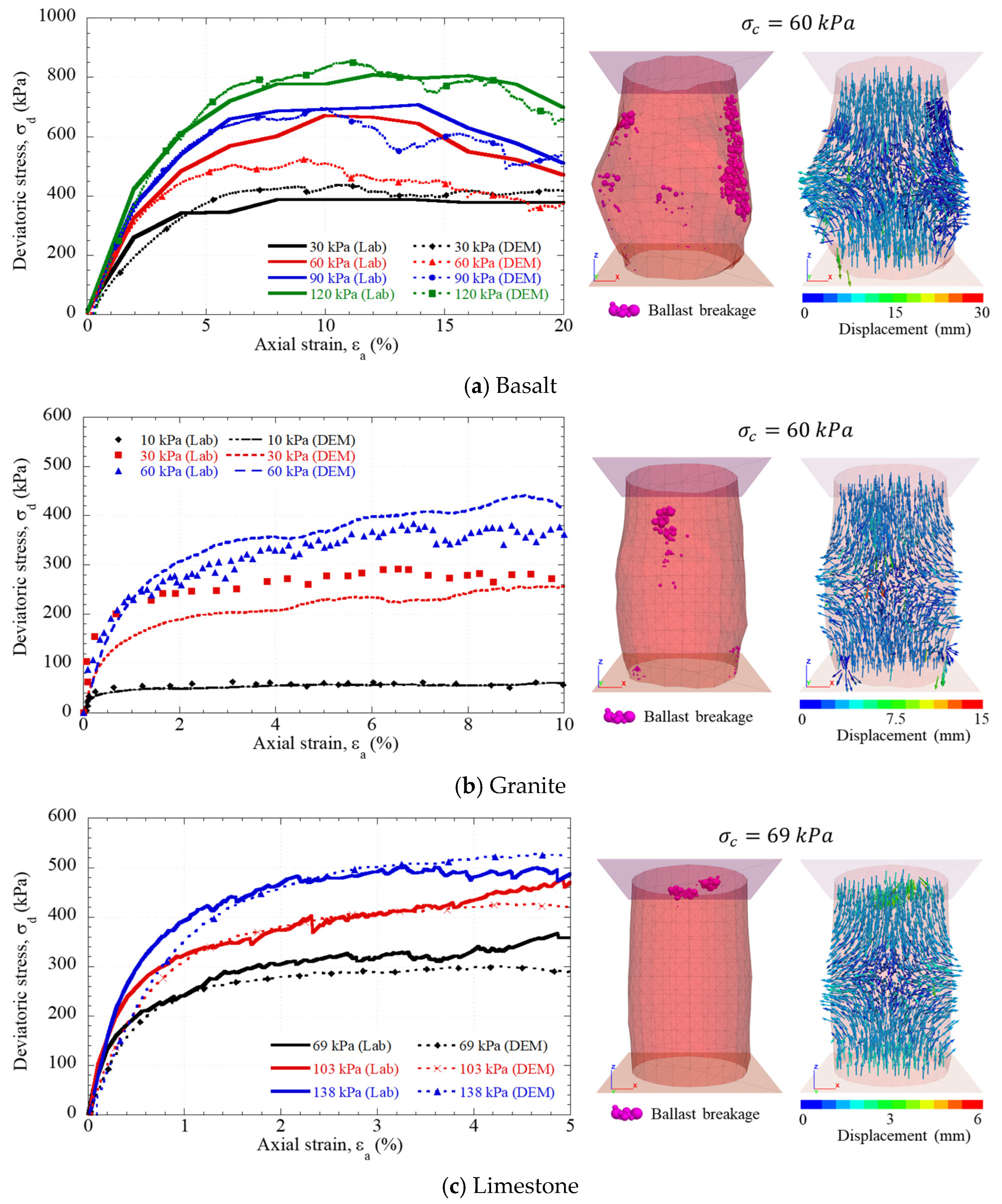
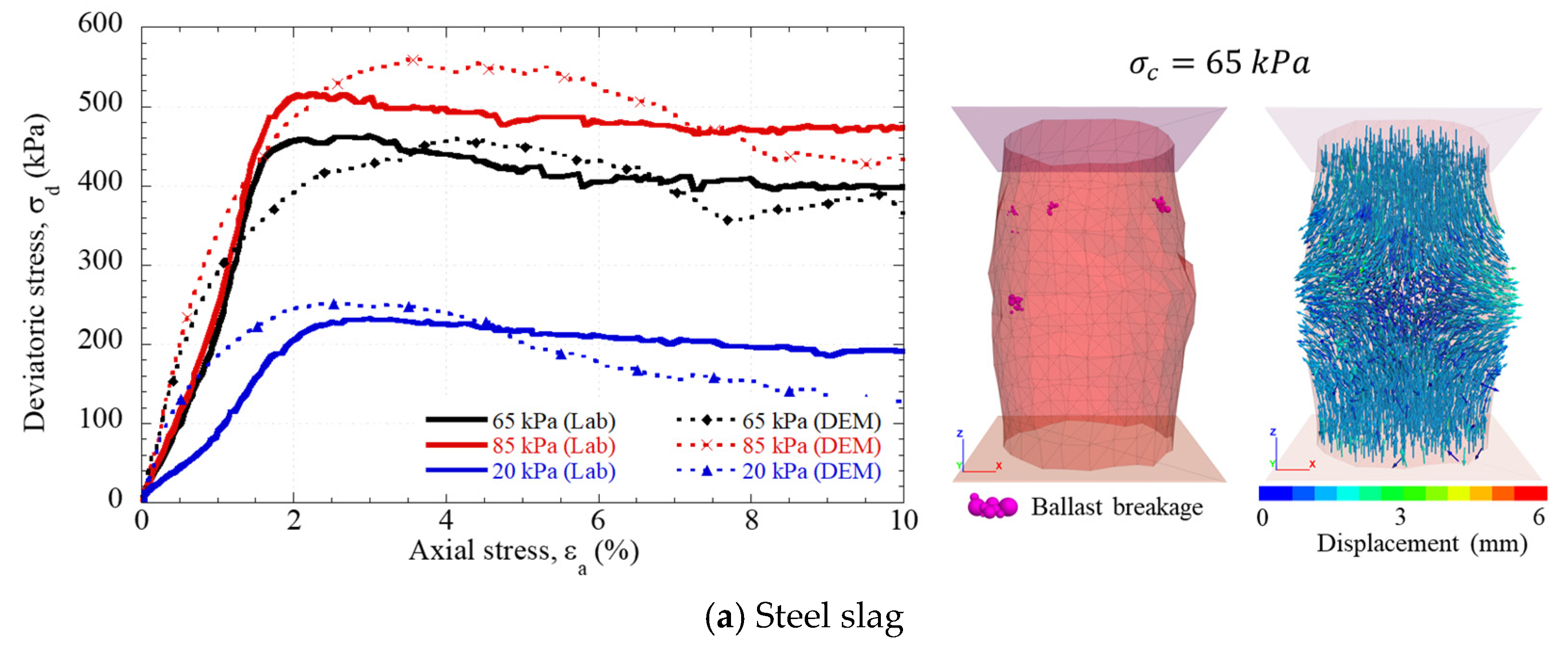
- The breakage indices, Bg, obtained from triaxial tests were low for all materials, indicating good mechanical behavior against fracture. It is important to mention that analysis under cyclic loading is recommended.
- Particle degradation was mainly concentrated in the <25 mm fractions, consistent with the ballast breakage index (BBI). Minimal differences were observed between curves, resulting in values of less than 5%, indicating good quality ballast.
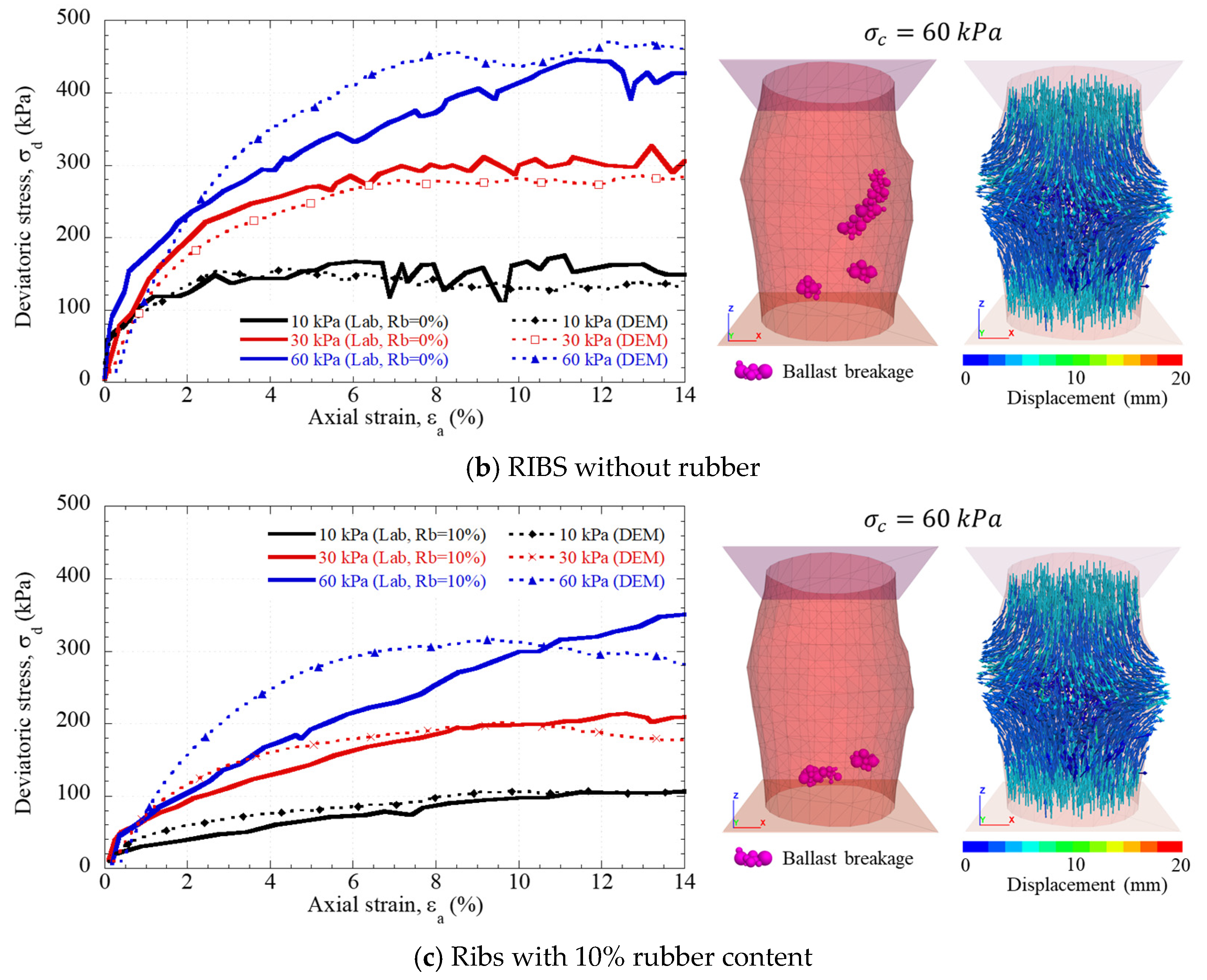
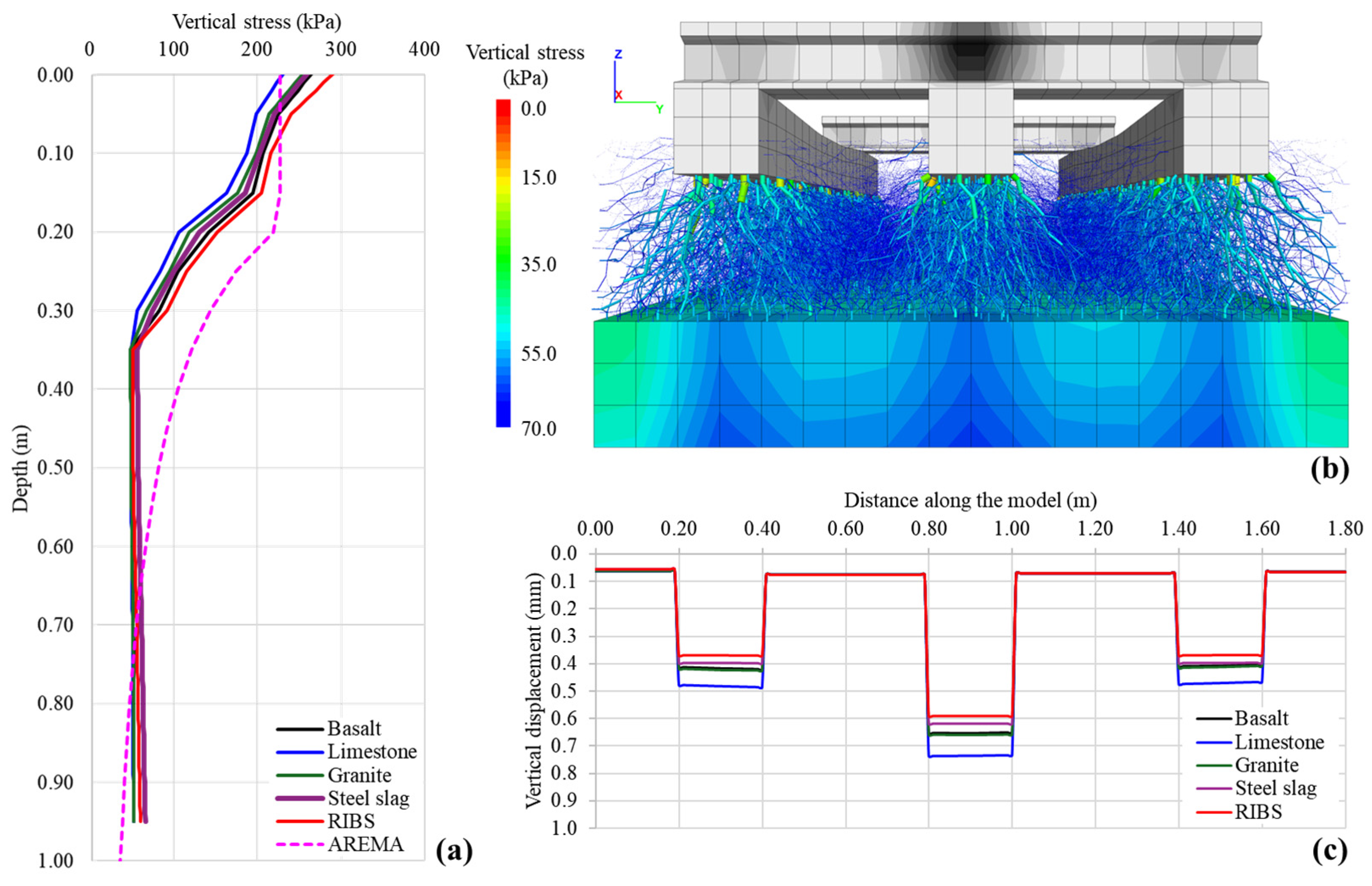
- The RIBS system (basalt mixed with rubber) showed the best overall performance, with the lowest fracture rate (0.05%) and reduced vertical displacements (<0.6 mm) under monotonic loading. From a practical perspective, the results question conventional empirical approaches, as in 80% of cases, stresses at the sleeper-ballast interface were higher than expected. In the models subjected to cyclic loading, a significant increase in vertical settlements was observed during the first cycles for the RIBS model. However, this model showed better stabilization of displacements compared to the others.
- The conventional materials (basalt, granite, and limestone) followed similar displacement trajectories, though with distinct magnitudes of settlement. Limestone showed the most significant final displacement (1.32 mm), followed by basalt (1.08 mm) and granite (0.71 mm). After 100 load cycles, all materials produced vertical stresses exceeding empirical estimates, except for the RIBS model, which reached a maximum stress of 177 kPa and exhibited a more uniform stress distribution.
- The incorporation of 10% rubber into the basalt ballast significantly improved mechanical performance: the BBI decreased by 51.0% (from 0.721 to 0.353), and the Marsal breakage index (Bg) reduced by 49.4% (from 7.373 to 3.729). These results confirm the effectiveness of rubber intermixing in reducing particle degradation and enhancing ballast resilience.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AREMA | American Railway Engineering and Maintenance-of-Way Association |
| BBI | Ballast Breakage Index |
| Bg | Breakage index Marsal |
| LA | Los Angeles index |
| MD | Micro-Deval index |
| DEM | Discrete element method |
| FDM | Finite difference method |
| RIBS | Rubber Intermixed ballast Systems |
References
- Selig, E.; Waters, J. Track Geotechnology and Substructure Management; Thomas Telford: London, UK, 1994. [Google Scholar]
- De Paiva, C.E.L.; Pereira, M.L. Sustainability of the Ballasted Track—A Comprehensive Review on Reducing the Use of Mineral Aggregates and the Role of Sub-ballast as a Protective Layer. In Sustainable Solutions for Railways and Transportation Engineering; Springer: Cham, Switzerland, 2018; pp. 67–100. [Google Scholar]
- Varandas, J.N.; Paixão, A.; Fortunato, E.; Hölscher, P. A Numerical Study on the Stress Changes in the Ballast Due to Train Passages. Procedia Eng. 2016, 143, 1169–1176. [Google Scholar] [CrossRef]
- Liu, H.; Zou, D. Associated generalized plasticity framework for modeling gravelly soils considering particle breakage. J. Eng. Mech. 2013, 139, 606–615. [Google Scholar] [CrossRef]
- Gräbe, P.J.; Clayton, C.R. Effects of principal stress rotation on permanent deformation in rail track foundations. J. Geotech. Geoenviron. Eng. 2009, 135, 555–565. [Google Scholar] [CrossRef]
- Mayoral Villa, J.M.; Olivera, N.; Tepalcapa, S.; Román, A.; Alcaraz, M. Numerical Assessment of Enhanced Urban-Train Support Systems. In Proceedings of the 10th European Conference on Numerical Methods in Geotechnical Engineering (NUMGE 2023), London, UK, 26–28 June 2023; International Society for Soil Mechanics and Geotechnical Engineering: London, UK, 2023; pp. 2903–2910. [Google Scholar]
- Shi, C.; Fan, Z.; Connolly, D.P.; Jing, G.; Markine, V.; Guo, Y. Railway ballast performance: Recent advances in the understanding of geometry, distribution and degradation. Transp. Geotech. 2023, 41, 101042. [Google Scholar] [CrossRef]
- Indraratna, B.; Salim, W. Mechanics of Ballasted Rail Tracks: A Geotechnical Perspective; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Indraratna, B.; Qi, Y.; Tawk, M.; Heitor, A.; Rujikiatkamjorn, C.; Navaratnarajah, S.K. Advances in ground improvement using waste materials for transportation infrastructure. Proc. Inst. Civ. Eng.-Ground Improv. 2022, 175, 3–22. [Google Scholar] [CrossRef]
- Indraratna, B.; Nimbalkar, S.; Rujikiatkamjorn, C. Track stabilisation with geosynthetics and geodrains, and performance verification through field monitoring and numerical modelling. Int. J. Railw. Technol. 2012, 1, 195–219. [Google Scholar] [CrossRef]
- Chen, C.; McDowell, G.R.; Thom, N.H. Investigating geogrid-reinforced ballast: Experimental pull-out tests and discrete element modelling. Soils Found. 2014, 54, 1–11. [Google Scholar] [CrossRef]
- Leshchinsky, B.; Ling, H. Effects of geocell confinement on strength and deformation behavior of gravel. J. Geotech. Geoenviron. Eng. 2013, 139, 340–352. [Google Scholar] [CrossRef]
- Indraratna, B.; Qi, Y.; Malisetty, R.S.; Navaratnarajah, S.K.; Mehmood, F.; Tawk, M. Recycled materials in railroad substructure: An energy perspective. Railw. Eng. Sci. 2022, 30, 304–322. [Google Scholar] [CrossRef]
- Naeini, M.; Mohammadinia, A.; Arulrajah, A.; Horpibulsuk, S. Recycled glass blends with recycled concrete aggregates in sustainable railway geotechnics. Sustainability 2021, 13, 2463. [Google Scholar] [CrossRef]
- Indraratna, B.; Qi, Y.; Ngo, T.; Malisetty, R.; Arachchige, C.K. Innovative and cost-effective rail track construction using recycled rubber. Railw. Eng. Sci. 2024, 33, 327–341. [Google Scholar] [CrossRef]
- Alves, R.; Rios, S.; Fortunato, E.; Viana da Fonseca, A.; Guimarães Delgado, B. Mechanical behaviour of steel slag–rubber mixtures: Laboratory assessment. Sustainability 2023, 15, 1563. [Google Scholar] [CrossRef]
- Sagar, N.; Hussain, A.; Hussaini, S.K.K. Experimental assessment of shear behavior of crumb rubber intermixed steel slag used as railway subballast. In Proceedings of the 4th Asia-Pacific Conference on Physical Modelling in Geotechnics (ACPMG 2024), Abu Dhabi, United Arab Emirates, 11–13 December 2024; International Society for Soil Mechanics and Geotechnical Engineering: London, UK, 2024. [Google Scholar] [CrossRef]
- Kaya, M. A Study on the Stress-Strain Behavior of Railroad Ballast Materials by Use of Parallel Gradation Technique. Ph.D. Thesis, Middle Eastern Technical University, Ankara, Turkey, 2004. [Google Scholar]
- Koh, T.; Moon, S.W.; Jung, H.; Jeong, Y.; Pyo, S. A feasibility study on the application of basic oxygen furnace (BOF) steel slag for railway ballast material. Sustainability 2018, 10, 284. [Google Scholar] [CrossRef]
- Esmaeili, M.; Nouri, R.; Yousefian, K. Experimental comparison of the lateral resistance of tracks with steel slag ballast and limestone ballast materials. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2017, 231, 175–184. [Google Scholar] [CrossRef]
- Arachchige, C.M.; Indraratna, B.; Qi, Y.; Vinod, J.S.; Rujikiatkamjorn, C. Deformation and degradation behaviour of Rubber Intermixed Ballast System under cyclic loading. Eng. Geol. 2022, 307, 106786. [Google Scholar] [CrossRef]
- Arachchige, C.M.K. Experimental and Numerical Study of Rubber Intermixed Ballast System Subjected to Monotonic and Cyclic Loading; University of Technology: Sydney, Australia, 2022. [Google Scholar]
- Bian, X.; Jiang, H.; Cheng, C.; Chen, Y.; Chen, R.; Jiang, J. Full-scale model testing on a ballastless high-speed railway under simulated train moving loads. Soil Dyn. Earthq. Eng. 2014, 66, 368–384. [Google Scholar] [CrossRef]
- Indraratna, B.; Hunt, H.; Malisetty, R.S.; Alagesan, S.; Qi, Y.; Rujikiatkamjorn, C. Optimization of inputs for the application of ANN to rail track granular materials. Can. Geotech. J. 2024, 62, 1–22. [Google Scholar] [CrossRef]
- Godson, M.D.; Rajesh, B.G.; Kumar, P. Electric arc furnace slag—A prospective alternative for railway sub-ballast layer. Constr. Build. Mater. 2025, 483, 141702. [Google Scholar] [CrossRef]
- Nasrollahi, K.; Dijkstra, J.; Nielsen, J.C.O. Towards real-time condition monitoring of a transition zone in a railway structure using fibre Bragg grating sensors. Transp. Geotech. 2024, 44, 101166. [Google Scholar] [CrossRef]
- Chen, J.; Liu, Y.; Hu, Q.; Gao, R. Effects of particle size and grading on the breakage of railway ballast: Laboratory testing and numerical modeling. Sustainability 2023, 15, 16363. [Google Scholar] [CrossRef]
- Li, W.; Bian, X.; Duan, X.; Tutumluer, E. Full-scale model testing on ballasted high-speed railway: Dynamic responses and accumulated settlements. Transp. Res. Rec. 2018, 2672, 125–135. [Google Scholar] [CrossRef]
- Sayeed, M.A.; Shahin, M.A. Design of ballasted railway track foundations using numerical modelling. Part I Development. Can. Geotech. J. 2018, 55, 353–368. [Google Scholar] [CrossRef]
- Edwards, J.R.; Gao, Z.; Wolf, H.E.; Dersch, M.S.; Qian, Y. Quantification of concrete railway sleeper bending moments using surface strain gauges. Measurement 2017, 111, 197–207. [Google Scholar] [CrossRef]
- Lu, M.; McDowell, G.R. Discrete element modelling of railway ballast under monotonic and cyclic triaxial loading. Géotechnique 2010, 60, 459–467. [Google Scholar] [CrossRef]
- Lim, W.L.; McDowell, G.R.; Collop, A.C. The application of Weibull statistics to the strength of railway ballast. Granul. Matter 2004, 6, 229–237. [Google Scholar] [CrossRef]
- Li, D.; Selig, E.T. Method for railroad track foundation design. I: Development. J. Geotech. Geoenviron. Eng. 1998, 124, 316–322. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- ASTM C136/C136M-19; Standard Test Method for Sieve Analysis of Fine and Coarse Aggregates. ASTM International: West Conshohocken, PA, USA, 2019.
- Indraratna, B.; Ionescu, D.; Christie, H.D. Shear behavior of railway ballast based on large-scale triaxial tests. J. Geotech. Geoenviron. Eng. 1998, 124, 439–449. [Google Scholar] [CrossRef]
- Xiao, J.; Zhang, D.; Wei, K.; Luo, Z. Shakedown behaviors of railway ballast under cyclic loading. Constr. Build. Mater. 2017, 155, 1206–1214. [Google Scholar] [CrossRef]
- Qian, Y.; Tutumluer, E.; Hashash, Y.M.; Ghaboussi, J. Triaxial testing of new and degraded ballast under dry and wet conditions. Transp. Geotech. 2022, 34, 100744. [Google Scholar] [CrossRef]
- Delgado, B.G.; da Fonseca, A.V.; Fortunato, E.; Maia, P. Mechanical behavior of inert steel slag ballast for heavy haul rail track: Laboratory evaluation. Transp. Geotech. 2019, 20, 100243. [Google Scholar] [CrossRef]
- Arachchige, C.M.; Indraratna, B.; Qi, Y.; Vinod, J.S.; Rujikiatkamjorn, C. Geotechnical characteristics of a rubber intermixed ballast system. Acta Geotech. 2022, 17, 1847–1858. [Google Scholar] [CrossRef]
- Jiang, M.J.; Yu, H.S.; Harris, D. A novel discrete model for granular material incorporating rolling resistance. Comput. Geotech. 2005, 32, 340–357. [Google Scholar] [CrossRef]
- Lu, M.M.G.R.; McDowell, G.R. The importance of modelling ballast particle shape in the discrete element method. Granul. Matter 2007, 9, 69–80. [Google Scholar] [CrossRef]
- Li, L.; Liu, W.; Ma, M.; Jing, G.; Liu, W. Research on the dynamic behaviour of the railway ballast assembly subject to the low loading condition based on a tridimensional DEM-FDM coupled approach. Constr. Build. Mater. 2019, 218, 135–149. [Google Scholar] [CrossRef]
- Xiao, Y.; Shen, Z.; Tan, P.; Hua, W.; Wang, M.; Jitsangiam, P. Evaluating enhancement effect of bottom groove shape on lateral resistance of frictional sleepers in ballasted railway track via hybrid DEM-FDM approach. Constr. Build. Mater. 2024, 436, 136755. [Google Scholar] [CrossRef]
- Jiang, M.J.; Shen, Z.F.; Wang, J.F. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances. Comput. Geotech. 2015, 65, 147–163. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, C.; Markine, V.; Jing, G.; Zhai, W. Calibration for discrete element modelling of railway ballast: A review. Transp. Geotech. 2020, 23, 100341. [Google Scholar] [CrossRef]
- Coetzee, C.J. Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar] [CrossRef]
- Itasca Consulting Group. PFC3D 6.0 Particle Flow Code in Three Dimensions, Theory and Implementation Volume; Itasca Consulting Group: Minneapolis, MN, USA, 2016. [Google Scholar]
- Ciantia, M.O.; Arroyo, M.; Calvetti, F.; Gens, A. An approach to enhance efficiency of DEM modelling of soils with crushable grains. Géotechnique 2015, 65, 91–110. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and fragmentation. J. Geophys. Res. 1986, 91, 1921–1926. [Google Scholar] [CrossRef]
- McDowell, G.R.; Bolton, M.D.; Robertson, D. The fractal crushing of granular materials. J. Mech. Phys. Solids 1996, 44, 2079–2101. [Google Scholar] [CrossRef]
- Li, H.Q.; Mcdowell, G.R. Discrete element modelling of under sleeper pads using a box test. Granul. Matter 2018, 20, 26. [Google Scholar] [CrossRef]
- Liu, F.; Wu, M.; Wang, H. Effect of particle size ratio and mix ratio on mechanical behavior of rubber-sand mixtures. J. Eng. Geol. 2019, 27, 376–389. [Google Scholar]
- Wang, C.; Deng, A.; Taheri, A. Three-dimensional discrete element modeling of direct shear test for granular rubber–sand. Comput. Geotech. 2018, 97, 204–216. [Google Scholar] [CrossRef]
- Perez, J.L.; Kwok, C.Y.; Senetakis, K. Micromechanical analyses of the effect of rubber size and content on sand-rubber mixtures at the critical state. Geotext. Geomembr. 2017, 45, 81–97. [Google Scholar] [CrossRef]
- Perez, J.L.; Kwok, C.Y.; Senetakis, K. Effect of rubber size on the behaviour of sand-rubber mixtures: A numerical investigation. Comput. Geotech. 2016, 80, 199–214. [Google Scholar] [CrossRef]
- Gong, L.; Nie, L.; Xu, Y.; Wang, H.; Zhang, T.; Du, C.; Wang, Y. Discrete element modelling of the mechanical behaviour of a sand-rubber mixture containing large rubber particles. Constr. Build. Mater. 2019, 205, 574–585. [Google Scholar] [CrossRef]
- Guo, Y.; Ji, Y.; Zhou, Q.; Markine, V.; Jing, G. Discrete element modelling of rubber-protected ballast performance subjected to direct shear test and cyclic loading. Sustainability 2020, 12, 2836. [Google Scholar] [CrossRef]
- Wu, H.; Zhu, L.; Song, W.; Xu, Z.; Xu, F.; Gong, H. Impact performance of ballast by incorporating waste tire-derived aggregates. Constr. Build. Mater. 2021, 288, 122992. [Google Scholar] [CrossRef]
- Zhang, F.; Yao, Q.; Wang, H.; Feng, H.; Chang, J.; Lu, L.; Jiang, M. DEM analysis of the cyclic behavior of ballast mixed with crumb rubber. Constr. Build. Mater. 2023, 375, 130975. [Google Scholar] [CrossRef]
- Ngo, T.; Indraratna, B.; Coop, M.; Qi, Y. Behaviour of ballast stabilised with recycled rubber mat under impact loading. Géotechnique 2023, 75, 192–212. [Google Scholar] [CrossRef]
- Tran, V.D.; Meguid, M.A.; Chouinard, L.E. Discrete element and experimental investigations of the earth pressure distribution on cylindrical shafts. Int. J. Geomech. 2014, 14, 80–91. [Google Scholar] [CrossRef]
- AREMA. American Railway Engineering and Maintenance-of-Way Association. Man. Railw. Eng. 2013, 2, 55–57. [Google Scholar]
- Mosayebi, S.A.; Zakeri, J.A.; Esmaeili, M. Some aspects of support stiffness effects on dynamic ballasted railway tracks. Period. Polytech. Civ. Eng. 2016, 60, 427–436. [Google Scholar] [CrossRef]
- Chen, J.; Vinod, J.S.; Indraratna, B.; Ngo, T.; Liu, Y. DEM study on the dynamic responses of a ballasted track under moving loading. Comput. Geotech. 2023, 153, 105105. [Google Scholar] [CrossRef]


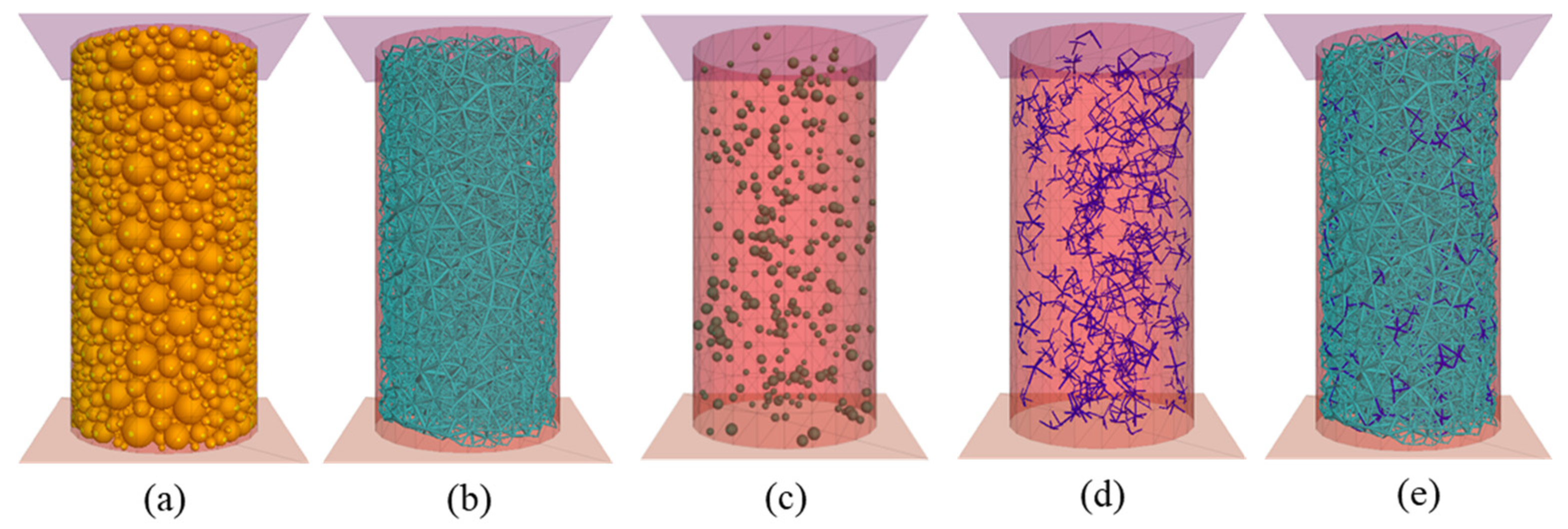
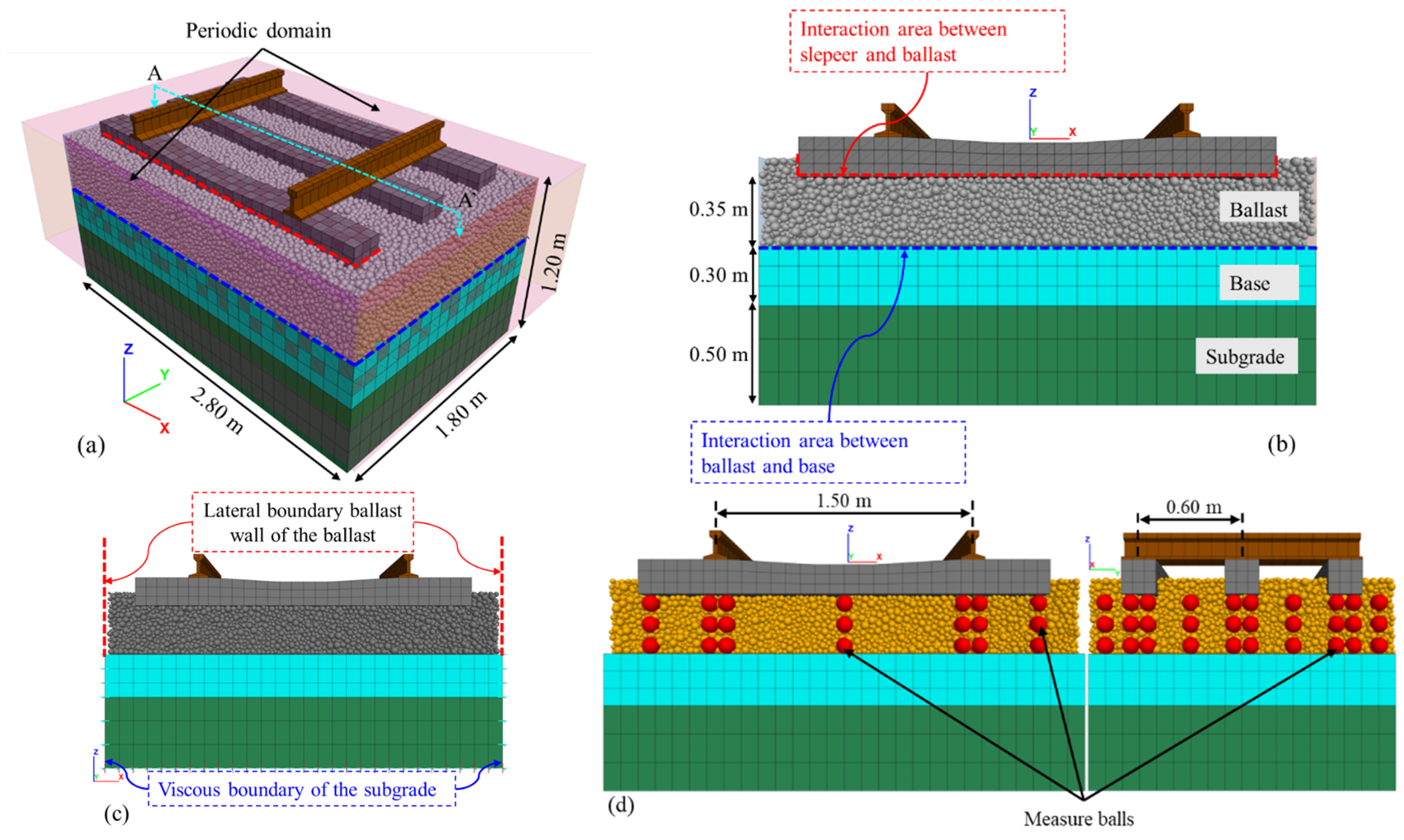
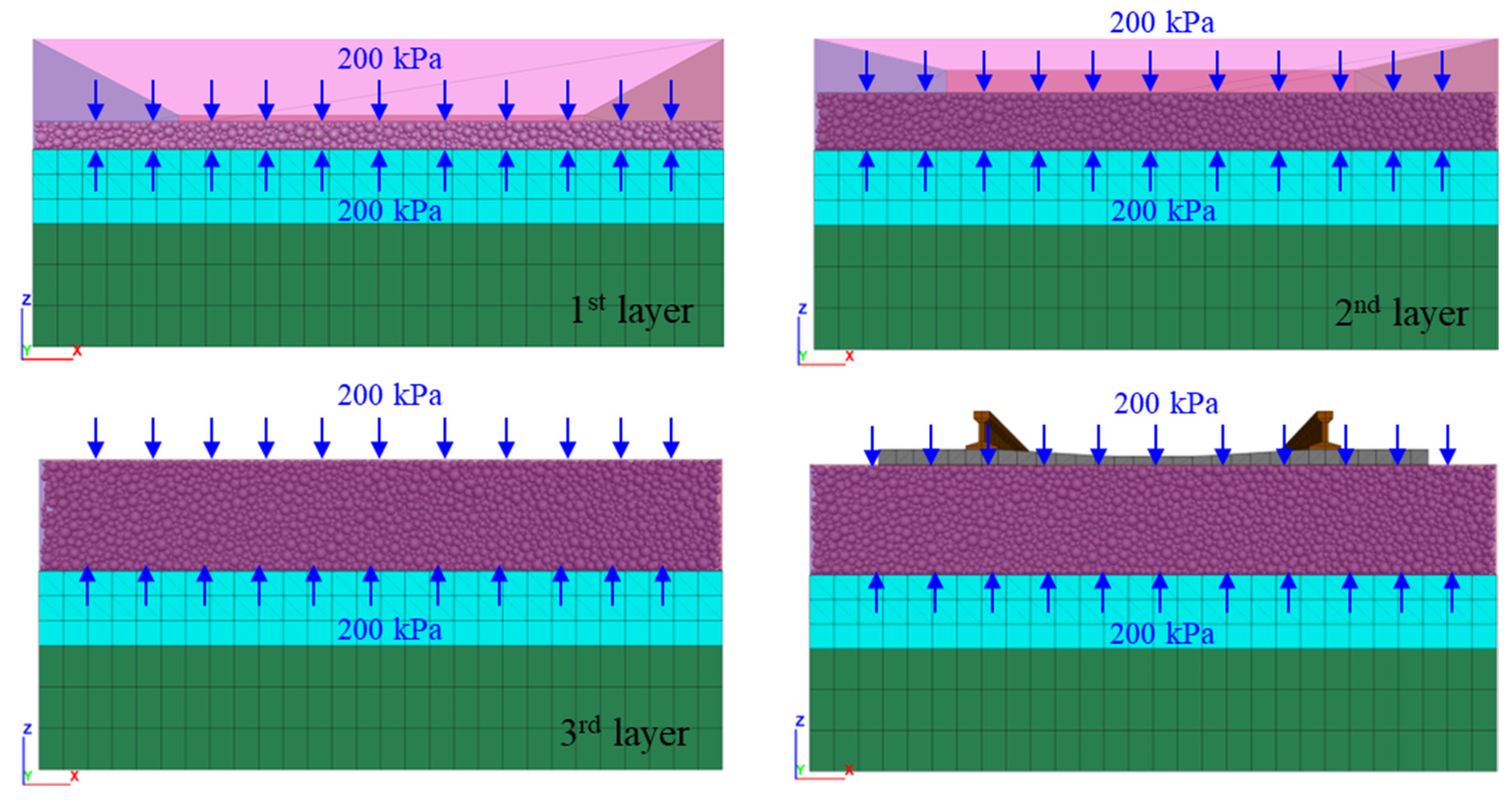
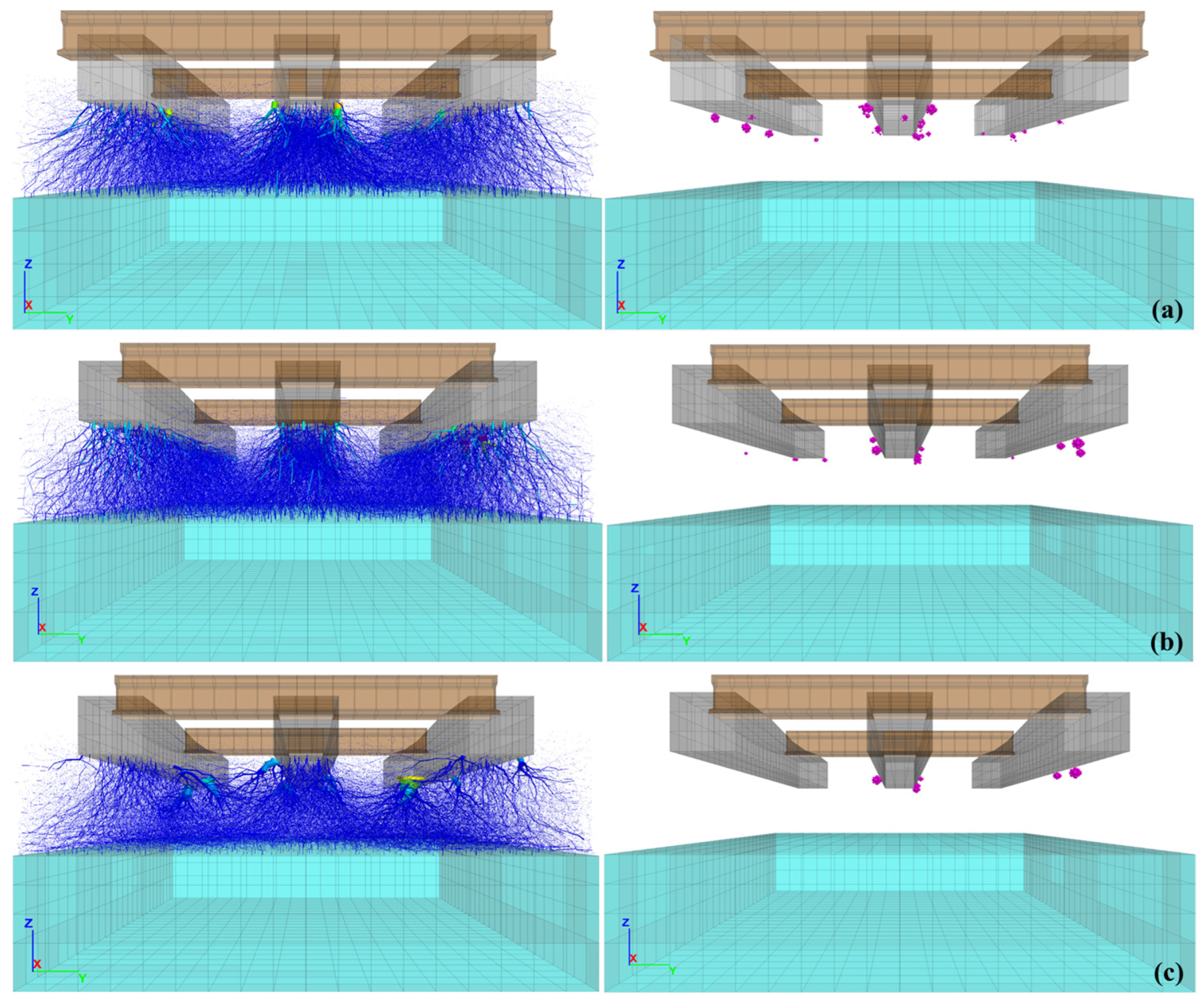



| Material | Density | MD 1 | LA 2 | Uniformity Coefficient, Cu | Coefficient of Curvature, Cc | Dmax | Dmin |
|---|---|---|---|---|---|---|---|
| ρ | (%) | (%) | (-) | (-) | (mm) | (mm) | |
| Basalt [36] | 2.60 | 5.10 | 12.10 | 1.48 | 0.99 | 53 | 13 |
| Granite [37] | 2.68 | 1.52 | 0.90 | 63 | 16 | ||
| Limestone [38] | 2.65 | 1.46 | 0.97 | 63 | 13 | ||
| Steel Slag [39] | 3.20 | 11.00 | 23.00 | 1.94 | 1.02 | 28 | 4 |
| RIBS [40] | 2.80 | 5.20 | 11.70 | 2.60 | 1.40 | 53 | 4.75 |
| Material | Type of Test | Void Ratio | Confining Pressure, (kPa) | Axial Strain, (%) |
|---|---|---|---|---|
| Basalt | Triaxial | 0.79–0.84 | 30/60/90/120 | 20 |
| Granite | Triaxial | - | 10/30/60 | 10 |
| Limestone | Triaxial | - | 69/103/138 | 5 |
| Steel Slag | Triaxial | - | 20/65/85 | 10 |
| RIBS | Triaxial | 0.76–0.82 | 10/30/60 | 20 |
| Material | Density (kg/m3) | Normal Stiffness, kn | Shear Stiffness, ks | Damping | Friction Coefficient, μ | Rolling Friction Coefficient, μr |
|---|---|---|---|---|---|---|
| (N/m) | (N/m) | - | - | - | ||
| Basalt | 2650 | 2 × 106 | 2 × 106 | 0.7 | 0.4 | 0.8 |
| Granite | 2680 | 3 × 108 | 3 × 108 | 0.7 | 0.5 | 0.6 |
| Limestone | 2600 | 2 × 107 | 2 × 107 | 0.7 | 0.5 | 0.7 |
| Steel slag | 3200 | 1 × 109 | 1 × 109 | 0.7 | 0.4 | 0.4 |
| RIBS | 2650 | 5 × 108 | 5 × 108 | 0.7 | 0.3 | 0.7 |
| Group | Constitutive Model | γ | c | ϕ | E | ν |
|---|---|---|---|---|---|---|
| (kN/m3) | (MPa) | (°) | (MPa) | (-) | ||
| Subgrade | Mohr–Coulomb | 22.0 | 0 | 43 | 143 | 0.30 |
| Base | Elastic | 17.6 | 9,590 | 0.35 | ||
| Sleeper | Elastic | 24.0 | 47,500 | 0.18 | ||
| Rail | Elastic | 79.0 | 210,000 | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayoral, J.M.; Olivera, N. Performance Evaluation of Conventional and Recycled Ballast Materials: A Coupled FDM-DEM Approach Considering Particle Breakage. Appl. Sci. 2025, 15, 11460. https://doi.org/10.3390/app152111460
Mayoral JM, Olivera N. Performance Evaluation of Conventional and Recycled Ballast Materials: A Coupled FDM-DEM Approach Considering Particle Breakage. Applied Sciences. 2025; 15(21):11460. https://doi.org/10.3390/app152111460
Chicago/Turabian StyleMayoral, Juan Manuel, and Nohemí Olivera. 2025. "Performance Evaluation of Conventional and Recycled Ballast Materials: A Coupled FDM-DEM Approach Considering Particle Breakage" Applied Sciences 15, no. 21: 11460. https://doi.org/10.3390/app152111460
APA StyleMayoral, J. M., & Olivera, N. (2025). Performance Evaluation of Conventional and Recycled Ballast Materials: A Coupled FDM-DEM Approach Considering Particle Breakage. Applied Sciences, 15(21), 11460. https://doi.org/10.3390/app152111460






