Short-Duration Monofractal Signals for Heart Failure Characterization Using CNN-ELM Models

Abstract

Monofractal analysis offers a promising framework for characterizing cardiac dynamics, particularly in the early detection of heart failure. However, most existing approaches rely on long-duration physiological signals and do not explore the classification of disease severity. In this study, we propose a hybrid CNN-ELM model trained exclusively on synthetic monofractal time series of short length (128 to 512 samples), aiming to assess its ability to distinguish between healthy individuals and varying degrees of heart failure defined by the NYHA functional classification. Our results show that Hurst exponent distributions reflect the progressive loss of complexity in cardiac rhythms as heart failure severity increases. The model successfully classified both binary (healthy vs. sick) and multiclass (NYHA I–IV) scenarios by grouping Hurst exponent values ($H_{0.1}$ to $H_{0.9}$) into clinical categories, achieving peak accuracy ranges of 97.3–98.9% for binary classification and 96.2–98.8% for multiclass classification across signal lengths of 128, 256, and 512 samples. Importantly, the CNN-ELM architecture demonstrated fast training times and robust generalization, outperforming previous approaches based solely on support vector machines. These findings highlight the clinical potential of monofractal indices as non-invasive biomarkers of cardiovascular health and support the use of short synthetic signals for scalable, low-cost screening applications. Future work will extend this framework to multifractal and real-world clinical data and explore its integration into intelligent diagnostic systems.

1. Introduction

The study of cardiovascular diseases is crucial, as they are one of the leading causes of mortality worldwide. The classification of heart diseases through the analysis of short time series, such as heart rate variability (HRV), allows for the detection of changes in cardiac activity over short time intervals, facilitating the early diagnosis of these conditions. The combination of this approach with artificial intelligence tools improves both the accuracy and speed in identifying anomalous patterns, which can transform monitoring and early detection of heart diseases, optimizing treatment and saving lives.

HRV analysis through the intervals between successive heartbeats (known as RR intervals) is a non-invasive technique that has proven useful for both the diagnosis and prognosis of heart diseases and neuropathies. Historically, statistical analysis of the RR signal was one of the first applied methods and remains highly effective. Similarly, spectral analysis of the RR sequence is another commonly used technique [1]. Both methods have been of great interest over the past 25 years due to their non-invasive nature. Currently, advances in machine learning have generated great interest in its application for the detection and classification of cardiovascular diseases [2,3,4]. These non-invasive methods provide a safer, simpler, and more cost-effective alternative compared to more complex invasive techniques. Among their main advantages are accessibility, safety, and the possibility of continuous monitoring, allowing detailed tracking of changes in HRV and, consequently, the patient’s health status.

Machine learning techniques, such as deep learning, support vector machines (SVM), random forests, and gradient boosting methods, have been successfully applied to classify patients with various heart conditions, grouping them into categories such as healthy, sick, and different subtypes of heart disease [5,6]. These approaches have proven to be highly effective in differentiating healthy individuals from those with heart pathologies [7,8,9]. The incorporation of machine learning and deep learning algorithms offers great potential for improving early detection, risk assessment, and treatment planning [10,11,12]. Models such as convolutional neural networks (CNNs) [13] and multilayer perceptrons (MLPs) [14] have shown promising results in diagnosing cardiovascular diseases based on clinical data [15,16].

HRV is a key indicator of cardiovascular health, as it reflects fluctuations in the time intervals between successive heartbeats. HRV analysis through short time series allows for the rapid detection of subtle changes in cardiac activity, which is crucial for identifying irregularities that may be early signs of heart disease. Time series are essential for studying data variation over time, enabling the identification of patterns and trends. While traditional time-series analysis focuses on long periods [17,18], in certain contexts, such as when data is limited or events occur over short intervals, it is essential to work with short time series [19,20,21]. In the case of cardiovascular series, short-term variations, occurring within seconds or minutes, are often related to specific events such as arrhythmias, whereas long-term variations may be linked to gradual changes in cardiovascular health [22,23].

Various artificial intelligence (AI) methods have proven effective in time-series classification. Deep learning has been widely used for prediction and anomaly detection [24,25,26,27]. Recurrent neural networks (RNNs), long short-term memory (LSTM) networks [28], and CNNs [29] are particularly effective models for time-series analysis, as they can capture complex patterns and handle sequences of varying lengths [30,31,32,33]. In a similar context, a CNN together with a non-iterative extreme learning machine (ELM) has also been used to analyze the severity of heart disease [34]. The ELM classifier is mainly valued for its fast training speed and generalization ability, comparable to conventional approaches [35,36,37].

In recent years, hybrid approaches combining convolutional layers with transformer mechanisms have emerged for the analysis of short physiological signals. For example, Hassanuzzaman et al. [38] proposed a residual 1D-CNN with attention transformer to classify short 5-second cardiac sound segments, achieving high accuracy even with brief recordings. Such architectures leverage convolutional layers’ local feature extraction with attention-based mechanisms to capture global dependencies across the signal. In the ECG domain, convolution + transformer models have been used for stress detection in an end-to-end fashion, avoiding handcrafted feature engineering [39]. More recently, PhysioWave, a multiscale wavelet-transformer framework, has demonstrated promising performance in representing non-stationary physiological signals across modalities [40].

Short monofractal time series analysis has revealed characteristics that are not evident in longer series [41,42]. Detrended fluctuation analysis (DFA) has been effective in studying short monofractal series [43], and its generalization for multifractal analysis has found applications in numerous fields [44]. This methodology has been successfully applied, for example, in the study of currency exchange rates [45,46].

As mentioned earlier, various AI-based methods allow for addressing the problem of classification using short time series. Furthermore, AI-based methods have been employed to classify short/very short monofractal series and, compared with traditional methods for mono-multifractal analysis, have achieved much better performance [33]. In particular, the authors of [33] used a CNN-SVM approach and compared its performance with DFA in classifying short monofractal time series, showing that CNN-SVM performs better than does DFA for monofractal series of length $L=128,256,512,1024$.

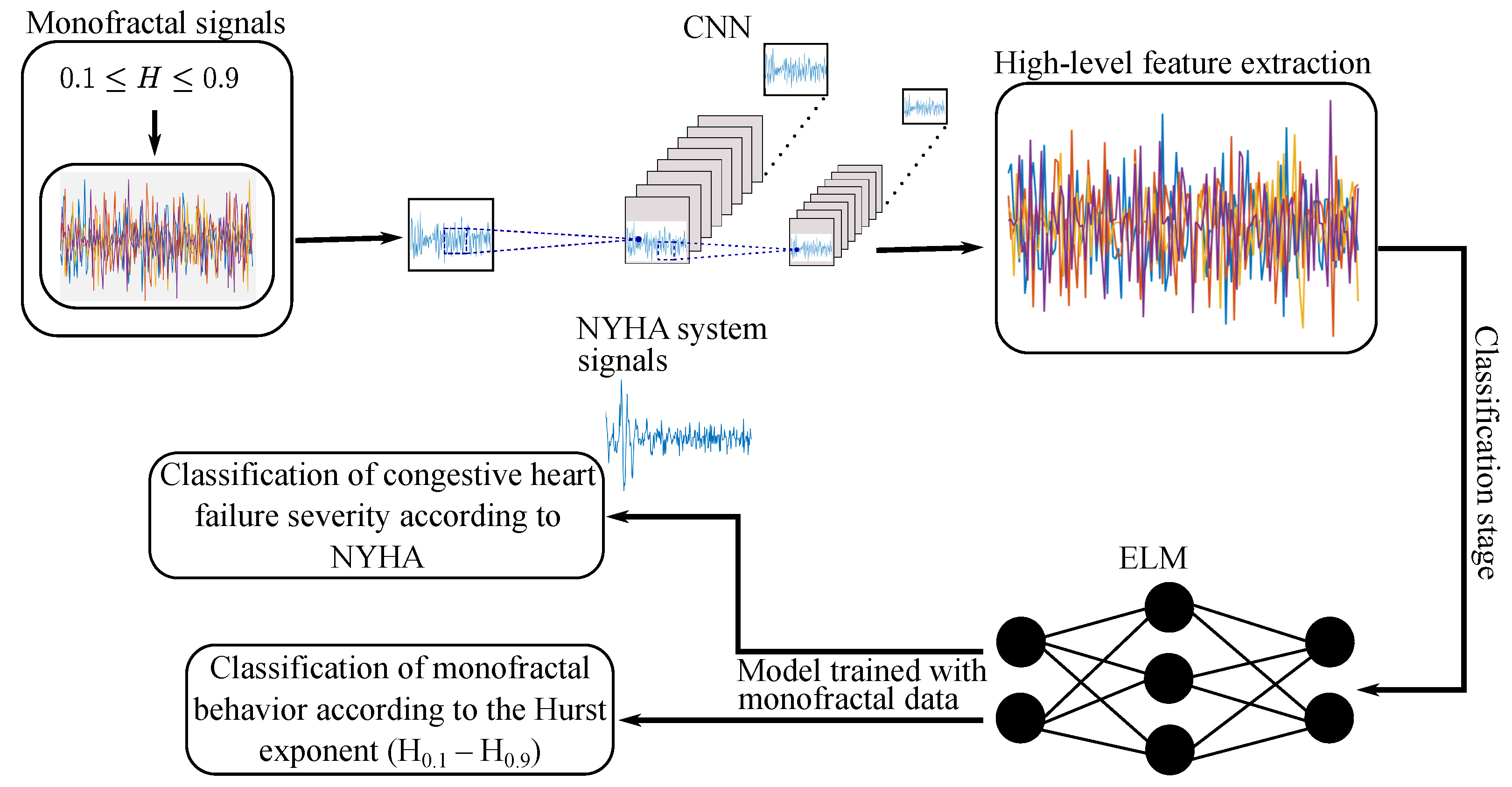
This work proposes the use of neural network models to establish a correspondence between degrees of heart disease (according to NYHA classification) and monofractal models derived from short HRV (RR intervals) time series. Specifically, a hybrid CNN-ELM approach is proposed, which integrates a CNN for monofractal feature extraction with an ELM classifier for disease severity distinction. The rationale for this scheme is that CNNs are capable of capturing hierarchical and multiscale patterns in time series, whereas ELM ensures fast training and reduces the risk of local minima. Furthermore, the performance of these models was evaluated based on the length of the RR intervals, highlighting, as an additional advantage, their fast training times, which surpassed those of previous methods.

2. Machine Learning Architectures

2.1. Convolutional Neural Network

Convolutional neural networks are deep learning models, initially designed for image-processing tasks [47,48]. Owing to their ability to learn local and global features, they have been successfully adapted to various applications, such as speech recognition, text analysis, and time-series models. Although there are multiple variants of the standard scheme, all share a basic structure, including the convolutional, pooling, and fully connected layers [48]. The deep layers, stacked on top of each other, efficiently capture and represent complex patterns in the data. A short description of these layers is provided below.

2.1.1. Convolution Layer

A convolution layer is the fundamental component of a CNN architecture, focused mainly on feature extraction through a series of combined linear and nonlinear operations. Precisely, a convolution operation maps linear features, while an activation function introduces nonlinearity in the output representation [49]. This convolution operator extracts meaningful patterns from the input tensor using a sliding kernel (filter). The sliding window generates a feature map, where each value is the sum of the element-to-element product between the kernel and the tensor at its corresponding position. By repeating this processing technique with multiple filters, the convolutional layer includes several feature maps, referred to in deep learning as depth (number of channels). In this instance, the number of channels and the kernel size are two key hyperparameters in the model’s performance, appropriately adjusted according to stride and padding. The stride has to do with the kernel displacement, while the padding (optional) handles the edges of the tensor by adding a border. For its part, the activation function introduces nonlinearity in the multiple feature maps, allowing the network to learn the complex representations of the inputs. Mathematically, given the input tensor $\mathit{X}$, the output of the convolutional layer ℓ is as follows [50]:

$$F_{i,j}^{(\ell )}=g\left(\sum _{p=1}^c\sum _{q=1}^c{K}_{p,q}^{(\ell )}·X_{i+p,j+q}^{(\ell -1)}+b^{(\ell )}\right),$$

(1)

where $K_{p,q}^{(\ell )}$ represents the convolutional kernel of size $c \times c$ in the ℓ-th layer, $X_{i+p,j+q}^{(\ell -1)}$ denotes the spatial position of the input tensor corresponding to the $(\ell -1)$ layer, and $g(·)$ is a nonlinear activation function. The sliding window extracts complex patterns from the input feature map using the dot product, enriched by the addition of a bias unit $b^{(\ell )}$.

Previous research has simulated the nonlinear behavior of information through smooth nonlinear functions, such as the sigmoid function or hyperbolic tangent [51]. Currently, the rectified linear unit (Relu) nonlinear activation function, defined as $g\left(x\right)=max\{0,x\}$, is the most commonly used in deep learning [51,52]. In addition to these transformations, other variants of Relu have been incorporated with success, such as leaky Relu, parametric Relu, and exponential linear unit [51].

2.1.2. Pooling Layer

The pooling layer operates on each of the feature maps or output channels of the convolutional layer. The main aim is to reduce the spatial dimension of the compact block of features coming from the convolutional layer. Despite reducing the resolution of the feature map, it always preserves the most relevant information. In this sense, a sliding filter, similar to convolution operations, significantly reduces the number of model parameters by appropriately setting the filter size, stride, and padding. With the architecture valuing only meaningful patterns over the feature map, several pooling operators have successfully performed this task. Among the most traditional transformations are max pooling, global average pooling, mixed pooling, $L_p$ pooling, and stochastic pooling [53]. Consider a numerical expression: Given the output feature map ${\mathit{F}}^{\left(n\right)}$ of the convolutional layer n, the output of the pooling layer n is as follows [54]:

$$P_{i,j}^{\left(n\right)}=h(F_{1+m(i-1),1+m(j-1)}^{\left(n\right)},\dots ,F_{mi,1+m(j-1)}^{\left(n\right)},\dots ,F_{1+m(i-1),mj}^{\left(n\right)},\dots ,F_{mi,mj}^{\left(n\right)}),$$

(2)

where $h(·)$ is the spatial reduction transformation, $m\times m$ is the size of the local spatial region, and $i,j=1,\dots ,{\displaystyle \frac{p-q+1}{m}}$. Here, p denotes the size of the input feature map, and q is the size of the kernel.

2.1.3. Fully Connected Layer

This last layer receives the flattened high-level features in a one-dimensional vector. These input features pass through a few hierarchical levels of the fully connected layer, processed through an affine transformation and a nonlinear function. In classification tasks, the model usually includes the Softmax function to convert the output features into class probabilities, as shown in the equation below [55]:

$$\mathrm{Softmax}\left({\theta }^i\mathit{x}\right)=P(y=i|\mathit{x};\theta )={\displaystyle \frac{\exp \left({\theta }^i\mathit{x}\right)}{{\displaystyle \sum _{j=1}^m\exp \left({\theta }^j\mathit{x}\right)}}},$$

(3)

where ${\theta }^i\mathit{x}$ represents the feature of the i-th class, m is the number of categories, and ${\theta }^i$ for $i=1,\dots ,d$ are the optimized parameters in the classification layer.

When the input feature vector is directly linked to the expected target, the operations involved are the same as those in a simple logistic regression or a standard MLP scheme. However, any machine learning model can be integrated to solve a specific task, such as a support vector machines, artificial neural networks, decision trees, and random forests. Among these classifiers, the MLP network is the most widely used method [34]. Formally, given the input vector $\mathit{x}$ and its corresponding objective vector $\mathit{y}$, the optimization problem includes a cost function defined between the predicted outputs and the desired objective:

$$\mathrm{minimize}:J(\theta ;\mathit{x},\mathit{y})={\displaystyle \frac{1}{2}}{\parallel {\mathit{h}}_{\theta }\left(\mathit{x}\right)-\mathit{y}\parallel }^2,$$

(4)

where $\theta$ is the set of weights and biases, and ${\mathit{h}}_{\theta }(·)$ is the output of the Softmax layer.

In addition to the least squares cost function introduced in Equation (4), there are other optimization approaches, such as hinge, Huber, and cross-entropy [56]. In the training and testing stages, the backpropagation learning mechanism and a gradient-based optimizer are two fundamental tools in the parameter update scheme [57].

2.2. Extreme Learning Machine Networks

The ELM network is an alternative approach for the fast training of conventional models, with successful applications in regression, classification, and clustering tasks [58,59]. Its randomized design avoids the use of backpropagation, overcoming common challenges such as local minima, learning rate sensitivity, and slow convergence. In addition, it stands out for its fast training speed, computational simplicity, and universal approximation capability [35,36]. The ELM structure consists of three layers—input, hidden, and output—connected by neurons through weights and biases. During the feature learning phase, the hidden weights and biases are randomly assigned, while the output weights are the adjustable parameters of the model. In this formulation, $\mathit{W}$ and $\mathit{b}$ represent the hidden weights and biases; $g(·)$ is an activation function; and N, d, and L correspond to the number of training samples, input features, and hidden neurons, respectively. The optimal search for parameters, denoted as $\beta \in {\mathbb{R}}^{L\times m}$ (m is the number of classes), is determined from the following optimization problem [35,37]:

$${\beta }^{*}=\arg \underset{\beta }{min}{\displaystyle \frac{1}{2}}{\parallel \mathit{H}\beta -\mathit{T}\parallel }_F^2+C{\parallel \beta \parallel }_2^2,$$

(5)

where C is the regularization coefficient involved in the efficiency of the model, ${\parallel ·\parallel }_F$ and ${\parallel ·\parallel }_2$ represent the Frobenius and Euclidean norm, $\mathit{H}\in {\mathbb{R}}^{N\times L}$ is the output matrix of the hidden layer, and $\mathit{T}\in {\mathbb{R}}^{N\times m}$ is the objective matrix.

The matrices presented in Equation (5) are explicitly expressed below:

$$\begin{array}{c}\mathit{H}=\left[\begin{array}{cccc}g({\mathit{w}}_1·{\mathit{x}}_1+b_1)& g({\mathit{w}}_2·{\mathit{x}}_1+b_2)& \dots & g({\mathit{w}}_n·{\mathit{x}}_1+b_n)\\ ⋮& ⋮& \ddots & ⋮\\ g({\mathit{w}}_1·{\mathit{x}}_N+b_1)& g({\mathit{w}}_2·{\mathit{x}}_N+b_2)& \dots & g({\mathit{w}}_n·{\mathit{x}}_N+b_n)\end{array}\right],\beta =\left[\begin{array}{c}{\beta }_1\\ ⋮\\ {\beta }_{d+n}\end{array}\right]\\ \mathrm{and}\mathit{T}=\left[\begin{array}{c}{t}_1\\ ⋮\\ t_N\end{array}\right].\hfill \end{array}$$

(6)

where ${\beta }_k={[{\beta }_{k1}{\beta }_{k2}\dots {\beta }_{kn}]}^T$ links the k-th input and hidden neuron to the output neurons, where $1\le k\le d+L$, and the vector of random weights $w_j={[w_{j1}{w}_{j2}\dots w_{jd}]}^T$ links the input neurons to the j-th hidden neuron, $1\le j\le d$. Likewise, $b_j$ is the bias of the j-th hidden neuron, and $x_i·x_j$ denotes the scalar product defined over ${\mathbb{R}}^d$.

Under condition C, the minimization problem (5) admits different closed-form solutions [60,61]. When $C=0$, the standard solution is ${\beta }^{*}={\mathit{H}}^{†}\mathit{T}$, where ${\mathit{H}}^{†}$ is the generalized Moore–Penrose inverse of $\mathit{H}$. On the other hand, when $C\ne 0$, the optimization approach corresponds to ridge regression, and its solution is defined by the following:

$${\beta }^{*}=\left\{\begin{array}{cc}{(\mathit{H}{\mathit{H}}^T+C\mathit{I})}^{-1}{\mathit{H}}^T\mathit{T},\hfill & \mathrm{si}N\gg L\hfill \\ {\mathit{H}}^T{(\mathit{H}{\mathit{H}}^T+C\mathit{I})}^{-1}\mathit{T},\hfill & \mathrm{si}N<L\hfill \end{array}\right.$$

(7)

The ELM is a subclass of models derived from the random link functional architecture, generated by eliminating the direct links between the input layer and the output layer [37,62]. This simplification reduces the complexity of the model and improves its efficiency, as training becomes faster and computationally less expensive [37].

3. Materials and Methods

In this section, we analyze the short synthetic monofractal time series with Hurst exponents in the range of $0.1<H<0.9$ with increments of 0.1 to train the CNN-ELM mixed approach. Specifically, the CNN was adopted for the extraction of synthetic monofractal features, while ELM classified patients according to the degree of disease, determined by the H value. Once this model was trained, short time series of normal sinus rhythm and congestive heart failure was applied to the models to classify and associate the different monofractal models with the degree of congestive heart failure. Additionally, the performance of the models was evaluated based on the length of the RR intervals. The overall workflow is illustrated in Figure 1.

3.1. Congestive Heart Failure

Congestive heart failure is commonly evaluated using the New York Heart Association (NYHA) classification system, which categorizes patients into four classes, ranging from class I, which includes patients with mild symptoms, to higher classes indicating more severe symptoms. This system is widely used in clinical practice to predict patient outcomes and assess the effectiveness of therapeutic interventions [63], as detailed in

Table 1. NYHA functional classification system.

Class	Manifestations of the Condition
I	Individuals without limitation of physical activity; habitual physical exertion does not cause fatigue, palpitations, or breathing difficulties.
II	Individuals with slight physical activity limitation; while not symptoms appear at rest, physical exertion during routine activities leads to fatigue, palpitations, or respiratory discomfort.
III	Individuals with marked limitation of physical capacity; there are no symptoms at rest, but minimal activity causes fatigue, palpitations, or shortness of breath.
IV	Individuals manifest signs of heart failure even at rest, and any physical activity intensifies the discomfort.

.

3.2. Selection and Preprocessing of RR Intervals

The analysis of short time series of RR intervals is of particular interest since most of the records are of short duration. In longer records, the signal dynamics may change over time, making it crucial to divide the data into shorter segments to capture these changes. For this study, interbeat (RR) interval databases were obtained directly from Physionet.org [64], a platform that supports research on complex physiological and clinical data. The selected data come from four groups of patients with congestive heart failure and one group with normal sinus rhythm, which were freely accessed on 1 August 2025 from https://physionet.org/content/chf2db/1.0.0/. Each record covers a 24 h period with a sampling frequency of 128 Hz. Short time series of lengths $2^k$ data points, where k takes values of 9, 8, and 7 were extracted and organized into a database containing 53,820 records for each length. Specifically, short signal segments of 128, 256, and 512 RR intervals (approximately 1.5, 3, and 6 min) were generated. This procedure enabled the creation of thousands of short signals from each original recording by randomly selecting segments and ensuring an adequate balance across classes, thereby enhancing the reliability of the analysis and mitigating the effects of imbalance. Importantly, the selected sample lengths (128, 256, 512) were not determined by direct physiological reasoning but rather by practical considerations related to the average consultation time available for patients. These lengths allow for the acquisition of sufficiently representative signals within short and realistic clinical time frames, thus making the approach suitable for primary care and rapid monitoring scenarios. The number of patients included in the study is provided in

Table 2. Databases for cardiovascular diseases.

Database Name	Description	Number of Subjects Study
Normal Sinus Rhythm RR Interval	Beat annotation files (about 24 h each) from 54 subjects in normal sinus rhythm.	54
MIT-BIH Normal Sinus Rhythm	This database includes 18 long-term ECG recordings of subjects referred to the Arrhythmia Laboratory at Boston’s Beth Israel Hospital. Subjects included in this database were found to have had no significant arrhythmias.	18
Congestive Heart Failure RR Interval	Beat annotation files (about 24 h each) from 29 subjects with congestive heart failure (NYHA classes 1, 2, and 3).	29
BIDMC Congestive Heart Failure	This database includes long-term ECG recordings from 15 subjects with severe congestive heart failure (NYHA class 3–4).	15

, while further details and metadata regarding the signals can be directly consulted in the Physionet repository. Additionally, the preprocessing steps applied to the signals are described in detail in [34]. Subsequently, the records were classified according to the NYHA system (see Table 1).

3.3. Monofractal Time Series

A monofractal time series exhibits self-similarity across all time scales, where the scaling properties are described by a single fractal dimension that reflects changes in patterns and structures as the scale varies [20,65,66]. Monofractal time series appear in various systems, including climate patterns, river flows, and physiological processes within the human body [21,67,68,69]. Based on this framework, synthetic monofractal signals were used in training to capture the long-range dependencies and scale-invariant correlations of RR interval variability, as quantified by the Hurst exponent. This simplified yet robust model enabled the network to learn persistence and antipersistence patterns, while the evaluation was conducted solely on real RR interval datasets. Synthetic series guided feature extraction, but classification was validated with real signals, showing that the learned representations generalize well and support monofractal models as valid proxies for training real physiological variability. We also acknowledge that real RR signals can exhibit multifractal and nonstationary components, which introduce additional complexity beyond what is captured by a monofractal framework. Such properties may lead to fluctuations across multiple temporal scales, potentially affecting classification when models are strictly tuned to monofractal dynamics. Nevertheless, our approach emphasizes short-duration monofractal signals as a simplified yet effective representation of long-range correlations, with the Hurst exponent capturing essential statistical dependencies even in the presence of multifractal components. While a full multifractal analysis could provide further insights, such an extension lies outside the scope of the present study.

3.4. Synthetic Monofractal Data

Different monofractal models were studied in the range $0.1<H<0.9$ with increments of 0.1. The models included white noise with a Hurst exponent (H) of 0.5, indicating the absence of long-range correlations, as well as models with H values greater than or less than $0.5$, reflecting the presence of correlations and anticorrelations, respectively. Artificial signals were generated to evaluate the effectiveness of various neural network techniques in categorizing monofractal time series, with the signal length being considered. Time series of various lengths, $2^k$, were used, where k takes values of 9, 8, and 7. To ensure robust analysis, multiple independent realizations were produced for each case according to [70,71], specifically 10 realizations for $k=20$, from which short time series were obtained.

The Hurst exponent reflects long-range correlations and temporal complexity in RR interval dynamics. In healthy subjects, autonomic regulation generates complex and adaptable fluctuations, typically associated with H values close to or above 0.5. In pathological states, loss of complexity and altered sympathetic–parasympathetic balance reduce variability and adaptability, shifting H values below 0.5. This transition indicates the predominance of more rigid and less resilient dynamics, consistent with impaired autonomic regulation observed in heart failure.

4. Results

Within this section, we provide details on the configuration and performance of the CNN-ELM approach, trained with monofractal synthetic signals of short length. Initially, the model classified the nine categories of the H-index, modeled through the Hurst exponents. Subsequently, the robustness of the CNN-ELM model, trained with synthetic data, was evaluated in the diagnosis of cardiovascular diseases. Specifically, the selected models grouped the NYHA signals according to the degree of heart disease.

4.1. Experimental Setup and Hyperparameters

To evaluate the performance of the CNN-ELM model with synthetic and real data, processed and organized by length, we employed the classical fivefold cross-validation scheme. This learning approach grouped the monofractal samples into five uniformly sized subsets. In each iteration, the CNN-ELM was trained with four of these folds, reserving the remaining fold to assess its generalization ability. Therefore, in this paper, the test statistic’s value is presented as the average of the five runs. This training and validation strategy, commonly adopted with machine learning models, provides more stable prediction estimates and mitigates the potential for biased metrics.

4.1.1. CNN for Feature Extraction

Given the stable behavior of the deep learning system discussed in [34], our study adopted this same methodology for feature extraction from the synthetic data. The input was processed using six fully connected deep learning blocks. Following common practice in this type of mechanism, each block in the proposed architecture included a convolutional layer and a pooling layer. The output representation of the convolutional layers was primarily processed by applying normalization techniques and the ReLU activation function. The length of the sliding windows and the convolutional kernel size in each block were the same values reported in a published paper [34]. For instance, in learning block six, the convolutional filter size was $3 \times 3 \times 32$ with a stride of 1, while for the max pooling layer, the filter size was $2 \times 2$ with a stride of 2. The Adam algorithm was adopted as the optimizer, configured with a learning rate of 0.001. In addition, an $L_2$ regularization rate of 0.001, a batch size of 64, and a total of four training epochs were incorporated.

4.1.2. ELM for Classification

For the H-index classification task, we employed an ELM model. This network was trained and validated using features extracted from convolutional layers 5 (Conv 5) and 6 (Conv 6), as described in the previously outlined cross-validation scheme. The unique training process of the ELM involved randomly assigning weights and biases to the hidden layer, which was then mapped to the output layer using a sigmoid activation function. Subsequently, the output weights were determined analytically through the generalized Moore–Penrose inverse, ensuring fast and reliable classification.

Optimization of the ELM’s performance involved a sensitivity analysis of its hyperparameters, C and L. This was performed by fixing the feature map extracted from the convolutional layer 6 for monofractal signals of length 128. We conducted a grid search for C from ${10}^k$ (where k ranged from $-10$ to 10), and for L from 100 to 500 with an arithmetic increment of 100. As shown in Figure 2, experimental results demonstrated superior model performance for C values ranging from ${10}^5$ to ${10}^{10}$ and L values from 500 to 2000 neurons. To ensure generalization, the optimal values of $C={10}^{10}$ and $L=500$ were chosen and applied to both monofractal and cardiovascular signals.

4.2. Classification with Monofractal Signals

This section focuses on the performance of the CNN-ELM model in classifying monofractal synthetic signals, following the previously established configuration. The central purpose was to evaluate its accuracy in synthetic signals of very short duration and, from these results, to select the most suitable model trained with these characteristics. This stage was crucial in supporting the applicability and capacity for further generalization of the proposed system to real cardiovascular signals.

The overall classification results of the CNN-ELM model are summarized in

Table 3. Classification accuracy of ELM approach on short-length monofractal signals.

Model	Signal Length	Convolutional Layer	Accuracy (%)
CNN-ELM	128	Conv 5	$67.59$
		Conv 6	$68.95$
CNN-ELM	256	Conv 5	$78.42$
		Conv 6	$81.39$
CNN-ELM	512	Conv 5	$89.24$
		Conv 6	$92.48$

according to signal length and convolutional architecture depth. As expected, the accuracy of the model improved progressively with increasing both signal length and CNN architecture depth. With the feature map associated with the sixth convolutional layer (Conv 6), the best accuracy rates were obtained, being 92.48% for longer signals and 68.95% for shorter signals. Overall, CNN-ELM demonstrated better generalization capability fora data of length 512.

In addition to overall accuracy, four classical machine learning metrics were employed to assess model performance in each H-category: accuracy (Acc), sensitivity (Sen), specificity (Spe), and positive predictive value (PPV) ()as described in [34]). These complementary metrics provide more specific indicators about the classification system. The classification statistical indices obtained by CNN-ELM are summarized in

Table 4. Performance of the CNN-ELM model in the classification of short monofractal signals of lengths 128, 256, and 512.

H-Index	Signal Length: 128				Signal Length: 256				Signal Length: 512
	Acc	PPV	Sen	Spe	Acc	PPV	Sen	Spe	Acc	PPV	Sen	Spe
$H_{0.1}$	95.5	78.8	82	97.2	97.4	88.0	88.6	98.5	99.0	95.7	95.4	99.5
$H_{0.2}$	91.2	59.9	62.2	94.8	94.9	76.0	78.6	96.9	98.0	90.1	92.4	98.7
$H_{0.3}$	91.3	60.9	59.9	95.2	94.9	77.3	76.2	97.2	98.1	92.6	90.3	99.1
$H_{0.4}$	91.3	61.2	59.8	95.3	94.7	76.3	75.6	97.1	98.0	90.8	91.0	98.8
$H_{0.5}$	91.2	60.7	58.9	95.2	94.4	75.3	74.1	97.0	97.7	89.4	89.5	98.7
$H_{0.6}$	91.6	62.5	60.8	95.4	94.6	75.8	76.1	97.0	97.7	89.3	89.7	98.7
$H_{0.7}$	92.9	68.5	67.6	96.1	95.9	81.8	81.3	97.7	98.2	92.0	92.1	99.0
$H_{0.8}$	94.9	76.6	78.2	97.0	97.2	87.0	88.0	98.3	98.8	94.6	94.8	99.3
$H_{0.9}$	97.9	90.5	91.1	98.8	98.8	95.1	94.1	99.4	99.5	98.0	97.1	99.8

for Conv 6. It can be seen from the table that the sensitivity was always lower than the specificity in the three scenarios, incrementing these values according to the length of the input monofractal data. In addition, for lengths 128, 256, and 512, the best-classified classes were $H_{01}$, $H_{07}$, $H_{08}$, and $H_{09}$. Overall, CNN-ELM demonstrated better generalization capability for a data of length 512.

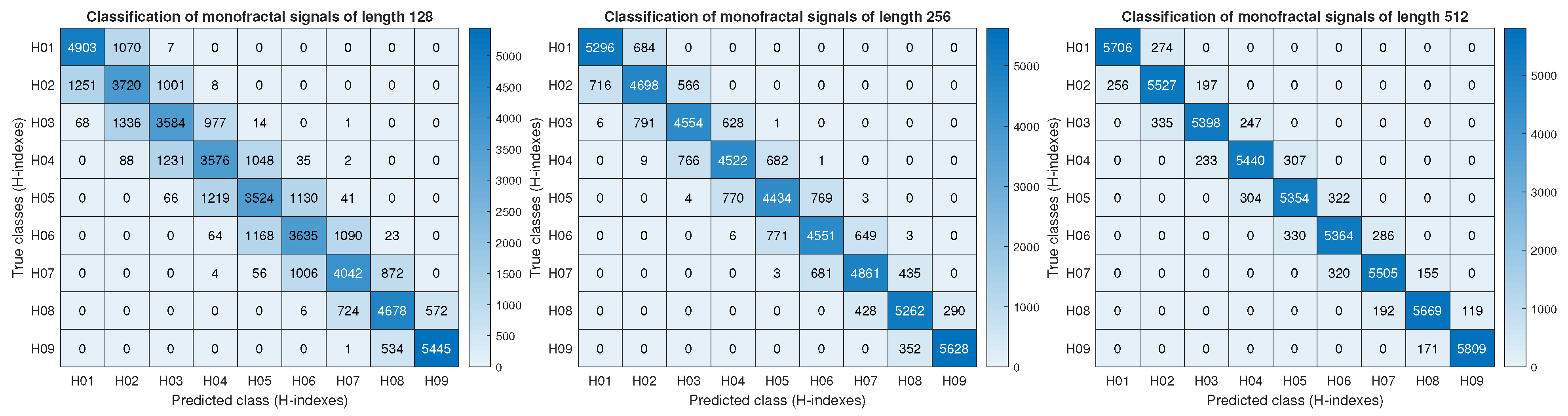
To reinforce the previous analysis, the correct and incorrect predictions of the Hurst index were summarized using a confusion matrix. Figure 3 illustrates the performance of the CNN-ELM model, constrained to the Conv 6 layer, using data with lengths of 128, 256, and 512. All matrices were generated through the cumulative sum of results obtained from fivefold cross-validation. For instance, in the $H_{01}$ category, an average of 55 signals were misclassified as $H_{02}$, while 1141 signals were correctly classified. This interpretation can be extended to the remaining entries of the matrix, allowing for a clear distinction between true positives, false positives, true negatives, and false negatives. This pattern reveals that the model struggles more with signals of length 128 compared to those of length 512, a limitation reflected in the error dispersion around the main diagonal of the H-index.

4.3. Classification of the Degree of Heart Disease According to NYHA

Monofractal research in the health domain is an emerging area, particularly with potential applications in the diagnosis of heart disease. Monofractal research in the health domain plays a crucial role, particularly in the diagnosis of heart disease. These approaches characterize heart rate variability using synthetic signals, offering a valuable tool for early detection. Numerous methods have been developed to address such anomalies, typically focusing on long-duration time series. Most studies analyze signals lasting between 6 and 24 h, with 2500 samples being the minimum length considered. This preference largely stems from the limitations of conventional models in accurately classifying short-duration cardiac anomalies. Moreover, to the best of our knowledge, no previous study has combined monofractal synthetic time series with an evaluation of the severity of heart disease.

Given the limited number of studies in this field, our research explored the relationship between short-duration monofractal signals and cardiovascular rhythm using machine learning strategies. Specifically, the CNN-ELM model, trained on short synthetic signals, was used to map Hurst index values to classes representing healthy individuals and to categories defined by the NYHA functional classification system. For the analysis, two scenarios were considered: the first differentiates between healthy and diseased subjects in general, while the second distinguishes between healthy subjects and different degrees of cardiovascular severity according to the criteria established by the NYHA. In both cases, the cumulative confusion matrix, along with the classic metrics mentioned above, was adopted as an evaluation tool to quantify the performance of the CNN-ELM model.

Table 5. Performance of the CNN-ELM model in the classification of real signals according to Hurst classes, for lengths 128, 256, and 512.

H-Index	Signal Length: 128				Signal Length: 256				Signal Length: 512
	Acc	PPV	Sen	Spe	Acc	PPV	Sen	Spe	Acc	PPV	Sen	Spe
$H_{0.1}$	48.0	3.5	0.2	95.8	48.4	4.7	0.2	96.6	47.5	2.8	0.2	94.7
$H_{0.2}$	52.2	89.1	5.2	99.3	54.5	89.5	10.3	98.8	51.7	89.7	4	99.4
$H_{0.3}$	90.7	—	—	90.7	90.6	—	—	90.6	91.6	—	—	91.6
$H_{0.4}$	90.2	—	—	90.2	87.2	—	—	87.2	88.5	—	—	88.5
$H_{0.5}$	83.9	—	—	83.9	85.8	—	—	85.8	84.5	—	—	84.5
$H_{0.6}$	82.6	—	—	82.6	81.2	—	—	81.2	73.1	—	—	73.1
$H_{0.7}$	68.0	—	—	68	70.7	—	—	70.7	72.0	—	—	72
$H_{0.8}$	92.4	—	—	92.4	93.3	—	—	93.3	98.2	—	—	98.2
$H_{0.9}$	97.3	—	—	97.3	98.9	—	—	98.9	97.2	—	—	97.2

shows the performance of the CNN-ELM model in classifying healthy individuals from sick individuals according to the Hurst index, with signals of lengths 128, 256, and 512 being considered. The results describe a clear pattern of difference between healthy and sick subjects. For low H values ($H_{0.1}$ and $H_{0.2}$), Acc ranged between 50% and 54%, with very low Sen and high Spe, indicating that the model correctly identifies healthy individuals but fails to detect sick individuals. In the intermediate categories ($H_{0.3}$–$H_{0.7}$), Acc reached values of 68% to 91%, while Sen and PPV were zero due to the absence of sick subjects; Spe remained high, reflecting the ability of CNN-ELM to recognize the cases present. In the upper classes ($H_{0.8}–H_{0.9}$), the pattern repeated, confirming that healthy subjects predominate. These results are consistent with monofractal theory, given that sick subjects tend to concentrate in H<0.5, while healthy subjects have high H values.

Figure 4 shows the cumulative confusion matrices for signals of lengths 128, 256, and 512, where the model distinguishes characteristic monofractal patterns within each group. Specifically, healthy subjects tended to concentrate in the $H\ge 0.5$ values, while sick subjects presented a higher concentration in the $H<0.5$ range. This behavior can be explained within the theoretical framework of the monofractal process. In the case of fractal Gaussian noise type signals, a value of $H\approx 0.5$ indicates random behavior, characteristic of a healthy heart; on the other hand, values of $H<0.5$ reflect anti-persistence, typical of pathological states. On the other hand, values of $H>0.5$ represent a more balanced or slightly persistent pattern, associated with healthy complexity, indicating balanced, adaptive physiological variability. In this context, the proposed model demonstrated its ability to differentiate between normal and abnormal heart rhythms in short-term scenarios, revealing a loss of complexity and dynamic stability in signals from patients with cardiovascular disease.

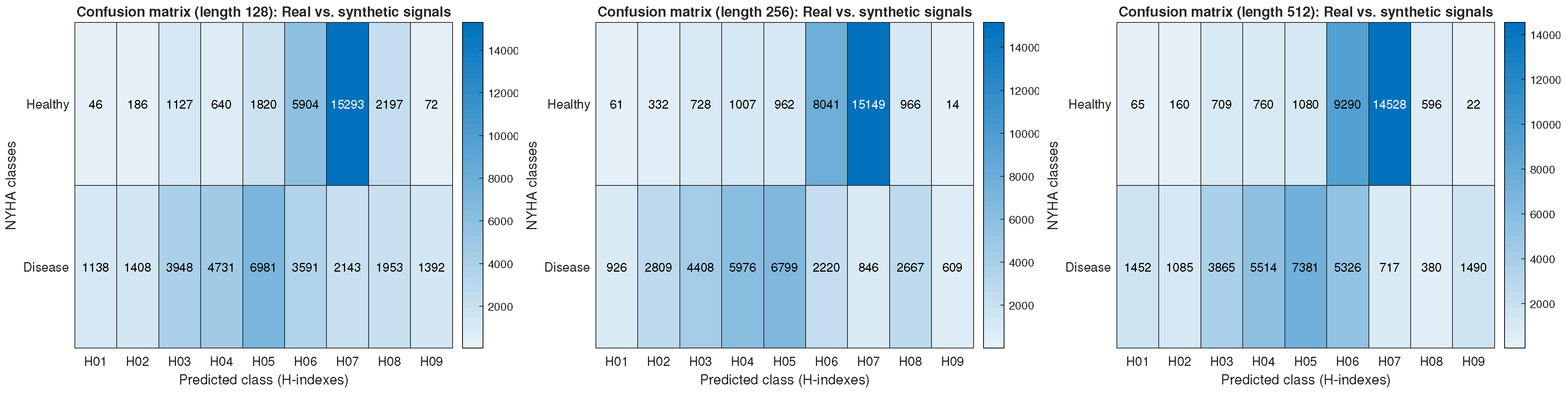
In the second scenario, the analysis was extended to a more specific classification, including both healthy individuals and the different grades of heart disease defined by the NYHA classification system (NYHA I, NYHA II, NYHA III, and NYHA IV). With the model previously trained with synthetic signals to identify monofractal variations, cumulative confusion matrices (see Figure 5) were generated for signals of lengths 128, 256, and 512. It was observed that healthy subjects exhibited a more concentrated distribution at values of $H\ge 0.5$, whereas H values tended to fall below $0.5$ when heart failure severity increased, suggesting greater irregularity in heart rate variability. This transition reflects a possible relationship between the degree of heart failure and anti-persistence in the time series, consistent with pathophysiological studies linking autonomic nervous system diffusion with heart rate variability.

Table 6. Performance of the CNN-ELM model for real versus synthetic signals according to NYHA classification, with signal lengths of 128, 256, and 512.

H-Index	Signal Length: 128				Signal Length: 256				Signal Length: 512
	Acc	PPV	Sen	Spe	Acc	PPV	Sen	Spe	Acc	PPV	Sen	Spe
$H_{0.1}$	75.5	1.3	0.3	94.2	76	1.9	0.4	94.8	76.4	0.6	0.1	95.4
$H_{0.2}$	79.9	13.9	5.7	94.4	79.9	12.3	5	94.5	79.8	0.6	0.2	95.4
$H_{0.3}$	73.1	23.3	9.9	90.5	71.8	26.1	16.3	87.1	75.8	26.4	10.3	93.8
$H_{0.4}$	67.8	17	14	81.9	71.7	25.9	19.4	85.4	69	17.9	17.9	82.4
$H_{0.5}$	66.3	16.9	15.6	80.1	63.1	18.5	21.8	74.3	61.5	17.3	25.6	71.4
$H_{0.6}$	82.3	—	—	82.3	84.9	—	—	84.9	79.6	—	—	79.6
$H_{0.7}$	85.9	—	—	85.9	85.7	—	—	85.7	83.4	—	—	83.4
$H_{0.8}$	91.7	—	—	91.7	95.7	—	—	95.7	98.6	—	—	98.6
$H_{0.9}$	96.2	—	—	96.2	97.4	—	—	97.4	98.8	—	—	98.8

reflects this behavior, showing that for H values from $H_{0.1}$ to $H_{0.2}$, the model achieved moderate Acc, with very low Sen and PPV, while Spe remained high. This indicates that healthy subjects are correctly identified with a low error rate, whereas patients with advanced heart failure, corresponding to NYHA III–IV, are more difficult to classify. In the range from $H_{0.3}$ to $H_{0.5}$, Sen and PPV increased, indicating improved discrimination of patients with mild-to-moderate heart failure, corresponding to NYHA I–III. For H values from $H_{0.6}$ to $H_{0.9}$, Acc and Spe reached high levels, while Sen and PPV were not calculated due to the absence of patients in these ranges, which included mostly healthy subjects. Overall, these quantitative results support the trend observed above, consistent with the theory of monofractal processes and findings on heart rate variability.

In contrast to studies based on integrated signals, where patients usually present H values close to 1 (very smooth cardiac signals), this study showed more chaotic and less predictable dynamics in patients with a higher degree of heart disease. Consequently, the CNN-ELM model distinguishes between healthy and diseased subjects and, in addition, recognizes the degree of clinical severity according to the distribution of Hurst indices.

5. Discussion

The results presented demonstrate that the proposed CNN-ELM model, trained with short-range monofractal signals, is capable of characterizing healthy subjects and distinguishing between different degrees of heart failure according to the NYHA classification system. These findings support the initial hypothesis that monofractal signals, defined by Hurst exponents, can capture complex patterns associated with disease severity. In contrast to [33], which classifies only H-indices extracted from synthetic signals using a support vector machine, this study incorporated the ELM classifier. Although the classification results were comparable, the incorporation of the ELM network significantly reduced the training times and showed a more stable generalization ability against real data.

The confusion matrices for the three window lengths show a pattern consistent with the clinical evidence. In particular, it was observed that the healthy and NYHA I categories tended to concentrate in the range $H_{05}$ to $H_{07}$, which is indicative of more regular and adaptive physiological signals. In contrast, NYHA classes II, III, and IV displayed a greater dispersion toward lower H values, reflecting less regularity and higher variability in the signals, which is characteristic of more advanced cardiac conditions. Specifically, the link between H values < 0.5 and pathological states supports early characterization of autonomic dysfunction and loss of cardiac variability complexity, suggesting that fractal-based indices may serve as non-invasive biomarkers to enhance risk stratification and patient monitoring in heart failure, complementing conventional clinical assessments such as the NYHA classification. Additionally, longer temporal windows are more effective in capturing the fractal properties associated with the severity of heart failure. Nevertheless, the dynamics of the model were maintained even with short signals (length 128), which supports the proposed objective of achieving effective classification using short-duration data.

From a clinical perspective, the model’s performance profile—characterized by consistently high specificity (>95% across most scenarios) but variable and generally low sensitivity (0.1–25.6%)—indicates that it operates most effectively as a rule-in diagnostic tool. This implies that a positive classification output substantially increases confidence in the presence of heart failure, supporting further confirmatory testing through established diagnostic procedures such as echocardiography or BNP measurement. However, the relatively low sensitivity highlights the need for cautious interpretation of negative results, particularly in high-risk or early-stage patients. Consequently, the proposed system is envisioned as a complementary decision-support tool capable of serving as an initial filtering mechanism within clinical workflows, aiding in the early identification of patients who may benefit from more comprehensive diagnostic evaluations. Future developments will focus on enhancing sensitivity while preserving the model’s high specificity to strengthen its applicability in both screening and diagnostic contexts.

This study differs from previous approaches by training the model only with monofractal features and demonstrating its ability to generalize to real data without relying on large volumes of clinical data. However, real signals may include multifractal or nonstationary components that are not fully represented in the synthetic ensemble. Although the model showed good classification results, its direct clinical application may require further validation in larger and more diverse cohorts. As future work, we propose extending this approach to multifractal signals, comparing the CNN-ELM with more recent architectures, such as transformers for biomedical signals, and exploring its integration into clinical workflows.

6. Conclusions

This study provides novel evidence supporting the feasibility of using short-duration synthetic signals to characterize cardiac dynamics and assess the severity of heart failure. The proposed CNN-ELM model successfully distinguished between healthy individuals and patients across the NYHA classification spectrum, even with time series as short as 128 samples. These findings reinforce the clinical relevance of the Hurst exponent as a biomarker of autonomic and cardiovascular function, particularly when associated with persistent or anti-persistent behavior in heart rate variability.

By focusing exclusively on monofractal features and avoiding the use of long or integrated real signals, the model demonstrated a strong capacity for generalization while minimizing computational cost and training time. Notably, the CNN-ELM architecture maintained consistent classification performance across different window lengths, aligning with known physiological patterns and clinical expectations.

This work stands apart from previous studies by integrating fractal theory with modern machine learning tools and by mapping the progression of heart failure through statistically meaningful H-index distributions. Nevertheless, further investigation is required to validate these results using real, multifractal, and potentially nonstationary data. Future studies should also explore alternative architectures, such as transformers, and assess the model’s integration into clinical decision-making processes.