Data-Driven Estimation of Reference Evapotranspiration in Paraguay from Geographical and Temporal Predictors

Abstract

Reference evapotranspiration (ET₀) is a fundamental variable for irrigation scheduling and water management. Conventional estimation methods, such as the FAO-56 Penman–Monteith equation, are of limited use in developing regions where meteorological data are scarce. This study evaluates the potential of machine learning (ML) approaches to estimate ET₀ in Paraguay, using only geographical and temporal predictors—latitude, longitude, altitude, and month. Five algorithms were tested: artificial neural networks (ANNs), k-nearest neighbors (KNN), random forest (RF), extreme gradient boosting (XGB), and adaptive neuro-fuzzy inference systems (ANFISs). The framework consisted of ET₀ calculation, baseline model testing (ML techniques), ensemble modeling, leave-one-station-out validation, and spatial interpolation by inverse distance weighting. ANFIS achieved the highest prediction accuracy (R² = 0.950, RMSE = 0.289 mm day⁻¹, MAE = 0.202 mm day⁻¹), while RF and XGB showed stable and reliable performance across all stations. Spatial maps highlighted strong seasonal variability, with higher ET₀ values in the Chaco region in summer and lower values in winter. These results confirm that ML algorithms can generate robust ET₀ estimates under data-constrained conditions, and provide scalable and cost-effective solutions for irrigation management and agricultural planning in Paraguay.

1. Introduction

Reference evapotranspiration (ET₀) is a critical variable for estimating crop water demand, designing efficient irrigation systems, and managing water resources sustainably. Its importance is especially pronounced in arid and semi-arid regions, where water scarcity poses a substantial constraint on agricultural productivity. The FAO-56 Penman–Monteith equation is widely recognized as the most robust and physically consistent method for ET₀ estimation [1]. However, the practical application of this method is often hindered in developing countries due to the unavailability or low quality of required meteorological data, such as air temperature, humidity, solar radiation, wind speed, and sunshine duration [2,3]. In response to these limitations, a range of low-input alternatives has been proposed. Empirical models such as Hargreaves–Samani or Priestley–Taylor require fewer inputs but often underperform across diverse climatic conditions due to their limited generalizability [4,5,6].

To address the trade-off between input simplicity and prediction accuracy, machine learning (ML) techniques have recently emerged as promising data-driven approaches. In recent years, different ML methods including artificial neural networks (ANNs), k-nearest neighbors (KNN), and adaptive neuro-fuzzy inference systems (ANFISs) have shown great potential for estimating ET₀ using a limited number of readily available input variables [7,8,9]. These approaches offer notable flexibility in the selection of inputs, making them particularly suitable for regions with sparse or incomplete meteorological records. Among these ML techniques, ensemble methods have attracted particular attention due to their superior predictive performance and robustness. By aggregating the outputs of multiple base learners, ensemble models—such as random forest (RF) and extreme gradient boosting (XGB)—can mitigate overfitting and enhance generalizability across varying environmental conditions. This is especially advantageous when modeling heterogeneous data collected from diverse climatic zones [10].

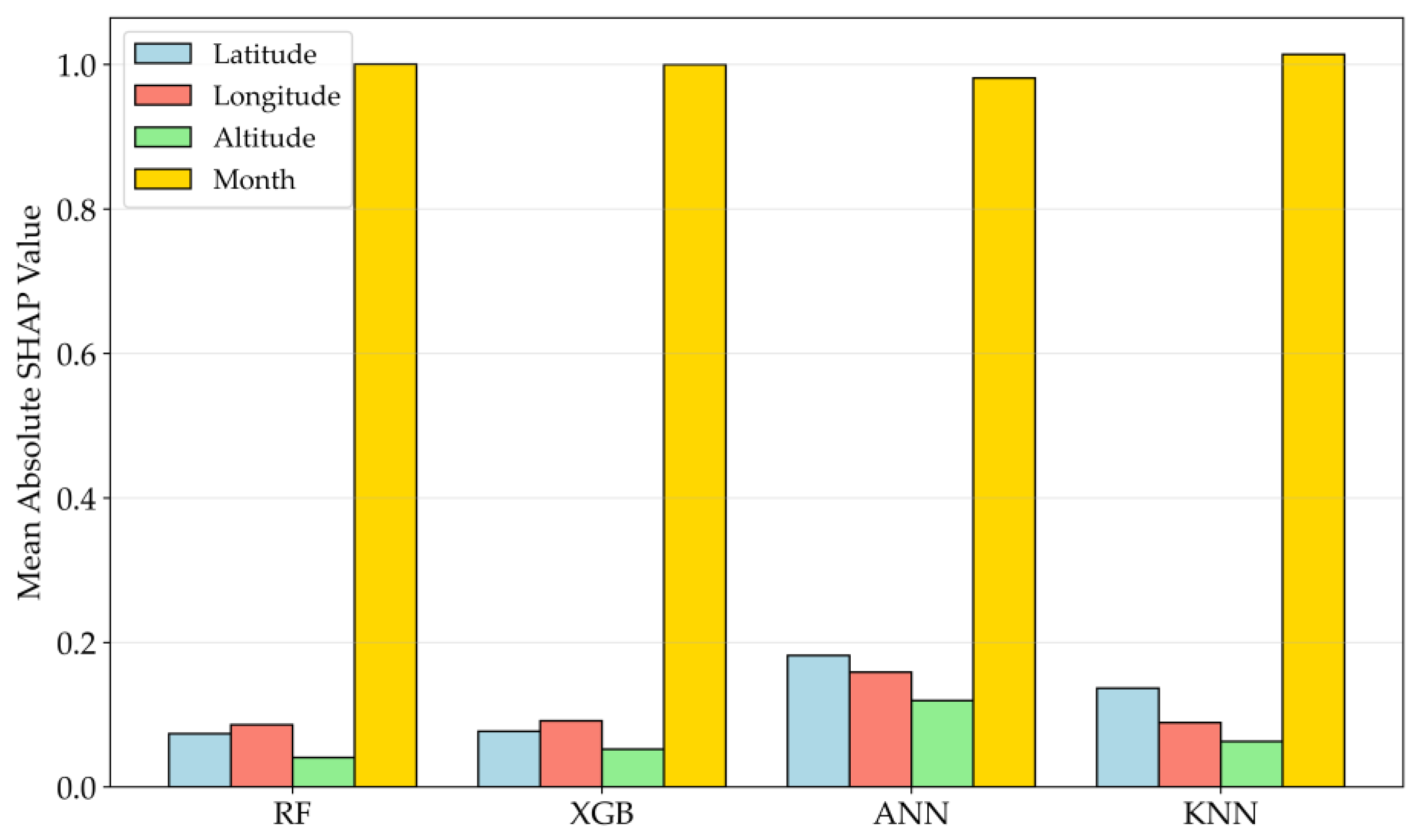
Building on this advantage, researchers have increasingly explored the potential of spatial and temporal features as sole predictors in ET₀ estimation. Several studies [11,12] have demonstrated the effectiveness of ML models using spatial–temporal inputs—such as latitude, longitude, altitude, and month number—for ET₀ estimation, even in the absence of meteorological variables.

This is because geographical variables such as latitude and altitude indirectly capture climatological influences by representing solar radiation, temperature gradients and atmospheric pressure, while the number of months serves as a proxy for seasonal variations [13]. Given the increasing climate variability and data scarcity in many parts of the world, such data-light approaches could significantly inform policy decisions related to sustainable agriculture and water allocation.

Despite their promising potential, the application of such models with little effort in geographically underrepresented and data-poor regions—such as Paraguay—is still limited. This study aims to evaluate the capability of modern ML algorithms to estimate ET₀ solely from geographic and temporal predictors, namely latitude, longitude, altitude, and the number of months. In this way, it addresses a critical gap in the literature concerning the robustness, accuracy, and spatial transferability of cost-effective, data-efficient ET₀ estimation frameworks within the South American context.

To fulfill this aim, a set of ML models was developed and evaluated for monthly ET₀ prediction using only four easily obtainable predictors: latitude, longitude, altitude, and month number. Five ML algorithms—ANN, KNN, ANFIS, RF, and XGB—were applied within a five-stage modeling framework, (1) ET₀ calculation (2) baseline model evaluation, (3) ensemble modeling, (4) leave-one-station-out validation, and (5) spatial interpolation, using the inverse distance weighting (IDW) method.

To further enhance the practical value of the developed models, spatially continuous ET₀ maps were generated using the IDW interpolation method. IDW is a simple yet effective geostatistical approach that estimates values at unsampled locations by weighting nearby observations based on their inverse distance. In the context of ET₀ estimation, IDW allows the conversion of point-based predictions into continuous surface maps, which are particularly useful for spatial decision-making in irrigation planning and water resource allocation. By visualizing ET₀ patterns across the landscape, stakeholders can identify high-demand areas, optimize crop selection, and implement region-specific water-saving strategies. This is especially important in data-scarce regions, where the lack of dense meteorological networks often limits spatially explicit water management practices.

The novelty of this research lies in its demonstration that robust and spatially continuous ET₀ estimates can be achieved in the absence of conventional meteorological data. This framework provides a scalable and economically viable alternative for ET₀ estimation in data-scarce environments. Given its cost-effectiveness and ease of implementation, the proposed approach holds strong potential to support irrigation scheduling, agricultural planning, and water management in developing regions.

2. Materials and Methods

2.1. Study Area

Paraguay lies between 19° and 28° south latitude and 54° and 63° west longitude and is located in a continental desert climate zone. Meteorological data from 19 stations over 5 years (2018–2022) were used for this study. Data from 19 stations of the Paraguayan Meteorological Service were used for this study. The locations of these stations in Paraguay are shown in Figure 1. The geographical coordinates of the stations can be found in

Table 1. Geographical characteristics of the meteorological stations in Paraguay.

Station Name	Region	Latitude (°S)	Longitude (°W)	Altitude (m)
General Bruguéz	Presidente Hayes	24°45′	58°50′	89
San Estanislao	San Pedro	24°40′	56°26′	183
Salto del Guairá	Canindeyú	24°03′	54°19′	297
Aeropuerto Silvio Pettirossi	Central	25°14′	57°31′	89
Paraguarí	Paraguarí	25°46′	57°15′	116
Capitán Meza	Itapúa	26°56′	55°12′	263
Concepción	Concepción	23°25′	57°18′	75
Mariscal Estigarribia	Boquerón	22°02′	60°37′	167
Encarnación	Itapúa	27°20′	55°50′	90
Coronel Oviedo	Caaguazú	25°28′	56°24′	159
Pilar	Ñeembucú	26°51′	58°19′	58
San Juan Bautista	Misiones	26°40′	57°09′	131
Caazapá	Caazapá	26°11′	56°22′	142
Aeropuerto Guaraní	Alto Paraná	25°21′	54°27′	247
Villarrica	Guairá	25°46′	56°26′	163
San Pedro	San Pedro	24°04′	57°06′	81
Pozo Colorado	Presidente Hayes	23°27′	58°52′	98
Pedro Juan Caballero	Amambay	23°35′	55°44′	563
Puerto Casado	Alto Paraguay	22°17′	57°56′	78

.

2.2. Methods

The methodology employed in this study was structured into a five-stage framework comprising (Figure 2): (1) ET₀ calculation (2), baseline model evaluation (ML algorithms), (3) ensemble learning implementation, (4) leave-one-station-out cross-validation, and (5) spatial interpolation using the IDW technique. In the first stage (Section 2.2.1), ET₀ was calculated for each of the 19 climatic stations and for each month of the study period using the traditional FAO-56 Penman–Monteith method based on monthly mean values of the required meteorological parameters. These computed ET₀ values then served as the output variable for training and testing the ML models. The second stage (Section 2.2.2), baseline models were evaluated to assess the individual performance of various ML algorithms using standard performance metrics. The third stage (Section 2.2.3) focused on ensemble averaging technique aiming to enhance predictive accuracy by integrating the strengths of multiple algorithms. In the fourth stage (Section 2.2.4), leave-one-station-out cross-validation was applied to examine the spatial generalizability and robustness of the models across different geographic locations. Finally (Section 2.2.5), the fifth stage, involved spatial interpolation of ET₀ distribution maps using the IDW method to generate continuous prediction surfaces from discrete station-level outputs.

2.2.1. ET₀ Calculation

In this study, ET₀ was calculated from the FAO-56 Penman–Monteith equation [1] using monthly averaged values along with the other necessary parameters in order to obtain stable long-term conditions for model development.

$$E{T}_0={\displaystyle \frac{\Delta (R_n-G)+{\rho }_a{c}_p(e_s-e_a)/r_a}{\left(\Delta +\gamma \left(1+\frac{r_s}{r_a}\right)\right){\rho }_w\lambda }}$$

(1)

where ET₀ represents the reference evapotranspiration (mm day⁻¹). The variable R_n denotes the net radiation flux density at the surface (MJ m⁻² day⁻¹), while G is the soil heat flux density (MJ m⁻² day⁻¹). The parameters e_s and e_a correspond to the saturation vapor pressure and actual vapor pressure of the air (kPa), respectively. The slope of the saturation vapor pressure–temperature curve is expressed as Δ (kPa °C⁻¹), and γ is the psychrometric constant (kPa °C⁻¹). The aerodynamic resistance to turbulent transfer of heat and water vapor from the surface to the reference height is defined as r_a (s m⁻¹), whereas the bulk surface resistance (r_s) accounts for the resistance to vapor flow from within the leaf, canopy, or soil to the atmosphere (s m⁻¹). Additional parameters include the air density (ρ_a, kg m⁻³), the specific heat of moist air at constant pressure (c_p, MJ kg⁻¹ °C⁻¹), the density of liquid water (ρ_w, kg m⁻³), and the latent heat of vaporization (λ, MJ kg⁻¹).

2.2.2. Machine Learning (ML) Algorithms

In this study, several ML algorithms were implemented to estimate ET₀ based solely on geographic and temporal predictors, including latitude, longitude, altitude, and number of months. These algorithms were selected due to their proven success in nonlinear regression tasks and their frequent use in hydrological and ecological modeling. The models were designed to estimate retrospective or contemporaneous monthly ET₀; forecasting future ET₀ values would require time-lagged predictors and was beyond the scope of this study. The ML models used in this study include:

Artificial neural networks (ANN): In the field of artificial intelligence, ANNs are recognized as computational paradigms inspired by the structural and functional characteristics of the neural networks of the human brain [14]. Due to their high flexibility and learning capability, they are widely used to solve complex nonlinear problems [15,16]. In this study, a feedforward multilayer perceptron (MLP) architecture was employed for ET₀ modeling. The MLP architecture is structured into an input layer, a hidden layer(s) and an output layer. The neurons in the hidden and output layers work by a weighted aggregation of the inputs followed by the application of a nonlinear activation function to enable complex mappings [17]. To optimize network performance, different activation functions—namely logsig, tansig, ReLU, and purelin—were employed and compared. Training was conducted using the Levenberg–Marquardt backpropagation algorithm, selected for its superior convergence properties and effectiveness in handling nonlinear regression tasks [18,19]. To prevent overfitting and enhance generalization, early stopping and regularization techniques were applied. Hyperparameter optimization was performed via grid search technique and tuning parameters including the number of hidden layers, number of hidden neurons, activation functions, and number of training epochs.

K-Nearest Neighbors (KNN): As a non-parametric and instance-based method, the KNN algorithm has been extensively applied in classification and regression tasks due to its simplicity and effectiveness [20,21]. In the context of regression, KNN predicts the target value of a query instance by identifying the k (the number of neighbors) most similar instances (neighbors) in the training dataset and averaging their corresponding output values. The similarity between data instances is usually measured using distance metrics such as Euclidean, Manhattan or Minkowski distance [22]. In this study, Euclidean distance was used as it is widely used and has proven to be useful for features with continuous value. The optimal value of k was determined using a grid search approach by minimizing the prediction error in the validation dataset.

Adaptive Neuro-Fuzzy Inference System (ANFIS): The ANFIS is a hybrid intelligent system that integrates the learning capabilities of ANNs with the reasoning mechanism of fuzzy logic [23]. This combination enables ANFIS to model complex, nonlinear relationships while maintaining interpretability through fuzzy if-then rules. The framework is particularly effective in capturing the uncertainty and imprecision inherent in many environmental and agricultural datasets [24,25,26]. ANFIS is typically based on the first-order Sugeno fuzzy inference system [27,28]. The architecture comprises five layers: (i) the fuzzification layer, which transforms crisp inputs into fuzzy sets using membership functions; (ii) the rule layer, where fuzzy if-then rules are applied; (iii) the normalization layer, which computes normalized firing strengths; (iv) the defuzzification layer, where output functions (usually linear or constant) are calculated; and (v) the output layer, which aggregates the final model output. The system learns by updating both the premise parameters (defining membership functions) and the consequent parameters (in the rule outputs) through a hybrid optimization approach. This typically involves a combination of least-squares estimation (for the consequent parameters) and backpropagation (for the premise parameters).

Random Forest (RF): Random Forest (RF) is an ensemble learning algorithm that constructs multiple decision trees during training and produces the final prediction by averaging the outputs of individual trees in regression tasks [29]. As a non-parametric, data-driven approach, RF is capable of modeling complex and nonlinear relationships between input features and the target variable, making it particularly suitable for environmental and agricultural application [30,31]. In the RF algorithm, each decision tree is trained on a bootstrap sample drawn from the original training dataset. Furthermore, at each node split, a random subset of predictor variables is selected to determine the best split. This randomization introduces diversity among the trees and helps reduce the risk of overfitting. The final model output is obtained by aggregating the predictions from all trees in the ensemble. Several hyperparameters affect the performance of the RF model, including the number of trees in the forest (n_estimators), the maximum depth of each tree (max_depth), the number of features considered at each split (max_features), the minimum number of samples required to split a node (min_samples_split), and the minimum number of samples required to be at a leaf node (min_samples_leaf). In this study, these parameters were optimized using grid search and cross-validation techniques to minimize prediction error and enhance model generalization.

Extreme Gradient Boosting (XGB): The XGB is an advanced implementation of gradient boosted decision trees designed for speed and performance [32]. It has gained widespread popularity due to its superior predictive accuracy, regularization capabilities, and computational efficiency. In regression tasks, XGB builds an ensemble of weak prediction models, typically decision trees, in a sequential manner where each new tree attempts to minimize the residuals of the previous ensemble. The XGB algorithm optimizes a regularized objective function that includes both a loss function and a penalty term for model complexity. This regularization mechanism helps prevent overfitting, a common issue in boosting-based algorithms. Additionally, XGB supports parallel processing, missing value handling, and sparse-aware learning, making it well-suited for large and complex datasets. Several hyperparameters influence the model’s performance, including the number of boosting rounds (n_estimators), maximum tree depth (max_depth), learning rate, and regularization parameters. In this study, these parameters were optimized through grid search and k-fold cross-validation based on validation set performance.

2.2.3. Parallel Hybrid Model

In this study, a parallel hybrid modeling framework was developed to enhance the accuracy of ET₀ predictions by integrating outputs from five ML algorithms: ANN, KNN, RF, XGB, and ANFIS. The individual predictions were combined using a weighted averaging ensemble technique, with weights systematically assigned based on each model’s performance metrics [33]. To optimize the final aggregated estimate, various weighting strategies were employed, including inverse error weighting (RMSE-based) and R²-based weighting [34,35,36]. Both methods stand out for their simplicity and low computational cost, and have been successfully applied in various environmental and hydrological prediction studies in the literature.

Inverse Error Weighting: In the inverse error weighting method, each model’s performance error (e.g., RMSE) is inverted and used as its weight. Models with lower errors receive higher weights. The normalized weights are then used to compute the final ensemble prediction according to Equation (2):

$$E{T}_{0,pre}(t)=\sum _{i=1}^m{w}_i\cdot E{T}_{0,i}(t); w_i={\displaystyle \frac{1/RMS{E}_i}{{\sum }_{j=1}^m(1/RMS{E}_j)}}$$

(2)

R²-Based Weighting: In the second method, the coefficient of determination (R²) of each model is directly used for weighting. As the model’s performance increases, its contribution rate also rises. The weights are normalized and expressed as Equation (3):

$$E{T}_{0,pre}(t)=\sum _{i=1}^m{w}_i\cdot E{T}_{0,i}(t); w_i={\displaystyle \frac{{R^2}_i}{{\sum }_{j=1}^m\left({R^2}_j\right)}}$$

(3)

where ET_0,pre(t) is ensemble-predicted reference evapotranspiration (mm day⁻¹) for observation t, ET_0,i(t) is reference evapotranspiration predicted by model i for observation t (mm day⁻¹), m is the number of base models in the ensemble, w_i is normalized weight assigned to model i, i is 1, …, m indexes the base models in the ensemble, t is 1, …, n indexes the data points (observations).

2.2.4. Leave-One-Station-Out Validation

In the leave-one-station-out validation (cross-validation), meteorological data collected from 19 different stations are partitioned into 19 subsamples, each corresponding to a specific station (Figure 3). All data within a given subsample originate exclusively from the same station. In each iteration, one subsample is held out as the validation set, while the model is trained on the remaining 18 subsamples. This procedure is repeated 19 times, ensuring that each station serves once as the validation set. In this way, every sample is tested independently, and the model’s spatial generalizability is effectively evaluated.

2.2.5. Spatial Maps of ET₀

The IDW method was employed to create monthly spatial maps of ET₀. IDW is a deterministic spatial interpolation method that estimates values at unsampled locations based on the values of nearby measured points, with the assumption that points closer to the target location have a greater influence on the estimated value than those further away. The weight assigned to each known point is inversely proportional to its distance from the location of the estimate and is usually raised to a power parameter [37]. In this study, the monthly ET₀ values calculated at 19 meteorological stations were spatially interpolated using the IDW method to produce continuous monthly maps for the entire study area. This approach enables the visualization of the spatial variability of ET₀ in regions lacking direct measurements.

2.2.6. Model Performance Criteria

The performance of the model was quantitatively assessed by statistical measures, namely the coefficient of determination (R²), the mean absolute error (MAE) and the root mean square error (RMSE), which together provide a complementary insight into the accuracy, precision and overall predictive ability.

$$R^2 = 1 - {\displaystyle \frac{{\sum }_{i=1}^n{\left(y_{cal,i} - y_{pre,i}\right)}^2 }{{\sum }_{i=1}^n{\left(y_{cal,i} - y_{mean}\right)}^2 }}$$

(4)

$$RMSE=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^n{\left(y_{cal,i} - y_{pre,i}\right)}^2}{n}}}$$

(5)

$$MAE={\displaystyle \frac{{\sum }_{i=1}^n\left|y_{cal,i} - y_{pre,i}\right|}{n}}$$

(6)

where y_cal,i is the calculated value, y_pre,i is the predicted value, y_mean is the mean of calculated values, and n is the number of data.

3. Results

3.1. Evaluation of FAO-56 Penman–Monteith Method

The FAO-56 Penman–Monteith analysis revealed clear seasonal and spatial variability in daily ET₀ across Paraguay (

Table 2. Monthly averages of daily ET₀ (mm day⁻¹).

Station	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
General Bruguez	5.08	4.88	4.07	3.40	3.22	3.54	3.30	2.81	3.33	3.67	3.94	5.06
San Estanislao	4.54	4.74	3.89	3.58	3.17	3.02	3.33	2.99	3.60	4.29	4.34	4.84
Salto del Guairá	4.50	4.39	4.33	3.93	4.35	3.90	3.13	3.32	4.29	4.35	3.94	4.47
Aeropuerto Silvio Pettirossi	4.98	4.84	4.08	3.77	3.67	3.49	3.09	3.54	3.38	3.88	4.75	5.15
Paraguarí	4.75	4.60	3.86	3.60	3.84	3.38	3.43	3.54	3.96	4.10	4.51	5.09
Capitán Meza	4.64	4.54	3.67	3.85	3.61	2.22	2.24	2.87	3.18	3.51	4.40	5.04
Concepción	4.07	3.85	3.38	2.79	2.00	1.62	1.66	2.07	2.69	3.41	3.79	3.96
Mariscal Estigarribia	5.21	4.77	3.82	3.09	1.88	1.50	1.67	2.24	2.99	3.93	4.59	4.86
Encarnación	4.73	4.68	3.10	2.93	1.81	1.33	1.37	2.01	2.70	3.18	3.55	5.09
Coronel Oviedo	4.88	4.78	4.05	3.78	3.68	3.51	3.65	3.25	3.71	3.99	4.53	5.04
Pilar	4.62	4.52	3.81	3.75	3.62	2.54	2.98	3.65	3.70	3.73	4.36	4.79
San Juan Bautista	4.60	4.68	4.09	3.86	3.78	2.71	3.39	3.69	3.35	3.94	4.33	5.15
Caazapá	4.67	4.48	3.99	3.66	3.88	3.44	2.91	3.77	3.44	3.84	4.17	5.02
Aeropuerto Guaraní	4.69	4.81	3.81	3.15	1.98	1.53	1.69	2.27	2.92	3.70	4.74	5.21
Villarrica	4.76	4.81	3.85	3.21	2.00	1.50	1.68	2.35	2.87	3.70	4.51	4.97
San Pedro	4.73	4.55	3.79	3.53	2.45	1.60	1.57	2.12	2.69	3.80	4.60	4.68
Pozo Colorado	5.37	4.85	4.16	3.53	2.35	1.62	2.23	2.58	3.17	4.07	4.82	5.22
Pedro Juan Caballero	4.42	4.20	3.67	3.33	2.16	1.85	1.87	2.54	3.11	3.68	4.27	4.58
Puerto Casado	4.87	4.54	3.92	3.83	2.55	1.53	2.46	2.37	3.55	3.93	4.63	5.01

). ET₀ values were highest during the austral summer months (December–February), often exceeding 5.0 mm day⁻¹ at stations such as Pozo Colorado (5.37 mm day⁻¹ in January) and General Bruguez (5.08 mm day⁻¹ in January), and lowest during winter (June–July), dropping below 2.0 mm day⁻¹ at stations like Encarnación (1.33 mm day⁻¹ in June) and Villarrica (1.50 mm day⁻¹ in June). Stations in the Chaco region of western Paraguay, including Pozo Colorado, Mariscal Estigarribia, and General Bruguez, consistently exhibited higher ET₀ throughout the year, reflecting the region’s semi-arid climate with high temperatures, low humidity, and reduced cloud cover. In contrast, stations in the eastern and southern regions, such as Encarnación, Villarrica, and Caazapá, showed more pronounced seasonal fluctuations, with lower ET₀ during winter months due to cooler temperatures and higher atmospheric moisture. Transitional months (April–May and September–October) displayed intermediate ET₀ values across most stations, corresponding to the seasonal shift between summer and winter. These results indicate that ET₀ in Paraguay is primarily controlled by seasonal climatic dynamics, with regional differences, particularly the elevated evaporative demand in the Chaco, strongly influencing its spatial distribution.

3.2. Evaluation of ML Algorithms

Data pre-processing constitutes an essential preliminary stage in the development of robust and reliable ML architectures. In this phase, the raw dataset undergoes systematic refinement to mitigate potential biases due to stochastic noise, incomplete observations, and structural inconsistencies. The implemented workflow included a number of well-established but methodologically critical procedures, including comprehensive data cleaning, variable transformation, and stratified partitioning to ensure a balanced representation of the subsets. For model calibration, 90% of the training data was used and hyperparameter tuning was performed on a randomly selected 90% subset of this training pool. This process was embedded in a ten-fold cross-validation scheme, ensuring statistical rigor, minimizing the risk, of overfitting and improving the external validity of the model’s performance metrics. The resulting optimal hyperparameter configurations for each algorithm are listed in

Table 3. Hyperparameter values used in machine learning algorithms.

Hyperparameters Tuned
ANN
Number of hidden layers	1
Number of hidden neurons	5
Activation function in hidden Layer	Tansig
Activation function in output Layer	Purelin
Number of epochs	300
Network structure	4–5–1
KNN
Optimal neighbor	3
Weights = ’uniform’	Uniform
Distance function	Euclidean distance function
RF
Number of estimators	173
Maximum depth	7
max_features	Sqrt
min_samples_leaf	2
min_samples_split	5
XGB
Number of estimators	135
Number of learning rates	0.159
Max dept	3

.

The performance metrics for the evaluated ML algorithms are summarized in

Table 4. MAE, RMSE, and R² statistics of the ANN, KNN, RF, and XGB algorithms in the training and testing phases.

Model	Training			Testing
	MAE (mm day−1)	RMSE (mm day−1)	R2	MAE (mm day−1)	RMSE (mm day−1)	R2
ANN	0.246	0.312	0.932	0.312	0.443	0.882
KNN	0.159	0.211	0.969	0.248	0.394	0.906
RF	0.178	0.228	0.964	0.244	0.379	0.913
XGB	0.168	0.220	0.966	0.243	0.387	0.910

for comparative assessment. At this stage of analysis, only geo-temporal predictors—namely latitude, longitude, altitude, and month number—were incorporated into the models. During the model development process, a range of ANN architectures was explored, including both single- and double-hidden-layer configurations with different neuron counts. The architecture that achieved the most favorable trade-off between training accuracy and generalization capacity consisted of a single hidden layer with five neurons. This network was trained for 300 epochs using the Levenberg–Marquardt (LM) optimization algorithm, applying the tansig activation function in the hidden layer and the purelin function in the output layer. While this design produced satisfactory results during training, its predictive accuracy in the testing phase was the lowest among all evaluated models (R² = 0.882), likely due to its limited representational capacity for capturing complex, nonlinear relationships. The KNN model, configured with three neighbors, uniform weighting, and the Euclidean distance metric, demonstrated strong performance despite its simplicity, achieving R² = 0.906 and RMSE = 0.394 mm day⁻¹ values comparable to those obtained by the RF and XGB models. The RF model employed 173 trees with a maximum depth of 7, a sqrt setting for the maximum number of features, and a minimum leaf size of 2. This configuration ranked among the top performers in the testing phase, delivering R² = 0.913 and RMSE = 0.379 mm day⁻¹. The XGB model, designed with a relatively low learning rate (0.159) and 135 trees, facilitated a more gradual and balanced learning process. Restricting the maximum depth to 3 helped mitigate overfitting, resulting in high predictive accuracy (R² = 0.910) and a low error rate (RMSE = 0.387 mm day⁻¹).

The influence of input features on model predictions was evaluated using SHapley Additive exPlanations (SHAP), a game-theoretic approach that provides consistent and locally accurate attribution values for each predictor. This method enables a detailed interpretation of feature contributions across different ML models, thereby improving the transparency and explainability of the predictive framework adopted in this study. Figure 4 presents the mean absolute SHAP values for four input variables (latitude, longitude, altitude, and month) across the RF, XGB, ANN, and KNN models. The results reveal that the “month” variable exerts the greatest influence in all models (≈1.0), underscoring the dominant role of seasonal variability in explaining ET₀. The variables (“latitude” and “longitude”) also display appreciable importance, particularly in the ANN model, where their contributions (0.18 and 0.16, respectively) are markedly higher compared with the other algorithms. This finding suggests that spatial positioning has a more pronounced impact on ANN-based predictions. Conversely, “altitude” consistently emerges as the least influential factor, with SHAP values between 0.04 and 0.12. Overall, these results indicate that temporal variability serves as the primary driver of model performance, while spatial factors—especially “latitude” and “longitude”—provide complementary explanatory power, and “altitude” contributes only marginally.

ANFIS models were developed and evaluated using various types of membership functions, including triangular (trimf), trapezoidal (trapmf), and Gaussian (gaussmf). As presented in

Table 5. MAE, RMSE, and R² statistics of the ANFIS models in the training and testing phases.

Model	Training			Testing
	MAE (mm day−1)	RMSE (mm day−1)	R2	MAE (mm day−1)	RMSE (mm day−1)	R2
ANFIS-Trimf	0.211	0.274	0.948	0.220	0.300	0.948
ANFIS-Trapmf	0.257	0.322	0.928	0.273	0.354	0.926
ANFIS-Gaussmf	0.200	0.266	0.951	0.202	0.289	0.950

, the ANFIS configuration employing the gaussmf membership function achieved superior performance, yielding the lowest error (RMSE = 0.289 mm day⁻¹) and the highest coefficient of determination (R² = 0.950) across both training and testing datasets. The trimf function also demonstrated strong predictive capability, although slightly below that of gaussmf, whereas the trapmf function exhibited comparatively lower accuracy. These findings indicate that the gaussmf is particularly effective at capturing the nonlinear dependencies inherent in the data, highlighting the suitability of ANFIS for ET₀ prediction. The principal advantage of ANFIS lies in its capacity for adaptive learning and its interpretable structure grounded in fuzzy logic, which enables both flexibility in modeling complex relationships and transparency in the decision-making process.

The comparative scatterplots of the calculated versus predicted ET₀ for each model are illustrated in Figure 5, providing a visual representation of the prediction accuracy across models. It is evident from both the scatterplots and the performance metrics that all models captured the general trends of ET₀ reasonably well, yet distinct differences in predictive precision are observed. ANFIS demonstrated the superior predictive performance among all evaluated models, achieving the lowest RMSE (0.289 mm day⁻¹) and the highest R² (0.950) on the testing dataset. This indicates its exceptional capability to capture complex nonlinear relationships in ET₀ dynamics. While RF and XGB models also provided strong accuracy (R² ≈ 0.910–0.915, RMSE ≈ 0.380–0.390 mm day⁻¹), their performance was slightly lower compared to ANFIS. KNN offered competitive results given its simplicity, whereas the shallow MLP model underperformed, reflecting its limited capacity to model intricate patterns in the data. Overall, these results highlight the effectiveness of combining fuzzy inference with adaptive learning in ANFIS for high-precision ET₀ prediction, while also emphasizing the trade-offs between interpretability, computational efficiency, and predictive accuracy among different ML approaches.

3.3. Enhancing Model Performance with Ensemble Methods

In this stage, a parallel hybrid modeling framework was implemented to enhance the predictive accuracy of the model outputs. Ensemble models were constructed using weighting strategies based on the R² and the inverse of the RMSE. The corresponding weight coefficients assigned to each model are presented in

Table 6. Weight coefficients (ω_i) of individual models under different weighting schemes in the training and testing phases.

Weighting Scheme	Model	Training	Testing
R2-based weighting	ANFIS	0.199	0.208
	RF	0.202	0.200
	XGB	0.202	0.199
	KNN	0.203	0.199
	ANN	0.195	0.193
Inverse RMSE-based weighting	ANFIS	0.183	0.257
	RF	0.212	0.196
	XGB	0.220	0.192
	KNN	0.230	0.188
	ANN	0.155	0.167

. Under the R²-based weighting scheme, the weights were relatively balanced across models, ranging between 0.193 and 0.208 in the testing phase. Notably, ANFIS received the highest weight (0.208), followed closely by KNN (0.203), RF (0.200), XGB (0.199), and ANN (0.193) indicating that all models contributed almost equally to the ensemble. This balanced distribution suggests that each algorithm demonstrated comparable predictive capacity when assessed using R² as the weighting criterion. In contrast, the inverse RMSE-based scheme resulted in a more pronounced variation in weight allocation. ANFIS achieved the highest testing-phase weight (0.257), substantially exceeding its allocation in the R²-based scheme. It was followed by RF (0.196), XGB (0.192), and KNN (0.188), while ANN consistently received the lowest weights (0.167), reflecting its weaker predictive performance. The markedly higher share of ANFIS under the inverse RMSE criterion highlights its superior capacity to capture underlying patterns in the data, thereby making a dominant contribution to the ensemble. These differences underscore that the weighting strategy plays a pivotal role in determining the relative contributions of individual models and can substantially influence the ensemble’s sensitivity to specific data characteristics.

The inverse RMSE-based weighting scheme achieved marginally better performance than the R²-based weighting in both training and testing phases. Although the improvements are relatively small, they indicate that assigning higher weights to models with lower prediction errors (as per inverse RMSE) slightly enhances the ensemble’s generalization ability. The consistently high R² values (>0.92) for both schemes confirm the robustness of the ensemble modeling framework (Figure 6). Notably, ANFIS emerged as the dominant contributor under the inverse RMSE-based weighting scheme, receiving a substantially larger weight allocation compared to other algorithms. This suggests that ANFIS was more effective in capturing complex, nonlinear patterns in the data, which likely played a key role in the improved accuracy of the ensemble. By contrast, ANN consistently received the lowest weights in both schemes, reflecting its comparatively weaker predictive performance.

3.4. Evaluation of Leave-One-Out Station Validation

The leave-one-out station validation showed clear differences in the prediction performance between the evaluated models (

Table A1. Leave-one-out station test results.

Station Name	Models	Training			Testing
		RMSE	MAE	R2	RMSE	MAE	R2
General Bruguéz	RF	0.270	0.193	0.952	0.247	0.177	0.965
	KNN	0.321	0.210	0.932	0.334	0.289	0.935
	ANN	0.460	0.314	0.861	0.308	0.231	0.954
	XGB	0.270	0.193	0.952	0.236	0.167	0.968
	ANFIS (trapmf)	0.222	0.278	0.928	0.196	0.242	0.922
San Estanislao	RF	0.386	0.292	0.902	0.201	0.262	0.930
	KNN	0.372	0.283	0.909	0.244	0.309	0.892
	ANN	0.430	0.300	0.879	0.304	0.420	0.886
	XGB	0.298	0.228	0.941	0.145	0.190	0.950
	ANFIS (gauss)	0.231	0.290	0.925	0.164	0.203	0.934
Salto del Guairá	RF	0.369	0.255	0.871	0.282	0.172	0.863
	KNN	0.370	0.256	0.872	0.303	0.245	0.803
	ANN	0.526	0.400	0.754	0.403	0.314	0.703
	XGB	0.370	0.255	0.872	0.265	0.173	0.855
	ANFIS (gauss)	0.382	0.286	0.864	0.281	0.223	0.830
Aeropuerto Silvio Pettirossi	RF	0.265	0.188	0.953	0.248	0.192	0.965
	KNN	0.265	0.188	0.954	0.300	0.242	0.948
	ANN	0.458	0.321	0.861	0.314	0.251	0.943
	XGB	0.265	0.188	0.954	0.231	0.175	0.969
	ANFIS (gauss)	0.296	0.218	0.942	0.254	0.200	0.965
Paraguarí	RF	0.278	0.201	0.949	0.249	0.196	0.963
	KNN	0.264	0.188	0.954	0.315	0.246	0.941
	ANN	0.483	0.336	0.846	0.284	0.239	0.952
	XGB	0.264	0.188	0.954	0.248	0.196	0.963
	ANFIS (gauss)	0.295	0.217	0.942	0.279	0.219	0.959
Capitán Meza	RF	0.265	0.189	0.954	0.228	0.177	0.968
	KNN	0.275	0.191	0.950	0.298	0.243	0.946
	ANN	0.438	0.312	0.873	0.534	0.446	0.827
	XGB	0.265	0.188	0.954	0.227	0.175	0.969
	ANFIS (trimf)	0.227	0.284	0.925	0.153	0.262	0.936
Concepción	RF	0.487	0.373	0.851	0.491	0.411	0.915
	KNN	0.475	0.374	0.921	0.389	0.362	0.975
	ANN	0.385	0.274	0.906	0.404	0.347	0.864
	XGB	0.400	0.328	0.951	0.401	0.382	0.982
	ANFIS (gauss)	0.300	0.223	0.942	0.183	0.154	0.981
Mariscal Estigarribia	RF	0.305	0.224	0.939	0.290	0.228	0.951
	KNN	0.273	0.188	0.951	0.294	0.234	0.950
	ANN	0.524	0.387	0.818	0.387	0.315	0.913
	XGB	0.274	0.198	0.950	0.296	0.229	0.949
	ANFIS (gauss)	0.195	0.238	0.944	0.258	0.327	0.938
Encarnación	RF	0.266	0.190	0.953	0.205	0.146	0.976
	KNN	0.276	0.193	0.950	0.332	0.284	0.938
	ANN	0.471	0.328	0.853	0.306	0.257	0.947
	XGB	0.266	0.190	0.953	0.192	0.139	0.979
	ANFIS (gauss)	0.297	0.219	0.942	0.321	0.275	0.970
Coronel Oviedo	RF	0.278	0.201	0.949	0.269	0.190	0.956
	KNN	0.264	0.188	0.954	0.238	0.174	0.966
	ANN	0.472	0.330	0.853	0.329	0.271	0.935
	XGB	0.264	0.188	0.954	0.255	0.180	0.961
	ANFIS (trimf)	0.320	0.243	0.932	0.332	0.266	0.949
Pilar	RF	0.266	0.189	0.953	0.304	0.239	0.941
	KNN	0.302	0.195	0.940	0.450	0.349	0.870
	ANN	0.577	0.424	0.781	0.651	0.583	0.621
	XGB	0.280	0.203	0.948	0.217	0.171	0.970
	ANFIS (trapmf)	0.382	0.306	0.904	0.356	0.293	0.926
San Juan Bautista	RF	0.262	0.186	0.955	0.331	0.236	0.929
	KNN	0.296	0.221	0.942	0.316	0.240	0.936
	ANN	0.413	0.293	0.888	0.327	0.247	0.931
	XGB	0.261	0.186	0.955	0.323	0.222	0.933
	ANFIS (gauss)	0.294	0.216	0.943	0.339	0.249	0.945
Caazapá	RF	0.269	0.190	0.952	0.255	0.204	0.960
	KNN	0.274	0.189	0.950	0.271	0.222	0.955
	ANN	0.467	0.325	0.856	0.278	0.227	0.953
	XGB	0.264	0.187	0.954	0.261	0.205	0.959
	ANFIS (trimf)	0.320	0.243	0.932	0.325	0.242	0.948
Aeropuerto Guaraní	RF	0.265	0.188	0.954	0.276	0.207	0.955
	KNN	0.264	0.188	0.954	0.276	0.206	0.955
	ANN	0.463	0.343	0.858	0.546	0.435	0.823
	XGB	0.264	0.188	0.954	0.276	0.206	0.955
	ANFIS (trimf)	0.320	0.243	0.932	0.348	0.273	0.928
Villarrica	RF	0.278	0.201	0.949	0.262	0.201	0.957
	KNN	0.263	0.187	0.954	0.253	0.194	0.960
	ANN	0.464	0.319	0.858	0.307	0.240	0.941
	XGB	0.265	0.189	0.954	0.277	0.209	0.952
	ANFIS (gauss)	0.295	0.217	0.943	0.640	0.560	0.952
San Pedro	RF	0.404	0.304	0.893	0.289	0.237	0.942
	KNN	0.332	0.252	0.928	0.250	0.196	0.957
	ANN	0.430	0.296	0.881	0.251	0.207	0.963
	XGB	0.300	0.215	0.941	0.268	0.216	0.950
	ANFIS (trimf)	0.320	0.242	0.933	0.375	0.306	0.939
Pozo Colorado	RF	0.267	0.190	0.953	0.296	0.229	0.949
	KNN	0.266	0.190	0.953	0.246	0.193	0.965
	ANN	0.479	0.331	0.848	0.395	0.312	0.910
	XGB	0.266	0.190	0.953	0.290	0.228	0.951
	ANFIS (gauss)	0.089	0.469	0.941	1.037	0.959	0.977
Pedro Juan Caballero	RF	0.495	0.386	0.841	0.447	0.363	0.829
	KNN	0.534	0.425	0.815	0.309	0.454	0.773
	ANN	0.528	0.395	0.819	0.356	0.496	0.717
	XGB	0.322	0.234	0.933	0.276	0.210	0.935
	ANFIS (gauss)	0.187	0.230	0.949	0.219	0.277	0.933
Puerto Casado	RF	0.403	0.306	0.893	0.376	0.308	0.909
	KNN	0.529	0.421	0.816	0.509	0.392	0.833
	ANN	0.466	0.326	0.857	0.270	0.208	0.953
	XGB	0.362	0.277	0.914	0.382	0.302	0.906
	ANFIS (gauss)	0.087	0.467	0.942	0.333	0.697	0.958

). The ensemble-based approaches such as RF and XGB, together with ANFIS, performed consistently better than ANN at most stations. At the Mariscal Estigarribia station, for example, RF and XGB achieved R² values of over 0.95 with a lower RMSE (~0.29–0.30 mm day⁻¹), while ANN yielded weaker results (R² = 0.913). The performance patterns varied slightly between stations. At the Puerto Casado station, ANN showed relatively strong generalization (R² = 0.953 during testing), but ANFIS maintained more stable accuracy during both training and testing. In Caballero and Pozo Colorado station, KNN and RF showed excellent predictive power, with KNN in Caballero station achieving an R² of 0.965 during testing. ANFIS often provided the highest accuracy under nonlinear conditions, as observed in Concepción and Encarnación station, where R² was above 0.97. ANN consistently had the lowest predictive skill, with higher errors observed especially in Pilar station (R² = 0.621 during the testing). In contrast, XGB often provided robust and stable predictions, especially in San Estanislao station (R² = 0.950) and Paraguarí (R² = 0.963). RF was also among the best models in several cases, such as in General Bruguéz (R² = 0.965) and Caazapá (R² = 0.960) stations. Overall, the results show that ensemble methods (RF and XGB) and neuro-fuzzy models (ANFIS) have superior predictive ability compared to ANN in leave-one-out station validation, confirming their suitability for capturing the complex and nonlinear relationships in station-based climate data.

3.5. Generation of Spatial Distribution Maps

Monthly spatial distribution maps of ET₀ in Paraguay were generated using the IDW interpolation method, based on quality-controlled and validated station observations (Figure 7). These maps provide a detailed assessment of the geographic and seasonal variability of ET₀ across the country. Results revealed a distinct annual cycle, with pronounced spatial heterogeneity influenced by topography, latitude, and seasonal climatic conditions.

The spatial and temporal evolution of ET₀ across Paraguay reveals a pronounced seasonal cycle. During the summer months (January–March), ET₀ reached its highest levels, with values typically exceeding 4.5 mm day⁻¹ and persistent hotspots in the northeastern and southeastern regions. From April to June, a steady decline was observed, culminating in the annual minimum in June when ET₀ ranged from 1.5 to 2 mm day⁻¹, particularly in the western Chaco. Beginning in July, ET₀ gradually increased, with averages rising from around 2.5 mm day⁻¹ in July to nearly 4 mm day⁻¹ by September, reflecting the transition into spring. The late spring and summer months (October–December) were characterized by a rapid recovery, with widespread values again surpassing 4.5 mm day⁻¹ and clear maxima in the northeastern and southeastern zones. Throughout the year, spatial patterns remained consistent, with the Chaco region generally exhibiting lower values and the eastern lowlands sustaining the highest atmospheric water demand. These findings emphasize the strong climatic control on ET₀ seasonality and the importance of accounting for regional variability in water resource management and agricultural planning.

4. Discussion

The comparative evaluation of ML and neuro-fuzzy inference systems in this study revealed substantial differences in predictive capability for estimating ET₀ using only geo-temporal predictors (latitude, longitude, altitude, and month number). While all models were able to capture the general seasonal dynamics of ET₀, their precision and robustness varied notably, reflecting differences in their ability to model the nonlinear and spatially heterogeneous nature of atmospheric water demand in Paraguay. These findings are broadly consistent with previous efforts to estimate ET₀ from limited or purely geo-temporal predictors [12], but the present study advances this line of research by providing a systematic, Paraguay-wide evaluation across 19 stations with monthly mean data.

The ANFIS configured with a Gaussian membership function consistently outperformed all other models, achieving the lowest RMSE (0.289 mm day⁻¹) and highest R² (0.950) during the testing phase. This superior performance is attributable to ANFIS’s hybrid architecture, which combines the adaptive learning capabilities of neural networks with the interpretability and flexibility of fuzzy logic. Previous studies have also highlighted the effectiveness of Gaussian-shaped membership functions for hydrometeorological modeling [24,38,39], and our results extend this evidence by demonstrating that such functions remain highly effective even under minimal predictor inputs restricted to latitude, longitude, altitude, and month.

Tree-based ensemble methods, particularly RF and XGB, provided highly competitive results (R² ≈ 0.910–0.915; RMSE ≈ 0.380 mm day⁻¹), with superior stability across stations compared to ANFIS. The strong generalization capacity of RF and XGB can be attributed to their ability to capture complex nonlinear interactions while controlling overfitting through ensemble averaging and regularization, respectively. Their robustness in the leave-one-station-out validation indicates that such methods are more resilient to the spatial variability and data sparsity typical of meteorological networks, a finding consistent with previous work on climate variable interpolation and prediction [40,41]. Our contribution includes the use of leave-one-station-out validation, allowing spatial generalizability to be explicitly assessed in a data-scarce national context, which adds value beyond the approaches typically used in earlier studies.

The KNN model achieved commendable accuracy given its algorithmic simplicity (R² = 0.906; RMSE = 0.394 mm day⁻¹) and produced exceptionally high performance at certain stations (e.g., R² > 0.96 at Pedro Juan Caballero). Nonetheless, its station-level variability in leave-one-station-out tests underscores its reliance on local data density and its sensitivity to spatial clustering effects. By contrast, the ANN, constrained by a shallow architecture, exhibited the weakest predictive performance overall (R² = 0.882), reaffirming that insufficient network depth and complexity limit the model’s capacity to approximate the highly nonlinear processes driving ET₀ variation. The sensitivity of KNN to local data density and the underperformance of a shallow ANN are consistent with earlier reports on the limitations of distance-based learners and under-parameterized neural networks in hydrological modeling tasks [42,43]. This comparison underlines the importance of selecting models with sufficient complexity and addressing spatial clustering effects when applying ML to ET₀ prediction.

The ensemble modeling framework further enhanced predictive accuracy, with the inverse RMSE-based weighting scheme yielding slightly better performance than the R²-based scheme (R² = 0.925 vs. 0.923 in testing). The increased weight assigned to ANFIS under the inverse RMSE criterion likely contributed to this improvement, as the scheme prioritized models with lower prediction errors. This finding is consistent with ensemble learning theory, which emphasizes the benefits of weighting base learners according to performance-related criteria [34,35,36]. Although the gains were modest, the consistently high R² values (>0.92) across weighting schemes demonstrate the robustness of the parallel hybrid framework.

From a climatological perspective, the spatial distribution maps of ET₀ revealed a clear and recurrent annual cycle, with maxima in summer (January–March) and minima in winter (May–July), modulated by Paraguay’s latitudinal extent, topographic variation, and seasonal shifts in temperature and solar radiation. Persistent hotspots in the northeast and southeast highlight regions of elevated atmospheric water demand, which may correspond to agricultural zones with high evapotranspiration losses. These patterns are in agreement with FAO-56 Penman–Monteith–based climatologist for similar subtropical regions in South America [44,45]. By explicitly mapping these dynamics with ML–derived estimates, our study extends earlier climatological assessments and provides a spatially detailed reference for irrigation planning in Paraguay.

It should be acknowledged that the models developed in this study were calibrated and validated using ET₀ values derived from the FAO-56 Penman–Monteith equation at 19 meteorological stations in Paraguay. Therefore, the ML models do not estimate ET₀ from physical principles directly, but rather approximate the Penman–Monteith outputs through geo-temporal predictors. While this approach is contingent on the spatial patterns of pre-calculated ET₀, it offers a data-efficient surrogate framework that can be particularly useful in regions where the full set of meteorological inputs required for Penman–Monteith is unavailable. In this sense, our methodology complements rather than replaces physically based methods, and its primary value lies in extending ET₀ estimation to data-scarce environments where conventional computation is impractical.

Regarding transferability, direct application of these models to other regions without recalibration may lead to biased or unreliable estimates, as also reported in previous ET₀ modeling studies that emphasize the need for local adjustment [24,46]. To ensure robust performance in different environments, the framework should be recalibrated using regionally derived Penman–Monteith (or equivalent) ET₀ values. Nevertheless, the conceptual framework is highly adaptable and can be extended to diverse climatic zones.

Finally, we note that the present models are intended for estimating ET₀ (mm day⁻¹) under existing climatic conditions. Prediction of future ET₀ would require the inclusion of time-lagged predictors and potentially dynamic climate projections, as highlighted in previous studies exploring ET₀ forecasting under climate change scenarios [47,48]. Incorporating such approaches represents a promising direction for future research and could further extend the applicability of data-driven ET₀ models in agricultural and water resource management.

5. Conclusions

This study demonstrated the effectiveness of ML algorithms and neuro-fuzzy inference systems for estimating ET₀ using only geo-temporal predictors such as latitude, longitude, altitude, and month. Among the evaluated approaches, ANFIS with Gaussian membership functions consistently achieved the highest accuracy, while ensemble-based models such as RF and XGB exhibited strong robustness and stability across stations. Furthermore, ensemble integration enhanced predictive skill, with inverse RMSE-based weighting performing slightly better than R²-based weighting. Spatial ET₀ distribution maps generated through IDW interpolation revealed pronounced seasonal variability, with higher evaporative demand in the Chaco region and lower values in eastern Paraguay, particularly during winter months. These findings confirm that data-efficient modeling strategies can serve as practical and cost-effective alternatives in data-scarce environments, supporting irrigation scheduling and agricultural planning.

Looking ahead, several promising research directions could further advance the applicability of the proposed framework. Incorporating additional climatic variables (e.g., temperature, solar radiation, humidity, and wind speed) would improve model sensitivity and capture short-term fluctuations. The adoption of advanced deep learning architectures such as Long Short-Term Memory (LSTM) networks and Convolutional Neural Networks (CNNs) may also enhance the ability to learn temporal and spatial dependencies, especially for forecasting tasks. In addition, integrating remotely sensed products (e.g., MODIS, Landsat, or ERA5 reanalysis) could enable scalable, spatially explicit ET₀ estimation in regions with sparse meteorological coverage. Finally, extending the methodology to other climatic zones and linking ET₀ predictions with crop growth models and irrigation management systems will strengthen its relevance for sustainable agriculture and water resource management under diverse and changing environmental conditions.