Efficient Reliability Block Diagram Evaluation Through Improved Algorithms and Parallel Computing

Abstract

Quantitative reliability evaluation is essential for optimizing control policies and maintenance strategies in complex industrial systems. While Reliability Block Diagrams (RBDs) are a natural formalism for modeling these hierarchical systems, modern applications require highly efficient, online reliability assessment on resource-constrained embedded hardware. This demand presents two fundamental challenges: developing algorithmically efficient RBD evaluation methods that can handle diverse custom distributions while preserving numerical accuracy, and ensuring platform-agnostic performance across diverse multicore architectures. This paper investigates these issues by developing a new version of the librbd open-source RBD library. This version includes advances in efficiency of evaluation algorithms, as well as restructured computation sequences, cache-aware data structures to minimize memory overhead, and an adaptive parallelization framework that scales automatically from embedded processors to high-performance systems. Comprehensive validation demonstrates that these advances significantly reduce computational complexity and improve performance over the original implementation, enabling real-time analysis of substantially larger systems.

1. Introduction

Quantitative reliability evaluation enables actionable insights that inform decisions-support systems with different aims, including, e.g., control policy synthesis, system architecture design, and maintenance planning that may involve contrasting measures and trade-offs. As systems become increasingly complex and highly integrated across various industrial sectors, the challenges in reliability assessment intensify. In highly integrated systems, component failures can cascade through interconnected subsystems, causing widespread disruptions that are difficult to isolate and mitigate. This integration trend, while offering significant functional benefits, demands more sophisticated and computationally efficient reliability assessment approaches capable of supporting online evaluation in resource-constrained environments. Reliability is defined as “the ability of a system or component to perform its required functions under stated conditions for a specified period of time” [1]. In probabilistic terms, reliability represents the probability that a system successfully performs its required functions during the time interval $[t_0,t)$ given correct operation at time $t_0$ [2]. This probabilistic definition forms the basis of reliability evaluation theory, enabling systematic quantitative assessment of system dependability.

Modern industrial applications increasingly require these evaluations to be performed online on embedded processors and low-power industrial controllers, where computational efficiency becomes a critical constraint rather than merely a performance optimization goal.

These challenges are widely recognized in the reliability engineering community. For instance, Hollander and Peña [3] introduced non-parametric methods to derive reliability curves for censored data through the survival function, while Xing [4] proposed a framework that simplifies network reliability assessment using Reduced Ordered Binary Decision Diagrams. Green and Vishakha [5] further explored computational efficiency by developing and comparing two parallel computation strategies—batch parallelism and pipeline parallelism—for non-sequential Monte Carlo simulations on multi-core architectures. Additionally, Nelissen et al. [6] proposed the deployment of inline run-time monitoring to realize run-time verification and ensure the required safety properties.

Recent industrial applications have further intensified these challenges, particularly in domains requiring real-time or quasi-runtime reliability assessment:

• Developing efficient and expressive modeling techniques for complex Cyber–Physical Systems and their reliability evaluation [7,8,9].
• Optimizing software rejuvenation scheduling in distributed environments through the reliability assessment of their software subsystems [10,11,12].

Our recent industrial case studies on software reliability monitoring and rejuvenation [13] and proactive maintenance [14] have further demonstrated scenarios requiring intensive library usage for quasi-runtime reliability assessment in embedded maintenance systems, revealing critical performance bottlenecks when deployed on resource-constrained hardware. These combined insights from the literature and our practical experience motivated three research questions:

RQ1

How can the system’s reliability be efficiently analyzed in presence of components with arbitrary, non-parametric (i.e., numerical) failure distributions?

RQ2

How can computational complexity be reduced for RBD evaluation while preserving numerical accuracy?

RQ3

Can modern multicore architectures—from embedded processors to high-performance systems—be effectively leveraged to achieve platform-agnostic performance improvements?

To address RQ1, we previously released librbd [15], an open-source library supporting RBD-based reliability evaluation. librbd was specifically created for the numerical computation of reliability curves for all basic RBD blocks with multiplatform compatibility, thereby fully addressing our first research question. This paper presents significant algorithmic and architectural advances addressing all three RQs. We introduce a novel optimized recursive strategy for evaluating complex KooN models, combined with parallel computation techniques that provide substantial performance gains across diverse hardware platforms. To the best of our knowledge, no existing open-source implementation provides this level of algorithmic efficiency, platform portability, and computational generality in a lightweight C library suitable for deployment in resource-constrained industrial environments.

The remainder of this paper is organized as follows: Section 2 provides a brief overview of existing methodologies to reliability evaluation; Section 3 presents the mathematical foundations of RBD reliability evaluation and introduces our algorithmic contributions for reducing computational complexity; Section 4 details the enhanced librbd 2.0 features and validates computed reliability curves through comparison with SHARPE [16,17]; Section 5 describes the experimental methodology and hardware platforms used for performance evaluation; Section 6 presents comprehensive performance results demonstrating the effectiveness of our approach across diverse system configurations.

2. Reliability Evaluation Methodologies

Since reliability evaluation is a fundamental step for the assessment of an industrial system, several modeling formalisms have been developed for reliability assessment, broadly classified into four categories:

• Combinatorial models exploit the assumption of statistically independent components, i.e., a failure of one component does not impact the failure rate of other components, to efficiently evaluate the reliability [18,19]. These models include Reliability Block Diagrams (RBDs) [20,21], Fault Trees (FTs) [22,23], Reliability Graphs (RGs) [24,25], and Fault Trees with Repeated Events (FTREs) [23,26].
• State-space-based models leverage Markov Processes that allow them to model statistical, temporal, and spatial dependencies among failures at the cost of state-space explosion [18,19]. These include Continuous Time Markov Chains (CTMCs) [27,28], Stochastic Petri Nets (SPNs), and extensions such as Generalized Stochastic Petri Nets (GSPNs) and Stochastic Timed Petri Nets (STPNs) [29,30,31,32], Stochastic Reward Nets (SRNs) [33,34], and Stochastic Activity Networks (SANs) [35,36].
• Hybrid models augment combinatorial models with time-dependent relationships through state-space-based models [18], including Dynamic RBDs (DRBDs) [37,38] and Dynamic FTs (DFTs) [39,40,41].
• Hierarchical models employ divide-and-conquer strategies by combining different formalisms across system layers [13,18,42,43,44], exploiting the benefits of both combinatorial and state-space-based approaches while mitigating their respective limitations.

Hierarchical models represent the state-of-the-art approach for reliability evaluation [18], particularly for highly integrated systems where component interactions significantly influence overall system behavior. As system complexity increases, decomposition into subsystems and components becomes necessary for tractable analysis, making RBDs a natural formalism for modeling hierarchical system architectures due to their intuitive graphical representation and computational efficiency.

3. Reliability Block Diagrams

In Section 3.1, we recall the definition of an RBD together with the mathematical formulas used to compute the probability that a block is correctly operating, i.e., its state is equal to success. In Section 3.2, we introduce notable tools used for the RBD modeling and evaluation, detailing their core capabilities. In Section 3.3, we analyze the recursive algorithm that is widely used to evaluate the reliability of KooN blocks with generic components, together with its main limitations. In Section 3.4, we propose novel mathematical formulas that can be successfully used to overcome such limitations. Finally, in Section 3.5, we propose novel mathematical formulas also for the computation of Bridge blocks.

3.1. RBD Definitions

An RBD is a graph showing the decomposition of a system into components that may independently fail, plus the logical connections needed for the correct working of the system [15,18,19,20,45]

Definition 1.

An RBD model is a Block Diagram that is used to evaluate the reliability of a system, or sub-system, through the definition of the logical connections needed for its successful operation.

Definition 2.

A basic block, for simplicity also called block, is the building unit of an RBD model. A block provides the basic logical connections needed to define an RBD model by aggregating other blocks.

A block has only two states, i.e., success and failure. An RBD modeling a system represents the success state of the system by means of success paths, that is, connections of the success states of its components.

Basic blocks come in five kinds, recursively defined as follows:

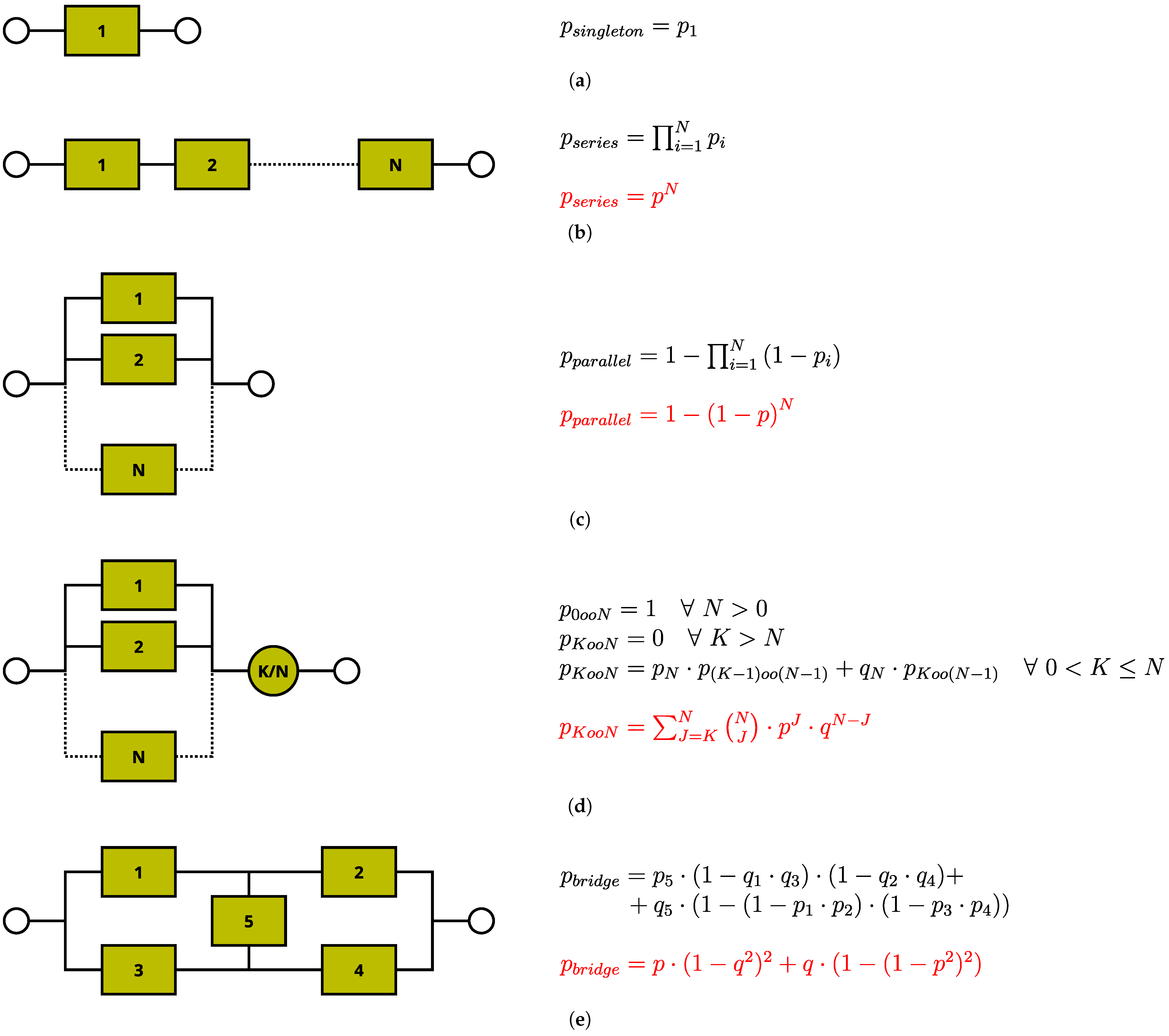
• Singleton. A component is a part of the physical system that is considered atomic w.r.t. failures. A physical component is visually represented inside the RBD model by a Singleton block. Singletons can be considered as the elementary bricks of the recursive structure of an RDB model. The state of a Singleton block is equal to success if and only if the associated component is working correctly. An example may be a stand-alone Power Supply.
• Series. This block is composed by N (sub-)blocks, and its state is equal to success if and only if all its sub-blocks are in success state. Examples are systems in which the single failure of any component produces the failure of the system.
• Parallel. This block is composed by N blocks, and its state is equal to success if and only if at least one of its sub-blocks is in success state, or, dually, a failure state of a Parallel block occurs if and only if all its blocks are in failure state. An example is a redundant Power Supply system with current sharing.
• K-out-of-N (KooN). This block is composed by N blocks, and its state is equal to success if and only if at least K blocks out of N are in success state. An example is a Triple Modular Redundancy computing system (TMR).
• Bridge. This block is introduced in order to model the possibility of an alternative success path in a parallel/series structure. As shown in Figure 1e, the block in the middle is used as a bridge between two parallel success paths, rerouting success to the other path in case of failure of one block. Typical examples can be found in network infrastructures.

Definition 3.

We denote as $p_i$ the probability that the state of the i-th component is equal to success, and as $q_i=1-p_i$ the probability that the state of the i-th component is equal to failure.

Definition 4.

A generic block uses heterogeneous components, also called generic components, i.e., $\exists i\ne j$ such that $p_i\ne p_j$. An identical block uses homogeneous components, also called identical components, i.e., $p_i=p_j=p\forall i,j$.

Figure 1 provides the graphical representation of the five kinds of basic blocks, visualizing the success paths among the related sub-blocks, together with the mathematical formulas that are used to perform the reliability analysis of each block according to [18,20]. In particular, Moskowitz [20] defines the formulas for computing the reliability as a probability of series and parallel models, also demonstrating the factoring theorem for simplifying the bridge model, and Trivedi and Bobbio [18] present the formulas for evaluating the reliability curve for series, parallel and KooN models, covering both the general case of generic components and the simplified case of identical components. More specifically, the formula in black is the one that can be used to evaluate blocks built with generic components, while the formula in red is the simplified one that can be used to evaluate blocks built with identical components.

For the sake of simplicity, the presented formulas express reliability as a probability. Nevertheless, the same formulations can be straightforwardly generalized to determine the time-varying reliability function. The correct probabilistic analysis of an RBD model requires that a failure probability function is associated to each Singleton block, reflecting the estimated failure probability of the modeled physical component. The Singleton blocks are statistically independent, i.e., given two Singletons A, B such that $A\ne B$, the probability of failure of A, $P\left(A\right)$, is not related with the probability of failure of B, $P\left(B\right)$, i.e., $P\left(A\right|B)=P(A)\forall A,B|A\ne B$.

Throughout the remainder of this paper, for simplicity of description, we consider RBD models composed of N Singleton blocks aggregated into a single system-level block. Also for clarity and simplicity, we refer to the Singleton blocks as components, and to the system-level block simply as block.

Figure 1. Layout of RBD blocks and mathematical formulas used to perform the respective reliability analysis under the generic case (black text) and under the identical case (red text): (a) Singleton. (b) Series. (c) Parallel. (d) KooN. (e) Bridge.

Figure 1. Layout of RBD blocks and mathematical formulas used to perform the respective reliability analysis under the generic case (black text) and under the identical case (red text): (a) Singleton. (b) Series. (c) Parallel. (d) KooN. (e) Bridge.

3.2. Existing RBD Modeling and Evaluation Tools

To facilitate the accurate definition and evaluation of RBD models, various supporting software tools have emerged. We can mention:

• Isograph Reliability Workbench: this commercial tool supports the hierarchical definition and analysis of scalable RBD models by means of submodels. It also supports the minimal cut-set analysis of the RBD model [46]. With respect to RQ1, this tool does not support the computation of the reliability curve.
• Relyence RBD: this commercial tool allows the definition and evaluation of series, parallel, and standby configurations, providing the reliability curve using analytical formulas or through Monte Carlo simulation [47]. With respect to RQ1, this tool only supports a set of parametric distributions for its input blocks.
• ALD RAM Commander—RBD Module: this commercial tool allows the definition and evaluation of series, parallel, and KooN configurations, providing the reliability curve using analytical formulas or through Monte Carlo simulation [48]. With respect to RQ1, this tool only supports a set of parametric distributions for its input blocks.
• SHARPE: the Symbolic Hierarchical Automated Reliability and Performance Evaluator (SHARPE) tool supports the definition of hierarchical stochastic models of dependability attributes, including reliability, availability, performance and performability, and the analysis of such models [16,17]. This tool supports several formalisms to define reliability models, including RBDs, and it supports time-dependent reliability analysis. With respect to RQ1, this tool only supports a set of parametric distributions for its input blocks.
• PyRBD is an open-source tool particularly effective to model and evaluate communication networks that employs a methodology that generates RBDs from network topologies and decomposes the diagrams for faster processing, with a core focus on utilizing minimal cut-sets and Boolean algebra to compute the steady-state availability [49,50]. With respect to RQ1, this tool does not support the computation of the reliability curve and it only supports a limited set of parametric distributions for its input blocks.
• PyRBD++ is the optimized evolution of PyRBD. While maintaining the same characteristics of its predecessor, it introduces a novel iterative conditional decomposition method to improve scalability performance [51,52]. As its predecessor, this tool does not support the computation of the reliability curve and it only supports a limited set of parametric distributions for its input blocks.

This comparative analysis highlights that no single existing tool fully satisfies the requirements of RQ1: specifically, the capability to compute the reliability curve using arbitrary, non-parametric input distributions. Therefore, we made the strategic decision to further enhance librbd, ensuring it uniquely provides the necessary computational foundation for our specialized research projects involving reliability modeling.

3.3. Quantitative Evaluation of KooN Blocks—Traditional Approach

The probability of success of a KooN block can be computed through the application of a divide and conquer recursive algorithm based on the formulas shown in Figure 1.

The recursive formulation is derived by conditioning on the state of the N-th component [15]. We denote as $p_N$ the probability of the N-th component being in success state, and as $q_N$ its probability of being in and failed state. If we consider the N-th component as correctly operating: for a KooN system to be correctly working, we need at least $K-1$ operating components out of the remaining $N-1$. If, on the other hand, the N-th component is failed, we need at least K operating components out of the remaining $N-1$ to have a correctly operating KooN system. The formulas that we report also below include two boundary cases that limit the domain of K and N to significant values and that are used as stop conditions for recursion.

$$\begin{array}{cc}\hfill & p_{0ooN}=1\forall N>0\hfill \\ \hfill & p_{KooN}=0\forall K>N\hfill \\ \hfill & p_{KooN}=p_N·p_{(K-1)oo(N-1)}+q_N·p_{Koo(N-1)}\forall 0<K\le N\hfill \end{array}$$

(1)

This approach can be modeled using an incomplete binary recursion tree since leaf nodes can be found at different depths due to the following two reasons: a node is a leaf node when one of the stop conditions is met, which can occur before the maximum reachable depth N; the initial value K affects the reachability of the stop conditions, with the worst case scenario occurring when $K = \raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. The theoretical upper limit to the number of recursive calls is given by a complete binary tree, i.e., ${\sum }_{i=1}^{i\le N}{2}^i=2^{N+1}-1$. Figure 2 shows this recursive approach over a 3oo5 block, where the the two numbers in each node represent, respectively, the two parameters K and N, magenta nodes are leaf nodes and cyan nodes are the internal ones.

This recursive approach, albeit simple and suitable to analyze KooN blocks with a limited number of components N, soon suffers from exponential blow-up of the number of recursive calls due to the following two reasons:

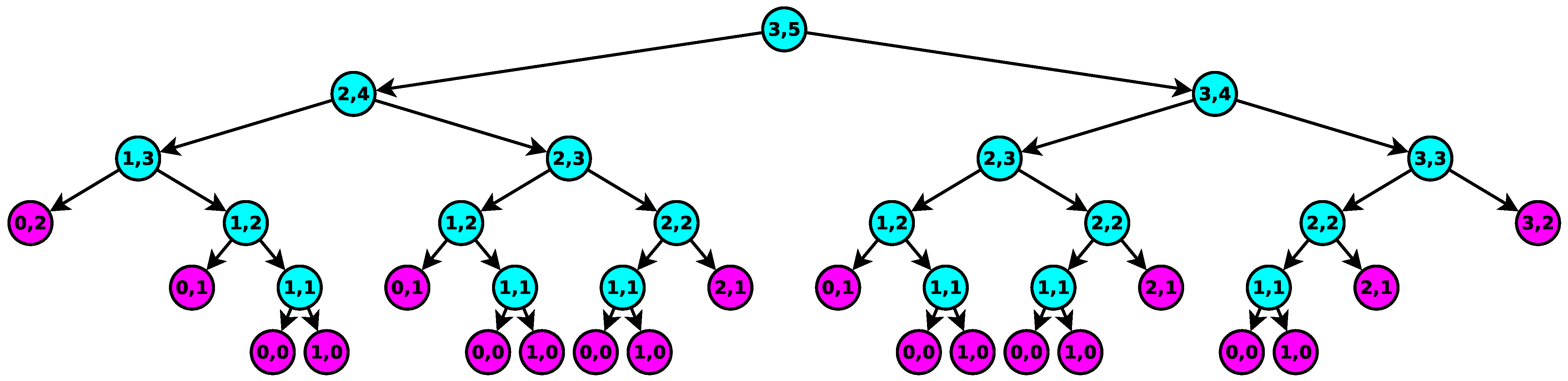
• The presented approach has trivial stop conditions that exponentially increase the number of leaf nodes, thus increasing the computation time. More specifically, it does not detect trivial KooN configurations such as Series (NooN) and Parallel (1ooN);
• Several different internal nodes with equivalent input parameters K and N are visited during the recursion tree. More specifically, in the example shown in Figure 2, two different nodes with the same parameters $K=2$ and $N=3$ are evaluated.

3.4. Quantitative Evaluation of KooN Blocks—Novel Approach

We propose novel mathematical formulas for the computation of KooN blocks with generic components that allow to reduce the computational complexity and, as a direct consequence, to decrease the computation time. Starting from Equation (1) and keeping in mind its main limitations, we propose two novel sets of mathematical formulas that can be successfully used to reduce the complexity of the already presented recursive algorithm. The first formula reduces the number of recursive calls for the analysis of trivial RBD blocks, hence the reliability of a KooN block can be computed as:

$$\begin{array}{cc}\hfill & p_{1ooN}=p_{parallel}=1-\prod _{i=1}^I\left(1-p_i\right)\forall N>0\hfill \\ \hfill & p_{KooN}=p_{series}=\prod _{i=1}^I{p}_i\forall K=N\hfill \\ \hfill & p_{KooN}=p_N·p_{(K-1)oo(N-1)}+q_N·p_{Koo(N-1)}\forall 1<K<N\hfill \end{array}$$

(2)

Figure 3 shows this recursive approach over the same 3oo5 block using the same notation. It can be easily observed that, by avoiding the analysis of series and parallel blocks, the number of visited nodes decreases drastically with respect to the recursion tree shown in Figure 2.

The other novel formula derives from the simplification of Equation (1) under the assumptions that $K>2$ and $K\le N-2$. In such case, the reliability of a KooN block can be computed as:

$$\begin{array}{cc}\hfill p_{KooN}& =p_N·p_{N-1}·p_{(K-2)oo(N-2)}+\hfill \\ \hfill & +(q_N·p_{N-1}+p_N·q_{N-1})·p_{(K-1)oo(N-2)}+\hfill \\ \hfill & +q_N·q_{N-1}·p_{Koo(N-2)}\hfill \end{array}$$

(3)

Using Equation (3), we can decrease N by 2 instead of 1, thus reducing the number of recursive calls. Furthermore, the two different recursive sub-trees with parameters $(K-1)$ and $(N-2)$, i.e., the first one for which component N is in failed state and component $N-1$ is in success state and second one for which component N is in success state and component $N-1$ is in failed state, collapse into a unified sub-tree. By using Equation (3) for all nodes such that $K>2$ and $K\le N-2$, the recursion tree ceases to be a binary tree and becomes a ternary tree.

The number of different internal nodes with equivalent input parameters K and N that are visited during the recursion tree achieved through the usage of Equation (3) can be further reduced by iteratively applying the same idea. In particular, let $h\in {\mathbb{N}}^{+}$ such that $K-h>1$ and $N-h\ge K$, then the reliability of a KooN block can be computed as:

$$p_{KooN}=\sum _{i=0}^h\left(\sum _{j=1}^{\left({\displaystyle \genfrac{}{}{0pt}{}{h}{i}}\right)}\left(\prod _{l\in C(h,i,j)}{p}_l·\prod _{m\notin C(h,i,j)}{q}_m\right)\right)·p_{(K-i)oo(N-h)}$$

(4)

where $\left({\displaystyle \genfrac{}{}{0pt}{}{h}{i}}\right)$ is the binomial coefficient and $C(h,i,j)$ is the function that returns the j-th unique combination of i working components out of h.

Increasing the value of h results in more identical sub-trees whose computation can be factorized (see the two sub-trees with root $(2,3)$ in Figure 3), leading to a reduction in the total number of recursive calls. Hence, to maximize the benefits of Equation (4), we need the maximum value h such that $K-h>1$ and $N-h\ge K$:

$$h=min(K-1,N-K)$$

(5)

where h is computed for each recursive call. Let H be the maximum of all h values computed. The recursive unfolding of Equation (4) follows a recursion tree with degree $H+1$. Figure 4 shows this recursive approach over the same 3oo5 block using the same notation. It can be easily observed that the number of visited nodes decreases drastically with respect to Figure 2. This reduction is caused by the node $(3,5)$, which is the only one, for this simple RBD model, that benefits from the new algorithm. Furthermore, this mathematical representation allows to reduce the number of visited internal nodes with equivalent input parameters K and N.

3.5. Quantitative Evaluation of Bridge Blocks—Novel Approach

As already pointed out, we propose novel mathematical formulas for the computation of Bridge blocks with both generic and identical components that allow us to reduce the computational complexity and, as a direct consequence, to decrease the computation time.

To reduce the complexity of Bridge blocks with generic components, we start from the generic equation shown in Figure 1e: after all occurrences of $q_i$ have been replaced with $1-p_i$, $i\in [1,5]$, we obtain the following formula that avoids the explicit computation of unreliability and maximizes the reuse of intermediate values:

$$\begin{array}{cc}\hfill va{l}_1& =(p_1+p_3-p_1·p_3)·(p_2+p_4-p_2·p_4)\hfill \\ \hfill va{l}_2& =p_1·p_2+p_3·p_4-p_1·p_2·p_3·p_4\hfill \\ \hfill p_{bridge}& =p_5·(va{l}_1-va{l}_2)+va{l}_2\hfill \end{array}$$

(6)

To reduce the complexity of Bridge blocks with identical components, we start from the identical equation shown in Figure 1e: after rearranging the order of operations, the computation of the Bridge block can be further simplified to the following formula that avoids a sum, hence it slightly reduces the computational complexity:

$$p_{bridge}=p·(1+q·(q·(q^2-2)+p·(2-p^2)))$$

(7)

4. RBD Computation Library—librbd 2.0

As already stated in Section 1, the purpose of this work is to enhance librbd [15,53], ensuring that the following original design requirements are fully preserved:

• to support the most common OSes, that is, Windows, MacOS and Linux;
• to support the numerical computation of the reliability curve for all RBD basic blocks; please note that this requirement is necessary to satisfy RQ1;
• to be available as a free software.

Section 4.1 briefly describes the design choices and features that were already integrated in librbd and that have been kept, while Section 4.2 provides the new requirements added to address RQs(2) and (3), also providing the detailed description of the new features. Finally, Section 4.3 shows the process used to validate librbd 2.0 and the obtained results.

4.1. Design Choices Already Present in librbd

The following design choices and features, which were already present in librdb [15], have been kept in librbd 2.0:

• The implementation of the resolution formulas for series, parallel, KooN, and bridge RBD blocks over time, up to 255 components per block.
• The availability of librbd on the majority of currently available OSes, i.e., Microsoft Windows, Linux, and MacOS.
• The implementation of librbd in C language for higher performance, introducing sporadic conditional compilation when interaction with the OS is deemed necessary [54].
• The availability of librbd as both a dynamic and static library.
• In order to minimize the numerical error, all computations use double-precision floating-point format (double) compliant with binary64 format [55].
• The implementation of formulas for RBD blocks both with generic components and with identical components.
• The implementation of several optimizations for the KooN RBD block computation, e.g., the minimization of computation steps when $N-K>K-1$ for blocks with identical components.
• The adoption of the Symmetric Multi-Processing (SMP), that can be enabled or disabled at compile time. When disabled, librbd is built as a Single Threaded (ST) library.

4.2. New Design Choices Introduced in librbd 2.0

This section details the significant enhancements and new requirements implemented in librbd 2.0, which extend the library’s capabilities to meet emerging computational challenges. Specifically, our primary contributions focus on performance optimization to address RQs (2) and (3):

• Algorithmic Complexity Reduction: To address RQ2, we implemented novel algorithms aimed at substantially reducing the computational complexity of KooN and Bridge blocks (detailed in Section 4.2.1).
• Cross-Platform Parallel Computation Techniques: To Address RQ3, ensuring optimal performance across diverse hardware architectures and OSes, this requirement necessitated several key developments:

  -

  Vectorization (SIMD): the addition of native support for the Single Instruction, Multiple Data (SIMD) paradigm for computation acceleration (Section 4.2.2).

  -

  Multi-Core Parallelism (SMP): the optimization of cache utilization within the SMP paradigm (Section 4.2.3), together with the addition of native SMP support for the Windows OS (Section 4.2.4).

4.2.1. Optimization of Algorithms for KooN and Bridge Blocks

The main limitation of librbd was its lower performance when computing the reliability of a KooN block with generic components when N is high and $K \approx \raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. The low performance was due to the fact that both algorithms implemented in librbd, i.e., the iterative and recursive one, were trivial and not optimized.

We propose a new version of the recursive algorithm, shown in Algorithm 1, that drastically reduces the number of recursive calls, hence decreasing the computation time. The first and second if statements are used to detect, respectively, series and parallel blocks and to treat them as such without using recursion, as shown in Equation (2). The innermost statements, i.e., the computation of h variable and the subsequent if statement, implement the optimized recursive algorithm as described in Equations (4) and (5). Finally, the last three statements, including the return, implement the classic recursive algorithm shown in Equation (1).

We state that the performance achieved using this new recursive algorithm is comparable to the one achieved with the iterative algorithm that was described in [15] when K is close to either 1 or N. Hence, the iterative algorithm, together with the heuristic used to select the proper algorithm, has been removed from librbd 2.0 to reduce source code complexity.

Algorithm 1: Computation of KooN block with generic components.

Input: Minimum number of working components k Input: Total number of components n Input: Array R of reliabilities, where $R\langle i\rangle$ is the reliability of i-th component Function R_KooN_Recursive(k, n, R)$\phantom{(}$   if $k=n$ then    # Evaluate noon block, i.e., Series block    $res=1$;    for $i\in [1,n]$ do     $res=res·R\langle i\rangle$;    return $res$;   if $k=1$ then    # Evaluate 1oon block, i.e., Parallel block    $res=1$;    for $i\in [1,n]$ do     $res=res·(1-R\langle i\rangle )$;    return $1-res$;   # Compute the best value h (see Equation (5))   $h=min(k-1,n-k)$;   if $h>1$ then    # Compute the reliability of koon (see Equation (4)) and store the result over $res$ variable    $res=1$;    for $i\in [0,h]$ do     # Compute ${\sum }_{j=1}^{\left({\displaystyle \genfrac{}{}{0pt}{}{h}{i}}\right)}\left({\prod }_{l\in C(h,i,j)}{p}_l·{\prod }_{m\notin C(h,i,j)}{q}_m\right)$ (see Equation (4)) and store the result over $step$ variable     $step=0$;     for $j\in [1,nCi]$ do       # Compute ${\prod }_{l\in C(h,i,j)}{p}_l·{\prod }_{m\notin C(h,i,j)}{q}_m$ (see Equation (4)) and store the result over $tmp$ variable       $tmp=1$;       for $l\in [1,h]$ do         if $l\in C(n,i,j)$ then           $tmp=tmp·R\langle l\rangle$;         else           $tmp=tmp·(1-R\langle l\rangle )$;       $step=step+tmp$;     $res=res+step·R\_KooN\_Recursive(k-i,n-h,R)$;    return $res$;   # The value h is equal to 1, use traditional recursive formula (see Equation (1))   $res=R\langle n\rangle ·R\_KooN\_Recursive(k-1,n-1,R)$;   $res=res+(1-R\langle n\rangle )·R\_KooN\_Recursive(k,n-1,R)$;   return $res$;

The key indicator of the performance of a recursive algorithm is the number of calls to the recursive function, which, for a KooN block, depends on both parameters K and N and, given N, it reaches its maximum when $K = \raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. Let $F_1(K,N)$, $F_2(K,N)$, and $F_3(K,N)$ be the functions used to compute the recursive calls using, respectively, Equations (1), (2) and (4), defined as follows:

$$F_1(K,N)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}K=0\mathrm{or}K>N\hfill \\ 1+F_1(K-1,N-1)+F_1(K,N-1)\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

$$F_2(K,N)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}K=1\mathrm{or}K=N\hfill \\ 1+F_2(K-1,N-1)+F_2(K,N-1)\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(9)

$$F_3(K,N)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}K=1\mathrm{or}K=N\hfill \\ 1+\sum _{i=0}^h{F}_3(K-i,N-h)\hfill & \mathrm{otherwise},\mathrm{with}h=min(K-1,N-K)\hfill \end{array}\right.$$

(10)

Figure 5 shows the trend, in logarithmic scale, of the number of recursive calls for the functions $F_1(\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,N)$, $F_2(\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,N)$, and $F_3(\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,N)$, where $\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ is the integer division, in particular for (a) N up to 20 to easily observe the benefits of the different algorithms and (b) N up to 255—the maximum number of components that can be grouped into a single block with librbd 2.0—to analyze the behavior at a larger scale.

We speculate that the observed trend at these two scales can be also extended for increasing values of N. We can observe that, as expected, the recursive algorithm described in Equation (1) is the one that maximizes the number of recursive calls and that this number follows, for the worst case $K = \raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$, an exponential function w.r.t. the parameter N. The usage of Equation (2) decreases the number of recursive calls, thus reducing the computational complexity as expected, but the trend is still exponential. Furthermore, for N values up to 20, we can observe that, for a given $n\in {\mathbb{N}}^{+}$, the following holds true: $F_1(\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,n)=F_2(\raisebox{1ex}{$n$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+1,n+2)$. Finally, the usage of Equation (4) massively decreases the number of recursive calls and the trend is no longer exponential. The number of recursive calls required to analyze a 10oo20 block using Equation (4) is lower than the one needed to analyze a 6oo11 block using Equation (2). The non-exponential trend is due to the different increment patterns that occur for each $N\ge 3$ when N is either even or odd. For odd N, the function exhibits a linear progression, i.e., $F_3(\raisebox{1ex}{$N$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,N)=F_3(\raisebox{1ex}{$N-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.,N-1)+1$. Conversely, for even N, the number of recursive calls is marked by a sharp increase, yet the overall number of recursive calls grows sub-exponentially.

For what concerns the computation algorithms of bridge blocks, we propose updated versions both for generic and identical components, which introduce the following benefits:

• they slightly reduce the complexity, hence they decrease the computation time;
• they can be easily implemented with the SIMD paradigm;
• they require a lower number of temporary variables/vectors and hence they decrease the computation time.

Algorithm 2 shows the computation of RBD bridge blocks with generic components, which exploits Equation (6).

Algorithm 2: Computation of Bridge block with generic components.

Input: Array R of reliabilities, where $R\langle i\rangle$ is the reliability of i-th component Function R_Bridge_Generic(R)   # Compute $val1$ and $val2$ variables (see Equation (6))   $val1=(R\langle 1\rangle +R\langle 3\rangle -(R\langle 1\rangle ·R\langle 3\rangle )·R\langle 2\rangle +R\langle 4\rangle -(R\langle 2\rangle ·R\langle 4\rangle \left)\right)$;   $val2=R\langle 1\rangle ·R\langle 2\rangle +R\langle 3\rangle ·R\langle 4\rangle -R\langle 1\rangle ·R\langle 2\rangle ·R\langle 3\rangle ·R\langle 4\rangle$;   # Compute reliability of Bridge block (see Equation (6))   return $R\langle 5\rangle ·(val1-val2)+val2$;

Algorithm 3 shows the computation of RBD bridge blocks with identical components, which exploits Equation (7).

Algorithm 3: Computation of bridge block with identical components.

Input: Reliability R of each component Function R_Bridge_Identical(R)   # Compute unreliability U of each component   $U=1-R$;   # Compute reliability of Bridge block (see Equation (7))   return $R·(1+U·(U·(U·U-2)+R·(2-R·R)\left)\right)$;

4.2.2. Single Instruction, Multiple Data (SIMD)

To further increase performance, the Single Instruction, Multiple Data (SIMD) paradigm has been introduced. SIMD is a type of parallel processing that allows the microprocessor or, in some architectures, a co-processor, to execute the same instruction over multiple data, by means of “SIMD extensions”. The SIMD extensions allow for the execution of a single instruction over vectors of data of different size, e.g., 64, 128, 256, and 512 bits. Since a 64-bit vector is able to host a single double-precision floating-point, our interest is placed on SIMD extensions capable of operating on vectors whose size is at least 128 bit. On one hand, the SIMD paradigm offers a parallelism which can greatly decrease the execution time; on the other hand, several considerations that may cause disadvantages must be taken into account:

• Usage of vectors requires large register files that increase the required chip area and the power consumption. Due to the power consumption increase, which causes higher CPU temperatures, Dynamic Frequency Scaling techniques may automatically decrease the CPU frequency.
• The implementation of an algorithm with SIMD instructions requires human effort since compilers typically do not generate SIMD instructions.
• Several SIMD extensions have restrictions on data alignment, thus increasing the complexity of the program. Even worse, different data alignment constraints may apply to different SIMD revisions or different processors of the same manufacturer.
• Due to the increased parallelism, a higher stress is put on the memory bus since a larger data flow is processed. This stress is further increased on multi-threading applications since different threads perform different but “concurrent” memory accesses.
• Specific instructions, like Fused Multiply-Add (FMA), are not available in some SIMD instruction sets.
• SIMD instruction sets are architecture-specific and some architectures lack SIMD instructions entirely, so programmers must provide a generic non-vectorized implementation and a different vectorized implementation for each covered architecture.

Table 1. SIMD extensions implemented in librbd 2.0.

Architecture	SIMD	Vector Size (Bits)	FMA Support
x86	SSE2	128	no
	AVX	256	no
amd64	FMA	256	yes
	AVX512F	512	yes
AArch64	NEON	128	yes

presents the list of SIMD extensions that have been implemented in librbd 2.0, together with their respective vector size and the support to FMA instructions. The SIMD functionality can be enabled or disabled at compile time.

4.2.3. Optimization of Cache Usage with SMP

One of the main difficulties with SMP programming is the subdivision of the entire task, which is responsible to process the whole dataset, into multiple batches, each one responsible for the processing a portion of the original data. librbd splits the entire data, i.e., the input reliability curves, into contiguous and non-interleaved batches. This trivial subdivision of the data into batches is affected by a performance issue that has been aggravated with the introduction of newer CPUs with an increased number of cores.

On older CPUs, the limited number of homogeneous cores were clocked at the same frequency. On modern CPUs, the increased number of cores are subdivided into two heterogeneous groups, the Performance Cores (P-Cores) and the Efficient Cores (E-Cores): P-Cores and E-Cores are, in general, clocked with different frequencies.

The performance issue of librbd is caused by the cache usage when SMP is used: the inner cache level, which is in general specific of a single core, contains a subset of a specific batch, while the outer cache levels, which are in general shared between multiple cores, contain data from different batches. When multiple threads need to concurrently access new data, i.e., data not available into the outer cache level, the accesses on the memory data bus are serialized, thus creating a bottleneck which reduces the performance. Due to this data organization of batches, and considering the clocking characteristics of both older and modern CPUs, the probability of such an event is non-negligible. This performance loss increases with the number of instantiated threads, thus limiting the benefits of SMP, and modern CPUs with an increased number of cores are then more penalized with respect to older CPUs.

librbd 2.0 splits the entire data into interleaved batches, i.e., given M threads and T time instants to be processed, the m-th thread processes the t time instants for which $tmodM\equiv m$. With this subdivision, both the inner and the outer cache levels contain data which are shared between several threads. Also in this case when multiple threads need to concurrently access new data, i.e., data not available into the cache, the accesses on the memory data bus are serialized. The main difference is that, after the first thread has retrieved the data from the external memory, all subsequent threads can access the spatially contiguous data from the outer cache levels, thus reducing the latency on memory data access time and minimizing the bottleneck on the memory data bus.

The introduction of the improved algorithms, already described in Section 4.2.1, and the optimization of cache usage when SMP is enabled allow us to increment the maximum batch size from 10,000 time instants to 20,000.

4.2.4. Native Support to SMP on Windows

librbd provided support to SMP through the usage of pthreads, a POSIX-compliant [56] library that implements the management of threads and is natively available on both Linux and MacOS.

Microsoft Windows, on the other hand, does not offer a native support to pthreads, although it is still possible to use it either through pthreads-win32 [57] or through Cygwin [58]. To limit the usage of external libraries, which may be not always available, we decided to refactor the SMP implementation on librbd 2.0 to support, through adequate conditional compiling, both pthreads and Win32 thread models, thus adding native support to SMP also on Microsoft Windows OSes.

4.3. Validation

To validate the librbd 2.0 library, we use the same methodology already presented in [15], i.e., we perform a comparison of the output provided by librbd 2.0 with respect to the ones provided by SHARPE [16,17]. For each RBD basic block, we generated two different RBD models, one using generic components and the other using identical components. During the validation process, we analyzed the 42 RBD models shown in Table 2. The validation process has been performed as follows:

• We used failure rate data from twenty components with constant failure rate, estimated according to Telcordia SR-332 [59] and reported in Table 3.
• We evaluated the RBD models for 100,000 h. By setting the sampling period to 1 h, the resulting reliability curve was determined across 100,000 time instants.

Table 2. RBD models used during validation.

RBD Block	Topology	Components
Series identical	20 components	C1
Series generic	20 components	All
Parallel identical	20 components	C1
Parallel generic	20 components	All
KooN identical	Koo20, $K\in [2,19]$	C1
KooN generic	Koo20, $K\in [2,19]$	All
Bridge identical	5 components C1
Bridge generic	5 components	From C1 to C5

Table 2. RBD models used during validation.

RBD Block	Topology	Components
Series identical	20 components	C1
Series generic	20 components	All
Parallel identical	20 components	C1
Parallel generic	20 components	All
KooN identical	Koo20, $K\in [2,19]$	C1
KooN generic	Koo20, $K\in [2,19]$	All
Bridge identical	5 components C1
Bridge generic	5 components	From C1 to C5

Table 3. Components and their respective failure rate λ.

Component	$\mathit{\lambda }$$({\mathit{h}}^{-1})$	Component	$\mathit{\lambda }$$({\mathit{h}}^{-1})$
C1	0.0000084019	C11	0.0000047740
C2	0.0000039438	C12	0.0000062887
C3	0.0000078310	C13	0.0000036478
C4	0.0000079844	C14	0.0000051340
C5	0.0000091165	C15	0.0000095223
C6	0.0000019755	C16	0.0000091620
C7	0.0000033522	C17	0.0000063571
C8	0.0000076823	C18	0.0000071730
C9	0.0000027777	C19	0.0000014160
C10	0.0000055397	C20	0.0000060697

Table 3. Components and their respective failure rate λ.

Component	$\mathit{\lambda }$$({\mathit{h}}^{-1})$	Component	$\mathit{\lambda }$$({\mathit{h}}^{-1})$
C1	0.0000084019	C11	0.0000047740
C2	0.0000039438	C12	0.0000062887
C3	0.0000078310	C13	0.0000036478
C4	0.0000079844	C14	0.0000051340
C5	0.0000091165	C15	0.0000095223
C6	0.0000019755	C16	0.0000091620
C7	0.0000033522	C17	0.0000063571
C8	0.0000076823	C18	0.0000071730
C9	0.0000027777	C19	0.0000014160
C10	0.0000055397	C20	0.0000060697

For each evaluated RBD model, we have produced two text output files, one generated using librbd 2.0 and the other one with SHARPE, that contain the reliability of each analyzed time instant. Each reliability value has been formatted using scientific notation with eight decimal places. Please note that the uncertainty of the comparison operations is limited by the chosen numerical representation, i.e., scientific notation with 8 decimal digits.

To perform this validation, we compiled librbd 2.0 as an ST, SISD library.

$$\begin{array}{cc}\hfill err\left(t\right)& ={\displaystyle \frac{ou{t}_{librbd}\left(t\right)-ou{t}_{SHARPE}\left(t\right)}{ou{t}_{SHARPE}\left(t\right)}}\hfill \\ \hfill RMSE& =\sqrt{{\displaystyle \frac{{\sum }_{t=0}^{max\_t}{\left(ou{t}_{librbd}\left(t\right)-ou{t}_{SHARPE}\left(t\right)\right)}^2}{max\_t}}}\hfill \\ \hfill MAE& ={\displaystyle \frac{{\sum }_{t=0}^{max\_t}\left|ou{t}_{librbd}\left(t\right)-ou{t}_{SHARPE}\left(t\right)\right|}{max\_t}}\hfill \end{array}$$

(11)

We decided to employ both RMSE and MAE to evaluate regression model performance. While both metrics quantify the mean discrepancy between values produced by the two tools, i.e., librbd 2.0 and SHARPE, they diverge in how individual errors are penalized: MAE treats all deviations equally by taking absolute values, whereas RMSE squares the deviations, thereby penalizing larger errors.

We chose this dual-metric approach for the following reasons. First, the error distribution is unknown a priori, and different metrics perform differently depending on the tail behavior of the error distribution [60]. Second, using both metrics allowed us to assess the robustness and stability of the error function: MAE provides an indication of average error magnitude under equal weighting, while RMSE emphasizes large deviations, offering insight into worst-case (or large error) behavior.

Finally, for each evaluated RBD block, we extracted both the minimum and maximum values for the relative error $err\left(t\right)$, thus computing the relative error range shown in Figure 6. For some RBD models, e.g., parallel block, SHARPE, and librbd 2.0 produce the same reliability curve, hence the relative error is $0.0$ for all time instants: this condition is visually represented in Figure 6 by not showing the relative error range.

We speculate that the relative error, when present, is due to implementative differences between the two tools, in particular regarding the exact sequencing of floating-point operations performed. This is supported by the observation that the largest error is obtained for series block, i.e., the one with reliability close to $0.0$ for high values of t. From the analysis of the obtained results, we can observe that the absolute value of the relative error for all evaluated topologies is lower than $1.0·{10}^{-8}$.

Table 4. librbd 2.0 validation against SHARPE—RMSE and MAE.

RBD Model	Generic		Identical
	RMSE	MAE	RMSE	MAE
Series	$3.272·{10}^{-15}$	$1.770·{10}^{-17}$	$5.840·{10}^{-16}$	$1.183·{10}^{-17}$
Parallel	$0.000·{10}^0$	$0.000·{10}^0$	$0.000·{10}^0$	$0.000·{10}^0$
Bridge	$0.000·{10}^0$	$0.000·{10}^0$	$0.000·{10}^0$	$0.000·{10}^0$
2oo20	$0.000·{10}^0$	$0.000·{10}^0$	$0.000·{10}^0$	$0.000·{10}^0$
3oo20	$1.924·{10}^{-11}$	$3.700·{10}^{-13}$	$1.049·{10}^{-11}$	$1.100·{10}^{-13}$
4oo20	$1.517·{10}^{-11}$	$2.300·{10}^{-13}$	$1.225·{10}^{-11}$	$1.500·{10}^{-13}$
5oo20	$1.549·{10}^{-11}$	$2.400·{10}^{-13}$	$1.265·{10}^{-11}$	$1.600·{10}^{-13}$
6oo20	$1.817·{10}^{-11}$	$3.300·{10}^{-13}$	$1.549·{10}^{-11}$	$2.400·{10}^{-13}$
7oo20	$1.761·{10}^{-11}$	$3.100·{10}^{-13}$	$1.225·{10}^{-11}$	$1.500·{10}^{-13}$
8oo20	$1.549·{10}^{-11}$	$2.400·{10}^{-13}$	$1.378·{10}^{-11}$	$1.900·{10}^{-13}$
9oo20	$1.643·{10}^{-11}$	$2.700·{10}^{-13}$	$1.549·{10}^{-11}$	$2.400·{10}^{-13}$
10oo20	$1.673·{10}^{-11}$	$2.800·{10}^{-13}$	$1.225·{10}^{-11}$	$1.500·{10}^{-13}$
11oo20	$1.703·{10}^{-11}$	$2.900·{10}^{-13}$	$1.483·{10}^{-11}$	$2.200·{10}^{-13}$
12oo20	$1.517·{10}^{-11}$	$2.300·{10}^{-13}$	$1.265·{10}^{-11}$	$1.600·{10}^{-13}$
13oo20	$1.225·{10}^{-11}$	$1.500·{10}^{-13}$	$1.140·{10}^{-11}$	$1.300·{10}^{-13}$
14oo20	$1.000·{10}^{-11}$	$1.000·{10}^{-13}$	$1.000·{10}^{-11}$	$1.000·{10}^{-13}$
15oo20	$9.487·{10}^{-12}$	$9.000·{10}^{-14}$	$8.367·{10}^{-12}$	$7.000·{10}^{-14}$
16oo20	$4.472·{10}^{-12}$	$2.000·{10}^{-14}$	$7.071·{10}^{-12}$	$5.000·{10}^{-14}$
17oo20	$5.477·{10}^{-12}$	$3.000·{10}^{-14}$	$0.000·{10}^0$	$0.000·{10}^0$
18oo20	$3.162·{10}^{-12}$	$1.000·{10}^{-14}$	$3.240·{10}^{-15}$	$1.500·{10}^{-17}$
19oo20	$0.000·{10}^0$	$0.000·{10}^0$	$6.686·{10}^{-16}$	$8.700·{10}^{-18}$

reports both the RMSE and MAE values obtained from the validation of librbd 2.0 w.r.t. SHARPE for both generic and identical component configurations. These results confirm an excellent agreement between librbd 2.0 and SHARPE across all RBD models. For the parallel, bridge and 2oo20 configurations, both RMSE and MAE values are effectively zero, confirming that librbd 2.0 reproduces the same reliability curves w.r.t. SHARPE.

For the other RBD models, the error remains extremely low—on the order of $1.0·{10}^{-11}$ for RMSE and $1.0·{10}^{-13}$ for MAE in most cases—indicating negligible numerical discrepancies. The slightly higher RMSE compared to MAE across all models is consistent with theoretical expectations, as RMSE magnifies larger deviations due to the squaring of residuals. The stability of both metrics across varying values of K further suggests that librbd 2.0 maintains numerical robustness independently of the redundancy level within the system.

In conclusion, the joint analysis of relative error, RMSE, and MAE supports the conclusion that librbd 2.0 achieves numerical equivalence with SHARPE across a wide range of RBD models, demonstrating high stability, robustness, and consistency irrespective of component heterogeneity. Reporting both metrics provides complementary insights—relative error showing a well-bounded percentage error, MAE confirming the uniform smallness of the errors, and RMSE ensuring that no large outliers are present. Our conclusion is that librbd 2.0 produces, for each implemented RBD basic block, the correct reliability curve.

5. Performance Evaluation Workbench

In this section, we present the methodology used during the performance evaluation of librbd 2.0. In particular, in Section 5.1, we present the materials, i.e., the PCs and their characteristics, used to evaluate the performance, while in Section 5.2, we discuss the actual methodology adopted to evaluate the performance of librbd 2.0.

5.1. Materials

The six PCs listed in

Table 5. PCs used for performance evaluation.

Name	CPU	Cores/Threads	RAM	OS & Compiler
PC1a	Intel i7-13700K	8/16 @ 5.4GHz + 8/8 @ 4.2GHz	64GB-DDR5 @ 5600MHz	Ubuntu 22.04 GCC 11.4.0
PC1b	Intel i7-13700K	8/16 @ 5.4GHz + 8/8 @ 4.2GHz	64GB-DDR5 @ 5600MHz	Windows 11 Visual Studio 2022
PC1c	Intel i7-13700K	8/16 @ 5.4GHz + 8/8 @ 4.2GHz	64GB-DDR5 @ 5600MHz	Windows 11 GCC 12.4.0
PC2	Apple M3	4/4 @ 4.06GHz + 4/4 @ 2.57GHz	16GB-LPDDR5 @ 3200MHz	Mac OS 14.5 clang 15.0.0
PC3	Intel i7-7700HQ	4/8 @ 3.8GHz	32GB-DDR4 @ 2400MHz	Ubuntu 22.04 GCC 11.4.0
PC4	Intel i7-6700HQ	4/8 @ 3.5GHz	16GB-LPDDR3 @ 2133MHz	Mac OS 10.13.6 clang 10.0.0
PC5	Broadcom BCM2712	4/4 @ 2.4GHz	8GB-LPDDR4X @ 2133MHz	Raspberry Pi OS 12 GCC 12.2.0
PC6	Broadcom BCM2837	4/4 @ 1.2GHz	1GB-LPDDR2 @ 900MHz	Raspberry Pi OS 11 GCC 10.2.1

have been used in order to measure the performance of librbd 2.0 [53]. Please note that (1) PC1 has been tested using three different combinations of OS and Compiler to evaluate the performance on the same hardware equipment; (2) the reported clock frequency corresponds to the maximum frequency: the actual frequency is, in general, set by the OS and/or the CPU itself based on the current CPU load and the number of used cores. To investigate the performance of librbd 2.0 also on embedded platforms, we have included into the set of used PCs two Raspberry Pi computers.

Both librbd 2.0 and test binaries have been compiled and linked using the maximum optimization level (−O3).

5.2. Methods

The performance evaluation has been conducted using a test application that has allowed us to measure the execution time needed by librbd 2.0 to analyze the RBD models shown in

Table 6. RBD models used during performance evaluation.

RBD Block	N
Series Generic	$N\in [2,3,4,5,7,10,12,15,20]$
Series Identical	$N\in [2,3,4,5,7,10,12,15,20]$
Parallel Generic	$N\in [2,3,4,5,7,10,12,15,20]$
Parallel Identical	$N\in [2,3,4,5,7,10,12,15,20]$
$N/2$ooN Generic	$N\in [2,3,4,5,7,10,12,15,20]$
$N/2$ooN Identical	$N\in [2,3,4,5,7,10,12,15,20]$
Bridge Generic	$N=5$
Bridge Identical	$N=5$
KooN Generic, $\forall 1<K<N$	$N=20$
KooN Identical, $\forall 1<K<N$	$N=20$

.

We analyzed each RBD model with different time instant configurations, i.e., 1000, 5000, 10,000, 20,000, 50,000, 100,000, and 200,000 time instants. Furthermore, we analyzed each RBD model with 1607 time instants: this number, albeit apparently random, allows us to validate the SIMD computation exploiting hybrid vector lengths of 64 (scalar double), 128, 256, and 512 bits.

To limit external impacts, e.g., the time consumed by the OS, each RBD model with each time instant configuration has been evaluated 15 times and, after all these 15 experiments were executed, we selected the median time of execution.

The failure rate $\lambda$ of each component, shown in Table 3, has been chosen using the criteria already described in Section 4.3.

To further investigate the performance improvements of SMP and SIMD, we repeated the experiments four times, once for each combination of SMP and SIMD options, i.e., ST and SISD, ST and SIMD, SMP and SISD, SMP and SIMD.

Please note that, as already stated in Section 4.3, librbd 2.0 has been validated with respect to SHARPE only when it is compiled as ST and SISD. During this phase, we compared the output for each produced RBD model with all different optimizations to validate that librbd 2.0 always produces the same results when changing the optimization features. Hence, the usage of all combinations of optimization features on the tested PCs allowed us to almost completely validate all possible versions of librbd 2.0. Please note that, since AVX512F ISA is not supported by any CPU used, the support to this SIMD extension is still untested. Nevertheless, the source code used when supporting this ISA is almost equal to the amd64 FMA one, which has been extensively stressed during the tests.

6. Results

To evaluate the performance of librbd 2.0, in Section 6.1, we present the performance analysis, while in Section 6.2, we discuss on the obtained results. In Section 6.3, we present the comparison of performance obtained with librbd 2.0 w.r.t. SHARPE. Finally, in Section 6.4, we discuss the current limitations that have been identified.

6.1. librbd 2.0 Performance Analysis

The performance analysis has been performed as described in Section 5.2, and the results are presented in this section as follows:

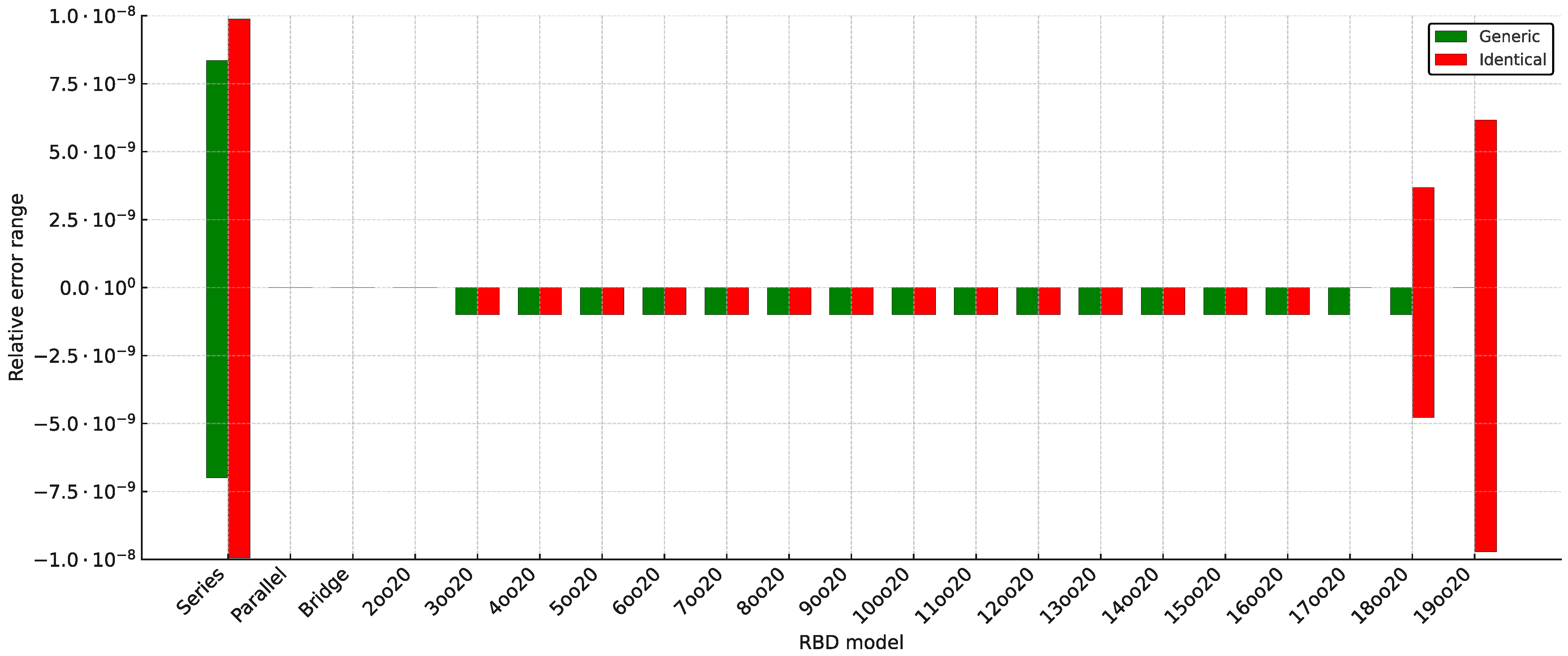
• For each combination of RBD model, time instants, PC used, and enabled optimizations, the reliability curve produced by the RBD computation has been stored to a file. This allows us to quickly compare the reliability curves both between different architectures and between different enabled optimizations. If the reliability curves for each modeled RBD are the same for all the sets of all enabled optimizations and the PC, then librbd 2.0 is fully validated.
• For each combination of modeled RBD, time instants, PC used, and enabled optimizations, the librbd 2.0 minimum, maximum, and median execution time observed on 15 different executions has been stored on a file. This has allowed us to quickly evaluate the performance both between different architectures and between different enabled optimizations.

6.1.1. Validation with Different Architectures and Enabled Optimizations

Using librbd 2.0 compiled as ST and SISD, we computed the reliability curves on the eight different architectures already presented in Table 5. We then computed the absolute value of the relative error between the reliability curve obtained with the reference architecture, i.e., PC1b since its results were previously validated with respect to SHARPE, and all other architectures. We observed that only the results obtained with PC5 differ from the expected ones: by further investigating, we observe that this difference is caused by a difference of computation of the input reliability curves, implemented through the usage of exp C library function. We suppose that this difference is caused by different versions of the C standard library. Nevertheless, across all the evaluated RBD models, the maximum RMSE and MAE between the reliability curves obtained with PC5 and PC1 are $1.053·{10}^{-6}$ and $1.046·{10}^{-6}$, respectively, indicating that the resulting reliability curves are essentially identical. For all other architectures, the reliability curves correspond to the one obtained with the reference architecture.

For each one of the eight target architectures used, the absolute value of the relative error computed between the reliability curve obtained with the reference library, i.e., the one compiled as ST and SISD, and the other three versions, i.e., SMP and SISD, ST and SIMD, SMP and SIMD, is limited to $1.0·{10}^{-8}$; hence, we can state that the result provided by librbd 2.0 is the same for all the sets of enabled optimizations and PCs.

6.1.2. Performance Analysis with Different Architectures and Enabled Optimizations

In Figure 7, we show the execution time of librbd 2.0 on the different PCs with different enabled optimizations.

The experimental results shown in Figure 7, which constitute a small subset of all experiments performed and already detailed in Table 6, constitute the worst case execution time of the performed experiments and hence are useful to correctly discuss the improvements introduced by SMP and SIMD.

6.2. Considerations on librbd 2.0 Performance

After the analysis of the execution time of librbd 2.0 already presented in Section 6.1, we can state that, in general, the adoption of SMP and SIMD considerably improves the performance; however, some exceptions warrant further analysis:

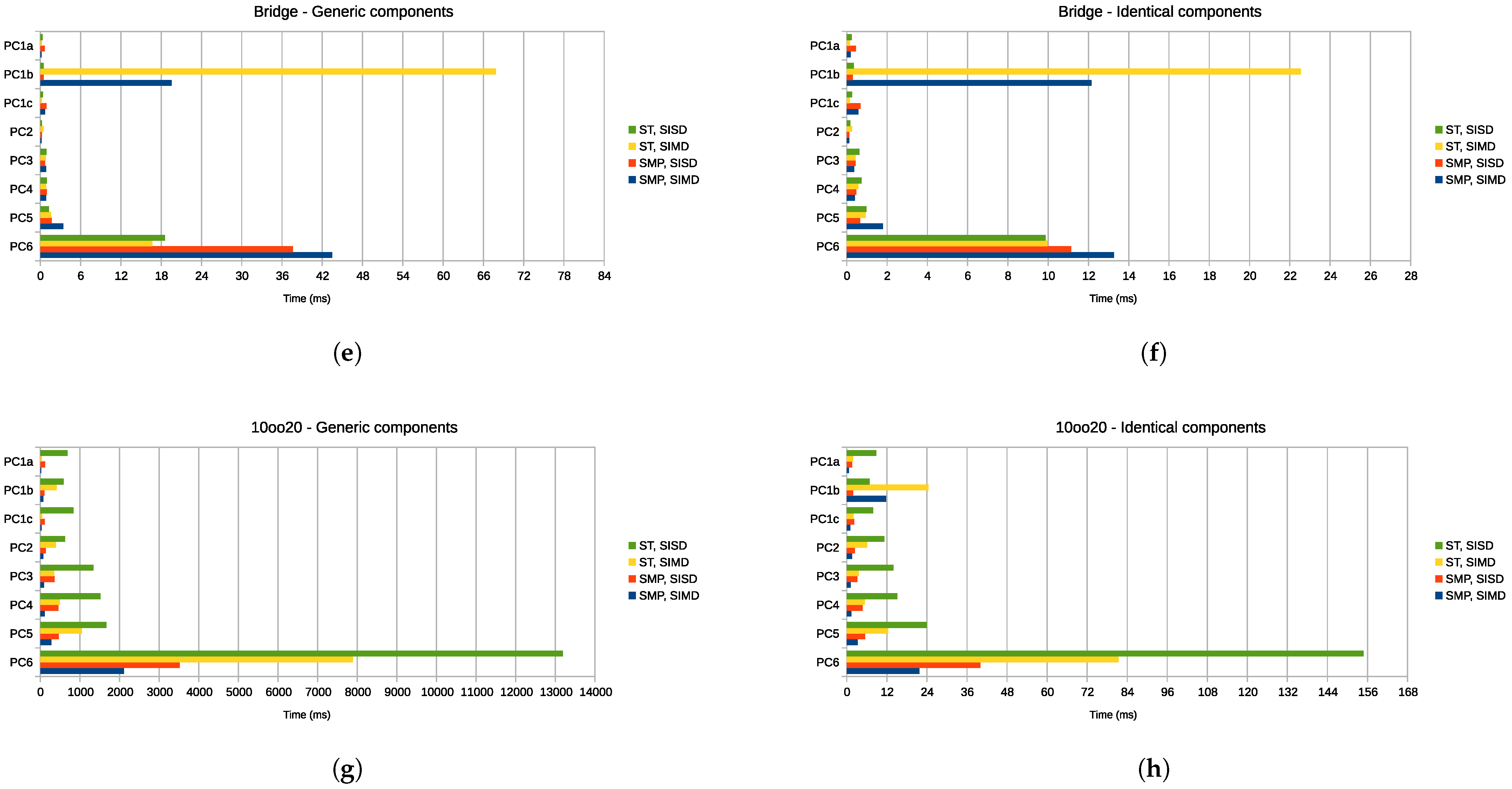
• Considering PC1b, the adoption of SIMD when compiling with Visual Studio 2022 causes a significant loss of performance. This loss of performance may be due to an incorrect setting of file-specific optimization flags or due to compiler issues that limit its capability to effectively optimize source code exploiting SIMD intrinsics.
• Considering PC1 in its three different configurations, i.e., OS and compiler, we observe that, with the exception of the ones involving SIMD and Visual Studio, the variation in the execution time among the different configurations is small, thus showing that librbd 2.0 can be effectively considered as a multi-platform library.
• Considering PC6, i.e., the PC with the lowest computational power, we observe that, in several occasions, e.g., series, parallel, and bridge with generic components, the introduction of SMP slightly degrades the performance. We suggest that this phenomenon may be caused by the memory latency, since this PC has very limited cache memory with a low bandwidth RAM. Despite PC6 being a low-power and dated embedded platform, its performance is anyway acceptable. Furthermore, its evolution, i.e., PC5, has performance results comparable with the other tested PCs.
• Considering the results obtained on all PCs, excluding the ones for 10oo20 blocks, we observe that, in several occasions, the adoption of SMP slightly degrades the performance. We suggest that this behavior may be caused by a non-optimized choice, for such simple models, of the batch size, i.e., the number of time instants concurrently processed by each thread. As already discussed in Section 4.2.3, the batch size should be properly tuned: if it is too high, a lower number of threads is instantiated, thus limiting the advantages of SMP; on the other side, if it is too low, each thread executes for a negligible amount of time and the overhead introduced by SMP, which includes the threads creation and termination, context switches, and race conditions on memory access, negates the advantages of SMP itself.
• With the exception of PC1b, the usage of SIMD extensions with ST library decreases the execution time. The actual decrease in computation time varies with the complexity of the analyzed block, i.e., more complex blocks with a higher number of computation steps per time instant have the greatest benefits.
• With respect to librbd [15], by comparing the results obtained with both librbd and librbd 2.0, we observe that bridge, parallel, and series blocks librbd 2.0 have, in general, performance comparable with the one achieved with librbd. This may be due to the fact that, for these trivial blocks, the benefits obtained with SIMD are, in general, comparable with the loss of performance due to complexity of the new source code required for the implementation of the new features. For what concerns KooN blocks, i.e., blocks characterized by a high complexity and a high number of computations per time instant, we observe huge benefits for both block with generic and identical components. For example, let us consider PC3: using librbd, an 8oo15 block with generic components on 200,000 time instants was analyzed in $2278.303$ ms, while librbd 2.0 analyzed the same block in just $22.184$ ms.
• Regarding RBDs presenting complex nestings of basic blocks, librbd 2.0 can be used by applying standard functional composition, that is, if a basic block B is used to compose basic blocks $B_1,\dots B_n$, if $P_B(p_1,\dots p_n)$ is the function computing its success probability, the overall success probability is given by $P_B(P_{B_1}(P_{B_{1_1}},\dots P_{B_{1_k}}),\dots P_{B_n}(P_{B_{n_1}},\dots P_{B_{n_m}}))$. Thus, execution time for each basic block adds up linearly.

6.3. Performance Comparison w.r.t. SHARPE

To compare the performance of librbd 2.0 w.r.t. SHARPE, we created series, parallel, bridge and Koo20, with $K\in [2,19]$, RBD models for the SHARPE tool, both using generic and identical components, and we performed the reliability evaluation for 200,000 time instants using PC1 with Windows OS. We then compared the obtained results with the ones that were already presented in Section 6.1 using PC1c with both SMP and SIMD enabled. Furthermore, we performed some stress tests to understand how the two different tools behave with KooN blocks for increasing values of N. In particular, we analyzed 15oo30, 20oo40, and 25oo50 models with both generic and identical components.

Table 7. librbd 2.0 and SHARPE analysis time in milliseconds (ms).

RBD Model	Generic		Identical
	SHARPE	librbd 2.0	SHARPE	librbd 2.0
Series	2140.0	0.1	1150.0	0.1
Parallel	2320.0	0.1	1350.0	0.1
Bridge	990.0	0.7	1010.0	0.6
2oo20	2480.0	2.5	1510.0	0.5
3oo20	2590.0	8.1	1640.0	0.7
4oo20	2690.0	16.7	1730.0	0.8
5oo20	2780.0	26.8	1820.0	1.0
6oo20	2910.0	32.6	1900.0	0.9
7oo20	3020.0	35.0	2000.0	1.0
8oo20	3010.0	33.5	2020.0	1.2
9oo20	3110.0	35.8	2070.0	0.9
10oo20	3050.0	33.2	2080.0	1.1
11oo20	3020.0	35.1	2090.0	1.1
12oo20	2970.0	35.0	2030.0	1.0
13oo20	2970.0	32.8	2010.0	1.0
14oo20	2840.0	31.6	1930.0	1.1
15oo20	2810.0	29.9	1900.0	1.0
16oo20	2730.0	25.8	1750.0	0.9
17oo20	2630.0	15.2	1650.0	0.7
18oo20	2410.0	7.3	1490.0	0.6
19oo20	2270.0	2.4	1340.0	0.6
15oo30	4870.0	2024.0	3510.0	1.2
20oo40	7300.0	53,901.3	5450.0	2.1
25oo50	10,150.0	2,277,788.3	7810.0	3.4

shows the result of such comparison.

In conclusion, the numerical approach of librbd 2.0 demonstrated a substantial speed advantage over SHARPE’s symbolic analytical technique for relatively simple RBD models with exponential distributions, confirming the superior efficiency of numerical solvers. However, for large and complex generic KooN models, e.g., 25oo50, librbd 2.0 experienced a severe performance drop. This behavior reflects an intrinsic limitation of its numerical nature: as detailed in Section 4.2.1, the computational complexity of the numerical evaluation grows sub-exponentially with model size, leading to a significant runtime increase for highly redundant systems.

Conversely, SHARPE’s analytical methods, which rely on closed-form expressions when failure rates follow expolynomial distributions, show a comparatively slower and almost linear growth in computational time as the model size increases. Nevertheless, this advantage rapidly diminishes when SHARPE must handle reliability curves departing from the expolynomial assumption. In such cases, e.g., when components follow a Weibull distribution, SHARPE internally approximates these distributions through expolynomial (phase-type) representations in order to preserve analytical tractability. This approximation process, while avoiding the need for simulation, introduces additional computational overhead and may impact numerical precision.

In contrast, the numerical foundation of librbd 2.0 ensures that its computational cost and numerical precision remain unaffected by the distributional form of the input reliability functions, providing a unified, accurate, and efficient framework for analyzing systems with non-expolynomial component behaviors.

6.4. Current Limitations

We have identified the following limitations:

• Limited support to compilers: librbd 2.0, since it exploits compiler-dependent features, requires the usage of one between GCC, Clang, and MSVC. We consider that this limitation is not important, since MSVC is the primary compiler for Microsoft Windows OSes, while both GCC and Clang are open-source compilers that are widely available over different OSes and architectures.
• Limited support to OSes: librbd 2.0 exploits both OS-dependent and compiler-dependent features to implement the SMP paradigm. As a result, when SMP is used, only Microsoft Windows, Linux, and MacOS are supported. We consider this limitation negligible, since these three OSes cover the majority of all OSes used nowadays. Furthermore, since this limitation applies to SMP version only, during compilation librbd 2.0 automatically detects the target OS and, if it is not supported, it automatically disables SMP.
• Limited support to SIMD: librbd 2.0 supports only SIMD extensions for x86, amd64, and AArch64 architectures. We believe that the supported SIMD extensions cover the majority of commercially available ones. Nonetheless, in future developments, support to additional SIMD extensions, e.g., PowerPC Vector Scalar Extension (VSX), could be introduced.
• Untested support to amd64 AVX512F SIMD: the support to AVX512F SIMD extension, which has been introduced in librbd 2.0, is still untested since the CPUs used during the performance analysis do not support this ISA. We consider this limitation not relevant due to the following two considerations: this ISA is supported by newer server CPUs only; the development of the algorithms exploiting this SIMD extension leverages the porting of FMA extension to AVX512F-specific intrinsics.
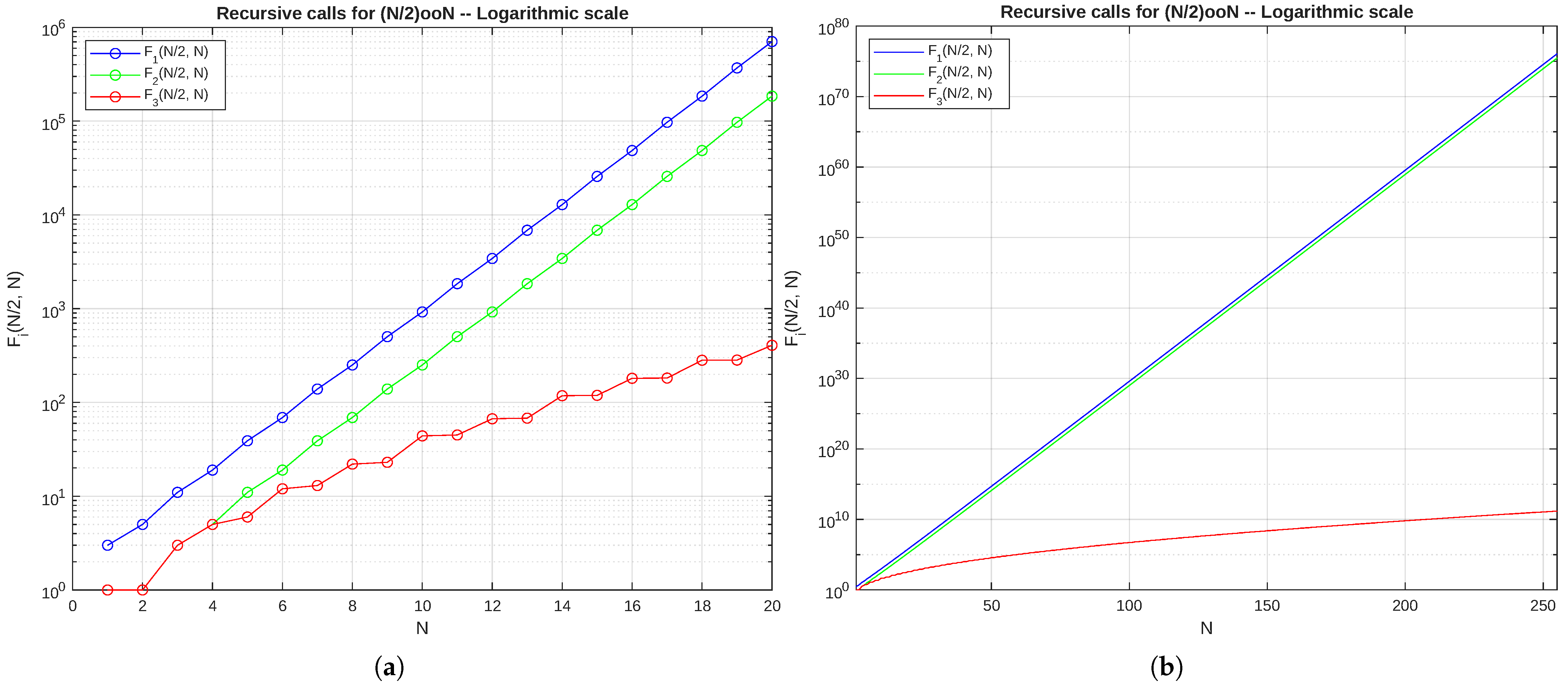
• Scalability limitations of KooN algorithm: the new algorithm designed and developed for the computation of KooN blocks with generic components is a huge improvement with respect to librbd, nonetheless its computational complexity is still an issue for big values of N. We consider this limitation negligible, since librbd 2.0 has shown that the computation of generic 10oo20 blocks is feasible in reasonable time even using low-performance PCs and given that this block can be reasonably considered a worse case scenario in practical RBD usage.

7. Conclusions and Future Developments

This work presented a significant enhancement and validation of librbd, an open-source library for RBDs computation, called librbd 2.0. librbd 2.0 successfully addresses the three core RQs posed in this study by introducing novel algorithmic and architectural improvements:

RQ1

Non-parametric reliability analysis. librbd was designed to compute the reliability of components with arbitrary, non-parametric failure distributions. Our validation against the established SHARPE tool confirms that librbd 2.0 maintains this crucial capability, with the absolute maximum relative error between the computed reliability curves remaining consistently below 1.0 $·{10}^{-8}$ across all models analyzed. This result ensures that the high numerical accuracy required by RQ1 is fully preserved.

RQ2

Reducing computational complexity through novel algorithms. The primary focus for reducing complexity was achieved through the implementation of novel mathematical formulas. Specifically, new algorithms were introduced to efficiently compute the reliability of the KooN block with generic components and the Bridge block with both generic and identical components. Performance analysis across various hardware platforms demonstrated the efficacy of these methods, showing a substantial reduction in computational complexity. Crucially, these new algorithms enabled the analysis of complex RBD models—such as large KooN configurations—that were previously unfeasible using librbd.

RQ3

Leveraging multicore architectures for platform-agnostic performance. To effectively utilize modern multicore architectures, as stipulated by RQ3, we implemented two key architectural improvements: an optimized usage of cache memory within the SMP paradigm, and native support for the SIMD programming paradigm. These techniques successfully increased the throughput of computed data and improved overall performance. Performance tests conducted on diverse PCs, CPUs, and OSes confirmed that these features contribute to achieving the platform-agnostic performance improvements necessary for deployment on a wide range of embedded and high-performance systems.

While the current work successfully addresses the proposed RQs, the following avenues for future research and development are identified to further enhance the utility and robustness of librbd 2.0:

• To promote broader adoption and ease of use, we are currently working on the definition of an RBD Description Language (RDL) based on the XML format. This RDL will be leveraged, alongside librbd 2.0, to develop an application for generic system-level reliability analysis.
• To address the identified threats to validity concerning SIMD extensions (limited support and untested AVX512F—specific code), we plan to perform a dedicated test session using server CPUs and to add support for additional SIMD extensions, such as PowerPC VSX.
• To resolve the observed performance discrepancy when using SIMD with the MSVC compiler, we plan to investigate the difference in the generated Assembly code between GCC and MSVC and implement necessary tweaks to MSVC-specific compiler options.