Analysis of Acoustic Wave Propagation in Defective Concrete: Evolutionary Modeling, Energetic Coercivity, and Defect Classification
Abstract
1. Introduction
2. State of the Art and Scientific Motivations
3. Materials and Methods
3.1. Conceptual Framework
3.2. Physical and Mathematical Model
3.3. Governing Equations
3.4. Extension of the Acoustic Wave Equation in Heterogeneous Concrete
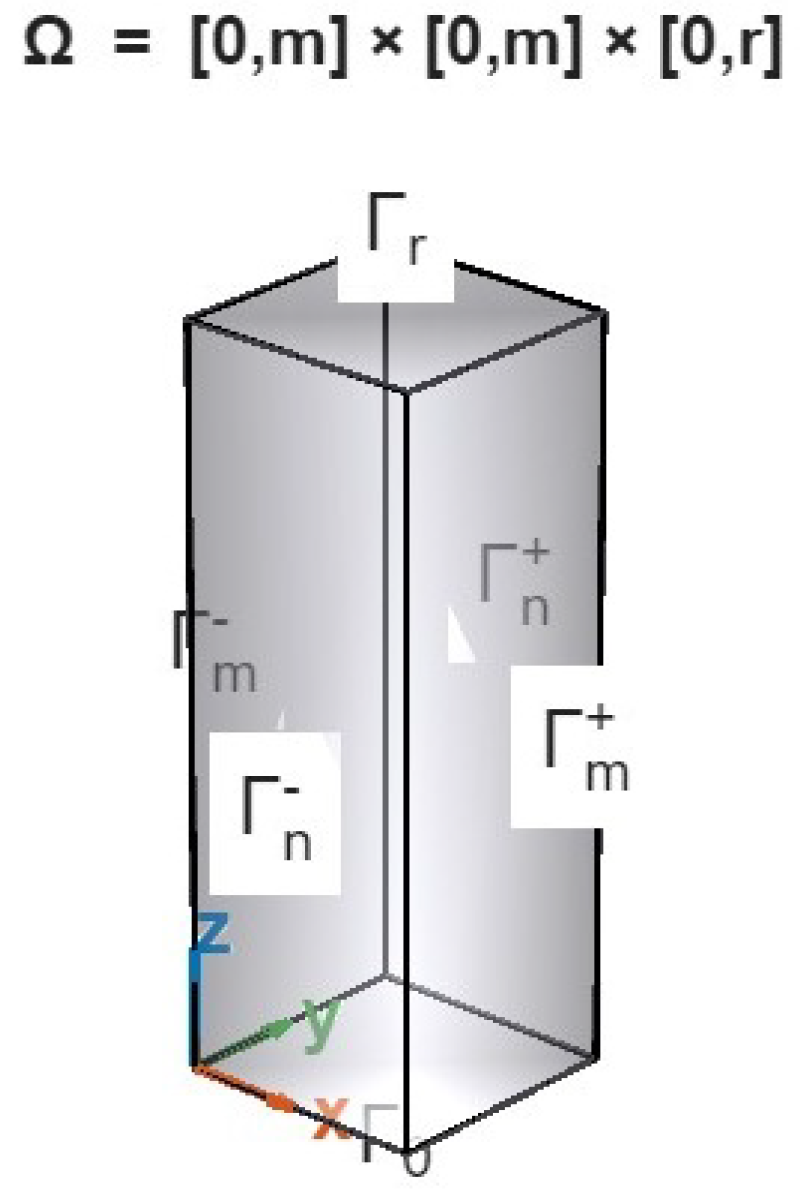
3.5. On Boundary and Initial Conditions
3.6. Evolutionary Reformulation
3.7. Abstract Formulation and Functional Setting
3.8. Functional Spaces and Bilinear Form
3.9. Numerical Implementation
3.10. Numerical Validation and Model Consistency
4. Some Interesting Theoretical Results
Some Theoretical Results
5. Numerical Results and Discussion
5.1. Physical Interpretation: Defects and Coercivity
5.2. Defect-Induced Stabilization: Setup and Sufficient Conditions
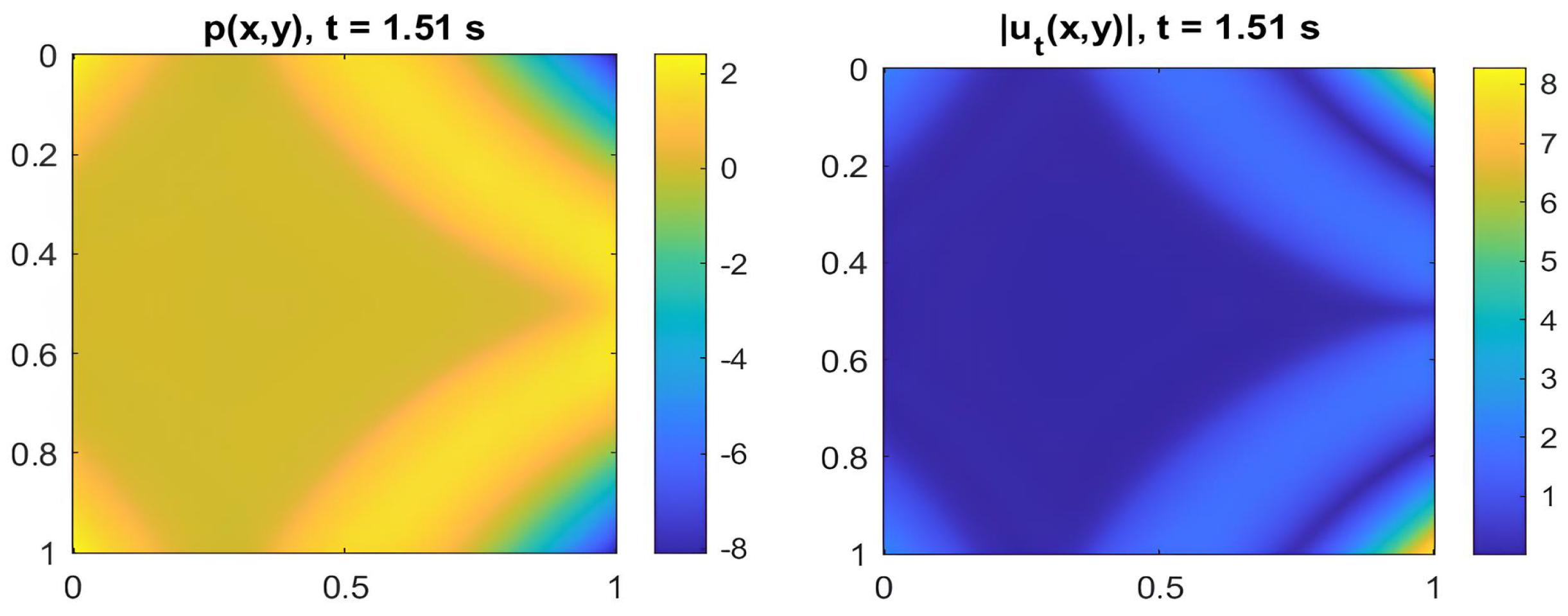
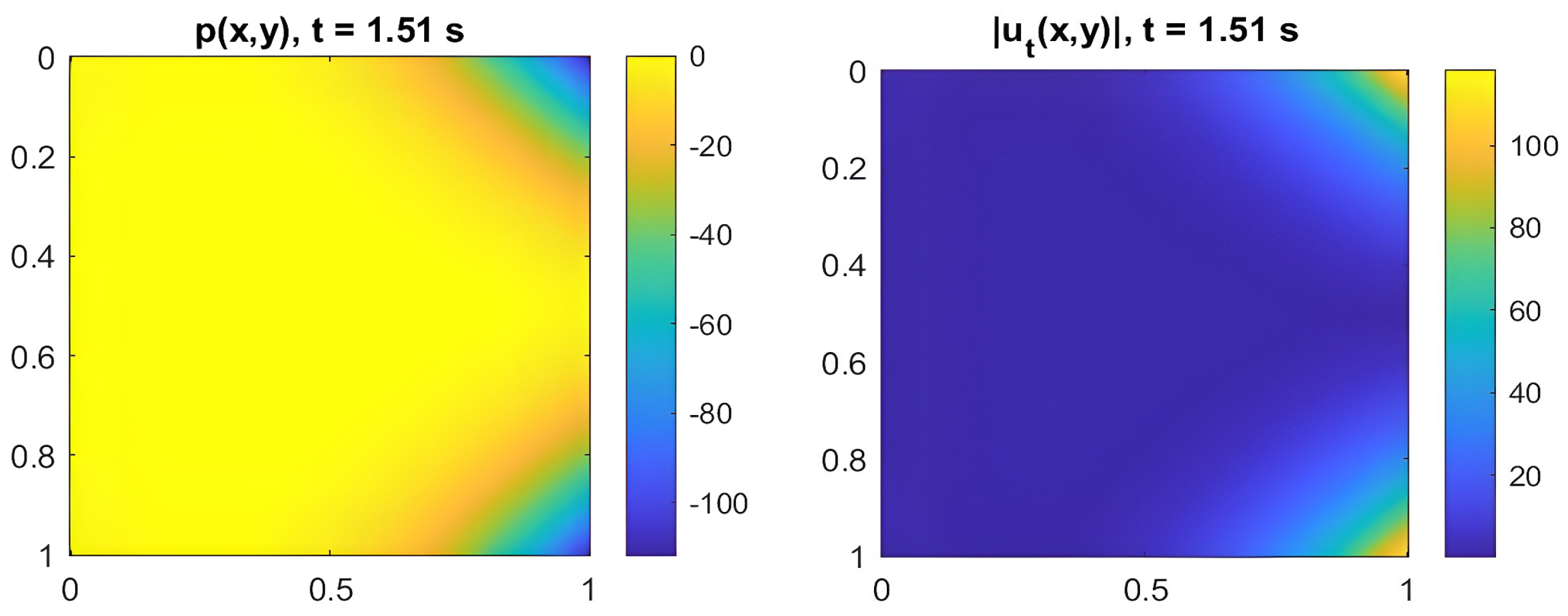
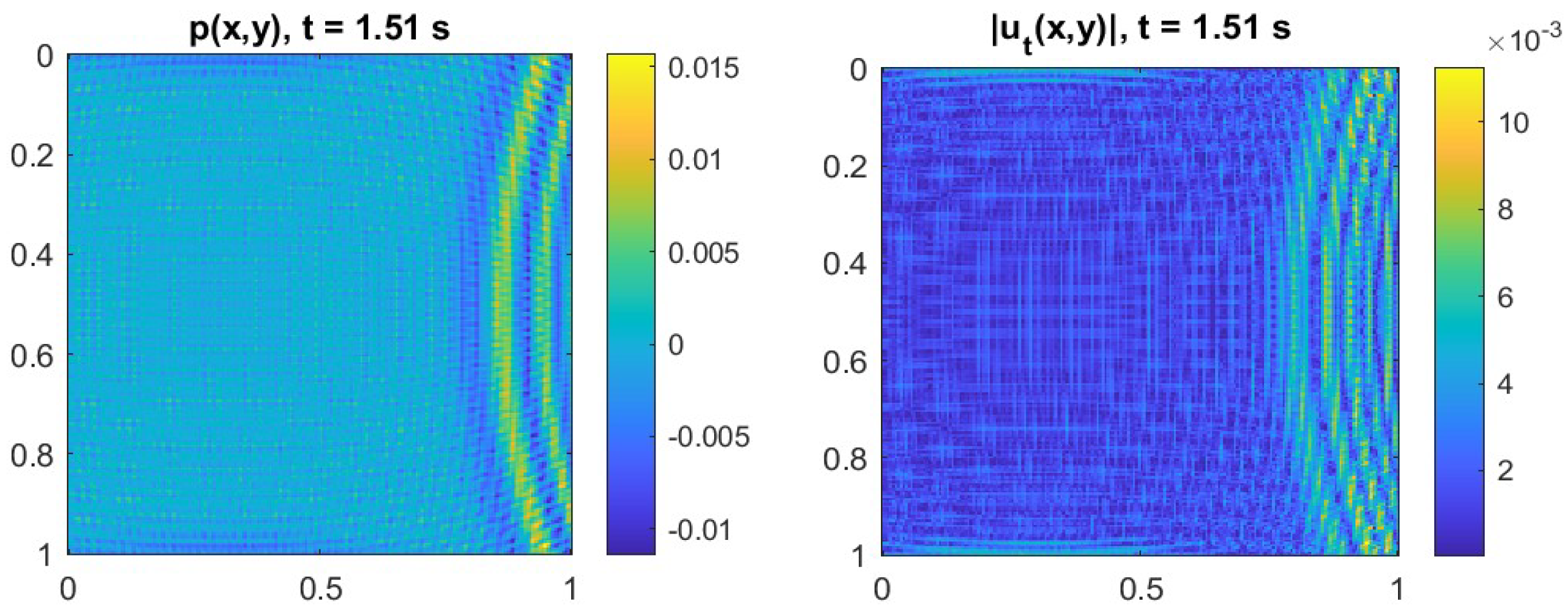
5.3. Energy Evolution and Defect Classification
5.4. Quantitative Comparison with Classical Models
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. Proof of Proposition 3
Appendix A.4. Proof of Proposition 5
- For every and for every ,
- For every and for every ,
Appendix A.5. Proof of Proposition 6
Appendix A.6. Proof of Theorem 2
References
- Li, E.D.; Shiying, T.; Wang, Z.; Zerfu, K. Eco-Friendly Fibre Reinforced Geopolymer Concrete: A Critical Review on the Microstructure and Long-Term Durability Properties. Case Stud. Constr. Mater. 2022, 16, e00894. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, L.; Wan, D.; Xue, Y. Research Progress and Trend Analysis of Solid Waste Resource Utilization in Geopolymer Concrete. Buildings 2025, 15, 3370. [Google Scholar] [CrossRef]
- Burrascano, P.; Di Schino, A.; Versaci, M. Efficient Estimation of Synthetic Indicators for the Assessment of Nonlinear Systems Quality. Appl. Sci. 2024, 14, 9259. [Google Scholar] [CrossRef]
- Angiulli, G.; Versaci, M.; Burrascano, P.; Laganá, F. A Data-Driven Gaussian Process Regression Model for Concrete Complex Dielectric Permittivity Characterization. Sensors 2025, 25, 6350. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, S. Algorithm for Acoustic Wavefield in Space–Wavenumber Domain of Vertically Heterogeneous Media Using NUFFT. Mathematics 2025, 13, 571. [Google Scholar] [CrossRef]
- Abdollahi-Mamoudan, F.; Ibarra-Castanedo, C.; Maldague, X.P.V. Non-Destructive Testing and Evaluation of Hybrid and Advanced Structures: A Comprehensive Review of Methods, Applications, and Emerging Trends. Sensors 2025, 25, 3635. [Google Scholar] [CrossRef]
- Angiulli, G.; Burrascano, P.; Ricci, M.; Versaci, M. Advances in the Integration of Artificial Intelligence and Ultrasonic Techniques for Monitoring Concrete Structures: A Comprehensive Review. J. Compos. Sci. 2024, 8, 531. [Google Scholar] [CrossRef]
- Versaci, M.; Laganà, F.; Manin, L.; Angiulli, G. Soft Computing and Eddy Currents to Estimate and Classify Delaminations in Biomedical Device CFRP Plates. J. Electr. Eng. 2024, 76, 72–79. [Google Scholar] [CrossRef]
- Simone, G.; Morabito, F.C.; Polikar, R.; Ramuhalli, P.; Udpa, L.; Udpa, S. Feature Extraction Techniques for Ultrasonic Signal Classification. Int. J. Appl. Electromagn. Mech. 2002, 15, 291–294. [Google Scholar] [CrossRef]
- Wang, H. Research on Ultrasonic Nondestructive Testing Method Based on Multimodal Sensor Fusion and Deep Learning. In Proceedings of the 8th International Conference on Advanced Algorithms and Control Engineering (ICAACE 2025), Shanghai, China, 21–23 March 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, H.; Jongmanns, M. Active Ultrasonic Measurements for Machine Condition Monitoring. In Proceedings of the 2025 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Chemnitz, Germany, 19–22 May 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, H.; Wang, W.; Wu, C.; Zhang, M.; He, L.; Liu, P.; Zhou, L.; Li, Y. Fuzzy Logic-Based Control of Superconducting Closed-Loop Current with a Linear-Motor Type Flux Pump. Cryogenics 2025, 150, 104148. [Google Scholar] [CrossRef]
- Cacciola, M.; Morabito, F.C.; Polimeni, D.; Versaci, M. Fuzzy Characterization of Flawed Metallic Plates with Eddy Current Tests. Prog. Electromagn. Res. 2007, 72, 241–252. [Google Scholar] [CrossRef]
- Gel’atko, M.; Hatala, M.; Botko, F.; Vandžura, R.; Hajnyš, J. Eddy Current Testing of Artificial Defects in 316L Stainless Steel Samples Made by Additive Manufacturing Technology. Materials 2022, 15, 6783. [Google Scholar] [CrossRef]
- Versaci, M. Fuzzy Approach and Eddy currents NDT/NDE Devices in Industrial Applications. Electron. Lett. 2016, 52, 943–945. [Google Scholar] [CrossRef]
- Fernandes, N.A.T.C.; Sharma, S.; Arieira, A.; Hinckel, B.; Silva, F.; Leal, A.; Carvalho, Ó. Experimental Validation of Time-Explicit Ultrasound Propagation Models with Sound Diffusivity or Viscous Attenuation in Biological Tissues Using COMSOL Multiphysics. Bioengineering 2025, 12, 946. [Google Scholar] [CrossRef] [PubMed]
- Bonfiglio, P. A mechanical relaxation test for the determination of the frequency dependent complex modulus of linear viscoelastic materials. npj Acoust. 2025, 1, 21. [Google Scholar] [CrossRef]
- Pawlik, L.; Wilk-Jakubowski, J.L.; Frej, D.; Wilk-Jakubowski, G. Applications of Computational Mechanics Methods Combined with Machine Learning and Neural Networks: A Systematic Review (2015–2025). Appl. Sci. 2025, 15, 10816. [Google Scholar] [CrossRef]
- Isidori, G.; Wilsch, F.; Wyler, D. The Standard Model Effective Field Theory at Work. Rev. Mod. Phys. 2024, 96, 015006. [Google Scholar] [CrossRef]
- Ghasemi, M.; Vetro, C.; Zhang, Z. Dirichlet μ-Parametric Differential Problem with Multivalued Reaction Term. Mathematics 2025, 13, 1295. [Google Scholar] [CrossRef]
- Younas, U.; Muhammad, J.; Ismael, H.F.; Sulaiman, T.A.; Emadifar, H.; Ahmed, K.K. The New Combined Kairat-II-X Differential Equation: Diversity of Solitary Wave Structures via New Techniques. J. Nonlinear Math. Phys. 2025, 32, 55. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M.; Kamandar, M. The LDG Finite-Element Method for Multi-Order FDEs: Applications to Circuit Equations. Fractal Fract. 2025, 9, 230. [Google Scholar] [CrossRef]
- Mosquera-Lois, I.; Kavanagh, S.R.; Klarbring, J.; Tolborg, K.; Walsh, A. Imperfections Are Not 0 K: Free Energy of Point Defects in Crystals. Chem. Soc. Rev. 2023, 52, 5812–5826. [Google Scholar] [CrossRef]
- Alsuhaibani, E. Nondestructive Testing of Externally Bonded FRP Concrete Structures: A Comprehensive Review. Polymers 2025, 17, 1284. [Google Scholar] [CrossRef]
- Elmoghazy, Y.H.; Safaei, B.; Asmael, M.; Sahmani, S.; Zeeshan, Q.; Qin, Z. Computational modelling and analysis of effect of viscoelastic materials on damping and vibrational behaviors of composite structures—An extensive review. Arch. Comput. Methods Eng. 2024, 31, 2611–2662. [Google Scholar] [CrossRef]
- Georgievskii, D. Table of Postulates of Continuum Mechanics and Principles of Forming Its Rows. J. Appl. Mech. Tech. Phys. 2024, 65, 1182–1188. [Google Scholar] [CrossRef]
- Römer, U.; Hartmann, S.; Tröger, J.A.; Anton, D.; Wessels, H.; Flaschel, M.; De Lorenzis, L. Reduced and all-at-once approaches for model calibration and discovery in computational solid mechanics. Appl. Mech. Rev. 2025, 77, 040801. [Google Scholar] [CrossRef]
- Gräßle, B.; Hiptmair, R.; Sauter, S. Stable Skeleton Integral Equations for General-Coefficient Helmholtz Transmission Problems. arXiv 2025, arXiv:2507.00991. [Google Scholar]
- Skvortsov, A.; MacGillivray, I.; Godin, O.A. Acoustic Waves in a Perforated Cylinder. J. Acoust. Soc. Am. 2025, 157, 1880–1888. [Google Scholar] [CrossRef]
- Raabe, D.; Mianroodi, J.R.; Neugebauer, J. Accelerating the design of compositionally complex materials via physics-informed artificial intelligence. Nat. Comput. Sci. 2023, 3, 198–209. [Google Scholar] [CrossRef]
- Hassani, S.; Dackermann, U. A systematic Review of Advanced Sensor Technologies for Non-Destructive Testing and Structural Health Monitoring. Sensors 2023, 23, 2204. [Google Scholar] [CrossRef]
- Ribeiro Junior, R.F.; Gomes, G.F. On the Use of Machine Learning for Damage Assessment in Composite Structures: A Review. Appl. Compos. Mater. 2024, 31, 1–37. [Google Scholar] [CrossRef]
- Zhang, P.; Ding, J.; Guo, J.; Wang, F. Fractal Analysis of Cement-Based Composite Microstructure and Its Application in Evaluation of Macroscopic Performance of Cement-Based Composites: A Review. Fractal Fract. 2024, 8, 304. [Google Scholar] [CrossRef]
- Khan, M.M.; Iqbal, M.A. Dynamic Increase Factor of Concrete Subjected to Compression and Tension by Using Split Hopkinson Pressure Bar Setup: Overview. Mech. Solids 2023, 58, 2115–21231. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Z.; Zhang, Q.; Yao, H.; Li, X.; Mi, J.; Wang, H. Breakthrough Underwater Physical Environment Limitations on Optical Information Representations: An Overview and Suggestions. J. Mar. Sci. Eng. 2024, 12, 1055. [Google Scholar] [CrossRef]
- Le Clainche, S.; Ferrer, E.; Gibson, S.; Cross, E.; Parente, A.; Vinuesa, R. Improving Aircraft performance using machine learning: A review. Aerosp. Sci. Technol. 2023, 138, 108354. [Google Scholar] [CrossRef]
- Siddique, J.L.; Ahmed, A.; Aziz, A.; Khalique, C.M. A Review of Mixture Theory for Deformable Porous Media and Applications. Appl. Sci. 2017, 7, 917. [Google Scholar] [CrossRef]
- Giorgio, I.; Galantucci, L.; Della Corte, A.; Del Vescovo, D. Piezo-Electromechanical Smart Materials with Distributed Arrays of Piezoelectric Transducers: Current and Upcoming Applications. Int. J. Appl. Electromagn. Mech. 2015, 47, 1051–1084. [Google Scholar] [CrossRef]
- Wang, E.; Carcion, J.M.; Liu, Y. Reflection and Transmission of Plane Elastic Waves at an Interface Between two Double-Porosity Media: Effect of Local Fluid Flow. Surv. Geophys. 2020, 41, 283–322. [Google Scholar] [CrossRef]
- Piroddi, L.; Abu Zeid, N.; Calcina, S.V.; Capizzi, P.; Capozzoli, L.; Catapano, I.; Cozzolino, M.; D’Amico, S.; Lasaponara, R.; Tapete, D. Imaging Cultural Heritage at Different Scales: Part I, the Micro-Scale (Manufacts). Remote Sens. 2023, 15, 2586. [Google Scholar] [CrossRef]
- Ferrari, A.; Luna, B.Q.; Spickermann, A.; Travelletti, J.; Krzeminska, D.; Eichenberger, J.; van Asch, T.; van Beek, R.; Bogaard, T.; Malet, J.-P.; et al. Techniques for the Modelling of the Process Systems in Slow and Fast-Moving Landslides. Mt. Risks Predict. Manag. Gov. 2014, 34, 82–129. [Google Scholar] [CrossRef]
- Aslam, M.A.; Li, Z. A Sustainable Approach to Boost Resilience in Fast-Moving Consumer Goods: The Critical Role of Suppliers and Transportation Capacity Explored Through PLS-SEM and NCA. Sustainability 2025, 17, 2625. [Google Scholar] [CrossRef]
- Zhan, L.; Liu, B.; Zhang, Y.; Lu, H. Rock Physics Modeling of Acoustic Properties in Gas Hydrate-Bearing Sediment. J. Mar. Sci. Eng. 2022, 10, 1076. [Google Scholar] [CrossRef]
- Smit, T.H. Finite Element Models of Osteocytes and Their Load-Induced Activation. Curr. Osteoporos. Rep. 2022, 20, 127–140. [Google Scholar] [CrossRef]
- Fuhg, J.N.; Anantha Padmanabha, G.; Bouklas, N.; Bahmani, B.; Sun, W.; Vlassis, N.N.; Flaschel, M.; Carrara, P.; De Lorenzis, L. A Review on Data-Driven Constitutive Laws for Solids. Arch. Comput. Methods Eng. 2025, 32, 1841–1883. [Google Scholar] [CrossRef]
- de Oliveira, D.; Gonçalves, M.V.; Ribeiro, G.M.; da Costa, A.L.S.; Regueiras, L.; Silva, T.; de Jesus, A.; Malcher, L.; Ziberov, M. On the Use of Compressed Air and Synthetic Biodegradable Cutting Fluid to Enhance the Surface Quality of WAAM–CMT Manufactured Low-Alloy Steel Parts During Post-Processing Milling with Different Cooling–Lubrication Strategies. J. Manuf. Mater. Process. 2025, 9, 193. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, M.; Li, X.; Jin, L.; Su, G.; Mo, Y.; Li, L.; Zhu, H.; Tian, Y. Research Progress in Application of 2D Materials in Liquid-Phase Lubrication System. Materials 2018, 11, 1314. [Google Scholar] [CrossRef]
- Banihashemi, S.; Assadimoghadam, A.; Hajirasouli, A.; LeNguyen, K.; Mohandes, S.R. Parametric design in construction: A new paradigm for quality management and defect reduction. Int. J. Constr. Manag. 2025, 25, 1534–1551. [Google Scholar] [CrossRef]
- Faris, N.; Zayed, T.; Fares, A. Review of Condition Rating and Deterioration Modeling Approaches for Concrete Bridges. Buildings 2025, 15, 219. [Google Scholar] [CrossRef]
- Hoxha, E.; Feng, J.; Sengupta, A.; Kirakosian, D.; He, Y.; Shang, B.; Gjinofci, A.; Xiao, J. Contrastive Learning for Robust Defect Mapping in Concrete Slabs Using Impact Echo. Constr. Build. Mater. 2025, 461, 139829. [Google Scholar] [CrossRef]
- Liu, W.K.; Li, S.; Park, H. Eighty Years of the Finite Element Method: Birth, Evolution, and Future. Arch. Comput. Methods Eng. 2022, 29, 4431–4453. [Google Scholar] [CrossRef]
- Hilal, W.; Gadsden, S.A.; Yawney, J. Cognitive Dynamic Systems: A Review of Theory, Applications, and Recent Advances. Proc. IEEE 2023, 111, 575–622. [Google Scholar] [CrossRef]
- Laganà, F.; Pullano, S.; Angiulli, G.; Versaci, M. Optimized Analytical-Numerical Procedure for Ultrasonic Sludge Treatment for Agricultural Use. Algorithms 2024, 17, 592. [Google Scholar] [CrossRef]
- Versaci, M.; Palumbo, A. Magnetorheological Fluids: Qualitative Comparison Between a Mixture Model in the Extended Irreversible Thermodynamics Framework and an Herschel–Bulkley Experimental Elastoviscoplastic Model. Int. J. Non-Linear Mech. 2020, 118, 103288. [Google Scholar] [CrossRef]
- Bilotta, G.; Barrile, V.; Bibbò, L.; Meduri, G.M.; Versaci, M.; Angiulli, G. Enhancing Land Cover Classification: Fuzzy Similarity Approach Versus Random Forest. Symmetry 2025, 17, 929. [Google Scholar] [CrossRef]
- Huang, H.; Chen, F.; Cao, K.; Zhang, X.; Li, R. Damage Evolution Characteristics of Steel-Fiber-Reinforced Cellular Concrete Based on Acoustic Emission. Buildings 2025, 15, 229. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, D.; Tang, Y.; Jian, Y. Compression Damage Precursors of Silane-Protected Concrete Under Sulfate Erosion Based on Acoustic Emission Characterization. Fractal Fract. 2025, 9, 254. [Google Scholar] [CrossRef]
- Mohammad, M.; Paivo, K.; Marjaana, K.; Zahra, A.; Lidija, K.; Vilma, D.; Ahmad, A.; Mirja, I. Im pacts of Casting Scales and Harsh Conditions on the Thermal, Acoustic, and Mechanical Properties of Indoor Acoustic Panels Made with Fiber-Reinforced Alkali-Activated Slag Foam Concretes. Materials 2019, 12, 825. [Google Scholar] [CrossRef] [PubMed]
- Zalegowski, K. Pore Structure Influence on Properties of Air-Entrained Concrete. Materials 2025, 18, 2885. [Google Scholar] [CrossRef]
- Beskopylny, A.N.; Shcherban’, E.M.; Stel’makh, S.A.; Elshaeva, D.; Chernil’nik, A.; Razveeva, I.; Panfilov, I.; Kozhakin, A.; Madenci, E.; Aksoylu, C.; et al. Porosity Analysis and Thermal Conductivity Prediction of Non-Autoclaved Aerated Concrete Using Convolutional Neural Network and Numerical Modeling. Buildings 2025, 15, 2442. [Google Scholar] [CrossRef]
- Singh, M.P.; Singh, R.K. Correlation Between Ultrasonic Velocity, Surface Tension, Density and Viscosity of Ionic Liquids. Fluid Phase Equilibria 2011, 30, 1–6. [Google Scholar] [CrossRef]
- Aghaei, H.; Penkov, G.M.; Solomoichenko, D.A.; Toorajipour, A.; Petrakov, D.G.; Jafarpour, H. Density-Dependent Relationship Between Changes in Ultrasonic Wave Velocities, Effective Stress, and Petrophysical-Elastic Properties of Sandstone. Ultrasonics 2023, 132, 106985. [Google Scholar] [CrossRef] [PubMed]
- Lay-Ekuakille, A.; Palamara, I.; Caratelli, D.; Morabito, F.C. Experimental Infrared Measurements for Hydrocarbon Pollutant Determination in Subterranean Waters. Rev. Sci. Instruments 2013, 84, 015103. [Google Scholar] [CrossRef] [PubMed]
- Ciarlet, P.; Jamelot, E. Explicit T-coercivity for the Stokes problem: A coercive finite element discretization. Comput. Math. Appl. 2025, 188, 137–159. [Google Scholar] [CrossRef]
- Mohapatra, A.R.D.; Deka, B. A non conforming temporal stabilizer-free finite element method for non-coercive eddy current problems. J. Comput. Appl. Math. 2026, 474, 116984. [Google Scholar] [CrossRef]
- Edwards, K.A.T.; Al-Abed, S.H.; Hosseini, S.; Brake, N.A. Properties of a Magnetic Concrete Core Transformer for Application in Wireless Power Transfer Systems. Constr. Build. Mater. 2019, 227, 117041. [Google Scholar] [CrossRef]
- Fomenko, E.V.; Knyazev, Y.V.; Akimochkina, G.V.; Semenov, S.V.; Yumashev, V.V.; Solovyov, L.A.; Anshits, N.N.; Bayukov, O.A.; Anshits, A.G. Mössbauer Research and Magnetic Properties of Dispersed Microspheres from High-Calcium Fly Ash. Magnetochemistry 2025, 11, 72. [Google Scholar] [CrossRef]
- Mustafa Mohamed, A.; Tayeh, B.A.; Ahmed, T.I.; Bashir, M.O.; Tobbala, D.E. Influence of nano-silica and nano-ferrite particles on mechanical and durability of sustainable concrete: A review. Nanotechnol. Rev. 2025, 14, 20250151. [Google Scholar] [CrossRef]
- Tabish, M.; Zaheer, M.M.; Baqi, A. Effect of nano-silica on mechanical, microstructural and durability properties of cement-based materials: A review. J. Build. Eng. 2023, 65, 105676. [Google Scholar] [CrossRef]
- Ventura, G.; Díaz, C.; Morales, H.; Brigola, R. Application Examples for Distributions. In Fourier Analysis and Distributions; Texts in Applied Mathematics; Springer: Cham, Switzerland, 2025; Volume 79. [Google Scholar] [CrossRef]
- Vala, J.; Tomáš, J. Damage Behaviour of Quasi-Brittle Composites: Mathematical and Computational Aspects. Appl. Sci. 2025, 15, 4214. [Google Scholar] [CrossRef]
- Spalvier, A.; Sánchez, J.; Pérez, N. 3D Modeling of Ultrasonic Wave Propagation in Pervious Concrete. J. Nondestruct. Eval. 2025, 44, 104. [Google Scholar] [CrossRef]
- Liu, C.; Hao, H.; Liu, J. Mesoscopic numerical investigation on wave attenuation in meta-concrete with cubic engineered aggregates. Eng. Struct. 2025, 344, 121360. [Google Scholar] [CrossRef]
- Korjakins, A.; Sahmenko, G.; Lapkovskis, V. A Short Review of Recent Innovations in Acoustic Materials and Panel Design: Emphasizing Wood Composites for Enhanced Performance and Sustainability. Appl. Sci. 2025, 15, 4644. [Google Scholar] [CrossRef]
- Wilk-Jakubowski, J.L.; Pawlik, L.; Frej, D.; Wilk-Jakubowski, G. The Evolution of Machine Learning in Vibration and Acoustics: A Decade of Innovation (2015–2024). Appl. Sci. 2025, 15, 6549. [Google Scholar] [CrossRef]
- Rostampour, M.A.; Mostofinejad, D.; Bahmani, H.; Mostafaei, H. Crack Assessment Using Acoustic Emission in Cement-Free High-Performance Concrete Under Mechanical Stress. J. Compos. Sci. 2025, 9, 380. [Google Scholar] [CrossRef]
- Nitka, M.; Rucka, M. 3D DEM Modelling of Acoustic Emission in Concrete: Insights into Elastic Waves Initiated by Microcracks. Ultrasonics 2025, 150, 107599. [Google Scholar] [CrossRef] [PubMed]
- Baktheer, A.; Aguilar, M.; Chudoba, R. Comprehensive Review of the Microplane Framework for Constitutive Modeling Focused on Homogenization Approaches. Arch. Comput. Methods Eng. 2025. [Google Scholar] [CrossRef]
- Kabantsev, O.; Kovalev, M. Failure Mechanisms and Parameters of Elastoplastic Deformations of Anchorage in a Damaged Concrete Base under Seismic Loading. Buildings 2022, 12, 78. [Google Scholar] [CrossRef]
- Al-Mistarehi, B.; Al-Omari, A.; Taamneh, M.; Imam, R.; Khafaja, D.A.-D. The effects of adding nano clay and nano zinc oxide on asphalt cement rheology. J. King Saud Univ.-Eng. Sci. 2023, 35, 260–269. [Google Scholar] [CrossRef]
- Bacharz, M.; Bacharz, K.; Trąmpczyński, W. Impact of Early-Age Curing and Environmental Conditions on Shrinkage and Microcracking in Concrete. Materials 2025, 18, 3185. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. Advances in Finite Element Modeling of Fatigue Crack Propagation. Appl. Sci. 2024, 14, 9297. [Google Scholar] [CrossRef]
- Ruiz Martínez, J.D.; Ríos, J.D.; Pérez-Soriano, E.M.; Cifuentes, H.; Leiva, C. Enhancing the matrix–fiber bond in ultra-high-performance fiber-reinforced concrete using a high performance plasticizer. Impact on the flowability, physical and mechanical properties. Constr. Build. Mater. 2025, 470, 140683. [Google Scholar] [CrossRef]
- Demiral, M. Strength in Adhesion: A Multi-Mechanics Review Covering Tensile, Shear, Fracture, Fatigue, Creep, and Impact Behavior of Polymer Bonding in Composites. Polymers 2025, 17, 2600. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, Z. Research on Dry Coupling Technology in the Ultrasonic Non-Destructive Testing of Concrete. Micromachines 2025, 16, 72. [Google Scholar] [CrossRef] [PubMed]
- Scavone, M.; Katicha, S.W.; Flintsch, G.W.; Amarh, E. On the TSD Deflection Velocity Measurements: A Revision to the Current State of the Art and Discussion over Its Applicability for Concrete Pavement Assessment. Int. J. Pavement Eng. 2023, 24, 2138881. [Google Scholar] [CrossRef]
- Zhang, J.; Pang, H.; Xing, Y. Mechanistic Analysis of Electromagnetic Ultrasonic Transverse Wave Detection of Steel Plates in High-Temperature Multi-Physical Environments. Measurement 2025, 245, 116601. [Google Scholar] [CrossRef]
- Aksoy, A.G.; Almira, J.M. Using the Baire Category Theorem to Explore Lions Problem for Quasi-Banach Spaces. Adv. Oper. Theory 2025, 10, 34. [Google Scholar] [CrossRef]
- Chakraborty, T.; Chakravarty, J.; Godet, V.; Paul, P.; Raju, S. The Hilbert Space of De Sitter Quantum Gravity. J. High Energy Phys. 2024, 2024, 132. [Google Scholar] [CrossRef]
- Versaci, M.; Laganà, F.; Morabito, F.C.; Palumbo, A.; Angiulli, G. Adaptation of an Eddy Current model for characterizing subsurface defects in CFRP plates using FEM Analysis based on Energy functional. Mathematics 2024, 12, 2854. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Lauriks, W.; Depollier, C.; Chapelon, J.-Y.; Angel, Y.C. Solution in Time Domain of Ultrasonic Propagation Equation in a Porous Material. Wave Motion 2003, 38, 151–163. [Google Scholar] [CrossRef]
- Salvi, N.; Tan, J. A Model-Based method for Sound Speed Measurement in Time-Variant Media. Measurement 2025, 244, 116524. [Google Scholar] [CrossRef]
- Biswas, M.; Guha, S. Influence of dynamic fiber volume fraction on Love wave velocity in PFRC plate imperfectly bonded with piezoelectric–viscoelastic substrate. Acta Mech. 2025, 236, 321–341. [Google Scholar] [CrossRef]
- Di Bella, C.; Wyrzykowski, M.; Lura, P. Evaluation of the ultimate drying shrinkage of cement-based mortars with poroelastic models. Mater. Struct. 2017, 50, 52. [Google Scholar] [CrossRef]
- Sabtiwu, M.; Dhandapani, Y.; Drewniok, M.; Adu-Amankwah, S.; Bernal, S.A. Carbonation induced changes in the mechanical performance, water and chloride permeability of Portland cement–slag–limestone ternary cement concretes. Cem. Concr. Compos. 2025, 163, 106222. [Google Scholar] [CrossRef]
- Bukhari, S.J.S.; Khanzadeh Moradllo, M. Multicriteria performance assessment of ‘low w/c + low cement + high dosage admixture’ concrete: Environmental, economic, durability, and mechanical performance considerations. J. Clean. Prod. 2025, 523, 146419. [Google Scholar] [CrossRef]
- Umar, I.H.; Tarauni, Z.A.; Bello, A.B.; Lin, H.; Hassan, J.I.; Cao, R. Performance Prediction and Optimization of High-Plasticity Clay Lime–Cement Stabilization Based on Principal Component Analysis and Principal Component Regression. Appl. Sci. 2025, 15, 7150. [Google Scholar] [CrossRef]
- Sharma, S.; Rathor, A.P.S.; Sharma, J.K.; Bhatia, D. Prediction of Settlement of Embankment on Soft Soil Using Machine Learning. Transp. Infrastruct. Geotech. 2025, 12, 211. [Google Scholar] [CrossRef]
- Lin, H.W. The Bulk Hilbert Space of Double Scaled SYK. J. High Energ. Phys. 2022, 2022, 60. [Google Scholar] [CrossRef]
- Hayotov, A.R.; Khayriev, U.N. Construction of an Optimal Quadrature Formula in the Hilbert Space of Periodic Functions. Lobachevskii J. Math. 2022, 43, 3151–3160. [Google Scholar] [CrossRef]
- Mashaan, N.S.; Ouano, C.A.E. An Investigation of the Mechanical Properties of Concrete with Different Types of Waste Plastics for Rigid Pavements. Appl. Mech. 2025, 6, 9. [Google Scholar] [CrossRef]
- Huang, Z.; Ding, M.; Hu, Z.; Long, Q.; Luo, Y. Mechanical Behavior of Discontinuous Cavity Structures in Prefabricated Tunnels. Results Eng. 2025, 26, 105400. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, S.; Wang, M.; Qin, J.; Fan, W.; Wu, Y. Experimental Study on Grouting Seepage Characteristics in Rough Single Microfissure Under Triaxial Stress States. Materials 2025, 18, 3746. [Google Scholar] [CrossRef]
- Shi, H.; Li, H.; Huang, F.; Li, L.; Dong, H.; Yang, Z. Study on Uniaxial Compressive Properties and Microfracture Toughness of Interface Transition Zones in Recycled Sand Concrete. Constr. Build. Mater. 2025, 477, 141365. [Google Scholar] [CrossRef]
- Wu, F.; Chen, J. Water and Fertilizer Retention Characteristics of Sustainable Bio-Based Aggregate Concrete for Vegetative Applications. Constr. Build. Mater. 2025, 493, 143266. [Google Scholar] [CrossRef]
- Pan, G.; Song, T.; Li, P.; Jia, W.; Deng, Y. Review on Finite Element Analysis of Meso-Structure Model of Concrete. J. Mater. Sci. 2025, 60, 32–62. [Google Scholar] [CrossRef]
- Yue, Z.Q. Matrix Solutions of Biot’s Poroelasticity in Saturated Multilayered Media. J. Elast. 2025, 157, 24. [Google Scholar] [CrossRef]
- de Castro Motta, J.; Rajagopal, K.; Saccomandi, G. Extensions of the Constitutive Relations to Describe the Response of Compressible Nonlinear Kelvin–Voigt Solids. Meccanica 2025. [Google Scholar] [CrossRef]
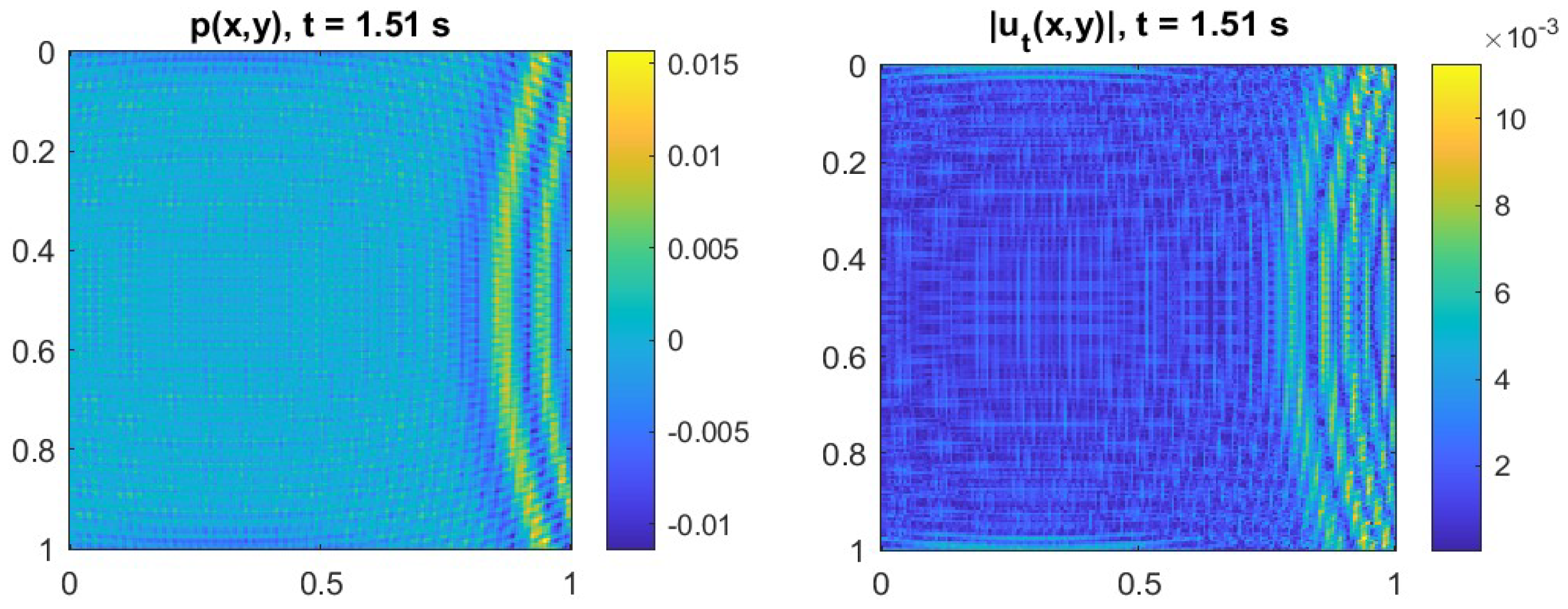
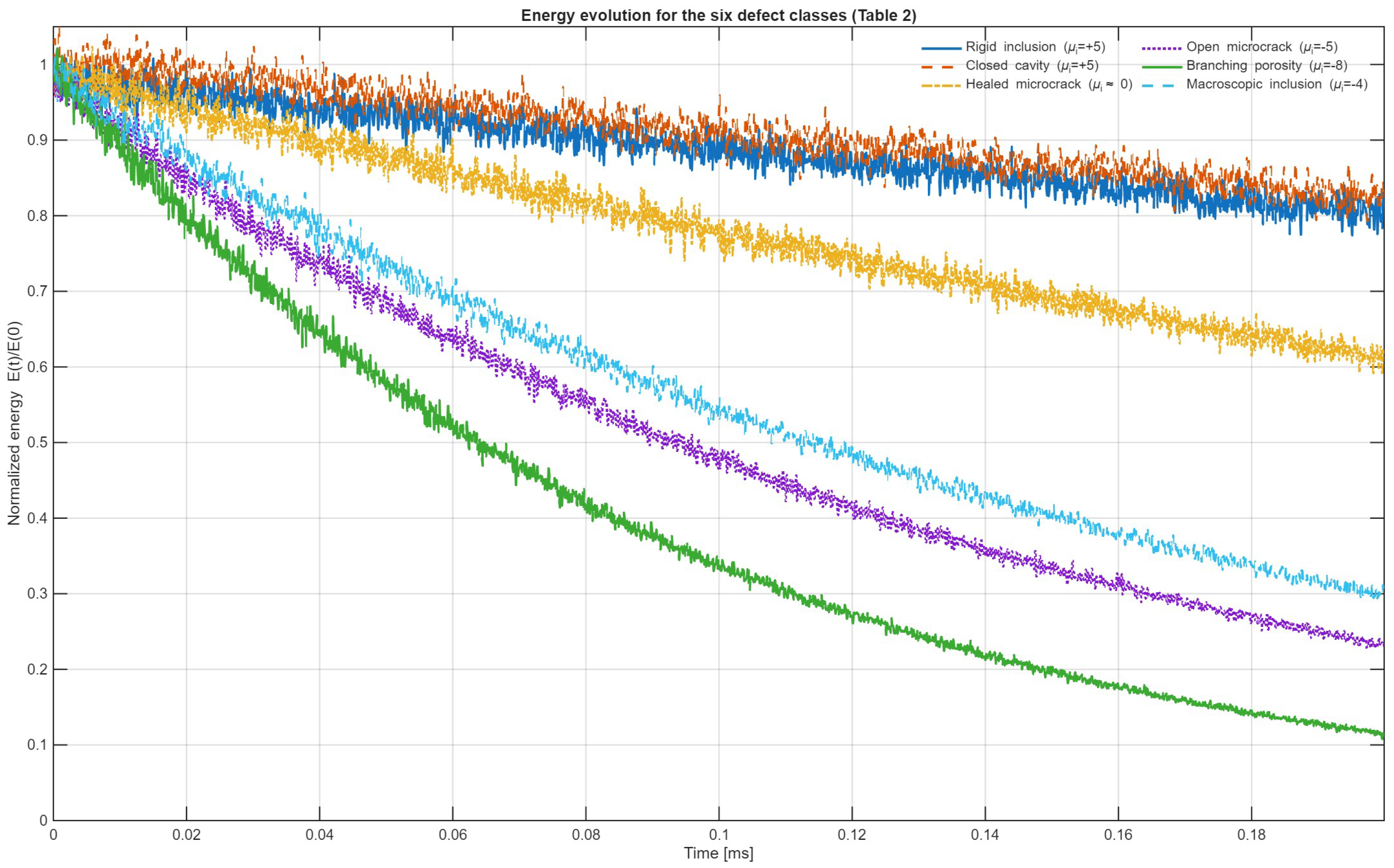
| Defect Type | Sign of | Energetic/Physical Behavior |
|---|---|---|
| Rigid inclusion or sealed crack | Stabilizing: It promotes local energy confinement and limits dissipation, enhancing coercivity. | |
| Neutral or homogeneous region | Neutral: Negligible influence on the global energy balance, corresponding to homogeneous propagation. | |
| Open crack or porous cavity | Dissipative: It induces scattering, attenuation, and loss of coercivity through increased heterogeneity. |
| Defect Type | Geometry/Size | Energetic Classification | Observed Physical Behavior | |
|---|---|---|---|---|
| Rigid inclusion | Disk, | Stabilizing | Strong reflection of the wavefront, local pressure accumulation, and nearly zero internal velocity. Total energy remains almost constant over time. | |
| Closed cavity | Disk, | Stabilizing | Temporary storage and elastic restitution of energy; slight and reversible attenuation in total energy. | |
| Healed microcrack | Thin line | Neutral | Minimal field disturbance; pressure and velocity nearly homogeneous; energy remains constant over time. | |
| Open microcrack | Open thin line | Dissipative | Strong velocity discontinuities and scattering; rapid energy decay due to leakage and attenuation. | |
| Branching porosity | Fractal network | Highly dissipative | Fragmented pressure field, complex velocity fluctuations, and pronounced and continuous energy loss. | |
| Macroscopic inclusion | Disk, | Destabilizing | Multiple reflections and internal resonances; irregular drops in total energy and local energetic instability. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Versaci, M.; Cacciola, M.; Laganà, F.; Angiulli, G. Analysis of Acoustic Wave Propagation in Defective Concrete: Evolutionary Modeling, Energetic Coercivity, and Defect Classification. Appl. Sci. 2025, 15, 11378. https://doi.org/10.3390/app152111378
Versaci M, Cacciola M, Laganà F, Angiulli G. Analysis of Acoustic Wave Propagation in Defective Concrete: Evolutionary Modeling, Energetic Coercivity, and Defect Classification. Applied Sciences. 2025; 15(21):11378. https://doi.org/10.3390/app152111378
Chicago/Turabian StyleVersaci, Mario, Matteo Cacciola, Filippo Laganà, and Giovanni Angiulli. 2025. "Analysis of Acoustic Wave Propagation in Defective Concrete: Evolutionary Modeling, Energetic Coercivity, and Defect Classification" Applied Sciences 15, no. 21: 11378. https://doi.org/10.3390/app152111378
APA StyleVersaci, M., Cacciola, M., Laganà, F., & Angiulli, G. (2025). Analysis of Acoustic Wave Propagation in Defective Concrete: Evolutionary Modeling, Energetic Coercivity, and Defect Classification. Applied Sciences, 15(21), 11378. https://doi.org/10.3390/app152111378









