Abstract
The fluid flow in underground reservoirs is directly related to resource recovery and hazard prevention. In this study, the evolution of fractured sandstone deformation and permeability under an in situ stress influence is investigated using the true triaxial percolation system. The results show that the strain of fractured sandstone increases logarithmically with the increase in axial stress. The evolution of axial strain is dominated by the maximum principal stress, and the minimum principal stress and the intermediate principal stress affect the strain amplitude. The fracture morphology of low-permeability sandstone affects permeability and strain evolution. Small fractures are more sensitive to the increase in the maximum principal stress, and the response in principal strain to the increase in principal stress is obvious in large fractures. There is a negative exponential relationship between pore pressure and the conductivity of fractures. When pore pressure is 0.3 MPa, the conductivity is the highest; meanwhile, when pore pressure is 1.8 MPa, the conductivity is the lowest. The decreasing range of the conductivity increases with the increase in fracture size. In situ stress significantly affects the evolution of principal strain and related permeability. The permeability decreases with an increase in the minimum and middle principal stresses. Under low pore pressure (0.3–0.6 MPa), the permeability decreases with an increase in the principal stress; meanwhile, under high pore pressure (0.6–1.8 MPa), permeability changes slightly with an increase in the principal stress. The findings provide reference to the engineering practice of underground mining.
1. Introduction
The world’s 4000 trillion cubic meters of unconventional resources are the potential clean energy of the future. Understanding fluid flow and migration in unconventional geology is beneficial to the mining and safety of natural resources. The geology structure composed of fractures and pores is directly related to the mechanical properties, permeability characteristics, and stress sensitivity, and it contributes to the fluid flow in resource reservoirs. The conductivity capacity of sandstone, characterized by permeability, is influenced by in situ-dependent pore fracture. The strain and permeability of fractured sandstone is significant to resource recovery. Numerous studies were conducted, and abundant achievements were obtained in this field [1,2,3,4].
To simulate the real geological environment, uniaxial and true triaxial tests were carried out with a consideration of fluid flow, ground stress, and geological conditions. In terms of uniaxial compression, Liu et al. [5] carried out uniaxial compression experiments with frozen weakly sandstone under different loading and unloading rates, and they revealed the failure mechanism of weakly frozen sandstone. Vasyliev et al. [6] used four experimental features to mathematically model the cracks in cylindrical rock samples and compared and verified the design strength with experimental data obtained from uniaxial compression. Abbas et al. [7] conducted uniaxial compression tests on sandstone–shale-sandstone composites, and based on the obtained mechanical properties and stress–strain relationships, it was pointed out that shale interlayers exert significant effects on the mechanical properties of the composites. Jiang et al. [8] used PFC2D particle-flow numerical simulation software to simulate the mechanical properties and damage evolution process of broken rock, and they discussed the multi-parameter stage characteristics and precursor information of acoustic emission under uniaxial compression. In terms of true triaxial compression, Ishibashi et al. [9,10] discussed the energy balance in the hydraulic shear process of granite fractures and pointed out the key role of the surrounding mass in the storage of elastic potential energy. Yu et al. [11] constructed a prediction model of sandstone permeability under the coupling effect of real triaxial stress field and pore pressure, and they pointed out that the permeability of sandstone is proportional to the pore pressure and inversely proportional to the principal stress. Niu et al. [12] studied the deformation, damage evolution, seepage characteristics, and energy response of columnar jointed basalt based on true triaxial compression experiments, and they pointed out that the permeability and axial strain of the sample have an exponential relationship. Lu et al. [13] obtained permeability under various true triaxial stresses using a newly developed multifunctional true triaxial geophysical (TTG) instrument, and a theoretical model was proposed to describe the permeability characteristics of composite coal rock under a real triaxial stress condition. Liu et al. [14] established a new mathematical model to predict the influence of shale permeability, considering true triaxial stress.
Solid deformation and fluid migration occurred during underground activity, and the coupling relationship was investigated through a simulation, a theoretical analysis, and an experimental test. And the characteristic of seepage, fracture propagation, and the strain response and the corresponding relationship was obtained [15,16,17,18,19,20,21,22,23,24,25]. Among them, Zhang et al. [26] conducted true triaxial tests on virtual granite samples using a properly calibrated DEM model to explore the grain-scale mechanism and energy release of the σ2 effects. Zhang et al. [27] numerically investigated the mechanics and failure characteristics of fractured rock samples under true triaxial compression, considering the effects of true triaxial loading parameters and pre-existing fracture geometry parameters. To investigate the damage evolution and stress dependency, Gao et al. [28] conducted a series of true triaxial cyclic loading tests on the collected intact and jointed marbles, irreversible strains and dissipated energy were calculated as damage variables, and progressive failure was analyzed. Wang et al. [29] studied the effects of true triaxial unloading on the deformation and failure characteristics of dacite, and they analyzed the strength and deformation behaviors caused by unloading σ3 based on the results of stress–strain curves. During the true triaxial experiment, the mechanical and conductivity parameter response to loading and unloading behavior was analyzed based on the acoustic emission (AE) methods of LVDT et al. [30,31,32,33,34,35,36]. Fracture as a conductivity medium significantly influences the mechanical behavior and conductivity capacity, while a rare study of the fractured rock response considered the influence of the loading path.
The behavior of geological reservoirs under disturbed stress conditions has been extensively investigated using a true triaxial experiment system. The true triaxial stress–strain and seepage characteristics in fractured sandstone significantly contribute to the resource extraction in tight resource reservoirs. In this study, the seepage, strain, and permeability response to the variation in in situ stress was analyzed in fractured sandstone. The correlations among permeability, pore pressure, stress, and strain were analyzed. A new method for predicting the permeability of fractured sandstone has been developed. The findings provide significant insight into the engineering practice.
2. Experimental Setup
2.1. Material Preparation
The experiment samples were collected from the Yanchang Formation 7–2, an ultra-low-permeability reservoir. The sandstone samples were machined into dimensions of 100 mm × 100 mm × 200 mm using the numerical control cutting equipment (Figure 1). Prefabricated fractures were created through splitting tests performed on a universal testing machine. The samples were sealed with NANDA 704 silicone rubber (Xiangyang High-Temp Resistant New Material Technology Co., Ltd., Xiangyang, China), which was applied evenly over the sandstone surface. This type of silicone rubber exhibits strong adhesion, high strength, non-corrosiveness, excellent sealing performance, and aging resistance, with a maximum curing depth of 3–5 mm. The coated specimens were allowed to cure for more than 24 h.

Figure 1.
Prefabricated cracks before and after experiment: (a) before experiment; (b) after experiment.
2.2. True Triaxial Gas–Solid Coupling Rock Mass Seepage Test System
The true triaxial gas-solid coupling system developed by Anhui University of Science and Technology was used to carry out the test. This test system can independently control the three-dimensional stress through the servo system σ1, σ2, σ3 (Figure 2). The experimental device can be used to study the deformation, failure and gas seepage of coal and rock mass under the coupling of true triaxial stress and gas pressure in a closed environment. The experimental system mainly includes hydraulic servo control system and monitoring control system. The main technical parameters of true triaxial gas–solid coupling rock mass seepage test system is shown in Table 1.
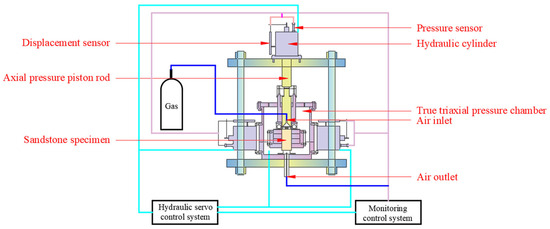
Figure 2.
True triaxial coupling experiment apparatus.

Table 1.
True triaxial gas–solid coupling rock mass seepage test system.
2.3. Experimental Scheme
To simulate the in situ stress condition, the experiment scheme was designed as below: firstly, gradually apply σ1 = σ2 = σ3 to a predetermined value of 2 MPa under hydrostatic pressure, and then apply 1 MPa carbon dioxide gas. After the gas is fully adsorbed and balanced, the gas pressure is changed to measure the permeability of the specimen under each gas pressure. After the measurement is completed, the gas permeability at each hydrostatic pressure is measured by applying σ1 = σ2 = σ3 to a predetermined value of 4, 6, and 8 MPa. Since the compressive strength of the specimen is much greater than 32 MPa, the stress state of the specimen can be changed by adding and releasing pressure. Then hold σ1 = 8 MPa unchanged and decrease σ2 = σ3 simultaneously to 2 MPa. Decrease σ1 = 4 MPa and determine the permeability of the test piece. Holding σ2 = σ3 = 2 MPa unchanged, increase σ1 to 8 MPa, σ2 = σ3 = 4 MPa, measure the permeability of the test piece, and then maintain σ2 = σ3 = 4 MPa unchanged, increasing successively σ1 = 12, 16, 20, 24, 28, and 32 MPa, measuring the permeability of the test piece throughout. Subsequently, reduce σ1 = 30 MPa, increase σ2 = σ3 = 6 MPa, and measure the permeability of the test piece concurrently. Then, maintaining σ2 = σ3 = 6 MPa unchanged, decrease σ1 successively to 24, 18, and 12 MPa, and determine the gas permeability. Subsequently, increase σ1 = 16 MPa, σ2 = σ3 = 8 MPa, measure the permeability of the test piece, and then hold σ2 = σ3 = 8 MPa unchanged, increasing σ1 successively to 24 and 32 MPa, and measure the permeability of the test piece. Finally, decrease the permeability of the test piece by setting σ1 = 6 MPa, σ2 = σ3 = 2 MPa, and then increase σ1 to 8, 10, 12, 14, and 16 MPa. The permeability of the test piece at each level of σ1 was measured. The permeability changes in specimens at pressure of 0.3, 0.6, 0.9, 1.2, 1.5 and 1.8 MPa were measured successively. The scheme is shown in Figure 3.
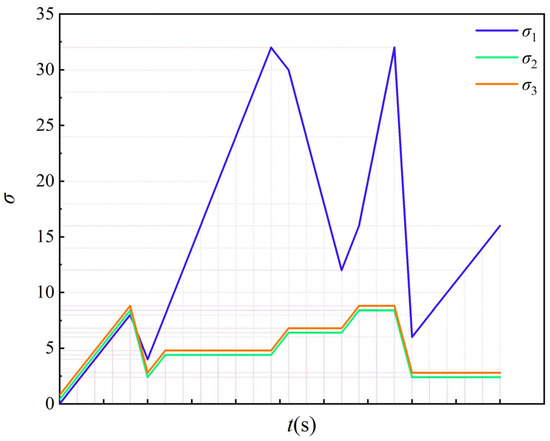
Figure 3.
Schematic diagram of stress loading.
3. Experimental Results and Discussion
3.1. Characteristics of Stress–Strain
Figure 4 presents the stress–strain curves of three sandstone samples (R1, R2, R3) under true triaxial loading. The results demonstrate that an increase in lateral stresses (σ2, σ3) enhances the yield strength of the rock. Under lower lateral stress, the rocks approach their strength limits as the axial stress increases, a trend particularly pronounced in sample R2. Based on the stress–strain relationships, no sample failure occurred as the axial stress was raised from 2 MPa to 32 MPa. The deformation process mainly involved compaction and elastic stages, with higher lateral stresses leading to more extended elastic deformation.
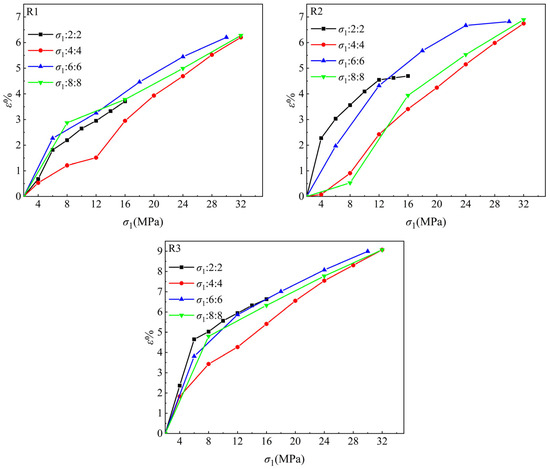
Figure 4.
Axial stress–strain relationship of true triaxial seepage test.
Axial strain generally increases with rising axial stress. However, due to inherent differences in initial rock properties, the stress responses varied among the samples. R1 and R2 exhibited distinct fractures, with R2 containing notably longer interconnected fractures, whereas R3 remain intact. This structural difference explains why R1 and R2 showed stronger responses to changes in σ2 and σ3 (especially R2), while R3 displayed minimal variation. The contrasting behaviors of R1, R2, and R3 underscore the critical influence of fracture structures on stress–strain evolution.
In summary, rock strength increases under higher triaxial stress levels. The evolution of axial strain is primarily controlled by the maximum principal stress, while the magnitudes of the intermediate and minimum principal stresses affect the strain amplitude.
3.2. The Influence of Pore Pressure on Permeability
Figure 5 illustrates the evolution of permeability under different pore pressures at a constant triaxial stress ratio. The results indicate a negative correlation between permeability and pore pressure. The characteristics of permeability evolution during pore pressure variations are mainly influenced by differences in fracture structures of the rock samples and the applied triaxial stress ratios.
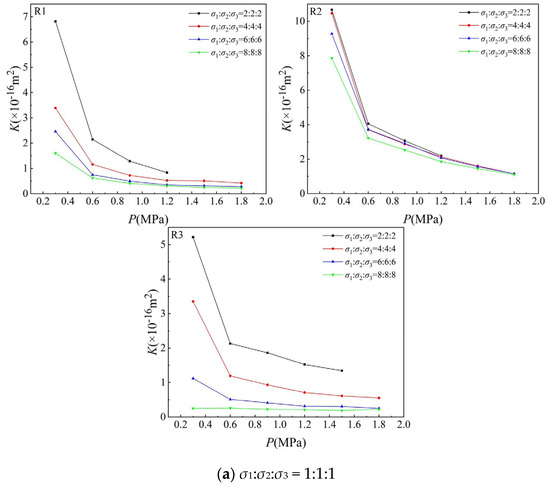
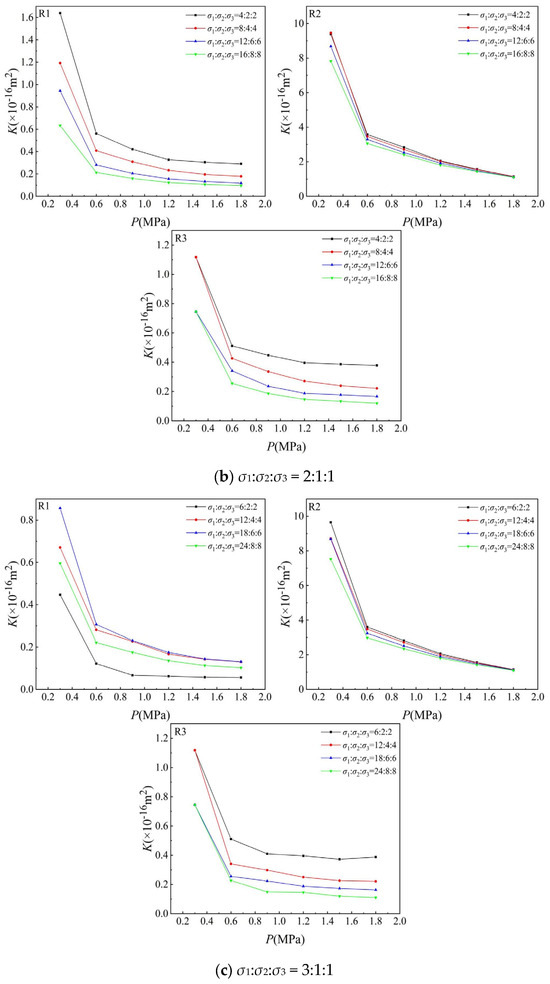
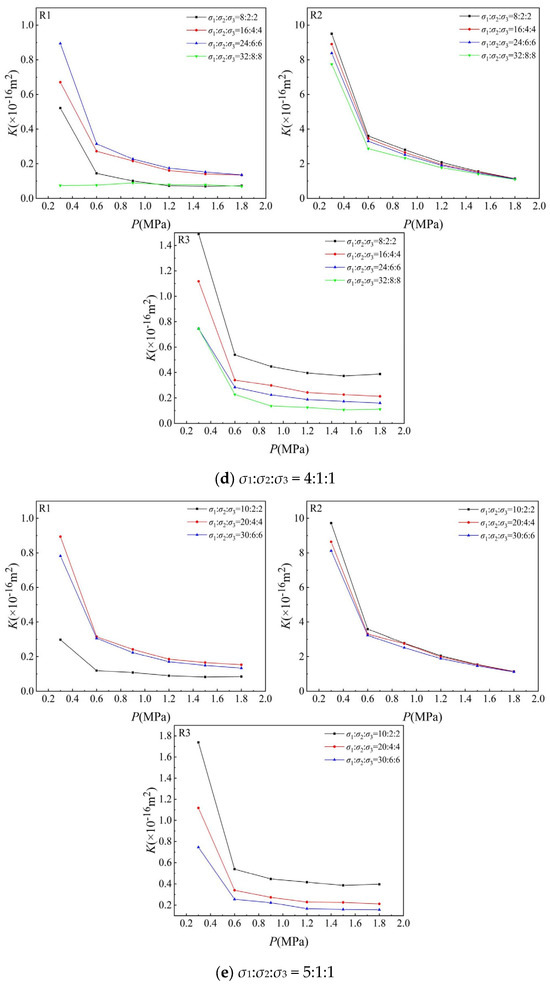
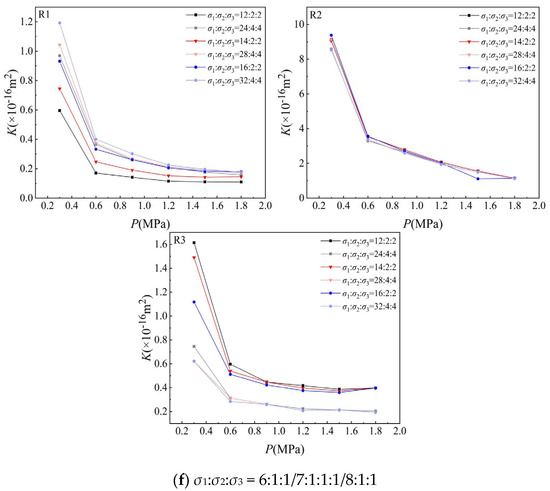
Figure 5.
Variation in permeability with pore pressure under the same stress ratio.
With respect to fracture structures of rock cores, it was observed that under the same triaxial stress ratio, higher stress levels lead to a more pronounced permeability response to pore pressure changes in R2 sample, followed by R1, with R3 exhibiting the least sensitivity. This finding is consistent with the stress–strain results in Section 3.1. Taking the triaxial stress ratio of 1:1:1 with σ1 = σ2 = σ3 = 2 MPa as an example, experimental results demonstrate that under identical stress conditions, when pore pressure increased from 0.3 MPa to 1.8 MPa, the permeability of samples R2, R1, and R3 decreased by 89.81%, 88.24%, and 75%, respectively.
Regarding the influence of triaxial stress ratios, results indicate that the stress ratio σ1:σ2:σ3 increased from 1:1:1 to 6:1:1, while permeability experienced dynamic decreases and slight increase in response to rising pore pressure. In detail, for sample R1, at stress ratios of 1:1:1 and 2:1:1, although the triaxial stress ratio is the same, with the increase in triaxial stress, the permeability decreases gradually under the same pore pressure, and σ1:σ2:σ3 = 1:1:1, the permeability decreases more than σ1:σ2:σ3 = 2:1:1. It illustrates that under increasing triaxial stress, original pore and cracks are gradually closed by three-dimensional compression, with essentially no crack propagation or new crack generation at this stage. And at higher stress ratios, 3:1:1, 4:1:1, 5:1:1, 6:1:1, 7:1:1 and 8:1:1, permeability varies with the stress ratio. Under low triaxial stress, permeability increases gradually with the increase in triaxial stress. When the triaxial stress reaches 24:8:8, 32:8:8, and 30:6:6, the permeability suddenly decreases, but it is still greater than the initial permeability under the corresponding stress ratio. This implies that micro cracks are generated in the fractured sandstone under high stress ratio, resulting in the increase in connected pores and thus enhanced permeability. As the triaxial stress increases from 24:8:8 to 30:6:6, both newly generated microcracks and pre-existing fractures are compressed and closed, resulting in an overall permeability reduction.
For sample R2, as the stress ratio increases from 1:1:1 to 8:1:1, permeability decreases gradually with the increase in triaxial stress, though the extent of decrease is relatively small. Therefore, the change in permeability is very different from R1. For sample R3, the permeability shows the same change trend as sample R2, and both show a gradual decrease with the increase in triaxial stress, but the change degree of permeability is greater than in sample R2. This can be attributed to the generation of new fractures in R3 under increasing triaxial stress, where the extent of fracture development exceeds the degree of compression-induced closure.
3.3. Influence of the Fracture on Permeability
Fracture conductivity, characterized by permeability during the true triaxial loading process, was identified as corresponding to small, medium, and large fractures in samples R1, R3, and R2, respectively. As the maximum principal stress increased, slight and dynamic permeability responses were observed in samples with large and small fractures. The phenomenon is different from the previous work [37,38], which reported that dynamic response typically occurs in fractures with large apertures. In these experiments, the maximum principal stress was applied parallel to the fracture orientation. Under this configuration, the increase in maximum principal stress only marginally influences the fluid flow channel through stress-dependent strain. In addition, the permeability response was weakened with the increase in the in situ stress. Fractures within the ultra-low-permeability sandstone significantly influence pore pressure distribution. Non-Dary flow behavior occurred at high pore pressure of 0.6–1.8 MPa, which can be attributed to the special fracture structures. This observation contrasts with findings from previous work [39,40]. Thus, the novelty of this study lies in identifying the facture contribution under different in situ stresses, particularly considering the influence of the maximum principal stress.
3.4. Influence of In Situ Stress on Permeability
The influence of in situ stress on the evolution of permeability was shown in Figure 6. The permeability was negatively correlated with the increase in in situ stress. In detail, for sample R1, under the stress condition σ1:σ2:σ3 = x:2:2, as the axial stress increases from 4 MPa to 8 MPa, the permeability decreases gradually, but the rate of decline decreases slowly. When the axial stress further increases from 8 MPa to 16 MPa, permeability begins to increase gradually with the increase in axial stress, and the permeability is always between the permeability change curves corresponding to the axial stress of 8 MPa and 4 MPa. Similarly, under the stress condition σ1:σ2:σ3 = x:4:4, the axial stress increases from 8 MPa to 12 MPa, while permeability decreases with the increase in axial stress. However, when the axial stress continues to increases from 12 MPa to 32 MPa, permeability shows an increasing trend. In contrast, under higher confining stress conditions σ1:σ2:σ3 = x:6:6 and x:8:8, permeability remains largely unchanged with increasing axial stress. Permeability shows different changes with the increase in axial stress, which is mainly because of the fact that when the triaxial stress is relatively small (σ1:σ2:σ3 = x:2:2 and x:4:4), the prefabricated fractures in the sandstone specimen, coupled with the high strength of the sandstone itself, basically do not develop pore fractures under low axial stress. These pore fractures close with the increase in low horizontal axial stress, resulting in the decrease in sandstone permeability. However, with further increase in axial stress, these prefabricated fractures begin to expand under a high level of axial stress, which increases the pore fractures in the sandstone and increases the permeability of the sandstone, when the triaxial stress is relatively large (σ1:σ2:σ3 = x:6:6 and x:8:8). With the increase in axial stress, the expansion of primary fractures and the development of new fractures in sandstone specimens are approximately consistent with the fracture rate of sandstone compression closure. It is observed that permeability basically does not change with the increase in axial stress.
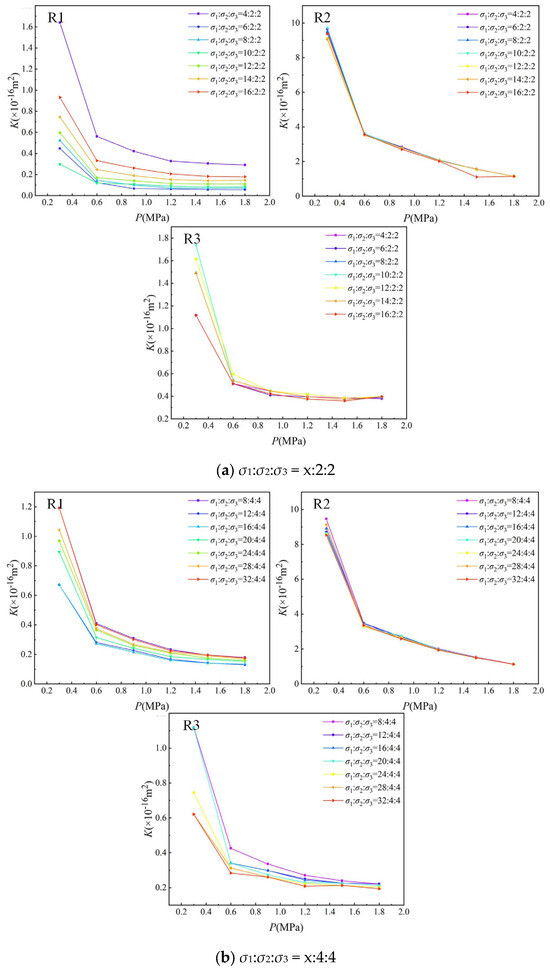
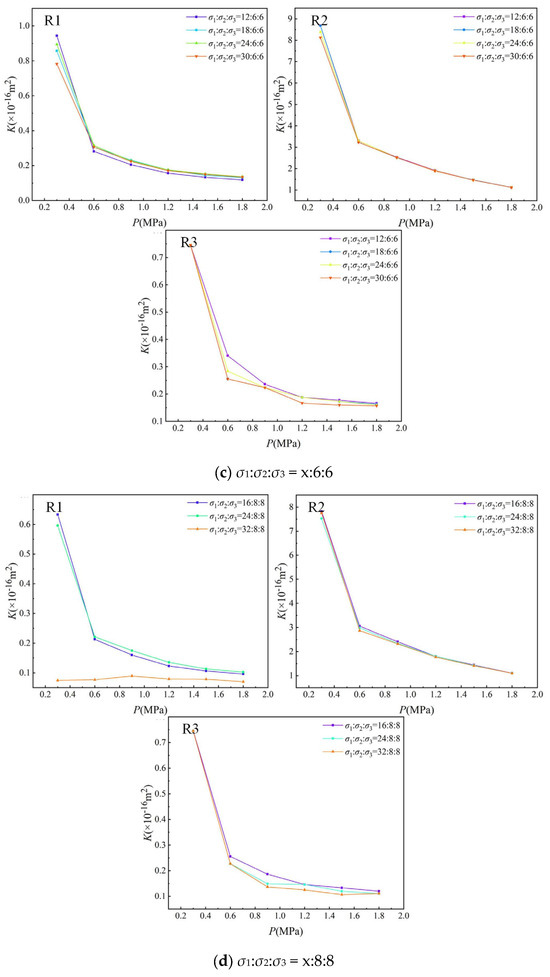
Figure 6.
Variation in permeability with pore pressure during the increase in axial stress.
For sample R2, the permeability remains largely unchanged with the increase in axial stress under different triaxial stress ratios. For sample R3, when σ1:σ2:σ3 = x:2:2, the permeability shows little variation as the axial stress increases from 4 MPa to 6 MPa. However, when the axial stress increases from 6 MPa to 10 MPa and further to 16 MPa, the permeability increases gradually. When σ1:σ2:σ3 = x:4:4, the permeability decreases gradually with the increase in axial stress. When σ1:σ2:σ3 = x:6:6 and x:8:8, the permeability stabilizes and shows no significant change with axial stress. The analysis shows that under a very low triaxial stress ratio (σ1:σ2:σ3 = x:2:2), multiple fractures were generated in the sandstone during the pre-fracturing process, and some tip fractures further expand and develop in the initial triaxial loading stage, resulting in an increase in pore-fracture connectivity and a gradual rise in permeability. However, when the triaxial stress ratio reaches σ1:σ2:σ3 = x:4:4, the high strength of sandstone prevents fracture tips from reaching the critical stress required for propagation. Under these conditions, the rate of fracture closure due to compression exceeds the rate of partial fracture extension. As a result, permeability gradually decreases with increasing axial stress. With the further increase in triaxial stress ratio (σ1:σ2:σ3 = x:6:6 and x:8:8), the applied stress approaches the fracture strength of the sandstone. At this time, the fracture closure rate is almost equal to the expansion rate of the new fracture. Consequently, permeability remains largely unchanged with increasing axial stress.
3.5. Relationship of Permeability and Axial Strain
The permeability evolution of the fractured sandstone is directly related to the increase in stress-dependent strain, as shown in Figure 7. A logarithmic relationship was observed between stain and stress in situ, while an exponential was identified between permeability and in situ stress. In detail, permeability initially decreases rapidly and then more gradually as pore pressure increases. The maximum permeability of 9 × 10−16 m2 presented at 0.3 MPa, while the minimum permeability of 0.1 × 10−16 m2 presented at 1.8 MPa. Gas conductivity decreased with the occurrence of turbulence flow due to the interaction of dynamic flow and limited connected channel. Permeability decreases with the increase minimum and intermediate principal stress. This decreasing trend in response to principal stress is pronounced at low pore pressure, while only a slight permeability response is observed at higher pore pressures ranging from 0.6 to 1.8 MPa.
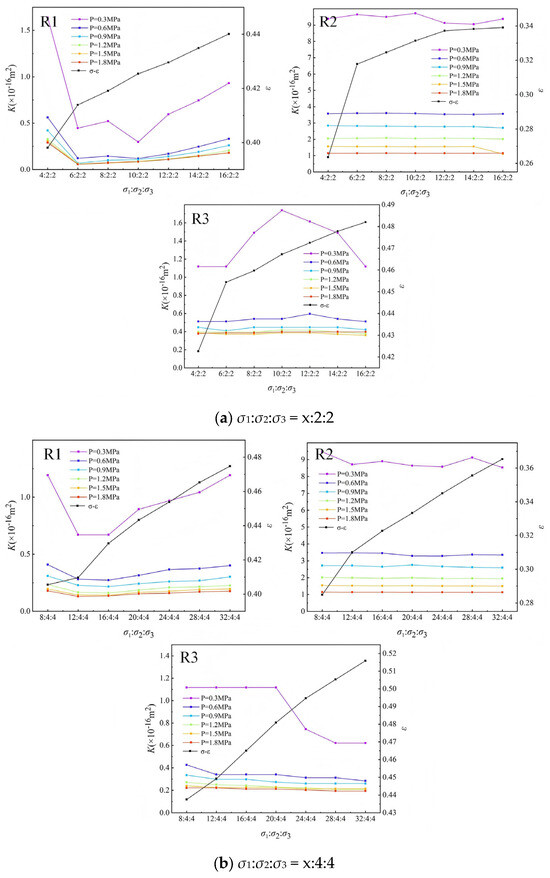
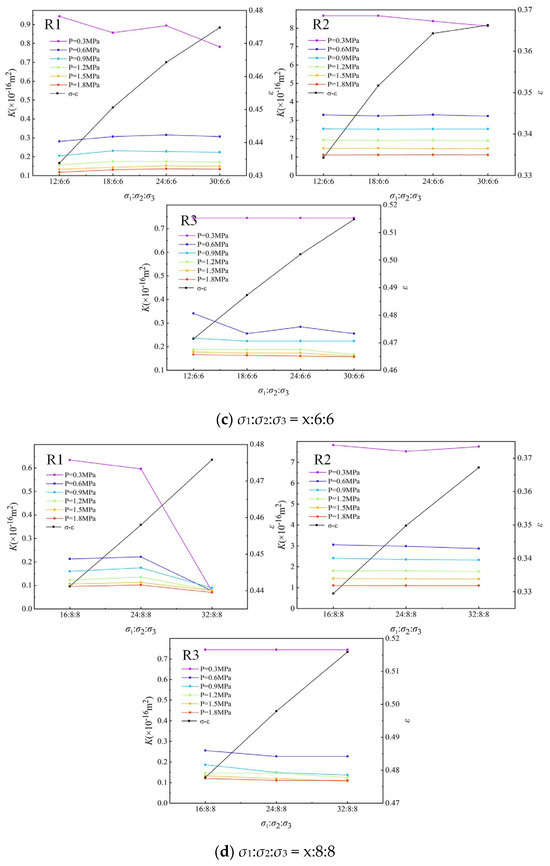
Figure 7.
Variation in permeability and axial strain.
3.6. Establishment of Stress-Dependent Permeability Theoretical Modeling
The influence of pore connectivity and fracture conductivity on the conductivity of intact rock was considered. In this study, the effective permeability ke was developed, which consists of two parts, namely kp of pore structure within rock matrix and kf of fracture. According to Darcy’s law,
where Qr, Qf, and Qp are the flow rates of whole rock, fracture and matrix pores, respectively, ke, kp and kf are the corresponding permeability, is the fluid pressure difference between the upstream and downstream, A is the cross-section area, L is the length of the flow path, and μ denotes the fluid viscosity.
Permeability values kf and kp can be correlated with fracture porosity and pore porosity according to the modified Kozeny–Carman model and Poiseuille equation, which are controlled by the following formula:
where a is rock matrix size, φf is the fracture porosity, φp is the pore porosity of the rock matrix, c, τ and S denote the Kozeny constant, tortuosity of the tube, and tube surface area per unit volume.
Partial differentiation of effective permeability ke to effective stress σe:
Rock compressibility Cf and pore medium compressibility Cp are defined as [41]
Taking Equations (6) and (7) into Equation (5), the effective permeability was deduced [42]:
Considering that compressibility varies with the applied effective stress, the stress-related fracture/pore compressibility can be calculated as follows:
where Cf0 and Cp0 are the initial fracture and pore compressibility, αf and αp are the declining rate of fracture or pore compressibility with the increase in the effective stress. The first-order Taylor formula expansion is carried out for Equations (9) and (10):
Taking Equations (11) and (12) into Equation (8), the equivalent effective model was established:
The validity of developed model was verified based on the experiment data, as shown in Figure 8. The coefficient of correlation for R2 was controlled at 0.9554, and the result demonstrates the developed stress-dependent permeability model can accurately predict the evolution of the pore-fracture rock fluid conductivity. The logarithmic strain-stress relationship observed in experiments (Figure 4) aligns with the exponential permeability–stress dependency predicted by the model (Equation (12)).
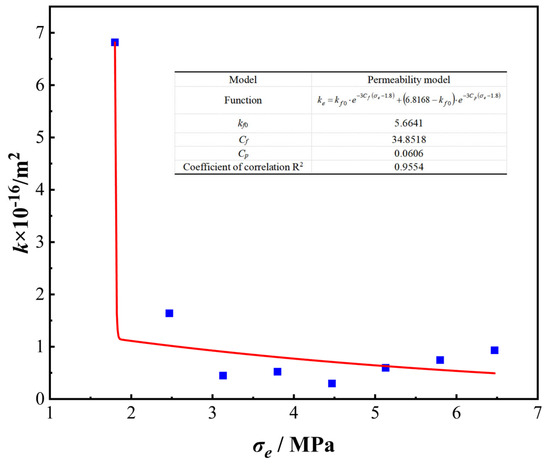
Figure 8.
Comparison of the model predicted and experimental data.
4. Conclusions
- (1)
- The morphology of fractures in low-permeability sandstone significantly influences the evolution of both permeability and strain. Among different fracture sizes, small fractures exhibit the greatest sensitivity to increases in the maximum principal stress, followed by medium and large fractures. In contrast, the most pronounced principal strain response to increasing principal stress occurs in large fractures, with medium and small fractures showing successively lower responses. Overall, fracture conductivity generally decreases, with minor variations observed specifically in small fractures.
- (2)
- Hydrodynamic pressure influences the fracture conductivity, and an exponential correlation was observed. The permeability of sandstone is negatively correlated to hydrodynamic pressure; the maximum permeability of 9 × 10−16 m2 presented at 0.3 MPa, and minimum permeability of 0.1 × 10−16 m2 presented at 1.8 MPa. The decrease in amplitude increased with the increase in fracture size. The gas conductivity decreased with the occurrence of turbulence flow due to the interaction of dynamic flow and limited connected channel.
- (3)
- In situ stress significantly influences the evolution of both principal strain and pore pressure-dependent permeability. Permeability decreases with increasing minimum and intermediate principal stresses. This decreasing trend in response to principal stress is pronounced at low pore pressures, while only a slight permeability response is observed at higher pore pressures ranging from 0.6 to 1.8 MPa in situ.
Author Contributions
Research design and original draft, Y.G.; supervision and editing, T.Z.; technical support, X.Y. (Xiang Yu); software development, Y.L.; data collection, X.Y. (Xin Yang). All authors have read and agreed to the published version of the manuscript.
Funding
This paper was supported by the National Natural Science Foundation (42477201), China; National key research and development plan (2021YFC28000903-05), China; the National Science and Technology Major Project (2024ZD1700201); the National Key Laboratory of Deep Coal Mining and Environmental Protection Fund (HNKY2024ZD201) China. Excellent Youth Project of Anhui Province (2022AH030086), China; the Anhui Provincial General Fund Project (2308085ME154), China; the Anhui Provincial Key Research and Development Program Fund Project (2023z04020001), China.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy considerations and ongoing research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dang, F.Q.; Li, S.Y.; Dong, H.; Wang, Z.J.; Zhu, J.Z. Experimental study on the oil recovery characteristics of CO2 energetic fracturing in ultralow-permeability sandstone reservoirs utilizing nuclear magnetic resonance. Fuel 2024, 366, 131370. [Google Scholar] [CrossRef]
- Tang, M.; Zhang, T.; Ma, Y.K.; Hao, D.Y.; Yang, X.; Li, Y.F. Experimental study on fracture effect on the multiphase flow in ultra-low permeability sandstone based on LF-NMR. Geoenergy Sci. Eng. 2023, 222, 211399. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, M.; Ma, Y.K.; Zhu, G.P.; Zhang, Q.H.; Wu, J.; Xie, Z.Z. Experimental study on CO2/Water flooding mechanism and oil recovery in ultralow—Permeability sandstone with online LF-NMR. Energy 2022, 252, 123948. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, M.; Yuan, L.; Zhu, G.P.; Zhang, C.; Liu, Y.; Li, Y.F.; Wang, W.; Yang, X. Experimental study on stress-dependent multiphase flow in ultra-low permeability sandstone during CO2 flooding based on LF-NMR. Energy 2023, 278, 127874. [Google Scholar] [CrossRef]
- Liu, J.Q.; Lyu, X.Z.; Liu, Y.; Zhang, P.P. Energy evolution and macro-micro failure mechanisms of frozen weakly cemented sandstone under uniaxial cyclic loading and unloading. Cold Reg. Sci. Technol. 2023, 214, 103947. [Google Scholar] [CrossRef]
- Vasyliev, L.; Malich, M.; Vasyliev, D.; Katan, V.; Rizo, Z. Improving a technique to calculate strength of cylindrical rock samples in terms of uniaxial compression. Min. Miner. Deposits 2023, 17, 43–50. [Google Scholar] [CrossRef]
- Abbas, H.A.; Mohamed, Z.; Kudus, S.A. Deformation behaviour, crack initiation and crack damage of weathered composite sandstone-shale by using the ultrasonic wave and the acoustic emission under uniaxial compressive stress. Int. J. Rock. Mech. Min. Sci. 2023, 170, 105497. [Google Scholar] [CrossRef]
- Jiang, X.Y.; Wu, D.; Zhao, Z.X.; Yang, Y.; Tian, J.W.; Wang, F.L. Experimental and numerical study on the damage evolution and acoustic emission multi-parameter responses of single flaw sandstone under uniaxial compression. Theor. Appl. Fract. Mech. 2024, 133, 104535. [Google Scholar] [CrossRef]
- Ishibashi, T.; Asanuma, H.; Mukuhira, Y.; Watanabe, N. Laboratory hydraulic shearing of granitic fractures with surface roughness under stress states of EGS: Permeability changes and energy balance. Int. J. Rock. Mech. Min. Sci. 2023, 170, 105512. [Google Scholar] [CrossRef]
- Ishibashi, T.; Yamaya, Y.; Asanuma, H. Experimental insights into coupled hydraulic, mechanical, and electrical behaviors of granite fractures: Implications for indirect estimation of crustal permeability changes. Int. J. Rock. Mech. Min. Sci. 2025, 188, 106060. [Google Scholar] [CrossRef]
- Yu, B.C.; Zhao, H.G.; Tian, J.B.; Liu, C.; Song, Z.L.; Liu, Y.B.; Li, M.H. Modeling study of sandstone permeability under true triaxial stress based on backpropagation neural network, genetic programming, and multiple regression analysis. J. Nat. Gas. Sci. Eng. 2021, 86, 103742. [Google Scholar] [CrossRef]
- Niu, Z.H.; Zhu, Z.D.; Que, X.C.; Xie, X.H.; Jin, K. Experimental study on damage evolution process, seepage characteristics, and energy response of columnar jointed basalt under true triaxial cyclic loading. Geoenergy Sci. Eng. 2024, 237, 212774. [Google Scholar] [CrossRef]
- Lu, J.; Yin, G.Z.; Deng, B.Z.; Zhang, W.Z.; Li, M.H.; Chai, X.W.; Liu, C.; Liu, Y.B. Permeability characteristics of layered composite coal-rock under true triaxial stress conditions. J. Nat. Gas. Sci. Eng. 2019, 66, 60–76. [Google Scholar] [CrossRef]
- Liu, C.; Yin, G.Z.; Li, M.H.; Deng, B.Z.; Song, Z.L.; Liu, Y.B.; Yin, S.Y. Shale permeability model considering bedding effect under true triaxial stress conditions. J. Nat. Gas. Sci. Eng. 2019, 68, 102908. [Google Scholar] [CrossRef]
- Duan, X.L.; Wang, W.; Liu, S.F.; Cao, Y.J.; Zheng, Z.; Zhu, Q.Z. Experimental investigation on mechanical behavior, energy evolution and gas permeability of anisotropic phyllite subjected to triaxial compression and cyclic loading. Geomech. Energy Environ. 2023, 35, 100483. [Google Scholar] [CrossRef]
- Liu, J.C.; Jia, W.S.; Duan, H.F.; Li, X.; Xia, K.W. Experimental study on the deformation and failure characteristics of cement stone under true triaxial stress state. Constr. Build. Mater. 2024, 449, 138397. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Long, Y.D.; Zhang, T.; Zhou, X.P. A true triaxial experiment investigation of the mechanical and deformation failure behaviors of flawed granite after exposure to high-temperature treatment. Eng. Fract. Mech. 2024, 306, 110273. [Google Scholar] [CrossRef]
- Zhou, H.Y.; Liu, Z.B.; Liu, F.J.; Shao, J.F.; Li, G.L. Anisotropic strength, deformation and failure of gneiss granite under high stress and temperature coupled true triaxial compression. J. Rock. Mech. Geotech. Eng. 2024, 16, 860–876. [Google Scholar] [CrossRef]
- Meng, F.B.; Shi, L.; Hall, S.; Baud, P.; Wong, T.F. Onset of pore collapse and dilatancy in porous sandstone under true triaxial compression: Experimental observation and micromechanical modeling. Int. J. Rock. Mech. Min. Sci. 2025, 186, 105983. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Meng, X.R.; Zhao, G.M.; Liu, C.Y.; Liu, Z.X.; Wu, X.K. Energy dissipation and damage mechanism of rocks under true triaxial graded perturbations. Soil. Dyn. Earthq. Eng. 2025, 190, 109192. [Google Scholar] [CrossRef]
- Singh, C.; Gupta, P.K. Numerical analysis of failure mechanics of concrete under true dynamic triaxial loading using a four-phase meso-model. Constr. Build. Mater. 2024, 450, 138661. [Google Scholar] [CrossRef]
- Wibisono, D.Y.; Gutierrez, M.; Majumder, D. Experimental investigation of tunnel damage and spalling in brittle rock using a true-triaxial cell. Int. J. Rock. Mech. Min. Sci. 2024, 182, 105884. [Google Scholar] [CrossRef]
- Couture, C.; Besuelle, P. A true triaxial experimental study on porous Vosges sandstone: From strain localization precursors to failure using full-field measurements. Int. J. Rock. Mech. Min. Sci. 2022, 153, 105031. [Google Scholar] [CrossRef]
- Lin, H.F.; Ji, P.F.; Kong, X.G.; Li, S.G.; Long, H.; Xiao, T.; Li, B. Experimental study on the influence of gas pressure on CH4 adsorption-desorption-seepage and deformation characteristics of coal in the whole process under triaxial stress. Fuel 2023, 333, 126513. [Google Scholar] [CrossRef]
- Gan, L.; Liu, Y.; Xu, F.; Ma, H.Y.; Xu, W.C. Experimental investigation of the seepage characteristics of a single fracture in limestone with different roughness and seepage fluids. J. Hydrol. 2023, 622, 129699. [Google Scholar] [CrossRef]
- Zhang, S.H.; Wu, S.C.; Duan, K. Study on the deformation and strength characteristics of hard rock under true triaxial stress state using bonded-particle model. Comput. Geotechnol. 2019, 112, 1–16. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Liu, S.J.; Kou, M.M.; Wang, Z.Q. Mechanical and failure characteristics of fissured marble specimens under true triaxial compression: Insights from 3-D numerical simulations. Comput. Geotechnol. 2020, 127, 103785. [Google Scholar] [CrossRef]
- Gao, Y.H.; Feng, X.T. Study on damage evolution of intact and jointed marble subjected to cyclic true triaxial loading. Eng. Fract. Mech. 2019, 215, 224–234. [Google Scholar] [CrossRef]
- Wang, S.S.; Xu, W.Y.; Yan, L.; Feng, X.T.; Xie, W.C.; Chen, H.J. Experimental investigation and failure mechanism analysis for dacite under true triaxial unloading conditions. Eng. Geol. 2020, 264, 105407. [Google Scholar] [CrossRef]
- Liu, C.Y.; Pan, C.; Zhao, G.M.; Xu, W.S.; Meng, X.R.; Liu, W.J.; Cheng, X. Experimental study on the failure mechanism of roadway surrounding rock under true triaxial loading: Insights from acoustic emission (AE) characteristics. Measurement 2025, 246, 116727. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Meng, X.R.; Zhao, G.M.; Li, Y.M.; Xu, W.S.; Liu, C.Y.; Liu, Z.X.; Wu, X.K.; Qin, Z.H.; Wang, K. Damage evolution and acoustic emission characteristics of sandstone under different true triaxial cyclic loading and unloading modes. Eng. Fail. Anal. 2025, 167, 108947. [Google Scholar] [CrossRef]
- Li, B.L.; Shi, W.H.; Zhang, H.J.; Long, Y. Failure behaviors and acoustic emission characteristics of flawed granite of different grain sizes: Insights from true triaxial experiments with a free face. Theor. Appl. Fract. Mech. 2024, 131, 104394. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Zhang, S.C.; Ma, X.F.; Zhang, X.H.; Zhang, S.P. Hydraulic fracture morphology and conductivity of continental shale under the true-triaxial stress conditions. Fuel 2023, 352, 129056. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, R.H.; Pan, P.Z.; Qi, J.H.; Su, G.S.; Zheng, H. Shear failure behaviors and degradation mechanical model of rock mass under true triaxial multi-level loading and unloading shear tests. Int. J. Min. Sci. Technol. 2024, 34, 1385–1408. [Google Scholar] [CrossRef]
- Huang, J.; Hu, Q.T.; Qin, C.Z.; Song, Z.L.; Wang, X.D. Pre-peak acoustic emission characteristics of tight sandstone failure under true triaxial stress. J. Nat. Gas. Sci. Eng. 2022, 102, 104576. [Google Scholar] [CrossRef]
- Gao, H.; Xie, H.P.; Zhang, Z.T.; Lu, J.; Zhang, D.M.; Zhang, R.; Wu, M.Y. True triaxial energy evolution characteristics and failure mechanism of deep rock subjected to mining-induced stress. Int. J. Rock. Mech. Min. Sci. 2024, 176, 105724. [Google Scholar] [CrossRef]
- Jiang, C.B.; Yang, Y.; Wei, W.H.; Duan, M.K.; Yu, T. A new stress-damage-flow coupling model and the damage characterization of raw coal under loading and unloading conditions. Int. J. Rock. Mech. Min. Sci. 2021, 138, 104601. [Google Scholar] [CrossRef]
- Fan, L.; Liu, S.M. Evaluation of permeability damage for stressed coal with cyclic loading: An experimental study. Int. J. Coal Geol. 2019, 216, 103338. [Google Scholar] [CrossRef]
- Yang, S.; Wen, G.C.; Yan, F.Z.; Li, H.L.; Liu, Y.B.; Wu, W.B. Swelling characteristics and permeability evolution of anthracite coal containing expansive clay under water-saturated conditions. Fuel 2020, 279, 118501. [Google Scholar] [CrossRef]
- Xue, Y.; Ranjith, P.G.; Gao, F.; Zhang, D.C.; Cheng, H.M.; Chong, Z.H.; Hou, P. Mechanical behaviour and permeability evolution of gas-containing coal from unloading confining pressure tests. J. Nat. Gas. Sci. Eng. 2017, 40, 336–346. [Google Scholar] [CrossRef]
- Jiang, T.W.; Yao, W.; Sun, X.W.; Qi, C.Y.; Li, X.; Xia, K.W.; Zhang, J.; Nasseri, M.H.B. Evolution of anisotropic permeability of fractured sandstones subjected to true-triaxial stresses during reservoir depletion. J. Petrol. Sci. Eng. 2021, 200, 108251. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, D.M.; Lu, J.; Yin, G.Z.; Wu, M.Y. Experimental study on infuence of intermediate principal stress on the permeability of sandstone. Transport. Porous Med. 2020, 135, 753–778. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).