Process Anomaly Detection in Cyber–Physical Production Systems Based on Conditional Discrete-Time Dynamic Graphs

Abstract

Various types of anomalies can arise in cyber–physical production systems, caused by either faulty devices or incorrect processes. Anomalies within individual devices can often be detected by applying machine learning techniques to the respective produced multivariate time series. While this data typically shows temporal and spatial changes and can therefore be efficiently utilized by models, detecting anomalies within the process is often more challenging, as process data usually only consists of events, binary signals, or changes in unique process states. Due to the low variance of data, existing anomaly detection methods struggle to detect anomalies effectively and accurately. To address this challenge, in this paper, we propose a novel concept for process anomaly detection based on conditional discrete-time dynamic graphs. Through the conditional connections of the graph, essential characteristics can be generated and utilized to effectively train machine learning models to detect anomalies in the process data. Identified anomalies can be related to the current graph, facilitating transparent and explainable detections. By evaluating the concept against process data from an industrial unit and achieving an F1-Score of 0.96 and 1 for the realized repetitive processes, the accuracy and effectiveness of the concept can be demonstrated.

1. Introduction

Due to the rising complexity and increasing interconnectivity of individual devices, and the focus on reduced production times, errors within modern cyber–physical production systems (CPPSs) or their individual components can significantly impact the entire production process. This can lead to faulty products, system breakdowns, or the propagation of errors throughout the entire production line. Therefore, early detection and analysis of faults are crucial for ensuring modern and safe CPPS [1].

Anomalies within such a system, like an unexpected torque value of a motor or an atypical process state, can indicate potential faults, serving as early warning signs for existing or emerging errors. In the context of a CPPS, an anomaly can be defined as any deviation from the intended, currently focused normal state of the system [2]. Detecting anomalies facilitates the early identification of potential errors, enabling rapid intervention and, ideally, preventing errors from occurring. Therefore, effective anomaly detection (AD) plays a decisive role in ensuring the reliability, safety, and performance of CPPSs.

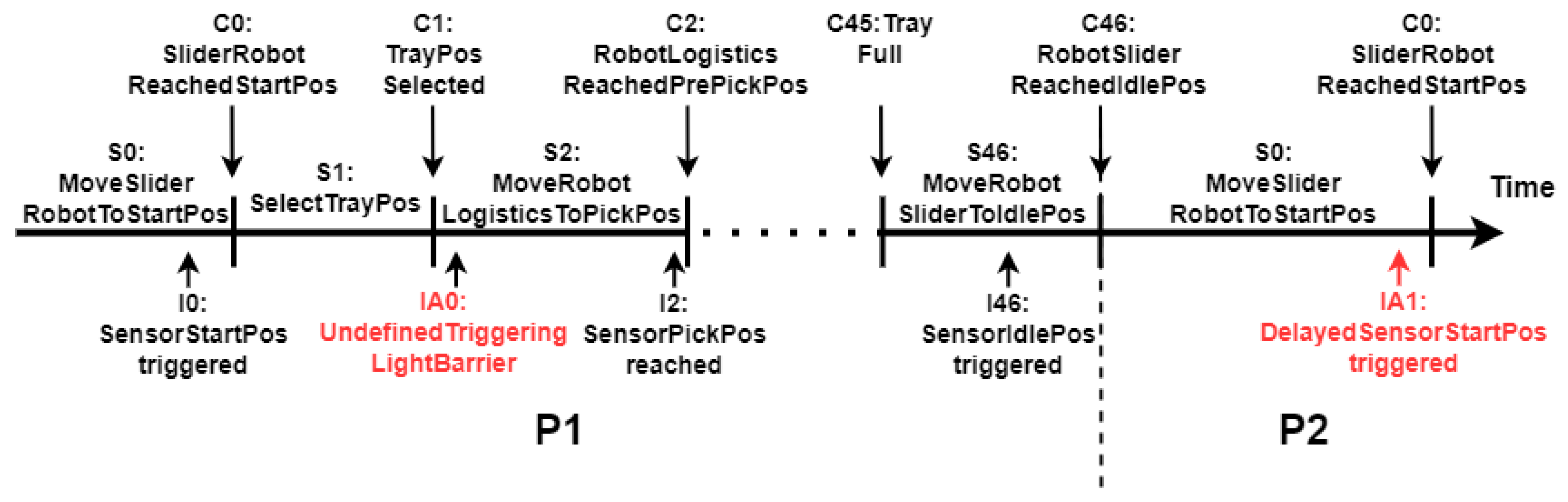
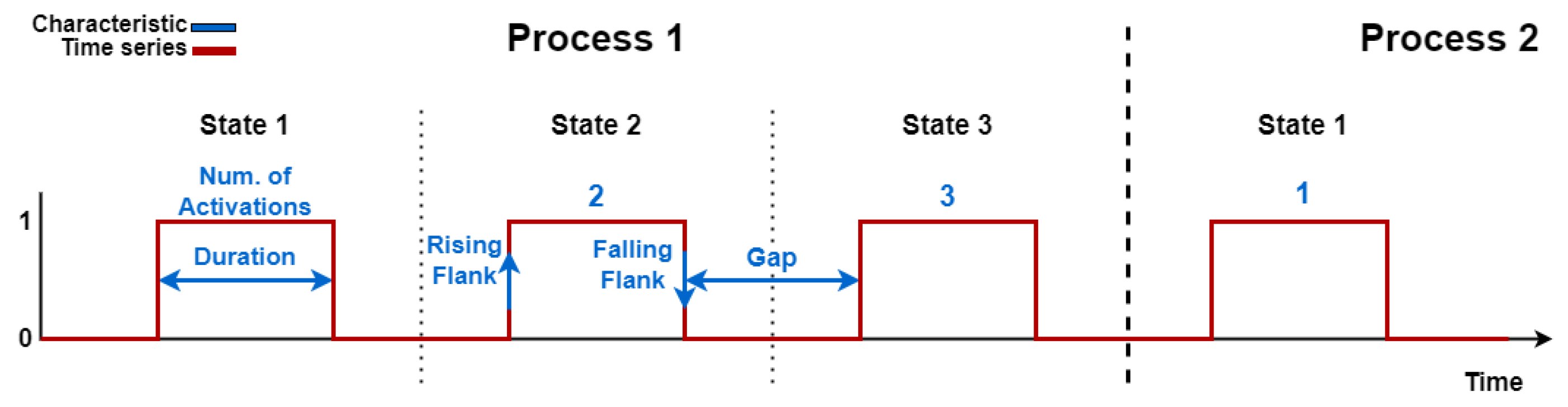
To establish a comprehensive AD, it is essential not only to consider separate devices but also the various processes executed within such a system [3]. An industrial process can be defined as a discrete event sequence in which a systematic series of operations or steps is performed to achieve a specific output or result, based on states and inputs [4]. Figure 1 visualizes such a sequence of states in a time diagram. The repetitive process passes through various states, whereby inputs occur, such as detecting a product by a sensor or reaching a defined axis position. These inputs represent external, variable influences that can trigger a condition. As a result, they can cause a change in state, either directly or indirectly, as a standalone event or as part of a sequence of events. Both the outputs and inputs can be physical or digital, such as commands to a control element to start the production process. In modern production systems, various sensors, actuators, mechanical systems, and control and monitoring devices interact with each other to realize these complex industrial processes.

In an industrial production system, the sequence of states is usually predefined and followed as a repetitive cycle. Because the trigger conditions rely on internal or external inputs, e.g., a signal from a sensor, these inputs provide essential features for detecting anomalies [5]. Two possible anomalies are visualized as examples in Figure 1; IA0 represents an undefined input, like the external triggering of a photoelectric sensors; IA1 shows a delayed input to the process by a sensor, indicating that the robot reaches the start position with a delay.

To detect anomalies within such processes, techniques from the field of AD can be used. These techniques can be categorized into two types: knowledge-based and data-based. Knowledge-based techniques rely on previously defined rules or precisely constructed representations of the entire system. Data-based techniques create models independently, using only the collected data [6].

While various devices within CPPSs usually provide a multivariate discrete data stream that can be optimally utilized for data-based techniques, only binary temporal data is generally available as information about inputs within the process [7]. This data often lacks depth and variance, making it hard to extract meaningful patterns and limiting the effective use of data-driven techniques.

At the same time, in many industrial systems, not only is the produced data available, but also additional background knowledge. This includes structural properties or extended process information, such as the design of the system, sequences, movement patterns, or standardized process concepts. Utilizing this information can enhance the analysis and understanding of the system in operation and can enable or improve AD.

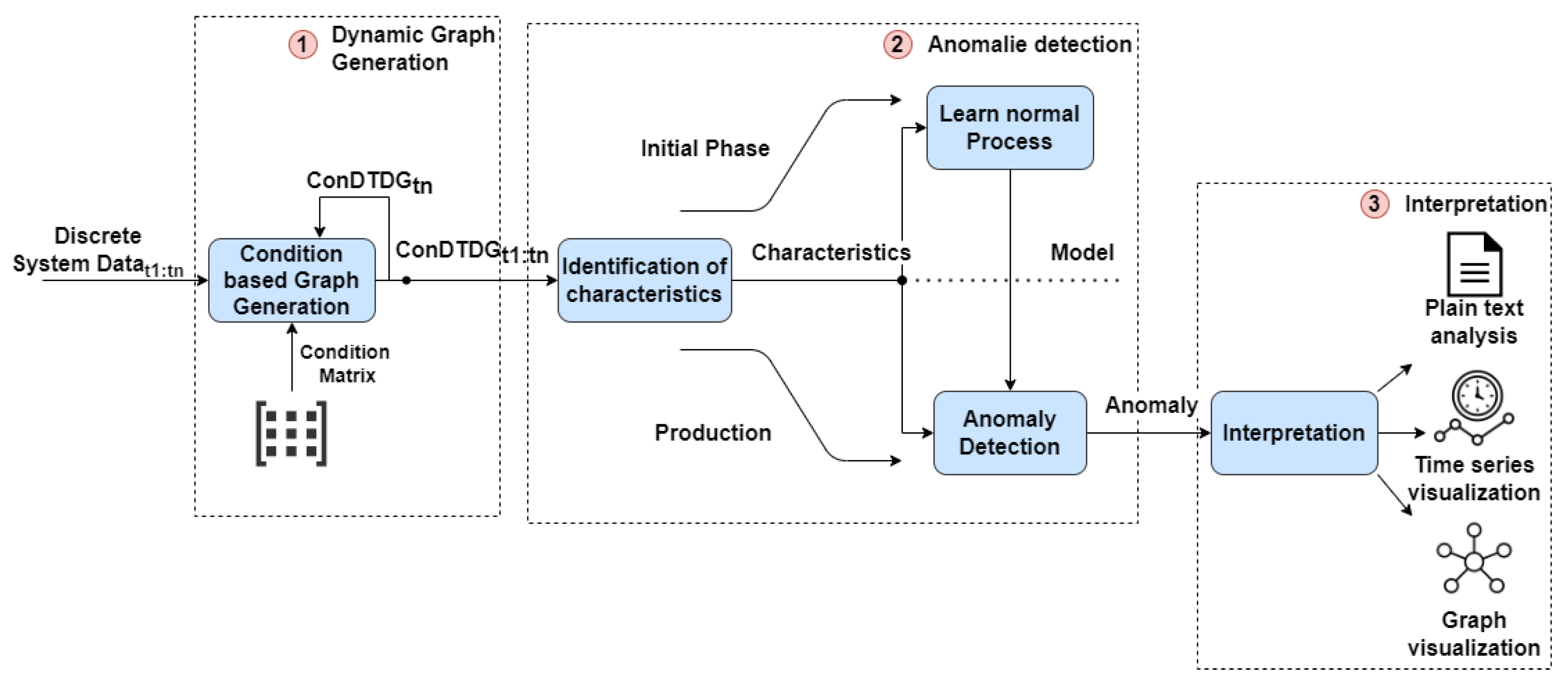
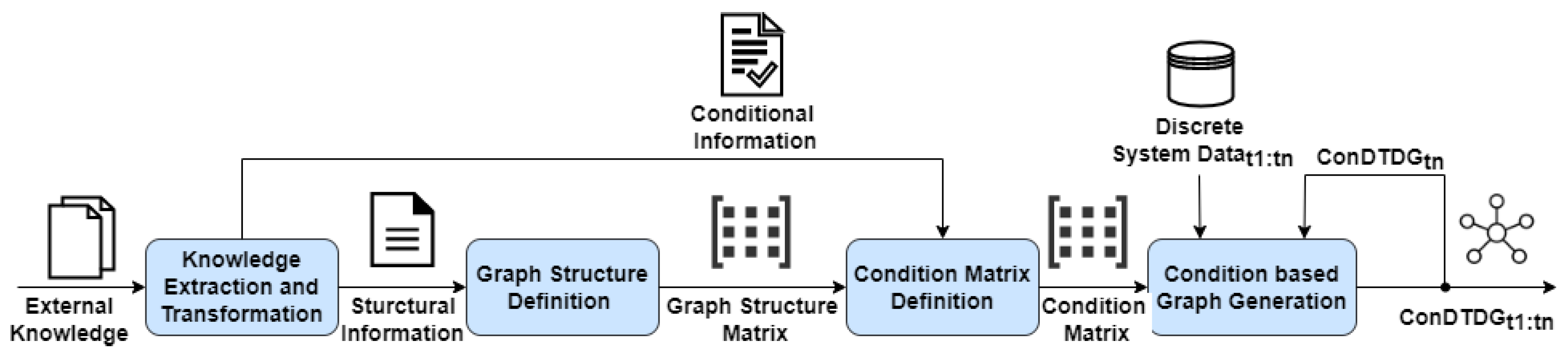
One solution to combine available background knowledge with process data is to transform all available information into a time-dynamic graph [8]. This graph will effectively represent the entire system and the production processes, facilitating a comprehensive analysis of the interdependencies and temporal relationships within the data. Therefore, individual motion devices, sensors, and products can be viewed as nodes. The interactions and relationships between devices and products can be modeled as dynamic edges, representing the actual process that depends on the current state and inputs. The resulting discrete-time dynamic graph represents the entire system, including all sub-processes, at any given time step within the overall process [9].

The graph or separate characteristics can then be utilized to identify anomalies in process data, providing deeper insights into the process, including the devices involved, their interactions, or temporal relationships. Such an approach enhances transparency and facilitates a deeper understanding of the dynamic process, thereby improving explainability and transparency. Thus, even users with limited technical knowledge can identify, interpret, and take action to resolve an anomaly if necessary.

In this paper, we present a novel concept for transforming an industrial production system, including the implemented processes, into a discrete-time dynamic graph based on predefined conditions. By considering the internal interdependencies and temporal relations of the conditional connections, we can extract essential characteristics to enhance low-variance process data. This enables the utilization of generated data to learn the normal process of the industrial production system based on different machine learning models. Identified anomalies can be contextualized with respect to the current graph, the specific process step, and the actual states, thereby enhancing the interpretability and transparency of anomalies. Finally, we implement the concept and conduct a comparative analysis of various models utilizing process data from a real industrial production system. The contribution of the work can be summarized as follows:

• We present a concept to transform a CPPS into a conditional discrete-time dynamic graph, including the realized processes.
• We provide a novel strategy to extract essential characteristics of the conditional connections to enrich low-variance process data.
• We implement and compare several sequential machine learning models to utilize filtered characteristics and detect process anomalies.
• We propose an evaluation scheme for analyzing detected anomalies that provides a threefold output, including plain text, time series analysis, and graph visualization, for optimized interpretation of detected anomalies depending on the knowledge of the users.
• We demonstrate the effectiveness of our approach through a comprehensive evaluation against process data from an industrial unit.

The remainder of the paper is organized as follows: Section 2 presents an analysis of existing related work. Section 3 provides essential basic information about graph theory and how to represent an industrial manufacturing system as a graph. In Section 4, we describe the concept of model-based AD based on conditional discrete-time dynamic graphs. Section 5 presents an experimental evaluation. Section 6 discusses important lessons learned during implementation and based on the results obtained. Finally, Section 7 summarizes the findings and provides an outlook on future work.

2. Related Work

Surveys of AD techniques can be found in [10,11,12]. As mentioned above, the individual techniques can be categorized into data-based and knowledge-based approaches.

Data-based techniques extract essential patterns and structures from the available data to automatically generate meaningful models. Since most available data from industrial processes are discrete time series, sequential models like recurrent neural networks (RNNs) [13] and transformers [14,15] are often employed due to their ability to capture long-range dependencies and interactions.

In [16], OC4Seq—a novel framework for detecting anomalies in discrete event sequences that effectively integrates local and global information based on one-class RNNs—is introduced. The resulting model can handle sequential dependencies and identify anomalies from both local and global perspectives. In [17], a multi-scale variational transformer was employed to extract important information from satellite time series data at different scales, thereby identifying potential correlations between individual sequences. The authors in [18] present a time series AD method utilizing stacked transformer representations as an encoder and 1D convolutional networks as a decoder. The proposed method can detect anomalies, considering both the global trend and local variability of the given time series. In [19], a variable temporal transformer model for detecting anomalies in multivariate time series was introduced. The shown self-attention mechanism captures both temporal dependencies and inter-variable relationships. It also increases the interpretability of the detection through a comparison of attention maps between the original and reconstruction data.

Data-based techniques have the advantage of not requiring any deep understanding of the system, as the models are created solely based on data, thereby saving development time and costs [20]. To effectively detect anomalies, data-based techniques require meaningful, information-rich, and varying data to extract and learn essential patterns and structures. Process data, such as binary signals, events, and status data, typically only exhibits temporal changes and no variation in its value range. Data-driven techniques often lack transparency because they do not reference the system, making it challenging to analyze and respond to detected anomalies. Therefore, pure data-driven methods are hardly applicable to process AD.

Knowledge-based techniques create detailed representations of the entire system for AD. Various model-based techniques are discussed in [21,22]. Rule-based methods used in industrial systems include Petri nets [23,24] and automata [25].

In [26], a rule-based approach for intrusion detection in the IoT domain using fuzzy-based classifiers is proposed. The developed model aimed to establish a good trade-off between interpretability and accuracy. In [27], a hybrid automata-based runtime verification method for online hazard prediction in train operations is introduced to improve safety. The method provides predictions of hazard-related train operations by analyzing all potential time position states of the train.

Model-based techniques allow the successful detection of anomalies even in less varied and information-poor data. Simultaneously, detections can be effectively and transparently interpreted and analyzed based on the models. The modeling and generation of such models require a deeper understanding of the system and a significant amount of work and time. Additionally, while Petri net and automata techniques check achieved states and change conditions, they do not consider the temporal occurrence of the respective inputs within the individual states. These inputs serve as external feedback to the process, which is essential for promptly responding to anomalies in complex production processes. To ensure interpretability and transparency, even for users with limited background knowledge, the interactions and relationships between individual devices and products also play a crucial role. This aspect cannot be determined solely from the pure process flow.

In an effort to combine the advantages of both approaches, more hybrid methods have recently been developed. Therefore, data-driven techniques are employed to develop precise system models, enabling the application of model-based methods. This approach simplifies the time-consuming system modeling process while maintaining the interpretability of the results [28].

The authors of [7] present an approach in which time automata are first generated automatically through deep learning. Later, based on the model, the system is used to recognize anomalies in a hybrid production environment. For this purpose, the authors applied deep belief networks to learn the system’s behavior and to detect anomalies through subsequent comparison. In [29], a concept for improving the interpretability of automatically learned time automata is presented. Therefore, knowledge about the time automata and the anomalies was combined in a knowledge graph and enhanced with technical knowledge about the system. Another method for detecting attacks on industrial control systems, utilizing a combination of Bayesian networks and timed automata, was presented in [30].

An alternative approach emphasizes the development of meaningful models to which data-based techniques can be effectively applied. In this context, the field of graph AD is rapidly evolving, utilizing available background knowledge to create graph structures. These structures serve as a basis for data-based methods, such as graph neural networks (GNNs), to be applied [31,32].

The authors of [33] present a novel GNN approach called Graph Deviation Network. This approach detects anomalies in multivariate time series data by learning the relationships between sensors as a graph and incorporating attention mechanisms for explainability. Experimental results on two real-world sensor datasets demonstrate the model’s accuracy while providing insights into the nature and causes of detected anomalies. In [34], a GNN autoencoder (AE) with a symmetric decoder capable of simultaneously reconstructing both edge and node features is demonstrated. The authors of [35] introduce a GNN-based AE for AD in particle physics, focusing on boosted jets to identify potential beyond standard model physics. By reconstructing graph-level features, including multidimensional edges, the method effectively distinguishes QCD jets from anomalous jet structures.

Utilizing data-driven techniques for graph structures enables effective and direct learning of the data while also ensuring the transparency and interpretability of AD through a model. On the other hand, creating a precise graph representation requires a deeper understanding of the entire system, while also demanding high computational resources to develop and execute the GNN.

In summary, various techniques and models for AD in the industrial sector exist. Many require data with high variance and detailed information, making the application solely on process data nearly impossible. Model-based techniques require considerable effort to create precise models of complex industrial systems. Yet, they often provide limited information about the interactions and relationships between devices and products in the process. At the same time, the interpretability and transparency of the detection play a crucial role in enabling a rapid and effective response to the detected anomaly.

Considering these points, we present a hybrid approach for AD in CPPSs. First, we model the entire system and the executed processes as a conditional discrete-time dynamic graph, leveraging available background knowledge. We learn essential characteristics of the conditional connection with respect to the executed process, which are then used for effective data-based AD in the CPPS. Finally, based on the modeled graph structure, anomalous detections can be quickly and transparently interpreted, enabling fast and effective reactions, even for users without a deeper understanding of the system.

3. System Representation as a Graph

3.1. Graph Theory

A graph $G=\{V,E\}$ can be described as a combination of nodes $V={\left\{v\right\}}_1^n$, connected by edges $E=\left\{e_{i,j}\right\}$, where n is the number of nodes and $e_{i,j}=(v_i,v_j)$ indicates an edge between nodes $v_i$ and $v_j$. Thereby, nodes represent separate entities, and edges represent relations between them. An adjacency matrix $A={\left[a_{i,j}\right]}_{nxn}$ defines how the nodes within the graph are connected (if $a_{i,j}=1$) and simultaneously indicates the receiver $v_i$ and the transmitter node $v_j$ for each connection [32].

In general, graphs can be divided into static and dynamic graphs. In static graphs, the nodes and connections are predefined and remain constant over time. Within dynamic graphs, both the structure (nodes can be added or removed) and the internal relations can be changed (by modifying the connections).

Dynamic graphs can be categorized into discrete-time and continuous-time graphs. A discrete-time graph can be seen as a sequence of snapshots of the respective graph, where the various structural properties and relations change over time. In contrast, a continuous-time graph changes an initial static graph based on observations. These observations are usually described as a combination of an event type, event, and time of the event.

Besides the basic structure of the graph, which provides information about the nodes, their interactions, and their relations, additional information can be stored in each graph component, e.g., background data or connection details.

3.2. CPPS as a Graph

As described previously, a CPPS can also be modeled as a graph. In this representation, individual motion devices, such as robot systems, and products, like processed components, are represented as separate nodes. The edges characterize the interactions and relationships between the entities.

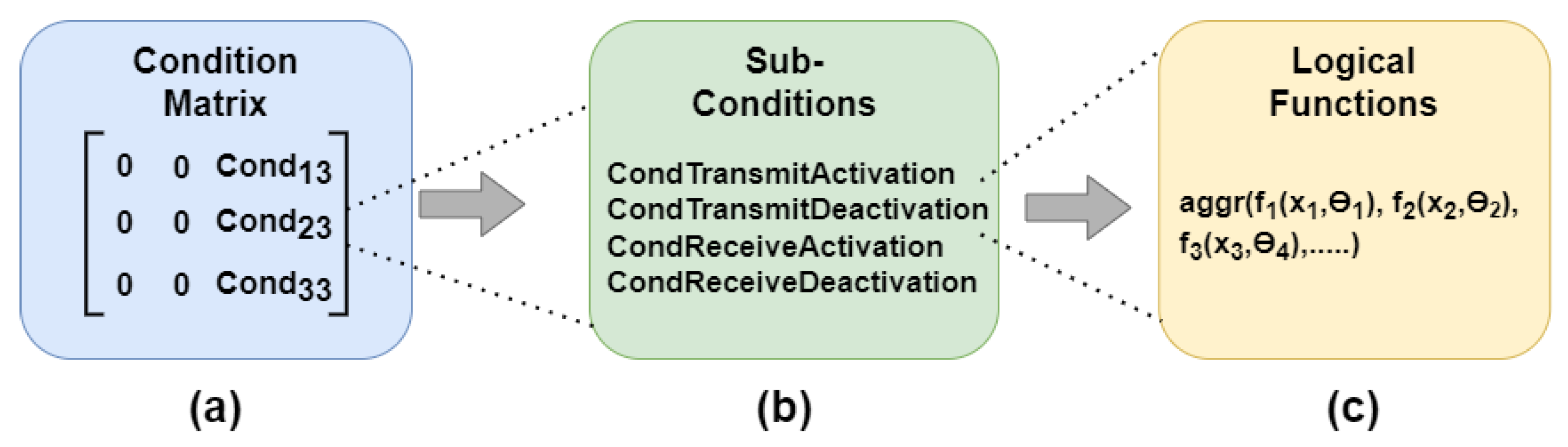
In such systems, interactions and relations, and therefore the edges, can change dynamically throughout the process. Hence, individual edges can be categorized as either static or dynamic connections. While static connections are fixed, for example, in the case of a mechanical link between two axes, the connection state of dynamic connections is based on the currently available system data, external inputs, and specific conditions. This enables the flexible addition or removal of connections between graph nodes based on the system’s current state.

In this paper, the term ‘activated’ is used when a connection between two units is established, while ‘deactivated’ means that the connection has been removed. Therefore, the state of potential connections within the process that are considered but not established at a certain point in time can be clearly defined. For example, when a robot fulfills a predefined condition by reaching a specific product pick-up position, the connection between the two entities is activated.

Since relations and interactions are constantly changing within the process, and the available data of individual devices are recorded at regulated intervals, the resulting graph of such a system can be defined as a conditional discrete-time dynamic graph.

4. Concept of Model-Based Process Anomaly Detection

To generate a dynamic graph of a system, detect process anomalies, and provide a logical and interpretable analysis, several steps must be executed. Figure 2 shows those steps, including dynamic graph generation, anomaly detection, and interpretation. In the following section, each individual step is described in detail.

4.1. Dynamic Graph Generation

Various nodes, edges, and required conditions must be predefined to enable the dynamic creation of the graph based on available discrete system data. One possibility is shown in Figure 3. First, essential data from available background knowledge is extracted and then transformed into conditional and structural information. Structural information defines the static structure of the graph, such as nodes and static edges, while conditional information describes the dynamic connections through a condition matrix. Combined with the discrete system data, the adjacency matrix and the corresponding system graph can be dynamically generated at any process time. The individual points will be discussed in more detail in the following sections.

4.1.1. Background Knowledge

Available background knowledge can be divided into structural and process knowledge.

Structural knowledge contains information about the design, built-in components, and system layout. For example, this includes blueprints of mechanical components or the placement of individual devices within the system. The data can be presented in various formats, such as design drawings, system visualizations, or digital twins. This information can be utilized to define the nodes and static connections of the intended graph.

Process knowledge encompasses details about individual sub-processes, including process variables, movement patterns, and process sequences. Data is usually available in the form of process visualizations or control programs. Utilizing the provided information, relationships and correlations among individual nodes, specifically conditional connections, along with various system states and the overall process sequence, can be characterized.

4.1.2. Knowledge Extraction and Transformation

Background knowledge is often supplied in various formats and from multiple sources. Therefore, it must be extracted and transformed to generate the structural and conditional matrix. Depending on available data, respective procedures must be adapted and individualized separately for each system. An example of the extraction and transformation process is explained in the next section.

4.1.3. Graph Structure Definition

Nodes in the graph are defined based on structural information, resulting in a structure matrix in the form of an adjacency matrix for the system. Static edges, which refer to mechanical connections, can be pre-classified within this matrix.

4.1.4. Condition Matrix Definition

Extracted process information defines individual conditions to create the condition matrix. As illustrated in Figure 4, each condition includes four distinct sub-conditions, each of which can contain one or more logical functions. The corresponding sub-condition defines whether data of the transmitter or receiver node (transmit/receive) is used, and which edge state (activation/deactivation) is established after the condition has been fulfilled. For example, the sub-condition CondTransmitActivation uses the current system values of the transmitter node. If this sub-condition, along with CondReceiveActivation—which uses the current system values of the receiver node—is met, the edge state is activated. This facilitates the straightforward creation, logical assignment, and transparent traceability of conditions, thereby enhancing the programmer’s ability to precisely define and manipulate these conditions.

If a node, such as a product, does not provide data for a specific condition, the associated sub-conditions can be neglected. The logical function $f_1$ (e.g., $=,>,\le$) uses a predefined literal value $x_1$, along with the current system value ${\Theta }_1$. The return values of each logical function are then aggregated using an operator, such as $all$ or $all$, within the sub-condition $y=aggr(f_1(x_1,{\Theta }_1),f_2(x_2,{\Theta }_2),\dots )$.

4.1.5. Condition-Based Graph Generation

The condition matrix enables the computation of the system graph based on discrete system data and the respective logical function. Depending on the recent state of the edge, the sub-conditions are checked. If the sub-conditions are satisfied, a 1 or 0 is set at the appropriate position in the adjacency matrix, activating or deactivating the connection.

4.1.6. Conditional Discrete-Time Dynamic Graph

The conditional graph $cond{G}_t=(V,E_t)$ can be generated based on conditional connections at each time step t over the whole process time T with

• $V=\{v_1,v_2,\dots .v_n\}$ — for a fixed set of n nodes over all $t\in T$,
• $E_t\subseteq V\times V$ — set of edges at t

For each time step t, the $cond{G}_t$ can be represented by an adjacency matrix $A_t\in {\{0,1\}}^{nxn}$ where

$${\left(A_t\right)}_{ij}=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\mathrm{activation}\mathrm{conditions}\mathrm{fulfilled}\hfill \\ 0\hfill & \mathrm{if}\mathrm{deactivation}\mathrm{conditions}\mathrm{fulfilled}\hfill \end{array}\right.$$

for the edge from node i to node j.

The resulting sequences of the conditional graphs can be defined as a conditional discrete-time dynamic graph $condDTD\mathcal{G}={\left\{cond{G}_t\right\}}_{t=1}^T$, with a three-dimensional process adjacency matrix $\mathcal{A}={\left\{A_t\right\}}_{t=1}^T$.

4.2. Anomaly Detection Based on Conditional Connections

Although production processes are repetitive, the process adjacency matrix can vary over time due to external influences or irregularities, such as sample or calculation times. To effectively and accurately identify anomalies in the binary temporal data of the process adjacency matrix, enriching existing data with additional characteristics is essential.

4.2.1. Identification of Temporal Process Characteristics

Examining the generated temporal process matrix reveals important characteristics through the activation and deactivation of the conditional connections. For example, the number of activations provides essential information on whether the correct number of products is being processed. The duration and the time gaps between activations are significant temporal characteristics that can highlight process errors in the event of substantial deviations. Figure 5 illustrates a binary time series of a conditional connection with various characteristics. All characteristics can be purely extracted from the process adjacency matrix. The resulting duration, gap, and activation matrices can be used as additional inputs to enhance AD by enriching the data with process information.

4.2.2. Anomaly Detection Model

Due to the high sequential dependencies in the resulting binary time series data, RNNs and their variants, such as Long Short-Term Memory (LSTM) networks, are particularly effective for learning and detecting anomalies in such sequences. Additionally, transformers can be considered, especially for multiple input steps and the resulting long sequences. Given the repetitive nature of the process data, employing reconstruction techniques presents a feasible and efficient method. To enhance the evaluation process and identify the most effective model, LSTM networks, bidirectional LSTM networks, and transformer architectures were systematically integrated and evaluated within the experimental scenario. A visualization of the networks used is shown in Figure 6.

4.3. Interpretation

Using the previously generated dynamic graph of the system, along with the embedded process information and individual conditional connections, immediate feedback can be provided in the event of a detection. This feedback includes the current process number, process status, and the involved nodes and connections. As shown in Figure 7, this can be visualized as a graph, within a time series, or as plain text. The text and graph can provide important information about the anomaly, even for users without domain knowledge. The time series includes detailed information about the overall process and can be utilized by specialists for future analysis and evaluation.

5. Experimental Evaluation

In the following section, the integration of the concept into a real CPPS is described.

5.1. Experimental Unit

A demonstration system from Yaskawa Europe GmbH, Hattersheim, Germany, the “Rotary table dispenser system”, was used as the experimental unit (Figure 8). A detailed structural description of the system can be found in [9]. The system is modeled after a real industrial production system and simulates various sub-processes, including transportation, pick-and-place, and sorting processes. The industrial standard PackML (https://www.omac.org/packml, accessed on 3 October 2025) (Packaging Machine Language), an approach to industrial automation that standardizes the integration and control of packaging machines, was used to design and program the system. Therefore, the components and sub-processes are divided into equipment modules (EMs), each with individual processes and states.

The EMs within the experimental unit can be described as follows:

EM0: Within EM0, a logistics robot picks up incoming containers from a central transfer position and places them in a storage unit. Once the storage unit is complete, it is moved synchronously with the logistics robot to the beginning of a conveyor belt using linear slides. After reaching this position, the logistics robot picks the containers from the storage unit and places them on the moving conveyor belt at predefined intervals.

EM1: In EM1, containers are picked up from the conveyor belt, emptied, and transferred to EM0. For this purpose, a production robot picks up the containers at the end of the conveyor belt, rotates them, and empties the collected objects onto a rotary table via a ramp. Afterwards, the containers are placed vertically in a central transfer position, where the logistic robot of EM0 can pick them up.

EM2: EM2 realizes the transportation of containers through the system while simultaneously sorting the objects into the containers. After the containers have been placed on the conveyor belt in EM0, they are moved in a circle around a rotary table at a constant speed. Various photoelectric sensors record the positions of the containers on the belt. A camera system detects the objects located on the rotary table. All positions are transferred to the pick-and-place robot, which picks up the objects and places them into moving containers.

An overview of the processes carried out, along with the integrated devices and sensors used for each EM, is provided in Appendix A.

5.2. Experimental Data

An OPC UA server was integrated to receive and store the required system data. In the initial phase, the discrete data packets were recorded over several production processes and stored in a database. For the conditional connections within the graph, 17 variables were recorded. With a process duration of approximately 3 min and a sample rate of 8 ms, this resulted in 382,500 data points per process. A total of 307 processes were recorded over a 16 h period.

Realistic anomalies were created within the experimental unit to validate the described concept. The system, processes, and products were influenced in compliance with safety standards and with the assistance of a domain expert. The anomalies shown were divided into four categories and later validated and marked in the time series by the domain expert. A list and description of the resulting anomalies are presented in

Table 1. Recorded test cases.

Anomaly	EM	Count	Anomaly Category	Anomaly Description
Worn intake	EM0	3	Wear	Worn vacuum suction of product by RL
Defect sensor	EM0	3	Defect	Additional random activations
RL blocked path	EM0	7	External Influence	Pick and/or place position not reachable by RL
Worn intake	EM1	4	Wear	Worn vacuum suction of product by RP
PR blocked path	EM1	5	External Influence	Pick and/or place position not reachable by RP
Wrong product	EM2	2	Product Irregularity	Wrong product on the belt
Human intervention	EM2	2	External Influence	External trigger of the photoelectric sensor
Missing product	EM2	4	Product Irregularity	Product removed during transportation
Added product	EM2	2	Product Irregularity	Additional product in the process

. Each anomaly was at least recorded twice, resulting in 32 anomalous processes. The anomalies can be categorized as follows.

Product irregularity: This category encompasses all anomalies directly generated by or through the product. In the experimental unit, anomalies were generated by manipulating the product, leading to different sensor activation times.

External influence: Anomalies caused by external sources, such as active intervention from a person, fall under this category. Such anomalies were generated by the irregular activation of feedback sensors at varying process times and frequencies.

Defect: This category encompasses anomalies resulting from defects in system components. In the experimental unit, such anomalies were produced by manipulating a sensor, such as the vacuum sensor, leading to incorrect sensor activation.

Wear: In this category, all anomalies arising from wear and tear on system components are summarized. In the experimental unit, such anomalies were generated by actively influencing the component, such as the robot vacuum suction, which prevents the robot from effectively picking and placing products.

5.3. Experimental Integration

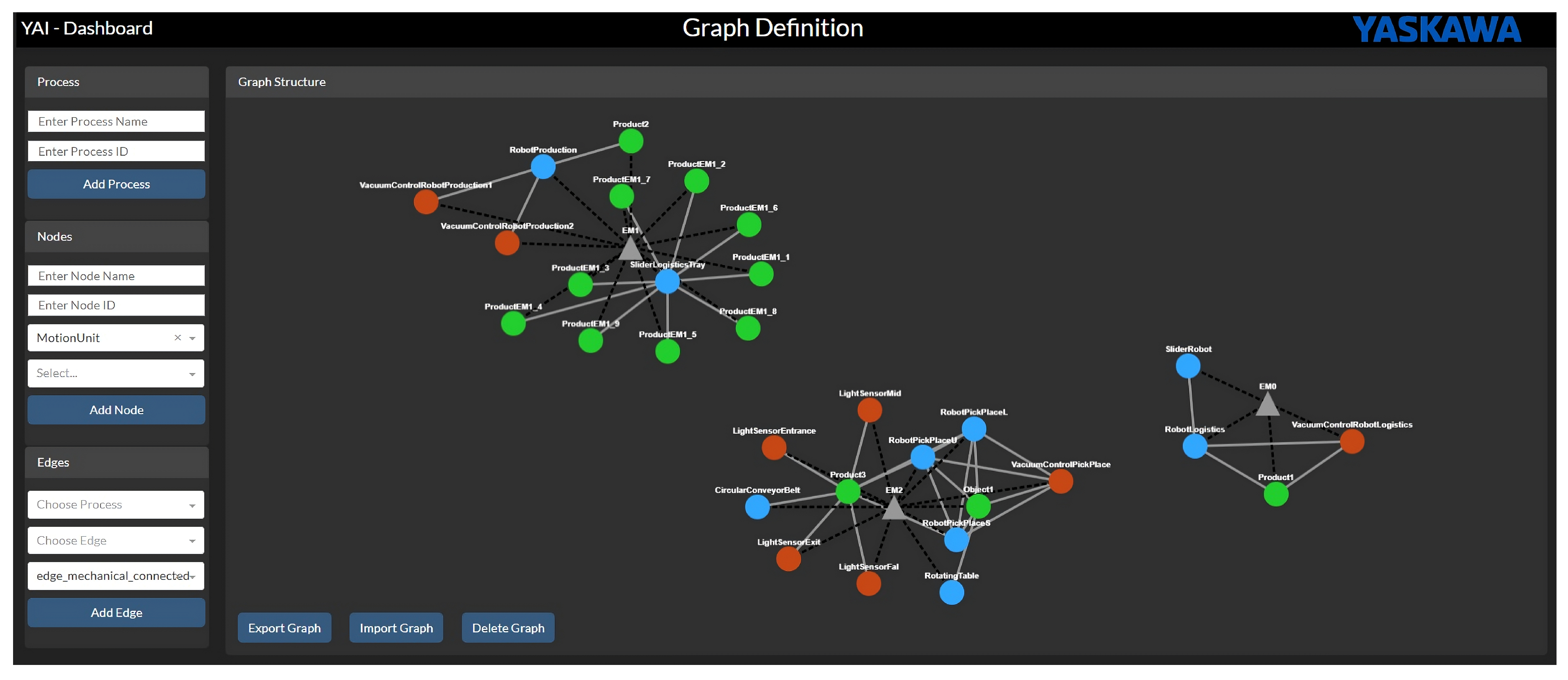
To define the static graph structure, connections, and conditions of the experimental system, available background knowledge was utilized. Since the system was programmed according to the industrial standard PackML, the entire static graph structure could be extracted from the control program. All integrated devices, including their definitions, groupings, and connections, can be found at predefined positions within the control program of the respective EM. Additionally, the definitions of the individual process states can be found within the control program.

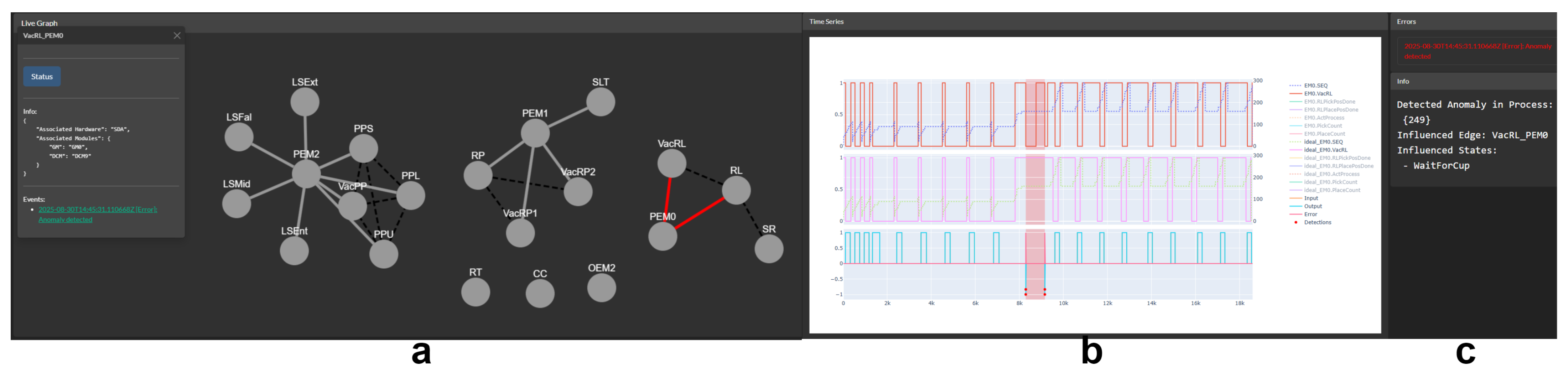
An intuitive graphical user interface (GUI) was developed to easily input all information, particularly the conditions, thereby automatically creating the condition matrix. Feedback from application engineers was considered to make the setup uncomplicated and straightforward. All graph entities and condition definitions edited in the GUI are saved to a database. As described above, the GUI is also used to visualize detections. Anomalies can be displayed in the graph structure, in conditional time series data, and as plain text relative to the overall process. A snapshot of the GUI for creating the graph is shown in Figure 9.

The integration of all functionalities and models was made based on a modular and hybrid integration concept [36] directly on an Intel NUC7i7DNB located next to the experiment unit. This demonstrates the ability to execute the proposed concept even with only limited computational resources. As programming language, Python 3.10.7 was used.

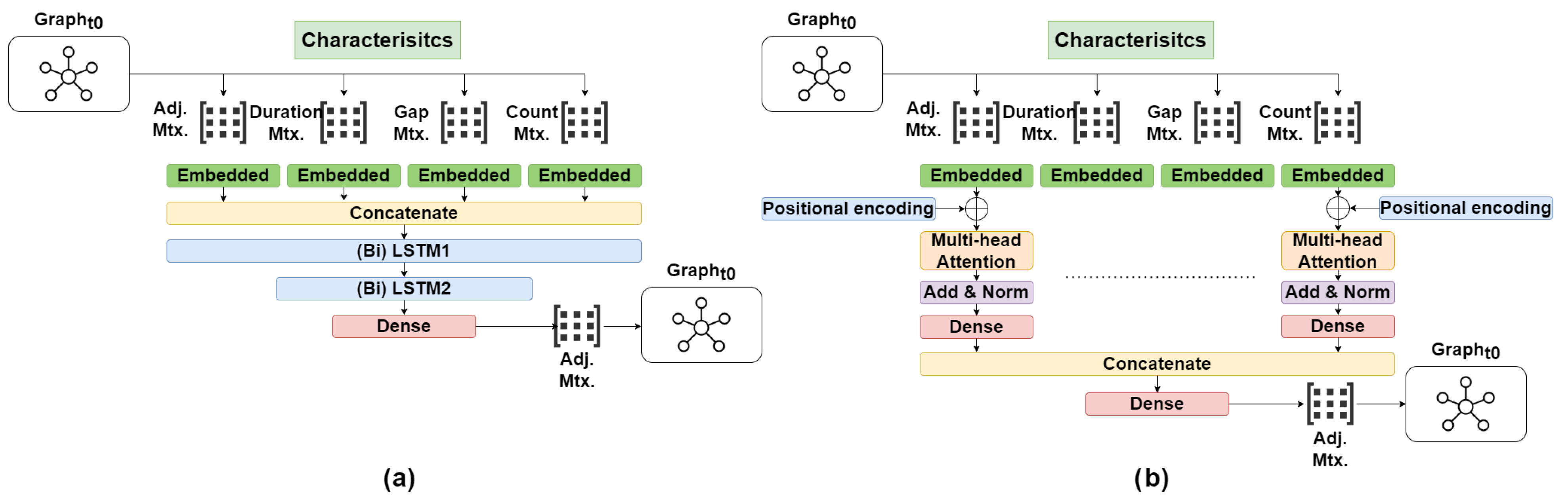
5.4. Model Development

LSTMs, bidirectional LSTMs, and transformers were selected as previously defined. To facilitate a comprehensive evaluation of the performance of the proposed concept, various test scenarios were generated to which the individual models were adapted. Each model was trained with only the adjacency matrix, the generated characteristics, and multiple time steps of the adjacency matrix, including the characteristics. The input dimensions were chosen based on the number of conditional connections, characteristics, and the number of time steps. The target of each model was set to reconstruct the actual adjacency matrix. To facilitate direct integration within industrial systems, parameters were optimized to construct the models as small as possible. Hyperparameter tuning, using the Python library Ray Tune, was conducted to identify the optimal models based on various parameters. The parameters set for the individual models are listed in

Table 2. Parameters for the model, along with their corresponding ranges for hyperparameter tuning; N—number of inputs.

Bi-/LSTM Model		Transformer
Dense Units	N,16,32,64	Dense Units	N,16,32,64
Patient	2,5,10	Patient	2,5,10
LSTM Units	16,32,64	Multi-Head Dimensions	16,32,64
		Number of Heads	1,2,4
		Number of Layers	2,4,5

. To effectively train the different models and speed up the hyperparameter tuning, a PC with an Intel (Intel, Santa Clara, Kalifornien, United States) Core i9-12900K processor and an NVIDIA GeForce RTX3080Ti GPU (NVIDIA, Santa Clara, CA, USA) was used.

5.5. Experimental Results

The recorded processes were divided into three datasets: training, validation, and testing. The individual processes could be distinguished based on the previously defined repetitive process states. For the training set, the first 20 normal processes were selected. The sample size was chosen to enable effective model training and to demonstrate that only a small number of recorded processes are needed for successful model development. The validation set included 226 normal processes used to evaluate the models’ reconstruction capabilities and identify potential false alarms. The test set contained 61 processes, including anomalous processes randomly positioned within the set, to assess the model’s ability to detect anomalies. After training the model, the threshold was automatically determined by reconstructing the training dataset and calculating the maximum absolute deviation. Given that the model was optimized to minimize the difference between the input and output, the resulting threshold values were very low. Initial test observations revealed that, due to the binary nature of the signals (0 or 1) and the sequential input of the time series data, anomalies tend to cause significant exceedances, often surpassing the threshold multiple times. Simultaneously, minor temporal variations in the input processes lead to minimal transgressions. To mitigate false alarms in the later industrial integration process, an additional scaling factor of 1.1 and an offset factor of 0.3 were systematically applied across all tests.

Thereafter, each process of the validation and test datasets was checked separately for anomalies. Successful detection was characterized by identifying an anomaly occurring within or shortly after a predetermined area. This definition can be justified by considering the inclusion of individual characteristics and their impact after the occurrence of an anomaly. For instance, an additional activation modifies the matrices for the entire subsequent process, potentially leading to further anomalies. The F1-score, precision, recall, and accuracy were selected as evaluation criteria. The detailed test results are presented in Appendix B. 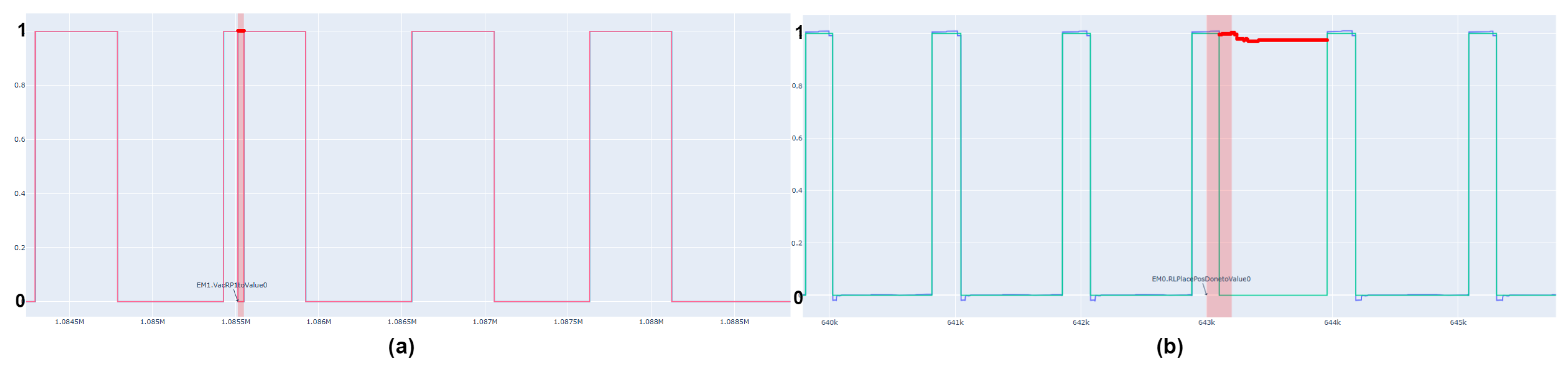Figure 10 presents some examples of the detections in time series.

As shown in the test results, models that consider the characteristics perform best across all EMs. On the other hand, detection based solely on conditional connections achieves the worst results. Additionally, the critical performance factor is not primarily the model used, but rather the characteristics and quality of the data being utilized.

This phenomenon is especially noticeable in the testing results related to EM2. The mechanical design of the EM2 leads to considerable time delays during the transportation of the containers, resulting in significant discrepancies between the processes in the recorded data. Since the concept and models are designed for repetitive processes, this leads to an inadequate detection rate.

6. Discussion

One important point to discuss is the manual work and expertise required to define the graph structure and conditions. For this purpose, several interviews were held with experts and people outside the technical field. In general, the programmer’s effort to define the graph structure and conditions is negligible, as all the necessary information is already needed to create the control program for the system. Even for domain experts, filtering and transforming the existing knowledge is simple, especially when using an industrial standard like PackML. However, for non-specialists, this can be challenging. A further goal would be automatically transforming the available knowledge into the corresponding conditions and graph structure to enhance the concept.

Another point of discussion is the use of separate EMs instead of an overall graph of the system. This strategy has several advantages. First, individual, smaller models can be generated, allowing for the direct integration of the models into the system without requiring a powerful external processing unit. Secondly, based on the processes performed, execution times and sampling rates vary in such a system. For example, the internal processing time for a transportation process is usually set significantly slower than for a pick-and-place operation of a robot to reduce the computational load on the control unit. For the integration of the concept, this can lead to a desynchronization or a reduction in the sampling time of all variables. By considering the individual EMs and processes, the models can be adjusted to their respective sampling rates, ensuring proper synchronization. Finally, the error susceptibility and maintenance of the concept can be reduced by splitting the overall process into smaller models, which also allows the other models to operate continuously in the event of an error in one model. Conversely, developing multiple models and adapting them to EMs requires greater effort and knowledge.

7. Conclusions and Future Work

Effective AD is crucial for the reliability, safety, and performance of modern CPPS. Identifying process anomalies in CPPSs based solely on available process data is often barely possible due to the limited variance and depth of the data. At the same time, ensuring transparency and interpretability of anomalies is essential for quick reactions and error prevention in such systems. Considering all these points, this paper presents a concept for an effective process AD using conditional discrete-time dynamic graphs. We first provide a concept for transforming a CPPS and its respective processes into a discrete-time dynamic graph using conditional connections. We introduce a novel technique to filter characteristics from the conditional connection and use them for training a data-based AD model, resulting in a threefold output for better transparency and interpretability. Finally, we conduct extensive tests using different models and setups with process data from an industrial production system and realistic anomalies to demonstrate the effectiveness and accuracy of the concept.

Despite the promising results of the concept, several directions for future research remain. As already mentioned, the structure and conditions must be defined manually, which can lead to increased workload for larger systems and require additional expertise. Methods that automate this procedure would provide enormous added value. Furthermore, the concept is designed and optimized for repetitive processes and sequential models. As the experimental results indicate, detection accuracy decreases with rapidly varying processes. Adapting the approach by using different model architectures, other baseline methods, or optimizing it for dynamic processes can enhance the concept and make it dynamically applicable. Until now, the concept has only been tested in one industrial production system. By integrating the concept into other systems, such as a complete production line, more tests can be conducted, and AD can be further improved.