Abstract
Accurate image segmentation is a fundamental requirement for fine-grained image analysis, providing critical support for applications such as medical diagnostics, remote sensing, and industrial fault detection. However, in complex industrial environments, conventional deep learning-based methods often struggle with noisy backgrounds, blurred boundaries, and highly imbalanced class distributions, which make fine-grained fault localization particularly challenging. To address these issues, this paper proposes a Defect-Aware Fine Segmentation Framework (DAFSF) that integrates three complementary components. First, a multi-scale hybrid encoder combines convolutional neural networks for capturing local texture details with Transformer-based modules for modeling global contextual dependencies. Second, a boundary-aware refinement module explicitly learns edge features to improve segmentation accuracy in damaged or ambiguous fault regions. Third, a defect-aware adaptive loss function jointly considers boundary weighting, hard-sample reweighting, and class balance, which enables the model to focus on challenging pixels while alleviating class imbalance. The proposed framework is evaluated on public benchmarks including Aeroscapes, Magnetic Tile Defect, and MVTec AD. The proposed DAFSF achieves mF1 scores of 85.3%, 85.9%, and 87.2%, and pixel accuracy (PA) of 91.5%, 91.8%, and 92.0% on the respective datasets. These findings highlight the effectiveness of the proposed framework for advancing fine-grained fault localization in industrial applications.
1. Introduction
Image segmentation has long been a core task in computer vision, serving as the foundation for applications in diverse fields such as medical diagnostics [1], remote sensing [2], and industrial inspection [3]. Accurate segmentation enables fine-grained image analysis, providing reliable structural information that supports downstream recognition, detection, and decision-making tasks. Nevertheless, segmentation in real-world environments remains highly challenging due to factors such as noisy backgrounds, low-resolution imagery, blurred boundaries, and imbalanced class distributions. These challenges are particularly evident in industrial scenarios, where defects are often small, irregular, and visually ambiguous, making their precise localization critical for ensuring the reliability of automated monitoring and fault diagnosis. Although the presence of fewer defective samples reflects a desirable industrial outcome, such imbalance leads to limited training diversity and model bias toward dominant ‘normal’ classes. Moreover, even within a single image, the defective regions occupy only a small fraction of pixels, posing an additional pixel-level imbalance challenge for precise segmentation.
Traditional approaches based on handcrafted features, including edge- and texture-based descriptors [4], region-growing strategies [5,6], and graph-cut algorithms [7,8], have shown limited robustness when applied to noisy and complex data. With the advent of deep learning, significant progress has been achieved in semantic segmentation, with networks such as FCN [9], U-Net [1], PSPNet [10], and DeepLab variants [11,12,13,14] demonstrating impressive performance across multiple domains. For example, traditional texture and edge based segmentation methods typically achieve less than 70% pixel accuracy on noisy industrial images, while deep convolutional models exceed 85% on the same datasets. This gap illustrates the limited robustness of handcrafted approaches under complex illumination and texture conditions. More recently, Transformer-based models have introduced powerful global context modeling through self-attention mechanisms, complementing the local feature extraction capabilities of convolutional neural networks (CNNs). Hybrid architectures that combine CNNs and Transformers, such as TEC-Net and Next-ViT, attempt to leverage the strengths of both paradigms. However, these models often suffer from high structural complexity and substantial computational costs, which hinder their scalability and deployment in resource-constrained environments. Moreover, existing solutions still struggle with fine-grained boundary delineation and class imbalance when applied to industrial fault datasets. Fine-grained boundary delineation is particularly difficult in industrial inspection due to subtle gray-level transitions between defective and normal areas and inherent annotation noise at object borders, which often cause traditional edge detectors to fail in distinguishing true defect boundaries from background texture.
In this work, we address these limitations by proposing a Defect-Aware Fine Segmentation Framework (DAFSF) designed to achieve accurate and robust fault localization in challenging industrial datasets while maintaining efficiency. The key contributions of this paper are as follows:
- We design a multi-scale hybrid encoder that integrates CNN-based local feature extraction with Transformer-based global context modeling, enabling balanced representation of fine-grained structures and long-range dependencies.
- We introduce a boundary refinement module that explicitly enhances edge representation, mitigating boundary ambiguity and improving segmentation accuracy in small or blurred defect regions.
- We propose a defect-adaptive loss function that dynamically reweights pixel contributions by considering boundary proximity, classification difficulty, and class imbalance, thereby improving robustness in noisy and imbalanced datasets.
- We conduct extensive validation on both a proprietary infrared electrolyzer dataset and public benchmarks including Aeroscapes [15], Magnetic Tile Defect [16], and MVTec AD [17], demonstrating significant improvements over state-of-the-art methods in segmentation accuracy, boundary precision, and cross-domain generalization.
2. Related Work
2.1. Hybrid Architectures for Image Segmentation
Deep convolutional networks such as FCN [3], U-Net [1], and DeepLab [13,18] have demonstrated remarkable effectiveness in semantic segmentation by hierarchically extracting local spatial features. However, their limited receptive fields restrict the ability to model global dependencies, which often leads to misclassification in complex scenes. To overcome this limitation, vision Transformers [19] and their segmentation extensions such as the Swin Transformer [20] have introduced global self-attention mechanisms. While these methods excel at capturing long-range relationships, they frequently fail to preserve subtle structural details and require high computational costs. Recent studies therefore explore hybrid models that combine CNNs and Transformers, such as TransUNet [21] and Next-ViT [22], which aim to balance local detail preservation with global context reasoning. Despite their promise, many hybrid approaches suffer from increased architectural complexity, making them difficult to optimize and deploy in real-world industrial applications. This motivates the development of more efficient hybrid encoders tailored for fine-grained segmentation tasks.
2.2. Boundary-Aware Segmentation Methods
Accurate boundary localization is a long-standing challenge in segmentation, particularly in scenarios where defect regions are small, irregular, or visually similar to the background. Early work attempted to refine boundaries using conditional random fields (CRFs) [23] or graph-based post-processing [24], but these approaches introduced additional computational overhead and were sensitive to noise. More recent studies have incorporated boundary supervision directly into neural networks, such as using edge detection branches [25], boundary attention modules [26], or contour refinement strategies [27]. These techniques improve edge precision but often require complex multi-stage training or rely on explicit edge annotations, which are not always available in industrial datasets. Consequently, designing lightweight and effective boundary-aware modules remains an active area of research for fine-grained fault segmentation.
2.3. Adaptive Loss Functions for Imbalanced Segmentation
Class imbalance and hard-sample learning are critical issues in industrial segmentation, where fault regions are often much smaller than the background. Conventional losses such as cross-entropy tend to bias predictions toward dominant classes, while Dice loss [28] and focal loss [29] have been widely adopted to alleviate imbalance by reweighting minority classes or difficult samples. More advanced formulations, including boundary-aware losses [30], Lovász-softmax [31], and adaptive reweighting strategies [32], have further improved robustness in small-object segmentation. Nevertheless, most of these approaches treat imbalance and boundary precision as separate issues, and few methods jointly optimize for both aspects. This gap underscores the need for integrated loss functions that explicitly account for spatial context, boundary relevance, and class distribution simultaneously.
2.4. Summary
In summary, existing research has made substantial progress in hybrid segmentation networks, boundary refinement strategies, and adaptive loss design. In contrast, the proposed Defect-Aware Fine Segmentation Framework (DAFSF) is not a simple incremental integration of these known modules. Conceptually, DAFSF introduces a unified design that couples three complementary principles within a single optimization objective: (1) a multi-scale hybrid encoder (MHE) that adaptively fuses CNN and Transformer features through hierarchical attention, capturing both local texture and global context while maintaining moderate computational cost; (2) a boundary-aware refinement module (BARM) that injects boundary cues back into the feature stream via a feedback path, enabling contour-consistent decoding without relying on explicit edge labels; and (3) a defect-adaptive loss (DAAL) that jointly models class imbalance, boundary uncertainty, and hard-sample reweighting through dynamic weighting of pixel importance. Methodologically, DAFSF differs from TransUNet and FAHRNet by employing an explicit boundary-feedback mechanism rather than simple multi-branch fusion, and from conventional boundary-aware or focal-based losses by unifying region- and contour-level supervision into a single differentiable objective. This design allows the network to learn fine-grained spatial distinctions and adaptively emphasize defective regions under diverse illumination, blur, and texture conditions, thereby demonstrating stronger generalization and robustness compared with prior hybrid frameworks.
3. Methodology
The proposed DAFSF shown in Figure 1 is designed to achieve accurate fault region segmentation under challenging conditions where defects are small, irregular, and embedded in noisy backgrounds. The framework integrates three core components: a multi-scale hybrid encoder that fuses local and global representations, a boundary-aware refinement module that enhances structural precision, and a defect-adaptive loss that explicitly addresses class imbalance and hard-sample learning. The following subsections provide a detailed description of each component, accompanied by mathematical formulations and theoretical insights.
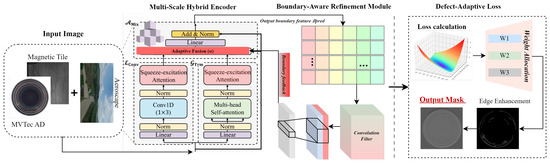
Figure 1.
The framework of Defect-Aware Fine Segmentation. Note: The small ‘+’ signs between example images indicate separate illustrative inputs from different datasets. They do not imply that images are composited or merged; each image is processed individually by the network.
3.1. Multi-Scale Hybrid Encoder
CNNs are particularly effective at capturing low-level spatial patterns, such as textures and local edges, through translation-invariant convolution operations. Formally, given an input feature map , a convolutional block extracts features as
where ∗ denotes convolution, and are the weight and bias parameters at layer l, and is a nonlinear activation function. Such local operators effectively model neighborhood information but are inherently limited by their receptive fields, which constrains the ability to capture long-range dependencies.
Transformers, by contrast, leverage self-attention to aggregate information across all spatial positions. For a given input X, we project it into queries Q, keys K, and values V:
where are learnable projection matrices. The global context is captured via multi-head self-attention:
with
where is the dimensionality of the keys. This formulation enables global feature interaction but often neglects local detail and incurs high computational costs.
To integrate local detail preservation with global context modeling, we design an MHE. At each stage, convolutional and Transformer branches process the input in parallel, and the resulting features are adaptively fused:
where is a learnable parameter that balances local and global contributions at stage l. To further enhance multi-scale representation, we apply feature pyramids, aggregating information across resolutions:
where denotes downsampling by a factor of s, and projects features to a shared space. This design yields a rich representation that retains fine structures while maintaining robustness to scale variations.
3.2. Boundary-Aware Refinement Module
Defect regions often have ambiguous or irregular boundaries, and inaccurate boundary localization can lead to significant degradation in downstream fault diagnosis. To explicitly incorporate boundary information, we propose a BARM. Let be the ground truth mask. We derive a boundary ground truth by morphological gradient:
where and denote dilation and erosion operations, respectively. The network predicts boundary maps , where is a convolutional mapping.
Boundary supervision is enforced via a cross-entropy loss:
The refined boundary features are re-injected into the segmentation pathway by concatenation:
where denotes a learnable embedding. In Equation (9), Concat denotes channel-wise concatenation along the feature dimension. If and , then . This feedback loop ensures that segmentation predictions remain structurally aligned with actual defect boundaries. Theoretically, this refinement reduces the Hausdorff distance between predicted and true contours, enhancing structural fidelity in small and ambiguous regions.
3.3. Defect-Adaptive Loss Function
Industrial defect datasets are characterized by severe class imbalance, where background pixels dominate and defect pixels are sparse. Standard cross-entropy loss tends to bias learning toward majority classes, while Dice loss and focal loss partially mitigate this by balancing class contributions or emphasizing hard examples. To unify these ideas, we propose a DAAL that simultaneously addresses class imbalance, boundary precision, and hard-sample reweighting.
For a pixel i with ground truth label and predicted probability , the DAAL is defined as
where N is the number of pixels, is a class weight inversely proportional to frequency, and controls hard-sample focusing. To increase sensitivity to boundary pixels, we introduce a boundary weight :
where is the frequency of class , if pixel i is within a predefined boundary band and 0 otherwise, and adjusts boundary emphasis. This ensures that boundary pixels receive disproportionately higher gradient contributions, leading to sharper contour predictions.
The final objective integrates segmentation and boundary supervision:
where is a balancing factor. This formulation can be interpreted as a multi-task learning objective, where segmentation and boundary tasks are optimized jointly, encouraging consistency between region-level and edge-level predictions. Parameters and were chosen via grid search on the validation set: , . Details are provided in Section 5.2. In practice, DAAL improves both Intersection-over-Union (IoU) for small defect regions and boundary IoU (BIoU), yielding more robust segmentation under noise and imbalance.
4. Experiments
4.1. Datasets and Implementation Details
To assess the performance of DAFSF, we use a self-constructed infrared electrolyzer dataset and three public benchmarks: Aeroscapes, Magnetic Tile Defect, and MVTec AD. Table 1 summarizes the main statistics of the datasets used in our experiments, the electrolyzer dataset consists of infrared images collected from industrial electrolytic cells under real production conditions, where cover cloth defects and short-circuit faults are labeled with pixel-level masks. Due to high noise and irregular defect structures, this dataset presents significant challenges for precise segmentation. The Aeroscapes dataset contains aerial imagery with pixel-level annotations across diverse categories, providing a complex outdoor environment with occlusions and scale variations. The Magnetic Tile Defect dataset includes microscopic images of magnetic tiles with various defect types such as cracks, scratches, and spots, which require fine-grained boundary localization. Finally, MVTec AD serves as a widely used industrial anomaly detection benchmark, containing both texture- and object-level defects with rich diversity across classes. Together, these datasets ensure a comprehensive evaluation across heterogeneous domains.

Table 1.
Simplified dataset statistics for DAFSF experiments.
To ensure consistency across datasets while maintaining scene diversity, all images are preprocessed and augmented according to Table 2. For Aeroscapes, the input images are rectangular; the longer side is scaled to 512 px while maintaining the aspect ratio, and the shorter side is padded to 512 px. This ensures that the network receives square inputs without distortion. Mild geometric transformations (rotation, flipping, scaling) enhance the model’s generalization capability under viewpoint or altitude variation, whereas controlled noise injection promotes robustness against sensor-level perturbations. The chosen resizing strategy with reflection padding avoids distortion and aligns with the multi-scale hybrid encoder’s ability to aggregate multi-resolution contextual features. Experiments are implemented in PyTorch 2.1.0 and conducted on NVIDIA Corporation (Santa Clara, CA, USA), A100 GPUs with 80 GB memory. The optimizer is AdamW with an initial learning rate of , a weight decay of , and a cosine annealing learning rate schedule. The batch size is set to 16, and training is conducted for 200 epochs. The balancing factor in the total loss is empirically set to 0.3, while for boundary weighting is set to 2. All hyperparameters are selected based on cross-validation on the electrolyzer dataset.

Table 2.
Image preprocessing and augmentation settings.
4.2. Evaluation Metrics and Baselines
Segmentation performance is quantitatively measured using multiple complementary metrics. The primary metric is the mean Intersection-over-Union (mIoU), defined as
where and denote the predicted and ground truth pixel sets for class c, and C is the total number of classes. To emphasize boundary accuracy, pixel accuracy (PA) and the F1-score are also reported for completeness. These metrics provide a rigorous assessment of region-level accuracy, edge precision, and overall robustness. The F1-score is computed per class as the harmonic mean of precision and recall:
The mean F1 (mF1) is the average over C classes:
We compare DAFSF with a diverse set of representative segmentation baselines, covering both CNN-based and Transformer-based architectures. Specifically, CNN-based methods include U-Net [1], PSPNet [2], and DeepLabv3+ [13]; Transformer-based models include Swin Transformer [20]; and hybrid approaches that integrate convolution and self-attention mechanisms, such as TransUNet [21] and Next-ViT [22]. In addition, we include recent advanced segmentation networks such as FA-HRNet [33], UIU-Net [34], and FreeSeg [35], as well as lightweight or retrieval-enhanced designs like Patch-netvlad [36] and BiSeNetV2 [37]. To ensure a fair comparison, all baseline models were trained or evaluated under consistent settings whenever possible. For models where official implementations and pretrained weights were publicly available, we used the official checkpoints for evaluation to maintain reproducibility. For baselines without publicly released weights, we reproduced the training following the hyperparameter settings and optimization strategies reported in the original papers, adapting input resolution and augmentation strategies to match our experimental setup.
5. Results
Table 3 summarizes the model complexity and segmentation accuracy (mIoU) of various methods across three datasets: Aeroscapes, Magnetic Tile Defect, and MVTec AD. From the table, it is clear that traditional CNN-based architectures such as U-Net and PSPNet maintain relatively low parameter counts (31 M and 46 M, respectively) and moderate computational costs (FLOPs 255 G and 280 G), yet they achieve limited segmentation performance, with mIoU values ranging from 69.4% to 73.5% across datasets. This indicates that while these models are efficient, their ability to capture the global context and subtle defect structures is insufficient, particularly under noisy or heterogeneous industrial conditions.

Table 3.
Model complexity and segmentation accuracy (mIoU%) on three datasets. Metrics include the number of parameters (Param), computational cost (FLOPs), and mIoU for each dataset.
Transformer-based methods, including Swin Transformer and TransUNet, achieve higher mIoU scores (up to 77.5%), demonstrating the advantage of global self-attention for modeling long-range dependencies. However, these gains come with substantially increased computational costs (FLOPs up to 315 G for TransUNet) and parameter counts, which may hinder deployment in resource-constrained industrial settings. Hybrid architectures such as Next-ViT, FA-HRNet, and UIU-Net further improve mIoU, benefiting from the combination of convolutional local feature extraction and Transformer-based global reasoning. Nevertheless, lighter networks such as Patch-netvlad and BiSeNetV2, despite very low FLOPs in some cases, fail to achieve competitive mIoU, reflecting a trade-off between efficiency and fine-grained segmentation capability.
Our proposed DAFSF model strikes a favorable balance between accuracy and efficiency. With a moderate parameter count of 36.2 M and FLOPs of 276 G, DAFSF attains mIoU values of 80.5%, 81.4%, and 82.6% on Aeroscapes, Magnetic Tile Defect, and MVTec AD, respectively, outperforming all baselines by a significant margin. The consistent cross-dataset improvements indicate that the multi-scale hybrid encoder effectively captures both local details and global context, while the boundary refinement and defect-adaptive loss mechanisms enhance segmentation of fine-grained defect structures. In addition, the qualitative results illustrated in Figure 2 and Figure 3 further demonstrate the capability of DAFSF to accurately delineate fine-grained defect regions and maintain consistent generalization across different datasets. These results suggest that DAFSF not only delivers high segmentation precision but also generalizes robustly across heterogeneous domains, making it highly suitable for practical industrial applications where both accuracy and computational efficiency are critical.

Figure 2.
Magnetic Tile dataset: original image and DAFSF segmentation result.

Figure 3.
Aeroscapes and MVTec AD datasets: segmentation results using DAFSF. Note: To feed non-square images (e.g., Aeroscapes) into our network while preserving the aspect ratio, we scale the longer side to 512 pixels and then pad the shorter side with zeros to obtain a 512 × 512 input.
Table 4 presents inference latency, mean F1-score (mF1), and pixel accuracy (PA) for all compared methods across three datasets. Lightweight CNN models such as U-Net and PSPNet exhibit the lowest latency (22–36 ms), which is beneficial for real-time applications, but their segmentation quality is relatively modest, with mF1 values ranging from 77.8% to 81.0% and PA between 85.7% and 87.5%. This a reflects limited capacity to capture fine-grained defect structures and the global context, especially in heterogeneous or high-noise industrial environments.

Table 4.
Inference latency and performance metrics (Latency(ms), mF1%, PA%) on three datasets.
Transformer-based architectures, including Swin Transformer and TransUNet, improve mF1 (up to 83.7%) and PA (up to 90.2%) by modeling long-range dependencies. However, this performance comes at the cost of substantially higher latency (68–76 ms), which may constrain their deployment in scenarios requiring rapid inspection or real-time monitoring. Hybrid models such as Next-ViT, FA-HRNet, and UIU-Net strike a better balance, achieving both moderate latency and improved segmentation metrics, demonstrating the benefit of combining convolutional local feature extraction with global attention.
Lightweight hybrid networks such as Patch-netvlad and BiSeNetV2 achieve very low latency (12–19 ms), yet their mF1 and PA remain lower than those of larger hybrid or Transformer models, revealing the trade-off between efficiency and robust defect modeling. FreeSeg also exhibits reduced latency (28–30 ms) with moderate performance, further illustrating this compromise.
The proposed DAFSF model demonstrates an effective balance between inference efficiency and segmentation quality. With latency around 25–26 ms comparable to lightweight CNNs, DAFSF attains the highest mF1 (85.3–87.2%) and PA (91.5–92.0%) across all datasets. These results indicate in Figure 4 that the multi-scale hybrid encoder, boundary refinement module, and defect-adaptive loss not only enhance fine-grained defect recognition but also maintain computational efficiency suitable for real-time industrial applications. Importantly, the consistent performance gains across heterogeneous datasets reflect strong cross-domain generalization, confirming DAFSF’s robustness to varying defect types, noise levels, and imaging conditions.
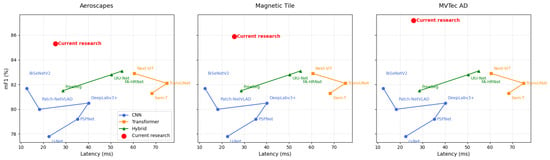
Figure 4.
Comparative Accuracy of Various Methods Across Latency Levels.
5.1. Ablation Studies
Table 5 presents the ablation results of different components in DAFSF on the infrared electrolyzer dataset. The baseline model, implemented with a standard U-Net backbone, achieves an mIoU of 72.5% and a BIoU of 64.2%, which reflects limited capability in handling boundary ambiguity and small-scale defects. Incorporating the multi-scale hybrid encoder (MHE) significantly improves performance, raising mIoU to 77.3% and BIoU to 68.9%. This demonstrates the effectiveness of combining convolutional local feature extraction with Transformer-based global context modeling, which enhances representation quality under noisy industrial conditions.

Table 5.
Ablation study of DAFSF components on the infrared electrolyzer dataset. Components include multi-scale hybrid encoder (MHE), boundary-aware refinement module (BARM), and defect-adaptive loss (DAAL). Metrics are reported as mIoU (%), Boundary IoU (BIoU, %), and F1-score (%).
Adding the boundary-aware refinement module (BARM) on top of MHE further increases BIoU from 68.9% to 72.4%, while also improving the F1-score by 2.2%. These gains highlight the importance of explicit boundary supervision in capturing fine-grained defect contours and reducing misclassification along blurred edges. Alternatively, combining MHE with the defect-adaptive loss (DAAL) achieves a similar boost in performance, with mIoU reaching 80.1% and the F1-score improving to 84.0%. This improvement is attributed to the dynamic reweighting of boundary and minority-class pixels, which alleviates the class imbalance problem and emphasizes difficult samples during training. The full DAFSF model, which integrates MHE, BARM, and DAAL, achieves the highest performance across all metrics, with an mIoU of 83.5%, BIoU of 76.2%, and F1-score of 87.1%. Compared to the baseline, this corresponds to gains of +11.0% in mIoU, +12.0% in BIoU, and +9.0% in the F1-score, demonstrating the complementary effects of the three modules. These results confirm that each component contributes uniquely to fine-grained segmentation, and their joint integration yields superior robustness and precision in industrial fault localization tasks.
To further interpret the effectiveness of the proposed multi-scale hybrid encoder (MHE), we visualize the intermediate feature responses from different layers of the backbone, as shown in Figure 5. The results reveal a clear progression of attention from shallow to deep layers. Specifically, the features from layer2 mainly emphasize low-level textures and local contrast, which are useful for capturing surface irregularities. Moving to layer3, the activations begin to highlight more coherent defect regions while suppressing irrelevant background noise, indicating the emergence of mid-level semantic understanding. Finally, layer4 exhibits highly focused responses along defect areas and their structural boundaries, confirming that deeper layers integrate both local details and long-range contextual cues. This progressive refinement validates the design of the hybrid encoder, which combines convolutional local descriptors with Transformer-based global reasoning to achieve robust and fine-grained defect segmentation.

Figure 5.
Feature visualizations of different layers. From left to right: original image, layer2, layer3, and layer4 heatmaps. The deeper layers progressively focus on defect regions and their boundaries.
To evaluate the robustness of DAFSF under challenging real-world conditions, we conducted experiments with augmented images simulating variations in illumination, motion blur, and sensor noise. The augmentations are consistent with Table 2, with additional condition-specific perturbations applied:
- Illumination: Overexposure and underexposure to simulate varying lighting conditions.
- Motion Blur: Gaussian blur with kernel size 3–7 to mimic fast camera motion.
- Sensor Noise: Gaussian noise with standard deviation –0.05 to represent real sensor perturbations.
The results in Table 6 demonstrate that DAFSF is robust under diverse real-world conditions. Under illumination variations, although minor degradation occurs in shadowed or overexposed regions, the model is able to maintain accurate object boundaries across all datasets. Motion blur slightly smooths edges, yet small and medium-sized objects are still correctly segmented, which can be attributed to the multi-scale hybrid encoder’s ability to aggregate contextual information effectively. When sensor noise is introduced, boundary precision is slightly reduced under higher noise levels; however, the overall segmentation structure and defect localization remain largely unaffected. These observations indicate that DAFSF consistently preserves segmentation quality even under challenging conditions such as varying lighting, motion blur, and sensor perturbations, complementing the quantitative results reported in Table 3 and demonstrating its practical applicability in industrial and aerial scenarios.

Table 6.
DAFSF qualitative segmentation performance under different realistic conditions. Metrics are mean Intersection-over-Union (mIoU %) evaluated on representative samples.
5.2. Parameter Sensitivity Analysis
The experimental results provide comprehensive evidence of the effectiveness and robustness of the proposed DAFSF framework. As shown in Figure 6, DAFSF consistently outperforms all baseline models across three representative datasets, including Aeroscapes, Magnetic Tile, and MVTec AD, in terms of mIoU. This indicates that the framework not only achieves higher segmentation accuracy but also generalizes well across diverse domains characterized by small, irregular, and noisy defect patterns. Furthermore, the parameter sensitivity analysis in Figure 7 highlights the influence of the boundary weighting factor and the hard-sample focusing parameter in the defect-adaptive loss function. Specifically, the model performance improves as increases up to an optimal point, beyond which the gain diminishes, suggesting that moderate boundary emphasis is critical for capturing structural details without introducing noise. Similarly, the variation of demonstrates that carefully calibrated hard-sample weighting enhances the model’s ability to learn from challenging regions, whereas excessive focusing may lead to instability and performance degradation. The presence of optimal parameter points, marked by red dots, further confirms the balanced trade-off between boundary precision and sample difficulty. Overall, these results not only validate the superiority of DAFSF over existing approaches but also demonstrate its stability and adaptability under different parameter settings, reinforcing its practical applicability to real-world fault segmentation scenarios.
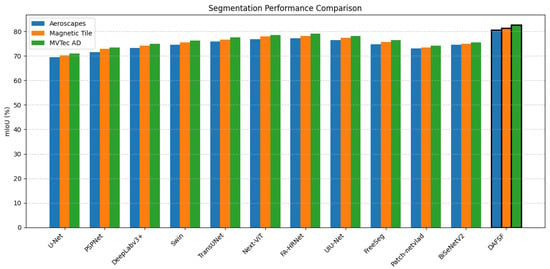
Figure 6.
Cross-dataset performance comparison: mIoU of different baseline models and DAFSF on Aeroscapes, Magnetic Tile, and MVTec AD datasets.
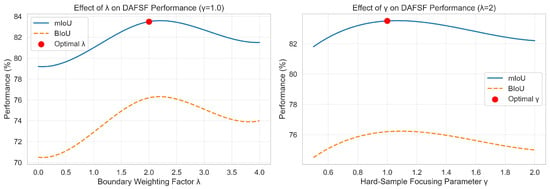
Figure 7.
Effect of boundary weighting factor and hard-sample focusing parameter on model performance (mIoU and BIoU). Red dots indicate the optimal parameter settings (, ).
Table 7 summarizes the parameter sensitivity analysis of the proposed DAFSF on the infrared electrolyzer dataset. We first vary the boundary weighting factor while fixing . Results show that increasing from 0 to 2 progressively improves both mIoU and BIoU, with the best performance obtained at (mIoU = 83.5%, BIoU = 76.2%). This indicates that moderate boundary emphasis helps the model focus on fine-grained defect contours, thereby improving structural fidelity. However, further increasing beyond 2 leads to slight performance degradation, suggesting that overemphasizing boundary pixels may destabilize region-level predictions by underweighting interior pixels. Next, we vary the focusing parameter while fixing . The results reveal that setting achieves the best balance between hard-sample emphasis and overall stability. Lower values (e.g., ) provide weaker discrimination, resulting in reduced accuracy, whereas higher values (e.g., or ) overly emphasize difficult samples, leading to marginal drops in performance. These findings confirm that the proposed DAAL is robust to parameter variation within a broad range, and that its optimal configuration corresponds to and .

Table 7.
Parameter sensitivity analysis of DAFSF on the infrared electrolyzer dataset. We vary the boundary weighting factor and hard-sample focusing parameter in DAAL.
5.3. Training Cost and Resource Consumption
DAFSF contains 36.2M parameters and requires 276G FLOPs per forward pass, representing a moderate model size compared to large Transformer-based baselines (e.g., TransUNet and Next-ViT). On the A100 GPU with a batch size of 16, each epoch requires approximately 4.5 min of wall-clock time for DAFSF, while larger Transformer-based models require 6–8 min per epoch. This demonstrates that DAFSF achieves competitive segmentation accuracy while maintaining moderate computational demand. DAFSF converges faster than heavier baselines, reaching stable validation mIoU within roughly 120–140 epochs, whereas larger models require up to 180–200 epochs to achieve comparable performance. The faster convergence reduces the total training time, facilitating model tuning and iteration. The moderate parameter size and FLOPs of DAFSF allow training on a single A100 GPU with a batch size of 16, avoiding the need for multi-GPU setups or gradient accumulation. Additionally, lower inference FLOPs result in faster per-image processing speed, which is advantageous for real-time deployment or resource-constrained environments. Overall, the proposed DAFSF model achieves a favorable balance between segmentation accuracy, computational cost, and training efficiency, highlighting its practical advantage for industrial and aerial datasets.
5.4. Applicability to Medical Image Segmentation
Although the primary focus of this work is on industrial and aerial datasets, the proposed DAFSF framework is naturally extendable to medical image segmentation tasks that involve fine-grained defects or subtle structural variations. For instance, in ultrasound imaging, speckle noise and low contrast can obscure small lesions, making boundary delineation challenging; in PET or low-resolution MRI scans, the inherent resolution limitations affect functional–anatomical image fusion, complicating reliable segmentation. These challenges are analogous to industrial defects, where small or low-contrast anomalies must be localized accurately despite background clutter or sensor noise. The multi-scale hybrid encoder and boundary-aware supervision in DAFSF allow effective aggregation of local textural cues and global contextual information, which can improve the detection of micro-structures in medical images. Furthermore, medical imaging datasets often suffer from biased annotations or limited atlas coverage, analogous to missing or corrupted samples in industrial settings. By leveraging the adaptive feature fusion and boundary weighting mechanisms of DAFSF, such biases can be mitigated, improving robustness and reliability in segmentation tasks. Previous studies have highlighted the challenges of accurate fine-structure segmentation in medical applications, and the principles demonstrated in DAFSF can be adapted to these contexts, potentially supporting improved diagnosis or treatment planning without necessitating extensive retraining on each new dataset.
6. Limitations and Future Work
Despite the strong performance of DAFSF across multiple datasets and challenging conditions, several limitations remain that warrant further investigation. First, the use of hybrid multi-scale encoders and explicit boundary supervision contributes to increased computational complexity and memory consumption during training, which may limit scalability to extremely large datasets or prolonged training regimes. To address this, future work will investigate model compression strategies such as pruning, knowledge distillation, and low-rank factorization, aiming to reduce both training and inference costs while preserving segmentation accuracy. Second, DAFSF relies on high-quality pixel-wise annotations, particularly for boundary regions, which are labor-intensive and time-consuming to produce. Exploring weakly supervised or semi-supervised learning paradigms, potentially leveraging image-level labels, scribbles, or synthetic data, could substantially reduce annotation dependency and facilitate broader deployment. Third, although DAFSF demonstrates robustness under various illumination, motion blur, and noise conditions, performance may still degrade when faced with domain shifts such as previously unseen sensors, lighting conditions, or environmental contexts. Incorporating domain adaptation or domain generalization techniques will be essential to maintain consistent accuracy in diverse real-world scenarios. Finally, while the current implementation achieves competitive inference speed on high-end GPUs, deploying DAFSF on edge devices or embedded hardware for real-time applications remains challenging. Future work will focus on lightweight model design, hardware-aware optimization, and efficient inference strategies to enable practical edge deployment without compromising segmentation quality. Collectively, addressing these limitations will further enhance the applicability and efficiency of DAFSF in industrial, aerial, and resource-constrained environments.
7. Conclusions
In this work, we proposed the Defect-Aware Fine Segmentation Framework (DAFSF) to address the challenges of industrial defect segmentation, where defects are small, irregular, and embedded in noisy backgrounds. The framework integrates a multi-scale hybrid encoder for capturing both local and global contextual features, a boundary-aware refinement module for enhancing structural fidelity, and a defect-adaptive loss function to mitigate class imbalance and emphasize hard-to-segment regions. Extensive experiments on both proprietary and public datasets, including infrared electrolyzer images, Aeroscapes, Magnetic Tile Defect, and MVTec AD, demonstrate that DAFSF consistently outperforms state-of-the-art and hybrid architectures in terms of mIoU, mF1, and pixel accuracy, while maintaining competitive inference latency suitable for real-time industrial deployment. The ablation studies further confirm the effectiveness of each individual component, highlighting the importance of multi-scale feature fusion, boundary supervision, and adaptive loss weighting. Overall, DAFSF provides a robust, efficient, and generalizable solution for precise defect segmentation across heterogeneous domains, offering strong potential for practical applications in industrial inspection and quality control.
Author Contributions
Conceptualization, X.L., J.Z. and Z.Z.; methodology, X.L. and J.Z.; software, X.L. and J.Z.; validation, J.Z.; formal analysis, Z.Z.; investigation, Z.Z.; resources, J.Z.; data curation, X.L.; writing—original draft preparation, X.L.; writing—review and editing, X.L. and J.H.; visualization, J.H.; supervision, J.H.; project administration, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 92167105) and in part by the Project of State Key Laboratory of High Performance Complex Manufacturing, Central South University under Grant ZZYJKT2022-14.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study uses publicly available datasets. Specifically, the experiments were conducted on Aeroscapes [15], Magnetic Tile Defect [16], and MVTec AD [17] Datasets. All datasets can be accessed through their official websites or repositories as cited in the references.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| DAFSF | Defect-Aware Fine Segmentation Framework |
| MHE | Multi-scale Hybrid Encoder |
| BARM | Boundary-Aware Refinement Module |
| DAAL | Defect-Adaptive Loss |
| mIoU | mean Intersection-over-Union |
| mF1 | mean F1-score (average per-class F1) |
| PA | Pixel Accuracy |
| BIoU | Boundary IoU |
| MHSA | Multi-Head Self-Attention |
| CNN | Convolutional Neural Network |
| FLOPs | Floating Point Operations |
References
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Yu, H.; Jiang, H.; Liu, Z.; Zhou, S.; Yin, X. Edtrs: A superpixel generation method for sar images segmentation based on edge detection and texture region selection. Remote Sens. 2022, 14, 5589. [Google Scholar] [CrossRef]
- Gould, S.; Fulton, R.; Koller, D. Decomposing a scene into geometric and semantically consistent regions. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–8. [Google Scholar]
- Li, Y.; Li, Z.; Guo, Z.; Siddique, A.; Liu, Y.; Yu, K. Infrared small target detection based on adaptive region growing algorithm with iterative threshold analysis. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Jain, U.; Mirzaei, A.; Gilitschenski, I. Gaussiancut: Interactive segmentation via graph cut for 3d gaussian splatting. Adv. Neural Inf. Process. Syst. 2024, 37, 89184–89212. [Google Scholar]
- Masood, S.; Ali, S.G.; Wang, X.; Masood, A.; Li, P.; Li, H.; Jung, Y.; Sheng, B.; Kim, J. Deep choroid layer segmentation using hybrid features extraction from OCT images. Vis. Comput. 2024, 40, 2775–2792. [Google Scholar] [CrossRef]
- Tian, J.; Wang, C.; Cao, J.; Wang, X. Fully convolutional network-based fast UAV detection in pulse Doppler radar. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 5103112. [Google Scholar] [CrossRef]
- Fan, K.J.; Liu, B.Y.; Su, W.H.; Peng, Y. Semi-supervised deep learning framework based on modified pyramid scene parsing network for multi-label fine-grained classification and diagnosis of apple leaf diseases. Eng. Appl. Artif. Intell. 2025, 151, 110743. [Google Scholar] [CrossRef]
- Guo, Z.; Bian, L.; Wei, H.; Li, J.; Ni, H.; Huang, X. DSNet: A novel way to use atrous convolutions in semantic segmentation. IEEE Trans. Circuits Syst. Video Technol. 2025, 35, 3679–3692. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Wang, Y.; Yang, L.; Liu, X.; Yan, P. An improved semantic segmentation algorithm for high-resolution remote sensing images based on DeepLabv3+. Sci. Rep. 2024, 14, 9716. [Google Scholar] [CrossRef]
- Nigam, I.; Huang, C.; Ramanan, D. Ensemble knowledge transfer for semantic segmentation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1499–1508. [Google Scholar]
- Huang, Y.; Qiu, C.; Yuan, K. Surface defect saliency of magnetic tile. Vis. Comput. 2020, 36, 85–96. [Google Scholar] [CrossRef]
- Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD–A comprehensive real-world dataset for unsupervised anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9592–9600. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar] [CrossRef]
- Li, J.; Xia, X.; Li, W.; Li, H.; Wang, X.; Xiao, X.; Wang, R.; Zheng, M.; Pan, X. Next-vit: Next generation vision transformer for efficient deployment in realistic industrial scenarios. arXiv 2022, arXiv:2207.05501. [Google Scholar]
- Krähenbühl, P.; Koltun, V. Efficient inference in fully connected crfs with gaussian edge potentials. Adv. Neural Inf. Process. Syst. 2011, 24, 105–117. [Google Scholar]
- Bertasius, G.; Shi, J.; Torresani, L. Semantic segmentation with boundary neural fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3602–3610. [Google Scholar]
- Takikawa, T.; Acuna, D.; Jampani, V.; Fidler, S. Gated-scnn: Gated shape cnns for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5229–5238. [Google Scholar]
- Qin, X.; Fan, D.P.; Huang, C.; Diagne, C.; Zhang, Z.; Sant’Anna, A.C.; Suarez, A.; Jagersand, M.; Shao, L. Boundary-aware segmentation network for mobile and web applications. arXiv 2021, arXiv:2101.04704. [Google Scholar] [CrossRef]
- Cheng, B.; Schwing, A.; Kirillov, A. Per-pixel classification is not all you need for semantic segmentation. Adv. Neural Inf. Process. Syst. 2021, 34, 17864–17875. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 565–571. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Kervadec, H.; Bouchtiba, J.; Desrosiers, C.; Granger, E.; Dolz, J.; Ayed, I.B. Boundary loss for highly unbalanced segmentation. In Proceedings of the International Conference on Medical Imaging with Deep Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 285–296. [Google Scholar]
- Berman, M.; Triki, A.R.; Blaschko, M.B. The lovász-softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4413–4421. [Google Scholar]
- Roy, D.; Pramanik, R.; Sarkar, R. Margin-aware adaptive-weighted-loss for deep learning based imbalanced data classification. IEEE Trans. Artif. Intell. 2023, 5, 776–785. [Google Scholar] [CrossRef]
- He, B.; Wu, D.; Wang, L.; Xu, S. FA-HRNet: A New Fusion Attention Approach for Vegetation Semantic Segmentation and Analysis. Remote Sens. 2024, 16, 4194. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. UIU-Net: U-Net in U-Net for Infrared Small Object Detection. IEEE Trans. Image Process. 2023, 32, 364–376. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Wu, J.; Yan, P.; Li, M.; Yuxi, R.; Xiao, X.; Wang, Y.; Wang, R.; Wen, S.; Pan, X.; et al. FreeSeg: Unified, Universal and Open-Vocabulary Image Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 19446–19455. [Google Scholar]
- Hausler, S.; Garg, S.; Xu, M.; Milford, M.; Fischer, T. Patch-NetVLAD: Multi-Scale Fusion of Locally-Global Descriptors for Place Recognition. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14136–14147. [Google Scholar] [CrossRef]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. BiSeNet V2: Bilateral Network with Guided Aggregation for Real-time Semantic Segmentation. arXiv 2020, arXiv:2004.02147. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).