Hydrodynamics of Toroidal Vortices in Torque-Flow Pumps

Abstract

This study investigates the role of toroidal vortex formation in torque-flow pumps and its influence on pump performance. A mathematical model of viscous fluid motion in toroidal coordinates was developed to describe the two-stage energy transfer mechanism, in which the impeller drives the toroidal vortex and the vortex subsequently imparts momentum to the main throughflow. The model identifies vortex deformation as a primary source of hydraulic losses. The theoretical framework was validated by computational fluid dynamics (CFD) simulations of a torque-flow pump. Analysis of the axial, circumferential, and vertical velocity components revealed a closed three-dimensional toroidal circulation loop within the free chamber, confirming the predictions of the mathematical model. A parametric study was conducted to assess the influence of impeller extension into the free chamber (Δb₂) on pump performance. Three characteristic regimes were identified. At Δb₂ ≈ 6 mm, the shaft power decreased to 120.3 kW (an 8.1% decrease compared to the baseline), with efficiency improving to 39.2%. At Δb₂ ≈ 10 mm, the pump achieved its best balance of parameters: efficiency increased from 34.0% to 42.8% (+8.7 percentage points), while head rose from 32.8 m to 38.5 m (+17.4%), with moderate power demand (122.3 kW). At Δb₂ ≈ 70 mm, the head reached 45.6 m (+39%), but power consumption rose to 146.9 kW (+12%), and the design shifted toward centrifugal-type operation, reducing reliability for abrasive fluids. Overall, the results provide both a validated mathematical description of toroidal vortex dynamics and practical guidelines for optimizing torque-flow pump design, with Δb₂ ≈ 10 mm identified as the most rational configuration.

1. Introduction

Up-to-date trends in designing modern energy-efficient technological equipment [1] are based on a comprehensive application of analytical and numerical solutions.

Nevertheless, there is still no exact mathematical description of the fluid flow in the flow part of torque-flow pumps. This is due to the peculiarities of the work process, which combines vortex and blade processes. Also, the main part of the flow does not interact directly with the impeller blades. Instead, the energy transfer takes place with the participation of a toroidal vortex, which acts as a “liquid blade”. Therefore, further investigation of the flow structure in a torque-flow pump, including the toroidal vortex, is crucial for enhancing energy efficiency and operational longevity.

The following state of the art on vortex formation in pumps highlights the significance of the stated problem. Particularly, Luo et al. [2] studied the unsteady flow in a centrifugal pump. As a result, the formation of the separation vortex and its characteristics at the tongue of the pump were evaluated numerically. Xin et al. [3] studied the effect of tip clearance flow on vortex formation in a high-speed centrifugal pump. The evolution of vortex structures was studied numerically using the relative vorticity transport equation and the relative vortex stretching. The results opened up new ways for improving the energy efficiency and operational stability of high-speed centrifugal pumps.

Zhou et al. [4] employed a numerical simulation approach to investigate the stall vortex structure and its kinematic characteristics in a multistage pump at various flow rates. The natural flow experiment and vibration signal decomposition enabled the detection of natural flow conditions, categorized into different flow modes (i.e., impeller stuck and passive rotation). Sun et al. [5] studied the effect of the shear-thinning property on vortex evolution and pressure fluctuation in an axial flow pump. As a result, the variation in viscosity of the guide vane was detected, and the interaction between vortices and the main stream, leading to higher pressure fluctuations, was analyzed.

Ji et al. [6] investigated vortex dynamics in the stall state of a mixed-flow pump. As a result, the effect of blade gap size was studied using the vortex dynamics diagnosis (VDD) approach. Zhao et al. [7] realized numerical approaches for vortex identification in a mixed-flow pump under low-flow conditions. As a result, the vane oblique vortex belt, tip vortex, tip separation vortex, passage vortex, and trailing edge separation vortex were detected as typical vortex structures in the impeller passage.

Tan et al. [8] analyzed the flow structure in a vortex pump under various design conditions and flow rates. As a result, it was found that the vortex structure in the non-blade cavity can be regarded as a Rankine-like vortex. Also, Tan et al. [9] studied the impact of operating conditions on a helico-axial pump’s vortex structure. As a result, it was found that the flow rate has a significant effect on the generation of vortex structures on the suction side and trailing edge of the blade.

Moreover, Song et al. [10] studied the formation and dynamic characteristics of the vortex in a pump. After the comprehensive application of experimental research and computational fluid dynamics (CFD) modeling, the dynamic characteristics of the vortex were analyzed. As a result, it was proven that the most significant velocity gradient occurs in the vortex core. Zhang et al. [11] studied the secondary vortex in an axial pump. The turbulent vortex flows were investigated numerically based on the Zwart–Gerber–Belamri cavitation model and the shear stress transport (SST) turbulence model. As a result, it was shown that the shear vortices are distributed gradually in the low-velocity area.

Xi and Lu [12] investigated the vortex formation mechanism in a side-pump system. Asymmetric adherent vortex in the side-pump sump was modeled using a combination of the simplified Navier–Stokes equations and SST and k-ε turbulence models. As a result, it was demonstrated that asymmetric friction affects the uneven distribution of inflow velocities. Moreover, the transverse velocity generates the asymmetric inspiratory vortex. Guo et al. [13] studied the unsteady vortex formation in a pump. It was found that the vertical pressure gradient has a negative impact on vortex formation. As a result, the research opened a new perspective on developing vortex formation mechanisms.

Yamade et al. [14] studied the origin, formation, and dynamics of vortices in a pump. Using large Eddy simulation (LES), various computational models, and different wall boundary conditions, the stretch of a viscous core for a submerged vortex was observed for swirl numbers ranging from 0.12 to 16.3. Oosterhuis et al. [15] proposed a 2D CFD model to evaluate the impact of the oscillatory flow on a cylindrical vortex in jet pumps with different geometries. As a result, various flow modes were detected, affecting the energy efficiency of the considered pumps.

After analyzing the research works mentioned above, the following research tasks were formulated:

–

To develop a mathematical model of the motion of viscous fluid in the toroidal vortex of a torque-flow pump to better understand the energy transfer process in the flow section.

–

Based on the developed mathematical model, the key parameter of energy efficiency of the torque-flow pump is increased by improving the energy transfer process in the blade and vortex working processes.

–

To increase the energy performance indicators (head) based on a deeper understanding of the energy transfer process in the torque flow pump.

Overall, the article aims to enhance the energy efficiency of torque-flow pumps by investigating the flow structure, with a primary focus on the toroidal vortex. This research aims to improve the performance and durability of pump equipment, ultimately leading to more sustainable and efficient pumping systems.

2. Materials and Methods

2.1. Kinematics of the Toroidal Vortex in a Torque Flow Pump

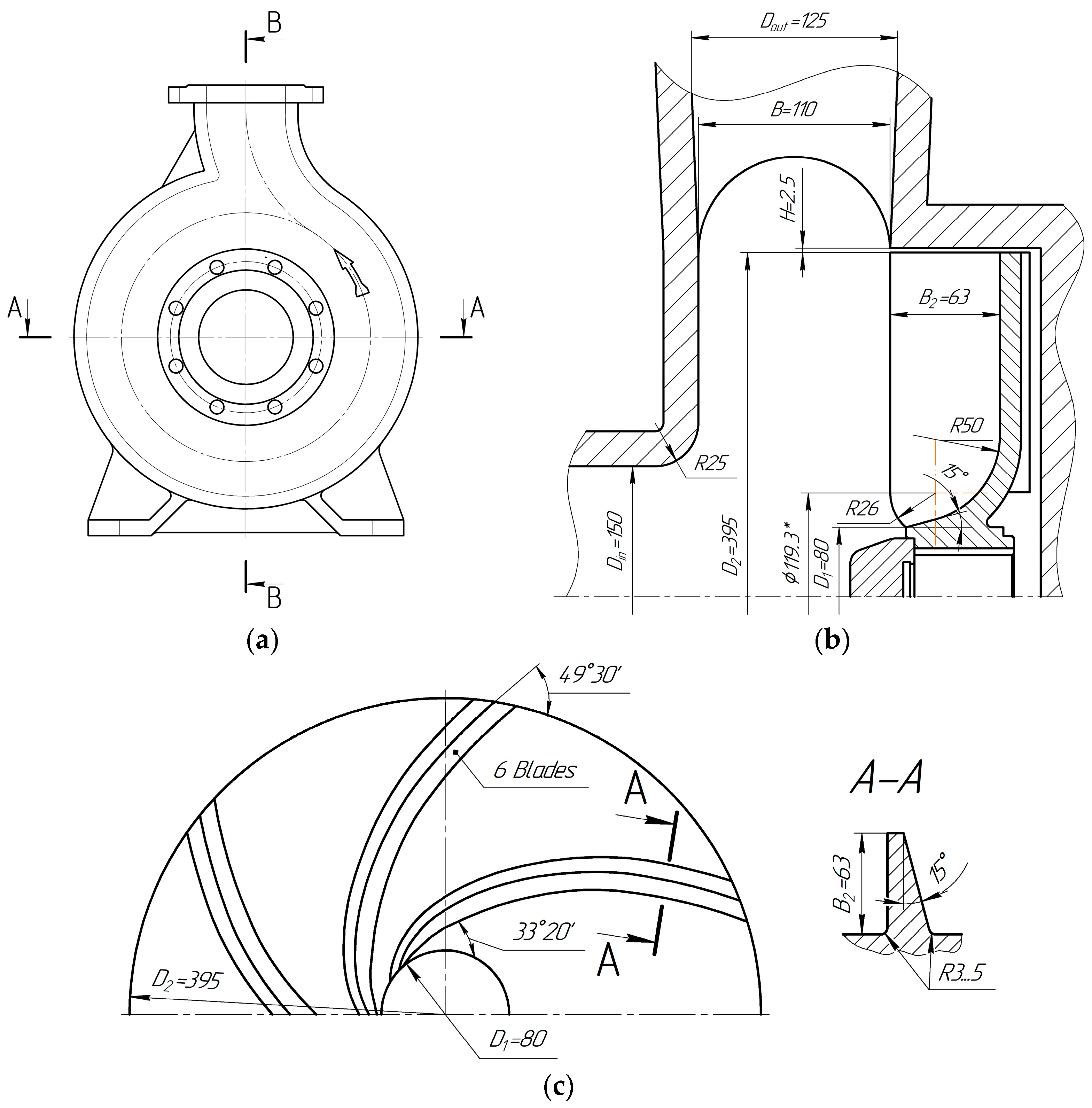
The “Turo” type torque flow pump of the basic design is characterized by the impeller’s location in the housing’s cylindrical bore. The movement of a fluid flow in a toroidal vortex is considered at the most characteristic section.

The research was conducted for a torque flow pump, SVN 500/32, with the following parameters: estimated flow rate at optimal mode—500 m³/h; estimated pressure head—32 m; and rotation frequency of the shaft—1500 rpm.

The design scheme of the torque flow pump is presented in Figure 1, and the main geometric parameters of the initial pump design are summarized in

Table 1. Geometric parameters of the flow part of the torque flow pump.

Parameter	Unit	Value
Impeller, Figure 1c
The inner diameter of the impeller	D1, m	0.080
The inlet angle	deg	33°20'
The outer diameter of the impeller	D2, m	0.395
The outlet angle	deg	49°30'
Blades, Figure 1c
The number of blades	z	6
The blade width	B2, m	0.063
The blade angle of inclination	deg	15°
The fillets radius	R, m	3–5
Free chamber, Figure 1b
The chamber width	B, m	0.110
The inlet diameter	Din, m	0.150
The outlet diameter	Dout, m	0.125
The radial gap	H, m	0.0025

.

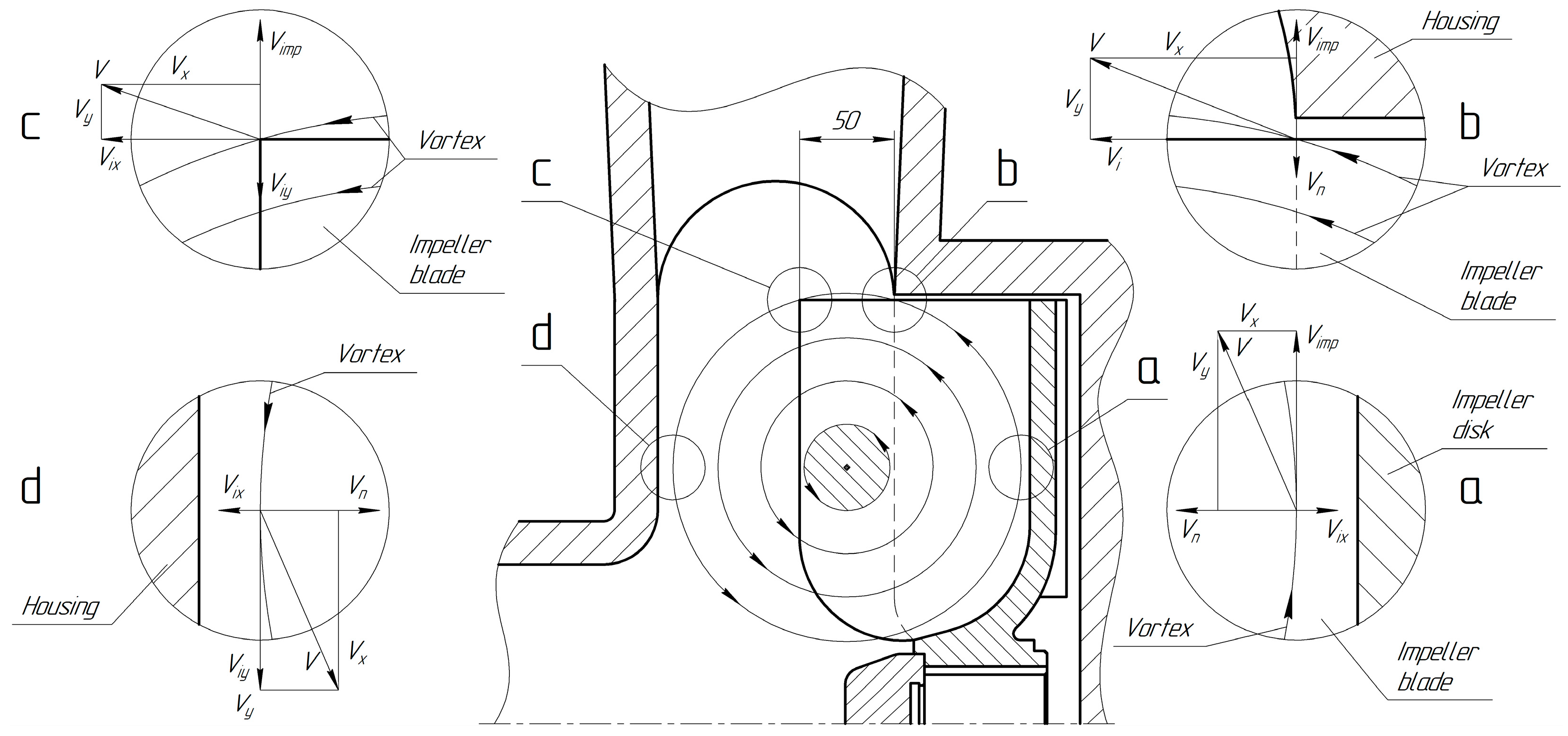
A toroidal vortex in the flow part of a torque flow pump is also schematically presented in Figure 2.

The resulting velocity v and its components v_x and v_y at each vortex point can be decomposed into components along the coordinate axes. This allows for considering each section in more detail.

First, near the impeller disc, liquid from the inlet pipe enters the flow part of the pump. This flow partially passes through the impeller. As a result, the inertial velocity component v_ix occurs. It is directed from the nozzle to the impeller along the pump axis. Simultaneously, the impeller disc opposes this fluid flow. The velocity component v_n is opposite to the direction of v_ix. Due to this, the toroidal vortex gradually changes its direction toward the impeller around the pump axis and away from the impeller on the periphery. As a result, under the action of centrifugal forces, an impeller’s velocity component v_imp in the radial direction occurs. The relationships between the velocity components mentioned above are as follows:

$$v_x=v_{ix}-v_n; v_y=v_{imp}.$$

(1)

Second, at the border of the cylindrical bore and the chamber (by the edges of the blades of the impeller), on the periphery of the impeller, the fluid flow of the toroidal vortex tries to break out of the cylindrical bore of the housing. This creates an inertial velocity v_i (with components v_ix and v_iy) directed from the impeller to the chamber. Simultaneously, the impeller continues to affect the fluid flow, creating a velocity component v_imp due to the action of centrifugal forces. As a result, the liquid flow is reflected from the cylindrical bore of the housing, creating a velocity component v_n. It is directed oppositely, i.e., from the periphery to the pump axis. The following relationships describe the statements mentioned above:

$$v_x=v_{ix}; v_y=v_{imp}-v_n.$$

(2)

Third, external forces do not act on the liquid in the axial direction in the chamber due to the significant distance from the solid surfaces. Thus, in this section, the liquid flow in the axial direction primarily moves under the action of inertial forces generated by the pump impeller. Simultaneously, in the radial direction, the fluid flow gradually changes its direction (from the center to the periphery near the impeller and from the periphery to the center—near the front wall of the housing) due to resistance forces. As a result, the following kinematic relationships can be written:

$$v_x=v_{ix}; v_y=v_{iy}.$$

(3)

Finally, near the housing, in the front part of the chamber, the liquid continues to move by inertia in the direction mentioned above. Due to the absence of moving elements, there is no interaction with the fluid flow in the radial direction. However, in the axial direction, the flow is reflected from the front wall of the housing, and it changes its direction, starting to move towards the impeller. As a result, the following formula can be used:

$$v_x=v_{ix}-v_n; v_y=v_{iy}.$$

(4)

In this pump design, the center of the toroidal vortex is located in a chamber. The asymmetry in the mutual arrangement of the blades and the vortex leads to the deformation of the latter. The interaction between the fluid and the flow in the area between the blade edge and the center of the toroidal vortex leads to changes in the shape of the toroidal vortex. This is the cause of additional hydraulic losses in the flow part of the pump.

This makes it necessary to modernize the flow part of the pump to avoid unnecessary energy losses. One way to achieve this is to increase the width of the impeller blades, which will enable the center of the torus vortex to be located directly on the edge of the blades. This prevents deformation of the vortex at the impeller outlet. At the same time, the circumferential speed of the transverse vortex increases, and the vortex cyclicity decreases. The energy transfer to the fluid flow is thus optimized, increasing the head and efficiency of the modernized pump.

Figure 3 shows the design scheme of the fluid flow in the modified torque flow pump with an increase in the width of the impeller blades (∆b₂ = +0.050 m).

In the toroidal vortex of the modified torque flow pump, the hydrodynamic processes are considered near the impeller disc (1), at the border of the cylindrical bore and the chamber (2), and near the housing (4), and are similar to those in the initial pump design.

Nevertheless, significant changes occur in the chamber where the blades of the modified impeller are located. In the axial direction, the liquid flow moves from the impeller to the front wall of the pump housing. Due to the absence of other external forces, the movement is caused predominantly by the forces of inertia. The anti-effect of the annular tap is preserved in the radial direction. Simultaneously, the impeller plays a crucial role, as it pushes the liquid toward the periphery due to the action of centrifugal forces. As a result, despite Formula (3), the kinematic dependencies take the following form:

$$v_x=v_{ix}; v_y=v_{imp}-v_{iy}.$$

(5)

One modernization approach is to reduce the width of the chamber. This leads to the displacement of the center of the toroidal vortex towards the edges of the impeller blades and further into the interblade channels. This design is typical for torque-flow pumps with a low specific speed.

Figure 4 presents the design scheme of the fluid flow in the modified torque flow pump with a reduced chamber width to the value when the center of the toroidal vortex is on the edge of the impeller blades.

In the toroidal vortex of the modified torque flow pump, when the center of the toroidal vortex is located on the edge of the impeller blades, the hydrodynamic processes near the impeller disc (1) and at the border of the cylindrical bore and the chamber (2) are similar to those in the initial pump design.

Nevertheless, near the front wall of the housing, the liquid flow movements by inertia, forming the components v_ix and v_iy of the inertial velocity v_i. Due to the reduction in the chamber width and the rotary elements’ approach, the velocity component v_imp appears. It is caused by the influence of the impeller and directed to the pump’s periphery. Simultaneously, in the axial direction, the flow is reflected from the front wall of the housing and gradually changes its direction, moving towards the impeller. As a result, despite Formula (4), the kinematic dependencies take the following form:

$$v_x=v_{ix}-v_n; v_y=v_{imp}-v_{iy}.$$

(6)

With a further decrease in the chamber width, the center of the toroidal vortex moves to the interblade channels of the impeller (Figure 5).

In the toroidal vortex of the modified torque flow pump, when the center of the toroidal vortex is on the edge of the impeller blades, the hydrodynamic processes near the impeller disc (1), on the border of the cylindrical bore and the chamber (2), are also similar to the initial pump design.

Nevertheless, significant changes occur near the housing. Due to the rapid change in the direction of movement of the toroidal vortex, the inertial components of the velocity v_ix and v_iy increase. The resistance of the housing walls remains, creating a velocity component v_n directed toward the impeller. Simultaneously, due to the reduction in the chamber width, the influence of the impeller becomes significant. It leads to the appearance of the velocity component v_imp, directed from the center to the periphery. As a result, despite Formula (4), the kinematic dependencies also take the form (6).

The effect mentioned above becomes essential for smaller chamber widths. At a particular moment, it can lead to the destruction of the toroidal vortex. As a result, a circulation flow disappears in the flow part, and all the liquid moves directly to the pressure pipe, increasing the pressure head.

All the Formulas (1)–(6) allow for summarizing the following generalized dependences:

$$v_x=v_{ix}-{\alpha }_{xn}{v}_n; v_y={\alpha }_{iy}{v}_{iy}+{\alpha }_{imp}{v}_{imp}-{\alpha }_{yn}{v}_n; v=\sqrt{v_x^2+v_y^2},$$

(7)

where α_xn, α_iy, α_imp, and α_yn—parameters that consider the pump’s section (

Table 2. The values of the coefficients α_xn, α_iy, α_imp, and α_yn in Formula (7).

Section	αxn	αiy	αimp	αyn
1. Near the impeller disc	1	0	1	0
2. On the border of the cylindrical bore and the chamber	0	0	1	1
3. In the chamber	0	1 − 2γ1	γ1	0
4. Near the housing	1	1 − 2γ2	γ2	0

); γ₁, γ_2,3—Boolean data that considers the design modification of the torque flow pump: 0—for the initial unmodified design (Figure 2); 1—for modified design (the 1st modification is presented in Figure 3, the 2nd—in Figure 4, and the 3rd—in Figure 5).

This analytical formulation should be regarded as an approximate description of the toroidal vortex rather than a complete solution for arbitrary Reynolds numbers. The neglect of specific convective terms and the quasi-axisymmetric assumption were introduced to achieve a tractable representation in toroidal coordinates, capturing the dominant energy transfer mechanisms. While these simplifications may affect local flow structures, they do not alter the global performance trends, which were corroborated by CFD simulations. In this sense, the model provides a theoretical framework for interpreting the interaction between the impeller blades and the vortex. However, its scope is limited, and further refinement is required for fully turbulent three-dimensional flows.

2.2. The Mathematical Model of the Toroidal Vortex Hydrodynamics

The corresponding mathematical model has been developed based on the design scheme presented in Figure 6 to study the hydrodynamics of the toroidal vortex in a torque flow pump.

The toroidal coordinate system was chosen with the following coordinates (Figure 6b): ψ—rotation angle of the cross-sectional area; and r, φ—radial and angular coordinates in the cross-section, respectively.

In this coordinate system, the main kinematic characteristics are as follows [16,17]:

$$v_r=\dot{r}; v_{\phi }=r\dot{\phi }; v_{\psi }=\left[a+rcos\left(\phi \right)\right]\dot{\psi },$$

(8)

where v_r, v_φ, and v_ψ—velocity components, and m/s; a—radius of a toroidal vortex, m.

Hydrodynamics of the fluid flow is determined by the continuity and Navier–Stokes equations that can be written in toroidal coordinates as follows:

$${\displaystyle \frac{\partial \left\{r\left[a+rcos\left(\phi \right)\right]v_r\right\}}{\partial r}}+{\displaystyle \frac{\partial \left\{\left[a+rcos\left(\phi \right)\right]v_{\phi }\right\}}{\partial \phi }}+{\displaystyle \frac{\partial \left(r{v}_{\psi }\right)}{\partial \psi }}=0;$$

(9)

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial v_r}{\partial t}}+v_r{\displaystyle \frac{\partial v_r}{\partial r}}+{\displaystyle \frac{v_{\phi }}{r}}{\displaystyle \frac{\partial v_r}{\partial \phi }}+{\displaystyle \frac{v_{\psi }}{a+rcos\left(\phi \right)}}{\displaystyle \frac{\partial v_r}{\partial \psi }}=-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial p}{\partial r}}+\nu \Delta v_r;\\ {\displaystyle \frac{\partial v_{\phi }}{\partial t}}+v_r{\displaystyle \frac{\partial v_{\phi }}{\partial r}}+{\displaystyle \frac{v_{\phi }}{r}}{\displaystyle \frac{\partial v_{\phi }}{\partial \phi }}+{\displaystyle \frac{v_{\psi }}{a+rcos\left(\phi \right)}}{\displaystyle \frac{\partial v_{\phi }}{\partial \psi }}=-{\displaystyle \frac{1}{\rho r}}{\displaystyle \frac{\partial p}{\partial \phi }}+\nu \Delta v_{\phi };\\ {\displaystyle \frac{\partial v_{\psi }}{\partial t}}+v_r{\displaystyle \frac{\partial v_{\psi }}{\partial r}}+{\displaystyle \frac{v_{\phi }}{r}}{\displaystyle \frac{\partial v_{\psi }}{\partial \phi }}+{\displaystyle \frac{v_{\psi }}{a+rcos\left(\phi \right)}}{\displaystyle \frac{\partial v_{\psi }}{\partial \psi }}=-{\displaystyle \frac{1}{\rho \left[a+rcos\left(\phi \right)\right]}}{\displaystyle \frac{\partial p}{\partial \phi }}+\nu \Delta v_{\psi },\end{array}\right.$$

(10)

where t—time, s; p—pressure, Pa; ν—kinematic viscosity, m²/s; Δ—Laplace operator determined as follows:

$$∆={\displaystyle \frac{1}{r\left[a+rcos\left(\phi \right)\right]}}\left({\displaystyle \frac{\partial }{\partial r}}\left\{r\left[a+rcos\left(\phi \right)\right]{\displaystyle \frac{\partial }{\partial r}}\right\}+{\displaystyle \frac{\partial }{\partial \phi }}\left\{{\displaystyle \frac{a+rcos\left(\phi \right)}{r}}{\displaystyle \frac{\partial }{\partial \phi }}\right\}+{\displaystyle \frac{\partial }{\partial \psi }}\left\{{\displaystyle \frac{r}{a+rcos\left(\phi \right)}}{\displaystyle \frac{\partial }{\partial \psi }}\right\}\right)$$

(11)

To solve Equation (10), the following assumptions and simplifications were considered. First, the stationary flow is considered. In this case, the partial derivatives with respect to time t can be neglected: ${\displaystyle \frac{\partial }{\partial t}}=0$. Second, the convective mass forces are considered low compared with the viscosity forces and the pressure difference. This eliminates the nonlinear components and reduces the differential Equation (10) to linear ones. The continuous Equation (9) is also satisfied for the quasi-axisymmetric case study, where the partial derivatives with respect to coordinates φ and ψ are neglected.

Under these assumptions, Equation (10) takes the following form:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial p}{\partial r}}={\displaystyle \frac{\mu }{r\left[a+rcos\left(\phi \right)\right]}}{\displaystyle \frac{\partial }{\partial r}}\left\{r\left[a+rcos\left(\phi \right)\right]{\displaystyle \frac{\partial v_r}{\partial r}}\right\};\\ {\displaystyle \frac{\partial p}{\partial \phi }}={\displaystyle \frac{\mu }{a+rcos\left(\phi \right)}}{\displaystyle \frac{\partial }{\partial r}}\left\{r\left[a+rcos\left(\phi \right)\right]{\displaystyle \frac{\partial v_{\phi }}{\partial r}}\right\};\\ {\displaystyle \frac{\partial p}{\partial \psi }}={\displaystyle \frac{\mu }{r}}{\displaystyle \frac{\partial }{\partial r}}\left\{r\left[a+rcos\left(\phi \right)\right]{\displaystyle \frac{\partial v_{\psi }}{\partial r}}\right\},\end{array}\right.$$

(12)

where μ = ρ·ν—dynamic viscosity, Pa·s.

The 1st equation of the system (12) is satisfied under the hypothesis of non-mixed layers of the toroidal vortex. In this case, the radial pressure gradient is not considered (${\displaystyle \frac{\partial p}{\partial r}}=0$), and the pressure function depends on the angular coordinates: p = p(φ, ψ).

The 1st differential equation of the system (12), considering the boundary condition for radial velocity v_r = 0 at the interfacial surface (r = R), is as follows:

$$v_r=C\ln \left[{\displaystyle \frac{r}{R}}{\displaystyle \frac{a+R\mathit{cos}\left(\phi \right)}{a+r\mathit{cos}\left(\phi \right)}}\right],$$

(13)

where C is an arbitrary constant that should be zero to avoid the singularity at r = 0.

Therefore, the radial velocity does not occur (v_r = 0), and the continuity Equation (9) is satisfied after considering the assumption stated before Equation (12).

After integrating the 2nd differential equation of the system (12), considering the boundary condition for angular velocity v_φ = 0 at r = 0, the following general solution can be obtained:

$$v_{\phi }={\displaystyle \frac{1}{2\mu }}\left\{r+a{\displaystyle \frac{\ln \left[1+\frac{r}{a}\mathit{cos}\left(\phi \right)\right]}{\mathit{cos}\left(\phi \right)}}\right\}{\displaystyle \frac{dp}{d\phi }}.$$

(14)

To avoid the singularity, the angular gradient of the pressure should be presented as follows:

$${\displaystyle \frac{dp}{d\phi }}=p_1\left(\phi ,\psi \right)\mathit{cos}\left(\phi \right),$$

(15)

where p₁—unknown pressure function, Pa:

$$p_1={\displaystyle \frac{2\mu v_{\phi s}}{R\mathit{cos}\left(\phi \right)+a\ln \left[1+\frac{R}{a}\mathit{cos}\left(\phi \right)\right]}},$$

(16)

where v_φs—the angular velocity v_φ at the interfacial surface of the vortex at r = R.

Overall, the angular velocity is determined by its surface value:

$$v_{\phi }={\displaystyle \frac{r\mathit{cos}\left(\phi \right)+a\ln \left[1+\frac{r}{a}\mathit{cos}\left(\phi \right)\right]}{R\mathit{cos}\left(\phi \right)+R\ln \left[1+\frac{R}{a}\mathit{cos}\left(\phi \right)\right]}}{v}_{\phi s}.$$

(17)

Under the assumption about the axisymmetric angular velocity at the interfacial surface, when v_φs = invar(ψ), the pressure function p₁ depends on the angle φ only. This fact allows for evaluating the pressure p(φ, ψ) as the following superposition:

$$p\left(\phi ,\psi \right)=p_{\phi }\left(\phi \right)+p_{\psi }\left(\psi \right),$$

(18)

of two angular components p_φ(φ) and p_ψ(ψ), Pa.

Analogously, after integrating the 3rd differential equation of the system (12), considering the boundary condition for angular velocity v_ψ = v_ψ0 at r = 0, the general solution can be obtained as follows:

$$v_{\psi }=v_{\psi 0}+{\displaystyle \frac{1}{2\mu }}{\displaystyle \frac{r\mathit{cos}\left(\phi \right)-a\ln \left[1+\frac{r}{a}\mathit{cos}\left(\phi \right)\right]}{{\mathit{cos}}^2\left(\phi \right)}}{\displaystyle \frac{dp}{d\psi }}.$$

(19)

To avoid the singularity, another angular gradient of the pressure should also be presented as follows:

$${\displaystyle \frac{dp}{d\psi }}=p_2\left(\phi ,\psi \right){\mathit{cos}}^2\left(\phi \right),$$

(20)

where p₂ is the unknown pressure function, Pa.

However, due to the superposition (18), the condition (20) can be achieved only for the trivial solution when p₂ = 0. This fact corresponds to the vortex cord hypothesis [18,19]. Therefore, the solution (18) reduces to the axisymmetric case study: v_ψ = v_ψ0. After considering this value and the angular velocity (17), a differential equation of streamlines can be written as follows:

$${\displaystyle \frac{rd\phi }{v_{\phi }}}={\displaystyle \frac{\left[a+r\mathit{cos}\left(\phi \right)\right]d\psi }{v_{\psi }}}.$$

(21)

Its general solution for an arbitrary initial point (φ₀, ψ₀) is as follows:

$$\psi ={\psi }_0-\underset{{\phi }_0}{\overset{\phi }{\int }}{\displaystyle \frac{v_{\psi 0}}{v_{\phi s}}}{\displaystyle \frac{r}{a+r\mathit{cos}\left(\theta \right)}}{\displaystyle \frac{R\mathit{cos}\left(\theta \right)+R\ln \left[1+\frac{R}{a}\mathit{cos}\left(\theta \right)\right]}{r\mathit{cos}\left(\theta \right)+a\ln \left[1+\frac{r}{a}\mathit{cos}\left(\theta \right)\right]}}d\theta ,$$

(22)

where θ—an angle changing in a range of φ₀ and φ.

2.3. The Simulation Model of the Vortex Flow

A 3D model of the pump flow part was created in SolidWorks 2021, and meshing was performed in ICEM CFD. An unstructured tetrahedral grid with local prismatic refinement near walls was applied to improve boundary layer resolution (Figure 7). The computational domain was divided into stator and rotor subdomains, containing ~3.2·10⁶ elements in total. A mesh independence test confirmed that further refinement did not affect the results.

To verify grid independence, three meshes of different densities were tested: coarse (1.6 million cells), medium (3.2 million cells), and fine (5.1 million cells). The calculated pump head and efficiency are summarized in

Table 3. Results of the grid sensitivity study.

Grid Size (Cells)	Grid Size (Cells)	Grid Size (Cells)
1.6 × 106 (coarse)	33.5	34.7
3.2 × 106 (medium)	33.9	34.5
5.1 × 106 (fine)	34.1	34.8

. The differences between the medium and fine grids were less than 1.2% for head and 0.8% for efficiency, confirming mesh independence. Therefore, the medium grid was used in all further simulations as it provides a reasonable compromise between accuracy and computational cost.

The computational domain of the torque-flow pump was generated in ICEM CFD and discretized using an unstructured tetrahedral grid with local prismatic refinement near solid boundaries to resolve the boundary layer accurately. The mesh was divided into two subdomains corresponding to the impeller (rotor) and the pump casing (stator). The final mesh topology is shown in Figure 7, which illustrates the overall flow passage as well as detailed views of the rotor and stator regions. This representation complements the grid sensitivity analysis (Table 3) and provides a clear visualization of the numerical setup.

Numerical simulations were performed in steady-state mode using water at 20 °C as the working medium. The standard k–ε turbulence model was used to close the Reynolds-averaged Navier–Stokes equations. This model is widely applied in pump simulations, where it provides a reliable compromise between computational cost and prediction accuracy. Its applicability to torque-flow pumps has been confirmed in previous studies [8,20]. Although advanced approaches, such as LES or DES, can offer a more detailed representation of transient vortex structures, they are beyond the scope of the present work and will be considered in future research.

The mass flow rate was set at the inlet, and the static pressure was measured at the outlet. The Y⁺ distribution (Figure 8) remained below 100 across most surfaces, confirming the appropriateness of the turbulence model. Convergence was achieved with a residual target of 10⁻⁴. Pump head and hydraulic efficiency were monitored during calculations.

To evaluate pump performance, the main hydraulic parameters were extracted directly from the CFD results. The following definitions were used for head, flow rate, shaft power, and overall efficiency:

$$H={\displaystyle \frac{〈p_t〉S_{out}-〈p_t〉S_{in}}{\rho g}},$$

(23)

where ρ—the fluid density, kg/m³; and g = 9.81 m/s²—gravitational acceleration (equivalently, 23 subsumes the static-pressure, velocity-head, and elevation terms of the Bernoulli head balance).

Section averages ⟨⋅⟩ are taken on planar cuts orthogonal to the axis: S_in is located upstream of the impeller inlet at a distance sufficient to avoid inlet recirculation; S_out is placed downstream of the diffuser outlet where the flow is fully developed.

Section-averaged total pressure is equal to:

$$p_t=p+{\displaystyle \frac{1}{2}}\rho v^2,$$

(24)

The flow rate is obtained from the inlet boundary condition and cross-checked from the outlet flux:

$$Q=\underset{S_{in}}{\int }\overrightarrow{v}·\overrightarrow{n}dS=\underset{S_{out}}{\int }\overrightarrow{v}·\overrightarrow{n}dS,$$

(25)

where $\overrightarrow{v}$—velocity vector, m/s; $\overrightarrow{n}$—normal vector to the cross-sectional area; and $S_{in}$, $S_{out}$—inlet and outlet cross-sectional areas, m².

The shaft (mechanical) power is computed from the torque on the rotating domain returned by the solver:

$$N=M·\omega ,$$

(26)

where M—the impeller torque obtained by integrating pressure and viscous stresses over the blade and hub surfaces, N·m; and ω—the angular velocity, rad/s.

Torque M is extracted directly from the rotating region monitor.

The pump efficiency is defined as the ratio of hydraulic power to shaft power:

$$\eta ={\displaystyle \frac{\rho gQH}{N}}.$$

(27)

All reported H, Q, N, and η correspond to converged steady-state solutions (residuals 10⁻⁴ and stable integral monitors).

3. Results

3.1. Three-Dimensional Velocity Field and Confirmation of the Toroidal Vortex

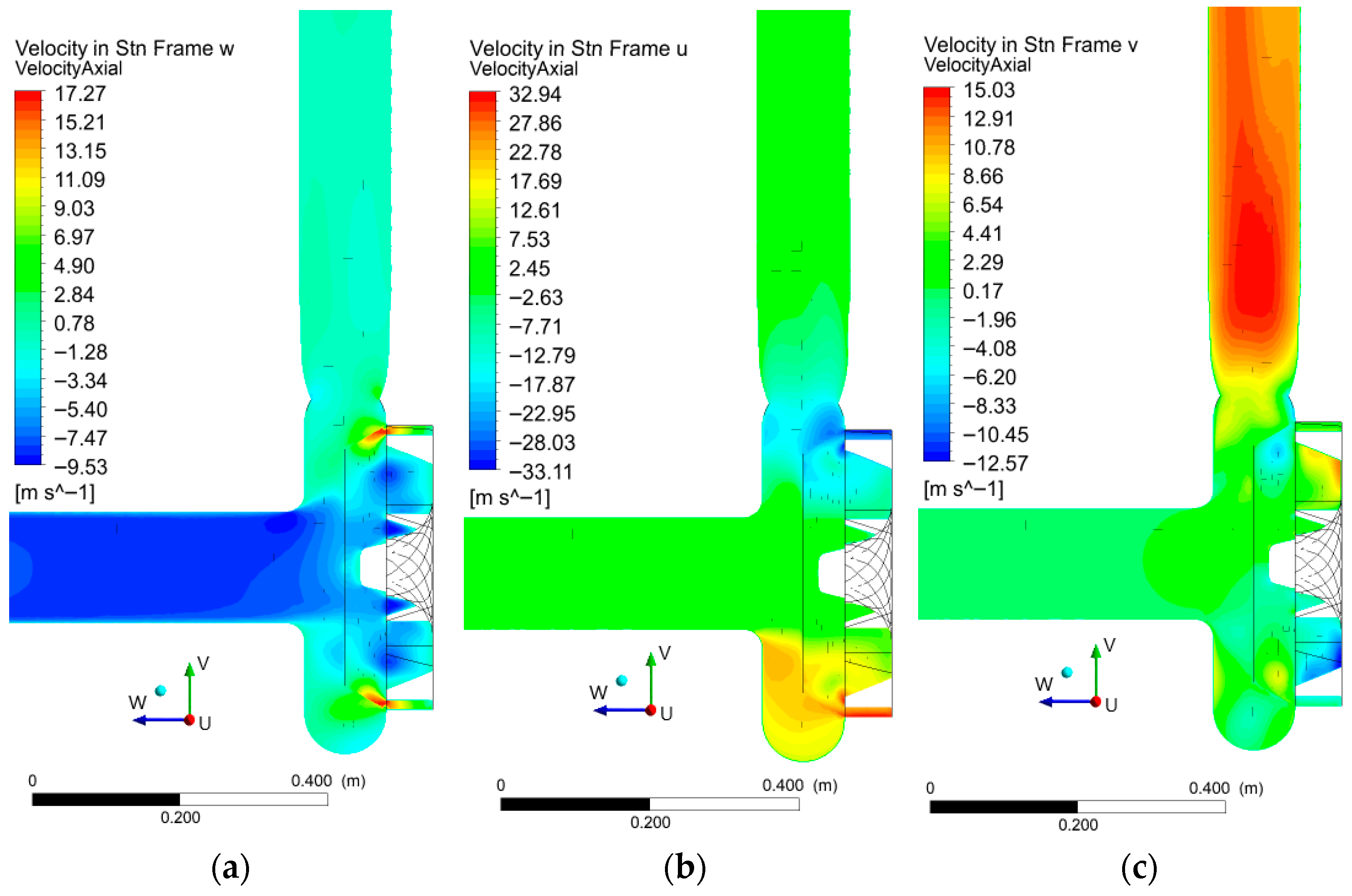
To verify the existence and characterize the structure of the toroidal vortex predicted by the mathematical model, the three components of the velocity field were analyzed in a longitudinal section of the pump. Figure 8 presents the axial (V_w), horizontal (V_u), and vertical (V_v) velocity distributions. The combined analysis of these components reveals a closed three-dimensional circulation loop, in which fluid motion alternates between forward and reverse directions in each coordinate plane. This confirms the presence of a fully developed toroidal vortex within the free chamber, governing both energy transfer and hydraulic losses in the torque-flow pump.

Figure 8a shows the axial velocity distribution in a longitudinal section of the torque-flow pump, highlighting the structure of the toroidal vortex. The velocity field reveals the circulating contour of the vortex, with characteristic regions of reverse axial flow indicated by negative velocity values (blue areas) adjacent to the impeller. These backflow zones correspond to the upward segment of the toroidal loop, while positive axial velocities (green–red regions) represent the downward jet returning toward the impeller inlet.

The image clearly demonstrates the closed circulation typical of a toroidal vortex: fluid accelerated by the impeller blades is redirected into the free chamber, where part of the flow reverses direction and forms a recirculating loop. This recirculation subsequently interacts with the main throughflow, transferring angular momentum and contributing to the overall head generation. The presence of high-velocity gradients near the blade edges indicates the regions of strongest momentum exchange, while the central low-velocity core corresponds to the vortex axis.

From the standpoint of the mathematical model, this longitudinal slice illustrates the two-stage energy transfer mechanism: (I) blade-to-vortex exchange, where the impeller drives the toroidal structure, and (II) vortex-to-throughflow transfer, where the vortex imparts momentum to the axial stream. The observed asymmetry of the velocity contours also reflects partial deformation of the vortex, which is a primary source of hydraulic losses in the base design.

Figure 8b depicts the distribution of the U-velocity component (V_u) on a longitudinal section, with the component oriented normal to the plotting plane (U–V plane). The color scale follows the sign convention: positive (red) values indicate motion toward the observer, whereas negative (blue) values indicate motion away from the observer. Two coherent lobes of opposite sign are observed across the free chamber and the impeller periphery, evidencing a through-plane rotational motion that, together with the axial component shown in Figure 8a, closes the three-dimensional toroidal circulation loop within the flow passage.

High-magnitude V_u regions localize near the blade edges and along the interface with the free chamber, marking zones of the strongest exchange of angular momentum between the impeller and the recirculating vortex. The sign reversal across the section (red–blue) is the kinematic signature of the vortex’s transverse branch: one side of the loop rotates toward the observer, the opposite side recedes, completing the 3D closed toroidal motion predicted by the mathematical model. Any asymmetry of these lobes reflects partial deformation of the toroidal core and is directly linked to additional hydraulic losses.

Figure 8c shows the distribution of the velocity component V_v in a longitudinal section of the torque-flow pump. This component is aligned with the vertical axis (V), and its distribution further confirms the presence of a closed toroidal vortex in the flow passage.

Regions of high positive velocity (red, up to 7 m/s) appear in the discharge channel above the impeller, corresponding to the upward branch of the vortex loop. In contrast, zones of negative velocity (blue, down to −12.6 m/s) are concentrated near the impeller periphery and in the lower part of the free chamber, indicating fluid motion in the opposite direction. Between these counter-directed streams, intermediate zones of low velocity (green–yellow) form the transitional shear layers that characterize vortex circulation.

The juxtaposition of upward and downward flows in the same longitudinal plane is a direct manifestation of the recirculating toroidal structure. Fluid is accelerated upward along one side of the vortex loop, while simultaneously returning downward on the opposite side. This establishes the closed circulation contour predicted by the mathematical model, in which momentum is continuously exchanged between the vortex and the main throughflow.

From a hydrodynamic perspective, the strong gradients at the vortex interface highlight the primary regions of dissipation, which also contribute to limiting pump efficiency in the base configuration. Together with Figure 8a,b, this plot confirms the existence of a three-dimensional toroidal vortex system, consisting of axial, circumferential, and vertical velocity components that form a closed, rotating energy-transfer mechanism within the free chamber.

3.2. Effect of Impeller Extension into the Free Chamber on Pump Performance

To investigate the influence of impeller geometry on pump characteristics, a parametric study was conducted by varying the impeller extension into the free chamber (Δb₂). Sixteen geometric configurations were analyzed, ranging from negative extensions (−10 mm, −6 mm, and −2 mm), where the impeller is recessed relative to the free chamber, to large positive extensions (up to 70 mm), where the blades penetrate deeply into the chamber. These variants are summarized in

Table 4. The values of the coefficients α_ix, α_iy, α_imp, and α_yn in Formula (7).

Test No.	1	2	3	4	5	6	7	8
Δb2, mm *	−10	−6	−2	0	2	6	10	14
Test no.	9	10	11	12	13	14	15	16
Test no.	18	22	26	30	40	50	60	70

* Δb₂ is the impeller extension into the free chamber (positive values correspond to blade widening).

, which provides the complete set of test cases used in the CFD simulations.

Figure 9, Figure 10 and Figure 11 summarize the numerical results in terms of head, efficiency, and shaft power. The data reveal distinct operating regimes, ranging from negative extensions, where the impeller is recessed relative to the free chamber, to large positive extensions, where the impeller blades penetrate deeply into the chamber. By analyzing the variation in pump parameters across this range, it becomes possible to identify design configurations that balance efficiency, head, and power consumption, and to determine the rational limits of impeller extension for practical applications.

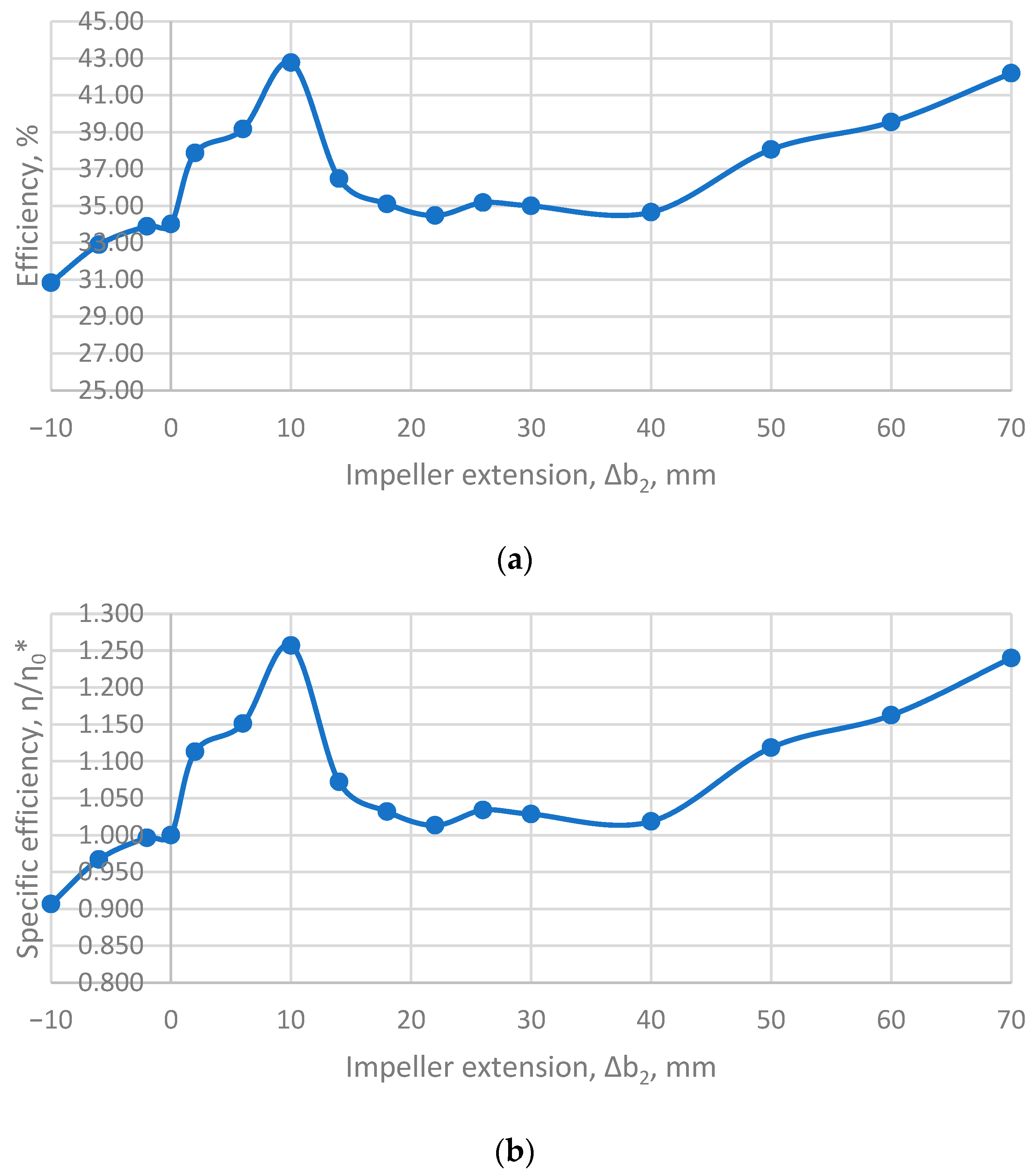
Figure 9 shows the variation in pump efficiency with the degree of impeller extension into the free chamber (Δb₂).

The reference configuration (Δb₂ = 0) yields a baseline efficiency of 34.0%. Negative extension reduces performance, with efficiency dropping to 30.8% at Δb₂ = –10 mm.

A moderate positive extension markedly improves efficiency. At Δb₂ = 6 mm, the efficiency increases to 39.2% (+15% relative to baseline), while the best result is observed at Δb₂ = 10 mm, where the efficiency reaches 42.8% (+25.7%).

Beyond this optimum, efficiency decreases when Δb₂ is extended further to 14–30 mm (≈34–36%), due to renewed vortex deformation and additional losses. However, a secondary efficiency rise is observed at larger extensions: Δb₂ = 70 mm yields η = 42.2%, comparable to the peak at 10 mm.

Overall, the efficiency curve exhibits two favorable operating zones: a primary optimum at Δb₂ ≈ 10 mm and a secondary plateau at Δb₂ ≈ 70 mm. These results highlight the sensitivity of torque-flow pump efficiency to the impeller–vortex interaction geometry.

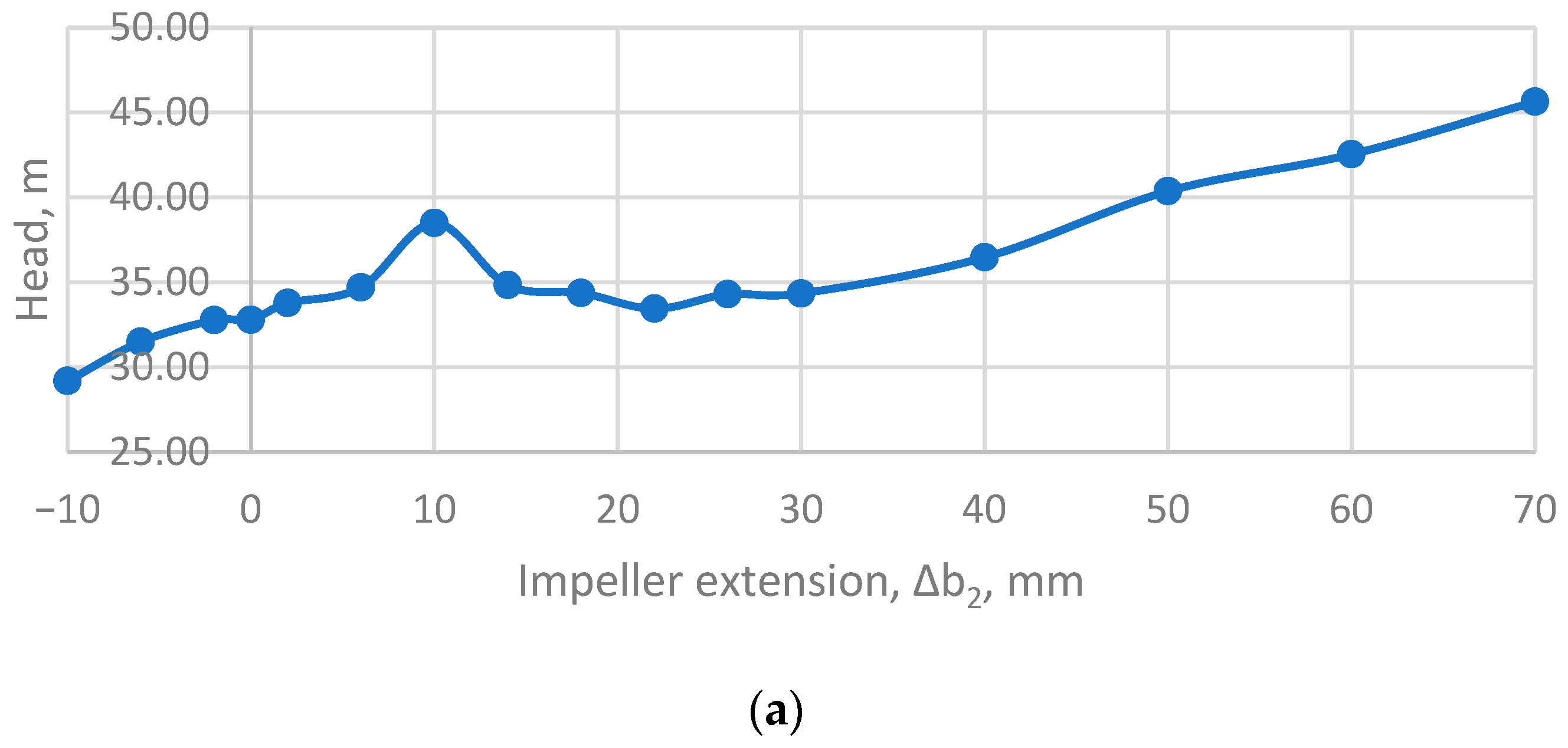
Figure 10 presents the variation in pump head with impeller extension Δb₂.

In the baseline configuration (Δb₂ = 0), the head equals 32.8 m. A small negative extension reduces head to 29.2 m (Δb₂ = –10 mm), while moderate positive extension produces a pronounced increase: H rises to 34.7 m at Δb₂ = 6 mm and peaks at 38.5 m at Δb₂ = 10 mm (+17.4% compared to baseline).

Beyond this optimum, the head continues to grow almost monotonically with increasing Δb₂, reaching 45.6 m at Δb₂ = 70 mm (+39.2%). According to the toroidal vortex model, this trend reflects the gradual transition from a vortex-dominated to a blade-dominated regime.

As the impeller blades penetrate deeper into the free chamber, the auxiliary circulating contour weakens, while the specific torque imparted directly by the blades increases. This enhances head generation, although it also introduces additional losses that limit efficiency growth (Figure 9).

Figure 11 presents the dependence of shaft power on the impeller extension into the free chamber. In the baseline configuration (Δb₂ = 0), the required power is 130.9 kW. For negative extensions, the pump head decreases (see Figure 2), which directly reduces the shaft power. At Δb₂ = –10 mm, the value falls to 128.6 kW, while at Δb₂ = –6 mm, it remains close to the baseline (130.0 kW). A slight rise to 131.3 kW is observed at –2 mm due to local variations in hydraulic losses.

For moderate positive extensions in the range of 2–14 mm, the required power decreases significantly due to higher efficiency, even though the head also increases, contributing to additional energy demand. The lowest value is obtained at Δb₂ = 6 mm, where N = 120.3 kW (–8.1% compared with baseline). At Δb₂ = 10 mm, where the maximum efficiency is achieved, the power is slightly higher (122.3 kW), but still below the reference configuration. With further extension to 14 mm, the value rises again to 129.7 kW, nearly returning to the baseline.

At larger extensions above 14 mm, the power consumption begins to rise steadily. In the range 18–26 mm, it remains above the baseline (133–136 kW), while at 30 mm, a local decrease to 125.2 kW is observed. Beyond this point, the growth becomes pronounced, reaching 143.0 kW at Δb₂ = 40 mm and peaking at 146.9 kW at Δb₂ = 70 mm, which is about 12% higher than the baseline.

The reliability of CFD approaches for torque-flow pumps has been confirmed in several published works, where numerical predictions have been shown to agree well with evaluating of head and efficiency [2,9]. On this basis, the present numerical results can be considered credible. Nevertheless, experimental verification of the modified designs is planned as part of our future research, which will be conducted within ongoing test campaigns at our laboratory.

4. Discussion

Figure 9 illustrates the dependence of pump efficiency on the impeller extension into the free chamber (Δb₂). The baseline configuration (Δb₂ = 0) provides an efficiency of 34.0%. Negative extensions further reduce efficiency to 30.8% at Δb₂ = –10 mm. A moderate positive extension, however, significantly improves performance: η rises to 39.2% at Δb₂ = 6 mm, and reaches a maximum of 42.8% at Δb₂ = 10 mm (+25.7% compared to baseline). This improvement is explained by the mathematical model of the toroidal vortex: shifting the vortex center toward the impeller blade edges minimizes vortex deformation, aligns the circumferential velocities of the vortex core and the blades, and ensures more effective energy transfer with reduced dissipation.

Further increasing Δb₂ moves the vortex into the interblade passages, resulting in new hydraulic losses and a corresponding drop in efficiency (approximately 34–36% at Δb₂ = 14–30 mm). Nevertheless, a secondary efficiency plateau is observed at larger extensions, with η = 42.2% at Δb₂ = 70 mm, close to the initial peak. This corresponds to a transition toward a blade-dominated regime: the circulating vortex weakens, the specific torque transferred by the blades increases, but an additional gap and recirculation losses prevent further growth of efficiency.

The analysis of Figure 10 reveals two essential features. First, the pump head increases almost monotonically with the degree of impeller extension into the free chamber, reaching its maximum value of 45.6 m at Δb₂ = 70 mm (+39% relative to the baseline). This confirms the model prediction that a deeper penetration of the blades suppresses the auxiliary toroidal vortex and strengthens the blade working process, thereby raising the specific torque delivered to the fluid.

Second, and more importantly from a design perspective, a local optimum appears at Δb₂ ≈ 10 mm, where the head rises to 38.5 m (+17%). This point coincides with the global maximum of efficiency (Figure 1) and a moderate power demand (Figure 3). The convergence of these three parameters indicates that Δb₂ ≈ 10 mm represents the most balanced configuration: the vortex center is aligned with the blade edges, deformation is minimized, and both blade and vortex processes contribute constructively to energy transfer.

Beyond the local optimum at Δb₂ ≈ 10 mm, the head continues to rise, reaching 45.6 m at Δb₂ = 70 mm. This growth is associated not with improved vortex–blade synergy, but rather with the gradual dominance of the blade working process over the vortex process. In this regime, the pump design effectively shifts toward the configuration of a classical centrifugal pump. While higher efficiencies generally characterize centrifugal pumps, they are also known to provide significantly lower reliability and durability when handling liquids with solid inclusions, especially abrasive particles.

Consequently, substantial impeller extensions cannot be considered a rational solution for torque-flow pumps designed for use with contaminated or abrasive fluids. The Δb₂ ≈ 10 mm configuration remains the most balanced design, ensuring both enhanced head (+17%) and maximum efficiency (+26%) while preserving the operational advantages of vortex-assisted energy transfer, namely stable performance and improved reliability in multiphase and solids-laden flows.

The observed variation in shaft power (Figure 11) with impeller extension can be explained by the redistribution of energy transfer mechanisms between the vortex and blade working processes, in accordance with the toroidal vortex model. When the blades are recessed relative to the free chamber (Δb₂ < 0 mm), the vortex dominates energy transfer, but it generates a lower head. Therefore, the overall power demand is reduced. The minor anomaly at –2 mm is associated with enhanced recirculation losses and does not alter the general downward trend.

For moderate positive extensions, the situation changes fundamentally. The alignment of the vortex core with the blade edges minimizes deformation and enhances momentum exchange, resulting in higher efficiency and, simultaneously, increased head. The combination of these effects results in a reduction in shaft power to its minimum at Δb₂ = 6 mm. At Δb₂ = 10 mm, the pump achieves its best overall balance, with a maximum efficiency of 42.8%, an increased head of 38.5 m, and a still moderate power consumption of 122.3 kW. This configuration can therefore be considered the most rational design solution.

At larger extensions, the blade process gradually becomes dominant over the vortex process. The pump increasingly behaves like a centrifugal design, generating a higher head, but at the cost of higher shaft power and lower robustness for multiphase or abrasive fluids. At Δb₂ between 50 and 70 mm, the shaft power rises above 140 kW, indicating a significant departure from the energy-saving characteristics of torque-flow pumps. Although such configurations may be attractive for applications where maximum head is required, they compromise one of the main advantages of torque-flow pump designs, namely their durability and reliability when handling contaminated or solids-laden liquids.

According to the obtained results, the operating process in a torque flow pump can be conditionally divided into several components. After the liquid enters the inlet pipe, the flow is divided into two main parts. One of its components forms a flow and is directed to the pressure pipe.

The second component circulates in the flow part while passing through the impeller’s interblade channels, forming a toroidal vortex. This vortex operates as a “liquid blade”, transferring the energy of the fluid flow that does not directly interact with the impeller’s blades. These results are consistent with studies [21,22,23], but significantly improve upon the analytical studies developed and the numerical simulation results obtained.

The mathematical formulation introduced certain simplifications, such as neglecting some convective terms and the dependence on ψ, to obtain an analytically tractable system in toroidal coordinates. These assumptions are justified because they retain the dominant contributions to the energy transfer mechanism, while the omitted components have only a secondary influence on global pump performance. Similar approaches have been applied in prior theoretical treatments of vortex structures in turbomachinery [13,15], and such reductions are also consistent with standard practices in CFD modeling [20]. As confirmed by the numerical simulations, the overall performance trends (head, efficiency, and shaft power) remain unaffected by these simplifications. Nevertheless, future work will include a sensitivity analysis to quantify the influence of the neglected terms more precisely.

The analysis of the velocity field confirms the existence of a closed three-dimensional toroidal vortex within the free chamber of the pump. The axial velocity distribution reveals the characteristic forward and reverse flow zones, while the circumferential component demonstrates counter-directed motion relative to the observation plane. The vertical velocity map shows the upward and downward branches of the circulation. Taken together, these three components provide a consistent picture of a toroidal vortex loop, in which the impeller accelerates the fluid, which is redirected into the free chamber and partially recirculated back toward the impeller inlet. This interaction explains the two-stage energy transfer mechanism predicted by the mathematical model: blade-to-vortex momentum exchange followed by vortex-to-throughflow transfer. The observed deformation of the vortex core also highlights the regions responsible for hydraulic losses and limited efficiency in the baseline configuration.

In this article, the scientific novelty lies in several key aspects related to mathematical modeling, numerical modeling, and the obtained results:

• Mathematical Modeling: Developing a detailed mathematical model to analyze toroidal vortex formation in a torque flow pump is a significant advancement. Previous studies have often focused on empirical observations or simplified models, whereas this research delves into complex fluid dynamics using a rigorous mathematical framework, providing a comprehensive understanding of the phenomenon.
• Numerical Modeling: Another novel aspect is using computational fluid dynamics (CFD) simulations to validate the mathematical model and analyze the flow patterns within the pump. CFD enables a detailed and quantitative analysis of fluid dynamics, providing insights that are not easily obtained through experimental methods alone. The accurate representation of toroidal vortex dynamics using CFD enhances the reliability of the results and facilitates the optimization of pump design.
• Obtained Results: The obtained results demonstrate the mathematical models’ and numerical simulations’ effectiveness in predicting toroidal vortex formation and its impact on pump performance. The ability to accurately predict the behavior of toroidal vortices under different operating conditions is a significant achievement, as it enables engineers to optimize pump design and enhance its efficiency and operational parameters. The modifications made to the pump based on these results resulted in tangible improvements in the efficiency and pressure head, highlighting the practical significance.

Overall, the scientific novelty of this article lies in its holistic approach to understanding and optimizing torque flow pump performance through a combination of advanced mathematical modeling, numerical simulations, and experimental validation.

From a practical perspective, the choice of impeller extension has direct implications for the operation of torque-flow pumps in abrasive and multiphase environments. It is well established that conventional centrifugal pumps exhibit reduced reliability and rapid wear when handling liquids laden with solids or those that are erosive. In contrast, torque-flow designs maintain higher resistance to erosion and clogging due to the dominant role of vortex energy transfer [8,13]. Our numerical results support this conclusion: while substantial extensions (Δb₂ = 50–70 mm) provide a higher head, they also shift the operating regime toward centrifugal-type behavior, which is less favorable for abrasive media. In contrast, the moderate extension (Δb₂ ≈ 10 mm) achieves improved efficiency and head while preserving the characteristic robustness of vortex-assisted operation, thus offering a rational compromise between performance and durability.

In this work, twelve impeller configurations with different Δb₂ values were analyzed, but the comparison was intentionally restricted to the nominal operating point corresponding to the optimal working regime of the pump. This allowed us to highlight the influence of blade extension under conditions that minimize additional hydraulic losses. A broader parametric study, including full H–Q and η–Q performance curves for several Δb₂ configurations, as well as a more detailed analysis of off-design regimes, will be conducted in our future research.

Further scientific research in the field of torque-flow pumps and toroidal vortex formation could explore several avenues to advance understanding and improve pump performance:

• Advanced Numerical Simulations: Utilize more sophisticated computational fluid dynamics (CFD) techniques, such as large eddy simulation (LES) or detached eddy simulation (DES), to capture finer details of toroidal vortex formation and its interaction with pump components. This can provide more accurate predictions and insights into flow behavior.
• Experimental Validation: Conduct more detailed experimental studies to validate numerical models and investigate toroidal vortex dynamics under a broader range of operating conditions. High-speed imaging and advanced flow visualization techniques can provide valuable data for comparison with simulations.
• Multi-Physics Modeling: Incorporate other physical phenomena, such as heat transfer and cavitation, into the numerical models to study their interactions with toroidal vortices and their effects on pump performance. This can lead to more comprehensive and realistic simulations.
• Material and Coating Research: Investigate using advanced materials and coatings for pump components to reduce friction losses and improve resistance to wear and corrosion, thereby enhancing pump efficiency and longevity.
• Environmental Impact Assessment: Conduct studies to assess the environmental impact of torque-flow pumps, considering the energy consumption, emissions, and lifecycle analysis to identify opportunities for reducing the environmental footprint.

Overall, further scientific research should aim to deepen the understanding of toroidal vortex dynamics in torque-flow pumps and leverage this knowledge to develop more efficient and reliable pumping systems for various industrial applications.

5. Conclusions

A mathematical model of viscous fluid flow in the toroidal vortex of a torque-flow pump has been developed. This model provides a more accurate understanding of the two-stage energy transfer process, in which the impeller drives the toroidal vortex and the vortex subsequently transfers momentum to the main stream. The analysis showed that deformation of the vortex is a key source of hydraulic losses in the base configuration.

The numerical study confirmed the existence of a three-dimensional toroidal vortex in the free chamber. CFD simulations of the axial, circumferential, and vertical velocity components demonstrated the closed circulation loop predicted by the mathematical model. The results validated the theoretical framework and quantified the interaction between the vortex and the impeller blades.

A parametric analysis of impeller extension into the free chamber (Δb₂) revealed three characteristic regimes. At Δb₂ ≈ 6 mm, shaft power was minimized (120.3 kW, an 8.1% decrease compared to the baseline), while efficiency increased to 39.2%. At Δb₂ ≈ 10 mm, the pump achieved the most balanced performance, with maximum efficiency of 42.8% (+8.7%), head of 38.5 m (+17.4%), and moderate power demand (122.3 kW). At Δb₂ ≈ 50–70 mm, the head reached its maximum of 45.6 m (+39%), but this regime was associated with increased power consumption (146.9 kW, +12%) and a shift toward centrifugal-type operation, which compromises the reliability of torque-flow pumps for abrasive and solid-laden fluids.

Overall, the study demonstrated that moderate impeller extension is the most rational approach to improving torque-flow pump performance. The configuration with Δb₂ ≈ 10 mm provides the optimal compromise between head, efficiency, and shaft power while preserving the advantages of vortex-assisted designs in terms of reliability and durability.