Dynamics of Long-Runout Landslides: A Review
Abstract
1. Introduction
2. Phenomenon and Characteristics of Long-Runout Landslides
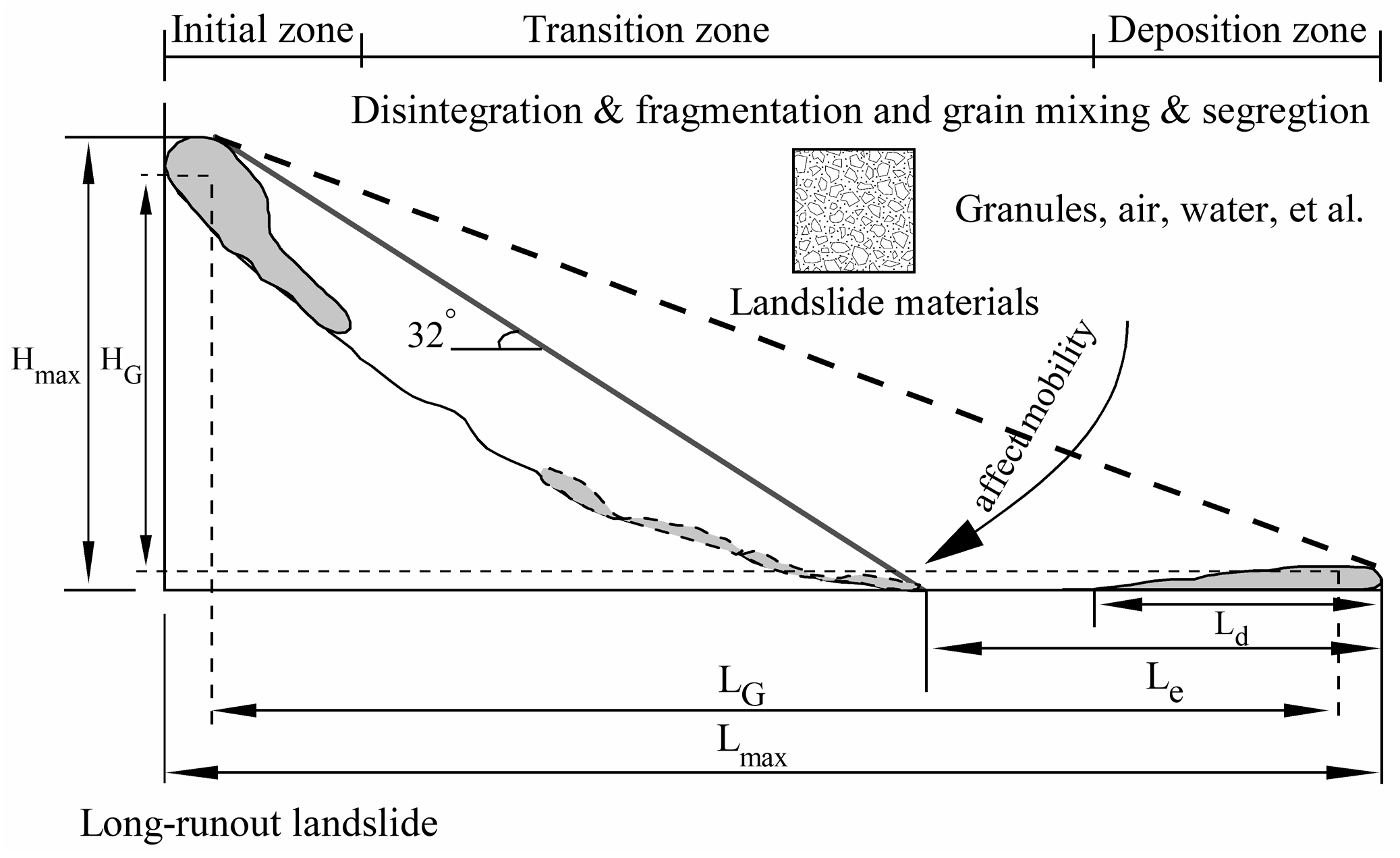
2.1. Phenomenon of Long-Runout Landslides
2.2. Characteristics of Long-Runout Landslides
3. Mobility of Long-Runout Landslides
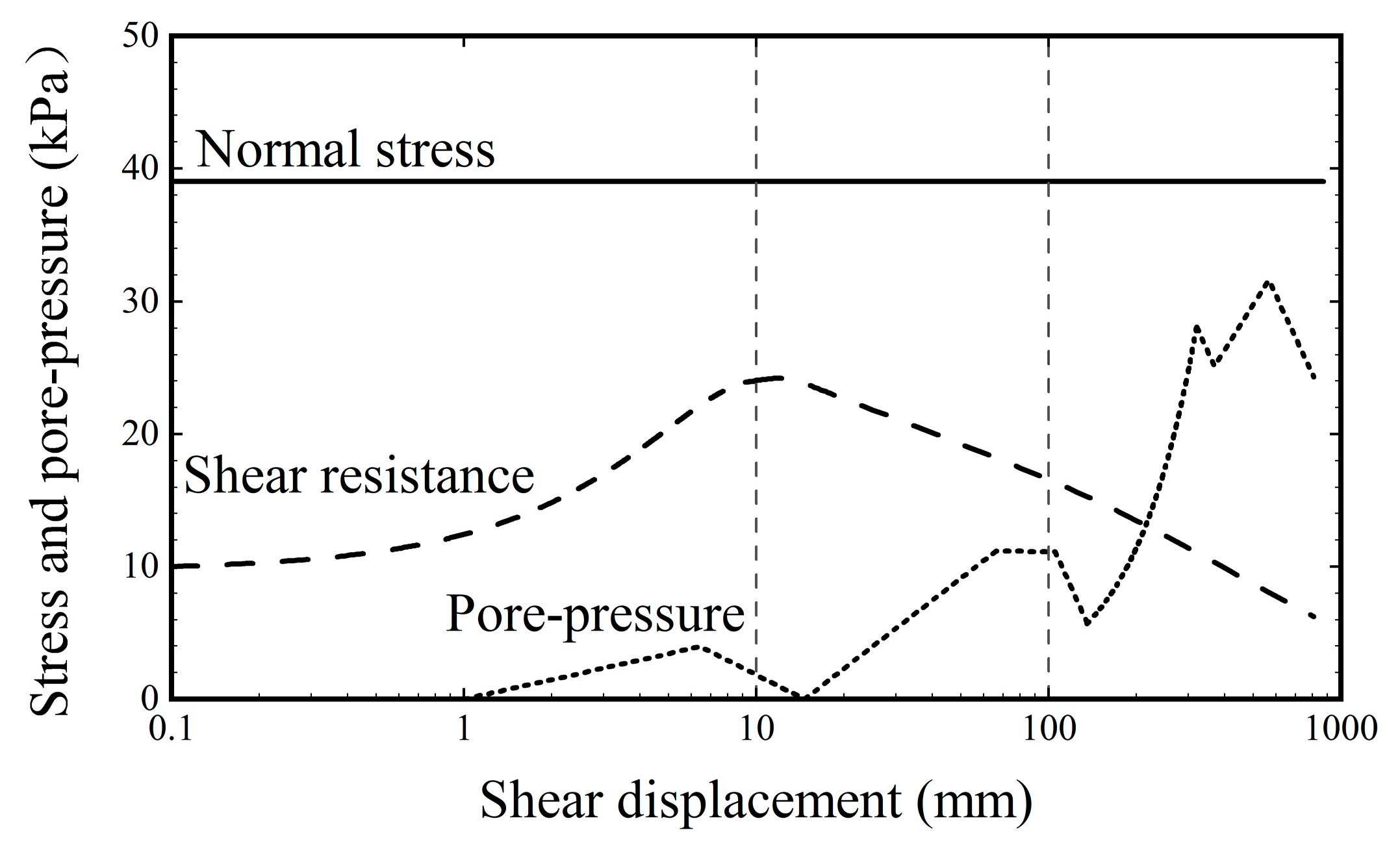
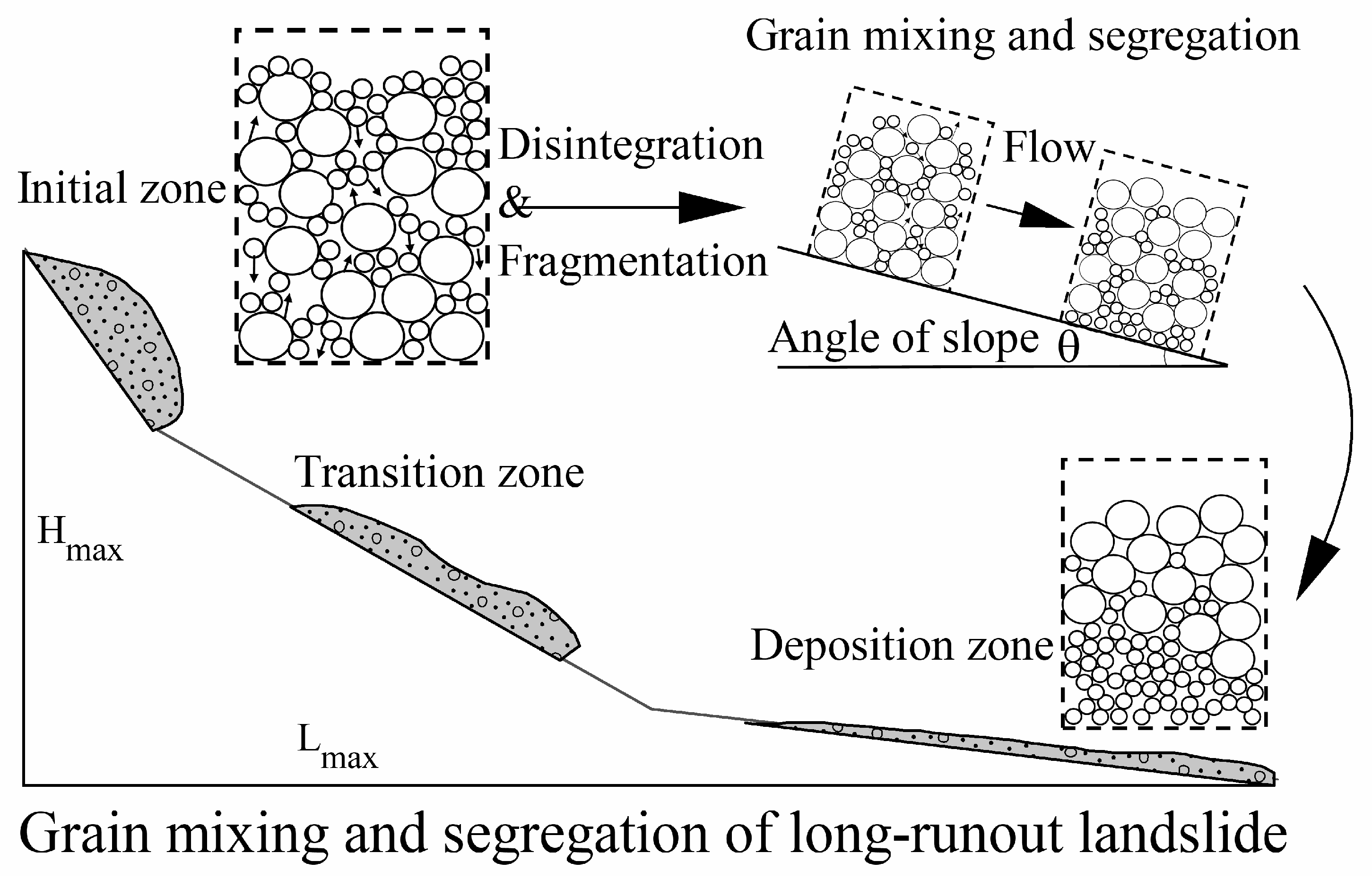
3.1. Role of Dynamic Disintegration and Fragmentation on Mobility of Long-Runout Landslides
3.2. Role of Dynamic Grain Segregation on Mobility of Long-Runout Landslides
3.3. Role of Air on Mobility of Long-Runout Landslides
3.4. Role of Water on Mobility of Landslides
3.5. Role of Ambient Settings on Mobility of Long-Runout Landslides
3.5.1. Role of Extraterrestrial Settings on Mobility of Long-Runout Landslides
3.5.2. Role of Submarine Settings on Mobility of Long-Runout Landslides
4. Dynamic Process of Long-Runout Landslides
4.1. Initial Process of Long-Runout Landslides
4.2. Transition Process of Long-Runout Landslides
4.3. Deposition Process of Long-Runout Landslides
5. Dynamic Mechanisms and Models for Long-Runout Landslides
5.1. Early Models for Long-Runout Landslides
5.2. Flash Heating Model for Long-Runout Landslides
5.3. Rheological Model for Long-Runout Landslides
6. Conclusions
Funding
Conflicts of Interest
Appendix A
| Landslides | (km3) | (km2) | Types of Landslides | References | |||
|---|---|---|---|---|---|---|---|
| Saidmarreh | 0.321 | 21 | / | 4800 | 15,000 | Subaerical landslides | [96] |
| Martinez | 0.246 | 0.38 | / | 1877 | 7600 | Subaerical landslides | [97] |
| Nevados Huascarán | 0.25 | 50~100 | 22.5 | 4000 | 16,000 | Subaerical landslides | [14] |
| Rubble Creek | 0.230 | 0.025 | / | 1060 | 4600 | Subaerical landslides | [98] |
| Bualtar I | 0.404 | 0.01 | / | 1940 | 4800 | Subaerical landslides | [22] |
| Bualtar II | 0.386 | 0.007 | / | 1430 | 3700 | Subaerical landslides | [22] |
| Bualtar III | 0.541 | 0.003 | / | 1300 | 2400 | Subaerical landslides | [22] |
| Pandemonium Creek | 0.222 | 0.005 | / | 2000 | 9000 | Subaerical landslides | [99] |
| Blackhawk | 0.125 | 0.28 | / | 1200 | 9600 | Subaerical landslides | [100] |
| Corno di desde | 0.324 | 0.02 | / | 1200 | 3700 | Subaerical landslides | [100] |
| Deyen, Glarus | 0.112 | 0.6 | / | 740 | 6600 | Subaerical landslides | [100] |
| Diablerets | 0.345 | 0.05 | / | 1900 | 5500 | Subaerical landslides | [100] |
| Disentis | 0.352 | 0.015 | / | 740 | 2100 | Subaerical landslides | [100] |
| Elm | 0.308 | 0.01 | / | 710 | 2300 | Subaerical landslides | [100] |
| Engelberg | 0.216 | 2.75 | / | 1600 | 7400 | Subaerical landslides | [100] |
| Fernpass | 0.089 | 1 | / | 1400 | 15,600 | Subaerical landslides | [100] |
| Flims | 0.128 | 12 | / | 2000 | 15,600 | Subaerical landslides | [100] |
| Frank | 0.248 | 0.03 | / | 870 | 3500 | Subaerical landslides | [100] |
| Garnish | 0.253 | 0.8 | / | 1900 | 7500 | Subaerical landslides | [100] |
| Goldau | 0.200 | 0.035 | / | 1200 | 6000 | Subaerical landslides | [100] |
| Gros Ventre | 0.164 | 0.038 | / | 560 | 3400 | Subaerical landslides | [100] |
| Kandertal | 0.191 | 0.14 | / | 1900 | 9900 | Subaerical landslides | [100] |
| Maligne Lake | 0.168 | 0.5 | / | 920 | 5470 | Subaerical landslides | [100] |
| Medicine Lake | 0.262 | 0.086 | / | 320 | 1220 | Subaerical landslides | [100] |
| Madison | 0.268 | 0.029 | / | 430 | 1600 | Subaerical landslides | [100] |
| Mombiel | 0.462 | 0.0008 | / | 370 | 800 | Subaerical landslides | [100] |
| Obersee GL | 0.360 | 0.12 | / | 1800 | 5000 | Subaerical landslides | [100] |
| Pamir | 0.241 | 2 | / | 1500 | 6200 | Subaerical landslides | [100] |
| Poshivo | 0.365 | 0.15 | / | 1500 | 4100 | Subaerical landslides | [100] |
| Saidmarreh | 0.079 | 20 | / | 1500 | 18,900 | Subaerical landslides | [100] |
| Schachental | 0.580 | 0.0005 | / | 1800 | 3100 | Subaerical landslides | [100] |
| Scimada Saoseo | 0.272 | 0.08 | / | 1500 | 5500 | Subaerical landslides | [100] |
| Sherman | 0.209 | 0.03 | / | 1300 | 6200 | Subaerical landslides | [100] |
| Siders | 0.137 | 1.5 | / | 2400 | 17,400 | Subaerical landslides | [100] |
| Tamins | 0.096 | 1.3 | / | 1300 | 13,500 | Subaerical landslides | [100] |
| Vaiont | 0.333 | 0.25 | / | 500 | 1500 | Subaerical landslides | [100] |
| Val Lagone | 0.418 | 0.00065 | / | 1005 | 2400 | Subaerical landslides | [100] |
| Voralpsee | 0.323 | 0.03 | / | 1100 | 3400 | Subaerical landslides | [100] |
| Wengen 1 | 0.454 | 0.0025 | / | 500 | 1100 | Subaerical landslides | [100] |
| Wengen 2 | 0.421 | 0.0055 | / | 590 | 1400 | Subaerical landslides | [100] |
| Tsergo ri | 0.0505 | 10 | / | 3030 | 60,000 | Subaerical landslides | [100] |
| Valpola | 0.2 | 0.34 | / | 800 | 4000 | Subaerical landslides | [101] |
| Ontake | 0.12 | 0.036 | / | 1550 | 12,000 | Subaerical landslides | [102,103,104] |
| Dusty Creek (1963) | 0.416 | 0.005 | / | 1000 | 2400 | Subaerical landslides | [105] |
| Dusty Creek (1984) | 0.5 | / | / | 1000 | 2000 | Subaerical landslides | [106] |
| Usoi | / | 0.5 | / | 1800 | / | Subaerical landslides | [107] |
| Slide Mountain | 0.254 | 0.013 | / | 420 | 1650 | Subaerical landslides | [2] |
| Queen Elization | 0.3591 | 0.045 | / | 950 | 2645 | Subaerical landslides | [2] |
| Johas Creek North | 0.307 | 0.00024 | / | 860 | 2800 | Subaerical landslides | [2] |
| Johas Creek South | 0.466 | 0.00049 | / | 900 | 1830 | Subaerical landslides | [2] |
| Claps de Luc | 0.462 | 0.0002 | / | 370 | 800 | Subaerical landslides | [2] |
| LA Madeleine | 0.277 | 0.09 | / | 1250 | 4500 | Subaerical landslides | [2] |
| Khait | 0.191 | 0.75 | 4.86 | 1421 | 7410 | Subaerical landslides | [108] |
| Hattian Bala | 0.307 | 0.98 | 0.202 | 737 | 2400 | Subaerical landslides | [109] |
| Mont Blanc Massif | 0.258 | 0.018 | / | 1860 | 7200 | Subaerical landslides | [110] |
| MountStelle | 0.24 | 0.06 | / | 2188 | 9120 | Subaerical landslides | [111] |
| Montserrat | 0.25 | 0.04 | / | 875 | 3500 | Subaerical landslides | [3] |
| Soufrière Guadeloupe | 0.142 | 0.5 | 25 | 1350 | 9500 | Volcanic landslides | [112] |
| St. Helens 20,000 BP | 0.109 | 1 | / | 1750 | 16,000 | Volcanic landslides | [112] |
| Vesuvius 1944 | 0.898 | 0.000179 | 0.022 | 575 | 640 | Volcanic landslides | [113] |
| Vesuvius 1944 | 0.537 | 0.0009 | 0.113 | 505 | 940 | Volcanic landslides | [113] |
| Vesuvius 1944 | 0.570 | 0.00055 | 0.099 | 285 | 500 | Volcanic landslides | [113] |
| Vesuvius 1944 | 0.490 | 0.000793 | 0.126 | 470 | 960 | Volcanic landslides | [113] |
| Vesuvius 1944 | 0.513 | 0.001 | 0.136 | 636 | 1240 | Volcanic landslides | [113] |
| Vesuvius 1944 | 0.529 | 0.0011 | 0.145 | 360 | 680 | Volcanic landslides | [113] |
| Vesuvius | 0.500 | 0.00116 | 0.161 | 410 | 820 | Volcanic landslides | [113] |
| Jocotitlan | 0.096 | 2.8 | 80 | 1150 | 12,000 | Volcanic landslides | [112] |
| Akagi | 0.126 | 4 | / | 2400 | 19,000 | Volcanic landslides | [100] |
| Asakusa | 0.154 | 0.04 | / | 1000 | 6500 | Volcanic landslides | [100] |
| Asama | 0.090 | 2 | 90 | 1800 | 20,000 | Volcanic landslides | [100] |
| Bandaisan | 0.109 | 1.5 | 34 | 1200 | 11,000 | Volcanic landslides | [100] |
| Bezymianni | 0.133 | 0.8 | 30 | 2400 | 18,000 | Volcanic landslides | [100] |
| Callaqui | 0.207 | 0.15 | / | 3100 | 15,000 | Volcanic landslides | [100] |
| Chaos Crags | 0.130 | 0.15 | 8 | 650 | 5000 | Volcanic landslides | [100] |
| Chimborazo | 0.103 | 8.1 | / | 3600 | 35,000 | Volcanic landslides | [100] |
| Chokai | 0.088 | 3.5 | / | 2200 | 25,000 | Volcanic landslides | [100] |
| Colima | 0.100 | 12.5 | 900 | 4000 | 40,000 | Volcanic landslides | [100] |
| Egmont | 0.084 | 7.5 | 250 | 2600 | 31,000 | Volcanic landslides | [100] |
| Egmont | 0.093 | 0.35 | 120 | 2500 | 27,000 | Volcanic landslides | [100] |
| Fuji | 0.104 | 1.8 | / | 2500 | 24,000 | Volcanic landslides | [100] |
| Galunggung | 0.076 | 2.9 | 175 | 1900 | 25,000 | Volcanic landslides | [100] |
| Iriga | 0.095 | 1.5 | 65 | 1050 | 11,000 | Volcanic landslides | [100] |
| Iwaki | 0.114 | 1.3 | / | 1600 | 14,000 | Volcanic landslides | [100] |
| Komagatake | 0.087 | 0.25 | / | 1000 | 11,500 | Volcanic landslides | [100] |
| Kurohime | 0.133 | 0.12 | / | 800 | 6000 | Volcanic landslides | [100] |
| Mageik | 0.089 | 0.09 | / | 800 | 9000 | Volcanic landslides | [100] |
| Mawenzi | 0.075 | 7.1 | 1150 | 4500 | 60,000 | Volcanic landslides | [100] |
| Meru | 0.078 | 15 | 1400 | 3900 | 50,000 | Volcanic landslides | [100] |
| Monbacho | 0.108 | 1 | 45 | 1300 | 12,000 | Volcanic landslides | [100] |
| Mt. St. Helens | 0.106 | 2.5 | 60 | 2550 | 24,000 | Volcanic landslides | [100] |
| Myoko (Sekikawa) | 0.105 | 0.8 | / | 2000 | 19,000 | Volcanic landslides | [100] |
| Myoko (Taguchi) | 0.175 | 0.23 | 10 | 1400 | 8000 | Volcanic landslides | [100] |
| Ovalnaya Zimina | 0.141 | 0.4 | / | 2400 | 17,000 | Volcanic landslides | [100] |
| Papandayan | 0.136 | 0.14 | / | 1500 | 11,000 | Volcanic landslides | [100] |
| Peteroa | 0.046 | 16 | / | 3900 | 85,000 | Volcanic landslides | [100] |
| Popa | 0.109 | 0.8 | / | 1200 | 11,000 | Volcanic landslides | [100] |
| Popocatepetl | 0.121 | 28 | / | 4000 | 33,000 | Volcanic landslides | [100] |
| Shasta | 0.071 | 26 | 450 | 3550 | 50,000 | Volcanic landslides | [100] |
| Shiveluch | 0.167 | 1.5 | 98 | 2000 | 12,000 | Volcanic landslides | [100] |
| Sierra Velluda | 0.136 | 0.5 | / | 3400 | 25,000 | Volcanic landslides | [100] |
| Socompa | 0.093 | 17 | 480 | 3250 | 35,000 | Volcanic landslides | [100] |
| Tashiro | 0.080 | 0.55 | / | 700 | 8800 | Volcanic landslides | [100] |
| Tateshina | 0.112 | 0.35 | / | 1400 | 12,500 | Volcanic landslides | [100] |
| Unzen | 0.131 | 0.34 | 12 | 850 | 6500 | Volcanic landslides | [100] |
| Usu | 0.077 | 0.3 | / | 500 | 6500 | Volcanic landslides | [100] |
| Yatsugatake (Nirasaki) | 0.075 | 9 | / | 2400 | 32,000 | Volcanic landslides | [100] |
| Yatsugatake (Otsukigawa) | 0.112 | 0.27 | 1988/ | 1400 | 12,500 | Volcanic landslides | [100] |
| Kitimat Slide | 0.033 | 0.2 | / | 200 | 6000 | Submarine landslides | [60] |
| A1 | 0.005 | 250 | / | 1700 | 370,000 | Submarine landslides | [60] |
| A2 | 0.009 | 22 | / | 1500 | 160,000 | Submarine landslides | [60] |
| A3 | 0.010 | 8.5 | / | 1400 | 140,000 | Submarine landslides | [60] |
| A4A | 0.010 | 27 | / | 1300 | 130,000 | Submarine landslides | [60] |
| A4B | 0.005 | 320 | / | 2000 | 400,000 | Submarine landslides | [60] |
| Kae Lae slideb | 0.083 | 40 | / | 5000 | 60,000 | Submarine landslides | [60] |
| Molokai slideb | 0.040 | 1100 | / | 5200 | 130,000 | Submarine landslides | [60] |
| Oahu slideb | 0.031 | 1800 | / | 5500 | 180,000 | Submarine landslides | [60] |
| Grant Banks | 0.003 | 76 | / | 365 | 110,000 | Submarine landslides | [61] |
| Hawaii | 0.013 | / | 2000 | 160,000 | Submarine landslides | [61] | |
| Kidnappers | 0.005 | 8 | / | 50 | 11,000 | Submarine landslides | [61] |
| Bay of Biscay | 0.012 | / | 250 | 21,000 | Submarine landslides | [61] | |
| Rockall | 0.002 | 300 | / | 330 | 160,000 | Submarine landslides | [61] |
| Bassein | 0.010 | / | 360 | 37,000 | Submarine landslides | [61] | |
| Agulhas | 0.004 | / | 375 | 106,000 | Submarine landslides | [61] | |
| Copper River Delta | 0.006 | / | 115 | 18,000 | Submarine landslides | [61] | |
| Albatross Bank | 0.057 | / | 300 | 5300 | Submarine landslides | [61] | |
| Portlock Bank | 0.031 | / | 200 | 6500 | Submarine landslides | [61] | |
| Kayak Trough | 0.008 | / | 115 | 15,000 | Submarine landslides | [61] | |
| Atlantic Coast | 0.009 | / | 30 | 3400 | Submarine landslides | [61] | |
| Unnamed | 0.017 | / | 80 | 4800 | Submarine landslides | [61] | |
| Unnamed | 0.008 | / | 18 | 2300 | Submarine landslides | [61] | |
| Magdalena | 0.058 | 0.3 | / | 1400 | 24,000 | Submarine landslides | [61] |
| Valdez | 0.131 | 0.075 | / | 168 | 1280 | Submarine landslides | [61] |
| Mississippi River Delta | / | 0.04 | / | 20 | / | Submarine landslides | [61] |
| Suva | / | 0.15 | / | 100 | / | Submarine landslides | [61] |
| Orkdalsfjord | 0.022 | 0.025 | / | 500 | 22,500 | Submarine landslides | [61] |
| Sandnesjoen | 0.150 | 0.005 | / | 180 | 1200 | Submarine landslides | [61] |
| Sokkelvik | 0.048 | 0.0005 | / | 120 | 2500 | Submarine landslides | [61] |
| Helsinki | 0.028 | 0.000006 | / | 11 | 400 | Submarine landslides | [61] |
| Storegga | 0.011 | 800 | / | 1700 | 160,000 | Submarine landslides | [61] |
| Typical Atlantic Ocean | 0.300 | / | / | 1200 | 4000 | Submarine landslides | [61] |
| Cape Fear | 0.023 | / | / | 700 | 30,000 | Submarine landslides | [61] |
| Blake Escarpment | 0.086 | 600 | / | 3600 | 42,000 | Submarine landslides | [61] |
| East Break East | 0.016 | 13 | 1150 | 70,000 | Submarine landslides | [61] | |
| East Break West | 0.010 | 160 | / | 1100 | 110,000 | Submarine landslides | [61] |
| Navarin Canyon | 0.029 | 5 | / | 175 | 6000 | Submarine landslides | [61] |
| Seward | 0.067 | 0.0027 | / | 200 | 3000 | Submarine landslides | [61] |
| Alsek | 0.010 | / | / | 20 | 2000 | Submarine landslides | [61] |
| Sur | 0.010 | 10 | / | 750 | 75,000 | Submarine landslides | [61] |
| Santa Barbara | 0.052 | 0.02 | / | 120 | 2300 | Submarine landslides | [61] |
| Alika-2b | 0.051 | 300 | / | 4800 | 95,000 | Submarine landslides | [61] |
| Nuuanub | 0.022 | 5000 | / | 5000 | 230,000 | Submarine landslides | [61] |
| Tristan de Cunhab | 0.075 | 150 | / | 3750 | 50,000 | Submarine landslides | [61] |
| Unnamed | 0.059 | 17,880 | 4716 | 7000 | 119,000 | Martian landslides | [56] |
| Unnamed | 0.043 | / | / | 2400 | 56,000 | Martian landslides | [56] |
| Unnamed | 0.100 | 4880 | 1175 | 7000 | 70,000 | Martian landslides | [56] |
| Unnamed | 0.102 | 4183 | 1244 | 8400 | 82,000 | Martian landslides | [56] |
| Unnamed | 0.072 | 4047 | 2200 | 6800 | 94,000 | Martian landslides | [56] |
| Unnamed | 0.085 | / | / | 4400 | 52,000 | Martian landslides | [56] |
| Unnamed | 0.095 | 3267 | 1287 | 7200 | 76,000 | Martian landslides | [56] |
| Unnamed | 0.125 | 2960 | 1675 | 8000 | 64,000 | Martian landslides | [56] |
| Unnamed | 0.108 | 2761 | 1144 | 6800 | 63,000 | Martian landslides | [56] |
| Unnamed | 0.108 | / | / | 5400 | 50,000 | Martian landslides | [56] |
| Unnamed | 0.130 | 1282 | 1244 | 8200 | 63,000 | Martian landslides | [56] |
| Unnamed | 0.096 | 833 | 1075 | 5400 | 56,000 | Martian landslides | [56] |
| Unnamed | 0.080 | 688 | 888 | 3600 | 45,000 | Martian landslides | [56] |
| Unnamed | 0.142 | 668 | 656 | 4400 | 31,000 | Martian landslides | [56] |
| Unnamed | 0.141 | 655 | 470 | 7600 | 54,000 | Martian landslides | [56] |
| Unnamed | 0.150 | 321 | 312 | 5400 | 36,000 | Martian landslides | [56] |
| Unnamed | 0.085 | 157 | 325 | 2800 | 33,000 | Martian landslides | [56] |
| Unnamed | 0.124 | 32 | 125 | 3600 | 29,000 | Martian landslides | [56] |
| Unnamed | 0.200 | 29 | 350 | 4000 | 20,000 | Martian landslides | [56] |
| Unnamed | 0.111 | 98 | 175 | 2000 | 18,000 | Martian landslides | [56] |
| Unnamed | 0.150 | 11 | 44 | 1200 | 8000 | Martian landslides | [56] |
| Unnamed | 0.305 | 38.5 | 84 | 6400 | 21,000 | Martian landslides | [56] |
| Unnamed | 0.310 | 37.1 | 81 | 6200 | 20,000 | Martian landslides | [56] |
| Unnamed | 0.326 | 30.1 | 66 | 6200 | 19,000 | Martian landslides | [56] |
| Unnamed | 0.313 | 23.1 | 50 | 5000 | 16,000 | Martian landslides | [56] |
| Unnamed | 0.365 | 9.8 | 22 | 6200 | 17,000 | Martian landslides | [56] |
| Unnamed | 0.314 | 6.3 | 13 | 2200 | 7000 | Martian landslides | [56] |
| Unnamed | 0.367 | 2.1 | 4 | 2200 | 6000 | Martian landslides | [56] |
| Ophir | 0.14 | 833 | / | 7280 | 52,000 | Martian landslides | [114] |
| OphirWest | 0.15 | 1500 | / | 7050 | 47,000 | Martian landslides | [114] |
| Coprates | 0.08 | 730 | / | 4960 | 62,000 | Martian landslides | [114] |
| Ius | 0.12 | 2600 | / | 7920 | 66,000 | Martian landslides | [114] |
| GangesLandslide1 | 0.10 | 530 | / | 5000 | 50,000 | Martian landslides | [114] |
| GangesLandslide2 | 0.13 | 19 | / | 2899 | 22,300 | Martian landslides | [3] |
| GangesLandslide3 | 0.14 | 9.95 | / | 3124 | 22,316 | Martian landslides | [3] |
| Olympus Mons | 0.40 | 0.165 | / | 1384 | 3460 | Martian landslides | [3] |
| Crater ManySlides1 | 0.24 | 0.0311 | / | 434 | 1810 | Martian landslides | [3] |
| Crater ManySlides2 | 0.23 | 0.0576 | / | 499 | 2169 | Martian landslides | [3] |
| Crater ManySlides3 | 0.30 | 0.0349 | / | 576 | 1920 | Martian landslides | [3] |
| Equatorial Crater | 0.13 | 11.3 | / | 598 | 4600 | Martian landslides | [3] |
| ShalbatanaVallis1 | 0.07 | 31.9 | / | 805 | 11,500 | Martian landslides | [3] |
| ShalbatanaVallis2 | 0.20 | 1 | / | 1120 | 5600 | Martian landslides | [3] |
| Malun | 0.123 | 24,000 | / | 7995 | 65,000 | Iapetus landslides | [3] |
| Iapetus2 | 0.118 | 1600 | / | 9440 | 80,000 | Iapetus landslides | [111] |
| Iapetus3 | 0.133 | 3000 | / | 7980 | 60,000 | Iapetus landslides | [111] |
| EuboeaMontes | 0.084 | 25,000 | / | 6804 | 81,000 | Io landslides | [3] |
| Yigong Landslide | 0.416 | 2.8~3 | 5 | 7280 | 8000 | Subaerical landslides | [19] |
| Landslide in Xikou Town | 0.483 | 0.0172 | / | 724 | 1500 | Subaerical landslides | [17] |
| Touzhaigou Landslide | 0.271 | 0.2 | / | 760 | 2800 | Subaerical landslides | [115] |
| Jiwei Mountain Landslide | 0.273 | 0.05 | 0.84 | 600 | 2200 | Subaerical landslides | [70] |
| Guanling Dazhai Landslide | 0.280 | 0.0179 | 0.72 | 420 | 1500 | Subaerical landslides | [72] |
| Donghekou | 0.267 | 0.15 | 1.28 | 640 | 2400 | Subaerical landslides | [48] |
| Zhaojiagou Landslide | 0.347 | 0.002 | / | 260 | 750 | Subaerical landslides | [116] |
| Shale Mountain Landslide | 0.187 | 0.05 | / | 300 | 1600 | Subaerical landslides | [116] |
| Sanxi Landslide | 0.299 | 0.015 | / | 377 | 1260 | Subaerical landslides | [117] |
| Pufu Landslide 1 | 0.340 | 0.45 | 1.1 | 1700 | 5000 | Subaerical landslides | [16] |
| Pufu Landslide 2 | 0.344 | 0.00005 | / | 1100 | 3200 | Subaerical landslides | [16] |
| Wenjiagou | 0.330 | 0.5 | 3 | 1320 | 4000 | Subaerical landslides | [50] |
| Shuimogou | 0.430 | 0.2 | 0.91 | 860 | 2000 | Subaerical landslides | [50] |
| Large House Foundation | 0.463 | 0.163 | 0.79 | 880 | 1900 | Subaerical landslides | [50] |
| Hongshigou | 0.385 | 0.134 | 0.68 | 1040 | 2700 | Subaerical landslides | [50] |
| Before The Nest | 0.350 | 0.12 | 0.59 | 560 | 1600 | Subaerical landslides | [50] |
| Xiaojia Mountain | 0.689 | 0.078 | 0.46 | 930 | 1350 | Subaerical landslides | [50] |
| Niumian Gou | 0.303 | 0.075 | 0.52 | 800 | 2640 | Subaerical landslides | [50] |
| Establish A Ditch | 0.433 | 0.0536 | 0.35 | 650 | 1500 | Subaerical landslides | [50] |
| Caocaoping | 0.433 | 0.0533 | 0.35 | 580 | 1340 | Subaerical landslides | [50] |
| Huoshi Gou | 0.530 | 0.0468 | 0.32 | 700 | 1320 | Subaerical landslides | [50] |
| Shibangou Village | 0.361 | 0.045 | 0.49 | 650 | 1800 | Subaerical landslides | [50] |
| Xiejiadianzi | 0.450 | 0.04 | 0.29 | 720 | 1600 | Subaerical landslides | [50] |
| Dashigou | 0.400 | 0.0314 | 0.24 | 560 | 1400 | Subaerical landslides | [50] |
| Changping | 0.417 | 0.0283 | 0.22 | 500 | 1200 | Subaerical landslides | [50] |
| Xiaomuling | 0.693 | 0.0273 | 0.21 | 710 | 1025 | Subaerical landslides | [50] |
| Baishuling | 0.517 | 0.0256 | 0.20 | 620 | 1200 | Subaerical landslides | [50] |
| Dawan Bay | 0.480 | 0.0248 | 0.20 | 480 | 1000 | Subaerical landslides | [50] |
| Zengjia Mountain | 0.573 | 0.0239 | 0.19 | 650 | 1135 | Subaerical landslides | [50] |
| Shi Zhouzi | 0.533 | 0.0192 | 0.16 | 640 | 1200 | Subaerical landslides | [50] |
| Long Beach | 0.636 | 0.0163 | 0.15 | 1050 | 1650 | Subaerical landslides | [50] |
| Hongma Gong | 0.413 | 0.0154 | 0.14 | 330 | 800 | Subaerical landslides | [50] |
| Baiguo Village | 0.325 | 0.0147 | 0.14 | 260 | 800 | Subaerical landslides | [50] |
| Qinglong Village | 0.333 | 0.0138 | 0.13 | 200 | 600 | Subaerical landslides | [50] |
| Pengjiashan | 0.580 | 0.0129 | 0.12 | 580 | 1000 | Subaerical landslides | [50] |
| Longwan Village | 0.535 | 0.0092 | 0.10 | 460 | 860 | Subaerical landslides | [50] |
| Zhang Zhengbo | 0.400 | 0.0091 | 0.10 | 320 | 800 | Subaerical landslides | [50] |
| Du Jiayan | 0.455 | 0.0086 | 0.094 | 400 | 880 | Subaerical landslides | [50] |
| Ma Flooring | 0.534 | 0.0085 | 0.094 | 395 | 740 | Subaerical landslides | [50] |
| Rock Watchtower Nest | 0.488 | 0.0082 | 0.092 | 390 | 800 | Subaerical landslides | [50] |
| Window Ditch | 0.440 | 0.0081 | 0.091 | 295 | 670 | Subaerical landslides | [50] |
| Zhao Jiashan | 0.400 | 0.007 | 0.082 | 280 | 700 | Subaerical landslides | [50] |
| Weiziping | 0.400 | 0.006 | 0.074 | 240 | 600 | Subaerical landslides | [50] |
| Caterpillar Mountain 2 # | 0.676 | 0.0056 | 0.070 | 500 | 740 | Subaerical landslides | [50] |
| Waqian Mountain | 0.403 | 0.0056 | 0.070 | 250 | 620 | Subaerical landslides | [50] |
| Muhongping | 0.433 | 0.0054 | 0.068 | 420 | 970 | Subaerical landslides | [50] |
| Daping Shang | 0.570 | 0.0051 | 0.065 | 365 | 640 | Subaerical landslides | [50] |
| Liushuping 2 | 0.414 | 0.004 | 0.054 | 240 | 580 | Subaerical landslides | [50] |
| Luanshibao Landslide | 0.200 | 0.7 | 4.36 | 821 | 4100 | Subaerical landslides | [50] |
| Big Light Bag | 0.429 | 7.42 | 6.2 | 1500 | 3500 | Subaerical landslides | [49] |
| Sucun Landslide | 0.239 | 0.004 | 0.235 | 320 | 1340 | Subaerical landslides | [52] |
| Hongao Landslide | 0.180 | 0.0232 | 0.385 | 126 | 700 | Subaerical landslides | [118] |
| Xinmo Landslide | 0.448 | 0.045 | / | 1120 | 2500 | Subaerical landslides | [73] |
| Walai Landslide | 0.320 | 0.51 | / | 1115 | 3480 | Subaerical landslides | [119] |
| Shuicheng Landslide | 0.366 | 0.0191 | 0.3 | 474 | 1296 | Subaerical landslides | [53] |
| Nixu Landslide | 0.184 | 0.33 | 0.55 | 860 | 4670 | Subaerical landslides | [120] |
| Heifangtai Landslide | 0.184 | 0.0127 | 0.1015 | 160 | 870 | Subaerical landslides | [67] |
| Yushu Bingda Landslide | 0.308 | 0.00009 | / | 552 | 1795 | Subaerical landslides | [69] |
| Best Power-Law Fit | R2 | |
|---|---|---|
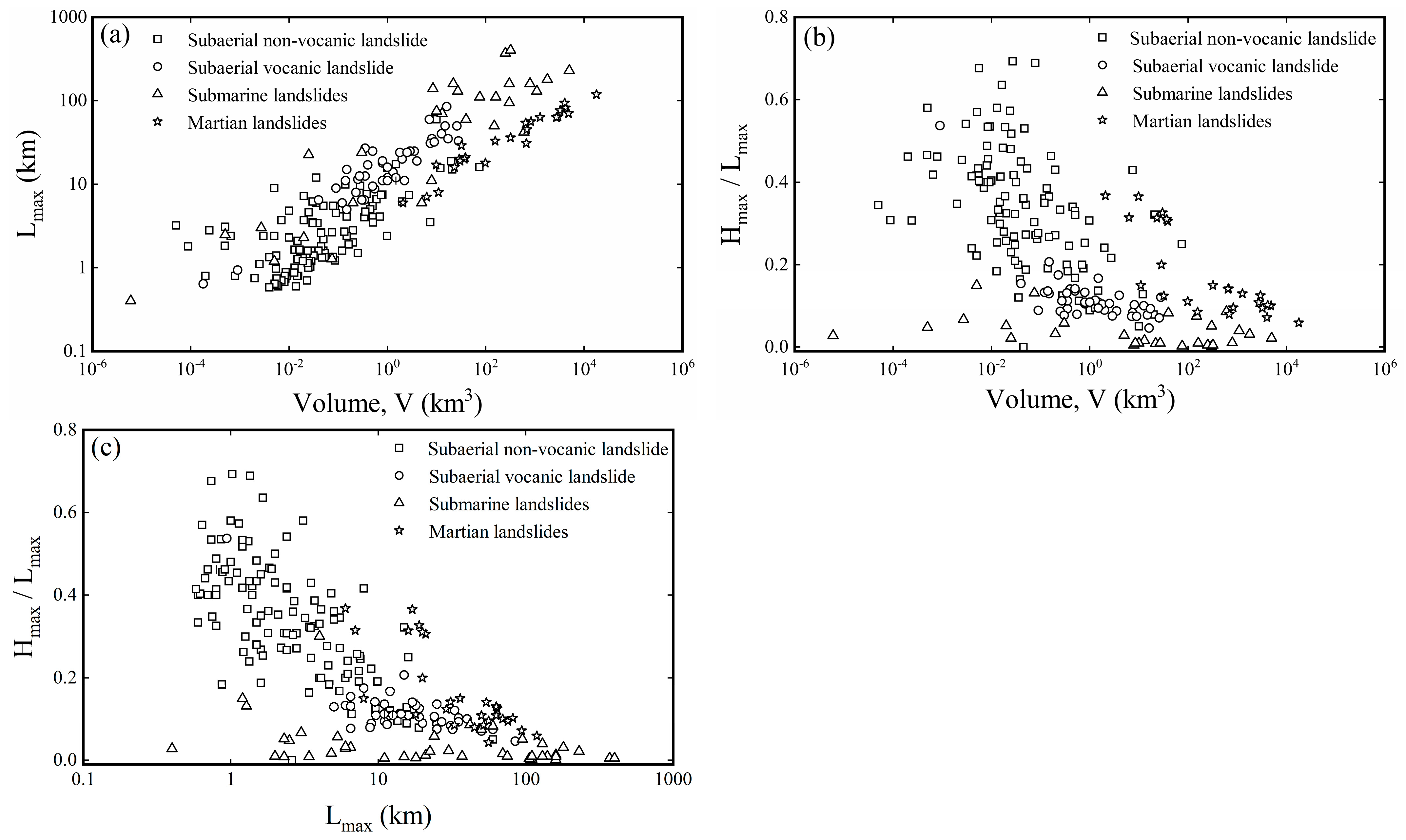
| Graph of Lmax versus V (Figure 2a) | ||
| Subaerial non-volcanic landslides | Lmax = 8V0.28 | 0.40 |
| Subaerial volcanic landslides | Lmax = 17V0.38 | 0.67 |
| Submarine landslides | Lmax = 52V0.18 | 0.42 |
| Martian landslides | Lmax = 7V0.3 | 0.94 |
| Graph of Hmax/Lmax versus V (Figure 2b) | ||
| Subaerial non-volcanic landslides | Hmax/Lmax = 0.27V−0.07 | 0.20 |
| Subaerial volcanic landslides | Hmax/Lmax = 0.12V−0.25 | 0.93 |
| Submarine landslides | Hmax/Lmax = 0.04V−0.05 | 0.11 |
| Martian landslides | Hmax/Lmax = 0.44V−0.20 | 0.68 |
| Graph of Hmax/Lmax versus Lmax (Figure 2c) | ||
| Subaerial non-volcanic landslides | Hmax/Lmax = 0.43Lmax−0.20 | 0.42 |
| Subaerial volcanic landslides | Hmax/Lmax = 0.60Lmax−0.65 | 0.89 |
| Submarine landslides | Hmax/Lmax = 0.07Lmax−0.24 | 0.11 |
| Martian landslides | Hmax/Lmax = 0.85Lmax−0.48 | 0.57 |
References
- Legros, F. The mobility of long-runout landslides. Eng. Geol. 2002, 63, 301–331. [Google Scholar] [CrossRef]
- Locat, P.; Couture, R.; Leroueil, S.; Locat, J.; Jaboyedoff, M. Fragmentation energy in rock avalanches. Can. Geotech. J. 2006, 43, 830–851. [Google Scholar] [CrossRef]
- Lucas, A.; Mangeney, A.; Ampuero, J. Frictional velocity-weakening in landslides on Earth and on other planetary bodies. Nat. Commun. 2014, 5, 3417. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, C.; Chen, H.; Ren, J.; Zhu, C. Investigation on catastrophic landslide of January 11, 2013 at ZhaoJiaGou, ZhenXiong County, YunNan Province. J. Eng. Geol. 2013, 21, 6–15. [Google Scholar]
- Hungr, O. Rock avalanche occurrence, process and modelling. Landslides Massive Rock Slope Fail. 2006, 49, 243–266. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhang, Z.; Huang, R. Study on dynamics of rock avalanches: State of the art report. J. Mt. Sci. 2007, 25, 72–84. [Google Scholar]
- Zhang, M.; Yin, Y.; Wu, S.; Zhang, Y. Development status and prospects of studies on kinematics of long-runout rock avalanches. J. Eng. Geol. 2010, 18, 805–817. [Google Scholar]
- Korup, O.; Schneider, D.; Huggel, C.; Dufresne, A. 7.18 Long-Runout Landslides. Treatise Geomorphol. 2013, 7, 183–199. [Google Scholar] [CrossRef]
- Li, K.; Wang, Y.; Lin, Q.; Chen, Q.; Wu, Y. Experiments on granular flow behavior and deposit characteristics: Implications for rock avalanche kinematics. Landslides 2021, 18, 1779–1799. [Google Scholar] [CrossRef]
- Gary, M.; McAffe, R.; Wolf, C. Glossary of Geology; American Geological Institute: Washington, DC, USA, 1972; p. 805. [Google Scholar]
- International Union of Geological Sciences Working Group on Landslide. A suggested method for describing the rate of movement of a landslide. Bull. Int. Assoc. Eng. Geol. 1995, 52, 75–78. [Google Scholar] [CrossRef]
- Heim, A. Bergsturz und Menschenleben; Fretz and Wasmuth Verlag: Zurich, Switzerland, 1932; p. 218. [Google Scholar]
- Buss, E.; Heim, A. Der Bergsturz von Elm. Z. Der Dtsch. Geol. Ges. 1881, 33, 540–564. [Google Scholar]
- Plafker, G.; Ericksen, G. Ericksen Nevados Huascaran avalanches Peru. Dev. Geotech. Eng. 1978, 14, 277–314. [Google Scholar] [CrossRef]
- Dunning, S.; Mitchell, W.; Rosser, N.; Petley, D. The Hattian Bala rock avalanche and associated landslides triggered by the Kashmir Earthquake of 8 October 2005. Eng. Geol. 2007, 93, 130–144. [Google Scholar] [CrossRef]
- Cheng, X.; Zhu, C.; Qi, W.; Qi, J.; Yuan, J. Formation conditions, development tendency and preventive measures of Pufu landslide in Luquan of Yunnan. Miner. Resour. Geol. 2015, 29, 395–401. [Google Scholar]
- Zhong, L. Geological disaster development mechanism and their prevention countermeasures in the “Three Rivers” juxtaposition area, Yunnan Province. Chin. J. Geol. Hazard Control 2007, 4, 6. [Google Scholar]
- Hu, M.; Cheng, Q.; Wang, F. Experimental study on formation of YiGong long-distance high-speed landslide. J. Rock Mech. Eng. 2009, 28, 138–143. [Google Scholar]
- Yin, Y. Study of the giant landslide of Bomi Yigong expressway in Tibet. Chin. J. Geol. Hazard Control 2000, 11, 103. [Google Scholar] [CrossRef]
- Wang, T.; Shi, J.; Wu, S.; Zhang, Y.; Li, B. Formation mechanism of wenjiagou high-speed and long-runout debris avalanche triggered by WenChuan earthquake. J. Eng. Geol. 2008, 18, 631–644. [Google Scholar]
- Pudasaini, P.; Miller, S. The hypermobility of huge landslides and avalanches. Eng. Geol. 2013, 157, 124–132. [Google Scholar] [CrossRef]
- Hewitt, K. Catastrophic landslide deposits in the karakoram Himalaya. Science 1988, 242, 64–67. [Google Scholar] [CrossRef]
- Davies, T.; McSaveney, M.; Hodgson, K. A fragmentation-spreading model for long-runout rock avalanches. Can. Geotech. J. 1999, 36, 1096–1110. [Google Scholar] [CrossRef]
- Bowman, E.; Take, W.; Rait, K.; Hann, C. Physical models of rock avalanche spreading behaviour with dynamic fragmentation. Can. Geotech. J. 2012, 49, 460–476. [Google Scholar] [CrossRef]
- Hardin, O. Crushing of Soil Particles. J. Geotech. Eng. 1985, 111, 1177. [Google Scholar] [CrossRef]
- Lin, Q.; Chen, Q.; Li, K.; Wang, Y.; Liu, S. Review on fragmentation-related dynamics of rock avalanches. J. Eng. Geol. 2023, 31, 815–829. [Google Scholar] [CrossRef]
- Strom, A. Morphology and internal structure of rockslides and rock avalanches: Grounds and constraints for their modelling. In Landslides from Massive Rock Slope Failure; Springer: Dordrecht, The Netherlands, 2006; pp. 305–326. [Google Scholar] [CrossRef]
- Friedmann, S.; Taberlet, N.; Losert, W. Rock-avalanche dynamics: Insights from granular physics experiments. Int. J. Earth Sci. 2006, 95, 911–919. [Google Scholar] [CrossRef]
- Crosta, G.; Frattini, P.; Fusi, N. Fragmentation in the Val Pola rock avalanche, Italian Alps. J. Geophys. Res. 2007, 112, F01006. [Google Scholar] [CrossRef]
- Gray, J. Particle segregation in dense granular flow. Annu. Rev. Fluid Mech. 2018, 50, 407–433. [Google Scholar] [CrossRef]
- Yu, F.; Su, L. Experimental investigation of mobility and deposition characteristics of dry granular flow. Landslides 2021, 18, 1875–1887. [Google Scholar] [CrossRef]
- Hu, W.; Chang, C.; McSaveney, M.; Huang, R.; Xu, Q.; Zheng, Y.; Yu, J. A weakening rheology of dry granular flows with extensive brittle grain damage in high-speed rotary shear experiments. Geophys. Res. Lett. 2020, 47, e2020GL087763. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, G. Effect of particle breakage-induced frictional weakening on the dynamics of landslides. Granul. Matter 2022, 24, 72. [Google Scholar] [CrossRef]
- Schneider, J.; Fisher, R.V. Transport and emplacement mechanisms of large volcanic debris avalanches: Evidence from the northwest sector of Cantal Volcano (France). J. Volcanol. Geotherm. Res. 1998, 83, 141–165. [Google Scholar] [CrossRef]
- Cruden, D.; Hungr, O. The debris of the Frank Slide and theories of rockslide-avalanche mobility. Can. J. Earth Sci. 1986, 23, 425–432. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Yang, G.; Chen, Y.; Jiang, J. A constitutive model for the state-dependent behaviors of rockfill material considering particle breakage. Sci. China Technol. Sci. 2014, 57, 1636–1646. [Google Scholar] [CrossRef]
- Yu, F. Particle breakage in granular soils: A review. Part. Sci. Technol. 2019, 39, 91–100. [Google Scholar] [CrossRef]
- Yu, F.; Su, L.; Peng, X. Influence of particle breakage on the isotropic compressibility of sands. J. Mt. Sci. 2022, 19, 2086–2099. [Google Scholar] [CrossRef]
- Wang, F.; Sassa, K.; Wang, G. Mechanism of a long-runout landslide triggered by the August 1998 heavy rainfall in Fukushima Prefecture, Japan. Eng. Geol. 2002, 63, 169–185. [Google Scholar] [CrossRef]
- Ottino, J.; Khakhar, D. Mixing and segregation of granular materials. Annu. Rev. Fluid Mech. 2000, 32, 55–91. [Google Scholar] [CrossRef]
- Zhou, D.; Hg, C. Numerical investigation of reverse segregation in debris flows by DEM. Granul. Matter 2010, 12, 507–516. [Google Scholar] [CrossRef]
- Kokelaar, B.; Graham, R.; Gray, J.; Vallance, J.W. Fine-grained linings of leveed channels facilitate runout of granular flows. Earth Planet. Sci. Lett. 2014, 385, 172–180. [Google Scholar] [CrossRef]
- Zhou, G.; Sun, Q.; Cui, P. Study on the mechanisms of solids segregation in granular debris flows. J. SiChuan Univ. Eng. Sci. Ed. 2013, 45, 28–36. [Google Scholar] [CrossRef]
- Li, T.; Fan, X.; Jiang, Y. A study on inverse grading and its influence on impact effect of landslide-debris flow. Yangtze River 2018, 49, 58–65. [Google Scholar] [CrossRef]
- Kent, P. The transport mechanism in catastrophic rock Falls. J. Geol. 1966, 74, 79–83. [Google Scholar] [CrossRef]
- Shreve, R. Sherman Landslide, Alaska. Science 1966, 154, 1639–1643. [Google Scholar] [CrossRef]
- Wu, S.; Wang, T.; Shi, L.; Sun, P.; Shi, J. Study on catastrophic landslides triggered by 2008 great WenChuan earthquake, Sichuan, China. J. Eng. Geol. 2010, 18, 145–159. [Google Scholar]
- Qi, C.; Xing, A.; Yin, Y.; Li, B. Numerical simulation of dynamic behavior of donghekou rockslide-debris avalanche. J. Eng. Geol. 2012, 20, 334–339. [Google Scholar]
- Zhang, W.; Huang, R.; Pei, X. Analysis on kinematics characteristics and movement process of Daguangbao landslide. J. Eng. Geol. 2015, 23, 866–885. [Google Scholar] [CrossRef]
- Zhan, W.; Huang, R.; Pei, X.; Li, W. Empirical prediction model for movement distance of gully type rock avalanches. J. Eng. Geol. 2017, 25, 154–163. [Google Scholar] [CrossRef]
- Sassa, K. Geotechnical model for the motion of landslides. In Proceedings of the 5th International Symposium on Landslides, Lausanne, Switzerland, 10–15 July 1988; pp. 37–55. [Google Scholar]
- Gan, J.; Fan, J.; Tang, C.; Wang, C.; Liu, Z. Sucun landslide in suichang county of zejiang province: Characteristicesand failure mechanism. J. Catastrophology 2017, 32, 73–78. [Google Scholar] [CrossRef]
- Zheng, G.; Xu, Q.; Liu, X.; Li, Y.; Dong, X.; Ju, N.; Guo, C. The JiChang landslide on July 23, 2019 in ShuiCheng, GuiZhou: Characteristics and failure mechanism. J. Eng. Geol. 2020, 28, 541–556. [Google Scholar] [CrossRef]
- Yu, F.; Su, L.; Li, X.; Zhao, Y. Impact dynamics of granular flow on rigid barriers: Insights from numerical investigation using material point method. J. Mt. Sci. 2024, 21, 4083–4111. [Google Scholar] [CrossRef]
- Yu, F.; Su, L.; Li, X.; Zhao, Y. Mobility and dynamic erosion process of granular flow: Insights from numerical investigation using material point method. J. Mt. Sci. 2024, 21, 2713–2738. [Google Scholar] [CrossRef]
- McEwen, A. Mobility of large rock avalanches: Evidence from Valles Marineris, Mars. Geology 1989, 17, 1111–1114. [Google Scholar] [CrossRef]
- Crosta, G.; Frattini, P.; Valbuzzi, E.; Blasio, F. Introducing a new inventory of large martian landslides. Earth Space Sci. 2018, 5, 89–119. [Google Scholar] [CrossRef]
- Watkins, J.A.; Ehlmann, B.L.; Yin, A. Long-runout landslides and the long-lasting effects of early water activity on Mars. Geol. Soc. Am. 2015, 43, 107–110. [Google Scholar] [CrossRef]
- Johnson, B.; Campbell, C. Drop height and volume control the mobility of long-runout landslides on the Earth and Mars. Geophys. Res. Lett. 2017, 44, 12091–12097. [Google Scholar] [CrossRef]
- Lipman, P.; Normark, W.; Moore, J.; Wilson, J.; Gutmacher, C. The giant submarine Alika debris slide, Mauna Loa, Hawaii. J. Geophys. Res. Soild Earth 1988, 93, 4279–4299. [Google Scholar] [CrossRef]
- Hampton, M.; Lee, H.; Locat, J. Submarine landslides. Rev. Geophys. 1996, 34, 33–59. [Google Scholar] [CrossRef]
- Masson, D.; Harbitz, C.; Wynn, R.; Pedersen, G.; Løvholt, F. Submarine landslides: Processes, triggers and hazard prediction. Philos. Trans. R. Soc. A 2006, 304, 2009–2039. [Google Scholar] [CrossRef]
- Harbitz, C.; Løvholt, F.; Bungum, H. Submarine landslide tsunamis:how extreme and how likely? Nat. Hazards 2014, 72, 1341–1374. [Google Scholar] [CrossRef]
- Iverson, R. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Moore, J.; Normark, W.; Holcomb, R. Giant Hawaiian landslides. Earth Sci. 1994, 22, 119–144. [Google Scholar] [CrossRef]
- Liu, P.; Lv, Q.; Wu, J.; Ma, J.; Liao, Z. A flume model test to investigate initation mechanisms of rainsstorm-induced shallow landslides. J. Eng. Geol. 2024, 33, 531–540. [Google Scholar] [CrossRef]
- Pan, R.; Liang, L.; Zhu, Y.; Wang, G. Field investigation and motion simulation study of high-speed long-range landslide in yushu, qinghai-tibet. Ind. Constr. 2023, 53, 579–584. [Google Scholar]
- Huang, R. Mechanism and geomechanical modes of landslide hazards triggered by WenChuan 8.0 earthquake. Chin. J. Rock Mech. Eng. 2009, 28, 1239–1249. [Google Scholar]
- Guo, F.; Zhang, L.; Wang, X.; Song, X. Analysis on evolution process and movement mechanism of the Luojiapo landslide in Heifangtai, Gansu Province. Chin. J. Geol. Hazard Control 2023, 34, 11–20. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, R.; Yin, Y.; Hou, S.; Dong, X.; Fan, X.; Tang, M. The Jiweishan landslide of June 5, 2009 in WuLong, ChongQing:characteristics and failure mechanis. J. Eng. Geol. 2009, 17, 433–444. [Google Scholar]
- Feng, Z.; You, Y.; Chen, L.; Wang, L. Numerical simulation study on kinematic post-failure process of large-scale landslide in the bailong river basin. J. Catastrophology 2024, 39, 45–50. [Google Scholar] [CrossRef]
- Yin, Y.; Zhu, J.; Yang, Y. Investigation of a high speed and long run-out rockslide-debris flow at DaZhai in GuanLing of GuiZhou province. J. Eng. Geol. 2010, 18, 445–454. [Google Scholar]
- Xu, Q.; Li, W.; Dong, X.; Xiao, X.; Fan, X.; Pei, X. The Xinmocun landslide on June 24,2017 in Maoxian, Sichuan: Characteristics and failure mechanism. Chin. J. Rock Mech. Eng. 2017, 36, 2612–2628. [Google Scholar] [CrossRef]
- Hsu, K.J. Catastrophic Debris Streams (Sturzstroms) Generated by Rockfalls. GSA Bull. 1975, 86, 129–140. [Google Scholar] [CrossRef]
- He, K.; Wang, Y.; Chen, Q.; Li, Q.; Shi, A. Research on the substrate entrainment dynamics of rock avalanches: State of the art. J. Eng. Geol. 2024, 32, 904–917. [Google Scholar] [CrossRef]
- Davies, T. Spreading of rock avalanche debris by mechanical fluidization. Rock Mech. 1982, 15, 9–24. [Google Scholar] [CrossRef]
- Li, K.; Cheng, Q.; Lin, Q.; Wang, Y.; Song, Z. State of the art on rock avalanche dynamics from granular flow mechanics. Earth Sci. 2022, 47, 893–912. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, C.; Miao, T.; Mu, Q. Kinematic block model of long run-out prediction for high-speed landslides. Chin. J. Rock Mech. Eng. 2000, 19, 742–746. [Google Scholar]
- Okura, Y.; Kitahara, H.; Sammori, T.; Kawanami, A. The effects of rockfall volume on runout distance. Eng. Geol. 2000, 58, 109–124. [Google Scholar] [CrossRef]
- Melosh, H. Acoustic fluidization: A new geologic process. J. Geophys. Res. Soild Earth 1979, 84, 7513–7520. [Google Scholar] [CrossRef]
- Collins, G.; Melosh, H. Acoustic fluidization and the extraordinary mobility of sturzstroms. J. Geophys. Res. Soild Earth 2003, 108, B102473. [Google Scholar] [CrossRef]
- Heaton, T.H. Evidence for and implications of self-healing pulses of slip in earthquake rupture. Phys. Earth Planet. Inter. 1990, 64, 1–20. [Google Scholar] [CrossRef]
- Tsutsumi, A.; Shimamoto, T. High velocity frictional properties of gabbro. Geophys. Res. Lett. 1997, 24, 699–702. [Google Scholar] [CrossRef]
- Rice, R. Heating and weakening of faults during earthquake slip. J. Geophys. Res. Soild Earth 2006, 111, B05311. [Google Scholar] [CrossRef]
- Goren, L.; Aharonov, E. Long runout landslides: The role of frictional heating and hydraulic diffusivity. Geophys. Res. Lett. 2007, 34, L07301. [Google Scholar] [CrossRef]
- Beeler, N.; Tullis, T.; Goldsby, D. Constitutive relationships and physical basis of fault strength due to flash heating. J. Geophys. Res. Soild Earth 2008, 113, B01401. [Google Scholar] [CrossRef]
- Goldsby, D.L.; Tullis, T.E. Flash heating leads to low frictional strength of crustal rocks at earthquake slip rates. Science 2011, 334, 216–218. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; He, S.; Hu, W. A thermo-poro-mechanics model predicts the transition from creep to rapid movement of large landslides. Rock Mech. Rock Eng. 2024, 57, 8243–8261. [Google Scholar] [CrossRef]
- GDR MiDi. On dense granular flows. Eur. Phys. J. E 2004, 14, 341–365. [Google Scholar] [CrossRef]
- da Cruz, F.; Emam, S.; Prochnow, M.; Roux, J.; Chevoir, F. Rheophysics of dense granular materials: Discrete simulation of plane shear flows. Phys. Rev. E 2005, 72, 021309. [Google Scholar] [CrossRef]
- Jop, P.; Forterre, Y.; Pouliquen, O.A. Constitutive law for dense granular flows. Nature 2006, 441, 727–730. [Google Scholar] [CrossRef]
- Hatano, T. Power-law friction in closely packed granular materials. Phys. Rev. E 2007, 75, 060301. [Google Scholar] [CrossRef]
- Ding, Z.; Hu, W.; Chang, C.; Li, Y.; Wang, G. Shear behaviors of confined flow: Insights for understanding the influences of fractal particle size distribution on high mobility of granular flows. Geophys. Res. Lett. 2024, 51, e2024GL108956. [Google Scholar] [CrossRef]
- Hu, W.; Zheng, Y.; McSaveney, M.; Xu, Q.; Asch, T. Fluidization of bed material caused by shear thinning during rock avalanche entrainment: Insights from flume tests and rheological experiments. Eng. Geol. 2023, 325, 107276. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, Q.; Li, K.; Shi, A.; Li, T. Review on rock avalanche dynamics. J. Earth Sci. Environ. 2021, 43, 164–181. [Google Scholar] [CrossRef]
- Harrison, J.; Falcon, N. An ancient landslip at saidmarreh in southwestern iran. J. Geol. 1938, 46, 296–309. Available online: http://www.jstor.org/stable/30081302 (accessed on 1 October 2025). [CrossRef]
- Bock, C. Martinez Mountain rock avalanche. Rev. Eng. Geol. 1977, 3, 155–168. [Google Scholar] [CrossRef]
- Moore, D.; Mathews, W. The Rubble Creek landslide, southwestern British Columbia. Can. J. Earth Sci. 1978, 15, 1039–1052. [Google Scholar] [CrossRef]
- Evans, S.; Clague, J.J.; Woodsworth, G.J.; Hungr, O. The Pandemonium Creek rock avalanche, British Columbia. Can. Geotech. J. 1989, 26, 427–446. [Google Scholar] [CrossRef]
- Hayashi, J.; Self, S. A comparison of pyroclastic flow and debris avalanche mobility. J. Geophys. Res. Soild Earth 1992, 97, 9063–9071. [Google Scholar] [CrossRef]
- Azzoni, A.; Chiesa, S.; Frassoni, A.; Govi, M. The Valpola landslide. Eng. Geol. J. 1992, 33, 123–139. [Google Scholar] [CrossRef]
- Anma, S.; Maikuma, H.; Yoshimura, M.; Fujita, Y.; Okusa, S. Dynamics of earthquake-induced slope failure of Ontake. Int. J. Rock Mech. Min. Sci. Geomech. 1989, 26, 89. [Google Scholar] [CrossRef]
- Voight, B.; Janda, R.; Glicken, H.; Douglass, P. Nature and mechanics of the Mount St.Helens rockslide-avalanche of 18 May 1980. Geotechnique 1980, 33, 243–273. [Google Scholar] [CrossRef]
- Voight, B.; Sousa, J. Lessons from Ontake-san: A comparative analysis of debris avalanche dynamics. Eng. Geol. 1994, 38, 261–297. [Google Scholar] [CrossRef]
- Clague, J.; Souther, J. The Dusty Creek landslide on Mount Cayley, British Columbia. Can. J. Earth Sci. 1982, 19, 524–539. [Google Scholar] [CrossRef]
- Lu, Z.; Cruden, D. Two debris flow modes on Mount Cayley, British Columbia. Can. Geotech. J. 1996, 33, 123–139. [Google Scholar] [CrossRef]
- Schuster, R.L.; Alford, D. Usoi landslide dam and lake sarez, pamir mountains, tajikistan. Environ. Eng. Geosci. 2004, 10, 151–168. [Google Scholar] [CrossRef]
- Evans, G.; Roberts, J.; Ischuk, A.; Delaney, K.; Morozova, G.; Tutubalina, O. Landslides triggered by the 1949 Khait earthquake, Tajikistan, and associated loss of life. Eng. Geol. 2009, 109, 195–212. [Google Scholar] [CrossRef]
- Basharat, M.; Rohn, J.; Ehret, D.; Baig, M. Lithological and structural control of Hattian Bala rock avalanche triggered by the Kashmir earthquake 2005, sub-Himalayas, northern Pakistan. J. Earth Sci. 2012, 23, 213–224. [Google Scholar] [CrossRef]
- Akçar, N.; Deline, P.; Ivy-Ochs, S.; Alfimov, V.; Hajdas, I.; Kubik, K.W.; Christl, M.; Schlüchter, C. The AD 1717 rock avalanche deposits in the upper Ferret Valley (Italy): A dating approach with cosmogenic 10Be. J. Quat. Sci. 2012, 27, 383–392. [Google Scholar] [CrossRef]
- Singer, K.N.; McKinnon, W.; Schenk, P.; Moore, J. Massive ice avalanches on Iapetus mobilized by friction reduction during flash heating. Nat. Geosci. 2012, 5, 574–578. [Google Scholar] [CrossRef]
- Siebe, C.; Komorowski, J.; Sheridan, M. Morphology and emplacement of an unusual debris-avalanche deposit at Jocotitlán volcano, Central Mexico. Bull. Volcanol. 1992, 54, 573–589. [Google Scholar] [CrossRef]
- Hazlett, R.; Buesch, D.; Anderson, J.; Elan, R.; Scandone, R. Geology, failure conditions, and implications of seismogenic avalanches of the 1944 eruption at Vesuvius, Italy. J. Volcanol. Geotherm. Res. 1991, 47, 249–264. [Google Scholar] [CrossRef]
- Lucas, A.; Mangeney, A.; Mège, D.; Bouchut, F. Influence of the scar geometry on landslide dynamics and deposits: Application to Martian landslides. J. Geophys. Res. Planets 2011, 116, E10001. [Google Scholar] [CrossRef]
- Zhong, L. History and enlightenment of land subsidence controlling in Tianjin City. Chin. J. Geol. Hazard Control 2008, 3, 59. [Google Scholar]
- Zhang, M.; Yin, Y. Dynamics, mobility-controlling factors and transport mechanisms of rapid long-runout rock avalanches in China. Eng. Geol. 2013, 167, 37–58. [Google Scholar] [CrossRef]
- Yin, Z.; Xu, Y.; Zhao, W. SanXi village landslide in DuJiangyan, SiChuan province on July 10, 2013. J. Eng. Geol. 2014, 22, 309–318. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Q.; Peng, D.; Zhao, K.; Guo, C. An experimental study of the permeability of the catastrophic landslide at the Shenzhen landfill. Hydrogeol. Eng. Geol. 2017, 44, 131–136+149. [Google Scholar] [CrossRef]
- Chen, J.; Chen, R.; Mi, D.; Zheng, X.; Gao, C. Kinematic processes and fragmentation characteristics of walai rock avalanche landslide in Tibet. Adv. Eng. Sci. 2020, 52, 30–39. [Google Scholar] [CrossRef]
- Yao, Y.; Gao, C.; Cui, J.; Wang, S.; Deng, J.; Yang, Z. Numerical simulation of the movement characteristics of the nixu long-runout landslide. J. Lanzhou Univ. Nat. Sci. 2021, 57, 767–774+782. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Z.; Mao, W.; Yu, F. Dynamics of Long-Runout Landslides: A Review. Appl. Sci. 2025, 15, 11300. https://doi.org/10.3390/app152111300
Lei Z, Mao W, Yu F. Dynamics of Long-Runout Landslides: A Review. Applied Sciences. 2025; 15(21):11300. https://doi.org/10.3390/app152111300
Chicago/Turabian StyleLei, Zhen, Wuwei Mao, and Fangwei Yu. 2025. "Dynamics of Long-Runout Landslides: A Review" Applied Sciences 15, no. 21: 11300. https://doi.org/10.3390/app152111300
APA StyleLei, Z., Mao, W., & Yu, F. (2025). Dynamics of Long-Runout Landslides: A Review. Applied Sciences, 15(21), 11300. https://doi.org/10.3390/app152111300







