Comparison of Machine Learning Models in Nonlinear and Stochastic Signal Classification
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. ECG Registration and Preprocessing
2.2. ECG Analysis
2.2.1. Higuchi Fractal Dimension (HFD)
2.2.2. Katz Fractal Dimension (KFD)
2.2.3. Detrended Fluctuation Analysis (DFA)
2.2.4. Approximate Entropy (ApEn)
2.2.5. Sample Entropy (SampEn)
2.2.6. Multiscale Entropy (MSE)
2.3. Feature Selection and Classification
2.3.1. Feature Selection
2.3.2. Feature Classification
2.3.3. Hyper-Parameter Optimization
2.3.4. Classification Performance
3. Results
3.1. Distributions of Nonlinear ECG Measures in Healthy Persons
3.2. Feature Importance Scores
3.3. Choice of the Best Classifier
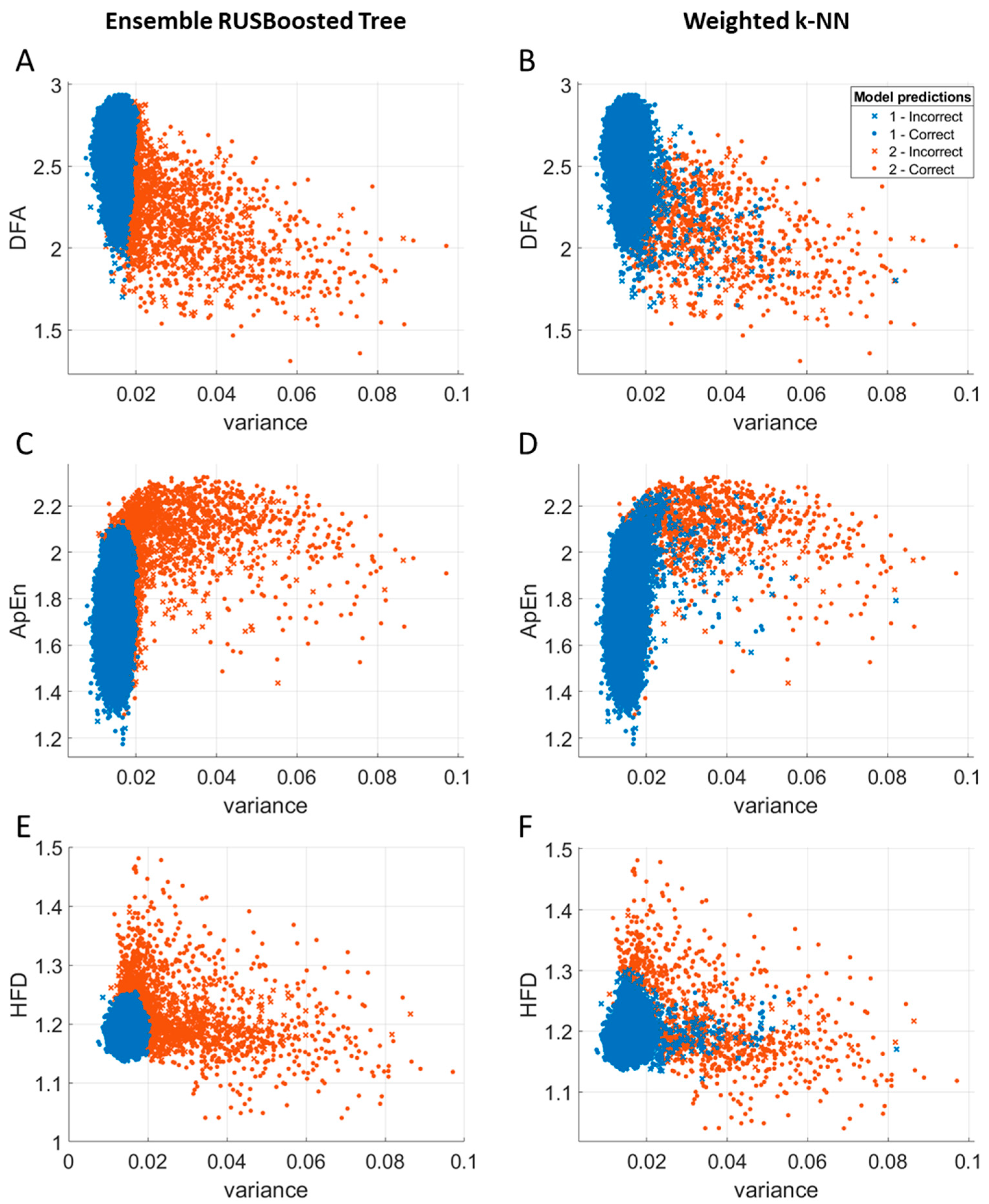
3.4. Comparison of Classifiers: The Ensemble RUSBoosted Trees and the Weighted k-NN Classifier
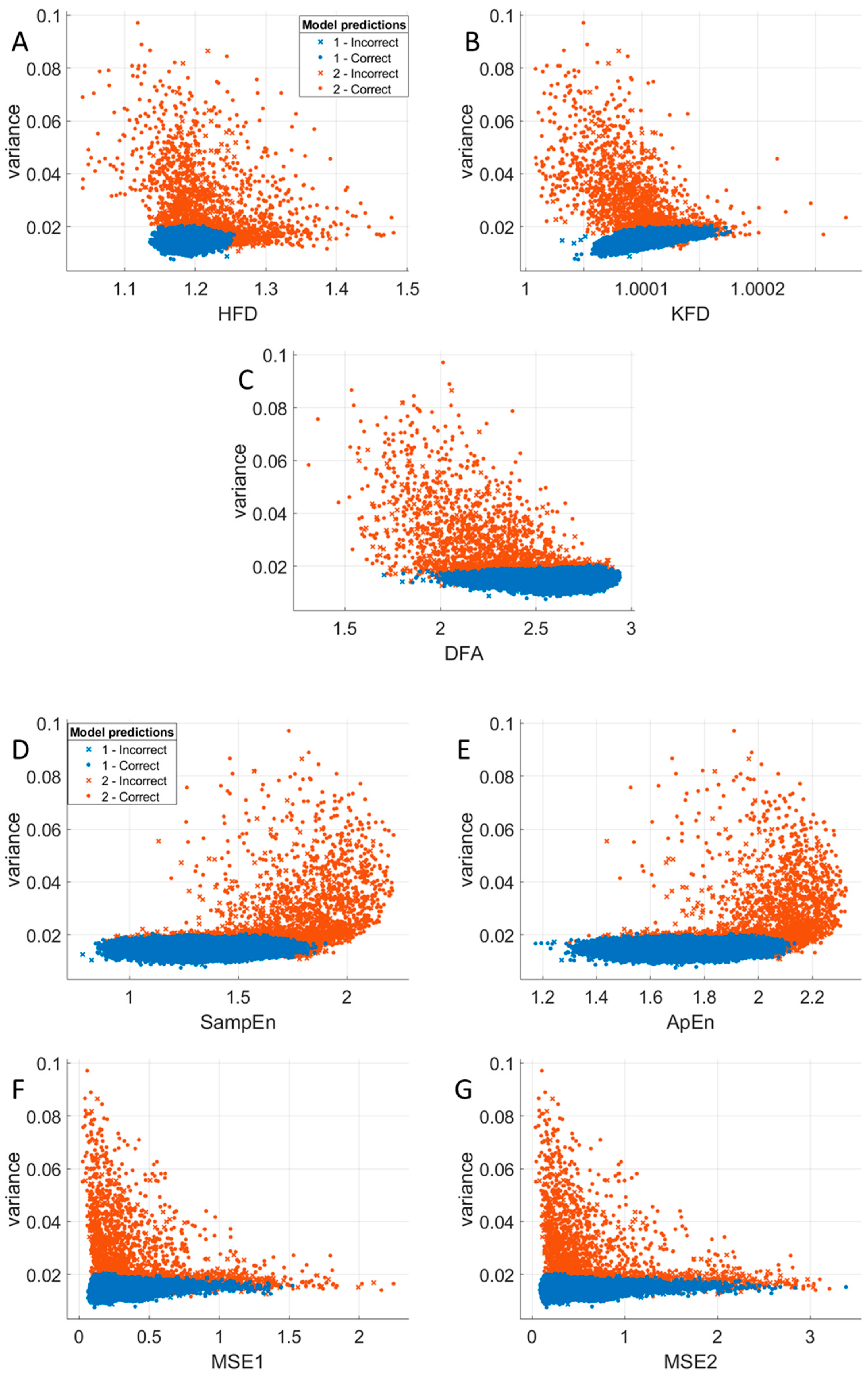
3.5. Relationships Between Variance and Nonlinear Measures
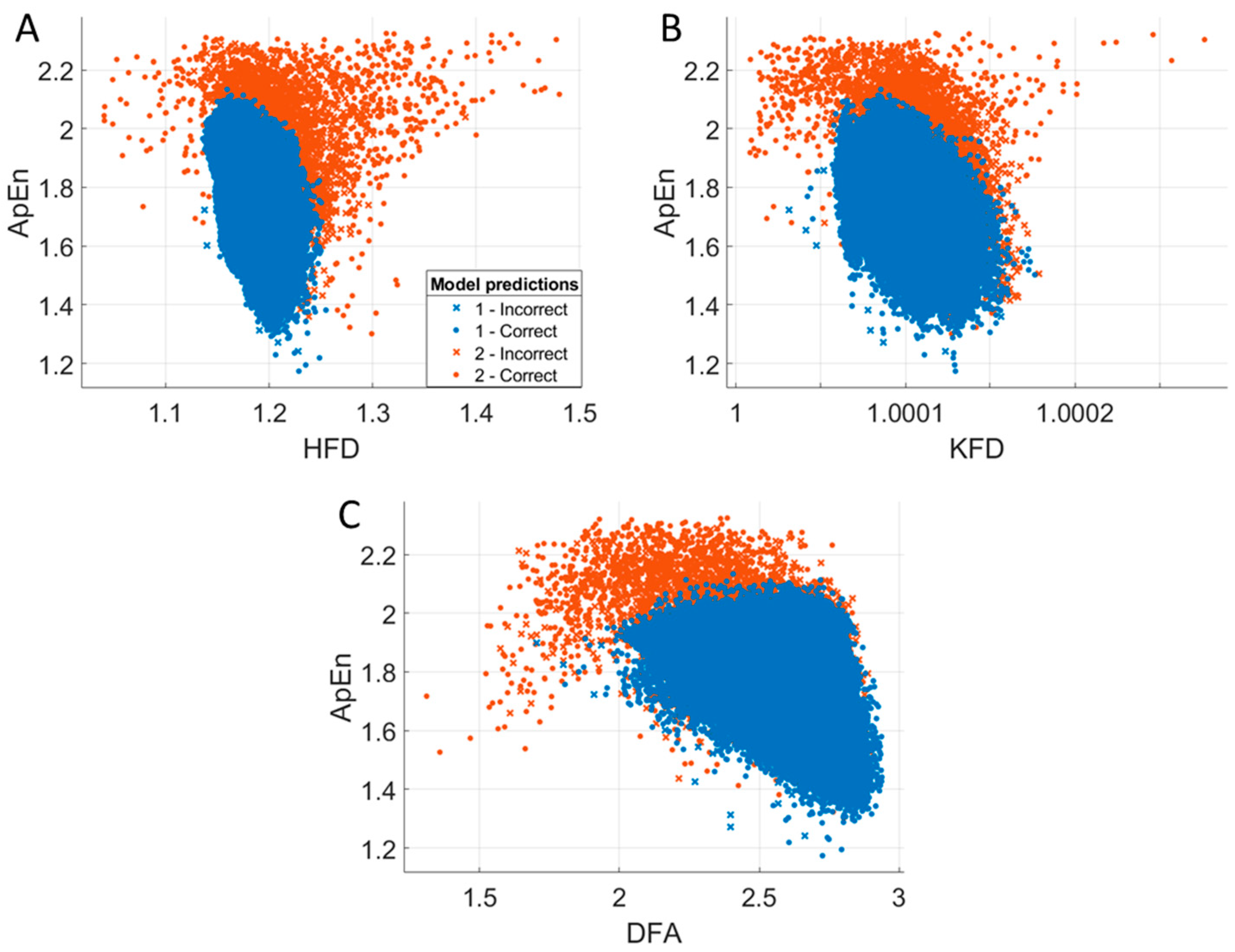
3.6. Relationships Between Entropy and Fractal Dimension Measures
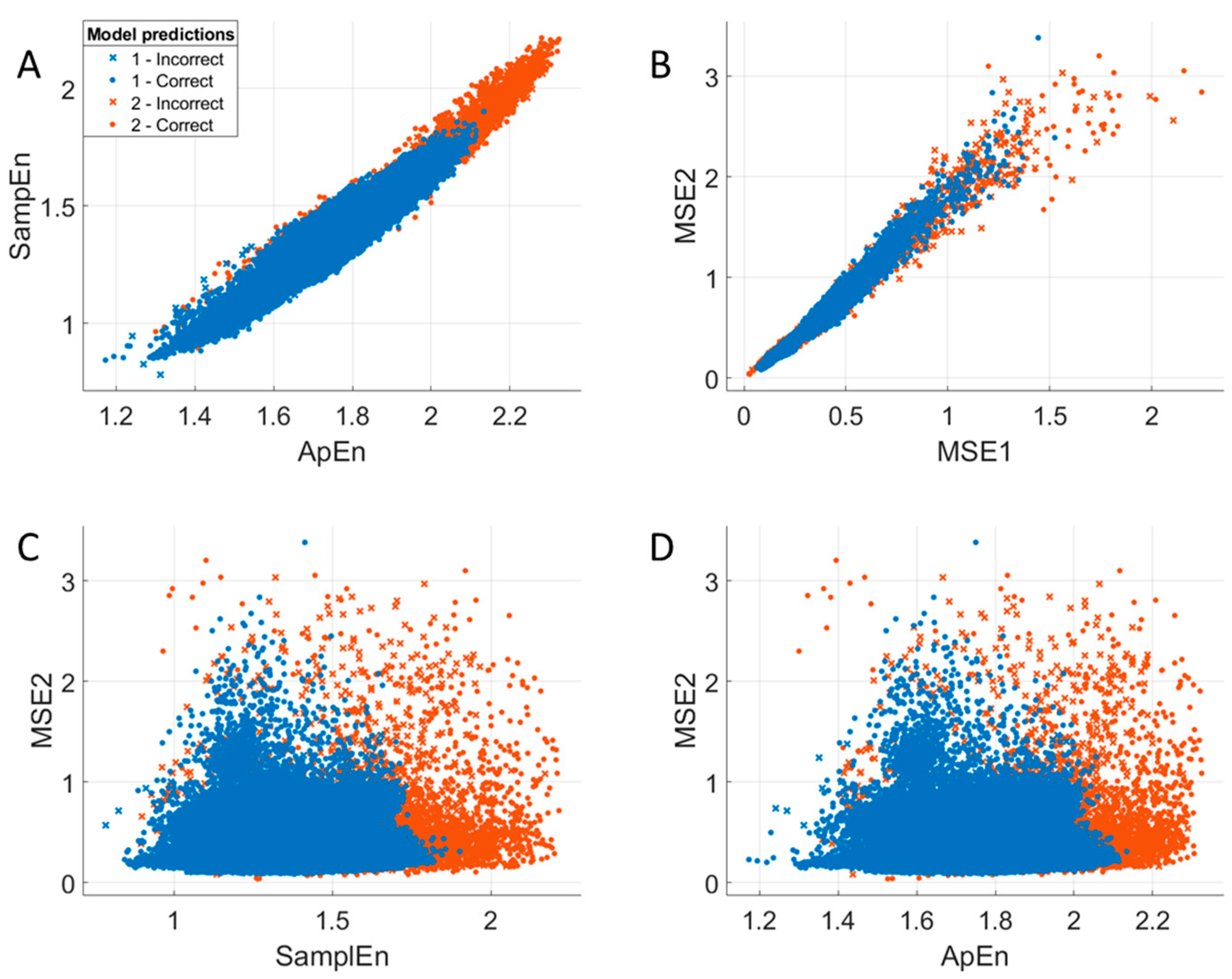
3.7. Relationships Between Entropy Measures
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ApEn | Approximate entropy |
| CD | Correlation dimension |
| CNN | Convolutional Neural Network |
| DFA | Detrended Fluctuation Analysis |
| DL | Deep learning |
| ECG | Electrocardiography |
| EMD | Empirical mode decomposition |
| EWT | Empirical wavelet transform |
| FN | False negative |
| FP | False positive |
| HFD | Higuchi fractal dimension |
| HRV | Heart rate variability |
| ICA | Independent component analysis |
| KFD | Katz fractal dimension |
| k-NN | k-Nearest Neighbors |
| LE | Lyapunov exponent |
| LSTM | Long short-term memory |
| MRMR | Minimum redundancy maximum relevance |
| MSE | Multiscale entropy |
| NPV | Negative predictive value |
| PPV | Positive predictive value (precision) |
| SampEn | Sample entropy |
| SVM | Support vector machine |
| TP | True positive |
| TN | True negative |
| VAR | Variance |
Appendix A. Evaluation of Energy Consumption Due to Model Training
Appendix B. Comparison of Model Performance
| H.NumNeighbors = 14; |
| H.Distance = ‘euclidean’; |
| H.DistanceWeight = ‘squaredinverse’; |
| H.Standardize = 1; |
| k = 5; % number of folds. |
| Mdl = fitcknn (features, classes, ‘Distance’, char(H.Distance), ... |
| ‘DistanceWeight’, char(H.DistanceWeight), ... |
| ‘NumNeighbors’, H.NumNeighbors, ... |
| ‘Standardize’, H.Standardize, ‘KFold’, k); |
| for i = 1:k |
| Labels = classes(Mdl.Partition.test(i)); |
| Pred = predict(Mdl.Trained{i}, features(Mdl.Partition.test(i), :)); |
| CM{i} = confusionmat(Labels, Pred); |
| end |
| Optimized Model | TP | FP | TN | FN | Sensitivity | Specificity | PPV | NPV | Accuracy |
|---|---|---|---|---|---|---|---|---|---|
| Tree | 43,016 | 140 | 219 | 73 | 0.998 | 0.610 | 0.997 | 0.750 | 0.995 |
| 43,028 | 161 | 199 | 61 | 0.999 | 0.553 | 0.996 | 0.765 | 0.995 | |
| 43,015 | 152 | 208 | 74 | 0.998 | 0.578 | 0.996 | 0.738 | 0.995 | |
| 43,011 | 133 | 227 | 77 | 0.998 | 0.631 | 0.997 | 0.747 | 0.995 | |
| 43,025 | 167 | 192 | 64 | 0.999 | 0.535 | 0.996 | 0.750 | 0.995 | |
| 0.998 | 0.581 | 0.997 | 0.750 | 0.995 | |||||
| Discriminant | 42,989 | 160 | 199 | 100 | 0.998 | 0.554 | 0.996 | 0.666 | 0.994 |
| 42,993 | 141 | 219 | 96 | 0.998 | 0.608 | 0.997 | 0.695 | 0.995 | |
| 42,998 | 150 | 210 | 91 | 0.998 | 0.583 | 0.997 | 0.698 | 0.994 | |
| 43,004 | 144 | 216 | 84 | 0.998 | 0.600 | 0.997 | 0.720 | 0.995 | |
| 43,008 | 129 | 230 | 81 | 0.998 | 0.641 | 0.997 | 0.740 | 0.995 | |
| 0.998 | 0.597 | 0.997 | 0.704 | 0.995 | |||||
| Naïve Bayes | 42,672 | 67 | 292 | 417 | 0.990 | 0.813 | 0.998 | 0.412 | 0.989 |
| 42,662 | 62 | 298 | 427 | 0.990 | 0.828 | 0.999 | 0.411 | 0.989 | |
| 42,640 | 68 | 292 | 449 | 0.990 | 0.811 | 0.998 | 0.394 | 0.988 | |
| 42,665 | 62 | 298 | 423 | 0.990 | 0.828 | 0.999 | 0.413 | 0.989 | |
| 42,656 | 57 | 302 | 433 | 0.990 | 0.841 | 0.999 | 0.411 | 0.989 | |
| 0.990 | 0.824 | 0.999 | 0.408 | 0.989 | |||||
| SVM | 43,040 | 148 | 211 | 49 | 0.999 | 0.588 | 0.997 | 0.812 | 0.995 |
| 43,031 | 157 | 203 | 58 | 0.999 | 0.564 | 0.996 | 0.778 | 0.995 | |
| 43,046 | 147 | 213 | 43 | 0.999 | 0.592 | 0.997 | 0.832 | 0.996 | |
| 43,024 | 148 | 212 | 64 | 0.999 | 0.589 | 0.997 | 0.768 | 0.995 | |
| 43,022 | 150 | 209 | 67 | 0.998 | 0.582 | 0.997 | 0.757 | 0.995 | |
| 0.999 | 0.583 | 0.997 | 0.789 | 0.995 | |||||
| k-NN | 43,037 | 125 | 234 | 52 | 0.999 | 0.652 | 0.997 | 0.818 | 0.996 |
| 43,048 | 135 | 225 | 41 | 0.999 | 0.625 | 0.997 | 0.846 | 0.996 | |
| 43,056 | 125 | 235 | 33 | 0.999 | 0.653 | 0.997 | 0.877 | 0.996 | |
| 43,038 | 134 | 226 | 50 | 0.999 | 0.628 | 0.997 | 0.819 | 0.996 | |
| 43,048 | 123 | 236 | 41 | 0.999 | 0.657 | 0.997 | 0.852 | 0.996 | |
| 0.999 | 0.643 | 0.997 | 0.842 | 0.996 | |||||
| Ensemble | 42,617 | 47 | 312 | 472 | 0.989 | 0.869 | 0.999 | 0.398 | 0.988 |
| 42,644 | 60 | 300 | 445 | 0.990 | 0.833 | 0.999 | 0.403 | 0.988 | |
| 42,579 | 47 | 313 | 510 | 0.988 | 0.869 | 0.999 | 0.380 | 0.987 | |
| 42,633 | 62 | 298 | 455 | 0.989 | 0.828 | 0.999 | 0.396 | 0.988 | |
| 42,643 | 43 | 316 | 446 | 0.990 | 0.880 | 0.999 | 0.415 | 0.989 | |
| 0.989 | 0.856 | 0.999 | 0.398 | 0.988 | |||||
| Neural Network | 43,022 | 141 | 218 | 67 | 0.998 | 0.607 | 0.997 | 0.765 | 0.995 |
| 43,023 | 148 | 212 | 66 | 0.998 | 0.589 | 0.997 | 0.763 | 0.995 | |
| 43,036 | 147 | 213 | 53 | 0.999 | 0.592 | 0.997 | 0.801 | 0.995 | |
| 43,024 | 147 | 213 | 64 | 0.999 | 0.592 | 0.997 | 0.769 | 0.995 | |
| 43,040 | 139 | 220 | 49 | 0.999 | 0.613 | 0.997 | 0.818 | 0.996 | |
| 0.999 | 0.598 | 0.997 | 0.783 | 0.995 |
| Sensitivity | Discriminant | Naïve Bayes | SVM | k-NN | Ensemble | Neural Network |
| Tree | 0.012654 | 0.000001 | 0.097824 | 0.002349 | 0.000003 | 0.087904 |
| Discriminant | 0.000001 | 0.009894 | 0.000472 | 0.000006 | 0.000494 | |
| Naïve Bayes | 0.000001 | 0.000002 | 0.020519 | 0.000002 | ||
| SVM | 0.054314 | 0.000015 | 0.587531 | |||
| k-NN | 0.000007 | 0.004663 | ||||
| Ensemble | 0.000007 | |||||
| Specificity | Discriminant | Naïve Bayes | SVM | k-NN | Ensemble | Neural Network |
| Tree | 0.609934 | 0.000317 | 0.918646 | 0.040432 | 0.000335 | 0.426127 |
| Discriminant | 0.000018 | 0.438621 | 0.048048 | 0.000131 | 0.941055 | |
| Naïve Bayes | 0.000011 | 0.000041 | 0.061452 | 0.000003 | ||
| SVM | 0.000524 | 0.000010 | 0.062232 | |||
| k-NN | 0.000001 | 0.000620 | ||||
| Ensemble | 0.000005 | |||||
| PPV | Discriminant | Naïve Bayes | SVM | k-NN | Ensemble | Neural Network |
| Tree | 0.614120 | 0.000320 | 0.913403 | 0.039895 | 0.000338 | 0.424345 |
| Discriminant | 0.000018 | 0.449108 | 0.046823 | 0.000132 | 0.926907 | |
| Naïve Bayes | 0.000011 | 0.000044 | 0.061923 | 0.000003 | ||
| SVM | 0.000514 | 0.000010 | 0.063177 | |||
| k-NN | 0.000001 | 0.000614 | ||||
| Ensemble | 0.000005 | |||||
| NPV | Discriminant | Naïve Bayes | SVM | k-NN | Ensemble | Neural Network |
| Tree | 0.027501 | 0.000000 | 0.078218 | 0.002126 | 0.000000 | 0.075628 |
| Discriminant | 0.000020 | 0.025051 | 0.000682 | 0.000010 | 0.001404 | |
| Naïve Bayes | 0.000023 | 0.000007 | 0.056455 | 0.000009 | ||
| SVM | 0.021545 | 0.000032 | 0.749565 | |||
| k-NN | 0.000006 | 0.002727 | ||||
| Ensemble | 0.000005 | |||||
| Accuracy | Discriminant | Naïve Bayes | SVM | k-NN | Ensemble | Neural Network |
| Tree | 0.242112 | 0.000001 | 0.087122 | 0.004320 | 0.000018 | 0.115168 |
| Discriminant | 0.000013 | 0.082095 | 0.001745 | 0.000009 | 0.009532 | |
| Naïve Bayes | 0.000010 | 0.000006 | 0.031457 | 0.000005 | ||
| SVM | 0.003499 | 0.000043 | 0.795631 | |||
| k-NN | 0.000014 | 0.000643 | ||||
| Ensemble | 0.000011 |
References
- Clifford, G.D.; Azuaje, F.; McSharry, P.E. Advanced Methods for ECG Analysis; Artech House: London, UK, 2006. [Google Scholar]
- Chatterjee, S.; Thakur, R.S.; Yadav, R.N.; Gupta, L.; Raghuvanshi, D.K. Review of noise removal techniques in ECG signals. IET Signal Proc. 2020, 14, 569–590. [Google Scholar] [CrossRef]
- Van der Bijl, K.; Elgendi, M.; Menon, C. Automatic ECG Quality Assessment Techniques: A Systematic Review. Diagnostics 2022, 12, 2578. [Google Scholar] [CrossRef]
- Siddiah, N.; Srikanth, T.; Kumar, Y.S. Nonlinear filtering in ECG Signal Enhancement. Int. J. Comput. Sci. Commun. Netw. 2012, 2, 123–128. [Google Scholar]
- Sarafan, S.; Vuong, H.; Jilani, D.; Malhotra, S.; Lau, M.P.H.; Vishwanath, M.; Ghirmai, T.; Cao, H. A Novel ECG Denoising Scheme Using the Ensemble Kalman Filter. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2022, 2022, 2005–2008. [Google Scholar]
- Khavas, Z.R.; Asl, B.M. Robust heartbeat detection using multimodal recordings and ECG quality assessment with signal amplitudes dispersion. Comput. Methods Programs Biomed. 2018, 163, 169–182. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y. SQI Quality Evaluation Mechanism of Single-Lead ECG Signal Based on Simple Heuristic Fusion and Fuzzy Comprehensive Evaluation. Front. Physiol. 2018, 9, 727. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Chang, K.M. Arrhythmia ECG noise reduction by ensemble empirical mode decomposition. Sensors 2010, 10, 6063–6080. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Liang, Y.; He, P.; Yang, J. Adaptive Motion Artifact Reduction Based on Empirical Wavelet Transform and Wavelet Thresholding for the Non-Contact ECG Monitoring Systems. Sensors 2019, 19, 2916. [Google Scholar] [CrossRef]
- Elouaham, S.; Dliou, A.; Jenkal, W.; Louzazni, M.; Zougagh, H.; Dlimi, S. Empirical Wavelet Transform Based ECG Signal Filtering Method. J. Electr. Comput. Eng. 2024, 2024, 9050909. [Google Scholar] [CrossRef]
- Sharanya, S.; Arjunan, P.D. Fractal Dimension Techniques for Analysis of Cardiac Autonomic Neuropathy. Biomed. Eng. Appl. Basis Commun. 2023, 35, 2350003. [Google Scholar] [CrossRef]
- Chen, C.; da Silva, B.; Ma, C.; Li, J.; Liu, C. Fast Sample Entropy Atrial Fibrillation Analysis Towards Wearable Device. In Proceedings of the 12th Asian-Pacific Conference on Medical and Biological Engineering. APCMBE 2023, Suzhou, China, 18–21 May 2023; Wang, G., Yao, D., Gu, Z., Peng, Y., Tong, S., Liu, C., Eds.; IFMBE Proceedings. Springer: Cham, Switzerland, 2024; Volume 103. [Google Scholar]
- Olejarczyk, E.; Raus-Jarzabek, E.; Massaroni, C. Automatic identification of movement and muscle artifacts in ECG based on statistical and nonlinear measures. In Proceedings of the 2024 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Florence, Italy, 29–31 May 2024. [Google Scholar]
- Alghieth, M. DeepECG-Net: A hybrid transformer-based deep learning model for real-time ECG anomaly detection. Sci. Rep. 2025, 15, 20714. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Chen, I.-Y.; Chiueh, H.; Liang, S.-F. A Low-Cost Implementation of Sample Entropy in Wearable Embedded Systems: An Example of Online Analysis for Sleep EEG. IEEE Trans. Instrum. Meas. 2021, 70, 4002412. [Google Scholar] [CrossRef]
- Gomolka, R.S.; Kampusch, S.; Kaniusas, E.; Thurk, F.; Szeles, J.C.; Klonowski, W. Higuchi Fractal Dimension of Heart Rate Variability During Percutaneous Auricular Vagus Nerve Stimulation in Healthy and Diabetic Subjects. Front. Physiol. 2018, 9, 1162. [Google Scholar] [CrossRef] [PubMed]
- Horie, T.; Burioka, N.; Amisaki, T.; Shimizu, E. Sample Entropy in Electrocardiogram During Atrial Fibrillation. Yonago Acta Med. 2018, 61, 49–57. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, C.; Wei, S.; Shen, Q.; Zhou, F.; Li, J. A New Entropy-Based Atrial Fibrillation Detection Method for Scanning Wearable ECG Recordings. Entropy 2018, 20, 904. [Google Scholar] [CrossRef]
- Alcan, V. Sample Entropy Analysis of heart rate variability in RR interval detection. Muhendis. Bilim. Ve Tasarım Derg. 2020, 8, 783–790. [Google Scholar] [CrossRef]
- Abdelrazik, A.; Eldesouky, M.; Antoun, I.; Lau, E.Y.M.; Koya, A.; Vali, Z.; Suleman, S.A.; Donaldson, J.; Ng, G.A. Wearable Devices for Arrhythmia Detection: Advancements and Clinical Implications. Sensors 2025, 25, 2848. [Google Scholar] [CrossRef]
- Ribeiro, P.; Sa, J.; Paiva, D.; Rodrigues, P.M. Cardiovascular Diseases Diagnosis Using an ECG Multi-Band Non-Linear Machine Learning Framework Analysis. Bioengineering 2024, 11, 58. [Google Scholar] [CrossRef] [PubMed]
- Noitz, M.; Mortl, C.; Bock, C.; Mahringer, C.; Bodenhofer, U.; Dunser, M.W.; Meier, J. Detection of Subtle ECG Changes Despite Superimposed Artifacts by Different Machine Learning Algorithms. Algorithms 2024, 17, 360. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, S.; Zhang, L.; Liu, C. Comparing the Performance of Random Forest, SVM and Their Variants for ECG Quality Assessment Combined with Nonlinear Features. J. Med. Biol. Eng. 2019, 39, 381–392. [Google Scholar] [CrossRef]
- Fu, F.; Xiang, W.; An, Y.; Liu, B.; Chen, X.; Zhu, S.; Li, J. Comparison of Machine Learning Algorithms for the Quality Assessment of Wearable ECG Signals Via Lenovo H3 Devices. J. Biol. Eng. 2021, 41, 231–240. [Google Scholar] [CrossRef]
- Karimulla, S.; Patra, D. An Optimal Methodology for Early Prediction of Sudden Cardiac Death Using Advanced Heart Rate Variability Features of ECG Signal. Arab. J. Sci. Eng. 2024, 49, 6725–6741. [Google Scholar] [CrossRef]
- Rasmussen, J.H.; Rosenberger, K.; Langbein, J.; Easie, R.R. An open-source software for non-invasive heart rate variability assessment. Methods Ecol. Evol. 2020, 11, 773–782. [Google Scholar] [CrossRef]
- El-Yaagoubi, M.; Goya-Esteban, R.; Jabrane, Y.; Munoz-Romero, S.; Garcia-Alberola, A.; Rojo-Alvarez, J.L. On the Robustness of Multiscale Indices for Long-Term Monitoring in Cardiac Signals. Entropy 2019, 21, 594. [Google Scholar] [CrossRef]
- Stapelberg, N.J.C.; Neumann, D.L.; Shum, D.H.K.; McConnell, H.; Hamilton-Craig, I. The sensitivity of 38 heart rate variability measures to the addition of artifact in human and artificial 24-hr cardiac recordings. Ann. Noninvasive Electrocardiol. 2018, 23, e12483. [Google Scholar] [CrossRef]
- Giles, D.A.; Draper, N. Heart rate variability during exercise: A comparison of artefact correction methods. J. Strength Cond. Res. 2018, 32, 726–735. [Google Scholar] [CrossRef]
- Ernst, G. Hidden Signals-The History and Methods of Heart Rate Variability. Front. Public Health 2017, 5, 265. [Google Scholar] [CrossRef]
- Massaroni, C.; Olejarczyk, E.; Lo Presti, D.; Schena, E.; Nusca, A.; Ussia, G.P.; Silvestri, S. Indirect Respiratory Monitoring via Single-Lead Wearable ECG: Influence of Motion Artifacts and Devices on Respiratory Rate Estimations. In Proceedings of the 2024 IEEE International Workshop on Metrology for Industry 4.0 & IoT, Florence, Italy, 29–31 May 2024. [Google Scholar]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Katz, M.J. Fractals and the analysis of waveforms. Comput. Biol. Med. 1988, 18, 145–156. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Hausdorff, J.M.; Mietus, J.E.; Stanley, H.E.; Goldberger, A.L. Fractal mechanisms and heart rate dynamics: Long-range correlations and their breakdown with disease. J. Electrocardiol. 1996, 28 (Suppl. S1), 59–64. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, R.J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, S.; Peng, L.; Zhong, Q.; He, L. A novel method based on shifted rank-1 reconstruction for removing EMG artifacts in ECG signals. Biomed. Signal Process. Control 2023, 85, 104967. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]

| Classifier Group | Ranges of Hyper-Parameters |
|---|---|
| Tree | split criterion: Gini’s diversity index; surrogate decision splits: off; maximum number of splits: 100 (fine), 20 (medium), 7 (coarse) optimized: maximum number of splits: 36 |
| Discriminant | in both linear and quadratic discriminant, a full covariance structure is used optimized: linear |
| Efficient Logistic Regression and Efficient Linear SVM | solver, regularization, and regularization strength (lambda) are automatic; relative coefficient tolerance (beta tolerance): 0.0001; multi-class coding: one-vs.-one |
| Naïve Bayes | standardize data; kernel, in contrast to Gaussian distribution for numeric predictors, uses unbounded support optimized: kernel type: triangle |
| SVM | multi-class coding: one-vs.-one; standardize data; box constraint level: 1; linear, quadratic, and cubic kernel function use automatic scale; Gaussian SVM scale: 0.71 (fine), 2.8 (medium), and 11 (coarse) optimized: kernel function: Gaussian; kernel scale: 1.7037 |
| k-NN | standardize data; distance metric: Euclidean (fine, medium, coarse, and weighted k-NN), Cosine (cosine k-NN), Minkowski (cubic k-NN); number of neighbors: k = 10, except fine k-NN (k = 1) and coarse k-NN (k = 100); distance weight: equal, except the weighted k-NN (squared inverse distance) optimized: distance metric: Euclidean; weighted k-NN; number of neighbors: k = 14 |
| Ensemble Trees | number of learners: 30; learner type: Decision Tree for AdaBoost, Bag, and RUSBoost, while Discriminant or Nearest Neighbors for Subspace Ensemble with subspace dimension equal to 4; all predictors to sample are used by Decision Tree learner; maximum number of splits: 20 for AdaBoost and RUSBoost with learning rate equal to 0.1, or 217,241 for Bag optimized: for RUSBoost: number of learners: 325; maximum number of splits: 139,269; learning rate: 0.50351; for Bagged Tree: number of learners: 112; maximum number of splits: 2451 |
| Neural Networks | standardize data; regularization strength (lambda): 0; activation: ReLU; iteration limit: 1000; number of layers: 1 (narrow, medium, and wide), 2 (bilayered), 3 (trilayered); layer size: 10, except medium (25) and wide (100) Neural Network optimized: lambda: 4.7042 × 10−6; activation: ReLU; number of layers: 1; layer size: 296 |
| Kernel | SVM or Logistic Regression Kernel; regularization strength (lambda): automatic; multi-class coding: one-vs.-one; kernel scale: automatic; iteration limit: 1000; number of expansion dimensions: automatic |
| Non-Standardized Data | ||||||||
| Measure | Variance | HFD | KFD | DFA | SampEn | AppEn | MSE1 | MSE2 |
| min | 0.008 | 1.04 | 1.0000 | 1.31 | 0.78 | 1.17 | 0.02 | 0.04 |
| max | 0.097 | 1.49 | 1.0003 | 2.95 | 2.22 | 2.32 | 2.25 | 3.38 |
| Standardized Data | ||||||||
| Measure | Variance | HFD | KFD | DFA | SampEn | AppEn | MSE1 | MSE2 |
| min | −0.0042 | −7.61 | −0.11 | −10.17 | −3.74 | −4.57 | −1.56 | −1.33 |
| max | −0.0040 | 15.86 | 0.20 | 2.53 | 5.55 | 4.49 | 17.95 | 15.13 |
| Classifier | Accuracy [%] | Total Cost | Prediction Speed [obs/s] | Training Time [s] | Model Size [kB] |
| Fine Tree | 99.5 | 1109 | 1,400,000 | 11 | 29 |
| Medium Tree | 99.5 | 1097 | 830,000 | 10 | 8 |
| Coarse Tree | 99.4 | 1294 | 870,000 | 9 | 5 |
| Linear Discriminant | 99.5 | 1169 | 610,000 | 9 | 5 |
| Quadratic Discriminant | 98.5 | 3193 | 580,000 | 8 | 8 |
| Binary GLM Logistic Regression | 99.4 | not applicable | 730,000 | 21 | 39,000 |
| Efficient Logistic Regression | 99.4 | 1354 | 770,000 | 16 | 12 |
| Efficient Linear SVM | 99.3 | 1436 | 730,000 | 19 | 12 |
| Gaussian Naïve Bayes | 98.4 | 3562 | 610,000 | 14 | 7 |
| Kernel Naïve Bayes | 98.9 | 2477 | 260 | 4729 | 53,000 |
| Linear SVM | 99.4 | 1229 | 180,000 | 911 | 222 |
| Quadratic SVM | 99.5 | 1109 | 360,000 | 3192 | 202 |
| Cubic SVM | 99.5 | 1048 | 540,000 | 5681 | 188 |
| Fine Gaussian SVM | 99.3 | 1516 | 26,000 | 2693 | 1000 |
| Medium Gaussian SVM | 99.5 | 993 | 78,000 | 908 | 232 |
| Coarse Gaussian SVM | 99.5 | 1124 | 60,000 | 452 | 202 |
| Fine k-NN | 99.5 | 1098 | 13,000 | 59 | 24,000 |
| Medium k-NN | 99.5 | 1042 | 5200 | 145 | 24,000 |
| Coarse k-NN | 99.5 | 1155 | 2400 | 382 | 24,000 |
| Cosine k-NN | 99.4 | 1242 | 1400 | 748 | 18,000 |
| Cubic k-NN | 99.5 | 1041 | 2900 | 317 | 24,000 |
| Weighted k-NN | 99.6 | 871 | 5600 | 160 | 24,000 |
| Ensemble Boosted Trees | 99.5 | 1050 | 69,000 | 376 | 273 |
| Ensemble Bagged Trees | 99.6 | 885 | 51,000 | 1092 | 5000 |
| Ensemble Subspace Discriminant | 99.4 | 1246 | 36,000 | 83 | 120 |
| Ensemble Subspace k-NN | 99.5 | 1045 | 5100 | 349 | 492,000 |
| Ensemble RUSBoosted Trees | 98.1 | 4076 | 98,000 | 130 | 273 |
| Narrow Neural Network | 99.5 | 1077 | 710,000 | 1350 | 7 |
| Medium Neural Network | 99.5 | 1023 | 780,000 | 2072 | 8 |
| Wide Neural Network | 99.5 | 1046 | 1,100,000 | 3419 | 14 |
| Bilayered Neural Network | 99.5 | 1156 | 710,000 | 1801 | 8 |
| Trilayered Neural Network | 99.5 | 1070 | 850,000 | 2165 | 10 |
| SVM Kernel | 99.4 | 1334 | 120,000 | 1138 | 11 |
| Logistic Regression Kernel | 99.4 | 1406 | 110,000 | 547 | 11 |
| Optimized Classifier Group | Accuracy [%] | Total Cost | Prediction Speed [obs/s] | Training Time [s] | Model Size [kB] |
| Tree | 99.5 | 1083 | 3,600,000 | 44 | 13 |
| Discriminant | 99.5 | 1169 | 2,200,000 | 35 | 5 |
| SVM | 99.6 | 927 | 130,000 | 29,587 | 314 |
| Naïve Bayes | 98.9 | 2466 | 270 | 51,166 | 53,000 |
| k-NN | 99.6 | 870 | 60,000 | 4140 | 24,000 |
| Ensemble Bagged Trees | 99.6 | 899 | 33,000 | 32,677 | 18,000 |
| Ensemble RUSBoosted Trees | 99.6 | 931 | 19,000 | 2372 | 53,000 |
| Neural Network | 99.6 | 957 | 590,000 | 39,444 | 31 |
| Optimized Classifier | Accuracy [%] | Total Cost | Prediction Speed [obs/s] | Training Time [s] | Model Size [kB] |
| Tree | 99.5 | 1083 | 3,200,000 | 2 | 13 |
| Discriminant | 99.5 | 1169 | 2,100,000 | 2 | 5 |
| SVM | 99.6 | 927 | 210,000 | 184 | 314 |
| Naïve Bayes | 98.9 | 2466 | 250 | 3629 | 53,000 |
| k-NN | 99.6 | 870 | 82,000 | 14 | 24,000 |
| Ensemble Bagged Trees | 99.6 | 899 | 51,000 | 316 | 18,000 |
| Ensemble RUSBoosted Trees | 99.6 | 933 | 20,000 | 130 | 53,000 |
| Neural Network | 99.6 | 953 | 600,000 | 483 | 31 |
| Classifier | TP | FP | TN | FN | Sensitivity | Specificity | PPV | NPV | Accuracy |
|---|---|---|---|---|---|---|---|---|---|
| 1. Fine Tree | 215,058 | 723 | 1075 | 386 | 99.8 | 59.8 | 99.7 | 73.6 | 99.5 |
| 2. Medium Tree | 215,073 | 726 | 1072 | 371 | 99.8 | 59.6 | 99.7 | 74.3 | 99.5 |
| 3. Coarse Tree | 215,029 | 879 | 919 | 415 | 99.8 | 51.1 | 99.6 | 68.9 | 99.4 |
| Optimized Tree | 215,090 | 729 | 1069 | 354 | 99.8 | 59.5 | 99.7 | 75.1 | 99.5 |
| 4. Linear Discriminant | 214,993 | 718 | 1080 | 451 | 99.8 | 60.1 | 99.7 | 70.5 | 99.5 |
| 5. Quadratic Discriminant | 212,575 | 324 | 1474 | 2869 | 99.7 | 82.0 | 98.8 | 33.9 | 99.5 |
| 6. Binary GLM Logistic Regression | 215,159 | 914 | 884 | 285 | 99.9 | 49.2 | 99.6 | 75.6 | 99.4 |
| 7. Efficient Logistic Regression | 215,163 | 1073 | 725 | 281 | 99.9 | 40.3 | 99.5 | 72.1 | 99.4 |
| 8. Efficient Linear SVM | 215,337 | 1329 | 469 | 107 | 100.0 | 26.1 | 99.4 | 81.4 | 99.3 |
| 9. Gaussian Naïve Bayes | 212,158 | 276 | 1522 | 3286 | 98.5 | 84.6 | 99.9 | 31.7 | 98.4 |
| 10. Kernel Naïve Bayes | 213,283 | 316 | 1482 | 2161 | 99.0 | 82.4 | 99.9 | 40.7 | 98.9 |
| Optimized Naïve Bayes | 213,291 | 313 | 1485 | 2153 | 99.0 | 82.6 | 99.9 | 40.8 | 98.9 |
| 11. Linear SVM | 215,240 | 1025 | 773 | 204 | 99.9 | 43.0 | 99.5 | 79.1 | 99.4 |
| 12. Quadratic SVM | 215,215 | 880 | 918 | 229 | 99.9 | 51.1 | 99.6 | 80.0 | 99.5 |
| 13. Cubic SVM | 215,210 | 814 | 984 | 234 | 99.9 | 54.7 | 99.6 | 80.8 | 99.5 |
| 14. Fine Gaussian SVM | 215,435 | 1507 | 291 | 9 | 100.0 | 16.2 | 99.3 | 97.0 | 99.3 |
| 15. Medium Gaussian SVM | 215,152 | 701 | 1097 | 292 | 99.9 | 61.0 | 99.7 | 79.0 | 99.5 |
| 16. Coarse Gaussian SVM | 215,189 | 869 | 929 | 255 | 99.9 | 51.7 | 99.6 | 78.5 | 99.5 |
| Optimized Gaussian SVM | 215,170 | 653 | 1145 | 274 | 99.9 | 63.7 | 99.7 | 80.7 | 99.6 |
| 17. Fine k-NN | 214,980 | 634 | 1164 | 464 | 99.8 | 64.7 | 99.7 | 71.5 | 99.5 |
| 18. Medium k-NN | 215,184 | 782 | 1016 | 260 | 99.9 | 56.5 | 99.6 | 79.6 | 99.5 |
| 19. Coarse k-NN | 215,202 | 913 | 885 | 242 | 99.9 | 49.2 | 99.6 | 78.5 | 99.5 |
| 20. Cosine k-NN | 215,132 | 930 | 868 | 312 | 99.9 | 48.3 | 99.6 | 73.6 | 99.4 |
| 21. Cubic k-NN | 215,181 | 778 | 1020 | 263 | 99.9 | 56.7 | 99.6 | 79.5 | 99.5 |
| 22. Weighted k-NN | 215,213 | 640 | 1158 | 231 | 99.9 | 64.4 | 99.7 | 83.4 | 99.6 |
| Optimized Weighted k-NN | 215,216 | 642 | 1156 | 228 | 99.9 | 64.3 | 99.7 | 83.5 | 99.6 |
| 23. Ensemble Boosted Trees | 215,078 | 684 | 1114 | 366 | 99.8 | 62.0 | 99.7 | 75.3 | 99.5 |
| 24. Ensemble Bagged Trees | 215,151 | 592 | 1206 | 293 | 99.9 | 67.1 | 99.7 | 80.5 | 99.6 |
| 25. Ensemble Subspace Discriminant | 215,918 | 720 | 1078 | 526 | 99.8 | 60.0 | 99.7 | 67.2 | 99.9 |
| 26. Ensemble Subspace k-NN | 215,277 | 878 | 920 | 167 | 99.9 | 51.2 | 99.6 | 84.6 | 99.5 |
| 27. Ensemble RUSBoosted Trees | 211,553 | 185 | 1613 | 3891 | 98.2 | 89.7 | 99.9 | 29.3 | 98.1 |
| Optimized Ensemble Bagged Trees | 215,144 | 599 | 1199 | 300 | 99.9 | 66.7 | 99.7 | 80.0 | 99.6 |
| Optimized Ensemble RUSBoosted Trees | 214,985 | 472 | 1326 | 459 | 99.8 | 73.7 | 99.8 | 74.3 | 99.6 |
| 28. Narrow Neural Network | 215,076 | 709 | 1089 | 368 | 99.8 | 60.6 | 99.7 | 74.7 | 99.5 |
| 29. Medium Neural Network | 215,080 | 659 | 1139 | 364 | 99.8 | 63.3 | 99.7 | 75.8 | 99.5 |
| 30. Wide Neural Network | 215,020 | 622 | 1176 | 424 | 99.8 | 65.4 | 99.7 | 73.5 | 99.5 |
| 31. Bilayered Neural Network | 215,076 | 688 | 1110 | 368 | 99.8 | 61.7 | 99.7 | 75.1 | 99.5 |
| 32. Trilayered Neural Network | 215,068 | 694 | 1104 | 376 | 99.8 | 61.4 | 99.7 | 74.6 | 99.5 |
| Optimized Neural Network | 215,098 | 611 | 1187 | 346 | 99.8 | 66.0 | 99.7 | 77.4 | 99.6 |
| 33. SVM Kernel | 215,183 | 1073 | 725 | 261 | 99.9 | 40.3 | 99.5 | 73.5 | 99.4 |
| 34. Logistic Regression Kernel | 215,127 | 1089 | 709 | 317 | 99.9 | 39.4 | 99.5 | 69.1 | 99.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olejarczyk, E.; Massaroni, C. Comparison of Machine Learning Models in Nonlinear and Stochastic Signal Classification. Appl. Sci. 2025, 15, 11226. https://doi.org/10.3390/app152011226
Olejarczyk E, Massaroni C. Comparison of Machine Learning Models in Nonlinear and Stochastic Signal Classification. Applied Sciences. 2025; 15(20):11226. https://doi.org/10.3390/app152011226
Chicago/Turabian StyleOlejarczyk, Elzbieta, and Carlo Massaroni. 2025. "Comparison of Machine Learning Models in Nonlinear and Stochastic Signal Classification" Applied Sciences 15, no. 20: 11226. https://doi.org/10.3390/app152011226
APA StyleOlejarczyk, E., & Massaroni, C. (2025). Comparison of Machine Learning Models in Nonlinear and Stochastic Signal Classification. Applied Sciences, 15(20), 11226. https://doi.org/10.3390/app152011226







