A Correlation Between Earthquake Magnitude and Pre-Seismic Gravity Field Variations over Its Epicenter
Abstract
1. Introduction
2. Materials and Methods
2.1. Proposed Methodology
2.2. Construction of Earthquake Datasets
2.3. Data Processing and Machine Learning
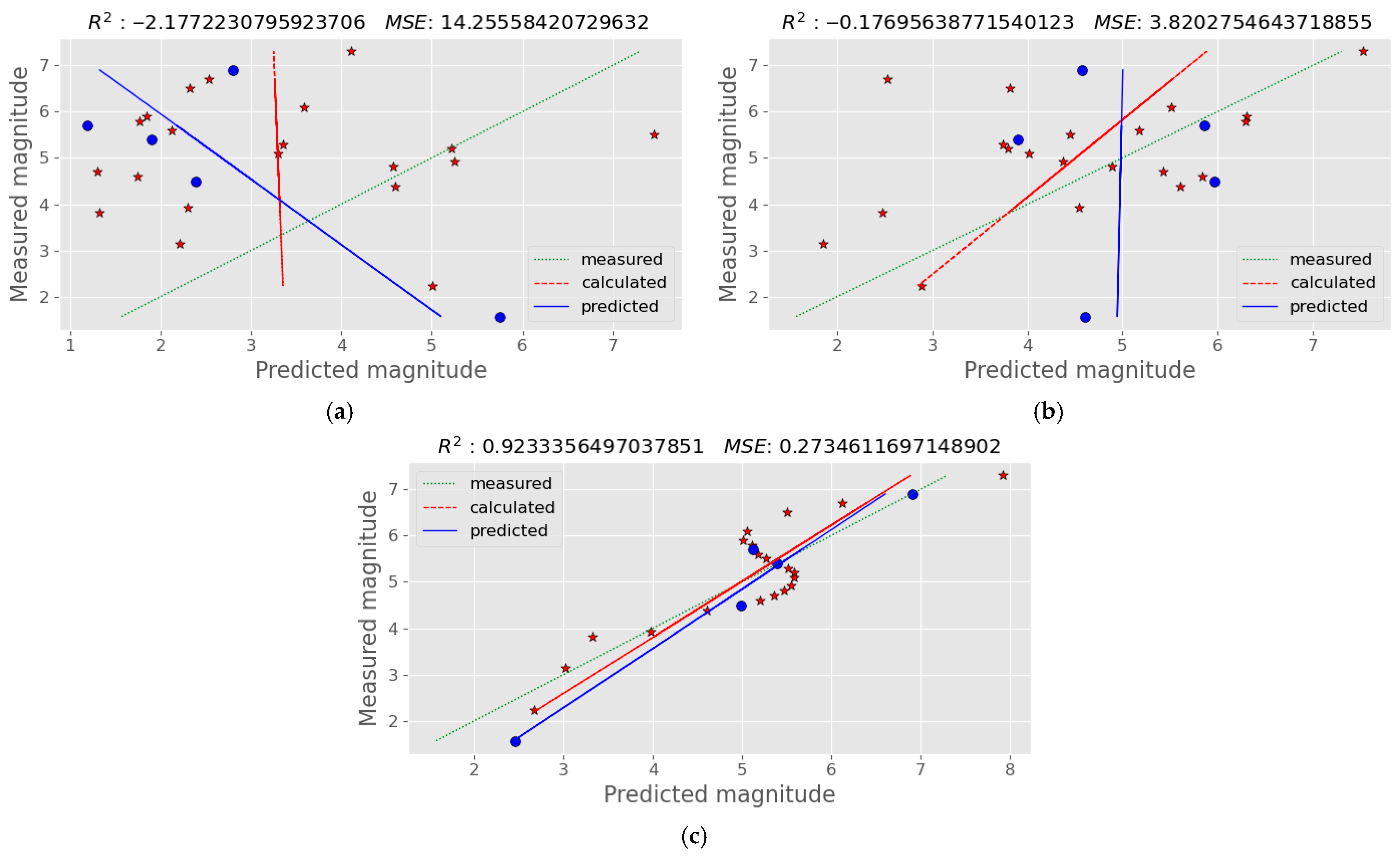
3. Results
3.1. Results on the Global Dataset
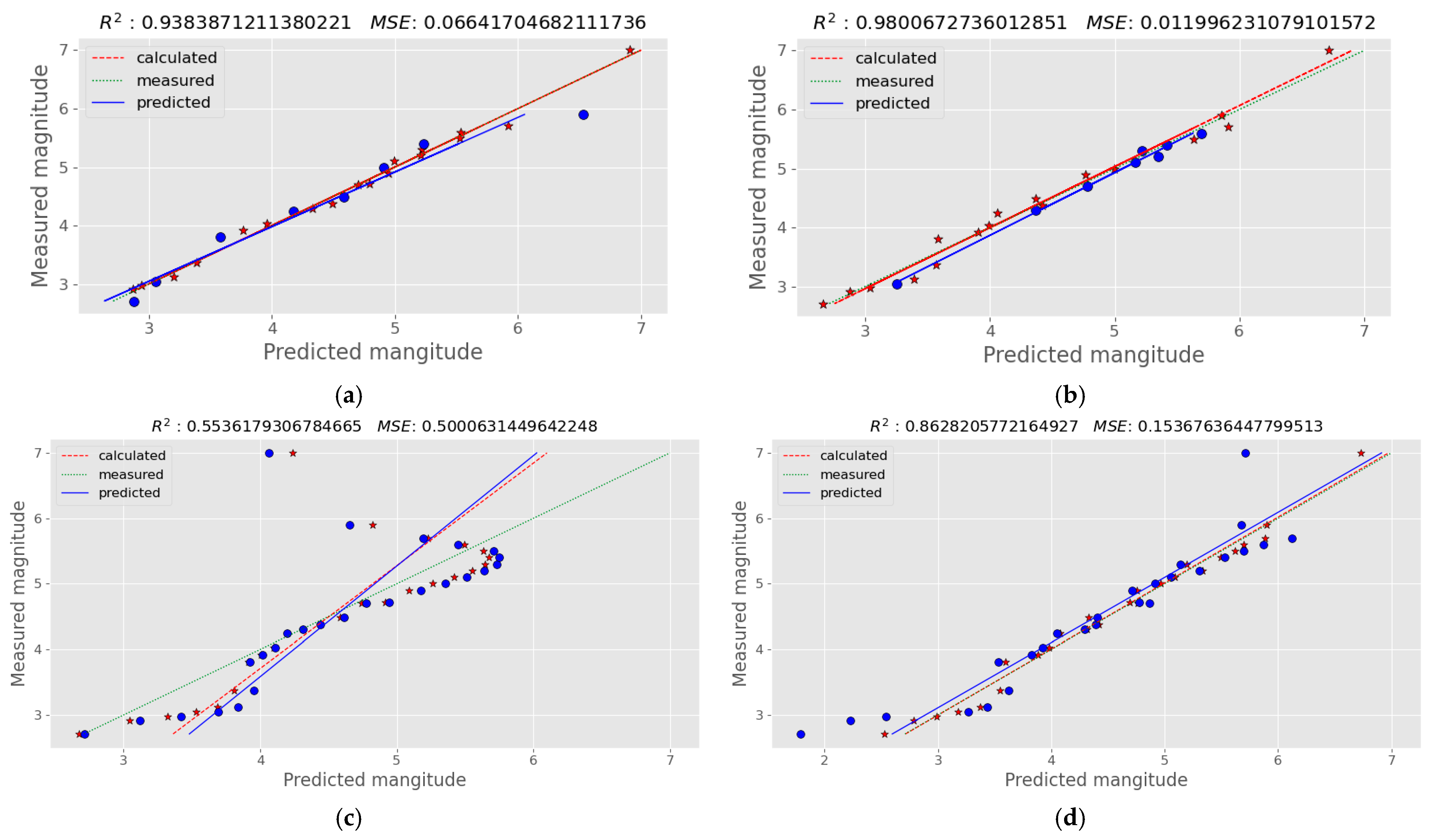
3.2. Results on the Greek Dataset
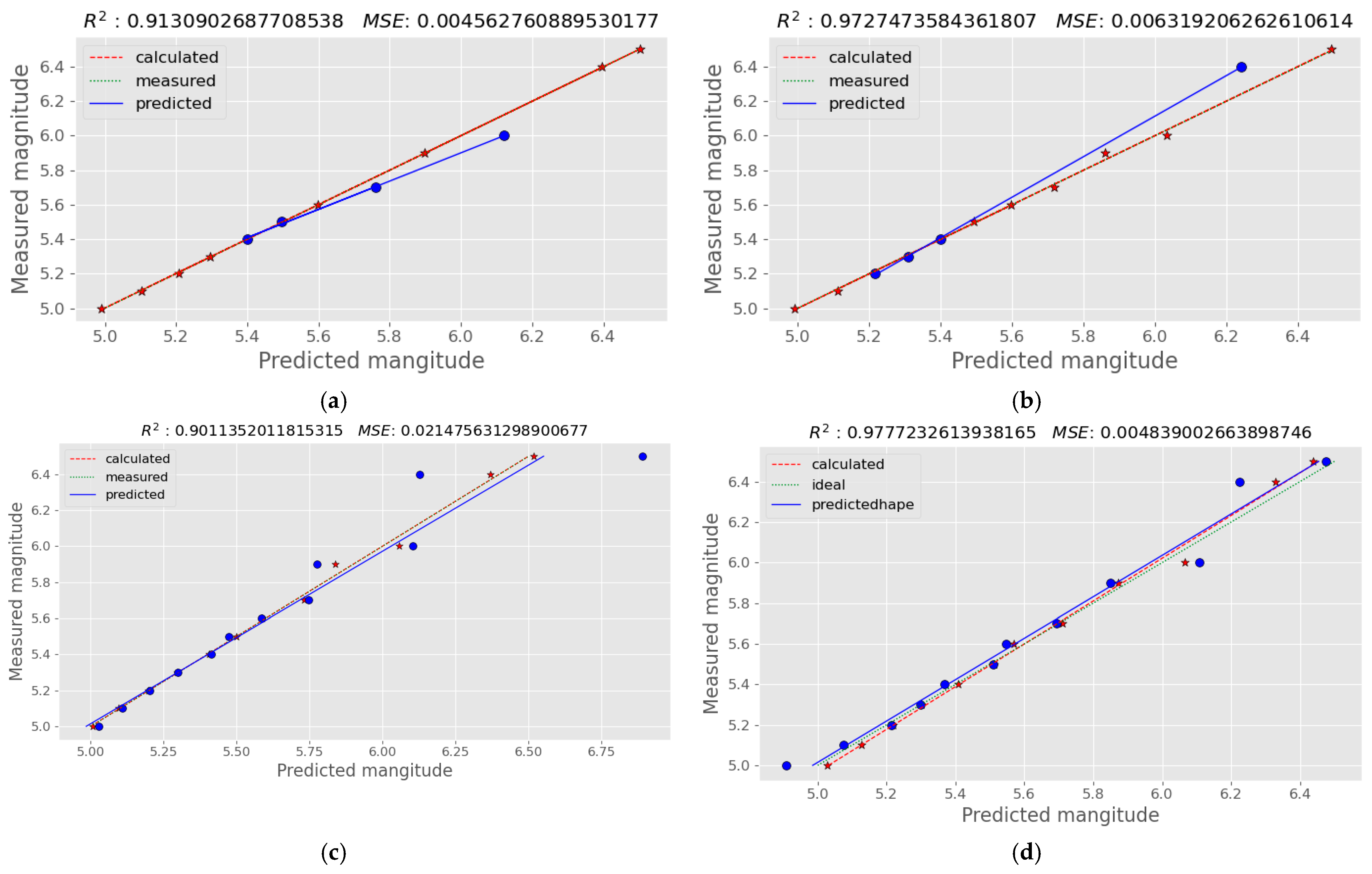
3.3. Results on the Hellenic Trench Dataset
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MLR | multiple linear regression |
| PLS | partial least squares |
| NN | neural networks |
| ULF | ultra-low frequency |
| VLF | very low frequency |
| Ms | surface wave magnitude |
| AI | artificial intelligence |
| USGS | United States Geological Survey Search Comprehensive Earthquake Catalogue |
| GRACE | Gravity Recovery and Climate Experiment |
| IGFS | International Gravity Field Service |
| COST-G | Combination Service for Time-Variable Gravity |
| μGal | microGalileo |
| MSE) | mean squared error |
Appendix A
| Time | Latitude | Longitude | Mag | Depth | magType | dmin | rms | net | Id | Place | horizontalError | Depth Error | magError | Mag Nst | locationSource | magSource |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2021-05-19 T10:41:12.805Z | 38,182 | −117,889 | 1 | 7.8 | ml | 0.025 | 0.08 | nn | Nn 00807589 | 30 km SE of Mina, Nevada | 0.5 | 0.24 | 8 | nn | nn | |
| 2021-05-01 T02:14:48.715Z | 32,116 | −102,162 | 2 | 5.9 | ml | 0.015 | 0.1 | tx | Tx 2021ilkv | 15 km NNW of Midland, Texas | 0.71 | 0.64 | 0.1 | 11 | tx | tx |
| 2021-05-13 T14:41:45.330Z | 18,004 | −66,760 | 3 | 11 | md | 0.158 | 0.15 | pr | Pr 2021133006 | 1 km SE of Magas Arriba, Puerto Rico | 0.33 | 0.24 | 0.16 | 10 | pr | pr |
| 2021-05-25 T04:24:46.561Z | 24,755 | 122,495 | 4 | 10 | mb | 0.55 | 0.82 | us | Us 6000efji | 60 km WNW of Yonakuni, Japan | 2.6 | 1.9 | 0.258 | 4 | us | us |
| 2021-05-27 T13:30:51.483Z | −27,092 | −70,936 | 4.1 | 54.44 | mb | 0.581 | 1.39 | us | Us 6000ef53 | 67 km WNW of Copiapo, Chile | 5.7 | 10.7 | 0.302 | 3 | us | us |
| 2021-05-03 T15:19:57.804Z | 53,802 | 160,385 | 4.5 | 71.99 | mb | 1298 | 0.58 | us | Us 7000dzq0 | 142 km NE of Petropavlovsk-Kamchatsky, Russia | 10.1 | 8.3 | 0.05 | 116 | us | us |
| 2021-05-03 T11:46:46.696Z | −61,875 | −81,575 | 4.6 | 10 | mb | 3296 | 0.68 | us | Us 7000dzp9 | 108 km SW of Sechura, Peru | 8.2 | 1.9 | 0.073 | 56 | us | us |
| 2021-05-16 T17:32:48.435Z | 27,745 | 52,142 | 4.7 | 10 | mb | 4588 | 0.75 | us | Us 7000e3l3 | 76 km WNW of Mohr, Iran | 8.6 | 1.5 | 0.057 | 94 | us | us |
| 2021-05-28 T13:06:35.311Z | 24,877 | 122,549 | 4.7 | 10 | mb | 0.586 | 0.53 | us | Us 6000egzm | 64 km NW of Yonakuni, Japan | 2.3 | 1.9 | 0.185 | 9 | us | us |
| 2021-05-21 T19:03:08.243Z | 34,519 | 99,048 | 4.9 | 10 | mb | 4100 | 0.94 | us | Us 7000e557 | Southern Qinghai, China | 7.8 | 1.8 | 0.057 | 98 | us | us |
| 2021-05-28 T07:24:16.071Z | 36,524 | 70,135 | 5 | 209.8 | mb | 0.697 | 0.78 | us | Us 6000efd7 | 25 km ESE of Farkhar, Afghanistan | 5.9 | 5.5 | 0.053 | 112 | us | us |
| 2021-05-29 T01:25:14.219Z | 1019 | 120,085 | 5.1 | 17.42 | mww | 0.702 | 0.88 | us | Us 6000efq7 | 214 km N of Palu, Indonesia | 4.8 | 3.3 | 0.086 | 13 | us | us |
| 2021-05-21 T23:56:16.899Z | 5887 | 126,646 | 5.2 | 10 | mb | 5131 | 0.78 | us | Us 7000e57i | 73 km SE of Pondaguitan, Philippines | 3.9 | 1.7 | 0.048 | 146 | us | us |
| 2021-05-05 T01:17:26.708Z | −20,697 | −173,463 | 5.3 | 10 | mww | 6939 | 0.73 | us | Us 7000e07n | 134 km SE of Pangai, Tonga | 8.7 | 1.8 | 0.098 | 10 | us | us |
| 2021-05-21 T01:37:36.219Z | −9889 | 160,446 | 5.4 | 16.49 | mww | 0.664 | 1.04 | us | Us 7000e4yd | 74 km SE of Honiara, Solomon Islands | 5.5 | 3.2 | 0.08 | 15 | us | us |
| 2021-05-29 T01:02:41.087Z | 36,311 | 141,987 | 5.5 | 12.04 | mww | 3055 | 0.85 | us | Us 6000efq6 | 122 km ENE of Hasaki, Japan | 2.3 | 3 | 0.071 | 19 | us | us |
| 2021-05-03 T08:46:39.830Z | 51,306 | 100,420 | 5.6 | 18 | mww | 2050 | 0.51 | us | Us 7000dznc | 28 km SW of Turt, Mongolia | 7.3 | 1.8 | 0.065 | 23 | us | us |
| 2021-05-25 T21:36:44.310Z | −17,576 | −174,808 | 5.7 | 201.18 | mww | 4551 | 0.83 | us | Us 7000e68h | 147 km NW of Neiafu, Tonga | 10.9 | 3.7 | 0.051 | 37 | us | us |
| 2021-05-21 T12:09:22.756Z | −8421 | 112,332 | 5.8 | 106 | mww | 1801 | 0.65 | us | Us 7000e50p | 33 km SSW of Sumberpucung, Indonesia | 3.6 | 1.9 | 0.062 | 25 | us | us |
| 2021-05-30 T20:47:51.021Z | −56,826 | −140,710 | 5.9 | 10 | mww | 27476 | 0.75 | us | Us 6000egs4 | Pacific-Antarctic Ridge | 15.2 | 1.8 | 0.086 | 13 | us | us |
| 2021-05-21 T13:48:37.193Z | 25,727 | 100,008 | 6.1 | 9 | mww | 4438 | 0.93 | us | Us 7000e532 | 25 km NW of Dali, China | 6.8 | 1.7 | 0.053 | 34 | us | us |
| 2021-05-21 T22:13:18.379Z | −16,601 | −177,373 | 6.5 | 10 | mww | 4518 | 0.96 | us | Us 7000e579 | 265 km SSE of Alo, Wallis and Futuna | 7.3 | 1.4 | 0.061 | 26 | us | us |
| 2021-05-12 T14:05:15.667Z | −17,387 | 66,314 | 6.7 | 10 | mww | 10669 | 0.68 | us | Us 7000e2ec | Mauritius-Reunion region | 8.2 | 1.7 | 0.036 | 75 | us | us |
| 2021-05-01 T01:27:27.215Z | 38,200 | 141,597 | 6.9 | 43 | mww | 2619 | 0.82 | us | Us 7000dz5t | 30 km SSE of Onagawa Cho, Japan | 7.3 | 1.9 | 0.041 | 58 | us | us |
| 2021-05-21 T18:04:13.565Z | 34,598 | 98,251 | 7.3 | 10 | mww | 4655 | 0.77 | us | Us 7000e54r | Southern Qinghai, China | 3 | 1.7 | 0.037 | 71 | us | us |
| Time | Latitude | Longitude | Mag | Depth | magType | dmin | rms | net | Id | Place | horizontalError | Depth Error | magError | Mag Nst | locationSource | magSource |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-07-22 T16:28:51.512Z | 39,669 | 19,763 | 2.7 | 10 | ml | 0.049 | 0.84 | us | us6000b2a3 | 8 km WNW of Kontokali | 6.6 | 2.0 | 0.097 | 14 | us | us |
| 2020-05-11 T09:33:07.394Z | 37,824 | 27,144 | 3.0 | 10 | ml | 1.297 | 0.67 | us | us70009dzb | 10 km WSW of Kusadasi | 5.3 | 2.0 | 0.085 | 18 | us | us |
| 2020-04-27 T20:15:03.107Z | 41,425 | 19,527 | 3.1 | 10 | ml | 1.023 | 0.62 | us | us60009dg4 | 9 km NNW of Shijak | 5.4 | 2.0 | 0.064 | 32 | us | us |
| 2020-06-01 T23:15:01.842Z | 40,459 | 21,483 | 3.2 | 10 | ml | 0.847 | 0.26 | us | us6000a40l | 7 km WSW of Emporio | 3.9 | 2.0 | 0.077 | 22 | us | us |
| 2020-04-13 T23:56:37.740Z | 41,603 | 28,747 | 3.3 | 10 | ml | 2.069 | 1.03 | us | us70008vrx | 33 km N of Durusu | 4.6 | 2.0 | 0.085 | 18 | us | us |
| 2020-02-20 T00:32:32.386Z | 35,272 | 23,962 | 3.6 | 10 | mb | 0.758 | 0.82 | us | us70007tbw | 17 km WNW of Chora Sfakion | 3.4 | 2.0 | 0.352 | 2 | us | us |
| 2020-10-30 T12:41:31.954Z | 37,797 | 26,977 | 4.0 | 10 | mb | 1.425 | 0.63 | us | us7000cask | 4 km N of Samos | 5.8 | 1.9 | 0.195 | 7 | us | us |
| 2020-04-18 T23:36:53.658Z | 38,073 | 20,321 | 4.1 | 21.78 | mb | 1.555 | 1.05 | us | us70008zl8 | 17 km SW of Lixouri | 5.0 | 6.2 | 0.100 | 27 | us | us |
| 2020-10-17 T20:31:59.067Z | 39,108 | 23,415 | 4.2 | 10 | mb | 1.224 | 0.7 | us | us6000c91f | 8 km SW of Skiathos | 4.9 | 1.9 | 0.264 | 4 | us | us |
| 2020-07-07 T15:19:51.452Z | 38,836 | 25,331 | 4.3 | 8.92 | mb | 2.118 | 0.74 | us | us7000ajhc | 38 km NNW of Psara | 4.5 | 5.9 | 0.126 | 18 | us | us |
| 2020-06-04 T04:51:18.397Z | 35,089 | 26,052 | 4.4 | 10 | mb | 0.972 | 0.75 | us | us6000a9vs | 14 km SSW of Sitia | 6.1 | 1.9 | 0.178 | 9 | us | us |
| 2020-02-04 T16:47:10.864Z | 38,997 | 27,941 | 4.5 | 10 | mb | 0.698 | 1.04 | us | us60007phg | 12 km NE of Akhisar | 4.7 | 1.9 | 0.105 | 27 | us | us |
| 2020-10-30 T09:20:36.917Z | 34,401 | 26,428 | 4.6 | 10 | mb | 1.291 | 0.58 | us | us7000catf | 89 km S of Palekastro | 5.1 | 1.9 | 0.164 | 11 | us | us |
| 2020-02-06 T09:24:16.857Z | 39,254 | 21,497 | 4.7 | 10 | mwr | 1.393 | 0.9 | us | us70007jsv | 10 km SSE of Anthiro | 2.9 | 1.7 | 0.068 | 21 | us | us |
| 2020-02-18 T16:09:23.758Z | 39,107 | 27,817 | 4.8 | 10 | mb | 0.534 | 0.68 | us | us70007sgb | 12 km E of Kirkagac | 2.8 | 1.8 | 0.060 | 87 | us | us |
| 2020-12-29 T08:06:09.922Z | 34,709 | 24,069 | 4.9 | 10 | mb | 0.887 | 1.12 | us | us6000d3y3 | 14 km S of Kastri | 5.0 | 1.4 | 0.052 | 149 | us | us |
| 2020-08-17 T07:27:02.373Z | 36,897 | 23,770 | 5.0 | 95.34 | mww | 1.502 | 0.61 | us | us6000bfuq | 56 km SSE of Hydra | 5.4 | 1.5 | 0.056 | 31 | us | us |
| 2020-05-22 T03:40:30.610Z | 34,483 | 25,886 | 5.1 | 10 | mww | 1.147 | 0.97 | us | us70009n06 | 60 km SSE of Ierapetra | 6.0 | 1.8 | 0.056 | 31 | us | us |
| 2020-10-12 T04:11:27.566Z | 35,644 | 26,246 | 5.2 | 10 | mww | 0.751 | 1.06 | us | us6000c7nd | 49 km N of Palekastro | 3.3 | 1.7 | 0.050 | 38 | us | us |
| 2020-10-30 T15:14:55.887Z | 37,831 | 26,822 | 5.3 | 10 | mww | 1.518 | 1.28 | us | us7000c7zh | 8 km NW of Kokkari | 5.2 | 1.9 | 0.098 | 10 | us | us |
| 2020-09-26 T22:50:25.082Z | 39,984 | 24,334 | 5.4 | 10.38 | mww | 1.585 | 0.58 | us | us6000c1rq | 31 km SSE of Karyes | 5.8 | 3.8 | 0.046 | 45 | us | us |
| 2020-01-28 T15:38:34.436Z | 35,218 | 27,891 | 5.5 | 10 | mww | 0.681 | 0.65 | us | us60007i7j | 69 km ESE of Karpathos | 5.2 | 1.7 | 0.052 | 35 | us | us |
| 2020-01-22 T19:22:16.298Z | 39,072 | 27,838 | 5.6 | 5.6 | mww | 0.567 | 0.66 | us | us60007d2r | 15 km ESE of Kirkagac | 4.1 | 3.1 | 0.057 | 30 | us | us |
| 2020-05-20 T23:43:16.920Z | 35,159 | 20,277 | 5.7 | 13.45 | mww | 2.416 | 0.52 | us | us70009m4x | 224 km SW of Methoni | 6.7 | 3.4 | 0.048 | 42 | us | us |
| 2020-09-18 T16:28:17.575Z | 35,036 | 25,303 | 5.9 | 44 | mww | 0.421 | 0.78 | us | us7000bpvt | 12 km SSE of Arkalochori | 5.9 | 1.9 | 0.050 | 39 | us | us |
| 2020-10-30 T11:51:27.348Z | 37,897 | 26,783 | 7.0 | 21 | mww | 1.518 | 0.59 | us | us7000c7y0 | 13 km NNE of Neon Karlovasi | 1.4 | 1.8 | 0.036 | 75 | us | us |
| Time | Latitude | Longitude | Mag | Depth | magType | dmin | rms | net | Id | Place | horizontalError | Depth Error | magError | Mag Nst | locationSource | magSource |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020-05-18 T11:48:07.371Z | 34.1328 | 25.5231 | 5.0 | 10 | mww | 1.265 | 0.71 | us | us70009jm3 | 98 km S of NΓ©a AnatolΓ, Greece | 7.1 | 1.8 | 0.075 | 17 | us | us |
| 2020-06-19 T07:43:21.049Z | 34.2871 | 25.5222 | 5.1 | 10 | mww | 1.126 | 0.62 | us | us6000aepr | 81 km S of NΓ©a AnatolΓ, Greece | 7.1 | 1.9 | 0.08 | 15 | us | us |
| 2020-05-18 T04:18:17.970Z | 34.1648 | 25.6205 | 5.2 | 10 | mww | 1.271 | 0.86 | us | us70009jdm | 93 km S of NΓ©a AnatolΓ, Greece | 6.9 | 1.8 | 0.05 | 39 | us | us |
| 2021-09-28 T04:48:08.650Z | 35.0817 | 25.2018 | 5.3 | 10 | mww | 0.328 | 0.94 | us | us7000ff36 | 9 km SW of ArkalochΓ3ri, Greece | 4.5 | 1.7 | 0.046 | 45 | us | us |
| 2020-06-03 T09:03:29.381Z | 34.3323 | 25.8927 | 5.4 | 10 | mww | 1.26 | 0.62 | us | us6000a52k | 76 km S of IerΓ’petra, Greece | 7.2 | 1.8 | 0.098 | 10 | us | us |
| 2020-01-30 T01:28:05.202Z | 35.1565 | 27.8845 | 5.5 | 10 | mww | 0.708 | 0.9 | us | us60007jpa | 72 km ESE of Karpathos, Greece | 5.3 | 1.8 | 0.055 | 32 | us | us |
| 2021-12-26 T18:59:02.711Z | 35.1923 | 26.9659 | 5.6 | 10 | mww | 0.388 | 1.09 | us | us6000gfhq | 25 km S of Fry, Greece | 5.7 | 1.8 | 0.056 | 31 | us | us |
| 2020-05-18 T23:22:35.162Z | 34.1855 | 25.5173 | 5.7 | 10 | mww | 1.215 | 0.6 | us | us70009k7k | 92 km S of NΓ©a AnatolΓ, Greece | 5.5 | 1.7 | 0.073 | 18 | us | us |
| 2020-09-18 T16:28:17.575Z | 35.0368 | 25.3034 | 5.9 | 44 | mww | 0.421 | 0.78 | us | us7000bpvt | 12 km SSE of ArkalochΓ3ri, Greece | 5.9 | 1.9 | 0.05 | 39 | us | us |
| 2019-11-27 T07:23:42.383Z | 35.7174 | 23.2284 | 6.0 | 69 | mww | 1.421 | 1.02 | us | us70006dlt | 45 km WNW of KΓssamos, Greece | 6.5 | 1.9 | 0.051 | 37 | us | us |
| 2021-10-12 T09:24:05.099Z | 35.1691 | 26.2152 | 6.4 | 20 | mww | 0.86 | 0.46 | us | us6000ftxu | 4 km SW of Palekastro, Greece | 6.1 | 1.8 | 0.048 | 42 | us | us |
| 2020-05-02 T12:51:05.561Z | 34.1818 | 25.7101 | 6.5 | 10 | mww | 1.293 | 1.01 | us | us700098qd | 91 km S of NΓ©a AnatolΓ, Greece | 6.7 | 1.8 | 0.048 | 42 | us | us |
References
- Sadhukhan, B.; Chakraborty, S.; Mukherjee, S. Predicting the Magnitude of an Impending Earthquake Using Deep Learning Techniques. Earth Sci. Inform. 2023, 16, 803–823. [Google Scholar] [CrossRef]
- Yegulalp, T.M.; Kuo, J.T. Statistical Prediction of the Occurrence of Maximum Magnitude Earthquakes. Bull. Seismol. Soc. Am. 1974, 64, 393–414. [Google Scholar] [CrossRef]
- Akhoondzadeh, M. Earthquake Prediction Using Satellite Data: Advances and Ahead Challenges. Adv. Space Res. 2024, 74, 3539–3555. [Google Scholar] [CrossRef]
- Huang, F.; Li, M.; Ma, Y.; Han, Y.; Tian, L.; Yan, W.; Li, X. Studies on Earthquake Precursors in China: A Review for Recent 50 Years. Geod. Geodyn. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Zhao, X.; Pan, S.; Sun, Z.; Guo, H.; Zhang, L.; Feng, K. State-of-the-Art Review Advances of Satellite Remote Sensing Technology in Earthquake Prediction. Nat. Hazards Rev. 2020, 22, 03120001. [Google Scholar] [CrossRef]
- Biswas, S. Exploring the Difficulties in Forecasting Earthquake Location with Inhomogeneous Ionospheric Perturbations. Nat. Hazards 2024, 120, 14727–14754. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Yamaguchi, H.; Hobara, Y. Observation of Ultra-Low-Frequency Wave Effects in Possible Association with the Fukushima Earthquake on 21 November 2016, and Lithosphere–Atmosphere–Ionosphere Coupling. Atmosphere 2023, 14, 1255. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, S.; Kumar, A. Earthquakes Associated Subionospheric VLF Anomalies Recorded at Two Low Latitude Stations in the South Pacific Region. J. Atmos. Sol. Terr. Phys. 2022, 229, 105834. [Google Scholar] [CrossRef]
- Surkov, V.V. An Overview of Theoretical Studies of Non-Seismic Phenomena Accompanying Earthquakes. Surv. Geophys. 2025, 46, 7–70. [Google Scholar] [CrossRef]
- Panet, I.; Narteau, C.; Lemoine, J.; Bonvalot, S.; Remy, D. Detecting Preseismic Signals in GRACE Gravity Solutions: Application to the 2011 Tohoku M w 9.0 Earthquake. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024542. [Google Scholar] [CrossRef]
- Tang, H.; Sun, W. Theories and Applications of Earthquake-Induced Gravity Variation: Advances and Perspectives. Earthq. Sci. 2023, 36, 376–415. [Google Scholar] [CrossRef]
- Wang, H.; Song, D.; Shan, X.; Bin Wang, A. A Method for Extracting the Pre-Seismic Gravity Anomalies over the Tibetan Plateau Based on the Maximum Shear Strain Using GRACE Data. Earth Planet. Phys. 2024, 8, 589–608. [Google Scholar] [CrossRef]
- Yang, J.; Chen, S.; Zhang, B.; Zhuang, J.; Wang, L.; Lu, H. Gravity Observations and Apparent Density Changes before the 2017 Jiuzhaigou Ms7.0 Earthquake and Their Precursory Significance. Entropy 2021, 23, 1687. [Google Scholar] [CrossRef] [PubMed]
- Fedotov, S.A.; Maguskin, M.A.; Kirienko, A.P.; Zharinov, N.A. Vertical Ground Movements on the Coast of the Kamchatka Gulf: Their Specific Features in the Epicentral Zone of the August 17, 1983, Earthquake M = 6.9, before and After. Tectonophysics 1992, 202, 157–162. [Google Scholar] [CrossRef]
- Fujii, Y.; Nakane, K. Case 24 Reevaluation of Anomalous Vertical Crustal Movement Associated with the 1964 Niigata, Japan, Earthquake. Pure Appl. Geophys. 1997, 149, 115–127. [Google Scholar] [CrossRef]
- Kaftan, V.I. An Analysis of Ground Movements and Deformations from 13-Year GPS Observations before and during the July 2019 Ridgecrest, USA Earthquakes. J. Volcanol. Seismol. 2021, 15, 97–106. [Google Scholar] [CrossRef]
- Shifflett, H.; Witbaard, R. Multiple Precursors to the Landers Earthquake. Bull. Seismol. Soc. Am. 1996, 86, 113–121. [Google Scholar] [CrossRef]
- Kopylova, G.N.; Boldina, S.V.; Serafimova, Y.K. Earthquake Precursors in the Ionic and Gas Composition of Groundwater: A Review of World Data. Geochem. Int. 2022, 60, 928–946. [Google Scholar] [CrossRef]
- Nakamura, Y.; Wakita, H. Precise Temperature Measurement of Groundwater for Earthquake-Prediction Study. Pure Appl. Geophys. 1984, 122, 164–174. [Google Scholar] [CrossRef]
- Orihara, Y.; Kamogawa, M.; Nagao, T. Preseismic Changes of the Level and Temperature of Confined Groundwater Related to the 2011 Tohoku Earthquake. Sci. Rep. 2014, 4, 6907. [Google Scholar] [CrossRef]
- Zhang, W.; Li, M.; Yang, Y.; Rui, X.; Lu, M.; Lan, S. Implications of Groundwater Level Changes before near Field Earthquakes and Its Influencing Factors—Several Earthquakes in the Vicinity of the Longmenshan-Anninghe Fault as an Example. Front. Earth Sci. 2025, 13, 1541346. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; Marchetti, D. Study of the Preparation Phase of Turkey’s Powerful Earthquake (6 February 2023) by a Geophysical Multi-Parametric Fuzzy Inference System. Remote Sens. 2023, 15, 2224. [Google Scholar] [CrossRef]
- Ganguly, N.D. Variation in Atmospheric Ozone Concentration Following Strong Earthquakes. Int. J. Remote Sens. 2009, 30, 349–356. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Cantzos, D.; Alam, A.; Dimopoulos, S.; Petraki, E. Electromagnetic and Radon Earthquake Precursors. Geosciences 2024, 14, 271. [Google Scholar] [CrossRef]
- Gupta, H.K.; Singh, H.N. Earthquake Swarms Precursory to Moderate to Great Earthquakes in the Northeast India Region. Tectonophysics 1989, 167, 285–298. [Google Scholar] [CrossRef]
- Kayal, J.R. Earthquake Prediction in Northeast India—A Review. Pure Appl. Geophys. 1991, 136, 297–313. [Google Scholar] [CrossRef]
- Bouih, M.; Panet, I.; Remy, D.; Longuevergne, L.; Bonvalot, S. Deep Mass Redistribution Prior to the 2010 Mw 8.8 Maule (Chile) Earthquake Revealed by GRACE Satellite Gravity. Earth Planet. Sci. Lett. 2022, 584, 117465. [Google Scholar] [CrossRef]
- Gunawan, I.; Wahyudi, E.J.; Alawiyah, S.; Kadir, W.G.A. Earthquake Events Detected by Continuous Gravimeters in Indonesia. J. Phys. Conf. Ser. 2024, 2734, 012006. [Google Scholar] [CrossRef]
- Kazama, T.; Okubo, S.; Sugano, T.; Matsumoto, S.; Sun, W.; Tanaka, Y.; Koyama, E. Absolute Gravity Change Associated with Magma Mass Movement in the Conduit of Asama Volcano (Central Japan), Revealed by Physical Modeling of Hydrological Gravity Disturbances. J. Geophys. Res. Solid. Earth 2015, 120, 1263–1287. [Google Scholar] [CrossRef]
- Liang, X.; Chen, S.; Chu, F.; Xu, R.; Sun, H.; Xiao, W.; Song, H.; Li, S. Resolution Analysis of the Gravity Survey Network in the Middle and South Sections of Tan-Lu Fault and Recent Changes in the Gravity Field. Geod. Geodyn. 2025, 16, 241–250. [Google Scholar] [CrossRef]
- Shimoda, T.; Juhel, K.; Ampuero, J.-P.; Montagner, J.-P.; Barsuglia, M. Early Earthquake Detection Capabilities of Different Types of Future-Generation Gravity Gradiometers. Geophys. J. Int. 2020, 224, 533–542. [Google Scholar] [CrossRef]
- Soosalu, H.; Key, J.; White, R.S.; Knox, C.; Einarsson, P.; Jakobsdóttir, S.S. Lower-Crustal Earthquakes Caused by Magma Movement beneath Askja Volcano on the North Iceland Rift. Bull. Volcanol. 2010, 72, 55–62. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Xing, L.; Liu, M.; He, Z. Gravity Changes Before and After the 2008 Mw 7.9 Wenchuan Earthquake at Pixian Absolute Gravity Station in More Than a Decade. Pure Appl. Geophys. 2020, 177, 121–133. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, X.; Liu, F.; Zhao, Y.; Wei, S.; Zhang, G. Progress and Prospect of the Time-Varying Gravity in Earthquake Prediction in the Chinese Mainland. Front. Earth Sci. 2023, 11, 1124573. [Google Scholar] [CrossRef]
- Barnes, D.F. Gravity Changes during the Alaska Earthquake. J. Geophys. Res. 1966, 71, 451–456. [Google Scholar] [CrossRef]
- Fujii, Y. Gravity Change in the Shock Area of the Niigata Earthquake, 16 Jun. 1964. Zisin J. Seismol. Soc. Jpn. 2nd Ser. 1966, 19, 200–216. [Google Scholar] [CrossRef]
- Hunt, T.M. Gravity Changes Associated with the 1968 Inangahua Earthquake. N. Z. J. Geol. Geophys. 1970, 13, 1050–1051. [Google Scholar] [CrossRef]
- Kisslinger, C. Processes during the Matsushiro, Japan, Earthquake Swarm as Revealed by Leveling, Gravity, and Spring-Flow Observations. Geology 1975, 3, 57. [Google Scholar] [CrossRef]
- Oliver, H.W.; Robbins, S.L.; Grannell, R.B.; Alewine, R.W.; Shawn, B. Surface and Subsurface Movements Determined by Remeasuring Gravity. In San Fernando, California, Earthquake of 9 February 1971; Oakeshott, G.B., Ed.; U.S. Government Printing Office: Sacramento, CA, USA, 1975; pp. 195–211. [Google Scholar]
- Yun-Tai, C.; Hao-Ding, G.; Zao-Xun, L. Variations of Gravity before and after the Haicheng Earthquake, 1975, and the Tangshan Earthquake, 1976. Phys. Earth Planet. Inter. 1979, 18, 330–338. [Google Scholar] [CrossRef]
- Hagiwara, Y. Gravity Changes Resulting from Earthquakes in China. J. Geod. Soc. Jpn. 1979, 25, 10–19. [Google Scholar] [CrossRef]
- Baldi, P.; Postpischl, D. Gravity Variations during Preseismic Crustal Deformations. Il Nuovo Cimento C 1978, 1, 457–464. [Google Scholar] [CrossRef]
- Lambert, A.; Bower, D.R. Constraints on the Usefulness of Gravimetry for Detecting Precursory Crustal Deformations. Tectonophysics 1991, 193, 369–375. [Google Scholar] [CrossRef]
- OKUBO, S. Advances in Gravity Analyses for Studying Volcanoes and Earthquakes. Proc. Jpn. Acad. Ser. B 2020, 96, 50–69. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y.; Kato, A.; Sugano, T.; Fu, G.; Zhang, X.; Furuya, M.; Sun, W.; Okubo, S.; Matsumoto, S.; Honda, M.; et al. Gravity Changes Observed between 2004 and 2009 near the Tokai Slow-Slip Area and Prospects for Detecting Fluid Flow during Future Slow-Slip Events. Earth Planets Space 2010, 62, 905–913. [Google Scholar] [CrossRef]
- Tanaka, Y.; Suzuki, T.; Imanishi, Y.; Okubo, S.; Zhang, X.; Ando, M.; Watanabe, A.; Saka, M.; Kato, C.; Oomori, S.; et al. Temporal Gravity Anomalies Observed in the Tokai Area and a Possible Relationship with Slow Slips. Earth Planets Space 2018, 70, 25. [Google Scholar] [CrossRef]
- Shahrisvand, M.; Akhoondzadeh, M.; Sharifi, M.A. Detection of Gravity Changes before Powerful Earthquakes in GRACE Satellite Observations. Ann. Geophys. 2014, 57, A0543. [Google Scholar] [CrossRef]
- Juhel, K.; Bletery, Q.; Licciardi, A.; Vallée, M.; Hourcade, C.; Michel, T. Fast and Full Characterization of Large Earthquakes from Prompt Elastogravity Signals. Commun. Earth Environ. 2024, 5, 561. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, R.; Dahm, T.; Zhou, S.; Heimann, S. Prompt Elasto-Gravity Signals (PEGS) and Their Potential Use in Modern Seismology. Earth Planet. Sci. Lett. 2020, 536, 116150. [Google Scholar] [CrossRef]
- Liu, X.; Chen, S.; Xing, H. Gravity Changes Caused by Crustal Fluids Invasion: A Perspective from Finite Element Modeling. Tectonophysics 2022, 833, 229335. [Google Scholar] [CrossRef]
- Lough, A.C.; Wiens, D.A.; Nyblade, A. Reactivation of Ancient Antarctic Rift Zones by Intraplate Seismicity. Nat. Geosci. 2018, 11, 515–519. [Google Scholar] [CrossRef]
- Rubin, A.M. Propagation of Magma-Filled Cracks. Annu. Rev. Earth Planet. Sci. 1995, 23, 287–336. [Google Scholar] [CrossRef]
- Rymer, H.; Brown, G. Gravity Fields and the Interpretation of Volcanic Structures: Geological Discrimination and Temporal Evolution. J. Volcanol. Geotherm. Res. 1986, 27, 229–254. [Google Scholar] [CrossRef]
- Chariskou, C.; Vrochidou, E.; Daniels, A.J.; Kaburlasos, V.G. Variable Selection on Reflectance NIR Spectra for the Prediction of TSS in Intact Berries of Thompson Seedless Grapes. Agronomy 2022, 12, 2113. [Google Scholar] [CrossRef]
- Govers, R.; Furlong, K.P.; van de Wiel, L.; Herman, M.W.; Broerse, T. The Geodetic Signature of the Earthquake Cycle at Subduction Zones: Model Constraints on the Deep Processes. Rev. Geophys. 2018, 56, 6–49. [Google Scholar] [CrossRef]
- McKenzie, D. Active Tectonics of the Mediterranean Region. Geophys. J. Int. 1972, 30, 109–185. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Papadimitriou, E.E.; Kiratzi, A.A.; Papazachos, C.B.; Louvari, E.K. Fault Plane Solutions in the Aegean Sea and the Surrounding Area and Their Tectonic Implication. Boll. Geofis. Teor. Appl. 1998, 39, 199–218. [Google Scholar]
- Shaw, B.; Jackson, J. Earthquake Mechanisms and Active Tectonics of the Hellenic Subduction Zone. Geophys. J. Int. 2010, 181, 966–984. [Google Scholar] [CrossRef]
- Herak, M. Conversion between the Local Magnitude (ML) and the Moment Magnitude (Mw) for Earthquakes in the Croatian Earthquake Catalogue. Geofizika 2020, 37, 197–211. [Google Scholar] [CrossRef]
- Scordilis, E.M. Empirical Global Relations Converting M S and m b to Moment Magnitude. J. Seismol. 2006, 10, 225–236. [Google Scholar] [CrossRef]
- Frankel, A.D.; Mueller, C.S.; Barnhard, T.P.; Leyendecker, E.V.; Wesson, R.L.; Harmsen, S.C.; Klein, F.W.; Perkins, D.M.; Dickman, N.C.; Hanson, S.L.; et al. USGS National Seismic Hazard Maps. Earthq. Spectra 2000, 16, 1–19. [Google Scholar] [CrossRef]
- U.S. Department of the Interior Earthquake Hazards Program. Available online: https://www.usgs.gov/programs/earthquake-hazards (accessed on 25 August 2025).
- GFZ Helmholtz Centre for Geosciences GFZ Data Services. Available online: https://dataservices.gfz-potsdam.de/web/ (accessed on 25 August 2025).
- COST-G Team International Combination Service for Time-Variable Gravity Fields (COST-G). Available online: https://cost-g.org/ (accessed on 25 August 2025).
- Calandra, S.; Teti, D. Correlation Study: Triggering and Magnitude of Earthquakes in Italy (≥M4. 3) in Relation to the Positions and Gravitational Forces of the Sun, Moon, and Planets Relative to Earth. New Concepts Glob. Tecton. J. 2024, 12, 1–26. [Google Scholar]
- Mahmud, S. The Combined Effects of the Gravitational Forces on the Tectonic Plates on Earth’s Surface Exerted by the Moon, the Sun and the Other Planets Are One of the Main Reasons of the Earthquakes. Int. J. Adv. Res. Phys. Sci. 2019, 6, 44–62. [Google Scholar]
- Romanet, P. Could Planet/Sun Conjunctions Be Used to Predict Large (Moment Magnitude ≥ 7) Earthquakes? Seismica 2023, 2, 1–6. [Google Scholar] [CrossRef]
- Senapati, B.; Kundu, B.; Jha, B.; Jin, S. Gravity-Induced Seismicity Modulation on Planetary Bodies and Their Natural Satellites. Sci. Rep. 2024, 14, 2311. [Google Scholar] [CrossRef] [PubMed]
- Straser, V. Variations in Gravitational Field, Tidal Force, Electromagnetic Waves and Earthquakes. New Concepts Glob. Tecton. Newsl. 2010, 57, 98–108. [Google Scholar]
- Neumeyer, J.; Hagedoorn, J.; Leitloff, J.; Schmidt, T. Gravity Reduction with Three-Dimensional Atmospheric Pressure Data for Precise Ground Gravity Measurements. J. Geodyn. 2004, 38, 437–450. [Google Scholar] [CrossRef]
- Rabbel, W.; Zschau, J. Static Deformations and Gravity Changes at the Earth’s Surface Due to Atmospheric Loading. J. Geophys. Z. Geophys. 1985, 56, 81–89. [Google Scholar]
- Namias, J. Summer Earthquakes in Southern California Related to Pressure Patterns at Sea Level and Aloft. J. Geophys. Res. Solid. Earth 1989, 94, 17671–17679. [Google Scholar] [CrossRef]
- Hasan, S.; Troch, P.A.; Boll, J.; Kroner, C. Modeling the Hydrological Effect on Local Gravity at Moxa, Germany. J. Hydrometeorol. 2006, 7, 346–354. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Z.; Wu, Q.; Teng, Y.; Zhang, X.; Du, F.; Jiang, Y. Hydrologic Changes of In-Situ Gravimetry. Geophysics 2022, 87, B117–B127. [Google Scholar] [CrossRef]
- Bragato, P.L. Statistical Relationship Between the Decrease of Major Seismicity and Drought in Southern California Since 1900. Front. Earth Sci. 2021, 9, 790412. [Google Scholar] [CrossRef]
- Johnson, C.W.; Fu, Y.; Bürgmann, R. Stress Models of the Annual Hydrospheric, Atmospheric, Thermal, and Tidal Loading Cycles on California Faults: Perturbation of Background Stress and Changes in Seismicity. J. Geophys. Res. Solid. Earth 2017, 122, 605–625. [Google Scholar] [CrossRef]
- Simon, V.; Kraft, T.; Maréchal, J.-C.; Helmstetter, A.; Diehl, T. Climate-Change-Induced Seismicity: The Recent Onset of Seasonal Microseismicity at the Grandes Jorasses, Mont Blanc Massif, France/Italy. Earth Planet. Sci. Lett. 2025, 666, 119372. [Google Scholar] [CrossRef]
- Kreemer, C.; Zaliapin, I. Spatiotemporal Correlation Between Seasonal Variations in Seismicity and Horizontal Dilatational Strain in California. Geophys. Res. Lett. 2018, 45, 9559–9568. [Google Scholar] [CrossRef]

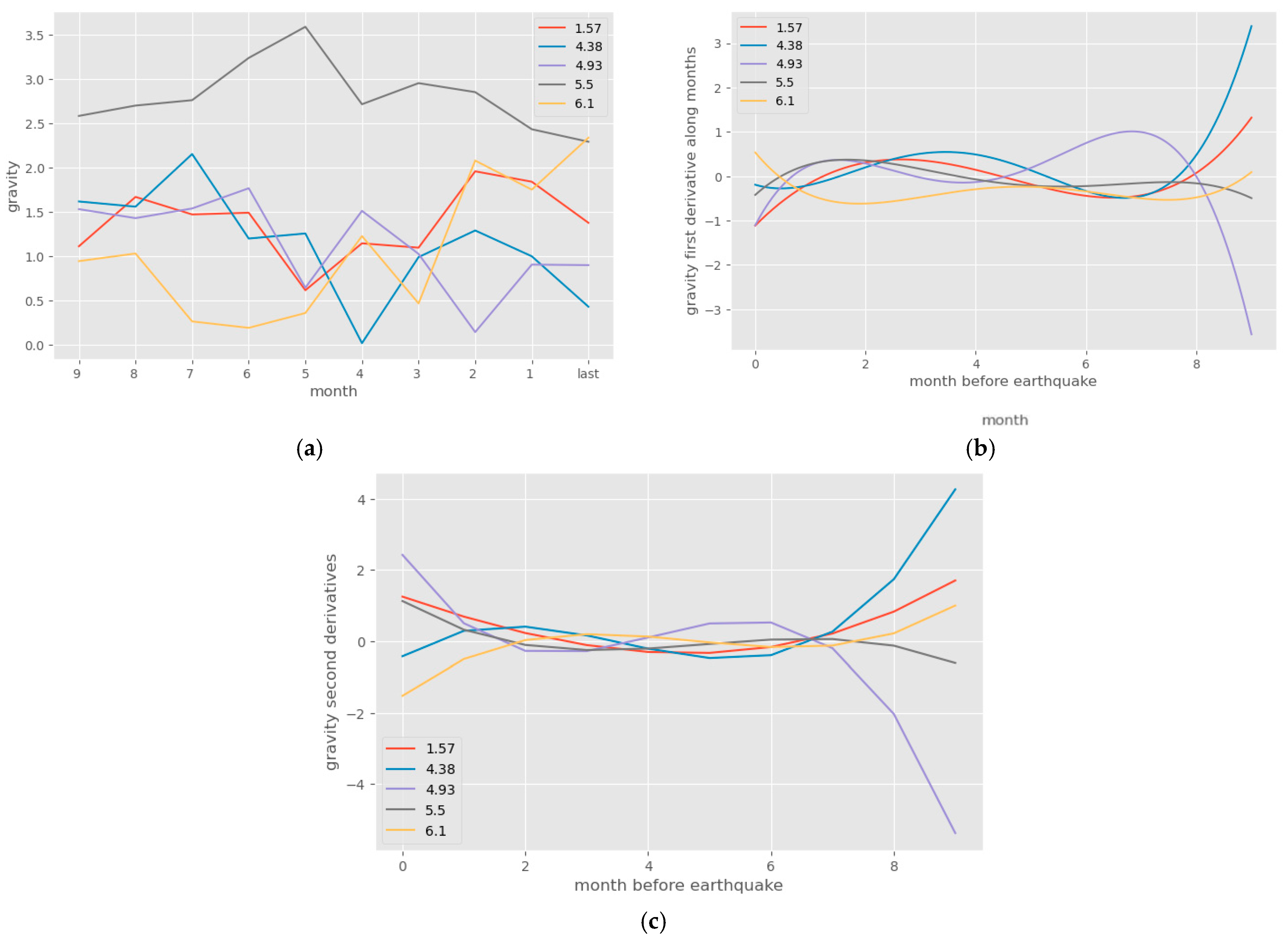

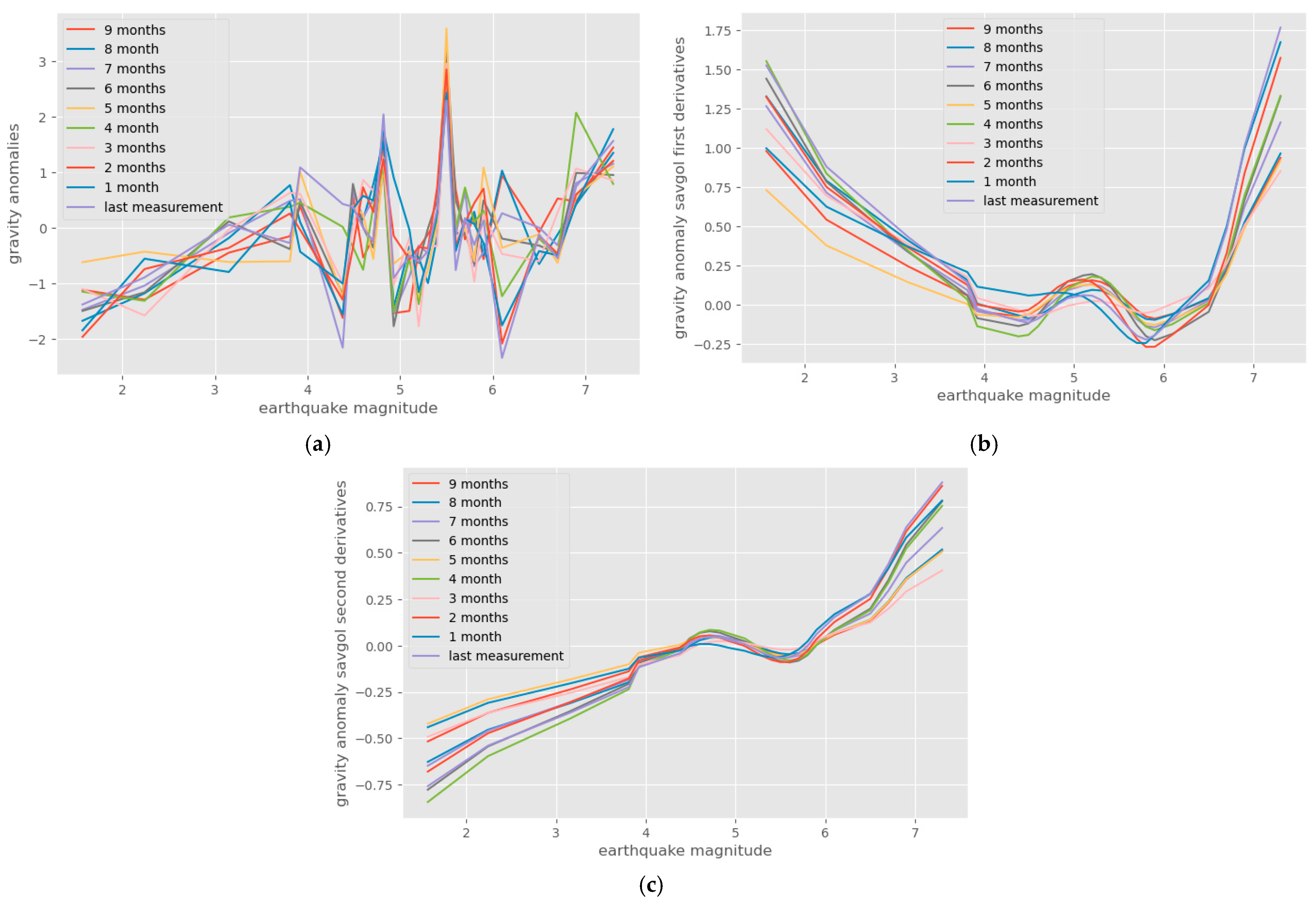
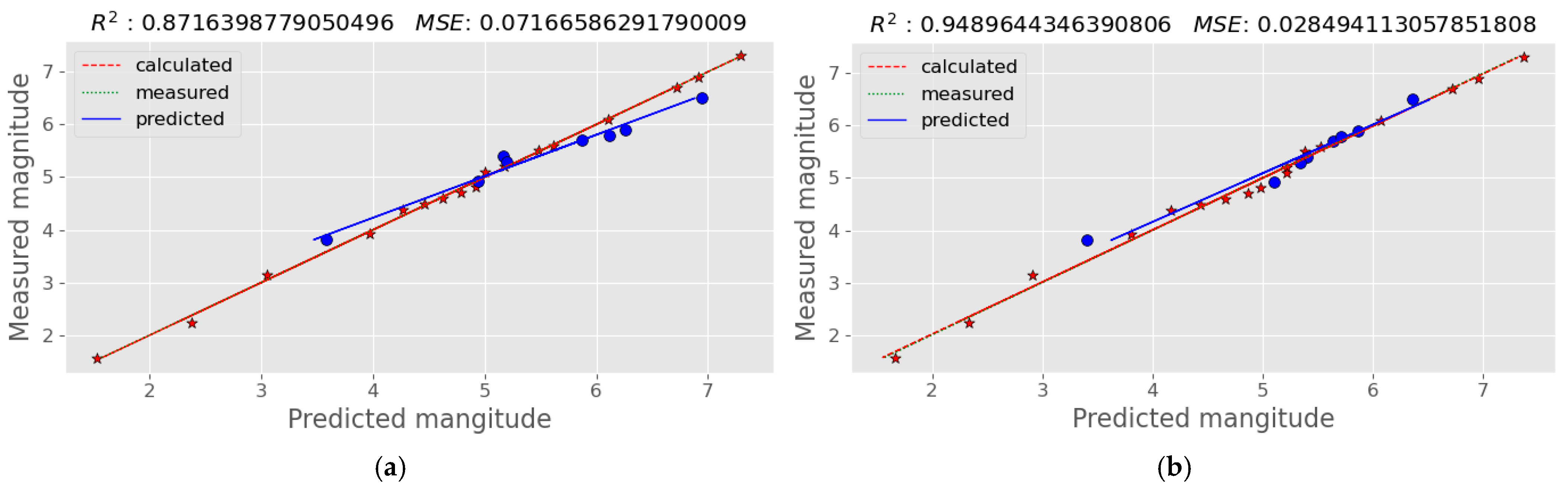
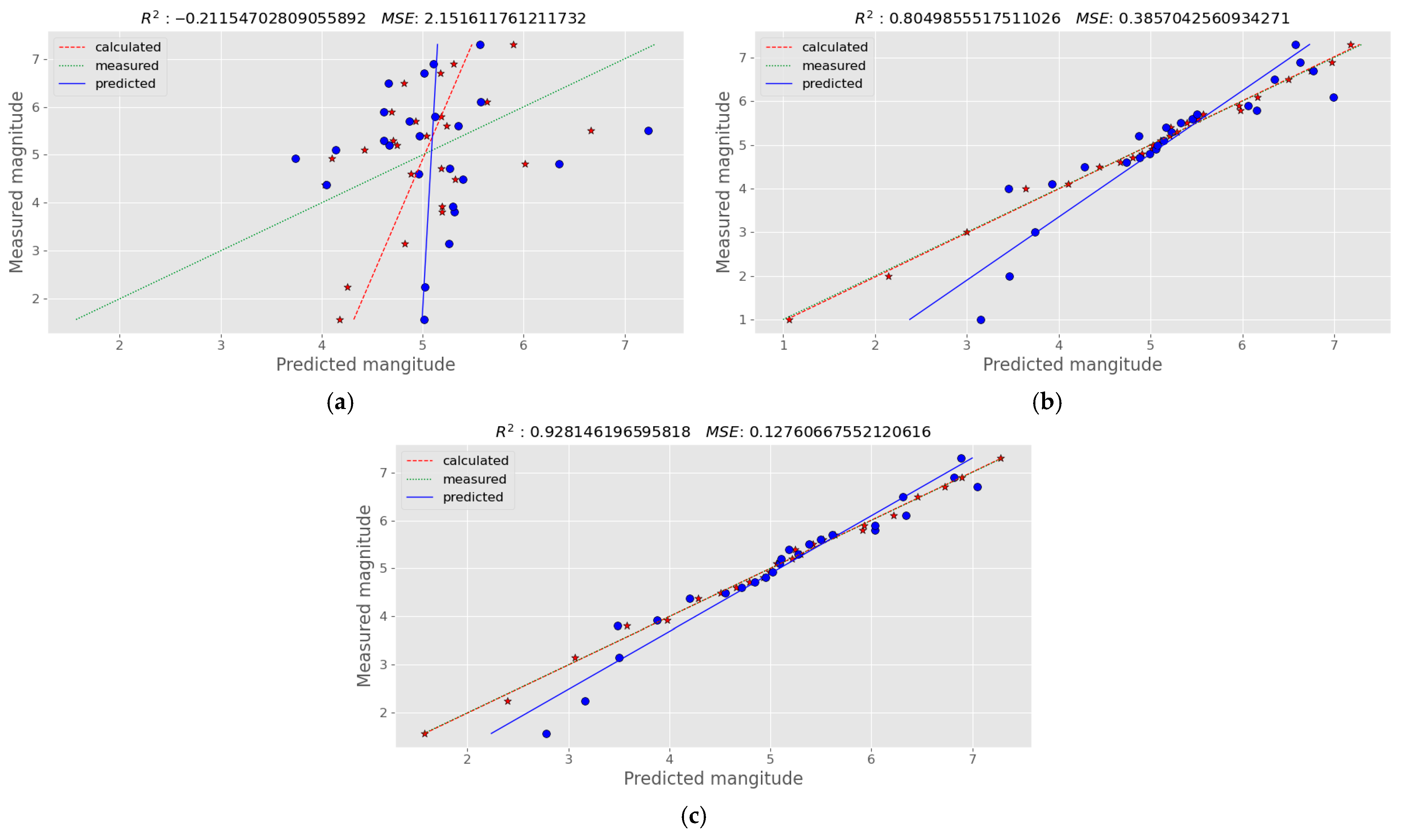

| Data Processing | MLR | PLS Regression | Neural Network |
|---|---|---|---|
| Data scaling by using the Standard scaler () function of the Scikit-learn 1.7.1 library. Calculation of derivatives by using the SavgolFilter () function of the Scipy 1.16.1 library. Calculation of the slope of gravity values through the months, by using the LinearRegression.fit () function of the Scikit-learn 1.7.1 library. | Used as callable function. Regression: linear. Test size: 0.3 Performance metrics: MSE, R2 score. Plotting predicted against actual magnitudes. | Used as callable function Number of components: The optimal determined by variable selection. Model regression function: PLS regression Metrics for evaluation of model performance and prediction: MSE, R2 score Plotting predicted against actual magnitudes | Used as callable function. Keras 3.10.0 model: sequential, regression. Test size: 0.2 Input shape: 10 Input layer: 10 nodes, activation: relu Hidden layers: one layer of three nodes, activation: relu Output layer: one node, activation: linear 200 epochs, batch size: 3 Performance metrics: MSE, R2 score Plotting predicted against actual magnitudes |
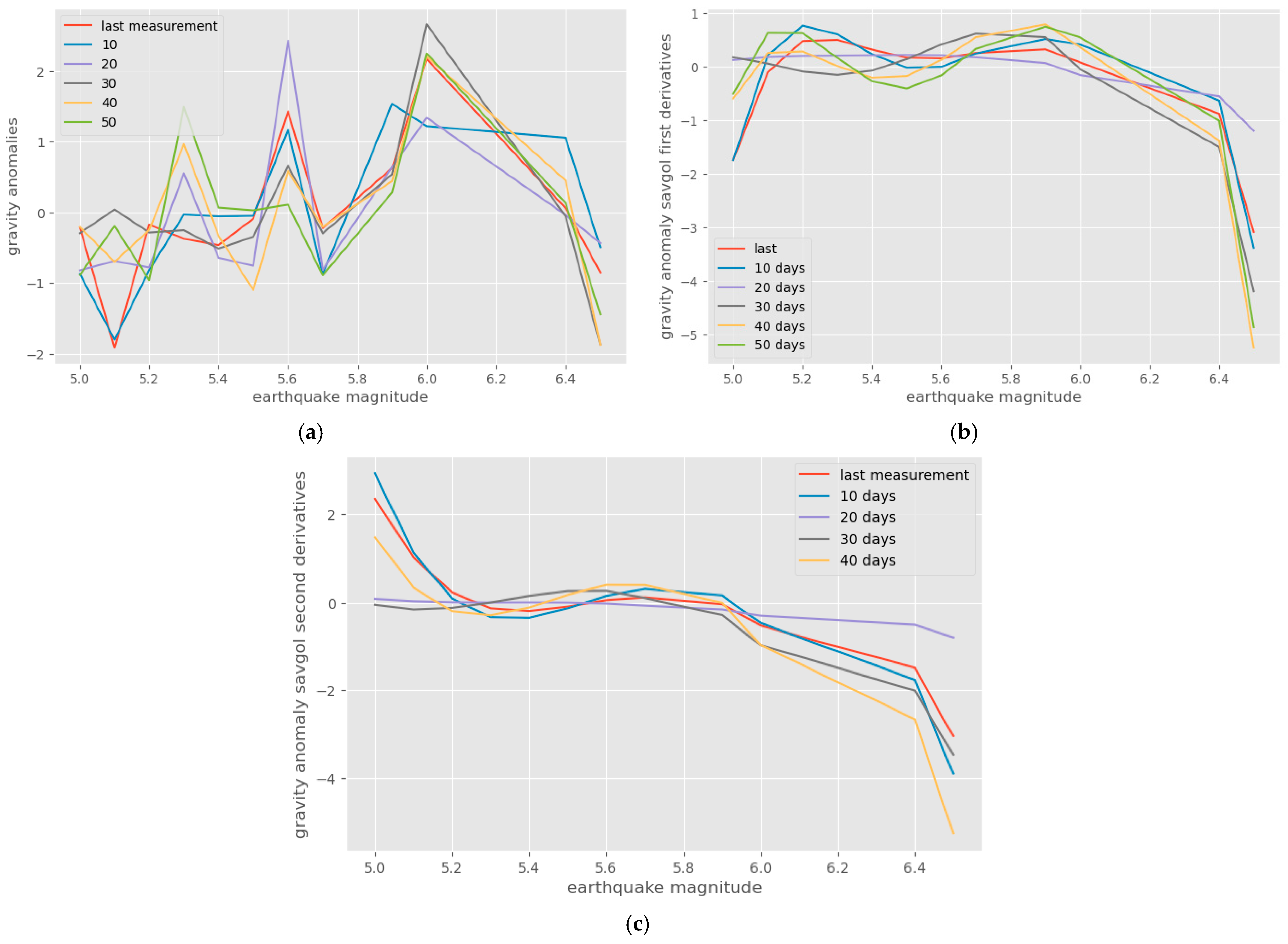
| Mag | Gravity Anomaly (µGal) Before the Earthquake Occurrence | Days After Last Measurement | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 Months | 8 Months | 7 Months | 6 Months | 5 Months | 4 Months | 3 Months | 2 Months | 1 Month | Last Measurement | ||
| 1.57 | −3.487 | −5.937 | −4.278 | −4.369 | −1.289 | −3.520 | −1.749 | −4.532 | −5.786 | −2.765 | 4 |
| 2.24 | −4.138 | −4.108 | −2.820 | −3.337 | −0.600 | −4.086 | −3.067 | −1.144 | −1.055 | −1.535 | 15 |
| 3.15 | −1.034 | −0.426 | 0.364 | 0.614 | −1.279 | 1.061 | 1.197 | −0.086 | −1.932 | 0.854 | 25 |
| 3.81 | 0.056 | 3.094 | 2.305 | −0.931 | −1.231 | 1.719 | 3.018 | 1.632 | 2.674 | 0.022 | 8 |
| 3.92 | 2.037 | 0.632 | 2.405 | 1.711 | 4.630 | 1.980 | 2.967 | 0.818 | −0.591 | 3.452 | 11 |
| 4.38 | −5.344 | −5.530 | −6.569 | −3.466 | −3.616 | 0.480 | −1.455 | −2.676 | −2.694 | 1.791 | 15 |
| 4.49 | 2.777 | 1.443 | 2.865 | 2.702 | 2.388 | −0.754 | 1.278 | −0.077 | 2.233 | 1.667 | 15 |
| 4.60 | −1.349 | 0.794 | 1.304 | 0.276 | 1.835 | −2.168 | 3.664 | 2.941 | 3.101 | 0.715 | 29 |
| 4.71 | −0.035 | 3.146 | 2.384 | −0.854 | −1.071 | 1.737 | 3.107 | 1.705 | 2.794 | 0.102 | 11 |
| 4.82 | 6.548 | 5.996 | 4.717 | 3.617 | 4.899 | 4.233 | 4.752 | 4.362 | 7.393 | 5.855 | 4 |
| 4.93 | −5.026 | −5.050 | −4.505 | −5.224 | −1.393 | −4.778 | −1.554 | 0.512 | 4.305 | −1.561 | 11 |
| 5.10 | −4.883 | −0.989 | −2.268 | −1.282 | −0.539 | −1.495 | 0.799 | −0.655 | 0.856 | −0.549 | 15 |
| 5.20 | −0.739 | −1.745 | −0.400 | −1.701 | −3.591 | −4.291 | −3.604 | −0.037 | −3.262 | −0.828 | 4 |
| 5.30 | 0.181 | −3.431 | −0.853 | 0.221 | −1.784 | −1.306 | 0.347 | −0.111 | −0.933 | −0.341 | 18 |
| 5.40 | 1.187 | −0.334 | 1.644 | 1.786 | 1.259 | 0.978 | 0.387 | 2.953 | 1.942 | 1.578 | 4 |
| 5.50 | 10.093 | 10.243 | 9.949 | 10.278 | 13.981 | 9.739 | 9.423 | 8.840 | 9.917 | 6.484 | 14 |
| 5.60 | 3.130 | −0.102 | 0.223 | 1.814 | −0.386 | 0.390 | 0.583 | 0.014 | −0.552 | −1.204 | 15 |
| 5.70 | −0.159 | −0.092 | 2.888 | 0.080 | 0.945 | 2.912 | 1.728 | 1.169 | 1.571 | 1.153 | 8 |
| 5.80 | 1.452 | 1.319 | −1.649 | −1.760 | −1.215 | 0.774 | −1.389 | 2.153 | 1.243 | −0.059 | 4 |
| 5.90 | −1.462 | −1.574 | −0.793 | 1.784 | 4.895 | 1.487 | 1.953 | 2.877 | −0.031 | 1.044 | 15 |
| 6.10 | 4.072 | 4.061 | 1.557 | −0.345 | −0.356 | −3.801 | −0.013 | −4.869 | −5.458 | −5.185 | 4 |
| 6.50 | 0.320 | −2.159 | 0.689 | −0.731 | 0.544 | −0.226 | −0.375 | 0.524 | −0.554 | 0.413 | 4 |
| 6.70 | 2.542 | −0.193 | −0.378 | −1.175 | −1.334 | −1.365 | 2.048 | −0.372 | −0.829 | −0.673 | 25 |
| 6.90 | 2.360 | 1.813 | 3.379 | 3.316 | 3.046 | 7.530 | 4.223 | 2.591 | 2.588 | 2.585 | 14 |
| 7.30 | 5.915 | 5.242 | 4.546 | 3.199 | 4.956 | 3.133 | 3.633 | 4.263 | 7.501 | 4.647 | 4 |
| MLR | PLS | NN | ||||
|---|---|---|---|---|---|---|
| MSE | R2 Score | MSE | R2 Score | MSE | R2 Score | |
| Gravity values | 2.864 | −4.130 | 2.151 | −0.211 | 11.860 | −1.545 |
| 1st magnitude derivative | 0.071 | 0.871 | 0.127 | 0.928 | 0.191 | 0.940 |
| 1st time derivative | 3.121 | −4.590 | 2.116 | −0.192 | 4.291 | −0.182 |
| 2nd magnitude derivative | 0.028 | 0.948 | 0.131 | 0.926 | 0.273 | 0.923 |
| 2nd time derivative | 3.626 | −5.495 | 1.978 | −0.114 | 7.553 | −1.030 |
| Slope 3rd magnitude derivative | 2.864 | −4.130 | 2.151 | −0.211 | 11.860 | −1.545 |
| Mag | Days After Last Measurement | Last Measurement | 10 Days | 20 Days | 30 Days | 40 Days | 50 Days |
|---|---|---|---|---|---|---|---|
| 2.71 | 7 | −0.665 | −0.386 | −0.503 | 0.238 | −0.438 | 0.052 |
| 2.91 | 6 | 0.817 | 1.031 | 0.517 | 0.728 | −0.660 | −1.309 |
| 2.98 | 2 | −1.483 | −0.964 | −1.787 | −0.573 | −1.319 | −2.641 |
| 3.05 | 5 | 0.439 | −0.586 | 0.164 | 1.085 | 1.670 | 1.638 |
| 3.12 | 8 | −0.022 | 3.567 | 0.120 | 2.772 | 5.024 | 0.111 |
| 3.37 | 15 | 2.155 | 4.949 | 3.695 | 2.672 | 3.271 | 2.827 |
| 3.81 | 5 | −3.674 | −2.813 | −2.314 | −3.629 | −2.234 | −2.255 |
| 3.92 | 3 | 0.962 | 0.408 | 2.035 | 0.966 | 1.041 | 0.533 |
| 4.03 | 2 | 1.892 | 2.155 | 2.863 | 3.689 | 4.217 | 3.337 |
| 4.30 | 2 | 1.552 | 2.646 | 2.042 | 1.738 | 2.334 | 3.304 |
| 4.38 | 9 | 1.248 | 1.552 | 1.050 | 1.180 | 1.161 | 1.099 |
| 4.49 | 9 | −0.583 | 1.290 | −2.100 | −2.683 | −2.627 | −4.802 |
| 4.25 | 5 | 3.745 | 3.237 | 3.858 | 2.852 | 1.635 | 2.059 |
| 4.70 | 1 | 3.966 | 5.240 | 3.552 | 2.874 | 2.715 | 1.944 |
| 4.71 | 13 | −0.280 | −0.442 | 1.513 | −1.728 | −2.296 | −2.171 |
| 4.90 | 8 | 4.907 | 0.536 | 4.569 | 4.866 | 3.655 | 1.786 |
| 5.00 | 2 | 4.779 | 3.889 | 3.028 | 4.914 | 3.689 | 4.271 |
| 5.10 | 7 | 0.748 | −0.082 | −0.064 | 0.200 | 0.148 | −2.086 |
| 5.20 | 7 | 2.771 | 1.793 | 1.597 | 2.318 | 1.574 | 1.103 |
| 5.30 | 5 | −3.235 | −2.493 | −2.009 | −3.333 | −1.940 | −1.945 |
| 5.40 | 1 | −0.950 | 0.526 | 0.808 | 0.394 | 1.118 | 0.587 |
| 5.50 | 3 | −0.994 | 1.306 | −2.422 | 0.198 | 0.441 | 0.643 |
| 5.60 | 7 | 1.457 | −1.820 | −2.383 | −2.275 | −4.461 | −5.903 |
| 5.70 | 5 | −0.248 | −1.054 | −1.715 | 0.706 | −0.062 | 0.368 |
| 5.90 | 3 | 1.744 | 2.939 | 1.980 | 1.220 | 1.351 | 0.532 |
| 7.00 | 5 | −3.205 | −2.497 | −2.036 | −3.357 | −1.949 | −1.975 |
| MLR | PLS | NN | ||||
|---|---|---|---|---|---|---|
| MSE | R2 Score | MSE | R2 Score | MSE | R2 Score | |
| Gravity values | 2.072 | −0.923 | 1.303 | −0.163 | 2.056 | −0.986 |
| 1st magnitude derivative | 0.066 | 0.932 | 0.500 | 0.553 | 0.436 | −0.603 |
| 1st time-derivative | 0.562 | 0.065 | 1.086 | 0.029 | 1.671 | −0.449 |
| 2nd magnitude derivative | 0.011 | 0.980 | 0.153 | 0.862 | 0.685 | 0.456 |
| 2nd time-derivative | 1.886 | −0.750 | 1.216 | −0.086 | 2.199 | −0.953 |
| Mag | Days After Last Measurement | Last Measurement | 10 Days | 20 Days | 30 Days | 40 Days | 50 Days |
|---|---|---|---|---|---|---|---|
| 5.00 | 3.6 | 0.636 | −0.295 | −0.323 | 0.191 | 0.403 | −1.514 |
| 5.10 | 4.4 | −1.615 | −1.544 | −0.118 | 0.604 | −0.320 | −0.301 |
| 5.20 | 3.6 | 0.688 | −0.223 | −0.260 | 0.202 | 0.341 | −1.644 |
| 5.30 | 8.0 | 0.423 | 0.835 | 1.844 | 0.242 | 2.119 | 2.656 |
| 5.40 | 8.0 | 0.305 | 0.800 | −0.043 | −0.080 | 0.220 | 0.159 |
| 5.50 | 1.5 | 0.799 | 0.810 | −0.223 | 0.127 | −0.906 | 0.091 |
| 5.60 | 6.9 | 2.807 | 2.447 | 4.805 | 1.373 | 1.564 | 0.232 |
| 5.70 | 3.7 | 0.622 | −0.308 | −0.319 | 0.186 | 0.403 | −1.524 |
| 5.90 | 3.3 | 1.744 | 2.939 | 1.980 | 1.221 | 1.352 | 0.533 |
| 6.00 | 6.9 | 3.786 | 2.515 | 3.083 | 3.846 | 3.931 | 3.982 |
| 6.40 | 2.6 | 0.996 | 2.296 | 0.914 | 0.485 | 1.366 | 0.274 |
| 6.50 | 7.3 | −0.207 | 0.213 | 0.285 | −1.760 | −2.037 | −2.490 |
| MLR | PLS | NN | ||||
|---|---|---|---|---|---|---|
| MSE | R2 Score | MSE | R2 Score | MSE | R2 Score | |
| Gravity values | 4.861 | −91.600 | 0.238 | −0.095 | 9.479 | −100.03 |
| 1st magnitude derivative | 0.004 | 0.913 | 0.021 | 0.901 | 1.064 | −2.549 |
| 1st time-derivative | 1.722 | −6.428 | 0.283 | −0.306 | 2.352 | −32.933 |
| 2nd magnitude derivative | 0.006 | 0.972 | 0.004 | 0.977 | 9.113 | −48.970 |
| 2nd time-derivative | 0.687 | −12.103 | 0.269 | −0.241 | 12.818 | −40.710 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chariskou, C.; Vrochidou, E.; Papakostas, G.A. A Correlation Between Earthquake Magnitude and Pre-Seismic Gravity Field Variations over Its Epicenter. Appl. Sci. 2025, 15, 11126. https://doi.org/10.3390/app152011126
Chariskou C, Vrochidou E, Papakostas GA. A Correlation Between Earthquake Magnitude and Pre-Seismic Gravity Field Variations over Its Epicenter. Applied Sciences. 2025; 15(20):11126. https://doi.org/10.3390/app152011126
Chicago/Turabian StyleChariskou, Chrysanthi, Eleni Vrochidou, and George A. Papakostas. 2025. "A Correlation Between Earthquake Magnitude and Pre-Seismic Gravity Field Variations over Its Epicenter" Applied Sciences 15, no. 20: 11126. https://doi.org/10.3390/app152011126
APA StyleChariskou, C., Vrochidou, E., & Papakostas, G. A. (2025). A Correlation Between Earthquake Magnitude and Pre-Seismic Gravity Field Variations over Its Epicenter. Applied Sciences, 15(20), 11126. https://doi.org/10.3390/app152011126










