A Parallel Network for Continuous Motion Estimation of Finger Joint Angles with Surface Electromyographic Signals

Abstract

The implementation of surface electromyographic (sEMG) signals in the interaction between human beings and machines is an important line of research. In the system of human–machine interaction, continuous-motion-estimation-based control plays an important role because it is more natural and intuitive than pattern recognition-based control. In this paper, we propose a parallel network consisting of a CNN with a multi-head attention mechanism and a BiLSTM (bidirectional long short-term memory) network to improve the accuracy of continuous motion estimation. The proposed network is evaluated in the Ninapro dataset. Six finger movements of 10 subjects were tested in the Ninapro DB2 dataset to evaluate the performance of the neural network and calculate the PCC (Pearson Correlation Coefficient) between the predicted joint angle sequence and the actual joint angle sequence. The experimental results show that the average accuracy (PCC) of the proposed network reaches 0.87 ± 0.02, which is significantly better than that of the BiLSTM network (0.79 ± 0.04, p < 0.05), CNN-Attention (0.80 ± 0.01, p < 0.05), CNN (0.70 ± 0.03, p < 0.05), CNN-BiLSTM (0.83 ± 0.02, p < 0.05), and TCN (0.76 ± 0.05, p < 0.05). It is worth noting that in this work, we extract multiple features from the raw sEMG signals and fuse them. We found that better continuous estimation accuracy can be achieved using multi-feature sEMG data. The model proposed in this paper skillfully integrates the convolutional neural network, multi-head attention mechanism, and bidirectional long short-term memory network, and its performance has good stability and accuracy. The model realizes more natural and accurate human–computer interaction.

1. Introduction

Electromyography (EMG) is used to record the electrical signals produced when muscles contract [1]. The EMG reflects the motor intention of the subject and contains a large amount of temporal and spatial information. Due to its low acquisition cost and easy acquisition, surface electromyography is widely used in gesture recognition [2], robot control [3], clinical diagnosis, sports science [4], and other fields. Surface electromyography is an important direction, providing a more natural method for human–computer collaboration.

Methods commonly used to decode human motion intentions include electromyography, video, inertial measurement unit (IMU), etc. Video-based techniques are vulnerable to environmental variables like lighting, noise, and camera placement, and require substantial computational resources. Inertial measurement unit (IMU)-based approaches are capable of accurately estimating joint angles. However, a large time delay is an unavoidable disadvantage of this method. EMG signals can give information about motor intention 50–100 milliseconds before the movement occurs [5]. Therefore, methods based on EMG signals can predict and estimate joint angles more naturally and fluently.

Overall, surface-EMG-based recognition tasks can be categorized as either classifying or regressing tasks. Classification tasks mainly include gesture recognition [6,7], body movement classification, etc. The regression task revolves around predicting continuous motion using EMG data. With the development of artificial intelligence, pure motion classification can no longer meet the requirements of human–computer interaction. Accurate continuous motion estimation plays a crucial role in realizing more natural human–computer interaction.

For EMG-based continuous motion prediction, both model-based and model-free approaches can be used [8]. Model-based methods estimate human motion parameters by building kinematic, dynamic, or musculoskeletal models. In this class of methods, Liu et al. [9] investigated a nonlinear EMG signal–torque model and an EMG signal amplitude estimation processor to estimate human joint torque. Wang et al. [10] studied and used the Hill-type model to estimate muscle force, and then obtained the moment arm through the musculoskeletal geometric model to achieve the purpose of predicting joint torque. The limitation of this type of method is that it requires more prior knowledge about human prostheses, and the number of parameters is large and difficult to estimate. Methods based on machine learning or deep learning, that is, model-free methods, do not include complex feature extraction or feature selection processes, which alleviate the requirements for kinematic modeling and are often better than model-based methods in terms of accuracy. For example, Chen et al. [11] proposed an LSTM-based upper limb motion model for multi-joint upper limb motion experiments. Gautam et al. [12] presented a deep learning model using a combination of CNNs and LSTMs, which can simultaneously classify the movement of the lower extremities and predict the corresponding knee angles. Chen et al. [13] used CNN, RNN, and traditional machine learning methods to continuously estimate the force of fingers with multiple degrees of freedom. Empirical findings indicate that the approach reliant upon neural networks is superior to the conventional technique. Ma et al. [14] aimed to predict joint angles with ten degrees of freedom and presented a novel method for surface electromyographic signal feature extraction for use in deep learning models. The proposed approach yields highly precise joint angle predictions. Zhang et al. [15] developed an adaptive radial basis function neural network (RBF NN)-based dynamics learning scheme to achieve the accurate identification of dominant dynamics of a robot under different failure modes. And physical experiments were conducted on a soft trunk robot. Jandaghi et al. [16] introduce a novel machine learning method, called deterministic learning, for training soft trunk robot models using radial basis function neural networks. The identification of fault occurrences during the operation of soft trunk robots is also investigated. Bodaghi et al. [17] present a flow-learning-based dimensionality reduction intermediate multimodal fusion network and compare various dimensionality reduction techniques for different variants of unimodal and multimodal networks.

In recent years, the utilization of deep learning techniques has grown in the field of recognizing patterns in biomedical signals. Due to the excellent performance of this method in terms of prediction accuracy, its future application scenarios are very broad. This paper presents a parallel network. The network consists of a convolutional neural network (CNN) with a multi-head attention mechanism and a bidirectional long short-term memory (BiLSTM) network. Six finger movements of 10 subjects were tested in the Ninapro DB2 dataset and benchmarked with five other deep learning methods. In addition, we also tested the network proposed in this paper in Ninapro DB7 for verifying the robustness of the network in different datasets. The test results show that the network has strong robustness.

The main contributions of this paper are the following four aspects: (1) We extract multiple features from the original sEMG signal and then fuse them. This effectively improves the accuracy of continuous estimation. (2) The network proposed in this paper skillfully combines the convolutional neural network, recurrent neural network, and attention mechanism. The special parallel mode ensures accuracy with high processing efficiency. (3) We tested the proposed model on a new database, and the results show that the model proposed in this paper has good robustness. (4) We also investigated the efficiency of the model, and the experimental results show that the model has a high inference speed, which meets the requirement of real-time continuous motion estimation (less than 100 ms).

The remainder of this paper is organized as follows: Section 2 discusses the dataset, the feature extraction method, the construction of the control model, and the PNCB model. Section 3 gives the evaluation metrics for continuous motion estimation and the test results of the PNCB model and the control model. Section 4 and Section 5 provide the discussion and conclusion of this paper.

2. Methods

2.1. Dataset

In order to evaluate the performance of the newly introduced algorithm and to compare it fairly with other traditional deep learning algorithms, this study chose the Ninapro open dataset. The Ninapro dataset records the motion data of multiple intact subjects and amputee subjects in the form of electromyography and is widely used in the development and testing of motion recognition control algorithms [18]. Ninapro is divided into 10 sub-datasets according to the type of experiment. In this study, we used the second one, referred to as DB2. This dataset contains motion data of 40 complete subjects.

During the process of obtaining hand movement data, subjects must follow the prompts to make corresponding actions and perform each movement for five seconds, alternating with rest positions for three seconds. Twenty-two joint angles were accurately measured at a sampling rate of 20 Hz using the CyberGlove II data glove. Surface EMG signals were measured and acquired through two models of dual differential surface EMG signal electrodes. One of the electrode combinations, called Delsys Trigno Wireless System, samples raw surface electromyography signals at a frequency of 2 kHz. It contains 12 wireless surface electromyography signal electrodes and a base station. In order to synchronize the frequency of data collected by the above two devices, the joint angles were resampled to 2 kHz.

In this study, we chose to use the 12-channel EMG to estimate 10 joint angles. As shown in Figure 1A, the ten joint angles selected, including the proximal interphalangeal and metacarpophalangeal joint points, were the primary active joints in the grasping movement. To ensure the generalizability of the algorithm, we selected 10 representative subjects from Ninapro DB2. Their height ranged from 169 to 187 cm and their weight ranged from 58 to 75 kg. Six different grasping actions were chosen for each participant, as shown in Figure 1B, since the focus of this paper is on the continuous estimation of joint angles for grasping actions. In order to verify the robustness of the model proposed in this paper, we also tested the same six grasping actions in Ninapro DB7 with a wide selection of 10 subjects.

2.2. Data Processing

Joint angle continuous motion is motion across multiple degrees of freedoms (DoFs). It represents a higher-dimensional and more complex target space and requires more comprehensive feature extraction methods. However, conventional deep learning feature extraction methods struggle to provide sufficient information for complex motion estimation across multiple degrees of freedom. Therefore, we used and fused multiple surface EMG signal feature extraction methods oriented to deep learning models. The extracted features such as Peak Stress (PS) and Shake Expectation (SE) are closely related to the strength and period of muscle contraction, which determines the accuracy of joint angle estimation.

In order to more completely extract data features, a sliding window of 100 ms, with a step size of 0.5 ms, was segmented from the surface electromyography signal and the resampled hand movement joint angle signal. Then, we extracted the following features from the segmented data intervals.

2.2.1. Root Mean Square (RMS)

Because of its simple calculation form and rich information, RMS is often used as a feature of surface electromyographic signals [19].

2.2.2. Peak Stress (PS)

Peak Stress (PS) is defined as a measurement that quantifies the amount of stress that becomes the peak in each sliding window. This feature is described using zeroth-, second-, and fourth-order moments. The calculation formulas are as follows:

$$PS={\displaystyle \frac{{\mathit{m}}_{\mathbf{4}}}{{\mathit{m}}_{\mathbf{2}}{\mathit{m}}_{\mathbf{0}}}}$$

where ${\mathit{m}}_{\mathbf{0}}$ represents the intensity of muscle contraction, ${\mathit{m}}_{\mathbf{2}}$ can be seen as a formula describing changes in surface electromyographic signals, and ${\mathit{m}}_{\mathbf{4}}$ describes the changes in ${\mathit{m}}_{\mathbf{2}}$. The quotient of ${\mathit{m}}_{\mathbf{4}}$ and ${\mathit{m}}_{\mathbf{2}}$ represents the stress change of the surface electromyographic signal, and then the stress of each unit can be obtained by dividing by ${\mathit{m}}_{\mathbf{0}}$.

2.2.3. Shake Expectation (SE)

The second derivative can explain the curvature of the surface EMG signal. Therefore, the amplitude changes the speed expectation of each sliding window, that is, Shake Expectation (SE) can be described by the average absolute second derivative of the surface electromyographic signal, and its calculation formula is

$$SE={\displaystyle \frac{\mathbf{1}}{\mathit{N}}}{\displaystyle \sum }_{\mathit{i}=\mathbf{0}}^{\mathit{N}-\mathbf{1}}\left|{\mathbf{\Delta }}^{\mathbf{2}}{\mathit{x}}_{\mathit{i}}\right|$$

where ${\mathbf{\Delta }}^{\mathbf{2}}$ represents the second derivative.

2.2.4. Unbiased Standard Deviation (USTD)

A sliding window of surface EMG signals can be viewed as a sample of movement progression. Unbiased Standard Deviation (USTD) uses unbiased estimators to evaluate the distribution of sample values. We assume that $\overline{\mathit{x}}$ is the prediction of the surface electromyographic signal amplitude in the sliding window, with the following calculation formula:

$$USTD=\sqrt{{\displaystyle \frac{\mathbf{1}}{\mathit{N}-\mathbf{1}}}{\displaystyle \mathbf{\sum }}_{\mathit{i}=\mathbf{0}}^{\mathit{N}-\mathbf{1}}{\mathbf{\left|}{\mathit{x}}_{\mathit{i}}-\overline{\mathit{x}}\mathbf{\right|}}^{\mathbf{2}}}$$

(1)

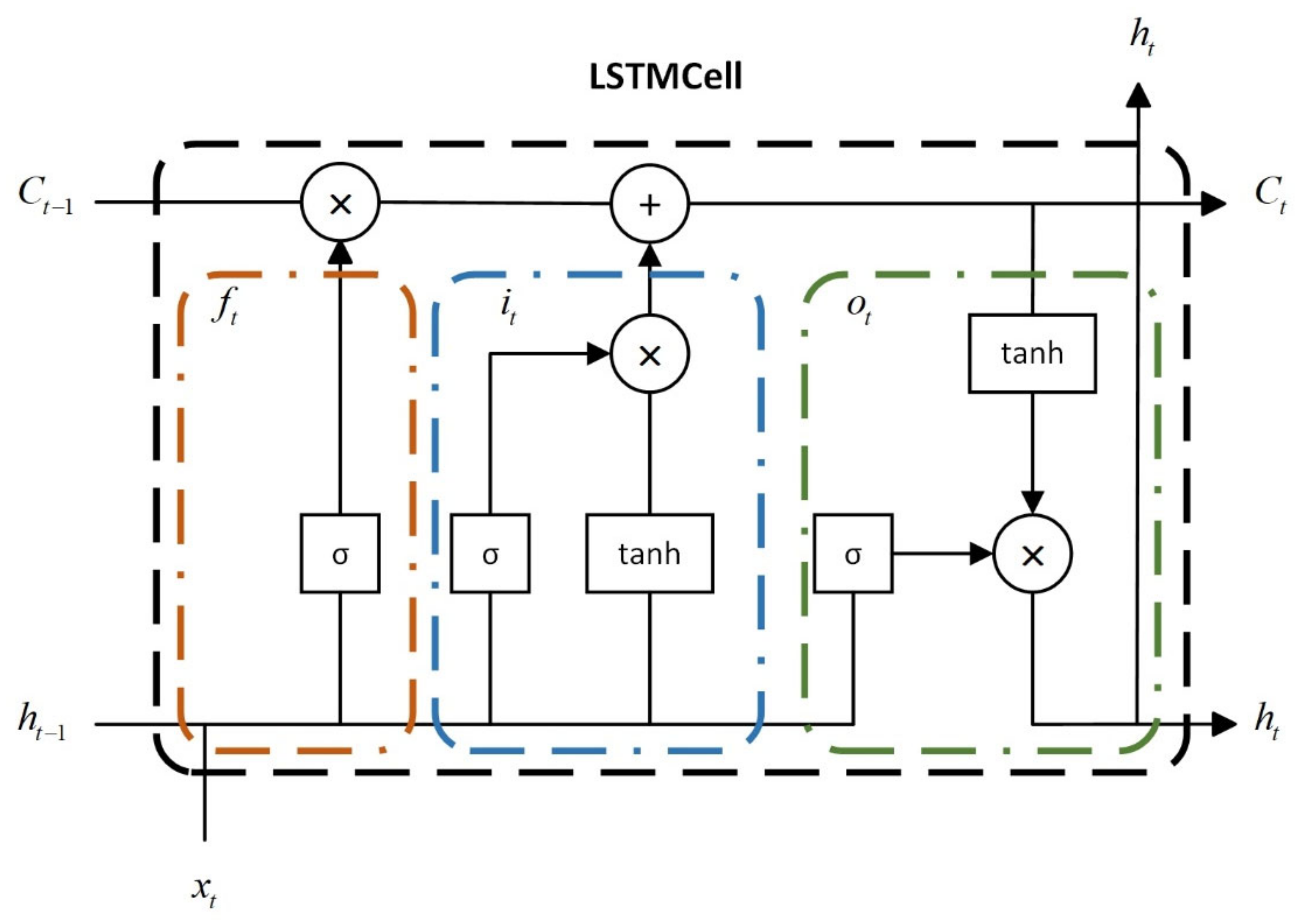
2.3. Bidirectional Long Short-Term Memory Network

The LSTM model was proposed to address the issue of vanishing gradients in conventional recurrent neural networks (RNNs). As a result, it demonstrates exceptional performance in capturing dependencies over longer distances. BiLSTM is an LSTM variant that connects in both directions. BiLSTM can effectively improve the long-term dependence of learning and further improve the model prediction accuracy [20]. Thus, the BiLSTM model finds extensive usage in natural language processing [21] and regression forecasting [22].

The fundamental component of the LSTM network consists of three gate structures, the forget gate, the input gate, and the output gate, as shown in Figure 2. The forget gate usually uses the Sigmoid function to achieve the purpose of retaining or deleting existing information. The input gate is made up of Sigmoid and Tanh layers that determine how much new information is being stored in memory. The output gate passes the information to the next LSTM unit. The specific mathematical formulas of the gates control unit are as follows:

$${\mathit{f}}_{\mathit{t}}=\mathit{\sigma }\left({\mathit{W}}_{\mathit{f}}\cdot \left[{\mathit{h}}_{\mathit{t}-\mathbf{1}},{\mathit{x}}_{\mathit{t}}\right]+{\mathit{b}}_{\mathit{f}}\right)$$

$${\mathit{i}}_{\mathit{t}}=\mathit{\sigma }\left({\mathit{W}}_{\mathit{i}}\cdot \left[{\mathit{h}}_{\mathit{t}-\mathbf{1}},{\mathit{x}}_{\mathit{t}}\right]+{\mathit{b}}_{\mathit{i}}\right)$$

$${\tilde{\mathit{C}}}_{\mathit{t}}=\mathbf{tanh}\left({\mathit{W}}_{\mathit{C}}\cdot \left[{\mathit{h}}_{\mathit{t}-\mathbf{1}},{\mathit{x}}_{\mathit{t}}\right]+{\mathit{b}}_{\mathit{C}}\right)$$

$${\mathit{C}}_{\mathit{t}}={\mathit{f}}_{\mathit{t}}\ast {\mathit{C}}_{\mathit{t}-\mathbf{1}}+{\mathit{i}}_{\mathit{t}}\ast {\tilde{\mathit{C}}}_{\mathit{t}}$$

$${\mathit{o}}_{\mathit{t}}=\mathit{\sigma }\left({\mathit{W}}_{\mathit{o}}\left[{\mathit{h}}_{\mathit{t}-\mathbf{1}},{\mathit{x}}_{\mathit{t}}\right]+{\mathit{b}}_{\mathit{o}}\right)$$

$${\mathit{h}}_{\mathit{t}}={\mathit{o}}_{\mathit{t}}\ast \mathbf{tanh}\left({\mathit{C}}_{\mathit{t}}\right)$$

where $\mathit{\sigma }$ and $\tanh$ are the Sigmoid and Tanh activation functions, respectively. The $\mathit{W}$ item is the weight matrix, and its value range is 0–1. The subscripts $\mathit{f}$, $\mathit{i}$, $\mathit{C}$, and $\mathit{o}$ represent the forget layer, input layer, hidden layer, and output layer, respectively. The $\mathit{b}$ item is the bias matrix of each layer. ${\mathit{f}}_{\mathit{t}}$, ${\mathit{i}}_{\mathit{t}}$, and ${\mathit{o}}_{\mathit{t}}$ represent the status of the forget layer, input layer, and output layer at time $\mathit{t}$, respectively. ${\mathit{C}}_{\mathit{t}}$ and ${\tilde{\mathit{C}}}_{\mathit{t}}$ represent the unit state vector. ${\mathit{h}}_{\mathit{t}}$ is the final unit state vector at time $\mathit{t}$.

In this study, we utilized a bidirectional long short-term memory network consisting of two layers, with a predetermined number of 64 hidden units. Our tests showed that this model structure performs well in terms of both training speed and accuracy. The output is generated via a fully connected layer.

2.4. Temporal Convolutional Network

It is well known that recurrent neural networks (RNNs) have excellent performance in processing time series problems, but they can only handle one time step at a time and cannot be processed in large-scale parallelism like convolutional neural networks. A Temporal Convolutional Network (TCN) using a convolutional architecture with extended causal convolutions and residual connections was introduced by Bai et al. [23]. Due to its excellent performance on time series problems, the TCN is widely used in fields such as signal processing [24] and regression prediction [25].

Causal convolution allows the network to only see future data and is a strictly time-constrained model. The size of the convolution kernel limits the time available for modelling by simple causal convolution. This requires a very deep network when processing tasks with a large workload, which will occupy a very large amount of computing resources. The extended causal convolution of the TCN effectively expands the receptive field of the convolutional neural network and solves this problem. The TCN incorporates a residual connection component that allows gradient transmission across layers to effectively prevent gradient disappearance.

In this study, we constructed a 5-layer TCN with 48 convolution channels and a convolution kernel size of 3. Finally, the output utilizes a fully connected layer. The above configuration was experimentally verified to achieve a relatively optimistic accuracy rate.

2.5. Parallel Network of CNN-Attention and BiLSTM

Convolution and recurrent neural networks are gaining ground in surface EMG signal processing and have shown good results in the past. However, when it comes to the regression problem based on surface electromyography signals, the above two networks have problems such as large prediction fluctuations and difficulty in convergence. Solving the above problems according to previous ideas requires expanding the scale of the network, but this will bring challenges to computing resources. To this end, we introduce a multi-head attention mechanism and combine it with a convolutional neural network, which is CNN-Attention. Considering the excellent performance of the BiLSTM network in solving long sequences, we connected it in parallel with the CNN-Attention network and finally obtained the model proposed in this article, called PNCB.

2.5.1. Multi-Scale Convolution

In the CNN module of the PNCB model, we adopt a multi-scale convolution module. The conventional convolution process has a small responsive area with a fixed filter size, which leads to the inadequate extraction of information when dealing with long sequence data like surface electromyographic signals. Therefore, in this study, we adopt a convolution operation with multiple size filters that can extract large-scale and small-scale information simultaneously. As shown in Figure 3, we set up convolution modules with three different convolution kernel sizes (the convolution kernel sizes used in this article are 3, 4, and 5, respectively). The preprocessed surface electromyography signal data pass through three convolution modules in a parallel manner. Each convolution module contains three parts, namely the convolution layer, maximum pooling layer, and ELU activation function. Finally, to obtain the output of the multi-scale convolution module, the results of the three convolution modules are combined based on their corresponding dimensions and then passed through a fully connected layer. Suppose the input signal is $\mathit{X}$; then, the output ${\mathit{X}}^{\mathbf{\prime }}$ of the multi-scale convolution module can be expressed by the following equation:

$${\mathit{X}}^{\mathbf{\prime }}=\mathit{\sigma }\left({\mathit{f}}^{{\mathit{n}}_{\mathbf{1}}\times \mathit{D};\mathit{C}}\left(\mathit{X}\right)\right)+\mathit{\sigma }\left({\mathit{f}}^{{\mathit{n}}_{\mathbf{2}}\times \mathit{D};\mathit{C}}\left(\mathit{X}\right)\right)+\mathit{\sigma }\left({\mathit{f}}^{{\mathit{n}}_{\mathbf{3}}\times \mathit{D};\mathit{C}}\left(\mathit{X}\right)\right)$$

where ${\mathit{f}}^{{\mathit{n}}_{\mathbf{1}}\times \mathit{D};\mathit{C}}$ denotes the convolution operation, $\mathit{C}$ is the number of convolution kernels, $\mathit{D}$ is the number of channels of the input signal, ${\mathit{n}}_{\mathbf{1}}$ is the convolution kernel size, and $\mathit{\sigma }$ is the ELU activation function.

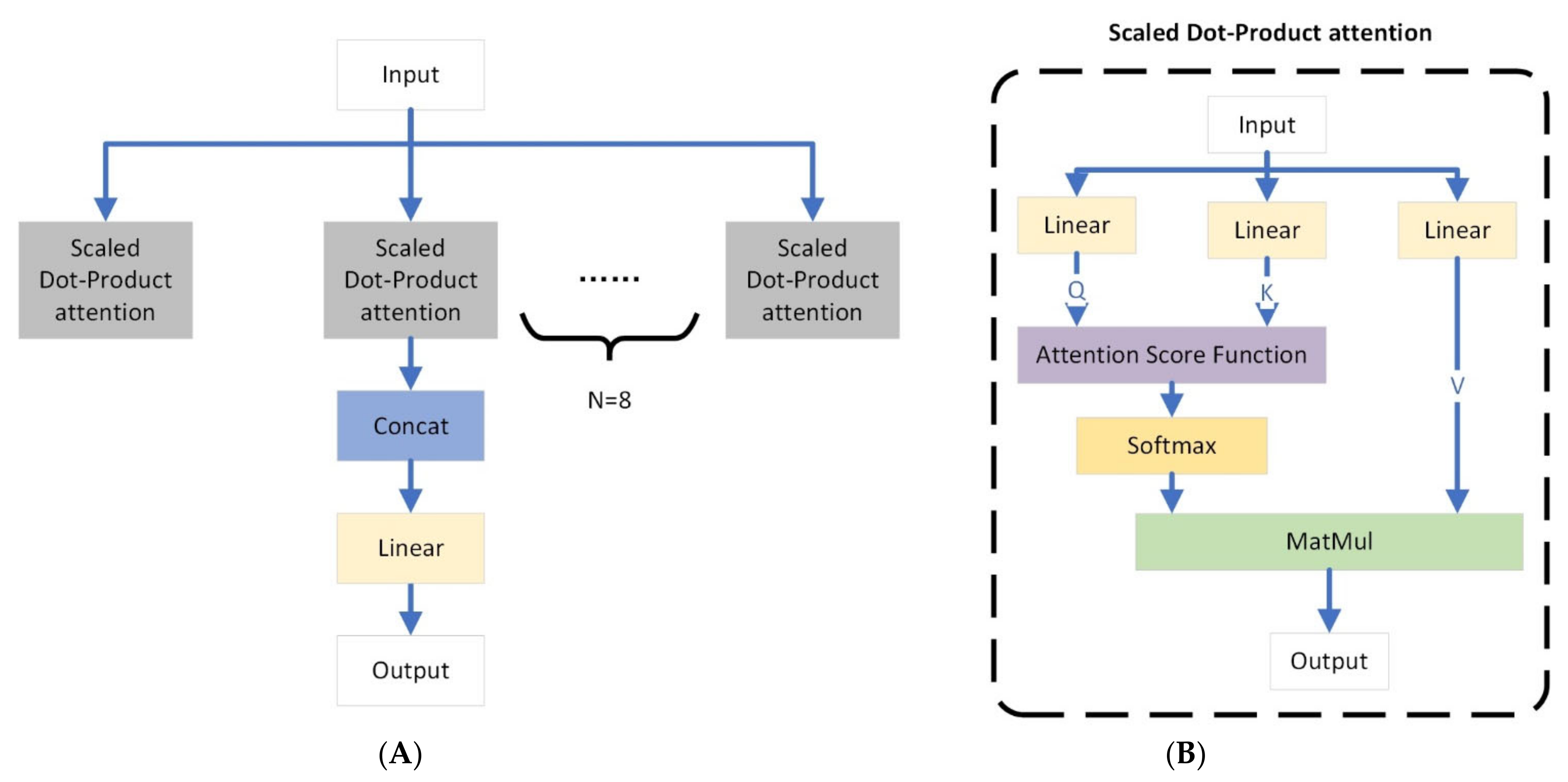
2.5.2. Multi-Head Attention Mechanism

The attention mechanism has found a wide range of applications in disciplines such as image processing [26] and machine translation [27] due to its superior parallelism and efficiency. The model of attention establishes an interactive relationship between a variety of input vectors in a linear space of projections. Multi-head attention aims to create distinct projections in multiple diverse projection spaces, perform different projections on the input matrix, and after obtaining many output matrices, splice them together. As shown in Figure 4B, in the context of single-head attention within multi-head attention, the network first calculates the attention between the key vector and the query vector and then calculates the weight value vector. The mathematical expressions for query vector $\mathit{Q}$, key vector $\mathit{K}$, weight value vector $\mathit{V}$, and attention $\mathit{A}\mathit{t}\mathit{t}\mathit{e}\mathit{n}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(\mathit{Q},\mathit{K},\mathit{V}\right)$ are as follows:

$$\mathit{Q}={\mathit{W}}_{\mathit{q}}\mathit{x}+{\mathit{b}}_{\mathit{q}}$$

$$\mathit{K}={\mathit{W}}_{\mathit{k}}\mathit{x}+{\mathit{b}}_{\mathit{k}}$$

$$\mathit{V}={\mathit{W}}_{\mathit{v}}\mathit{x}+{\mathit{b}}_{\mathit{v}}$$

$$\mathit{A}\mathit{t}\mathit{t}\mathit{e}\mathit{n}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left(\mathit{Q},\mathit{K},\mathit{V}\right)=\mathit{s}\mathit{o}\mathit{f}\mathit{t}\mathit{m}\mathit{a}\mathit{x}\left({\displaystyle \frac{\mathit{Q}\cdot {\mathit{K}}^{\mathit{T}}}{\sqrt{{\mathit{d}}_{\mathit{k}}}}}\right)·\mathit{V}$$

where ${\mathit{W}}_{\mathit{q}}$, ${\mathit{W}}_{\mathit{k}}$, and ${\mathit{W}}_{\mathit{v}}$ are in ${\mathit{R}}^{\mathit{C}\times \mathit{C}}$, and ${\mathit{b}}_{\mathit{q}}$, ${\mathit{b}}_{\mathit{k}}$, and ${\mathit{b}}_{\mathit{v}}$ are in ${\mathit{R}}^{\mathit{C}}$. $\mathit{C}$ here refers to the channel dimension of the single-head attention mechanism layer. ${\mathit{d}}_{\mathit{k}}$ is the dimension of $\mathit{Q}$ and $\mathit{K}$.

As shown in Figure 4A, we set up a multi-head attention mechanism with 8 heads (n = 8) in parallel. This module divides the input sequence into n groups according to dimensions. Then, it splices the outputs of multiple single-head attention layers according to the corresponding dimensions. Finally, a fully connected layer provides the output of the multi-head attention module. The mathematical expressions of this process are as follows:

$$\mathit{h}\mathit{e}\mathit{a}{\mathit{d}}_{\mathit{i}}=\mathit{A}\mathit{t}\mathit{t}\mathit{e}\mathit{n}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\left({\mathit{Q}}_{\mathit{i}},{\mathit{K}}_{\mathit{i}},{\mathit{V}}_{\mathit{i}}\right)$$

$$\mathit{M}\mathit{u}\mathit{l}\mathit{t}\mathit{i}\mathit{H}\mathit{e}\mathit{a}\mathit{d}=\mathit{C}\mathit{o}\mathit{n}\mathit{c}\mathit{a}\mathit{t}\left(\mathit{h}\mathit{e}\mathit{a}{\mathit{d}}_{\mathbf{1}},\dots ,\mathit{h}\mathit{e}\mathit{a}{\mathit{d}}_{\mathit{n}}\right)\mathit{W}+\mathit{b}$$

where $\mathit{W}$ is in ${\mathit{R}}^{\mathit{D}\times \mathit{D}}$ and $\mathit{b}$ is in ${\mathit{R}}^{\mathit{D}}$.

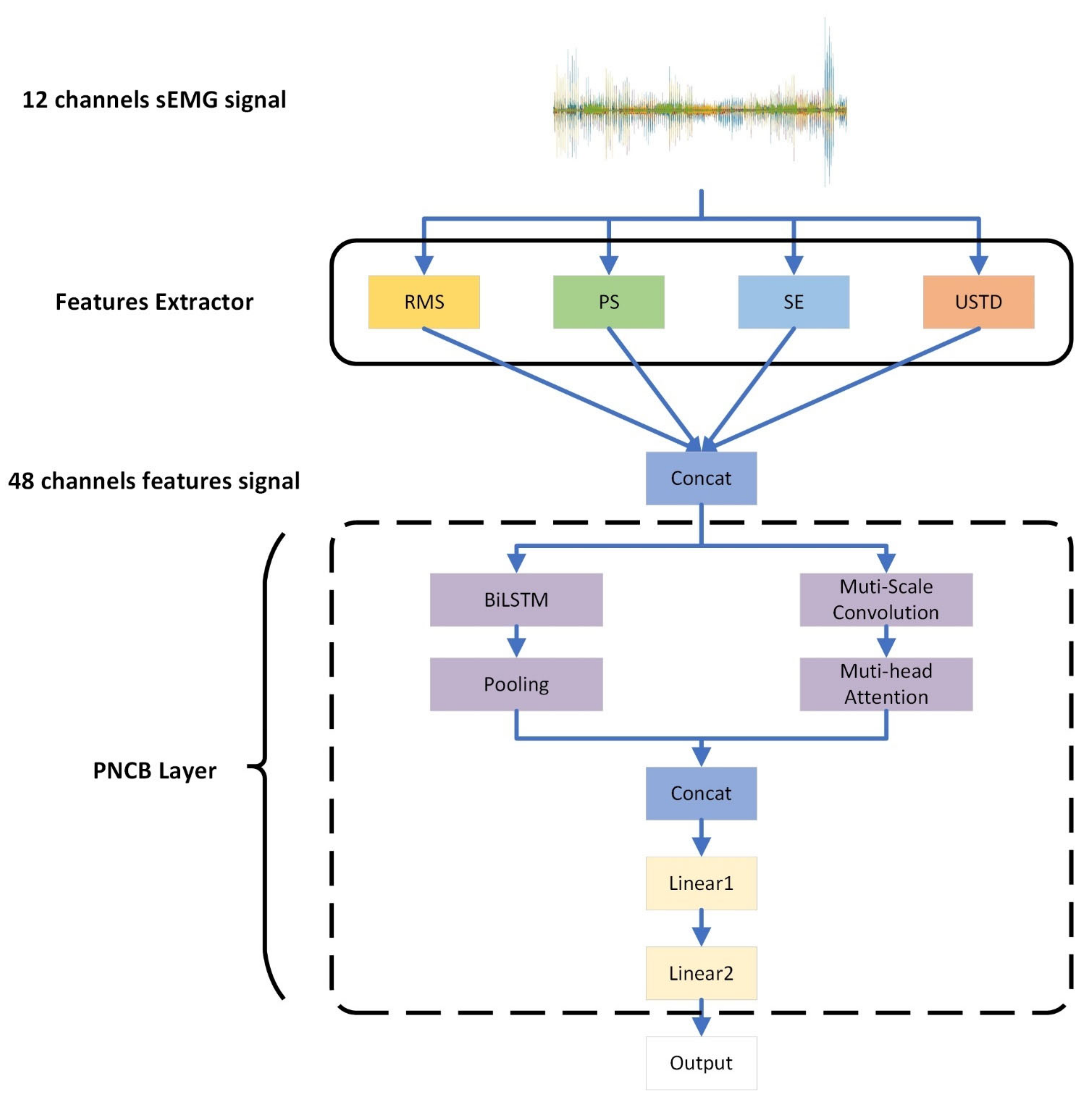
2.5.3. PNCB Model Structure

As shown in Figure 5, the original surface EMG signals are sent to the feature extractor, respectively, to extract the four features mentioned in Section 2.2. The data after feature extraction are spliced according to the channel dimension to obtain 48-channel feature signal data. The processed data are then input into the PNCB model, and predictions of 10 joint angles are finally obtained. The PNCB model has two parallel branches. One branch is a CNN-Attention network composed of multi-scale convolution modules and multi-head attention mechanism modules in series. The parameters and specific implementation of this branch are described in Section 2.5.1. And the other branch is composed of BiLSTM and a maximum pooling layer. The parameters of this branch of the BiLSTM remain the same as those mentioned in Section 2.3. The outputs of the two branches are spliced according to the channel dimension, and finally the features are mapped to 10 target angles through two fully connected layers.

It is worth noting that in addition to testing the TCN and BiLSTM network as control experiments, we also tested three sub-module networks in the PNCB model. They are multi-scale convolution modules, namely the CNN, CNN-Attention network, and CNN-BiLSTM network (the network that removes the multi-head attention module in the PNCB model). The purpose of this is not only to enrich the control experiment, but also to test whether each module of the model promotes the entire system.

3. Result

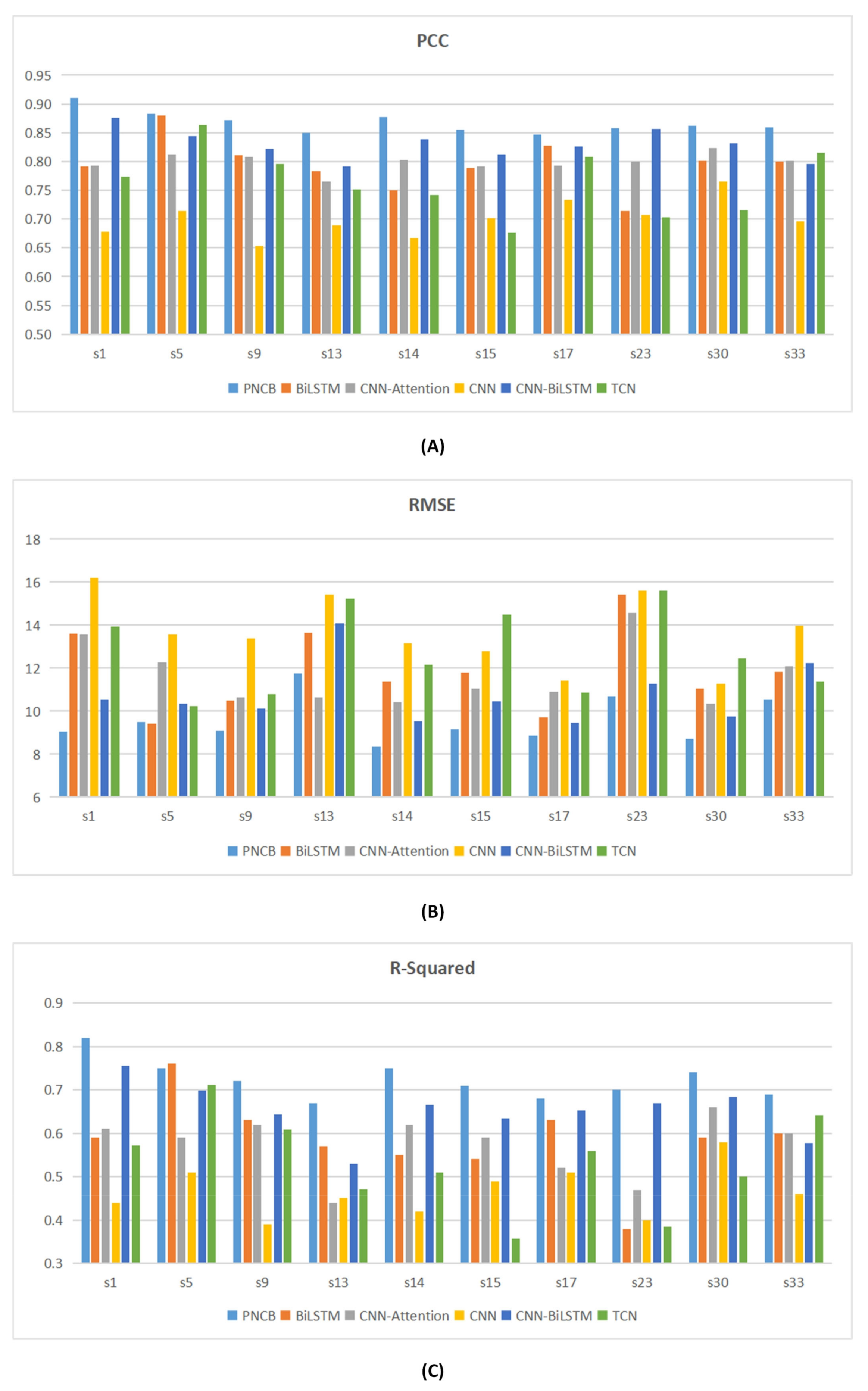
3.1. Evaluation Metrics

In this study, we use the Pearson Correlation Coefficient (PCC) to assess the association between the expected and actual joint angles, and thus the accuracy and effectiveness of the algorithm. The closer the PCC is to 1, the more accurate the algorithm is. Its mathematical expression is as follows:

$$\mathit{P}\mathit{C}\mathit{C}={\displaystyle \frac{{{\displaystyle \sum }}_{\mathit{i}=\mathbf{1}}^{\mathit{N}}\left({\mathit{\theta }}_{\mathit{e}\mathit{s}\mathit{t}}-\overline{{\mathit{\theta }}_{\mathit{e}\mathit{s}\mathit{t}}}\right)\left({\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}-\overline{{\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathbf{l}}}\right)}{\sqrt{{{\displaystyle \sum }}_{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\left({\mathit{\theta }}_{\mathit{e}\mathit{s}\mathit{t}}-\overline{{\mathit{\theta }}_{\mathit{e}\mathit{s}\mathit{t}}}\right)}^{\mathbf{2}}}\sqrt{{{\displaystyle \sum }}_{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\left({\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}-\overline{{\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}}\right)}^{\mathbf{2}}}}}$$

where ${\mathit{\theta }}_{\mathit{e}\mathit{s}\mathit{t}}$, $\overline{{\mathit{\theta }}_{\mathit{e}\mathit{s}\mathit{t}}}$, ${\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}$, and $\overline{{\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}}$ represent joint angle estimates, average joint angle estimates, actual joint angle values, and actual joint angle averages, respectively.

The deviation between the prediction and the actual value is the root-mean-square error (RMSE). This article uses the RMSE to indicate the amount of error in degrees (°) between the predicted and actual joint angle.

R2 objectively assesses the overall accuracy of the algorithm as a comprehensive evaluation index. The coefficient of determination represents the percentage of variance in the predicted value that can be explained by the prediction. The indicator range lies between 0 and 1. The better the estimation performance of the algorithm, the higher the value of the indicator. The calculation formula is

$${\mathit{R}}^{\mathbf{2}}=\mathbf{1}-{\displaystyle \frac{{{\displaystyle \sum }}_{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\left({\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}-{\mathit{\theta }}_{\mathit{e}\mathit{s}\mathit{t}}\right)}^{\mathbf{2}}}{{{\displaystyle \sum }}_{\mathit{i}=\mathbf{1}}^{\mathit{N}}{\left({\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}-\overline{{\mathit{\theta }}_{\mathit{r}\mathit{e}\mathit{a}\mathit{l}}}\right)}^{\mathbf{2}}}}$$

3.2. Experimental Parameters and Statistical Analysis

We maintain consistency in the training parameters, including the type of loss function, the type of optimizer, and the learning rate, when training a neural network in this study. The loss function used is the mean squared error, with Adam optimization as the optimizer, and the learning rate is uniformly set to 0.0002. In regression prediction problems, mean squared error is a commonly used loss function. As an effective deep learning optimizer, Adam optimization has often been used in the fields of signal processing and image processing in recent years. It is based on the Stochastic Gradient Descent Technique [28]. We keep the network structure parameters in the control experimental algorithms CNN, CNN-Attention, CNN-BiLSTM, and BiLSTM consistent with those of the corresponding modules of PNCB. All neural networks are built on the Pytorch framework.

The t-test uses the theory of the t-distribution to infer the probability of a difference occurring, and thus to compare whether the difference between two sets of data is significant or not. It is applicable to normal distributions with a small sample size and unknown overall standard deviation. In this article, we used it to examine the differences between the comparison algorithm used in the experiment and the model proposed in this article. The dependent variables used in this study were PCC, RMSE, and R2 of the evaluation indicators. In this research, the statistical significance threshold was established at p value < 0.05.

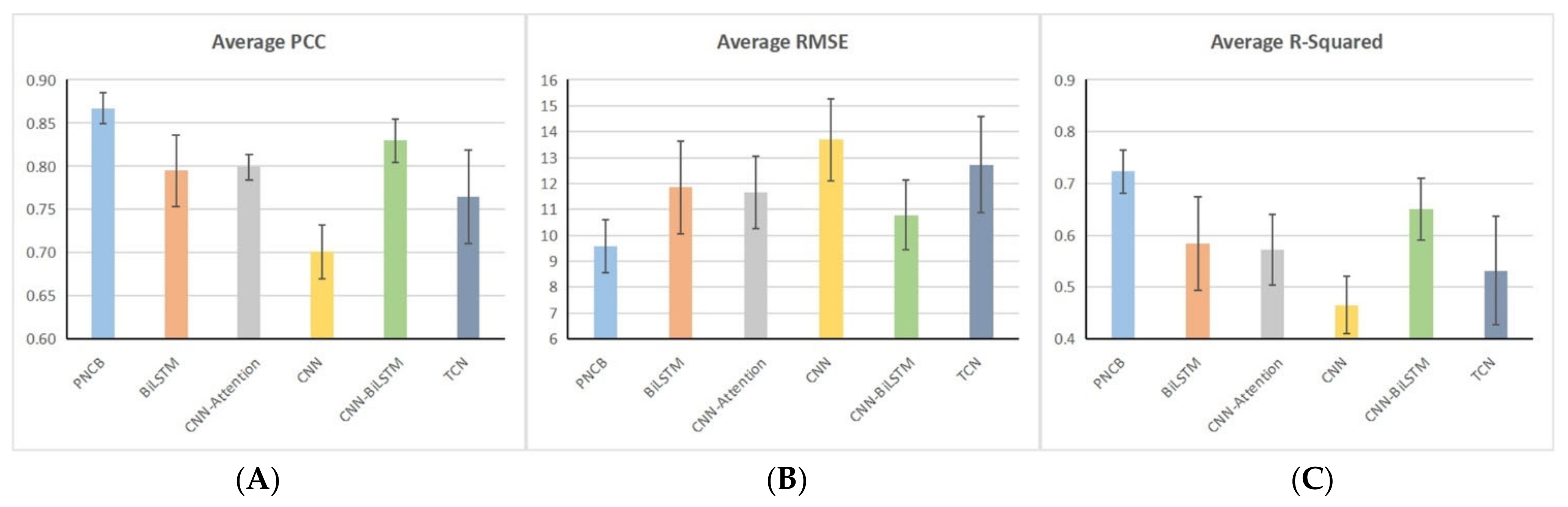
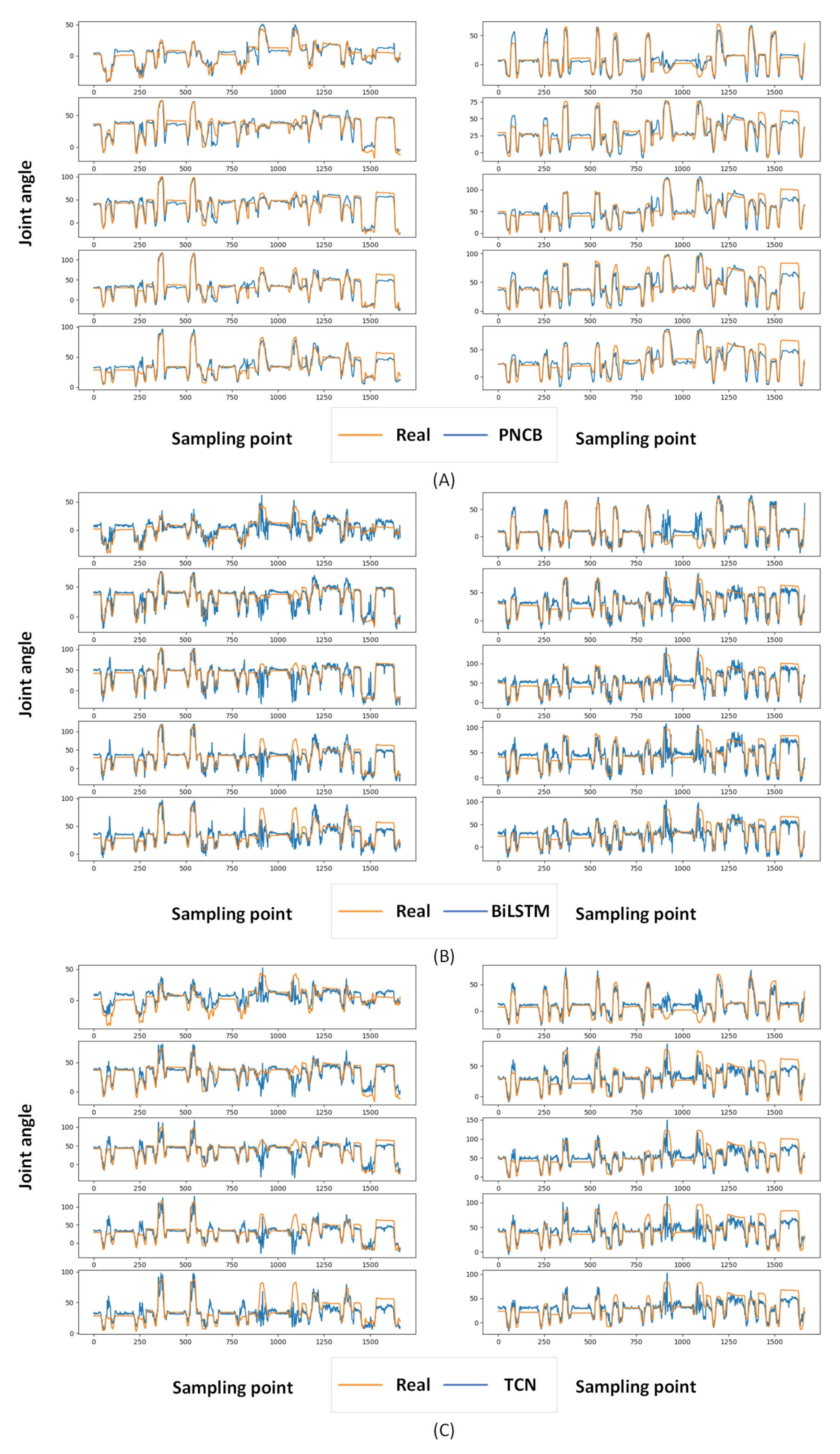
3.3. Experimental Results

The general performance of the PNCB model and the other five comparison algorithms for the continuous motion estimation of finger joints is shown in Figure 6. Figure 6A–C show the average PCC, RMSE, and R2 of the six deep learning algorithms on 10 subjects, respectively. The experimental results show that the mean value of the PCC of the PNCB model is 0.87 ± 0.02, and the average PCC values of the other five comparison algorithms are BiLSTM (0.79 ± 0.04, p < 0.05), CNN-Attention (0.80 ± 0.01, p < 0.05), CNN (0.70 ± 0.03, p < 0.05), CNN-BiLSTM (0.83 ± 0.02, p < 0.05), and TCN (0.76 ± 0.05, p < 0.05). The average RMSE of the PNCB model is 9.57 ± 1.01, and the average RMSEs of the other five comparison algorithms are BiLSTM (11.85 ± 1.80, p < 0.05), CNN-Attention (11.65 ± 1.38, p < 0.05), CNN (13.69 ± 1.59, p < 0.05), CNN-BiLSTM (10.78 ± 1.36, p < 0.05), and TCN (12.72 ± 1.87, p < 0.05). The average R2 value of the PNCB model is 0.72 ± 0.04, and the average R2 values of the other five comparison algorithms are BiLSTM (0.58 ± 0.09, p < 0.05), CNN-Attention (0.57 ± 0.07, p < 0.05), CNN (0.47± 0.06, p < 0.05), CNN-BiLSTM (0.65 ± 0.06, p < 0.05), and TCN (0.53 ± 0.10, p < 0.05). Our proposed PNCB model outperforms the other five comparative algorithms on three evaluation indicators, as shown by the experimental results. The p-values are all below 0.05. This means that there is a statistically significant difference in performance between the six methods.

Figure 7A–C show the accuracy performance of the PNCB model and other five comparison algorithms among 10 subjects. The PCC value of the PNCB model remains consistently high across all subjects, exceeding 0.85 and indicating a very strong level of correlation. Additionally, the PNCB model maintains a lower RMSE and higher R2 on each of the 10 subjects. The results above show that the PNCM is superior to the other five algorithms compared and is more widely applicable.

Figure 8A–C show joint angle curves predicted by PNCB, BiLSTM and the TCN alongside the actual joint angle curves. It is not difficult to see from the figure that the predicted joint angle curve of PNCB has the best consistency with the actual joint angle curve, which is better than those of BiLSTM and the TCN. The joint angle curve predicted by BiLSTM agrees well with the actual joint angle curve. However, the prediction curves of some action segments fluctuate greatly, and the prediction curves have more prominent abnormalities. The TCN-predicted joint angle curves fluctuated greatly and did not match the actual joint angle curves well enough.

In order to verify the robustness of PNCB, we selected the same six actions from a wide range of 10 more subjects in Ninapro DB7 and performed a continuous estimation test. The experimental results show that the average PCC value is 0.86 ± 0.03, the average RMSE is 9.38 ± 1.05, and the average R2 value is 0.72 ± 0.06. The experimental results indicate that PNCB is robust enough to be applied to other datasets. In addition, we have also conducted a study on the efficiency of the PNCB model. The size of the model is 0.991 MB, and the inference time of the model on a GeForce RTX3060 graphics card is 10.92 ms. Although the PNCB model has a large number of parameters, its inference time is very short and the model is efficient because it can be computed in parallel.

4. Discussion

This paper introduces the PNCB model, which skillfully integrates multi-scale convolutional neural networks, multi-head attention mechanisms, and bidirectional long short-term memory networks to improve the accuracy and universality of continuous estimation of hand joint angles. And 10 subjects were extensively selected in the Ninapro DB2 dataset to conduct a continuous estimation of hand motion joint angles for six daily grasping movements. Five other algorithms were also tested as control experiments.

To ensure precise and quantitative evaluation of the PNCB model and other control algorithms, we measured three evaluation indicators: PCC, RMSE, and R2. The findings of this study demonstrate that the PNCB model, as presented in this paper, outperforms the control algorithm in terms of both overall and individual subject performance. And it has good stability and universality. It is worth noting that the comparison algorithms CNN, CNN-Attention, and CNN-BiLSTM all come from certain modules of the PNCB model. The purpose of this is to enrich the control experiments and to test whether the stacking method of each module of the PNCB model promotes the overall performance of the model. It is not difficult to see from the experimental results (Figure 6) that the CNN with only one multi-scale convolution module performed worst among the control algorithms. The comparison algorithms CNN-Attention and CNN-BiLSTM stacked by the two modules have better performance than CNN, and their performance has been greatly improved. This shows that each module of PNCB promotes model performance.

To more intuitively see the accuracy of the PNCB model, BiLSTM, and TCN in the continuous estimation of hand motion joints, we drew the actual joint angle curves and the predicted joint angle curves of the above three networks, as shown in Figure 8. The superiority of the PNCB model is further verified. The predicted joint angle curve of the PNCB model is more stable and smoother than those of BiLSTM and the TCN, and it has a high degree of fit with the actual curve. There are several reasons for the excellent performance of the PNCB model. The first is the use of a multi-head attention mechanism, which can obtain global and local relationships in one step in a parallel manner. However, the BiLSTM network acquires global information in a recursive manner and is susceptible to noise, leading to reduced accuracy. In the same way, the TCN obtains global information through layering and the receptive field is not large enough, which has the same problem as BiLSTM. In addition, multi-scale convolution can obtain the characteristics of different scales of surface electromyographic signals, further improving the performance of the PNCB model. Finally, we added BiLSTM to the model in parallel and used its unique loop structure to once again improve the performance of the model. The advantage of using a parallel form of adding BiLSTM is that this can fully utilize the strengths of the different networks, avoid the weaknesses, and also improve the processing efficiency of the model.

The following shortcomings may exist in this study. There are many factors that affect EMG, including electrode movement, noise, and arm position [29]. These factors actually exist and can reduce the accuracy of the continuous estimation of the model. In future research, we will consider modeling these factors by adding noise to the data to test and improve the model to make it more robust. In addition, it is our goal to use the model in real-world scenarios such as smart prosthetics and controlling robotic hands using EMG. In the future, we are considering testing the model on edge devices so that we can apply the model to real-world scenarios.

5. Conclusions

This paper proposes a parallel model that cleverly integrates convolutional neural networks, multi-head attention mechanisms, and bidirectional long short-term memory networks, taking full advantage of the benefits of each neural network. And the continuous estimation of hand motion joints was tested on the Ninapro dataset. Its performance is significantly better than those of the five comparison algorithms mentioned in this article and has good stability and universality. Furthermore, upon comparing the experimental outcomes, it is apparent that the stacking technique for each module in the PNCB model proposed encourages the overall performance of the model and can suggest insights on constructing deep learning networks. It is worth noting that we also innovatively extracted multiple features of the surface electromyographic signal and fused them, which improved the accuracy of continuous estimation of hand motion. We also test it on a wide selection of subjects in different datasets, and the experimental results show that PNCB possesses strong robustness. In brief, it is anticipated that PNCB will have a significant role in the continuous motion assessment area that depends on the surface electromyography method in the future.