Reduction of Q-Barton Uncertainty: Proposal of a New Methodology Based on a Factual Geological–Geotechnical Database to Apply in Tunnels

Abstract

The main goal of this study is to analyse and quantify errors, doubts, and uncertainties associated with the use of Q-Barton system parameters. This study also analyses how related factors influence the observer in tunnel openings. Data from six penstock tunnels of an underground hydraulic circuit at a hydroelectric power plant were used to study the application of the Q-Barton index. Records of values adopted at tunnel opening faces were compared with values calculated and quantified objectively. The values adopted by a geologist at the tunnel opening (Q-Barton-geologist) were compared with statistical values of the Q-Barton (Q-Barton-GGDB) generated from a factual database. This comparison enables the evaluation of the accuracy and influence of the Q-Barton system in tunnel openings, as well as the consequences on labour days and geotechnical support costs associated with a structure represented by the sample used. Using Q-Barton-GGDB, savings of 17.5% on geotechnical supports and 12.9% on labour days will be achieved. Final results highlight the need to explore the issues discussed here further.

1. Introduction

In any tunnel, a careful geological–geotechnical survey is one of the keys to success. It is often the primary tool, if not the main tool, for avoiding additional costs, accidents and undesirable delays in the excavation work. However, it is impossible to define the behaviour and resistance of a rock mass as a structure with great precision, since it is not possible to observe the mass thoroughly, and there is a possibility of significant variability. In other words, the same rock mass can react differently depending on the stress imposed on it, which, in turn, depends on the type, dimensions, and particularities of the excavation work.

Over time, rock mass classification methods have been updated and improved in order to define and characterise rock masses ever more precisely. These methods make it possible to gather the information needed to initially design and pre-dimension underground structures, such as tunnels, caverns, shafts, or even the foundations of large structures. However, unlike soil characterisation, when it comes to classifying rock masses, particularly for underground works, no universally used methodology or classification system can be used for this type of underground construction. There are several different classification systems, each with its specifications and particularities, used according to the designer’s choice and preference.

One of the most widely used classification systems for rock masses is the Q-Barton system [1,2,3,4]; due to its simplicity and usability, it has been increasingly accepted in the geotechnical community for design purposes.

The utilisation of the Q-Barton system has been the object of several improvements and refinements throughout the years. The joint characteristics (Jr, Ja, and Jn) with the RQD can induce mischaracterisation of the Q-Barton index, but as with other classifications, the assessment of the rock mass quality depends on the parameters that characterise it and how these are defined in the excavation tunnel [5]. How the parameters’ field measurements in tunnelling are made [6], and the use of empirical methods to calculate the mechanical parameters of the rock mass [7], could be eventual solutions to decrease the uncertainties related to the acquisition of this type of data.

The RQD is one of the parameters of the Q-Barton system, with several studies made regarding its practical measurement [8,9,10,11,12].

The variation in measuring rock joints, the number of discontinuity sets, and the discontinuity spacing in rocks of tunnels are relevant to the evaluation of the degree of rock jointing [13,14,15,16,17]. In this sense, the automated method for extracting and analysing rock discontinuities from point clouds, based on a digital surface model of the rock mass [18], is an enhancement.

Estimating the joint roughness coefficient of discontinuities in rocks using different and expeditious methods [19] or by visual comparison [20] are approaches that could clarify this parameter evaluation.

Some authors apply statistical methods (e.g., Bayesian, Random Set Theory, and Fuzzy Logic) for updating geomechanical parameters and uncertainty quantification and determining the parameter range in rock masses [21,22,23,24].

Taxonomy to characterise the uncertainty and variability of taxonomic terms, as well as the quantity and quality of information, and its effectiveness through application to common problems found in rock engineering is also developed [25].

It is important to note that employment of the Monte Carlo Simulation (MCS) technique probabilistically assesses the rock mass properties and responses, and, utilising appropriate empirical correlations for the Q-value distribution, it is also used as input for a finite element model to probabilistically evaluate excavation-induced tunnel displacement [26]. These authors also conducted a probabilistic sensitivity analysis to rank the relative importance of the input parameters in the Q-Barton system based on the regression coefficients, Spearman’s rank-order correlation coefficients, and their contributions to variance and effects on output mean.

The GGDB-based method is applied during excavation works, while probabilistic or statistical methods (e.g., Bayesian, Fuzzy Logic, and Monte Carlo) are implemented after the construction cycle. The GGDB method is easy to implement and requires only basic knowledge of geology and geotechnics, used objectively and consistently.

It is known that conservative deterministic analysis methods, which were used in the design and construction phases, can inflate the costs of underground construction [27].

In this context, this proposal aims to improve the accuracy of some Q-Barton system classification parameters, as well as to evaluate the consequences associated with inaccurate rock mass classification. It is known that the uncertainty in system rock mass classifications results from uncertainty in parameter acquisition [28]. Using real data obtained from the excavation of a hydraulic circuit under construction, an attempt is made to translate the impact of a less precise definition in the base parameters in two ways: (i) in the costs to apply the geotechnical supports; (ii) in the labour days required to carry out these supports.

1.1. Use of Q-Barton in Excavation Works

In the site’s daily work, the geotechnical support solutions were implemented on the excavation tunnel faces as a function of the Q-Barton, based on parameters estimated with varying degrees of empiricism (Q-Barton-geologist). The ultimate aim of the present study is to optimise the determination of the Q-Barton index, thereby maximising the use of methods for objective quantification of basic parameters (Q-Barton-GGDB). The gap between the Q-Barton determined in tunnel face openings (Q-Barton-geologist) and the Q-Barton quantified with this approach (Q-Barton-GGDB) is considered to be a geotechnical risk factor that should be eliminated in excavation works.

The sample used in the present study is not statistically representative of all dam projects, as the sampling criteria were systematic but not random in a strictly statistical sense, focusing on tunnel faces that were accessible. However, it can be assumed that the sampling represents a hypothetical real underground work that is similar to the set of cases studied.

In the current approach, this methodology has proven to apply to high-grade metamorphic rocks. Its application to low-grade metamorphic rocks, igneous rocks, and sedimentary rocks will only be conditioned by the possibility of objective and consistent measurement of the characteristics of discontinuities and rock mass.

The Q-Barton system is based on the definition of a quality index (Q) derived from the analysis of six parameters relevant to defining and characterising the behaviour of rock mass. The Q-value defines qualitative rock mass classes that are correlated with stability and stand-up time requirements in underground excavations, as well as the type and quantity of geotechnical support recommended for a given rock mass.

The Q ranges between 10⁻³ and 10³ and is determined by Equation (1) [29]:

$$\mathrm{Q}={\displaystyle \frac{\mathrm{R}\mathrm{Q}\mathrm{D}}{\mathrm{J}\mathrm{n}}}\times {\displaystyle \frac{\mathrm{J}\mathrm{r}}{\mathrm{J}\mathrm{a}}}\times {\displaystyle \frac{\mathrm{J}\mathrm{w}}{\mathrm{S}\mathrm{R}\mathrm{F}}}$$

(1)

where RQD is the rock quality designation, Jn is the joint set number, Jr is the joint roughness number, Ja is the joint alteration number, Jw is the joint water reduction factor, and SRF is the Stress Reduction Factor.

Combined, the Q-Barton parameters express the three main factors, which describe the stability in underground openings: RQD/Jn, degree of jointing or block size; Jr/Ja, joint friction or inter-block shear strength; Jw/SRF, active stress.

1.2. Geological–Geotechnical Characterisation of the Hydropower Project

The present study was conducted in the penstock tunnels of a hydropower project. The geological and geotechnical characteristics are briefly described in the following subsections.

1.2.1. Geological Setting

The regional geology of the hydroelectric power plant site is composed, at the top, of a group of metasedimentary rocks approximately 100 m thick, deposited in a sub-horizontal contact, formed by an angular unconformity over a gneissic basement of Archean age (3000 Ma to 3500 Ma). These metasedimentary rocks are formed of metarenites, metasiltites, and conglomeratic breccias. In the area surrounding the dam, on both banks of the river, there are cliffs of metasedimentary rocks forming subvertical walls up to 100 m high. At the foot of the cliffs, there are gravel deposits and colluvial deposits of decimetre thickness. In the region of the dam, a few metres above the riverbed, at approximately elevation 750 m, gneisses of the Archean age basement outcrop. The contact between the gneiss and the overlying metasedimentary complex gradually rises towards the main centre area, where it outcrops at approximately 800 m elevation. Thus, the entire complex of tunnels and the main central cave is built entirely into the gneissic complex.

The gneissic complex is composed of amphibolitic gneiss that is folded and frequently has pinch-and-swell layers. This gneissic complex suffered intense deformation, which developed a metamorphic foliation (Sn) and gave the rock mass a gneissic banding (strike ≈ NW-SE and dip ≈ upright). After this metamorphic phase, there was an episode of retrometamorphism in greenschists facies, which is characterised by the formation of epidote and chlorite. In these rocks, associated with these later facies, occur veins of epidote that can reach metric thicknesses. Calcite appears later, due to the precipitation of calcium carbonate from an aqueous solution in existing fractures, with hard calcite infillings of centimetre thickness.

1.2.2. Rock Mass Characterisation

The gneissic rock mass was characterised according to the variation in the parameters of weathering (W), fracturing (F), and strength (R) [30,31], in six penstock tunnels. The geomechanical characteristics of these rock mass tunnels (W, F, and R) had been recorded at length segments corresponding to each blasting advance (Figure 1).

The majority of the six-penstock tunnels are characterised by good conditions of weathering (W1—fresh rock), strength (R4—strong rock), and fracturing (F2—little fractured rock). Only one penstock tunnel presents the worst conditions on average; i.e., it has higher weathering (W2 to W3—slightly to moderately weathered rock), the least strength (R2/R3—weak to medium-strong rock), and the highest fractures spacing (F3 to F4—moderately to very fractured rock).

1.2.3. Geomechanical Classification of Penstock Tunnels

The geomechanical base parameters are determined based on data acquired at the tunnel faces by the geologist during the production cycles of the penstock tunnel openings. This site task involved performing the in-cycle geomechanical classification of rock mass (Q-Barton-geologist). The Q-Barton parameters—RQD, Jn, Jr, Ja, Jw, and SRF, which characterised the penstock tunnel opening used in this study, are shown in Figure 2.

The parameter values most frequent achieved for RQD are in the classes 50% to 75% and 75% to 90%, respectively; rock mass quality is fair and good; Jn is 9–12 (≈98%), which corresponds to a rock mass with three joint sets and three joint sets plus random joints; Jr is 1.5 (≈90%), which means the rock wall is in contact with a surface roughness and waviness of rough irregular planar; Ja is 1–2 (≈70%), which means the rocks are all in contact only with coating with an unaltered joint wall to slightly altered joint wall non-softening mineral coatings; Jw is 1 (≈95%), which means dry excavation with mineral inflow; SRF is 1 (≈70%), which indicates competent rock with low or favourable stress condition, mainly massive rock with medium stresses and favourable stress conditions.

2. Materials and Methods

The non-rigorous nature of standards and specifications regarding the elements to be collected, particularly when evaluating a rock mass using geomechanical classification, means that subjective factors intrinsic to the observer are included in obtaining the necessary parameters. The main skill required for mobilising these tasks is professional experience, which enables each technician to make a personal selection of which parameters to consider and how to evaluate them. Related to this subjectivity, there is a certain geotechnical risk that has two aspects: a more conservative assessment that results in an over-dimensioned support (an approach from a security standpoint) and higher costs with longer execution times.

This study proposes a comparative analysis between the daily work completed by a geologist in tunnel openings (Q-Barton-geologist) and a more objective approach based on the quantification of Q-Barton parameters (Q-Barton-GGDB).

A more optimistic evaluation of Q-Barton parameters will translate into lower costs and faster execution, but may also increase uncertainty in terms of safety. In this study, an attempt was made to objectively measure the parameters of the rock quality designation (RQD), number of discontinuity sets (Jn), joint roughness number (Jr), and joint alteration number (Ja) of the Q-Barton. The purpose is to reduce the uncertainties and errors associated with these and to statistically study their consequences for the classification of the rock mass and its geotechnical treatment. The joint water reduction factor (Jw) and the Stress Reduction Factor (SRF) were not addressed in this study.

The six–penstock tunnels (PTs) used for this study are parallel to each other and have the references PT01, PT02, PT03, PT04, PT05, and PT06. They have a length between 1.872 km for PT06 and 2.004 km for PT01. The rock excavation method for each tunnel was carried out according to the New Austrian Tunnelling Method (NATM) as defined in the project. This involved starting with two attack tunnels, one located downstream and the other upstream, each divided into two tunnel opening phases.

The samples comprised 48 tunnel faces where the site geologist applied the Q-Barton system during daily work, and simultaneously, they were calculated using the proposed methodology (

Table 1. Sampling characteristics of 48 tunnel faces (Q-Barton values determined by the site geologist).

Sampling Characteristics
Number of tunnel face openings	48
Tunnels Geology	Amphibolitic gneiss
Full-section tunnel	40%	(100%)
Two-phase tunnel (heading and benching)	60%
Tunnel faces of Class I (Q-Barton > 20)	0%	(100%)
Tunnel faces of Class II (3 < Q-Barton < 20)	67%
Tunnel faces of Class III (0.3 < Q-Barton < 3)	31%
Tunnel faces of Class IV (0.01 < Q-Barton < 0.3)	2%
Tunnel faces of Class V (Q-Barton < 0.01)	0%

).

The selection of the excavation tunnel face openings did not correspond to any statistical sampling criteria, so they are not representative of the hydraulic circuits of penstock tunnels. Instead, this sample will be representative of the hydraulic tunnels whose overall characteristics, in terms of the two types of excavation sections and the three rock mass classes, are statistically represented by the sample studied.

As explained above, the data used in this study come from two sources (

Table 2. Number of values considered for each Q-Barton parameter.

Values	Quantity of Data (Determined by a Geologist and Used on Design—Q-Barton-Geologist)	Quantity of Data (Maximum Amount Calculated—Q-Barton-GGDB)
Values of RQD	1	3
Values of Jn	1	4
Values of Jr	1	3
Values of Ja	1	3
Values of Jw	1	1 1
Values of SRF	1	1 1
Values of Q-Barton	1	108

¹ The value was adopted that was determined at the tunnel face by the geologist.

):

-

Q-Barton parameter values obtained by the geologists on the tunnel face and used to define the geotechnical support for each advance during the normal NATM work cycle. A Q-Barton value was calculated based on the six values corresponding to the six basic parameters considered for each advance;

-

As part of the proposed methodological approach, various objective calculation processes were employed for the Q-Barton parameters. This method involved determining various values for the parameters, which, when combined in six different ways, generated a maximum of 108 Q-Barton values for each tunnel face, for each Q-Barton value of tunnel opening.

This proposal methodology (Q-Barton-GGDB) focused only on the RQD, Jn, Jr, and Ja parameters. The Jw and SRF values recorded by the geologist at the tunnel face (Q-Barton-geologist) were used. The values provided by the geologist at the construction site were used because, at this stage of the present study, no other objective identification parameters with immediate application at the construction site had been identified that could be correlated with Jw and SRF.

The Q-Barton-GGDB proposed herein is based on diverse criteria for calculating the Q-Barton parameters (

Table 3. Methodology proposed in the present study to Q-Barton calculation (Q-Barton-GGDB)—for details and references, see the next section.

Q-BARTON Parameters	Criterion 1	Criterion 2	Criterion 3	Criterion 4
RQD	Jv Method	λ Method	In situ Method	-
Jn	5 m (or 10 m) Statistic	5 m (or 10 m) Design	10 m Statistic	10 m Design
Jr	5 m	10 m	More representative	-
Ja	5 m	10 m	More representative	-
Jw	Jw-Geologist	-	-	-
SRF	SRF-Geologist	-	-	-

).

The GGDB framework includes input information such as rock mass and discontinuities data acquisition, field data description, Q-Barton parameters criteria, and statistical analysis. Based on this input, the framework produces output information that ultimately defines the Design Rock Mass Classes (Figure 3).

Discontinuities, i.e., waviness and smoothness, as defined in [30,33], are noted according [32] and are shown in Figure 4.

Discontinuities, i.e., wall contact types, wall opening types, and wall alteration types, as per INTT notations [32], are illustrated in simplified sketches (Figure 5, Figure 6 and Figure 7) to facilitate understanding.

The following section (Section 2.1. Q-Barton calculus) presents the methodology in detail for calculating the Q-Barton parameters used in this proposal (Table 3; Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7).

2.1. Q-Barton Calculus

To calculate the Q-Barton base parameters, it was necessary to select calculation methods, establish criteria for collecting geological–geotechnical data, and make decisions about the value of field data.

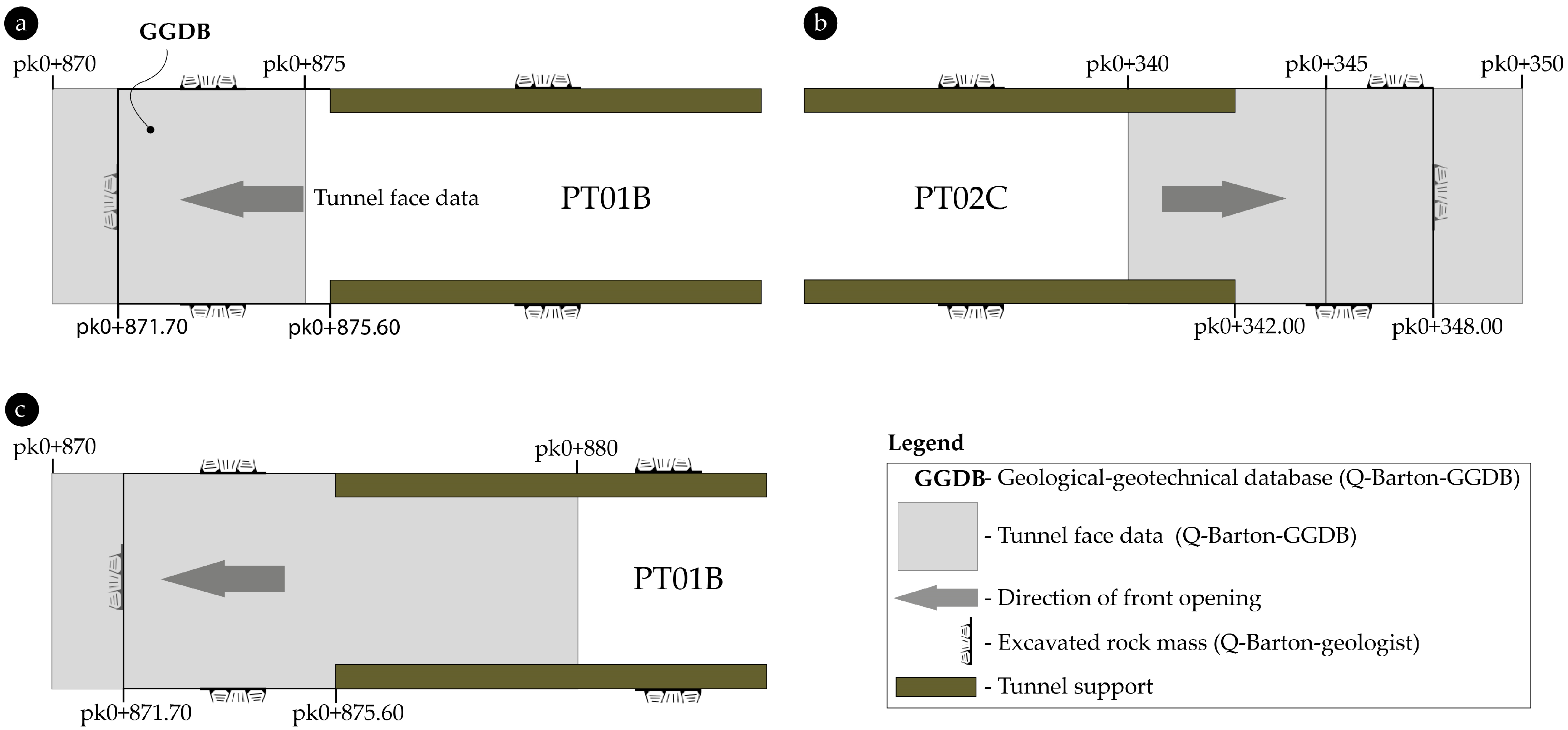
In the penstock tunnels studied, data relating to the geology–geotechnics of the tunnel face openings and the characteristics of the discontinuities were recorded in the geological–geotechnical database (GGDB), generally at opening advances of 5 m by 5 m. In none of the cases did this theoretical interval coincide with the real advances of the tunnel face openings used in this research. To match the data from a single opening with the data recorded in the GGDB, criteria had to be defined. So, in the sampling sections, the data used to determine the Q-Barton parameters were obtained following two criteria:

-

The 5 m tunnel criterion—the most representative characteristics of the 5 m mapped tunnel were used. This criterion was most used in the studied sections (Figure 8a); in the case of the opening section under study, it was covered in equal parts between two recorded rows on GGDB, and the study was carried out with the data from both rows, using the most penalising row in terms of the Q-Barton quality index (see the example of the Figure 8b);

-

The 10 m tunnel criterion—the most representative characteristics of the 10 m mapped tunnel were used. This criterion was most used in the studied sections (Figure 8c).

2.1.1. RQD Parameter Methodology

Originally, the RQD parameter was defined from NQ drill cores with the aim of being applied as a simple classification system for rock mass stability and has been used to measure the degree of strength in competent rocks [10,14,29,33]. It is defined as ‘the percentage of intact core pieces longer than 100 mm in the total length of the core’ [29].

The geologists on the tunnel face, depending on their individual experience and whether they had used an expeditious methodology (probably one of the three methods described below in this subsection) to eliminate personal subjectivity, determined this parameter for each tunnel face advance. In this way, an RQD value was calculated for each tunnel face, which was used to determine the Q-Barton index that defined the geotechnical support to be applied. This RQD calculation was used to obtain the Q-Barton-geologist.

Following the primary aim of this study, the procedure of autonomously calculating the RQD parameter was adopted using at least one of the three methods that were applied on tunnel faces (Q-Barton-GGDB):

(1)

The Jv method—Equation (2) [10],

$$\mathrm{R}\mathrm{Q}\mathrm{D}=115-3.3\mathrm{J}\mathrm{v}$$

(2)

(2)

The λ method—Equation (3) [14],

$$\mathrm{R}\mathrm{Q}\mathrm{R}=100{\mathrm{e}}^{-0.1\mathsf{\lambda }}(1+0.1\mathsf{\lambda })$$

(3)

where λ is the total joint frequency.

(3)

In the RQD in situ method [10], by applying a scan-line, the RQD values can be found as the percentage of core pieces greater than 10 cm.

For each studied tunnel face, one RQD value was obtained to calculate Q-Barton (Q-Barton-geologist), and three RQD values were obtained to calculate three Q-Barton values (Q-Barton-GGDB).

2.1.2. Jn Parameter Methodology

The Jn parameter, which is defined according to the number of discontinuity sets present on each tunnel face, is not necessarily an indicator of rock fractures. That is, a very fractured rock mass may be associated with a small number of discontinuity sets and vice versa. The term discontinuities was used herein to refer to any natural discontinuity surface with zero or very low tensile strength embedding joints, cracks, fissures, fractures, or fault planes [17].

A set of discontinuities is defined by a set of discontinuities with approximately the same orientation and characteristic spacing. In contrast, discontinuities that do not occur systematically or are spaced several meters apart are called random discontinuities [5].

The definition of a discontinuity set for the Jn calculus is not only based on the constant spacing between parallel or almost parallel discontinuities but also depends on the length and height of the underground excavation (tunnel section). Suppose the spacing between discontinuities is generally greater than the length and height of the excavation. In that case, the blocks formed are too large to be mapped, and in these cases, the discontinuities should be considered random. In underground excavations, the number of discontinuity sets may not be easily identified directly.

This parameter is highly dependent on the geologist’s experience and their own definition of discontinuity sets; however, there are no absolutely rigid criteria for classifying a group of fractures or joints as a set. This absence of specific standards for determining this parameter is associated with errors that can have consequences for both the classification of the rock mass and the support to be applied.

In the penstock, this parameter was determined at the tunnel face openings by the geologist through simply observing the rock mass; the sets were constituted by the direct visualisation of the fractures or joints, checking for parallelism and geometrical characteristics. With this procedure, the Jn-value was calculated for one Q-Barton value (Q-Barton-geologist).

The discontinuity data obtained in each tunnel advance were processed using stereographic projection software (Stereonet v. 11, outputs enhanced by the authors) to generate the main sets. The goal of the procedure was to verify if the design discontinuity sets are represented in the openings and have been considered in the stability project.

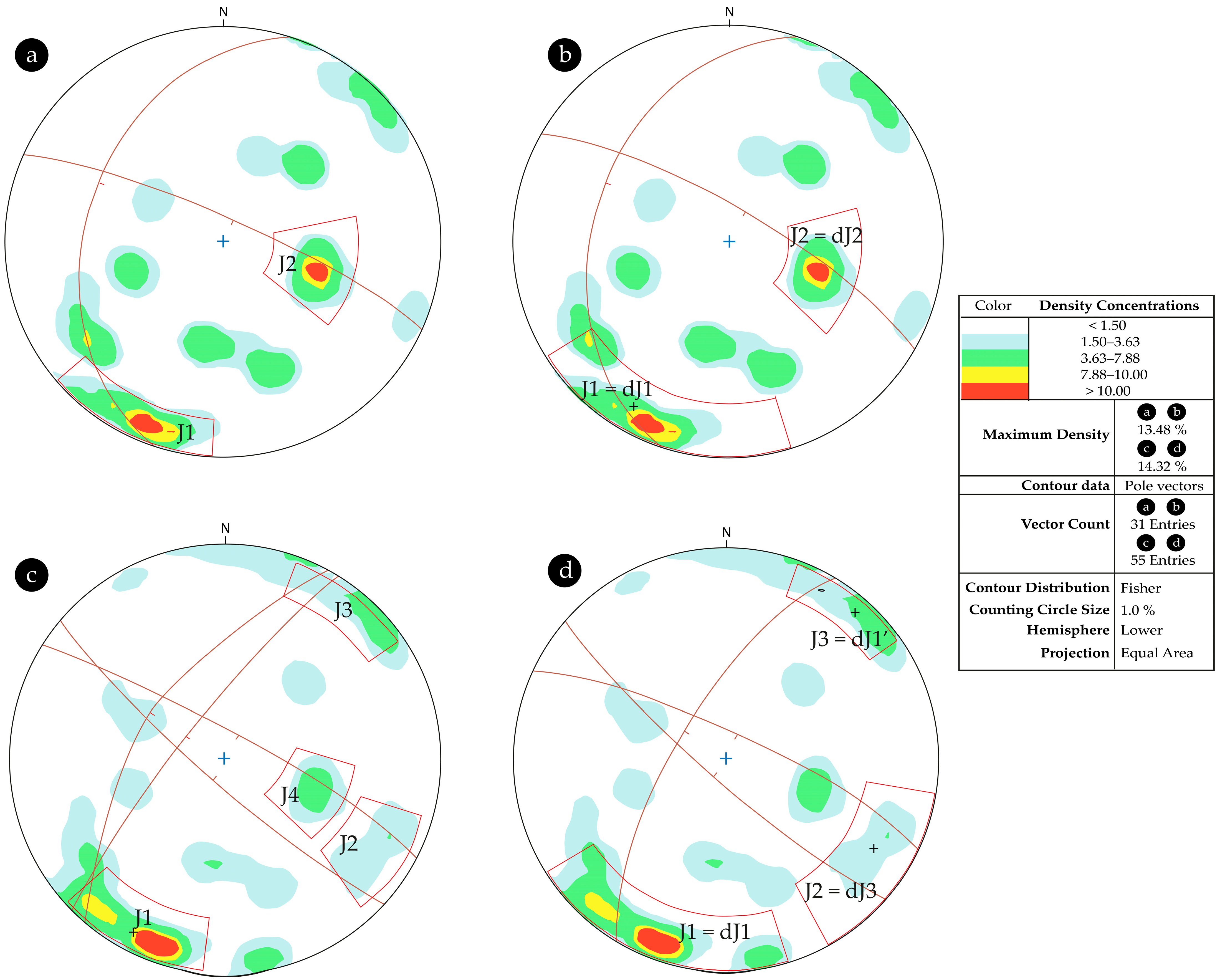
For the objectives of this study, data from the GGDB were used to obtain discontinuity data representative of the study cases. The discontinuities of tunnel faces were recorded in this database in rows with 5 m length sections, from the starting point of the attack of each penstock tunnel. In none of the 48 study cases did the ‘pk’ of the section advance match the 5 m length section GGDB rows. To solve this problem and obtain the Jn-value, four criteria were used to select the discontinuities to be used. Four Jn-values were achieved, which were representative for the calculation of section Q-Barton (Q-Barton-GGDB):

(Criterion 1)—The discontinuities surveyed in the widest 5 m of the section studied were used, and when the section is also covered by two 5 m mapped sections, this parameter is assessed according to the two sections (Figure 9a); the sets were defined independently of the design families;

(Criterion 2)—‘Criterion 1’ is applied, but taking into account the sets defined in the design (Figure 9a);

(Criterion 3)—The discontinuities mapped in the adjacent 10 m section that included the section studied were used (Figure 9c); the sets were defined independently of the design sets;

(Criterion 4)—‘Criterion 3’ is applied, but taking into account the sets defined in the design (Figure 9d).

The establishment of a criterion to define a set could be discussible. In this approach, a criterion was adopted based on the number of pole discontinuities belonging to a statistical spot and their concentration.

In order to evaluate the Jn parameter equally in all the study cases and reduce the uncertainties associated with the lack of standards, the discontinuity sets were defined according to the following rules:

-

A discontinuity set is a cluster of fractures greater than or equal to the minimum number described (

Table 4. Minimum number of poles to establish discontinuity sets.

Total Number of Projected Poles	Minimum Number of Poles to Establish a Discontinuity Set
<15	3
[15–25]	3–4
[25–35]	4–5
>35	5–6

), with at least a concentration of projected poles of 10% per 1% of the area;

-

It constitutes a discontinuity set if the number of projected poles coinciding with the design discontinuity sets is greater than three (only for criterion two and criterion four);

-

Random discontinuities are considered to be present when the number of poles that are not a discontinuity set is ≥ 20% of the total number of projected poles.

The most accurate method of defining the Jn parameter involves the use of stereographic projection software, which enables the statistical analysis of geological data collected in the field, specifically the in situ orientation of discontinuity surfaces and those in boreholes [4].

To better understand the application of the four criteria described above, stereographic projections are shown along with the identification of the number of the discontinuity sets for the Jn parameter, e.g., for one section of the penstock tunnel PT01B (Figure 9 and

Table 5. Definition of discontinuity sets for the studied section PT01B (pk0+871.70 to pk0+875.60).

Tunnel Section and Jn Parameter	Criteria
	Criterion 1 (5 m most relevant)	Criterion 2 (5 m most relevant/design discontinuity sets)	Criterion 3 (10 m most relevant)	Criterion 4 (10 m most relevant/design discontinuity sets)
Mapped section	(pk0+870.0 to pk0+875.0)	(pk0+870.0 to pk0+875.0)	(pk0+870.0 to pk0+880.0)	(pk0+870.0 to pk0+880.0)
Jn	2 sets + random—(6)	2 sets + random—(6)	4 or more sets—(15)	3 sets + random—(12)

).

2.1.3. Jr and Ja Parameters Methodology

The calculation method of Jr and Ja parameters proposed in this study consists of counting all the mapped discontinuities and their characteristics in the 5 m or 10 m sections most relevant to each section.

To calculate Jr, the waviness and smoothness of discontinuities were used, and to calculate Ja, the type of contact, opening, and wall alteration of discontinuities were used. The discontinuity parameters were recorded at the tunnel opening and are presented in the GGDB (Q-Barton-GGDB).

The discontinuities considered to be the most significant in each section studied follow three criteria:

Criterion 1—Analysis of the selected characteristics of all the discontinuities mapped in the 5 m most relevant to the section;

Criterion 2—Analysis of the selected characteristics mapped in the 10 m most relevant for the section;

Criterion 3—Analysis the selected characteristics of the discontinuities considered in a tunnel face opening as the most significant for the studied section.

For Jr parameter, the analysis referred to ‘criterion 1’ and ‘criterion 2’ was carried out based on the GGDB data of all discontinuities and their characteristics mapped in the six penstock tunnels. It consists of evaluating the discontinuities according to their waviness and smoothness, associated with a value of Jr, according to the geologist’s field data. The analysis referred to ‘criterion 3’ used the data from the ‘structural synthesis’, which was recorded in every geological–geotechnical mapping of the tunnel faces, characterising the three most important families of discontinuities on each front.

To obtain the Jr-value, the average values of the waviness and smoothness parameters associated with each of the three criteria described above were used, thus obtaining three representative values of this parameter for each of the 48 sections evaluated.

The Jr parameter is a Q-Barton index, which is usually easy to characterise in the tunnel faces, but it can also raise doubts depending on the type and conditions of the discontinuity planes. As this parameter is generally obtained by simply geological observation of the rock mass, it is highly dependent on the geologist’s assessment of the surface characteristics of the discontinuities.

To obtain a value representative of the Jr of each tunnel opening section, it was estimated using the waviness and smoothness surface characteristics recorded in the tunnel faces to describe the mapped discontinuities. To avoid the subjectivity associated with determining the Jr values obtained in the tunnel faces, they were replaced by statistical analyses of the mapped characteristics.

The transformation of waviness values (irregular or stepped (IR), undulating (UN), planar (PL)), and smoothness (rough (RG), smooth (SM), and slickensided (SK)—using INTT notations [32]) recorded in the discontinuities in the tunnel face, into Jr parameter values—0.5, 1.0, 1.5, 2.0, 3.0, and 4.0—for calculating the Q-Barton, followed the equivalences contained in published charts [35].

For a better understanding of the following procedure, an example is provided for the tunnel opening section from pk0+871.70 to pk0+875.60 of PT01 (

Table 6. Example of the procedure used to obtain the Jr-values (pk0+871.70 to pk0+875.60—PT01).

Advance PT01 from pk0+871.70 to pk0+875.60
Discontinuities Characteristics			Counting Discontinuities Criteria
Surface waviness	Surface smoothness	Jr	Most relevant in the tunnel face (pk0+871.70 to pk0+875.60)	5 m most relevant (pk0+870.00 to pk0+875.00)	10 m most relevant (pk0+870.00 to pk0+880.00)
Number of discontinuities considered in each criterion			3	10	16
Irregular or stepped (IR)	Rough (RG)	4.0 3.0 2.0	-	-	-
Undulating (UN)	Smooth (SM)	3.0 2.0 1.5	1 - -	5 - -	6 - -
Planar (PL)	Slickensided (SK)	1.5 1.0 0.5	2 - -	5 - -	6 - -
Average value			2	2.25	2.06

).

Relative to the Ja parameter, the reason for analysing a section according to three discontinuity criteria above mentioned in this subsection (criterion 1, criterion 2, and criterion 3) is that all the criteria are equally representative of the section under study, making it possible to obtain not one but three Ja-values that characterise this parameter for each section, making it possible to visualise the limits and variation Ja value in each section.

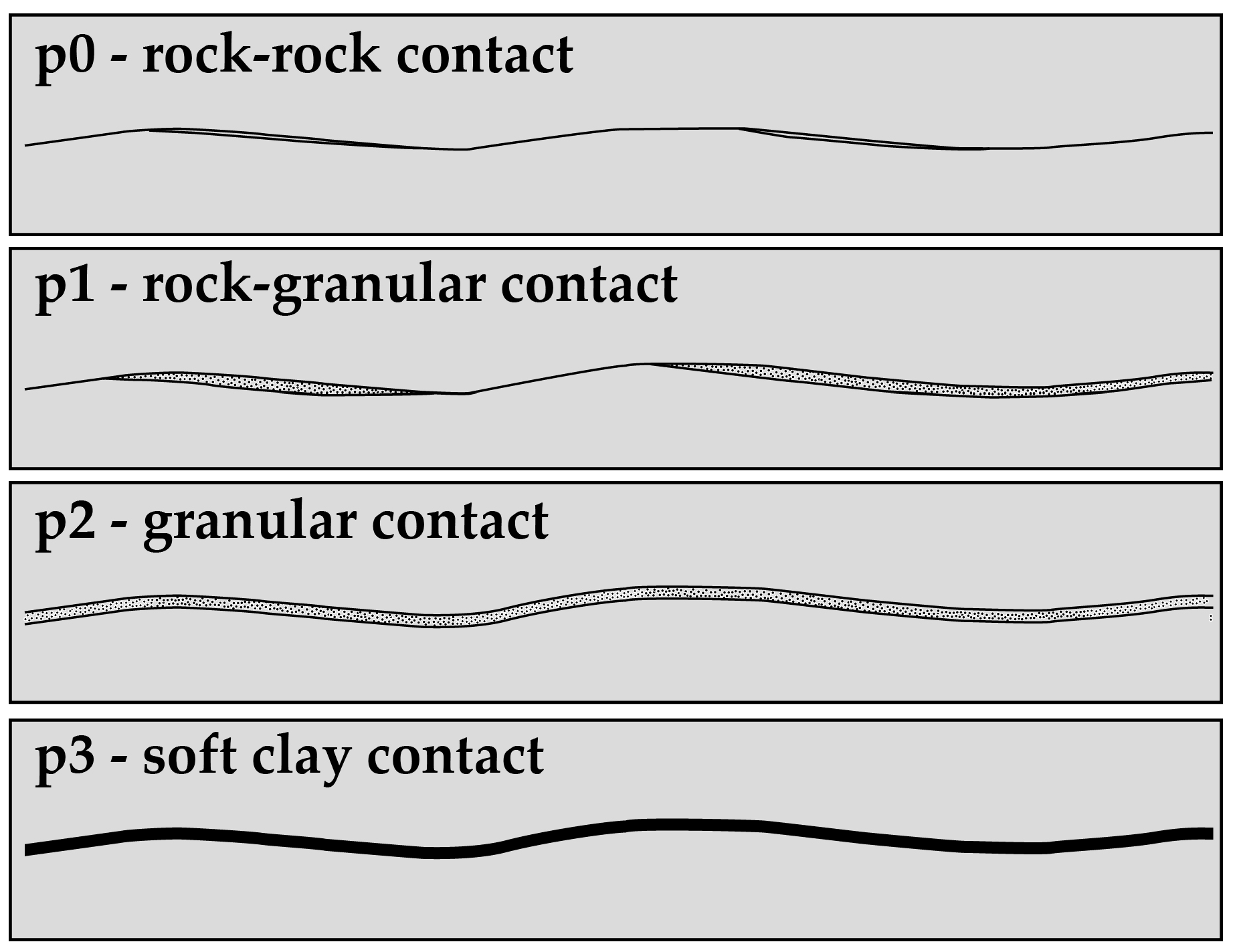
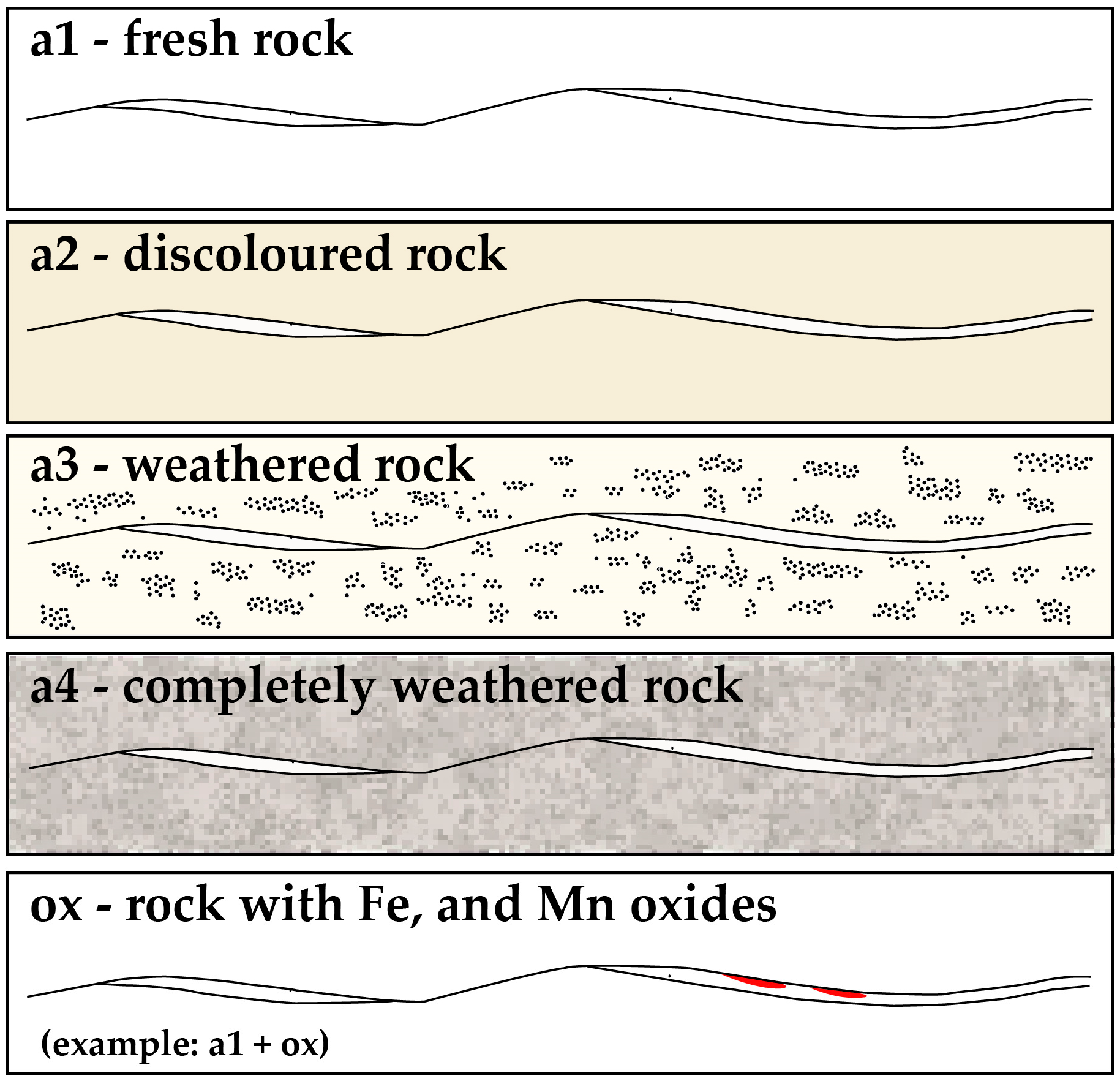
The Ja parameters characterise the degree of mechanical strength of the discontinuity walls in the Q-Barton system, penalising or favouring the Q-index depending on the type of wall contact (p), wall opening (E), and wall alteration (a) of the discontinuities using INTT notations [32], as well as the characteristics of the joint infill material. This parameter, however, is difficult for geologists in the field to define, and it sometimes raises doubts when assigning a value that accurately defines the joint alteration number.

In order to quantify the Ja objectively, we analysed the type of contact (p) and the opening (E) of the discontinuity walls, as well as their wall alteration (a), recorded for the discontinuities at the tunnel faces.

To be able to transform the characteristics of the discontinuities—type of wall contact (p0, p1, p2, and p3), type of wall opening (E1, E2, E3, and E4), and type of wall alteration (a1, a2, a3, a4, and ox)—into Ja-values of 0.75, 1, 2, 3, 4, 5, 6, 8, 8–12, and 13–20—it was necessary to establish a set of empirical equivalences (Table S1). The unpublished equivalences, developed within the scope of this study, are necessarily subject to a continuous process of revision.

Table 7. Ja-values related to the characteristics of the discontinuities (type of wall contact, type of wall opening, and type of wall alteration).

Ja	Smoothness/Discontinuities Type	Contact Type (p)	Opening (E)	Alteration (a)
(a) Rock-wall contact (no mineral fillings, only coatings)
0.75		p0	E1	a1
1		p0	E1	a2, ox
2		p1	E1 (E2)	a2 (a3), ox
3		p1	E2	a3, ox
4		p1	E2 (E3)	a3, ox
(b) Rock-wall contact before 10 cm shear (thin mineral fillings)
4		p1	E2 (E3)	a2
6		p1/p2	E2 (E3)	a3
8		p2	E2 (E3)	a3
8–12		p2	E2 (E3)	a4
(c) No rock-wall contact when sheared (thick mineral fillings > 5 mm)
6	SK/fault	p2/p3	E3	a2
8	SK/fault	p2/p3	E3	a3
8–12	SK/fault	p2/p3	E3	a4
10	SK/fault	p3	E4	a2
13	SK/fault	p3	E4	a3
13–20	SK/fault	p3	E4	a4

shows the values of the Ja parameter corresponding to the characteristics of the discontinuities (wall contact type (p)/wall opening (E)/wall alteration (a)).

In order to demonstrate the methodology used to calculate the Ja-values for the 48 studied sections,

Table 8. Example of the methodology used to obtain the Ja-values (PT01B—pk0+871.70 to pk0+875.60).

Discontinuities Characteristics					Counting Discontinuities Criteria
Ja	Smoothness/Discontinuities Type	Contact Type (p)	Opening (E)	Alteration (a)	Most Relevant in the Tunnel Face (pk0+871.70 to pk0+875.60)	5 m Most Relevant (pk0+870.00 to pk0+875.00)	10 m Most Relevant (pk0+870.00 to pk0+880.00)
(a) Rock-wall contact (no mineral fillings, only coatings)
0.75		p0	E1	a1	1	10	15
1		p0	E1	a2, ox	1	-	-
2		p2	(E1) E2	a2 (a3)	1	-	-
3		p2	E2	a3	-	-	-
4		p2	E2	a3	-	-	-
(b) Rock-wall contact before 10 cm shear (thin mineral fillings)
4		p1 (p2)	E2 (E3)	a3	-	-	-
6		p1	E2 (E3)	a2	-	-	-
8		p3	E2 (E3)	a3	-	-	-
8–12		p3	E2 (E3)	a4	-	-	-
(c) No rock-wall contact when sheared (thick mineral fillings > 5 mm)
6	SK/fault	p1/p3	E3	a2	-	-	-
8	SK/fault	p1/p3	E3	a3	-	-	-
8–12	SK/fault	p1/p3	E3	a4	-	-	-
10	SK/fault	p3	E4	a2	-	-	-
13	SK/fault	p3	E4	a3	-	-	-
13–20	SK/fault	p3	E4	a4	-	-	-
Average value					2	2.25	2.06

shows an example of the procedure for the PT01B section from pk0+871.70 to pk0+875.60.

2.2. Costs of Execution Time and Geotechnical Support

The economic consequences of the 48 sampling cases classified according to the two sets of Q-Barton indices obtained from different parameterisations (Q-Barton-geologist, estimated by the geologist during the tunnel opening; and Q-Barton-GGDB, calculated by combining the discontinuity parameters recorded at GGDB) were compared. The geotechnical costs associated with each class of rock mass (Classes I to V of Q-Barton) were characterised. The costs shown below have been calculated for 10 m of advance in each tunnel class, applied in the penstock of the hydropower hydraulic circuit, considering the costs of support and drainage of the rock mass (

Table 9. Production cycles characterisation in the tunnel opening.

Classes	Average of Advances (m/Day)	Length of Advances (m/Advance)	Duration of Production Cycles (day/Advance)
Class I	3.02	4.53	1.50
Class II	1.83	4.53	2.47
Class III	1.42	4.50	3.16
Class IV 1	0.99	3.61	3.64
Class V	-	-	-

¹ Excluding the application of the secondary support.

):

-

Advances in rock mass of Class I, Class II, and Class III were carried out definitively, including, within the tunnel opening cycle, the application of shotcrete, anchor bolts, and eventual piped weep holes and, outside the excavation cycle, the application of a drainage borehole;

-

Advances in rock mass of Class IV and Class V were divided into two phases: the first, within the tunnel opening cycle, in which primary support was applied—shotcrete, anchor bolts, and eventual piped weep holes—and the second, outside the tunnel opening cycle, where secondary support was applied—structural concrete application.

The number of labour days for the 48 studied samples was calculated by multiplying the number of advances per rock mass class (sampling) by the average value of the number of labour days for each production cycle (defined by Q-Barton Classes in Table 9).

For the unit price of any product or service, a monetary basis index equal to 1.0 unit was chosen (

Table 10. Geotechnical support costs for a 10 m advance on Q-Barton Classes. Monetary base index equal to 1.0 u; Φ—diameter; L—length; Fy—yield strength; t—thickness.

Q-Barton Rock Mass Classes	Geotechnical Support	Units	Quantities for 10 m	Unitary Price (u)
Class I	-Anchor bolt- (Φ 25 mm, L = 4 m, Fy = 500 MPa, eventual, every 4 m)	m	30.0	3.90
Class II	(Φ 25 mm, L = 4 m, Fy = 500 MPa, systematic 2.3 m)		121.7
Class III	(Φ 25 mm, L = 4 m, Fy = 500 MPa, systematic 1.7 m)		235.3
Class IV	(Φ 25 mm, L = 4 m, Fy = 500 MPa, systematic 1.4 m)		571.4
Class V	(Φ 32 mm, L = 4 m, Fy = 500 MPa, systematic 1.0 m)		1120.0
Classes I, II and III	-Shotcrete- (Steel fibre reinforced, t = 8 cm, fibre rate = 30 kg/m3)	m3	22.8	58.00
Class IV	(Conventional, t = 15 cm)		42.8	54.00
Class V	(Conventional, t = 30 cm)		85.6
Class I	-Piped weep hole- (Φ 50 mm, L = 0.50 m)	m	0.5	4.00
Class II			1.0
Class III			1.5
Class IV			2.0
Class V			2.5
Classes I, II and III	-Drainage borehole- (Φ 50 mm, spacing = 2.5 m × 2.5 m)	m	140.0	2.00
Classes IV and V	-Injection with cement mortar- (Φ 50 mm, L = 3 m, spacing = 2.0 m × 2.0 m)	m	210.0	2.67
Classes IV and V	-Wire mesh- (Φ 42 mm, Fy = 600 MPa, 10 cm × 10 cm)	m2	285.2	1.00
Class V	-Steel arch-	unit	10.0	366.70
Class IV	-Structural shotcrete- (C30/37 A400)	m3	486.5	26.70
Class V			469.2
Total costs for each Q-Barton Class
Class I	Class II	Class III	Class IV	Class V
1721.4 u	2081.0 u	2526.1 u	18,383.1 u	26,040.9 u

, unitary price (u))—the other unitary prices are defined as a function of this minor price = 1.0 u – and, therefore, the costs for geotechnical supports, total costs, and labour days, instead of any currency, so that, on the one hand, a stable ratio among unit prices and costs was established, which is not subject to exchange fluctuations and, on the other hand, the costs have a more universal application.

The cost of the geotechnical support was obtained for each Q-Barton Class by analysing the cost of the supports applied for 10 m of tunnel advance per class and the total sampling length for each Class of rock mass (Table 10). The cost of supports applied to Class IV and Class V, where a lining is applied, out of the production cycle, which reduces the hydraulic section, is around 10 times higher than for the other classes.

This cost analysis did not include prices associated with labour days, equipment, or any cost associated with the application of additional geotechnical supports, due to the unpredictability and significant variability of these costs. The indirect costs are already reflected to some extent in the increase in time needed to carry out the geotechnical support applied. In the construction works, the additional costs related to additional geotechnical support (e.g., punctual anchors, bolts, and localised iron mesh) were residual; for this reason, it is not possible to give any objective cost percentage that would apply to other construction contexts.

3. Results and Discussion

3.1. RQD Parameter

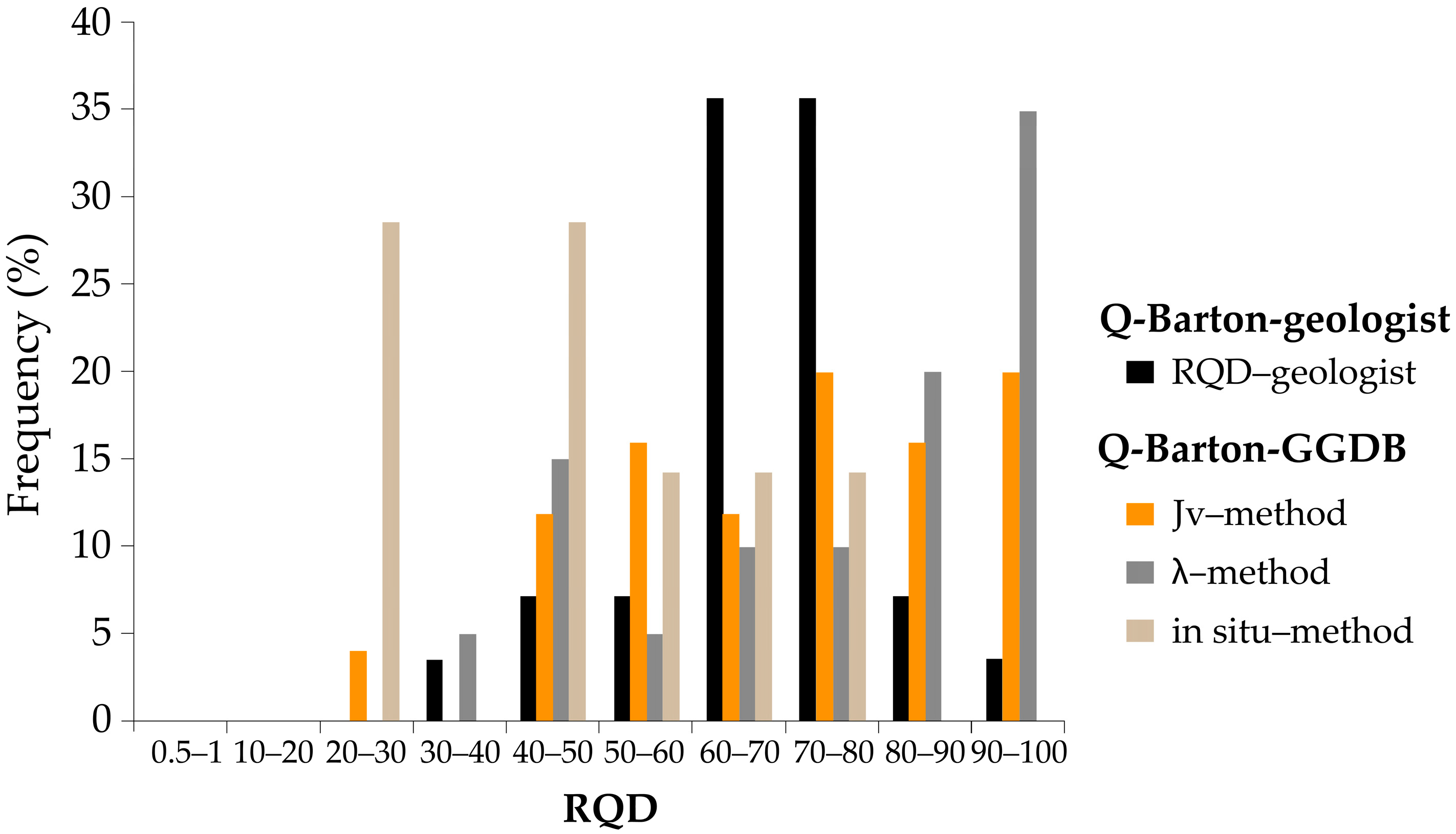
The RQD values estimated and used on site by the geologist to characterise the respective tunnel faces, as well as those obtained independently by the three above-mentioned methods (see Section 2.1.1), are organised by penstock tunnel. In general, these RQD values are not coincident (Figure 10). The RQD determined by the geologist has the most frequent values in the 60% to 80% range. The autonomous calculation of the RQD parameters on 48 samples, using Jv and λ methods, shows a tendency towards higher RQD values, with more frequent classes in the 70% to 100% RQD range. In turn, the in situ RQD method, despite having a sample size of only seven measurements, shows lower RQD values, with more frequent occurrences in the 20% to 30% and 40% to 50% ranges. The method considered most robust is that of Palmström [10]. Comparatively, the method of Priest and Hudson [14] overestimates the value of Q-Barton, and the location of the scan-line is always debatable. In turn, the in situ method [10] is difficult to choose the rock mass site where it is applied, and it is the most subjective of all methods.

In summary, the calculated values (Q-Barton-GGDB) are higher than those estimated and adopted by the geologist (Q-Barton-geologist) for the tunnel face openings, which suggests that conservative values were chosen when estimating this parameter during the tunnel support application cycle.

3.2. Jn Parameter

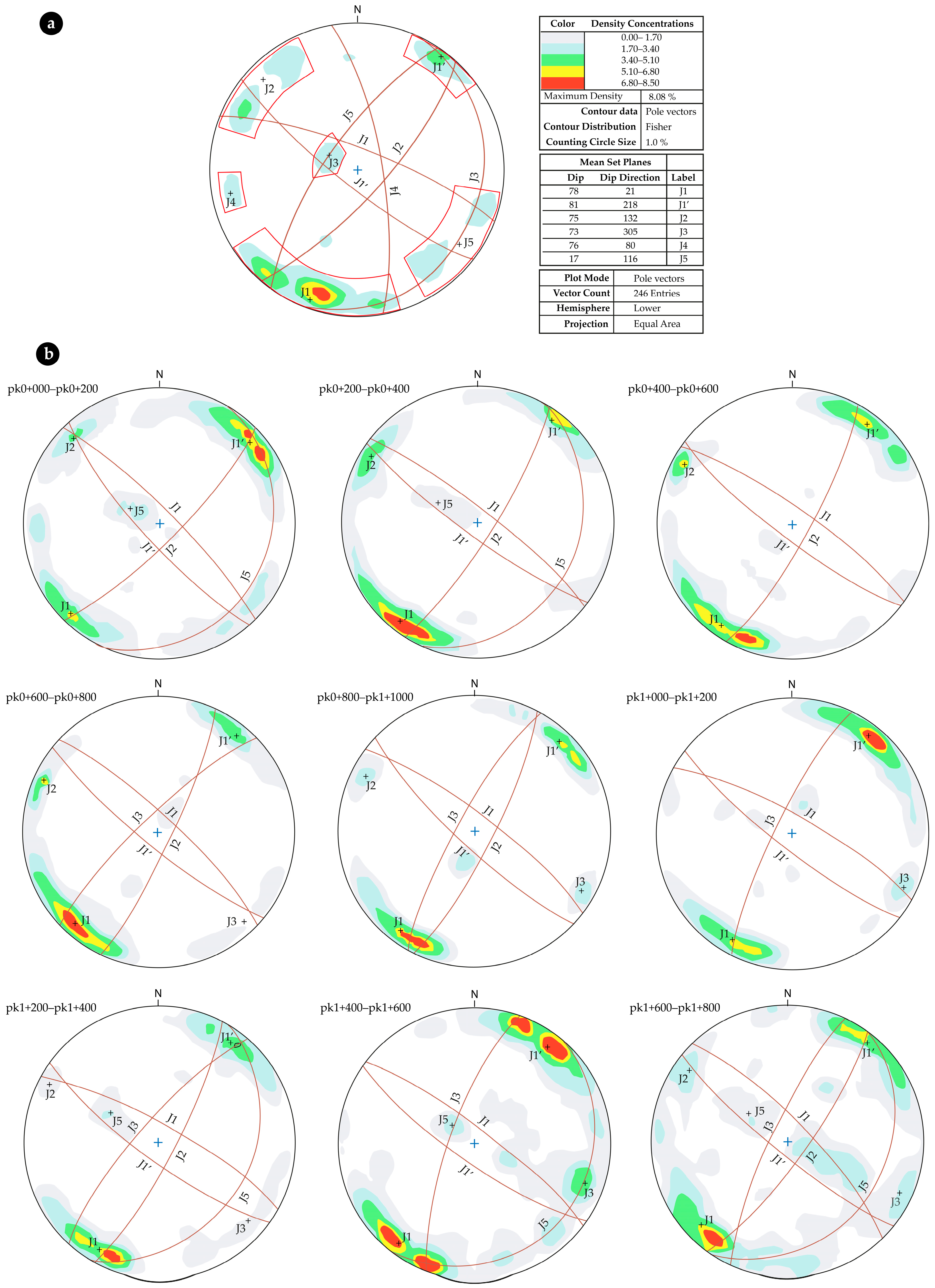
The design with the most frequent discontinuity sets (Figure 11a) mapped in the tunnel face openings are the J1 and J1’ sets, which coincide with the gneissic foliation (Sn) and with the more frequent regional faults. These sets have similar strike but dip in opposite directions.

The validity of the design set discontinuities (Figure 11a) in defining the geotechnical support for the penstock tunnels was analysed retrospectively. Sections of 200 m of tunnel were considered, and a comparison was made between the discontinuity sets mapped in each section and the design sets. The density stereograms of the discontinuity poles drawn up for each 200 m of tunnel PT03 are shown in Figure 11b.

By analysing the stereograms in Figure 11b, it can be stated that the discontinuity sets identified during the excavation of PT03 correspond to the discontinuity sets defined in the design (Figure 11a). A first consequence of this finding is to conclude that, statistically, the geotechnical support defined in the design meets the geological conditions of the rock mass.

The question is whether this statistical homogeneity observed in 1800 m of tunnel and in 200 m sections (Figure 11) is maintained in sections with an average of 5 m or 10 m corresponding to each tunnel penstock opening.

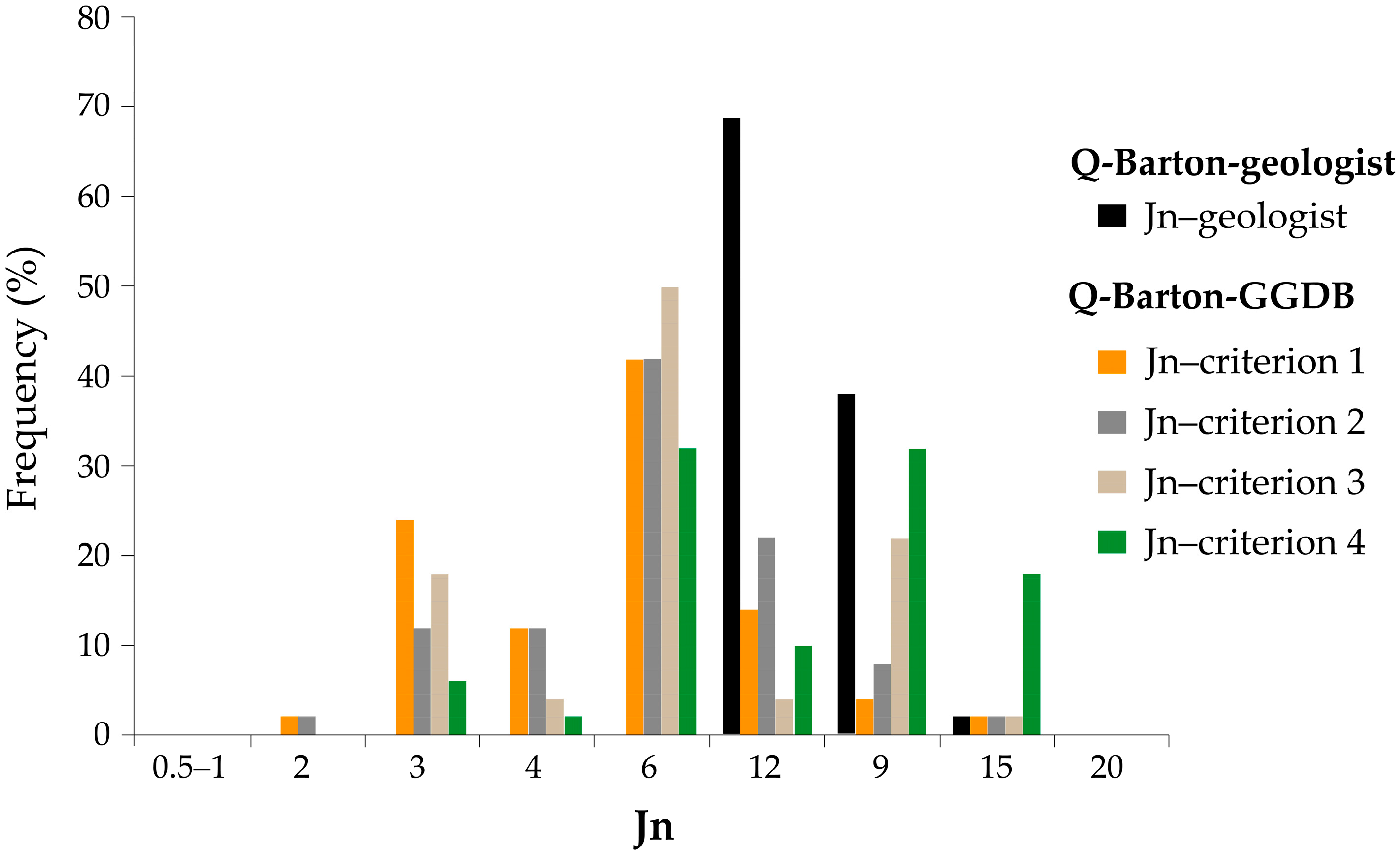
Analysing the Jn-values calculated using the four criteria based on 5 m and 10 m of tunnel (GGDB; see Section 2.1.2) in comparison with the Jn-values determined at the tunnel faces by the geologist, it could be seen that, usually, the Jn-values were calculated objectively (GGDB) (Figure 12), which is a situation that favours greater values of the Q-Barton index. In the tunnel faces, almost all of the estimated Jn-values were between Jn = 9 and Jn = 12. The consideration of discontinuities in 5 m sections (criteria 1 and 2) determines lower Jn-values, with considerable percentages of values (40%) of Jn = 6, while the consideration of 10 m sections (criterion 3) determines higher Jn-values.

The calculation criterion that most closely approximated the Jn-values determined at the tunnel face was criterion 4 (Figure 12). In this criterion, a 10 m section was considered, and to establish the number of discontinuity sets, only those defined statistically that matched the design discontinuity sets were considered.

Criteria 1 and 2 have unimodal distributions, while criteria 3 and 4 have bimodal distributions, likely due to the samples belonging to two different rock masses (Class II and Class III of tunnels).

3.3. Jr Parameter

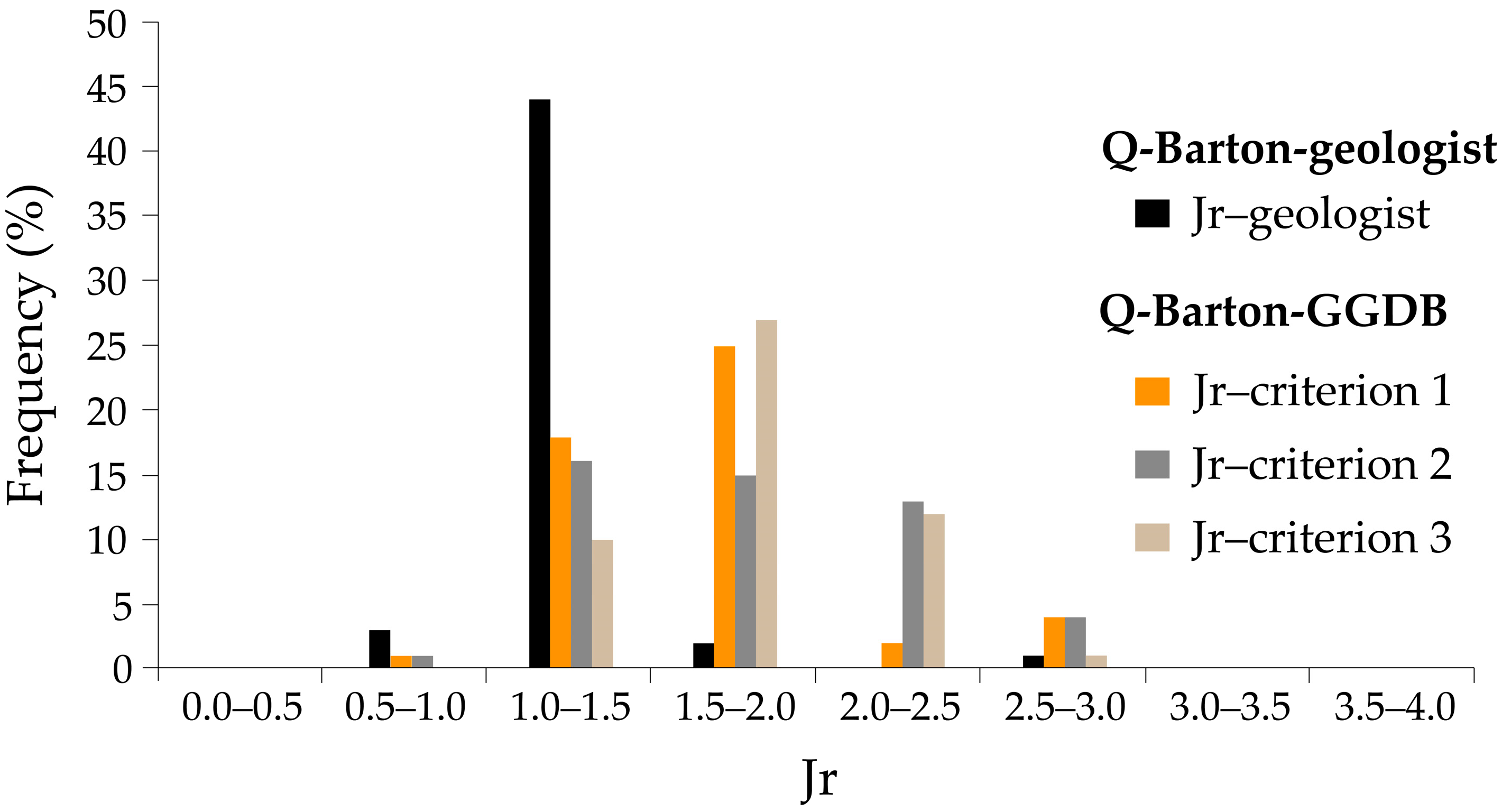
The Jr parameter adopted in tunnel face openings has its highest frequency in the 1.0–1.5 range, and it can be seen that most of the values are equal to or greater than the aforementioned range, which once again, suggests a conservative tendency in the evaluation of this parameter in tunnel faces by the geologist (Figure 13).

The comparative analysis of the three Jr criteria obtained indicates that the use of discontinuities in the tunnel face openings (Table 3; criterion 1) concentrates the values in the Jr = 1.5–2.0 range, while criteria 2 and 3 (Table 3)—statistical calculation of discontinuities recorded in 5 m and 10 m of tunnel face opening—show a broader distribution with values in the Jr = 1.5–2.5 interval. Criterion 3 (Table 3) shows a normal distribution with the centre class in the range Jr = 1.5–2.0 (Figure 13).

The use of more objective methods (Q-Barton-GGDB) allows for the determination of greater Jr-values and, consequently, higher Q-Barton values. Taking into account all Q-Barton-GGDB criteria, it was found that criterion 3 presents the values closest to a normal distribution.

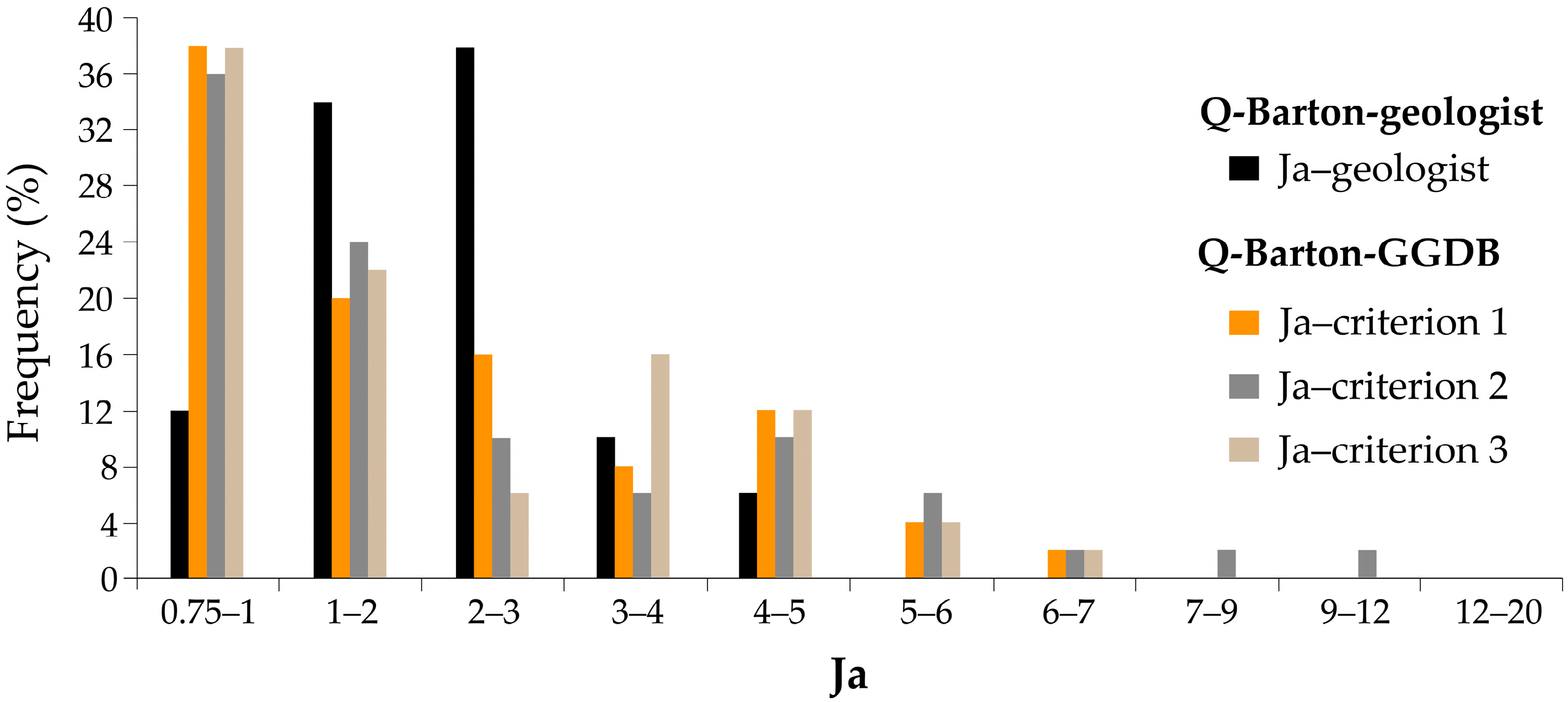
3.4. Ja Parameter

The Ja parameter indicates that more than half of the calculated values are lower than the values determined on tunnel faces (54.4%), 31.5% are higher, and only 14.1% are equal to the values determined on tunnel faces (Figure 14).

The Ja-values calculated according to the three criteria using GGDB show a very similar pattern of values, with a maximum in the lowest class ranging from Ja = 0.75 to Ja = 1, and an asymmetry to the right, or positive asymmetry, for higher values (Figure 14).

Since Ja is the denominator in the expression for calculating Q-Barton, higher Ja-values are associated with lower Q-Barton values and vice versa, which, once again, suggests a tendency for the quality index of the Q-Barton to increase in relation to the value estimated on tunnel face openings.

Of the three methods considered in this proposal, criteria 1 and 2 are closest to a regular statistical distribution, specifically, the lognormal distribution. Of these two methods, criterion 1 is the simplest to use, as it requires less data.

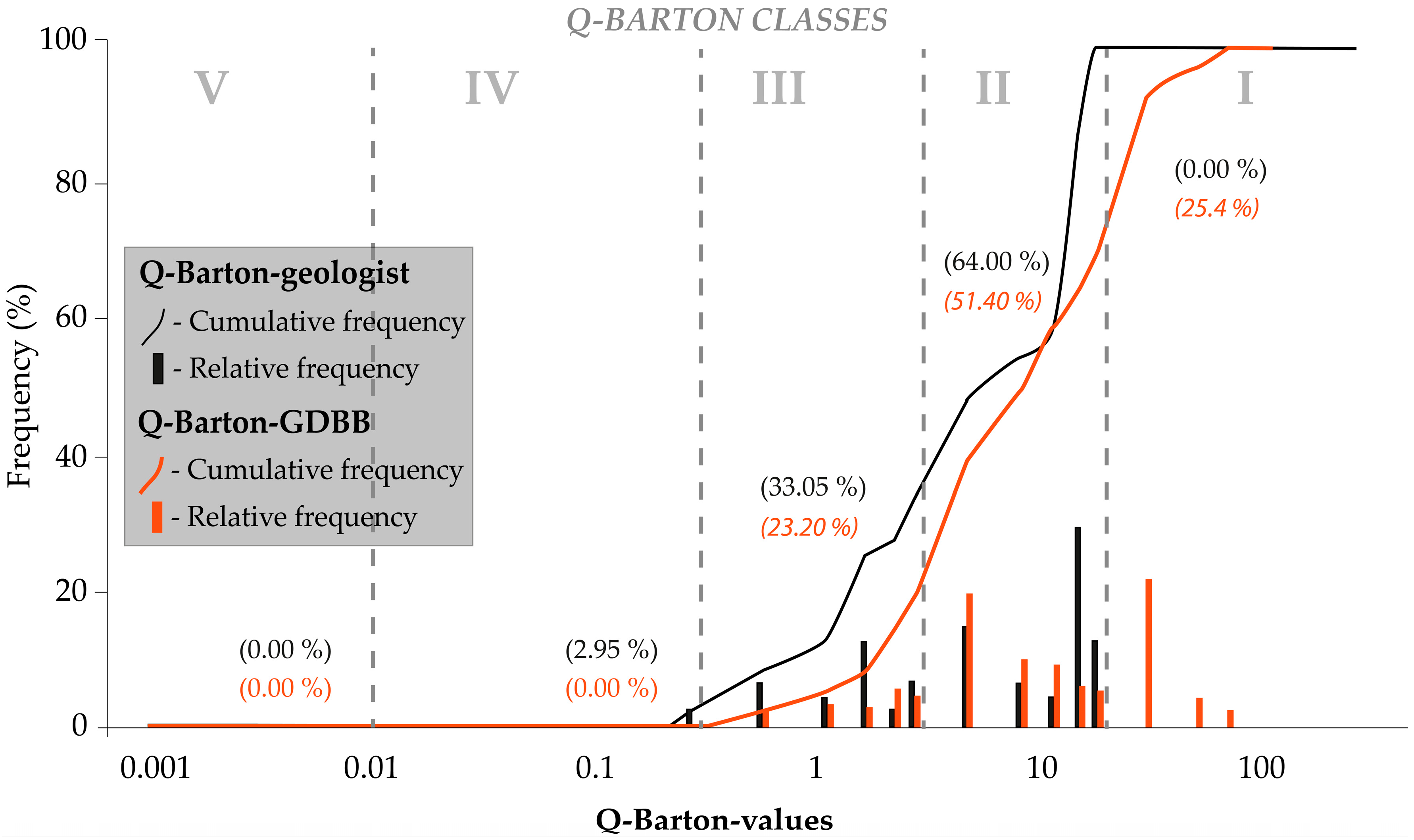
3.5. Q-Barton

The Q-Barton values determined on tunnel faces (48 values of Q-Barton-geologist) ranged from Class I to Class V, with values of 0%, 64%, 33.05%, 2.95%, and 0%, respectively (Figure 15). On the other hand, the Q-Barton values calculated by combining parameters (3252 values of Q-Barton-GGDB) ranging from Class I to Class V are 25.4%, 51.4%, 23.2%, 0%, and 0%, respectively (Figure 15).

Making a comparative analysis between the two methods to obtain the Q-Barton, there is a slight shift to the right (greater Q-values) of the line corresponding to the cumulative frequencies obtained by the calculated ‘Q-Barton-GGDB’ relative to ‘Q-Barton-geologist’ (Figure 15). The Q-Barton values obtained on faces in the upper second half of Class II are moving to higher Q-values and would generally increase rock mass values to Class I (Q-Barton value > 20). Similarly, it can be seen that the relative frequency of Q-values in the upper second half of Class III decreases, with a consequent increase for rock mass values to Class II (Q-Barton > 3.0).

3.6. Cost Analysis of the Labour Days and Geotechnical Supports

The application of geotechnical support of the 48 samples according to Q-Barton-geologist took 131.34 labour days and had a direct cost of 56,530.07 u (

Table 11. Number of labour days and cost of geotechnical support defined by Q-Barton Classes for the 48 samples of Q-Barton-geologist (A) and Q-Barton-GGDB (B), respectively. Monetary basis index = 1.0 u (see explanation in Section 2.2).

(A)	Q-Barton-geologist
Classes	Advance number (sample)	%	Advance day	Labour days	Advance (m)	Advance Class (sample)	Geotechnical support cost−10 m advance—(u)	Geotechnical support cost —sample—(u)
column (1)	column (2)	column (3)	column (4)	column (5)	column (6)	column (7)	column (8)	column (9) 1
Class I	0.00	0.00	1.50	0.00	4.53	0.00	1721.4	0.00
Class II	30.72	64.00	2.47	76.00	4.53	139.08	2081.0	29,092.38
Class III	15.86	33.05	3.16	50.20	4.50	71.43	2526.1	18,043.93
Class IV	1.42	2.95	3.64	5.15	3.61	5.11	18,383.1	9393.76
Class V	0.00	0.00	0.00	0.00	0.00	0.00	26,040.9	0.00
Total	48	100		131.34				56,530.07
(B)	Q-Barton-GGDB
Classes	Advance number (sample)	Classes	Advance number (sample)	Classes	Advance number (sample)	Classes	Advance number (sample)	Classes
column (1)	column (2)	column (3)	column (4)	column (5)	column (6)	column (7)	column (8)	column (9) 1
Class I	12.19	25.40	1.50	18.29	4.53	55.23	1721.4	9507.29
Class II	24.67	51.40	2.47	60.94	4.53	117.70	2081.0	24,493.37
Class III	11.14	23.20	3.16	35.19	4.50	50.14	2526.1	12,665.87
Class IV	0.00	0.00	3.64	0.00	3.61	0.00	18,383.1	0.00
Class V	0.00	0.00	0.00	0.00	0.00	0.00	26,040.9	0.00
Total	48	100		114.42				46,666.53

¹ The calculation of the geotechnical support cost of sample (GSCs)—column (9)—is based on the following formula: $GSCs={\displaystyle \frac{ACs\ast GSC10}{10}}$, where ACs is the advance class (sample)—column (7), and GSC10 is the geotechnical support cost (10 m advance)—column (8).

(A); columns (5) and (9), respectively). If the same geotechnical support were determined based on the Q-Barton-GGDB value, it would take 114.42 labour days with an associated cost of 46,666.53 u (Table 11 (B); columns (5) and (9), respectively).

In analysing Table 11, it was found that there is a difference of approximately 17 labour days and 9863.54 u between the two Q-Barton methods on the same sample. This difference results in a total saving of around 12.9% in labour days and 17.5% in geotechnical support costs if the parameters associated with the Q-Barton classification were calculated using the Q-Barton-GGDB methodology. Comparing the values of labour days, it can be concluded that, in general, 12.9% of labour days is saved, essentially due to the Class I rock mass (Q-Barton-GGDB) classified as Class II (Q-Barton-geologist) and the Class II rock mass (Q-Barton-GGDB) classified as Class III (Q-Barton-geologist). When matching the cost of geotechnical support, the 17.5% difference between the samples classified by the Q-Barton-geologist and the same samples classified by the Q-Barton-GGDB is mainly due to the absence of Class IV, the decrease in Classes III and II, and the increase in Class I.

The difference in values is quite significant if considering that the sample analysed is representative of the hydropower hydraulic circuit. This difference tends to be greater, as factors such as delays on the tunnel openings, more likely to happen at higher Q-Barton classes, have not been considered labour days; the costs associated with labour and machinery and other costs directly related to the number of labour days have not been accounted for at a national economic level.

It is considered that this difference in costs is due to inaccuracy and subjectivity associated with the parameterisation of the Q-Barton system (when comparing Q-Barton-GGDB with Q-Barton-geologist), particularly in the 48 studied cases, but that it is characteristic for an underground construction that, overall, it is represented by the general characteristics of the sampling.

Higher Q-Barton values can represent higher geological–geotechnical risks. However, the GGDB method facilitates a deeper understanding of potential rupture mechanisms (e.g., wedge and planar sliding) and the dynamics of these structures. The GGDB method requires a cooperative relationship between the two technicians; these rupture features are better weighted by comparing the geologist’s independent observations.

3.7. Essential Elements for the Application of Q-Barton-GGDB Methodology in Tunnel Construction

The use of Q-Barton-GGDB on tunnel openings requires attention to some aspects:

• Presence of two geologists, a junior geologist, and a senior geologist carrying out together the Q-Barton-GGDB methodology; two technicians on the excavation of an underground construction achieves a more consistent, reliable classification with fewer uncertainties in the characterisation of the properties of the rock mass and discontinuities; this option is economically viable because the reduction in the cost of oversizing and unnecessary labour days offsets the cost of the second technician. The presence of a second technician in tunnel face openings also helps to minimise human error when assessing geotechnical risk situations;
• Acquisition of data on a tablet at the tunnel face openings, recording Q-Barton parameters, mass rock, and discontinuity characteristics; while the senior geologist makes the geological–geotechnical mapping and performs a global evaluation of the face opening—including the geotechnical zoning, the junior geologist takes the rock mass and discontinuity measurements by filling out the digital GGDB form;
• Determination of Q-Barton at the tunnel face openings (Q-Barton-geologist); after doing the global evaluation, the senior geologist determines the Q-Barton;
• Calculation of Q-Barton parameters (Q-Barton-GGDB); using the data carried on the GGDB, this Q-Barton will be calculated by the senior geologist at the office;
• Decision on Q-Barton index; this decision will be taken by the senior geologist, taking into account the different results obtained; the big challenge will be to keep Q-Barton-geologist validated by Q-Barton-GGDB statistical analyses or adopt a new one—the Q-Barton-GGDB.

These five aspects form the basis for utilising the Q-Barton-GGDB methodology to achieve the technical and cost advantages mentioned above.

4. Conclusions

This work proposes a new methodology for calculating the Q-Barton in underground tunnel openings based on a geological–geotechnical database (Q-Barton-GGDB).

The GGDB is constructed with objective/quantitative data relative to the rock mass (RQD) and its discontinuities (roughness and smoothness, wall contact type, wall opening, and wall alteration).

To calculate the Q-Barton parameters Jn, Jr, and Ja, several objective criteria from the GGDB data were proposed.

The adopted methodology for calculating the RQD, Jn, Jr, and Ja proved to be suitable for determining the Q-Barton-GGDB, enabling statistically valid values to be generated.

In general, the Q-Barton-geologist values were substantially more conservative than the Q-Barton-GGDB statistical values, resulting in an underestimation of the rock mass and geotechnical support quality.

Using the Q-Barton-GGDB methodology, 29% of the openings had a relatively consistent probability of being classified for the Q-Barton class below that adopted with Q-Barton-geologist. This value is relatively high, and although the conclusions of the sampling cannot be extended to the entire hydropower hydraulic circuit, it suggests a very conservative approach in assigning Q-Barton-geologist parameters, with significant consequences in terms of costs and labour days.

Analysing the consequences of carrying out a generic design with the same geotechnical support and excavation advances with the penstock hydraulic circuit studied, which results in economic savings, which may be higher, around 12% of labour days and 17.5% of the costs of the geotechnical support applied.

These values are considered to be quite high if the dimension and costs associated with a design of this type are considered, as well as the effect that less good characterisation of the rock mass can have.

The use of two technicians/geologists on the tunnel face openings, i.e., having two geologists present in the tunnel face openings, allows for a better understanding of geological–geotechnical risk.

The Q-Barton-GGDB implies collaboration between two geologists, which reduces subjectivity and the misestimating of Q-Barton parameters. In any case, the geologist team can compare the Q-Barton-geologist with Q-Barton-GGDB and balance the two Q-Barton values; this analysis reduces the risk related to an eventual underestimation of support requirements.

This approach could be replicated in other tunnels in rock masses with different lithologies. The tunnel faces that served as the basis for the present approach were built entirely in gneiss, and it is suggested that the proposed methodology could be extended to other types of rock masses.

The present study did not analyse geotechnical risk in the strict sense, but the analysis of deviations in the Q-Barton index could be considered a risk analysis. An assessment of the geotechnical risk, combined with a similar study of the geotechnical parameters of Q-Barton, is suggested for future development.