Next Article in Journal
Reduction of Q-Barton Uncertainty: Proposal of a New Methodology Based on a Factual Geological–Geotechnical Database to Apply in Tunnels
Previous Article in Journal
On Stability Analysis of Car-Following Models with Various Discrete Operators
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 20
10.3390/app152011074
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Surgical Tightening Torque on the Pull-Out Strength of Screws in Vertebral Body Tethering

by
Freddy Patricio Moncayo-Matute
1,2,*,
Rafael Claramunt
1,
Álvaro Guzmán-Bautista
1,
Paúl Bolívar Torres-Jara
2 and
Enrique Chacón-Tanarro
1
1
Mechanical Engineering Department, ETSI Industriales, Universidad Politécnica de Madrid, 28040 Madrid, Spain
2
Grupo de Investigación en Nuevos Materiales y Procesos de Transformación (GIMAT), Universidad Politécnica Salesiana, Cuenca 010105, Ecuador
*
Author to whom correspondence should be addressed.
Appl. Sci. 2025, 15(20), 11074; https://doi.org/10.3390/app152011074
Submission received: 10 September 2025 / Revised: 6 October 2025 / Accepted: 8 October 2025 / Published: 16 October 2025
Browse Figures
Versions Notes

Abstract

Background/Objectives: Screw loosening and vertebral fractures remain common after vertebral body tethering (VBT). Because tightening torque sets screw preload, its biomechanical effect warrants explicit modeling. In this paper, a Finite Element (FE) model, supported by ex vivo porcine vertebral tests, was developed and validated that incorporates torque-induced pre-tension to quantify vertebral stress, aiming toward customizable VBT planning. Methods: An FE model with pre-tension and axial extraction failure was parameterized using ex vivo tests on five porcine vertebrae. A laterally inserted surgical screw in each specimen was tightened to 5.9 ± 0.80 Nm. Axial extraction produced failure loads of 2.1 ± 0.31 kN. This is also considered in the FE model to validate the failure scenario. Results: Torque alone generated peak von Mises stresses of 16.1 ± 0.86 MPa (cortical bone 1) and 2.1 ± 0.13 MPa (trabecular), lower than prior reports. With added axial load, peaks rose to 141.1 ± 0.70 MPa and 19.7 ± 0.23 MPa, exceeding typical ranges. However, predicted failure agreed with experiments, showing 0.58 mm displacement and a conical displacement distribution around the washer. Conclusions: Modeling torque-induced pre-tension is essential to reproduce realistic stress states and anchor failure in VBT. The framework enables patient-specific assessment (bone geometry/density) to recommend safe tightening torques, potentially reducing screw loosening and early fractures.

1. Introduction

The vertebral body tethering (VBT) technique is an innovative surgical approach for correcting idiopathic scoliosis in adolescents [1]. The anchorage system involves a surgical screw and a washer inserted into the vertebral body through the lateral convex side. These anchorage systems are subsequently tensioned using a polyethylene terephthalate cord connecting the screw heads, which reduces spinal deformity and halts its progression [1].
Clinical follow-up studies over more than two years [2,3] have demonstrated improvements in Cobb angles ranging from 45.3 ° ± 11.7 ° to 18.7 ° ± 13.4 ° using the VBT technique, confirming its effectiveness in improving patient outcomes and ensuring safety during treatment [4,5,6,7,8,9,10,11,12,13,14,15,16].
Unlike spinal fusion techniques, VBT has been experimentally shown to preserve vertebral motion, including flexion, extension, axial rotation, and lateral bending stability [1,3,17]. Additionally, it accommodates vertebral growth, with differential growth observed in thoracic vertebrae: the concave side grew by 2.2 mm compared to 1.5 ± 2.3 mm on the convex side [18]. Despite these clinical successes, the lack of computational models for evaluating the effects of VBT has been highlighted [1,3,17,19,20,21,22,23]. For instance, the numerical study by Nicolini et al. [24] examined VBT effects with cord tensions up to 300 N but did not account for tightening torque, a factor that significantly influences postoperative biomechanical loading. Therefore, more robust computational models validated against experimental data are needed to accurately understand VBT mechanics.
Among previous works, biomechanical studies have reported the forces that vertebrae endure during surgery and the postoperative behavior of patients in motion [18]. Proper control of these forces prevents complications such as overcorrection that might affect the lungs, implant loosening, cord failure, or vertebral fracture [3,17,18]. Improvements in screw design, anchoring typologies, and better insertion orientation have been proposed to mitigate these issues [19,20,21]. These forces also participate in screw loosening, a critical concern in surgical fixation. Implant treatments generally show failure rates of 5 to 10 % , primarily associated with loosening [25].
Screw loosening occurs in two stages. First, cyclic loading causes bone wear at the screw–bone interface, reducing the existing preload due to friction between the thread and bone. In the second stage, this loss of preload exacerbates the loosening due to rotational pull-out forces from external loads and vibration [20,21]. Specifically in VBT, the tension in the polyethylene terephthalate cord generates a bending moment on the spine, creating compression on the convex side and tension on the concave side of the vertebral bodies.
This effect has been previously studied via finite element analysis (FEA), evaluating stress distribution in vertebrae under screw pull-out forces [26,27].
A critical yet understudied factor in anchor fixation is the final tightening torque applied to screws after insertion. The effects of tightening torque in bicortical screw fixations, as in VBT, remain insufficiently explored [28]. Experimental evidence suggests that torque values inducing stresses close to 75 % of the screw’s elastic limit optimize anchor strength and reduce loosening [22]. In dental applications, proper tightening torque ensures structural stability even under masticatory pressure, preventing loosening [29,30,31]. This underscores the importance of achieving structural stiffness to minimize screw loosening in vertebral anchoring. In most current surgical techniques, tightening torque relies on the surgeon’s experience or is applied using a torque wrench following certain standards [32].
These methods introduce variability, compounded by the uncertain mechanical properties of the bone being fixed [33].
This study proposes an FEA methodology that incorporates a representative value for surgical torque and axial extraction force, both obtained from our experimental campaign conducted on porcine thoracic vertebrae under controlled conditions that simulate the insertion technique used in the vertebral body tethering (VBT) procedure. Unlike other studies, this study does not seek to compare different torque levels or establish an optimal value, but rather to evaluate the mechanical behaviour of the screw–bone system under realistic surgical conditions.

2. Methodology

To facilitate the understanding of the FEA methodology developed in this study, this section first presents the experimental campaign conducted for its formulation. This approach aims to provide a clearer insight into the challenges associated with anchoring systems using surgical screws in the VBT technique and the influence of the analyzed factor, the tightening torque. Given the challenges of conducting experimental studies on human vertebrae, various authors have demonstrated that porcine spine models are the most suitable for analysing the behaviour of human thoracic vertebrae T6 to T10 [19,20], which are commonly targeted in VBT procedures. To replicate the conditions of VBT surgery in the laboratory, a methodology for sample preparation, tightening torque application, and screw pull-out testing was established. This approach aimed to simulate real surgical conditions as closely as possible. The experimental results were then used as inputs for the FEA model, ensuring its accuracy and reliability.

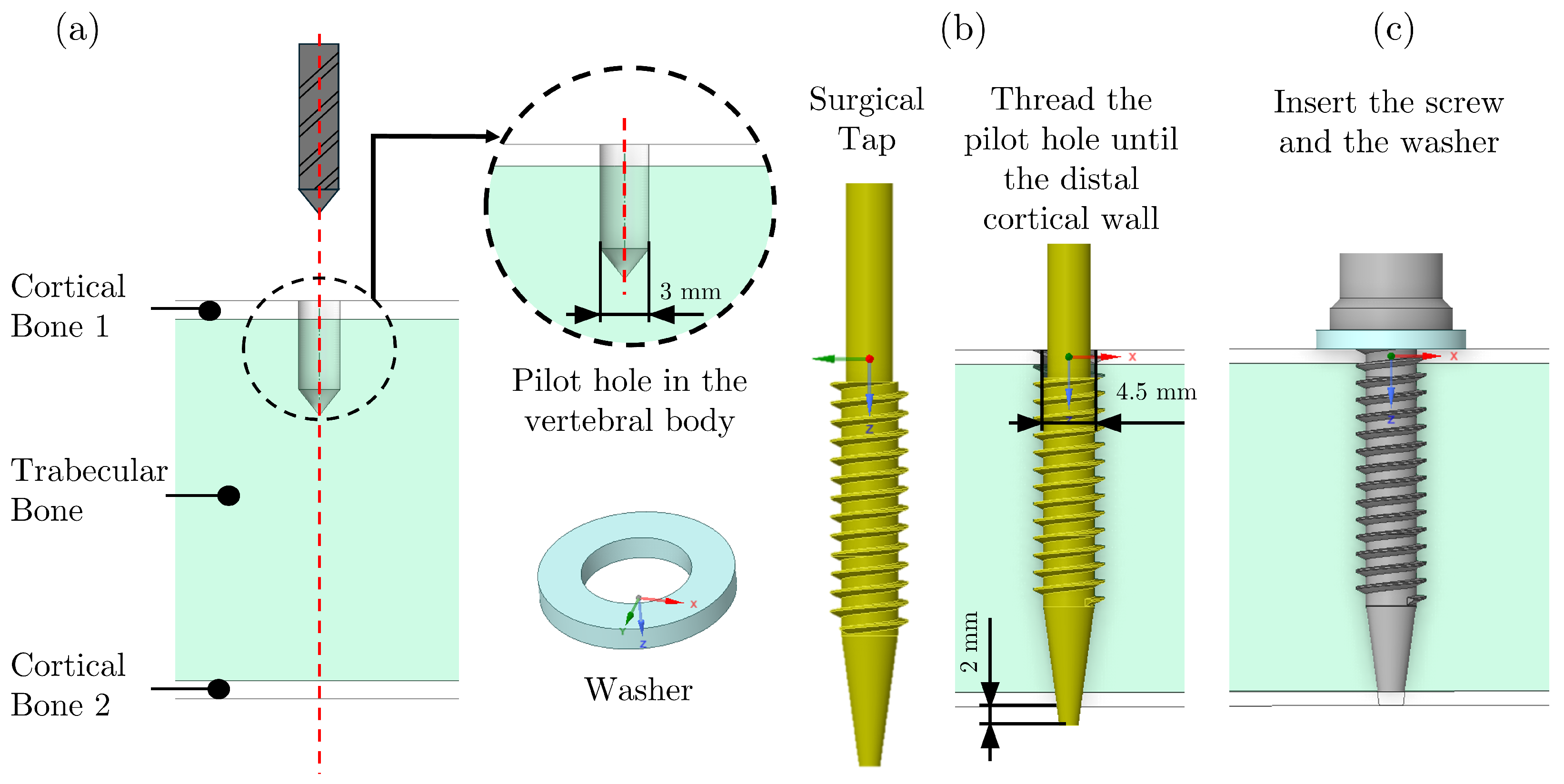
2.1. Sample Preparation

The preparation of all tested samples followed the procedure described in Figure 1. First, a 3 mm pilot hole was drilled in the center of the lateral surface of the porcine thoracic vertebrae, extending deep enough to penetrate the first cortical layer (Figure 1a). Next, a surgical tap with an outer diameter of 4.5 mm and an inner diameter of 3.8 mm was used to thread the pilot hole until reaching the second cortical wall (Figure 1b). To ensure bicortical support, the tip of the tap was extended 2 mm beyond the outer surface of the second cortical layer.
After tapping, the surgical screw and the washer were inserted (Figure 1c), overcoming the required insertion torque. The washer serves a dual purpose: enabling the application of tightening torque between the screw and vertebra and ensuring the correct insertion depth within the vertebral body. The distal cortical interface supports the screw, without any threading. This ensures the screw lateral stability but does not contribute mechanically during pull-out. Figure 2 illustrates the anchorage elements and their nomenclature. Additionally, Table 1 compiles the surgical screw dimensions used for numerical simulation, whereas Table 2 shows the washer dimensions.
Once the screw was fully inserted, the tightening torque was manually applied in a controlled manner using a torque wrench. The tightening process involved progressively increasing the torque until it stabilized. At this point, a final slight rotation of approximately 3 degrees was applied. This method aligns with the usual medical practice during surgery.
If the torque value recorded after this final rotation showed no drop compared to the stabilized value, it was taken as the reference tightening torque for the test. Otherwise, the sample was discarded. A total of five samples were prepared for the pull-out tests following this procedure.

2.2. Pull-Out Test

The experimental evaluation of pull-out strength was performed through a universal testing machine (Instron, Boston, MA, USA), operating under displacement control at 2 mm min − 1 [34,35,36,37,38]. The load measurements were taken via a 5 kN load cell (Class 0.5 according to standard ISO 7500-1 [39]: 1 N resolution, maximum measurement uncertainty lower than 0.5 % of the measured value in 2018), fixed to the actuator through a ball joint. This ensures a purely axial pull-out. The porcine thoracic vertebrae, prepared according to the simulated VBT surgical procedure described in Section 2.1, were fixed to the base as shown in Figure 3b,c.
Figure 3a shows the load–displacement curves for the five samples evaluated (E1–E5), with the points corresponding to the maximum load indicated. Based on these results, an average extraction force F r = 2.1 ± 0.31 kN was obtained. This value was subsequently used as the axial load condition in the finite element analysis (FEA) model, representing the clinical scenario of screw extraction after surgical tightening.
Figure 3c,d illustrate the volume of bone displaced after screw removal, observed at the end of each test. The results indicate that applying surgical torque increases the amount of bone material displaced around the screw threads, suggesting a localized stiffness effect induced by mechanical preloading.

2.3. Geometric Model

The preparation of the FEA model begins with the screw 3D modeling in ANSYS WORKBENCH 2024 R1, following the specifications detailed in the Figure 1. The cortical bone thickness was set to 1.5 mm , consistent with porcine thoracic vertebrae, as determined from the tested samples. The geometry of the surgical screw and washer was also incorporated into the model, with the screw inserted laterally into the thoracic vertebra.
A Boolean operation was performed to remove the bone volume occupied by the screw. It is important to note that the screw head does not rest directly on the cortical bone, which is why the washer is used.
Ideally, the vertebra 3D model would be based on DICOM (Digital Imaging and Communications in Medicine) images of a patient undergoing VBT screw placement, obtained using a CT (computed tomography) scanner. However, the FEA of the geometric model derived from tomographic images presents several challenges. These include the generation of an excessive number of surfaces and singularities, particularly at contact points, leading to prolonged simulation times and potentially incoherent results, such as unrealistically high stresses at specific nodes. For this reason, it was deemed appropriate in this study to simplify the geometric model (Figure 4) to focus on analyzing the effects of tightening torque and pull-out force. The simplified model only represents the threaded length of the screw, forgoing the tip. This is done owing to the fact that the screw tip only serves as a balancing point in the case of transversal loads, and does not produce any effect in the case of pull-out loads.

2.4. Mechanical Properties

This section defines the mechanical properties of the volumes considered in the previous section (surgical screw, washer, porcine cortical bone, and trabecular bone). As supported by other authors in similar studies [1,33,40,41,42,43,44,45,46,47,48,49], both cortical and trabecular bone can be considered isotropic for FEA purposes.
Accordingly, all elements in the model were assumed to exhibit elastic linear and homogeneous behavior, with mechanical properties derived from the referenced literature, as summarized in Table 3.

2.5. Mesh

The geometry of the model and the mechanical properties of the solids were imported into ANSYS WORKBENCH 2024 R1. The meshing of all volumes was performed using SOLID187 10-node quadratic tetrahedrical 3D elements, which are well-suited for meshing irregular geometries, such as the surgical screw [53,54,55,56]. As shown in Table 4, the selected element size varied across geometries. Refinement tests ensured convergence, with stress values within ± 5 % of the finest mesh value. Consequently, stress values remained within this range when further refining the mesh, which implies that a finer mesh does not provide a significant increase in result accuracy.
Using the configuration detailed in Table 4, the meshed geometric model of the simplified anchorage assembly is shown in Figure 5.

2.6. Model Formulation

This subsection will focus on the definition of load cases and boundary conditions for the presented FEA model.

2.6.1. Load Cases

Two load cases were studied in this work: screw tightening and screw pull-out. In the first case, only the tightening torque is applied on the screw, whereas in the second case, both the tightening torque and the extraction load are present.
To model the tightening torque (T), several simplifications are assumed. Simulating the physical process of applying torque and nut rotation is computationally expensive and does not improve result accuracy. Instead, a common practice in FEA modeling is replicating the shortening of the grip length (which induces a preload tension) by splitting the bolt into two sections and applying a preload at both ends [57]. This is known as a bolt pre-tension model.
In bolt pre-tension models, the bolt is represented as a cylinder divided into two halves, and two coinciding nodes (i and j) are selected at the interface of the halves. Constraint equations are then defined to link the relative motion of these nodes. By specifying the force applied ( F t ) to the spring connecting nodes i and j, a tensile load is introduced into both halves of the cylinder, effectively simulating the bolt pre-tension (see Figure 6).
Therefore, the bolt pre-tension condition is applied to the shaft of the surgical screw, as illustrated in Figure 6a. To apply this condition, it is essential to determine the pre-tension load ( F t ) induced by the tightening torque ( T ) , which is related through Equation (1), as described in [57].
F t = T K d 1
where d 1 = 5.4 mm is the screw diameter, and ( K ) is a torque coefficient that can be assumed as 0.2 [2]. The bolt pre-tension condition applies the load ( F t ) (Figure 6b) to simulate the stress state equivalent to applying the tightening torque, allowing this effect to transfer to the surrounding structures. This pre-tension condition shall be applied in a region of the screw that is not in contact with the surrounding structure to accurately model the actual loading condition applied by the fastener. In this case, this location is the screw region surrounded by the steel washer, at 9.35 mm from the screw head. Lastly, this simplification assumes no shear loads may be transferred in the pre-tension region, and requires the small rotation and large deflection formulations to be considered for this model.
This allows slight rotational movement of the surgical screw along its axial direction under tensile loading within the cortical and trabecular bone, offering a more realistic simulation than fixing the tension direction strictly along the thread’s axial axis. For the second load case, this pre-tension stress state is maintained, and a second loading condition is then applied: the axial pull-out force ( F r ) on the screw (see Figure 7).

2.6.2. Boundary Conditions

The configuration of surface contacts between the various bodies can be modeled under two conditions: post-surgical and osseointegration (occurring more than four months after surgery). These conditions dictate how the internal contacts between the vertebral structures and the implant are defined. If the aim is to simulate screw extraction, it is crucial to determine whether the screw has undergone osseointegration. For an osseointegrated screw, a bonded contact type should be used to simulate the screw being adhered to the bone. Conversely, in a post-surgical scenario where osseointegration has not yet occurred, a frictional contact should be applied [58,59]. This post-surgical scenario is the object of study in the present work.
For the surface contacts between the threads of the titanium screw and its housing in the cortical bone, a coefficient of friction of 0.12 was applied [58]. This value was extracted from previous studies regarding bone–screw interaction. The reported experimental values range between 0.1 and 0.3, depending on bone quality, surface finish, and testing conditions. In this range, a value of 0.12, close to the lower bound of 0.1, provides a worst-case scenario of shear load transfer. Additionally, in this FEA, the mechanical behavior of the screw is not generally considered, other than its elasticity properties. Thus, the present study focuses on stress distribution and vertebral bone failure scenarios.
However, for the contacts between the steel washer and the external surface of the cortical bone, as well as the screw threads and the trabecular bone, a frictionless contact was implemented. This type of contact is characterized by the absence of tangential forces, allowing the surfaces to slide over each other without resistance. This aligns with the bolt pre-tension model previously outlined, which implied no shear loads may be transferred between the screw threads and the trabecular bone. In the normal direction, the surfaces can separate but cannot penetrate each other. In the case of the contact between the washer and the cortical bone, this approach is particularly useful, as it may simulate well-lubricated interfaces where friction can be neglected [60]. In this clinical scenario, the lubricant is blood, making this condition a realistic approximation of actual surgical conditions.
As for the cortical–trabecular bone interface, the surface contact between these structures is defined as bonded, as these layers do not separate. The outer fixed constraint should be positioned sufficiently far from the screw’s insertion site—approximately 11 times the screw’s outer diameter—to define a fixed boundary condition and facilitate numerical calculations. The defined contact conditions are illustrated in Figure 7.
The described FEM model provides von Mises stress values in the vertebral system. These values may be used as a qualitative indicator for stress concentration analyses, and location of possible anchoring failure regions.

3. Results and Discussion

Given the availability of experimental pull-out tests, this section provides simulation results which focus on reproducing their equivalent experimental tests. This reproduction is performed under the same loading conditions, aiming to provide a comparison of general trends between experimental tests and simulations. This analysis is not an absolute quantitative validation, but a coherence check between simulation and experimental failure modes. The experimental tightening torque values of the five samples (E1–E5) were used, with a mean value of 5.9 ± 0.80 Nm. Substituting this value in Equation (1), the obtained pre-tension load was F t = 546.3 N . For pull-out load, an average value of F r = 2.1 ± 0.31 kN , was considered, as commented in the Methodology section.
Additionally, specimen-specific simulations (E1–E5) were performed using the experimentally recorded tightening torque for each case. The graphical simulations presented in the following figures correspond to the mean torque condition, followed by the application of the mean axial pull-out load. Table 5 summarizes the maximum von Mises stresses in cortical and trabecular bone under two scenarios: (i) tightening torque only (green columns), where stresses remained below the critical ranges reported in the literature, and (ii) tightening torque combined with pull-out load (red columns), where cortical stresses exceeded the fracture thresholds of bone tissue. These simulations were not restricted to the mean torque value but encompassed the full experimental range observed across the five specimens (5.2–7.0 Nm), thereby providing a parametric analysis of bone response. This approach supports the consistency of the model and strengthens the interpretation of stress evolution under progressive loading conditions.

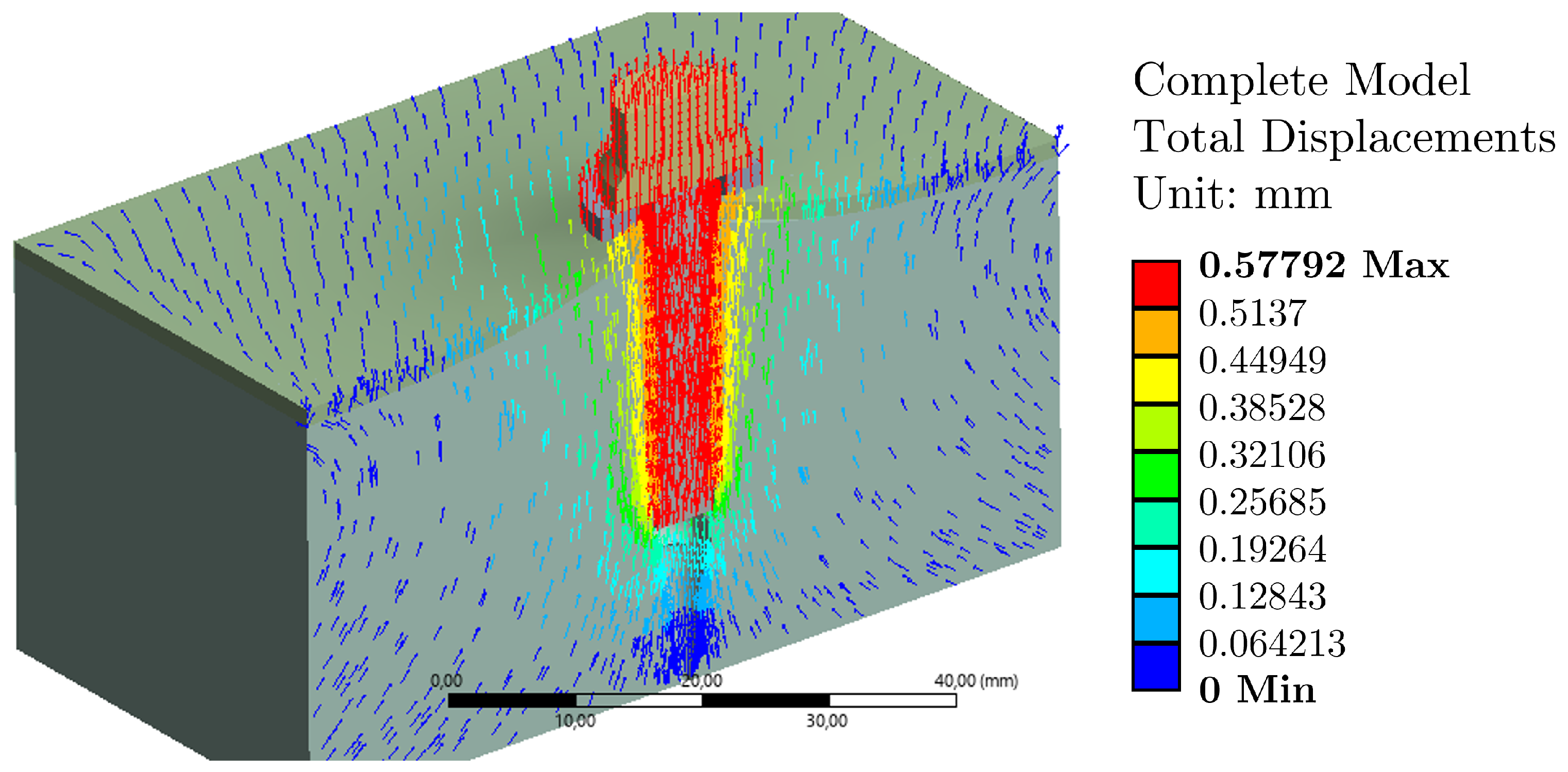
3.1. Load Case 1: Effect of Tightening Torque

The stress distribution generated by ( F t ) was analysed separately for the trabecular and cortical bones. This stress distribution arises primarily from the compression exerted by the screw threads on the bone structures. Under this load, the bone–screw interface’s rigidity is enhanced, reducing the likelihood of loosening under static and dynamic loads.
Figure 8 shows the von Mises stress distribution in the trabecular bone resulting from the tightening torque. The stress concentration is homogeneously scattered throughout the threads, with the maximum value reached in the last thread. This is the expected behavior of the trabecular bone under a tightening torque, as the screw pulls the trabecular bone threading against the cortical bone on the left-hand side.
The maximum stress reached was 2.1 ± 0.13 MPa, which lies below the strength range of 5–15 MPa shown in Table 3. Therefore, under the applied tightening torque, trabecular bone exhibited stress levels well below the reported failure threshold, indicating that this loading condition does not critically compromise the trabecular structure.
Figure 9 shows the stress values in cortical bone 1 (screw head side, left-hand side), as well as cortical bone 2 (screw tip side, right-hand side). The screw preload induces von Mises stresses only in the screw head side cortical layer, as it is the layer which supports the trabecular bone preload. This stress value reaches a maximum of 16.1 ± 0.86 MPa, which is well below the cortical bone strengths reported in Table 3. Cortical bone 2, on the other hand, does not contribute to the preload stage. This aligns with the notions of surgical and experimental procedure, as the screw tip should not perform any function for tightening or pull-out purposes.
As a last remark for von Mises stress distributions for the tightening torque load case, Figure 10 shows the stress values across the entire model. The maximum stress value is located in the screw thread, and reaches a value of 58.7 ± 0.16 MPa. This is the expected behavior for the anchorage, where the load is mainly withstood by the stiffest element (i.e., the titanium screw). The complete stress diagram also shows that the stress is mainly distributed in the vertebra across the first cortical bone layer, in the region close to the steel washer. This result does not inform about the trabecular bone fibers reorientation due to the effect of tightening the screw. This will be shown in Section 3.2, where displacements are discussed.

3.2. Load Case 2: Plus Tightening Torque/Effect of Pull-Out Load

The primary purpose of the pull-out load simulation is to assess stress distribution in the vertebral bone under the combined effect of tightening torque and axial extraction load. Figure 11 presents the von Mises stresses in trabecular bone after applying the experimental pull-out load. The maximum value reached was 19.7 ± 0.23 MPa, exceeding the 5–15 MPa range reported in the literature for trabecular bone strength.
Since the von Mises criterion is not fully appropriate for evaluating bone failure, these results must be interpreted with caution. Nevertheless, they suggest that under combined loading, the trabecular region is subjected to stresses that may exceed physiological limits, consistent with experimental observations of screw loosening and failure.
This may be explained by the reorientation of trabecular bone fibers caused by tightening. This is further validated in Figure 12 and Figure 13, where this reorientation is seen by means of material displacements in the trabecular bone.
In Figure 12, a conic shape can be observed, indicating a reorganization of trabecular fibers, from the end of the trabecular threading towards the steel washer. This reorganization causes an increase of bone stiffness [29]. This conic shape aligns with the pull-out behavior observed in the experimental campaign, where the volume displaced by the screw during extraction is greater than the threading bounding cylinder. Additionally, Figure 12 and Figure 13 exhibit a maximum displacement value of 0.58 mm .
This result shows good agreement with the experimental findings when vertebral settling within the testing device is considered. The model reproduces the stress distribution patterns associated with the applied pull-out load, highlighting the trabecular region as the critical site under this condition. The simulation also indicates that the highest stress concentrations occur at the last trabecular thread crests, where the bone has not been sufficiently compacted by the previously applied tightening torque and is therefore more susceptible to subsequent extraction forces.
Regarding cortical bone 1, applying the tightening torque and extraction load, the stress levels are observed in the Figure 14. The maximum stress obtained in cortical bone ( 141.1 ± 0.7 MPa) exceeded the upper limit of the ranges reported in the literature (80–120 MPa). This difference is explained by the local stress concentration generated at the interface between the washer and the cortical surface, resulting from the combined effect of the applied surgical torque and the axial pull-out load, which induces an additional increase in local stresses compared to the average values observed under pure pull-out conditions. Furthermore, the reference values reported in previous studies correspond to experimental scenarios involving pure screw extraction [26], without systems incorporating washers and torque-induced pretension, and therefore represent a lower threshold for tissue damage. Consequently, the results of this study provide a more comprehensive representation of the biomechanical behavior of the anchorage under realistic surgical conditions. As in the case of the trabecular bone, the pre-tension increases the internal stiffness of the bone sections, making it significantly more difficult to detach the structures during the pull-out load. This effect was not accounted for in previous studies. The reference loads from the literature are based on purely axial extraction without considering additional effects, such as those introduced by pre-tension and other factors analyzed in this study.
Overall, the model suggests that pull-out failure is initiated by the collapse of the trabecular threads, after which the cortical layer alone cannot withstand the stresses induced by screw extraction. This outcome corresponds to the expected clinical scenario and is consistent with the experimental observations. It should be noted, however, that this conclusion is based on von Mises stress distributions, which, in this study, are used as a qualitative indicator of stress concentration rather than a direct failure criterion for brittle materials such as bone. This approach can be utilized for clinical exploration under varying boundary conditions that may lead to vertebral failure, enabling further investigations and optimizations.

3.3. Limitations of the Model and Future Prospects

One limitation of this study is the use of an isotropic, linear model to represent bone tissue, which does not fully capture its heterogeneity or post-elastic behavior. Although this simplification is commonly adopted in finite element analyses to reduce computational complexity [58], it may significantly affect stress magnitudes, particularly in trabecular regions, where heterogeneous tissue properties have been shown to influence local stress concentrations and failure patterns [61].
Consequently, the absolute stress values reported here should be interpreted with caution, as they may be underestimated compared with more realistic orthotropic models. Nevertheless, previous studies have validated this approach for analyses primarily aimed at stress distribution and the initial mechanical behavior of fixation systems [57,58,62].
In addition, this simplification improves computational stability, especially in simulations involving complex contact with threaded geometries. Incorporating heterogeneous models derived from bone density maps could enhance accuracy, particularly for evaluating bone damage progression or implant loosening risk. This line of research is proposed for future work.

4. Conclusions

This study presents an experimental campaign to determine the pull-out force in porcine thoracic vertebrae using the VBT technique. Although the experimental methodology provides information on the load capacity of the screw–bone interface, these tests have limitations in quantifying damage when applying surgical torque to the ultimate failure strength and they do not reflect the internal distribution of stresses. To overcome these limitations and gain a deeper understanding of the behavior of the anchorage, a simplified and homogeneous finite element model based on a 3D geometric representation of the screw–vertebra system is developed. The model matches the experimental torque and pull-out conditions and enables effective application of finite element analysis. In this simplified model, the mechanical behavior of the surgical screw was not explicitly represented, as the primary aim was to analyze the bone–screw interaction and no screw failure was found in the experimental campaign.
When applying to the model only the average tightening torque of the experimental campaign (5.9 ± 0.80 Nm), the analyses confirmed that stresses in trabecular and cortical bone remained below the ranges reported in the literature. After imposing the mean experimental pull-out force (2.1 ± 0.31 kN) to that tightening torque, the model identified peak stress intensities in cortical and trabecular bone which approached or exceeded values reported in the literature and could be interpreted as qualitative indicators of failure.
Under the application of the average surgical torque ( 5.9 ± 0.8 Nm), the vertebral body did not exhibit critical stress levels, suggesting mechanically safe behavior within the torque range commonly used in clinical practice. However, when the axial pull-out load ( 2.1 ± 0.31 kN) was applied to the pre-tensioned model, maximum stresses reached up to 141 MPa, exceeding the reported cortical strength limit (80–120 MPa). This condition represents a state of localized failure induced by the combined effect of torque and axial loading, which should not be considered mechanically safe. Therefore, the study distinguishes between a safe pre-tension regime (torque only) and a critical combined regime, in which stresses surpass the material limits. This finding is clinically relevant for establishing more precise and safer surgical torque thresholds during vertebral anchorage.
However, several important limitations of this work have to be taken into consideration. First, the authors believe that understanding the behavior of the surgical screw becomes relevant due to variations in parameters such as diameter, pitch, length, and material, as stated by previous studies [32,33,34,35,63]. Furthermore, the experimental campaign demonstrated that the use of large-dimension screws can trigger vertebral failure due to the substantial volume inserted. Such failures may originate from factors like bone porosity, existing pathologies, and the patient’s age [58,64], and may be mitigated by previously simulating the surgical scenario.
A second limitation is that the cortical layer was explicitly dimensioned based on the experimental study. Measurements of the cortical thickness in the porcine samples were taken, yielding an average value. While this thickness could influence the final results, the stress values obtained correlate well with those reported in the literature. Additionally, it is computationally feasible to identify the point of structural failure by parameterizing the thickness of the cortical walls, providing further insight into their role in biomechanical behavior.
In addition, the mechanical properties of the porcine specimen were sourced from various finite element studies. The wide range of values considered poses a limitation that must be accounted for when representing different stress states. Replacing the numerical methodology in this study with the mechanical properties of human thoracic vertebrae could provide a correlation coefficient, demonstrating the relevance and applicability of the simulation method to both specimens. This would enhance the study’s relevance and broaden its scope for clinical applications.
It is important to emphasize that von Mises stress was used in this study, but solely as a qualitative indicator of stress intensity, and not as an absolute failure criterion for brittle tissues such as bone. This consideration defines the scope of the conclusions and ensures that the findings are interpreted in terms of relative stress distributions and comparative trends, rather than as absolute predictions of strength.

Author Contributions

F.P.M.-M.: Conceptualization, Data Curation, Methodology, Resources, and Writing—Original Draft. R.C.: Formal Analysis, Investigation, and Validation. Á.G.-B.: Software, Visualization, Writing—Original Draft, and Writing—Review and Editing. P.B.T.-J.: Data Curation and Validation. E.C.-T.: Conceptualization, Project Administration, Supervision, and Writing—Review and Editing. All authors have read and agreed to the published version of the manuscript.

Funding

There are no financial conflicts of interest to disclose.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Acknowledgments

The authors would like to thank the Mechanical Engineering Department, ETSI Industriales, Universidad Politécnica de Madrid, for their support throughout the development of this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Ames, R.J.; Samdani, A.F.; Betz, R.R. Anterior scoliosis correction in immature patients with idiopathic scoliosis. Oper. Tech. Orthop. 2016, 26, 247–257. [Google Scholar] [CrossRef]
  2. Driscoll, M.; Aubin, C.E.; Moreau, A.; Parent, S. Biomechanical comparison of fusionless growth modulation corrective techniques in pediatric scoliosis. Med. Biol. Eng. Comput. 2011, 49, 1437–1445. [Google Scholar] [CrossRef] [PubMed]
  3. Cunin, V. Early-onset scoliosis–current treatment. Orthop. Traumatol. Surg. Res. 2015, 101, S109–S118. [Google Scholar] [CrossRef] [PubMed]
  4. Fairhurst, H.; Little, J.P.; Adam, C.J. Intra-operative measurement of applied forces during anterior scoliosis correction. Clin. Biomech. 2016, 40, 68–73. [Google Scholar] [CrossRef] [PubMed]
  5. Gould, S.L.; Cristofolini, L.; Davico, G.; Viceconti, M. Computational modelling of the scoliotic spine: A literature review. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3503. [Google Scholar] [CrossRef]
  6. Cobetto, N.; Parent, S.; Aubin, C.E. 3D correction over 2 years with anterior vertebral body growth modulation: A finite element analysis of screw positioning, cable tensioning and postoperative functional activities. Clin. Biomech. 2018, 51, 26–33. [Google Scholar] [CrossRef]
  7. Yaszay, B.; Doan, J.D.; Parvaresh, K.C.; Farnsworth, C.L. Risk of Implant Loosening after Cyclic Loading of Fusion-less Growth Modulation Techniques: Nitinol Staples vs Flexible Tether. Spine 2017, 42, 443–449. [Google Scholar] [CrossRef]
  8. Brink, R.C.; Schlösser, T.P.; van Stralen, M.; Vincken, K.L.; Kruyt, M.C.; Hui, S.C.; Viergever, M.A.; Chu, W.C.; Cheng, J.C.; Castelein, R.M. Anterior-posterior length discrepancy of the spinal column in adolescent idiopathic scoliosis—A 3D CT study. Spine J. 2018, 18, 2259–2265. [Google Scholar] [CrossRef]
  9. Helenius, I.; Remes, V.; Yrjönen, T.; Ylikoski, M.; Schlenzka, D.; Helenius, M.; Poussa, M. Harrington and Cotrel-Dubousset instrumentation in adolescent idiopathic scoliosis: Long-term functional and radiographic outcomes. J. Bone Joint Surg. Am. 2003, 85, 2303–2309. [Google Scholar] [CrossRef]
  10. Helenius, L.; Diarbakerli, E.; Grauers, A.; Lastikka, M.; Oksanen, H.; Pajulo, O.; Löyttyniemi, E.; Manner, T.; Gerdhem, P.; Helenius, I. Back pain and quality of life after surgical treatment for adolescent idiopathic scoliosis at 5-year follow-up: Comparison with healthy controls and patients with untreated idiopathic scoliosis. J. Bone Jt. Surg. Am. 2019, 101, 1460–1466. [Google Scholar] [CrossRef]
  11. Marks, M.C.; Bastrom, T.P.; Petcharaporn, M.; Shah, S.A.; Betz, R.R.; Samdani, A.; Lonner, B.; Miyanji, F.; Newton, P.O. The effect of time and fusion length on motion of the unfused lumbar segments in adolescent idiopathic scoliosis. Spine Deform. 2015, 3, 549–553. [Google Scholar] [CrossRef] [PubMed]
  12. Parsch, D.; Gaertner, V.; Brocai, D.; Carstens, C. The effect of spinal fusion on the long-term outcome of idiopathic scoliosis: A case-control study. J. Bone Surg. Brit. 2001, 83, 1133–1136. [Google Scholar] [CrossRef]
  13. Keenan, B.E.; Izatt, M.T.; Askin, G.N.; Labrom, R.D.; Pettet, G.J.; Pearcy, M.J.; Adam, C.J. Segmental torso masses in adolescent idiopathic scoliosis. Clin Biomech. 2014, 29, 773–779. [Google Scholar] [CrossRef]
  14. Moncayo-Matute, F.P.; Vázquez-Albornoz, J.H.; Vázquez-Silva, E.; Hidalgo-Bravo, A.J.; Torres-Jara, P.B.; Moya-Loaiza, D.P. 3D Printing and Virtual Surgical Planning in Craniofacial and Thoracic Surgery: Applications to Personalised Medicine. J. Pers. Med. 2025, 15, 397. [Google Scholar] [CrossRef]
  15. Vázquez-Silva, E.; Bohorquez-Vivas, D.; Peña-Tapia, P.; Moncayo-Matute, F.; Torres-Jara, P.; Moya-Loaiza, D. Oculopalpebral prosthesis prototype design using the additive manufacturing technique: A case study. JPRAS Open 2024, 39, 228–236. [Google Scholar] [CrossRef]
  16. Moncayo-Matute, F.P.; Peña-Tapia, P.G.; Vázquez-Silva, E.; Torres-Jara, P.B.; Moya-Loaiza, D.P.; Abad-Farfán, G.; Andrade-Galarza, A.F. Surgical planning and finite element analysis for the neurocraneal protection in cranioplasty with PMMA: A case study. Heliyon 2022, 8, e10706. [Google Scholar] [CrossRef]
  17. Desroches, G.; Aubin, C.E.; Sucato, D.J.; Rivard, C.H. Simulation of an anterior spine instrumentation in adolescent idiopathic scoliosis using a flexible multi-body model. Med. Biol. Eng. Comput. 2007, 45, 759–768. [Google Scholar] [CrossRef]
  18. Wall, E.J.; Jain, V.V.; Crawford, A.H.; Bylski-Austrow, D.I.; Reynolds, J.E. Spine growth modulation in early adolescent idiopathic scoliosis: Prospective US FDA IDE pilot study of titanium clip-screw implant at two to five years. Spine Deform. 2019, 7, 899–909. [Google Scholar] [CrossRef] [PubMed]
  19. Hamad, A.; Ahmed, E.B.; Tsirikos, A.I. Adolescent idiopathic scoliosis: A comprehensive approach to aetiology, diagnostic assessment and treatment. Orthop. Trauma 2017, 31, 343–349. [Google Scholar] [CrossRef]
  20. Cobetto, N.; Aubin, C.E.; Parent, S. Surgical planning and follow-up of anterior vertebral body growth modulation in pediatric idiopathic scoliosis using a patient-specific finite element model integrating growth modulation. Spine Deform. 2018, 6, 344–350. [Google Scholar] [CrossRef]
  21. Burwell, R.G.; Dangerfield, P.H.; Moulton, A.; Grivas, T.B. Adolescent idiopathic scoliosis (AIS), environment, exposome and epigenetics: A molecular perspective of postnatal normal spinal growth and the etiopathogenesis of AIS with consideration of a network approach and possible implications for medical therapy. Scoliosis 2011, 6, 26. [Google Scholar] [CrossRef]
  22. Fogel, G.R.; Parikh, R.D.; Ryu, S.I.; Turner, A.W. Biomechanics of lateral lumbar interbody fusion constructs with lateral and posterior plate fixation. J. Neurosurg. Spine 2014, 20, 291–297. [Google Scholar] [CrossRef]
  23. Cappuccino, A.; Cornwall, G.B.; Turner, A.W.; Fogel, G.R.; Duong, H.T.; Kim, K.D.; Brodke, D.S. Biomechanical analysis and review of lateral lumbar fusion constructs. Spine 2010, 35, S361–S367. [Google Scholar] [CrossRef]
  24. Nicolini, L.F.; Beckmann, A.; Laubach, M.; Hildebrand, F.; Kobbe, P.; de Mello Roesler, C.R.; Fancello, E.A.; Markert, B.; Stoffel, M. An experimental-numerical method for the calibration of finite element models of the lumbar spine. Med. Eng. Phys. 2022, 107, 103854. [Google Scholar] [CrossRef]
  25. Jung, R.E.; Pjetursson, B.E.; Glauser, R.; Zembic, A.; Zwahlen, M.; Lang, N.P. A systematic review of the 5-year survival and complication rates of implant-supported single crowns. Clin. Oral Implants Res. 2008, 19, 119–130. [Google Scholar] [CrossRef]
  26. Cleek, T.M.; Reynolds, K.J.; Hearn, T.C. Effect of screw torque level on cortical bone pullout strength. J. Orthop. Trauma 2007, 21, 117–123. [Google Scholar] [CrossRef]
  27. Krishnan, V.; Varghese, V.; Kumar, G.S. Comparative analysis of effect of density, insertion angle and reinsertion on pull-out strength of single and two pedicle screw constructs using synthetic bone model. Asian Spine J. 2016, 10, 414. [Google Scholar] [CrossRef] [PubMed]
  28. Hsieh, M.K.; Lee, D.M.; Li, Y.D.; Peng, C.C.; Tsai, T.T.; Lai, P.L.; Chen, W.P.; Tai, C.L. Biomechanical evaluation of position and bicortical fixation of anterior lateral vertebral screws in a porcine model. Sci. Rep. 2023, 13, 454. [Google Scholar] [CrossRef] [PubMed]
  29. Geng, J.P.; Tan, K.B.; Liu, G.R. Application of finite element analysis in implant dentistry: A review of the literature. J. Prosthet. Dent. 2001, 85, 585–598. [Google Scholar] [CrossRef] [PubMed]
  30. Vázquez-Silva, E.; Abad-Farfán, G.; Pena-Tapia, P.G.; Torres-Jara, P.B.; Moncayo-Matute, F.P.; Viloria-Avila, T.J.; Vergara-Paredes, M.J. Composites and hybrid materials used for implants and bone reconstruction: A state of the art. Contemp. Eng. Sci. 2022, 15, 105–135. [Google Scholar] [CrossRef]
  31. Moncayo-Matute, F.P.; Pena-Tapia, P.G.; Vázquez-Silva, E.; Torres-Jara, P.B.; Abad-Farfán, G.; Moya-Loaiza, D.P.; Andrade-Galarza, A.F. Description and application of a comprehensive methodology for custom implant design and surgical planning. Interdiscip. Neurosurg. 2022, 29, 101585. [Google Scholar] [CrossRef]
  32. Singh, H.; Sonkesriya, S.; Patel, B.J.; Rathod, V.; Gupta, B.; Vyas, T.; Sawhney, A.; Makkad, R.S. Implant abutment using hand drivers versus torque wrench. Bioinformation 2023, 19, 221. [Google Scholar] [CrossRef] [PubMed]
  33. Song, C.H.; Park, J.S.; Choi, B.W.; Lee, J.S.; Lee, C.S. Computational investigation for biomechanical characteristics of lumbar spine with various porous Ti–6Al–4V implant systems. Appl. Sci. 2021, 11, 8023. [Google Scholar] [CrossRef]
  34. Le Cann, S.; Cachon, T.; Viguier, E.; Miladi, L.; Odent, T.; Rossi, J.M.; Chabrand, P. Pedicle screw fixation study in immature porcine spines to improve pullout resistance during animal testing. PLoS ONE 2015, 10, e0127463. [Google Scholar] [CrossRef]
  35. Conrad, B.P.; Cordista, A.G.; Horodyski, M.; Rechtine, G.R. Biomechanical evaluation of the pullout strength of cervical screws. Clin. Spine Surg. 2005, 18, 506–510. [Google Scholar] [CrossRef]
  36. Abad-Coronel, C.; Bravo, M.; Tello, S.; Cornejo, E.; Paredes, Y.; Paltan, C.A.; Fajardo, J.I. Fracture Resistance Comparative Analysis of Milled-Derived vs. 3D-Printed CAD/CAM Materials for Single-Unit Restorations. Polymers 2023, 15, 3773. [Google Scholar] [CrossRef]
  37. Vázquez-Silva, E.; Pintado-Pintado, J.A.; Moncayo-Matute, F.P.; Torres-Jara, P.B.; Moya-Loaiza, D.P. Effect of Infill Density on the Mechanical Properties of Natural Peek Processed by Additive Manufacturing. Polymers 2025, 17, 347. [Google Scholar] [CrossRef]
  38. Matute, F.P.M.; Alonso, R.C.C.; Terán, J.V.B.; Tanarro, E.C. Influencia del Par de Apriete en las Cargas Axiales de Extracción de Tornillos Quirúrgicos de Cuerpos Vertebrales en Técnicas Vbt. In Proceedings of the XVI Congreso Iberoamericano de Ingeniería Mecánica (CIBIM 2024), Concepción, Chile, 22–24 October 2024. [Google Scholar]
  39. UNE-EN ISO 7500-1:2018; Metallic Materials—Calibration and Verification of Static Uniaxial Testing Machines—Part 1: Tension/Compression Testing Machines—Calibration and Verification of the Force-Measuring System. International Organization for Standardization: Geneva, Switzerland, 2018.
  40. Moncayo-Matute, F.P.; Vázquez-Silva, E.; Peña-Tapia, P.G.; Torres-Jara, P.B.; Moya-Loaiza, D.P.; Viloria-Ávila, T.J. Finite Element Analysis of Patient-Specific 3D-Printed Cranial Implant Manufactured with PMMA and PEEK: A Mechanical Comparative Study. Polymers 2023, 15, 3620. [Google Scholar] [CrossRef]
  41. Balladares, A.O.; Abad-Coronel, C.; Ramos, J.C.; Fajardo, J.I.; Paltán, C.A.; Martín Biedma, B.J. Comparative Study of the Influence of Heat Treatment on Fracture Resistance of Different Ceramic Materials Used for CAD/CAM Systems. Materials 2024, 17, 1246. [Google Scholar] [CrossRef] [PubMed]
  42. Mejía Rodríguez, M.; González-Estrada, O.A.; Villegas-Bermúdez, D.F. Finite Element Analysis of Patient-Specific Cranial Implants under Different Design Parameters for Material Selection. Designs 2024, 8, 31. [Google Scholar] [CrossRef]
  43. Moncayo-Matute, F.; Vázquez-Silva, E.; Torres-Jara, P.; Peña-Tapia, P.; Moya-Loayza, D.; Abad-Farán, G. Mechanical analysis for personalized implant for neurocranial protection manufactured with Polymethylmethacrylate. J. Phys. Conf. Ser. 2023, 2516, 012005. [Google Scholar] [CrossRef]
  44. Torres-Jara, P.; Vázquez-Silva, E.; Moncayo-Matute, F.; Peña-Tapia, P.; Moya-Loayza, D.; Abad-Farán, G. Application of a comprehensive methodology for the development of personalized bone implants: Exemplification through three cases. J. Phys. Conf. Ser. 2023, 2516, 012004. [Google Scholar] [CrossRef]
  45. Bermejillo Barrera, M.D.; Franco-Martínez, F.; Díaz Lantada, A. Artificial Intelligence Aided Design of Tissue Engineering Scaffolds Employing Virtual Tomography and 3D Convolutional Neural Networks. Materials 2021, 14, 5278. [Google Scholar] [CrossRef]
  46. Cobos, C.M.; Ferrandiz, S.; Garzón, L.; López, J.; Rayon, E. Exploring the mechanical response of PLA/MWCNT and PLA/HNT composites obtained by additive manufacturing. Rapid Prototyp. J. 2025, 31, 179–188. [Google Scholar] [CrossRef]
  47. Abad-Coronel, C.; Córdova, J.; Merchán, A.; Larriva, J.; Bravo, A.; Bernal, B.; Paltán, C.A.; Fajardo, J.I. Comparative Analysis of the Fracture Resistance of a Polymeric Material for 3D Printing and a Milled Polymethylmethacrylate Material as Interim Material for Fixed Partial Dentures: New Material Updated. Designs 2023, 7, 118. [Google Scholar] [CrossRef]
  48. Abad-Coronel, C.; Freire Bonilla, C.; Vidal, S.; Rosero, F.; Encalada Abad, C.; Mena Córdova, N.; Paltán, C.A.; Fajardo, J.I.; Aliaga, P. Evaluating a Novel 3D-Printed Resin for Dental Restorations: Fracture Resistance of Restorations Fabricated by Digital Press Stereolithography. Polymers 2025, 17, 2322. [Google Scholar] [CrossRef]
  49. Abad-Coronel, C.; Calle, C.; Abril, G.; Paltán, C.A.; Fajardo, J.I. Fracture Resistance Analysis of CAD/CAM Interim Fixed Prosthodontic Materials: PMMA, Graphene, Acetal Resin and Polysulfone. Polymers 2023, 15, 1761. [Google Scholar] [CrossRef]
  50. Kocis, J.; Navrat, T.; Florian, Z.; Wendsche, P. Biomechanical testing of spinal segment fixed by thoracolumbar spine locking plate on the swine lumbar spine. Biomed. Pap. Med. Fac. Univ. Palacky Olomouc Czech Repub. 2010, 154, 345–354. [Google Scholar] [CrossRef]
  51. Lv, Q.B.; Gao, X.; Pan, X.X.; Jin, H.M.; Lou, X.T.; Li, S.M.; Yan, Y.Z.; Wu, C.C.; Lin, Y.; Ni, W.F.; et al. Biomechanical properties of novel transpedicular transdiscal screw fixation with interbody arthrodesis technique in lumbar spine: A finite element study. J. Orthop. Transl. 2018, 15, 50–58. [Google Scholar] [CrossRef]
  52. Zanetti, E.M.; Salaorno, M.; Grasso, G.; Audenino, A.L. Parametric analysis of orthopedic screws in relation to bone density. Open Med. Inform. J. 2009, 3, 19. [Google Scholar] [CrossRef]
  53. Carson, W.L.; Duffield, R.C.; Arendt, M.; Ridgely, B.J.; Gaines, R.W., Jr. Internal forces and moments in transpedicular spine instrumentation the effect of pedicle screw angle and transfixation—The 4R-4Bar linkage concept. Spine 1990, 15, 893–901. [Google Scholar] [CrossRef]
  54. Fan, W.; Guo, L.X.; Zhao, D. Stress analysis of the implants in transforaminal lumbar interbody fusion under static and vibration loadings: A comparison between pedicle screw fixation system with rigid and flexible rods. J. Mater. Sci. Mater. Med. 2019, 30, 118. [Google Scholar] [CrossRef]
  55. Moncayo-Matute, F.P.; Gerardo Peña-Tapia, P.; Vázquez-Silva, E.; Torres-Jara, P.B.; Patricia Moya-Loaiza, D.; Abad-Farfán, G. Surgical planning for the removal of cranial espheno-orbitary meningioma through the use of personalized polymeric prototypes obtained with an additive manufacturing technique. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Online, 20–21 July 2023; pp. 1–7. [Google Scholar]
  56. Torres-Jara, P.B.; Bohorquez Vivas, D.D.; Moya-Loaiza, D.P.; Peña-Tapia, P.G. Análisis de Elementos Finitos de un Implante Personalizado a Base de PMMA/PEEK: Acople Con el Hueso Craneal y Sistema de Anclaje; Universidad de Concepción: Concepción, Chile, 2024. [Google Scholar]
  57. Burguete, R.L.; Johns, R.B.; King, T.; Patterson, E.A. Tightening characteristics for screwed joints in osseointegrated dental implants. J. Prosthet. Dent. 1994, 71, 592–599. [Google Scholar] [CrossRef]
  58. Chen, S.I.; Lin, R.M.; Chang, C.H. Biomechanical investigation of pedicle screw–vertebrae complex: A finite element approach using bonded and contact interface conditions. Med. Eng. Phys. 2003, 25, 275–282. [Google Scholar] [CrossRef]
  59. Moncayo-Matute, F.P.; Torres-Jara, P.B.; Vázquez-Silva, E.; Peña-Tapia, P.G.; Moya-Loaiza, D.P.; Abad-Farfán, G. Finite element analysis of a customized implant in PMMA coupled with the cranial bone. J. Mech. Behav. Biomed. Mater. 2023, 146, 106046. [Google Scholar] [CrossRef] [PubMed]
  60. Straumal, B.; Gornakova, A.; Kiselevskiy, M.; Anisimova, N.Y.; Nekrasov, A.; Kilmametov, A.; Strug, R.; Rabkin, E. Optimal surface roughness of Ti6Al4V alloy for the adhesion of cells with osteogenic potential. J. Mater. Res. 2022, 37, 2661–2674. [Google Scholar] [CrossRef]
  61. Harrison, N.M.; McDonnell, P.F.; O’Mahoney, D.C.; Kennedy, O.D.; O’Brien, F.J.; McHugh, P.E. Heterogeneous linear elastic trabecular bone modelling using micro-CT attenuation data and experimentally measured heterogeneous tissue properties. J. Biomech. 2008, 41, 2589–2596. [Google Scholar] [CrossRef] [PubMed]
  62. Andreucci, C.A.; Fonseca, E.M.; Jorge, R.N. Bio-lubricant properties analysis of drilling an innovative design of bioactive kinetic screw into bone. Designs 2023, 7, 21. [Google Scholar] [CrossRef]
  63. Solórzano-Requejo, W.; Martinez Cendrero, A.; Altun, A.A.; Nohut, S.; Ojeda, C.; Garcia Molleja, J.; Molina-Aldareguia, J.; Schwentenwein, M.; Diaz Lantada, A. Topology optimisation and lithography-based ceramic manufacturing of short-stem hip prostheses with enhanced biomechanical and mechanobiological performance. Virtual Phys. Prototyp. 2024, 19, e2387280. [Google Scholar] [CrossRef]
  64. Bonney, H.; Colston, B.; Goodman, A. Regional variation in the mechanical properties of cortical bone from the porcine femur. Med. Eng. Phys. 2011, 33, 513–520. [Google Scholar] [CrossRef]
Applsci 15 11074 g001
Figure 1. Anchoring procedure. (a) Pilot hole to guide the tap. (b) Bone threading. (c) Screw tightening.
Figure 1. Anchoring procedure. (a) Pilot hole to guide the tap. (b) Bone threading. (c) Screw tightening.
Applsci 15 11074 g001
Applsci 15 11074 g002
Figure 2. Anchoring elements and geometric nomenclature. (a) Surgical Ti-6Al-4V screw. (b) Thread profile with main geometric parameters. (c) A36 steel washer with geometric parameters.
Figure 2. Anchoring elements and geometric nomenclature. (a) Surgical Ti-6Al-4V screw. (b) Thread profile with main geometric parameters. (c) A36 steel washer with geometric parameters.
Applsci 15 11074 g002
Applsci 15 11074 g003
Figure 3. Results of the pull-out test: (a) Experimental pull-out load (kN)–displacement (mm) results. (b) Lateral positioning of the screw within the vertebra. (c) Screw extraction, showing bone debris adhered to the screw threads. (d) Vertebral cross-section and evacuated volume following the test (sample E1).
Figure 3. Results of the pull-out test: (a) Experimental pull-out load (kN)–displacement (mm) results. (b) Lateral positioning of the screw within the vertebra. (c) Screw extraction, showing bone debris adhered to the screw threads. (d) Vertebral cross-section and evacuated volume following the test (sample E1).
Applsci 15 11074 g003
Applsci 15 11074 g004
Figure 4. Finite element analysis, simplified model performed in the ANSYS SpaceClaim module. The study volume dimensions are 75 mm × 75 mm × 37.5 mm, including two 1.5 mm thick cortical bone layers and a trabecular bone core.
Figure 4. Finite element analysis, simplified model performed in the ANSYS SpaceClaim module. The study volume dimensions are 75 mm × 75 mm × 37.5 mm, including two 1.5 mm thick cortical bone layers and a trabecular bone core.
Applsci 15 11074 g004
Applsci 15 11074 g005
Figure 5. Anchorage system and vertebral model mesh. (a) Isometric view of the steel washer, cortical bones 1 and 2, trabecular bone, and threaded hole. (b) Cross-section of the previous view. (c) Detail of the screw head, locating the steel washer and cortical bone 1. (d) Screw geometry and mesh.
Figure 5. Anchorage system and vertebral model mesh. (a) Isometric view of the steel washer, cortical bones 1 and 2, trabecular bone, and threaded hole. (b) Cross-section of the previous view. (c) Detail of the screw head, locating the steel washer and cortical bone 1. (d) Screw geometry and mesh.
Applsci 15 11074 g005
Applsci 15 11074 g006
Figure 6. Bolt pre-tension model. (a) Numerical modeling of the bolt pre-tension. (b) Detail of the screw pre-tension.
Figure 6. Bolt pre-tension model. (a) Numerical modeling of the bolt pre-tension. (b) Detail of the screw pre-tension.
Applsci 15 11074 g006
Applsci 15 11074 g007
Figure 7. Vertebral system boundary conditions, front view of the screw pull-out (legend on the right-hand side of the figure). Of note, the pre-tension location is indicated with a white cross sign.
Figure 7. Vertebral system boundary conditions, front view of the screw pull-out (legend on the right-hand side of the figure). Of note, the pre-tension location is indicated with a white cross sign.
Applsci 15 11074 g007
Applsci 15 11074 g008
Figure 8. Stress distribution in trabecular bone; cross-sectional view of the threaded area.
Figure 8. Stress distribution in trabecular bone; cross-sectional view of the threaded area.
Applsci 15 11074 g008
Applsci 15 11074 g009
Figure 9. Stress distribution in the external cortical walls due to tightening torque.
Figure 9. Stress distribution in the external cortical walls due to tightening torque.
Applsci 15 11074 g009
Applsci 15 11074 g010
Figure 10. Stress distribution throughout the model.
Figure 10. Stress distribution throughout the model.
Applsci 15 11074 g010
Applsci 15 11074 g011
Figure 11. Stress distribution in the trabecular bone due to the effect of a tightening torque and an extraction load. The purple areas indicate regions where the trabecular bone stress becomes greater than 5 MPa, indicating failure.
Figure 11. Stress distribution in the trabecular bone due to the effect of a tightening torque and an extraction load. The purple areas indicate regions where the trabecular bone stress becomes greater than 5 MPa, indicating failure.
Applsci 15 11074 g011
Applsci 15 11074 g012
Figure 12. Displacement distribution in the trabecular bone due to effect of a tightening torque and an extraction load.
Figure 12. Displacement distribution in the trabecular bone due to effect of a tightening torque and an extraction load.
Applsci 15 11074 g012
Applsci 15 11074 g013
Figure 13. Displacement distribution across the model.
Figure 13. Displacement distribution across the model.
Applsci 15 11074 g013
Applsci 15 11074 g014
Figure 14. Stress distribution in the cortical bones due to tightening torque and an extraction load.
Figure 14. Stress distribution in the cortical bones due to tightening torque and an extraction load.
Applsci 15 11074 g014
Table 1. Surgical screw dimensions.
Table 1. Surgical screw dimensions.
d 1 (mm) d 2 (mm) a 1 (°) a 2 (°) r 1 (mm) r 2 (mm)s (mm)p (mm)L (mm)
5.46.565251.20.80.21.837.5
Table 2. Washer dimensions.
Table 2. Washer dimensions.
Washer
d e (mm) d i (mm)e (mm)
6.55.45
Table 3. Model elements’ mechanical properties.
Table 3. Model elements’ mechanical properties.
StructuresMechanical
Strength (MPa)		Young’s
Modulus (MPa)		Poisson
Ratio		References
Porcine Cortical Bone80–12013,5000.3[9,50,51,52]
Porcine Trabecular Bone5–152000.2[28,32,51,52]
Washer (Structural Steel—A36)400–450210,0000.3[8]
Surgical Screw (Ti-6Al-4V)895107,0000.3[8]
Table 4. Element mesh properties.
Table 4. Element mesh properties.
StructureSize (mm)Number of NodesNumber of Elements
Cortical Bone0.582,65055,474
Trabecular Bone0.183,85877,985
Surgical Screw0.378,55649,481
Round Washer0.179,75838,958
Table 5. Internal verification: specimen-specific loading conditions and von Mises stresses under two cases.
Table 5. Internal verification: specimen-specific loading conditions and von Mises stresses under two cases.
SpecimenExp. Torque (Nm)Exp. Pull-Out (kN)von Mises Cortical (MPa)von Mises Trabecular (MPa)von Mises Cortical (MPa)von Mises Cortical (MPa)
Tightening onlyTightening onlyTightening + pull-outTightening + pull-out
E17.02.3614.242.17141.5619.77
E25.21.7816.122.05141.6019.27
E36.51.8316.952.02140.2319.90
E45.41.9916.572.13140.8020.09
E55.42.5716.612.11141.3219.74
Mean ± SD5.90 ± 0.802.1 ± 0.3116.1 ± 0.862.1 ± 0.13141.1 ± 0.7019.7 ± 0.23
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Moncayo-Matute, F.P.; Claramunt, R.; Guzmán-Bautista, Á.; Torres-Jara, P.B.; Chacón-Tanarro, E. Effect of Surgical Tightening Torque on the Pull-Out Strength of Screws in Vertebral Body Tethering. Appl. Sci. 2025, 15, 11074. https://doi.org/10.3390/app152011074

AMA Style

Moncayo-Matute FP, Claramunt R, Guzmán-Bautista Á, Torres-Jara PB, Chacón-Tanarro E. Effect of Surgical Tightening Torque on the Pull-Out Strength of Screws in Vertebral Body Tethering. Applied Sciences. 2025; 15(20):11074. https://doi.org/10.3390/app152011074

Chicago/Turabian Style

Moncayo-Matute, Freddy Patricio, Rafael Claramunt, Álvaro Guzmán-Bautista, Paúl Bolívar Torres-Jara, and Enrique Chacón-Tanarro. 2025. "Effect of Surgical Tightening Torque on the Pull-Out Strength of Screws in Vertebral Body Tethering" Applied Sciences 15, no. 20: 11074. https://doi.org/10.3390/app152011074

APA Style

Moncayo-Matute, F. P., Claramunt, R., Guzmán-Bautista, Á., Torres-Jara, P. B., & Chacón-Tanarro, E. (2025). Effect of Surgical Tightening Torque on the Pull-Out Strength of Screws in Vertebral Body Tethering. Applied Sciences, 15(20), 11074. https://doi.org/10.3390/app152011074

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop