On Stability Analysis of Car-Following Models with Various Discrete Operators

Abstract

This paper investigates a car-following model that incorporates both classical and fractional discrete operators. While classical models have been extensively studied, the influence of discrete fractional operators on the stability of such systems has not yet been systematically analyzed. Stability conditions are derived and rigorously proven for systems employing three widely used fractional h-difference operators—Grünwald–Letnikov, Riemann–Liouville, and Caputo—as well as the classical h-difference operator. The analysis reveals that the established conditions are independent of the specific operator used. Furthermore, a comprehensive numerical study validates the theoretical findings and demonstrates that the fractional models can significantly extend the stability bound for the step size from $h<6.67$ (classical case) to $h<22.3$ (fractional case).

1. Introduction

The car-following model (CFM) describes how a driver adjusts position and speed to follow the vehicle ahead in the same lane [1,2,3]. The concept of CFM originated in 1933 with the work of Greenshields [4,5], who was the first to experimentally investigate traffic flow, density, and speed using photographic measurement techniques. At that time, the term “flow” was not yet established; Greenshields instead referred to “density-vehicles per hour” or “second-kind density.” He proposed a linear relationship between vehicle speed and traffic density. Early research on highway capacity followed two primary approaches: analyzing the speed–density relationship and examining vehicle spacing at high traffic densities. Greenshields’ findings laid the foundation for the development of multi-regime models [6]. Since then, various strategies have emerged to address traffic flow challenges. One prominent approach is the platoon model [7,8,9], where the behavior of vehicles resembles that of a train, with a leading vehicle controlling the motion of the following ones [10]. Another approach is Adaptive Cruise Control (ACC), which enables individual vehicles to autonomously address traffic flow issues. Among these, bilateral control models (BCMs) [11,12,13,14,15,16] stand out, aiming to maintain a vehicle equidistant from both the vehicle ahead and the one behind. Another line of recent research focuses not on individual vehicle behavior, but on optimizing shared mobility systems as a whole. For example, studies on electric vehicle car-sharing platforms explore how scalable infrastructure and dynamic pricing policies can significantly improve system performance, highlighting the role of global design strategies—such as fleet sizing, charger placement, and pricing rules—in enhancing both user satisfaction and economic viability [17,18].

These developments have motivated us to propose a generalized CFM by incorporating fractional operators, offering a novel perspective grounded in fractional calculus, an area of applied mathematics. The integration of fractional operators into CFMs introduces deeper insights into vehicle dynamics. There are several key motivations for this approach. First, memory effects. Classical CFMs often assume instantaneous reactions to changes in the leading vehicle’s behavior. In reality, drivers respond based on past experiences. Fractional calculus captures these memory effects by accounting for the history of vehicle interactions. The next one is that fractional derivatives inherently model non-local behavior, acknowledging that a driver’s reaction depends not only on the current state of the leading vehicle but also on its past behavior. This enhances the model’s realism and improves its ability to capture complex traffic dynamics. Driver behavior also depends on psychology, experience, and anticipation. Fractional calculus provides tools to model these variations, improving the robustness and applicability of CFMs. In summary, applying fractional operators to car-following models offers a more realistic and nuanced representation of traffic dynamics by incorporating memory effects, non-local interactions, and human behavioral complexity. For a comprehensive overview of this field, the reader is referred to [19,20,21,22,23,24,25,26,27].

Previous studies on fractional-order car-following models have primarily considered continuous-time formulations. For instance, Ref. [28] introduced a fractional variant of the classical Pipe’s model, and Ref. [29] proposed a fractional Optimal Velocity Model (FOOV) to incorporate driver memory effects. Later, Ref. [30] extended fractional calculus to macroscopic traffic flow models through local fractional PDEs. More recently, Ref. [31] introduced a fractional-order car-following model with random delay, optimized via an enhanced whale optimization algorithm, further demonstrating the potential of Caputo-based fractional models to enhance stability and robustness under uncertain driving conditions. These works, however, were limited to continuous fractional derivatives, focused on specific operator definitions, and offered only numerical demonstrations of stability rather than general proofs.

In contrast, the present paper is, to the best of our knowledge, the first to conduct a rigorous stability analysis of discrete-time car-following systems involving multiple fractional h-difference operators—namely the Grünwald–Letnikov, Riemann–Liouville, and Caputo operators—alongside the classical discrete operator. The study provides analytically proven sufficient conditions for asymptotic stability that are shown to be independent of the chosen operator, thereby unifying previously fragmented approaches to discrete fractional dynamics. Moreover, by introducing an arbitrary discrete step size h, the authors generalize existing results to encompass digital or sampled implementations, a feature absent in earlier continuous formulations.

Moreover, it is worth noting that fractional-order controllers have been successfully applied to Adaptive Cruise Control (ACC) and cooperative ACC (CACC) systems, demonstrating improved string stability and robustness in vehicle platoons [32,33]. In particular, the Grünwald–Letnikov fractional PID (GL-PID) has been shown to outperform classical PID controllers by delivering smoother acceleration/deceleration profiles and better disturbance rejection in realistic driving scenarios [34]. These results reinforce the potential of discrete fractional models like ours to be deployed in automated vehicle control frameworks and intelligent transportation systems.

Our numerical experiments demonstrate that the proposed fractional-order discrete models significantly extend the stability region compared with the classical model (e.g., from h $<6.7$ in the integer case to $h<22.3$ for $\alpha$ = 0.5), and that among the fractional formulations, the Caputo operator yields the most physically realistic vehicle responses. Such a comparative evaluation of multiple discrete fractional operators within a car-following context has not been reported previously. We explore the application of Grünwald–Letnikov, Riemann–Liouville, and Caputo fractional h-difference operators to classical CFMs. Our goal is to determine whether these modifications enhance model stability. Specifically, we assess whether stability can be achieved in cases where the classical model is unstable, and whether fractional operators accelerate convergence in cases where the classical model is already stable.

The key contributions of this paper that advances the literature are summarized as follows:

• use of fractional operators to capture memory effects and non-local interactions;
• derivation of system stability conditions involving the three principal fractional-order operators: Grünwald–Letnikov, Riemann–Liouville, and Caputo, together with the classical case;
• incorporation of models with an arbitrary step size h, aligning more closely with real-world applications;
• establishing rigorous, operator-independent stability criteria for fractional discrete CFMs;
• integrating three fractional operator definitions in a unified discrete framework;
• demonstrating, both analytically and numerically, the superior stability and implementation potential of fractional-order discrete models—particularly those based on the Caputo operator—over classical integer-order formulations.

The paper is structured as follows. The symbols used are listed in

Table 1. List of symbols and abbreviations used in the paper.

Symbol/Abbreviation	Description
${\mathbb{N}}_0=N\cup \left\{0\right\}$	Set of non-negative integers
$h\mathbb{N}=\{h,2h,3h,\dots \}$	Discrete-time grid with step size $h>0$
$R_{+}$	Set of positive real numbers
$\mathrm{Spec}\left(A\right)=\{\lambda :det(A-\lambda I)=0\}$	Spectrum of matrix A (set of its eigenvalues)
${\Delta }_h$	Forward h-difference operator
${\Delta }_h^{\alpha }$	Fractional h-difference operator of order $\alpha$
${}^{G}L\Delta _h^{\alpha }$	Grünwald–Letnikov fractional h-difference operator
${}^{R}L\Delta _h^{\alpha }$	Riemann–Liouville fractional h-difference operator
${}^C\Delta _h^{\alpha }$	Caputo fractional h-difference operator
$k_d,k_v$	Position and velocity feedback gains
s	Desired inter-vehicle (safe) distance
h	Discretization step size
$\alpha$	Fractional-order parameter ($0<\alpha \le 1$)
$Y_i\left(k\right)={(x_i\left(k\right),v_i\left(k\right))}^T$	State vector of the i-th vehicle

. In the Section 2, we introduce the necessary definitions and foundational results. Section 3 presents the proposed model and our main theoretical findings. In particular, we provide theorems establishing sufficient conditions for the asymptotic stability of CFMs with fractional operators Grünwald–Letnikov, Riemann–Liouville, and Caputo, together with the classical operator—equivalent to the stability of the original systems. Additionally, in the last section, we provide extensive simulations that demonstrate the impact of fractional operators on system behavior, covering both stable and unstable classical model scenarios. These examples not only validate our theoretical findings but also enable a comparative analysis of the operators’ effects.

To highlight the contribution of this work in the context of existing research,

Table 2. Comparative summary of selected related works and identified research gaps.

Reference	Model/System	Operator/Order	Main Focus	Limitation/Gap
[1,2,4]	Classical macroscopic or empirical traffic relations	Integer-order (continuous)	Foundational modeling of flow–density relations	No fractional or discrete dynamics; limited microscopic interpretation
[7,8]	Vehicle platoon/control systems	Integer-order (continuous)	Optimal control and error regulation for vehicle strings	Continuous models only; no fractional extensions
[10,11,12,13]	Mixed or bilateral car-following models	Integer-order	Stability and eigenvalue analysis in bilateral/mixed traffic	No discrete fractional operators; no operator comparison
[20,21,22,23]	General fractional systems theory	Fractional calculus (continuous/discrete)	Mathematical framework and stability of fractional systems	No car-following applications; mainly theoretical results
[35,36]	Discrete fractional linear systems	Caputo/Riemann–Liouville-type	Stability of discrete fractional systems	Not applied to car-following; single-operator focus
[24,25,37]	Consensus and flocking models	Fractional (Caputo, Grünwald–Letnikov)	Behavior and numerical analysis of fractional systems	No comparative study among operators; not focused on CFMs
[28,29]	Fractional car-following models	Fractional (Caputo/continuous)	Simulation and demonstration of memory effects	Continuous-time analysis only; lacks discrete framework
[30]	Macroscopic traffic models (LWR type)	Local fractional PDEs	Computational fractional analysis of traffic flow	Macroscopic scale; not applicable to microscopic CFM stability
[31]	Fractional car-following with random delays	Caputo (continuous)	Optimization and improved robustness under delay	Operator-specific; lacks unified discrete stability conditions
This work	Discrete car-following model (microscopic)	Grünwald–Letnikov, Riemann–Liouville, Caputo, classical	Unified discrete stability analysis; operator-independent sufficient conditions; extensive numerical validation	Fills the gap by providing theoretical and numerical comparison of three discrete fractional operators; links results to ACC/CAV applications

summarizes several representative studies on car-following and fractional-order models, indicating their main focus and the research gaps addressed by the present paper.

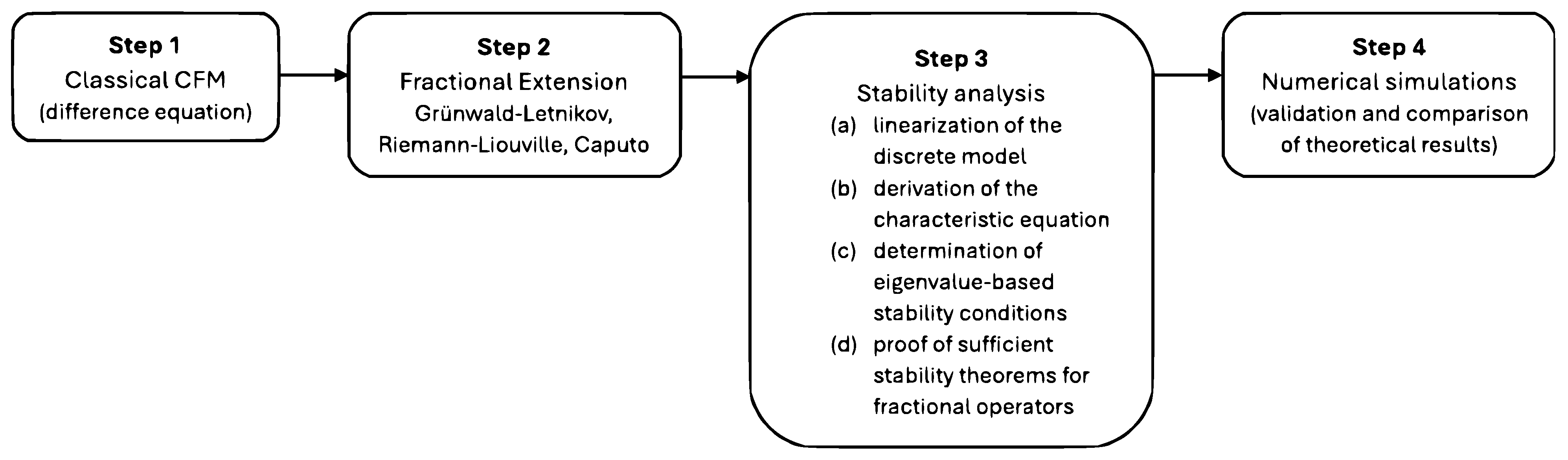
For the convenience of the reader we present a diagram summarizing the methodological workflow used in the article (see Figure 1).

2. Preliminaries

Let $\alpha >0$. We define the following sequence:

$$a^{\left(\alpha \right)}\left(k\right):=\left\{\begin{array}{ccc}1\hfill & \mathrm{f}\mathrm{o}\mathrm{r}& k=0\\ {(-1)}^k{\displaystyle \frac{\alpha (\alpha -1)\dots (\alpha -k+1)}{k!}}\hfill & \mathrm{f}\mathrm{o}\mathrm{r}& k\in \mathbb{N}.\end{array}\right.$$

(1)

Note that $a^{\left(\alpha \right)}\left(k\right)$ can also be defined in the recurrence way by the following:

$$\begin{array}{c}{a}^{\left(\alpha \right)}\left(0\right):=1,\hfill \\ a^{\left(\alpha \right)}\left(k+1\right):=\left(1-{\displaystyle \frac{\alpha +1}{k+1}}\right)a^{\left(\alpha \right)}\left(k\right),k\in {\mathbb{N}}_0.\hfill \end{array}$$

(2)

Definition 1

([35]). Let $h>0$. For a function $x:{\left(h\mathbb{N}\right)}_0\to \mathbb{R}$ the forward h-difference operator is defined as

$$\left({\Delta }_{h}x\right)\left(kh\right):={\displaystyle \frac{x\left(\right(k+1\left)h\right)-x\left(kh\right)}{h}}.$$

(3)

Let $q\in \mathbb{N}$ and ${\Delta }_h^q:=\underset{qtimes}{\underbrace{{\Delta }_h\circ \dots \circ {\Delta }_h}}$ be q-fold application of operator ${\Delta }_h$, i.e.,

$${\Delta }_h^{q}x=\underset{qtimes}{\underbrace{{\Delta }_h\left({\Delta }_h\left(\dots {\Delta }_{h}x\right)\right)}}$$

and we write $\left({\Delta }_h^{0}x\right)\left(kh\right):=x\left(kh\right)$.

Using the sequence (2) one can define the following difference operator.

Definition 2

([35]). For a function $x:{\left(h\mathbb{N}\right)}_0\to \mathbb{R}$ the fractional h-sum of order $\alpha >0$ is given by

$$\left({\Delta }_h^{-\alpha }x\right)\left(kh\right):=h^{\alpha }\sum _{i=0}^k{a}^{(-\alpha )}(k-i)x\left(ih\right),$$

(4)

where $k\in {\mathbb{N}}_0.$

Henceforth, we confine our analysis to the case $\alpha \in (0,1]$.

Definition 3

([35]). Let $\alpha \in (0,1]$. The Grünwald–Letnikov fractional h-difference operator ${}^{GL}\Delta _h^{\alpha }$ of order α for a function $x:{\left(h\mathbb{N}\right)}_0\to \mathbb{R}$ is defined by

$$\left({}^{GL}\Delta _h^{\alpha }x\right)\left(kh\right):=h^{-\alpha }\sum _{i=0}^k{a}^{\left(\alpha \right)}\left(i\right)x\left((k-i)h\right),$$

(5)

where ${\left(a^{\left(\alpha \right)}\left(i\right)\right)}_{i\in {\mathbb{N}}_0}$ is the sequence given by (2) or equivalently, by (1).

Observe that, for $\alpha =0$ and $h=1$ we have $\left({}^{GL}\Delta _h^{\alpha }x\right)\left(k\right)=x\left(k\right)$ and for $\alpha =1$ we get $\left({}^{GL}\Delta _h^{\alpha }x\right)\left(k\right):=x\left(k\right)-x(k-1)$.

Definition 4

([35]). Let $\alpha \in (0,1]$. The Riemann–Liouville fractional h-difference operator ${}^{RL}\Delta _h^{\alpha }$ of order α for a function $x:{\left(h\mathbb{N}\right)}_0\to \mathbb{R}$ is defined by

$$\left({}^{RL}\Delta _h^{\alpha }x\right)\left(kh\right):=\left({\Delta }_h\left({\Delta }_h^{\alpha -1}x\right)\right)\left(kh\right).$$

(6)

Remark 1

(cf. [35]). The Riemann–Liouville and Grünwald–Letnikov fractional h-difference operators are equivalent.

Definition 5

([35]). Let $\alpha \in (0,1]$. The Caputo fractional h-difference operator ${}^C\Delta _h^{\alpha }$ of order α for a function $x:{\left(h\mathbb{N}\right)}_0\to \mathbb{R}$ is defined by

$$\left({}^C\Delta _h^{\alpha }x\right)\left(kh\right):=\left({\Delta }_h^{\alpha -1}\left({\Delta }_{h}x\right)\right)\left(kh\right).$$

(7)

Let us consider linear system with Riemann–Liouville fractional h-difference operator

$$\left({}^{RL}\Delta _h^{\alpha }x\right)\left(kh\right)=Ax\left(kh\right),$$

(8)

where $A\in {\mathbb{R}}^{n\times n}$.

Remark 2

(cf. [37]). For the scalar system $A=\lambda <0$ and $\alpha \in (0,1]$ we have, it is asymptotically stable if and only if $\left|\lambda \right|<{\left({\displaystyle \frac{2}{h}}\right)}^{\alpha }$.

Remark 3

([37]). There is a possibility to have asymptotic stability if $\lambda =0\in Spec\left(A\right)$, when zero eigenvalue is singular.

Now let us consider a linear system with the Caputo fractional h-difference operator.

$$\left({}^C\Delta _h^{\alpha }x\right)\left(kh\right)=Ax\left(kh\right),$$

(9)

where $A\in {\mathbb{R}}^{n\times n}$.

Proposition 1

(cf. [35]). Systems (8) or (9), with $\alpha \in (0,1]$ are asymptotically stable if and only if both conditions are satisfied

1. 

There is $k\in {\mathbb{N}}_0$ such that

$$arg{\lambda }_i\in [a,b],$$

where $a=2\pi$frac$\left\{\alpha (k+{\displaystyle \frac{1}{4}})\right\}$, $b=2\pi (1-$frac$\left\{\alpha ({\displaystyle \frac{1}{4}}-k)\right\})$ and $\mathrm{frac}\left\{x\right\}:=x-\lfloor x\rfloor$.

2. 

For all $i=1,\dots ,n$ and $k,s\in \mathbb{Z}$

$$|{\lambda }_i|<{\left({\displaystyle \frac{2}{h}}\left|sin{\displaystyle \frac{arg{\lambda }_i-\alpha \frac{\pi }{2}-2(\beta k+s)\pi }{2-\alpha }}\right|\right)}^{\alpha },i=1,\dots ,n,$$

where $arg{\lambda }_i$ and $|{\lambda }_i|$ are, respectively, the main argument and modulus of ${\lambda }_i\in Spec\left(A\right)$.

Remark 4

(cf. [36]). Let $\lambda \in \mathbb{R}$. Then system (9) takes the following form

$${}^C\Delta _h^{\alpha }\left(kh\right)=\lambda x\left(kh\right),$$

(10)

where $\alpha \in (0,1]$. If

$$-{\left({\displaystyle \frac{2}{h}}\right)}^{\alpha }<\lambda <0.$$

then Equation (10) is asymptotically stable.

3. Car-Following Model

We start our investigation with the classical continuous-time framework, and consider n autonomous vehicles in a car-following system, where i-th vehicle follows the $(i-1)$-th vehicle. The dynamics of the system are considered by modeling the position of the i-th vehicle at time t as $x_i\left(t\right)$, with its velocity defined as $v_i\left(t\right)={\dot{x}}_i\left(t\right)$. The pair $\{x_i\left(t\right),v_i\left(t\right)\}$ defines the full state of vehicle i. The vehicle’s behavior is modulated through its acceleration ${\dot{v}}_i\left(t\right)={\ddot{x}}_i\left(t\right)$, which is determined by a control mechanism. In the context of the car-following model, the acceleration is modeled as follows:

$${\dot{v}}_i=k_d(x_{i-1}-x_i-s)+k_v(v_{i-1}-v_i),$$

(11)

where s represents the desired inter-vehicle spacing, commonly referred to as the safe distance. The parameters $k_d>0$ and $k_v>0$ are control gains associated with position and velocity feedback, respectively. This formulation implies that each vehicle adjusts its motion based solely on the relative distance and relative speed to the vehicle immediately ahead. In ideal conditions, all vehicles maintain the safe distance s from one another and travel at a constant speed $v_0$. In such a configuration, the system is at equilibrium, with all accelerations ${\dot{v}}_i$ equal to zero.

One can consider a discrete-time system, accordingly, based on a discretized formulation of the dynamics. Then Equation (11) gets the form

$${\Delta }_h{v}_i\left(k\right)=k_d(x_{i-1}\left(k\right)-x_i\left(k\right)-s)+k_v(v_{i-1}\left(k\right)-v_i\left(k\right)),$$

(12)

where ${\Delta }_h$ is h-difference operator, ${\Delta }_h{v}_i\left(k\right):={\displaystyle \frac{v_i(k+h)-v_i\left(k\right)}{h}}$.

Further, assuming that the velocity of the first, leading car remains constant, the system of dynamics for the first vehicle can be written as

$$\left\{\begin{array}{c}{x}_1(k+h)=x_1\left(k\right)+h{v}_1\left(k\right)\hfill \\ v_1(k+h)=v_1\left(k\right)\hfill \end{array}\right.$$

while that for the rest of the vehicles is as follows:

$$\left\{\begin{array}{cc}{x}_i(k+h)=x_i\left(k\right)+h{v}_i\left(k\right)\hfill & \\ v_i(k+h)=k_{d}h(x_{i-1}\left(k\right)-x_i\left(k\right)-s)+k_{v}h(v_{i-1}\left(k\right)-v_i\left(k\right))+v_i\left(k\right)\hfill & \mathrm{f}\mathrm{o}\mathrm{r} i=2,\dots ,n.\hfill \end{array}\right.$$

Then the pair $\{x_i\left(k\right),v_i\left(k\right)\}$ is the state of the i-th car, where $x_i\left(k\right)$ is the position of i-th car and $v_i\left(k\right)$ is its velocity at the moment k. For $Y_i\left(k\right)=\left(\begin{array}{c}{x}_i\left(k\right)\\ v_i\left(k\right)\end{array}\right)$, let $Y\left(k\right)={(Y_1\left(k\right),\dots ,Y_n\left(k\right))}^T$ be the state vector containing the states of all cars in the traffic system at the moment k. Subsequently, a linear system of the general form is considered:

$$\left({\Delta }_{h}Y\right)\left(k\right)=AY\left(k\right),$$

(13)

where $k_d>0$ is the proportional gain, $k_v>0$ is the derivative gain, $h>0$ is the step size, $k\in {\mathbb{N}}_0$, and

$$A=\left(\begin{array}{ccccccc}0& 1& 0& 0& \dots & 0& 0\\ 0& 0& 0& 0& \dots & 0& 0\\ 0& 0& 0& 1& \dots & 0& 0\\ k_d& k_v& -k_d& -k_v& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \dots & 0& 0& 0& 1\\ 0& 0& \dots & k_d& k_v& -k_d& -k_v\end{array}\right)\in {\mathbb{R}}^{2n\times 2n}.$$

(14)

Observe that the second row of matrix A is composed entirely of zeros. This arises from the fact that we assume that the velocity of the first, leading vehicle remains constant, i.e., $v_1(k+h)=v_1\left(k\right)$, for all moments of k. Consequently, the acceleration of the leading vehicle is zero, reflecting the absence of any change in its velocity.

Next, system (13) can then be written in discrete matrix form as follows:

$$Y(k+h)=(I+hA)Y\left(k\right),$$

(15)

where matrix A is given by (14).

3.1. Car-Following Model with Fractional h-Difference Operators

In this section, our investigation centers on three of the most well-known fractional operators: Grünwald–Letnikov, Riemann–Liouville, and Caputo. We examine the stability of the system and derive sufficient conditions under which stability is guaranteed. For this purpose, let us discretize the model given by (11) using fractional h-difference operators. We consider a linear system in the following general form:

$$\left({\Delta }_h^{\alpha }Y\right)\left(kh\right)=AY\left(kh\right),$$

(16)

where ${\Delta }_h^{\alpha }$ is the Grünwald–Letnikov ${}^{GL}\Delta _h^{\alpha }$, Caputo ${}^C\Delta _h^{\alpha }$, or Riemann–Liouville ${}^{RL}\Delta _h^{\alpha }$ fractional h-difference operator, $k_d>0$ is the proportional gain, $k_v>0$ is the derivative gain, $h>0$ is the step size, $\alpha \in (0,1],k\in {\mathbb{N}}_0$, and matrix A is given by (14).

To investigate the stability problem of system (16), let us consider the transformation of this system as follows:

$$\left\{\begin{array}{c}{\overline{x}}_{i-1}=x_i-x_1,\hfill \\ {\overline{v}}_{i-1}=v_i-v_1,i=2,\dots ,n.\hfill \end{array}\right.$$

(17)

Then, system (16) can be written as

$$\left({\Delta }_h^{\alpha }\overline{Y}\right)\left(kh\right)=\overline{A}\overline{Y}\left(kh\right),$$

(18)

where $\overline{Y}={({\overline{Y}}_1,\dots ,{\overline{Y}}_{n-1})}^T,{\overline{Y}}_i\left(k\right)=\left(\begin{array}{c}{\overline{x}}_i\left(k\right)\\ {\overline{v}}_i\left(k\right)\end{array}\right),i=1,\dots ,n-1$ and

(19)

Observe that the discrete form of system (18) with Riemann–Liouville fractional h-difference operator is the following:

$${\displaystyle \overline{Y}\left((k+1)h\right)=(h^{\alpha }\overline{A}+\alpha I)\overline{Y}\left(kh\right)-\sum _{i=2}^{k+1}{a}^{\left(\alpha \right)}\left(i\right)\overline{Y}\left((k-i+1)h\right)}$$

(20)

and with Caputo fractional h-difference operator it is

$$\overline{Y}\left(kh\right)=(I+h^{\alpha }\overline{A})\overline{Y}\left((k-1)h\right)-\sum _{i=1}^{k-1}{a}^{(\alpha -1)}(k-i)\left(\overline{Y}\left(ih\right)-\overline{Y}\left((i-1)h\right)\right).$$

(21)

Lemma 1.

For matrix $\overline{A}$ defined by (19) it holds

$$Spec\left(\overline{A}\right)=\left\{\underset{(n-1)-\mathit{times}}{\underbrace{{\displaystyle \frac{-k_v-\sqrt{k_v^2-4k_d}}{2}}}},\underset{(n-1)-\mathit{times}}{\underbrace{{\displaystyle \frac{-k_v+\sqrt{k_v^2-4k_d}}{2}}}}\right\}.$$

Proof. 

Let us observe that matrix $\overline{A}$ is a lower triangular block matrix. Using this fact, one gets

Thus

$Spec\left(\overline{A}\right)=\left\{\underset{(n-1)-\mathrm{times}}{{\displaystyle \underbrace{\frac{-k_v-\sqrt{k_v^2-4k_d}}{2}}}},\underset{(n-1)-\mathrm{times}}{{\displaystyle \underbrace{\frac{-k_v+\sqrt{k_v^2-4k_d}}{2}}}}\right\}.$□

Subsequently, we can provide the sufficient condition for the stability of system (18).

Theorem 1.

Let us consider system (18). If one of the following assumptions holds as follows:

1. 

$k_v^2\ge 4k_d$, $-{\displaystyle \frac{2^{\alpha +1}}{h^{\alpha }}}<-k_v\pm \sqrt{k_v^2-4k_d}<0$ for $k_v,k_d,h>0,\alpha \in (0,1]$,

2. 

$k_v^2<4k_d$, $k_d<{\left({\displaystyle \frac{2}{h}}\left|sin{\displaystyle \frac{arg\lambda -\alpha \frac{\pi }{2}}{2-\alpha }}\right|\right)}^{2\alpha }$ for $\lambda \in Spec\left(\overline{A}\right),k_v,k_d,h>0,\alpha \in (0,1]$,

then system (18) is asymptotically stable.

Proof. 

First, let us consider the case when $k_v^2\ge 4k_d$. Along with the assumption $-{\displaystyle \frac{2^{\alpha +1}}{h^{\alpha }}}<-k_v\pm \sqrt{k_v^2-4k_d}<0$, one gets $-{\displaystyle \frac{2^{\alpha }}{h^{\alpha }}}<-{\displaystyle \frac{k_v\pm \sqrt{k_v^2-4k_d}}{2}}<0$, for $k_v,k_d,h>0$. By Lemma 1, $\lambda \in Spec\left(\overline{A}\right)$ is equal to $\lambda ={\displaystyle \frac{-k_v+\sqrt{k_v^2-4k_d}}{2}}$ or $\lambda ={\displaystyle \frac{-k_v-\sqrt{k_v^2-4k_d}}{2}}$. It follows that for any $\lambda \in Spec\left(\overline{A}\right)$ one gets $\left|\lambda \right|<{\left({\displaystyle \frac{2}{h}}\right)}^{\alpha }$ and by Remarks 1, 2, and 4, system (18) is asymptotically stable.

Next, let us assume that $k_v^2<4k_d$. Then, according to Lemma 1, $\lambda \in Spec\left(\overline{A}\right)$ is equal to $\lambda ={\displaystyle \frac{-k_v}{2}}+j{\displaystyle \frac{\sqrt{4k_d-k_v^2}}{2}}$ or $\lambda ={\displaystyle \frac{-k_v}{2}}-j{\displaystyle \frac{\sqrt{4k_d-k_v^2}}{2}}$. We observe that for $\alpha \in (0,1]$, it follows that ${\displaystyle \frac{3\pi }{2}}\le 2\pi -\alpha {\displaystyle \frac{\pi }{2}}<2\pi$. If $\lambda ={\displaystyle \frac{-k_v}{2}}+j{\displaystyle \frac{\sqrt{4k_d-k_v^2}}{2}}$, then one gets $\phi =arctan\left({\displaystyle \frac{\sqrt{4k_d-k_v^2}}{-k_v}}\right)$ and since $\phi$ lies in the second quadrant, the main argument is $arg\lambda =\pi -arctan\left({\displaystyle \frac{\sqrt{4k_d-k_v^2}}{k_v}}\right)\in \left[{\displaystyle \frac{\pi }{2}},\pi \right]$. Using the previous observation, it can be limited to $arg\lambda \in \left[\alpha {\displaystyle \frac{\pi }{2}},2\pi -\alpha {\displaystyle \frac{\pi }{2}}\right]$. Similarly, for $\lambda ={\displaystyle \frac{-k_v}{2}}-j{\displaystyle \frac{\sqrt{4k_d-k_v^2}}{2}}$, one gets $arg\lambda =\pi +arctan\left({\displaystyle \frac{\sqrt{4k_d-k_v^2}}{k_v}}\right)\in \left[\pi ,{\displaystyle \frac{3\pi }{2}}\right]\subset \left[\alpha {\displaystyle \frac{\pi }{2}},2\pi -\alpha {\displaystyle \frac{\pi }{2}}\right]$. Hence, $arg\lambda \in \left[\alpha {\displaystyle \frac{\pi }{2}},2\pi -\alpha {\displaystyle \frac{\pi }{2}}\right]$ for each $\lambda \in Spec\left(\overline{A}\right)$ and condition 1 in Proposition 1 is fulfilled with $k=0$. In addition, observe that $\left|\lambda \right|=\sqrt{k_d}$ for every $\lambda \in Spec\left(\overline{A}\right)$. By assumptions we obtain $\left|\lambda \right|<{\left({\displaystyle \frac{2}{h}}\left|sin{\displaystyle \frac{arg\lambda -\alpha \frac{\pi }{2}}{2-\alpha }}\right|\right)}^{\alpha }$, which means that condition 2 in Proposition 1 is satisfied with $k=s=0$. Hence, by Proposition 1 and Remark 1 it follows that system (18) is asymptotically stable. □

The asymptotic stability of system (18) implies $v_i\to v_1$ and $x_i\to x_1,i=2,\dots ,n$. However, in physical systems, to prevent collisions, a safe distance s is maintained. This constraint leads to the modified condition that the positions of the vehicles approach $x_i\to x_1+i\times s$ for $i=2,\dots ,n$, thereby ensuring the necessary separation between the vehicles. Once system (18) reaches stability, all vehicles move with a uniform velocity $v_1$.

3.2. Car-Following Model—Classical Case

In this subsection, we focus on the classical discretized car-following model given as follows:

$${\Delta }_{h}Y\left(k\right)=AY\left(k\right)$$

(22)

where $Y={(Y_1,\dots ,Y_n)}^T$ is the state vector that contains the states of all cars in the traffic system with $Y_i\left(k\right)=\left(\begin{array}{c}{x}_i\left(k\right)\\ v_i\left(k\right)\end{array}\right)$ where $x_i\left(k\right)$ is the position of the i-th car and $v_i\left(k\right)$ is its velocity at the moment k and matrix A is given by (14).

Again, to investigate stability, we use the transformation

$$\left\{\begin{array}{c}{\overline{x}}_{i-1}=x_i-x_1,\hfill \\ {\overline{v}}_{i-1}=v_i-v_1,i=2,\dots ,n.\hfill \end{array}\right.$$

(23)

Then system (22) with step $h>0$ can be rewritten as

$$\overline{Y}(k+h)=(I+h\overline{A})\overline{Y}\left(k\right).$$

(24)

where $\overline{A}\in {\mathbb{R}}^{2(n-1)\times 2(n-1)}$ is given by (19).

Let us recall the classical fact on asymptotic stability for discrete-time systems.

Proposition 2

([38]). A discrete-time system $x(k+1)=Ax\left(k\right)$ is asymptotically stable if and only if the matrix A is a Schur matrix, i.e., all eigenvalues λ of A satisfy $\left|\lambda \right|<1$.

Theorem 2.

Let us consider system (24). If one of the following assumptions holds,

1. 

$k_v^2\ge 4k_d$, $-{\displaystyle \frac{4}{h}}<-k_v\mp \sqrt{k_v^2-4k_d}<0$,

2. 

$k_v^2<4k_d$, $k_d<{\displaystyle \frac{k_v}{h}}$,

then system (24) is asymptotically stable.

Proof. 

First, consider the case where $k_v^2\ge 4k_d$. By Lemma 1 and basic algebraic properties it follows that

$Spec(I+h\overline{A})=\left\{\underset{(n-1)-\mathrm{times}}{\underbrace{1+h{\displaystyle \frac{-k_v-\sqrt{k_v^2-4k_d}}{2}}}},\underset{(n-1)-\mathrm{times}}{\underbrace{1+h{\displaystyle \frac{-k_v+\sqrt{k_v^2-4k_d}}{2}}}}\right\}$, which together with the assumption $-{\displaystyle \frac{4}{h}}<-k_v\mp \sqrt{k_v^2-4k_d}<0$ implies that $\left|\lambda \right|<1$ for each $\lambda \in Spec(I+h\overline{A})$ and system (24) is asymptotically stable.

Next, consider $k_v^2<4k_d$. Then using, again, Lemma 1 and basic algebraic properties, we get $Spec(I+h\overline{A})=\left\{\underset{(n-1)-\mathrm{times}}{\underbrace{1+h{\displaystyle \frac{-k_v-j\sqrt{4k_d-k_v^2}}{2}}}},\underset{(n-1)-\mathrm{times}}{\underbrace{1+h{\displaystyle \frac{-k_v+j\sqrt{4k_d-k_v^2}}{2}}}}\right\}$. Observe that $\left|\lambda \right|=\sqrt{1-h{k}_v+h^2{k}_d}$ for every $\lambda \in Spec(I+h\overline{A})$. By assumption $k_d<{\displaystyle \frac{k_v}{h}}$, we obtain $\sqrt{1-h{k}_v+h^2{k}_d}<1$, which implies that the matrix $(I+h\overline{A})$ is a Schur matrix. Hence, by Proposition 2, system (24) is asymptotically stable. □

4. Numerical Simulations

This section presents numerical simulations that illustrate and validate the theoretical results discussed earlier. Various scenarios are analyzed to demonstrate the stability properties of classical and fractional-order models under different parameter settings.

Example 1.

Consider a scenario involving $n=4$ vehicles with randomly selected initial conditions given by $Y\left(0\right)=[7,2,6,1,4,3,2,4]$. The control gains are set to $k_d=0.06$ and $k_v=0.5$. To prevent collisions between vehicles, a safety distance of $s=2$ was enforced during the simulations.

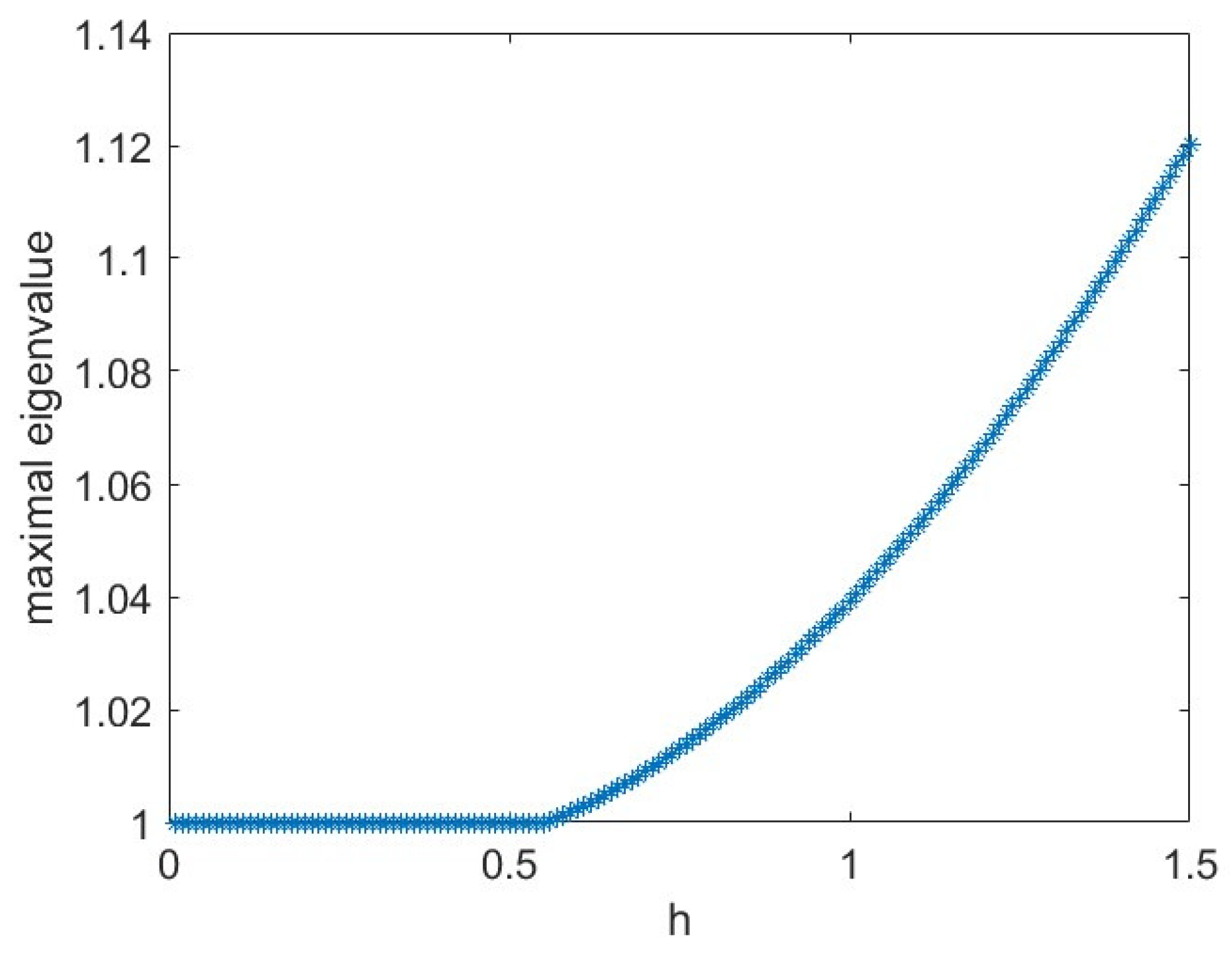
Figure 2 illustrates the dependence of the eigenvalues of system (22) as a function of the discretization step h. The results indicate that the classical model remains stable for step sizes smaller than approximately $h=6.7$. Note that for $k_d=0.06$ and $k_v=0.5$ the assumption 1 of Theorem 2 is satisfied. Based on condition 1 of Theorem 2, and given that the specified values of $k_d$ and $k_v$ yield real eigenvalues, the theoretical stability condition imposes an upper bound of $h<6.67$.

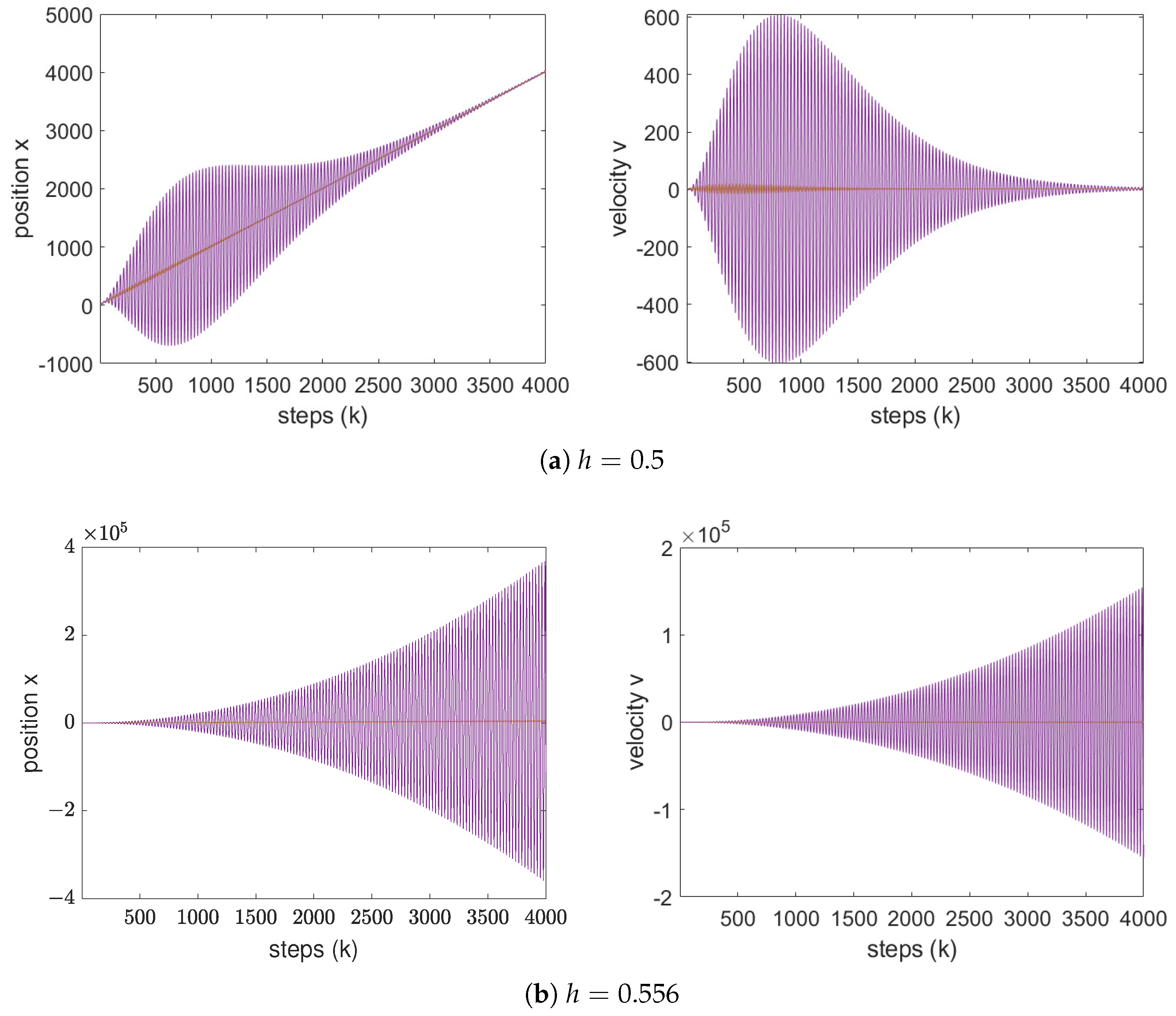
This analytical result is supported by numerical simulations. Figure 3 presents the evolution of the positions and velocities of the vehicles for selected values of h in the classical model. When the step size exceeds the theoretical bound (e.g., $h=6.7$), the system becomes unstable, as evidenced by the lack of convergence of vehicle velocities to that of the leader and the absence of coordinated, parallel motion.

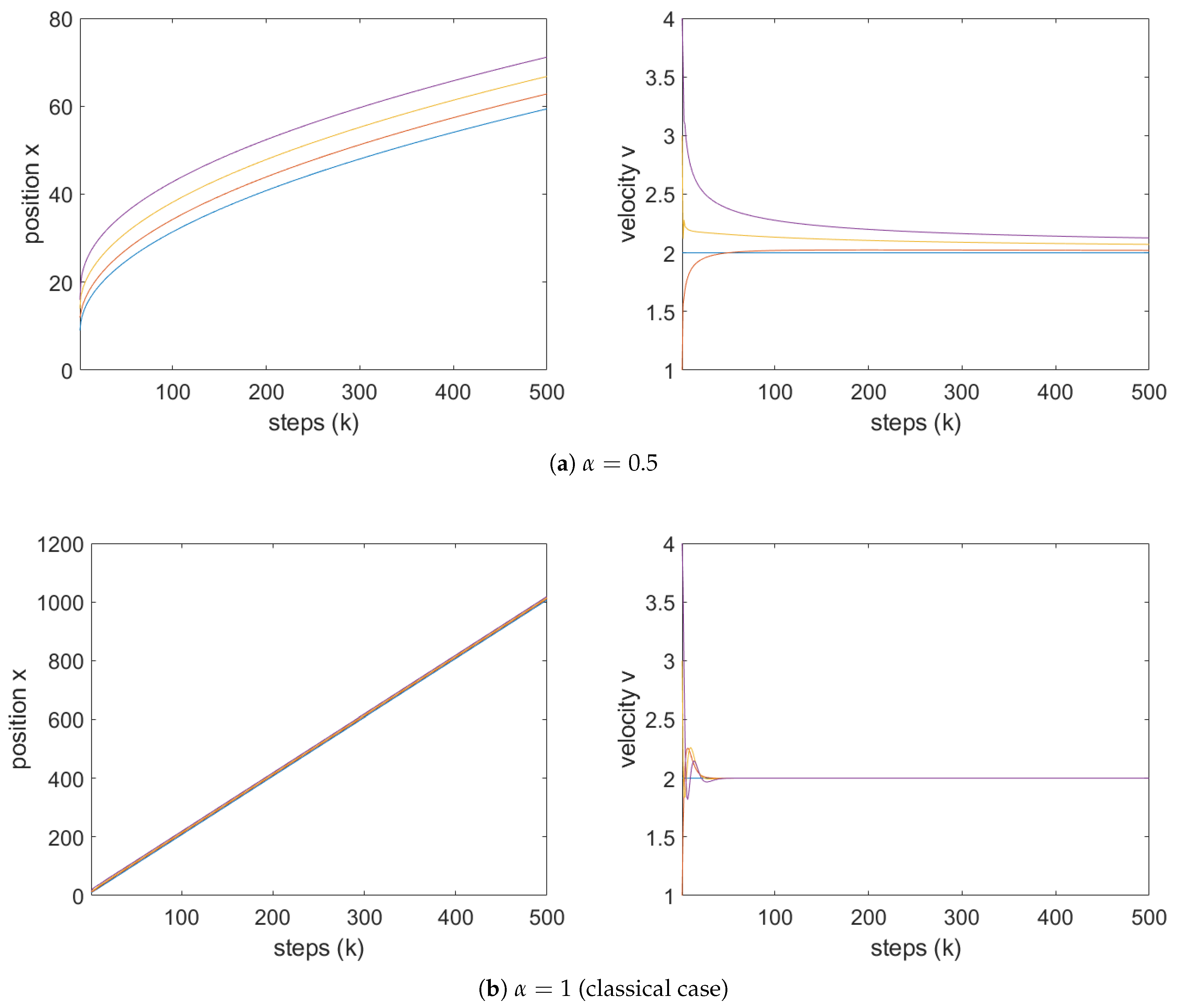
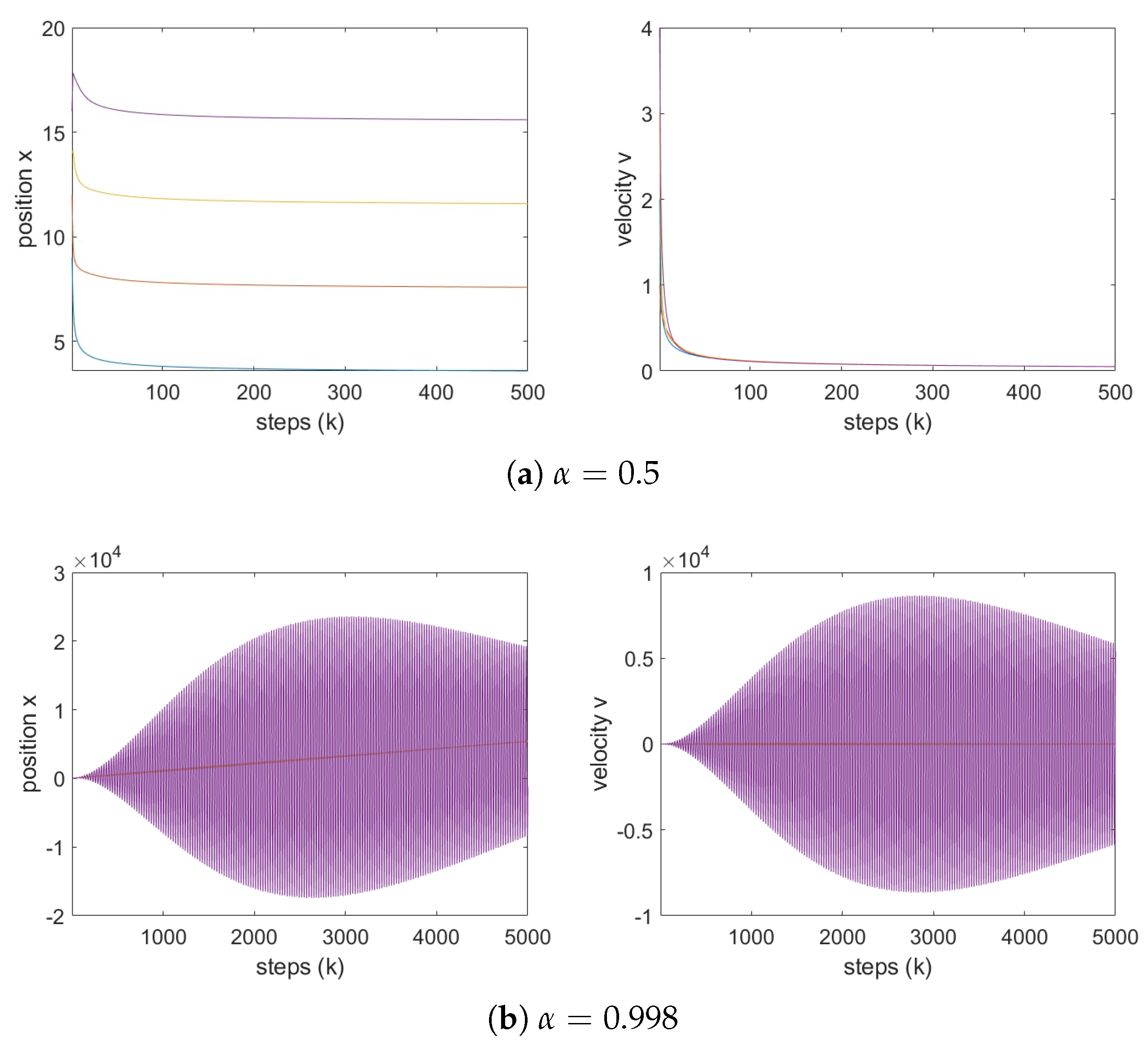
Next, we fix the step size $h=1$ and analyze the system behavior for various values of $\alpha \in (0,1]$. Observe that for $k_d=0.06$ and $k_v=0.5$ the assumption 1 of Theorem 1 is satisfied. According to condition 1 of Theorem 1, a system incorporating a fractional h-difference operator remains stable for any $\alpha$ within this interval. The stability condition from the theorem reduces in this case to the following: $-2^{\alpha +1}<-0.5$ which clearly holds for all $\alpha \in (0,1]$.

Figure 4 and Figure 5 present numerical simulations of vehicle positions and velocities for models employing the Grünwald–Letnikov and Caputo fractional differential operators, respectively, with $h=1$. In agreement with the theoretical analysis, both models exhibit convergence for any $\alpha \in (0,1]$.

As $\alpha \to 1$, the models approach the classical case. However, for small values of $\alpha$, the system governed by the Grünwald–Letnikov operator tends to drive vehicle velocities toward zero—a behavior that is undesirable in practical applications. In contrast, although the Caputo-based model converges slightly more slowly, it avoids this degradation in velocity, rendering it more suitable for real-world implementations.

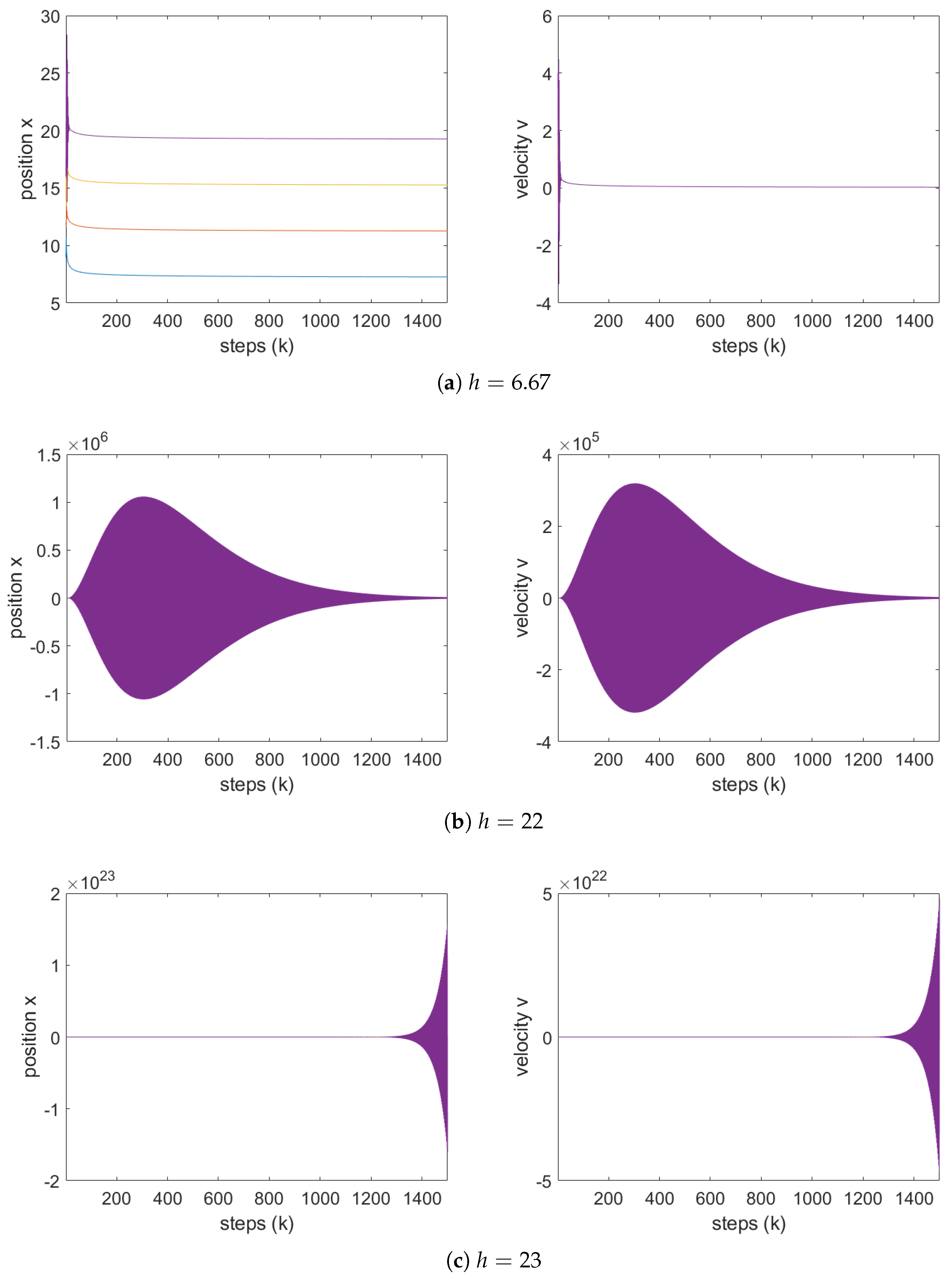
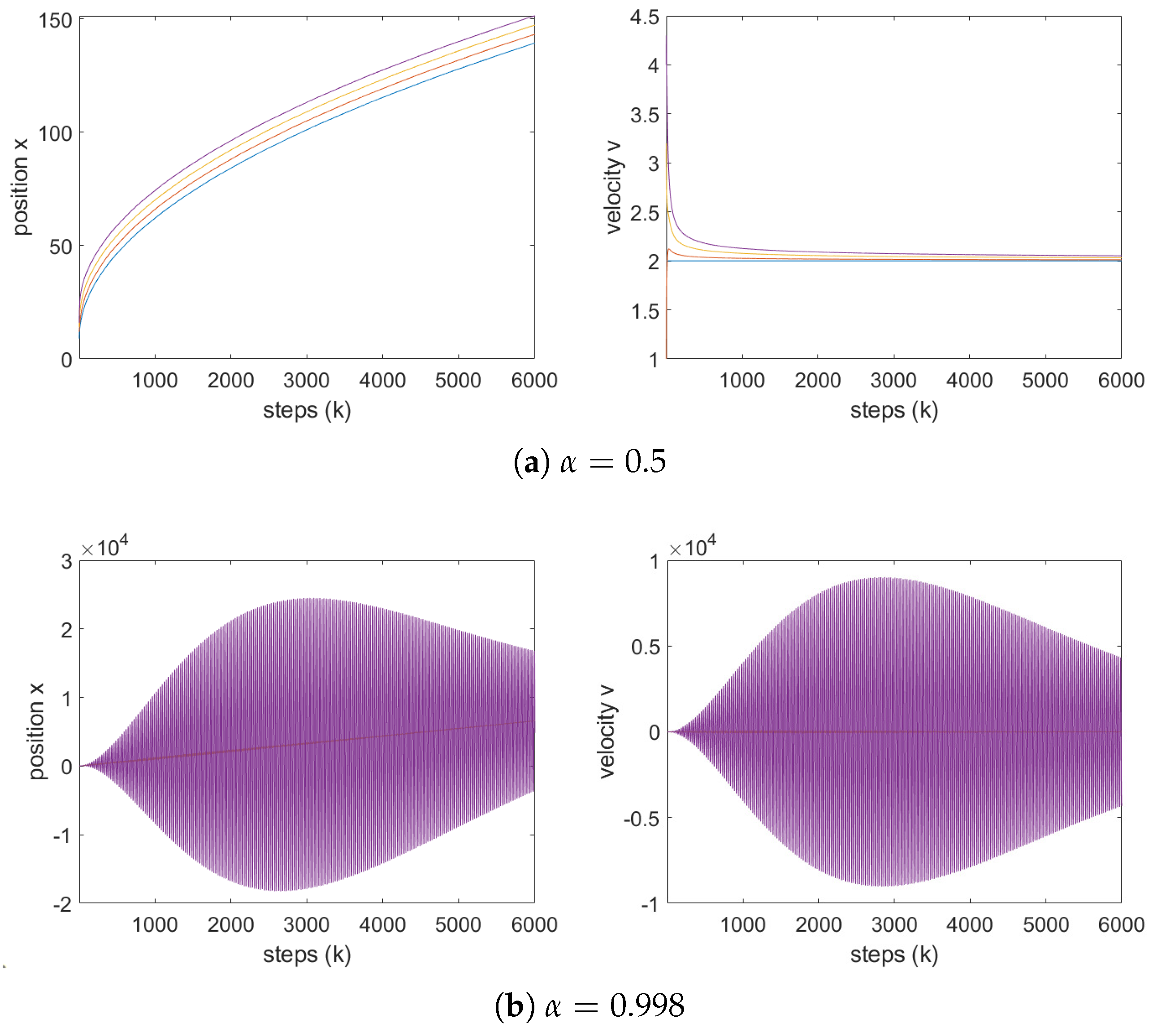
To further investigate the influence of step size, we fix $\alpha =0.5$ and perform simulations for varying values of h in both fractional models. The results are shown in Figure 6 and Figure 7. According to point 1 of Theorem 1, the stability condition in this case becomes the following: $-{\displaystyle \frac{2^{1.5}}{h^{0.5}}}<-0.6,$ which leads to the constraint $h<22.3$. Notably, this represents a significant improvement compared to the classical model, where stability is only ensured for $h<6.67$. These calculations are fully supported by the numerical results shown in Figure 6 and Figure 7, corresponding to the Grünwald–Letnikov and Caputo operators, respectively.

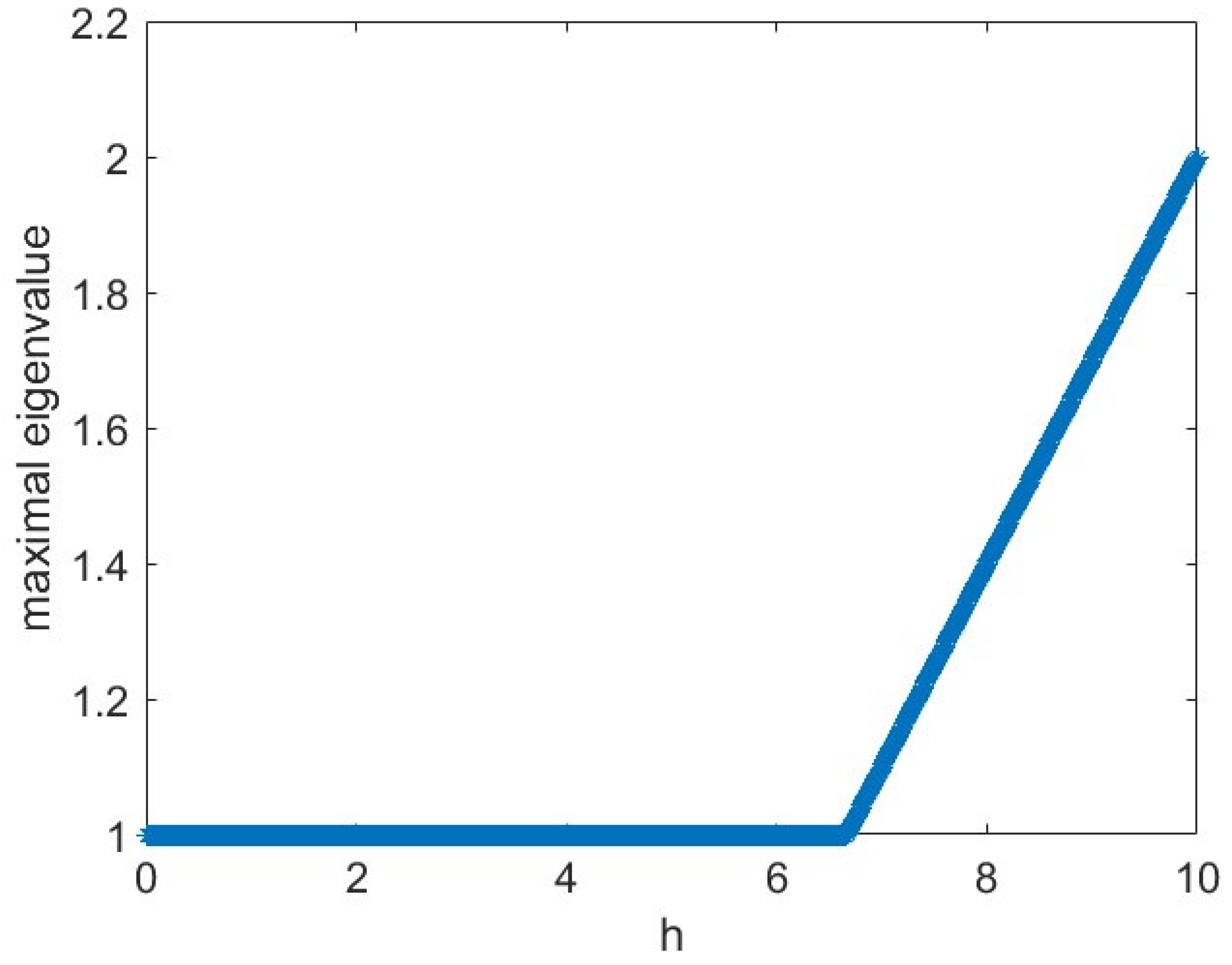
Example 2.

Consider $n=4$ vehicles, using the same initial conditions as before, $Y\left(0\right)=[7,2,6,1,4,3,2,4]$, but with control gains set to $k_d=0.18$ and $k_v=0.1$. The safety distance is again assumed to be $s=2$.

Observe that for $k_d=0.18$ and $k_v=0.1$ the assumption 2 of Theorem 2 is satisfied. The chosen parameter values lead to complex eigenvalues of system (22). Consequently, point 2 of Theorem 2 can be used to determine the range of the step size h for which the classical model remains stable. Specifically, the condition $0.18<{\displaystyle \frac{0.1}{h}}$ leads to the bound $h<0.556$.

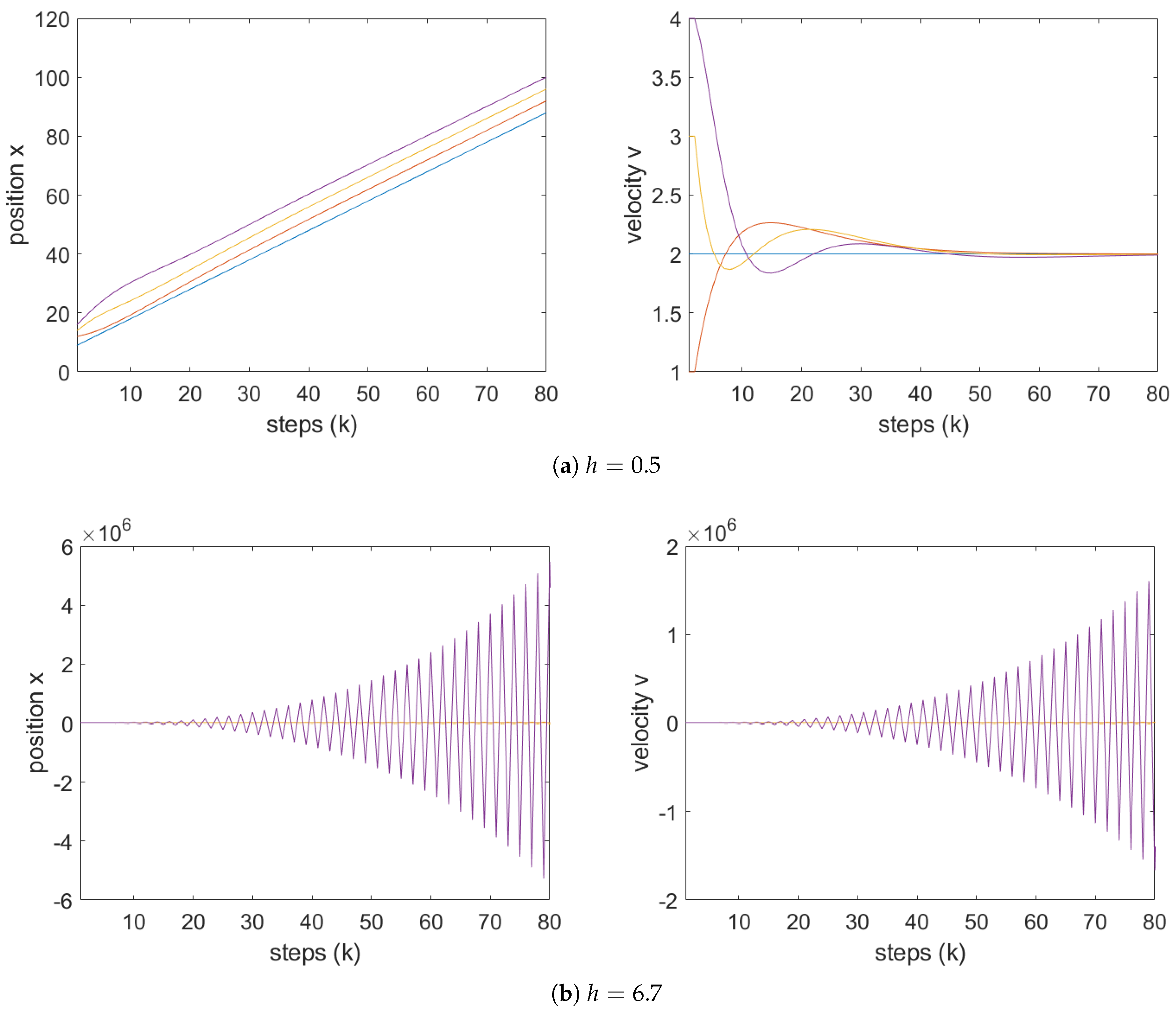
This calculation is confirmed by the simulation results presented in Figure 8, which shows the maximum real part of the eigenvalues of the classical system as a function of h. Further confirmation is provided by the time-domain simulations of vehicle positions and velocities for the given parameters in the classical model, shown in Figure 9. For step sizes $h\ge 0.556$, the vehicle velocities no longer converge to that of the leader, indicating instability.

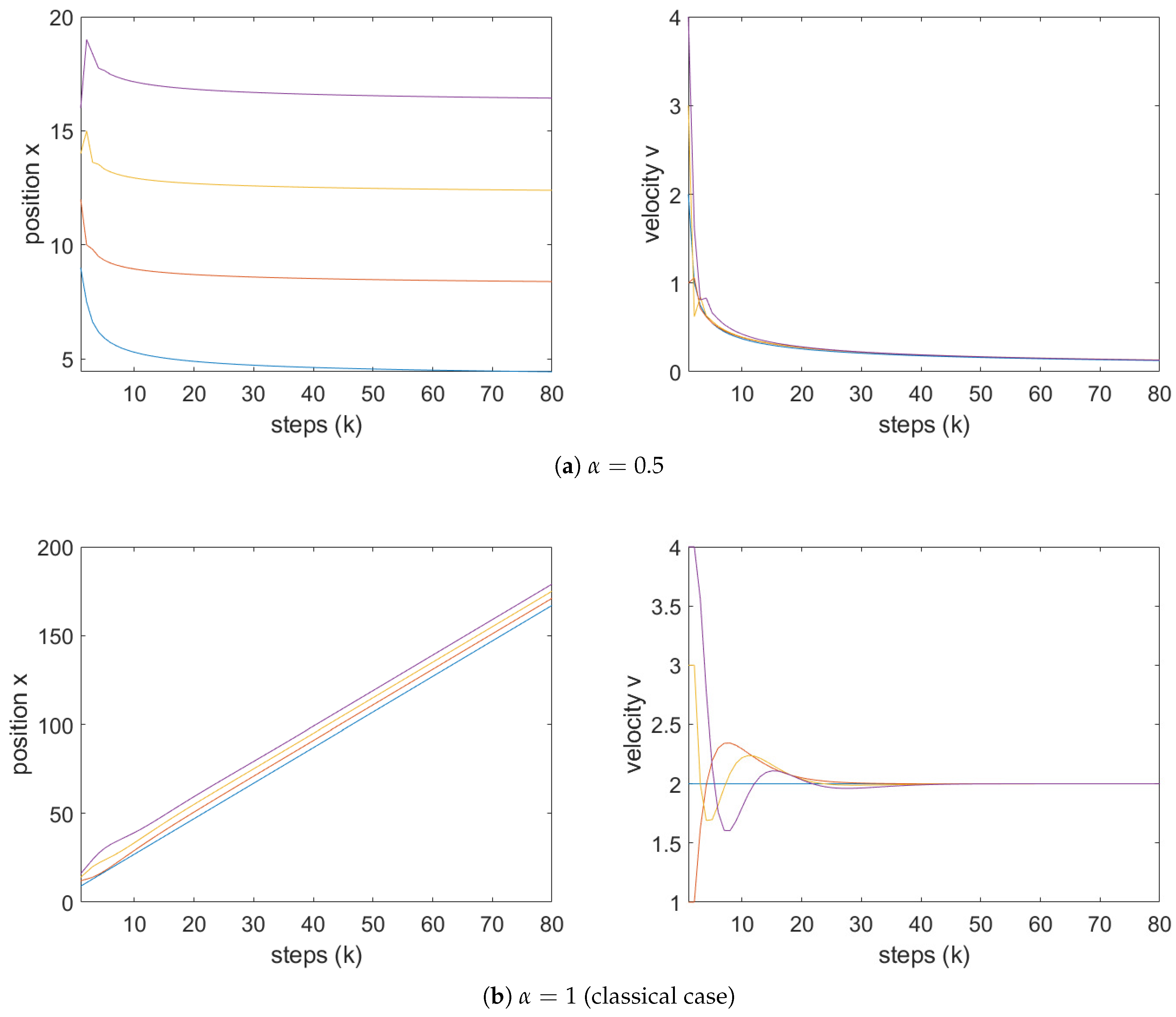
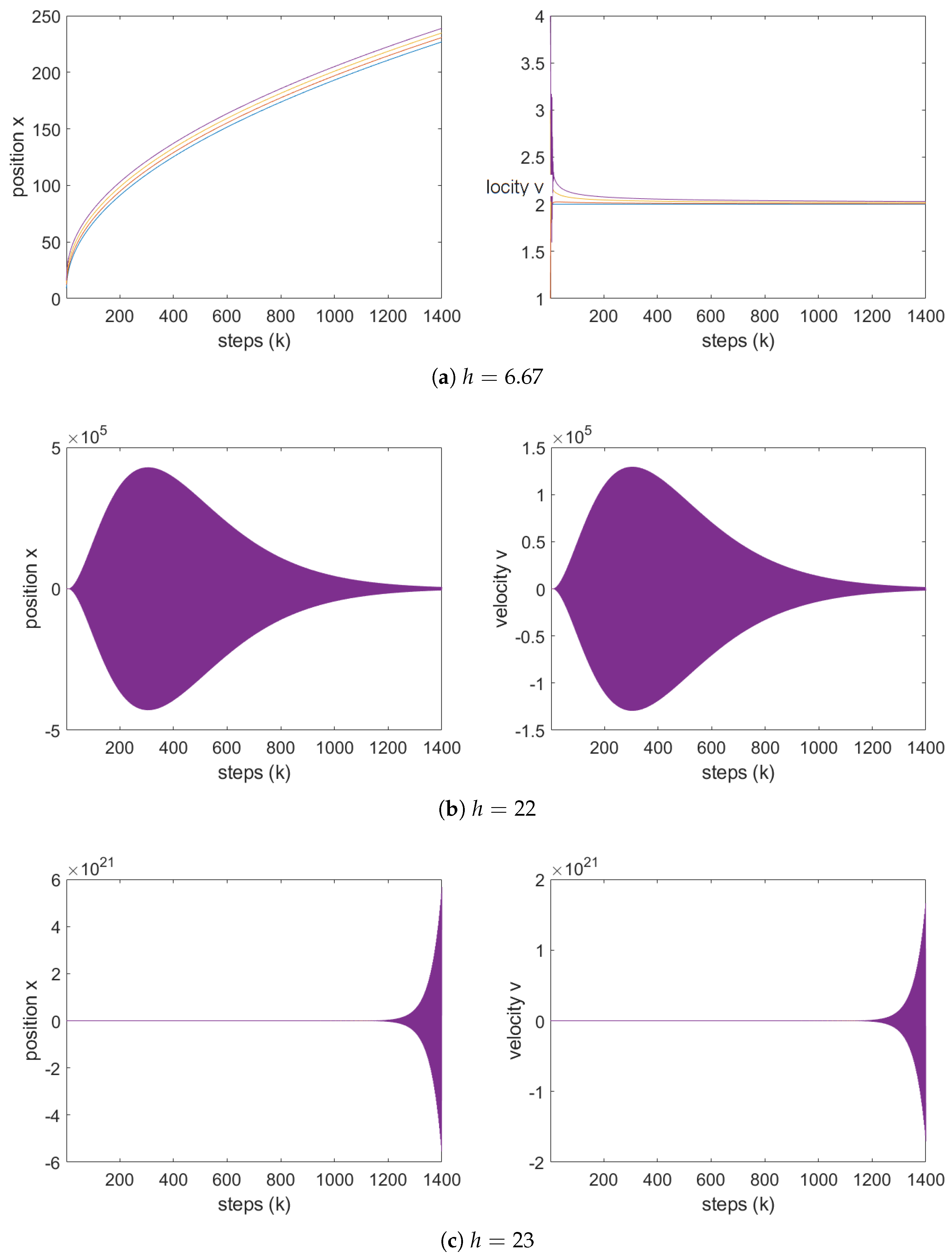
Now, fix $h=0.556$, for which the classical model becomes unstable when using the gains $k_d=0.18$ and $k_v=0.1$. Figure 10 and Figure 11 illustrate the system’s behavior under the Grünwald–Letnikov and Caputo fractional differential operators, respectively, for $h=0.556$ and several values of $\alpha \in (0,1]$.

As observed from the simulations, both fractional-order models maintain stability for $\alpha \le 0.998$. Observe that for $k_d=0.18$ and $k_v=0.1$ the assumption 2 of Theorem 1 is satisfied. The obtained result is consistent with Theorem 1. The eigenvalues of the system are given by ${\lambda }_1=-0.05+0.4213j$ and ${\lambda }_2=-0.05-0.4213j$, with corresponding arguments $arg\left({\lambda }_1\right)=0.537\pi$ and $arg\left({\lambda }_2\right)=-0.537\pi$. For $\alpha =0.998$, condition 2 in Theorem 1 leads to the following inequality:

$$k_d<{\left({\displaystyle \frac{2}{0.556}}\left|sin\left({\displaystyle \frac{\pm 0.537\pi -0.998\frac{\pi }{2}}{2-0.998}}\right)\right|\right)}^{2·0.998}.$$

These yield bound $k_d<0.1808$. Since the chosen gain $k_d=0.18$ satisfies inequality, the system remains stable under the corresponding condition.

It is worth noting that for $\alpha =1$, the model reduces to the classical (integer-order) case, which is unstable in this configuration. Therefore, the application of fractional-order differential operators significantly enhances the stability of the system.

Remark 5.

It should be noted that all simulations presented in this study are based on synthetic data. This approach allows full control of system parameters and facilitates direct validation of the theoretical stability conditions. Nevertheless, the developed framework could also be applied to real-world vehicle trajectory datasets, such as NGSIM or HighD, which provide high-resolution measurements of car-following behavior under natural driving conditions. In future studies, the proposed framework could be calibrated and validated using such datasets to further assess its realism and practical applicability.

5. Conclusions

This article focused on the analysis of a car-following model enhanced with fractional- and integer-order dynamics. Specifically, the Grünwald–Letnikov, Riemann–Liouville, and Caputo fractional as well as classical h-difference operators were incorporated into the model to investigate the stability of the considered systems.

For the first time, sufficient stability conditions for the car-following model employing each of the mentioned fractional operators were formulated and rigorously proved. The theoretical results were complemented by extensive numerical simulations, which provided illustrative comparisons between the fractional and classical formulations.

The simulation results confirmed that the use of fractional-order operators can substantially extend the admissible discretization step size and improve the stability properties of the system. In particular, the Caputo operator demonstrated favorable characteristics for practical applications, avoiding undesired behaviors such as velocity decay observed in other formulations.

From a practical perspective, the observed differences between the Grünwald–Letnikov and Caputo formulations may have important implications for real-world control systems such as Adaptive Cruise Control (ACC) and Connected Autonomous Vehicles (CAVs). The smoother convergence behavior of the Caputo-based model suggests that it may provide greater robustness against abrupt changes in leader velocity and better comfort for passengers—both key requirements in automated driving. In contrast, the Grünwald–Letnikov formulation, while theoretically valid and faster to converge, can produce overly aggressive corrections or excessive damping, which may be undesirable in practical implementations. Therefore, fractional models based on the Caputo operator appear more suitable for control-oriented applications in intelligent transportation systems.

These findings support the relevance and effectiveness of fractional calculus in improving the performance and robustness of car-following models and open new avenues for its application in traffic flow analysis and control. Future research could focus on several directions that naturally extend the present work. First, stochastic formulations of the fractional car-following model could be developed to account for variability and uncertainty in driver behavior. Another promising avenue involves the extension of the current single-lane framework to multi-lane, enabling the study of lane-changing interactions and collective dynamics. Finally, further validation using empirical vehicle trajectory datasets or controlled experiments (i.e., NGSIM or HighD) could provide deeper insights into the applicability of fractional-order dynamics in real-world traffic environments.