Abstract
This study introduces a novel generative approach for crafting phrase-oriented rhythmic patterns in jazz solos, leveraging statistical analyses of a comprehensive corpus, the Weimar Jazz Database. Jazz solos, celebrated for their improvisational complexity, require a delicate interplay between rhythm and melody, making the generation of authentic rhythmic patterns a challenging task. This work systematically explores the relationships among rhythmic elements, including phrases, beats, divisions, and patterns. The generative method employs a Markov chain framework to synthesize rhythmic divisions and patterns, ensuring stylistic coherence and diversity. An extensive evaluation compares original and generated datasets through statistical and machine learning metrics, validating the generative model’s ability to replicate key rhythmic characteristics while fostering innovation. The findings underscore the potential of this approach to contribute significantly to the fields of computational creativity and algorithmic music composition, providing a robust tool for generating compelling jazz solos.
1. Introduction
Jazz is a musical genre celebrated for its improvisational nature, particularly evident in instrumental solos, where musicians create unrehearsed melodic lines that adhere to intricate constraints of music theory. These melodic lines, monophonic sequences of notes and rests, are typically guided by the harmonic framework provided by the underlying chord progression. While this harmonic structure imposes theoretical constraints, jazz musicians enjoy considerable creative freedom to explore unconventional melodic and rhythmic ideas. This delicate balance between constraint and freedom is a hallmark of jazz, allowing for unique and captivating performances.
The crafting of an engaging jazz solo requires a nuanced interplay between pitch and rhythm [1]. A melodically innovative sequence of pitches paired with monotonous or uninspired rhythms fails to captivate audiences, just as a rhythmically dynamic solo with poor pitch selection may sound incoherent or lack direction. Among these two dimensions, rhythm often serves as the driving force, providing energy, groove, and syncopation that are quintessential to jazz. Rhythmic patterns, therefore, play a vital role in shaping the character and emotional impact of a solo. Recent studies, such as Daikoku’s work on rhythmic pattern perception, emphasize the significance of rhythm for cognitive and aesthetic aspects of music generation, highlighting its importance for jazz improvisation [2].
In jazz soloing, sequences of notes delineated by rests are typically organized into phrases. These phrases serve as structural units within solos, acting as building blocks that contribute to the overall coherence and narrative of the performance. Phrases allow for repetition, variation, and transformation over time, which are key elements in developing engaging musical content. By focusing on phrases, musicians can explore the interplay of melody, rhythm, and harmony within smaller, manageable segments, a process that facilitates both spontaneous creativity and structured improvisation. This phrase-oriented perspective has been widely recognized as a cornerstone of effective music generation and improvisation in jazz [3,4].
Despite its importance, rhythm has often been overshadowed by melody and harmony in generative music research, especially in the context of jazz. This paper seeks to address this gap by proposing a novel method for generating rhythmic patterns tailored for phrase-oriented jazz solos. The method leverages a statistical analysis of rhythmic patterns observed in a comprehensive corpus of jazz solos, namely the Weimar Jazz Database [5]. This database, renowned for its extensive collection of annotated jazz performances, provides a rich resource for studying the rhythmic and melodic characteristics of jazz improvisation. By extracting statistical insights from this corpus, the proposed method identifies common rhythmic motifs and their variations, enabling the generation of rhythmically compelling and stylistically authentic jazz solos.
The statistical approach presented in this paper emphasizes the balance between innovation and adherence to stylistic norms. It introduces a degree of unpredictability to generate fresh and interesting rhythmic patterns while maintaining coherence with the characteristic structures of jazz. This balance is particularly important for improvisational genres like jazz, where musicians strive to surprise and engage their audience without deviating too far from established conventions. By focusing on rhythmic patterns at the phrase level, this work contributes to the broader field of generative music by addressing a critical yet underexplored dimension of jazz improvisation.
1.1. Related Work
The Weimar Jazz Database (WJD) [5,6] has become a valuable resource for jazz research. Researchers have utilized the database to explore various aspects of jazz music, such as evaluating automated melody extraction algorithms based on jazz improvisations [7], comparing the improvisatory styles of iconic jazz musicians like Miles Davis and John Coltrane [8], and investigating metrical dependence in jazz solos [9]. The same authors conducted a study that focused on the pitch, intervallic, and rhythmic aspects of these musical motifs [9]. Furthermore, the Weimar Jazz Database has been used in corpus studies to analyze jazz solos and explore insights relevant to jazz, groove, microrhythm studies, and music perception [6]. Cross et al. investigated whether licks in jazz solos are metrically dependent, shedding light on the relationship between interval patterns and metrical position in jazz music [9]. The Jazz Transformer is a generative model that incorporates structural events from the WJazzD to induce structures in AI-composed jazz music [10]. The research conducted by [11] emphasizes the importance of pattern recognition in music and the exploration of music metadata. Ref. [12] introduced a novel time-swing ratio representation called swingogram, which captures information related to the swing ratio over time in jazz performances.
In the domain of generative jazz, pioneering work by [13,14] resulted in GenJam, a genetic algorithm-based system developed to generate jazz solos. The interactive genetic algorithm maintains hierarchically related populations of melodic ideas that are mapped to specific notes through scales suggested by the chord progression being played, simulating the learning process of a novice jazz musician. This approach was further explored by [15] in their study on generating four-part harmony using genetic algorithms. GenJam has been a prominent case study for applying evolutionary computation to improvisation [16]. Ref. [17] also presented a system to produce jazz melodies using a genetic algorithm and pattern learning based on variable-length chromosomes with geometric crossover to accommodate the variable length, creating a jazz melody according to the preference of the user and the training data.
Backman and Dahlstedt presented a system based on probabilistic and evolutionary strategies to create artificial jazz solos [18]. The generation of the improvisatory material uses interactive evolution based on a dual genetic representation: a basic melody line representation with energy constraints and a hierarchic structure of operators that processes the various parts of this basic melody.
Impro-Visor [19,20,21] is a music notation program designed to assist jazz musicians in composing and hearing solos similar to their own. Ref. [22] used deep belief networks (DBNs), a multi-layered composition of restricted Boltzmann machines (RBMs), to generate jazz melodies over chord progressions. JazzGAN, a GAN that utilizes recurrent neural networks (RNNs) to improvise monophonic jazz melodies over chord progressions, has also been integrated into Impro-Visor [23].
Some generative music methods are not genre-specific. To solve the problem of insufficient data for automatic generation of jazz, ref. [24] introduced a recurrent variational auto-encoder as the generative model, using a genre-unspecified dataset as the source dataset and a jazz-only dataset as the target dataset.
More recently, Row and colleagues introduced the JAZZVAR dataset [25], which consists of variations found within solo piano performances of jazz standards. The dataset includes 502 pairs of original and variation performances that were manually extracted from solo jazz piano performances. Overall, the JAZZVAR dataset provides a valuable resource for studying variations within solo piano performances of jazz standards.
In sum, the particularities of jazz have made it a prominent research topic in the realm of symbolic generative music. In this sense, from the early days of rule-based systems, such as jazz grammars [19], passing to machine learning methods such as genetic algorithms [13], stochastic approaches [26,27], and neural networks [28,29,30], to the more recent advances in the deep learning field [31,32], researchers have tried to develop symbolic techniques to generate jazz solos that use machine learning to mimic human styles [33]. For a comparative assessment of Markov models and recurrent neural networks (RNNs) for jazz music generation, the reader is referred to [34].
The comparison in Table 1 shows that while deep neural methods (e.g., GANs, Transformers) excel at capturing long-term musical dependencies, they demand large training corpora and computational resources. Evolutionary and grammar-based systems emphasize interactivity and rule encoding but are less suitable for corpus-driven rhythmic modeling. In contrast, low-order Markov chains strike a balance of interpretability, computational efficiency, and data efficiency, making them particularly appropriate for phrase-level rhythmic generation from the Weimar Jazz Database subsets used here.

Table 1.
Comparison of generative approaches for jazz solos found in the literature.
For a comprehensive review of general-purpose generative music methods beyond the jazz domain, interested readers are referred to [35].
1.2. Research Gap and Motivation
While significant advancements have been made in the field of generative music, particularly in modeling melodic and harmonic structures, the rhythmic dimension—especially in the context of jazz improvisation—remains comparatively underexplored. Existing generative models often prioritize pitch-related aspects, leaving rhythm treated as a secondary concern or relying on simplistic, quantized approaches that fail to capture the nuanced phrasing and syncopation characteristic of jazz solos. This oversight is particularly limiting given that rhythm in jazz serves not only as a temporal scaffold but as a central expressive force, shaping groove, swing, and emotional contour.
Moreover, most rhythm generation methods in the literature operate at a low structural level—focusing on individual notes or beats—without sufficient consideration for larger musical units such as phrases. Yet, phrases are fundamental to how jazz musicians organize and develop musical ideas over time. The lack of phrase-oriented rhythmic modeling thus represents a critical gap, restricting the potential of generative systems to produce solos that are both stylistically convincing and musically engaging.
This study is motivated by the need to develop a generative framework that gives rhythm a more prominent and structured role in the creation of jazz solos. By leveraging the annotated richness of the Weimar Jazz Database and employing a statistically grounded Markov chain model, the proposed method aims to synthesize rhythmic patterns that reflect the diversity and coherence observed in authentic jazz improvisation. The focus on phrase-level generation seeks to bridge the gap between low-level rhythmic modeling and high-level musical structuring, offering a more holistic approach to algorithmic composition in jazz.
Through this work, we aim to contribute to the broader domain of computational creativity by highlighting the generative potential of rhythm and demonstrating how statistical models can yield both stylistic fidelity and creative diversity. This emphasis on rhythm, particularly in a phrase-oriented context, not only enriches the capabilities of generative systems but also aligns more closely with how jazz musicians conceive and perform improvised solos.
2. Materials and Methods
2.1. The Dataset
To analyze and model rhythmic patterns in jazz solos, we started with an event dump of the WJD, the Events dataset, containing a list of all 289,000 note events along with various annotations [5], particularly rhythmical and metrical information as well as phrase segmentation (manually annotated in the WJD) and metadata. From this, we created the Phrases dataset, by extracting phrases. Each entry in this dataset provided detailed information about specific musical events, including their phrase positions, rhythmic characteristics, performer, style, and tempo. The Phrases dataset was constructed to capture higher-level rhythmic structures derived from the Events data, and it includes fields essential for analyzing and modeling jazz phrase structures. From the Phrases dataset, we further derived the Bigrams dataset, focusing on transitions between rhythmic events to capture the probabilistic structures in rhythmic generation.
2.1.1. Phrases, Beats, Divisions, and Rhythmic Patterns
For the following, we first need to delineate some basic musical concepts and their representation as used in the WJD and, consequently, in our datasets:
- Beats (mapped in blue in Figure 1) provide the foundational temporal structure in the WJD, indicating the regular pulse over which rhythms are created. Beats are typically grouped into metrical units, called bars or measures (mapped in purple in Figure 1), which, in the WJD, are almost exclusively groups of four beats (4/4 m). Beats are virtual time-points inferred from the musical surface and used by all players as an internal time reference to coordinate their interplay.
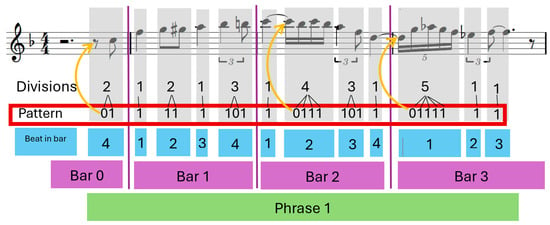 Figure 1. First phrase (lick) of the solo “Billie’s Bounce” by Charlie Parker: length (beats) = 12; rhythmic pattern = 01,1,11,1,101,1,0111,101,1,01111,1,1.
Figure 1. First phrase (lick) of the solo “Billie’s Bounce” by Charlie Parker: length (beats) = 12; rhythmic pattern = 01,1,11,1,101,1,0111,101,1,01111,1,1. - Divisions refer to the subdivision of beats into smaller virtual timepoints (tatums), on which observed events are located. This allows efficient representation of rhythmic complexity, ranging from straightforward rhythms to intricate, syncopated patterns. In contrast to many other systems, each beat carries its own optimal subdivision, instead of imposing a fixed grid across the whole solo. A note event in the WJD is uniquely annotated with information of the surrounding metrical frame, the position of the surrounding beat in a bar, and the position in the surrounding beat indexed by local beat division and position in the local tatum grid (see Figure 1).
- Rhythm Patterns (highlighted in the red box in Figure 1) are our main object of interest. Each beat in a solo is associated with a certain number of subdivisions, or tatum positions, depending on its rhythmic complexity. Within each beat, note events are mapped to these tatum positions. This mapping can be compactly represented as a binary string, where each position corresponds to a tatum subdivision: a 1 indicates the presence of an event, and a 0 indicates its absence (see orange arrows in Figure 1). The length of this binary string reflects the number of subdivisions used in that beat. A solo can therefore be described as a sequence of these binary rhythm patterns, each linked to its corresponding beat. If a beat contains no events—such as during a rest or a sustained note—it is either annotated with a single 0 or omitted entirely.
- Bigrams capture local transitions between rhythmic events by considering all pairs of adjacent binary rhythm patterns within a phrase. Each bigram consists of two consecutive rhythm patterns, providing a compact representation of rhythmic progression across beats. This allows analysis of how rhythmic ideas evolve locally within phrases, revealing tendencies such as repetition, variation, or syncopated displacement. Bigrams are especially useful for identifying characteristic transitions in the rhythmic language of a performer or style.
- Phrases are perceptual and productive groupings of sequences of note events that represent a coherent musical thought or expression (a rhythmic gestalt), spanning a variable number of note events, beats, and bars (see Figure 1). Each phrase in our dataset inherits the contextual metadata from the containing solo, such as tempo, style, and performer, allowing us to analyze the specific characteristics associated with various jazz artists and general musical parameters.
- Midlevel Annotation is an analytical grouping system, specifically devised for jazz solos [36]. Its components, the midlevel units (MLUs), describe “playing ideas” that the soloist uses to create the musical surface. There are nine main categories (lick, line, melody, rhythm, theme, void, fragment, expressive, quote), each with distinct musical and referential characteristics, including different rhythmic designs. The most common categories, line and lick, differ mainly in their typical length (number of notes) and, most importantly, the fact that line MLUs have a much more uniform rhythmic design than lick MLUs. A single phrase can consist of one or more MLUs.
Together, phrases, MLUs, beats, divisions, and rhythm patterns provide a structured framework for analyzing and generating jazz solos at the rhythmic and structural levels. By modeling these elements, we aim to capture key aspects of jazz rhythm, enabling the generation of new solos that retain the rhythmic essence of the original performances. Figure 1 presents an example of a phrase and its corresponding divisions sequence and rhythm pattern.
2.1.2. First Level of Detail: Phrases Dataset
The Phrases Dataset provides a foundational level of detail for understanding and generating jazz solo structures. This dataset, saved in phrases.csv, compiles essential information on phrase-level features, offering insights into the rhythmic, stylistic, and performative aspects of each phrase within a jazz solo.
Each entry in the Phrases Dataset represents an individual phrase with attributes that describe its rhythmic structure, stylistic context, and performer details. The primary fields included are as follows:
- mlu: This field categorizes each phrase into one or more musical types, such as lick or line, which represent playing ideas typical in jazz improvisation as described above.
- notes: Counts the number of notes within each phrase, offering a basic measure of the phrase’s complexity and rhythmic density.
- length: Represents the phrase duration in beats, capturing the temporal span and aiding in comparisons of phrase length across different tempos and styles.
- divisions: Specifies the subdivisions within each beat, providing detailed insight into the rhythmic intricacies, including syncopation and variations in beat subdivision that are characteristic of jazz.
- rhythm: Encodes the rhythmic pattern of each phrase as a sequence. This field is crucial for modeling rhythmic patterns and serves as a reference for evaluating generated rhythms.
Table 2 presents a very small excerpt from the dataset phrases.csv, showcasing a lick and a line performed by Art Pepper in a COOL jazz style with an UP tempo and SWING feel.

Table 2.
Excerpt of phrases.csv (four licks and two lines).
2.1.3. Second Level of Detail: Bigrams Dataset
To encode rhythmic transitions within jazz solos, we constructed the Bigrams Dataset from the Phrases Dataset. This dataset focuses on pairs of consecutive rhythmic units within each phrase, referred to as “bigrams”. By examining bigrams, we can analyze the 1st-order Markov transition probabilities based on beat divisions and tatum positions. This facilitates a more detailed understanding of the rhythmic flow and nuances of jazz phrases.
The Bigrams Dataset is organized into the following fields, each offering insights into different aspects of rhythmic transition:
- position: This indicates the bigram’s position within the phrase, allowing for analysis of how rhythmic patterns evolve from the beginning to the end of a phrase.
- division: This denotes the specific beat subdivision of the first unit in the bigram. This field provides the initial rhythmic context, capturing where the transition begins within a beat.
- division follower: This specifies the beat subdivision of the second unit in the bigram. This transition from Division to Division Follower provides insights into how rhythmic subdivisions are developed or shifted.
- division bigram: This represents the combined sequence of Division and Division Follower, encapsulating the entire rhythmic transition within the bigram. This allows for efficient comparison and analysis of distinct subdivision patterns.
- pattern: This encodes the rhythmic pattern that encompasses the bigram, allowing us to contextualize the transition within broader rhythmic motifs.
- follower: This details the rhythmic position following the bigram.
- bigram: This represents the entire sequence of rhythmic events and subdivisions within the bigram.
Table 3 presents an excerpt from the bigrams.csv dataset, focusing on six consecutive bigrams extracted from a melodic line performed by Art Pepper in the COOL style and UP tempo. Each row corresponds to a specific position within the line and provides detailed information about the musical structure, including the melodic line unit (MLU), division and its follower, and their paired bigram, as well as the associated rhythmic pattern and follower sequences represented in binary form.

Table 3.
Excerpt of bigrams.csv (six bigrams of a line).
By focusing on rhythmic transitions, the Bigrams Dataset provides a second level of detail for understanding jazz rhythms at a microstructural level. This dataset is fundamental for training and evaluating generative models to accurately predict rhythmic transitions, capturing not only isolated rhythms but also the contextual flow and progression within phrases. Together with the Phrases Dataset, this dataset enables a comprehensive approach to modeling and generating realistic jazz solos with authentic rhythmic variations.
For both datasets (phrases and bigrams), we also have the inherited metadata, which are the following:
- style: This defines the broader stylistic category of the phrase, such as “BEBOP”, “HARDBOP”, “POSTBOP”, and “COOL”, providing context on the overall aesthetic and rhythmic tendencies associated with the style.
- tempo: This indicates the tempo at which the phrase is performed, with values such as “UP”, “MEDIUM UP”, “MEDIUM”, and “MEDIUM SLOW”. These tempo categories impact the rhythmic feel and articulation, as well as the density of notes within each phrase.
- performer: This identifies the musician responsible for the phrase, allowing for an analysis of how individual performers interpret rhythm and phrase structure within different tempos and styles.
Several of the features in the dataset, such as position, division, pattern, and bigram, are treated as categorical variables. At first glance, this could give the impression that these variables belong to potentially infinite spaces, since some of them are represented as strings of varying length. In practice, however, all categories are simply defined as the union of all observed values in the dataset, and therefore remain finite. For clarity, we report the number of unique categories for each feature. The style covers 4 main categories: POSTBOP, HARDBOP, COOL, and BEBOP. Tempo is distributed across 4 categories, namely UP, MEDIUM UP, MEDIUM, and MEDIUM SLOW. The dataset further includes 54 unique performers, 12 unique values for division, 13 for division_follower, 118 for division_bigram, 180 for pattern, 176 for follower, and 3021 for bigram. While some of these feature spaces are large and lead to sparsity, this sparsity is intrinsic to the nature of jazz improvisation, where diversity and variation are central, and our statistical framework is explicitly designed to handle this richness.
2.2. Statistical Analysis
This section provides an in-depth evaluation of the rhythmic and structural characteristics present in the original corpus, examining both the Phrases and Bigrams datasets. By conducting statistical tests and exploring various metrics, we aim to gain insights into the rhythmic patterns, subdivisions, and stylistic variations inherent to jazz solos. The subsections that follow detail two levels of analysis: Phrases Analysis investigates phrase-level metrics such as note count, rhythmic length, and stylistic consistency, while Bigrams Analysis examines the finer-grained rhythmic transitions between subdivisions within phrases.
2.2.1. Determining Dependent and Independent Variables in Phrases
To better understand the dependencies among key phrase-level variables, we computed pairwise Cramér’s V values, a statistical measure of association between categorical variables. This analysis aims to identify which variables are most likely to influence others, thereby distinguishing dependent from independent factors. Figure 2 presents a heatmap of the resulting Cramér’s V values for variables such as style, performer, mlu, tempo, length, divisions, and rhythm. Values closer to 1 indicate a strong association, while values near 0 suggest independence. These results guide the selection of variables for downstream modeling tasks by revealing the underlying structure of dependencies within the dataset.
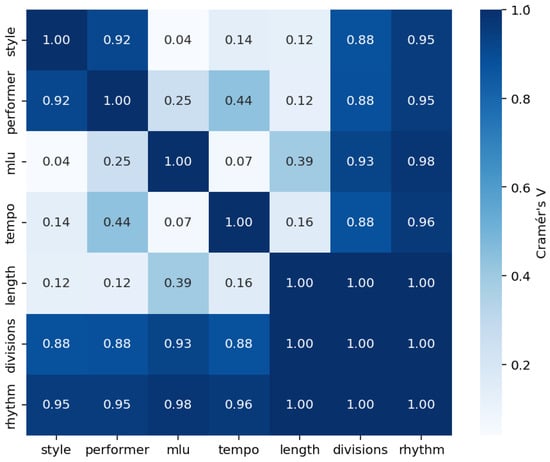
Figure 2.
Cramér’s V Heatmap for “style”, “performer”, “mlu”, “tempo”, “length”, “divisions”, and “rhythm”.
- Strong Associations:
- –
- style and performer (Cramér’s V = 0.9166): This strong association suggests that specific styles are closely linked to particular performers.
- –
- style and rhythm (Cramér’s V = 0.9520): A high association indicates that rhythm patterns are significantly influenced by the style, implying a strong relationship between these two variables.
- –
- performer and rhythm (Cramér’s V = 0.9540): This value suggests that rhythm is also highly associated with the performer, indicating that each performer likely follows distinct rhythmic patterns.
- –
- mlu and rhythm (Cramér’s V = 0.9789): This near-perfect association shows that rhythmic patterns are heavily dependent on mlu.
- –
- length and divisions (Cramér’s V = 1.0000), length and rhythm (Cramér’s V = 1.0000), and divisions and rhythm (Cramér’s V = 1.0000): These values of 1.0000 indicate perfect associations, meaning that length, divisions, and rhythm are entirely dependent on each other.
- Moderate Associations:
- –
- performer and divisions (Cramér’s V = 0.8368): This suggests a strong but not perfect link between the performer and divisions.
- –
- mlu and divisions (Cramér’s V = 0.9152): This is a high association, indicating that the mlu variable strongly correlates with divisions.
- –
- tempo and rhythm (Cramér’s V = 0.9601): This strong association implies that tempo has a significant impact on rhythm, suggesting tempo-specific rhythmic patterns.
- –
- performer and tempo (Cramér’s V = 0.4356): This moderate association suggests that certain tempos are more common among specific performers.
- Weak or Low Associations:
- –
- style and mlu (Cramér’s V = 0.0398): The low association between style and mlu suggests that these two variables are mostly independent.
- –
- mlu and tempo (Cramér’s V = 0.0659): This indicates a minimal relationship, suggesting that mlu and tempo vary independently of each other.
- –
- tempo and length (Cramér’s V = 0.1585): This low association shows that the tempo does not strongly affect the length.
- Justification for Excluding style as a Variable for Generating rhythm:Despite the high association between style and rhythm (Cramér’s V = 0.9520), other variables such as length, divisions, and performer demonstrate equally strong or even stronger associations with rhythm. Since both performer and divisions are already highly dependent on style (Cramér’s V values of 0.9166 and 0.8320, respectively), the effect of style on rhythm may be adequately captured indirectly through these variables. Consequently, incorporating style directly in a generative model for rhythm may be redundant, as its influence can be represented through the other strongly associated variables, simplifying the model without sacrificing predictive accuracy.
2.2.2. Feature Importance Analysis
To determine the most influential variables for predicting both divisions and rhythm in the dataset, we used a Random Forest Classifier, configured with a test size of 0.2, 100 estimators, and a fixed random seed of 42 for reproducibility. This approach enables a robust assessment of feature importance by leveraging an ensemble of decision trees, each trained on a random subset of features and samples. Results are depicted in Figure 3 and Figure 4.
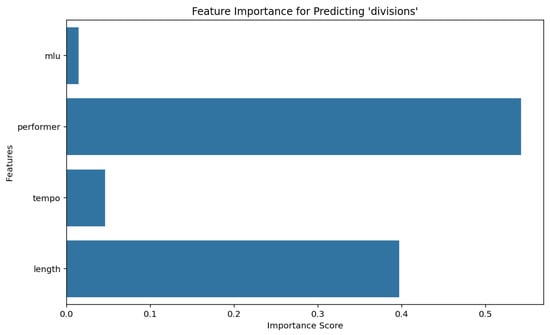
Figure 3.
Feature importance for predicting divisions using a Random Forest classifier.
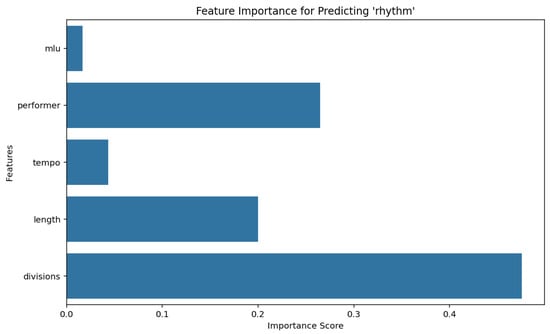
Figure 4.
Feature importance for predicting rhythm using a Random Forest classifier.
The analysis was conducted in two stages, as summarized in Figure 3 and Figure 4. This sequential design is motivated by the fact that divisions play a foundational role in shaping rhythmic patterns and must be generated before rhythm.
- Prediction of divisions: First, we trained a Random Forest model to predict divisions. The feature importance results indicated which variables significantly contribute to the formation of divisions in the dataset.
- Prediction of rhythm given divisions: In the second stage, we trained a separate Random Forest model to predict rhythm, using divisions as one of the predictive features. By analyzing the feature importances for rhythm, we identified the variables most critical to defining rhythmic structures once divisions had been established.
2.2.3. Justification for Sequential Generation of Variables
The results from the feature importance analysis support a sequential approach in generating divisions before rhythm. The high dependency of rhythm on divisions implies that attempting to predict rhythm prior to generating divisions would introduce inaccuracies and result in less coherent patterns. This sequential generation aligns with the underlying structure of jazz phrasing, where rhythmic patterns (rhythm) are heavily informed by subdivisions and meter (divisions). Consequently, by first predicting divisions and then utilizing it as an input for predicting rhythm, we achieve a more reliable model that reflects the dependencies inherent in the data.
2.2.4. Determining Dependent and Independent Variables in Bigrams
To understand the interdependencies within bigram-level representations of musical phrases, we analyze the associations between key categorical variables using Cramér’s V. This statistical measure quantifies the strength of association between pairs of categorical variables, helping to identify which variables are closely related and which are largely independent. Figure 5 presents the pairwise associations, where values close to 1 indicate strong relationships and values near 0 denote weak or no dependency. This analysis provides a basis for selecting dependent and independent variables, revealing both strongly coupled pairs (such as style and performer) and more isolated variables (such as position) within the context of bigram-based rhythmic modeling.
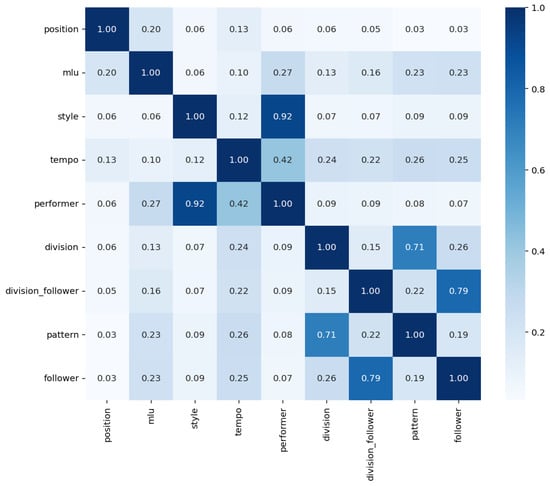
Figure 5.
Association matrix (Cramér’s V) for categorical variables in bigrams.
- Strong Associations:
- –
- style and performer exhibit a very strong association (0.9205), suggesting that particular styles are closely associated with specific performers.
- –
- division_follower and follower show a high association (0.7900), indicating that the follower division is strongly influenced by the division_follower variable.
- –
- division and pattern also show a significant association (0.7091), suggesting that divisions are closely tied to specific patterns.
- Moderate Associations:
- –
- tempo and performer have a moderate association (0.4150), indicating that certain tempos may be more common among particular performers.
- –
- tempo and pattern (0.2566), as well as division and follower (0.2564), display moderate associations. This suggests some influence of tempo and division on pattern and follower, respectively.
- –
- mlu and performer (0.2729), as well as mlu and follower (0.2333), show moderate associations, indicating that mlu values may correlate with specific performers and followers.
- Weak or Low Associations:
- –
- Variables such as position show low associations with most other variables, with the highest association being 0.1971 with mlu. This indicates that position is relatively independent in the dataset.
- –
- division_follower has weak associations with most variables except for follower and pattern.
- –
- The relationships between style and variables like division (0.0709) and division_follower (0.0685) are also weak, suggesting minimal dependence.
- Conclusion: Overall, the dataset contains both strong and weak associations among the variables. Strong associations, such as between style and performer or division_follower and follower, suggest dependencies that may be useful for modeling. However, variables with low association values, such as position, are relatively independent and might contribute less directly to predictive models targeting other variables.
2.2.5. Feature Importance Analysis with Random Forest Classifier
To determine the most influential variables for predicting both pattern and division follower in the dataset, we used a Random Forest Classifier, configured with a test size of 0.2, 100 estimators, and a fixed random state of 42 for reproducibility. This approach enables a robust assessment of the importance of features using a set of decision trees, each trained on a random subset of features and samples. Results are depicted in Figure 6 and Figure 7.
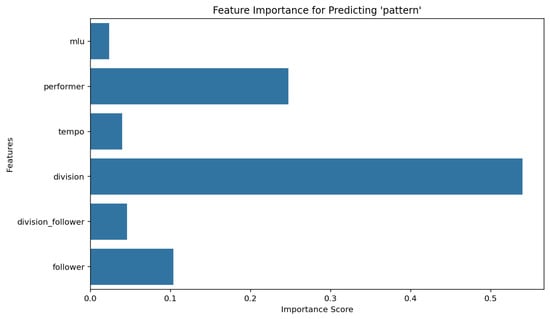
Figure 6.
Feature importance for predicting pattern using a Random Forest classifier.
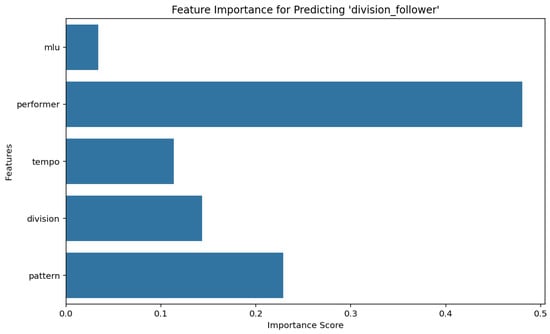
Figure 7.
Feature importance for predicting division follower using a Random Forest classifier.
2.3. Generative Method
This section details the phrase-oriented generative method for rhythmic patterns, which forms the core of this paper. As discussed in the previous section, we consider performer, tempo, and mlu as independent variables. Consequently, it is assumed that these variables are already defined when generating the rhythmic pattern for a phrase. The first step involves generating the length (in beats) of the phrase, using the probabilities of length occurrences conditioned on the given combination of the three initial variables (performer, tempo, and mlu). If a predefined target length is specified, this step can be omitted.
Once the four initial parameters are established, the next step is to generate the sequence of divisions within the phrase using a Markov chain approach. The first division in the sequence, called seed division, is randomly selected based on the probabilities of the first division values in the original dataset for the combination of parameters given. Subsequent divisions are generated stochastically, using a Markov transition matrix that encodes the probabilities of division transitions within the filtered portion of the training dataset (filtered by performer, tempo, and mlu). If a “0” division is generated at any step, a new seed division is selected, and the process continues.
Following the generation of the division sequence, a probability matrix is constructed based on the filtered dataset and the specific divisions present in the sequence. This matrix is then used to probabilistically generate the corresponding rhythmic pattern. For each division in the sequence, a segment of the rhythmic pattern is sampled and appended to form the full phrase-level rhythmic structure.
Figure 8 illustrates this process step by step, showing how a division sequence is first generated using a Markov chain model and subsequently transformed into a rhythmic pattern sequence. This example corresponds directly to Sample 1 (John Coltrane, Line Up), where the final output rhythmic pattern is [1101, 01, 11, 11, 11], as also shown in Figure 9. The complete generative method is formally described in Algorithm 1.
| Algorithm 1: Phrase-oriented generative method for rhythmic patterns |
 |
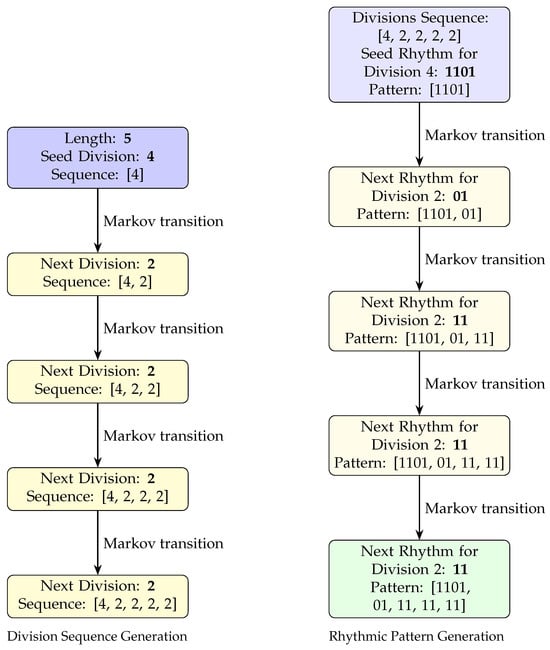
Figure 8.
Step-by-step division sequence and rhythmic pattern generation, exemplified with Sample 1.

Figure 9.
Sample 1–John Coltrane, Line Up, generated rhythmic pattern: 1101,01,11,11,11.
From a musical perspective, low-order Markov chains provide a desirable balance between predictability and variability. First-order transitions capture local dependencies between adjacent divisions or rhythmic patterns, enabling stylistically coherent outputs, while still allowing for enough stochasticity to generate creative variation. Higher-order models, on the other hand, tend to reproduce longer deterministic subsequences from the training data, thereby reducing generative novelty and potentially leading to overfitting. Conversely, purely random or uniform selection mechanisms neglect stylistic coherence altogether. Therefore, the adoption of low-order Markov chains is not only computationally efficient and data-appropriate, but also musically aligned with the objective of generating coherent yet varied rhythmic sequences.
3. Results
Before generating new phrases, the original datasets (phrases and bigrams) were randomly shuffled and split into separate training and test sets. The original phrases dataset was divided into phrases_train.csv containing 80% of the records (5246 entries) and phrases_test.csv containing the remaining 20% (1312 entries). Similarly, the bigrams dataset was split into bigrams_train.csv with 52,297 records and bigrams_test.csv with 13,075 records.
The training subsets were used to train the generative method described in Section 2.3. Once trained, this method was used to generate a new dataset of phrases for evaluation purposes. To ensure a fair comparison, the size of the generated dataset matches that of the test dataset.
In the remainder of this section, we present a statistical validation of the generative method by comparing the generated data to the original test sets. Following the quantitative assessment, we showcase a selection of listenable jazz solos generated by the model to illustrate its musical effectiveness and stylistic plausibility.
3.1. Phrases Statistics: Test vs. Generated
Table 4 presents a comparison of descriptive statistics between the test and generated datasets, focusing on the notes (number of notes per phrase) and length (duration in beats) features. The means are nearly identical for both features—16.36 vs. 16.31 for notes and 8.40 for length in both cases—indicating that the generative model accurately reproduces the average phrase size and duration found in the original data. The standard deviations are also closely aligned, suggesting that the generative model maintains the same variability as the original dataset. Minimum and maximum values match exactly, showing that the generated data spans the same range as the original. The percentiles (25th, 50th, and 75th) further confirm this correspondence, though a slight deviation appears in the 75th percentile of length (12 vs. 11), hinting at a modest tendency toward slightly longer phrases in the generated data. Overall, these statistics suggest that the generated phrases exhibit strong statistical similarity to the original phrases in terms of both note count and temporal structure. This alignment supports the model’s ability to replicate key surface-level features of the original corpus.

Table 4.
Comparison of descriptive statistics between original and generated data for the notes and length features.
Figure 10 presents a comparison of the distributions of key features between the test and generated datasets. Subfigure (a) shows the frequency of phrases per performer, ordered in descending order of occurrence. The generated data successfully mirrors the overall distribution, suggesting that the model captures performer-specific stylistic tendencies. Subfigure (b) displays the distribution of phrase lengths in beats, where a close match can be observed, with both datasets exhibiting a similar range and modal values. Subfigure (c) focuses on the MLU (line and lick), showing strong alignment between datasets. Finally, Subfigure (d) compares the distribution of tempo values, revealing that the generative model effectively maintains the temporal context of the original phrases. Together, these plots provide evidence that the model retains crucial categorical and numerical distributional properties from the source material.
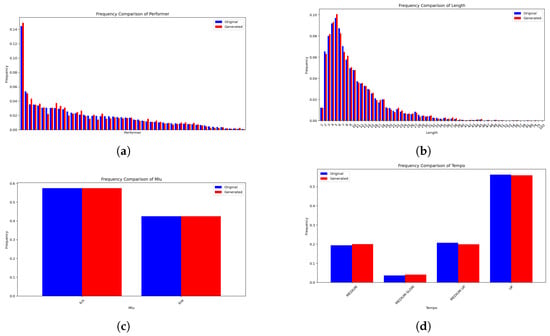
Figure 10.
Frequencies comparison in phrases between original (test) and generated data. (a) Performer (ordered by frequency descending). (b) Length. (c) MLU. (d) Tempo.
3.1.1. Statistical Tests for Notes in Phrases
To assess the similarity between the test and generated datasets for the variable notes, we performed three statistical tests: T-test, Kolmogorov–Smirnov (KS) test, and Mann–Whitney U test. The results are as follows:
- T-test: t-statistic = 0.2430, p-value = 0.8080. Since the p-value is greater than 0.05, we conclude there is no significant difference in the means of notes between the test and generated datasets. This indicates that the generative model produces phrases with a similar average number of notes.
- KS-test (Kolmogorov–Smirnov): KS-statistic = 0.0061, p-value = 0.9998. The high p-value suggests no significant difference in the overall distribution of notes between datasets. This result implies that the generative model closely replicates the distribution of notes.
- Mann–Whitney U: U-statistic = 18,429,602.5000, p-value = 0.8829. The p-value further confirms no significant difference in the ranks of notes values, indicating similar distributions and order between the test and generated datasets.
Figure 11 presents a comparative evaluation of the notes variable between test and generated phrases. The left panel shows a KDE (Kernel Density Estimate) plot, highlighting the distribution similarity between the original dataset (blue) and the generated dataset (red). The right panel presents boxplots for both datasets, illustrating comparable medians, interquartile ranges, and the presence of outliers. The analysis demonstrates that the generative model closely replicates the statistical properties of the original data in terms of the number of notes per phrase.
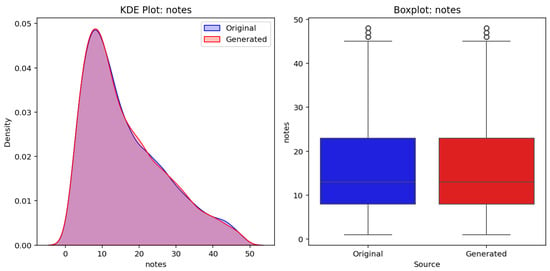
Figure 11.
Comparative evaluation of the notes variable between original (test) and generated phrases.
3.1.2. Statistical Tests for Length in Phrases
As before, to assess the similarity between the test and generated phrases datasets for the variable length, we performed the same three statistical tests: T-test, Kolmogorov–Smirnov (KS) test, and Mann–Whitney U test. The results are as follows:
- T-test: t-statistic = −0.0673, p-value = 0.9463. The p-value is well above 0.05, showing no significant difference in the means of length between datasets. This suggests that the generative model produces phrases with lengths close to those of the original data.
- KS-test: KS-statistic = 0.0056, p-value = 1.0000. This high p-value suggests that the distribution of length is nearly identical between the test and generated datasets.
- Mann–Whitney U: U-statistic = 18,392,262.0000, p-value = 0.9629. The p-value further supports that there is no significant difference in the distribution ranks of length values between the datasets.
Figure 12 shows a comparison of the length variable between original test and generated phrases. The left panel presents a KDE plot, showcasing the distribution overlap between the original dataset (blue) and the generated dataset (red), indicating similar statistical properties. The right panel displays boxplots for both datasets, illustrating the central tendency and variability. The results suggest that the generative model maintains a comparable distribution for phrase lengths, with minimal discrepancies between the two datasets.
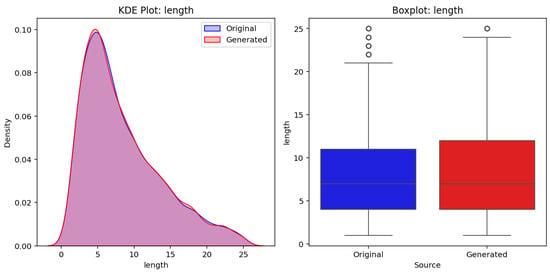
Figure 12.
Comparative evaluation of the length variable between original (test) and generated phrases.
3.1.3. PCA-Based Analysis of Notes and Length in Phrases
To conclude the statistical evaluation of the phrase generation method, Figure 13 presents a PCA (Principal Component Analysis) projection of the original and generated phrases based on the variables notes and length. The scatter plot illustrates the distribution of data points in a reduced two-dimensional space, where blue points correspond to the original dataset and red points to the generated dataset. The substantial overlap between the two distributions indicates that the generative model successfully captures and preserves the underlying structure of the original data in terms of phrase characteristics.
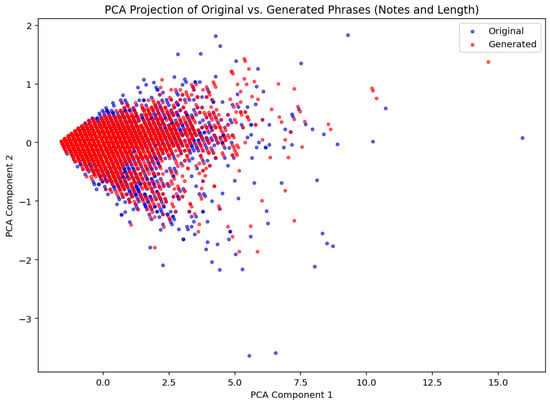
Figure 13.
PCA projection of the original (test) and generated phrases, based on the variables notes and length.
3.2. Bigrams Statistics: Test vs. Generated
From the generated phrases dataset (phrases_generated.csv), we extracted the corresponding bigrams dataset (bigrams_generated.csv). This section presents an evaluation of the generated bigrams by comparing them with the test bigrams dataset (bigrams_test.csv), which contains the 20% of the original data reserved for testing and not used during model training.
Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 show the frequency comparison of the top 95% most frequent values for the variables pattern and division follower across different tempo and MLU categories. Each row represents a distinct tempo–MLU pair: UP, MEDIUM UP, MEDIUM, and MEDIUM SLOW. For each pair, the left plot illustrates the distribution of pattern values (Figure 14, Figure 16, Figure 18 and Figure 20), while the right plot displays the distribution of division follower values (Figure 15, Figure 17, Figure 19 and Figure 21). The visualizations highlight notable similarities between the test and generated datasets, suggesting that the generative method accurately captures the distributional structure of these variables across different rhythmic and temporal contexts.
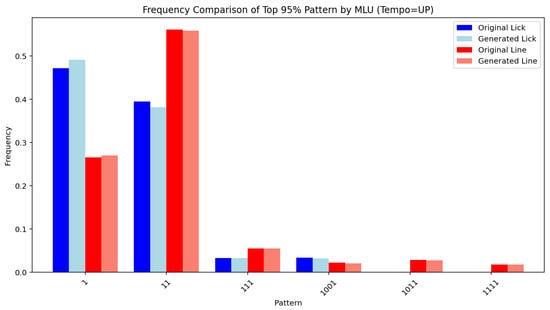
Figure 14.
Pattern (UP).
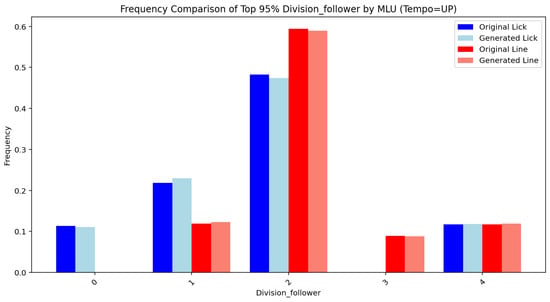
Figure 15.
Division follower (UP).
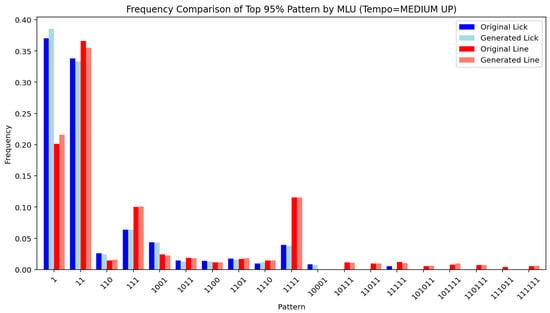
Figure 16.
Pattern (MEDIUM UP).
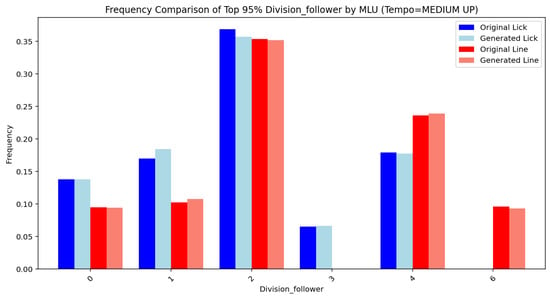
Figure 17.
Division follower (MEDIUM UP).
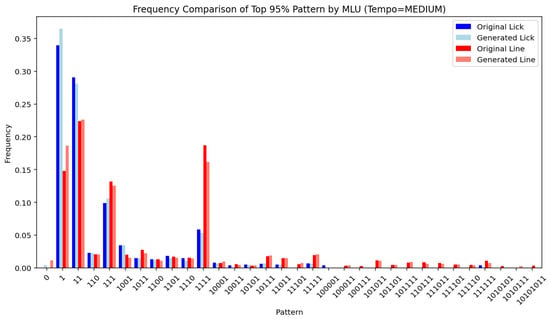
Figure 18.
Pattern (MEDIUM).
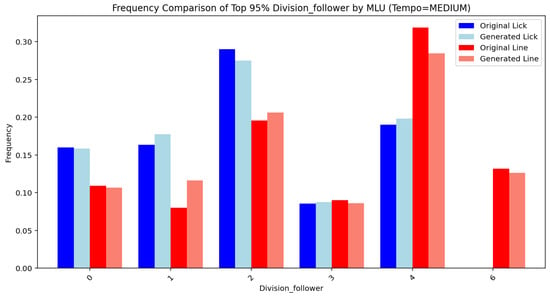
Figure 19.
Division follower (MEDIUM).
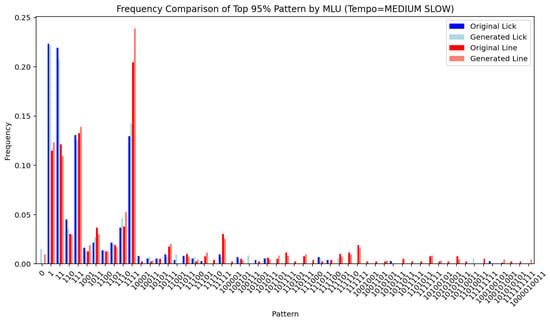
Figure 20.
Pattern (MEDIUM SLOW).
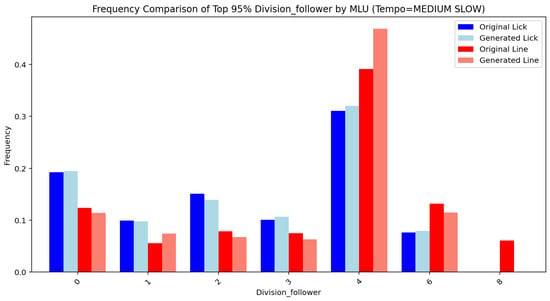
Figure 21.
Division follower (MEDIUM SLOW).
3.2.1. Statistical Tests for Pattern in Bigrams
We conducted statistical tests to evaluate the similarity between the test and generated datasets for the variable pattern. The following results were obtained:
- T-test: t-statistic = −0.0943, p-value = 0.9249. Since the p-value is greater than 0.05, there is no significant difference in the means of pattern between the datasets. This suggests that the generative model is producing patterns with similar average values as the original dataset.
- KS-test (Kolmogorov–Smirnov): KS-statistic = 0.0174, p-value = 0.9777. The p-value indicates no significant difference in the overall distribution of pattern between the test and generated datasets, suggesting that the generative model closely replicates the original distribution.
- Mann–Whitney U: U-statistic = 1,133,057.0000, p-value = 0.5512. The p-value suggests no significant difference in the ranks of pattern values, indicating that the generative model produces a similar distribution and order of patterns.
Moreover, Figure 22 presents the analysis of the variable pattern for the original test and generated datasets. The left panel shows a KDE plot comparing the density distributions of the original test (blue) and generated (red) datasets, demonstrating strong alignment in the overall shapes and spreads. The right panel presents a boxplot of pattern, highlighting similarities in medians, interquartile ranges, and the distribution of outliers between the two datasets. These results indicate the generative model’s ability to replicate the statistical properties of pattern effectively.
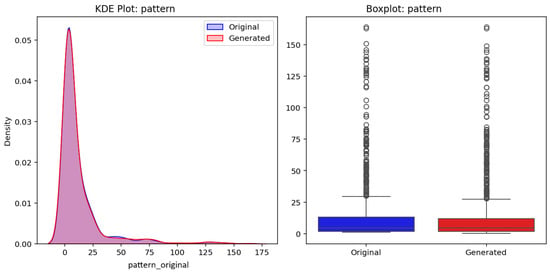
Figure 22.
Evaluation of the variable pattern for the original test (blue) and generated (red) datasets.
3.2.2. Statistical Tests for Division_Follower in Bigrams
As for the pattern_encoded variable, we also conducted statistical tests to evaluate the similarity between the test and generated datasets for the variables division_follower. The following results were obtained:
- T-test: t-statistic = 0.2752, p-value = 0.7832. The p-value indicates no significant difference in the means of division_follower between the datasets, showing that the generative model approximates the average values of the original dataset.
- KS-test: KS-statistic = 0.0261, p-value = 0.6897. This result indicates no significant difference in the overall distribution of division_follower, suggesting that the generative model is producing values with a similar distribution to the original data.
- Mann–Whitney U: U-statistic = 1,131,436.0000, p-value = 0.5988. The p-value suggests no significant difference in ranks, further confirming the similarity in distribution and order of division_follower values between the original test and generated datasets.
Moreover, Figure 23 presents the evaluation of the variable division_follower for the test and generated datasets. The left panel shows a KDE plot comparing the density distributions of the original test (blue) and generated (red) datasets, indicating close alignment in their shapes and spreads. The right panel presents a boxplot of the same variable, illustrating similarities in medians, interquartile ranges, and the distribution of outliers between the two datasets. Overall, the results demonstrate the generative model’s effectiveness in reproducing the statistical properties of division_follower.
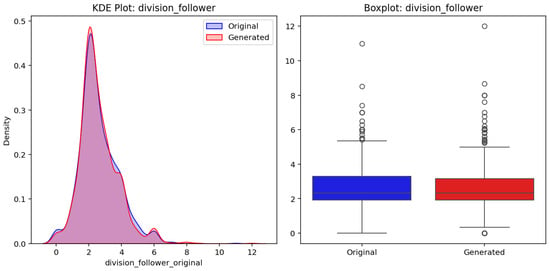
Figure 23.
Evaluation of the variable division_follower for the original test (blue) and generated (red) datasets.
3.3. Generative Music Solos Examples
To complement the statistical evaluation, we present a set of illustrative examples demonstrating the generative model’s output in a musically meaningful form. These examples highlight the model’s ability to reproduce stylistically coherent jazz rhythmic phrases under varying conditions of tempo. The harmonic context for each example was generated using the method proposed by Raposo and Soares [37], which produces plausible jazz chord progressions. The accompanying bass lines were created by arpeggiating the notes of the underlying chords, providing harmonic grounding and forward motion. Melodic solo lines were constructed using arbitrary sequences of chord tones to maintain harmonic coherence.
Most importantly, the rhythmic patterns of the solos were generated using the method presented in this paper, showcasing the model’s effectiveness in producing realistic and stylistically appropriate jazz rhythms.
3.3.1. Example 1 (300 BPM)
The example solo presented in Figure 24 was generated at a fast tempo (300 BPM), highlighting the model’s ability to maintain rhythmic coherence and stylistic integrity even under high-speed conditions. The solo features syncopations, rests, and phrase groupings that reflect common rhythmic practices in bebop and hard bop styles. The full arrangement, including accompaniment, can be listened to at https://musescore.com/user/101346721/scores/26537644 (accessed on 12 October 2025).

Figure 24.
Solo example 1 (300 BPM). It can be heard in context with accompaniment at https://musescore.com/user/101346721/scores/26537644 (accessed on 12 October 2025).
3.3.2. Example 2 (200 BPM)
The example solo presented in Figure 25 was generated at a medium tempo (200 BPM), allowing for more space between phrases and a different rhythmic feel. In this example, the generative model produces longer note durations, smoother transitions, and occasional anticipations, illustrating its adaptability across different rhythmic contexts. The complete audio, including harmonic and bass accompaniment, can be heard at https://musescore.com/user/101346721/scores/26538247 (accessed on 12 October 2025).

Figure 25.
Solo example 2 (200 BPM). It can be heard in context with accompaniment at https://musescore.com/user/101346721/scores/26538247 (accessed on 12 October 2025).
3.3.3. Example 3 (148 BPM)
The example solo presented in Figure 26, was generated at a slower tempo of 148 BPM, providing space for greater rhythmic nuance and expressive phrasing. This example demonstrates the model’s capability to produce relaxed, swing-inspired patterns that balance syncopation with sustained notes. The rhythm exhibits characteristic features of medium swing jazz, including offbeat accents and varied note groupings. The full version, including accompaniment, can be heard at https://musescore.com/user/101346721/scores/26538610 (accessed on 12 October 2025).

Figure 26.
Solo example 3 (148 BPM). It can be heard in context with accompaniment at https://musescore.com/user/101346721/scores/26538610 (accessed on 12 October 2025).
3.3.4. Supplementary Examples
A set of generated solos for popular jazz standards is included as MIDI files in the Supplementary Materials (see Table 5). These examples allow experienced jazz listeners to assess the stylistic coherence and rhythmic plausibility of the generated solos, providing a qualitative evaluation of the model’s output across different tempos. The MIDI files represent performances by a jazz ensemble trio—upright bass, piano, and tenor saxophone. While the files are computer-generated and not performed by humans, which may influence the realism of the instrumental interpretation, they nevertheless convey the human-like feel and stylistic character of the generated solos.

Table 5.
Generated jazz solos included as Supplementary MIDI files.
4. Discussion
The statistical evaluation of the generative model provides a detailed understanding of its ability to replicate essential characteristics of the original dataset. By employing rigorous statistical tests—including the T-test, Kolmogorov–Smirnov (KS) test, and Mann–Whitney U test—the analysis assesses the degree of alignment between the generated and original data in terms of central tendency, distribution shape, and rank-based similarity. These complementary tests offer a robust and multifaceted perspective on the model’s performance.
For the variables notes and length, the results reveal no statistically significant differences between the generated and original datasets. This suggests that the model effectively captures the note density and phrase durations characteristic of the original jazz solos. Similarly, the variables pattern_encoded and division_follower, which reflect rhythmic motifs and structural transitions, also show no significant differences across all tested conditions. These findings indicate that the model successfully replicates both local rhythmic detail and higher-level temporal structure.
A direct comparison with existing methods was not conducted, as—to the best of our knowledge—no prior work focuses exclusively on rhythm generation for jazz solos. While some generative systems explore melody, harmony, or multi-dimensional music generation, rhythm is often treated as a secondary feature rather than a standalone creative axis. Our work therefore fills an important gap by emphasizing rhythm generation as an independent and central objective in the context of jazz improvisation.
To complement the statistical analysis, we also provide audio examples of the generated phrases. While subjective, these examples offer an opportunity for musical and artistic evaluation, inviting listeners to assess the stylistic plausibility and expressive qualities of the outputs. Despite these encouraging results, some limitations remain. The current evaluation framework focuses on statistical similarity rather than musical expressiveness or creative value, which are inherently subjective and harder to quantify. Additionally, the model does not yet incorporate rest positions between phrases, an essential element for achieving natural phrasing and articulation in jazz. Furthermore, the analysis is limited to a specific subset of variables—mainly rhythm-related—leaving expressive dimensions such as dynamics, articulation, and microtiming unaddressed.
Future work will aim to address these limitations and extend the model’s capabilities. Planned developments include the integration of rest handling to produce more natural and expressive rhythms, the addition of a pitch-generation module to enable full solo creation, and the modeling of expressive parameters such as dynamics, articulation, and phrasing. To evaluate the artistic quality and creative potential of the generated material, we also intend to conduct user studies involving both expert musicians and general listeners. These efforts aim to bridge the gap between statistical fidelity and artistic expression, ultimately contributing to a more musically meaningful approach to generative jazz solo creation.
5. Conclusions
This study presented a novel generative method for creating phrase-oriented rhythmic patterns in jazz solos, grounded in a thorough statistical analysis of the Weimar Jazz Database. By modeling the intricate relationships among rhythmic elements such as phrases, beats, divisions, and patterns within a Markov chain framework, the proposed approach successfully synthesizes rhythmic sequences that maintain stylistic coherence and diversity.
The comprehensive evaluation, combining statistical analyses with illustrative musical examples, demonstrated that the generative method produces rhythmic patterns that are both realistic and musically convincing. These results indicate that the model successfully captures the essential rhythmic characteristics of jazz solos, while still allowing for creative variation. While it might seem that the method merely reproduces dataset statistics, generating coherent and stylistically plausible jazz rhythms at the phrase level is far from a trivial task. To the best of our knowledge, this specific problem—modeling and generating phrase-level rhythmic structures in jazz solos using a statistically principled approach—has not been previously addressed. The ability of our method to produce novel, musically coherent rhythmic patterns that retain the stylistic characteristics of the original dataset represents a meaningful contribution, both from a methodological and a creative perspective.
Overall, this work contributes a valuable tool for computational creativity and algorithmic music composition, offering promising applications in jazz generation systems. Future research may explore extending this framework to incorporate melodic and harmonic dimensions, further enriching the authenticity and expressiveness of generated jazz solos.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/app152011058/s1, GenJazz_075bpm_Autumn_Leaves.mid, GenJazz_090bpm_Misty.mid, GenJazz_120bpm_Blue_Bossa.mid, GenJazz_140bpm_So_What.mid, GenJazz_160bpm_Take_The_A_Train.mid, GenJazz_180bpm_Caravan.mid, GenJazz_200bpm_Donna_Lee.mid, GenJazz_260bpm_Giant_Steps.mid.
Author Contributions
Conceptualization, A.N.R. and V.N.G.J.S.; methodology, A.N.R. and V.N.G.J.S.; software, A.N.R.; validation, V.N.G.J.S.; formal analysis, A.N.R. and V.N.G.J.S.; data curation, A.N.R.; writing—original draft preparation, A.N.R. and V.N.G.J.S.; writing—review and editing, A.N.R. and V.N.G.J.S.; funding acquisition, V.N.G.J.S. All authors have read and agreed to the published version of the manuscript.
Funding
V.N.G.J.S. and A.N.R. acknowledge that work is funded by FCT/MECI through national funds and when applicable co-funded EU funds under UID/50008: Instituto de Telecomunicações.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The authors would like to thank Klaus Frieler for granting access to the dataset and for his valuable suggestions, which greatly contributed to the development of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WJD | Weimar Jazz Database |
| MLU | Midlevel Unit |
| KDE | Kernel Density Estimate |
| PCA | Principal Component Analysis |
References
- Ó Nuanáin, C. Connecting Time and Timbre: Computational Methods for Generative Rhythmic Loops in Symbolic and Signal Domains. Ph.D. Thesis, Universitat Pompeu Fabra, Barcelona, Spain, 2018. [Google Scholar]
- Daikoku, T. Temporal dynamics of uncertainty and prediction error in musical improvisation across different periods. Sci. Rep. 2024, 14, 22297. [Google Scholar] [CrossRef] [PubMed]
- Naruse, D.; Takahata, T.; Mukuta, Y.; Harada, T. Pop Music Generation with Controllable Phrase Lengths. In Proceedings of the 23rd International Society for Music Information Retrieval Conference, ISMIR 2022, Bengaluru, India, 4–8 December 2022; pp. 125–131. [Google Scholar]
- Bhandari, K.; Colton, S. Motifs, Phrases, and Beyond: The Modelling of Structure in Symbolic Music Generation. arXiv 2024, arXiv:2403.07995. [Google Scholar] [CrossRef]
- Pfleiderer, M.; Frieler, K.; Abeßer, J.; Zaddach, W.G.; Burkhart, B. (Eds.) Inside the Jazzomat–New Perspectives for Jazz Research; Schott Campus: Mainz, Germany, 2017. [Google Scholar]
- Corcoran, C.; Frieler, K. Playing It Straight: Analyzing Jazz Soloists’ Swing Eighth-note Distributions with the Weimar Jazz Database. Music Percept. 2021, 38, 372–385. [Google Scholar] [CrossRef]
- Frieler, K.; Basaran, D.; Höger, F.; Crayencour, H.C.; Peeters, G.; Dixon, S. Don’t hide in the frames: Note- and pattern-based evaluation of automated melody extraction algorithms. In Proceedings of the 6th International Conference on Digital Libraries for Musicology, DLfM ’19, The Hague, The Netherlands, 9 November 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 25–32. [Google Scholar] [CrossRef]
- Frieler, K. Miles Vs. Trane: Computational and Statistical Comparison of the Improvisatory Styles of Miles Davis and John Coltrane. Jazz Perspect. 2020, 12, 123–145. [Google Scholar] [CrossRef]
- Cross, P.; Goldman, A. Interval patterns are dependent on metrical position in jazz solos. Music. Sci. 2023, 27, 299–312. [Google Scholar] [CrossRef]
- Wu, S.; Yang, Y. The Jazz Transformer on the Front Line: Exploring the Shortcomings of AI-composed Music through Quantitative Measures. arXiv 2020, arXiv:2008.01307. [Google Scholar] [CrossRef]
- Frieler, K.; Höger, F.; Pfleiderer, M.; Dixon, S. Two Web Applications for Exploring Melodic Patterns in Jazz Solos. In Proceedings of the 19th International Society for Music Information Retrieval Conference (ISMIR), Paris, France, 23–27 September 2018; pp. 32–39. [Google Scholar]
- Dittmar, C.; Pfleiderer, M.; Balke, S.; Müller, M. A swingogram representation for tracking micro-rhythmic variation in jazz performances. J. New Music Res. 2018, 47, 97–113. [Google Scholar] [CrossRef]
- Biles, J. GenJam: A Genetic Algorithm for Generation Jazz Solos. In Proceedings of the International Computer Music Conference, Aarhus, Denmark, 12–17 September 1994; pp. 131–137. [Google Scholar]
- Merz, E. Implications of Ad Hoc Artificial Intelligence in Music. In Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment, Virtual, 11–15 October 2021; Volume 10, pp. 35–39. [Google Scholar] [CrossRef]
- Wiggins, G.; Papadopoulos, G. A genetic algorithm for the generation of jazz melodies. In Proceedings of the Finnish Conference on Artificial Intelligence (STeP’98), Jyväskylä, Finnland, 7–9 September 1998. [Google Scholar]
- Miranda, E.R.; Biles, J.A. (Eds.) Evolutionary Computer Music; Springer: London, UK, 2007. [Google Scholar] [CrossRef]
- Nam, Y.W.; Kim, Y.H. Automatic Jazz Melody Composition Through a Learning-Based Genetic Algorithm. In Proceedings of the Computational Intelligence in Music, Sound, Art and Design, Leipzig, Germany, 24–26 April 2019; Springer: Cham, Switzerland, 2019; pp. 217–233. [Google Scholar]
- Bäckman, K.; Dahlstedt, P. A Generative Representation for the Evolution of Jazz Solos. In Proceedings of the Applications of Evolutionary Computing, Naples, Italy, 26–28 March 2008; Giacobini, M., Brabazon, A., Cagnoni, S., Di Caro, G.A., Drechsler, R., Ekárt, A., Esparcia-Alcázar, A.I., Farooq, M., Fink, A., McCormack, J., et al., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 371–380. [Google Scholar]
- Gillick, J.; Tang, K.; Keller, R.M. Machine Learning of Jazz Grammars. Comput. Music J. 2010, 34, 56–66. [Google Scholar] [CrossRef]
- Putman, A.M.; Keller, R.M. A Transformational Grammar Framework for Improvisation. In Proceedings of the First International Conference on New Music Concepts (ICNMC), Treviso, Italy, 7–8 March 2015. [Google Scholar]
- Yaconelli, J.; Keller, R.M. Discovery and Utilization of Jazz Motifs for Computer-Generated Solos. In Proceedings of the 3rd Conference on Computer Simulation of Musical Creativity, Dublin, Ireland, 20–22 August 2018. [Google Scholar] [CrossRef]
- Bickerman, G.; Bosley, S.; Swire, P.; Keller, R.M. Learning to Create Jazz Melodies Using Deep Belief Nets. In Proceedings of the International Conference on Computational Creativity, Lisbon, Portugal, 7–9 January 2010; pp. 228–237. [Google Scholar]
- Trieu, N.; Keller, R.M. JazzGAN: Improvising with Generative Adversarial Networks. In Proceedings of the 6th International Workshop on Musical Metacreation (MUME 2018), Salamanca, Spain, 25–26 June 2018. [Google Scholar] [CrossRef]
- Hung, H.T.; Wang, C.Y.; Yang, Y.H.; Wang, H.M. Improving Automatic Jazz Melody Generation by Transfer Learning Techniques. In Proceedings of the 2019 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Lanzhou, China, 18–21 November 2019. [Google Scholar]
- Row, E.; Tang, J.; Fazekas, G. JAZZVAR: A Dataset of Variations found within Solo Piano Performances of Jazz Standards for Music Overpainting. arXiv 2023, arXiv:2307.09670. [Google Scholar] [CrossRef]
- Scirea, M.; Barros, G.; Shaker, N.; Togelius, J. SMUG: Scientific music generator. In Proceedings of the 6th International Conference on Computational Creativity, ICCC 2015, Park City, UT, USA, 29 June–2 July 2015; pp. 204–211. [Google Scholar]
- Frieler, K.; Zaddach, W.G. Evaluating an Analysis-by-Synthesis Model for Jazz Improvisation. Trans. Int. Soc. Music Inf. Retr. 2022, 5, 20–34. [Google Scholar] [CrossRef]
- Johnson, D.D.; Keller, R.M.; Weintraut, N. Learning to Create Jazz Melodies Using a Product of Experts. In Proceedings of the Eighth International Conference on Computational Creativity (ICCC), Atlanta, GA, USA, 19–23 June 2017. [Google Scholar]
- Kritsis, K.; Kylafi, T.; Kaliakatsos-Papakostas, M.; Pikrakis, A.; Katsouros, V. On the Adaptability of Recurrent Neural Networks for Real-Time Jazz Improvisation Accompaniment. Front. Artif. Intell. 2021, 3, 508727. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Composing jazz music pieces using LSTM neural networks approach. Appl. Comput. Eng. 2024, 68, 128–136. [Google Scholar] [CrossRef]
- Briot, J.P.; Hadjeres, G.; Pachet, F.D. Deep Learning Techniques for Music Generation; Springer: Cham, Switzerland, 2020; Volume 1. [Google Scholar]
- Yadav, P.S.; Khan, S.; Singh, Y.V.; Garg, P.; Singh, R.S. A Lightweight Deep Learning-Based Approach for Jazz Music Generation in MIDI Format. Comput. Intell. Neurosci. 2022, 2022, 2140895. [Google Scholar] [CrossRef] [PubMed]
- Miller, B.A. All of the Rules of Jazz: Stylistic Models and Algorithmic Creativity in Human-Computer Improvisation. Music Theory Online 2020, 26. [Google Scholar] [CrossRef]
- Hsu, C.; Greer, R. Comparative Assessment of Markov Models and Recurrent Neural Networks for Jazz Music Generation. arXiv 2023, arXiv:2309.08027. [Google Scholar] [CrossRef]
- Kaliakatsos-Papakostas, M.; Floros, A.; Vrahatis, M.N. Chapter 13–Artificial intelligence methods for music generation: A review and future perspectives. In Nature-Inspired Computation and Swarm Intelligence; Yang, X.S., Ed.; Academic Press: Cambridge, MA, USA, 2020; pp. 217–245. [Google Scholar] [CrossRef]
- Frieler, K.; Pfleiderer, M.; Zaddach, W.G.; Abeßer, J. Midlevel analysis of monophonic jazz solos: A new approach to the study of improvisation. Music. Sci. 2016, 20, 143–162. [Google Scholar] [CrossRef]
- Raposo, A.N.; Soares, V.N.G.J. Generative Jazz Chord Progressions: A Statistical Approach to Harmonic Creativity. Information 2025, 16, 504. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).