DARTS Meets Ants: A Hybrid Search Strategy for Optimizing KAN-Based 3D CNNs for Violence Recognition in Video
Abstract
1. Introduction
2. Related Work
2.1. Evolutionary Hyperparameter Tuning
2.2. Differentiable Architecture Search
2.3. KAN in Related Works
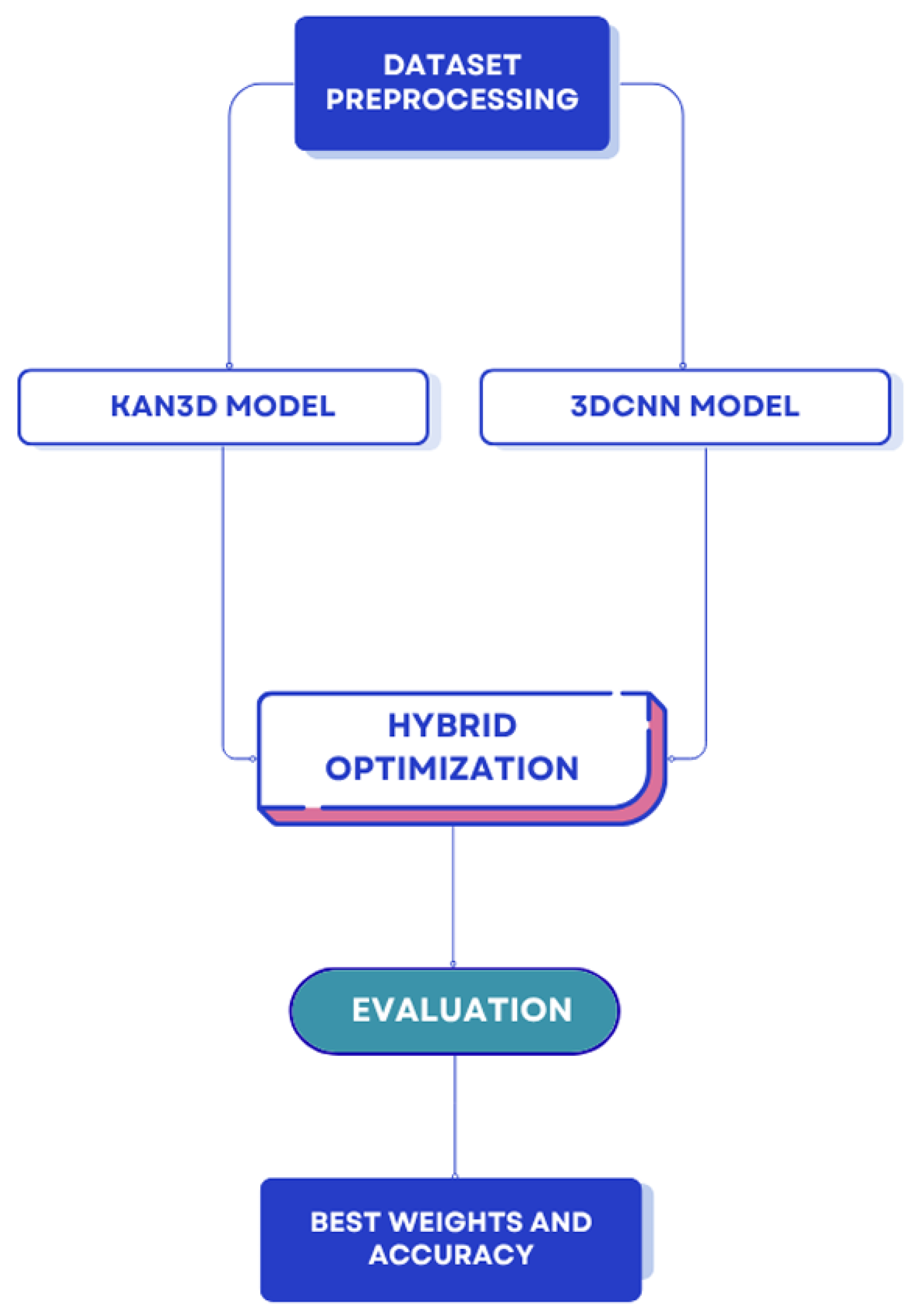
3. Methods
3.1. Dataset
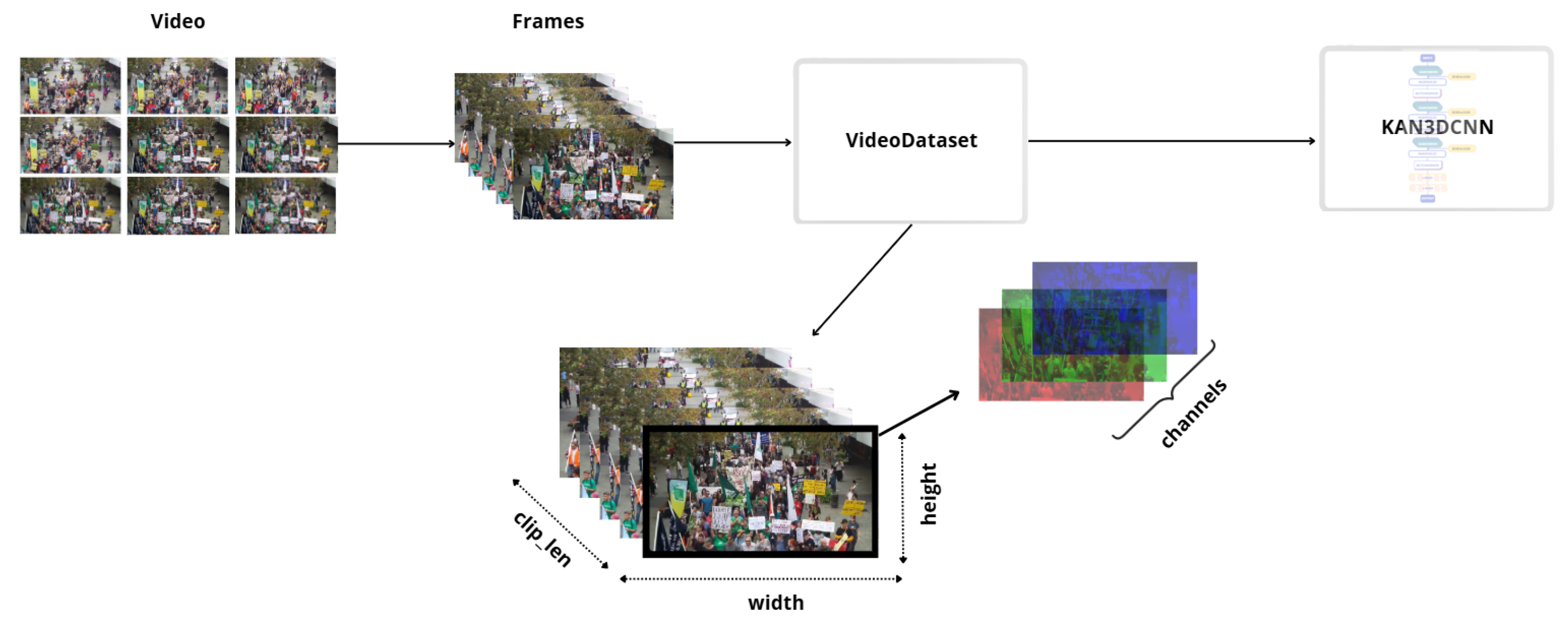
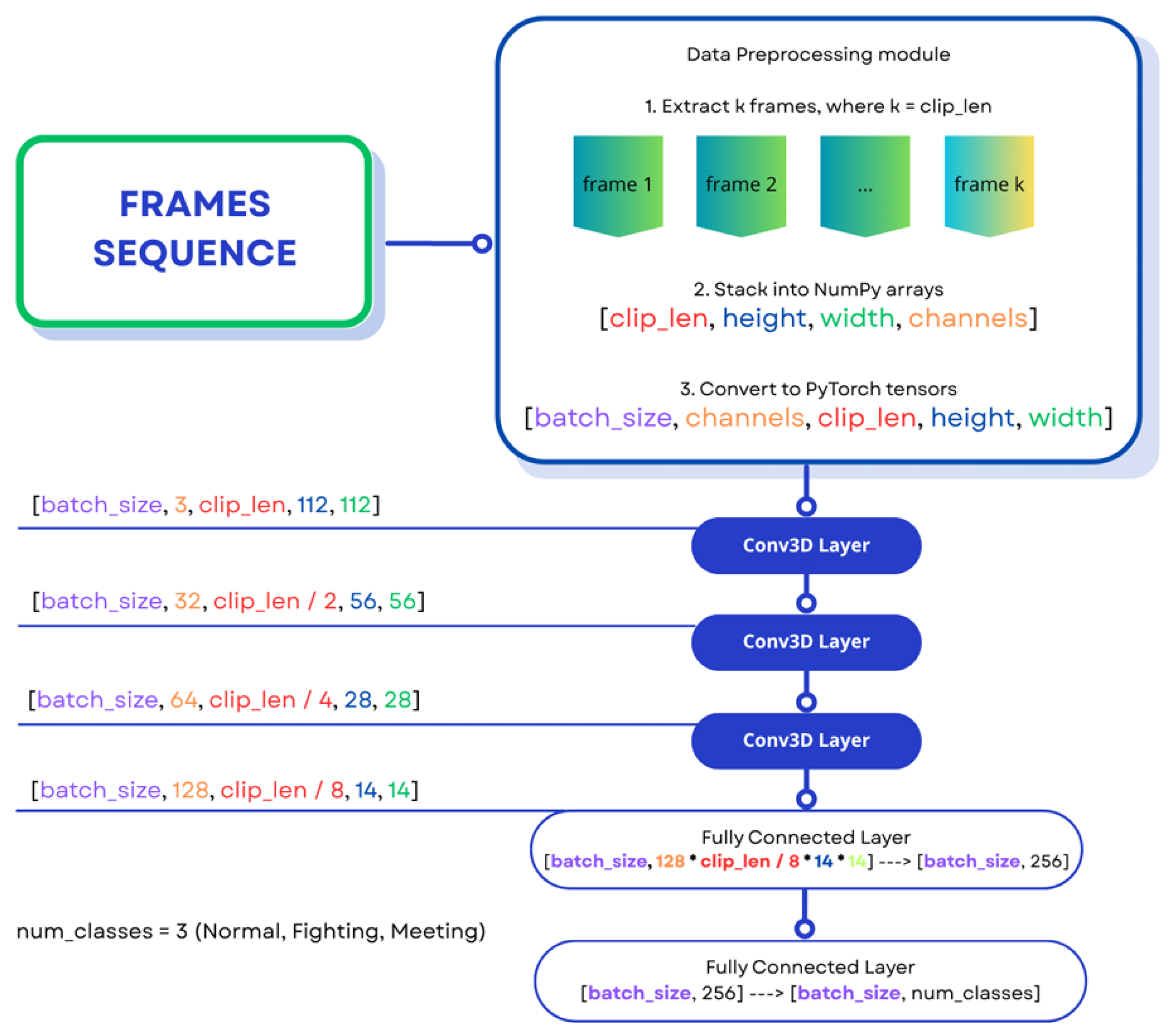
3.2. Dataflow in 3D-CNN
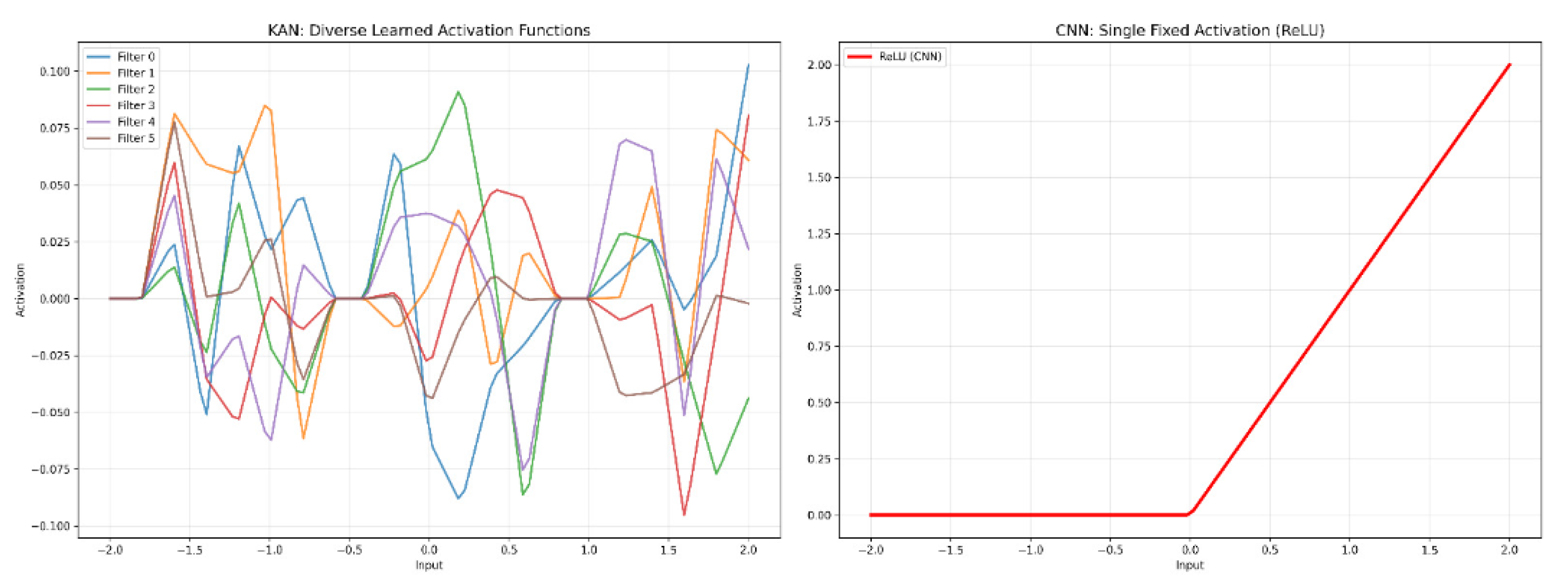
3.3. Dataflow in KAN3DCNN
3.4. Training
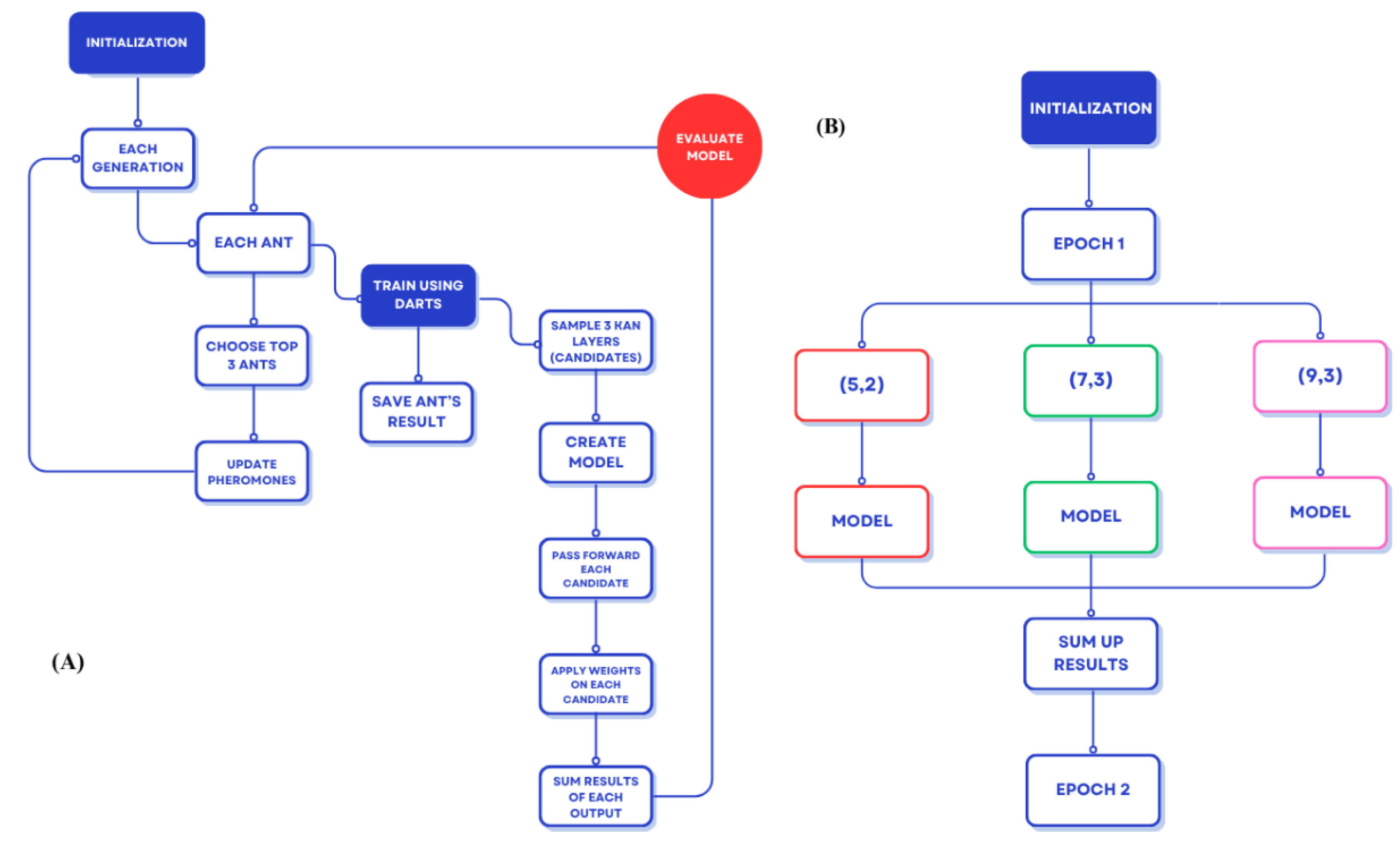
3.4.1. MMAS Level Training
3.4.2. DARTS Level Training
4. Evaluation
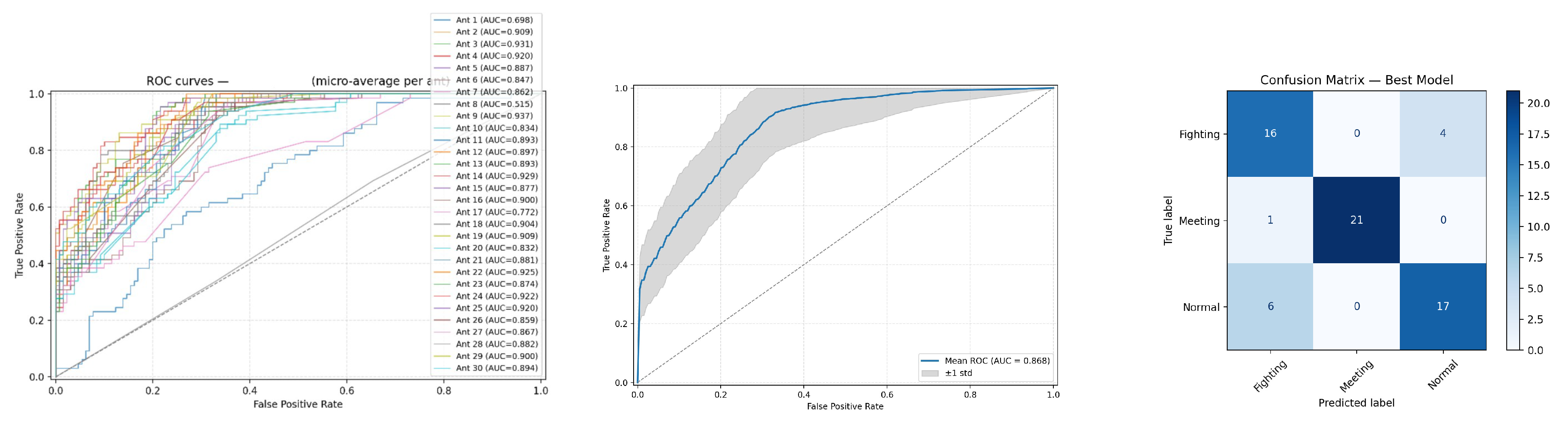
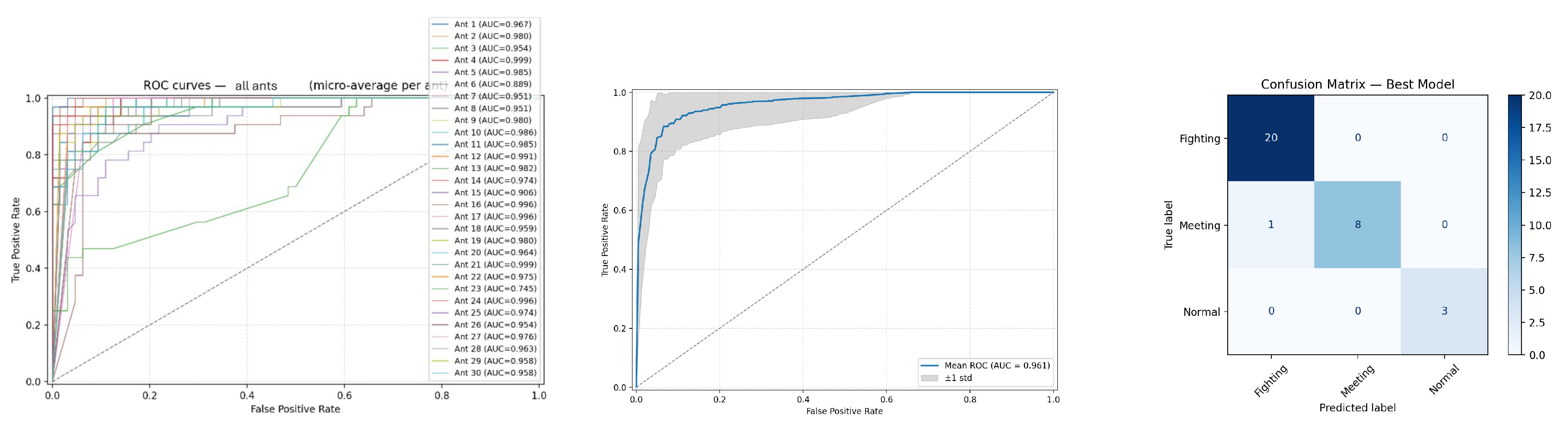
5. Results
Experimental Results
6. Discussion
6.1. Analysis of Results
6.2. Comparison with Other Methods
6.3. Future Research
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, J.H.; Mahmoud, M.; Kang, H.S. Conv3D-based video violence detection network using optical flow and RGB data. Sensors 2024, 24, 317. [Google Scholar] [CrossRef]
- Karim, A.; Razin, J.I.; Ahmed, N.U.; Shopon; Alam, T. An automatic violence detection technique using 3D convolutional neural network. In Sustainable Communication Networks and Application: Proceedings of ICSCN 2020; Springer: Singapore, 2021; pp. 17–28. [Google Scholar]
- Chakole, P.D.; Satpute, V.R. Analysis of anomalous crowd behavior by employing pre-trained efficient-X3D net for violence detection. Sādhanā 2025, 50, 30. [Google Scholar] [CrossRef]
- Maqsood, R.; Bajwa, U.I.; Saleem, G.; Raza, R.H.; Anwar, M.W. Anomaly recognition from surveillance videos using 3D convolution neural network. Multimed. Tools Appl. 2021, 80, 18693–18716. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Tegmark, M. Kan: Kolmogorov-arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar] [PubMed]
- Long, Q.; Wang, B.; Xue, B.; Zhang, M. A Genetic Algorithm-Based Approach for Automated Optimization of Kolmogorov-Arnold Networks in Classification Tasks. arXiv 2025, arXiv:2501.17411. [Google Scholar]
- Sen, A.; Mazumder, A.R.; Dutta, D.; Sen, U.; Syam, P.; Dhar, S. Comparative evaluation of metaheuristic algorithms for hyperparameter selection in short-term weather forecasting. In Proceedings of the 15th International Joint Conference on Computational Intelligence—ECTA, Rome, Italy, 13–15 November 2023; pp. 238–245. [Google Scholar]
- Liu, H.; Simonyan, K.; Yang, Y. DARTS: Differentiable architecture search. arXiv 2018, arXiv:1806.09055. [Google Scholar]
- Mohtavipour, S.M.; Saeidi, M.; Arabsorkhi, A. A multi-stream CNN for deep violence detection in video sequences using handcrafted features. Vis. Comput. 2022, 38, 2057–2072. [Google Scholar] [CrossRef]
- Rendón-Segador, F.J.; Álvarez-García, J.A.; Salazar-González, J.L.; Tommasi, T. Crimenet: Neural structured learning using vision transformer for violence detection. Neural Netw. 2023, 161, 318–329. [Google Scholar] [CrossRef]
- Shanmughapriya, M.; Gunasundari, S.; Fenitha, J.R.; Sanchana, R. Fight detection in surveillance video dataset versus real time surveillance video using 3DCNN and CNN-LSTM. In Proceedings of the 2022 International Conference on Computer, Power and Communications (ICCPC), Chennai, India, 14–16 December 2022; IEEE: New York, NY, USA, 2022; pp. 313–317. [Google Scholar]
- Kachitvichyanukul, V. Comparison of three evolutionary algorithms: GA, PSO, and DE. Ind. Eng. Manag. Syst. 2012, 11, 215–223. [Google Scholar] [CrossRef]
- Sen, A.; Mazumder, A.R.; Sen, U. Differential evolution algorithm based hyper-parameters selection of transformer neural network model for load forecasting. In Proceedings of the 2023 IEEE Symposium Series on Computational Intelligence (SSCI), Mexico City, Mexico, 5–8 December 2023; IEEE: New York, NY, USA, 2023; pp. 234–239. [Google Scholar]
- Verma, K.K.; Singh, B.M. Deep multi-model fusion for human activity recognition using evolutionary algorithms. Int. J. Interact. Multimedia Artif. Intell. 2021, 7, 44–58. [Google Scholar] [CrossRef]
- Abdelmoaty, A.M.; Ibrahim, I.I. Comparative Analysis of Four Prominent Ant Colony Optimization Variants: Ant System, Rank-Based Ant System, Max-Min Ant System, and Ant Colony System. arXiv 2024, arXiv:2405.15397. [Google Scholar]
- Ren, P.; Xiao, Y.; Chang, X.; Huang, P.Y.; Li, Z.; Chen, X.; Wang, X. A comprehensive survey of neural architecture search: Challenges and solutions. ACM Comput. Surv. 2021, 54, 1–34. [Google Scholar] [CrossRef]
- Latypov, V.; Hvatov, A. Exploring convolutional KAN architectures with NAS. In Proceedings of the First Conference of Mathematics of AI, Sochi, Russia, 24–28 March 2025. [Google Scholar]
- Wang, S.; Park, S.; Kim, J.; Kim, J. Safety helmet monitoring on construction sites using YOLOv10 and advanced transformer architectures with surveillance and body-worn cameras. J. Constr. Eng. Manag. 2025, 151, 04025186. [Google Scholar] [CrossRef]
- Tang, H.; Liu, J.; Yan, S.; Yan, R.; Li, Z.; Tang, J. M3net: Multi-view encoding, matching, and fusion for few-shot fine-grained action recognition. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 1719–1728. [Google Scholar]
- Vaca-Rubio, C.J.; Blanco, L.; Pereira, R.; Caus, M. Kolmogorov-arnold networks (KANs) for time series analysis. In Proceedings of the 2024 IEEE Globecom Workshops (GC Wkshps), Cape Town, South Africa, 8–12 December 2024. [Google Scholar]
- Cheon, M. Demonstrating the efficacy of kolmogorov-arnold networks in vision tasks. arXiv 2024, arXiv:2406.14916. [Google Scholar] [CrossRef]
- Genet, R.; Inzirillo, H. Tkan: Temporal kolmogorov-arnold networks. arXiv 2024, arXiv:2405.07344. [Google Scholar] [CrossRef]
- Drokin, I. Kolmogorov-Arnold Convolutions: Design Principles and Empirical Studies. arXiv 2024, arXiv:2407.01092. [Google Scholar] [CrossRef]
- Szeghalmy, S.; Fazekas, A. A comparative study of the use of stratified cross-validation and distribution-balanced stratified cross-validation in imbalanced learning. Sensors 2023, 23, 2333. [Google Scholar] [CrossRef]
- Vrskova, R.; Hudec, R.; Kamencay, P.; Sykora, P. Human activity classification using the 3DCNN architecture. Appl. Sci. 2022, 12, 931. [Google Scholar] [CrossRef]
- Bodner, A.D.; Tepsich, A.S.; Spolski, J.N.; Pourteau, S. Convolutional kolmogorov-arnold networks. arXiv 2024, arXiv:2406.13155. [Google Scholar]
- He, P.; Jiang, G.; Lam, S.K.; Sun, Y. ML-MMAS: Self-learning ant colony optimization for multi-criteria journey planning. Inf. Sci. 2022, 609, 1052–1074. [Google Scholar] [CrossRef]
- Jing, K.; Chen, L.; Xu, J. An architecture entropy regularizer for differentiable neural architecture search. Neural Netw. 2023, 158, 111–120. [Google Scholar] [CrossRef]
- Ali, Y.A.; Awwad, E.M.; Al-Razgan, M.; Maarouf, A. Hyperparameter search for machine learning algorithms for optimizing the computational complexity. Processes 2023, 11, 349. [Google Scholar] [CrossRef]


| Model | Recall | Precision | F1-Score | Accuracy |
|---|---|---|---|---|
| 3D-CNN (GA) | 0.69 | 0.69 | 0.68 | 0.69 |
| 3D-CNN (DE) | 0.67 | 0.68 | 0.67 | 0.67 |
| 3D-CNN (MMAS) | 0.73 | 0.76 | 0.73 | 0.73 |
| KAN3D (Ant) | 0.82 | 0.82 | 0.82 | 0.81 |
| KAN3D (Genetic) | 0.84 | 0.84 | 0.84 | 0.83 |
| KAN3D (MMAS) | 0.85 | 0.87 | 0.86 | 0.85 |
| KAN3D (DARTS) | 0.76 | 0.80 | 0.78 | 0.77 |
| KAN3D-MMAS-DARTS | 0.85 | 0.90 | 0.87 | 0.87 |
| Model | Recall | Precision | F1-Score | Accuracy |
|---|---|---|---|---|
| SEBlock3D + RandomOverSampler (big_dataset) | 0.80 | 0.80 | 0.80 | 0.80 |
| SEBlock3D + update_lambda_a (big_dataset) | 0.81 | 0.82 | 0.81 | 0.82 |
| SEBlock3D + update_lambda_a | 0.83 | 0.83 | 0.79 | 0.80 |
| KANConv3D (without SEBlock3D) | 0.95 | 0.87 | 0.90 | 0.94 |
| SEBlock3D + RandomOverSampler | 0.89 | 0.98 | 0.93 | 0.97 |
| Accuracy | Candidates | |
|---|---|---|
| 0.9688 | 0.00661 | (4, 7), (4, 5), (2, 11) |
| 0.9375 | 0.00052 | (4, 9), (4, 11), (2, 7) |
| 0.9375 | 0.00037 | (5, 5), (1, 11), (5, 5) |
| 0.9062 | 0.00610 | (3, 11), (3, 7), (5, 5) |
| 0.9062 | 0.00530 | (4, 9), (3, 5), (4, 11) |
| 0.9062 | 0.00002 | (3, 5), (2, 5), (5, 5) |
| 0.9062 | 0.00173 | (3, 7), (4, 7), (2, 3) |
| 0.8750 | 0.00109 | (5, 9), (2, 11), (3, 7) |
| 0.8750 | 0.00223 | (1, 5), (3, 5), (4, 9) |
| 0.1250 | 0.00706 | (4, 5), (2, 11), (3, 7) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buribayev, Z.; Zhassuzak, M.; Aouani, M.; Zhangabay, Z.; Abdirazak, Z.; Yerkos, A. DARTS Meets Ants: A Hybrid Search Strategy for Optimizing KAN-Based 3D CNNs for Violence Recognition in Video. Appl. Sci. 2025, 15, 11035. https://doi.org/10.3390/app152011035
Buribayev Z, Zhassuzak M, Aouani M, Zhangabay Z, Abdirazak Z, Yerkos A. DARTS Meets Ants: A Hybrid Search Strategy for Optimizing KAN-Based 3D CNNs for Violence Recognition in Video. Applied Sciences. 2025; 15(20):11035. https://doi.org/10.3390/app152011035
Chicago/Turabian StyleBuribayev, Zholdas, Mukhtar Zhassuzak, Maria Aouani, Zhansaya Zhangabay, Zemfira Abdirazak, and Ainur Yerkos. 2025. "DARTS Meets Ants: A Hybrid Search Strategy for Optimizing KAN-Based 3D CNNs for Violence Recognition in Video" Applied Sciences 15, no. 20: 11035. https://doi.org/10.3390/app152011035
APA StyleBuribayev, Z., Zhassuzak, M., Aouani, M., Zhangabay, Z., Abdirazak, Z., & Yerkos, A. (2025). DARTS Meets Ants: A Hybrid Search Strategy for Optimizing KAN-Based 3D CNNs for Violence Recognition in Video. Applied Sciences, 15(20), 11035. https://doi.org/10.3390/app152011035







