Shear Characteristics and Failure Evolution Process of the Cantilever Anti-Floating Ledge in Rock Strata: A Case Study of Guangzhou Metro Stations

Abstract

Based on the high strength and superior deformation control capabilities of rock strata, a novel cantilever anti-floating ledge has been proposed to resist the floating of underground structures in rock strata. To explore the actual anti-floating effect and working performance of the structure, laboratory shear tests were designed based on the actual project. The shear characteristics and failure evolution process were then discussed using the Particle Flow Code (PFC) numerical simulation. The main conclusions are as follows. The shear stress–shear displacement curve of the cantilever anti-floating ledge can be described as six stages according to the different states of stress and deformation. With the increase in groundwater buoyancy, the damage to the cantilever anti-floating ledge occurs successively from the ledge, the concrete–rock interface, the connection between the ledge and the side wall, and the connection between the ledge and the bottom plate. Local damage and delamination of the interface do not affect the structural strength, but structural cracks should be prevented from continuing to form and connect. It is necessary to pay attention to the stress and deformation state of the crack-prone area mentioned above, improve the reinforcement ratio in the crack-prone area, and strengthen the bond between the concrete and the rock.

1. Introduction

Underground structures constructed in water-rich areas, such as subway stations, underground parking lots, and underground commercial spaces, must consider anti-floating effects to prevent buoyancy issues. Anti-floating measures commonly used in current engineering projects mainly include ballasting, drainage and pressure reduction, uplift piles, and anti-floating anchors [1,2,3,4]. These measures should be selected and designed appropriately based on specific geological conditions, surrounding environments, and structural requirements.

In central and western China, due to the presence of shallow and high-quality rock layers, underground structures often employ uplift piles and anti-floating anchors to counteract buoyancy forces. Extensive research has revealed the anti-floating capacity and friction behavior of uplift piles in rock layers, providing robust theoretical support for engineering applications. For example, finite element simulations have elucidated the load-bearing characteristics of uplift piles in rock layers [5,6]. Laboratory and field test results have quantified the lateral friction force distribution patterns of uplift piles in weathered rock layers [7,8]. Computational theoretical advancements include methods for estimating the ultimate bearing capacity of uplift piles in soil–rock composite strata [9] and a hyperbolic model for capturing the nonlinear displacement–friction relationship at the pile–rock interface [10]. Additionally, the pile group effect and optimization strategies have been explored, including enhancing the uplift resistance of pile groups under composite loads, predicting the final acting force in shallow cover layers using incomplete displacement curves, and the local uplift stability of the foundation [11,12,13]. Based on anti-floating piles, anti-floating anchors have emerged as an optimized variant, enhancing performance by reducing the size and spacing of individual piles while increasing their number. Special applications include fiber-reinforced polymer (FRP) versions tested for pullout behavior in moderately weathered granite [14,15], and full-length steel pipe prestressed compression anchors for reinforcing existing structures [16]. To better utilize the inherent shear strength of rock layers, variable-section piles, achieved by enlarging the base cross-section of uplift piles, are gaining attention as an effective solution for anti-floating of the underground structures. Compared to traditional uplift piles, enlarging the bottom cross-section size can significantly enhance uplift resistance by approximately 1.5 to 3 times, depending on factors such as rock type, embedment depth, enlargement angle, and soil density [17,18,19]. This enhancement primarily stems from the enlarged base increasing end bearing capacity and shear resistance [20,21].

However, achieving optimal anti-floating effects in underground structures typically requires the installation of a large number of uplift piles or anti-floating anchors in the foundation, which significantly increases economic costs and construction schedules. Drawing inspiration from the load transfer mechanism of variable-section piles, a novel anti-floating strategy is proposed: a cantilever anti-floating ledge at the toe of the underground structure, which resists buoyancy through the shear locking effect between the concrete and rock layers (Figure 1). It is worth noting that the adoption of this measure is based on the premise that the excavation pit is supported by suspended diaphragm walls—i.e., the bottom of the diaphragm walls is located above the pit bottom—a common practice in shallow rock layer sites [22,23,24]. This novel anti-floating measure significantly reduces the number of required uplift piles or anti-floating anchors, offering notable economic advantages, and has been successfully applied in a subway station project in Guangzhou City, Guangdong Province, China. However, its theoretical foundation and design methods remain incomplete, with limited engineering precedents, necessitating further research to provide theoretical support.

Laboratory shear tests can directly reveal the shear failure characteristics of strata and structures [1,25,26,27,28,29,30,31]. Additionally, particle flow numerical simulations provide microscopic insights into the failure evolution process of the interface [32,33,34,35].

This study aims to combine laboratory shear tests with Particle Flow Code (PFC) numerical simulation, using the actual engineering of a subway station in Guangzhou, China, as a case, to explore the anti-floating performance of the cantilever anti-floating ledge, clarify its shear mechanical characteristics and failure evolution process in the rock layer, and identify the critical crack-prone zones. This provides theoretical and practical guidance for design optimization in underground engineering.

2. Engineering Context

2.1. Project Overview

A subway station in Guangzhou is located at the intersection of Yizhou Road and Yuejiang Road, extending east–west along Yizhou Road. To the north of the station are Boya Bay Residential Community, Guangzhou TV Tower Park, Zhujiang Dijing Residential Community, and Chigang River. To the south are the Guangdong Museum of Art (under construction), Chigang Tower Park, and Chigang Tower. Red lines restrict the site and are adjacent to several important buildings, posing major challenges for construction. The geographical location of the subway station is shown in Figure 2.

The station is a four-story underground island platform station constructed using the open-cut method. The total length of the station is 276.2 m, with a standard excavation cross-sectional width of 47.1 m and a depth ranging from 32.98 m to 33.63 m. The cross-section of the station is shown in Figure 3.

2.2. Lithological and Hydrogeological Conditions

The strata in the station area, from top to bottom, are as follows: ① miscellaneous fill, ② mucky soil, ③ completely weathered sandstone, ④ strongly weathered sandstone, ⑤ medium weathered sandstone, and ⑥ slightly weathered sandstone, as shown in Figure 3. It is worth noting that the sandstone with complete weathering and strong weathering has an extremely high degree of weathering and can therefore be classified as soil, with the soil–rock interface located at a depth of approximately 12.0 m. The main body of the station is primarily embedded in hard rock layers. This formation is part of the Mesozoic sedimentary sequence in the Guangzhou area, characterized by fluvial-deltaic depositional cycles that produced layered sandstone structures with mudstone and calcareous cementation. Stratigraphic relationships show a continuous transition from medium weathered (⑤) to slightly weathered sandstone (⑥), reflecting a gradual decrease in weathering intensity with increasing depth. The slightly weathered sandstone rock mass is generally intact, with a basic quality grade of III to IV. The thickness of each layer, along with the key physical and mechanical parameters, is detailed in

Table 1. The thickness and the key physical and mechanical parameters of the strata.

Number	Layer	Thickness /m	Unit Gravity γ/(kN/m3)	Elastic Modulus E/MPa	Poisson’s Ratio μ/-	Cohesion c/kPa	Friction Angle φ/(°)	Void Ratio e/-	Permeability Coefficient k/(cm/s)
①	Miscellaneous fill	3.0	18.8	2	0.15	8.0	10.0	0.842	3.42 × 10−9
②	Mucky soil	2.5	17.0	6	0.35	7.6	-	1.365	2.36 × 10−12
③	Completely weathered sandstone	3.5	20.2	1600	0.28	36.3	19.7	0.620	0.295 × 10−9
④	Strongly weathered sandstone	2.0	20.2	2000	0.25	41.6	24.3	0.547	0.496 × 10−9
⑤	Medium weathered sandstone	8.0	25.3	2300	0.22	120.0	36.0	0.340	0.649 × 10−9
⑥	Slightly weathered sandstone	-	25.6	6500	0.20	280.0	43.0	0.160	0.295 × 10−9

.

The north side of the station is bordered by the Chigang River, which has a width of approximately 6 m and a depth of around 3 m. The minimum distance from the station is 12 m and remains hydraulically connected to the underlying geological strata. The groundwater level at the site is relatively shallow; pumping tests indicate an initial water level of 2.6–3.5 m (elevation 4.23–5.50 m) and a stable water level of 2.2–3.1 m (elevation 4.73–5.86 m). Groundwater exhibits significant seasonal fluctuations, with an annual variation range of 1.5–2.5 m.

2.3. The Cantilever Anti-Floating Ledge

The permeability coefficient of slightly weathered sandstone beneath the site ranges from 2.55 × 10⁻⁴ cm/s to 6.36 × 10⁻⁴ cm/s. According to the „Code for Engineering Geological Investigation of Water Resources and Hydropower” (GB50487-2008) in China [36], it can be classified as a moderately permeable layer, necessitating anti-floating design measures. To fully utilize the excellent shear properties of the rock layers, it is recommended to install the cantilever anti-floating ledge at the toe of the underground structure. The shear locking effect between the ledge and the rock layers will resist buoyancy. Additionally, multiple uplift piles should be installed within the structural base plate as auxiliary supports, as shown in Figure 3.

3. Laboratory Shear Test of the Cantilever Anti-Floating Ledge

3.1. Test Design and Boundary Condition Determination

The cantilever anti-floating ledge achieves anti-floating through shear interaction with the rock layer. Therefore, a laboratory shear test was designed to investigate its shear mechanical properties from the perspective of the ultimate state. Figure 4 shows a partial generalization diagram of the cantilever anti-floating ledge. In actual engineering, the cantilever anti-floating ledge extends outward by 1.0 m, with a ledge height of 2.2 m and a 30 ° incline at the top. The red dashed box in Figure 4 represents the key area that plays a crucial role in preventing floating. This area was scaled down by a factor of 1/30 to fit the shear testing machine, resulting in final dimensions of 200 mm × 100 mm × 50 mm.

It is essential to emphasize that this scaled test focuses on the qualitative similarity of shear behavior rather than the quantitative prediction of bearing capacity. Therefore, materials were not prepared using similar materials at a similar scale ratio. Instead, geometric similarity and authentic material properties were employed to capture real-world interface interactions and reflect cracking and failure characteristics of both interfaces and materials. Such qualitative insights are commonly used in geotechnical model tests when strict similarity is difficult to achieve due to material scaling limitations [37,38].

To accurately simulate the stress state of the cantilever anti-floating ledge in engineering, it is necessary to determine the boundary conditions of the test sample. Referring to Figure 5, the boundary conditions to be determined include the following:

① The boundary AB is subjected to axial force N_AB, shear force F_AB, and bending moment M_AB. Due to the nature of the shear test, F_AB is ignored because its direction is consistent with the direction of the applied shear force. Therefore, only N_AB and M_AB are considered.

② The boundary BC is a free boundary with zero pressure.

③ The boundary CD is subjected to axial force N_CD, shear force F_CD, and bending moment M_CD. Similarly, since the direction of shear force F_CD is the same as the direction of the applied shear force, N_CD is ignored in the shear test, and only F_CD and M_CD are considered.

④ The boundary EF is connected to the rock and designated as a fixed boundary.

The finite difference software FLAC^3D5.0 was used to determine the stress conditions around the cantilever anti-floating ledge, which were then converted into boundary conditions of the shear sample. The numerical model developed in FLAC^3D5.0 is shown in Figure 6. The process of determining these boundary conditions is as follows:

(1)

A comprehensive numerical model of the station was constructed in FLAC^3D5.0 to simulate the entire anti-floating process.

(2)

The stress states near the cantilever anti-floating ledge were extracted from the simulation results.

(3)

These stresses were converted into specific boundary loads using the FISH programming language in FLAC^3D5.0.

(4)

The corresponding boundary load conditions for the shear tests were derived using a dimensional similarity ratio.

Due to space limitations and the fact that these topics are not the focus of this paper, detailed explanations of model establishment, parameter selection, boundary conditions, and simulation processes will not be provided here.

Figure 7 illustrates the process for determining load boundary conditions in shear tests. Using FLAC^3D calculations, the actual load boundary conditions for the cantilever anti-floating ledge were obtained. Load boundary conditions in the shear test require proportional scaling according to the following principle: forces reduced by a factor of 30², moments reduced by a factor of 30³ (accounting for lever arms). The converted loads are adapted to the test scale. Since both concrete and rock are brittle materials, their deformation remains minimal until failure. Thus, bending moments can be simplified as equivalent to a pair of equal and opposite forces acting on the structure, ultimately forming the load boundary conditions for the shear test. Additionally, during the operation of the cantilevered buoyancy platform, the concrete base plate imposes constraints on the lateral displacement of the structure. Consequently, displacement boundary conditions are defined as locally rigid constraints in the vertical direction, with no constraints in the horizontal shear direction.

To achieve the aforementioned displacement and load boundary conditions, the right boundary CD of the concrete is extended outward by 40 mm to facilitate shear forces, while the forces at boundaries AB and CD are converted into uniformly distributed loads along boundaries AB and DD’. The final schematic diagram of the shear test, along with its related annotations, is shown in Figure 8.

A steel plate was pre-installed at boundary AB to ensure even load distribution, with the load acting directly on the steel plate via the testing machine. The uniform load at boundary DD’ is applied via the right-hand loading device, with specific details to be detailed later. During the shear test, boundary AG remains fixed while the jack pushes boundary DE to generate a shear force.

3.2. Test Materials

The test materials primarily consist of slightly weathered sandstone and C35 concrete (with a characteristic compressive strength of 35 MPa after 28 days of curing). The slightly weathered sandstone was sourced from the construction site, is relatively soft, and has a rock mass rating of Grade III to IV.

The C35 concrete is of the same grade as that used for the underground structures at the site. Its mix design includes coarse aggregate (crushed stone with a particle size of 1–5 mm), fine aggregate (river sand), cement, water, fly ash, and admixtures (water-reducing agent), with specific proportions detailed in

Table 2. Material ratio of C35 concrete.

Materials	Coarse Aggregate	Fine Aggregate	Cement	Fly Ash	Water	Water Reducer
Material ratio	5.279	5.752	2	0.364	1	0.054

. This mix design is based on “Code for Design of Concrete Structures” (GB50010-2010) in China [39] with appropriate admixtures such as water-reducing agents and fly ash added according to experience to enhance the concrete’s workability.

3.3. Test Device and System

(1)

Test device

To achieve the boundary conditions, the test apparatus is designed as shown in Figure 9. The sample is placed on the loading platform, with both the left and upper jacks fixed, while the right jack applies the load. The right-side loading device 1 (Figure 9a) is installed in the upper right corner of the device. It connects to the right-side loading device 2 (Figure 9b) via two steel strands. Two tension gauges with a measurement range of 500 N and an accuracy of ±2.5 N are attached to the strands. During testing, load control is achieved by monitoring the tension gauge readings. The right-side loading device 1 consists of an upper steel plate (dimensions: 520 mm × 40 mm × 5 mm (length × width × thickness)), a lower steel plate (100 mm × 40 mm × 5 mm (length × width × thickness)), and connecting bolts (M5 × 70 mm). Device 2 includes pulley 1 (diameter 140 mm), pulley 2 (diameter 20 mm), steel strand (length 2000 mm, diameter 3 mm), a steel frame (1200 mm × 1500 mm (width × height)), and counterweights (maximum 10 kg), where pulley 1 is fixed to the steel frame and pulley 2 is fixed to the testing machine.

(2)

Test system

The testing system consists of a loading subsystem and a data acquisition subsystem. The loading subsystem uses a WDAJ-600 microcomputer-controlled electro-hydraulic servo rock shear rheological testing machine. The data acquisition subsystem includes an integrated data recorder for the shear testing machine, an acoustic emission system, and a digital image correlation system.

3.4. Test Process

The rock material described in Section 3.2 was cut and polished to produce rock samples of the required size for testing. The processed rock samples were then placed in a special mold, which was filled with C35 concrete to form the final samples. The samples were subjected to standard curing for 28 days at a temperature of 20 ± 2 °C and a relative humidity of no less than 95% before testing. Complete saturation of the samples was achieved using a vacuum saturator. Spots were formed on the surface of the samples by spraying, and acoustic emission probes were installed at the upper left, lower left, upper right, and lower right positions on the opposite side of the samples. The preparation process of the shear test samples is shown in Figure 10. To minimize variability in test results, three sets of duplicate samples were prepared.

The right-side loading device was installed, and the testing machine was started. During the initial stage, the sample was pre-contacted and loaded using a vertical jack. When the pressure at the boundary AB stabilized at the target value of 1.142 kN, the axial displacement device was fixed to establish a fixed boundary. Subsequently, counterweights were added to the right-side loading device 2, and the pressure at the DD’ interface was adjusted to the target value of 0.875 kN based on the tension gauge reading. Subsequently, the sample underwent pre-contact via a horizontal loading jack and was subjected to shear at a constant rate of 0.3 mm/min. Concurrently, acoustic emission and digital image correlation data acquisition were initiated. The shear test setup is illustrated in Figure 11. When the shear stress of the samples exhibits a significant decrease, the test is terminated, indicating that the shear process is complete.

4. Results of the Shear Test

4.1. Shear Mechanical Characteristics

Figure 12 shows the shear stress–shear displacement curves of the shear samples. The differences in peak shear stress and displacement are attributed to random joints in the sandstone, the heterogeneous nature of the concrete material, and variations in interfacial bonding. However, the curves of the three groups of samples exhibit consistent patterns during loading until failure. The core parameters (peak shear strength and elastic modulus) show minimal variation. This confirms that heterogeneity effects remain within an acceptable range (<10%). Taking Group 2 as a representative example to analyze the evolution of strength and deformation during shear tests. The shear stress–shear displacement relationship can be divided into six stages:

① Initial compaction stage (OA): The sample is in close contact with the loading jack of the testing machine, causing internal microcracks to close.

② Approximate linear elastic compression–shear deformation stage (AB): The sample undergoes approximate linear elastic deformation under compression-shear action.

③ Initial microcrack initiation and propagation stage (BC): Microcracks appear at stress concentration points, accompanied by a slight decrease in stress.

④ Slow compression-shear nonlinear deformation stage (CD): Some microcracks close, causing shear stress to redistribute; simultaneously, other regions maintain shear strength until new cracks form, triggering subsequent stress decline.

⑤ Stress brittle drop stage (DE): When the peak strength τ_p is reached, the shear stress rapidly drops, internal cracks merge, and strength is significantly lost.

⑥ Plastic flow deformation stage (EF): The sample fails due to shear and continues to deform under the residual strength τ_f.

During the shear process, the BC and CD stages may repeat multiple times (as observed in the first group), indicating the presence of numerous microcracks or the repeated expansion and closure of individual microcracks. It is worth noting that since the test samples were made of real rock and concrete materials rather than simulated materials scaled based on similarity ratios, the peak shear stress obtained cannot directly characterize the ultimate load-bearing capacity of the cantilever anti-floating ledge in actual engineering applications. However, the shear characteristics, deformation behavior, and failure evolution process captured in the tests provide precise and reliable insights into structural performance.

4.2. Deformation Evolution Characteristics

The XTDIC 3D optical speckle system can elucidate the structural deformation evolution characteristics during the shearing process from a macro perspective [40,41]. It is worth noting that in the XTDIC system, horizontal displacement to the right is considered positive, and vertical displacement downward is also considered positive. Similarly, analyze the experimental results represented by Group 2 to clarify general patterns.

Figure 13 shows the horizontal displacement evolution of the cantilever anti-floating ledge during the entire loading process. To minimize rotational errors caused by the sample adapting to the loading head during the initial stage, the basic point is established at approximately 120 s, and subsequent stages record only relative displacement. During the initial loading stage, the sample is in a compacted state, and overall deformation is primarily uniformly distributed. In Stage I, under the combined action of the lower plate tangential jack and the upper right tensile device, a tensile–shear crack appears at the upper right corner, causing local horizontal displacement to suddenly change due to twisting deformation (transitioning to Stage II). In Stage III, the oblique cracks extend outward from the protruding part of the lower plate, intersect with the initial cracks, and trigger rock surface collapse. In Stage IV, under the combined effects of axial constraint and the left lateral top plate, an oblique crack forms at the upper left corner, extending toward the protruding part of the lower plate, accompanied by a slight decrease in stress. Stage V exhibits horizontal deformation zoning characteristics; the upper right corner and left triangular zone displace to the right, while the fracture surface and sample move to the left, with slight noticeable displacement in other areas. Finally, in Stage VII, oblique cracks from the upper left and upper right corners converge at the step interface, leading to the loss of shear resistance and structural failure.

Figure 14 shows the vertical displacement evolution of the cantilever anti-floating ledge throughout the loading process. During the initial loading stage, the sample deforms uniformly. In Stages I to III, as cracks form and propagate in the upper right corner, the vertical displacement in this region gradually increases from the center toward the right outer side. In Stages IV to V, oblique cracks appear in the upper left corner, causing rock fragments on the surface to displace downward, while the upper right corner continues to move upward. During Stages VI to VII, the upper left corner undergoes upward uplift, and the crack further extends, connecting with the stop block interface and the upper right crack by Stage VII, ultimately leading to shear failure. Similarly to horizontal deformation, vertical deformation also exhibits distinct zonation characteristics; the upper half of the sample undergoes uplift (including the left-upper crack, the step interface, and the area above the right-upper crack), showing significant gradient changes under axial roof confinement, while the lower half remains nearly stationary in terms of vertical displacement.

Figure 15 shows the distribution characteristics of the total displacement field of the cantilever anti-floating ledge after shear failure. After failure, the total displacement field of the structure exhibits significant displacement on the right side of the upper plate and throughout the entire lower plate region, while the displacement on the left side of the upper plate is relatively small. Based on the distribution of the intensity of displacement changes in the total displacement field, key displacement change regions can be identified: the region extending from the upper left corner to the cantilever edge (Region I), the left interface region (Region II), and the right interface region (Region III). The deformation distribution pattern of the sample is extremely complex, and these displacement change regions are the primary zones where cracks form.

4.3. Crack Development Characteristics

The industrial camera was used to capture the initial formation and propagation of cracks in the samples during the loading process, thereby revealing the crack development mechanism in the cantilever anti-floating ledge, as shown in Figure 16. Under the synergistic action of the right-side loading device and the horizontal jack, tensile-shear cracks first appeared near the right side of the concrete–rock interface and propagated toward the upper left corner along the direction of the horizontal jack. This phenomenon occurred at 40% of the loading process, when the shear stress reached 10% of the peak value (I). From 40% to 55% of the loading process, damage primarily manifested as crack propagation and elongation (II). At 65% of the loading process, collapse occurred in the lower right region, accompanied by peeling and sliding at the left concrete–rock interface, with shear stress rising to 50% of the peak value (III). At 80% of the loading process, compression-shear cracks began to form from the upper left corner and propagated toward the cantilevered ledge; the initial cracks intensified, causing stress to temporarily drop to 70% of the peak value (IV). Finally, as the cracks extended and merged at the concrete–rock interface and the cantilevered ledge, shear strength sharply decreased to only 20% of the peak stress (V).

According to the test results, when the underground structure encounters significant groundwater buoyancy (approximately 10% of the ultimate bearing capacity of the cantilevered anti-floating platform), tensile shear cracks will appear along the side walls above the cantilever anti-floating ledge. These cracks will propagate from the interface between the concrete and rock toward the bottom plate. Subsequently, localized damage may occur along the crack path, accompanied by separation and displacement of the base of the cantilever anti-floating ledge from the rock. The cracks may then extend diagonally along the bottom plate toward the protruding area of the cantilevered platform. Due to stress concentration at the cantilevered platform, these cracks tend to extend toward that direction and eventually converge. It is worth noting that from the initial stage of damage to a longer period (10–50% of the ultimate bearing capacity), only local damage appears near the upper sidewall of the cantilevered platform. The most direct mitigation measure is to reinforce the structure, particularly by increasing the longitudinal tensile reinforcement. For highly weathered or jointed rock layers, grouting reinforcement should be carried out within the influence range of the anti-floating structure. Additionally, enhancing the bond between concrete and rock is critical, while closely monitoring stress levels and mechanical conditions at the connections between the rock and the structure. Reinforcement ratios should be increased as necessary.

4.4. AE Results

During the shear testing of the samples, a series of acoustic emission (AE) events occur alongside the continuous generation and propagation of microcracks, with each event marking the occurrence of a discrete microdamage event. Therefore, AE counting is employed to characterize the evolution of microdamage. Additionally, AE energy—the energy released by AE signals within a given time interval—serves as another reliable indicator for defining the closure, initiation, and propagation of internal microcracks. Consequently, AE counts and energy are selected as key indicators to facilitate a comprehensive analysis of crack evolution within the samples throughout the loading process by integrating them with the loading curve.

Figure 17 shows the AE signal curves of the sample during shear loading, where Figure 17a displays the AE count, and Figure 17b displays the AE energy. Overall, the patterns reflected by the AE count are highly consistent with those of the AE energy. The damage development of the sample was further analyzed in conjunction with the crack development described in detail in the previous section (Figure 16). During the initial loading stage, the AE signals were weak, and the damage primarily manifested as local compression and microcracks. At approximately 135 s, the first AE signal peak was detected, corresponding to the observable crack extending from the right-side loading jack toward the upper left corner of the sample (Figure 16I). Subsequently, AE activity weakened to a stable level until a second peak appeared at approximately 180 s, at which point the initial crack exhibited partial squeezing, surrounded by dense fine cracks, and partial peeling occurred at the left–lower concrete–rock interface, leading to a significant increase in overall damage (Figure 16II). The period before 180 s was defined as Stage I, characterized by the sequential formation of local cracks. From 180 s onwards, the AE signal intensity continued to increase, with continuous monitoring indicating that cracks continued to form, expand, and merge. A third peak occurred at 270 s, accompanied by a slight decrease in stress in the loading curve, and compressive shear cracks appeared from the upper left corner toward the ledge (Figure 16IV). By 340 s, cracks at the concrete–rock interface and the ledge extended, expanded, and eventually merged, resulting in the loss of shear strength (Figure 16V). The period from 180 s to 340 s constitutes Stage II. After 340 s, the sample suffered severe damage under residual strength, marking the beginning of Stage III.

From an engineering practice perspective, the cantilever anti-floating ledge can be considered relatively safe in Stage I. Although tensile shear cracks may easily form along the side walls, these cracks do not accompany progressive damage. Additionally, in actual engineering applications, retaining structures are often embedded with reinforcing bars, which significantly enhances their tensile strength. However, upon entering Stage II, the structure enters the failure stage as loads increase, internal cracks continue to form and expand, successively affecting multiple weak areas, ultimately leading to the loss of load-bearing capacity. To ensure structural safety and optimal anti-floating performance, it is essential to prevent the structure from entering Stage II.

5. PFC Numerical Simulation

5.1. Numerical Calculation Model

A numerical model for shear tests of the cantilever anti-floating ledge was developed using the particle flow numerical calculation software PFC^2D5.0, which enables the microscopic revelation of the failure evolution process and addresses the limitations of physical shear tests in macro-scale descriptions. The PFC model employs the Discrete Element Method (DEM), treating materials as aggregates of rigid spherical particles. Interactions occur via contact points—distinguished as ball-ball contacts (for internal cohesion) and ball-facet contacts (for boundaries). This approach realistically simulates heterogeneous behavior at the concrete–rock interface, where particle interactions reproduce real-world discontinuities and stress concentrations. The Linear Parallel Bond Model (LPBM) captures cohesive forces between particles, with bonds providing tensile, shear, and rotational stiffness to achieve the typical brittle failure mode of rock-concrete composites.

The shape, dimensions, and loading scheme of the model are consistent with those of the shear test. Concrete primarily consists of cementitious materials (cement), fine aggregates (sand), and coarse aggregates (stone). To replicate its mechanical properties in the simulation, it is divided into two components: mortar matrix and randomly generated blocky stone aggregates. The blocky stones are generated using the Monte Carlo method, and randomly generated polygons within the model using the FISH language. Key steps include randomizing the particle size, position coordinates, and shape of the blocky stones [42]. The concrete is configured based on the actual stone content and particle size distribution, along with the final computational model, as shown in Figure 18. To simulate the stress state of the cantilever anti-floating ledge, the model boundary conditions are set as follows; the lower EF segment and upper AB segment are fixed boundaries, and the remaining segments are free boundaries. A wall pressure P1 = 7339 N/m is applied at DD’ (consistent with the experiment). The shear test boundary conditions are also marked in Figure 18.

5.2. Calibration of Microscopic Parameters

The accuracy of PFC numerical simulation results mainly depends on the reasonable selection of model parameters. Due to the unclear relationship between the macroscopic mechanical properties of materials and the microscopic parameters of the model, it is challenging to derive microscopic parameters directly from macroscopic physical properties. Therefore, model calibration is crucial; through iterative adjustment of microscopic parameters, the numerical results can be made highly consistent with physical experimental results, thereby accelerating the acquisition of reliable simulation results. Parameters were iteratively calibrated through uniaxial compression tests on slightly weathered sandstone and concrete samples, ensuring macroscopic outputs (elastic modulus, peak shear strength) deviated from laboratory results by less than 5%. This calibration not only reproduces material heterogeneity—58% aggregate and 42% mortar in concrete—but also facilitates tracking the initiation of microcracks driven by stress concentration, which evolves into macroscopic failure, thereby overcoming the limitations of continuum models like FLAC^3D.

(1)

Parameter calibration of the slightly weathered sandstone

According to the micro-mechanical parameter calibration procedure proposed by Huang et al. (2022) [43], the parameters of slightly weathered sandstone were calibrated through uniaxial compression tests. First, physical uniaxial compression tests were conducted on cylindrical samples with dimensions of Φ50 × 100 mm to obtain their macroscopic mechanical properties. Considering the heterogeneity of the samples, three parallel tests were conducted to obtain their uniaxial compression curves, as shown in Figure 19. As seen, the three test curves exhibit certain differences, but these remain within an acceptable range. We selected Group 2, the middle group, as the calibration group for determining the PFC microparameters.

Simultaneously, a numerical model of the same dimensions was constructed. Through iterative adjustments of the micro-parameters, the simulation results were highly consistent with the physical test results, as shown in Figure 20. The final micro-parameters of the slightly weathered sandstone are presented in

Table 3. Microscopic calibration parameters of the slightly weathered sandstone.

Particle Density/(kg/m)	Minimum Particle Radius/m	Maximum Particle Radius/m	Particle Friction Factor/-	Particle Elastic Modulus/kPa	Particle Contact Stiffness Ratio/-
2650	5 × 10−4	7.5 × 10−4	0.6	3 × 106	1.3
Parallel bond radius factor/-	Parallel bond elastic modulus/kPa	Parallel bond stiffness ratio/-	Parallel bond normal stiffness/kPa	Parallel bond tangential stiffness/kPa	-
0.22	2.17 × 105	1.3	1.55 × 104	1.55 × 104	-

.

(2)

Parameter calibration of the concrete

The calibration process for the micro-parameters of concrete is consistent with that for rocks. The stress–strain curves of concrete were obtained through numerical simulation and laboratory tests, as shown in Figure 21. The final micro-parameters are detailed in

Table 4. Microscopic calibration parameters of the concrete aggregate.

Particle Density/(kg/m)	Minimum Particle Radius/m	Maximum Particle Radius/m	Particle Friction Factor/-	Particle Elastic Modulus/kPa	Particle Contact Stiffness Ratio/-
2650	5 × 10−4	7.5 × 10−4	0.5	3 × 106	1.3
Parallel bond radius factor/-	Parallel bond elastic modulus/kPa	Parallel bond stiffness ratio/-	Parallel bond normal stiffness/kPa	Parallel bond tangential stiffness/kPa	-
0.22	2 × 106	1.3	1.5 × 105	1.5 × 105	-

and

Table 5. Mesoscopic calibration parameters of the concrete mortar matrix.

Particle Density/(kg/m)	Minimum Particle Radius/m	Maximum Particle Radius/m	Particle Friction Factor/-	Particle Elastic Modulus/kPa	Particle Contact Stiffness Ratio/-
2000	5 × 10−4	7.5 × 10−4	0.5	3 × 106	1.3
Parallel bond radius factor/-	Parallel bond elastic modulus/kPa	Parallel bond stiffness ratio/-	Parallel bond normal stiffness/kPa	Parallel bond tangential stiffness/kPa	-
0.22	2 × 105	1.3	8.5 × 104	8.5 × 104	-

.

Overall, parameter calibration yielded favorable results for both slightly weathered sandstone and concrete materials. However, given material heterogeneity, sensitivity analysis of parameters remains necessary. Current research on PFC parameter calibration is extensive, primarily focusing on key parameters such as bond strength, friction coefficient, and interfacial stiffness [33,34,35]. Bond strength significantly influences peak shear stress; increased bond strength markedly elevates peak stress and enhances post-peak ductility, while reduced bond strength accelerates crack propagation and may shorten failure time. The friction coefficient primarily affects shear crack density and interfacial debonding. Stiffness variations have minimal impact on stress–strain curves but influence energy dissipation patterns.

5.3. Comparison with the Test Results

Figure 22 compares the numerical simulation results with the shear test results. The peak shear stress obtained from the simulation is 7.63 MPa, and the peak shear displacement is 2.79 mm, which is highly consistent with the test values of 7.67 MPa and 2.87 mm. Additionally, the failure modes of the samples were similar. Integrating parameter calibration (Figure 20 and Figure 21) with comparative analysis (Figure 22) further confirms the high consistency between simulation and experimental results (peak stress/displacement deviation < 3%), validating the model’s applicability for further investigation of micro-damage. The load curves obtained from the PFC simulation exhibit greater fluctuations compared to the test curves. Notably, the test curve experiences a sudden drop after reaching its peak, whereas the simulated curve exhibits more pronounced oscillatory behavior. This discrepancy primarily stems from the slight retraction of the axial loading jack in the physical test, which did not fully satisfy the fixed upper boundary conditions. This led to rapid convergence of internal cracks, resulting in a swift decline in strength. In contrast, the strict boundary constraints in the simulation suppressed crack propagation, resulting in dense cracks in Region 2. In fact, the ledge is prone to pressure concentration, which can potentially generate numerous compressive cracks. Additionally, the tensile shear cracks initially formed on the right side (Region 1) of the samples in the test were absent in the simulation. In fact, these observed cracks indicate delamination between rock and concrete at the upper right interface, caused by the right-side loading device and horizontal jack—a phenomenon well captured in the simulation. During the test, due to the need to space the test equipment apart, the right-side horizontal loading jack did not fully contact the right side of the sample, resulting in the sample cracking in Region 1 due to stress concentration.

5.4. Damage Evolution Law

Figure 23 illustrates the evolution of microcracks in the sample during the shear process. This result is derived from PFC numerical simulations and provides a more intuitive visualization of the internal microdamage development process compared to physical laboratory tests. Additionally, the simulation avoids errors caused by experimental conditions or sample preparation. The shear process underwent 240,000 cycles, with the state recorded every 40,000 cycles, and the loading sequence until failure was divided into six equally spaced segments. During the initial loading phase, the sample primarily underwent compression under axial and tangential forces, with minimal internal damage (Stage I). As shear stress increases, the region of the ledge undergoes compression, and tensile cracks form under the combined action of compression and shear. Simultaneously, due to stress concentration, shear cracks form along the ledge in a leftward-inclined direction (Stage II). Additionally, under the synergistic action of the right-side loading device and the tangential loading jack, the concrete and rock at the upper right corner gradually separate along the interface, consistent with the initial crack orientation observed in the test. As the load is further applied, cracks near the ledge become denser and interconnected, forming the main crack zones along the ledge, the upper left corner, and the concrete–rock interface (Stages III to IV), while the upper right corner tends to fracture. As cracks at the ledge expand and connect to the left and right interfaces, shear strength decreases. Unlike the sudden drop observed in the test, the simulation reveals plastic deformation after the peak, characterized by widespread cracking in the concrete and rock near the ledge, accompanied by local fractures and fragmentation (Stage V). The final failure is characterized by the separation along the interface, the complete destruction of the ledge, and fractures extending diagonally from the ledge to the upper left and lower right corners (Stage VI).

Simulation results indicate that the failure evolution process in shear samples exhibits minor differences compared to observations in laboratory tests. On one hand, experimental limitations—such as the incomplete rigid constraints of the axial loading jack and imperfect contact between the right-side tangential jack and the sample surface—contributed to these differences. On the other hand, the simulation revealed the internal accumulation of damage processes. From a microscopic perspective, varying degrees of damage accumulated within the samples, but these damages were weakly manifested at the macroscopic level. Therefore, based on the findings from shear tests, strict precautions must be taken to prevent internal damage in the cantilever anti-floating ledge in actual engineering applications. In particular, the tensile reinforcement at the ledge sections and the stirrups in the lower half of the ledge should be reinforced. Additionally, fiber-reinforced concrete can be used to suppress the development of microcracks in concrete.

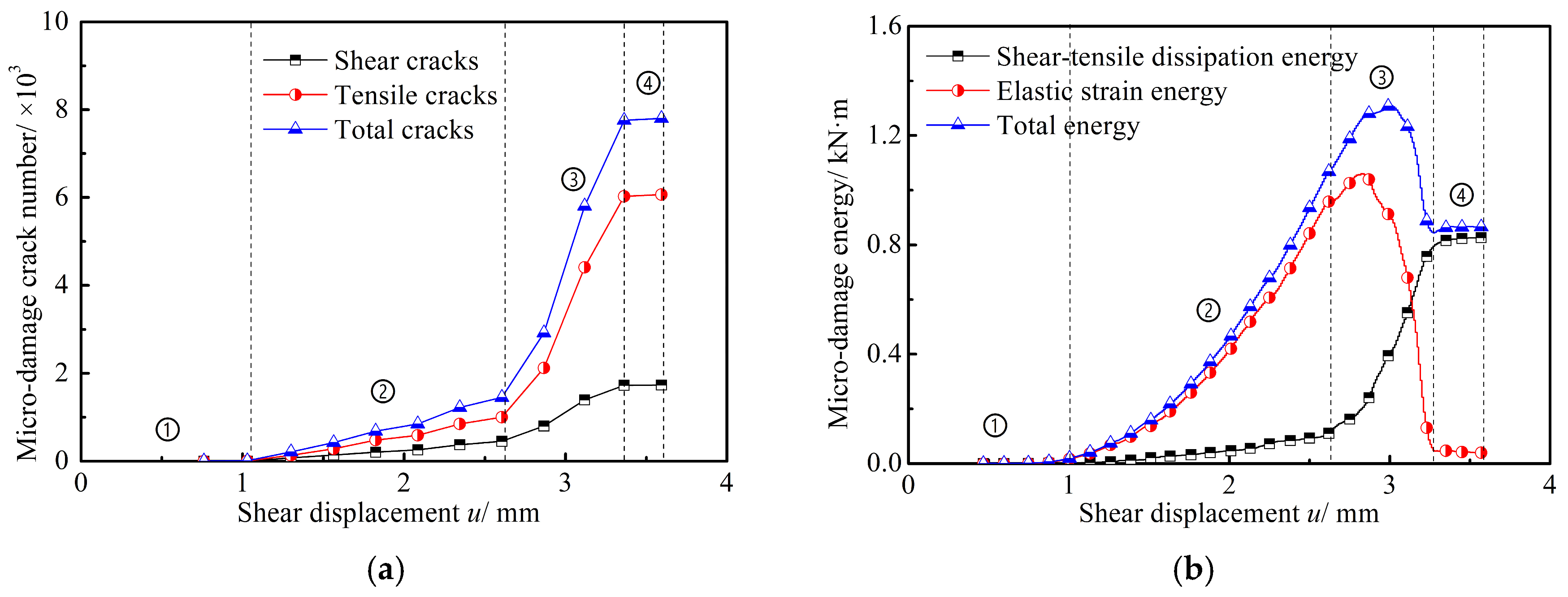
5.5. Micro-Damage Crack Number and Micro-Damage Energy

Figure 24 shows the relationship between the micro-damage crack number and micro-damage energy as a function of shear displacement. Micro-damage cracks are primarily classified into tensile cracks and shear cracks, both of which increase gradually with increasing shear displacement; among these, tensile cracks are significantly more numerous than shear cracks. The increase in crack numbers can be divided into four stages. In Stage ①, almost no micro-damage cracks form, and the sample is in the initial compaction stage. Upon entering stage ②, crack growth accelerates significantly, with damage first initiating in the stress concentration zones at the ledge. Stage ③ is characterized by a sharp increase in the number of micro-damage cracks; as shown in Figure 23, cracks are densely distributed at the ledge and propagate outward, primarily as tensile cracks. In stage ④, the number of cracks stabilizes, indicating that the sample has been completely sheared. Similarly, the evolution of micro-damage energy can also be divided into four stages. Stage ① is characterized by extremely low shear-tensile dissipation energy and elastic strain energy. In Stage ②, both increase with increasing shear displacement, but the growth rate of elastic strain energy is much higher than that of shear-tensile dissipation energy. As the peak shear stress is approached, Stage ③ begins, where the growth of elastic strain energy slows down and decreases, while shear-tensile dissipation energy increases sharply, causing the total energy to first rise and then fall. In Stage ④, the damage energy remains constant, indicating that the sample has completely failed. The four-stage classification of micro-damage crack number and micro-damage energy is basically consistent.

It can be further concluded that, under actual operating conditions, the cantilever anti-floating ledge is safest when restricted to stage ①. Suppose unexpected high groundwater buoyancy or local failure of auxiliary anti-floating components (such as uplift piles) causes the structure to enter stage ②. In that case, special attention must be paid to the formation of cracks near the ledge and the potential risk of separation from the rock layer. It should be ensured that the cantilever anti-floating ledge does not enter the stage ③.

Underlying causes of shear characteristics include geometric stress concentrations at the ledge bulge and material mismatches at the concrete–rock interface, leading to tensile-dominant cracks and sequential damage. Effects manifest as progressive strength degradation post-Stage II, with energy shifts from elastic storage to dissipation, indicating irreversible failure.

6. Discussion

6.1. The Limitations of the Shear Test and Subsequent Work

Although laboratory shear tests provide valuable insights into the shear behavior and failure mechanisms of the cantilever anti-floating ledge, it must be acknowledged that these tests have certain limitations. Shear tests examine the cantilever anti-floating ledge in isolation, simplifying the influence of the base slab and side walls on the anti-floating structure, and the impact of these factors on test results remains unevaluated. The 1/30-scale specimens may not fully reflect size effects present in full-scale structures, such as size-dependent fracture toughness or boundary effects. Simultaneously, the use of real materials (C35 concrete and slightly weathered sandstone) deviates from strict similarity laws, rendering the results less effective for evaluating bearing capacity. Material heterogeneity introduces additional uncertainty, as uneven bonding between natural sandstone joints and concrete may amplify discrepancies between laboratory and field conditions. During testing, axial jack retraction caused misalignment of the fixed constraints, resulting in a sudden drop in post-peak stress. Furthermore, the test assumed static loading at a constant rate of 0.3 mm/min, neglecting dynamic or periodic groundwater fluctuations common in water-saturated strata. Such fluctuations could accelerate interfacial delamination or fatigue damage.

To expand the experimental research, subsequent work should address current limitations. This includes employing advanced fixtures to more accurately replicate field constraints, exploring the feasibility of using similar materials for testing, and comprehensively considering boundary conditions under the influence of the entire structure. Additionally, multi-scenario shear tests should be conducted to evaluate the cantilever anti-floating ledge under varying conditions. This includes testing interface bond durability using rocks of different weathering grades (e.g., medium weathered sandstone), while varying platform dimensions and reinforcement ratios to quantify their impact on shear strength and crack resistance. Dynamic or cyclic loading protocols will also be introduced to simulate real-world groundwater buoyancy fluctuations, potentially revealing fatigue effects unobservable in static testing.

6.2. Advancements over Classical Methods and Existing Limitations

The proposed PFC model surpasses classical continuous medium methods (such as finite element analysis) by inherently capturing discontinuous behaviors like microcrack initiation and propagation at the concrete–rock interface. Finite element methods struggle to simulate discrete failure due to mesh dependency and the absence of additional damage criteria. While excelling in large-scale stress analysis, finite elements are complemented by PFC, which provides micro-scale insights into energy evolution and crack partitioning. This hybrid multi-scale approach enables more accurate prediction of shear failure in heterogeneous rock formations. This integration reveals mechanisms such as interfacial debonding due to material mismatch, which triggers strength loss—effects unobservable in purely continuum models.

Despite significant advantages, PFC models retain limitations. Substantial computational demands (240,000 cycles per iteration in this simulation); assumptions of two-dimensional plane strain that may underestimate three-dimensional spatial effects; and reliance on calibration parameters sensitive to material variability, where uncertainty in geological conditions (e.g., varying rock weathering) can introduce parameter errors that reduce computational accuracy. Future research may extend to three-dimensional PFC modeling of complex geometries, incorporate probabilistic sensitivity analysis to address uncertainties in groundwater buoyancy or jointed rock masses, and validate findings through field data from similar projects. This model enables reliable predictions under uncertain conditions by adjusting parameters based on field testing, providing a robust basis for anti-buoyancy design in medium-permeability rock formations with known variability.

7. Conclusions

In this paper, based on the actual engineering background, the shear test of the cantilever anti-floating ledge was designed. The working characteristics, shear characteristics, and failure process of the structure in anti-floating underground structures in rock strata were explored. On this basis, the PFC numerical calculation software was further utilized to investigate the failure evolution process and micro-damage evolution laws from a microscopic perspective. The following conclusions are drawn:

(1)

The shear stress–shear displacement relationship curve of the cantilever anti-floating ledge can be divided into six stages: ① initial compression stage, ② approximate linear elastic compression–shear deformation stage, ③ initial microcrack initiation and propagation stage, ④ slow compression–shear nonlinear deformation stage, ⑤ stress brittle drop stage, and ⑥ plastic flow deformation stage.

(2)

During the initial loading phase, the sample remains compacted, with deformation primarily occurring as uniform overall deformation. Subsequently, the upper right corner of the sample begins to warp, and a diagonal crack extending to the ledge appears in the upper left corner, exhibiting typical deformation zonation. After failure, the total displacement field of the structure exhibits significant displacement on the right side of the upper plate and the entire lower plate region. The key displacement change regions are the region extending from the upper left corner to the edge of the cantilever beam (Region I), the left interface region (Region II), and the right interface region (Region III).

(3)

In the initial stage, the cantilever anti-floating ledge primarily exhibits localized microcracks. Subsequently, tensile shear cracks first form near the concrete–rock interface of the side walls, followed by localized failure of the rock mass near the ledge and interface debonding. This process is referred to as Stage I. Subsequently, the structure undergoes continuous cracking, expansion, and penetration; compressive shear cracks form from the base plate to the cantilever ledge; and the loading curve shows a small stress drop until the cracks connect, leading to structural failure. This process is referred to as Stage II. Thereafter, the structure continues to undergo severe damage under residual strength, referred to as Stage III. It is essential to avoid entering Stages II and III.

(4)

The micro-damage process of cantilever anti-floating ledge generally goes through four stages. Stage ①: With a few microcracks, the structure is compacted, and the shear–tensile dissipation energy and elastic strain energy are small. Stage ②: Crack growth accelerates, damage begins at ledge areas, and elastic strain energy increases rapidly. Stage ③: Rapid increase in crack growth, extensive crack propagation at ledge areas, decrease in elastic strain energy, and a sharp increase in shear–tensile dissipated energy, with total energy first increasing and then decreasing. Stage ④: Crack growth and energy remain constant, and the structure fails.

(5)

To fully utilize the performance of the cantilever anti-floating ledge, special attention should be paid to the stress and deformation conditions at the connection between the ledge and the side walls and bottom plate. The reinforcement ratio of the tensile reinforcing bars at the connection points between the ledge and the side walls, as well as at the protruding parts of the ledge, should be increased. The stirrups at the lower half of the ledge should be strengthened, and the bond strength between the ledge and the rock layer should be enhanced. If the rock layer has a high degree of weathering or well-developed joints, additional reinforcement of the rock layer should be carried out within the influence zone of the ledge.