New Prediction Model of Rock Cerchar Abrasivity Index Based on Gene Expression Programming
Abstract
1. Introduction
2. Database Creation and Statistics Analysis
2.1. Database Creation
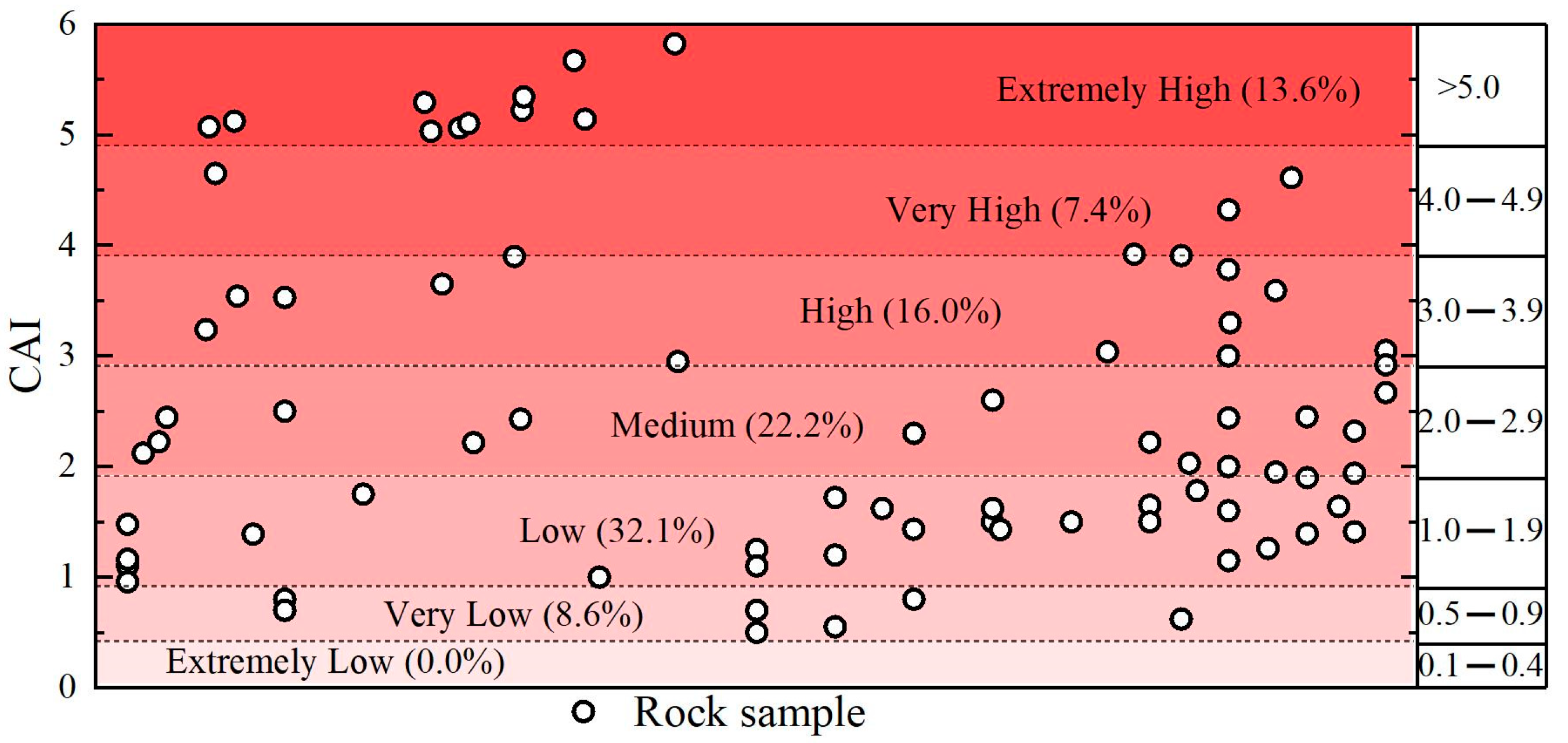
2.2. Statistics Analysis
3. Gene Expression Programming
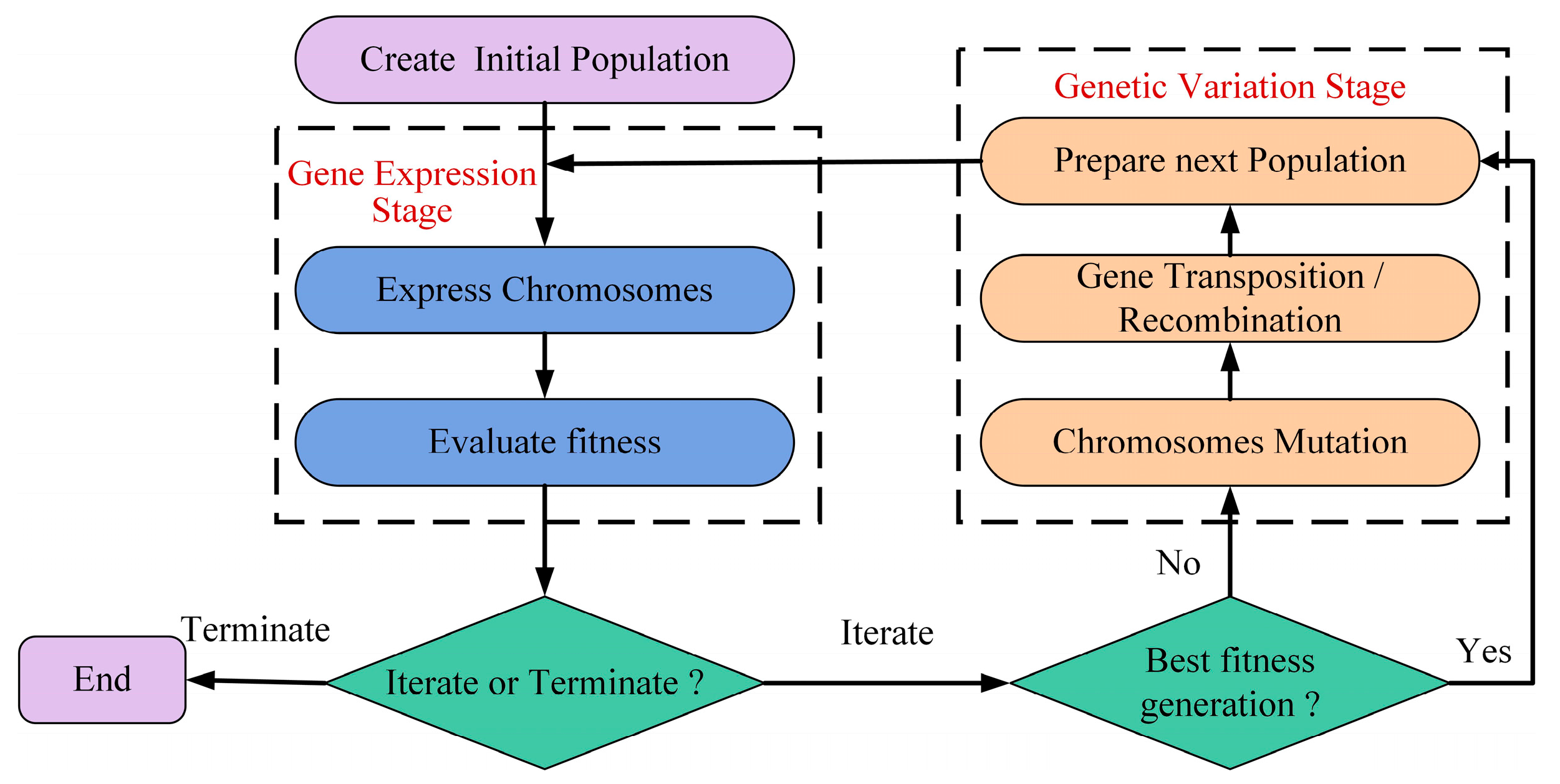
3.1. Overview of GEP Algorithm
3.2. GEP Algorithm Parameters
3.3. Fitness Evaluation Method
4. Results and Discussion
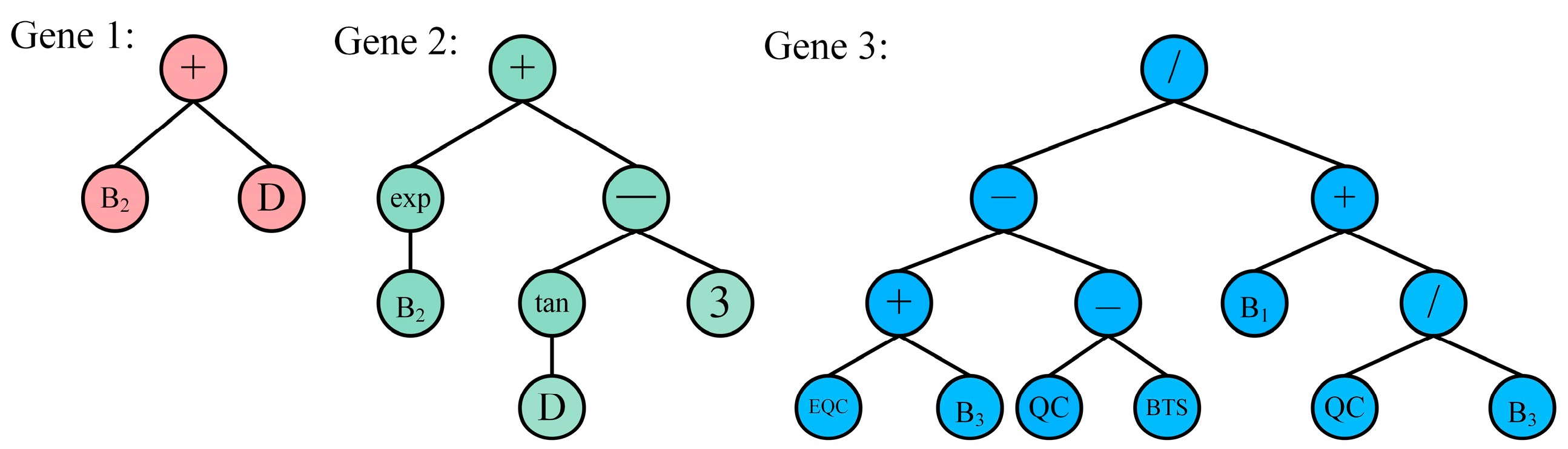
4.1. GEP-Based Model
4.2. Multiple Linear Regression Model
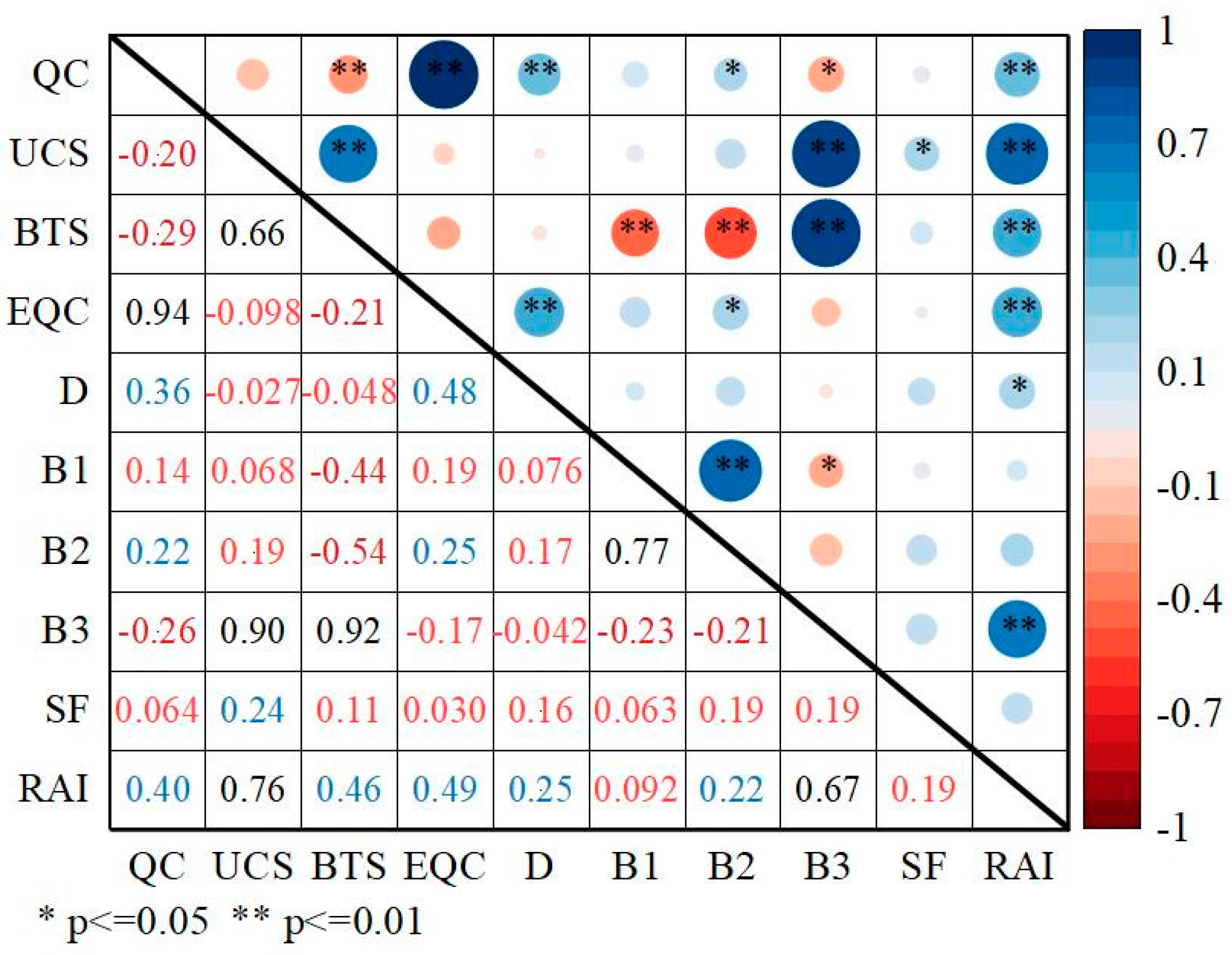
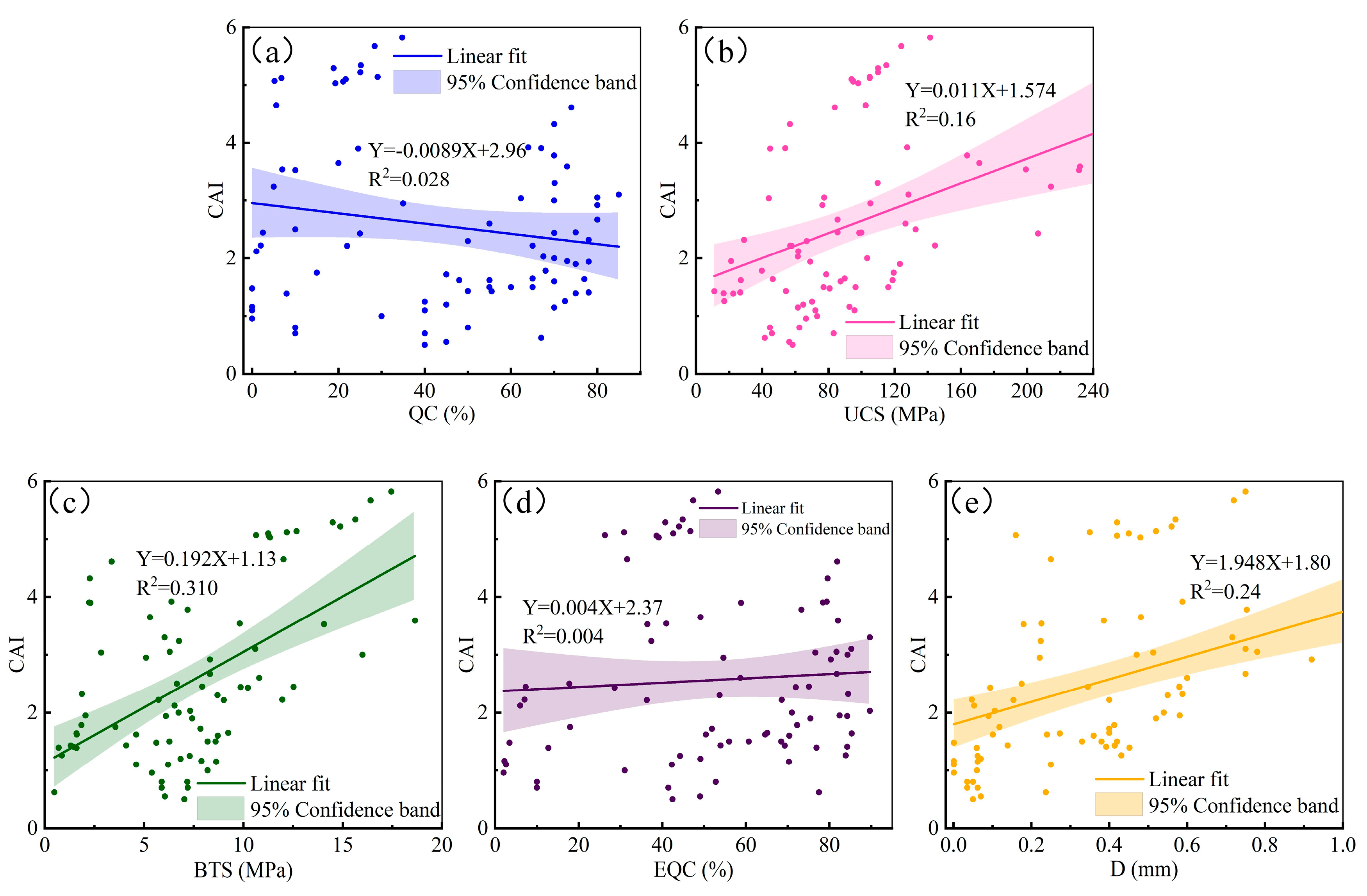
4.3. Models’ Goodness of Fit
4.4. Limitation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Rock Type | QC/% | UCS/MPa | BTS/MPa | EQC/% | D/mm | B1 | B2 | B3/MPa | SF-a/N/mm | RAI | CAI |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Granodiorite [19] | 25.10 | 110.00 | 14.88 | 44.01 | 0.56 | 7.39 | 0.76 | 28.61 | 3.67 | 48.41 | 5.22 |
| 2 | Monzogranite [19] | 21.10 | 95.00 | 11.28 | 38.63 | 0.42 | 8.42 | 0.79 | 23.15 | 1.83 | 36.70 | 5.06 |
| 3 | Monzogranite [19] | 19.30 | 98.00 | 11.34 | 39.15 | 0.48 | 8.64 | 0.79 | 23.57 | 2.13 | 38.37 | 5.03 |
| 4 | Monzogranite [19] | 28.40 | 124.00 | 16.41 | 47.40 | 0.72 | 7.56 | 0.77 | 31.90 | 5.60 | 58.78 | 5.67 |
| 5 | Monzogranite [19] | 25.20 | 115.00 | 15.64 | 44.89 | 0.57 | 7.35 | 0.76 | 29.99 | 4.00 | 51.62 | 5.34 |
| 6 | Granodiorite [19] | 18.90 | 110.00 | 14.50 | 40.73 | 0.42 | 7.59 | 0.77 | 28.24 | 2.48 | 44.80 | 5.29 |
| 7 | Monzonite [19] | 6.80 | 105.00 | 12.19 | 30.87 | 0.35 | 8.61 | 0.79 | 25.30 | 1.32 | 32.41 | 5.12 |
| 8 | Granodiorite [19] | 21.70 | 94.00 | 11.25 | 42.61 | 0.45 | 8.36 | 0.79 | 22.99 | 2.16 | 40.06 | 5.10 |
| 9 | Monzonite [19] | 5.60 | 102.50 | 12.02 | 31.59 | 0.25 | 8.53 | 0.79 | 24.82 | 0.95 | 32.38 | 4.65 |
| 10 | Monzogranite [19] | 29.10 | 105.00 | 12.68 | 46.73 | 0.52 | 8.28 | 0.78 | 25.80 | 3.08 | 49.07 | 5.14 |
| 11 | Granodiorite [19] | 34.80 | 141.50 | 17.45 | 53.37 | 0.75 | 8.11 | 0.78 | 35.14 | 6.98 | 75.51 | 5.82 |
| 12 | Monzonite [19] | 5.20 | 95.00 | 10.64 | 26.29 | 0.16 | 8.93 | 0.80 | 22.48 | 0.45 | 24.97 | 5.07 |
| 13 | Dolerite [29] | 5.00 | 214.50 | 6.76 | 37.39 | 0.22 | 31.73 | 0.94 | 26.93 | 0.57 | 80.19 | 3.24 |
| 14 | Dolerite [29] | 7.00 | 199.30 | 9.82 | 40.96 | 0.23 | 20.30 | 0.91 | 31.28 | 0.91 | 81.63 | 3.54 |
| 15 | Granite [29] | 74.00 | 83.81 | 3.37 | 81.86 | 1.10 | 24.87 | 0.92 | 11.88 | 3.04 | 68.61 | 4.61 |
| 16 | Granite [29] | 73.00 | 231.99 | 18.65 | 82.06 | 0.39 | 12.44 | 0.85 | 46.51 | 5.91 | 190.38 | 3.59 |
| 17 | Granite [29] | 24.60 | 44.80 | 2.30 | 58.85 | 2.50 | 19.48 | 0.90 | 7.18 | 3.38 | 26.37 | 3.90 |
| 18 | Migmatite [29] | 70.01 | 56.76 | 2.27 | 79.58 | 1.22 | 25.00 | 0.92 | 8.03 | 2.19 | 45.17 | 4.32 |
| 19 | Andesite [29] | 10.01 | 231.46 | 14.07 | 36.42 | 0.18 | 16.46 | 0.89 | 40.35 | 0.92 | 84.30 | 3.53 |
| 20 | Diorite [29] | 20.01 | 171.20 | 5.30 | 49.16 | 0.48 | 32.30 | 0.94 | 21.30 | 1.25 | 84.16 | 3.65 |
| 21 | Granite [29] | 67.00 | 53.90 | 2.23 | 78.45 | 1.19 | 24.12 | 0.92 | 7.76 | 20.00 | 42.28 | 3.907 |
| 22 | Phyllite [29] | 50.00 | 54.33 | 4.10 | 53.95 | 0.14 | 13.25 | 0.86 | 10.55 | 22.00 | 29.31 | 1.433 |
| 23 | Dolomite [29] | 2.00 | 144.43 | 11.96 | 7.04 | 0.05 | 12.08 | 0.85 | 29.39 | 30.00 | 10.17 | 2.223 |
| 24 | Sandstone [16] | 75.00 | 85.54 | 7.93 | 75.09 | 0.58 | 10.79 | 0.83 | 18.42 | 3.45 | 64.23 | 2.45 |
| 25 | Sandstone [16] | 80.01 | 77.45 | 6.29 | 81.69 | 0.78 | 12.31 | 0.85 | 15.61 | 4.01 | 63.27 | 3.05 |
| 26 | Sandstone [16] | 70.01 | 87.36 | 8.71 | 70.40 | 0.36 | 10.03 | 0.82 | 19.51 | 2.21 | 61.50 | 1.60 |
| 27 | Sandstone [16] | 60.01 | 77.05 | 6.28 | 60.70 | 0.33 | 12.27 | 0.85 | 15.55 | 1.26 | 46.77 | 1.50 |
| 28 | Sandstone [16] | 55.00 | 116.20 | 8.60 | 56.01 | 0.38 | 13.51 | 0.86 | 22.35 | 1.83 | 65.08 | 1.50 |
| 29 | Siltstone [16] | 70.01 | 61.51 | 8.63 | 70.33 | 0.06 | 7.13 | 0.75 | 16.29 | 0.38 | 43.26 | 1.15 |
| 30 | Siltstone [16] | 30.01 | 73.20 | 8.20 | 31.02 | 0.06 | 8.93 | 0.80 | 17.32 | 0.15 | 22.71 | 1.00 |
| 31 | Siltstone [16] | 40.01 | 70.10 | 7.30 | 44.25 | 0.06 | 9.60 | 0.81 | 16.00 | 0.20 | 31.02 | 1.25 |
| 32 | Siltstone [16] | 50.01 | 62.50 | 7.18 | 52.80 | 0.05 | 8.70 | 0.79 | 14.98 | 0.19 | 33.00 | 0.80 |
| 33 | Mudstone [16] | 10.01 | 44.65 | 5.89 | 10.00 | 0.04 | 7.58 | 0.77 | 11.47 | 0.02 | 4.47 | 0.80 |
| 34 | Mudstone [16] | 10.01 | 45.86 | 5.89 | 10.00 | 0.04 | 7.79 | 0.77 | 11.62 | 0.02 | 4.59 | 0.70 |
| 35 | Sandstone [16] | 75.01 | 123.21 | 7.42 | 75.45 | 0.52 | 16.61 | 0.89 | 21.38 | 2.91 | 92.96 | 1.90 |
| 36 | Sandstone [16] | 70.01 | 103.40 | 6.74 | 71.03 | 0.54 | 15.34 | 0.88 | 18.67 | 2.59 | 73.45 | 2.00 |
| 37 | Sandstone [16] | 65.01 | 89.79 | 9.24 | 65.12 | 0.40 | 9.72 | 0.81 | 20.37 | 2.41 | 58.47 | 1.65 |
| 38 | Sandstone [16] | 45.01 | 78.65 | 7.84 | 51.90 | 0.40 | 10.03 | 0.82 | 17.56 | 1.63 | 40.82 | 1.72 |
| 39 | Siltstone [16] | 40.01 | 83.20 | 7.20 | 41.45 | 0.06 | 11.56 | 0.84 | 17.31 | 0.19 | 34.49 | 0.70 |
| 40 | Sandstone [16] | 80.01 | 76.33 | 8.32 | 80.35 | 0.92 | 9.17 | 0.80 | 17.82 | 6.15 | 61.33 | 2.92 |
| 41 | Sandstone [16] | 65.01 | 56.93 | 5.73 | 68.60 | 0.40 | 9.94 | 0.82 | 12.77 | 1.57 | 39.05 | 2.22 |
| 42 | Sandstone [16] | 65.01 | 96.40 | 8.20 | 68.47 | 0.42 | 11.76 | 0.84 | 19.88 | 2.36 | 66.01 | 1.50 |
| 43 | Sandstone [16] | 55.01 | 126.60 | 10.80 | 58.70 | 0.60 | 11.72 | 0.84 | 26.15 | 3.80 | 74.31 | 2.60 |
| 44 | Sandstone [16] | 50.01 | 66.92 | 8.70 | 53.72 | 0.55 | 7.69 | 0.77 | 17.06 | 2.57 | 35.95 | 2.30 |
| 45 | Sandstone [16] | 70.01 | 98.64 | 9.86 | 71.95 | 0.58 | 10.00 | 0.82 | 22.05 | 4.11 | 70.97 | 2.44 |
| 46 | Siltstone [16] | 40.01 | 58.31 | 7.03 | 42.45 | 0.05 | 8.29 | 0.78 | 14.32 | 0.15 | 24.75 | 0.50 |
| 47 | Siltstone [16] | 45.01 | 64.81 | 6.84 | 49.13 | 0.07 | 9.48 | 0.81 | 14.89 | 0.24 | 31.84 | 1.20 |
| 48 | Sandstone [16] | 40.01 | 72.14 | 6.21 | 42.29 | 0.25 | 11.62 | 0.84 | 14.97 | 0.66 | 30.51 | 1.10 |
| 49 | Sandstone [16] | 80.01 | 85.56 | 8.32 | 81.75 | 0.75 | 10.28 | 0.82 | 18.87 | 5.10 | 69.95 | 2.67 |
| 50 | Siltstone [16] | 45.01 | 56.37 | 6.05 | 49.05 | 0.07 | 9.32 | 0.81 | 13.06 | 0.21 | 27.65 | 0.55 |
| 51 | Sandstone [16] | 85.00 | 128.40 | 10.60 | 85.23 | 0.75 | 12.11 | 0.85 | 26.09 | 27.00 | 109.44 | 3.1 |
| 52 | Siltstone [29] | 22.01 | 57.88 | 9.02 | 36.31 | 0.15 | 6.42 | 0.73 | 16.15 | 0.50 | 21.02 | 2.22 |
| 53 | Sandstone [29] | 68.01 | 39.80 | 1.85 | 72.27 | 0.41 | 21.56 | 0.91 | 6.06 | 0.55 | 28.77 | 1.78 |
| 54 | Sandstone [29] | 67.01 | 41.55 | 0.48 | 77.51 | 0.24 | 86.56 | 0.98 | 3.16 | 0.09 | 32.20 | 0.62 |
| 55 | Sandstone [29] | 64.01 | 127.60 | 6.38 | 79.36 | 0.59 | 20.00 | 0.90 | 20.18 | 2.98 | 101.26 | 3.92 |
| 56 | Sandstone [29] | 78.01 | 26.73 | 1.45 | 84.26 | 0.39 | 18.47 | 0.90 | 4.40 | 0.48 | 22.52 | 1.41 |
| 57 | Sandstone [29] | 62.31 | 44.00 | 2.84 | 76.63 | 0.51 | 15.50 | 0.88 | 7.90 | 1.12 | 33.72 | 3.04 |
| 58 | Sandstone [29] | 70.11 | 109.73 | 6.03 | 89.70 | 0.72 | 18.20 | 0.90 | 18.19 | 3.87 | 98.43 | 3.30 |
| 59 | Sandstone [29] | 67.51 | 61.51 | 7.32 | 89.69 | 0.11 | 8.40 | 0.79 | 15.00 | 0.70 | 55.17 | 2.03 |
| 60 | Sandstone [29] | 55.51 | 11.04 | 1.31 | 69.31 | 0.41 | 8.43 | 0.79 | 2.69 | 0.38 | 7.65 | 1.43 |
| 61 | Sandstone [29] | 78.01 | 29.04 | 1.87 | 84.47 | 0.59 | 15.53 | 0.88 | 5.21 | 0.93 | 24.53 | 2.32 |
| 62 | Sandstone [29] | 75.01 | 16.69 | 0.70 | 76.91 | 0.45 | 23.84 | 0.92 | 2.42 | 0.24 | 12.84 | 1.39 |
| 63 | Sandstone [29] | 73.01 | 21.18 | 2.05 | 82.43 | 0.58 | 10.33 | 0.82 | 4.66 | 0.98 | 17.46 | 1.95 |
| 64 | Sandstone [29] | 55.01 | 27.09 | 1.61 | 64.62 | 0.24 | 16.82 | 0.89 | 4.67 | 0.25 | 17.50 | 1.62 |
| 65 | Sandstone [29] | 77.01 | 46.40 | 1.60 | 85.33 | 0.27 | 29.00 | 0.93 | 6.09 | 0.37 | 39.59 | 1.64 |
| 66 | Sandstone [29] | 72.51 | 17.07 | 0.86 | 83.90 | 0.43 | 19.85 | 0.90 | 2.71 | 0.31 | 14.32 | 1.26 |
| 67 | Sandstone [29] | 78.01 | 69.04 | 6.10 | 84.26 | 0.09 | 11.32 | 0.84 | 14.51 | 0.46 | 58.17 | 1.94 |
| 68 | Dolomite [29] | 1.01 | 61.84 | 6.54 | 6.01 | 0.05 | 9.46 | 0.81 | 14.22 | 0.02 | 3.71 | 2.12 |
| 69 | Dolomite [29] | 2.51 | 99.93 | 12.53 | 7.32 | 0.35 | 7.98 | 0.78 | 25.02 | 0.32 | 7.32 | 2.45 |
| 70 | Dolomite [29] | 10.01 | 132.70 | 6.65 | 17.77 | 0.18 | 19.95 | 0.90 | 21.01 | 0.21 | 23.57 | 2.50 |
| 71 | Limestone [29] | 0.01 | 95.78 | 4.60 | 2.60 | 0.00 | 20.80 | 0.91 | 14.85 | 0.00 | 2.49 | 1.10 |
| 72 | Limestone [29] | 0.01 | 80.70 | 5.62 | 3.44 | 0.00 | 14.36 | 0.87 | 15.06 | 0.00 | 2.77 | 1.48 |
| 73 | Limestone [29] | 0.01 | 66.45 | 5.39 | 2.03 | 0.00 | 12.33 | 0.85 | 13.38 | 0.00 | 1.35 | 0.96 |
| 74 | Limestone [29] | 0.01 | 92.75 | 7.89 | 2.22 | 0.00 | 11.75 | 0.84 | 19.13 | 0.00 | 2.06 | 1.16 |
| 75 | Tuff [32] | 70.00 | 313.20 | 16.00 | 84.34 | 0.47 | 19.58 | 0.90 | 50.06 | 5.00 | 264.15 | 3 |
| 76 | Sandstone [32] | 48.00 | 118.80 | 4.60 | 50.44 | 0.10 | 25.83 | 0.93 | 16.53 | 7.00 | 59.92 | 1.62 |
| 77 | Mudstone [32] | 8.00 | 22.50 | 1.60 | 12.75 | 0.06 | 14.06 | 0.87 | 4.24 | 10.00 | 2.87 | 1.39 |
| 78 | Sandstone [32] | 35.00 | 105.40 | 5.10 | 54.63 | 0.22 | 20.67 | 0.91 | 16.39 | 11.00 | 57.58 | 2.95 |
| 79 | Sandstone [32] | 25.00 | 206.70 | 10.23 | 28.62 | 0.09 | 20.21 | 0.91 | 32.52 | 13.00 | 59.16 | 2.43 |
| 80 | Sandstone [32] | 70.00 | 163.83 | 7.19 | 73.31 | 0.75 | 22.79 | 0.92 | 24.27 | 14.00 | 120.10 | 3.78 |
| 81 | Sandstone [32] | 15.00 | 119.46 | 3.56 | 17.93 | 0.12 | 33.56 | 0.94 | 14.58 | 16.00 | 21.42 | 1.75 |
References
- Zhang, S.-R.; She, L.; Wang, C.; Wang, Y.-J.; Cao, R.-L.; Li, Y.-L.; Cao, K.-L. Investigation on the relationship among the Cerchar abrasivity index, drilling parameters and physical and mechanical properties of the rock. Tunn. Undergr. Space Technol. 2021, 112, 103907. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, S.; Deng, M.; Wang, C. Nonlinear dynamic analysis and damage evaluation of hydraulic arched tunnels under mainshock–aftershock ground motion sequences. Tunn. Undergr. Space Technol. 2020, 98, 103321. [Google Scholar] [CrossRef]
- Abu Bakar, M.Z.; Majeed, Y.; Rostami, J. Effects of rock water content on Cerchar abrasivity index. Wear 2016, 368–369, 132–145. [Google Scholar] [CrossRef]
- Sun, J.; Wang, K.; Wei, J.; Shang, Y.; Sun, C.; Ma, F. A mechanics model of constant cross-section type disc cutter based on dense core forming mechanism. Tunn. Undergr. Space Technol. 2023, 140, 105301. [Google Scholar] [CrossRef]
- Zhang, G.; Konietzky, H.; Song, Z.; Zhang, M. Study of Cerchar abrasive parameters and their relations to intrinsic properties of rocks for construction. Constr. Build. Mater. 2020, 244, 118327. [Google Scholar] [CrossRef]
- Kahraman, S.; Alber, M.; Fener, M.; Gunaydin, O. The usability of Cerchar abrasivity index for the prediction of UCS and E of Misis Fault Breccia: Regression and artificial neural networks analysis. Expert Syst. Appl. 2010, 37, 8750–8756. [Google Scholar] [CrossRef]
- Golovanevskiy, V.A.; Bearman, R.A. Gouging abrasion test for rock abrasiveness testing. Int. J. Miner. Process. 2008, 85, 111–120. [Google Scholar] [CrossRef]
- Perez, S.; Karakus, M.; Sepulveda, E. A preliminary study on the role of acoustic emission on inferring Cerchar abrasivity index of rocks using artificial neural network. Wear 2015, 344–345, 1–8. [Google Scholar] [CrossRef]
- Deliormanlı, A.H. Cerchar abrasivity index (CAI) and its relation to strength and abrasion test methods for marble stones. Constr. Build. Mater. 2012, 30, 16–21. [Google Scholar] [CrossRef]
- Yaralı, O.; Duru, H. Investigation into effect of scratch length and surface condition on Cerchar abrasivity index. Tunn. Undergr. Space Technol. 2016, 60, 111–120. [Google Scholar] [CrossRef]
- Sun, J.; Shang, Y.; Wang, K.; Wang, C.; Ma, F.; Sun, C. A new prediction model for disc cutter wear based on Cerchar abrasivity index. Wear 2023, 526–527, 204927. [Google Scholar] [CrossRef]
- Aydın, H. Investigating the effects of various testing parameters on Cerchar abrasivity index and its repeatability. Wear 2019, 418–419, 61–74. [Google Scholar] [CrossRef]
- Michalakopoulos, T.N.; Anagnostou, V.G.; Bassanou, M.E.; Panagiotou, G.N. The influence of steel styli hardness on the Cerchar abrasiveness index value. Int. J. Rock Mech. Min. Sci. 2006, 43, 321–327. [Google Scholar] [CrossRef]
- Teymen, A. The usability of Cerchar abrasivity index for the estimation of mechanical rock properties. Int. J. Rock Mech. Min. Sci. 2020, 128, 104258. [Google Scholar] [CrossRef]
- Ko, T.Y.; Kim, T.K.; Son, Y.; Jeon, S. Effect of geomechanical properties on Cerchar abrasivity index (CAI) and its application to TBM tunnelling. Tunn. Undergr. Space Technol. 2016, 57, 99–111. [Google Scholar] [CrossRef]
- Yaralı, O.; Yaşar, E.; Bacak, G.; Ranjith, P.G. A study of rock abrasivity and tool wear in coal measures rocks. Int. J. Coal Geol. 2008, 74, 53–66. [Google Scholar] [CrossRef]
- Alber, M. Stress dependency of the Cerchar abrasivity index (CAI) and its effects on wear of selected rock cutting tools. Tunn. Undergr. Space Technol. 2008, 23, 351–359. [Google Scholar] [CrossRef]
- Moradizadeh, M.; Cheshomi, A.; Ghafoori, M.; TrighAzali, S. Correlation of equivalent quartz content, Slake durability index and Is50 with Cerchar abrasiveness index for different types of rock. Int. J. Rock Mech. Min. Sci. 2016, 86, 42–47. [Google Scholar] [CrossRef]
- Er, S.; Tuğrul, A. Correlation of physico-mechanical properties of granitic rocks with Cerchar abrasivity index in Turkey. Measurement 2016, 91, 114–123. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.-L.; Zhou, A.; Yin, Z.-Y.; Lyu, H.-M. Prediction of disc cutter life during shield tunneling with AI via the incorporation of a genetic algorithm into a GMDH-Type neural network. Engineering 2021, 7, 238–251. [Google Scholar] [CrossRef]
- Qi, H.; Zhou, J.; Khandelwal, M.; Onifade, M.; Lawal, A.I.; Li, C.; Bada, S.O.; Genc, B. An optimized machine learning framework for prediction of coal abrasive index: Leveraging supervised learning, metaheuristic optimization, and interpretability analysis. Fuel 2026, 403, 136065. [Google Scholar] [CrossRef]
- Houshmand, N.; Esmaeili, K.; Goodfellow, S.; Carlos Ordóñez-Calderón, J. Predicting rock hardness using Gaussian weighted moving average filter on borehole data and machine learning. Miner. Eng. 2023, 204, 108448. [Google Scholar] [CrossRef]
- Geng, Q.; Huang, Y.; Chen, J.; Wang, X.; Liu, W.; Luo, Y.; Zhang, Z.; Ye, M. Prediction of rock-breaking forces of tunnel boring machine (TBM) disc cutter based on machine learning methods. Tunn. Undergr. Space Technol. 2025, 163, 106682. [Google Scholar] [CrossRef]
- Shin, Y.J.; Kwon, K.; Bae, A.; Choi, H.; Kim, D. Machine learning-based prediction model for disc cutter life in TBM excavation through hard rock formations. Tunn. Undergr. Space Technol. 2024, 150, 105826. [Google Scholar] [CrossRef]
- Tripathy, A.; Singh, T.N.; Kundu, J. Prediction of abrasiveness index of some Indian rocks using soft computing methods. Measurement 2015, 68, 302–309. [Google Scholar] [CrossRef]
- Onifade, M.; Lawal, A.I.; Bada, S.O.; Khandelwal, M. Predictive modelling for coal abrasive index: Unveiling influential factors through Shallow and Deep Neural Networks. Fuel 2024, 374, 132319. [Google Scholar] [CrossRef]
- Barzegari, G.; Khodayari, J.; Rostami, J. Evaluation of TBM cutter wear in Naghadeh water conveyance tunnel and developing a new prediction model. Rock Mech. Rock Eng. 2021, 54, 6281–6297. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, H.; Hong, K.; Chen, K.; Zhou, J.; Li, F.; Zhang, B.; Song, F.; Yang, Y.; He, R. A practical TBM cutter wear prediction model for disc cutter life and rock wear ability. Tunn. Undergr. Space Technol. 2019, 85, 92–99. [Google Scholar] [CrossRef]
- Majeed, Y.; Abu Bakar, M.Z. Statistical evaluation of Cerchar abrasivity index (CAI) measurement methods and dependence on petrographic and mechanical properties of selected rocks of Pakistan. Bull. Eng. Geol. Environ. 2016, 75, 1341–1360. [Google Scholar] [CrossRef]
- Rostami, J.; Ghasemi, A.; Alavi Gharahbagh, E.; Dogruoz, C.; Dahl, F. Study of dominant factors affecting Cerchar abrasivity index. Rock Mech. Rock Eng. 2014, 47, 1905–1919. [Google Scholar] [CrossRef]
- Capik, M.; Yilmaz, A.O. Correlation between Cerchar abrasivity index, rock properties, and drill bit lifetime. Arab. J. Geosci. 2017, 10, 15. [Google Scholar] [CrossRef]
- He, J.; Li, S.; Li, X.; Wang, X.; Guo, J. Study on the correlations between abrasiveness and mechanical properties of rocks combining with the microstructure characteristic. Rock Mech. Rock Eng. 2016, 49, 2945–2951. [Google Scholar] [CrossRef]
- Ozdogan, M.V.; Deliormanli, A.H.; Yenice, H. The correlations between the Cerchar abrasivity index and the geomechanical properties of building stones. Arab. J. Geosci. 2018, 11, 604. [Google Scholar] [CrossRef]
- Torrijo, F.J.; Garzón-Roca, J.; Company, J.; Cobos, G. Estimation of Cerchar abrasivity index of andesitic rocks in Ecuador from chemical compounds and petrographical properties using regression analyses. Bull. Eng. Geol. Environ. 2019, 78, 2331–2344. [Google Scholar] [CrossRef]
- Plinninger, R.; Käsling, H.; Thuro, K.; Spaun, G. Testing conditions and geomechanical properties influencing the Cerchar abrasiveness index (CAI) value. Int. J. Rock Mech. Min. Sci. 2003, 40, 259–263. [Google Scholar] [CrossRef]
- Hucka, V.; Das, B. Brittleness determination of rocks by different methods. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1974, 11, 389–392. [Google Scholar] [CrossRef]
- Shaffiee Haghshenas, S.; Shirani Faradonbeh, R.; Mikaeil, R.; Haghshenas, S.S.; Taheri, A.; Saghatforoush, A.; Dormishi, A. A new conventional criterion for the performance evaluation of gang saw machines. Measurement 2019, 146, 159–170. [Google Scholar] [CrossRef]
- Sarıdemir, M. Genetic programming approach for prediction of compressive strength of concretes containing rice husk ash. Constr. Build. Mater. 2010, 24, 1911–1919. [Google Scholar] [CrossRef]
- Korkmaz, E.; Tarım, S. Comprehensive analysis of impeller trimming modifications on submersible pump characteristics using a gene expression programming approach. Measurement 2025, 254, 117876. [Google Scholar] [CrossRef]
- Abdullah, A.; Saddiqi, H.A.; Qasim, M.; Khitab, A.; Khan, M.; Ahmad, S. Anemia prediction using gene expression programming (GEP) and explainable artificial intelligence approaches. Comput. Biol. Med. 2025, 196, 110856. [Google Scholar] [CrossRef] [PubMed]



| Researchers | Year | Analysis Method | Rock Properties | ||||||
|---|---|---|---|---|---|---|---|---|---|
| QC | EQC | UCS | BTS | Is50 | D | N | |||
| Ko [15] | 2016 | Regression analysis | √ | √ | √ | √ | |||
| Barzegari [27] | 2021 | Statistical analysis | √ | √ | √ | ||||
| Sun [28] | 2019 | Experiment analysis | √ | √ | |||||
| Yaralı [16] | 2008 | Regression analysis | √ | √ | √ | √ | √ | √ | √ |
| Deliormanlı [9] | 2012 | Regression analysis | √ | √ | |||||
| Alber [17] | 2008 | Theoretical analysis | √ | √ | √ | √ | √ | ||
| Perez [8] | 2015 | Neural network | √ | √ | √ | √ | |||
| Moradizadeh [18] | 2016 | Statistical analysis | √ | √ | √ | √ | |||
| Er [19] | 2016 | Regression analysis | √ | √ | √ | √ | √ | ||
| Zhang [1] | 2021 | Regression analysis | √ | √ | √ | √ | |||
| Majeed [29] | 2015 | Statistical analysis | √ | √ | √ | √ | √ | ||
| Rostami [30] | 2014 | Experiment analysis | √ | √ | √ | ||||
| Capik [31] | 2017 | Regression analysis | √ | √ | √ | √ | |||
| He [32] | 2016 | Regression analysis | √ | √ | √ | √ | √ | √ | |
| Ozdogan [33] | 2018 | Regression analysis | √ | √ | |||||
| Torrijo [34] | 2019 | Regression analysis | √ | √ | |||||
| Plinninger [35] | 2003 | Regression analysis | √ | √ | |||||
| Teymen [14] | 2020 | Regression analysis | √ | √ | √ | √ | |||
| Parameter | Maximum | Minimum | Average | Standard Deviation | |
|---|---|---|---|---|---|
| Input | QC/% | 0.01 | 85.00 | 43.91 | 27.32 |
| UCS/MPa | 11.04 | 313.20 | 92.28 | 53.64 | |
| BTS/MPa | 0.48 | 18.65 | 7.48 | 4.22 | |
| EQC/% | 2.03 | 89.70 | 53.23 | 25.50 | |
| D/mm | 0.00 | 2.50 | 0.39 | 0.37 | |
| B1 | 6.42 | 86.56 | 14.90 | 10.41 | |
| B2 | 0.73 | 0.98 | 0.85 | 0.06 | |
| B3/MPa | 2.42 | 50.06 | 18.16 | 9.53 | |
| SF-a/N/mm | 0.00 | 30.00 | 3.62 | 5.89 | |
| RAI | 1.35 | 264.15 | 47.79 | 40.08 | |
| Output | CAI | 0.50 | 5.82 | 2.57 | 1.46 |
| Type | Parameters/Hyperparameters | Value/Symbol |
|---|---|---|
| General setting | Input parameters | QC, UCS, BTS, EQC, D, B1, B2, B3, SF-a, RAI |
| Function symbol | +,−,*,/,sqrt,exp,^2,^3,tan,^(1/3) | |
| Fitness method | R2 | |
| Population size | 60 | |
| Iteration number | 3000 | |
| Linking function | + | |
| Genetic variation parameters | Mutation | 0.2 |
| Inversion | 0.2 | |
| IS transposition | 0.15 | |
| RIS transposition | 0.15 | |
| One-point recombination | 0.15 | |
| Two-point recombination | 0.15 | |
| Gene recombination | 0.1 |
| Model | Sum of Squares | df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|---|
| 1 | Regression | 52.51 | 1 | 52.51 | 35.45 | 0.00 |
| Residual | 117.01 | 79 | 1.48 | |||
| Total | 169.52 | 80 | ||||
| 2 | Regression | 98.09 | 2 | 49.05 | 53.56 | 0.00 |
| Residual | 71.43 | 78 | 0.916 | |||
| Total | 169.52 | 80 | ||||
| 3 | Regression | 105.34 | 3 | 35.11 | 42.13 | 0.00 |
| Residual | 64.18 | 77 | 0.83 | |||
| Total | 169.52 | 80 | ||||
| 4 | Regression | 127.27 | 4 | 31.82 | 57.24 | 0.00 |
| Residual | 42.247 | 76 | 0.56 | |||
| Total | 169.52 | 80 | ||||
| Model | Unstandardized Coefficients | t | Sig. | R2 | ||
|---|---|---|---|---|---|---|
| B | Std. Error | |||||
| 1 | Constant | 1.13 | 0.28 | 4.09 | 0.00 | 0.31 |
| BTS | 0.19 | 0.03 | 5.95 | 0.00 | ||
| 2 | Constant | 0.26 | 0.25 | 1.02 | 0.31 | 0.58 |
| BTS | 0.20 | 0.03 | 7.90 | 0.00 | ||
| D | 2.06 | 0.29 | 7.06 | 0.00 | ||
| 3 | Constant | 0.84 | 0.31 | 2.70 | 0.01 | 0.62 |
| BTS | 0.18 | 0.03 | 7.06 | 0.00 | ||
| D | 2.37 | 0.30 | 7.96 | 0.00 | ||
| QC | −0.01 | 0.004 | −2.95 | 0.00 | ||
| 4 | Constant | 0.16 | 0.27 | 0.60 | 0.55 | 0.75 |
| BTS | 0.16 | 0.02 | 7.46 | 0.00 | ||
| D | 1.57 | 0.28 | 5.70 | 0.00 | ||
| QC | −0.07 | 0.01 | −7.14 | 0.00 | ||
| EQC | 0.07 | 0.01 | 6.28 | 0.00 | ||
| Indices | GEP-Based | MLR-Based | |||
|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | ||
| R2 | 0.906 | 0.31 | 0.58 | 0.62 | 0.75 |
| RMSE | 0.46 | 1.20 | 0.94 | 0.90 | 0.73 |
| MAPE | 0.18 | 0.48 | 0.38 | 0.36 | 0.28 |
| MAE | 0.37 | 1.00 | 0.79 | 0.75 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Fan, X.; Wang, H.; Shang, Y.; Sun, C. New Prediction Model of Rock Cerchar Abrasivity Index Based on Gene Expression Programming. Appl. Sci. 2025, 15, 10901. https://doi.org/10.3390/app152010901
Sun J, Fan X, Wang H, Shang Y, Sun C. New Prediction Model of Rock Cerchar Abrasivity Index Based on Gene Expression Programming. Applied Sciences. 2025; 15(20):10901. https://doi.org/10.3390/app152010901
Chicago/Turabian StyleSun, Jingdong, Xiaohua Fan, Hao Wang, Yong Shang, and Chaoyang Sun. 2025. "New Prediction Model of Rock Cerchar Abrasivity Index Based on Gene Expression Programming" Applied Sciences 15, no. 20: 10901. https://doi.org/10.3390/app152010901
APA StyleSun, J., Fan, X., Wang, H., Shang, Y., & Sun, C. (2025). New Prediction Model of Rock Cerchar Abrasivity Index Based on Gene Expression Programming. Applied Sciences, 15(20), 10901. https://doi.org/10.3390/app152010901







