Visual Mamba-Inspired Directionally Gated State-Space Backtracking for Chemical Gas Source Localization

Abstract

Rapidly pinpointing the origin of accidental chemical gas releases is essential for effective response. Prior vision pipelines—such as 3D CNNs, CNN–LSTMs, and Transformer-based ViViT models—can improve accuracy but often scale poorly as the temporal window grows or winds meander. We cast recursive backtracking of concentration fields as a finite-horizon, multi-step spatiotemporal sequence modelling problem and introduce Recursive Backtracking with Visual Mamba (RBVM), a Visual Mamba-inspired, directionally gated state-space backbone. Each block applies causal, depthwise sweeps along ${\mathrm{H}}^{\pm }$, ${\mathrm{W}}^{\pm }$, and ${\mathrm{T}}^{\pm }$ and then fuses them via a learned upwind gate; a lightweight MLP follows. Pre-norm LayerNorm and small LayerScale on both branches, together with a layer-indexed, depth-weighted DropPath, yield stable stacking at our chosen depth, while a 3D-Conv stem and head keep the model compact. Computation and parameter growth scale linearly with the sequence extent and the number of directions. Across a synthetic diffusion corpus and a held-out NBC_RAMS field set, RBVM consistently improves Exact and hit $\le 1$ over strong 3D CNN, CNN–LSTM, and ViViT baselines, while using fewer parameters. Finally, we show that, without retraining, a physics-motivated two-peak subtraction on the oldest reconstructed frame enables zero-shot dual-source localization. We believe RBVM provides a compact, linear-time, directionally causal backbone for inverse inference on transported fields—useful not only for gas–release source localization in CBRN response but more broadly for spatiotemporal backtracking tasks in environmental monitoring and urban analytics.

1. Introduction

Accidental or malicious releases of toxic industrial chemicals (TICs)—including chlorine, sulfur dioxide, and anhydrous ammonia—have repeatedly demonstrated their potential for severe harm to public health, industry, and ecosystems. Large-scale field trials and incident reports alike show that dense gases hug the surface, weave around obstacles, and traverse long distances within minutes. Under such constraints, the practical value of a localization system is decided in the earliest stage: quickly inferring the emission origin guides evacuation corridors, prioritises mobile or fixed sensor deployment, and informs remediation teams. While the conceptual ideal would be a dense, always-on lattice of chemical detectors, the reality is constrained by cost, power, maintenance, and social acceptance; in practice, responders pair sparse measurements with operational dispersion tools such as ALOHA and HPAC to delineate hazard footprints [1,2]. The resulting observability gap motivates methods that can reason from sparse measurements or image-like surrogates of concentration fields, with early mobile-robotics work demonstrating gas-concentration gridmaps from sparse sensors [3].

A natural direction is to treat the gridded concentration map—obtained from fast surrogates, physics simulators, or interpolated sensor mosaics—as a spatiotemporal signal and to pose source localization as a data-driven inference task. Early pipelines based on 3D convolutional neural networks (3D CNNs) or hybrid CNN–LSTM stacks (e.g., ConvLSTM [4]) learn useful local motion features, but their compute and memory grow unfavourably with temporal horizon, cubically for deep 3D CNNs (to achieve large receptive fields) and at least quadratically for CNN–LSTM variants that carry recurrent state over long windows [5,6]. Parallel optimization and Bayesian inversions remain attractive for small grids [7,8], yet they typically require explicit wind-field estimates and degrade as resolution or domain size increases. More recently, Transformer-based approaches have recast localization as recursive frame prediction: given recent frames, a model iteratively predicts earlier snapshots until the origin emerges [9]. Transformer models have also been widely adapted to vision tasks [10]. Video Vision Transformer (ViViT) further improved single-pass accuracy [11]; however, global self-attention incurs $\mathcal{O}\left(L^2\right)$ cost in sequence length L, which constrains temporal reach and throughput, and prior studies primarily address single-source incidents. Related video backbones such as SlowFast and the Temporal Shift Module (TSM) have also been widely adopted for efficient temporal modelling [12,13]. Recent surveys and designs on efficient video backbones further motivate axis-wise, linear-time operators for streaming use cases (see, e.g., [14]).

State-space sequence models (SSMs) offer a principled path to linear-time sequence modelling without global attention. Mamba replaces global attention with content-aware kernels that propagate a latent state at $\mathcal{O}\left(L\right)$ cost [15], and visual extensions apply directional scans along image axes to capture spatial dependencies [16,17]. Building on these ideas, we adopt a Visual Mamba-inspired formulation tailored to dispersion grids: rather than implementing explicit associative scans, we realize each axis-wise state update with a one-sided, causal, depthwise operator and learn a convex combination over directions via an upwind gate. This preserves linear scaling, encodes physical causality along the operated axis, and maps cleanly to commodity GPUs through grouped convolutions. In effect, directional depthwise stencils play the role of stable, axis-aligned transports, while the gate adapts to local flow regimes (global/local/hybrid), which we ablate in Section 5.3. Beyond gas release response, we view this combination as a general backbone for inverse inference on transported fields, i.e., spatiotemporal backtracking tasks in environmental monitoring and urban analytics.

Within this design space, we introduce Recursive Backtracking with Visual Mamba (RBVM), a directionally gated visual state-space backbone for source localization. Each residual block applies causal, depthwise sweeps along ${\mathrm{H}}^{\pm }$, ${\mathrm{W}}^{\pm }$, and ${\mathrm{T}}^{\pm }$ and then fuses them via a learned upwind gate; a lightweight two-layer GELU MLP follows. Small LayerScale coefficients modulate both the directional aggregate and the MLP branch, and a layer-indexed, depth-weighted DropPath schedule stabilizes training across blocks. A $1\times 3\times 3$ 3D-Conv stem embeds the single-channel lattice into C channels, while a symmetric $1\times 3\times 3$ head produces logits for all time slices. Causal padding strictly prevents look-ahead along the operated axis, aligning the inductive bias with advective transport. The six-direction variant adds a backward temporal branch (${\mathrm{T}}^{-}$) and improves robustness under meandering winds, whereas the five-direction variant (omitting ${\mathrm{T}}^{-}$) may be considered for strictly causal regimes. In all cases, computation and memory scale linearly with the spatiotemporal volume $THW$ and with the number of directions $\left|\mathcal{D}\right|$.

Our inference protocol follows the recursive backtracking paradigm. The model ingests a conditioning window of recent frames and recursively predicts earlier snapshots in reverse chronological order, with dataset-specific choices of window length and backtracking depth (cf. [9,11]). The last predicted slice provides the probability map for localization. Training uses a supervised loss that blends per-slice reconstruction MSE with a BCE-with-logits term computed over the backtracked slices (including the oldest), encouraging sharp, well-localized peaks. To further stabilize learning, we maintain a Polyak/EMA [18] teacher of the student parameters, and, after a short warm-up, add consistency terms (probability-space MSE and logit-space BCE) whose coefficients ramp linearly with epoch [19]. Because dispersion in our synthetic generator is additive, a simple two-peak subtraction applied post hoc to the oldest slice enables zero-shot dual-source localization without retraining.

We evaluate on two complementary domains. A controlled synthetic benchmark—flat terrain with stochastic yet strictly causal advection—isolates algorithmic design effects and supplies dual-source sequences for stress testing. In addition, we rigorously evaluate the model using diffusion data spanning diverse experimental conditions and meteorological environments generated via the Nuclear–Biological–Chemical Reporting and Modelling System (NBC_RAMS) [9,11]. A held-out subset of these runs captures urban channelling, shear, and occasional wind reversals. Models are trained only on single-source synthetic sequences and then evaluated on NBC_RAMS as-is, under the same protocol, as in prior work [9,11]. Across both domains, we compare RBVM against strong baselines—3D-CNN, CNN–LSTM, and ViViT—and report geometry-aware localization metrics (RMSE/AED, hit $\le 1$, Exact) together with model compactness (parameter count).

In summary, this paper makes three contributions in a unified framework. First, it presents a Visual Mamba-inspired, directionally gated visual SSM that aggregates causal depthwise operators via a learned upwind gate, achieving linear-time scaling with a hardware-friendly implementation. Second, it demonstrates robust performance under meandering, urban flows—yielding a favourable accuracy–compactness trade-off relative to 3D-CNN, CNN–LSTM, and ViViT—without resorting to quadratic-cost attention. Third, it shows that a parameter-free, physics-motivated two-peak subtraction enables zero-shot dual-source localization on synthetic stress tests, indicating that RBVM learns a physically meaningful representation rather than a brittle lookup. The remainder of the paper develops the preliminaries on linear-time state-space modelling, details the RBVM architecture and training protocol, specifies datasets and experimental procedures, and reports quantitative and qualitative results before concluding with a brief outlook.

Paper organization. We first lay the groundwork in Section 2, reviewing linear-time state-space modelling, introducing notation, and motivating directional causality for dispersion grids. Next, Section 3 presents RBVM end-to-end: we unpack the block design (causal depthwise operators and DirGate), the stem/head, training objectives and schedules, the inference protocol, and the zero-shot dual-source postprocessing step. We then turn to the experimental setup in Section 4, detailing datasets, splits, preprocessing, the common evaluation protocol, and baseline implementations, ensuring like-for-like comparisons. With the stage set, Section 5 presents the evidence: we begin with the NBC_RAMS field benchmark (Section 5.1), then turn to the synthetic benchmark (Section 5.2), and round out the section with targeted analyses—sensitivity highlights (Section 5.3) and qualitative overlays (Section 5.1 and Section 5.2). Finally, Section 6 distils the main takeaways, limitations, and practical guidance, and Section 7 closes with a brief outlook and opportunities for extension.

Scope and positioning. We address the real-time inverse task on short windows of solver-generated concentration fields under strict latency and input-availability constraints (no winds or solver calls at inference). Directional state-space modelling matches advective transport while retaining linear-time scaling and streaming readiness; physics-based solvers and their adjoint and data assimilation variants solve the forward problem, while we study a compact, directionally causal inverse layer that consumes their rasters at decision time.

Novelty—what is new vs. prior art.

(i)

Directionally causal visual SSM. Axis-wise one-sided, depthwise stencils with an upwind gate (global/local/hybrid), preserving per-axis causality and linear scaling—contrasted with bidirectional scans or quadratic attention.

(ii)

Flipped-time joint decoding. A reverse-index causal temporal design that predicts all backtracked slices in one pass and is trained with BCE-on-logits across slices plus light EMA consistency, limiting exposure bias without iterative rollout.

(iii)

Deployment posture. A learned inverse layer that consumes solver rasters under strict latency without winds or online solver calls, with optional calibration/abstention for operations—complementing (not replacing) physics stacks.

Contributions.

• A directionally causal, depthwise state-space backbone with an upwind gate that preserves linear-time scaling in sequence length and respects per-axis causality.
• On NBC_RAMS and synthetic diffusion, the model improves localization accuracy while remaining compact (with a compact parameter budget and linear-time scaling).
• A zero-shot dual-source postprocess with explicit assumptions and lightweight safeguards (non-negative residual clamping, small-radius NMS, uncertainty flag).

2. Preliminaries

2.1. Linear-Time State-Space Modelling and Directional Causality

A continuous-time state-space model (SSM) drives a latent state $h\left(t\right)\in {\mathbb{R}}^d$ with input $x\left(t\right)$ via

$$\dot{h}\left(t\right)=Ah\left(t\right)+Bx\left(t\right),y\left(t\right)=Ch\left(t\right),$$

(1)

which, under uniform sampling with period $\Delta$, yields the discrete update $h_t=\overline{A}{h}_{t-1}+\overline{B}{x}_t$ with $\overline{A}=exp(\Delta A)$ and $\overline{B}=A^{-1}\left(exp(\Delta A)-I\right)B$ (for invertible A; otherwise via the series/Van Loan formulation). Absorbing C into a learned readout shows that the induced dynamics form a (causal) 1-D convolution, giving linear time and memory in sequence length L and motivating modern SSM kernels such as S4/Hyena [20,21].

Recent SSMs (e.g., Mamba) replace fixed coefficients with selective, input-conditioned parameters and compute latent updates with $\mathcal{O}\left(Ld\right)$ cost, providing a principled alternative to quadratic self-attention [15]. Visual and multi-dimensional extensions apply directional scans or structured kernels on images/videos [16,17,22,23]. In this paper, we adopt a directional, causal, depthwise formulation that preserves the linear scaling and inductive bias of SSMs while remaining simple and hardware-friendly: instead of explicit associative scans, we realize each axis-wise update with a one-sided, depthwise convolution and learn the (upwind) combination of directions. This aligns the inductive bias with advective transport and keeps operators GPU-friendly via grouped depthwise convolutions, anticipating ablations in Section 5.3.

2.1.1. Notation and Operators

Let $X\in {\mathbb{R}}^{B\times T\times H\times W\times C}$ be a normalized (concentration) tensor (channels-last inside blocks), and let $\mathrm{LN}\left(X\right)$ denote pre-normalized features. We define the direction sets ${\mathcal{D}}_6=\{{\mathrm{H}}^{+},{\mathrm{H}}^{-},{\mathrm{W}}^{+},{\mathrm{W}}^{-},{\mathrm{T}}^{+},{\mathrm{T}}^{-}\}$ and ${\mathcal{D}}_5={\mathcal{D}}_6\setminus \left\{{\mathrm{T}}^{-}\right\}$, where $\mathrm{H}/\mathrm{W}/\mathrm{T}$ denotes the height/width/time axes ${\mathrm{and}}^{ +}{/}^{-}$ chooses the causal side (forward vs. backward) along that axis. For $d\in {\mathcal{D}}_6$, the operator ${\mathcal{O}}_d$ is a depthwise convolution (kernel width 3) that scans only along the operated axis with one-sided causal padding on the upwind side (zeros elsewhere); spatial $({\mathrm{H}}^{\pm },{\mathrm{W}}^{\pm })$ use masked 2D depthwise kernels, while temporal $\left({\mathrm{T}}^{\pm }\right)$ use 1D depthwise kernels on the flipped timeline (see the paragraph on temporal causality). Unless stated otherwise, our main experiments use the 6-dir set ${\mathcal{D}}_6$; the 5-dir set ${\mathcal{D}}_5$ appears only in sensitivity snapshots. Per-block complexity is $\mathcal{O}\left(\right|\mathcal{D}\left|CTHW\right)$, i.e., linear in sequence extent.

2.1.2. Directional Operator

For $d\in \left\{{\mathrm{T}}^{\pm }\right\}$ we apply a 1-D depthwise convolution of width 3 along time; for $d\in \{{\mathrm{H}}^{\pm },{\mathrm{W}}^{\pm }\}$, we apply a separable depthwise 2-D convolution whose kernel is $3\times 1$ (for $\mathrm{H}$) or $1\times 3$ (for $\mathrm{W}$), so the operation is effectively 1-D along the selected spatial axis:

$$Z_d={\mathcal{O}}_d\left(\mathrm{LN}\left(X\right)\right)\in {\mathbb{R}}^{B\times T\times H\times W\times C},$$

(2)

with past/future (time) or top/bottom/left/right (space) causal padding chosen ${\mathrm{by}}^{ \pm }$. Each ${\mathcal{O}}_d$ is depthwise and thus costs $\mathcal{O}\left(CTHW\right)$.

We consider two direction sets: ${\mathcal{D}}_5=\{H^{+},H^{-},W^{+},W^{-},T^{+}\}$ and ${\mathcal{D}}_6={\mathcal{D}}_5\cup \left\{T^{-}\right\}$. The sole architectural difference between 5-dir and 6-dir is the inclusion of the reverse-index temporal sweep $T^{-}$. DirGate forms a convex mixture over ${\mathcal{D}}_5$ or ${\mathcal{D}}_6$ with identical logits initialization, temperature, LayerScale, and DropPath. The added parameters are limited to the extra gate logit and one LayerScale scalar per channel (order ${10}^3$ at our scale, $<1\%$ of total); hidden widths are unchanged.

2.1.3. Learned Upwind Gating (DirGate)

We mix directional responses with a temperature-controlled softmax:

$$\begin{array}{cc}\hfill \pi \left(X\right)& =\mathrm{softmax}\left(\frac{1}{\tau }W\varphi \left(X\right)\right)\in {\Delta }^{\left|\mathcal{D}\right|-1},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \varphi \left(X\right)& =\left\{\begin{array}{cc}{\mathrm{mean}}_{t,h,w}\left(\mathrm{LN}\left(X\right)\right)\in {\mathbb{R}}^{B\times C}\hfill & \left(\mathrm{global}\right),\hfill \\ \mathrm{LN}\left(X\right)\in {\mathbb{R}}^{B\times T\times H\times W\times C}\hfill & \left(\mathrm{local}\right),\hfill \end{array}\right.\hfill \end{array}$$

(4)

where W maps $\varphi \left(X\right)$ to $\left|\mathcal{D}\right|$ logits and $\tau >0$ is a temperature. In our main experiments, the gate is global, providing one mixture per sample. We zero-initialize W so that training starts from a uniform mixture. Hybrid gating (global backbone modulated by a shallow local adaptor) is considered in Section 5.3; the block equations remain unchanged.

2.1.4. Block Update with LayerScale and DropPath

Denoting ${\pi }_d\left(X\right)$ the d-th mixture weight (broadcast to $B\times T\times H\times W\times 1$), the residual update in each block is

$$X\leftarrow X+\mathrm{DropPath}\left(\sum _{d\in \mathcal{D}}{\gamma }_d{\pi }_d\left(X\right){\mathcal{O}}_d\left(\mathrm{LN}\left(X\right)\right)\right)+\mathrm{DropPath}\left({\gamma }_{\mathrm{mlp}}\mathrm{MLP}\left(\mathrm{LN}\left(X\right)\right)\right),$$

(5)

with learnable LayerScale scalars ${\gamma }_d$ (per direction) and ${\gamma }_{\mathrm{mlp}}$ initialized small (∼${10}^{-3}$) for stability. In practice, we use a layer-indexed, depth-weighted DropPath probability across blocks (static during training).

2.1.5. Complexity

Each block performs $\left|\mathcal{D}\right|$ depthwise operations, plus a small gate and MLP. Overall, computation scales linearly with the spatiotemporal volume $THW$ and with $\left|\mathcal{D}\right|$; memory scales linearly with $CTHW$ (or $\left|\mathcal{D}\right|CTHW$ if all directional responses are buffered). Our main configuration uses six directions; the 5-dir variant drops ${\mathrm{T}}^{-}$ and appears only as an ablation.

2.2. Synthetic Benchmark

We introduce a controlled synthetic benchmark to support sensitivity analyses and stress tests under known physics. Following the general recipe of [9], we simulate passive gas transport on a discrete $H\times W$ lattice under a Fickian advection–diffusion process driven by a piecewise-steady stochastic wind. Each scenario starts from an impulse-like initial condition and evolves forward to yield a short sequence of concentration fields exhibiting advection and dilution. This construction makes the recursive backtracking task well posed while avoiding any commitment to a particular temporal horizon.

The corpus contains single-source sequences used for training and model selection, and dual-source sequences reserved for stress testing. Variants cover representative wind and flow conditions, including meandering winds and so on. We employ a fully vectorized generator for high-throughput sampling. Exact lattice size, boundary conditions, denoising/normalization choices, and dataset-specific window and backtracking lengths are specified in Section 4.2.

2.3. Baseline Architectures

We compare RBVM against three representative families that span the common design space for spatiotemporal modelling on dispersion grids: a 3D convolutional backbone, a CNN–LSTM hybrid, and a Transformer-based video classifier (ViViT). Unless stated otherwise, all baselines ingest the same preprocessed input as RBVM (a recent conditioning window of frames on an $H\times W$ lattice with per-frame min–max normalization) and predict the source cell on the oldest slice as a multi-class classification task. Given our emphasis on NBC_RAMS [9,11], baseline capacities are adjusted per domain, while the synthetic setting uses lighter, overfit-resistant variants for sensitivity and stress tests.

3D–CNN (VideoGasNet–style). We implement a compact I3D-style backbone akin to VideoGasNet [24,25]: a stack of blocks, each comprising a 3D convolution, batch normalization, ReLU activation, and spatiotemporal pooling with small kernels; these stages are followed by global average pooling and a classifier. Dropout is applied in the head for regularization. This family provides a strong convolutional baseline but typically requires deeper stacks to cover longer temporal horizons, increasing compute and memory cost as the window grows.

CNN–LSTM (per-frame encoder + temporal RNN). Frames are encoded framewise by a shallow 2D CNN with weights shared across time; the resulting per-frame features are then aggregated over the sequence by a unidirectional LSTM, akin to CNN–LSTM pipelines (cf. [4]). We pass the LSTM output to a lightweight MLP classifier. Training uses a standard cross-entropy classification objective. This hybrid keeps parameter growth linear with sequence length through recurrence, at the cost of reduced parallelism compared with fully convolutional designs.

ViViT (Video Vision Transformer). We re-implement ViViT [26] as a single-stream, tubelet-tokenised video classifier, following prior practice [11]. Given $V\in {\mathbb{R}}^{T\times H\times W\times 1}$, we extract non-overlapping tubelets $x_i\in {\mathbb{R}}^{t\times h\times w\times 1}$, linearly project them to tokens $E{x}_i\in {\mathbb{R}}^d$, prepend a learned class token $z_{\mathrm{cls}}$, and add learned positional embeddings p to obtain

$$z^0=(z_{\mathrm{cls}},E{x}_1,\dots ,E{x}_N)+p\in {\mathbb{R}}^{(N+1)\times d}.$$

A stack of L Transformer encoder layers with multihead self-attention (MSA), pre-norm LayerNorm, and a two-layer GELU MLP produces $z^L$; the classifier reads $\mathrm{LN}\left(z_{\mathrm{cls}}^L\right)$ and outputs 625 logits. Our default instantiation (mirroring the internal supplement) is as follows: $L=10$, heads $k=8$, embedding width $d=128$, feed-forward width $d_{ff}=512$, and tubelet sizes $(t,h,w)=(2,12,13)$. ViViT offers strong single-pass accuracy on spatiotemporal grids but incurs quadratic attention cost in token count and non-trivial memory overhead as the token grid grows.

Baseline training and complexity at a glance. All baselines share the same data splits and preprocessing pipeline as RBVM. Supervision is cross-entropy on the 625-way source label from the oldest slice; early stopping and model selection are based on validation loss. For CNN–LSTM and 3D-CNN, we adopt Adam (LR ${10}^{-3}$) with $L_2$ weight decay ${10}^{-4}$ and dropout as stated above; for ViViT, we follow the configuration listed above. Hyperparameters were tuned once on the synthetic validation split and then frozen for the NBC_RAMS transfer. For comparability, we report both absolute metrics (Exact/hit $\le 1$, RMSE, macro precision/recall/$F_1$) and efficiency (latency, peak GPU), and we keep parameter counts within a reasonable budget range across baselines when possible; when this is not feasible (e.g., ViViT’s positional table vs. CNN recurrent state), we additionally comment on accuracy–efficiency trade-offs rather than raw accuracy alone.

Complexity viewpoint. 3D-CNNs scale roughly with the spatiotemporal receptive field (depth increases to “see” longer horizons); CNN–LSTM scales linearly in frames but loses parallelism due to recurrence; ViViT keeps parameter count nearly constant with T (positional table aside) but attention cost scales quadratically in tokens. In contrast, RBVM uses causal, depthwise directional operators with a learned upwind mixture and scales linearly in $THW$ (product) and in the number of directions $\left|\mathcal{D}\right|$.

Section 5 reports a head-to-head comparison on the synthetic benchmark and the held-out NBC_RAMS corpus under the common protocol above.

2.4. Related Works

We group prior art into three strands, and clarify how our approach differs.

2.4.1. Physics-Based Source Inversion and Hybrid Approaches

Operational CBRN pipelines run forward dispersion solvers coupled with meteorology and turn them into inverse estimators via adjoint optimization or data assimilation. Classical references cover inverse theory and source–receptor relationships [27,28], while operational stacks such as RAMS/HYSPLIT illustrate realistic transport under terrain and synoptic variability [29,30]. Ensemble Kalman filtering/smoothing remains a common choice [31,32]. Physics-informed learning amortises computation by injecting PDE constraints or learning operators [33,34]. Our design is complementary: we consume solver-generated rasters and learn a compact inverse layer that localizes sources online without solver calls or wind inputs at inference.

2.4.2. Vision Backbones for Spatiotemporal Fields

Generic video architectures have been applied to scientific rasters: 3D CNNs learn local motion features [35,36]; CNN–RNN hybrids (e.g., ConvLSTM) add recurrent memory [4]; ViT-based backbones (ViViT/ TimeSformer/MViT) capture long-range interactions [26,37,38]. These are accurate but can be heavy or quadratic in attention length, complicating streaming. In contrast, we use directionally causal, depthwise operators with an upwind gate, retaining linear-time behaviour and aligning with advective transport.

2.4.3. State-Space Sequence Models and Visual Extensions

Structured state-space models achieve linear-time scanning and stable long-range memory on 1D sequences [39], with selective variants improving the capacity–efficiency trade-off [15]. Visual extensions adapt SSMs to images/videos via axis-wise scans [17]. We enforce axis-wise one-sided stencils to respect per-axis causality and mix directions via an upwind gate, yielding an inductive bias consistent with advection–diffusion while remaining streaming-ready.

2.4.4. Positioning vs. PDE-Constrained and Hybrid Routes

PDE-constrained inversions (adjoint/DA) offer strong physical priors but assume meteorology and iterative solves; physics-informed learning can reduce cost yet remains coupled to PDE constraints. Our approach operates downstream of physics: given solver-consistent rasters, we perform the inverse mapping online with axis-wise one-sided sweeps and an upwind gate—no online solver dependencies and linear complexity—with a path to confidence calibration/abstention for reliability; see also work on probabilistic outputs in other domains (e.g., paragraph-based sentiment) [40], and complementary watermarking for provenance in deployment [41].

3. Methodology

3.1. RBVM: Directionally Gated Visual SSM Backbone

Long-horizon backtracking requires a model that (i) preserves temporal causality, (ii) propagates information efficiently across space and time, and (iii) scales linearly with the sequence extent so that compute and memory remain bounded as the look-back window grows. In dispersion grids, the spatiotemporal signal is moreover anisotropic: advection makes information travel primarily along an upwind/downwind axis that can change over time. These constraints motivate a state-space formulation with directional propagation.

Why Mamba? Transformers provide global context but incur $\mathcal{O}\left(L^2\right)$ time and memory in sequence length L. Three-dimensional CNNs scale linearly but need deep stacks to connect distant voxels; CNN–LSTM hybrids lose parallelism and grow memory with horizon. State-space sequence models such as Mamba replace global attention with content-aware latent dynamics that advance in $\mathcal{O}\left(L\right)$, enable streaming, and keep memory flat with horizon.

Why Visual Mamba? Backtracking must move information along spatial axes as well as time. Visual Mamba extends SSMs with directional scans on images (and videos), yielding short communication paths across H and W while preserving linear complexity. In dispersion grids, this is a good inductive bias: gaseous filaments meander and split, but transport is largely directional instant-to-instant; directional scans approximate these flows with lightweight operators.

Why advance beyond prior Visual Mamba? Standard visual SSM implementations often use bidirectional (non-causal) passes or associative scans [17,23] that, while powerful, are heavier than needed here and can blur temporal causality. We tailor the formulation to dispersion by (i) enforcing axis-wise causality with one-sided, depthwise operators (e.g., [42,43]); (ii) introducing an upwind gate (DirGate) that learns a convex mixture over directions $\{{\mathrm{H}}^{\pm },{\mathrm{W}}^{\pm },{\mathrm{T}}^{\pm }\}$, routing information along the current flow; and (iii) using a 3D–Conv stem/head for compact I/O, with small LayerScale coefficients and a layer-indexed, depth-weighted DropPath for stable stacking [44,45]. This Mamba-inspired design keeps the linear-time advantage, encodes physical causality, and is hardware-friendly (grouped depthwise ops dominate cost).

Concretely, we parameterise RBVM as follows: Let the input be $X\in {\mathbb{R}}^{B\times 1\times T\times H\times W}$ (one channel); the stem maps to C channels and we then operate on $\tilde{X}=\mathrm{LN}\left(X_{\mathrm{feat}}\right)\in {\mathbb{R}}^{B\times T\times H\times W\times C}$ (pre-norm, channels-last inside the block). For notational consistency in this section, we denote the channels-last features by $U\equiv \tilde{X}\in {\mathbb{R}}^{B\times T\times H\times W\times C}$.

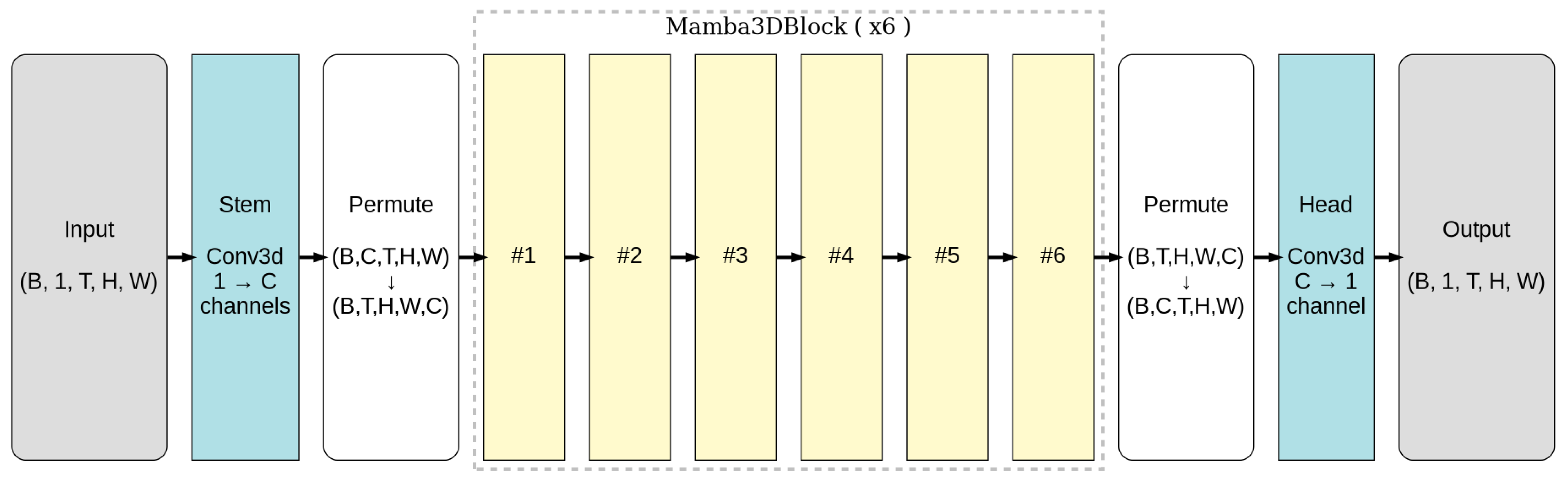
Model overview. The model structure comprises a 3D-Conv stem that embeds inputs $(B,1,T,H,W)$ into C channels, a stack of Mamba3D blocks operating in channels-last form $(B,T,H,W,C)$, and a 3D-Conv head that maps back to one channel of logits for all T slices; inside each block, six directional NDLayer3D operators $({\mathrm{H}}^{\pm },{\mathrm{W}}^{\pm },{\mathrm{T}}^{\pm })$ are applied with causal padding and mixed by an upwind DirGate. 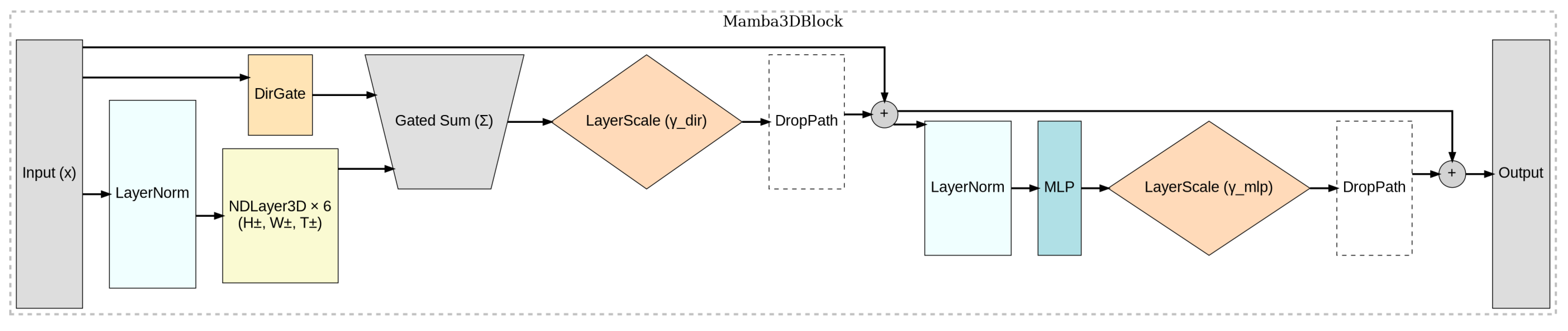LayerScale and optional DropPath are used on both the directional and MLP branches with residual skips, while NDLayer3D permutes/reshapes to apply 2D depthwise convolutions along space and 1D depthwise convolutions along time before restoring the $(B,T,H,W,C)$ layout (Figure 1, Figure 2 and Figure 3).

Operational inputs. The model consumes gridded concentration rasters exported by an upstream dispersion stack (e.g., NBC_RAMS/HPAC-family). No wind vectors are used at inference. The same interface applies to other operational stacks that export concentration fields on a regular grid.

3.1.1. Temporal Causality and Time Flip

We index the conditioning window so that the oldest slice used for evaluation aligns with the causal boundary (via a simple time flip). Temporal branches $T^{+}$ and $T^{-}$ then perform one-sided sweeps on this flipped timeline, with padding applied only on the causal (upwind) side. All temporal operations remain within the observed window; no operator can access frames earlier than the oldest target, and the head unflips the index before producing logits. The time flip is a non-learned re-indexing that preserves gradients to all supervised frames; it does not grant access to frames earlier than the oldest target and does not remove supervision from any FUT index. Normalization statistics are taken from the conditioning window only; we do not peek into frames earlier than the oldest target, so no information leakage is introduced by normalization.

3.1.2. Temporal Windowing

Let the conditioning window cover $\{t_0-T+1,\dots ,t_0\}$ with $t_0 \ge 5$ min. We apply a time flip so the oldest frame is the decoding target and supervise all backtracked frames within this window. By construction, neither training nor metrics require frames earlier than $t_0$, and excluding the first five minutes avoids near-field transients beyond the scope of this study.

3.1.3. Optional Raster Adaptor for Irregular Sensing

When only sparse/irregular measurements are available, a lightweight adaptor constructs a working raster $X\in {\mathbb{R}}^{T\times H\times W}$ together with a co-registered uncertainty/support map $U\in {[0,1]}^{T\times H\times W}$. We can use conservative kernel interpolation (e.g., inverse-distance or Gaussian kernels with mass normalization) or standard kriging to populate X, and define U from local support (e.g., distance-to-sample or posterior variance). The model then consumes $[X;U]$ (uncertainty as an auxiliary channel) with no change to the backbone. At inference, U is folded into the decision rule by tightening abstention thresholds when support is low (higher U). This adaptor runs before the directional sweeps, thus keeping linear-time behaviour and per-axis causality intact. This optional raster adaptation is documented for deployment completeness.

3.1.4. Directional Operators (Causal, Depthwise)

Each operator ${\mathcal{O}}_d$ performs a causal sweep along one axis/direction, propagating information only from the past (or from the upwind side) without peeking ahead. In gas dispersion, this matches physics: under advection, the most informative context at $(t,h,w)$ lies immediately upwind or in the preceding time step. We therefore use one-sided stencils (kernel width 3) with causal padding along the operated axis. Kernels are depthwise (groups $=C$) so each channel evolves with its own small filter; cross-channel mixing is deferred to the gated fusion and the MLP head. This yields short communication paths and excellent hardware efficiency while preserving the state-space flavour of axis-wise propagation. While each operator acts along a single axis ($H^{\pm }$ or $W^{\pm }$), stacking blocks composes these short paths into oblique or curved trajectories; the upwind gate shifts the dominant orientation across blocks and time, and the post-aggregation MLP mixes channels to couple axes. This compositional routing suffices to capture meanders and off-axis transport in our data; if tightly wound eddies dominate, diagonal variants are a drop-in extension that leave the rest of the stack unchanged.

3.1.5. Orientation Extensions

For scenes dominated by rotational or swirling transport, we can extend the direction set to ${\mathcal{D}}_8=\{H^{\pm },W^{\pm },D_{45}^{\pm },D_{135}^{\pm }\}$, where $D_{45}^{\pm },D_{135}^{\pm }$ are one-sided, depthwise diagonal stencils implemented as oriented masked kernels with causal support on the upwind half-plane. As with $H^{\pm }/W^{\pm }$, padding is causal with respect to the operated direction and evaluation index, so per-direction causality is preserved. This change is modular and increases complexity linearly with $\left|\mathcal{D}\right|$ (still $\mathcal{O}\left(\right|\mathcal{D}\left|CTHW\right)$).

Define the direction set ${\mathcal{D}}_6=\{{\mathrm{H}}^{+},{\mathrm{H}}^{-},{\mathrm{W}}^{+},{\mathrm{W}}^{-},{\mathrm{T}}^{+},{\mathrm{T}}^{-}\}$ (our default), with ${\mathcal{D}}_5={\mathcal{D}}_6\setminus \left\{{\mathrm{T}}^{-}\right\}$ used only in sensitivity snapshots. For $d\in \mathcal{D}$, we apply a one-sided, depthwise kernel of width 3 with causal padding along the operated axis:

$$\begin{array}{cc}\hfill Z_d& ={\mathcal{O}}_d\left(U\right),\hfill \\ \hfill Z_d& \in {\mathbb{R}}^{B\times T\times H\times W\times C},\hfill \\ \hfill {\mathcal{O}}_{{\mathrm{T}}^{\pm }}& ={\mathrm{DW}-\mathrm{Conv}1\mathrm{D}}_t,{\mathcal{O}}_{{\mathrm{H}}^{\pm }}={\mathrm{DW}-\mathrm{Conv}2\mathrm{D}}_h,{\mathcal{O}}_{{\mathrm{W}}^{\pm }}={\mathrm{DW}-\mathrm{Conv}2\mathrm{D}}_w.\hfill \end{array}$$

(6)

3.1.6. Implementation Note

${\mathrm{T}}^{+}$ processes the sequence in index order (consistent with streaming), while ${\mathrm{T}}^{-}$ adds a backward temporal branch that helps under meandering winds; ${\mathrm{H}}^{\pm }$ and ${\mathrm{W}}^{\pm }$ use $(1\times 3)$ stencils with padding applied only on the upwind side. We permute/reshape tensors so these become depthwise 1D/2D grouped convolutions on contiguous memory. Across blocks, alternation of $H^{\pm }/W^{\pm }$ sweeps with gate-driven orientation changes yields oblique information flow without breaking per-axis causality. On the flipped timeline, $T^{+}$ and $T^{-}$ are both one-sided with causal padding, so adding $T^{-}$ improves robustness to meanders without introducing bidirectional look-ahead.

3.1.7. Upwind Gate (DirGate)

The five (or six) directional responses are not equally informative at every site. When the plume drifts east, for example, ${\mathrm{W}}^{+}$ (eastward) should carry more weight; when winds reverse or channel, the optimal mixture shifts accordingly. DirGate learns this upwind routing as a temperature-controlled softmax over directions. At each block, we normalize features, project to $\left|\mathcal{D}\right|$ logits, scale by $\tau$, and apply softmax to obtain a convex mixture. Smaller $\tau$ sharpens the distribution; a larger $\tau$ encourages smoother mixing. We zero-initialize the projection so training starts from a uniform mixture.

3.1.8. Formal Definition and Modes

Directional responses ${\left\{Z_d\right\}}_{d\in {\mathcal{D}}_6}$ are combined by a convex mixture where a lightweight summary $\varphi \left(U\right)$ feeds zero-initialized logits W with temperature $\tau$. We support global, local, and a hybrid (global prior + local refinement); operators are unchanged across modes and preserve linear complexity:

$$g=\mathrm{softmax}\left(W\varphi \left(U\right)/\tau \right),\widehat{Z}=\sum _{d\in {\mathcal{D}}_6}{g}_d{Z}_d.$$

Here $\varphi (·)$ summarizes U (global pooling for global; identity or $1\times 1$ projection for local); W are gate logits (zero-initialized; uniform start), and $\tau$ controls mixture entropy.

3.1.9. Gating with Additional Orientations

DirGate naturally generalizes to ${\mathcal{D}}_8=\{H^{\pm },$$W^{\pm },D_{45}^{\pm },D_{135}^{\pm }\}$ by producing convex weights over the enlarged set. Alternatively, a compact dynamic-orientation variant replaces fixed diagonals with K learned-orientation atoms (small K, e.g., $K\le 4$) and gates over these atoms (global or local mode). Zero-initialized logits and a moderate temperature $\tau$ avoid premature collapse; the added cost is linear in K, and streaming behaviour is unchanged. At higher resolutions, a local DirGate (per-voxel mixtures) can replace or refine the global mixture while keeping linear complexity; an optional patchify/strided stem lets global gating operate on a reduced token grid, with the patch stride chosen to balance latency and spatial fidelity. Note that DirGate supports three modes. Global gating predicts a single convex mixture over directions for the whole sample (our default at $25\times 25$). Local gating predicts a mixture per voxel (and time index), enabling spatially varying routing when heterogeneity increases. A hybrid option combines a global prior with local refinement. Logits are zero-initialized (uniform start) and the temperature $\tau$ controls entropy; for local mode, we optionally apply a small spatial smoothing on pre-softmax logits. Switching modes leaves the directional operators unchanged and preserves linear complexity in $THW$ (and in $\left|\mathcal{D}\right|$).

3.1.10. Degeneracy Mitigation

We zero-initialize gate logits (uniform start) and use a moderate temperature ($\tau =1.0$) to avoid overly sharp mixtures. Small LayerScale on both branches (${\gamma }_{\mathrm{dir}},{\gamma }_{\mathrm{mlp}}\approx {10}^{-3}$ at init) prevents any single direction from dominating early; global gating (default at modest grids) further stabilizes routing by averaging over space–time. Local/hybrid variants remain available when heterogeneity increases.

3.1.11. Block, Stem, Head, and Complexity

Each residual block first aggregates directional responses using DirGate and then refines them with a lightweight two-layer GELU MLP. We use pre-norm LayerNorm on both branches so gradients flow through identity skips; small LayerScale coefficients $({\gamma }_d,{\gamma }_{\mathrm{mlp}}\sim {10}^{-3})$ stabilize early training; and a layer–indexed, depth-weighted DropPath regularizes across blocks without adding inference cost. A $1\times 3\times 3$ 3D-Conv stem maps the single-channel lattice to C channels, and a symmetric head maps back to one channel of logits at all time steps. Conceptually, stacking such blocks alternates axis-wise message passing (short, causal stencils) with channel mixing (MLP), so long-range dependencies emerge through depth rather than wide filters.

3.1.12. Block, Stem, and Head (Modular View)

Stem. Conv3D maps $1\to C$; an optional patchify/strided reduction maps $H\times W\to (H/p)\times (W/p)$ before the sweeps.

Block. Six axis-wise depthwise paths $(H^{\pm },W^{\pm },T^{\pm })$ operate on $\mathrm{LN}\left(U\right)$ to produce $\left\{Z_d\right\}$; DirGate yields g, and the gated sum is added with LayerScale and optional DropPath:

$$U\leftarrow U+\mathrm{DropPath}\left(\sum _{d\in {\mathcal{D}}_6}{\gamma }_{\mathrm{dir},d}{g}_d{\mathcal{O}}_d\left(\mathrm{LN}\left(U\right)\right)\right),U\leftarrow U+\mathrm{DropPath}\left({\gamma }_{\mathrm{mlp}}\mathrm{MLP}\left(\mathrm{LN}\left(U\right)\right)\right).$$

Residual form. We initialize ${\gamma }_{\mathrm{dir},d}$ and ${\gamma }_{\mathrm{mlp}}$ at ${10}^{-3}$. Small residual scales ease early optimization in deep residual/Transformer-style stacks while preserving capacity.

Head. Conv3D maps $C\to 1$ logits on the cell grid; temporal alignment follows the flip convention in Sec. Temporal causality. Deployment safeguards (calibration/abstention) are wrappers and do not alter the backbone.

3.1.13. Scaling and Input Reduction

Patchify at input. For large rasters, we optionally apply a non-overlapping $p\times p$ patchify (or a strided $1\times 3\times 3$ stem) to coarsen $H\times W\to (H/p)\times (W/p)$ before the directional sweeps; the head symmetrically upsamples to cell logits. Because the operators remain depthwise and one-sided, axis-wise causality and the linear-time profile are preserved. Gating (global/local/hybrid) is orthogonal to this reduction and leaves the directional operators unchanged. Gating Under Patchify Global DirGate operates unchanged on patch tokens; local DirGate (per token) is also supported when heterogeneity increases with resolution. Both retain linear complexity and reuse the same directional responses. Gating granularity does not alter the backbone’s cost profile: axis-wise, one-sided depthwise operators remain the dominant term. The gate adds a per-sample (global) or per-voxel (local) convex mixture whose overhead is linear in volume. When resolution increases, a patchify/strided stem maps $H\times W\to (H/p)\times (W/p)$ tokens before the directional sweeps; global or hybrid gating then operates on the compact token grid, with optional local refinement if sub-grid heterogeneity persists.

3.1.14. Cost Drivers and Permutations

Per-block cost scales linearly in $THW$ (and $\left|\mathcal{D}\right|$); grouped depthwise convolutions dominate runtime. We keep a channels-last layout $(B,T,$$H,W,C)$ throughout the body so most permutations are metadata (stride) changes, only stem/head swap layouts. In practice, permutation overhead is negligible relative to depthwise stencils on current GPUs. Adding diagonal or learned-orientation stencils increases the per-block constant proportionally to the number of directions/orientation atoms, but does not change the linear dependence on sequence extent; memory overhead grows linearly with the volume and linearly with the number of directional buffers.

3.1.15. Tiling with Causal Halos

For very large rasters, we process overlapping tiles with a small causal halo so one-sided stencils remain valid at tile boundaries; logits are then stitched without seams.

Compute and memory are dominated by depthwise grouped convolutions and thus scale linearly with the spatiotemporal volume $THW$ and with $\left|\mathcal{D}\right|$. DirGate (a single linear projection + softmax) and LayerScale add negligible overhead. This keeps the backbone compact while allowing look-back horizons to extend without quadratic penalties.

3.1.16. Pseudocode (Forward and One Training Step)

Listing A1 provides ASCII-safe pseudocode for one forward pass (incl. optional patchify) and one training step reflecting the equations. Optional regularizers/safeguards are flagged and disabled in the main tables unless stated. For quick lookup, see Appendix A.

3.2. Training Objective and Schedules

We adopt a finite-horizon backtracking protocol parameterised by the conditioning-window length COND and the backtracking depth FUT (cf. [9,11]). Given a mini-batch $X_{1:\mathtt{COND}}$, the network returns logits ${\widehat{L}}_{1:\mathtt{FUT}}\in {\mathbb{R}}^{B\times \mathtt{FUT}\times H\times W}$ for the earlier slices. During training we apply a time flip so that the index $k=\mathtt{FUT}$ corresponds to the oldest slice (closest to $t\approx 0$), aligning targets and losses with the evaluation slice used at test time.

3.2.1. Joint Decoding

We decode all backtracked frames jointly from the same conditioning window and supervise the entire FUT stack in parallel. Concretely, the network produces ${\widehat{L}}_{1:\mathtt{FUT}}$ (and ${\widehat{P}}_{1:\mathtt{FUT}}$) in one forward pass; we do not feed ${\widehat{P}}_t$ as input to predict ${\widehat{P}}_{t+1}$. The temporal operators $T^{\pm }$ are one-sided causal sweeps over the latent representation aligned to the observed window (via time flip), not an auto-regressive rollout. This joint design mitigates per-step error accumulation and exposure bias typical of strictly auto-regressive decoders; the “oldest” evaluation slice is a direct head output rather than the result of repeated prediction chaining.

All FUT slices are decoded from the same conditioning window on a flipped index; both temporal branches remain one-sided with respect to the evaluation boundary, so training cannot leak information from frames earlier than the oldest target.

No forgetting via joint supervision. We supervise the entire FUT stack jointly from the same conditioning window, aggregating per-frame terms across all FUT indices (oldest included) in the supervised loss. Because all targets are optimized together, the model does not preferentially fit only the most recent slice; random window sampling across epochs further rehearses every FUT index.

Per-frame min–max yields invariance to unknown affine rescaling (emission strength, sensor gain), which is desirable for localization across heterogeneous sources. The model thus learns shape/transport patterns rather than absolute amplitude; when absolute mass is needed operationally, the optional amplitude channel provides that cue without altering the backbone or loss.

3.2.2. Loss Decomposition

The objective encourages two complementary behaviours: (i) faithful reconstruction of the earlier maps (to learn dynamics, not merely a point label) and (ii) sharp localization on the oldest slice, where the source imprint is most concentrated. Let $\widehat{P}=\sigma \left(\widehat{L}\right)$ and $Y\in {[0,1]}^{B\times \mathtt{FUT}\times H\times W}$. We blend per-pixel regression (MSE) with a classification-style term (BCE) applied to the logits over all backtracked frames (including the oldest):

$${\mathcal{L}}_{\sup }=\underset{{\mathcal{L}}_{\mathrm{MSE}}}{\underbrace{\frac{1}{B}\sum {\parallel \widehat{P}-Y\parallel }_2^2}}+\lambda \underset{{\mathcal{L}}_{\mathrm{BCE}}}{\underbrace{\frac{1}{B}\sum \mathrm{BCEWithLogits}(\widehat{L},Y)}},\lambda =\mathtt{LAM}.$$

(7)

Applying BCE on logits improves gradients when probabilities saturate; $\lambda$ trades off geometric fidelity and peak sharpness (default $\lambda =0.1$). Losses use reduction=”sum” internally and are normalized by batch size in logging.

3.2.3. Complementarity of BCE-on-Logits and MSE

Writing $p=\sigma (\ell )$, the logistic loss on logits satisfies ${\nabla }_{\ell }{L}_{\mathrm{BCE}}=p-y$, while MSE on probabilities gives ${\nabla }_{\ell }{L}_{\mathrm{MSE}}=2(p-y)p(1-p)$ by the chain rule; the latter attenuates near saturation ($p\approx 0$ or 1). We therefore use $L=L_{\mathrm{MSE}}+\lambda L_{\mathrm{BCE}}$ with $\lambda =0.1$: BCE-on-logits supplies non-vanishing sharpening signal under saturation, and MSE preserves geometric fidelity elsewhere. For numerical stability, we compute BCE with logits and evaluate MSE on clipped probabilities; post hoc temperature scaling (optional) can further refine calibration without altering the objective.

3.2.4. Class Imbalance and Weighting

Because positives occupy a small fraction of cells on the oldest slice, the dense $L_{\mathrm{MSE}}$ term prevents trivial all-zero solutions and enforces the global plume shape, while $L_{\mathrm{BCE}}$ focuses learning on the sparse high-probability region and maintains gradients under saturation. For simplicity and robustness across datasets, we use a single $\lambda$ for all backtracked frames; this setting was stable in our experiments.

3.2.5. SWA/Polyak Teacher Consistency

Backtracking stacks several predictions; small calibration errors can compound. To stabilize training without affecting inference cost, we maintain a Polyak/EMA teacher (AveragedModel) and add light consistency terms after a short warm-up:

$$\begin{array}{cc}\hfill {\widehat{L}}^{\mathrm{ema}}& =f_{\mathrm{avg}}\left(X_{1:\mathtt{COND}}\right),{\widehat{P}}^{\mathrm{ema}}=\sigma \left({\widehat{L}}^{\mathrm{ema}}\right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{cons}}& =\alpha {\parallel \widehat{P}-{\widehat{P}}^{\mathrm{ema}}\parallel }_2^2+\beta \mathrm{BCEWithLogits}(\widehat{L},{\widehat{P}}^{\mathrm{ema}}),\hfill \end{array}$$

(9)

with $(\alpha ,\beta )$ ramped linearly by $\mathtt{schedule}\_\mathtt{coeff}$. The total loss is $\mathcal{L}={\mathcal{L}}_{\sup }+{\mathcal{L}}_{\mathrm{cons}}$.

3.2.6. EMA Teacher and Schedule

Let ${\theta }_t$ be the student parameters and ${\theta }_t^{\mathrm{ema}}$ the teacher. We update the teacher as ${\theta }_t^{\mathrm{ema}}\leftarrow \rho {\theta }_{t-1}^{\mathrm{ema}}+(1-\rho ){\theta }_t$ with a high decay $\rho$, so the teacher prediction is a temporally smoothed copy of the student. After a short warm-up, the consistency weights $(\alpha ,\beta )$ are ramped linearly from 0 to modest values so the EMA target does not act as a strong prior early in training. The teacher uses the same inputs and indexing as the student (including the time flip that makes the oldest slice the target), receives no external wind or solver signals, and is updated with stop-gradient. Thus, the consistency loss improves calibration and temporal coherence across FUT slices without introducing information leakage or exogenous bias.

3.2.7. Robustness Under Meanders

When winds meander or reverse, student and teacher may transiently disagree; keeping $(\alpha ,\beta )$ modest ensures supervised terms dominate in low-confidence cases, while the EMA acts as a gentle stabilizer rather than a hard constraint.

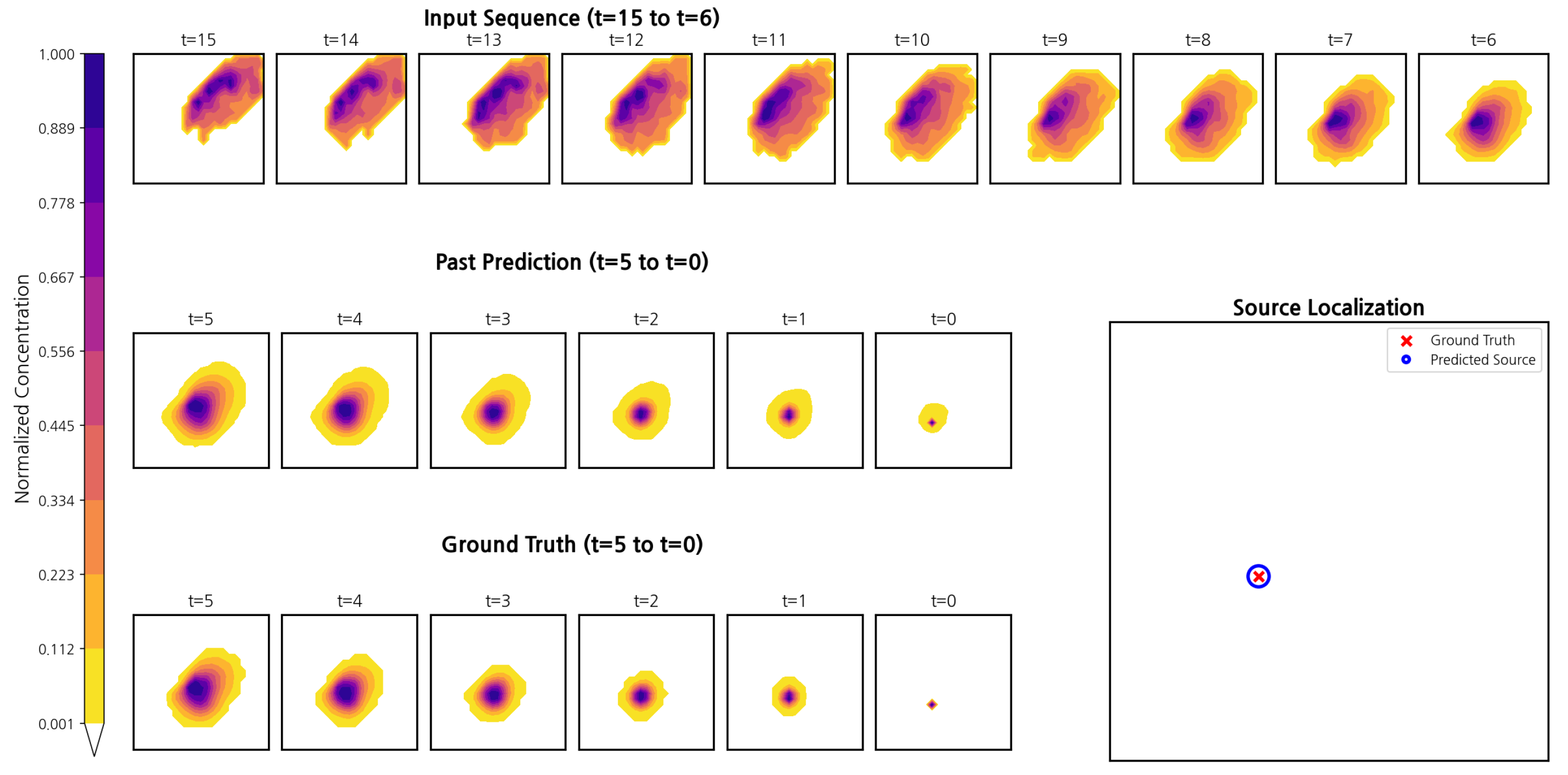
3.2.8. Inference

At test time, we feed the most recent $\mathtt{COND}$ frames and obtain ${\widehat{L}}_{1:\mathtt{FUT}}$. After the same time flip used in training, ${\widehat{P}}_{\mathtt{FUT}}=\sigma ({\widehat{L}}_{\mathtt{FUT}})$ is the estimate at $t\approx 0$. The predicted source cell is the spatial argmax:

$$(\widehat{x},\widehat{y})=\underset{(x,y)\in \{1,\dots ,H\}\times \{1,\dots ,W\}}{arg\; max}{\widehat{P}}_{\mathtt{FUT}}(x,y).$$

(10)

We report geometry-aware metrics—Exact hit, hit $\le 1$ (Chebyshev $d_{\infty }$), and RMSE (px). Using the same per-frame normalization at train/test time avoids bias from dilution-induced dynamic-range shifts. All FUT slices are produced in a single pass from the same conditioning window, so no predicted slice is reused as input at test time. At test time, we run a single forward pass on the observed window; temporal sweeps are one-sided on the flipped index, so no information beyond the window can be accessed.

3.2.9. Uncertainty and Abstention (Optional)

Alongside the point estimate on the oldest predicted slice ${\widehat{P}}_{\mathtt{FUT}}$, we provide an optional confidence score built from two quantities: (i) the top-two probability margin $\Delta p=p_{\left(1\right)}-p_{\left(2\right)}$ at the argmax cell and (ii) the predictive entropy $H\left({\widehat{P}}_{\mathtt{FUT}}\right)=-{\sum }_{h,w}{\widehat{P}}_{\mathtt{FUT}}(h,w)log\left({\widehat{P}}_{\mathtt{FUT}}(h,w)+\epsilon \right)$. An abstention policy can be enabled at deployment: emit a hard decision only if $\Delta p\ge ϵ$ and $H\le \kappa$; otherwise, return uncertain. These thresholds are chosen on a held-out validation set and kept fixed. For reliability, logits may be post hoc calibrated by temperature scaling ($\ell \to \ell /T$; T fit on validation); when enabled, we recommend reporting the expected calibration error (ECE) on the oldest slice. All of these components are optional knobs for deployment and are disabled in the main tables unless explicitly stated.

3.2.10. Stabilizers

We use a DropPath schedule across blocks, an EMA teacher for light consistency after warm-up, and gradient clipping. These discourage sample-idiosyncratic routing and help the gate avoid collapse, without changing the backbone.

3.2.11. Deployment Note

In practice, we keep the validation-selected thresholds $(ϵ,\kappa )$ fixed at deployment, optionally apply temperature scaling for calibration, and log both the margin and entropy with each prediction. The abstention safeguard remains disabled in the main accuracy tables unless stated.

3.2.12. Optional Stabilizer for Very Low-Wind Plateaus

Episodes with near-stagnant flow can produce broad, low-contrast concentration fields. As an optional stabilizer that leaves the backbone unchanged, we add a light mass-balance term on the oldest slice,

$$L_{\mathrm{mb}}={\lambda }_{\mathrm{mb}}·\left|\sum _{h,w}{\widehat{P}}_{\mathtt{FUT}}-\sum _{h,w}{Y}_{\mathtt{FUT}}\right|,$$

and we recommend mixing low- and moderate-wind windows within a mini-batch to avoid collapse onto trivial flat solutions. When used, $L_{\mathrm{mb}}$ is applied after a short warm-up with a small weight ${\lambda }_{\mathrm{mb}}$ tuned on validation.

3.2.13. Conceptual Algorithms (For Clarity)

Algorithms 1 and 2 give compact, ASCII-safe pseudocode for the forward pass (causal directional sweeps + DirGate) and a single training step (BCE-with-logits across backtracked slices; after warm-up, a light EMA-consistency term). These conceptual listings include only the interfaces needed for reproduction and do not alter the backbone.

Algorithm 1 Forward pass with directional sweeps and DirGate

Input:  $X\in {\mathbb{R}}^{B\times 1\times T\times H\times W}$

Stem: $U=\mathrm{Conv}3\mathrm{D}\left(X\right)$; permute to $(B,T,H,W,C)$

For each block:

For $d\in \{H^{+},H^{-},W^{+},W^{-},T^{+},T^{-}\}$: $Z_d={\mathcal{O}}_d\left(\mathrm{LN}\left(U\right)\right)$ (depthwise, causal)

$g=\mathrm{softmax}\left(W\varphi \right(U)/\tau )$ (global or local DirGate)

$U\leftarrow U+\mathrm{DropPath}\left({\sum }_d{\gamma }_d{g}_d\odot Z_d\right)$

$U\leftarrow U+\mathrm{DropPath}\left({\gamma }_{\mathrm{mlp}}\mathrm{MLP}\left(\mathrm{LN}\left(U\right)\right)\right)$

Head: permute to channels-first and apply $\mathrm{Conv}3\mathrm{D}$ to produce logits

Algorithm 2 One training step

Input: conditioning window $X_{1:\mathtt{COND}}$, targets $Y_{1:\mathtt{FUT}}$ (time-flipped)

Forward: logits ${\widehat{L}}_{1:\mathtt{FUT}}$, probs $\widehat{P}=\sigma \left(\widehat{L}\right)$

Loss:  ${\mathcal{L}}_{\sup }=\mathrm{MSE}(\widehat{P},Y)+\lambda \mathrm{BCEWithLogits}(\widehat{L},Y)$

After warm-up: teacher EMA gives ${\widehat{P}}^{\mathrm{ema}}$; add $\alpha \mathrm{MSE}(\widehat{P},{\widehat{P}}^{\mathrm{ema}})+\beta \mathrm{BCEWithLogits}(\widehat{L},{\widehat{P}}^{\mathrm{ema}})$

Update: mixed-precision backprop, gradient clipping, EMA update

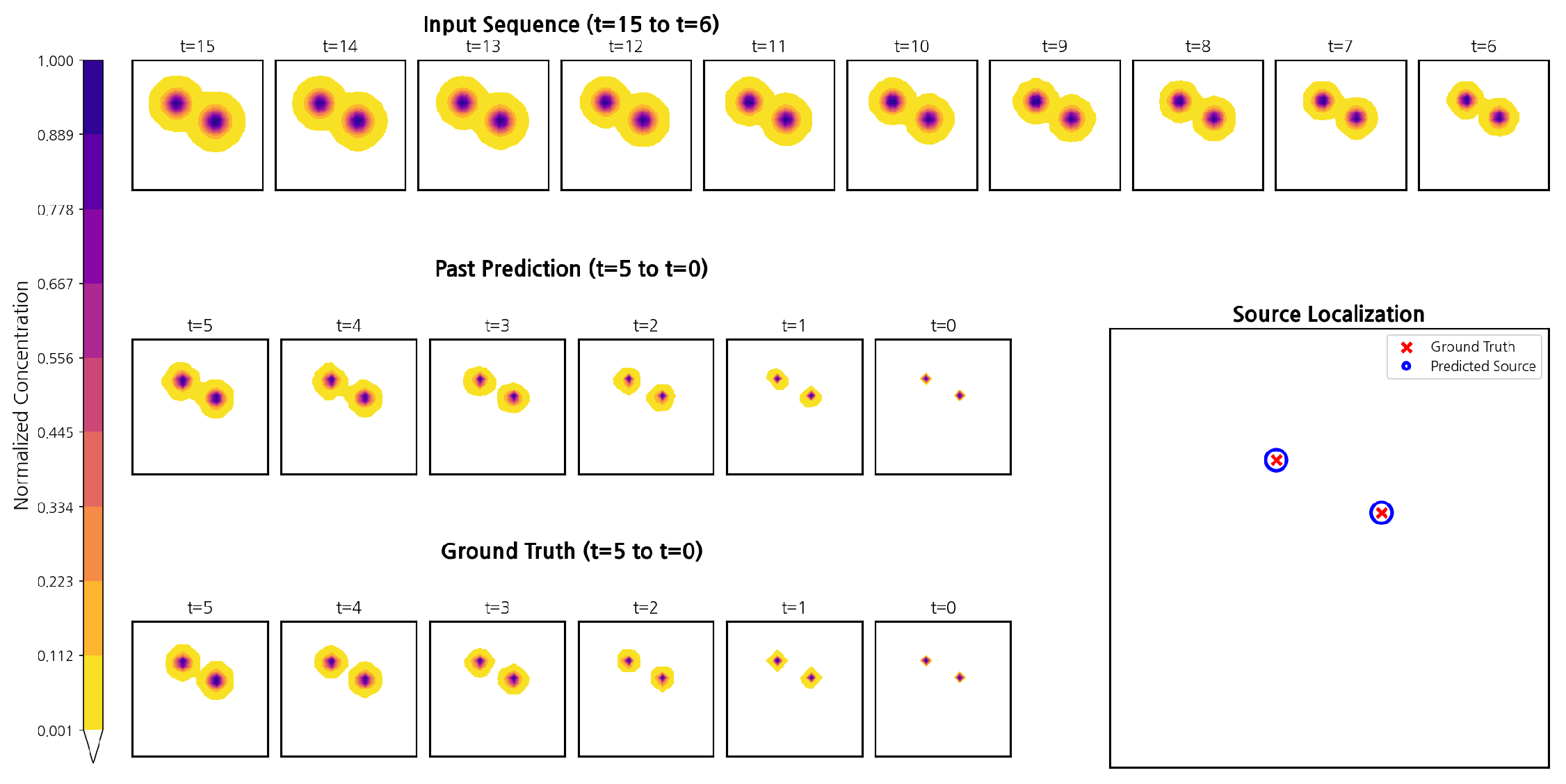
3.3. Dual-Source Stress Test (Zero-Shot)

We frame the dual-source experiment as a stress test under additive transport assumptions: it is parameter-free, states its assumptions/safeguards, and is intended to probe qualitative behaviour rather than to assert fully general multi-source performance in the absence of solver-backed multi-release data.

Scope and assumptions. We cast dual-source localization as a zero-shot stress test under passive advection–diffusion: (i) approximate linear superposition over the short observation window; (ii) after backtracking, the oldest slice exhibits at least moderate peak separation so that the global maximum is attributable to a single emitter; and (iii) subtraction uses an isotropic template by default, or an oriented/elliptical template when a coarse wind prior is available.

Safeguards. We clamp residuals to be non-negative, apply small-radius NMS before the second pick, and flag “uncertain” when the top-two probability margin on the oldest slice is small, in which case we defer a hard two-source decision.

Optional upgrades (kept off by default). A compact two-Gaussian mixture fit or a short unrolled residual decoder trained on synthetic superpositions can improve deblending under stronger overlap while remaining near-linear at our lattice size and leaving the backbone unchanged.

Real incidents may involve more than one emitter. Because the synthetic generator is additive (linear superposition), we keep the backbone unchanged and apply a lightweight, physics-aware postprocess on the oldest slice. We treat ${\widehat{P}}_{\mathtt{FUT}}$ as a superposition of two diffusion kernels and perform a two-peak subtraction: (i) locate the global maximum, subtract a fixed isotropic heat-kernel template scaled by that peak, and clamp to zero; (ii) repeat once on the residual and return the two peak coordinates. This deterministic, parameter-free procedure introduces no learned weights, runs in $\mathcal{O}\left(HW\right)$ time, and provides a practical zero-shot baseline for dual-source localization without retraining.

Multi-source extension (documented). For $K>2$, we apply a sequential K-peak procedure on the oldest slice: (1) pick the current global maximum; (2) subtract a scaled template (isotropic by default, oriented if a coarse wind prior is available); (3) clamp residuals to non-negative; (4) apply small-radius NMS; (5) repeat until a residual mass criterion is met. We stop when the residual mass falls below a fraction ${\theta }_{\mathrm{res}}$ of the original or after $K_{max}$ picks (e.g., $K_{max}=4$). A minimum-separation guard (≥1 cell) and a top-two margin check prevent over-segmentation. This runs in linear time per pick and leaves the backbone unchanged.

Optional refinements (kept off by default). For overlapping lobes, a K-component Gaussian mixture may be fitted from the subtractor initialization (means at picked peaks; amplitudes from subtracted scales; optionally shared covariance) and refined by a few EM steps. Alternatively, a tiny residual decoder (a shallow conv head on the residual) trained on synthetic superpositions improves deblending while preserving the linear-time profile and leaving the directional operators/gating unchanged.

For $K>1$, we expose a per-pick confidence based on the local top-two margin and the residual mass curve; if either falls below thresholds, the routine halts further picks and flags uncertain. This confidence is combined with predictive entropy into a single actionable score.

4. Experimental Setup

4.1. NBC_RAMS Field Benchmark

To assess performance under realistic urban flow—and to prioritise an operationally relevant setting—we adopt a primary benchmark curated from the Nuclear–Biological–Chemical Reporting and Modelling System (NBC_RAMS) [9,11]. NBC_RAMS couples a 3D mesoscale meteorology model (winds/temperature with terrain and building effects) and an Eulerian dispersion module to produce gridded concentration sequences over a $5\mathrm{km}\times 5\mathrm{km}$ area (cell size 200 m). Each run spans 30 min at 1 min cadence, yielding $25\times 25$ rasters; we vary wind sector/speed and payloads to generate diverse scenarios for training/validation/testing. Functionally, NBC_RAMS is analogous to HPAC (v6) [46] and has been used in prior studies for comparable tasks [9,11].

Following prior practice [9,11], we discard the first 5 min of near-field turbulence and use the remaining frames as follows: ten recent frames are retained for conditioning (COND = 10), and six earlier frames are reconstructed back to $t\approx 0$ (FUT = 6). This empirically grounded setting keeps the learning/evaluation pipeline identical across domains. We randomize diffusion/wind broadly in synthetic generation and evaluate cross-domain on a distinct NBC_RAMS terrain without fine-tuning.

We omit the first five minutes after release, following standard NBC_RAMS practice, to exclude the highly transient near-field jet regime that is difficult to sense reliably and poorly represented at $25\times 25$ resolution. In our setup, the conditioning window begins at $t_0\ge 5$ min and spans recent frames; evaluation is always performed on the oldest frame in this window. This reflects common operational timelines (earliest observations arrive with a short delay) and focuses the task on mid-field transport patterns used by responders.

All 5-dir/6-dir comparisons use identical data splits, optimizer, schedule, and training budget; only the direction set differs. A parameter-matched 5-dir control (e.g., slightly wider MLP to match the extra $T^{-}$ parameters) is left for future large-scale ablations; current gains arise with <1% parameter change.

4.1.1. Variability and Scale

We sweep payload mass (${\mathrm{SF}}_6$, 0.0005 to 0.0025 kg with 0.0005 kg steps), wind speed 1 ${\mathrm{ms}}^{-1}$ to 3 ${\mathrm{ms}}^{-1}$ (step 0.5 ${\mathrm{ms}}^{-1}$), wind direction (eight sectors), and source positions (all 625 cells), yielding 125,000 single-source scenarios. This breadth exposes models to channelling, shear, and occasional reversals that are absent in the flat synthetic regime.

4.1.2. Preprocessing and Usage

We apply per-frame min–max normalization to $[0,1]$, clip sub-threshold numerical noise, and use a light Gaussian blur to suppress isolated sensor-like outliers; frames are already $25\times 25$, so no spatial resize is needed. We adopt the same 70:20:10 split across scenarios. In all single-source experiments, we use the same conditioning/backtracking protocol (cf. [9]). Dual-source experiments are not available in NBC_RAMS and are evaluated only on synthetic data. Unless otherwise stated, we reuse a consistent preprocessing/evaluation pipeline across datasets. When reporting results, we use geometry-aware metrics on the oldest slice: RMSE (px) and AED (m) with AED computed as $\mathrm{RMSE}\times 200\mathrm{m}$ (1 px = 200 m), plus hit $\le 1$ and Exact; model compactness is summarized by parameter count. Unless otherwise stated, we use global DirGate at $25\times 25$. For higher-resolution exports, we enable the patchify/strided stem and, if needed, switch to local or hybrid gating following the guidance in Section 6.

• Data splits. We split at the scenario level to avoid leakage. A scenario is the tuple 〈release–location id, wind–sector bin, wind–speed bin, payload id〉; all windows from a scenario are assigned in full to exactly one of train/val/test. Splits are grouped and stratified so that the wind–sector and wind–speed marginals are comparable across splits while keeping overall proportions fixed.
• Leakage controls. The model employs LayerNorm (no BatchNorm), and all augmentations are applied only within the training split. No window from a scenario appears in more than one split, and no re-shuffling occurs during training.
• Illustrative samples. Figure 4 illustrates gas dispersion at one-minute intervals from 1 to 15 min post-release. Each tile corresponds to a fixed time index ($t=1,\dots ,15$); the red “×” marks the true source location. Normalized concentration is overlaid on a satellite basemap, revealing the plume’s growth, transport, and dilution as it advects along urban corridors and experiences shear. As time elapses, near-source concentrations diminish due to atmospheric dilution, while downwind lobes broaden and may split as flow channels and meanders. Figure 5 shows the corresponding preprocessed input fed to the model. From each simulation we extract a consecutive window of $\mathtt{COND}$ frames after an initial near-field transient so that early, unstable slices do not dominate the learning signal. Candidate windows are validated and discarded if too sparse (e.g., if more than $\mathtt{COND}/3$ frames contain no detectable concentration), ensuring that each sample carries sufficient dispersion information. To align with RBVM’s training contract, frames are rasterised to a $25\times 25$ lattice, min–max-normalized per frame to $[0,1]$ to avoid dilution-induced dynamic-range bias, and lightly denoised by clipping isolated single-pixel spikes (numerical noise). These preprocessed time-series frames are the model inputs; the label is the source grid cell on the oldest slice in the extracted window.
• Operational input rasters. All experiments consume gridded concentration rasters exported by an upstream dispersion stack (NBC_RAMS), which couples mesoscale meteorology with Eulerian transport and can perform upstream assimilation when measurements are available. Consequently, the regular lattice is defined by the dispersion stack; RBVM operates downstream on these solver-produced rasters and does not ingest raw irregular samples. When higher-resolution exports are provided (e.g., $100\times 100$), our input interface supports them directly.

4.2. Synthetic Benchmark for Sensitivity and Stress Tests

Our synthetic corpus follows the physics recipe of [9] but is reimplemented in a fully vectorized PyTorch 2.3 pipeline for high-throughput sampling. We model horizontal gas motion on a $25\times 25$ lattice under the advection–diffusion equation [47,48]:

$${\displaystyle \frac{\partial C}{\partial t}}=k{\nabla }^{2}C-\mathit{v}·\nabla C,$$

(11)

with concentration $C(x,y,t)$, diffusion k, and horizontal wind $\mathit{v}=(v_x,v_y)$. For an instantaneous point release at ${\mathit{r}}_0$ (time $t_0$) in ${\mathbb{R}}^2$, the Green solution [47] is

$$C(\mathit{r},t)={\displaystyle \frac{C_0}{4\pi k(t-t_0)}}exp\left(-{\displaystyle \frac{{∥\mathit{r}-{\int }_{t_0}^t\mathit{v}\left(\tau \right)\mathrm{d}\tau -{\mathit{r}}_0∥}^2}{4k(t-t_0)}}\right),$$

(12)

i.e., a diffusive Gaussian that drifts with the time-integrated wind, consistent with standard atmospheric–dispersion treatments [48]. Each scenario randomizes the source ${\mathit{r}}_0$, diffusion k, initial mass $C_0$, and a piecewise-steady wind ${\mathit{v}}_n=(s_{n}cos{\theta }_n,s_{n}sin{\theta }_n)$, where the main direction is drawn from eight equal angular sectors and perturbed by ${\theta }_n\sim \mathcal{U}(-\pi /3,\pi /3)$; the speed $s_n$ is sampled from a chosen range. This choice yields strictly causal transport on flat terrain, allowing us to isolate algorithmic effects without orographic confounds.

4.2.1. Sequences, Conditioning, and Targets

Each synthetic sequence contains 16 frames as in [9]: a one-hot Kronecker delta at $t=0$ (true source) followed by 15 advecting/decaying plumes. We use the latest 10 frames as the conditioning window and recursively backtrack the earlier 6 frames; this mirrors [9], keeps the inference horizon fixed across methods, and makes evaluation comparable to field data. To match RBVM’s training contract, we apply per-frame min–max normalization to $[0,1]$ to prevent dilution-induced dynamic-range shifts from biasing the optimizer, and we clip isolated single-pixel spikes caused by numerical noise. The regression targets are the six earlier frames; the classification target is the source on the oldest slice.

4.2.2. Rationale for Synthetic Use

The synthetic set provides a controllable arena to verify (i) whether axis-wise causality and the upwind mixture suffice in strictly causal flows; and (ii) how far a single-source model generalizes when the generator emits dual-source sequences. We do not train on dual-source; those sequences are used only as a zero-shot stress test (Section 3.3). Unless stated, data are split 70:20:10 (train/val/test), and all baselines and RBVM are trained on the same images for fairness.

4.2.3. Evaluation Slice and Metrics

We always score on the oldest reconstructed slice (closest to $t=0$). Reported metrics are RMSE (px) and AED (m = RMSE $\times 200$), plus hit $\le 1$ and Exact. Using the identical slice across methods avoids favouring architectures that implicitly bias a different time index.

4.3. Experimental Instantiation of the Proposed Method

We instantiate RBVM for all main experiments. The backbone comprises a $1\times 3\times 3$ 3D–Conv stem ($1\to C$), $N_{\mathrm{blk}}$ residual blocks, and a symmetric $1\times 3\times 3$ head ($C\to 1$) producing logits for all T frames. Each block applies causal, depthwise directional sweeps over ${\mathcal{D}}_6$ (six directions by default; ${\mathcal{D}}_5={\mathcal{D}}_6\setminus \left\{{\mathrm{T}}^{-}\right\}$ is used only in sensitivity snapshots), fuses them via a temperature-controlled DirGate (global by default, zero-initialized so training starts uniform), and refines with a two-layer GELU MLP. We use pre-norm LayerNorm on both branches; small LayerScale coefficients ${\gamma }_d,{\gamma }_{\mathrm{mlp}}\sim {10}^{-3}$ stabilize residuals; and a layer-indexed, depth-weighted DropPath regularizes across blocks (static during training).

4.3.1. Default Hyperparameters

Unless stated otherwise, we set embed $C=192$, blocks $N_{\mathrm{blk}}=6$, VARIANT=6dir (the 5dir variant appears only in ablations), drop_path_rate = 0.2, gate_mode = global, $\tau =1.0$, and ${\gamma }_{\mathrm{init}}={10}^{-3}$. Optimization follows Section 3.2.1, Section 3.2.2, Section 3.2.3, Section 3.2.4, Section 3.2.5, Section 3.2.6, Section 3.2.7 and Section 3.2.8. Defaults are BATCH_SIZE = 16, EPOCHS = 30, WARMUP_EPOCHS=3, $\mathtt{LAM}=0.1$, $\alpha =1.0$, and $\beta =0.1$.

4.3.2. Fairness Controls and Protocol Consistency

All methods—including 3D–CNN, CNN–LSTM, and ViViT—are trained on the same splits with identical preprocessing and are scored on the same oldest slice using RMSE/AED, hit $\le 1$, and Exact. We also report parameter count for model compactness. This protocol ensures that observed gains derive from modelling choices (directional causality, upwind gating) rather than differences in data handling or evaluation timing. Consistent with Section 5, we report NBC_RAMS first and use the synthetic benchmark primarily for sensitivity analyses and the dual-source stress test under the same evaluation protocol.

Per-frame min–max normalization. We normalize each input frame with a small stabilizer $\epsilon$ and apply the same policy at train and test; statistics are computed only from the observed conditioning window.

$${\tilde{X}}_t(h,w)={\displaystyle \frac{X_t(h,w)-{min}_{h,w}{X}_t}{{max}_{h,w}{X}_t-{min}_{h,w}{X}_t+\epsilon }},\epsilon ={10}^{-6}.$$

Targets $Y_t$ are normalized independently with the same transform, making the loss effectively scale-invariant. This avoids domination by high-intensity frames, improves stability under dilution, and preserves relative morphology. If absolute scale is required, an optional single-channel per-frame summary $a_t$ (e.g., framewise max or integral) can be concatenated to the input; our default experiments keep this off to prioritise localization from morphology.

4.3.3. Ablation Protocol and Findings

To isolate LayerScale/DropPath effects under limited compute, we define an ablation split that uses one third of the full training set (same val/test as the main results). We sweep ${\gamma }_{\mathrm{init}}\in \{{10}^{-4},{10}^{-3},{10}^{-2}\}$ and drop_path_rate $\in \{0.1,0.2,0.3\}$ under identical budgets and report ratios relative to the default $({\gamma }_{\mathrm{init}}={10}^{-3}$, $\mathtt{drop}\_\mathtt{path}\_\mathtt{rate}=0.2)$. Around this default, performance remains essentially unchanged (ratios $\approx 1.00$), while a higher DropPath of $0.3$ consistently worsens RMSE (ratio $>1$) and slightly reduces Exact (ratio $<1$); ${\gamma }_{\mathrm{init}}\le {10}^{-3}$ is stable on this split. Results are summarized in Appendix B. No training instabilities were observed on this split (no NaN/Inf; gradients remained bounded under clip = 1.0). With a small LayerScale ${\gamma }_{\mathrm{init}}\le {10}^{-3}$ and a moderate drop_path_rate of $0.2$, we observed a mild regularization gain without any loss in convergence speed.

5. Results

This section presents RBVM results on the high-fidelity NBC_RAMS Field Benchmark, our primary focus, and, secondarily, on a controlled Synthetic Benchmark for sensitivity analyses and a dual-source stress test. Unless noted, we follow Section 4: a COND(=10)-frame conditioning window, FUT(=6) recursive backtracking steps, and evaluation on the oldest reconstructed slice ${\widehat{P}}_{\mathtt{FUT}}$. We report geometry-aware localization metrics (RMSE/AED, hit $\le 1$, Exact), model compactness via parameter count, and qualitative overlays. The core tables report Exact/hit ≤1/RMSE as before. Uncertainty and abstention are documented as deployment-facing options; when enabled, we suggest reporting the abstention rate at the chosen margin/entropy thresholds and ECE after temperature scaling, but these diagnostics are not required for the main results.

5.1. NBC_RAMS Field Benchmark

5.1.1. Setup

We evaluate on NBC_RAMS simulations under an as-is protocol, consistent with recent practice [9,11]. By default, we reuse the training settings from our previous study [11]. The NBC_RAMS terrain used here differs from that in [11], but we intentionally keep all model and baseline configurations unchanged to enable a clean cross-terrain comparison. NBC_RAMS introduces urban complexity (channelling, shear, occasional wind reversals), making it the primary test of operational relevance. Classification metrics (Exact and hit $\le 1$) are computed on the oldest slice, and geometric error is reported as Average Error Distance (AED) in metres, obtained by converting pixel offsets with a ground sampling distance of 200 m per cell. For source localization, we regard geometry-aware metrics—Exact, hit $\le 1$, and RMSE/AED—as primary indicators of operational performance.

5.1.2. Main Results

Table 1. NBC_RAMS field benchmark (evaluated on the oldest slice). Metrics: RMSE/AED reported jointly as pixels/metres on the $25\times 25$ grid, with AED computed as $\mathrm{RMSE}\times 200\mathrm{m}$ (1 px = 200 m); hit $\le 1$ = accuracy within Chebyshev distance 1; Exact = exact hit. RBVM (6-dir) attains the lowest RMSE/AED and the highest hit/Exact while using the fewest parameters.

Model	Params [M]	RMSE/AED [px/m]	hit $\le 1$ [%]	Exact [%]
3D–CNN	6.74	0.63 / 126	96.87	74.30
CNN–LSTM	9.87	0.32 / 64	99.55	91.74
ViViT	2.11	0.28 / 56	99.49	94.19
RBVM (6-dir)	0.95	0.20 / 40	99.86	96.70

summarizes geometry-aware metrics and parameter counts. RBVM (6-dir) achieves the best scores across all measures while using the fewest parameters (0.95 M): RMSE $0.20\mathrm{px}$ (AED $40\mathrm{m}$), hit $\le 1$$99.86\%$, and Exact $96.70\%$. Compared with the strongest baseline by Exact (ViViT, 2.11 M params), RBVM reduces AED by about $29\%$ ($56\mathrm{m}\to 40\mathrm{m}$) and raises Exact by $+2.51$ pp, with roughly $55\%$ fewer parameters. Relative to CNN–LSTM (9.87 M), AED improves by $38\%$ ($64\mathrm{m}\to 40\mathrm{m}$) and Exact by $+4.96$ pp, with about $90\%$ fewer parameters. Against 3D–CNN, the gains are larger (AED $126\mathrm{m}\to 40\mathrm{m}$, $68\%$ reduction; Exact $+22.4$ pp) despite an $\sim 86\%$ smaller parameter budget. Note that hit $\le 1$ is near the ceiling for several models (all $\approx 99\%$), so Exact and AED are more discriminative at the operating point; RBVM improves both, shifting the accuracy–compactness frontier relative to 3D–CNN, CNN–LSTM, and ViViT. These gains persist on a terrain different from prior work under unchanged configurations (cf. Setup), underscoring robustness across urban layouts. The 6-dir improvement persists despite a negligible parameter delta relative to 5-dir. Since DirGate remains a single convex mixture and all training budgets/hyperparameters are identical, we attribute the gain to the reverse-index causal sweep $T^{-}$, which stabilizes routing under per-frame angle noise and partial wind reversals, rather than to added capacity.

5.1.3. Qualitative View

Figure 6 presents a representative case. The top row ($t=15\to 6$) is the input conditioning window; the middle row ($t=5\to 0$) shows the model’s recursively backtracked frames; the bottom row shows the corresponding ground truth. The right panel overlays the predicted source (blue marker) and the ground truth (red “×”). As the sequence is rolled back, the predicted plumes follow the dominant wind channels, gradually contract, and concentrate near the origin, closely matching the ground-truth frames. This illustrates that RBVM captures the governing advective pattern and reconstructs the past consistently, which in turn yields accurate source localization. These visual trends are consistent with Table 1: RBVM produces sharper, better-localized peaks on the oldest slice, reduces overshoot and near-miss confusions in the neighbourhood of the source, and better preserves source geometry under meandering winds, aligning with the improved Exact and lower AED.

5.2. Synthetic Benchmark: Sensitivity and Stress Tests

5.2.1. Setup

The synthetic study isolates algorithmic effects in strictly causal flows on a flat domain and is used primarily for sensitivity analyses. We compare RBVM against 3D–CNN, CNN–LSTM, and ViViT, trained/evaluated on the same images and evaluation slice. For RBVM we report both 5-dir (${\mathrm{H}}^{\pm },{\mathrm{W}}^{\pm },{\mathrm{T}}^{+}$) and 6-dir (${\mathrm{T}}^{-}$ added) variants. Unless noted, we evaluate on the oldest reconstructed slice and report geometry-aware metrics (RMSE/AED, hit $\le 1$, Exact) together with parameter count.

5.2.2. Main Results

Table 2. Synthetic benchmark (strictly causal flows; oldest slice evaluation). RMSE/AED are reported jointly as pixels/metres on the $25\times 25$ grid, with AED computed as $\mathrm{RMSE}\times 200\mathrm{m}$ (1 px = 200 m).

Model	Params [M]	RMSE/AED [px/m]	hit $\le 1$ [%]	Exact [%]
3D–CNN	0.272	0.851 / 170.	91.34	29.15
CNN–LSTM	9.868	0.334 / 66.8	100.0	67.68
ViViT	0.789	0.398 / 79.6	100.0	60.61
RBVM (5-dir)	0.128	0.186 / 37.2	99.76	83.17
RBVM (6-dir)	0.130	0.022 / 4.40	100.0	97.80

reports the geometry-aware view (RMSE/AED, hit $\le 1$, Exact) and parameter count. On this controlled benchmark, 6-dir decisively outperforms 5-dir—with a much lower RMSE/AED and higher Exact—while keeping essentially the same parameter size, indicating that the gain stems from the backward temporal branch rather than model capacity.

5.2.3. Where the Gains Come from

Causal, depthwise directional operators keep communication paths short; DirGate adapts the mixture to the dominant flow; and a lightweight MLP supplies channel mixing without attention’s quadratic costs. In this regime, adding the backward temporal branch (${\mathrm{T}}^{-}$) markedly improves robustness to per-frame angle noise and cumulative drift, yielding ∼8.5× lower AED (4.40 m vs. 37.2 m) and $+14.63$ percentage points (pp) in Exact over 5-dir, with a negligible change in parameter count (0.130 M vs. 0.128 M). hit $\le 1$ also improves from $99.76\%$ to $100.0\%$.

5.2.4. Scope of the Toy Synthetic Benchmark

For a sanity check and ablations, we used a lean Mamba–3D variant and a lightweight, fully vectorized data pipeline. Each sample provides 16 frames on a $25\times 25$ grid; we condition on the most recent 10 frames and evaluate on the oldest reconstructed slice after a 6-step rollout (COND $=10$, FUT $=6$). The dataset is split 70:20:10 (seed 42). Unless noted, training uses AdamW (LR $=3\times {10}^{-4}$, weight decay $={10}^{-4}$), cosine annealing over 30 epochs, AMP, and gradient clipping at $1.0$; the best checkpoints are selected by validation RMSE (pixels). The toy backbone is intentionally minimal: embed width $C=96$, blocks $N_{\mathrm{blk}}=3$; each block stacks causal, depthwise axis-wise operators (no DirGate/LayerScale/DropPath), followed by a two-layer GELU MLP; the stem/head are 3D convolutions with padding and a sigmoid head. The direction set is controlled by a single flag (VARIANT$\in \{\mathtt{5}\mathtt{dir},\mathtt{6}\mathtt{dir}\}$), enabling paired comparisons under identical capacity.

The supervised objective combines a reconstruction term over the returned sequence with a small, source-sharpening term on the oldest slice:

$$\mathcal{L}=\mathrm{MSE}\left(Y,\widehat{Y}\right)+0.1\mathrm{BCE}\left(Y_{\mathrm{oldest}},{\widehat{Y}}_{\mathrm{oldest}}\right),$$

and the model is evaluated with RMSE (px) and Exact (%) on the oldest slice; AED (m) is reported as RMSE $\times 200$ given the grid scale (1 px $\approx 200\mathrm{m}$). For numerical stability in time-reversed slicing and flips, tensors are made contiguous in both the dataset and rollout paths. Synthetic runs follow the controlled setup in Section 4.2.

5.3. Sensitivity Highlights

We provide brief snapshots that relate design choices to observed behaviour (geometry-aware metrics on the oldest slice unless noted):

• Direction set (5-dir vs. 6-dir). In strictly causal synthetic flows, 5-dir and 6-dir can be close, consistent with the absence of reversals. On NBC_RAMS, adding the backward temporal branch (${\mathrm{T}}^{-}$) improves Exact and reduces RMSE, indicating value under meandering winds and urban channelling.
• Gating mode (global vs. local). At the $25\times 25$ scale, a global gate (one mixture per sample) performs on par with, or slightly better than, a local gate; sample-level mixtures suffice at this resolution. Larger domains may benefit from local gating.
• DropPath rate. A small, layer-indexed DropPath suffices on the toy synthetic split. On NBC_RAMS, a higher maximum rate acts as a useful regularizer and yields better hit $\le 1$ / Exact without altering model capacity.

5.4. Dual-Source Stress Test (Zero-Shot)

Finally, we assess zero-shot behaviour on dual-source synthetic sequences. Following Section 3.3, we keep RBVM as-is and apply a parameter-free, physics-aware two-peak subtraction on the oldest slice ${\widehat{P}}_{\mathtt{FUT}}$ (no retraining, no architectural change).

Table 3. Zero-shot dual-source localization on synthetic sequences (two-peak subtraction on ${\widehat{P}}_{\mathtt{FUT}}$). SR@ $r$ denotes the fraction of test cases where both sources are within radius $r\mathrm{m}$. SL-$F_1$ uses a $200\mathrm{m}$ success threshold.

Model (Variant)	${\mathbf{RMSE}}_{\mathit{m}}$ [m]	SR@100 [%]	SR@200 [%]	SL-${\mathit{F}}_1$
RBVM (5-dir)	184.1	59.9	83.9	0.907
RBVM (6-dir)	118.2	89.7	95.1	0.969

reports results for both variants: the six-direction model achieves ${\mathrm{RMSE}}_m=118.2\mathrm{m}$, $\mathrm{SR}@100=89.7\%$, $\mathrm{SR}@200=95.1\%$, and $\mathrm{SL}-F_1=0.969$; the five-direction model attains ${\mathrm{RMSE}}_m=184.1\mathrm{m}$, $\mathrm{SR}@100=59.9\%$, $\mathrm{SR}@200=83.9\%$, and $\mathrm{SL}-F_1=0.907$. Thus, adding the backward temporal branch (${\mathrm{T}}^{-}$) reduces distance error by $\approx 36\%$ (118.2 m vs. 184.1 m) and improves success rates by $+29.8$ pp (SR@100) and $+11.2$ pp (SR@200), while maintaining essentially the same parameter budget (∼0.13 $\mathrm{M}$).

• Timeline visualisation. For qualitative inspection, Figure 7 presents a 16-frame timeline per sequence: the top row shows the 10 conditioning inputs ($t=15\to 6$), the middle row shows the 6 recursively backtracked predictions ($t=5\to 0$), and the bottom row shows the corresponding ground-truth frames. The right panel overlays localization on the oldest slice ($t\approx 0$): “×” marks the two ground-truth emitters, and open circles mark the two predicted sources obtained via a parameter-free two-peak subtraction on ${\widehat{P}}_{\mathtt{FUT}}$. Predictions follow the dominant wind, contract backward in time, and concentrate at the sources, consistent with the ground truth.

For threshold sensitivity at this map resolution (100 m = half-cell, 200 m = one-cell), see Appendix D, in which we report mean ± std over 10 seeds for ${\mathrm{RMSE}}_m$, SR@100, SR@200, and SL $F_1$.

Our quantitative focus is the dual-source stress test; the documented $K>2$ extension is intended for application-specific benchmarking in future work.

6. Discussion

6.1. Main Findings on NBC_RAMS

Across both benchmarks, RBVM improves localization accuracy while remaining compact relative to 3D-CNN, CNN–LSTM, and ViViT; here we prioritise the field setting. On NBC_RAMS, where winds meander and urban channelling occurs, the six-direction variant (adds ${\mathrm{T}}^{-}$) consistently raises Exact and lowers RMSE compared with five directions (Table 1). Two design elements appear most influential in the field: (i) applying BCE-with-logits to all backtracked slices (including the oldest) sharpens peaks without probability saturation, improving decision boundaries near the source; and (ii) an EMA-based consistency term stabilizes calibration along the six-step rollout, reducing near-miss confusions even when Exact is already high. From a scaling standpoint, depthwise grouped operators dominate cost, while DirGate and LayerScale are negligible. Hence compute and memory scale linearly with the spatiotemporal volume $THW$ and with the number of directions $\left|\mathcal{D}\right|$, enabling predictable extension of the look-back horizon. Adding $T^{-}$ introduces one additional one-sided temporal stencil that preserves causality and adds robustness to reverse-index transport; the overhead is linear and modest (one more sweep), whereas the observed benefit under meanders points to a physics-aligned gain rather than capacity-driven effects.

6.2. Dual-Source Localization: Importance and Implications

Multi-emitter incidents matter operationally—ambiguity in early response often arises from overlapping plumes. Our zero-shot treatment keeps the backbone fixed and applies a parameter-free, physics-aware two-peak subtraction on the oldest slice ${\widehat{P}}_{\mathtt{FUT}}$. On the synthetic stress test, this recovers both emitters within $200\mathrm{m}$ in $95.1\%$ of cases, with ${\mathrm{RMSE}}_m=118.2\mathrm{m}$ (Table 3, Figure 7). The approach works because (a) backtracking concentrates mass near the origin, and (b) the generator is additive, so a first-order “deblending” via subtraction is effective. Beyond gas releases, the same template applies to other transported fields—e.g., source separation in environmental monitoring or urban analytics—whenever superposition is a reasonable approximation and the oldest slice carries the sharpest imprint. As for the robustness across runs, we report SR@100 m and SR@200 m as mean±std over 10 random seeds (independent initialization and shuffle, identical budgets) to characterise variability; success rates remain consistent and method ranking is stable across runs.

The subtract-and-pick baseline is intended for short windows and passive releases, where backtracking typically increases peak separability on the oldest slice. In anisotropic urban winds, an oriented (elliptical) kernel aligned to a coarse wind prior further stabilizes results. We explicitly defer (flag “uncertain”) when emitters are nearly co-located, turbulence induces highly non-Gaussian lobes, or chemistry violates additivity; a small mixture fit or shallow residual decoder is a documented extension that improves deblending while preserving the linear-time profile.

The uncertainty flagging here is consistent with our deployment UQ/abstention policy (top-2 margin and predictive entropy on the oldest slice), ensuring conservative behaviour in low-SNR or plateaued cases.

When the oldest slice is heavily diffused or noisy, we prioritise decision quality over forced guesses. On ${\widehat{P}}_{\mathtt{FUT}}$, we compute the top-two margin $m=p_{\left(1\right)}-p_{\left(2\right)}$ and predictive entropy H; if $m<ϵ$ or $H>\eta$, the system flags uncertain rather than emitting a hard argmax. This confidence-aware abstention reduces false precision in low-SNR regimes and enables a clear coverage–accuracy trade-off. If desired, a tiny temporal pooling/decoder over the last few backtracked slices can further stabilize low-SNR cases without altering the backbone or its linear-time profile.

6.2.1. Overlapping Emitters and Limits

Near-coincident sources or elongated, intersecting lobes challenge purely subtractive schemes. Our default policy is conservative: stop early and mark uncertain rather than over-commit. When heavier deblending is required, two drop-ins remain lightweight: a subtractor-initialized mixture fit and a tiny residual decoder; both preserve linear-time inference and do not alter the directional operators or upwind gating.

6.2.2. Rotational Eddies and Orientation Extensions

While stacked axis-wise sweeps plus DirGate already form curved information paths, explicit diagonal (or learned) orientations can further align computation with local swirling cells or street-canyon recirculation. Because the added stencils remain depthwise and one-sided, the linear-time and causality guarantees hold. In deployments where rotational signatures are anticipated, enabling diagonals—or a small orientation basis—provides a practical, low-overhead enhancement without altering the backbone.

6.2.3. Scaling with Resolution and Domain Size

For domains beyond $25\times 25$, two practical routes preserve throughput: (i) patchify the input (e.g., $p=4$ maps $100\times 100$ to $25\times 25$ tokens) so the backbone runs at constant token count; (ii) process full resolution when needed—cost and memory then grow linearly with $THW$ and $CTHW$, respectively. In both cases, runtime remains dominated by the grouped depthwise stencils; permutations are comparatively cheap due to the channels-last body. The choice of p trades spatial fidelity and latency without altering the causal directional design.

6.3. Possible Failure Modes and Practical Guidance

Typical issues are shared across methods and can be mitigated with lightweight extensions: Boundary sources lose context near edges; boundary-aware padding or scoring on an inset region reduces this bias. Intersecting plumes may yield shallow residuals after subtraction; a small residual decoder or a learned mixture head (two-kernel deblender) can stabilize the second peak. Very low winds produce broad plateaus; mixing low- and moderate-wind episodes during training maintains Exact without extra inference cost. These considerations do not alter the backbone and preserve the linear-time, directionally causal design. Very low-wind episodes often yield broad plateaus for which a single-cell decision provides limited operational value. We therefore document two optional safeguards that preserve our linear-time profile: a light mass-balance regularizer at training time and a confidence-aware abstention rule at inference (top-two margin and entropy). When enabled in deployment, these reduce over-confident decisions on plateaus.

We prefer per-frame min–max over per-sequence or global z-score to prevent domination by high-intensity frames and to stabilize optimization under dilution. If absolute-scale reasoning is mission-critical (e.g., rate estimation), adding the amplitude channel or incorporating a solver-derived prior is a straightforward extension that preserves the model’s linear-time profile.

Near-field minutes (0–5) are dominated by jetting, strong verticals, and building-scale recirculation that can violate a coarse 2D lattice assumption. Our study targets the mid-field inverse task on solver-produced rasters under real-time constraints. As a near-term extension, earlier minutes can be incorporated by pairing higher-resolution or patchified stems with short-horizon synthetic jets, without altering the directional operators or gating and while preserving linear-time inference.

6.3.1. Vertical and Terrain Effects

Our current lattice is 2D at the screen level, which abstracts vertical stratification (e.g., stable/unstable boundary layers) and building-induced recirculation. Two lightweight extensions are natural. (i) Shallow-3D: introduce a small vertical depth Z (e.g., 2–8 levels from a solver export or coarse lidar) and add axis-wise one-sided sweeps $Z^{\pm }$. Because operators remain depthwise and one-sided, the per-block cost stays linear in $T+H+W+Z$; memory also scales linearly in $C\times T\times H\times W\times Z$. A learned vertical pooling/projection (few modes) can further reduce Z while preserving key stratification cues. (ii) Auxiliary priors: supply coarse vertical/terrain proxies as static channels (e.g., mixing height, stability, roughness/orography, building height/street-canyon masks) and use them to bias DirGate (additive logits or temperature modulation) without requiring online solver calls. These priors can be precomputed at low cadence and broadcast over the conditioning window. Both routes preserve our linear-time profile and streaming readiness while improving robustness to OOD flows with vertical structure.

6.3.2. Transfer and Operationalisation

NBC_RAMS supplies high-fidelity, terrain-aware flows but is still a proxy for live incidents. Our pathway is to (i) pretrain on breadth (synthetic + NBC_RAMS), (ii) validate in controlled field exercises (surrogate releases with ground truth), and (iii) optionally enable light calibration and confidence-aware abstention at deployment as operational safeguards. This positions RBVM as a downstream inverse layer over physics-consistent rasters while retaining a clear route to field validation.

6.3.3. Positioning vs. Physics-Based Inversions

RBVM serves as a compact learned inverse layer running downstream of a physics-based stack: physics supplies terrain/ meteorology-aware rasters, and RBVM performs source localization online without solver calls or winds. This division of labour matches operational practice and maintains predictable, linear-time latency. For deployment, light post hoc calibration (temperature scaling with ECE) and an uncertainty-aware abstention policy are documented as optional safeguards; they do not change the backbone and are not used for the core results.

6.3.4. Operational Inputs and Irregular Sensing

Our inverse layer targets solver-produced rasters, matching emergency-response practice. Where a solver grid is not available, an uncertainty-aware raster adaptor provides a working lattice and a support map that integrate seamlessly with RBVM and the abstention policy. A graph-based analogue—causal directional message passing on sensor graphs with upwind-inspired gating—is a natural extension; we leave it as future work to keep the present backbone unchanged and linear-time.

6.3.5. Spatial Heterogeneity and Gating Granularity

When flows are relatively uniform or grids are compact, global gating offers the best accuracy–efficiency trade-off. As spatial heterogeneity increases (e.g., urban canyons) or grids become larger, local gating—or a hybrid global prior plus local refinement—captures spatially varying winds while keeping the directional operators and linear-time scaling intact. In practice, we recommend patchify/stride → global (or hybrid) as a first step, enabling local refinement only where persistent sub-grid variation is observed. A systematic analysis of gate dynamics (e.g., entropy distributions across wind regimes) is an interesting direction for future work.

6.3.6. Generalization

Beyond our current domain randomization and cross-domain test, future work will (i) widen the randomization ranges for diffusion/wind/diurnal variability and (ii) inject coarse solver priors as optional channels to bias gating—both preserving the linear-time backbone while improving OOD robustness.

6.3.7. Operational Thresholds and Reporting (Optional)

A simple default (e.g., $\epsilon =0.05$ for the margin and a modest entropy cap $\kappa$) balances coverage and false positives on validation and can be fixed for deployment. We recommend logging the top-two margin, entropy, and calibrated confidence (after temperature scaling) together with the final action (“localize” vs. “uncertain”). Under broad plateaus or diffuse plumes—where point decisions carry low operational value—the abstention rule avoids over-confident mis-localizations. When resources permit, a few MC-DropPath samples can be turned on to obtain uncertainty bands without changing the backbone. These safeguards mirror our low-SNR guidance and remain purely post hoc.

Stability to split choice is important. Because our grouping jointly encodes source location and meteorology, we expect model ranking to be robust under stratified re-sampling; a full multi-split study is left to follow-on work enabled by the released indices and splitter.

Taken together, the results support RBVM as a compact, linear-time, directionally causal backbone for inverse inference on transported fields in both field and synthetic settings. At larger spatial extents, we use a patchify/strided stem and, if needed, a two-stage coarse-to-fine schedule: a coarse predictor backtracks on the reduced grid and a fine predictor refines on a local crop. Both stages share the same directional operators and gating.

7. Conclusions and Future Work

We presented Recursive Backtracking with Visual Mamba (RBVM), a compact, Visual-Mamba-inspired visual state-space framework that infers the origin of a gas release from a short conditioning window. The backbone aggregates causal, depthwise directional operators along $\{{\mathrm{H}}^{\pm },{\mathrm{W}}^{\pm },{\mathrm{T}}^{+}[,{\mathrm{T}}^{-}]\}$ via an upwind gate (DirGate) and uses pre-norm LayerNorm with a small LayerScale and a layer-indexed, depth-weighted DropPath for stable stacking. Because grouped depthwise convolutions dominate the cost, compute and memory scale linearly with the spatiotemporal extent, yielding predictable behaviour as the look-back horizon increases.

Our contributions are threefold and mutually reinforcing. Architecturally, we replace heavy spatiotemporal mixing with axis-wise, one-sided depthwise operators that preserve physical causality, while DirGate learns a convex directional mixture that follows the flow and remains hardware-friendly. In training/inference, a simple recipe—time flip alignment, BCE-with-logits across all backtracked slices (including the oldest), and an EMA-based consistency term—produces sharp, well-calibrated peaks on the evaluation slice without complicating optimization. Empirically, across a field corpus with urban channelling and wind variability and a strictly causal synthetic benchmark, RBVM improves geometry-aware localization metrics with a small parameter budget relative to attention-centric trackers. The six-direction variant (with a backward temporal branch) proves more robust than five directions in settings with meandering winds, and in a dual-source stress test, a parameter-free, physics-aware two-peak subtraction on the oldest slice provides a practical zero-shot extension without changing the backbone.

To maintain clarity and comparability, we scoped evaluation around two complementary settings. Field analyses follow an as-is protocol, and synthetic experiments follow a controlled setup used for sensitivity studies and the dual-source stress test. This design yields clean, like-for-like baselines and forms a springboard for broader field corpora and additional synthetic variants.

Looking ahead, we aim to broaden RBVM’s applicability while preserving its linear-time core. Priorities include handling sparser or irregular observations, strengthening generalization across diverse wind and terrain conditions with physics-aware extensions, scaling to larger domains, and improving multi-source separation—all within a streaming, hardware-friendly pipeline.

By marrying linear-time, directional state-space modelling with visual grid inputs, RBVM offers a practical alternative to attention-centric trackers and advances toward real-time decision support in CBRN emergencies. Beyond this domain, we view RBVM as a compact, directionally causal backbone for inverse inference on transported fields, useful more broadly for spatiotemporal backtracking tasks in environmental monitoring and urban analytics. Future work will pursue controlled comparisons against solver-backed inversions under harmonised I/O and budgets, and explore light hybridisation via auxiliary priors or gating biases while retaining linear-time inference.