An Asymmetric SiC Power Module Directly Integrated with Vapor Chamber for Thermal Balancing in MMC
Abstract
Featured Application
Abstract
1. Introduction
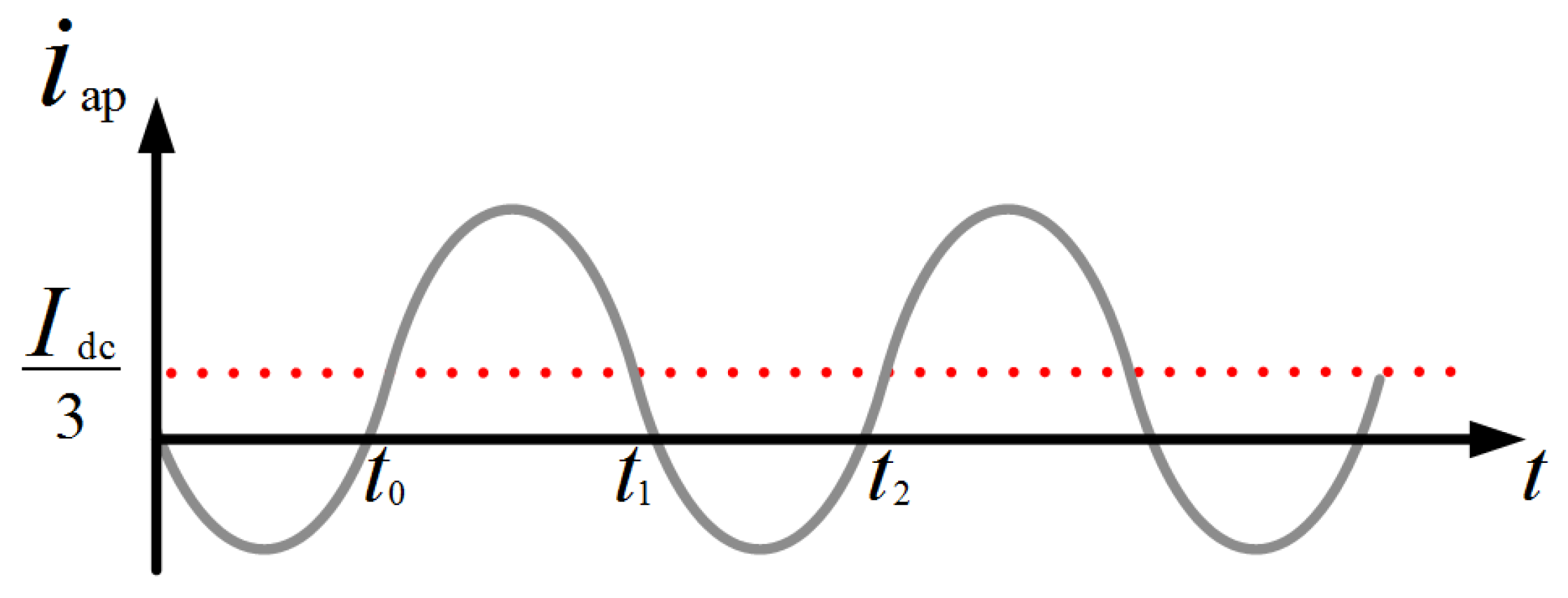
2. Principle of Uneven Loss Distribution Inside the SMs of MMC
3. Theoretical Analysis of Heat Transfer and Mechanical Structural Design
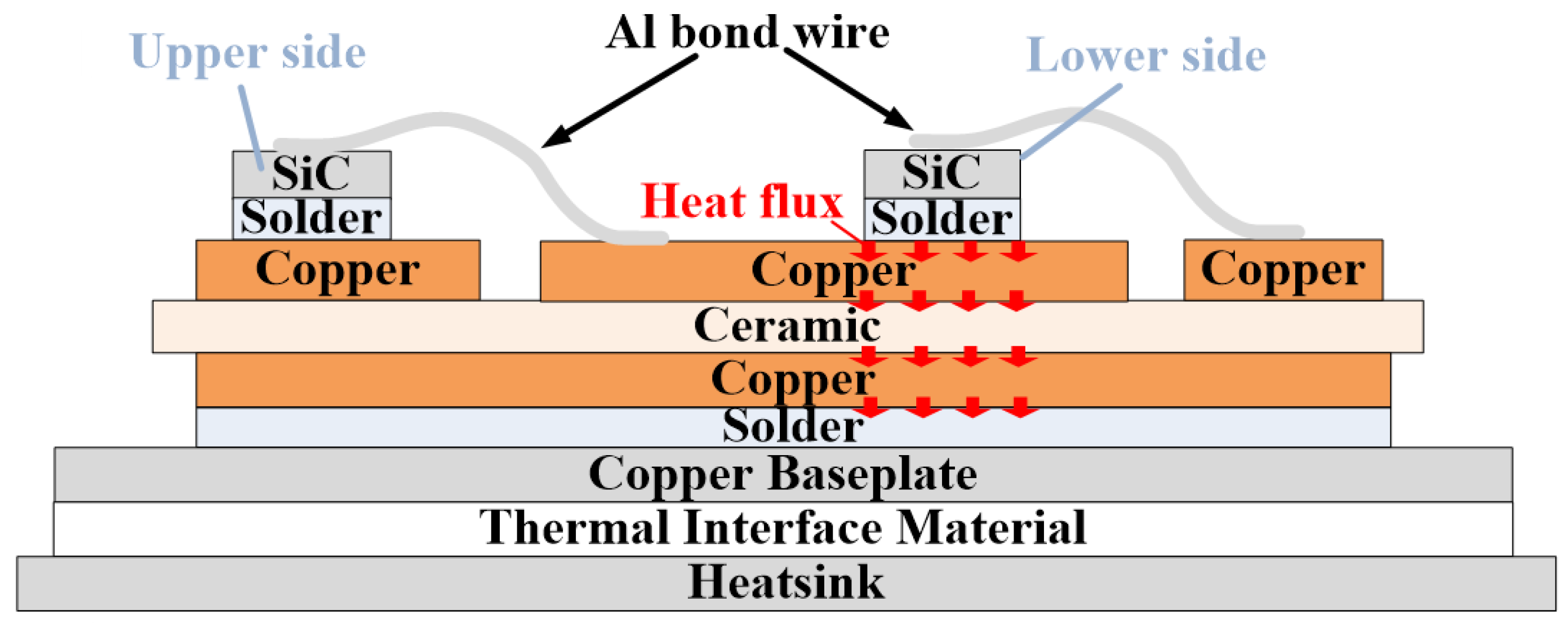
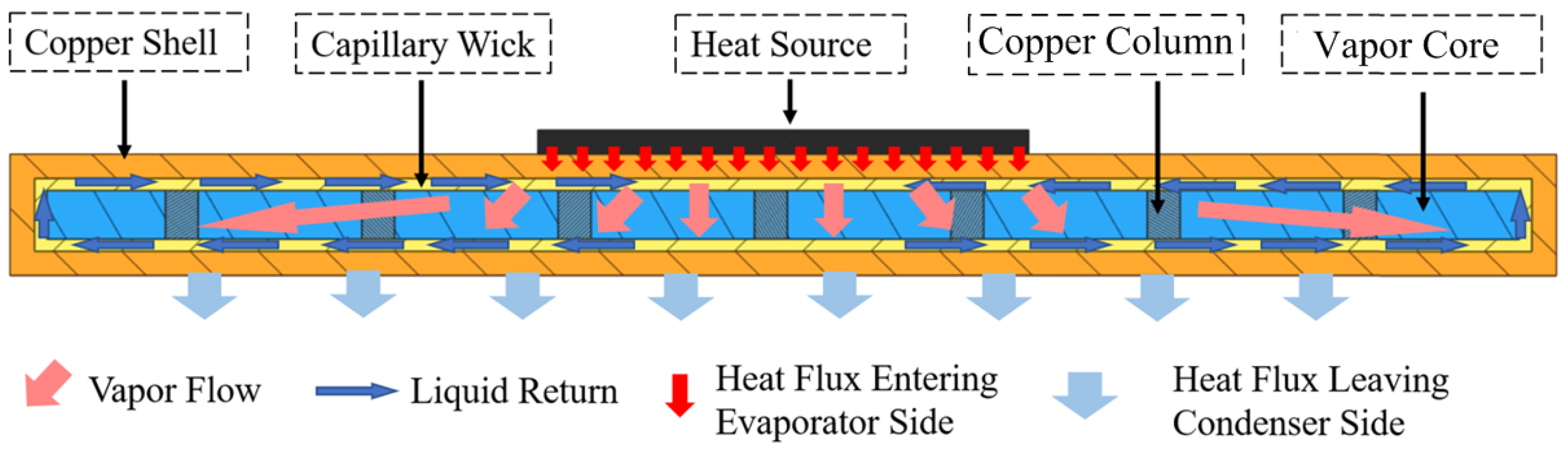
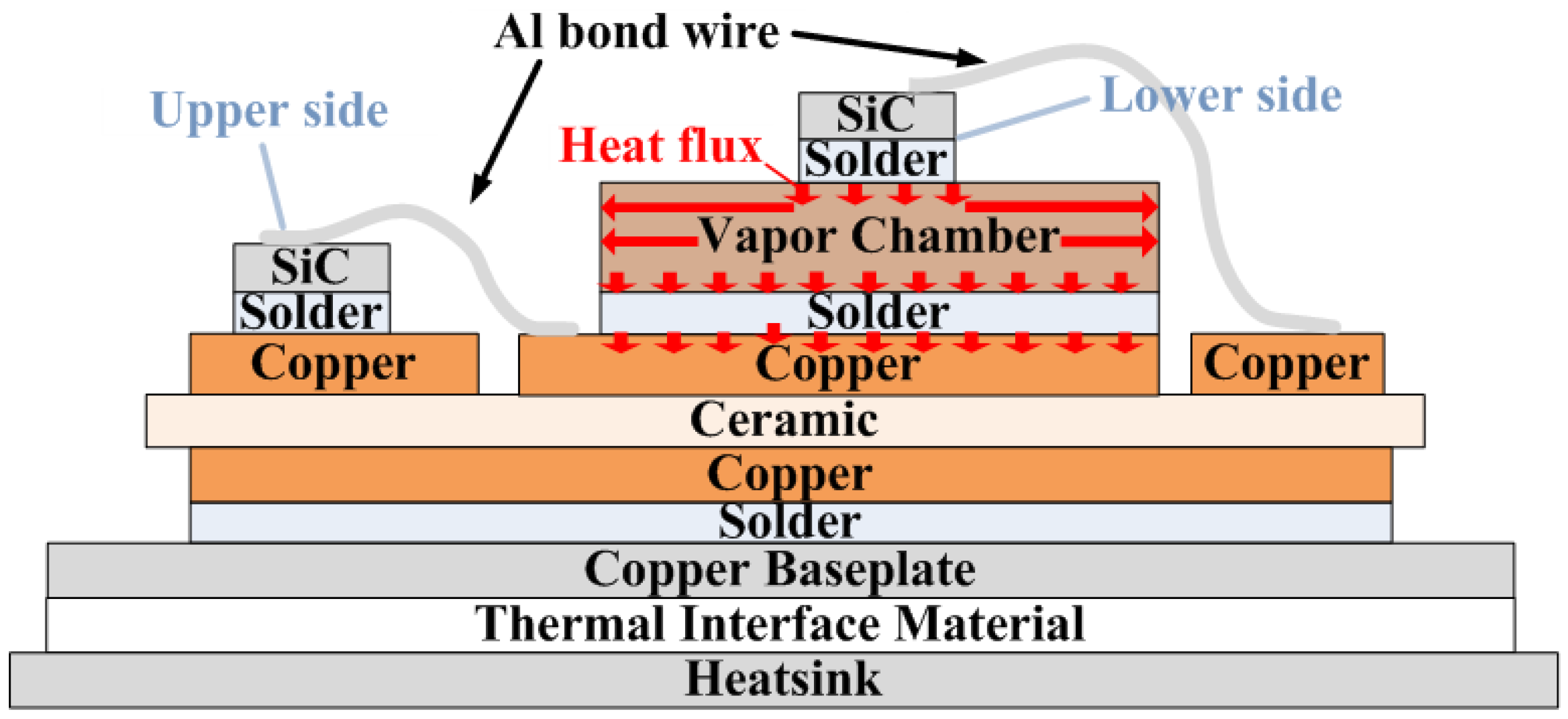
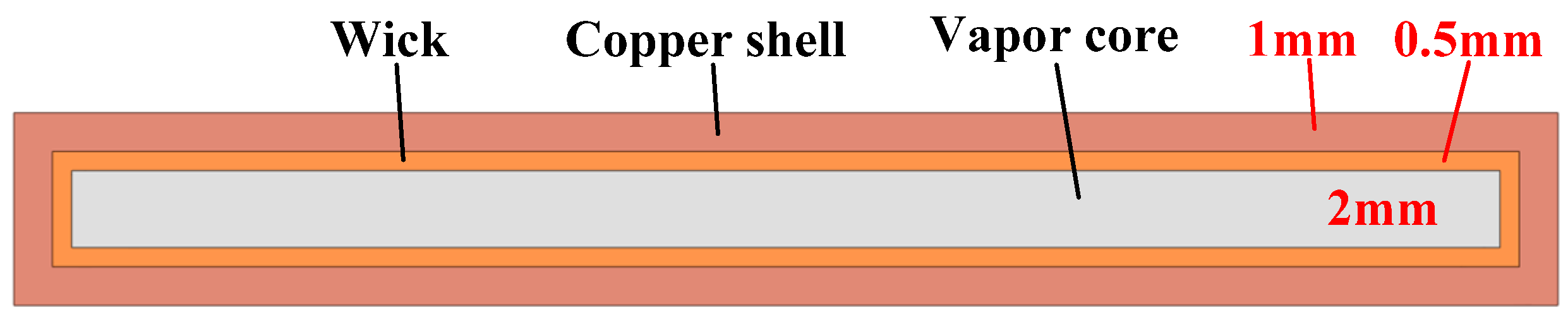
3.1. Theoretical Analysis of Heat Transfer
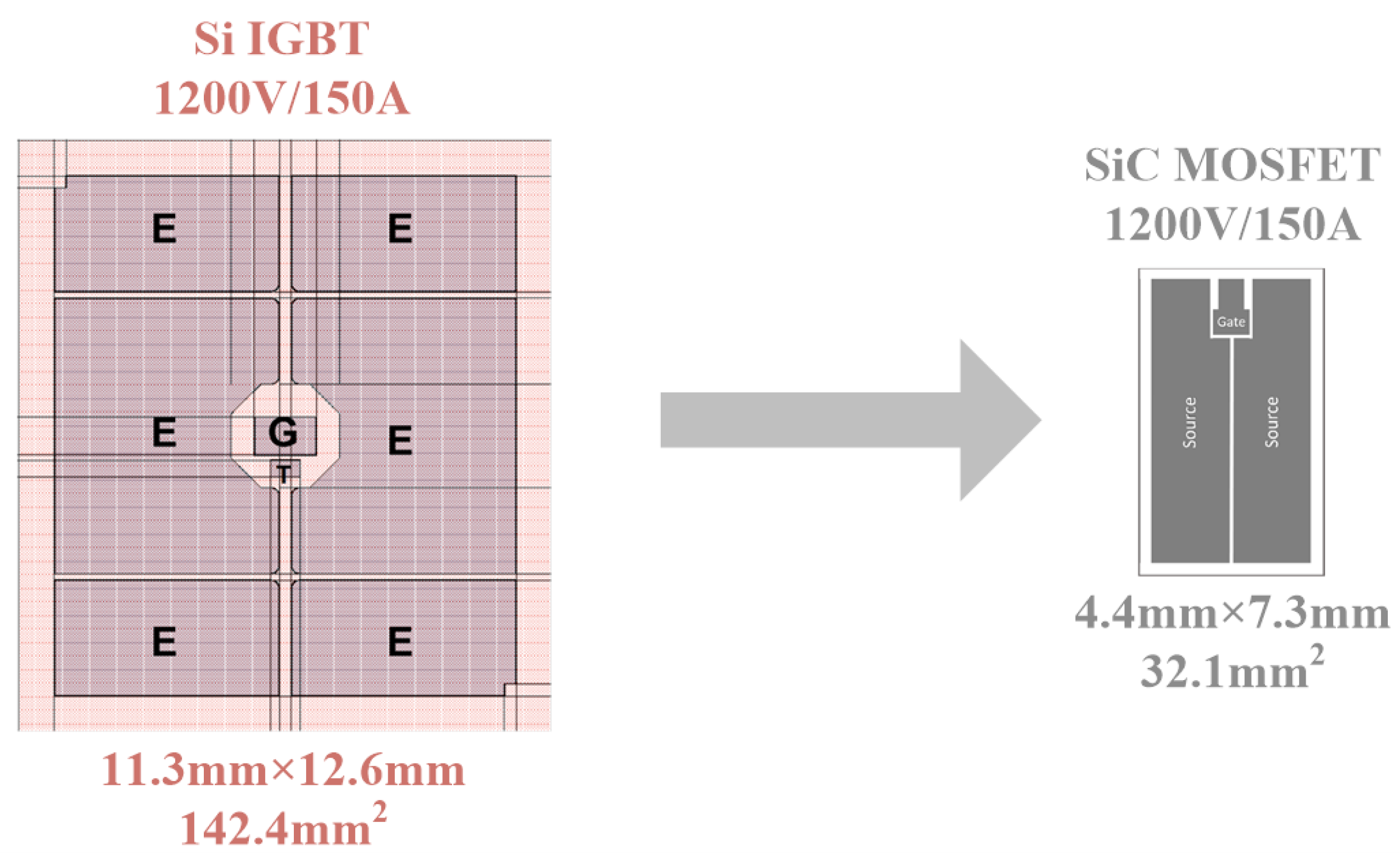
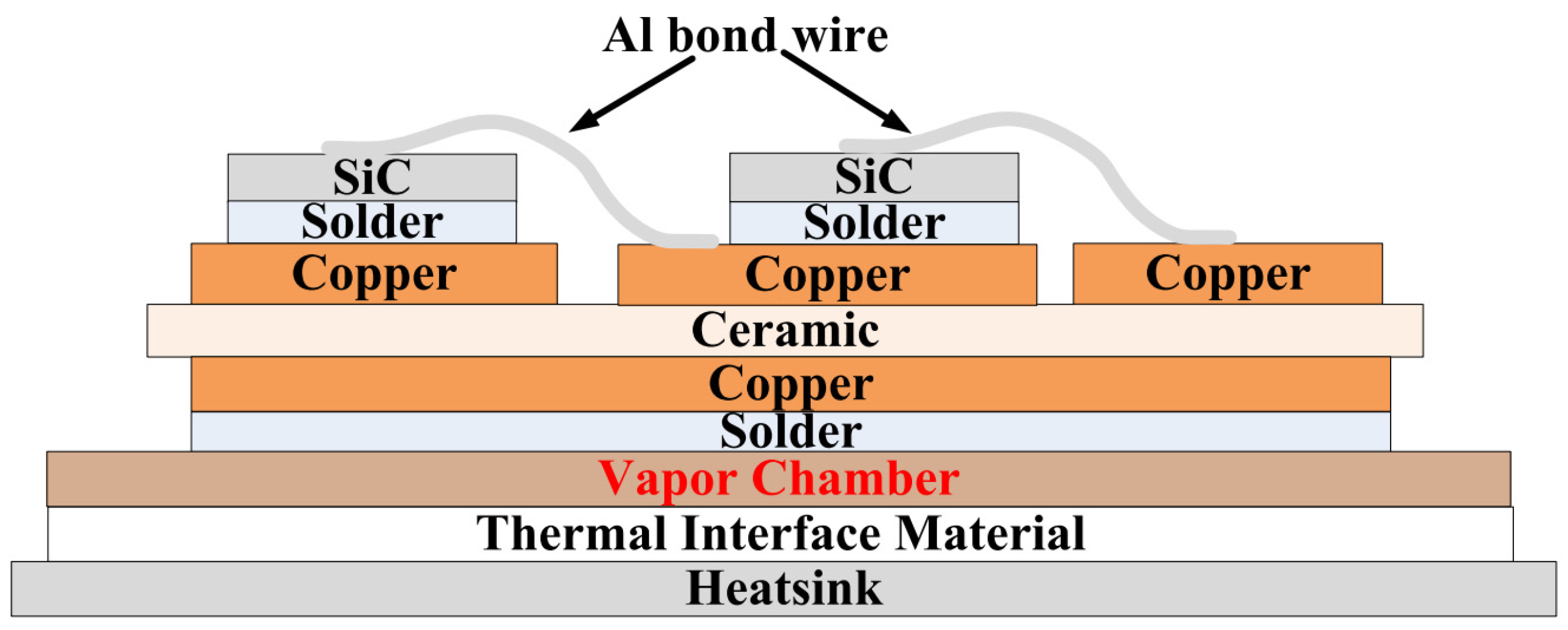
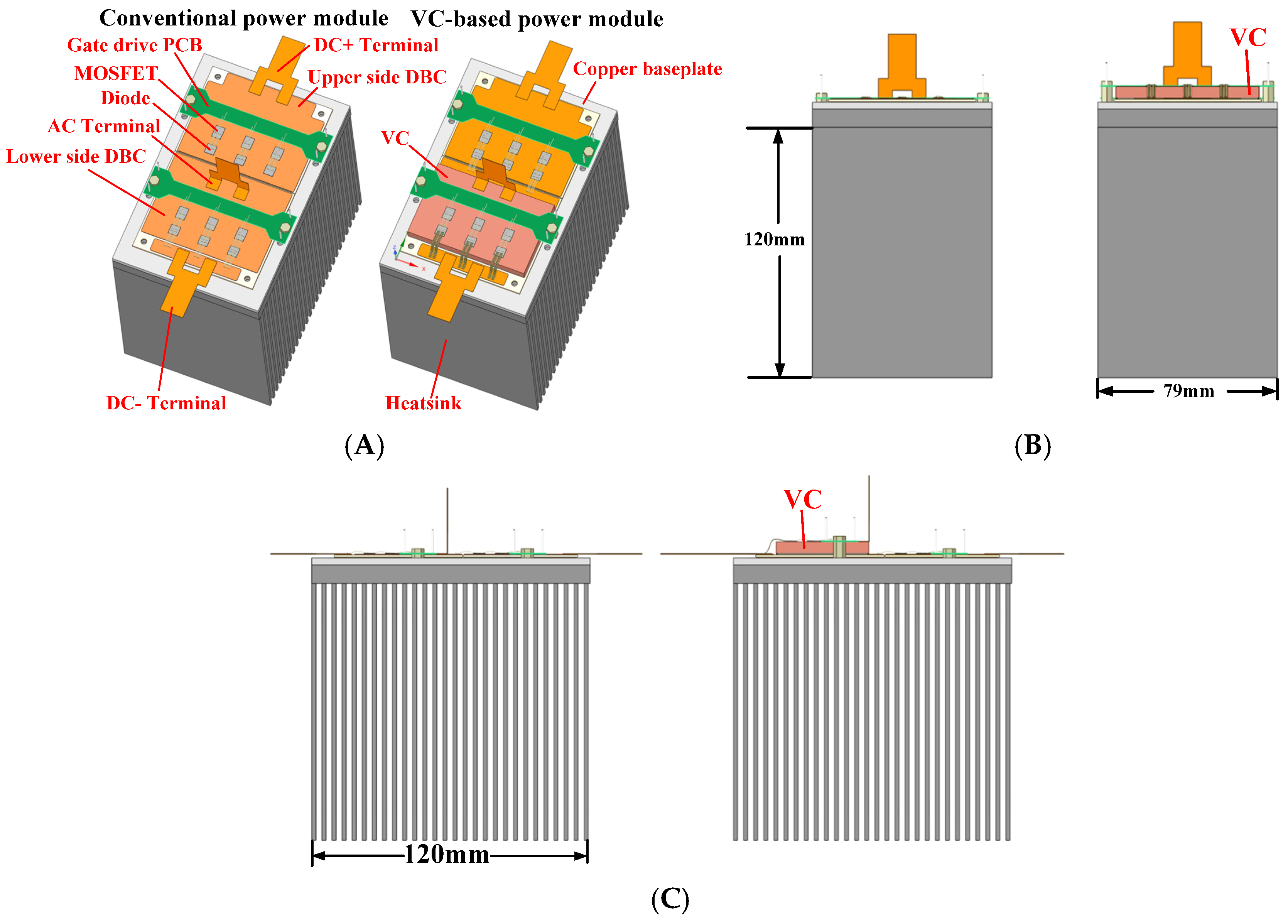
3.2. Mechanical Structural Design of the SiC Power Module
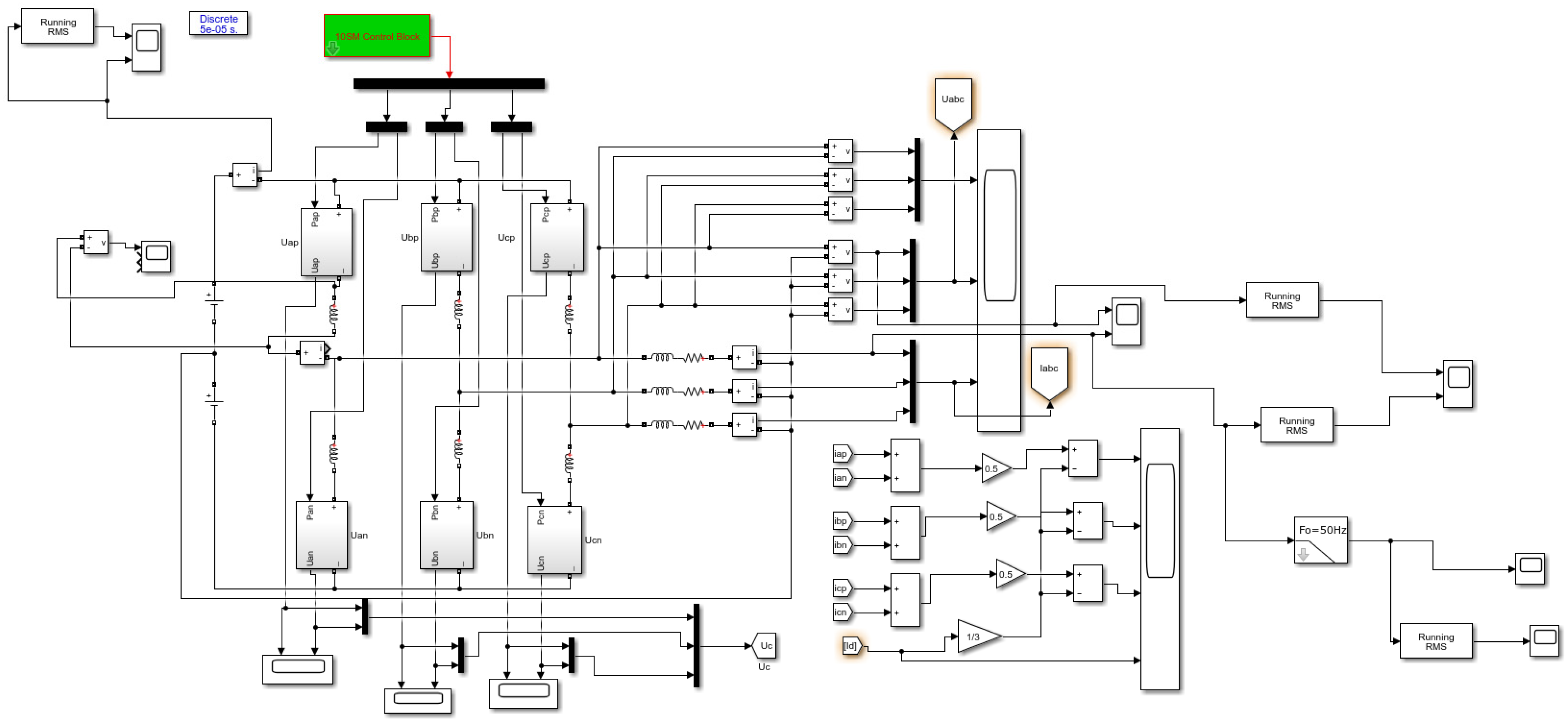
4. Thermal Simulation and Lifetime Analysis
4.1. Three-Dimensional Model of the Power Module
4.2. Mission Profiles of MMC System and Power Devices
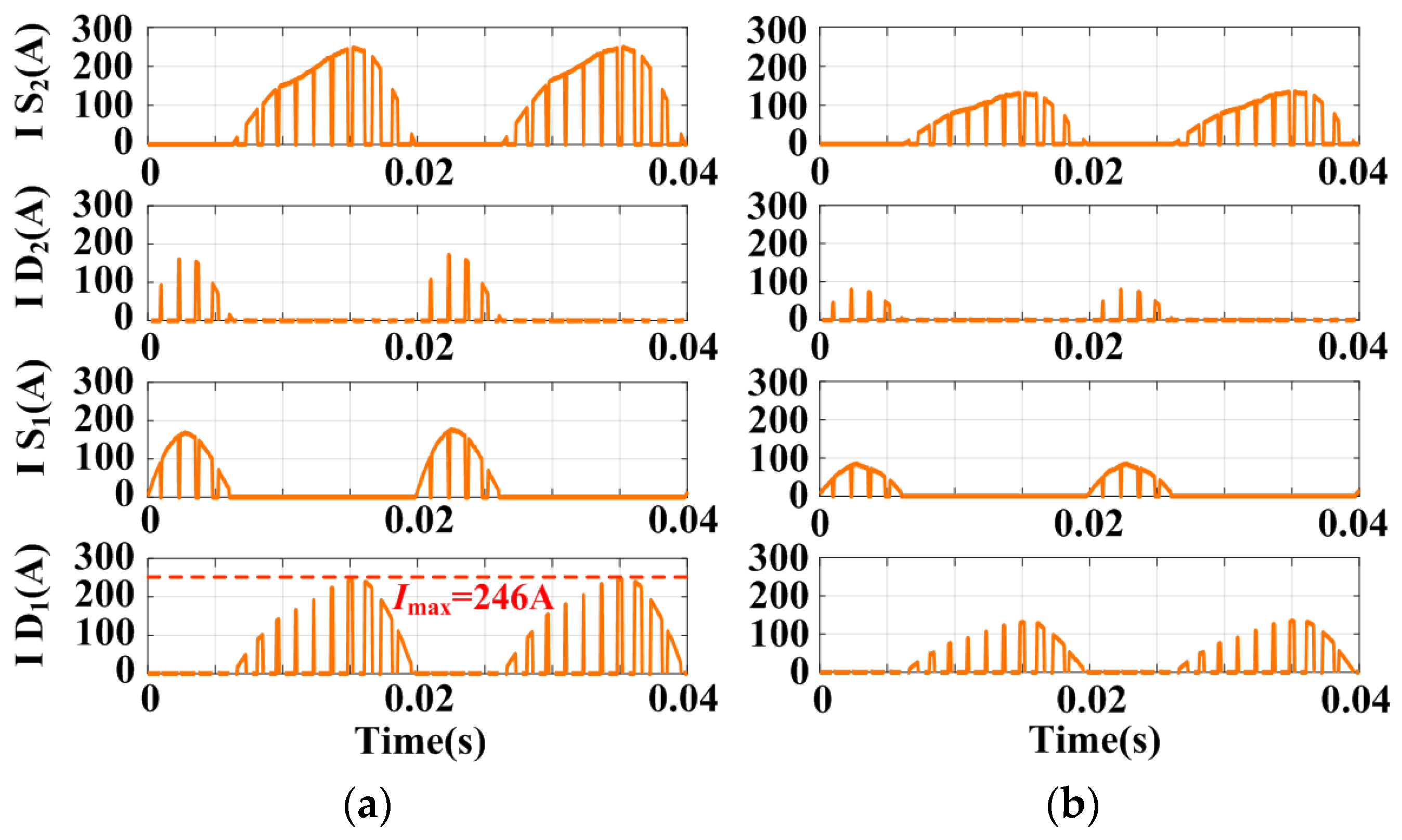
4.3. Heat Sources Calculation
- (1)
- The power module exhibits high symmetry in terms of terminal shape/position and chip layout.
- (2)
- Reference [46] points out that the positive temperature coefficient of the on-resistance (Ron) of SiC MOSFETs balances the static current across parallel devices.
- (3)
- Unbalanced dynamic current distribution is more likely to occur in high-switching-frequency applications [46]. However, MMCs operate at relatively low switching frequencies.
- (4)
- This study focuses on the temperature uniformity of the four devices in the HB module, rather than that of the parallel dies.
- (5)
- The paralleled chips are from the same production batch.
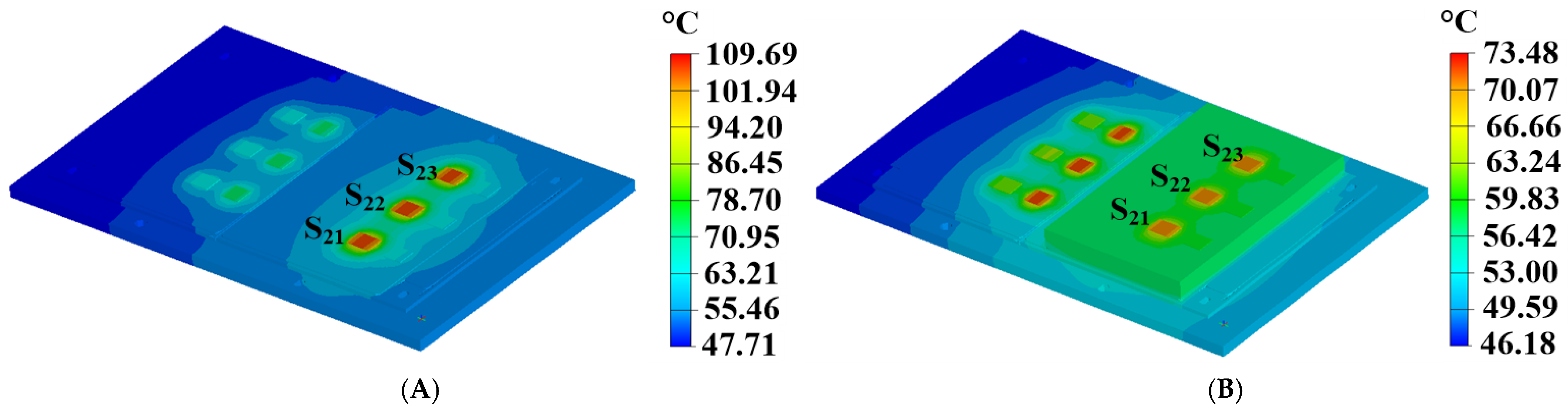
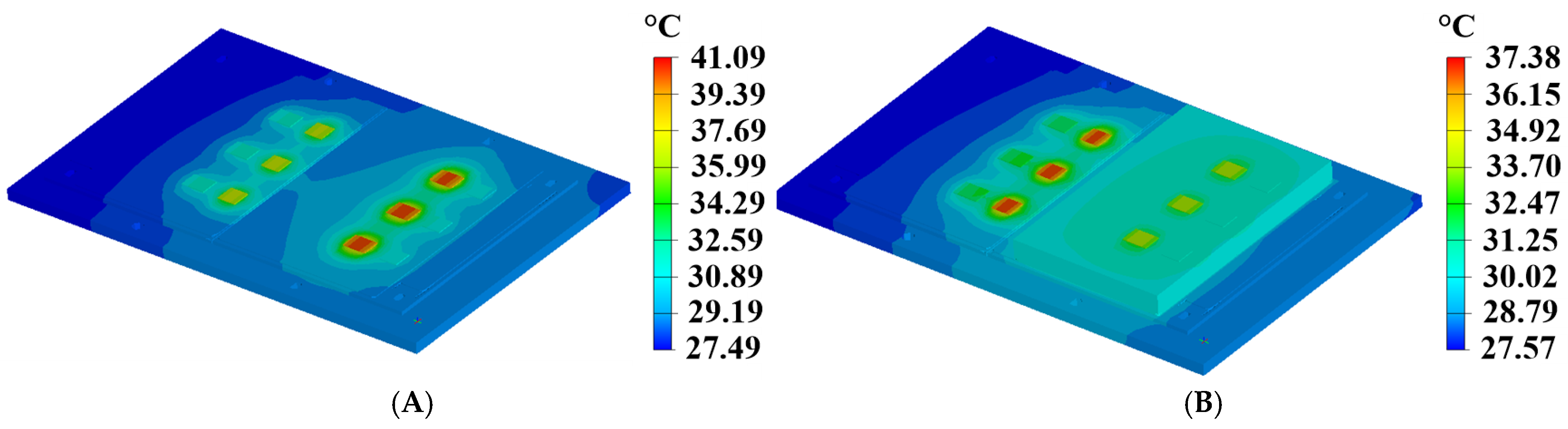
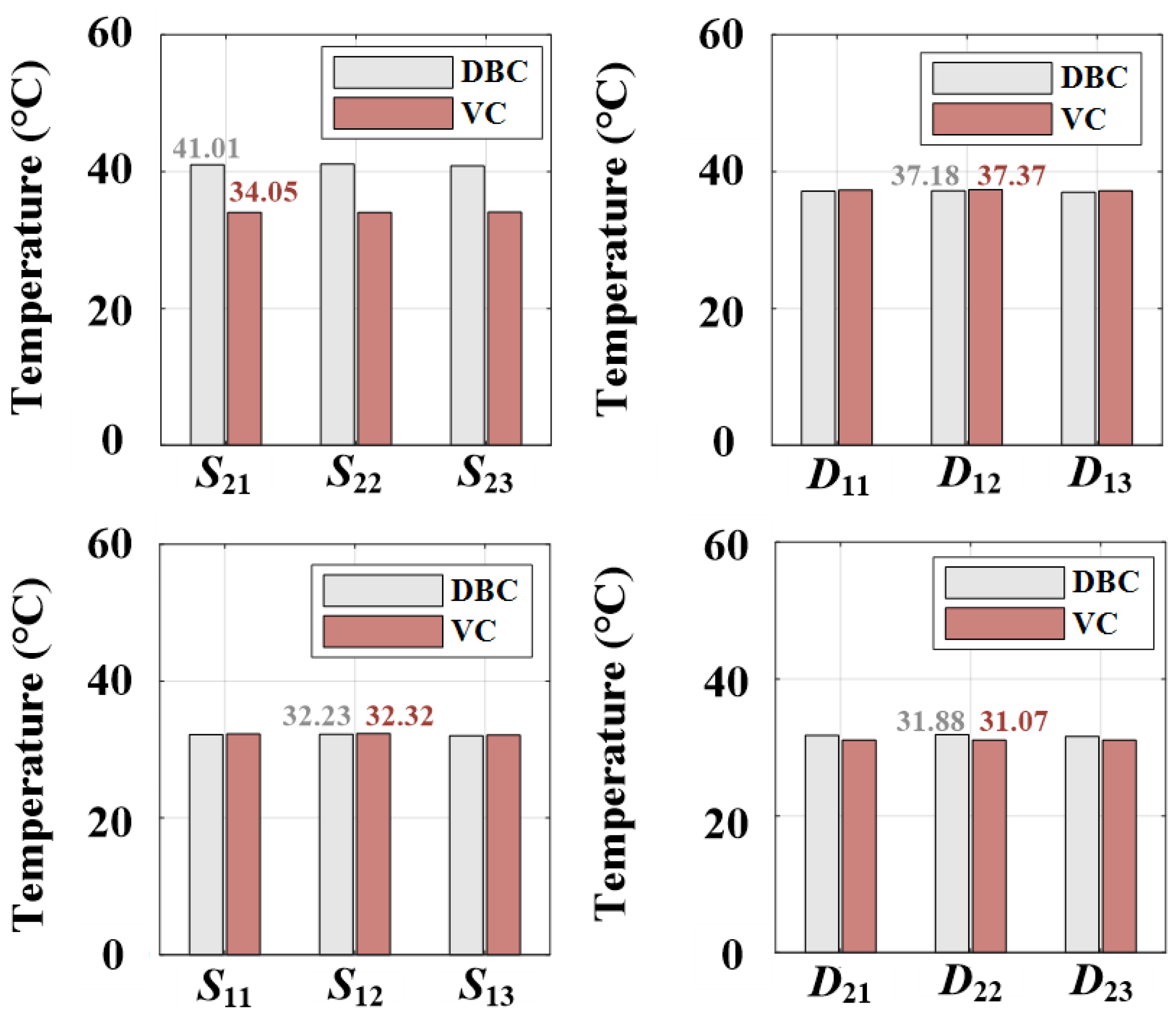
4.4. FEM Simulation
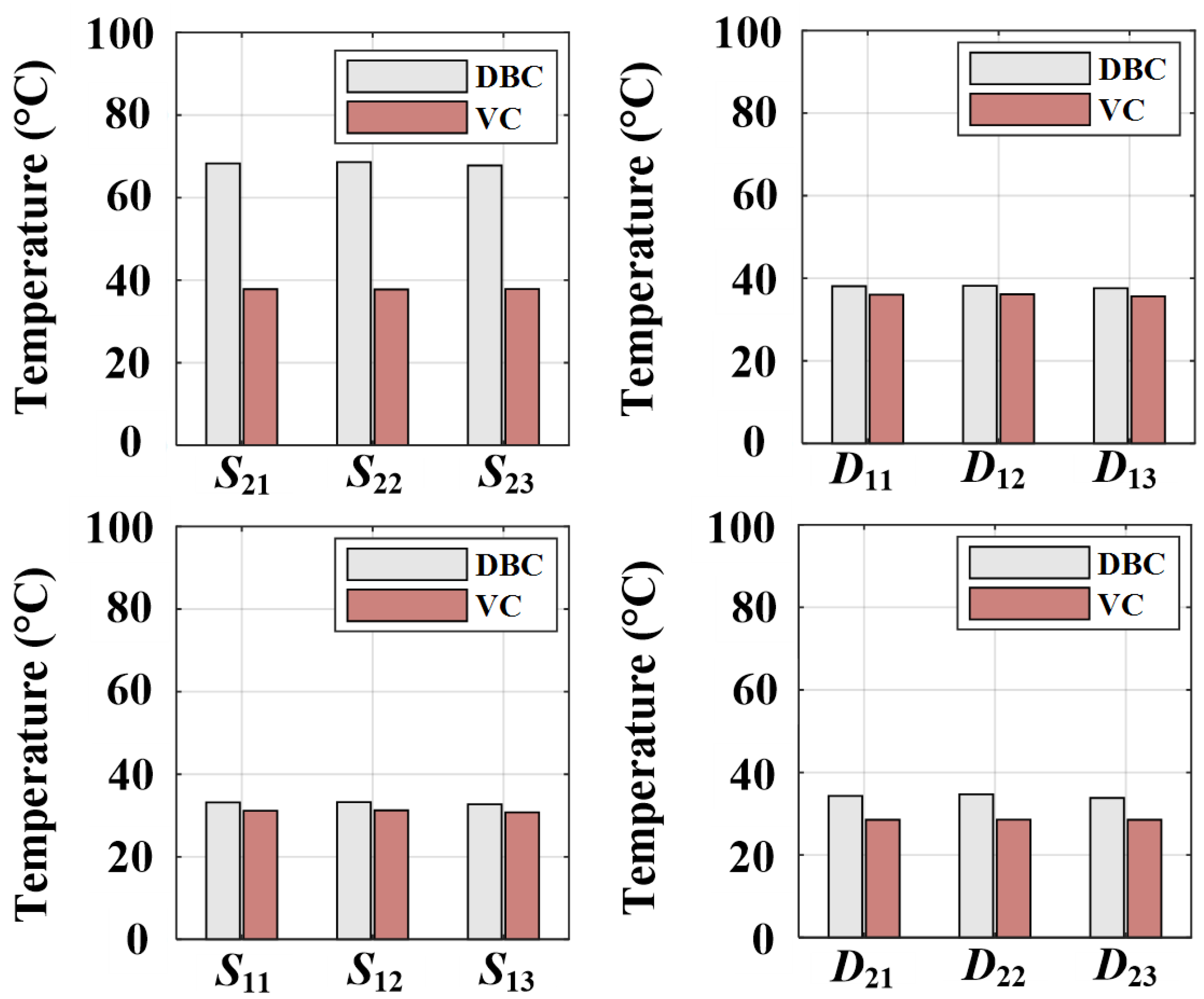
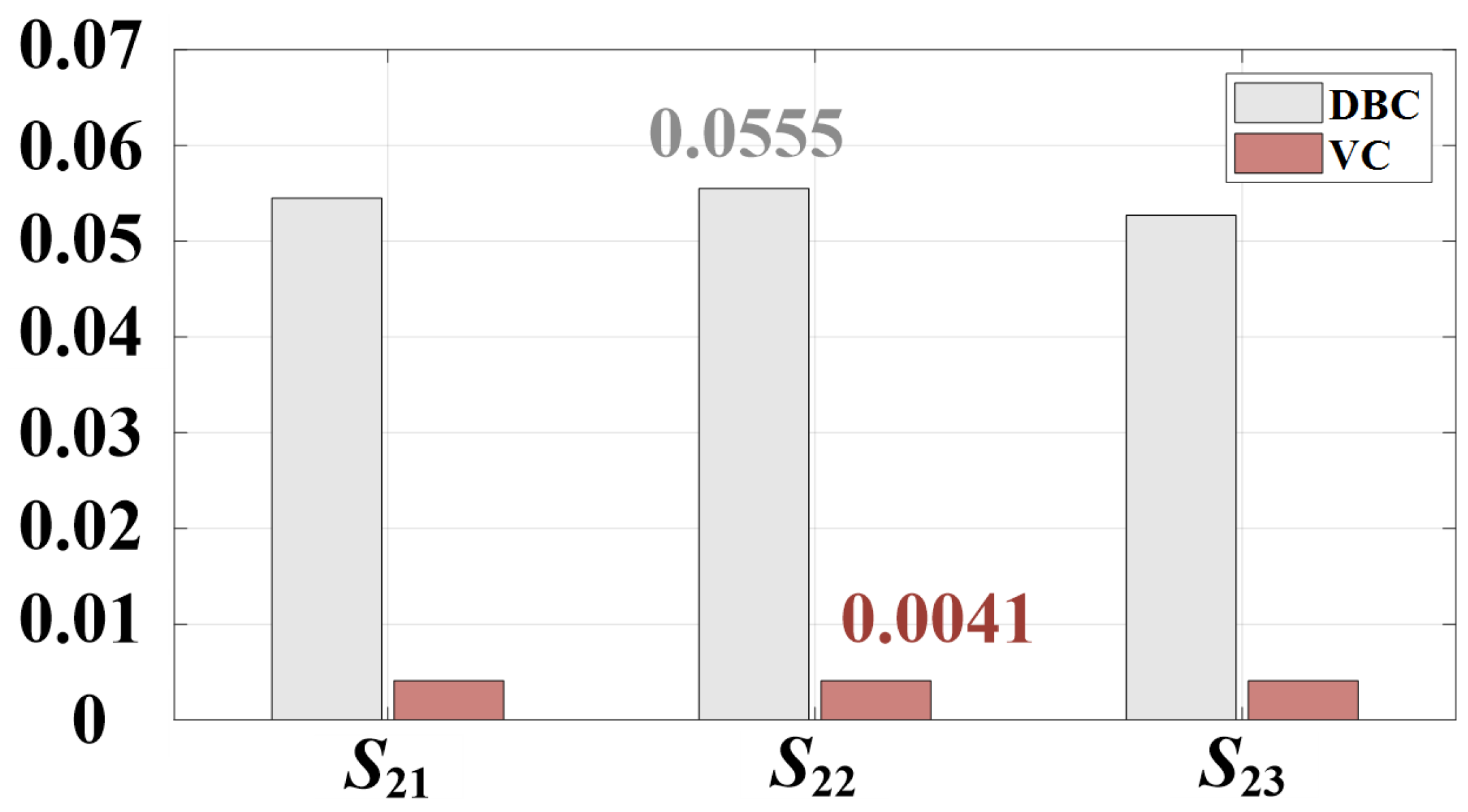
4.5. Lifetime Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Alyami, H.; Mohamed, Y. Review and development of MMC employed in VSC-HVDC systems. In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–6. [Google Scholar]
- Song, S.; Liu, J.; Ouyang, S.; Chen, X. An improved high-frequency common-mode voltage injection method in modular multilevel converter in motor drive application. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 2496–2500. [Google Scholar]
- Farias, J.V.M.; Cupertino, A.F.; Ferreira, V.D.N.; Pereira, H.A.; Seleme, S.I.; Teodorescu, R. Reliability-Oriented Design of Modular Multilevel Converters for Medium-Voltage STATCOM. IEEE Trans. Ind. Electron. 2020, 67, 6206–6214. [Google Scholar] [CrossRef]
- Wu, L.; Qin, J.; Saeedifard, M.; Wasynczuk, O.; Shenai, K. Efficiency Evaluation of the Modular Multilevel Converter Based on Si and SiC Switching Devices for Medium/High-Voltage Applications. IEEE Trans. Electron Devices 2015, 62, 286–293. [Google Scholar] [CrossRef]
- Xu, C.; He, J.; Lin, L. Research on Capacitor-Switching Semi-Full-Bridge Submodule of Modular Multilevel Converter Using Si-IGBT and SiC-MOSFET. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 4814–4825. [Google Scholar] [CrossRef]
- Chen, C.; Huang, Z.; Chen, L.; Tan, Y.; Kang, Y.; Luo, F. Flexible PCB-Based 3-D Integrated SiC Half-Bridge Power Module with Three-Sided Cooling Using Ultralow Inductive Hybrid Packaging Structure. IEEE Trans. Power Electron. 2019, 34, 5579–5593. [Google Scholar] [CrossRef]
- Yin, T.; Lin, L.; Xu, C.; Zhu, D.; Jing, K. A Hybrid Modular Multilevel Converter Comprising SiC MOSFET and Si IGBT with Its Specialized Modulation and Voltage Balancing Scheme. IEEE Trans. Ind. Electron. 2022, 69, 11272–11282. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, L.; Huang, X.; Palmer, J.; Wang, F.; Tolbert, L.M. A Novel Voltage Balancing Control With dv/dt Reduction for 10-kV SiC MOSFET-Based Medium Voltage Modular Multilevel Converter. IEEE Trans. Power Electron. 2020, 35, 12533–12543. [Google Scholar] [CrossRef]
- Pan, J.; Ke, Z.; Al Sabbagh, M.; Li, H.; Potty, K.A.; Perdikakis, W.; Na, R.; Zhang, J.; Wang, J.; Xu, L. 7-kV 1-MVA SiC-Based Modular Multilevel Converter Prototype for Medium-Voltage Electric Machine Drives. IEEE Trans. Power Electron. 2020, 35, 10137–10149. [Google Scholar] [CrossRef]
- Yin, T.; Xu, C.; Lin, L.; Jing, K. A SiC MOSFET and Si IGBT Hybrid Modular Multilevel Converter with Specialized Modulation Scheme. IEEE Trans. Power Electron. 2020, 35, 12623–12628. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Mu, W.; Qin, M.; Yang, F.; Liu, J.; Tomoyuki, Y.; Tatsuhiko, F. Thermal Performances and Annual Damages Comparison of MMC Using Reverse Conducting IGBT and Conventional IGBT Module. IEEE Trans. Power Electron. 2021, 36, 9806–9825. [Google Scholar] [CrossRef]
- Mu, W.; Wang, L.; Wang, B.; Zhang, T.; Yang, F.; Gan, Y.; Zhang, H. Direct Integration of Optimized Phase-change Heat Spreaders into SiC Power Module for Thermal Performance Improvements Under High Heat Flux. IEEE Trans. Power Electron. 2021, 37, 5398–5410. [Google Scholar] [CrossRef]
- Aranzabal, I.; de Alegría, I.M.; Delmonte, N.; Cova, P.; Kortabarria, I. Comparison of the Heat Transfer Capabilities of Conventional Single- and Two-Phase Cooling Systems for an Electric Vehicle IGBT Power Module. IEEE Trans. Power Electron. 2019, 34, 4185–4194. [Google Scholar] [CrossRef]
- Hu, B.; Gonzalez, J.O.; Ran, L.; Ren, H.; Zeng, Z.; Lai, W.; Gao, B.; Alatise, O.; Lu, H.; Bailey, C.; et al. Failure and Reliability Analysis of a SiC Power Module Based on Stress Comparison to a Si Device. IEEE Trans. Device Mater. Reliab. 2017, 17, 727–737. [Google Scholar] [CrossRef]
- Liu, H.; Ma, K.; Qin, Z.; Loh, P.C.; Blaabjerg, F. Lifetime Estimation of MMC for Offshore Wind Power HVDC Application. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 504–511. [Google Scholar] [CrossRef]
- Wang, L.; Xu, J.; Wang, G.; Zhang, Z. Lifetime estimation of IGBT modules for MMC-HVDC application. Microelectron. Reliab. 2018, 82, 90–99. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Ma, D.; Wang, L.; Yang, F.; Li, X.; Tan, Y. A Lifetime Estimation Method of MMC Submodules based on the Combination of FEA and Physical Lifetime Model. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 1–5 June 2019; pp. 1–6. [Google Scholar]
- Farias, J.V.M.; Cupertino, A.F.; Ferreira, V.N.; Seleme, S.I.; Pereira, H.A.; Teodorescu, R. Design and lifetime analysis of a DSCC-MMC STATCOM. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Júnior, P.R.M.; Cupertino, A.F.; Mendonça, G.A.; Pereira, H.A. On lifetime evaluation of medium-voltage drives based on modular multilevel converter. IET Electr. Power Appl. 2019, 13, 1453–1461. [Google Scholar] [CrossRef]
- Ye, Y.; Lutz, J.; Zeng, G.; Alvarez, R.; Correa, P. Thermal Calculation Methodology for Lifetime Estimation of Semiconductor Devices in MMC Application. In Proceedings of the PCIM Europe 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 16–18 May 2017; pp. 1–6. [Google Scholar]
- Zhang, Y.; Wang, H.; Wang, Z.; Yang, Y.; Blaabjerg, F. The impact of mission profile models on the predicted lifetime of IGBT modules in the modular multilevel converter. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7980–7985. [Google Scholar]
- Zhang, Y.; Wang, H.; Wang, Z.; Yang, Y.; Blaabjerg, F. Impact of lifetime model selections on the reliability prediction of IGBT modules in modular multilevel converters. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4202–4207. [Google Scholar]
- Zhang, Y.; Wang, H.; Wang, Z.; Blaabjerg, F.; Saeedifard, M. Mission Profile-Based System-Level Reliability Prediction Method for Modular Multilevel Converters. IEEE Trans. Power Electron. 2020, 35, 6916–6930. [Google Scholar] [CrossRef]
- Khanzadeh, B.; Tang, C.; Thiringer, T. A Study on the Lifetime of Q2L-MMC-DAB’s Switches for Wind Turbine Applications. In Proceedings of the 2020 Fifteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 September 2020; pp. 1–6. [Google Scholar]
- Fu, W.; Wang, L. Reliability Evaluation for the Press-pack Submodule in MMC-HVDC Application. In Proceedings of the 2020 4th International Conference on HVDC (HVDC), Xi’an, China, 6–9 November 2020; pp. 362–368. [Google Scholar]
- Guo, W.; Liu, Z.; Ma, D.; Wang, L. The Reliability of Press-pack IGBT in MMC Based on Electro-Thermo-Mechanical Simulation. In Proceedings of the 2020 17th China International Forum on Solid State Lighting & 2020 International Forum on Wide Bandgap Semiconductors China (SSLChina: IFWS), Shenzhen, China, 23–25 November 2020; pp. 266–270. [Google Scholar]
- Sheng, J.; Yang, H.; Li, C.; Chen, M.; Li, W.; He, X.; Gu, X. Active Thermal Control for Hybrid Modular Multilevel Converter Under Overmodulation Operation. IEEE Trans. Power Electron. 2020, 35, 4242–4255. [Google Scholar] [CrossRef]
- Yang, Q.; Saeedifard, M. Active thermal loading control of the modular multilevel converter by a multi-objective optimization method. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 4482–4487. [Google Scholar]
- Qiu, H.; Wang, J.; Tu, P.; Tang, Y. Device-Level Loss Balancing Control for Modular Multilevel Converters. IEEE Trans. Power Electron. 2020, 36, 4778–4790. [Google Scholar] [CrossRef]
- Merlin, M.M.C.; Mitcheson, P.D. Active power losses distribution methods for the modular multilevel converter. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–6. [Google Scholar]
- Yin, T.; Lin, L.; Xu, C. Adaptive Thermal Control for MOSFET-Based Modular Multilevel Converter. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. P.1–P.7. [Google Scholar]
- Bakhshizadeh, M.K.; Ma, K.; Loh, P.C.; Blaabjerg, F. Indirect thermal control for improved reliability of Modular Multilevel Converter by utilizing circulating current. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 2167–2173. [Google Scholar]
- Zhao, J.; Deng, F.; Hu, W.; Du, Y.; Abulanwar, S. Thermal Optimization Strategy Based on Second-Order Harmonic Circulating Current Injection for MMCs. IEEE Access 2021, 9, 80183–80196. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, F.; Liu, C.; Yu, Q.; Wang, Q.; Zhang, J. Harmonic circulating current injection based power losses optimization control of bottom switch/diode for modular multilevel converters. CSEE J. Power Energy Syst. 2021, 7, 1213–1226. [Google Scholar] [CrossRef]
- van der Broeck, C.H.; Ruppert, L.A.; Lorenz, R.D.; De Doncker, R.W. Methodology for active thermal cycle reduction of power electronic modules. IEEE Trans. Power Electron. 2019, 34, 8213–8229. [Google Scholar] [CrossRef]
- Zhang, J.; Du, X.; Zeng, C.; Sun, P.; Tai, H. A lifetime extension strategy for power devices in the wind power converters based on the distribution characteristics of consumed lifetime. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 761–766. [Google Scholar]
- Yerasimou, Y.; Pickert, V.; Ji, B.; Song, X. Liquid Metal Magnetohydrodynamic Pump for Junction Temperature Control of Power Modules. IEEE Trans. Power Electron. 2018, 33, 10583–10593. [Google Scholar] [CrossRef]
- Wang, X.; Castellazzi, A.; Zanchetta, P. Observer based dynamic adaptive cooling system for power modules. Microelectron. Reliab. 2016, 58, 113–118. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Castellazzi, A. Reduced active and passive thermal cycling degradation by dynamic active cooling of power modules. In Proceedings of the 2015 IEEE 27th International Symposium on Power Semiconductor Devices & IC’s (ISPSD), Hong Kong, China, 10–14 May 2015; pp. 309–312. [Google Scholar]
- Castellazzi, A.; Onifade, M.; Wang, X.; Zanchetta, P. State-space modeling of power assemblies for advanced thermal management solutions. In Proceedings of the 2012 IEEE 13th Workshop on Control and Modeling for Power Electronics (COMPEL), Kyoto, Japan, 10–13 June 2012; pp. 1–8. [Google Scholar]
- Wang, B.; Wang, L.; Yang, F.; Mu, W.; Qin, M.; Zhang, F.; Ma, D.; Wang, J.; Liu, J. Air-Cooling System Optimization for IGBT Modules in MMC Using Embedded O-Shaped Heat Pipes. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3992–4003. [Google Scholar] [CrossRef]
- Chen, Y.; Li, B.; Wang, X.; Wang, X.; Yan, Y.; Li, X.; Wang, Y.; Qi, F.; Li, H. Direct Phase-Change Cooling of Vapor Chamber Integrated With IGBT Power Electronic Module for Automotive Application. IEEE Trans. Power Electron. 2021, 36, 5736–5747. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Wu, S.; Hou, Z.; Mu, W.; Yang, F.; Liu, J.; Gan, Y. An Evaluation on Thermal Performance Improvements for SiC Power Module Integrated with Vapor Chamber in MMC. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 5214–5225. [Google Scholar] [CrossRef]
- Zhang, C.; Ge, X.; Lin, C.; Luo, D.; Wang, H.; Xiao, X. Optimization and Analysis of Thermal Conductivity Structure for IGBT Module Embedded with the Vapor Chamber. IEEE Trans. Compon. Packag. Manuf. Technol. 2023, 13, 798–807. [Google Scholar] [CrossRef]
- Avenas, Y.; Gillot, C.; Bricard, A.; Schaeffer, C. On the use of flat heat pipes as thermal spreaders in power electronics cooling. In Proceedings of the 2002 IEEE 33rd Annual IEEE Power Electronics Specialists Conference. Proceedings (Cat. No.02CH37289), Cairns, QLD, Australia, 23–27 June 2002; Volume 2, pp. 753–757. [Google Scholar]
- Zhao, C.; Wang, L.; Zhang, F.; Yang, F. A Method to Balance Dynamic Current of Paralleled SiC MOSFETs With Kelvin Connection Based on Response Surface Model and Nonlinear Optimization. IEEE Trans. Power Electron. 2021, 36, 2068–2079. [Google Scholar] [CrossRef]
- Yang, X.; Lin, Z.; Ding, J.; Long, Z. Lifetime Prediction of IGBT Modules in Suspension Choppers of Medium/Low-Speed Maglev Train Using an Energy-Based Approach. IEEE Trans. Power Electron. 2019, 34, 738–747. [Google Scholar] [CrossRef]
- Reigosa, P.D.; Wang, H.; Yang, Y.; Blaabjerg, F. Prediction of Bond Wire Fatigue of IGBTs in a PV Inverter Under a Long-Term Operation. IEEE Trans. Power Electron. 2016, 31, 7171–7182. [Google Scholar]
- Ma, K.; Liserre, M.; Blaabjerg, F.; Kerekes, T. Thermal Loading and Lifetime Estimation for Power Device Considering Mission Profiles in Wind Power Converter. IEEE Trans. Power Electron. 2015, 30, 590–602. [Google Scholar] [CrossRef]
- Ciappa, M. Selected failure mechanisms of modern power modules. Microelectron. Reliab. 2002, 42, 653–667. [Google Scholar] [CrossRef]
- Hanif, A.; Yu, Y.; DeVoto, D.; Khan, F. A Comprehensive Review Toward the State-of-the-Art in Failure and Lifetime Predictions of Power Electronic Devices. IEEE Trans. Power Electron. 2019, 34, 4729–4746. [Google Scholar] [CrossRef]
- Huang, H.; Mawby, P.A. A Lifetime Estimation Technique for Voltage Source Inverters. IEEE Trans. Power Electron. 2013, 28, 4113–4119. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, 159–164. [Google Scholar] [CrossRef]
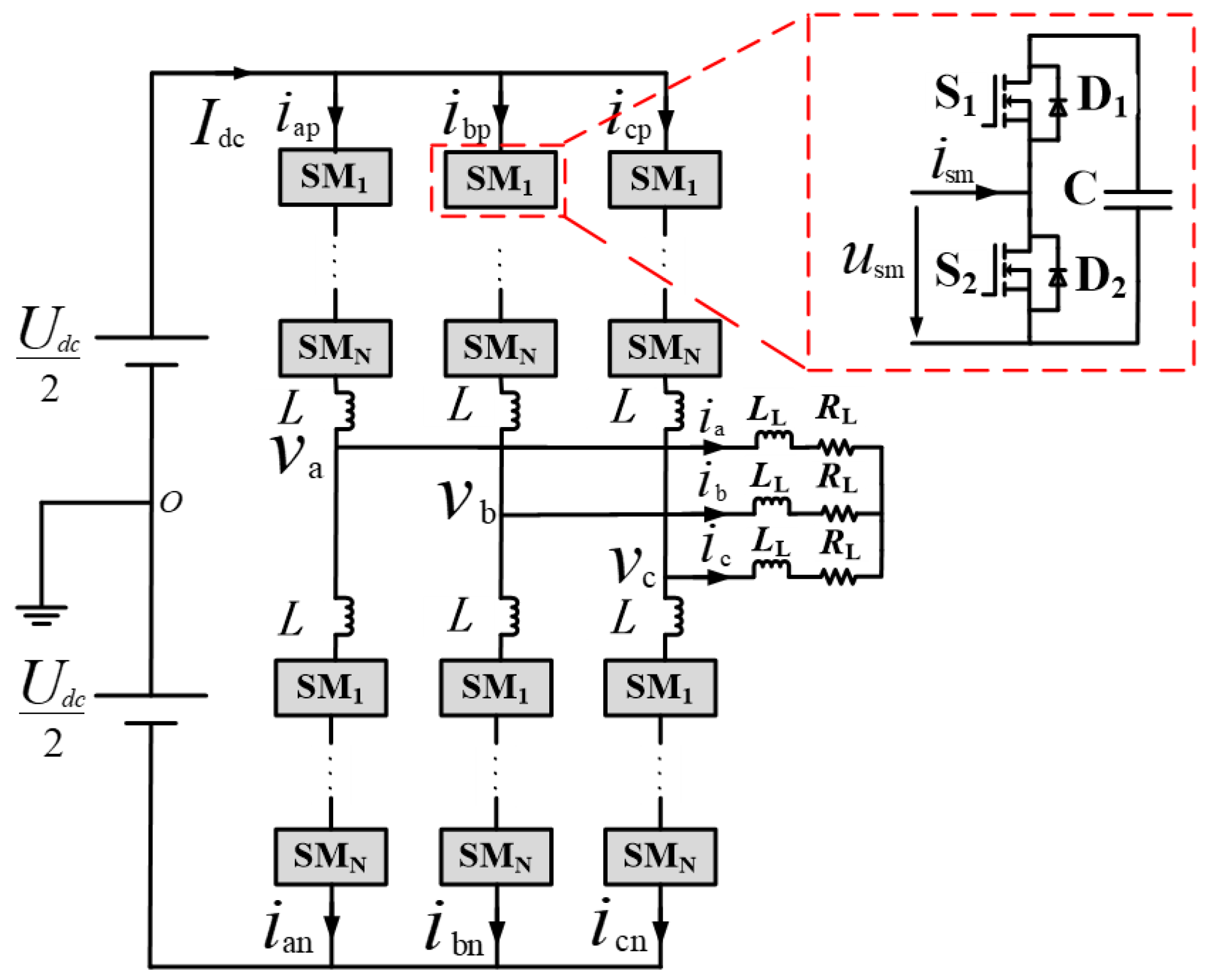






| Modes | S1 | S2 | ism | usm |
|---|---|---|---|---|
| A | 0 | 1 | ism > 0 | 0 |
| B | 0 | 0 | ism > 0 | uc |
| C | 0 | 0 | ism < 0 | 0 |
| D | 1 | 0 | ism < 0 | uc |
| Parameters | Value |
|---|---|
| VC size | 60 mm 40 mm 5 mm |
| Thickness of the copper shell | 1 mm |
| Thickness of the wick | 0.5 mm |
| Height of the vapor core | 2 mm |
| Working fluid | Water |
| Working fluid filling weight | 1.5 g |
| Vacuum degree | 9.31 Pa (9.19 10−5 atm) |
| Sheet | Materials | Thickness mm | Ther. Conduct W/m·K | Spec. Heat J/kg·K |
|---|---|---|---|---|
| MOSFET | SiC | 0.175 | 490 | 690 |
| Diode | SiC | 0.11 | 490 | 690 |
| Chip solder | Pb40Sn60 | 0.1 | 32.7 | 150 |
| Top copper | Copper | 0.3 | 400 | 385 |
| Ceramic | Al2O3 | 0.635 | 24 | 30 |
| Bottom Copper | Copper | 0.3 | 400 | 385 |
| DBC solder | Pb40Sn60 | 0.3 | 32.7 | 150 |
| Baseplate | Copper | 3 | 400 | 385 |
| TIM | Thermal grease | 0.1 | 5 | 1000 |
| Symbol | Meaning | Value |
|---|---|---|
| SN | System rated apparent power | 0.83 MVA |
| P | System active power | 0.75 MW |
| Udc | DC-link voltage | 3 kV |
| Um | Amplitude of ac side phase voltage | 1.35 kV |
| N | Number of SMs | 5 |
| L | Arm inductor | 5 mH |
| RL | Load resistor | 2.965 |
| LL | Load inductor | 4.58 mH |
| C | SM capacitor | 4.7 mF |
| fs | Switching frequency | 1 k Hz |
| f | Fundamental frequency | 50 Hz |
| m | Modulation index | 0.9 |
| Parameters | [V] | [Ω] | [1] | [1] |
|---|---|---|---|---|
| 0.9428 | 9 × 10−3 | −1.39 × 10−3 | 8.85 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Zhou, X.; Zhu, Y.; Qi, M.; Lin, H.; Yao, B.; Huang, S.; Wang, X.; Wu, Q.; Liu, W. An Asymmetric SiC Power Module Directly Integrated with Vapor Chamber for Thermal Balancing in MMC. Appl. Sci. 2025, 15, 10869. https://doi.org/10.3390/app152010869
Wang B, Zhou X, Zhu Y, Qi M, Lin H, Yao B, Huang S, Wang X, Wu Q, Liu W. An Asymmetric SiC Power Module Directly Integrated with Vapor Chamber for Thermal Balancing in MMC. Applied Sciences. 2025; 15(20):10869. https://doi.org/10.3390/app152010869
Chicago/Turabian StyleWang, Binyu, Xiwei Zhou, Yawen Zhu, Mengfei Qi, Hai Lin, Bobin Yao, Shaohua Huang, Xuetao Wang, Qisheng Wu, and Weiyu Liu. 2025. "An Asymmetric SiC Power Module Directly Integrated with Vapor Chamber for Thermal Balancing in MMC" Applied Sciences 15, no. 20: 10869. https://doi.org/10.3390/app152010869
APA StyleWang, B., Zhou, X., Zhu, Y., Qi, M., Lin, H., Yao, B., Huang, S., Wang, X., Wu, Q., & Liu, W. (2025). An Asymmetric SiC Power Module Directly Integrated with Vapor Chamber for Thermal Balancing in MMC. Applied Sciences, 15(20), 10869. https://doi.org/10.3390/app152010869








