Abstract
Magnetic resonance imaging (MRI) using a simultaneous multislice technique can measure dynamic vascular elasticity over time. However, conventional k-space undersampling can cause signal interference, owing to vertical projection between blood vessels within the same hemisphere. Here, we proposed a radial projection method that can reduce signal interference between the blood vessels and aimed to verify the theoretical and practical effects of this method. A dataset from the internal and common carotid arteries (ICA and CCA) was used for both projection methods. Pulse wave velocity (PWV) was calculated using the ICA and CCA time series, and the methods were compared using the mean absolute error of PWV. The feasibility of the radial projection method in an actual MRI environment was also evaluated. PWVs of the radial projection method were statistically indistinguishable from the ground truth. And the radial projection method was less sensitive to background noise levels and showed similar results to the ground truth. This method could effectively avoid signal interference between vessels and was feasible for use in real MRI environments, maintaining high temporal resolution even with fewer sampling timepoints. Therefore, it can contribute to the early diagnosis and treatment of cerebrovascular diseases through accurate and dynamic PWV measurements.
1. Introduction
Pulse wave velocity (PWV) refers to the speed at which a pulse wave propagates through a blood vessel. An elevated PWV is indicative of increased arterial stiffness, which leads to reduced arterial elasticity and restricted vascular dilation, resulting in higher pressure within the vessel [1]. Owing to these characteristics, PWV serves as a crucial physiological marker for assessing arterial stiffness, enabling early diagnosis of cerebrovascular diseases, such as cerebral aging and infarction [2,3,4,5,6,7].
Representative noninvasive methods for measuring PWV in blood vessels include phase-contrast magnetic resonance imaging (MRI), arterial tonometry, and Doppler ultrasound [8,9]. The measurement of PWV using tonometry involves placing pressure sensors at two points, typically along the carotid and femoral arteries, to record arterial pressure waveforms. The pulse wave transit time between two measuring sites is measured, and PWV is calculated by dividing the distance between these sites by the transit time [10,11]. Although tonometry has the advantage of providing direct pressure waveforms, its accuracy can vary depending on sensor placement and the patients’ vascular condition, thereby affecting measurement consistency [12]. Additionally, when calculating the distance between two measurement sites, this method uses a certain ratio based on the patient’s height rather than using the actual length of the blood vessels, which can reduce the accuracy of the distance [13].
Another method for measuring PWV involves the use of Doppler ultrasound. In this technique, an ultrasound probe is placed at the vessel of interest, such as the carotid artery, and the blood pressure and diameter information at the site are obtained to calculate the stiffness index and PWV [14,15]. Doppler ultrasound is efficiently utilized in clinical settings because it does not require special preparation or recovery time and is a simple and quick measurement technique [16,17]. However, the accuracy of Doppler measurement can vary based on the precise placement and angle of the probes, making the results highly dependent on the operator’s skill [9,18,19,20,21]. Additionally, because of the low ultrasound penetration rate, this method may be limited in obtaining information from deeper blood vessels, such as cerebral vessels, as it can be affected by factors, such as skin thickness, tissue density, and bone [22,23].
The limitations of PWV measurement using tonometry and Doppler ultrasound can be overcome by the features of MRI, which offers high resolution and contrast among various tissues, as well as the ability to quantitatively assess deep blood vessels [24,25]. Using MRI sequences with a high temporal resolution, blood flow signal waveforms can be obtained at two arterial locations, and the pulse wave transit time can be calculated by measuring the peak difference between two blood flow signal waveforms [8]. PWV is then calculated by dividing the distance between two imaging points by the transit time. Simultaneous multislice imaging (SMS) with a multiband radio frequency pulse, which excites multiple slices simultaneously, allows for the simultaneous acquisition of images from two different blood vessels, eliminating the need to synchronize the blood flow timing in the two vessels for pulse wave transit time calculation [26]. Combining the keyhole technique with the SMS method (SMS-K) enables rapid scanning, allowing for the evaluation of real-time changes in PWV, thereby measuring dynamic vascular elasticity over time [27].
In a previous study, the SMS-K technique was proposed to measure cerebrovascular stiffness by generating vascular waveforms and calculating PWV in the internal and common carotid arteries (ICA and CCA), thus confirming the basic research findings and clinical utility of the SMS-K method [27]. In the SMS-K technique, undersampling of the k-space with parallel encoding during image reconstruction can result in a vertical projection effect. This causes the ICA and CCA, which are located vertically in the same hemisphere, to overlap on the same vertical line in the transaxial image, leading to signal interference between the vessels. This interference can distort the original blood flow signal waveforms, potentially hindering accurate PWV calculations. Although an image rotation technique has been proposed to minimize the signal interference between vessels, it only solves the problem in the case of two specific vessels aligned vertically, and there is still the possibility of signal interference with other vessels located in different positions.
The limitations of vertical projection caused by parallel encoding can be resolved by radial projection using data acquired through radial encoding. Radial encoding acquires images by encoding in various directions, not just vertically [28], resulting in more frequent sampling of the center of k-space point than with vertical encoding. This preserves low-frequency components, leading to a higher signal-to-noise ratio (SNR) [29,30]. Additionally, when a structural image is used to identify the positional information of various vessels, including the ICA and CCA, which are located in the same hemisphere, each vessel can be projected at an optimal angle to avoid interference with other vessels. Therefore, this technique can prevent signal interference between vessels, allowing for accurate PWV calculation using undisturbed blood flow signal waveforms from the ICA and CCA.
In this study, we propose a new vascular stiffness measurement technique that can significantly reduce signal interference between blood vessels, which is a limitation of the vertical projection method. Additionally, we explored the validity of this technique using imaging parameters similar to those of an actual MRI environment and analyzed its potential through simulation. We considered that a projection method that can produce results similar to the actual PWV and obtain the full sampling effect despite undersampling in the k-space can contribute to a more accurate early diagnosis of vascular aging and diseases.
2. Materials and Methods
2.1. Simulation Data
In a previous study, the temporal resolution was set to 48 ms for an image reconstructed using three k-space lines, and PWV was calculated based on signals from 500 timepoints in the ICA and CCA vessels. However, there was still a limitation: the peaks of the corresponding vascular pulse waveforms could not be sensitively detected, owing to the low sampling rate [27]. To overcome this limitation, in this study, the sampling rate was increased by 10× to improve the temporal resolution in the simulation data. We assumed undersampled acquisition from brain tissue images acquired using the SMS technique with the following parameters: imaging sequence = 2-dimensional gradient echo (2D GRE), temporal resolution = 4.8 ms, matrix size = 256 × 256, resolution = 1.0 mm × 1.0 mm × 3.0 mm, time series = 1000 points, flip angle = 30, bandwidth = 320 Hz/Px, distance between two slices (Δd) = 60 mm, and total acquisition time = 4.8 s.
Brain tissue images from five individuals, previously acquired using the SMS technique, were used as the background. Four regions of interest (ROIs), presumed to be the left and right ICA and CCA, were manually extracted from each image. Two simulated pulse waveforms were applied to each ROI to generate 10 sample waveforms (Figure 1). The ICA and CCA pulse waveforms were generated using the simulated pulse waveform database comprising healthy adult samples provided by Charlton et al. [31], considering an average heart rate of 60–100 beats per minute, with the interval between peaks within the same vessel averaging 640 ms. Subsequently, the ground truth images to be used for the simulation were temporally generated with Gaussian noise. Gaussian noise was set with a mean of 0 and standard deviation equal to the background of the brain tissue image, ranging from approximately 2.99 to 3.91. The accuracy of peak detection can decrease with the level of temporal noise, potentially affecting PWV values. Therefore, to assess the accuracy of the PWV measurements according to temporal noise levels, 10 ground truth images were generated per sample, with Gaussian noise levels varying from 10% to 100%.
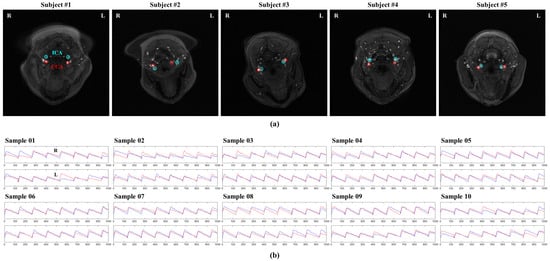
Figure 1.
Ground truth samples used in the simulation. (a) The regions of interest (ROIs) in the internal and common carotid arteries (ICA and CCA, respectively) were extracted from time-of-flight magnetic resonance angiography using simultaneous multislice images from five patients. (b) Two different pulse waveforms were applied to each ROI for simulation, resulting in a total of 10 waveforms. The time series for the left and right hemispheres of each sample were plotted, and the blue and red lines represent the time series of ICA and CCA, respectively.
2.2. Projection Methods
In the vertical projection method, each ground truth image was transformed into k-space using the Fourier transform, and the undersampled k-space lines were selected based on the DC component lines [27]. The number of parallel encoding lines was selected to be equal to the number of angles used in the radial projection. The time series in the undersampled k-space were plotted based on the ICA and CCA ROIs that were manually extracted from the ground truth images (Figure 2).
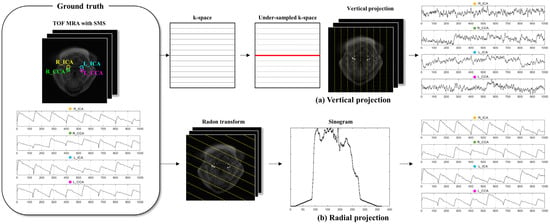
Figure 2.
Workflow for the comparison of the vertical and radial projection methods. (a) Vertical projection method. The images acquired from simultaneous multislice (SMS) images for time-of-flight magnetic resonance angiography (TOF MRA) are Fourier transformed. Additionally, k-space is undersampled using parallel encoding based on the DC component (red line), and the undersampled k-space is reconstructed. The internal and common carotid artery (ICA and CCA) time series are then plotted using the average intensity within each ROI. The difference between the peaks of the ICA and CCA is used to calculate the pulse wave velocity (PWV). (b) Radial projection method. The ground truth image, i.e., the SMS image, is Radon transformed at selected projection angles to generate sinograms. The time series are created from the average signal within each ROI in these sinograms. The PWV is calculated based on the time series of the ICA and CCA obtained from the same or different angles. The yellow line indicates the projection direction.
The radial projection method data were extracted from the sinogram derived by Radon transforming the ground truth image into a projection angle, and the time series of ICA and CCA were plotted (Figure 2). The projection angle was selected as the angle at which signal interference between blood vessels did not occur during radial projection, and isolation was assessed with the sinogram generated by Radon transforming the ROI template from 1° to 180° (Figure 3). Owing to individual variations in vascular distribution, this method allows the selection of projection angles, in which none of the ROIs overlap, ranging from a minimum of one angle to a maximum equivalent to the number of ROIs. Each vessel’s time series was generated by Radon transformation at angles where they could be isolated, and the PWV calculation was performed based on the time series derived from the same or different angles.

Figure 3.
Method for selecting the projection angles in the radial projection method. Templates with the time series of the internal and common carotid arteries are constructed from the ground truth image (red dashed box). These templates are then Radon transformed across all angles from 1° to 180°. The resulting sinograms for each angle are used to select the optimal projection angles to avoid signal interference between vessels. The number of selected projection angles can range from a minimum of one to a maximum equivalent to the number of ROIs. Note that each angle line in the right panel shows the selected vessel being isolated, not the center of the image. TOF MRA, time-of-flight magnetic resonance angiography; SMS, simultaneous multislice; ROI, region of interest.
Finally, additional experiments were conducted to verify whether the simulation results could be applied in an actual MRI environment. Although the simulation was based on a dataset generated with a temporal resolution of 1.6 ms, achieving such a temporal resolution in an actual MRI environment is challenging. Therefore, the simulation dataset was undersampled by a factor of 10, thereby simulating images acquired at a temporal resolution of 16 ms in an actual MRI environment. This undersampled dataset was resampled by a factor of 10 to create the interpolated dataset. The differences between the simulation, undersampled, and interpolated datasets were analyzed based on the mean PWV in the patients and hemispheres, both with and without 100% Gaussian temporal noise. All processes involving vertical and radial projections were performed using MATLAB software (R2020b version, Mathworks, Natick, MA, USA).
2.3. PWV Calculation
PWV calculations were performed using the time series extracted from 1000 timepoints obtained using both vertical and radial projection methods. First, the time series were smoothed to reduce noise and ensure accurate peak point detection. The findpeak function in MATLAB R2020b was used to identify the peak points in the time series. PWV was calculated by applying the difference between the peak points of ICA and CCA within the same hemisphere, as in Equation (1):
2.4. Evaluation with Error Analysis
The accuracy of the projection methods was evaluated by calculating the mean absolute error (MAE) and standard deviation (SD) based on the differences between the PWVs from the ground truth images with full sampling and those obtained using the vertical and radial projection methods. Additionally, a one-way non-parametric analysis of variance (Kruskal–Wallis test) was performed to assess the differences between the ground truth, vertical projection, and radial projection PWVs and further evaluate the feasibility of the proposed technique in an actual MRI environment. Furthermore, Bonferroni correction was applied to the results of all Kruskal–Wallis tests. All statistical analyses were conducted using Jamovi version 2.4.8 (https://www.jamovi.org (accessed on 30 September 2024)) and Dwass–Steel–Critchlow–Fligner (DSCF) post-hoc tests.
3. Results
The accuracy of the PWVs from the ground truth images was evaluated according to Gaussian noise levels. The vertical projection method showed an average difference of 3.400 ± 0.280 m/s, regardless of the noise level. By contrast, the radial projection method exhibited an average difference of 1.644 ± 0.798 m/s. The MAE in the radial projection method increased as the noise level increased (Table 1), and the average MAEs in both hemispheres were 0.397 and 0.647 m/s at noise levels of 10 and 20%, 1.016 and 1.686 m/s at 30 and 60%, and 2.045 and 2.816 m/s at 70 and 100%, respectively. However, these differences were much smaller than the MAE in the vertical projection method.

Table 1.
Accuracy evaluation of the methods using the MAE of PWVs.
Furthermore, the PWVs were significantly different between the ground truth, vertical projection, and radial projection across different Gaussian noise levels (p < 0.05), except for in the left hemisphere at the 10%, 20%, 30%, and 80% noise level (Table 2). Post-hoc tests using DSCF pairwise comparisons indicated that radial projection PWVs were not significantly different from ground truth PWVs, except for in the left hemisphere at the 90% noise level and right hemisphere at the 100% noise level. By contrast, the vertical-projection PWVs were significantly different from the ground truth PWVs in all cases, except for in the left hemisphere at the 10% and 20% noise levels.

Table 2.
Mean differences between the ground truth, vertical projection, and radial projection PWVs (Kruskal–Wallis test).
Finally, the feasibility of the proposed technique was evaluated using the differences in PWVs between the simulation, undersampled, and interpolated datasets, and there was a significant difference (p < 0.001), regardless of the presence of noise (Table 3). Furthermore, the post-hoc test results showed no significant difference between the simulation and interpolated datasets (p > 0.05), whereas there was a significant difference between the simulation and undersampled datasets (p < 0.001), regardless of the presence of noise. Additionally, as shown in Figure 4, although the time series of the simulation, undersampled, and interpolated datasets exhibited similar trends, a detailed view of the eight peaks indicated that the peak points of the undersampled dataset were substantially different from those of the simulation dataset, especially at peaks 02, 03, 05, 06, and 08 (Figure 4).

Table 3.
Feasibility assessment of the radial projection method (Kruskal–Wallis test).
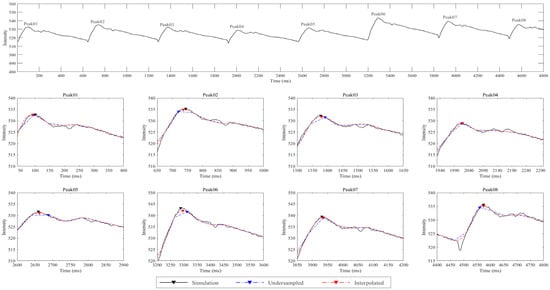
Figure 4.
Comparison of time series and peak points among the simulation, undersampled, and interpolated datasets. The top panel shows the time series from the simulation dataset over the range of 0–4800 ms. The bottom two panels provide detailed views of the eight waveform peaks (Peak 01 to Peak 08). The black, blue, and red arrowheads indicate the peak points for the simulation, undersampled, and interpolated datasets, respectively. The interpolated dataset closely followed the simulation dataset, indicating effective reconstruction of the original signal. Although the undersampled dataset showed a similar trend to the time series of the simulation dataset, there were noticeable differences in the peak positions.
4. Discussion
This study demonstrated that the radial projection method can resolve the problem of interference between vascular signals, which is a limitation of the vertical projection method. The results indicated that the ground truth PWV was very similar to that of the radial projection method but not to that of the vertical projection method. This also demonstrates that the radial projection method can achieve effects similar to those of full sampling in terms of PWV measurement, even with k-space undersampling. Additionally, interpolation showed that the same effects observed in the simulation could be obtained in an actual MRI environment, suggesting the potential for future in vivo applications.
To evaluate the accuracy of the radial projection method, the MAE of the PWVs across different levels of temporal noise were compared with those of the ground truth and vertical projection methods. The results show that the average MAE in both hemispheres using the radial projection method was much lower than that of the vertical projection method at all noise levels. Additionally, while the MAE in the radial projection method tended to increase with higher noise levels, the MAE in the vertical projection method was consistently higher, regardless of the noise level (Table 1). Furthermore, on comparing the PWVs between the ground truth and projection methods, the PWVs were not significantly different between the ground truth and radial projection method (Table 2). By contrast, the PWVs in the vertical projection method were significantly different from the ground truth PWVs in all cases, except for in the left hemisphere at the 10% and 20% noise levels.
These findings demonstrate that the radial projection method is less sensitive to background noise than the vertical projection method and that the radial method can provide results similar to the ground truth. This can be attributed to the effective avoidance of signal interference between the arterial vessels using the radial projection method. Specifically, during radial projection, stronger signals from the ICA and CCA are kept separate to prevent signal interference. Furthermore, the signals from the ICA and CCA do not mix with those from other vessels, resulting in only minor interference from the surrounding tissues or background noise. Consequently, the time series derived from the ICA and CCA are minimally affected by other vessels, leading to low and stable MAE and SD values. Additionally, the radial projection method collects data from multiple angles, not only preventing signal overlap between blood vessels but also improving the signal-to-noise ratio (SNR) by more frequently sampling low-frequency components in k-space.
By contrast, the vertical projection method is prone to significant signal interference between major vessels. In such cases, temporal noise from the primary vessel is also affected by temporal noise from other large vessels, thereby amplifying the overall signal interference. This persistent interference results in consistently high MAE values, irrespective of the temporal noise levels, indicating that the vertical projection method should have sufficient k-space sampling lines. The radial projection method was shown to be more effective than the vertical projection method, as its performance was stable even at various temporal noise levels, suggesting its potential as an important tool for early diagnosis and treatment evaluation in cerebrovascular diseases.
To determine the feasibility of implementing the radial projection method in an actual MRI environment, we compared the PWVs between the simulation, undersampled, and interpolated datasets. The results confirmed the feasibility of the radial projection method, as there was no significant difference in PWVs between the simulation and interpolated datasets (Table 3), indicating that the interpolated dataset could maintain an accuracy comparable to that of the simulation dataset. Furthermore, the findings suggest that a high accuracy can be sufficiently preserved even with data acquired at fewer sampling timepoints in an actual MRI environment. Figure 4 illustrates the peak detection accuracy across various peak points in the simulation, undersampled, and interpolated datasets. The interpolated dataset showed a peak detection performance similar to that of the simulation dataset, indicating that it can detect peak points with high sensitivity, similar to the data acquired at high temporal resolution.
This study demonstrated that the radial projection method is feasible in an actual MRI environment and can maintain high accuracy and temporal resolution even with fewer sampling timepoints. However, this study has certain limitations. Currently, this method uses projection angles to avoid major vessels, such as the ICA and CCA. Surrounding vessels, apart from the ICA and CCA, may influence the waveforms of these major arteries. Therefore, it is necessary to select projection angles that can avoid all surrounding vessels, which requires further research. Moreover, the distance between the two vessels used for PWV calculation in this study may not be accurate because it does not account for the curvature of the actual vascular structures. Thus, it is necessary to utilize vessel segmentation techniques to calculate the actual path length between target vessels for more precise PWV measurements. Additionally, this study did not thoroughly analyze the potential influence of vascular diameters and locations on the mean absolute error (MAE). Future research could benefit from a more detailed investigation of these factors to enhance the robustness and accuracy of the proposed method. Finally, the proposed radial projection method requires additional evaluation through MRI sequence implementation and further assessments involving patients. For clinical application, additional quantitative evaluations and technical improvements are necessary. Further studies to enhance the performance of the radial projection method by increasing its temporal and cost efficiency could aid in obtaining accurate PWV measurements, which are crucial for the early diagnosis and treatment of cerebrovascular diseases. Additionally, the clinical application of the radial projection method could potentially improve patient care and provide more efficient healthcare services.
5. Conclusions
In conclusion, the radial projection method can maintain a high temporal resolution through interpolation, even with images acquired at fewer sampling timepoints in an actual MRI environment. This could enhance time efficiency while enabling accurate and dynamic PWV calculations. Sensitive peak point detection is crucial for precise PWV calculations because it is essential for the early diagnosis of vascular aging and diseases.
Author Contributions
J.-M.S., C.-K.K. and Y.-D.S. were involved in conceptualization, data curation, formal analysis, investigation, methodology, resources, software, validation, visualization, and writing of the original draft. C.-K.K. and Y.-D.S. were involved in funding acquisition, project administration, supervision, writing, reviewing, and editing as corresponding authors. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF), funded by the Korean government (MSIT), under Grants 2020R1A2C1004355 and 2022R1F1A1062766, and by the Gachon University Research Fund of 2023 under Grant GCU-202308040001.
Institutional Review Board Statement
The study was conducted in accordance with the guidelines of the Declaration of Helsinki and approved by the Institutional Review Board (or Ethics Committee) of Gachon University Gil Medical Center (GU-GMC) (protocol code: GDIRB2018-143 and date of approval: 8 May 2018).
Informed Consent Statement
Informed consent was obtained from the subject involved in the study. Written informed consent has been obtained from the subject to publish this paper.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Cecelja, M.; Chowienczyk, P. Role of Arterial Stiffness in Cardiovascular Disease. JRSM Cardiovasc. Dis. 2012, 1, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-L.; Kim, S.-H. Pulse Wave Velocity in Atherosclerosis. Front. Cardiovasc. Med. 2019, 6, 41. [Google Scholar] [CrossRef] [PubMed]
- Gąsecki, D.; Rojek, A.; Kwarciany, M.; Kowalczyk, K.; Boutouyrie, P.; Nyka, W.; Laurent, S.; Narkiewicz, K. Pulse Wave Velocity Is Associated with Early Clinical Outcome after Ischemic Stroke. Atherosclerosis 2012, 225, 348–352. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Cha, M.-J.; Lee, D.H.; Lee, H.S.; Nam, C.M.; Nam, H.S.; Kim, Y.D.; Heo, J.H. The Association between Cerebral Atherosclerosis and Arterial Stiffness in Acute Ischemic Stroke. Atherosclerosis 2011, 219, 887–891. [Google Scholar] [CrossRef] [PubMed]
- Laurent, S.; Katsahian, S.; Fassot, C.; Tropeano, A.-I.; Gautier, I.; Laloux, B.; Boutouyrie, P. Aortic Stiffness Is an Independent Predictor of Fatal Stroke in Essential Hypertension. Stroke 2003, 34, 1203–1206. [Google Scholar] [CrossRef]
- Fiori, G.; Fuiano, F.; Scorza, A.; Conforto, S.; Sciuto, S.A. Non-Invasive Methods for PWV Measurement in Blood Vessel Stiffness Assessment. IEEE Rev. Biomed. Eng. 2022, 15, 169–183. [Google Scholar] [CrossRef]
- Darnaud, C.; Courtet, A.; Schmitt, A.; Boutouyrie, P.; Bouchard, P.; Carra, M.C. Association between Periodontitis and Pulse Wave Velocity: A Systematic Review and Meta-Analysis. Clin. Oral. Investig. 2021, 25, 393–405. [Google Scholar] [CrossRef]
- Wentland, A.L.; Grist, T.M.; Wieben, O. Review of MRI-Based Measurements of Pulse Wave Velocity: A Biomarker of Arterial Stiffness. Cardiovasc. Diagn. Ther. 2014, 4, 193. [Google Scholar]
- Jiang, B.; Liu, B.; McNeill, K.L.; Chowienczyk, P.J. Measurement of Pulse Wave Velocity Using Pulse Wave Doppler Ultrasound: Comparison with Arterial Tonometry. Ultrasound Med. Biol. 2008, 34, 509–512. [Google Scholar] [CrossRef]
- Laurent, S.; Cockcroft, J.; Van Bortel, L.; Boutouyrie, P.; Giannattasio, C.; Hayoz, D.; Pannier, B.; Vlachopoulos, C.; Wilkinson, I.; Struijker-Boudier, H.; et al. Expert Consensus Document on Arterial Stiffness: Methodological Issues and Clinical Applications. Eur. Heart J. 2006, 27, 2588–2605. [Google Scholar] [CrossRef]
- Urban, M.W. Understanding Arterial Biomechanics with Ultrasound and Waveguide Models. Acoust. Today 2023, 19, 46. [Google Scholar] [CrossRef] [PubMed]
- Vappou, J.; Luo, J.; Okajima, K.; Di Tullio, M.; Konofagou, E. Aortic Pulse Wave Velocity Measured by Pulse Wave Imaging (PWI): A Comparison with Applanation Tonometry. Artery Res. 2011, 5, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Bossuyt, J.; Van De Velde, S.; Azermai, M.; Vermeersch, S.J.; De Backer, T.L.M.; Devos, D.G.; Heyse, C.; Filipovsky, J.; Segers, P.; Van Bortel, L.M. Noninvasive Assessment of Carotid-Femoral Pulse Wave Velocity: The Influence of Body Side and Body Contours. J. Hypertens. 2013, 31, 946–951. [Google Scholar] [CrossRef] [PubMed]
- Yi, K.-K.; Park, C.; Yang, J.; Lee, Y.-B.; Kang, C.-K. Quantitative Thermal Stimulation Using Therapeutic Ultrasound to Improve Cerebral Blood Flow and Reduce Vascular Stiffness. Sensors 2023, 23, 8487. [Google Scholar] [CrossRef]
- Graf, S.; Craiem, D.; Barra, J.G.; Armentano, R.L. Estimation of Local Pulse Wave Velocity Using Arterial Diameter Waveforms: Experimental Validation in Sheep. J. Phys. Conf. Ser. 2011, 332, 012010. [Google Scholar] [CrossRef]
- Price, D.J.A. Tissue Doppler Imaging: Current and Potential Clinical Applications. Heart 2000, 84, ii11–ii18. [Google Scholar] [CrossRef]
- Atkinson, P.; Wells, P.N.T. Pulse-Doppler Ultrasound and Its Clinical Application. Yale J. Biol. Med. 1977, 50, 367. [Google Scholar]
- Pilz, N.; Heinz, V.; Ax, T.; Fesseler, L.; Patzak, A.; Bothe, T.L. Pulse Wave Velocity: Methodology, Clinical Applications, and Interplay with Heart Rate Variability. Rev. Cardiovasc. Med. 2024, 25, 266. [Google Scholar] [CrossRef]
- Calabia, J.; Torguet, P.; Garcia, M.; Garcia, I.; Martin, N.; Guasch, B.; Faur, D.; Vallés, M. Doppler Ultrasound in the Measurement of Pulse Wave Velocity: Agreement with the Complior Method. Cardiovasc. Ultrasound 2011, 9, 13. [Google Scholar] [CrossRef]
- Rabben, S.I.; Stergiopulos, N.; Hellevik, L.R.; Smiseth, O.A.; Slørdahl, S.; Urheim, S.; Angelsen, B. An Ultrasound-Based Method for Determining Pulse Wave Velocity in Superficial Arteries. J. Biomech. 2004, 37, 1615–1622. [Google Scholar] [CrossRef]
- Rubens, D.J.; Bhatt, S.; Nedelka, S.; Cullinan, J. Doppler Artifacts and Pitfalls. Radiol. Clin. N. Am. 2006, 44, 805–835. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.F.A. Transcranial Doppler Ultrasonography (Uses, Limitations, and Potentials): A Review Article. Egypt. J. Neurosurg. 2021, 36, 20. [Google Scholar] [CrossRef]
- Purkayastha, S.; Sorond, F. Transcranial Doppler Ultrasound: Technique and Application. Semin. Neurol. 2013, 32, 411–420. [Google Scholar] [CrossRef]
- Geva, T. Magnetic Resonance Imaging: Historical Perspective. J. Cardiovasc. Magn. Reson. 2006, 8, 573–580. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, C.H., 3rd; Herfkens, R.J. Magnetic Resonance Imaging and Measurement of Blood Flow. West. J. Med. 1994, 160, 237. [Google Scholar]
- Barth, M.; Breuer, F.; Koopmans, P.J.; Norris, D.G.; Poser, B.A. Simultaneous Multislice (SMS) Imaging Techniques. Magn. Reson. Med. 2016, 75, 63–81. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.-Y.; Lee, Y.-B.; Kang, C.-K. Novel Technique to Measure Pulse Wave Velocity in Brain Vessels Using a Fast Simultaneous Multi-Slice Excitation Magnetic Resonance Sequence. Sensors 2021, 21, 6352. [Google Scholar] [CrossRef]
- Feng, L. Golden-Angle Radial MRI: Basics, Advances, and Applications. Magn. Reson. Imaging 2022, 56, 45–62. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, S.; Cheng, L.; Bao, S. Review: K-Space Trajectory Development. In Proceedings of the 2013 IEEE International Conference on Medical Imaging Physics and Engineering, Shenyang, China, 19–20 October 2013; pp. 356–360. [Google Scholar] [CrossRef]
- Berry, E.S.K.; Jezzard, P.; Okell, T.W. The Advantages of Radial Trajectories for Vessel-Selective Dynamic Angiography with Arterial Spin Labeling. Magn. Reson. Mater. Phys. Biol. Med. 2019, 32, 643–653. [Google Scholar] [CrossRef]
- Charlton, P.H.; Harana, J.M.; Vennin, S.; Li, Y.; Chowienczyk, P.; Alastruey, J. Pulse Wave Database (PWDB): A Database of Arterial Pulse Waves Representative of Healthy Adults. Heart Circ. 2019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).