Resource-Efficient Acoustic Full-Waveform Inversion via Dual-Branch Physics-Informed RNN with Scale Decomposition
Abstract
1. Introduction
- (1)
- we propose a novel dual-branch PIRNN architecture for VSP acoustic FWI. This architecture facilitates efficient information transfer and conversion between models at different scales, enabling more accurate and computationally efficient inversion processes.
- (2)
- our proposed approach incorporates scale decomposition, allowing the transformation of loss information from the original-scale model to a reduced-scale model. This enables PIRNN-based VSP acoustic FWI across multiple scales, significantly enhancing both computational efficiency and inversion accuracy.
- (3)
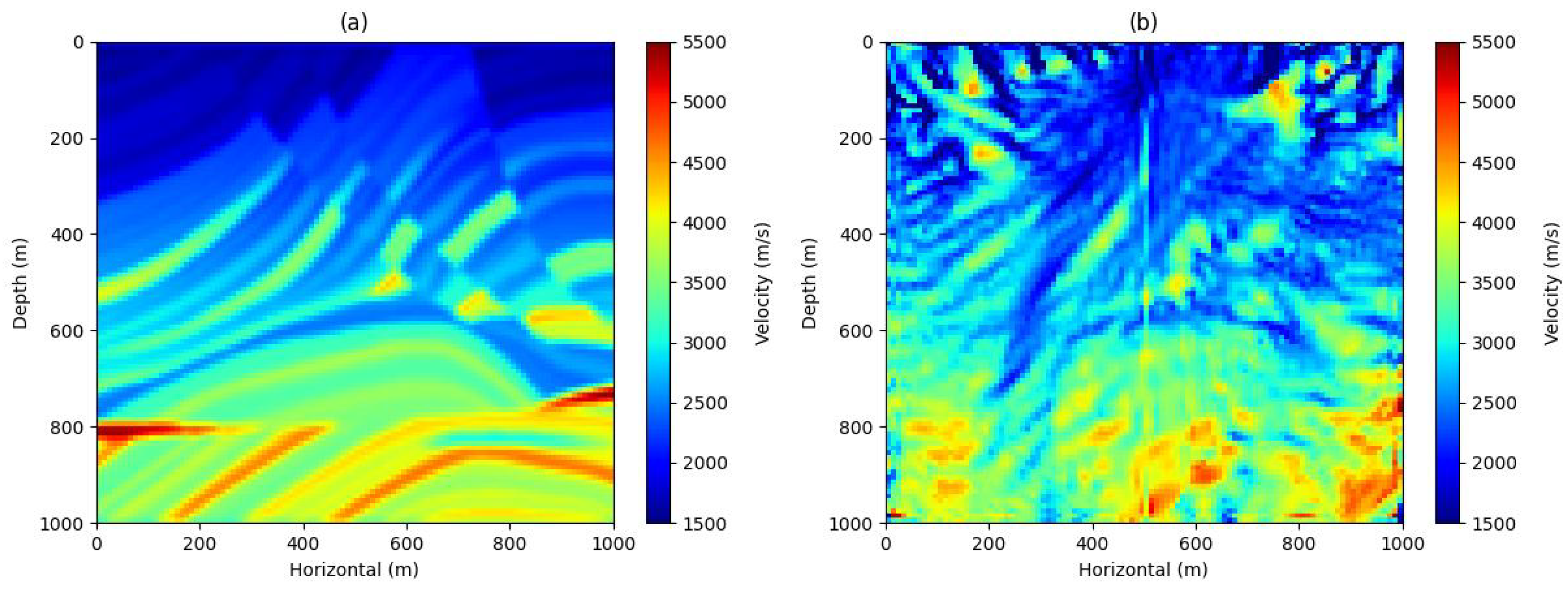
- we validate the proposed dual-branch PIRNN FWI network through simulation experiments on a homogeneous layered model and the Marmousi model. The results demonstrate that our approach substantially reduces GPU resource consumption while maintaining high inversion accuracy, confirming its effectiveness for practical applications.
2. Theory
2.1. FWI Math Model
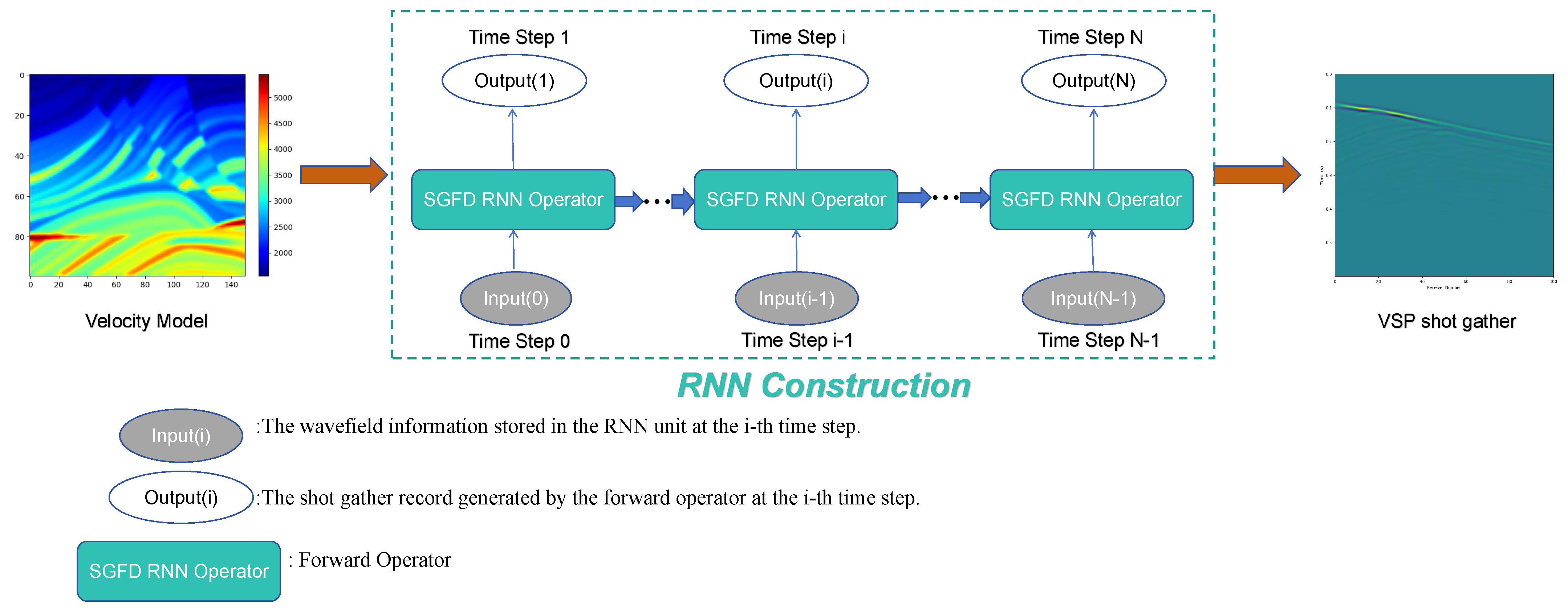
2.2. PIRNN Forward Modeling
2.3. PIRNN Velocity Model Inversion
3. Methodology
3.1. Network Structure
3.2. SGFD RNN Operator
3.3. Scale Decomposition
4. Numerical Examples
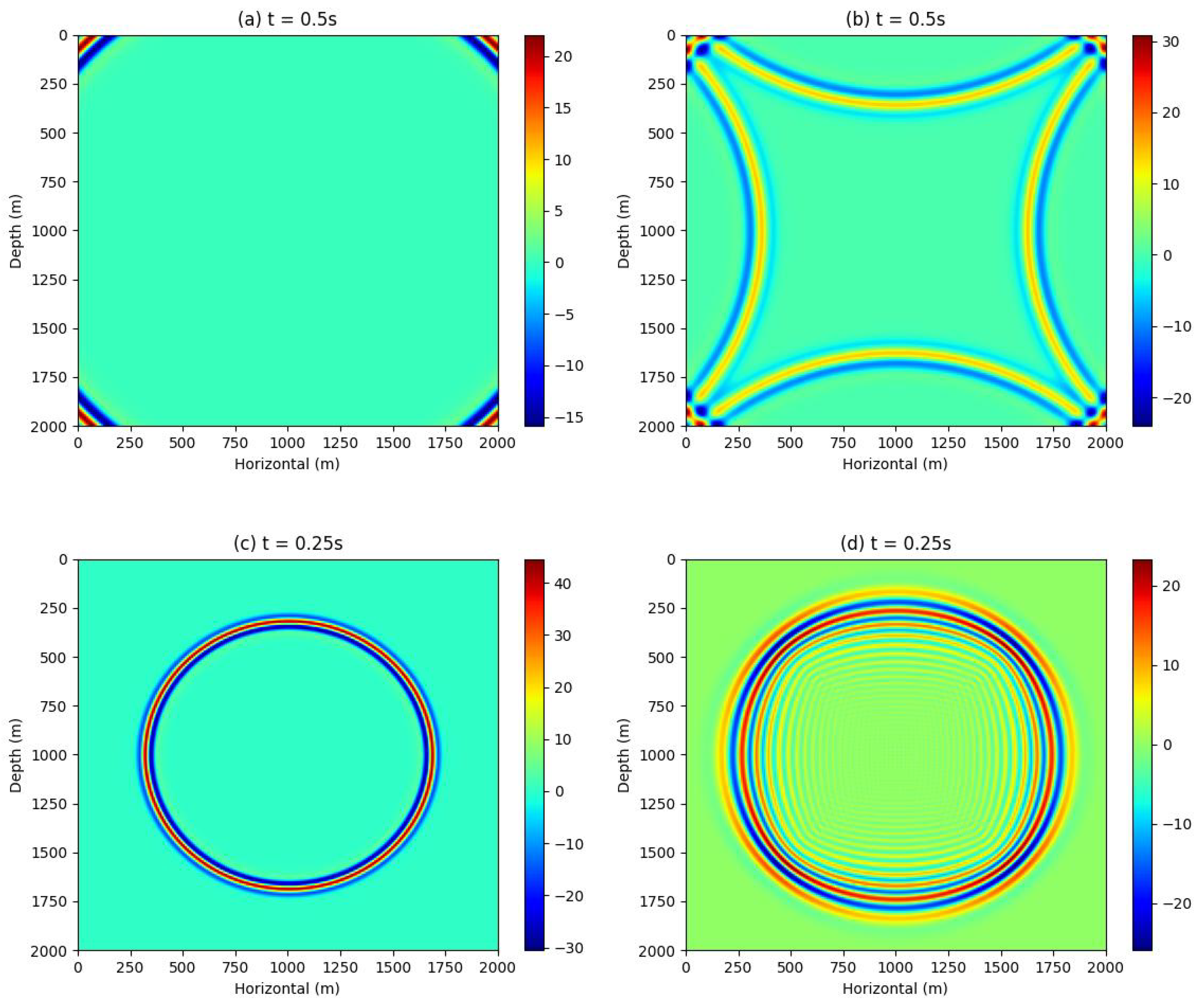
4.1. Forward Modeling
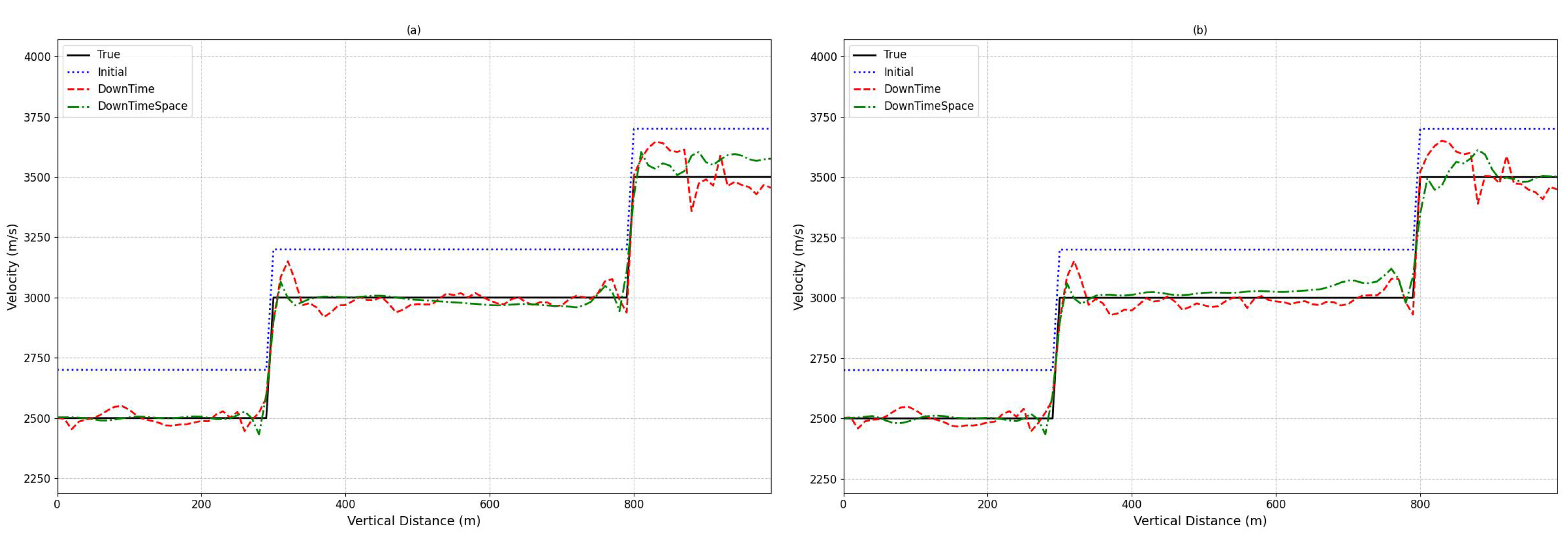
4.2. Homogeneous Layer Model
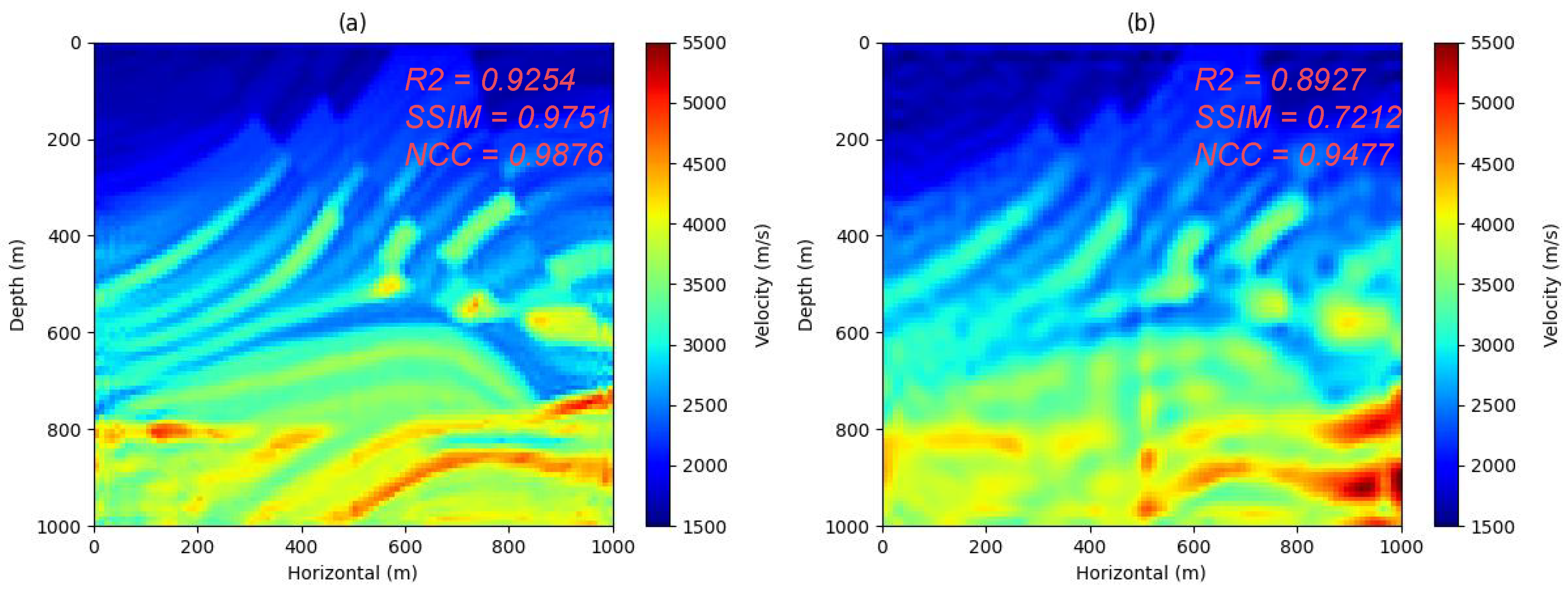
4.3. Marmousi Model
4.4. GPU Memory Usage Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tarantola, A. Linearized inversion of seismic reflection data. Geophys. Prospect. 1984, 32, 998–1015. [Google Scholar] [CrossRef]
- Pratt, R.G.; Shin, C.; Hick, G. Gauss–Newton and full Newton methods in frequency–space seismic waveform inversion. Geophys. J. Int. 1998, 133, 341–362. [Google Scholar] [CrossRef]
- Shin, C.; Cha, Y.H. Waveform inversion in the Laplace domain. Geophys. J. Int. 2008, 173, 922–931. [Google Scholar] [CrossRef]
- Warner, M.; Guasch, L. Adaptive waveform inversion: Theory. Geophysics 2016, 81, R429–R445. [Google Scholar] [CrossRef]
- Pan, W.; Innanen, K.A.; Geng, Y.; Li, J. Interparameter trade-off quantification for isotropic-elastic full-waveform inversion with various model parameterizations. Geophysics 2019, 84, R185–R206. [Google Scholar] [CrossRef]
- Sun, B.; Alkhalifah, T. The application of an optimal transport to a preconditioned data matching function for robust waveform inversion. Geophysics 2019, 84, R923–R945. [Google Scholar] [CrossRef]
- Ta, Q.B.; Pham, Q.Q.; Pham, N.L.; Huynh, T.C.; Kim, J.T. Smart Aggregate-Based Concrete Stress Monitoring via 1D CNN Deep Learning of Raw Impedance Signals. Struct. Control Health Monit. 2024, 2024, 5822653. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Ta, Q.B.; Ho, D.D.; Kim, J.T.; Huynh, T.C. A method for automated bolt-loosening monitoring and assessment using impedance technique and deep learning. Dev. Built Environ. 2023, 14, 100122. [Google Scholar] [CrossRef]
- Das, V.; Pollack, A.; Wollner, U.; Mukerji, T. Convolutional neural network for seismic impedance inversion. Geophysics 2019, 84, R869–R880. [Google Scholar] [CrossRef]
- Puzyrev, V. Deep learning electromagnetic inversion with convolutional neural networks. Geophys. J. Int. 2019, 218, 817–832. [Google Scholar] [CrossRef]
- Moghadas, D. One-dimensional deep learning inversion of electromagnetic induction data using convolutional neural network. Geophys. J. Int. 2020, 222, 247–259. [Google Scholar] [CrossRef]
- Wang, H.; Liu, W.; Xi, Z.z.; Fang, J.h. Nonlinear inversion for magnetotelluric sounding based on deep belief network. J. Cent. South Univ. 2019, 26, 2482–2494. [Google Scholar] [CrossRef]
- Liao, X.; Shi, Z.; Zhang, Z.; Yan, Q.; Liu, P. 2D inversion of magnetotelluric data using deep learning technology. Acta Geophys. 2022, 70, 1047–1060. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comput. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
- Mao, Z.; Jagtap, A.D.; Karniadakis, G.E. Physics-informed neural networks for high-speed flows. Comput. Methods Appl. Mech. Eng. 2020, 360, 112789. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ellsworth, W.L.; Zhu, W.; Chuang, L.Y.; Beroza, G.C. Earthquake transformer—An attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 2020, 11, 3952. [Google Scholar] [CrossRef] [PubMed]
- Moseley, B.; Markham, A.; Nissen-Meyer, T. Solving the wave equation with physics-informed deep learning. arXiv 2020, arXiv:2006.11894. [Google Scholar]
- Waheed, U.; Haghighat, E.; Alkhalifah, T.; Song, C.; Hao, Q. Eikonal solution using physics-informed neural networks. In Proceedings of the EAGE 2020 Annual Conference & Exhibition Online, Online, 8–11 December 2020; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2020; Volume 2020, pp. 1–5. [Google Scholar]
- Lu, C.; Zhang, C. Seismic velocity inversion via physical embedding recurrent neural networks (RNN). Appl. Sci. 2023, 13, 13312. [Google Scholar] [CrossRef]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for wave propagation and full waveform inversions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023120. [Google Scholar] [CrossRef]
- Sun, J.; Niu, Z.; Innanen, K.A.; Li, J.; Trad, D.O. A theory-guided deep-learning formulation and optimization of seismic waveform inversion. Geophysics 2020, 85, R87–R99. [Google Scholar] [CrossRef]
- Virieux, J.; Operto, S. An overview of full-waveform inversion in exploration geophysics. Geophysics 2009, 74, WCC1–WCC26. [Google Scholar] [CrossRef]
- Fichtner, A. Full Seismic Waveform Modelling and Inversion; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Borisov, D.; Modrak, R.; Gao, F.; Tromp, J. 3D elastic full-waveform inversion of surface waves in the presence of irregular topography using an envelope-based misfit function. Geophysics 2018, 83, R1–R11. [Google Scholar] [CrossRef]
- Hardage, B.A. Vertical seismic profiling. Lead. Edge 1985, 4, 59. [Google Scholar] [CrossRef]
- Plessix, R.É.; Baeten, G.; de Maag, J.W.; ten Kroode, F.; Rujie, Z. Full waveform inversion and distance separated simultaneous sweeping: A study with a land seismic data set. Geophys. Prospect. 2012, 60, 733–747. [Google Scholar] [CrossRef]
- Brossier, R.; Operto, S.; Virieux, J. Velocity model building from seismic reflection data by full-waveform inversion. Geophys. Prospect. 2015, 63, 354–367. [Google Scholar] [CrossRef]
- Plessix, R.E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophys. J. Int. 2006, 167, 495–503. [Google Scholar] [CrossRef]
- Fichtner, A.; Trampert, J. Resolution analysis in full waveform inversion. Geophys. J. Int. 2011, 187, 1604–1624. [Google Scholar] [CrossRef]
- Tarantola, A. Inversion of seismic reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Yang, P. A Numerical Tour of Wave Propagation. ResearchGate 2014. Available online: https://www.researchgate.net/profile/Pengliang-Yang/publication/262936022_A_numerical_tour_of_wave_propagation/links/57d3e6de08ae601b39a80917/A-numerical-tour-of-wave-propagation.pdf (accessed on 1 December 2024).














| Parameters | Original Scale | DownScale |
|---|---|---|
| Grid size | nz = nx = 100 | nz = nx = 100 |
| Gird spacing | dz = dx = 10 | dz = dx = 5 |
| Number of shots | 11 | 11 |
| Numbers of receivers | 100 | 100 |
| Source sampling rate | 4000 Hz | 2000 Hz |
| Central frequency | 40 Hz | 40 Hz |
| Time step | 0.5 ms | 0.5 ms |
| Parameters | Forward Modeling |
|---|---|
| Finite-Difference parameter | nz = nx = 200, Order = 4/10 |
| PML Width | 20 |
| Width of velocity model | 2000 m |
| Depth of velocity model | 2000 m |
| Central frequency | 20/40 Hz |
| Source Location | Center of model |
| Velocity value | 3000 m/s |
| Parameters | Original Scale | DownTime | DownTimeSpace |
|---|---|---|---|
| Grid Points | nz = nx = 100 | nz = nx = 100 | nz = nx = 50 |
| Grid Spacing | dz = dx = 10 | dz = dx = 5 | dz = dx = 5 |
| Number of timesteps | 1400 | 700 | 350 |
| Central frequency | 40 Hz | 40 Hz | 40 Hz |
| Source sampling rate | 4000/8000 Hz | 2000 Hz | 2000 Hz |
| Total data scale | 11 × 100 × 100 × 1400 | 11 × 100 × 100 × 700 | 11 × 50 × 50 × 350 |
| Parameters | Original Scale | DownTime | DownTimeSpace |
|---|---|---|---|
| Grid Points | nz = nx = 100 | nz = nx = 100 | nz = nx = 50 |
| Grid Spacing | dz = dx = 10 | dz = dx = 5 | dz = dx = 5 |
| Number of timesteps | 1600 | 800 | 400 |
| Central frequency | 40 Hz | 40 Hz | 40 Hz |
| Source sampling rate | 4000/8000 Hz | 2000 Hz | 2000 Hz |
| Total data scale | 11 × 100 × 100 × 1400 | 11 × 100 × 100 × 800 | 11 × 50 × 50 × 400 |
| Model | Scale Strategy | R2 | SSIM | NCC |
|---|---|---|---|---|
| Homogeneous | DownTime | 0.9574 | 0.5478 | 0.9805 |
| DownTimeSpace | 0.7978 | 0.6254 | 0.9449 | |
| Marmousi ( = 5) | DownTime | 0.9254 | 0.9751 | 0.9876 |
| DownTimeSpace | 0.8927 | 0.7212 | 0.9477 | |
| Marmousi ( = 10) | DownTime | 0.9421 | 0.8746 | 0.9711 |
| DownTimeSpace | 0.8736 | 0.6972 | 0.9373 |
| Components | Original Scale | DownTime | DownTimeSpace |
|---|---|---|---|
| Intermediate activations | 32.1 Gb | 16 Gb | 2.3 Gb |
| Model parameters | 1.8 Gb | 1.6 Gb | 1.6 Gb |
| Optimizers Status | |||
| Other usage |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Liu, J.; Qu, L.; Gao, J.; Cai, H.; Liang, J. Resource-Efficient Acoustic Full-Waveform Inversion via Dual-Branch Physics-Informed RNN with Scale Decomposition. Appl. Sci. 2025, 15, 941. https://doi.org/10.3390/app15020941
Lu C, Liu J, Qu L, Gao J, Cai H, Liang J. Resource-Efficient Acoustic Full-Waveform Inversion via Dual-Branch Physics-Informed RNN with Scale Decomposition. Applied Sciences. 2025; 15(2):941. https://doi.org/10.3390/app15020941
Chicago/Turabian StyleLu, Cai, Jijun Liu, Liyuan Qu, Jianbo Gao, Hanpeng Cai, and Jiandong Liang. 2025. "Resource-Efficient Acoustic Full-Waveform Inversion via Dual-Branch Physics-Informed RNN with Scale Decomposition" Applied Sciences 15, no. 2: 941. https://doi.org/10.3390/app15020941
APA StyleLu, C., Liu, J., Qu, L., Gao, J., Cai, H., & Liang, J. (2025). Resource-Efficient Acoustic Full-Waveform Inversion via Dual-Branch Physics-Informed RNN with Scale Decomposition. Applied Sciences, 15(2), 941. https://doi.org/10.3390/app15020941






