Physics-Informed Neural Networks for Modal Wave Field Predictions in 3D Room Acoustics
Abstract
1. Introduction
2. Room Acoustic Application
2.1. Case Study Setup
2.2. Analytic Solution
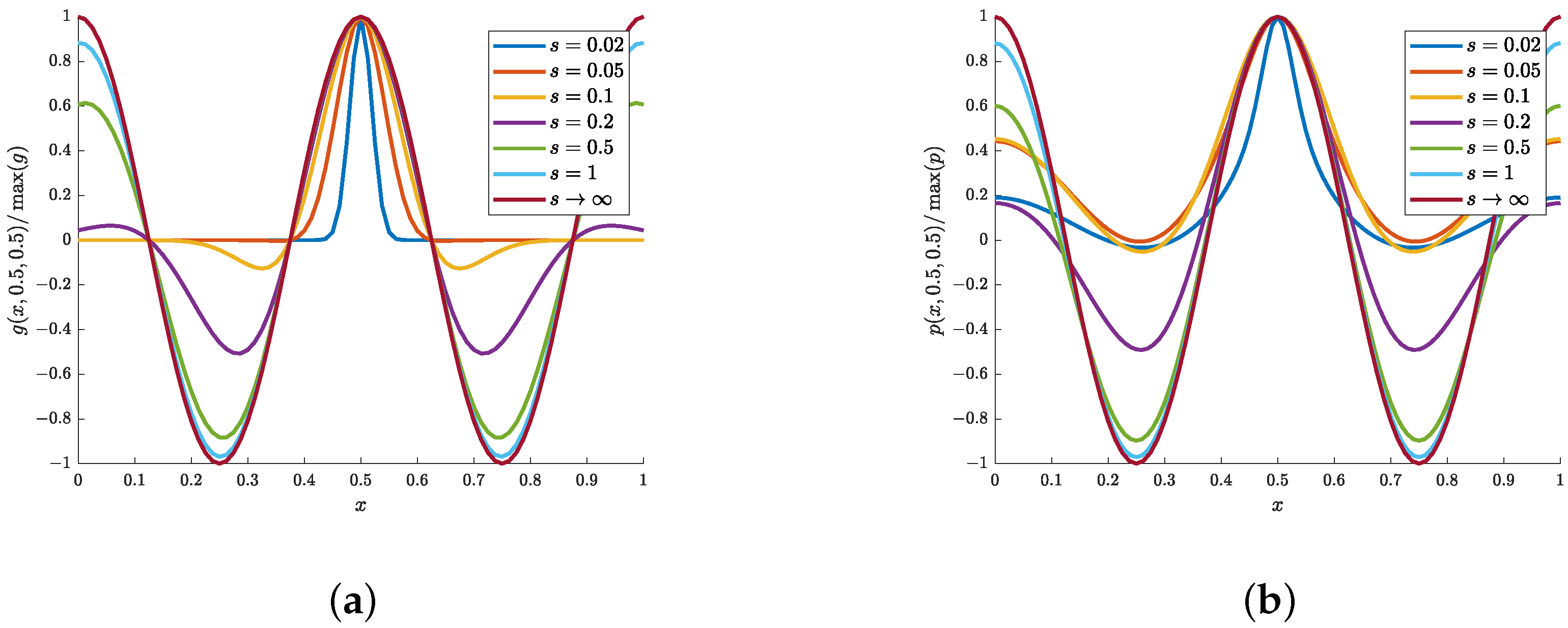
2.3. Spatial Frequency Content
2.4. Validated FEM Reference Simulation
3. Physics-Informed Neural Networks for Wave-Based Room Acoustics
3.1. Initial Setup [5]
3.2. Hyperparameter Study
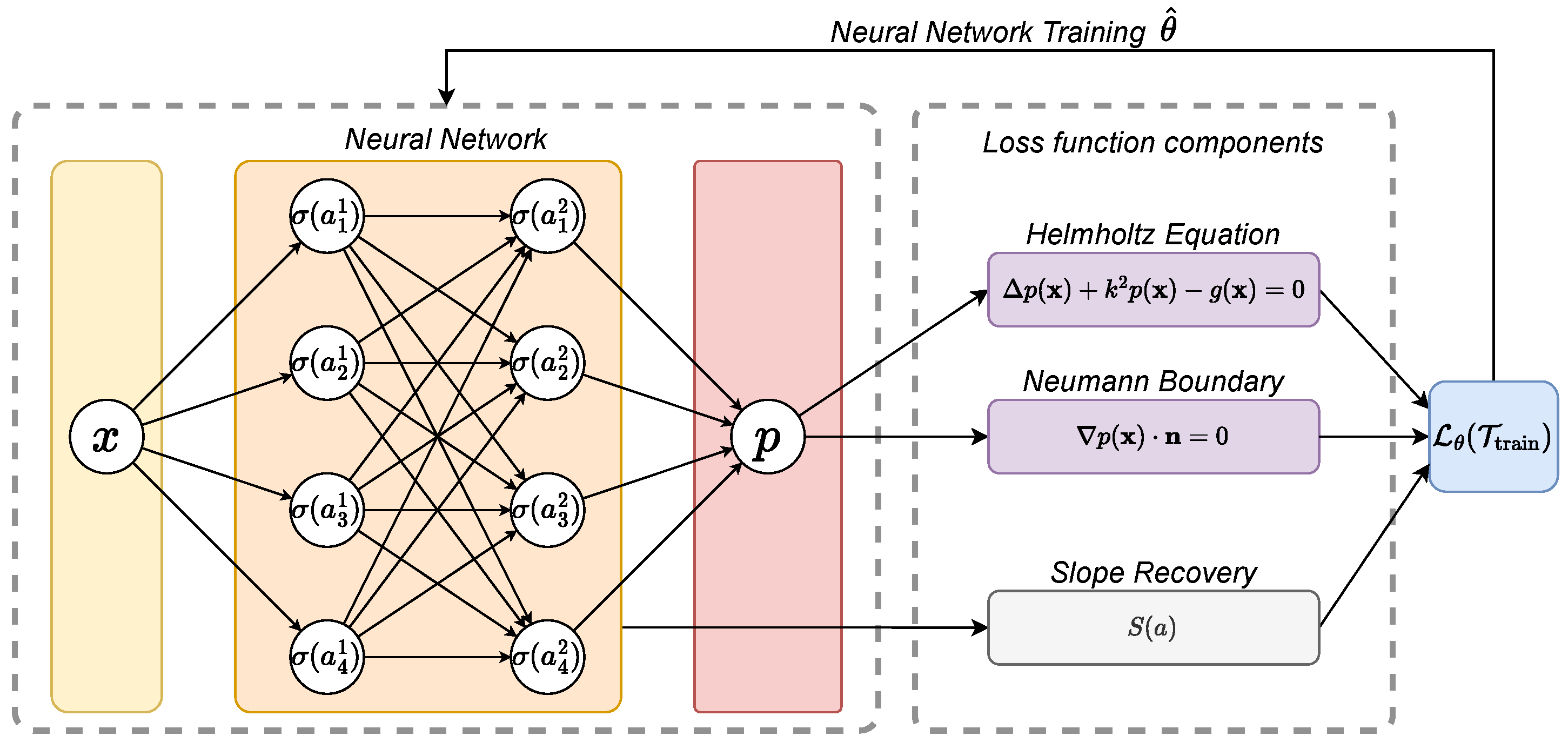
3.3. Locally Adaptive Activation Functions
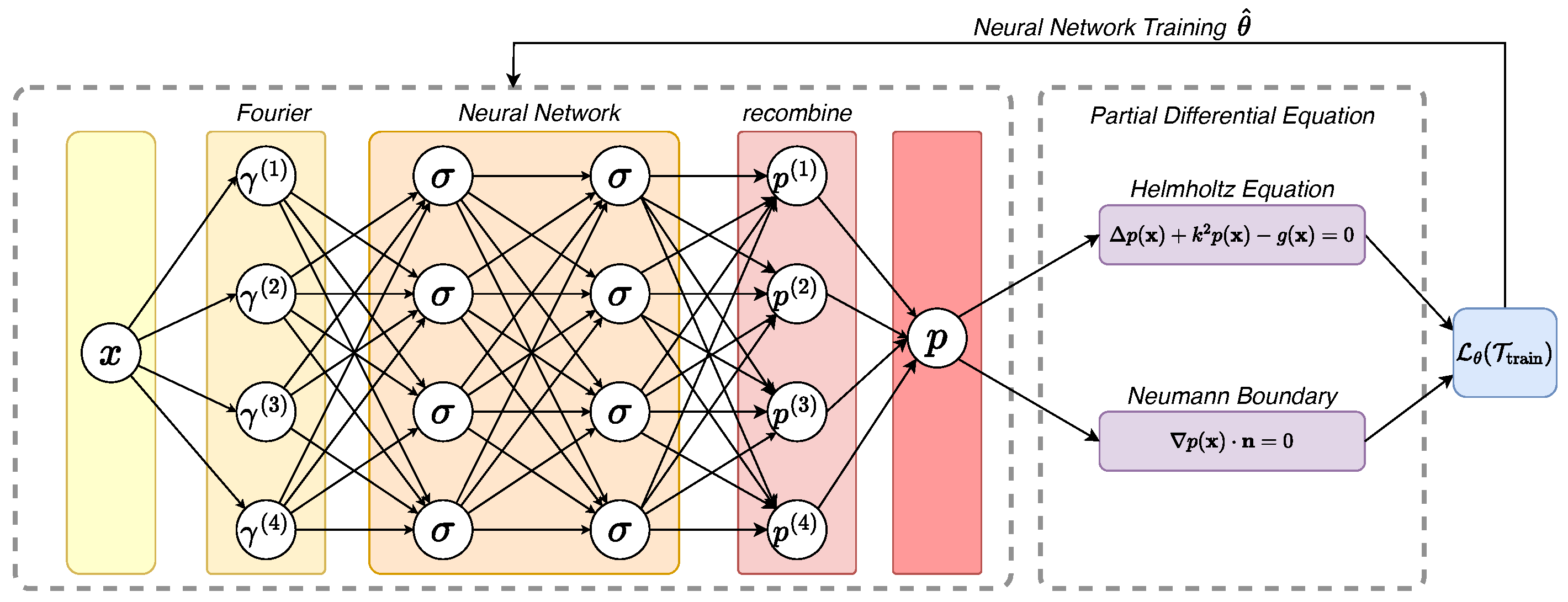
3.4. Multi-Scale Fourier Feature Networks
3.5. Validation and Testing Procedure
4. Hypotheses
5. Results
5.1. Explorative Hyperparameter Study for 1 m
5.2. Adaptive Refinement of Training Set
5.3. Multi-Scale Fourier Feature Networks
5.4. Input Feature Generation
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeong, C.H. Room acoustic simulation and virtual reality-Technological trends, challenges, and opportunities. J. Swed. Acoust. Soc. (Ljudbladet) 2022, 1, 27–30. [Google Scholar]
- Vorländer, M. Computer simulations in room acoustics: Concepts and uncertainties. J. Acoust. Soc. Am. 2013, 133, 1203–1213. [Google Scholar] [CrossRef] [PubMed]
- Schmid, J.D.; Bauerschmidt, P.; Gurbuz, C.; Eser, M.; Marburg, S. Physics-informed neural networks for acoustic boundary admittance estimation. Mech. Syst. Signal Process. 2024, 215, 111405. [Google Scholar] [CrossRef]
- Kraxberger, F.; Kurz, E.; Weselak, W.; Kubin, G.; Kaltenbacher, M.; Schoder, S. A Validated Finite Element Model for Room Acoustic Treatments with Edge Absorbers. Acta Acust. 2023, 7, 48. [Google Scholar] [CrossRef]
- Schoder, S.; Kraxberger, F. Feasibility study on solving the Helmholtz equation in 3D with PINNs. arXiv 2024, arXiv:2403.06623. [Google Scholar]
- Lu, L.; Pestourie, R.; Yao, W.; Wang, Z.; Verdugo, F.; Johnson, S.G. Physics-informed neural networks with hard constraints for inverse design. SIAM J. Sci. Comput. 2021, 43, B1105–B1132. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, L.; Karniadakis, G.E.; Dal Negro, L. Physics-informed neural networks for inverse problems in nano-optics and metamaterials. Opt. Express 2020, 28, 11618–11633. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific machine learning through physics–informed neural networks: Where we are and what’s next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Song, C.; Alkhalifah, T.; Waheed, U.B. Solving the frequency-domain acoustic VTI wave equation using physics-informed neural networks. Geophys. J. Int. 2021, 225, 846–859. [Google Scholar] [CrossRef]
- Escapil-Inchauspé, P.; Ruz, G.A. Hyper-parameter tuning of physics-informed neural networks: Application to Helmholtz problems. Neurocomputing 2023, 561, 126826. [Google Scholar] [CrossRef]
- Gladstone, R.J.; Nabian, M.A.; Meidani, H. FO-PINNs: A First-Order formulation for Physics Informed Neural Networks. arXiv 2022, arXiv:2210.14320. [Google Scholar] [CrossRef]
- Wu, Y.; Aghamiry, H.S.; Operto, S.; Ma, J. Helmholtz-equation solution in nonsmooth media by a physics-informed neural network incorporating quadratic terms and a perfectly matching layer condition. Geophysics 2023, 88, T185–T202. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Shin, Y.; Kawaguchi, K.; Karniadakis, G.E. Deep Kronecker neural networks: A general framework for neural networks with adaptive activation functions. Neurocomputing 2022, 468, 165–180. [Google Scholar] [CrossRef]
- Rasht-Behesht, M.; Huber, C.; Shukla, K.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for wave propagation and full waveform inversions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023120. [Google Scholar] [CrossRef]
- Shukla, K.; Di Leoni, P.C.; Blackshire, J.; Sparkman, D.; Karniadakis, G.E. Physics-informed neural network for ultrasound nondestructive quantification of surface breaking cracks. J. Nondestruct. Eval. 2020, 39, 61. [Google Scholar] [CrossRef]
- Khan, M.R.; Zekios, C.L.; Bhardwaj, S.; Georgakopoulos, S.V. A Physics-Informed Neural Network-Based Waveguide Eigenanalysis. IEEE Access 2024, 12, 120777–120787. [Google Scholar] [CrossRef]
- Pan, Y.Q.; Wang, R.; Wang, B.Z. Physics-informed neural networks with embedded analytical models: Inverse design of multilayer dielectric-loaded rectangular waveguide devices. IEEE Trans. Microw. Theory Tech. 2023, 72, 3993–4005. [Google Scholar] [CrossRef]
- Schoder, S.; Museljic, E.; Kraxberger, F.; Wurzinger, A. Post-processing subsonic flows using physics-informed neural networks. In Proceedings of the 2023 AIAA Aviation Forum, AIAA, San Diego, CA, USA, 12–16 June 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Markidis, S. The old and the new: Can physics-informed deep-learning replace traditional linear solvers? Front. Big Data 2021, 4, 669097. [Google Scholar] [CrossRef]
- Xu, Z.Q.J.; Zhang, Y.; Luo, T.; Xiao, Y.; Ma, Z. Frequency principle: Fourier analysis sheds light on deep neural networks. arXiv 2019, arXiv:1901.06523. [Google Scholar]
- Kraxberger, F.; Kurz, E.; Merkel, L.; Kaltenbacher, M.; Schoder, S. Finite Element Simulation of Edge Absorbers for Room Acoustic Applications. In Proceedings of the Fortschritte der Akustik—DAGA 2023, Hamburg, Germany, 6–9 March 2023; pp. 1292–1295. [Google Scholar]
- Schoder, S.; Spieser, É.; Vincent, H.; Bogey, C.; Bailly, C. Acoustic modeling using the aeroacoustic wave equation based on Pierce’s operator. AIAA J. 2023, 61, 4008–4017. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://tensorflow.org (accessed on 20 October 2024).
- Bradbury, J.; Frostig, R.; Hawkins, P.; Johnson, M.J.; Leary, C.; Maclaurin, D.; Necula, G.; Paszke, A.; VanderPlas, J.; Wanderman-Milne, S.; et al. JAX: Composable Transformations of Python+NumPy Programs. 2018. Available online: https://jax.readthedocs.io (accessed on 15 November 2024).
- Jagtap, A.D.; Kawaguchi, K.; Em Karniadakis, G. Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks. Proc. R. Soc. A 2020, 476, 20200334. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wang, H.; Perdikaris, P. On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2021, 384, 113938. [Google Scholar] [CrossRef]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Schoder, S.; Roppert, K. openCFS: Open Source Finite Element Software for Coupled Field Simulation—Part Acoustics. arXiv 2022, arXiv:2207.04443. [Google Scholar] [CrossRef]
- Ainsworth, M. Discrete dispersion relation for hp-version finite element approximation at high wave number. SIAM J. Numer. Anal. 2004, 42, 553–575. [Google Scholar] [CrossRef]
- Kaltenbacher, M. Numerical Simulation of Mechatronic Sensors and Actuators: Finite Elements for Computational Multiphysics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Hoboken, NJ, USA, 1998. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Sardinia, Italy, 13–15 May 2010; Proceedings of Machine Learning Research. Teh, Y.W., Titterington, M., Eds.; Volume 9, pp. 249–256. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Clanuwat, T.; Bober-Irizar, M.; Kitamoto, A.; Lamb, A.; Yamamoto, K.; Ha, D. Deep learning for classical japanese literature. arXiv 2018, arXiv:1812.01718. [Google Scholar]
- Srl, B.T.; Brescia, I. Semeion Handwritten Digit Data Set; Semeion Research Center of Sciences of Communication: Rome, Italy, 1994. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 12–14 December 2011; Volume 2011, p. 4. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.semanticscholar.org/paper/Learning-Multiple-Layers-of-Features-from-Tiny-Krizhevsky/5d90f06bb70a0a3dced62413346235c02b1aa086 (accessed on 15 November 2024).
- Cao, Y.; Fang, Z.; Wu, Y.; Zhou, D.X.; Gu, Q. Towards understanding the spectral bias of deep learning. arXiv 2019, arXiv:1912.01198. [Google Scholar]
- Rahaman, N.; Baratin, A.; Arpit, D.; Draxler, F.; Lin, M.; Hamprecht, F.; Bengio, Y.; Courville, A. On the spectral bias of neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: Cambridge MA, USA, 2019; pp. 5301–5310. [Google Scholar]
- Ronen, B.; Jacobs, D.; Kasten, Y.; Kritchman, S. The convergence rate of neural networks for learned functions of different frequencies. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Rucz, P.; Ulveczki, M.Á.; Heinz, J.; Schoder, S. Analysis of the co-rotating vortex pair as a test case for computational aeroacoustics. J. Sound Vib. 2024, 587, 118496. [Google Scholar] [CrossRef]
- Wurzinger, A.; Schoder, S. pyCFS-data: Data Processing Framework in Python for openCFS. arXiv 2024, arXiv:2405.03437. [Google Scholar]
- Allen, J.B.; Berkley, D.A. Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 1979, 65, 943–950. [Google Scholar] [CrossRef]
- Krishnapriyan, A.; Gholami, A.; Zhe, S.; Kirby, R.; Mahoney, M.W. Characterizing possible failure modes in physics-informed neural networks. Adv. Neural Inf. Process. Syst. 2021, 34, 26548–26560. [Google Scholar]
- Zeng, C.; Burghardt, T.; Gambaruto, A.M. Training dynamics in Physics-Informed Neural Networks with feature mapping. arXiv 2024, arXiv:2402.06955. [Google Scholar]
- Sallam, O.; Fürth, M. On the use of Fourier Features-Physics Informed Neural Networks (FF-PINN) for forward and inverse fluid mechanics problems. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2023, 237, 846–866. [Google Scholar] [CrossRef]


| in % | CPU Time | |||
|---|---|---|---|---|
| 20 | 1.35 | 1.69 | 5 s | |
| 25 | 0.73 | 1.18 | 15 s | |
| 30 | 0.34 | 0.66 | 33 s | |
| 35 | 0.35 | 0.46 | 1 min 11 s | |
| 40 | 0.43 | 0.33 | 3 min 43 s | |
| 45 | 0.22 | 0.20 | 5 min 12 s | |
| 50 | - | - | 15 min 30 s |
| s in m | 0.2 | 0.1 | 0.05 | 0.02 |
| in % | 4.52 | 5.72 | 7.05 | no convergence |
| W | Training Sequence | in % | ||||
|---|---|---|---|---|---|---|
| 1 | 180 | 5 | sin | P | 90,000 Adams | nc |
| 2 | 180 | 5 | sin | P | 90,000 Adams | 0.77 |
| 3 | 180 | 5 | sin | P | 90,000 Adams | 0.45 |
| 4 | 180 | 5 | sin | P | 90,000 Adams | 0.14 |
| 5 | 180 | 5 | sin | P | 90,000 Adams | 0.07 |
| 1 | 180 | 5 | sin | P | 90,000 Adams + 15,000 LBFGS | nc |
| 2 | 180 | 5 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.61 |
| 3 | 180 | 5 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.42 |
| 4 | 180 | 5 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.13 |
| 5 | 180 | 5 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.07 |
| 1 | 180 | 5 + 50 | sin | P | 90,000 Adams + 15,000 LBFGS | nc |
| 2 | 180 | 5 + 50 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.28 |
| 3 | 180 | 5 + 50 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.42 |
| 4 | 180 | 5 + 50 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.13 |
| 5 | 180 | 5 + 50 | sin | P | 90,000 Adams + 15,000 LBFGS | 0.07 |
| 2 | 180 | 0.02 | sin | P | 90,000 Adams | 24.15 |
| 2 | 180 | 0.2 | sin | P | 90,000 Adams | 9.20 |
| 2 | 180 | 1 | sin | P | 90,000 Adams | 7.19 |
| 2 | 180 | 5 | sin | P | 90,000 Adams | 0.77 |
| 2 | 180 | 50 | sin | P | 90,000 Adams | 0.70 |
| 2 | 180 | 500 | sin | P | 90,000 Adams | 0.019 |
| 3 | 180 | 5 | sin | P | 90,000 Adams | 0.45 |
| 3 | 180 | 50 | sin | P | 90,000 Adams | 0.39 |
| 3 | 180 | 500 | sin | P | 90,000 Adams | 0.041 |
| W | Training Sequence | in % | ||||
|---|---|---|---|---|---|---|
| 2 | 20 | 5 | sin | P | 90,000 Adams | 6.78 |
| 2 | 40 | 5 | sin | P | 90,000 Adams | 0.48 |
| 2 | 60 | 5 | sin | P | 90,000 Adams | 3.49 |
| 2 | 120 | 5 | sin | P | 90,000 Adams | 2.34 |
| 2 | 180 | 5 | sin | P | 90,000 Adams | 0.77 |
| 2 | 240 | 5 | sin | P | 90,000 Adams | 3.90 |
| 2 | 300 | 5 | sin | P | 90,000 Adams | 5.57 |
| 3 | 20 | 5 | sin | P | 90,000 Adams | 11.36 |
| 3 | 40 | 5 | sin | P | 90,000 Adams | 2.35 |
| 3 | 60 | 5 | sin | P | 90,000 Adams | 1.79 |
| 3 | 120 | 5 | sin | P | 90,000 Adams | 1.32 |
| 3 | 180 | 5 | sin | P | 90,000 Adams | 0.45 |
| 3 | 240 | 5 | sin | P | 90,000 Adams | 0.18 |
| 3 | 300 | 5 | sin | P | 90,000 Adams | 3.01 |
| 2 | 20 | 50 | sin | P | 90,000 Adams | nc |
| 2 | 40 | 50 | sin | P | 90,000 Adams | 0.76 |
| 2 | 60 | 50 | sin | P | 90,000 Adams | 1.39 |
| 2 | 120 | 50 | sin | P | 90,000 Adams | 1.81 |
| 2 | 180 | 50 | sin | P | 90,000 Adams | 0.70 |
| 3 | 20 | 50 | sin | P | 90,000 Adams | 5.44 |
| 3 | 40 | 50 | sin | P | 90,000 Adams | 1.32 |
| 3 | 60 | 50 | sin | P | 90,000 Adams | 2.02 |
| 3 | 120 | 50 | sin | P | 90,000 Adams | 0.057 |
| 3 | 180 | 50 | sin | P | 90,000 Adams | 2.37 |
| W | Training Sequence | in % | Training Time in s | ||||
|---|---|---|---|---|---|---|---|
| 2 | 120 | 50 | sin | P(A100) | 90,000 Adams | 1.59 | 591 |
| 2 | 120 | 50 | sin | P | 90,000 Adams | 1.81 | 1502 |
| 3 | 120 | 50 | sin | P | 90,000 Adams | 0.057 | 2304 |
| 2 | 120 | 50 | sin | T1 | 90,000 Adams | 0.70 | 765 |
| 3 | 120 | 50 | sin | T1 | 90,000 Adams | 0.13 | 1268 |
| 2 | 120 | 50 | sin | T2 | 90,000 Adams | 0.55 | 825 |
| 3 | 120 | 50 | sin | T2 | 90,000 Adams | 0.39 | 1263 |
| 2 | 120 | 50 | sin | J | 90,000 Adams | 0.42 | 1168 |
| 3 | 120 | 50 | sin | J | 90,000 Adams | 0.34 | 2046 |
| W | Training Sequence | in % | ||||
|---|---|---|---|---|---|---|
| 2 | 180 | 5 | sin | P | 90,000 Adams | 0.77 |
| 2 | 180 | 5 | ELU | P | 90,000 Adams | nc |
| 2 | 180 | 5 | GELU | P | 90,000 Adams | 1.56 |
| 2 | 180 | 5 | ReLU | P | 90,000 Adams | nc |
| 2 | 180 | 5 | SELU | P | 90,000 Adams | nc |
| 2 | 180 | 5 | sigmoid | P | 90,000 Adams | nc |
| 2 | 180 | 5 | SiLU | P | 90,000 Adams | 9.77 |
| 2 | 180 | 5 | swish | P | 90,000 Adams | 6.09 |
| 2 | 180 | 5 | tanh | P | 90,000 Adams | 2.53 |
| W | Training Sequence | in % | ||||
|---|---|---|---|---|---|---|
| 2 | 180 | 5 | sin | P | 90,000 Adams | 0.77 |
| 2 | 180 | 5 | LAAF-n 1 | T1 | 90,000 Adams | 0.086 |
| 2 | 180 | 5 | LAAF-n 2 | T1 | 90,000 Adams | 0.370 |
| 2 | 180 | 5 | LAAF-n 4 | T1 | 90,000 Adams | 0.120 |
| 2 | 180 | 5 | LAAF-n 8 | T1 | 90,000 Adams | 0.096 |
| Overall Best | Best Sin | Best Sigmoid | Fastest | |
|---|---|---|---|---|
| in % | 0.1938 | 0.195 | 0.21 | 0.204 |
| Training time in s | 621 | 404 | 89 | 50 |
| Learning rate | 0.0009 | 0.00077 | 0.025 | 0.001 |
| 9 | 3 | 10 | 2 | |
| W | 80 | 80 | 12 | 35 |
| tanh | sin | sigmoid | sin | |
| 1 | 0.1 | 4.7 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schoder, S. Physics-Informed Neural Networks for Modal Wave Field Predictions in 3D Room Acoustics. Appl. Sci. 2025, 15, 939. https://doi.org/10.3390/app15020939
Schoder S. Physics-Informed Neural Networks for Modal Wave Field Predictions in 3D Room Acoustics. Applied Sciences. 2025; 15(2):939. https://doi.org/10.3390/app15020939
Chicago/Turabian StyleSchoder, Stefan. 2025. "Physics-Informed Neural Networks for Modal Wave Field Predictions in 3D Room Acoustics" Applied Sciences 15, no. 2: 939. https://doi.org/10.3390/app15020939
APA StyleSchoder, S. (2025). Physics-Informed Neural Networks for Modal Wave Field Predictions in 3D Room Acoustics. Applied Sciences, 15(2), 939. https://doi.org/10.3390/app15020939








