Featured Application
Patient-specific finite element models of degenerative cervical myelopathy (DCM) patients correlate with neurological function, assess disease severity, and can potentially guide personalized surgical planning.
Abstract
Degenerative cervical myelopathy (DCM) is characterized by progressive neurological dysfunction, yet the contribution of intramedullary stress and strain during neck motion remains unclear. This study used patient-specific finite element models (FEMs) of the cervical spine and spinal cord to examine the relationship between spinal cord biomechanics and neurological dysfunction. Twenty DCM patients (mean age 62.7 ± 11.6 years; thirteen females) underwent pre-surgical MRI-based modeling to quantify von Mises stress and maximum principal strains at the level of maximum spinal cord compression during simulated neck flexion and extension. Pre-surgical functional assessments included hand sensation, dexterity, and balance. During flexion, the mean intramedullary stress and strain at the level of maximum compression were 7.6 ± 3.7 kPa and 4.3 ± 2.0%, respectively. Increased intramedullary strain during flexion correlated with decreased right-hand sensation (r = −0.58, p = 0.014), impaired right-hand dexterity (r = −0.50, p = 0.048), and prolonged dexterity time (r = 0.52, p = 0.039). Similar correlations were observed with intramedullary stress. Patients with severe DCM exhibited significantly greater stress during flexion than those with mild/moderate disease (p = 0.03). These findings underscore the impact of dynamic spinal cord biomechanics on neurological dysfunction and support their potential utility in improving DCM diagnosis and management.
1. Introduction
Degenerative cervical myelopathy (DCM) is the most common cause of spinal cord dysfunction in older adults and an important cause of disability and impaired quality of life [1]. Intramedullary stress and strain during neck motion are known contributors to axonal and myelin injury in DCM [2]. However, it is not known if intramedullary stress and strain are linked to neurological dysfunction in DCM. This critical knowledge gap has limited our understanding of the clinical relevance and potential utility of incorporating spinal cord biomechanics into clinical decision-making for DCM patients. Although the direct measurement of intramedullary stress and strain is not feasible in humans, methods to estimate intramedullary stress and strain are expected to improve the evaluation of ongoing spinal cord damage, thereby boosting the accuracy of the diagnosis and management of DCM.
Validated finite element models (FEMs) of the human cervical spine provide a non-invasive assessment of clinical spine biomechanics in relation to its normal biomechanical function (intrinsic-cord-related and external-range-of-motion-related load transfer), injury, degeneration, or surgery [3,4,5]. A FEM is a computational method used to predict the behavior of materials under external mechanical loading, simulating physiological activities [6,7]. Advances in computational capabilities and engineering software have broadened the applications of FEMs in medicine. In spine surgery, FEMs have been used to quantify implant biomechanics, evaluate load distributions in spinal structures, and predict the biomechanical effects of surgical interventions on spinal alignment and stability under physiological conditions [8,9,10]. Additionally, advancements in 3D modeling have enabled the development of patient-specific anatomical models from imaging modalities like MRI and CT.
Prior approaches to the 3D FEM of the cervical spinal cord, however, have used a generic spinal cord model with geometric and material properties from animal and cadaver spinal cord tissue [11,12,13,14]. These generic models do not incorporate the specific geometries of the individual patient’s cervical spine, which are well-known contributors to intramedullary stress and strain [15,16]. While a comprehensive review of patient-specific and generic FEMs is beyond the scope of this study, prior review articles have highlighted challenges faced by previous studies in developing patient-specific models. Some of these challenges include a limited scope for studying generic responses, a lack of advanced imaging tools to obtain accurate patient-specific geometries, and in some cases, limited interdisciplinary collaboration between clinical personnel and modeling teams, which are often based in engineering disciplines [17,18,19,20,21].
The lack of patient-specific data in these models has limited the clinical translation of biophysical modeling. Patient-specific FEMs can quantify intramedullary stress and strain for individual patients more accurately and have greater potential for clinical translation. However, no prior studies have directly linked patient-specific FEM outputs to neurological dysfunction in DCM patients. This study addresses this critical gap by utilizing patient-specific FEMs to determine the relationship between pre-surgical spinal cord biomechanics and pre-surgical neurological function in DCM. By incorporating individualized spinal cord geometries, we aim to assess how intramedullary stress and strain correlate with functional impairments and clinical severity in DCM.
2. Materials and Methods
We prospectively recruited 20 DCM patients between the ages of 18 and 90 who were scheduled for cervical spine surgery at a single academic medical center. All patients were clinically diagnosed with DCM by a board-certified spine surgeon. For enrollment in the study, the diagnosis of DCM included the following features: (1) one or more signs of myelopathy (gait ataxia, positive Romberg’s sign, inability to tandem walk, corticospinal motor deficits, hand atrophy, hyperreflexia, a positive Hoffman sign, upgoing plantar reflexes, or lower limb spasticity); (2) one or more symptoms of myelopathy (impaired hand dexterity, numb hands, gait impairment, bilateral hand paresthesia, L’Hermitte’s phenomena, and/or weakness in arms or legs); and (3) evidence of cervical spinal cord compression during magnetic resonance imaging (MRI). Any subjects unable to tolerate MRI for any reason were also excluded. We excluded patients with a history of trauma, syringomyelia, prior cervical spine surgery, spinal cord hemorrhage, tumor, pregnancy, and patients with other neuromuscular diseases that could explain their symptoms. Institutional review board approval was obtained, and all participants provided written informed consent.
2.1. Generation of Patient-Specific Surface Model from MRI
Patient-specific FEMs of the osteo-ligamentous spine were created from their pre-surgical MRI. A 3T General Electric Premier MRI Scanner was used to acquire a T2-weighted fast spin echo image with a 3D isotropic resolution of 0.8 × 0.8 × 0.8 mm with a TR/TE of 2500/122 ms. Sagittal MRI was used to record the spinal cord level of maximum compression and grade intervertebral disc degeneration at all cervical spine levels [22]. Vertebral body and spinal cord surface geometries were developed from the DICOM images using the Mimics v26.0 (Materialise NV, Leuven, Belgium) software package. Surface patches were applied to delineate the endplate and facet regions. The MRI-derived surface geometry was exported as computer-aided design geometry.
2.2. Finite Element Modeling of Cervical Spine
The 3D cervical spine surface model was imported into ANSA software v22.1.0 (BETA CAE Systems, Farmington Hills, MI, USA) for finite element meshing. T2-weighted MRI was used to grade disk degeneration at each level [22], and the corresponding disk properties were incorporated into the model. The spinal cord FEM model consisted of spinal cord parenchyma, pia mater, dura mater, denticulate ligaments, and cerebrospinal fluid [15]. The model used material properties from human spinal cord tissue that have been reported previously [15]. This patient-specific spinal cord FEM was integrated with the cervical spine model for analysis (Figure 1).
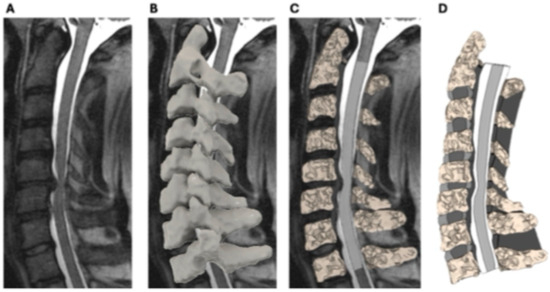
Figure 1.
Illustration of the patient-specific finite element modeling of the cervical spine and spinal cord. Sagittal T2-weighted MRI of the cervical spine showing spinal cord compression at the C5–C6 level (A). MRI data were imported into Mimics software (Materialise NV, Leuven, Belgium) to generate a 3D surface model of the cervical spine (B). Mesh representation of the finite element model, illustrating segmentation of the vertebrae, intervertebral discs, and spinal cord for biomechanical analysis (C,D).
2.3. Loading and Boundary Conditions
The patient-specific FEMs were constrained at the inferior surface of the T1 vertebra in all degrees of freedom, and the sagittal loadings were applied at the superior vertebra. The pure moment load level was 2 Nm each in the flexion and extension modes. An additional follower force of 75 N to simulate the head’s mass and muscle force was applied during flexion and extension using the method described by Patwardhan et al. [23]. The 75 N loading was maintained using LS-PrePost v4.3 and LS-Dyna v9.0.1 (Livermore, CA, USA). Motion-related biomechanical outputs, including the segmental range of motion (ROM), segmental von Mises stress (VMS), and maximum principal strain (MPS) in the spinal cord, were calculated (Figure 2). MPS and vMS at the level of maximum spinal cord compression, as well as the maximum MPS and vMS across the entire cervical spinal cord, were recorded.
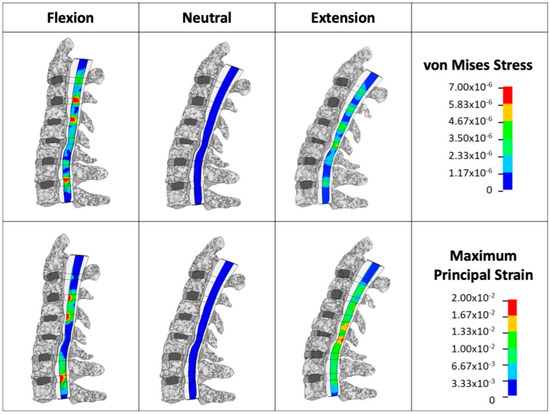
Figure 2.
Finite element model simulation: loading and boundary condition illustration of applied boundary conditions and loading in the patient-specific FEM during simulated neck flexion and extension. Sagittal loadings of 2 Nm and a follower force of 75 N simulate head mass and muscle forces. Segmental von Mises stress (VMS) and maximum principal strain (MPS) were calculated for the spinal cord under these conditions.
2.4. Assessment of Neurological Function
All DCM participants underwent pre-surgical functional testing. Functional measures included the modified Japanese Orthopedic Association scale (mJOA) and Myelopathy Disability Index (MDI), both myelopathy-specific symptom surveys, and the Quick Disabilities of Arm, Shoulder, and Hand (QuickDASH), which surveys upper limb dysfunction during activities of daily living. The Berg Balance Scale (BBS) was used to assess balance. Short Form 36 Physical Component Score version 2 (SF36 PCS) was used to assess quality of life. Upper limb strength, sensation, and dexterity were measured using the Graded Redefined Assessment of Strength, Sensibility, and Prehension Version-Myelopathy (GRASSP-M) [24]. Handgrip strength and pinch strength were assessed separately for the right and left hands using a Jamar Plus Hand Dynamometer and Jamar Digital Pinch Gauge, respectively. The average of three trials for each hand was used for analysis.
2.5. Statistical Analysis
Descriptive statistics were used for demographics and pre-surgical functional scores. FEM outputs and neurological function were related using partial correlations controlling for age. The statistical significance of each relationship was calculated using two-tailed hypothesis tests for the correlation coefficients (r), with significance set at p < 0.05. Statistical analysis was performed using MATLAB (Boston, MA, USA), SPSSv23 (IBM, Armonk, NY, USA), and statistical significance was set at p < 0.05.
3. Results
3.1. Demographics and Pre-Surgical Functional Scores
A total of 20 participants (7 males and 13 females) with a mean age of 62.7 ± 11.6 years were included in this study. Patient demographic information and pre-surgical functional survey scores are summarized in Table 1.

Table 1.
Demographics and Functional Scores.
3.2. Pre-Surgical Intramedullary Stress and Strain
The mean intramedullary stress and strain at the level of maximum compression during flexion was 7.57 ± 3.66 kPa and 0.04 ± 0.02, respectively. Across subjects, the maximum stress/strain in the cervical spinal cord during flexion was 10.6 ± 5.04 kPa and 0.05 ± 0.02, respectively. The mean intramedullary stress and strain at the level of maximum compression during extension was 5.63 ± 2.56 kPa and 0.02 ± 0.01, respectively. Across subjects, the maximum stress/strain in the cervical spinal cord during extension was 7.7 ± 3.32 kPa and 0.03 ± 0.011, respectively (Figure 3). The most common cervical spine level of maximum compression was C5–C6 (40%, n = 8), followed by C6–C7 (25%, n = 5), C4–C5 (20%, n = 4), and C3–C4 (15%, n = 3). In 40% of patients (n = 8), the level of maximum compression coincided with the level of maximum von Mises stress during flexion. The stress and strain during flexion and extension are summarized in Table 2.
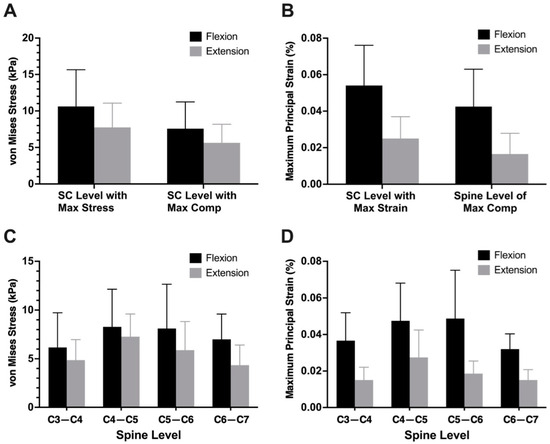
Figure 3.
Mean intramedullary von Mises stress (A) and principal strain (B) during neck flexion and extension from patient-specific finite element models. Mean von Mises stress (C) and principal strain (D) at each cervical spine level during neck flexion and extension. Error bars represent standard deviations.

Table 2.
Mean Intramedullary stress and strain from patient-specific finite element models (n = 20) during flexion and extension.
3.3. Association Between Spinal Cord Biomechanics and Pre-Surgical Neurological Function
Increased intramedullary strain during flexion at the level of maximum compression was correlated with decreased right-hand sensation (r = −0.58, p = 0.014), decreased right-hand dexterity (r = −0.50, p = 0.048), and increased right-hand dexterity time (r = 0.52, p = 0.039). Increased intramedullary stress at the level of maximum cord compression during flexion was associated with decreased right-hand sensation (r = −0.55, p = 0.023), decreased right-hand dexterity (r = −0.536, p = 0.032), and increased right-hand dexterity time (r = 0.55, p = 0.026). The correlation coefficients between spinal cord biomechanics and pre-surgical neurological function are summarized in Figure 4. Spinal cord biomechanics was able to discriminate between DCM severity groups. Intramedullary stress at maximum spinal cord compression during flexion was significantly greater for patients with severe DCM (11.1 ± 4.4 kPa) compared to those with mild/moderate DCM (6.7 ± 3.0 kPa, p = 0.03).
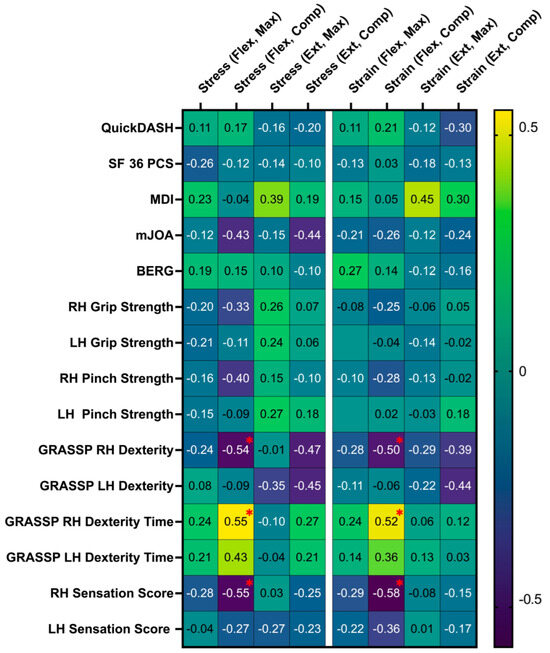
Figure 4.
Partial correlation coefficient (r) matrix relating intramedullary stress and strain under flexion and extension with the neurological function of DCM patients. Statistically significant correlations (p < 0.05) are highlighted with a red asterisk. Abbreviations: RH, right hand; LH, left hand; QuickDASH, Quick Disabilities of the Arm, Shoulder, and Hand; SF 36 PCS, Short Form 36 Physical Component Score; MDI, Myelopathy Disability Index; mJOA, Modified Japanese Orthopedic Association scale; BERG, Berg Balance Scale; GRASSP, Graded Redefined Assessment of Strength, Sensibility, and Prehension; Flex, flexion; Max, maximum; Comp, compression; Ext, extension.
4. Discussion
This study demonstrates for the first time the relationship between intramedullary stress/strain and neurological dysfunction in degenerative cervical myelopathy. Intramedullary stress and strain at the level of maximum spinal cord compression during neck flexion were significantly correlated with sensorimotor hand dysfunction and disease severity. The results of this study highlight the potential clinical utility of spinal cord biomechanics for the diagnoses of degenerative cervical myelopathy.
There is increasing evidence that intrinsic spinal cord forces due to the stress and strain of the cord during neck motion are important contributors to neural injury in DCM [2]. Human cadaver studies have shown that longitudinal stretch (strain) along the spinal cord during flexion is accentuated in the presence of spinal cord compression or kyphosis [25]. Neck motion creates chronic, repetitive stretch injuries that produce neural injury. Evidence for cellular pathways that mediate stretch-associated axonal [26] and myelin [27] injury further supports a larger role for intramedullary stress and strain in the pathophysiology of DCM. The contribution of spinal cord biomechanics to the structural spinal cord suggests a possible mechanism by which intramedullary stress and strain relate to neurological dysfunction in DCM.
Although extrinsic spinal cord compression contributes to spinal cord damage, there is increasing evidence that intrinsic spinal cord forces due to the stress and strain of the cord during neck motion are important contributors to neural injury in DCM [2]. During neck flexion, increased spinal cord strain at the level of maximum cord compression is noted in the dorsal half of the spinal cord affecting the dorsal column–medial lemniscus pathway, which relates to light touch sensation and proprioception relative to the brain. We found that flexion-related intramedullary stress and strain were correlated to hand sensation, and this link is potentially due to the effect of neck flexion on the dorsal columns. In addition, we found that higher pre-surgical intramedullary stress and strain are linked to decreased hand dexterity and prolonged dexterity time. The corticospinal tracts, which control hand dexterity, are located in the dorsal half of the spinal cord, and these tracts experience increased spinal cord tension during neck flexion. Increased tension or deformation in these tracts may disrupt the precision and speed of neural transmission necessary for coordinated hand movements. Together, neck flexion is correlated with sensorimotor dysfunction in DCM due to increased intramedullary stress and strain at the level of maximum cord compression.
There are several possible pathophysiological mechanisms that affect the dorsal spinal cord during neck flexion in DCM patients. Vascular disruption occurs as neck flexion induces elongation and tension in the posterior spinal arteries, leading to a zigzagging pattern and transient reductions in lumen size, which diminish blood flow and increase the risk of ischemic damage to the dorsal columns [28,29,30]. This is compounded by increased intramedullary pressure due to the flexion-related deformation of the spinal cord, which impedes microcirculatory efficiency and could provoke ischemia within the dorsal neural tissues, disrupting the functionality of the dorsal columns and corticospinal tracts [31,32,33]. Moreover, the mechanical tension exerted on the dorsal spinal cord can distort mechanosensitive ion channels [34] and the axonal and myelin [35,36] structures within these pathways, impairing axoplasmic transport and leading to sensory and motor dysfunctions. Additionally, shear stresses from pathological flexion or torsional movements significantly impact the dorsal spinal cord, misaligning or displacing neural tissues, which adversely affects the integrity and function of the dorsal columns and associated neural pathways [37,38].
The findings of this study highlight the potential clinical utility of spinal cord biomechanics in DCM. DCM is characterized by clinico-radiological discordance, where DCM patients with substantial neurological dysfunction may have minimal cord compression [39,40,41]. This can contribute to delays in diagnosis and difficulties with the prognostication of the post-surgical recovery of functions. In these patients, the quantification of spinal cord biomechanics may potentially support an earlier diagnosis and improve the accuracy of predicting post-surgical function. Spinal cord biomechanics can also assist with the diagnosis of certain forms of cervical myelopathy, such as Hirayama’s disease [42], where dynamic spinal cord compression is the primary contributor to neurological dysfunction. The quantification of patient-specific spinal cord biomechanics can also be used for surgical planning. In those patients with high intramedullary stress and strain during neck flexion, motion-preserving surgeries such as cervical laminectomy or laminoplasty are unlikely to provide durable benefits compared to fusion surgeries that will reduce adverse spinal cord tension during neck motion. Our previous work has demonstrated that patient-specific FEMs can be successfully developed for the post-surgical spine, enabling longitudinal assessments of spinal cord biomechanics [15,43,44]. Assessing the link between post-surgical spinal cord biomechanics and function is a goal of future studies.
The limitations of this study include its small sample size, which restricts generalizability and reduces statistical power; a larger sample size would address these issues. Our FEMs also did not differentiate between gray and white matter, as separate gray and white matter properties for the human spinal cord are currently not available. In future studies, we will include patient-specific axial rotation, as well as lateral bending, for a more comprehensive understanding of spinal cord mechanics. Our study is also limited by the lack of patient-specific spinal cord tissue properties in FEMs. Deriving patient-specific tissue properties of the spinal cord is not feasible given the risk of profound neurological damage, and cadaver spinal cord specimens may not reflect true in vivo tissue properties. One technique is the use of advanced microstructural MRI, such as diffusion tensor imaging (DTI). DTI can provide an estimate of spinal cord microstructure, and in our ongoing studies, we are evaluating the link between spinal cord DTI and tissue biomechanics. These studies may create a pathway for non-invasively estimating patient-specific tissue properties to improve the accuracy of patient-specific FE modeling. Despite these limitations, this is the largest study to perform patient-specific cervical spinal cord FEM, and the first to correlate FEM outputs to the patient-reported measures of neurological function.
5. Conclusions
Intramedullary stress and strain contribute to neurological dysfunction in degenerative cervical myelopathy (DCM). This study demonstrates an association between increased stress and strain during neck flexion and pre-surgical impairments in sensory and motor function. These findings emphasize the role of dynamic mechanical forces in DCM and support the potential clinical value of biomechanical modeling. By integrating these spinal cord biomechanics into patient assessments, patient-specific FEMs may improve diagnostic precision and inform surgical strategies.
Author Contributions
Conceptualization, N.Y. and A.V.; methodology, M.R., K.B.D., B.H. and A.V.; software, K.B.D. and B.H.; validation, K.B.D., B.H., N.Y. and A.V.; formal analysis, A.V., M.R. and K.B.D.; investigation, N.Y. and A.V.; resources, N.Y. and A.V.; data curation, M.R., K.B.D. and A.V.; writing—original draft preparation, M.R., K.B.D., O.C. and A.V.; writing—review and editing, M.R., A.V. and N.Y.; visualization, M.R. and B.H.; supervision, A.V. and N.Y.; project administration, A.V.; funding acquisition, A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by AO Spine North America, the North American Spine Society (NASS), and the NIH/NINDS (5R01NS129724).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the Institutional Review Board of Medical College of Wisconsin (protocol code: PRO00043133; date of initial approval: 21 June 2002).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- New, P.W.; Cripps, R.A.; Bonne Lee, B. Global Maps of Non-Traumatic Spinal Cord Injury Epidemiology: Towards a Living Data Repository. Spinal Cord 2014, 52, 97–109. [Google Scholar] [CrossRef] [PubMed]
- Henderson, F.C.; Geddes, J.F.; Vaccaro, A.R.; Woodard, E.; Berry, K.J.; Benzel, E.C. Stretch-Associated Injury in Cervical Spondylotic Myelopathy: New Concept and Review. Neurosurgery 2005, 56, 1101–1113; discussion 1101–1113. [Google Scholar]
- Wheeldon, J.A.; Stemper, B.D.; Yoganandan, N.; Pintar, F.A. Validation of a Finite Element Model of the Young Normal Lower Cervical Spine. Ann. Biomed. Eng. 2008, 36, 1458–1469. [Google Scholar] [CrossRef]
- John, J.D.; Saravana Kumar, G.; Yoganandan, N. Cervical Spine Morphology and Ligament Property Variations: A Finite Element Study of Their Influence on Sagittal Bending Characteristics. J. Biomech. 2019, 85, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Yoganandan, N.; Choi, H.; Purushothaman, Y.; Jebaseelan, D.; Baisden, J.; Kurpad, S. Effects of Different Severities of Disc Degeneration on the Range of Motion of Cervical Spine. J. Craniovertebral Junction Spine 2020, 11, 269–275. [Google Scholar] [CrossRef]
- Welch-Phillips, A.; Gibbons, D.; Ahern, D.P.; Butler, J.S. What Is Finite Element Analysis? Clin. Spine Surg. 2020, 33, 323–324. [Google Scholar] [CrossRef]
- Liu, W.K.; Li, S.; Park, H.S. Eighty Years of the Finite Element Method: Birth, Evolution, and Future. Arch. Comput. Methods Eng. 2022, 29, 4431–4453. [Google Scholar] [CrossRef]
- Chen, H.; Wu, T.; Pan, S.; Zhang, L.; Zhao, Y.; Chen, X.; Sun, Y.; Lu, W.W.; Zhou, F. Finite Element Analysis of a New Preoperative Traction for Cervical Kyphosis: Suspensory Traction. Med. Biol. Eng. Comput. 2024, 62, 2867–2877. [Google Scholar] [CrossRef]
- Li, W.; Han, J.; Xin, Q.; Liu, Q.; Feng, C.; Liu, Y.; Zhang, D. Finite Element Mechanical Analysis of Ipsilateral Approach and Contralateral Approach in Unilateral Bilateral Endoscopic Spine Surgery. J. Orthop. Surg. Res. 2023, 18, 979. [Google Scholar] [CrossRef]
- Purushothaman, Y.; Choi, H.; Yoganandan, N.; Jebaseelan, D.; Baisden, J.; Kurpad, S. A Comparison Study of Four Cervical Disk Arthroplasty Devices Using Finite Element Models. Asian Spine J. 2021, 15, 283–293. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, K.; Ozawa, H.; Sakamoto, N.; Minegishi, Y.; Sato, M.; Itoi, E. Influence of Intramedullary Stress on Cervical Spondylotic Myelopathy. Spinal Cord 2013, 51, 761–764. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nishida, N.; Kanchiku, T.; Imajo, Y.; Suzuki, H.; Yoshida, Y.; Kato, Y.; Nakashima, D.; Taguchi, T. Stress Analysis of the Cervical Spinal Cord: Impact of the Morphology of Spinal Cord Segments on Stress. J. Spinal Cord Med. 2016, 39, 327–334. [Google Scholar] [CrossRef] [PubMed]
- Lévy, S.; Baucher, G.; Roche, P.-H.; Evin, M.; Callot, V.; Arnoux, P.-J. Biomechanical Comparison of Spinal Cord Compression Types Occurring in Degenerative Cervical Myelopathy. Clin. Biomech. 2021, 81, 105174. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.; Paul, R.; Dhar, U.K.; Doulgeris, J.; O’Connor, T.E.; Tsai, C.-T.; Vrionis, F.D. A Review of Finite Element Modeling for Anterior Cervical Discectomy and Fusion. Asian Spine J. 2023, 17, 949–963. [Google Scholar] [CrossRef]
- Vedantam, A.; Purushothaman, Y.; Harinathan, B.; Scripp, S.; Budde, M.D.; Yoganandan, N. Spinal Cord Stress After Anterior Cervical Diskectomy and Fusion: Results from a Patient-Specific Finite Element Model. Ann. Biomed. Eng. 2023, 51, 1040–1051. [Google Scholar] [CrossRef]
- Nikkhoo, M.; Cheng, C.-H.; Wang, J.-L.; Khoz, Z.; El-Rich, M.; Hebela, N.; Khalaf, K. Development and Validation of a Geometrically Personalized Finite Element Model of the Lower Ligamentous Cervical Spine for Clinical Applications. Comput. Biol. Med. 2019, 109, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Fagan, M.J.; Julian, S.; Mohsen, A.M. Finite Element Analysis in Spine Research. Proc. Inst. Mech. Eng. H 2002, 216, 281–298. [Google Scholar] [CrossRef]
- Yoganandan, N.; Myklebust, J.B.; Ray, G.; Sances, A. Mathematical and Finite Element Analysis of Spine Injuries. Crit. Rev. Biomed. Eng. 1987, 15, 29–93. [Google Scholar]
- Yoganandan, N.; Kumaresan, S.; Voo, L.; Pintar, F.A. Finite Element Applications in Human Cervical Spine Modeling. Spine 1996, 21, 1824–1834. [Google Scholar] [CrossRef]
- Voo, K.; Kumaresan, S.; Pintar, F.A.; Yoganandan, N.; Sances, A. Finite-Element Models of the Human Head. Med. Biol. Eng. Comput. 1996, 34, 375–381. [Google Scholar] [CrossRef] [PubMed]
- Gilbertson, L.G.; Goel, V.K.; Kong, W.Z.; Clausen, J.D. Finite Element Methods in Spine Biomechanics Research. Crit. Rev. Biomed. Eng. 1995, 23, 411–473. [Google Scholar] [CrossRef]
- Suzuki, A.; Daubs, M.D.; Hayashi, T.; Ruangchainikom, M.; Xiong, C.; Phan, K.; Scott, T.P.; Wang, J.C. Magnetic Resonance Classification System of Cervical Intervertebral Disk Degeneration: Its Validity and Meaning. Clin. Spine Surg. 2017, 30, E547–E553. [Google Scholar] [CrossRef]
- Patwardhan, A.G.; Havey, R.M.; Ghanayem, A.J.; Diener, H.; Meade, K.P.; Dunlap, B.; Hodges, S.D. Load-Carrying Capacity of the Human Cervical Spine in Compression Is Increased under a Follower Load. Spine 2000, 25, 1548–1554. [Google Scholar] [CrossRef] [PubMed]
- Kalsi-Ryan, S.; Clout, J.; Rostami, P.; Massicotte, E.M.; Fehlings, M.G. Duration of Symptoms in the Quantification of Upper Limb Disability and Impairment for Individuals with Mild Degenerative Cervical Myelopathy (DCM). PLoS ONE 2019, 14, e0222134. [Google Scholar] [CrossRef] [PubMed]
- Breig, A.; Turnbull, I.; Hassler, O. Effects of Mechanical Stresses on the Spinal Cord in Cervical Spondylosis. A Study on Fresh Cadaver Material. J. Neurosurg. 1966, 25, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, W.L.; McCreath, B.J.; Graham, D.I.; Gennarelli, T.A. Cytochemical Evidence for Redistribution of Membrane Pump Calcium-ATPase and Ecto-Ca-ATPase Activity, and Calcium Influx in Myelinated Nerve Fibres of the Optic Nerve after Stretch Injury. J. Neurocytol. 1995, 24, 925–942. [Google Scholar] [CrossRef]
- Maxwell, W.L.; Kosanlavit, R.; McCreath, B.J.; Reid, O.; Graham, D.I. Freeze-Fracture and Cytochemical Evidence for Structural and Functional Alteration in the Axolemma and Myelin Sheath of Adult Guinea Pig Optic Nerve Fibers after Stretch Injury. J. Neurotrauma 1999, 16, 273–284. [Google Scholar] [CrossRef]
- Breig, A. Adverse Mechanical Tension in the Central Nervous System: An Analysis of Cause and Effect: Relief by Functional Neurosurgery; Almqvist & Wiksell International: New York, NY, USA; Wiley: Stockholm, Sweden, 1978; ISBN 978-0-471-04237-2. [Google Scholar]
- Stember, D.M.; Hanson, R.M.; Staudinger, R. Spinal Cord Infarction in Degenerative Cervical Spondylosis. Neurol. Clin. Pract. 2020, 10, e33–e34. [Google Scholar] [CrossRef]
- Fukuda, H.; Kitani, M. Unilateral posterior spinal artery syndrome of the upper cervical cord associated with vertebral artery occlusion. Rinsho Shinkeigaku 1994, 34, 1171–1174. [Google Scholar] [PubMed]
- Jarzem, P.F.; Quance, D.R.; Doyle, D.J.; Begin, L.R.; Kostuik, J.P. Spinal Cord Tissue Pressure during Spinal Cord Distraction in Dogs. Spine 1992, 17, S227–S234. [Google Scholar] [CrossRef]
- Tachibana, S.; Kitahara, Y.; Iida, H.; Yada, K. Spinal Cord Intramedullary Pressure. A Possible Factor in Syrinx Growth. Spine 1994, 19, 2174–2178; discussion 2178–2179. [Google Scholar] [CrossRef] [PubMed]
- Kitahara, Y.; Iida, H.; Tachibana, S. Effect of Spinal Cord Stretching Due to Head Flexion on Intramedullary Pressure. Neurol. Med. Chir. 1995, 35, 285–288. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sorum, B.; Docter, T.; Panico, V.; Rietmeijer, R.A.; Brohawn, S.G. Pressure and Ultrasound Activate Mechanosensitive TRAAK K+ Channels through Increased Membrane Tension. bioRxiv 2023. [Google Scholar] [CrossRef]
- Cinelli, I.; Destrade, M.; McHugh, P.; Duffy, M. Effects of Nerve Bundle Geometry on Neurotrauma Evaluation. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3118. [Google Scholar] [CrossRef]
- Shi, R.; Whitebone, J. Conduction Deficits and Membrane Disruption of Spinal Cord Axons as a Function of Magnitude and Rate of Strain. J. Neurophysiol. 2006, 95, 3384–3390. [Google Scholar] [CrossRef]
- Harrison, D.E.; Cailliet, R.; Harrison, D.D.; Troyanovich, S.J.; Harrison, S.O. A Review of Biomechanics of the Central Nervous System—Part II: Spinal Cord Strains from Postural Loads. J. Manip. Physiol. Ther. 1999, 22, 322–332. [Google Scholar] [CrossRef]
- Harrison, D.E.; Cailliet, R.; Harrison, D.D.; Troyanovich, S.J.; Harrison, S.O. A Review of Biomechanics of the Central Nervous System—Part III: Spinal Cord Stresses from Postural Loads and Their Neurologic Effects. J. Manip. Physiol. Ther. 1999, 22, 399–410. [Google Scholar] [CrossRef]
- Nagata, K.; Yoshimura, N.; Muraki, S.; Hashizume, H.; Ishimoto, Y.; Yamada, H.; Takiguchi, N.; Nakagawa, Y.; Oka, H.; Kawaguchi, H.; et al. Prevalence of Cervical Cord Compression and Its Association with Physical Performance in a Population-Based Cohort in Japan: The Wakayama Spine Study. Spine 2012, 37, 1892–1898. [Google Scholar] [CrossRef]
- Nemani, V.M.; Kim, H.J.; Piyaskulkaew, C.; Nguyen, J.T.; Riew, K.D. Correlation of Cord Signal Change with Physical Examination Findings in Patients with Cervical Myelopathy. Spine 2015, 40, 6–10. [Google Scholar] [CrossRef]
- Rhee, J.M.; Heflin, J.A.; Hamasaki, T.; Freedman, B. Prevalence of Physical Signs in Cervical Myelopathy: A Prospective, Controlled Study. Spine 2009, 34, 890–895. [Google Scholar] [CrossRef]
- Foster, E.; Tsang, B.K.-T.; Kam, A.; Storey, E.; Day, B.; Hill, A. Hirayama Disease. J. Clin. Neurosci. 2015, 22, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.; Palmer, P.; Harinathan, B.; Banurekha Devaraj, K.; Yoganandan, N.; Vedantam, A. Using Finite Element Models to Assess Spinal Cord Biomechanics after Cervical Laminoplasty for Degenerative Cervical Myelopathy. Diagnostics 2024, 14, 1497. [Google Scholar] [CrossRef] [PubMed]
- Vedantam, A.; Harinathan, B.; Warraich, A.; Budde, M.D.; Yoganandan, N. Differences in Spinal Cord Biomechanics after Laminectomy, Laminoplasty, and Laminectomy with Fusion for Degenerative Cervical Myelopathy. J. Neurosurg. Spine 2023, 39, 28–39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).