1. Introduction
Flow control is the branch of fluid mechanics where techniques to manipulate a flow in view of a technological objective are studied. Among the most pursued goals of flow control, aerodynamic drag reduction and noise reduction stand out as crucial technological challenges.
The former is particularly relevant in the turbulent regime, where the comparatively large wall shear stresses lead to a large consumption of energy required to drive the flow, for instance, as energy required to pump a fluid through a duct or to propel a body through a still fluid. A large number of drag-reducing techniques have been developed over the last decades; they are typically classified as ‘passive’ or ‘active’, depending on whether or not energy is introduced in the flow [
1]. Losses due to skin-friction are particularly difficult to abate, as they are intrinsic of near-wall turbulence and descend directly from the interaction between the structure of turbulence and the solid wall. A classic example of a passive skin-friction drag reduction technique is represented by riblets, which are probably the most promising passive approach to date. Riblets are tiny streamwise corrugations of the wall surface which yield skin-friction reduction up to 9% in a turbulent channel flow at low speed [
2]. This figure is bound to reduce significantly down to 1–2% of the aerodynamic drag once a typical aircraft in cruise flight is considered [
3]. Hence, to achieve larger drag reduction, active approaches are considered. Among them, a class known as ‘spanwise forcing’ stands out for its robustness, performance, and simplicity. A recent review of spanwise forcing for drag reduction can be found in Ref. [
4]. In this type of forcing, the boundary condition of the spanwise component of the flow velocity at the wall is imposed as an unsteady, spatially periodic distribution. The most efficient technique of this class is the use of streamwise traveling waves of spanwise velocity (StTWs), introduced by Quadrio et al. [
5]. Within this framework, the spanwise velocity component of the velocity at the wall varies in time and space according to
where
A is the amplitude of the forcing,
and
are the spatial and temporal frequencies of the waves, and
x and
t denote the streamwise and temporal coordinates, respectively. StTWs modify the near-wall velocity profile and are capable of reducing skin-friction drag with rates up to
for intermediate values of
A; furthermore, this kind of control yields the largest net energy savings among the active techniques [
5]. Experimental realizations of such forcing were provided in a pipe flow [
6]; the actuator was later adapted to planar geometry [
7,
8]. Gallorini and Quadrio [
9] characterized the spatially discrete waveform that is typical of these experiments. The effects of the Reynolds number (
) on skin-friction reduction induced by StTWs was assessed in the thorough study by Gatti et al. [
10]. The compressibility effects in a plane channel flow were assessed by Gattere et al. [
11], who showed that no beneficial or detrimental effects derive from compressibility, once the comparison with the unmanipulated flow is carried out properly. The performance of StTWs in non-planar geometries was analyzed by Quadrio et al. [
12]. The latter study carried out a preliminary analysis on the effects of StTWs applied on a transonic wing slab: they employed direct numerical simulations (DNSs) to simulate the turbulent flow around the wing at a cruise Mach number and at a relatively small value of the Reynolds number. Their analysis was recently extended by Berizzi et al. [
13], who carried out a parametric study on the same setup by varying the control input of the forcing and the angle of attack of the airflow. It was shown that the drag of the airfoil alone can be reduced up to 4%; extrapolating the savings to a full aircraft, a potential reduction of 12% in the total drag force of the aircraft at a negligible power cost was estimated. They also provided the first description of the effects of StTWs on the flow field on the wing, focusing in particular on the interaction between the control effects, the suction-side shock wave, and the turbulent boundary layer.
Flow control for noise reduction is clearly a different topic, where again active and passive strategies coexist. Passive techniques for noise reduction rely, for example, on superficial roughness or on porous media coatings [
14]. The primary effect of the surface treatment is the partial dissipation of acoustic energy into heat, or its reflection towards the original source [
1]. Another important example of passive noise reduction is the technique adopted in the jet flows exiting from airplane engines: since the radiated noise increases with the Mach number, the solution typically exploited is to increase the so-called ‘bypass ratio’ of the outflow, thus reducing the speed and the temperature of the outflow, eventually lowering noise. Recently, the reduction in the tonal, trailing-edge noise of a NACA0012 airfoil at relatively low Reynolds and Mach numbers was attempted by placing small superficial roughness elements at the wall [
15,
16]. Examples of active control techniques for noise reduction in aeronautical applications are the blowing and/or suction of the boundary layer [
17] and the use of plasma actuators [
18]. A third group of sound-abating technologies is made by the ‘reactive’ noise suppression systems [
1]. These rely on the generation of additional noise which, due to its amplitude and phase, interferes destructively with the noise generated by the sound source, thus reducing it locally. Also in this case, a supply of energy is required; the approach is inevitably more complicated than the former ones, as elements such as an acoustic sensor and a controller for generating the so-called “anti-sound” are needed. These kinds of systems have been employed successfully, for example, in combustion chambers, where they have drastically reduced noise and flame instabilities, thus improving the performance and efficiency of this component of thermal engines.
Flow control for turbulent drag and noise reduction are typically two distinct research domains and are thus seldom addressed together. Hence, only a limited number of studies exists, where the effect of one kind of flow control on the goal of the other is considered. Two of the few examples are the recent work by Zhang et al. [
14], who showed the effects of a uniform porous coating on both drag and noise reduction in a cylinder configuration, and by Muhammad and Chong [
19], who performed an experiment by placing riblets on a portion of an aerodynamic profile; they concluded that the passive device could potentially reduce the airfoil self-noise in low and high frequency ranges. To the authors’ knowledge, the effects of spanwise forcing for skin-friction drag reduction on the aeroacoustic field have never been considered so far in the literature. The present study intends to investigate, via direct numerical simulations (DNSs), the effects of spanwise forcing for turbulent drag reduction on the near-field pressure fluctuations around a transonic wing. Our goal is to assess the near-field changes induced by the control, and to observe whether this type of forcing, that is very effective in drag reduction, possibly yields noise increase as an undesired side effect. To this aim, the dataset produced by Berizzi et al. [
13] will be studied for the physical setup of a compressible, transonic flow around a wing slab with a shock wave. While the simulations have been carried out and described in that previous study, their analysis presented here is entirely original.
The paper is structured as follows:
Section 2 briefly presents the numerical methods adopted for the computations, while
Section 3 shows the main modifications of the near-wing flow field ensuing from the forcing.
Section 4 describes the main effects of StTWs on the noise field close to the profile by focusing on its intensity and frequency content, while in
Section 5 we further analyze the noise modifications in relationship with the classically adopted performance indicators of the wing. Finally,
Section 6 presents the conclusions of the study.
3. The Near-Field Flow
We start by describing the effects of flow control via StTWs on the wall stresses close to the trailing edge of the wing, linking them to the modifications of the near-field velocity field, with a particular emphasis on its wake. Our previous analysis described in Ref. [
13] was focused on the aerodynamic forces acting on the wing, and did not consider the flow field around it.
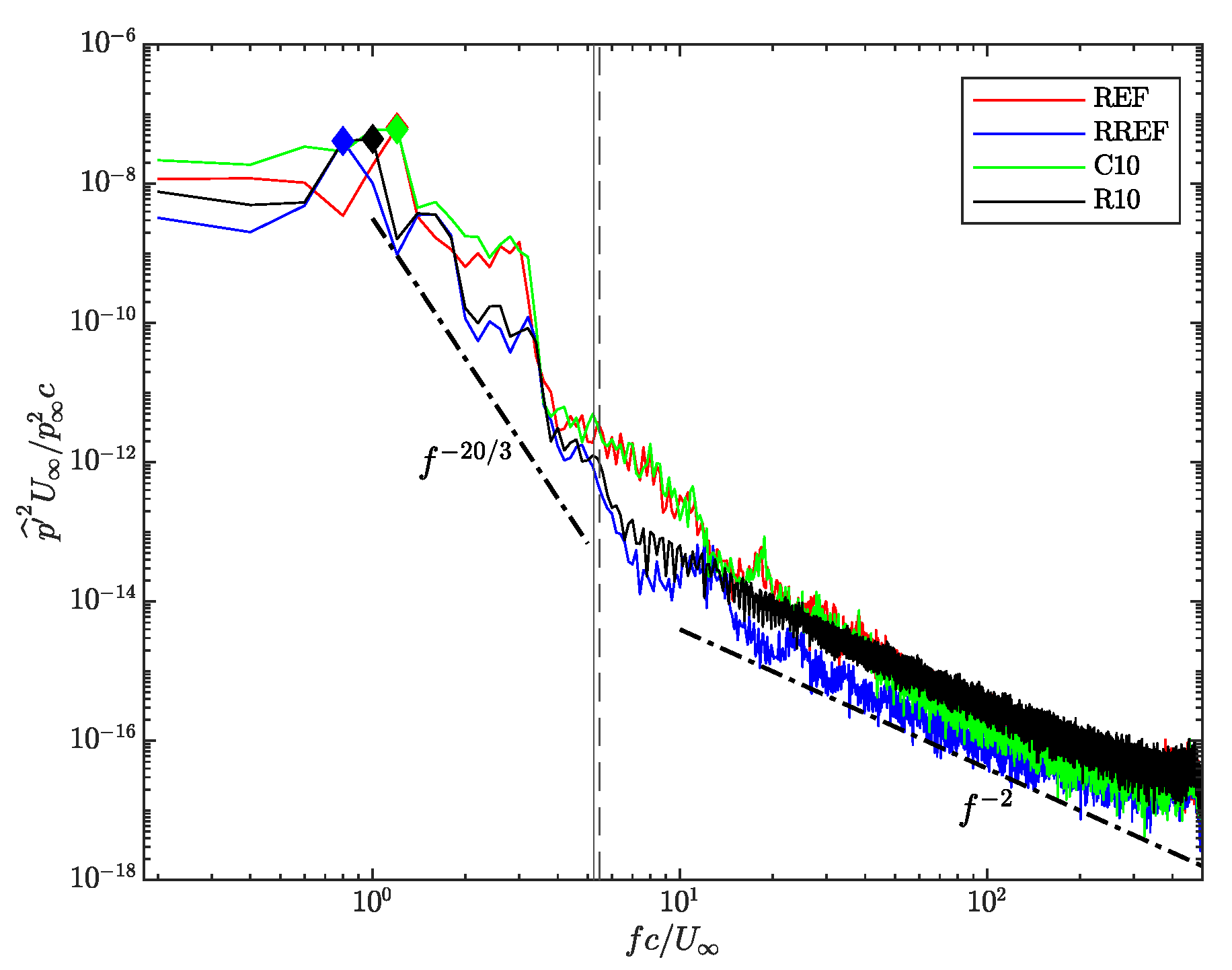
Figure 3 plots an instantaneous snapshot of the spatial distribution of the pressure fluctuations of the transonic flow around the wing in the reference uncontrolled (REF) simulation. The figure gives an overview of the rich physics of the flow, and of how well it can be captured with a DNS. A thorough description of the flow was already given in [
12,
13] and will not be repeated in detail here. In a nutshell, the initially subsonic flow is compressed and slowed down by approaching the leading edge. Then, on the suction side the airflow undergoes an abrupt acceleration (or ‘expansion’) and rapidly becomes supersonic, remaining so for about half the profile chord. The supersonic region (delimited by the white sonic line) is terminated by a shock wave, which results from the compression of the supersonic flow in the aft part of the wing. The shock interacts with the boundary layer, increasing its thickness and enhancing pressure fluctuations downstream of the interaction. Close to the trailing edge, the flow is further slowed down by the adverse pressure gradient, which eventually causes flow separation. On the pressure side, instead, the flow is accelerated downstream of the leading edge, but does not reach supersonic conditions. The most intense pressure fluctuations are detected in the post-shock region above the suction side, and below the pressure side. Large-scale eddies, visualized as pressure fluctuations of alternating signs, characterize the wake and the boundary layers. The latter, which become turbulent downstream of the tripping (see
Section 2), feature different characteristics depending on the wing side: on the suction side, fluctuations are relatively weak down to the shock wave/boundary layer interaction region, which enhances turbulence (a common source of noise, together with the trailing-edge separation). Beneath the profile, instead, pressure fluctuations are significant only in the trailing-edge region.
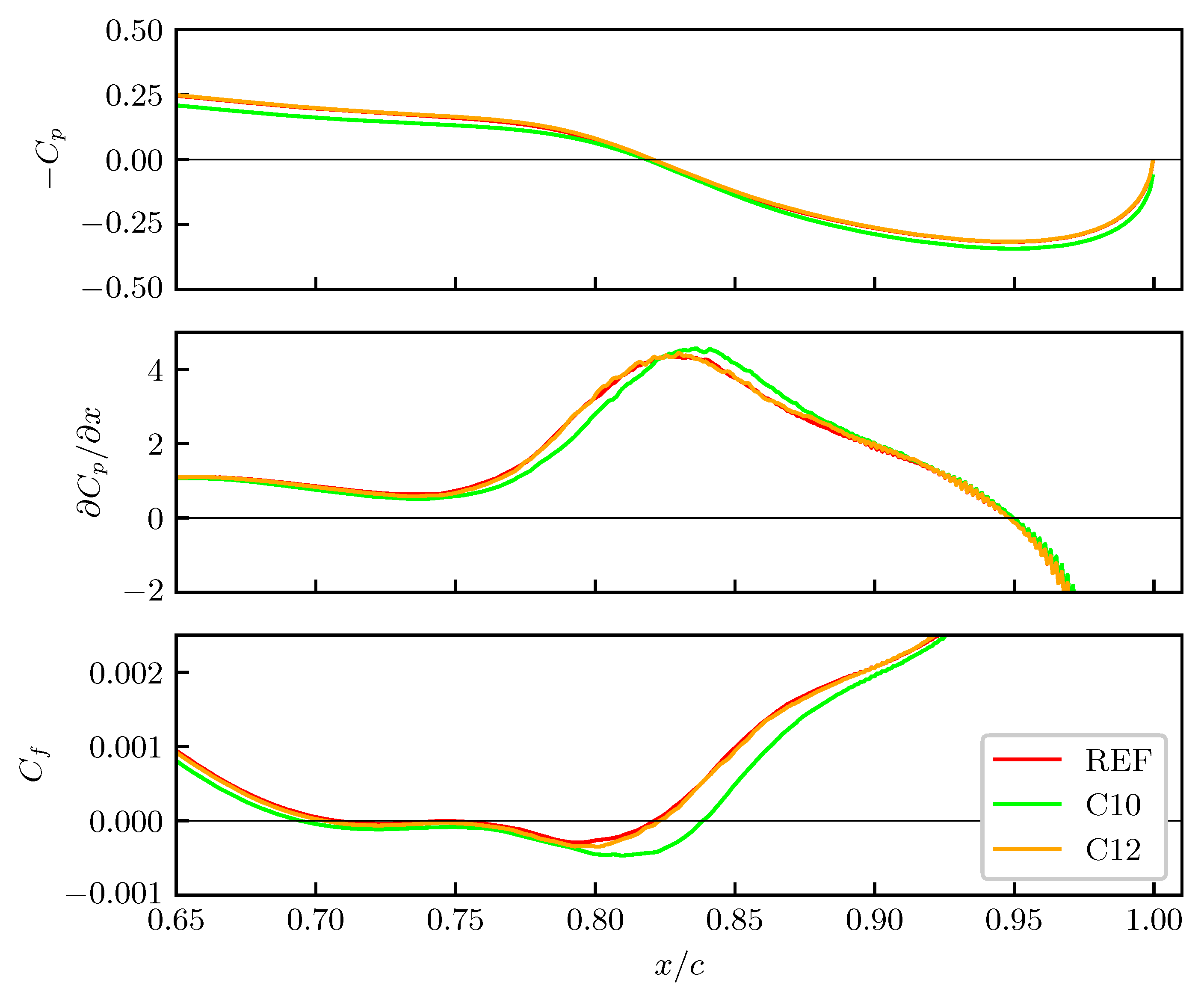
Figure 4 plots, for cases REF, C10, and C12, a detail of the mean pressure (
) and friction (
) coefficients, together with the
x-derivative of the pressure gradient (
), close to the trailing edge of the wing on its pressure side. StTWs, albeit applied on the suction side only, do have a minimal influence on the flow properties of the pressure side too, as a consequence of the changes to the airfoil circulation. On the upper panel, the pressure coefficients of cases REF and C12 basically overlap. The curve relative to simulation C10, instead, features slightly higher values of
. In the lower panel, a region of separated flow is detected by the negative values of the friction coefficient: the regions where
in cases REF and C12 overlap, while the one relative to case C10 is larger by some percent chord units. In Ref. [
13], it was shown for the suction side how the StTWs contribute to the generation of a recirculation bubble in the region of the shock foot. In particular, it was shown that spanwise forcing induces a separation, whose extension is enlarged in a measure that depends on the the position of the shock and on the skin-friction reduction rate. Here, on the contrary, we observe that on the opposite pressure side, separation is already present in the unmanipulated flow. Interestingly, StTWs modify the adverse pressure gradient on the pressure side; this is shown in the central panel via the
x-derivative of the pressure coefficient. When lift is increased (case C10), the peak of
observed in case REF is slightly delayed and intensified, thus leading to a stronger separation. The link between the forcing applied on the suction side and the recirculation bubble below the pressure side is arguably a variation in the characteristics of the wake and of the circulation around the profile.
The left panel of
Figure 5 shows the velocity profile in the wake, for the reference simulation (black dashed line) and for a subset of ten simulations extracted among cases C1–C20. At a first glance, the wake profiles for the controlled cases appear to overlap with the non-controlled one. However, it is possible to observe that, in general, the wake is slightly translated downstream when the control is applied. Furthermore, the colormap, which encodes the variation in the lift coefficient of the wing, brings to light that larger increases in the lift coefficient correspond to larger shifts of the wake towards negative values of
.
For each point of the wake profile, the percentage variation in the controlled cases with respect to the reference simulation is computed as
and the results are shown in the right panel of
Figure 5. The already mentioned downward shift of the wake, which in the left panel is somehow difficult to identify, becomes evident here as positive values of
in the upper half, and negative values in the lower half of the wake. The only case in which the velocity in the wake is globally reduced with respect to the reference case is simulation C12, i.e., the one in which the control parameters of StTWs yield skin-friction increase and lift decrease (indeed,
). In this case, in fact,
is negative for the whole transversal extent of the wake. Finally, it is worth highlighting that the percentage variations in the velocity profiles never exceed
.
5. Discussion
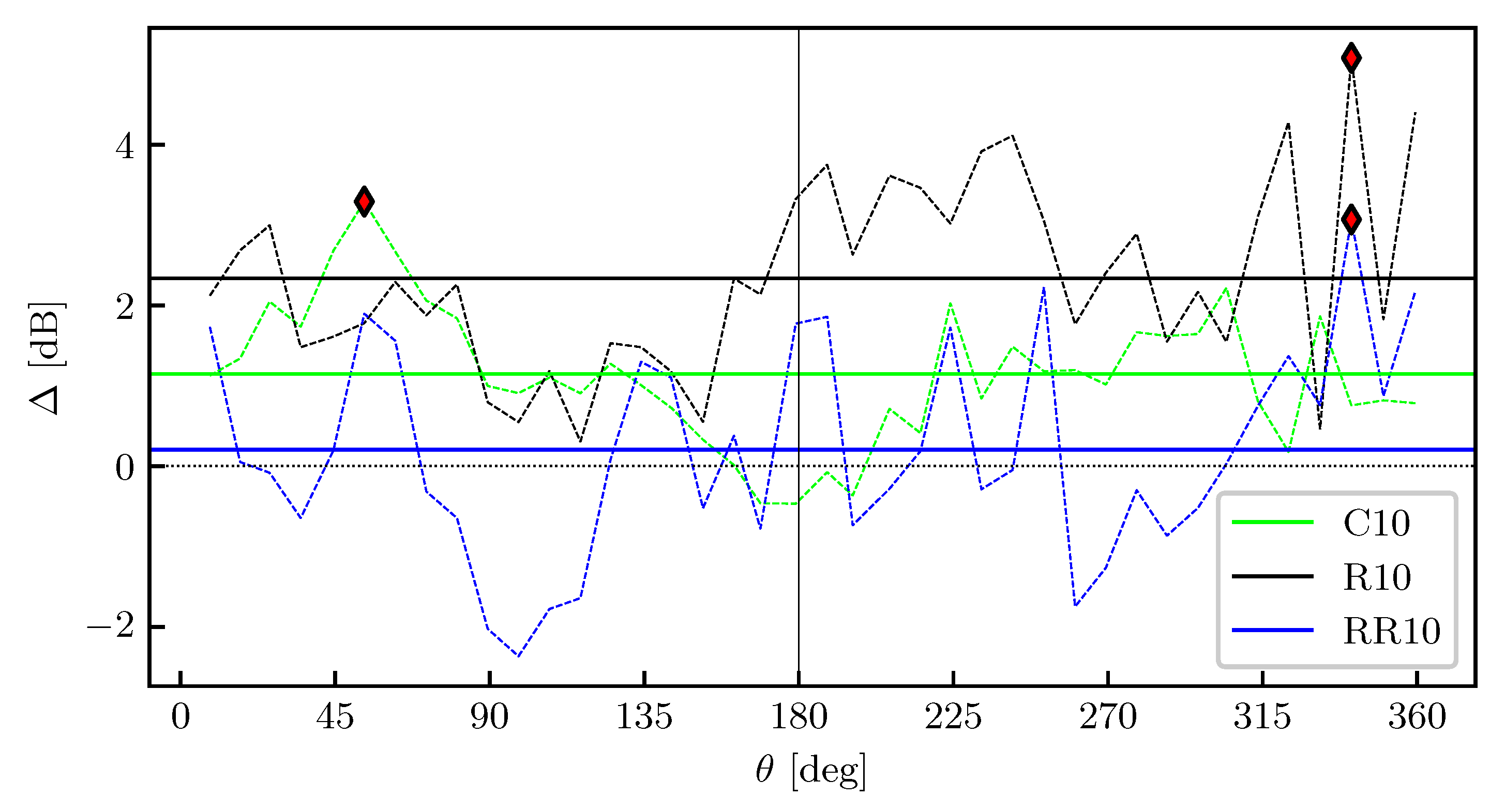
In this section, we connect the application of flow control via StTWs to the variation in noise intensity, previously discussed in
Section 4. In particular, we consider the relationship between the changes
plotted in
Figure 7 and the percentage increase in the lift and drag coefficients of the wing (
and
, respectively) that derive from the activation of spanwise forcing.
We have also observed that mean, azimuthally averaged changes in OASPL
and the lift coefficient do not share a similar dependency on the control parameters. A quantitative link between OASPL and the drag coefficient, instead, is provided in
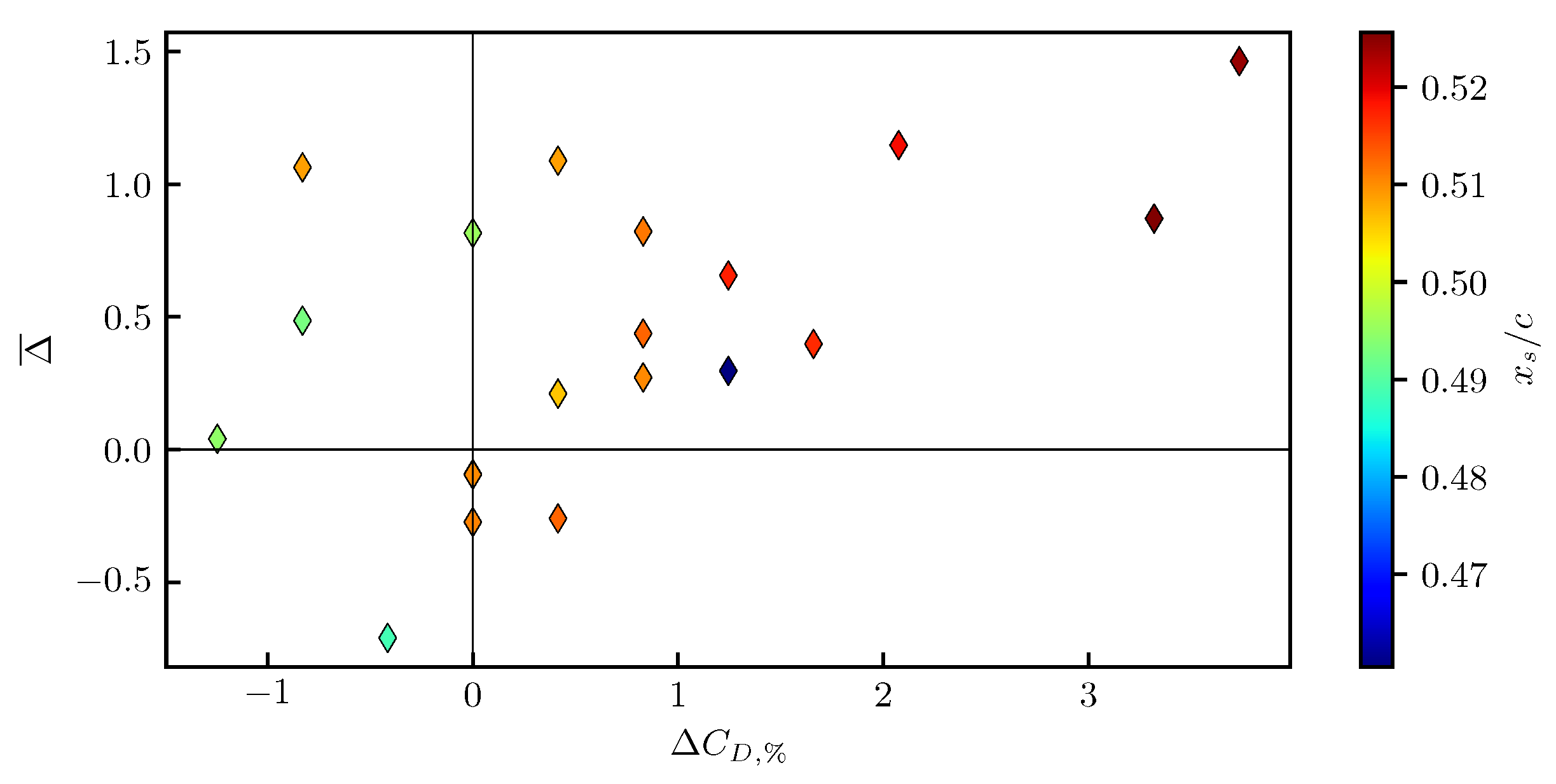
Figure 10. Here, we compare the averaged change
of OASPL with the percentage change in the drag coefficient
for the simulations at constant forcing intensity
A and angle of attach
, namely cases C1–C20. The figure shows that the larger is
, the larger is the mean increase in the overall sound pressure level, and vice versa. The mean position of the shock wave
, which affects the lift and the drag coefficients [
13], is color-coded in
Figure 10. While the cases with the largest drag reduction also feature the most delayed shock,
Figure 10 does not provide evidence for the existence of a clear relationship between
and
. For instance, the data point corresponding to the largest
is the one featuring the largest
, but the simulation with the lowest drag increase (
) does not yield the most upstream shock. Hence, we conclude that the observed noise increase should be arguably related to the increase in the aerodynamic drag, and not to the displacement of the shock wave.
In
Section 4.2, we have described the variations in the frequency content of the noise signal measured by a single specific observer. It is useful to verify whether or not those observations can be extended to probes in other azimuthal positions. Hence, we investigate the Fourier transforms for the acoustic signals of all observers in the reference uncontrolled case (REF), and in one controlled case at
(C10).
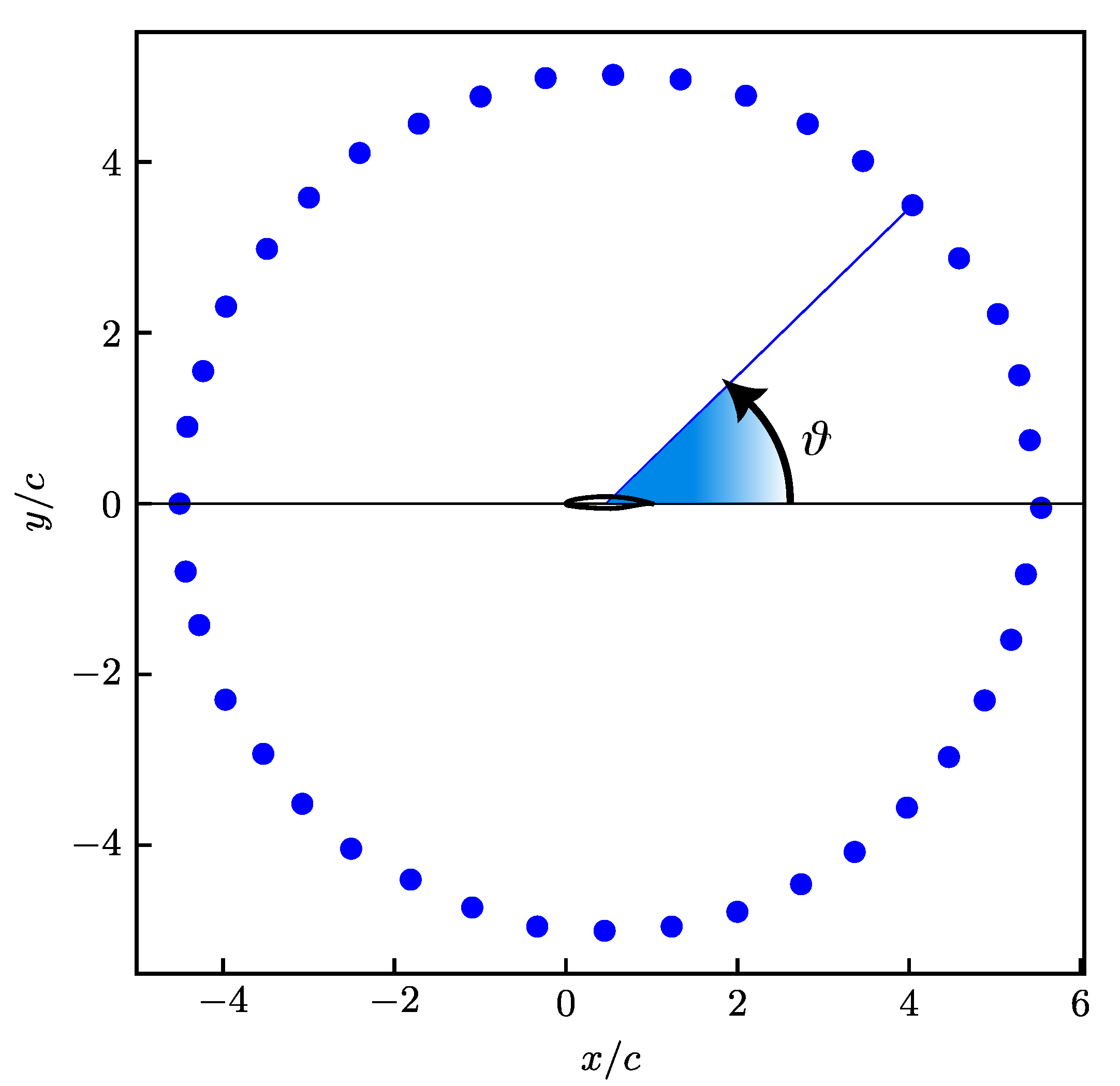
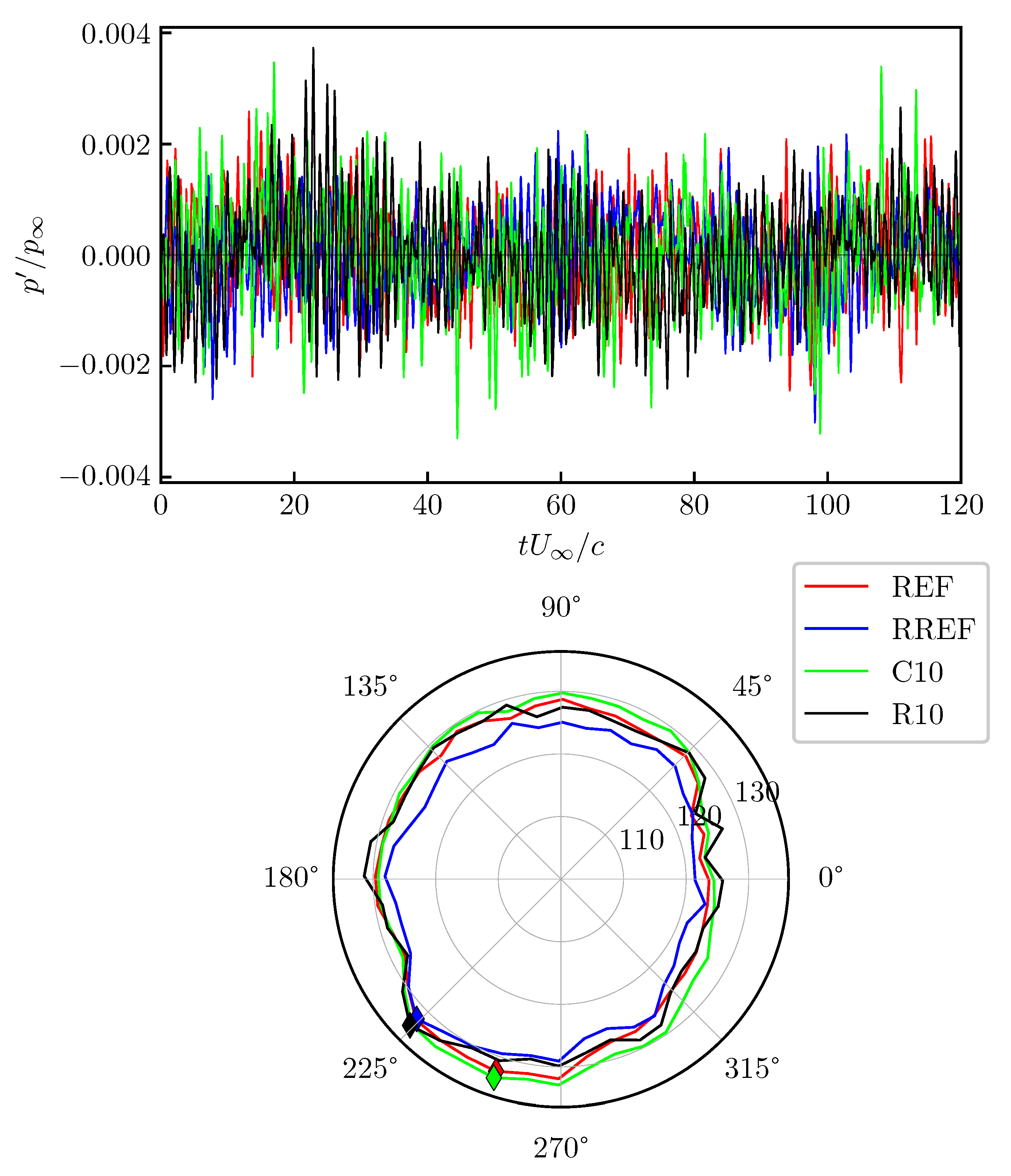
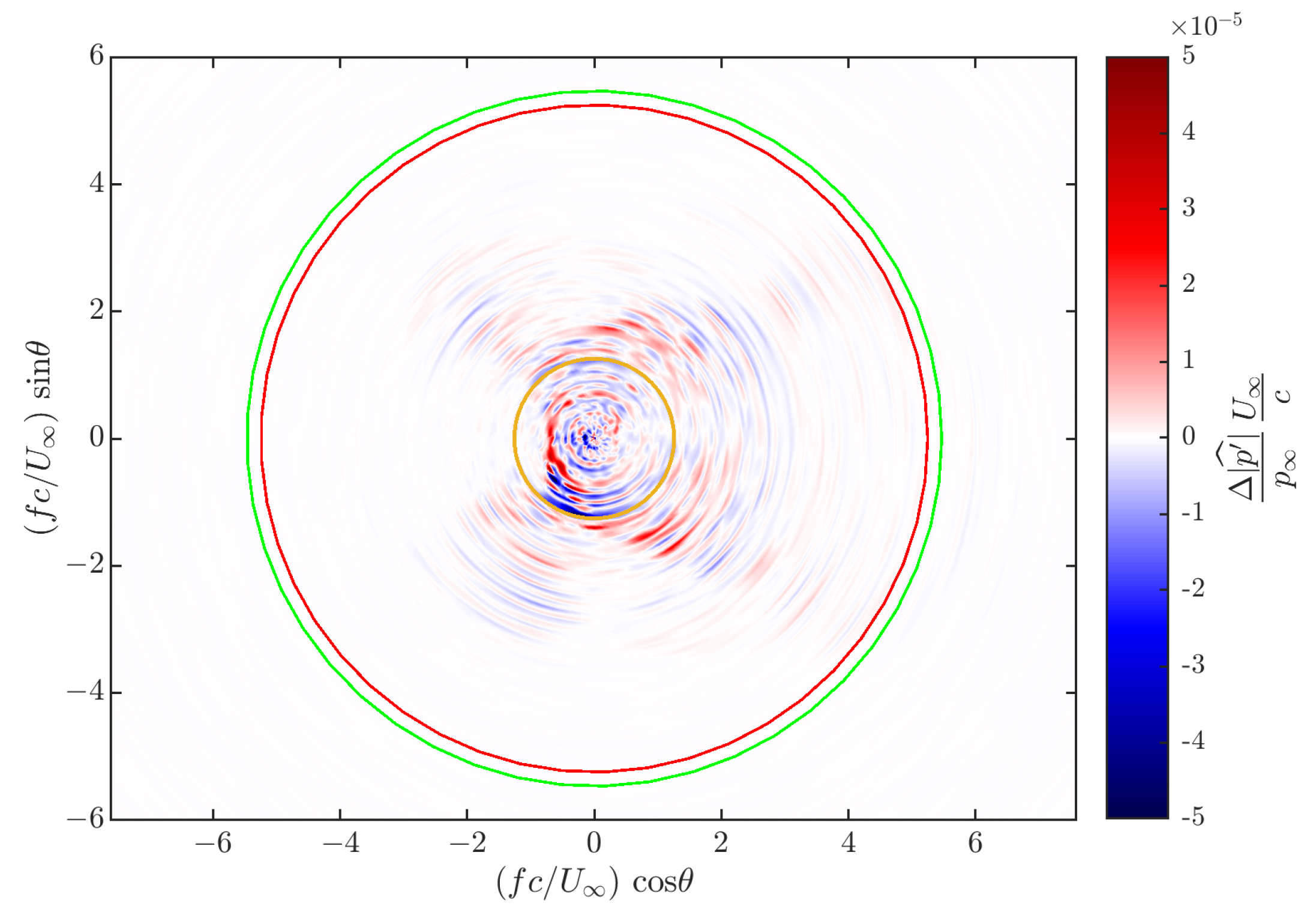
Figure 11 represents at once the absolute value of the Fourier coefficients obtained from the data of all the probes in the REF case (left panel) and in case C10 (right panel). In each panel, the distance of a point from the center of the picture represents a fixed value of frequency (for instance, the radius of the red circle corresponds to the temporal frequency of the forcing in case C10). The angle identified by the position vector of a point in the plot and the horizontal axis, instead, represents the angular position
of the probe. Since only 40 discrete probes are available, the values of this ‘directional’ Fourier transform between the probes have been azimuthally interpolated for the plot.
In the left panel, the largest values of the Fourier transform are found, as expected by the previous analysis of the OASPL presented in
Section 4, in the direction opposite to the shock wave, i.e., at
. The distinct peaks at
and
could be the trace of tonal noise, probably generated at the trailing edge of the wing. In fact, the presence of a separation bubble in this region (previously mentioned in
Section 3) is the necessary condition for the generation of tonal noise, as explained by Nash et al. [
31]. Their experimental study considered subsonic flow at moderate values of the Reynolds number, with almost zero turbulence intensity: instabilities due to laminar–turbulent transition above the laminar separation bubble were the cause for tonal noise development. Indeed, the interaction between the upper and lower surface boundary layers at the trailing edge can produce either tonal noise (if one flow is turbulent and the other is transitional) or broadband noise (if both flows are turbulent) [
32]. Pröbsting et al. [
33] studied experimentally the self-noise of a NACA0012 airfoil with both tripped and non-tripped boundary layers. In particular, they studied the tonal noise as a function of the Reynolds number and the angle of attack. When tripping was applied on both sides, they observed a drastic reduction in the tonal component, which becomes negligible for
at
. Hence, since the current study involves a numerical tripping on both sides of the airfoil (see
Section 2), the source of such tonal component is unclear. We hypothesize that either an instability in the separated trailing edge, pressure-side shear layer, or an additional fixed-frequency vortex shedding in the wake might explain the observed presence of tonal noise; other factors which may play a role are the asymmetric geometry of the V2C airfoil (as opposed to the symmetric NACA0012 profile), as well as the presence of the shock wave above the suction side. However, in
Section 4 we have ruled out a connection between tonal noise observed at
and buffeting, since the frequencies corresponding to the two peaks of the Fourier transforms are separated (see
Figure 9).
Broadband noise is perceived at
(i.e., in the region of the maximum OASPL, see
Figure 6). This kind of noise, generated by turbulence, characterizes four symmetric ‘branches’ at
, and
, together with the already mentioned
. Indeed, turbulence is probably the reason why most of the high-frequency contributions are perceived by the observers located at the angles
: these, in fact, are the regions facing the turbulent boundary layers (downstream of the numerical tripping) and the wake. On the contrary, negligible contributions are perceived in front of the leading edge, where the incoming airflow is in fact laminar (see
Section 2). It should be remembered that, at this relatively low value of
, the required artificial boundary layer tripping is quite large, and can therefore generate some noise by itself. For example, the two symmetric branches observed in front of the leading edge at
and
could be ascribable to the body force employed for tripping the boundary layer. Tonal noise due to tripping, however, can be ruled out, because of the random nature of the body force ([
23]).
In the controlled C10 case, shown in the right panel of
Figure 11, the largest Fourier coefficients are detected in the direction opposite to the shock, albeit weak scattered spots appear above the suction side at
and
. On the pressure side, the peak at
previously observed is slightly intensified, whereas a reduction in the frequency content at
is observed. Finally, the broadband noise in the aforementioned branches at
, and
is slightly intensified; this is also reflected in the higher OASPL values perceived at the same angles (see
Figure 6). It is worth highlighting that the scale of these differences is tiny. Once again, the presence of tonal noise specifically related to the forcing can be ruled out, since the Fourier coefficients at the frequency corresponding to StTWs in cases C10 and R10 (
) are negligible.
In view of the importance of applying StTWs at the reduced incidence to obtain the lift of the uncontrolled wing with less drag, we also compute the directional Fourier transform for the controlled R10 simulation, in which
while the control parameters match those of case C10. We plot in
Figure 12 the difference between the magnitudes of the Fourier coefficients between cases R10 and REF (labeled as
), with the same rationale behind curve RREF of
Figure 7 in
Section 4. The largest effects are observed at low frequencies, as above
the two transforms are basically identical regardless of
. In terms of directions, the probes located upstream of the leading edge detect little to no difference in the frequency content of noise. In fact, the larger effects are observed on symmetric branches at
, and
. This pattern resembles indeed what was previously described in
Figure 7 for the curve RR10. Furthermore, we note a general reduction in the low-frequency content below the pressure side of the wing (
), which could be the cause of the lower OASPL values depicted in
Figure 6 in the same region. Finally, we wish to remark that the values of
induced by StTWs, combined with those caused by the reduction in the angle of attack, are tiny from the point of view of the frequency content, too.
In conclusion, this preliminary near-field analysis has determined only a slight intensification of the aeroacoustics noise when StTWs are employed on a transonic wing slab to reduce drag. The frequency content of noise is minimally altered, too. Once the angle of attack of the wing is reduced to take into account the increased lift due to the forcing and to actually achieve drag reduction, both the noise intensification and the modification of its frequency content become negligible.
6. Conclusions
In this paper, we have extended the analysis recently carried out in Ref. [
13], where it was studied how spanwise forcing for turbulent skin-friction drag reduction (StTW) affects the transonic flow field surrounding a supercritical wing slab with a shock wave above the suction side. The dataset considered in this work derives from the previous study; here, we describe the near-field modifications in terms of wake characteristics and radiated sound. This work represents the first of its kind, as to our knowledge no study of the interaction between spanwise forcing for skin-friction reduction and the aeroacoustic field has been published so far.
We have shown that, when flows with and without control are compared at the same angle of attack, spanwise forcing results into a small downwards displacement of the wake, as a consequence of the increased lift. On the contrary, when the control parameters of StTWs were such that skin-friction drag was actually increased, lift was diminished, and the flow velocity in the wake was further reduced. However, the percentage variation in the velocity component parallel to the free stream in the wake was quite limited, and was never found to exceed 2%. We have also shown that StTWs, which are applied on the suction side only, do bear a minimal influence on the flow on the pressure side of the airfoil, mediated by the downward displacement of the wake: in fact, when lift is increased, the small recirculation bubble that is naturally present beneath the wing becomes slightly enlarged, due to the stronger adverse pressure gradient experienced by the flow.
This paper has presented the first assessment of the acoustic effects of spanwise forcing implemented via StTWs, in terms of the near-field acoustic signals extracted from a number of equally spaced probes placed on a circumference of radius centered on the profile. We have shown that, for cases at a constant angle of attack, noise is slightly increased at almost all angular positions as an effect of the forcing. The direction in which the largest sound intensity is perceived, which does not match the direction of the shock wave, is not altered by the application of control, and depends instead on the flow incidence only. However, in this application, StTWs are meant as a strategy to reduce the aerodynamic drag through an increase in aerodynamic efficiency of the wing. Therefore, one should compare with the flow at the reduced angle of attack that restores the original lift. When the comparison with/without StTWs is carried out at constant lift, the noise perceived by all probes is, on average, unaltered. The frequency spectrum of the pressure fluctuations is not particularly affected by the presence of this type of flow control technology. In fact, both the spectrum of the probe detecting the largest sound intensity and the directional Fourier transforms show but minimal alterations after the forcing is applied. The available evidence thus indicates that no negative interaction takes place between spanwise forcing and the aeroacoustics of the wing.
This work only constitutes a preliminary study, and its results are limited. Work is ongoing to employ more advanced tools such as wavelets transforms and spatial correlations of the pressure signals in order to analyze changes in the acoustic signature around the profile. Furthermore, we are planning to investigate modifications to the far-field aeroacoustic noise. Changes away from the profile, indeed, may differ from the variation in the near-field acoustics. We also plan to consider the wall-pressure signature, which could be more sensitive to changes in the boundary conditions with respect to near-field (or far-field) acoustic signals. Finally, the possibility that StTWs could be employed as a means to alter the noise generated by the turbulent flow cannot be ruled out, provided the combination of parameters is properly tuned towards a goal that is different from turbulent skin-friction drag reduction.