Predictive and Cross-Validation Analysis of Aerobic and Anaerobic Performance Based on Maximum Strength
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Approach
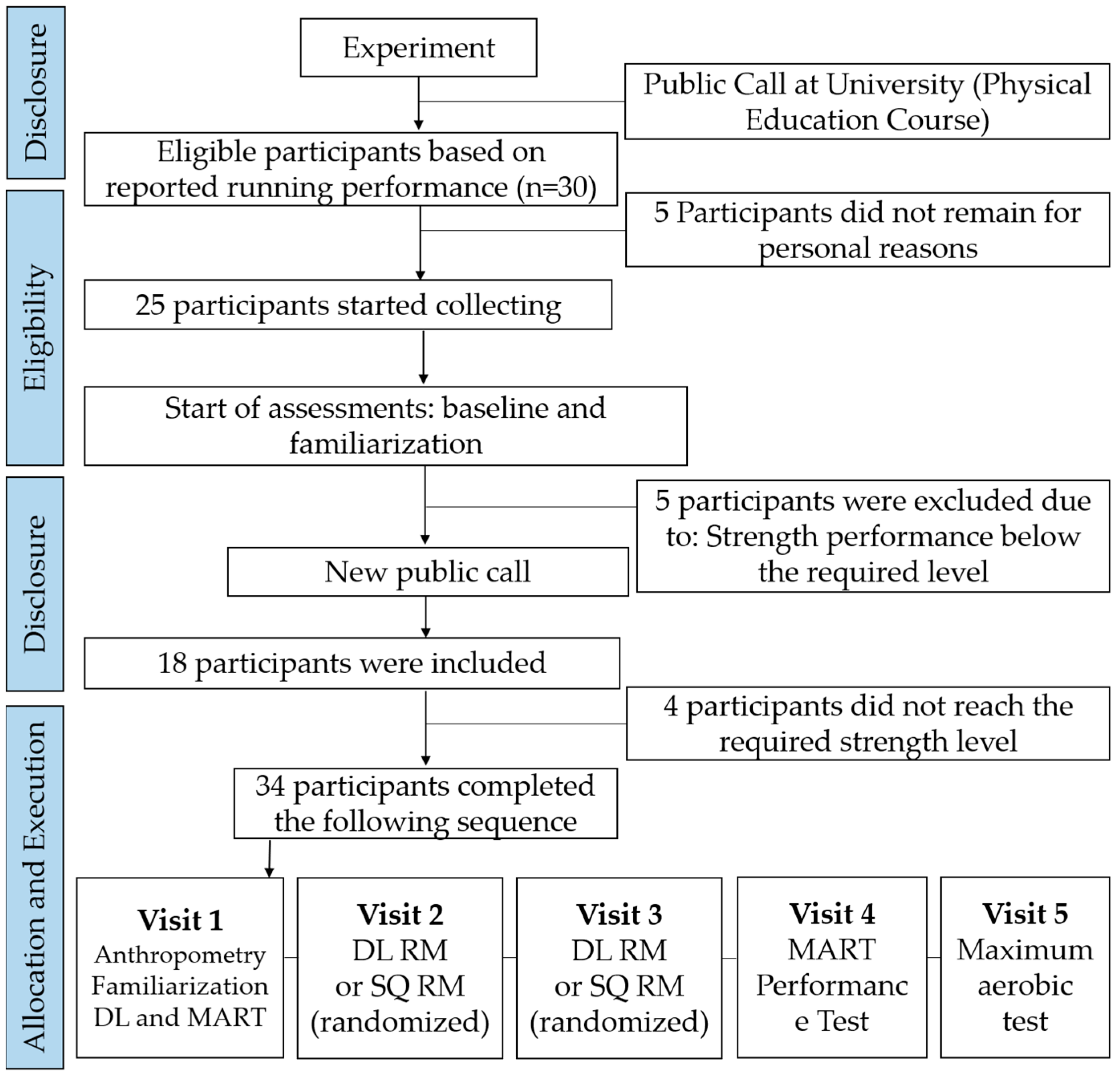
2.2. Study Design
2.2.1. First Data Collection (For the Development of the Equation)
2.2.2. Second Data Collection (To Test the Validity of the Equation)
2.3. Sample
2.4. Procedures
2.4.1. Morphological and Anthropometric Procedures
2.4.2. One-Repetition Maximum Test
2.4.3. Anaerobic Performance Test (MART)
2.4.4. Progressive Maximal Effort Performance Test
2.4.5. Allometry
2.4.6. Stratification of Training Levels
2.4.7. Data Analysis and Processing
2.5. Statistical Analysis
3. Results (First Collection)
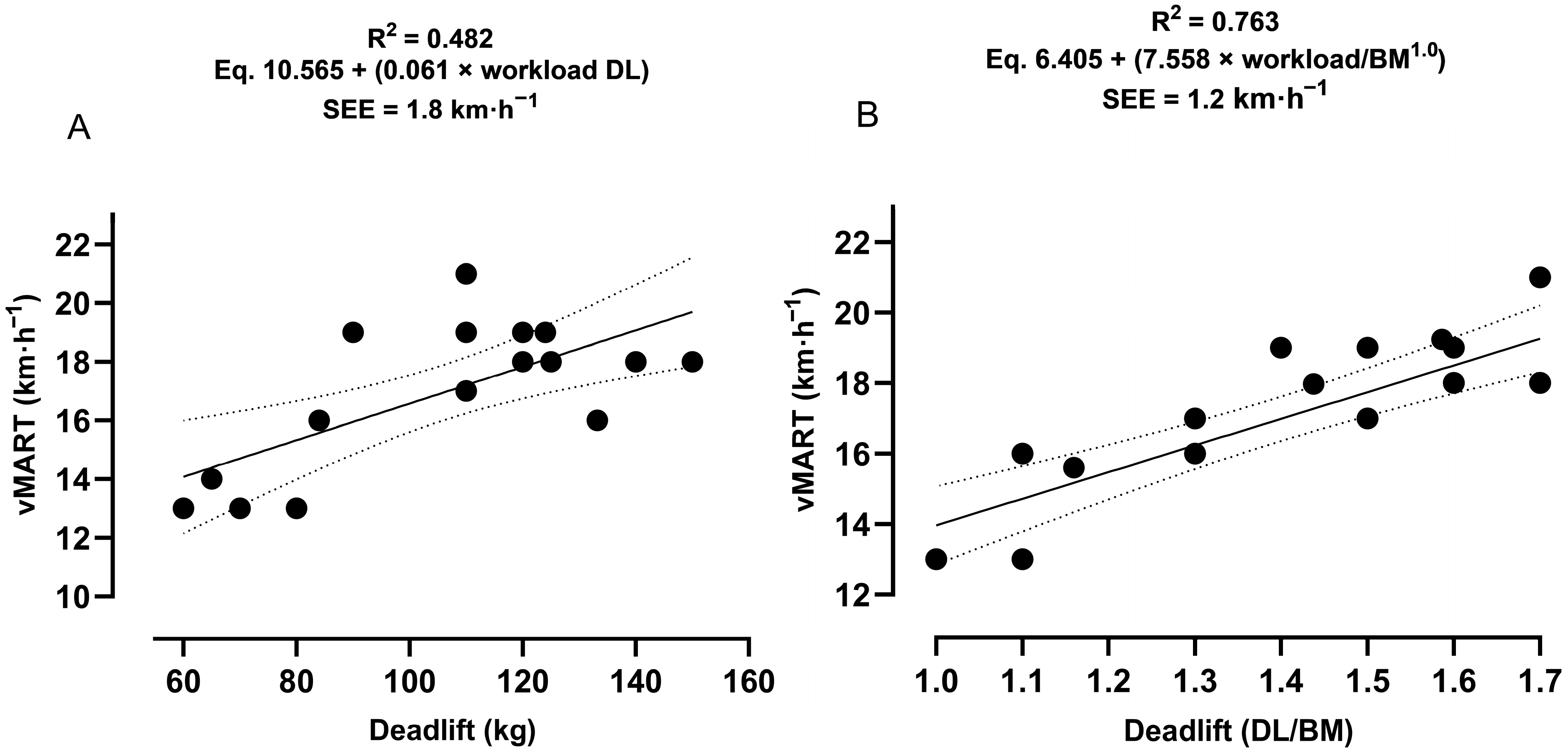
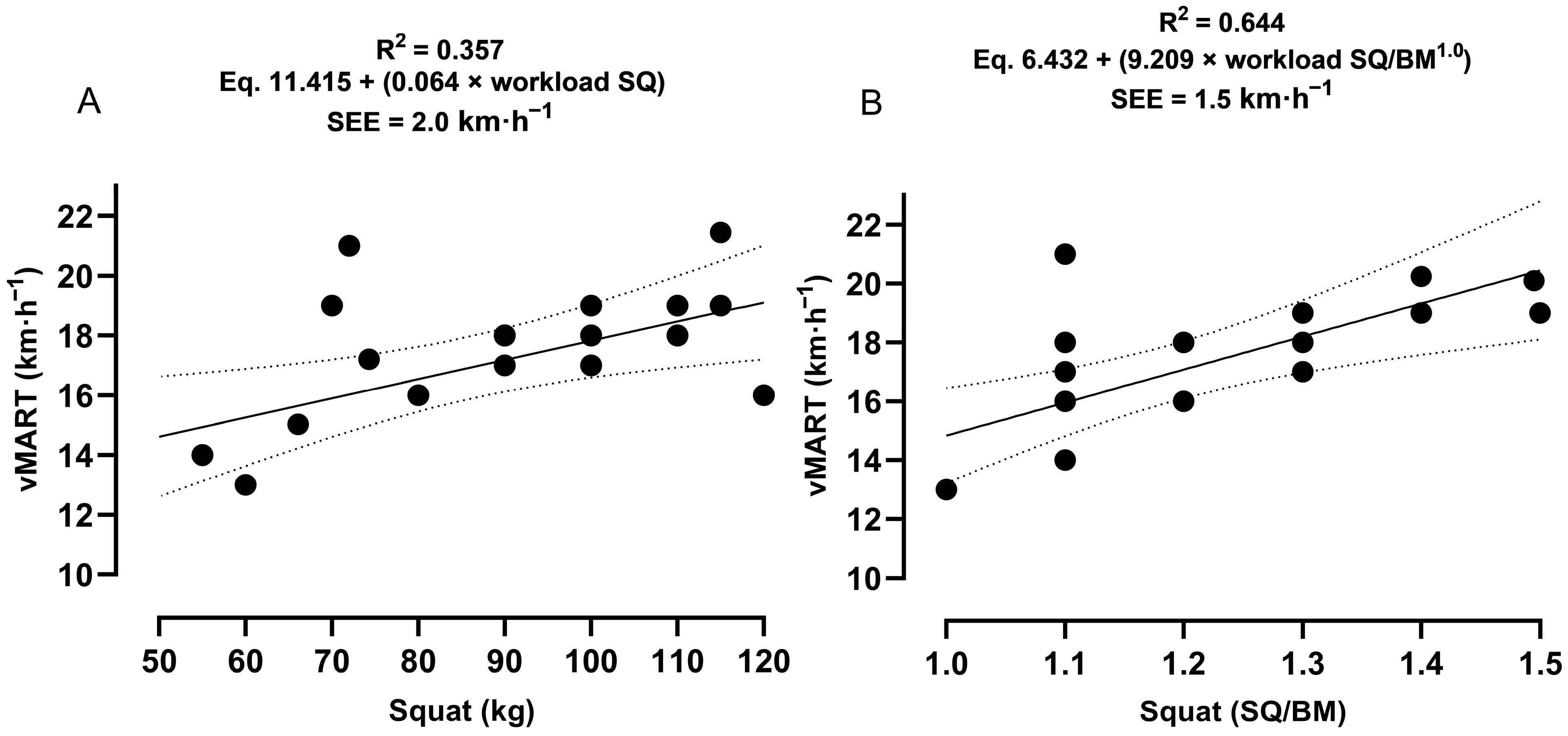
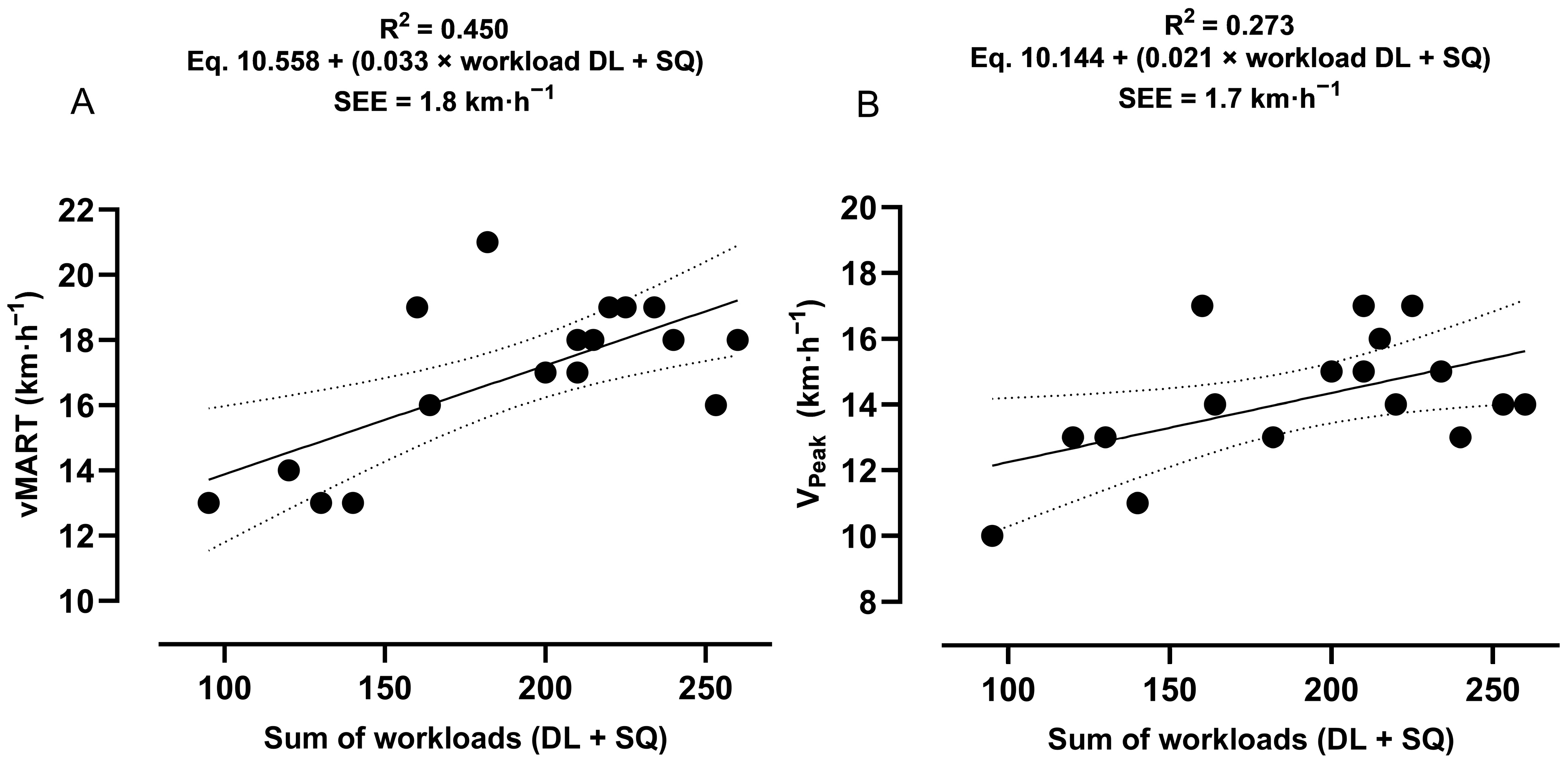
3.1. Primary Outcomes
3.2. Secondary Outcome
3.3. Tertiary Outcome
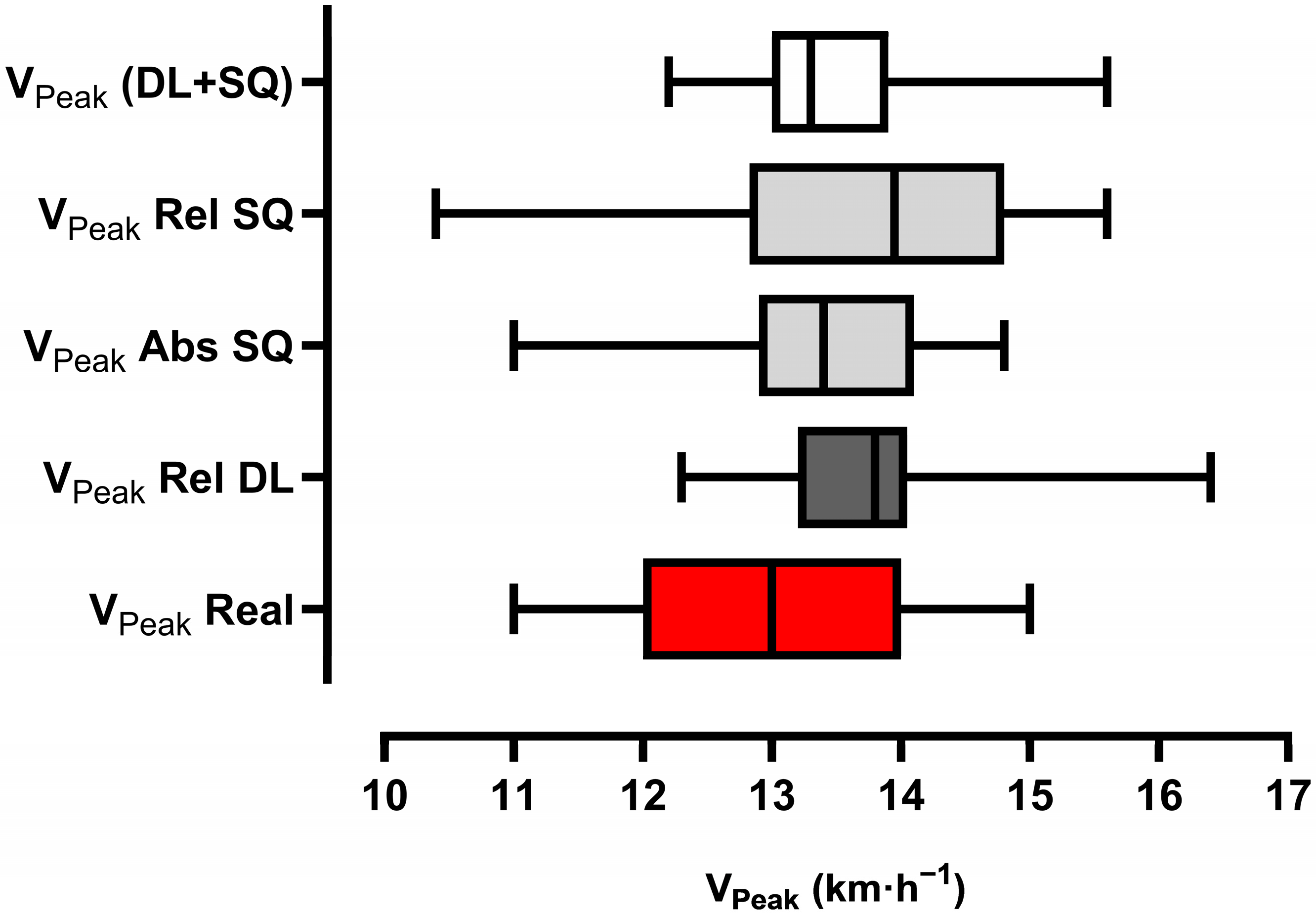
4. Cross-Validation Results (Second Collection)
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheatham, S.W.; Kolber, M.J.; Cain, M.; Lee, M. The effects of self-myofascial release using a foam roll or roller massager on joint range of motion, muscle recovery, and performance: A systematic review. Int. J. Sports Phys. Ther. 2015, 10, 827–838. [Google Scholar] [PubMed]
- Machado, S.; Jansen, P.; Almeida, V.; Veldema, J. Is TDCS an Adjunct Ergogenic Resource for Improving Muscular Strength and Endurance Performance? A Systematic Review. Front. Psychol. 2019, 10, 1127. [Google Scholar] [CrossRef] [PubMed]
- Bonilla, D.A.; Boullosa, D.; Del Coso, J. Advances in Nutrition, Dietary Supplements and Ergogenic Aids for Athletic Performance: Trends and Future Prospects. Nutrients 2023, 15, 2246. [Google Scholar] [CrossRef]
- Billat, V.; Pycke, J.R.; Vitiello, D.; Palacin, F.; Correa, M. Race Analysis of the World’s Best Female and Male Marathon Runners. Int. J. Environ. Res. Public Health 2020, 17, 1177. [Google Scholar] [CrossRef]
- Paavolainen, L.; Nummela, A.; Rusko, H. Muscle Power Factors and VO2max as Determinants of Horizontal and Uphill Running Performance. Scand. J. Med. Sci. Sports 2000, 10, 286–291. [Google Scholar] [CrossRef]
- Paavolainen, L.M.; Nummela, A.T.; Rusko, H.K. Neuromuscular Characteristics and Muscle Power as Determinants of 5-Km Running Performance. Med. Sci. Sports Exerc. 1999, 31, 124–130. [Google Scholar] [CrossRef]
- Noakes, T.D.; Myburgh, K.H.; Schall, R. Peak Treadmill Running Velocity during the Vo2 Max Test Predicts Running Performance. J. Sports Sci. 1990, 8, 35–45. [Google Scholar] [CrossRef]
- Doma, K.; Deakin, G.B. The Effects of Strength Training and Endurance Training Order on Running Economy and Performance. Appl. Physiol. Nutr. Metab. 2013, 38, 651–656. [Google Scholar] [CrossRef]
- Beattie, K.; Kenny, I.C.; Lyons, M.; Carson, B.P. The Effect of Strength Training on Performance in Endurance Athletes. Sports Med. 2014, 44, 845–865. [Google Scholar] [CrossRef]
- Aagaard, P.; Andersen, J.L. Effects of Strength Training on Endurance Capacity in Top-Level Endurance Athletes. Scand. J. Med. Sci. Sports 2010, 20, 39–47. [Google Scholar] [CrossRef]
- Balsalobre-Fernández, C.; Santos-Concejero, J.; Grivas, G.V. Effects of Strength Training on Running Economy in Highly Trained Runners: A Systematic Review with Meta-Analysis of Controlled Trials. J. Strength Cond. Res. 2016, 30, 2361–2368. [Google Scholar] [CrossRef] [PubMed]
- Houmard, J.A.; Costill, D.L.; Mitchell, J.B.; Park, S.H.; Chenier, T.C. The Role of Anaerobic Ability in Middle Distance Running Performance. Eur. J. Appl. Physiol. Occup. Physiol. 1991, 62, 40–43. [Google Scholar] [CrossRef] [PubMed]
- Rohleva, M. Exploring the Relationship between Endurance and Strength Training in Power Sports. J. Educ. Train. Stud. 2017, 5, 204. [Google Scholar] [CrossRef][Green Version]
- Sentija, D.; Marsic, T.; Dizdar, D. The Effects of Strength Training on Some Parameters of Aerobic and Anaerobic Endurance. Coll. Antropol. 2009, 33, 111–116. [Google Scholar]
- Delecluse, C. Influence of Strength Training on Sprint Running Performance. Current Findings and Implications for Training. Sports Med. 1997, 24, 147–156. [Google Scholar] [CrossRef]
- Meylan, C.M.P.; Cronin, J.; Oliver, J.L.; Hopkins, W.G.; Pinder, S. Contribution of Vertical Strength and Power to Sprint Performance in Young Male Athletes. Int. J. Sports Med. 2014, 35, 749–754. [Google Scholar] [CrossRef]
- Chelly, S.M.; Denis, C. Leg power and hopping stiffness: Relationship with sprint running performance. Med. Sci. Sports Exerc. 2001, 33, 326–333. [Google Scholar] [CrossRef]
- Furlong, L.A.M.; Harrison, A.J.; Jensen, R.L. Measures of Strength and Jump Performance Can Predict 30-m Sprint Time in Rugby Union Players. J. Strength Cond. Res. 2021, 35, 2579–2583. [Google Scholar] [CrossRef]
- Loturco, I.; Kobal, R.; Kitamura, K.; Fernandes, V.; Moura, N.; Siqueira, F.; Cal Abad, C.C.; Pereira, L.A. Predictive Factors of Elite Sprint Performance: Influences of Muscle Mechanical Properties and Functional Parameters. J. Strength Cond. Res. 2019, 33, 974–986. [Google Scholar] [CrossRef]
- Eihara, Y.; Takao, K.; Sugiyama, T.; Maeo, S.; Terada, M.; Kanehisa, H.; Isaka, T. Heavy Resistance Training Versus Plyometric Training for Improving Running Economy and Running Time Trial Performance: A Systematic Review and Meta-Analysis. Sports Med. Open 2022, 8, 138. [Google Scholar] [CrossRef]
- Cunningham, D.J.; West, D.J.; Owen, N.J.; Shearer, D.A.; Finn, C.V.; Bracken, R.M.; Crewther, B.T.; Scott, P.; Cook, C.J.; Kilduff, L.P. Strength and Power Predictors of Sprinting Performance in Professional Rugby Players. J. Sports Med. Phys. Fit. 2013, 53, 105–111. [Google Scholar]
- Llanos-Lagos, C.; Ramirez-Campillo, R.; Moran, J.; Sáez de Villarreal, E. Effect of Strength Training Programs in Middle- and Long-Distance Runners’ Economy at Different Running Speeds: A Systematic Review with Meta-Analysis. Sports Med. 2024, 54, 895–932. [Google Scholar] [CrossRef] [PubMed]
- McBride, J.M.; Blow, D.; Kirby, T.J.; Haines, T.L.; Dayne, A.M.; Triplett, N.T. Relationship between Maximal Squat Strength and Five, Ten, and Forty Yard Sprint Times. J. Strength Cond. Res. 2009, 23, 1633–1636. [Google Scholar] [CrossRef] [PubMed]
- Schiemann, S.; Keiner, M.; Wirth, K.; Lohmann, L.H.; Wagner, C.M.; Behm, D.G.; Warneke, K. The Magnitude of Correlation between Deadlift 1RM and Jumping Performance Is Sports Dependent. Front. Sports Act. Living 2024, 6, 1345213. [Google Scholar] [CrossRef]
- Choe, K.H.; Coburn, J.W.; Costa, P.B.; Pamukoff, D.N. Hip and Knee Kinetics During a Back Squat and Deadlift. J. Strength Cond. Res. 2021, 35, 1364–1371. [Google Scholar] [CrossRef]
- von Elm, E.; Altman, D.G.; Egger, M.; Pocock, S.J.; Gøtzsche, P.C.; Vandenbroucke, J.P. The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) Statement: Guidelines for Reporting Observational Studies. Int. J. Surg. 2014, 12, 573–577. [Google Scholar] [CrossRef]
- Santos Junior, E.R.T.; De Salles, B.F.; Dias, I.; Ribeiro, A.S.; Simão, R.; Willardson, J.M. Classification and Determination Model of Resistance Training Status. Strength Cond. J. 2021, 43, 77–86. [Google Scholar] [CrossRef]
- Serdar, C.C.; Cihan, M.; Yücel, D.; Serdar, M.A. Sample Size, Power and Effect Size Revisited: Simplified and Practical Approachin Pre-Clinical, Clinical and Laboratory Studies. Biochem. Med 2021, 31, 27–53. [Google Scholar] [CrossRef]
- Jackson, A.S.; Pollock, M.L. Generalized Equations for Predicting Body Density of Men. Br. J. Nutr. 1978, 40, 497–504. [Google Scholar] [CrossRef]
- Jackson, A.S.; Pollock, M.L.; Ward, A. Generalized Equations for Predicting Body Density of Women. Med. Sci. Sports Exerc. 1980, 12, 175–182. [Google Scholar] [CrossRef]
- William, E. Siri Body Composition From Fluid Spaces and Density: Analysis of Methods. Nutrition. 1993, 9, 480–491. [Google Scholar]
- Nummela, A. Reliability and Validity of the Maximal Anaerobic Running Test. Int. J. Sports Med. 1996, 17, S97–S102. [Google Scholar] [CrossRef] [PubMed]
- Nummela, A.T.; Paavolainen, L.M.; Sharwood, K.A.; Lambert, M.I.; Noakes, T.D.; Rusko, H.K. Neuromuscular Factors Determining 5 Km Running Performance and Running Economy in Well-Trained Athletes. Eur. J. Appl. Physiol. 2006, 97, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Motulsky, H.; Christopoulos, A. Fitting Models to Biological Data Using Linear and Nonlinear Regression; GraphPad Software Inc.: San Diego, CA, USA, 2004; pp. 1–351. [Google Scholar]
- Tibana, R.A.; Neto, I.V.d.S.; de Sousa, N.M.F.; Romeiro, C.; Hanai, A.; Brandão, H.; Dominski, F.H.; Voltarelli, F.A. Local Muscle Endurance and Strength Had Strong Relationship with CrossFit® Open 2020 in Amateur Athletes. Sports 2021, 9, 98. [Google Scholar] [CrossRef]
- Tibana, R.; de Souza, N.; Cunha, G.; Prestes, J. Correlação Das Variáveis Antropométricas e Fisiológicas Com o Desempenho No Crossfit®. RBPFEX-Rev. Bras. Prescrição Fisiol. Exerc. 2018, 11, 880–887. [Google Scholar]
- Meier, N.; Rabel, S.; Schmidt, A. Determination of a Crossfit® Benchmark Performance Profile. Sports 2021, 9, 80. [Google Scholar] [CrossRef]
- Bellar, D.; Hatchett, A.; Judge, L.W.; Breaux, M.E.; Marcus, L. Herthe Relationship of Aerobic Capacity, Anaerobic Peak Power and Experience to Performance in CrossFit Exercise. Biol. Sport 2015, 32, 315–320. [Google Scholar] [CrossRef]
- Grgic, J.; Lazinica, B.; Schoenfeld, B.J.; Pedisic, Z. Test–Retest Reliability of the One-Repetition Maximum (1RM) Strength Assessment: A Systematic Review. Sports Med. Open 2020, 6, 31. [Google Scholar] [CrossRef]
- Browne, M.W. Cross-Validation Methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef]
- Latin, R.W.; Berg, K.E. The Accuracy of the ACSM and a New Cycle Ergomefry Equation for Young Women. Med. Sci. Sports Exerc. 1994, 26, 642–646. [Google Scholar] [CrossRef]
- Williford, H.N.; Scharff-Olson, M.; Wang, N.; Blessing, D.L.; Smith, F.H.; Duey, W.J. Cross-Validation of Non-Exercise Predictions of VO(2peak) in Women. Med. Sci. Sports Exerc. 1996, 28, 926–930. [Google Scholar] [CrossRef] [PubMed]
- Mahar, M.T.; Guerieri, A.M.; Hanna, M.S.; Kemble, C.D. Estimation of Aerobic Fitness from 20-m Multistage Shuttle Run Test Performance. Am. J. Prev. Med. 2011, 41, S117–S123. [Google Scholar] [CrossRef] [PubMed]
- Sayers, S.P.; Harackiewicz, D.V.; Harman, E.A.; Frykman, P.N.; Rosenstein, M.T. Cross-Validation of Three Jump Power Equations. Med. Sci. Sports Exerc. 1999, 31, 572–577. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, H.M.; Coelho E Silva, M.J.; Figueiredo, A.J.; Goncalves, C.E.; Castagna, C.; Philippaerts, R.M.; Malina, R.M. Cross-Validation and Reliability of the Line-Drill Test of Anaerobic Performance in Basketball Players 14–16 Years. J. Strength Cond. Res. 2011, 25, 1113–1119. [Google Scholar] [CrossRef]



| High Strength Score | Low Strength Score | |||||||
|---|---|---|---|---|---|---|---|---|
| Age | BM | Height | BMI | Age | BM | Height | BMI | |
| (Years) | (kg) | (m) | (kg·m−2) | (Years) | (kg) | (m) | (kg·m−2) | |
| Mean | 28.0 | 73.9 | 1.71 | 25.1 | 26.6 | 75.6 | 1.75 | 24.5 |
| SD | 8.1 | 11.4 | 0.08 | 2.7 | 6.3 | 11.9 | 0.09 | 3.2 |
| High Strength Score | Low Strength Score | |||||||
|---|---|---|---|---|---|---|---|---|
| DL | DL/BM | SQ | SQ/BM | DL | DL/BM | SQ | SQ/BM | |
| (kg) | (kg/kg) | (kg) | (kg/kg) | (kg) | (kg/kg) | (kg) | (kg/kg) | |
| Mean | 145.3 | 2.0 | 111.1 | 1.5 | 105.4 * | 1.4 * | 86.3 * | 1.1 * |
| SD | 21.6 | 0.1 | 16.4 | 0.3 | 27.9 | 0.3 | 22.7 | 0.2 |
| High Strength Score | Low Strength Score | |||||||
|---|---|---|---|---|---|---|---|---|
| VO2Max | VPeak | VO2 | MART | VO2Max | VPeak | VO2 | vMART | |
| mL·kg−1·min−1 | km·h−1 | mL·kg−1·min−1 | km·h−1 | mL·kg−1·min−1 | km·h−1 | mL·kg−1·min−1 | km·h−1 | |
| Mean | 53.3 | 14.9 | 95.9 | 18.0 | 50.8 | 14.2 | 90.5 | 16.9 |
| SD | 5.5 | 1.6 | 8.3 | 1.6 | 6.6 | 2.0 | 12.5 | 2.4 |
| High Strength Score | Low Strength Score | |
|---|---|---|
| (kg) | (kg) | |
| Mean | 256.5 | 191.7 * |
| SD | 33.5 | 49.1 |
| Age | BM | Fat | DL/BM | SQ/BM | |
|---|---|---|---|---|---|
| (Years) | (kg) | (%) | (kg/kg) | (kg/kg) | |
| Mean | 26.0 | 68.4 | 18.6 | 1.3 | 1.1 |
| SD | 5.7 | 14.3 | 12.3 | 0.2 | 0.1 |
| DL | SQ | vMART | VPeak | |
|---|---|---|---|---|
| (kg) | (kg) | (km·h−1) | (km·h−1) | |
| Mean | 90.6 | 74.4 | 15.3 | 12.6 |
| SD | 29.5 | 17.1 | 1.9 | 1.5 |
| Eq. Prediction DL | Eq. Prediction SQ | Sum | |||
|---|---|---|---|---|---|
| (Abs) | (Rel) | (Abs) | (Rel) | (DL+SQ) | |
| vMART Real | r = 0.766; p = 0.001 * | r = 0.757; p = 0.001 * | r = 0.545; p = 0.024 * | r = 0.125; p = 0.634 | r = 0.683; p = 0.003 * |
| VPeak Real | r = 0.651; p = 0.005 * | r = 0.430; p = 0.085 | r = 0.089; p = 0.733 | r = 0.573; p = 0.016 * | |
| vMART | |||||
|---|---|---|---|---|---|
| DL | DL/BM | SQ | SQ/BM | DL+SQ | |
| (km·h−1) | |||||
| TME (Abs) | 0.87 | 0.95 | 1.54 | 2.70 | 0.98 |
| TME (Rel) | 5.5% | 6.0% | 9.9% | 17.3% | 6.3% |
| VPeak | |||||
| DL | DL/BM | SQ | SQ/BM | DL+SQ | |
| (km·h−1) | |||||
| TME (Abs) | 2.67 | 1.30 | 2.26 | 0.89 | |
| TME (Rel) | 18.7% | 10.0% | 17.4% | 6.9% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sá Filho, A.S.; Inacio, P.A.; Aprigliano, V.; Leonardo, P.S.; Oliveira-Silva, I.; Cunha, R.M.; Chiappa, G.R.; Fajemiroye, J.O.; Vieira, R.P.; Lopes-Martins, R.A.B.; et al. Predictive and Cross-Validation Analysis of Aerobic and Anaerobic Performance Based on Maximum Strength. Appl. Sci. 2025, 15, 693. https://doi.org/10.3390/app15020693
Sá Filho AS, Inacio PA, Aprigliano V, Leonardo PS, Oliveira-Silva I, Cunha RM, Chiappa GR, Fajemiroye JO, Vieira RP, Lopes-Martins RAB, et al. Predictive and Cross-Validation Analysis of Aerobic and Anaerobic Performance Based on Maximum Strength. Applied Sciences. 2025; 15(2):693. https://doi.org/10.3390/app15020693
Chicago/Turabian StyleSá Filho, Alberto Souza, Pedro Augusto Inacio, Vicente Aprigliano, Patricia Sardinha Leonardo, Iransé Oliveira-Silva, Raphael Martins Cunha, Gaspar R. Chiappa, James Oluwagbamigbe Fajemiroye, Rodolfo P. Vieira, Rodrigo Alvaro Brandão Lopes-Martins, and et al. 2025. "Predictive and Cross-Validation Analysis of Aerobic and Anaerobic Performance Based on Maximum Strength" Applied Sciences 15, no. 2: 693. https://doi.org/10.3390/app15020693
APA StyleSá Filho, A. S., Inacio, P. A., Aprigliano, V., Leonardo, P. S., Oliveira-Silva, I., Cunha, R. M., Chiappa, G. R., Fajemiroye, J. O., Vieira, R. P., Lopes-Martins, R. A. B., & Sales, M. M. (2025). Predictive and Cross-Validation Analysis of Aerobic and Anaerobic Performance Based on Maximum Strength. Applied Sciences, 15(2), 693. https://doi.org/10.3390/app15020693










