Quadrature-Phase-Locked-Loop-Based Back-Electromotive Force Observer for Sensorless Brushless DC Motor Drive Control in Solar-Powered Electric Vehicles
Abstract
1. Introduction
1.1. General Context
1.2. Sensorless Control of BLDCMs
1.3. Proposed Work and Contributions
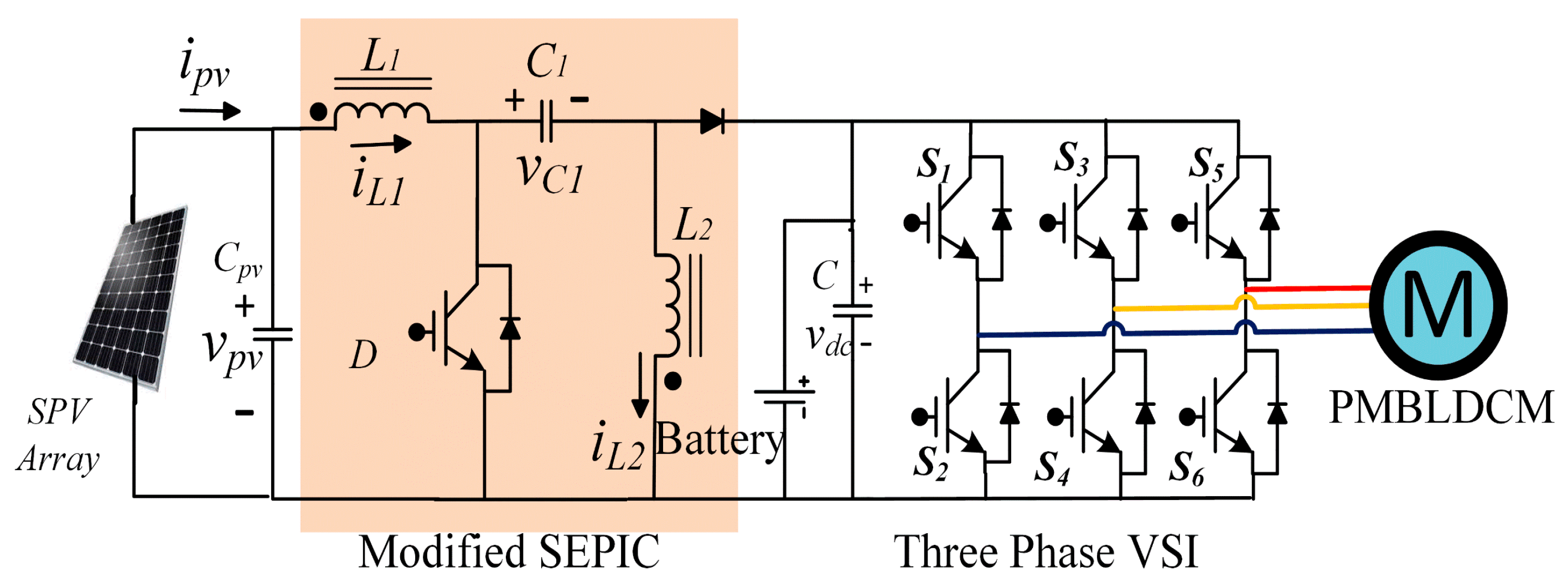
2. System Design and Configuration
2.1. Rating and Specifications of the Solar Panel
2.2. Design and Control of the SEPIC
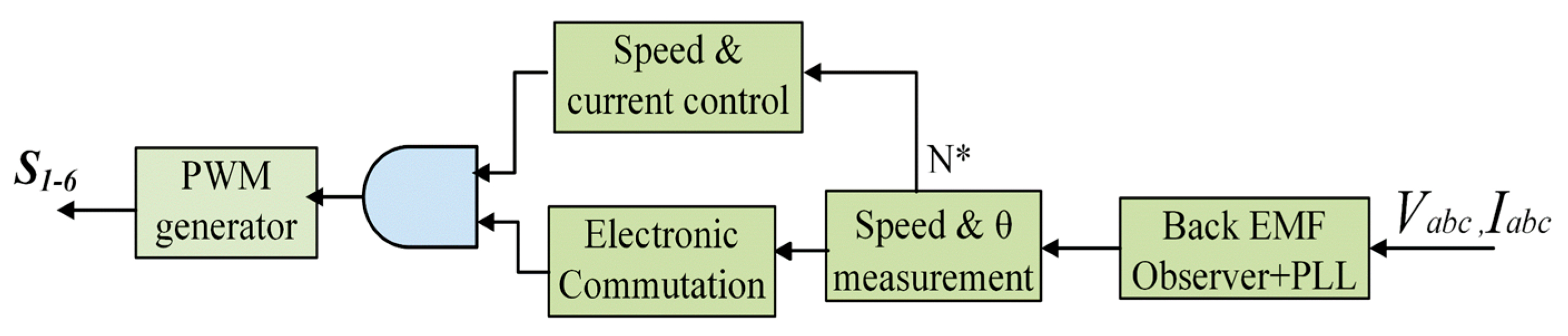
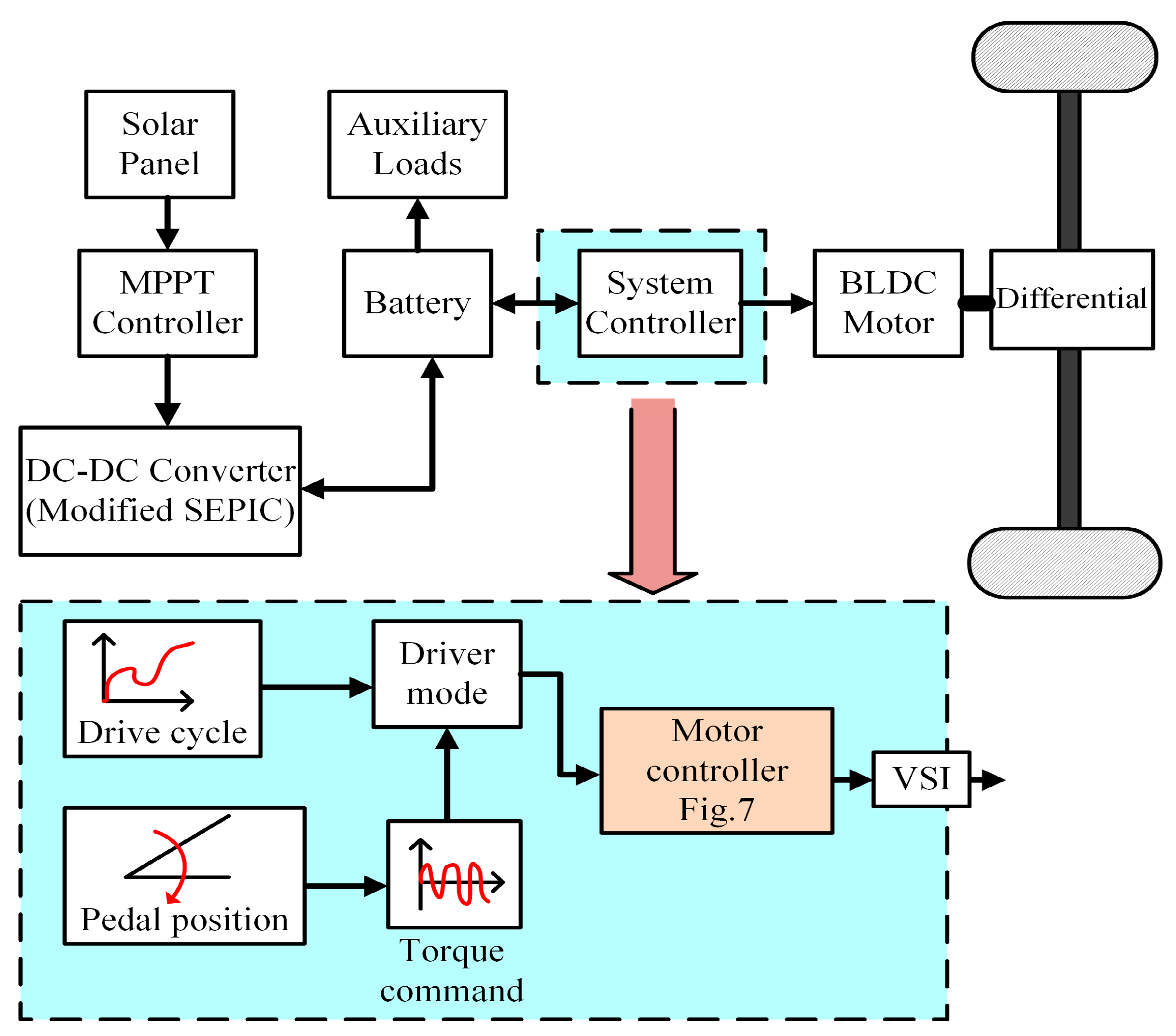
3. Control System Architecture
3.1. Control of the Solar PV Array
3.2. Sensorless Control with Conventional Back-EMF Observer
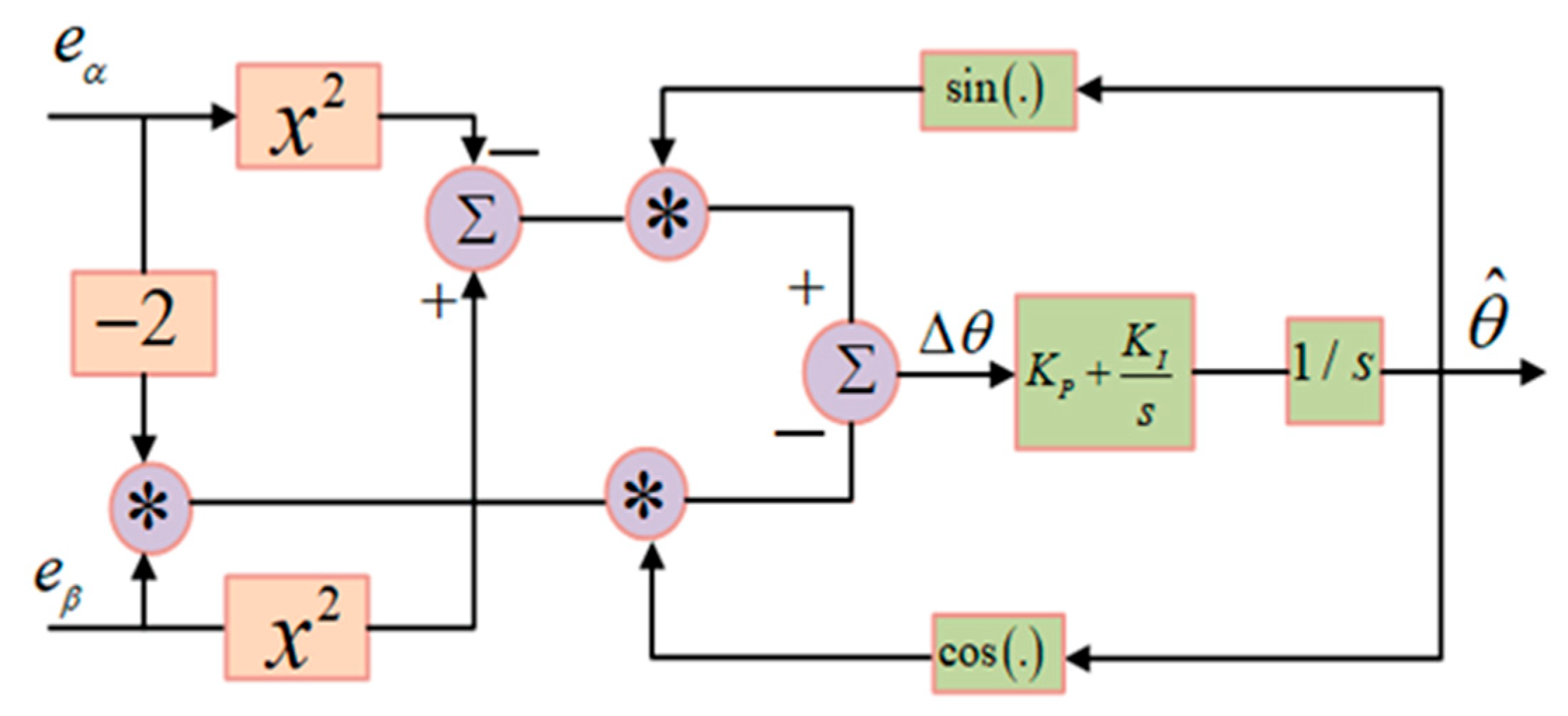
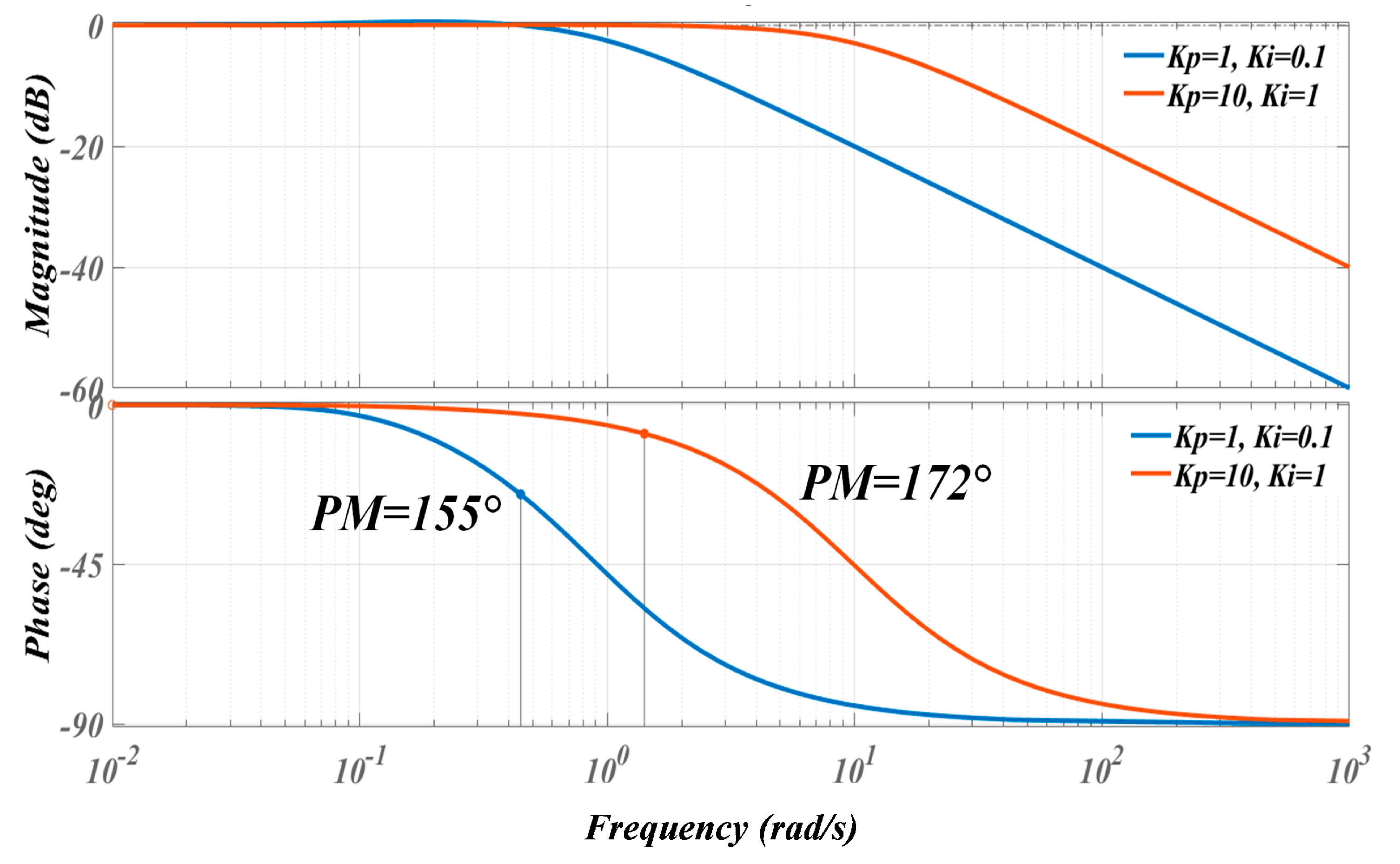
3.3. Modified Observer with Improved QPLL
3.4. Speed Controller
3.5. Regenerative Braking Control
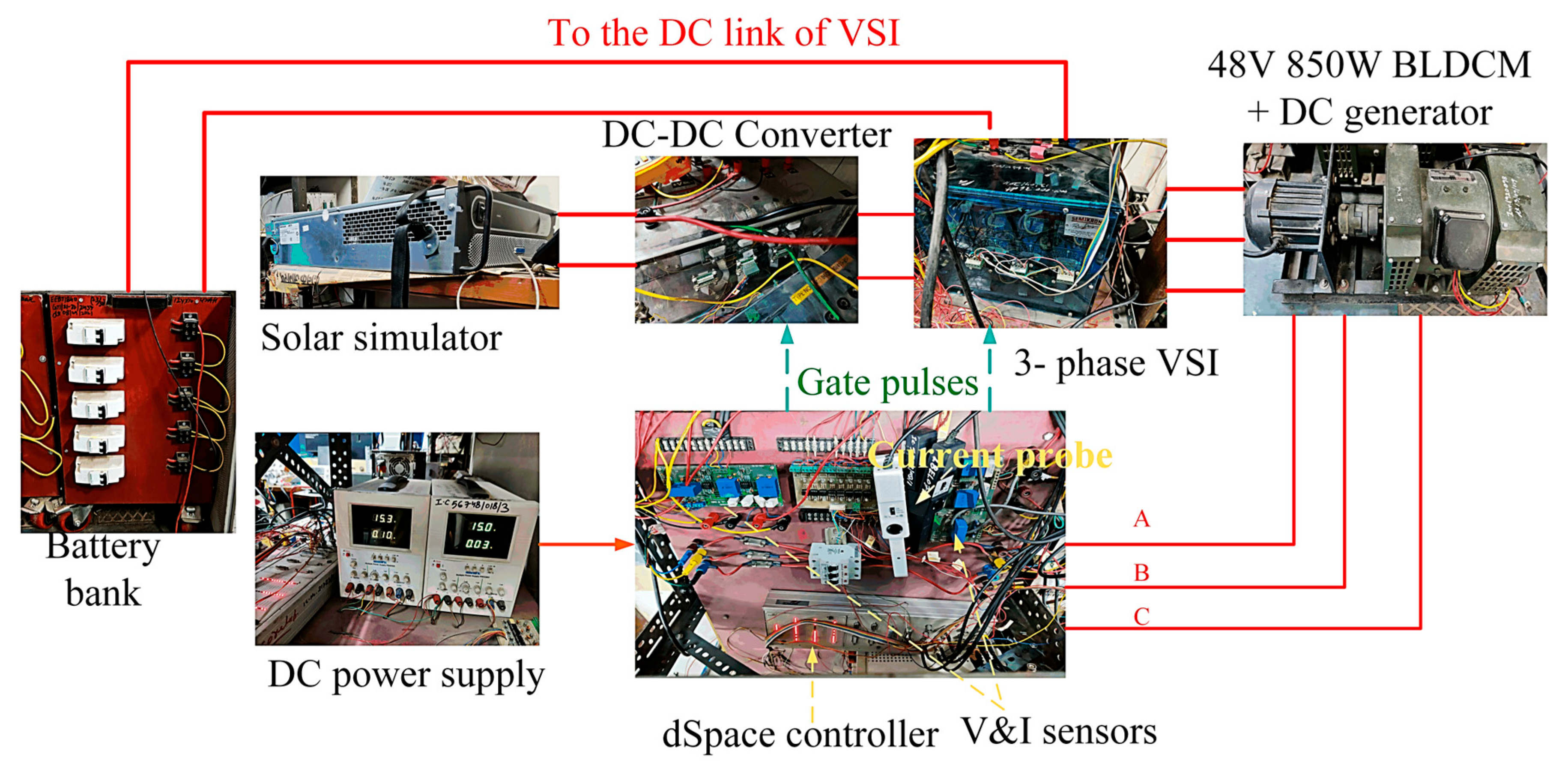
4. Experimental Testbench
5. Results and Analysis
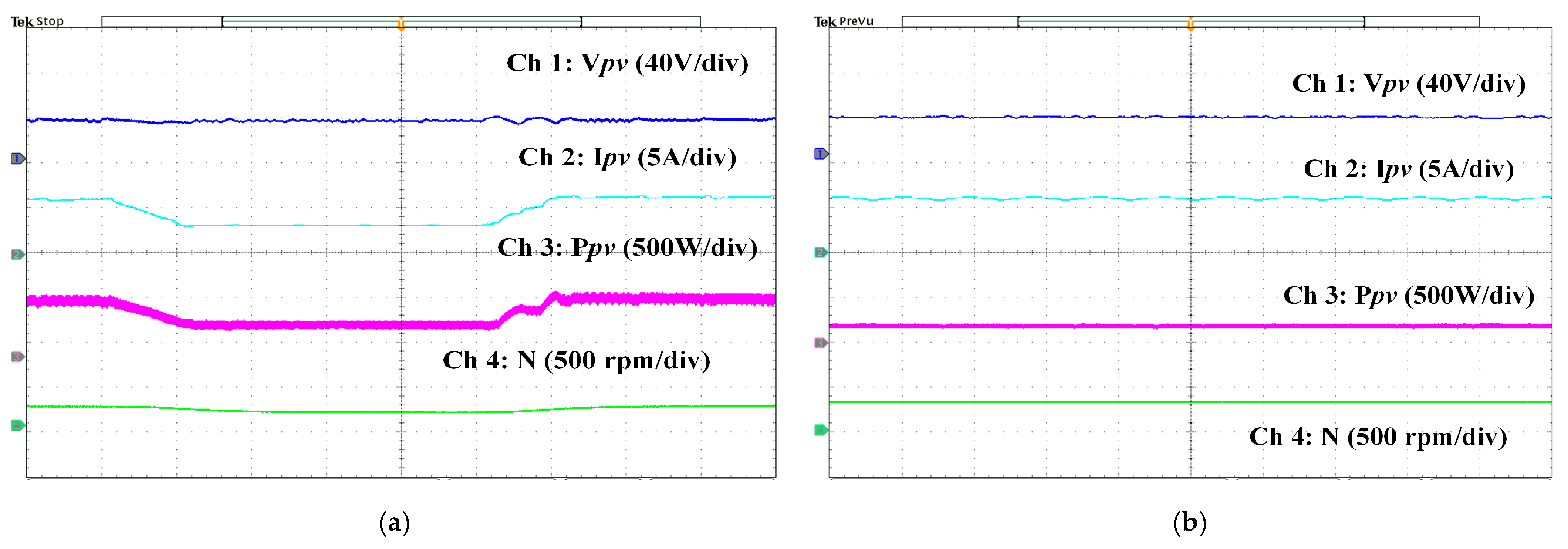
5.1. Performance of the Solar PV Array and Converter
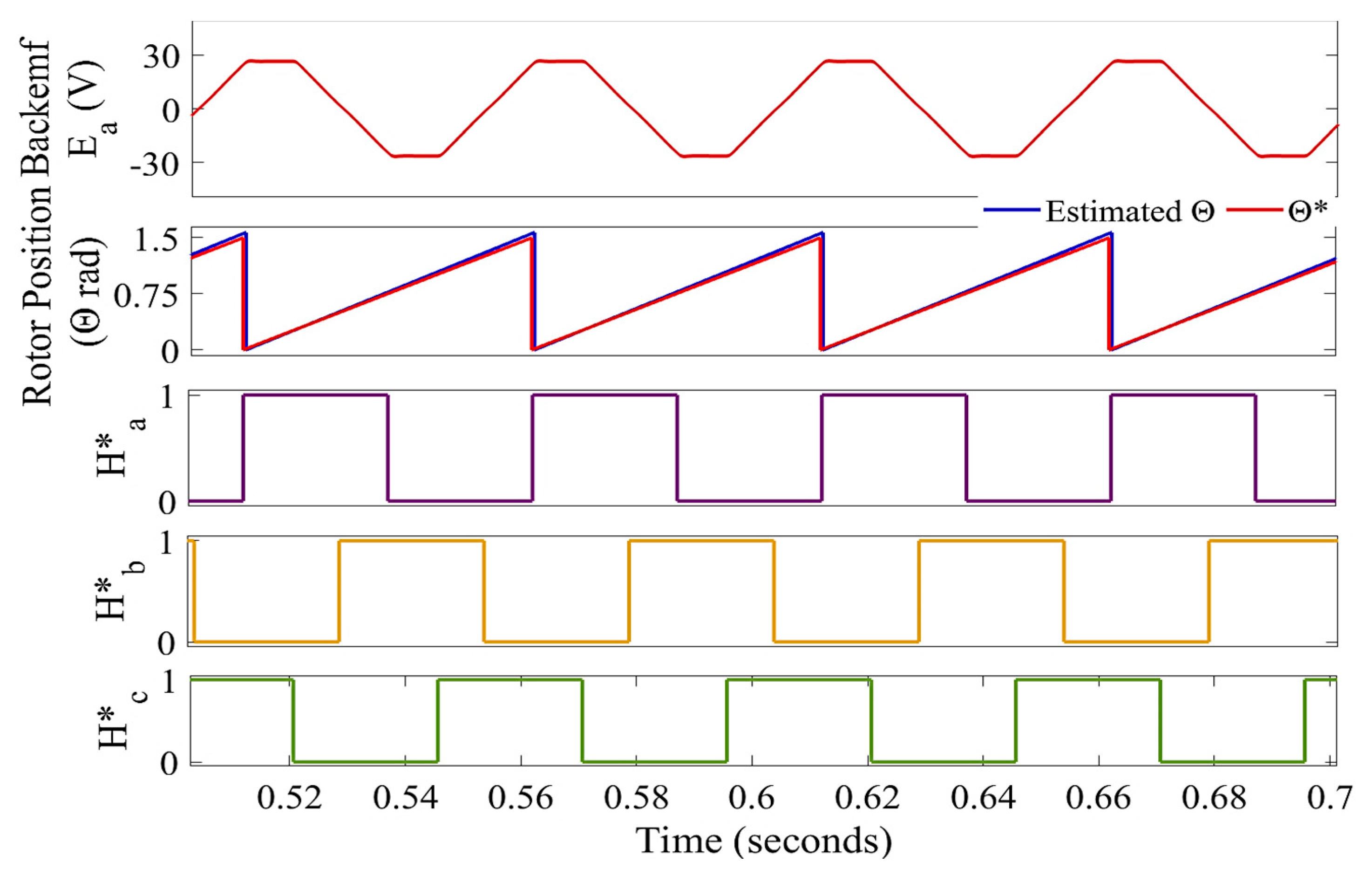
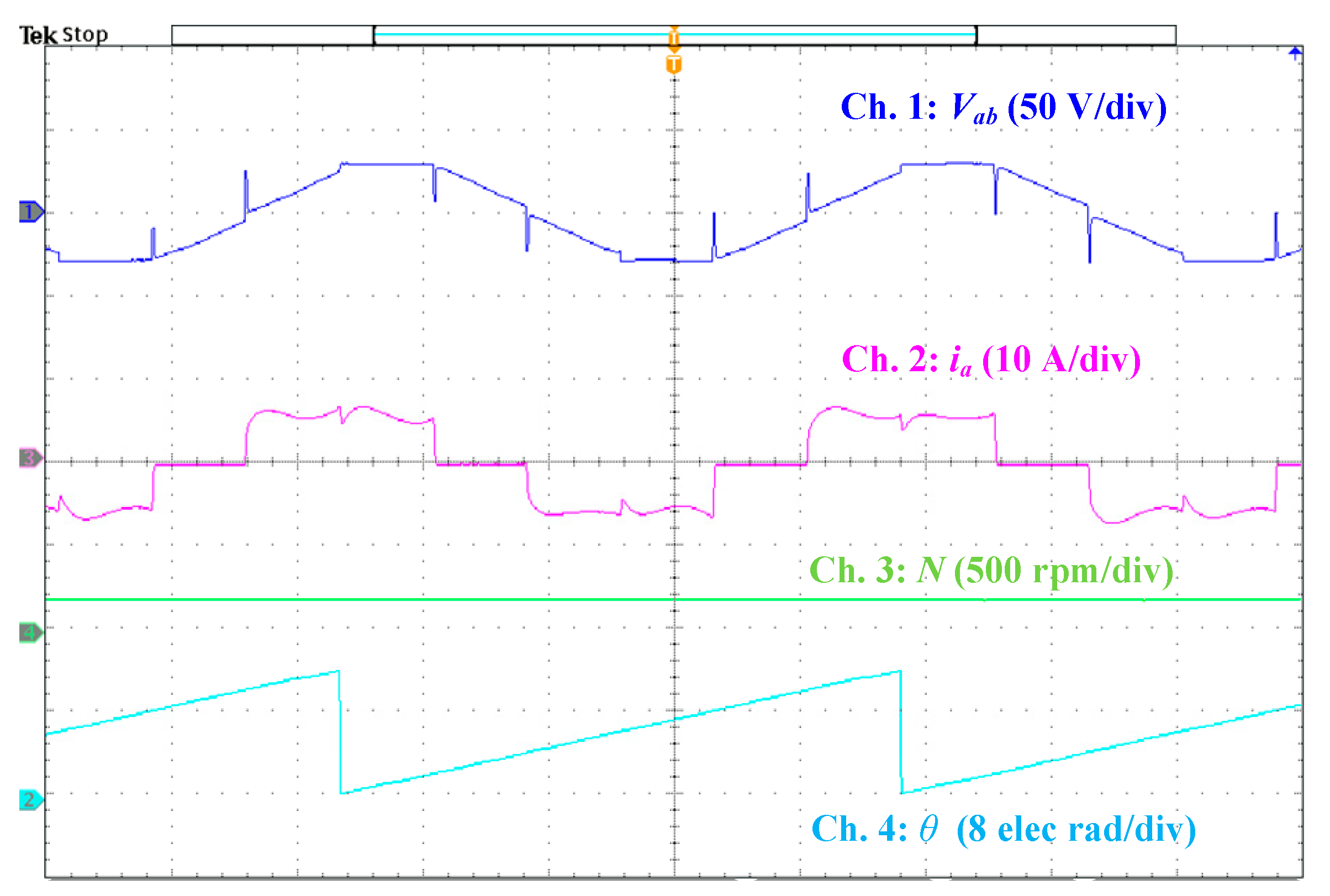
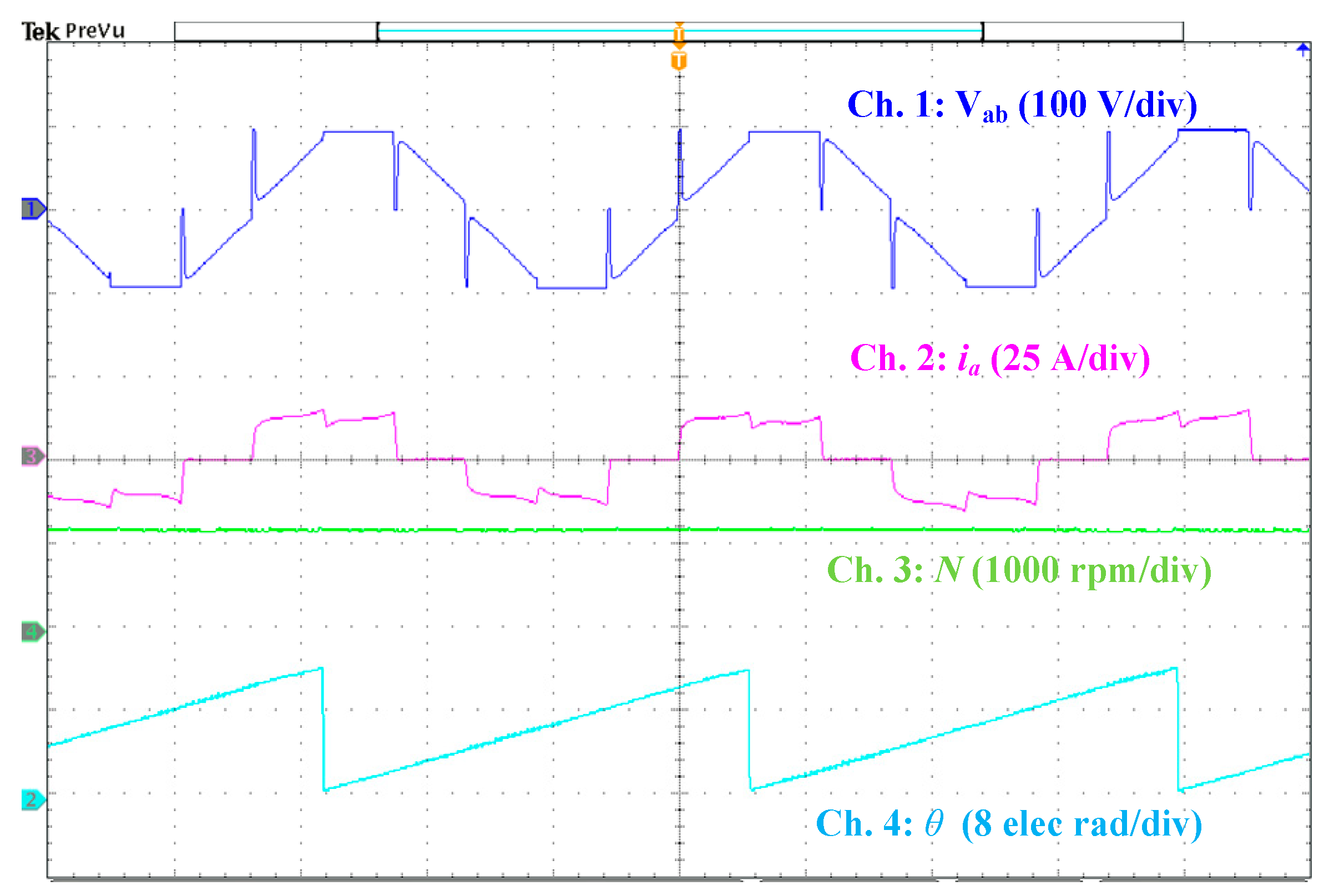
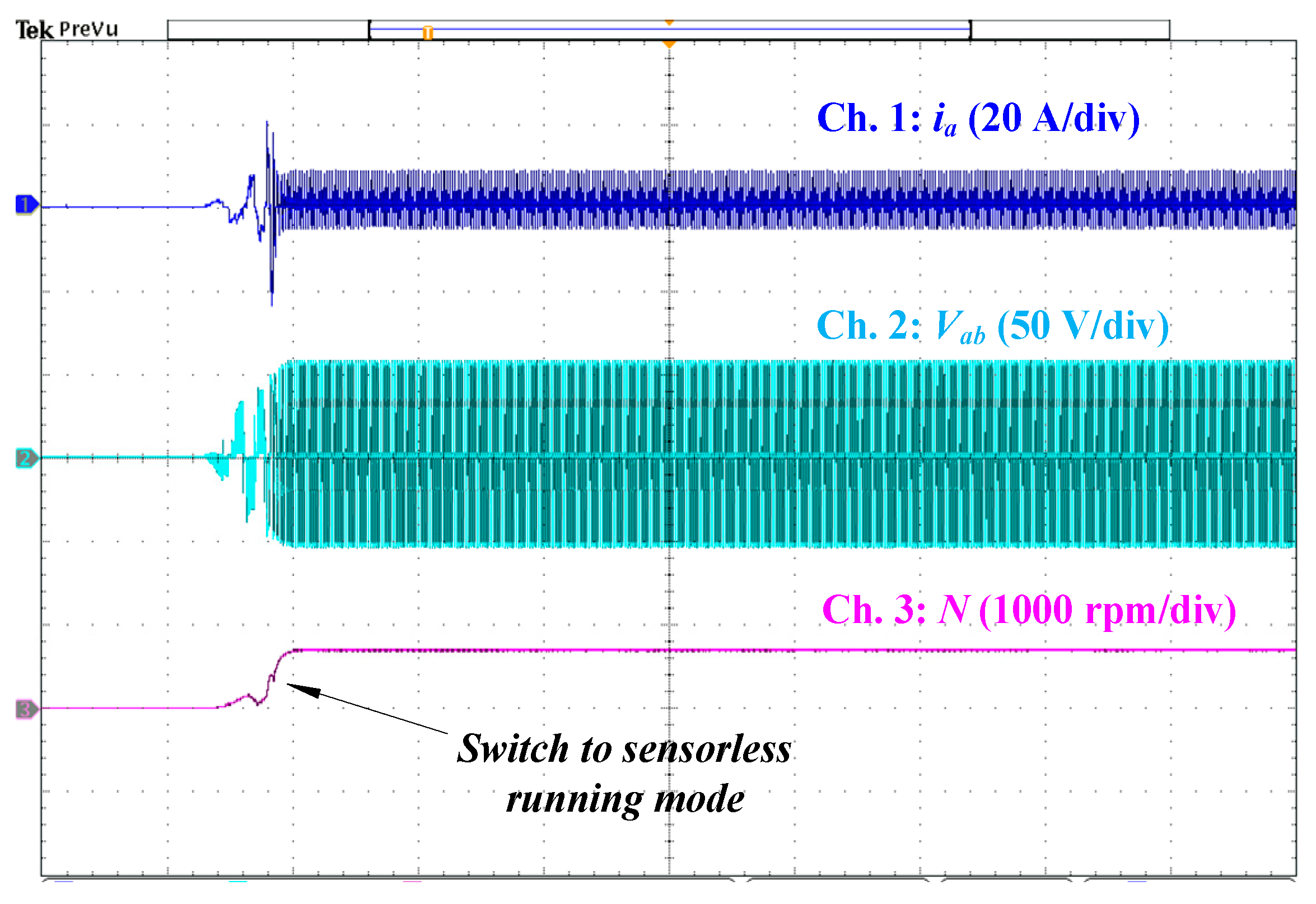
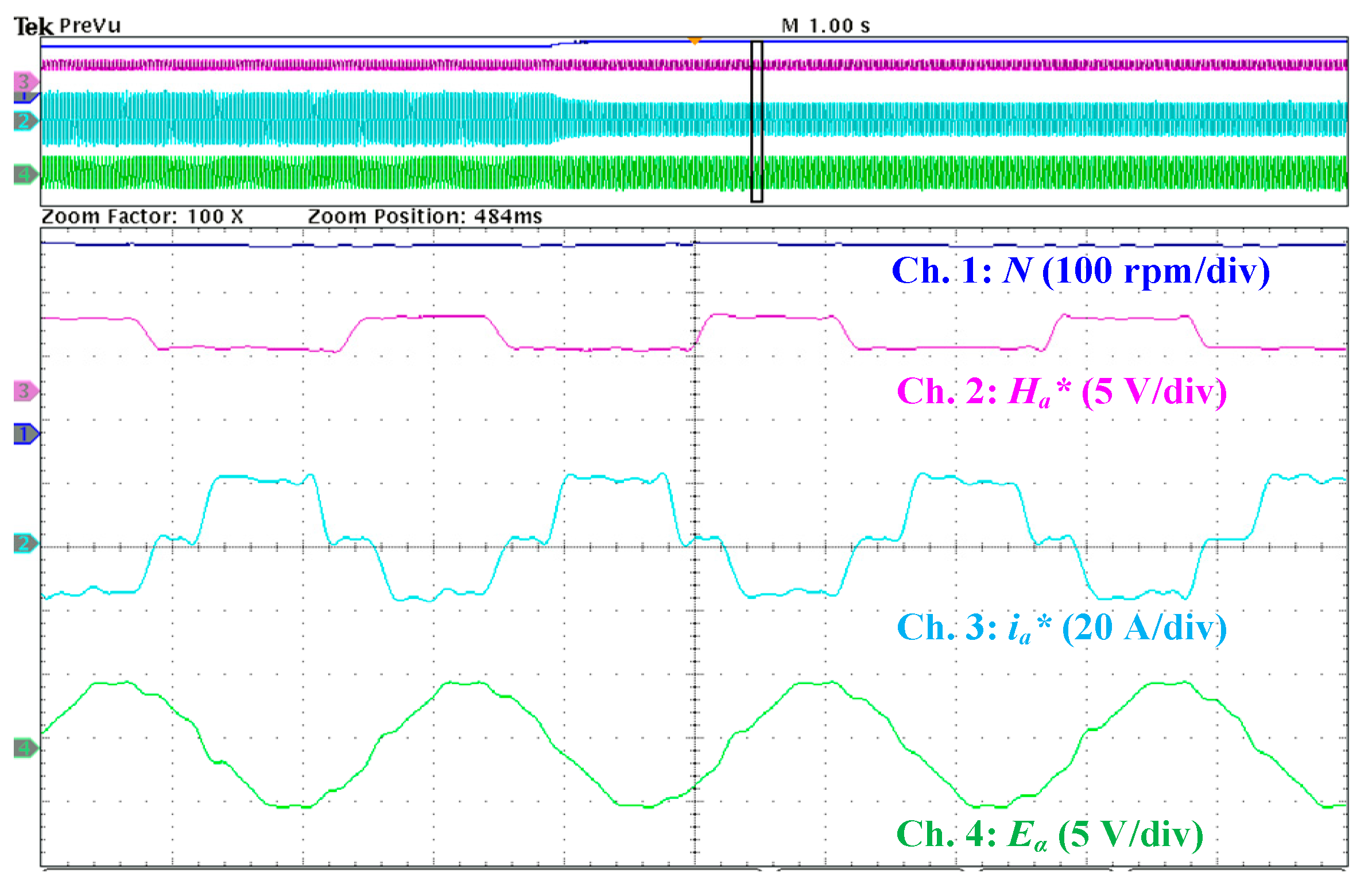
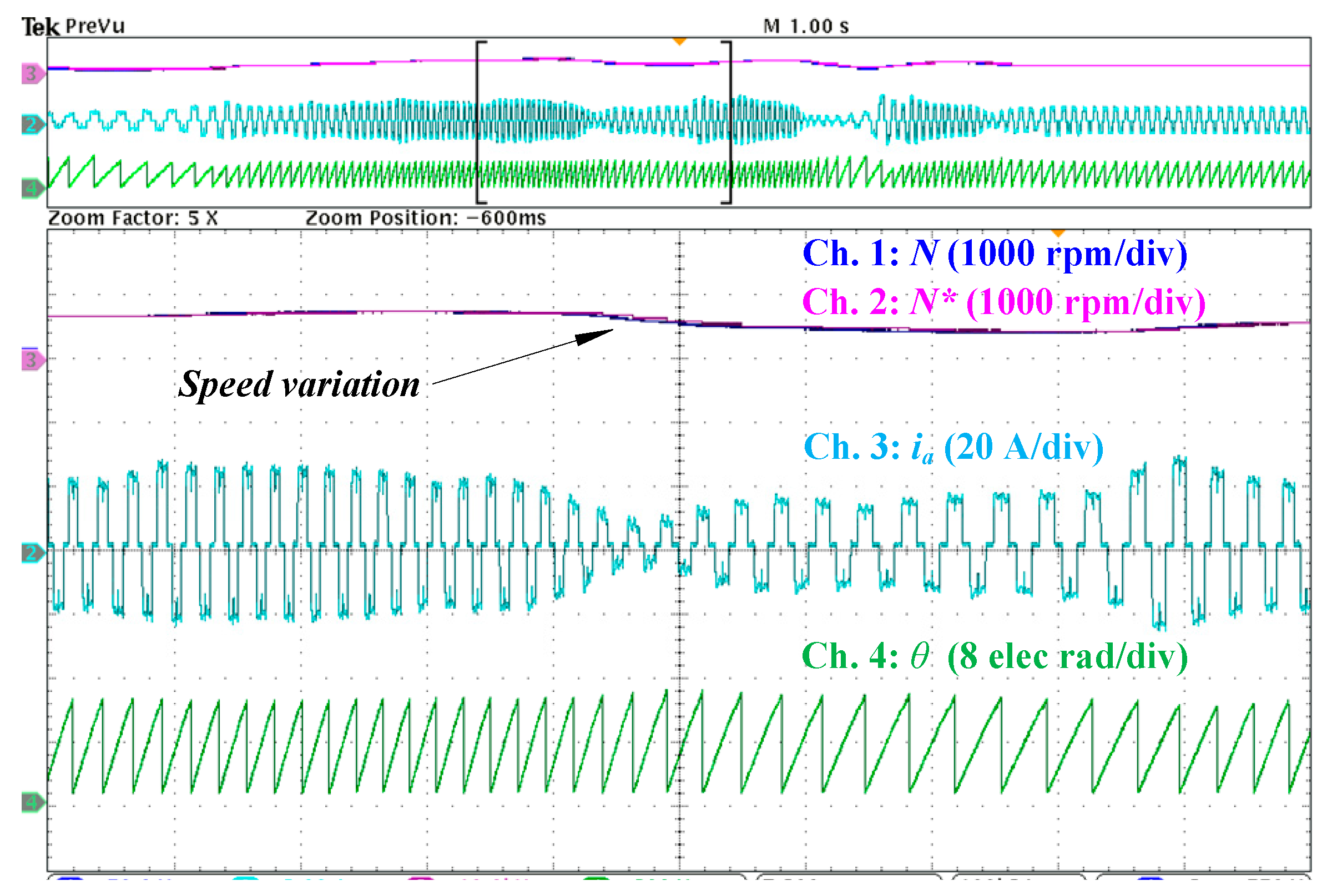
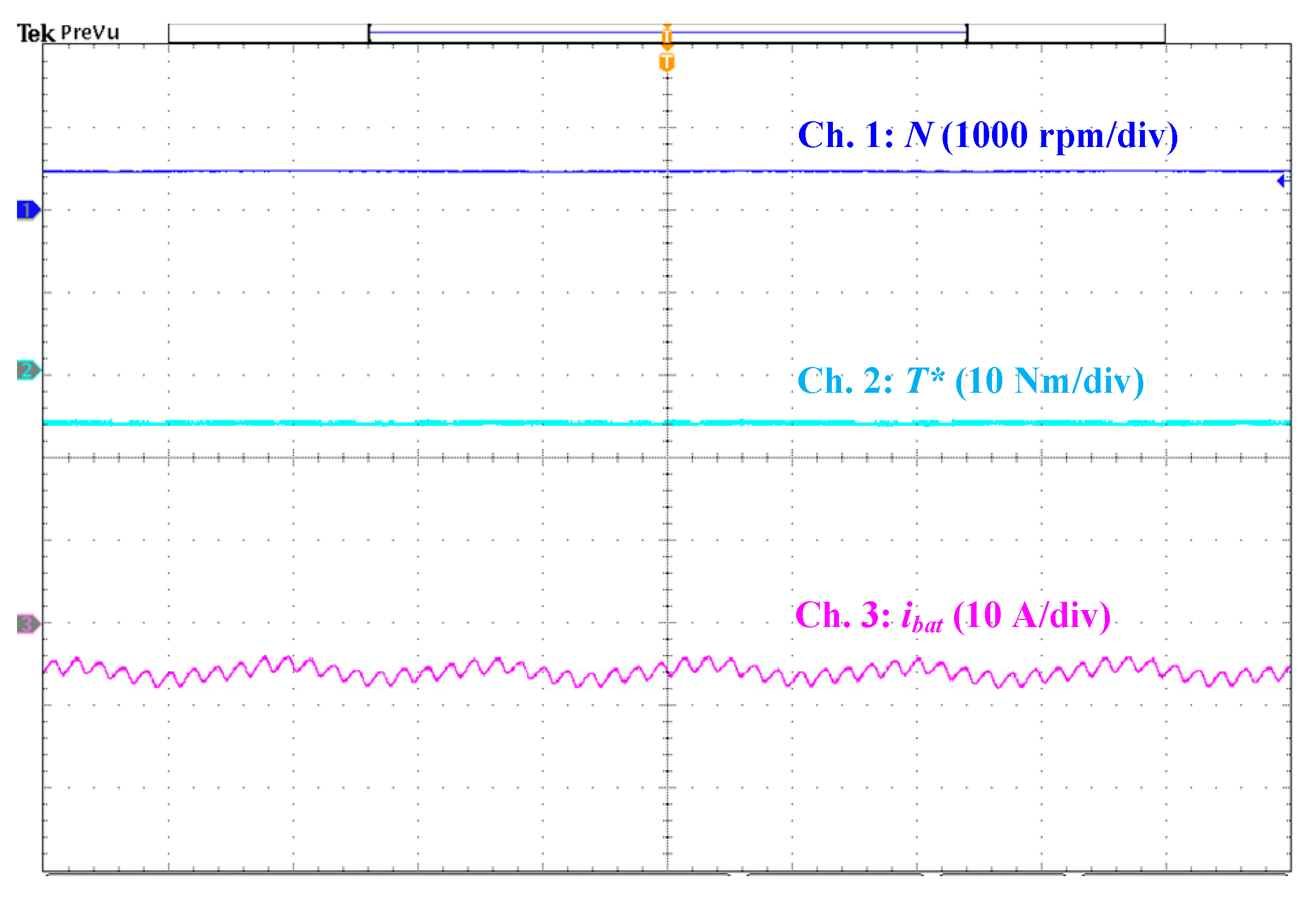
5.2. Performance of the Sensorless BLDCM Drive Control
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vaidehi, S.D.; Jayakumar, A.; Lavanya, R.; Kumar, M.D. Techno-Economic Assessment of Various Motors for Three-Wheeler E-Auto Rickshaw: From Indian Context. Mater. Today Proc. 2021, 45, 6572–6579. [Google Scholar] [CrossRef]
- Prabhu, N.; Thirumalaivasan, R.; Ashok, B. Critical Review on Torque Ripple Sources and Mitigation Control Strategies of BLDC Motors in Electric Vehicle Applications. IEEE Access 2023, 11, 115699–115739. [Google Scholar] [CrossRef]
- Akrami, M.; Jamshidpour, E.; Frick, V. Application of Hall Position Sensor in Control and Position Estimation of PMSM—A Review. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; pp. 1–6. [Google Scholar]
- Akrami, M.; Jamshidpour, E.; Nahid-Mobarakeh, B.; Pierfederici, S.; Frick, V. Sensorless Control Methods for BLDC Motor Drives: A Review. IEEE Trans. Transp. Electrif. 2025; Early Access. [Google Scholar] [CrossRef]
- Mohammad, K.; Rashid, M.F.; Rahat, H.; Khan, F.; Rahman, K. Detailed Analysis of DC-DC Converters Fed with Solar-PV System with MPPT. In Proceedings of the 2022 International Conference for Advancement in Technology (ICONAT), Goa, India, 21–23 January 2022; pp. 1–6. [Google Scholar]
- Sutikno, T.; Samosir, A.S.; Aprilianto, R.A.; Purnama, H.S.; Arsadiando, W.; Padmanaban, S. Advanced DC–DC Converter Topologies for Solar Energy Harvesting Applications: A Review. Clean Energy 2023, 7, 555–570. [Google Scholar] [CrossRef]
- Saha, B.; Singh, B. Back-EMF Observer Based Sensorless BLDC Motor Drive with SEPIC Converter for EV Application. In Proceedings of the 2021 IEEE 6th International Conference on Computing, Communication and Automation (ICCCA), Arad, Romania, 17–19 December 2021; pp. 94–99. [Google Scholar]
- Bahrami, M.; Mokhtari, H.; Dindar, A. Energy Regeneration Technique for Electric Vehicles Driven by a Brushless DC Motor. IET Power Electron. 2019, 12, 3397–3402. [Google Scholar] [CrossRef]
- Nian, X.; Peng, F.; Zhang, H. Regenerative Braking System of Electric Vehicle Driven by Brushless DC Motor. IEEE Trans. Ind. Electron. 2014, 61, 5798–5808. [Google Scholar] [CrossRef]
- Ahmad, F.; Pandey, M.; Zaid, M. Sensorless Control of Brushless DC Motor by Zero-Crossing Detection Pulse Generation with Adaptive Power Factor Control Technique. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Yang, L.; Zhu, Z.Q.; Bin, H.; Zhang, Z.; Gong, L. Virtual Third Harmonic Back-EMF-Based Sensorless Drive for High-Speed BLDC Motors Considering Machine Parameter Asymmetries. IEEE Trans. Ind. Appl. 2021, 57, 306–315. [Google Scholar] [CrossRef]
- Antonello, R.; Ortombina, L.; Tinazzi, F.; Zigliotto, M. Enhanced Low-Speed Operations for Sensorless Anisotropic PM Synchronous Motor Drives by a Modified Back-EMF Observer. IEEE Trans. Ind. Electron. 2018, 65, 3069–3076. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, L.; Li, H.; Zheng, S.; Jin, H.; Chen, B. Commutation Point Optimization Method for Sensorless BLDC Motor Control Using Vector Phase Difference of Back-EMF and Current. IEEE/ASME Trans. Mechatron. 2024, 29, 423–433. [Google Scholar] [CrossRef]
- Filho, C.J.V.; Xiao, D.; Vieira, R.P.; Emadi, A. Observers for High-Speed Sensorless PMSM Drives: Design Methods, Tuning Challenges and Future Trends. IEEE Access 2021, 9, 56397–56415. [Google Scholar] [CrossRef]
- Nair, S.V.; Hatua, K.; Prasad, N.V.P.R.D.; Reddy, D.K. A Quick I-f Starting of PMSM Drive with Pole Slipping Prevention and Reduced Speed Oscillations. IEEE Trans. Ind. Electron. 2021, 68, 6650–6661. [Google Scholar] [CrossRef]
- Wang, T.; Huang, J.; Ye, M.; Chen, J.; Kong, W.; Kang, M.; Yu, M. An EMF Observer for PMSM Sensorless Drives Adaptive to Stator Resistance and Rotor Flux Linkage. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1899–1913. [Google Scholar] [CrossRef]
- Yang, S.-C.; Chen, G.-R. High-Speed Position-Sensorless Drive of Permanent-Magnet Machine Using Discrete-Time EMF Estimation. IEEE Trans. Ind. Electron. 2017, 64, 4444–4453. [Google Scholar] [CrossRef]
- Ok, S.; Xu, Z.; Lee, D.-H. A Sensorless Speed Control of High-Speed BLDC Motor Using Variable Slope SMO. IEEE Trans. Ind. Appl. 2024, 60, 3221–3228. [Google Scholar] [CrossRef]
- Cai, J.; Gu, Y.; Cheok, A.D.; Yan, Y. A Survey of Phase-Locked Loop Technologies in Sensorless Position Estimation of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Instrum. Meas. 2024, 73, 1504016. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, Y.; Cao, X.; Yuan, D.; Liu, J. Estimated Position Error Suppression Using Novel PLL for IPMSM Sensorless Drives Based on Full-Order SMO. IEEE Trans. Power Electron. 2022, 37, 4463–4474. [Google Scholar] [CrossRef]
- Li, J.; Sun, Y.; Lin, J.; Li, X.; Zhou, F.; Dan, H. Reduced-Order Adaptive Observer with Asymptotic Stability for Sensorless Control of SPMSM. IEEE Trans. Power Electron. 2025, 40, 588–598. [Google Scholar] [CrossRef]
- Wang, B.; Shao, Y.; Yu, Y.; Dong, Q.; Yun, Z.; Xu, D. High-Order Terminal Sliding-Mode Observer for Chattering Suppression and Finite-Time Convergence in Sensorless SPMSM Drives. IEEE Trans. Power Electron. 2021, 36, 11910–11920. [Google Scholar] [CrossRef]
- Woldegiorgis, A.T.; Ge, X.; Wang, H.; Hassan, M. A New Frequency Adaptive Second-Order Disturbance Observer for Sensorless Vector Control of Interior Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2021, 68, 11847–11857. [Google Scholar] [CrossRef]
- Masoudi, H.; Kiyoumarsi, A.; Madani, S.M.; Ataei, M. Torque Ripple Reduction of Nonsinusoidal Brushless DC Motor Based on Super-Twisting Sliding Mode Direct Power Control. IEEE Trans. Transp. Electrif. 2023, 9, 3769–3779. [Google Scholar] [CrossRef]
- Li, P.; Sun, W.; Shen, J.-X. Flux Observer Model for Sensorless Control of PM BLDC Motor with a Damper Cage. IEEE Trans. Ind. Appl. 2019, 55, 1272–1279. [Google Scholar] [CrossRef]
- Bendjedia, B.; Chouireb, S. Comparative Study Between Sensorless Vector Control of PMSM Drives Based on MRAS, SMO, and EKF Observers. In Proceedings of the 2023 International Conference on Advances in Electronics, Control and Communication Systems (ICAECCS), Blida, Algeria, 9–11 May 2023; pp. 1–6. [Google Scholar]
- Cao, R.; Jiang, N.; Lu, M. Sensorless Control of Linear Flux-Switching Permanent Magnet Motor Based on Extended Kalman Filter. IEEE Trans. Ind. Electron. 2020, 67, 5971–5979. [Google Scholar] [CrossRef]
- Chen, D.; Wang, J.; Zhou, L. Adaptive Second-Order Active-Flux Observer for Sensorless Control of PMSMs with MRAS-Based VSI Nonlinearity Compensation. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3076–3086. [Google Scholar] [CrossRef]
- Bierhoff, M.H. A General PLL-Type Algorithm for Speed Sensorless Control of Electrical Drives. IEEE Trans. Ind. Electron. 2017, 64, 9253–9260. [Google Scholar] [CrossRef]
- Tong, L.; Zou, X.; Feng, S.; Chen, Y.; Kang, Y.; Huang, Q.; Huang, Y. An SRF-PLL-Based Sensorless Vector Control Using the Predictive Deadbeat Algorithm for the Direct-Driven Permanent Magnet Synchronous Generator. IEEE Trans. Power Electron. 2014, 29, 2837–2849. [Google Scholar] [CrossRef]
- Wu, X.; Li, J.; Chen, S.; Ma, Z.; Han, Y.; Zhang, X. Sensorless Control of Permanent Magnet Synchronous Motor Based on Double-Cost-Function Finite-Position-Set Phase-Locked Loop. IEEE Trans. Ind. Electron. 2025; Early Access. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. Three-Phase PLLs: A Review of Recent Advances. IEEE Trans. Power Electron. 2017, 32, 1894–1907. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, S.; Liu, A.; Xu, Y.; Li, Z.; Liu, X. Robustness Improvement of Model-Based Sensorless SPMSM Drivers Based on an Adaptive Extended State Observer and an Enhanced Quadrature PLL. IEEE Trans. Power Electron. 2021, 36, 4802–4814. [Google Scholar] [CrossRef]
- Song, X.; Han, B.; Zheng, S.; Fang, J. High-Precision Sensorless Drive for High-Speed BLDC Motors Based on the Virtual Third Harmonic Back-EMF. IEEE Trans. Power Electron. 2018, 33, 1528–1540. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, G.; Zhou, X.; Zheng, S. High-Precision Sensorless Optimal Commutation Deviation Correction Strategy of BLDC Motor with Asymmetric Back EMF. IEEE Trans. Ind. Inform. 2021, 17, 5250–5259. [Google Scholar] [CrossRef]
- Santra, S.B.; Chatterjee, A.; Chatterjee, D.; Padmanaban, S.; Bhattacharya, K. High Efficiency Operation of Brushless DC Motor Drive Using Optimized Harmonic Minimization Based Switching Technique. IEEE Trans. Ind. Appl. 2022, 58, 2122–2133. [Google Scholar] [CrossRef]
- Zuo, Y.; Lai, C.; Iyer, L.V. Improved Single Current Sensor Based PMSM Control under Low Frequency Ratio Using Discrete-Time Adaptive Luenberger Observer. IEEE Trans. Ind. Electron. 2024, 71, 10297–10308. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.T.; Le, K.M.; Tran, H.N.; Jeon, J.W. An Adaptive Backstepping Sliding-Mode Control for Improving Position Tracking of a Permanent-Magnet Synchronous Motor with a Nonlinear Disturbance Observer. IEEE Access 2023, 11, 19173–19185. [Google Scholar] [CrossRef]
- Sun, L. Low Speed Sensorless Control Method of Brushless DC Motor Based on Pulse High Frequency Voltage Injection. Alex. Eng. J. 2022, 61, 6457–6463. [Google Scholar] [CrossRef]
- Kwon, Y.-C.; Lee, J.; Sul, S.-K. Recent Advances in Sensorless Drive of Interior Permanent-Magnet Motor Based on Pulsating Signal Injection. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6577–6588. [Google Scholar] [CrossRef]
- Sun, X.; Cai, F.; Yang, Z.; Tian, X. Finite Position Control of Interior Permanent Magnet Synchronous Motors at Low Speed. IEEE Trans. Power Electron. 2022, 37, 7729–7738. [Google Scholar] [CrossRef]
- Saha, B.; Singh, B.; Sen, A. Solar PV Integration to E-Rickshaw with Regenerative Braking and Sensorless Control. IEEE Trans. Ind. Appl. 2022, 58, 7680–7691. [Google Scholar] [CrossRef]
- Basu, A.; Singh, M. An Efficient Energy Recovery Approach of a BLDC Driven E-Rickshaw in Regenerating Braking Mode. Sci. Iran. 2024. [Google Scholar] [CrossRef]
- Basu, A.; Singh, M.; Vardhan, A.S.S. Energy Regeneration of a Position Sensorless BLDC-Driven PV E-Rickshaw with Regenerative Braking. Electr. Eng. 2024, 106, 1357–1372. [Google Scholar] [CrossRef]






| Sensorless Technology | Merits | Demerits |
|---|---|---|
| Back-EMF zero-crossing |
|
|
| Third harmonic back-EMF variation |
|
|
| Conventional back-EMF observer |
|
|
| Sliding mode observer (SMO) |
|
|
| Super-twisting SMO (STO) |
|
|
| Flux-based observer |
|
|
| Extended Kalman Filter (EKF) |
|
|
| Luenberger observer |
|
|
| Linear disturbance observer (LDO) |
|
|
| Frequency-adaptive observers (SOGI, MSOGI, DSOGI) |
|
|
| Multiple harmonic elimination (MHE) observers |
|
|
| Machine parameter-adaptive observers (RLS, MRAS, adaptive PI) |
|
|
| Saliency-based observers |
|
|
| Proposed QPLL-based back-EMF observer |
|
|
| Parameter | Value | Units |
|---|---|---|
| Rated power | 850 | W |
| Peak power | 1250 | W |
| Rated voltage | 48 | V |
| Rated current | 21 | A |
| Peak current | 50 | A |
| Rated speed | 3000 | rpm |
| Stator per-phase resistance | 0.18 | Ω |
| Stator per-phase inductance | 50 | mH |
| Rated torque | 2.7 | Nm |
| Peak torque | 20 | Nm |
| Pole pairs | 2 | |
| Inertia | 0.02 | kg·m2 |
| Component or Characteristic | Value or Type |
|---|---|
| Propulsion type | Electrical, 850 W BLDCM |
| Drive mode | Torque control |
| Maximum speed | 25 km/h |
| Wheel diameter | 304.80 mm |
| Vehicle dimensions | 2850 × 1050 × 1800 mm |
| Net weight | 190 kg |
| Peak loading capacity | 400 kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saha, B.; Sen, A.; Singh, B.; Mahtani, K.; Sánchez-Fernández, J.A. Quadrature-Phase-Locked-Loop-Based Back-Electromotive Force Observer for Sensorless Brushless DC Motor Drive Control in Solar-Powered Electric Vehicles. Appl. Sci. 2025, 15, 574. https://doi.org/10.3390/app15020574
Saha B, Sen A, Singh B, Mahtani K, Sánchez-Fernández JA. Quadrature-Phase-Locked-Loop-Based Back-Electromotive Force Observer for Sensorless Brushless DC Motor Drive Control in Solar-Powered Electric Vehicles. Applied Sciences. 2025; 15(2):574. https://doi.org/10.3390/app15020574
Chicago/Turabian StyleSaha, Biswajit, Aryadip Sen, Bhim Singh, Kumar Mahtani, and José A. Sánchez-Fernández. 2025. "Quadrature-Phase-Locked-Loop-Based Back-Electromotive Force Observer for Sensorless Brushless DC Motor Drive Control in Solar-Powered Electric Vehicles" Applied Sciences 15, no. 2: 574. https://doi.org/10.3390/app15020574
APA StyleSaha, B., Sen, A., Singh, B., Mahtani, K., & Sánchez-Fernández, J. A. (2025). Quadrature-Phase-Locked-Loop-Based Back-Electromotive Force Observer for Sensorless Brushless DC Motor Drive Control in Solar-Powered Electric Vehicles. Applied Sciences, 15(2), 574. https://doi.org/10.3390/app15020574








