1. Introduction
The huge amount of data in many areas leads to the formation of high-dimensional datasets. Large amounts of data and a massive number of attributes increase computational complexity and decrease the efficiency of data mining [
1,
2] and learning processes [
3]. The large amount of data also leads to a problem in classification tasks known as the curse of dimensionality [
2,
4]. Feature selection (FS) is a crucial process for shrinking the size of a dataset by removing duplicated and useless features to enhance classification performance and/or reduce computational costs [
2].
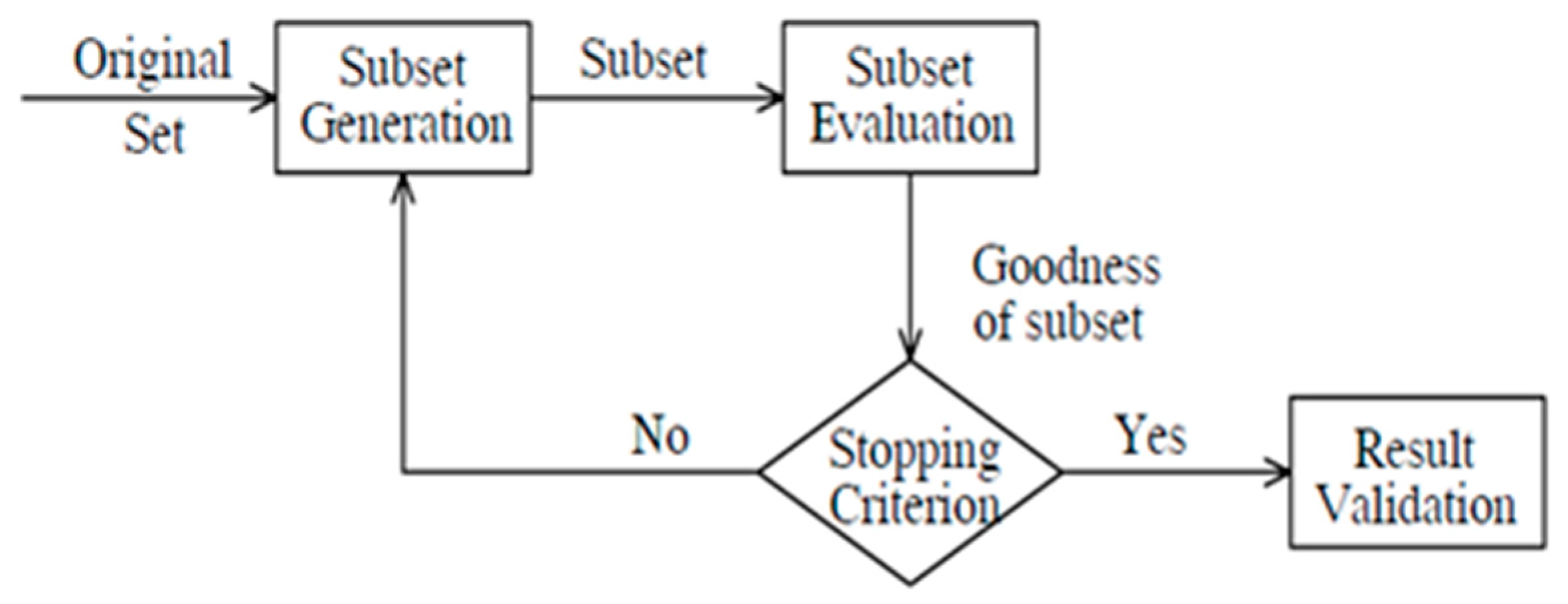
The FS process consists of four steps, as shown in
Figure 1 [
5]. The four steps are subset generation, subset evaluation, verification for a stopping criterion, and result validation. Subset generation is the process of searching for feasible solutions to generate candidate feature subsets for evaluation. Subset evaluation is then used to evaluate the newly generated subset by comparing it with a previous best one in terms of a certain evaluation criterion. The new subset may replace the previous best subset if the former is found to be better than the latter. The stopping criterion determines whether the feature selection process must be stopped or not due to, for example, achieving a certain minimum number of features or reaching a certain maximum number of iterations. Finally, result validation is used to measure the accuracy of the result. It is responsible for evaluating the FS approach by validating the selected subset of features using a testing dataset.
The search algorithms that are commonly used to search for the best representative features in a dataset can be categorized into three different classes, namely, exhaustive, random, and heuristic search techniques [
2,
6]. An exhaustive search technique is time-consuming and, consequently, exhibits high costs since it investigates all possible solutions [
2,
7]. A random search technique generates a random subset of features from the dataset [
8]. A heuristic search technique is faster than the former two searching techniques since it allows the user to obtain the near-optimal subset by applying some heuristic behavior without having to check all possible feature subsets [
9].
To evaluate the generated feature subsets, filter, wrapper, and hybrid approaches can be used [
10]. The filter approach evaluates a new subset of features based on a certain ranking method to return the most important attributes without applying any learning algorithm [
11]. The wrapper approach evaluates the chosen features based on the feedback from a learning algorithm which takes, for example, classification accuracy into account [
12]. The hybrid approach benefits from the advantages of both the filter and wrapper methods [
13].
Metaheuristics are frequently used in the literature to solve optimization problems, specifically with broad searching areas to find the best solution in a reasonable time [
14]. This paper focuses on metaheuristic search strategies to deal with the FS optimization problem. Swarm intelligence (SI) algorithms are metaheuristic methods that have been broadly used to resolve a variety of optimization issues [
10]. These algorithms imitate the social attitudes of animals, insects, or birds when seeking food. SI suffers from falling into the local optima, especially when searching in a high-dimensional search space. Such algorithms require a balance between global search, i.e., exploration, and local search, i.e., exploitation, to discover promising areas in the search space and find a global optimum. The focus of this paper is to provide a heuristic solution to achieve this balance.
In this paper, three hybrid FS optimization approaches are proposed. The proposed approaches combine the Grey Wolf Optimization (GWO) [
15,
16] and Particle Swarm Optimization (PSO) [
17,
18] algorithms by applying GWO followed by PSO, and then each approach manipulates the solutions obtained by both algorithms in a different way. This combination aims to overcome the GWO stuck-in-local-optima problem that might occur by leveraging the PSO-wide search space exploration ability on the solutions obtained by GWO. The three proposed approaches are all named Improved Binary Grey Wolf Optimization (IBGWO) and each of them is abbreviated to IBGWO and appended to the approach number. The proposed work in this paper adds significant extensions to the work proposed in [
19].
The FS optimization problem considered in this paper is a binary problem since the features are represented as a bit string of 0’s and 1’s to reflect the non-selected and selected features, respectively [
20,
21]. Transfer functions (TFs) are the mechanisms that are used to transform continuous solutions into binaries [
22]. Two types of TF, namely, S-shaped and V-shaped, are used in this work. The three proposed hybrid approaches are based on the binary versions of both PSO and GWO to resolve the FS optimization problem.
Each of the three proposed approaches combines GWO with PSO by applying GWO followed by PSO and then each approach manipulates the solutions obtained by both algorithms in a different way. The first approach is named IBGWO2 and it performs peer-to-peer (P2P) comparisons between the PSO solutions and the corresponding GWO solutions and keeps the fittest solutions for the next iteration. The second approach is named IBGWO3 and it ranks all the solutions that are obtained from both GWO and PSO and keeps the fittest solutions from both algorithms together. The third approach is named IBGWO4. It is like IBGWO3 in ranking all the solutions that are obtained from both GWO and PSO and it adds the initially generated solutions to select the optimal solutions from these three populations, i.e., those obtained by GWO, PSO, and the initial population.
The performances of the three approaches were evaluated and compared with each other in addition to making comparisons with the original binary PSO (BPSO), binary GWO (BGWO), and other state-of-the-art metaheuristics used for FS optimization in the literature. The comparisons were performed using nine high-dimensional, cancer-related human gene expression datasets. The evaluations were performed in terms of a set of evaluation metrics, namely, average classification accuracy, average number of selected features, average fitness values, average computational time, and computational complexity.
The results showed that the proposed S-shaped optimizer, IBGWO3-S, achieved more than 0.9 average classification accuracy while selecting the fewest number of features in most of the datasets. The proposed V-shaped optimizer named IBGWO4-V achieved more than 0.95 average classification accuracy while also selecting the fewest number of features in most of the datasets. The results also confirmed the superiority of the proposed IBGWO4-V approach when compared with the original BGWO and BPSO. Moreover, the results confirmed the superiority of the proposed IBGWO4-V approach over other state-of-the-art metaheuristics selected from the literature in most of the datasets. Finally, the computational complexity analysis of the three proposed approaches showed that the best approach in terms of classification accuracy, fitness value, and number of selected features had the highest computational complexity.
This paper is organized as follows. Related works are discussed in
Section 2.
Section 3 introduces GWO, PSO, and their binary versions. The details of the proposed approaches are provided in
Section 4. The evaluation metrics are described in
Section 5. The datasets and experimental setup are presented in
Section 6. The evaluation results are discussed in
Section 7. A discussion of the evaluation results is summarized in
Section 8. Conclusions and future work directions are presented in
Section 9. Finally,
Appendix A lists all abbreviations used throughout the paper.
2. Related Works
Metaheuristic algorithms are broadly employed to resolve optimization issues [
23]. Metaheuristics are frequently used to determine the appropriate subset of features in a reasonable time. Such methods have been classified into a set of classes as classified in [
24]. Such classes include physics-based [
25,
26], social-based [
27], music-based, chemistry-based, sport-based, math-based, biology-based [
28], and swarm-based [
20].
Since the focus of this work is on swarm-based metaheuristic optimizers, a more detailed listing of such metaheuristics is provided as follows. Examples of swarm-based metaheuristics include PSO [
17,
18,
20,
29], Honey Bee Mating Optimization (HBMO) [
30], Whale Optimization Algorithm (WOA) [
31], Harris Hawks Optimizer (HHO) [
32], Dragonfly Algorithm (DA) [
33], Ant Colony Optimization (ACO) [
34,
35], Ant Lion Optimizer (ALO) [
36,
37,
38], GWO [
15,
16,
21,
39,
40,
41], Bacterial Foraging Optimization (BFO) [
42], Spotted Hyena Optimization (SHO) [
43], and many others.
Many researchers have proposed hybrid metaheuristics to improve the exploration and exploitation aspects of searching techniques to avoid local optima. For example, a hybrid firefly algorithm with a mutation operator was used for FS optimization to detect intrusions in a network [
44]. This hybrid approach was utilized to choose the best features without becoming stuck in the local optima. A hybrid algorithm that combines WOA with the flower pollination algorithm for feature selection to detect a spam email was proposed in [
45].
Genetical Swarm Optimization (GSO) was proposed in [
46], which provided a combination of Genetic Algorithms (GAs) and PSO. This technique was used to optimize the FS problem for digital mammogram sets of data. Another hybrid approach was proposed in [
47] that combined GWO and WOA to create a wrapper-based FS method. A hybrid model that combined SHO with Simulated Annealing (SA) for FS optimization is called SHOSA and was proposed in [
43]. The findings indicated the superiority of SHOSA in finding the best features. A hybrid algorithm called (MBA–SA) combined the Mine Blast Algorithm (MBA) with SA to optimize the FS problem and is presented in [
48].
A binary algorithm that combined GWO with HHO to select the optimal features from the datasets was proposed in [
49]. This hybrid algorithm is called HBGWOHHO. The results indicated that the proposed algorithm outperformed some well-known FS optimization algorithms. A hybrid algorithm based on PSO to boost SHO’s hunting methodology was proposed in [
50]. The findings showed that the proposed algorithm outperformed four metaheuristic algorithms when tested on thirteen well-known benchmark functions including unimodal and multimodal functions.
An improved binary GWO algorithm was proposed in [
51]. This work attempted to improve the accuracy of the classification process when compared with the original BGWO algorithm. The proposed improved BGWO algorithm was analyzed by tuning a set of parameters in the original GWO algorithm to achieve an acceptable balance between the exploration and the exploitation capabilities of the original GWO. A set of approaches based on this sensitivity analysis were implemented and compared against each other. This work is similar to our work in the sense that it aimed to solve the GWO exploration-exploitation balance problem. However, our approach combines the binary PSO algorithm with the binary GWO algorithm instead of implementing a kind of sensitivity analysis like the one proposed in that work.
An improved BPSO algorithm was proposed in [
52]. This work aimed to enhance the exploration ability of the original PSO by modifying its population search process. This modification was based on applying two trained surrogate models, where each model was used to approximate the fitness values of the individuals in a separate sub-population. This work is also similar to our work in its ability to enhance the exploration capability of the original BPSO algorithm. However, the main objective of our work is different in the sense that it attempts to combine BGWO with BPSO algorithms to enhance the exploration capability of the original BGWO algorithm by leveraging the original BPSO algorithm.
A multi-objective differential evolutionary algorithm for optimizing FS was proposed in [
53]. This algorithm was proposed to provide a tradeoff between the diversity and convergence of non-dominating solutions. Like our proposed work, this work addressed the problem of optimizing the FS problem. However, it did not include SI in its proposed mechanism.
An improved binary pigeon-inspired optimizer was proposed in [
54] and applied to the FS optimization problem. This optimizer was proposed to overcome the stuck-in-local-optima problem of the original binary pigeon-inspired optimizer [
55]. The objective of this work is like our proposed approaches in the sense that it tried to overcome the effect of the local optimal solution on the optimization process. Our work is different in applying the improvement to the BGWO algorithm by combining it with the BPSO algorithm.
A hybrid SI approach that combined the BGWO with BPSO algorithms was proposed in [
56]. This approach is very similar to our work since it combined the same two metaheuristic approaches applied in our work. Like our work, the objective of this study was to provide a balance between exploration and exploitation of the search space. However, the way of combining the two metaheuristic approaches, i.e., GWO and PSO, differs from our proposed work since the two approaches were used in an alternative fashion, where BGWO was applied in the even iterations while BPSO was applied in the odd ones. The approaches proposed in this work combined both BGWO and BPSO algorithms together in each iteration, which, logically speaking, results in lower classification errors and better fitness values.
A recent hybrid swarm intelligence metaheuristic optimization approach was proposed in [
57] to optimize the FS process. This work combined the BPSO, BGWO, and tournament selection [
58] algorithms. Like our work, the objective of this combination was to provide a balance between exploration and exploitation of the solution space to achieve a near-global optimal solution.
Another recent hybrid SI metaheuristic optimization approach was proposed in [
59] to optimize the FS problem. This work combined ACO with GWO to enhance the exploration power of GWO while preserving its strong exploitation characteristic. This is the same objective of our work with the difference in combining GWO with ACO instead of PSO.
In general, there does not exist an algorithm that is able to resolve all FS optimization issues for all datasets [
60]. Therefore, there is always a strong requirement to design novel algorithms, approaches, and techniques to address the FS optimization problem. This emphasizes the significance of the work proposed in this paper.
3. Background
Kennedy and Eberhart proposed the original PSO algorithm in 1995 [
17]. It imitates the social interactions of flocking birds when seeking food [
17,
61]. PSO is an SI metaheuristic algorithm that explores the problem space for the optimal solution using a set of particles called a swarm. The position of a particle represents a probable solution in the problem space, and the velocity is utilized to adjust the particle to transfer at a particular speed and direction during the searching process. The new velocity of each particle, vl
new, is updated as shown in the following equation:
where vl
old is the particle’s old velocity and x
old is the particle’s old position. pbest and gbest are the personal and global best positions, respectively. The two numbers, rand1 and rand2, are two random numbers in the set [0, 1]. The acceleration factors c1 and c2 refer to the particle’s confidence in itself and its neighbors, respectively. The two factors are set to 2 as a generally accepted setting for most optimization problems, as mentioned in [
17,
62,
63,
64,
65]. iw is an inertia weight that decreases linearly or non-linearly to regulate the exploration and exploitation phases during the search process [
66,
67,
68,
69]. A new position, x
new, for each particle is calculated by the following equation:
- b.
Grey Wolf Optimization
GWO is a metaheuristic algorithm that was proposed by Mirjalili et al. [
15] to resolve optimization problems in different fields. It simulates the hunting technique of grey wolves in detecting prey positions by applying an intelligent searching methodology. The social hierarchy of the grey wolves is based on the hunting skills of the individuals. This hierarchy classifies the wolves into four types: α, β, δ, and ω. In the GWO algorithm, the initial grey wolves are set randomly. Each wolf represents a candidate solution in the problem space. The best solutions are considered as α, β, and δ, while the remaining candidate solutions are considered as ω. The hunting techniques of the grey wolves are explained in more detail in [
15,
16]. These techniques are summarized mathematically by the following set of equations:
where X
(t+1) is the new location of each wolf in the pack depending on the three best locations X
α, X
β, and X
δ. This is determined by the distance D between each wolf and the locations of α, β, and δ. The two coefficient vectors A and C are calculated by the following two equations:
where r1 and r2 are random vectors, whose values are in the set [0, 1]. Vector a is decreased linearly during the iterations from 2 to 0 and calculated using the following equation:
where a is a vector that tunes the exploration and exploitation of the GWO algorithm. It is linearly reduced from 2 to 0 during the iterations depending on the current iteration, currIter, and the maximum number of iterations, maxIter [
15,
16].
GWO offers a natural transition from exploration to exploitation through its adaptive encircling and shrinking mechanisms. However, GWO’s exploration can be limited in certain cases because the wolves tend to converge prematurely around the best solutions, i.e., α, β, and δ, thus reducing diversity in later stages of the search. On the other hand, PSO includes mechanisms that help escape local optima. Its velocity update formula incorporates both cognitive and social components, with random coefficients adding stochasticity to the search. This enables particles to explore new regions even after they cluster around promising solutions. Therefore, the combination of GWO and PSO is motivated by the need to overcome the limitations of GWO in maintaining exploration and diversity while leveraging PSO’s ability to escape local optima and refine solutions.
- c.
Binary Optimization Algorithms for the FS Problem
FS can be considered a binary problem where all features in a dataset can be represented by a series of zeros and ones, where zeros represent the unselected features and ones represent the selected features. According to Mirjalili and Lewis [
22], the conversion from continuous solutions to their corresponding binary solutions is based on two types of TFs, namely, S-shaped and V-shaped. The mathematical formulas of these TFs are shown in [
22,
33]. The binary versions of both PSO and GWO are discussed in [
37,
62]. S2-TF and V2-TF, defined in Equations (13) and (14), are utilized in this work to convert the attributes into binaries. The two equations are shown as follows:
4. Proposed Approaches
An optimization problem entails determining the most effective and optimal solution from all possible solutions. The FS process is an optimization problem that aims to obtain the best and most optimized features in a given dataset. Four different SI approaches are described in this section as wrapper-based FS methods. These approaches are used to identify the most significant feature subsets that optimize the classification task. Searching strategies must provide a balance between the exploration and exploitation phases to identify the optimum solution. Throughout this paper, the PSO algorithm with powerful exploration potential is combined with the GWO algorithm, which has a good exploitation capability. This combination is employed in four different approaches to increase search efficiency and decrease the chances of falling in the local optimum. In this work, the continuous solutions are converted to binary solutions using the S2 and V2 TFs mentioned in [
22,
37].
The GWO algorithm has a good exploitation ability; however, new wolves may drop in a local optimum [
70]. According to the GWO algorithm’s searching strategy, the new wolves in the pack follow the three best solutions,
α,
β, and
δ. These best solutions may not be the optimal ones, particularly when the search is in a high-dimensional space. This increases the probability of being trapped in a local optimum. To improve GWO’s searching capability and the accuracy of its solutions, GWO is combined with PSO. This combination is proposed and implemented in the form of four different approaches. These approaches are explained in more detail in the following subsections.
The first approach is named Improved Binary Grey Wolf Optimization 1 (IBGWO1). This approach was previously proposed in [
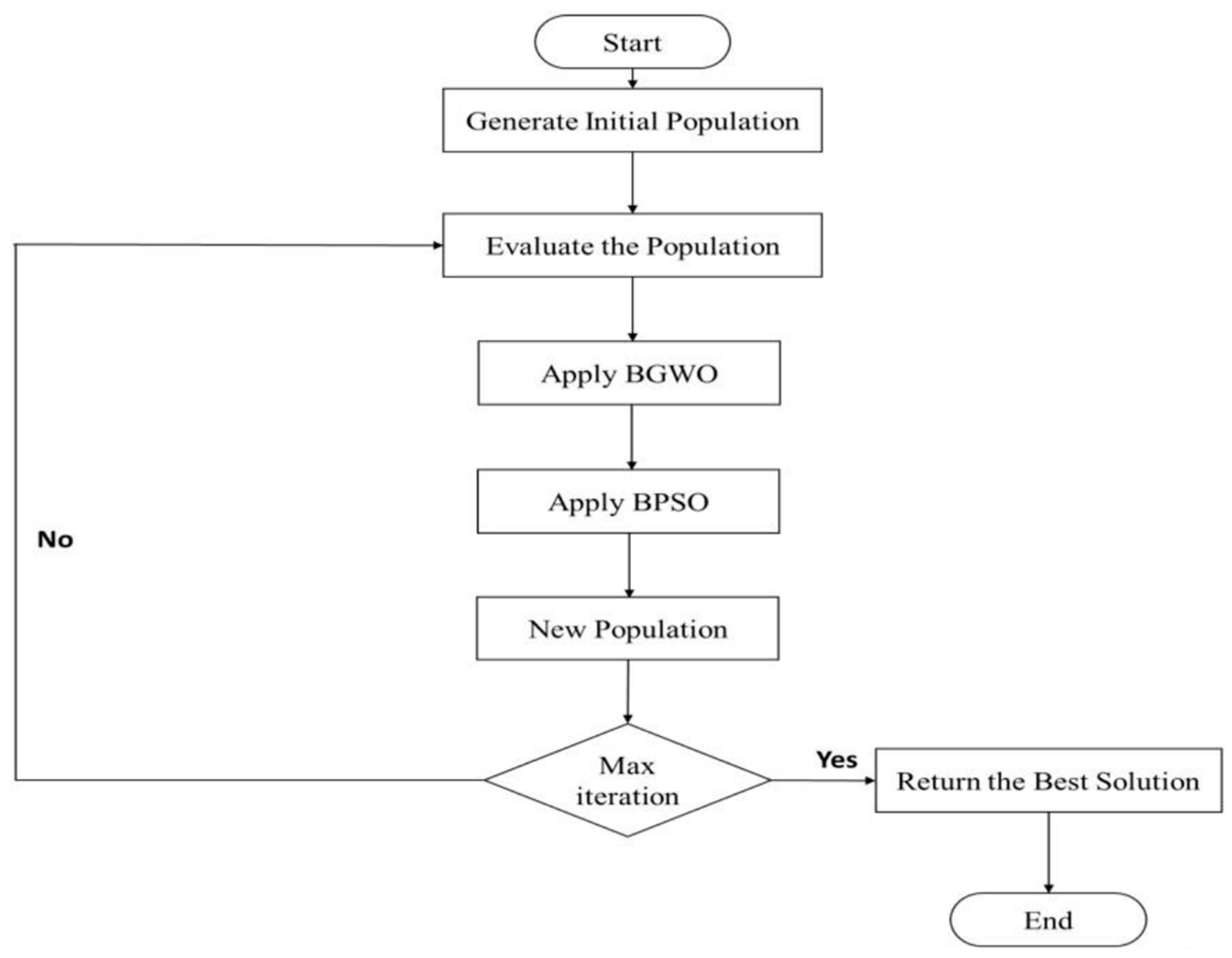
19]. IBGWO1 is presented here for completeness and comparison with three newly proposed approaches in this paper.
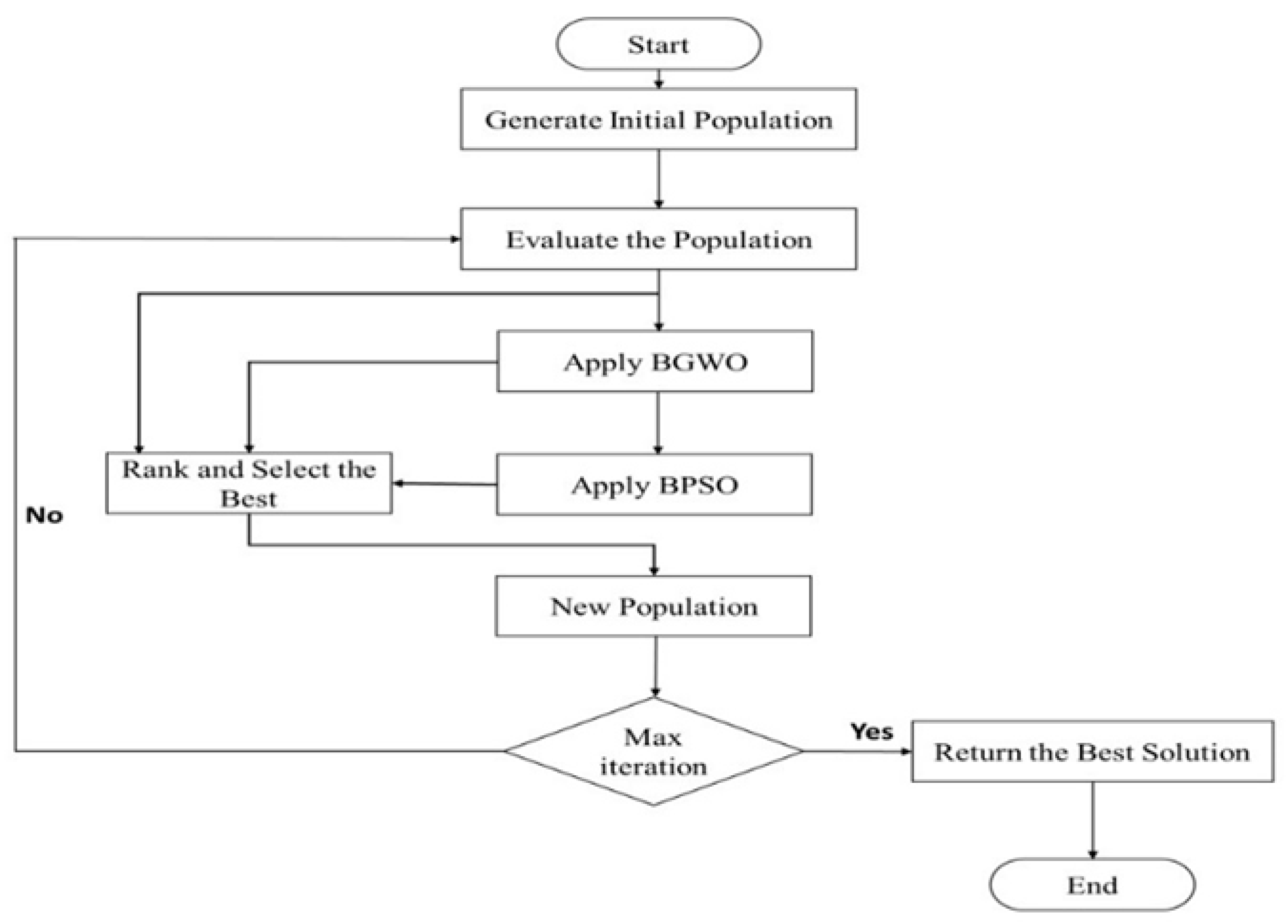
Figure 2 shows the flowchart of IBGWO1. As shown in the figure, IBGWO1 applies GWO followed by PSO to obtain a new population in each iteration. The initial population of GWO is generated randomly and then GWO improves the solutions of the obtained population according to its algorithm. The improved solutions of GWO are used as the initial population of the PSO algorithm, which, in turn, improves the solutions based on its algorithm. These steps are repeated until either the optimal solution or the maximum number of iterations is reached.
- b.
IBGWO2
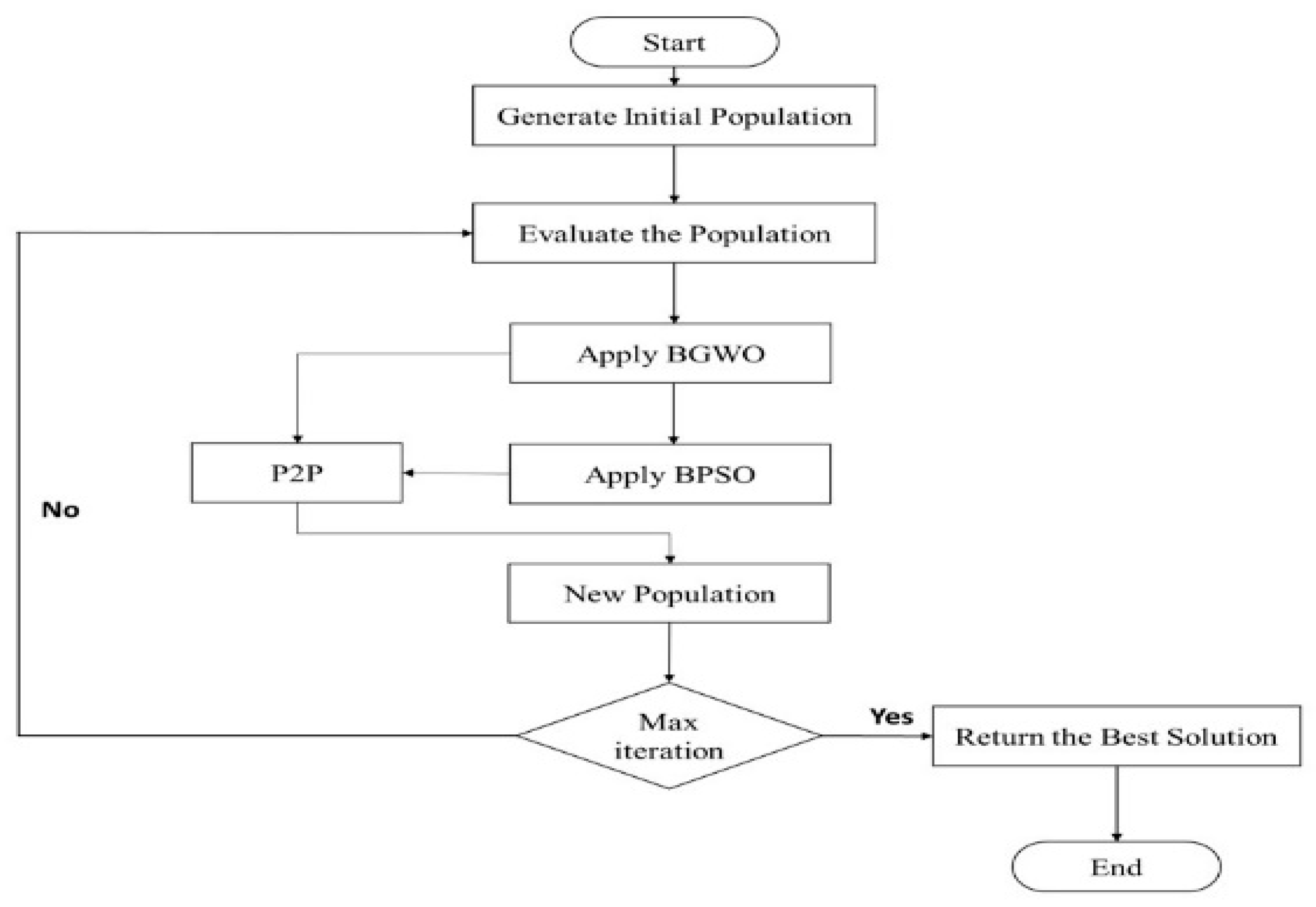
As previously described in the IBGWO1 approach, the GWO’s enhanced population serves as the initial population of the PSO algorithm. Some of GWO’s generated solutions may provide higher fitness than PSO’s generated solutions; however, these robust solutions are updated after implementing the PSO algorithm. Therefore, IBGWO2 proposes the employment of P2P comparisons to preserve the best solutions. The P2P comparisons are used to compare GWO’s solutions to those of their PSO peers, with the fittest solutions being stored. In this approach, the enhanced GWO population is saved before performing PSO. Then, P2P comparisons between GWO’s solutions and PSO’s solutions are performed. These steps are repeated if the stopping criteria are not met.
Algorithm 1 presents the IBGWO2 pseudo-code, while
Figure 3 illustrates its flowchart. In lines 1 to 6, the maximum number of iterations, T, and the population size, P, are initialized. Afterwards, the positions are generated randomly and all GWO and PSO parameters are initialized. In lines 9 to 17, the solutions are updated according to the GWO algorithm and the new positions are saved in a new population. The new population obtained by GWO is then updated according to the PSO equations and another new population is obtained as shown in lines 18 to 24. In lines 25 to 29, P2P comparisons are performed and the best solutions are kept for the next iteration. These steps are repeated until either the optimal solution or the maximum number of iterations is achieved.
| Algorithm 1: IBGWO2 |
1: Start
2: Set the maximum number of iterations T
3: Set the population size P
4: Initialize the individuals’ positions and velocities
5: Initialize the GWO parameters a, A, C
6: Initialize the PSO c1 and c2
7: t ← 1
8: While t < T do
9: Calculate individuals’ fitness values
10: Find best three solutions Xα, Xβ, and Xα
11: p ← 1
12: For p < P do
13: Update GWO individuals’ positions using Equations (3)–(9)
14: Convert the new individuals’ positions to binary using Equations (13) and (14)
15: Update a, A, C using Equations (10)–(12)
16:End For
17: Save the GWO population
18: p ← 1
19: For p < P do
20: Find pbest
21: Update individuals’ velocities using Equation (1)
22: Update individuals’ positions using Equation (2)
23: Convert the new individuals’ positions to binary using Equations (13) and (14)
24: End For
25: Save the PSO population
26: p ← 1
27: For p < P do
28:Compare GWO’s solutions with its corresponding pair in PSO’s solutions
29: Save the fittest solutions for the next iteration
30: End For
31: t++
32: End While
33: Return the best solution
34: End |
- c.
IBGWO3
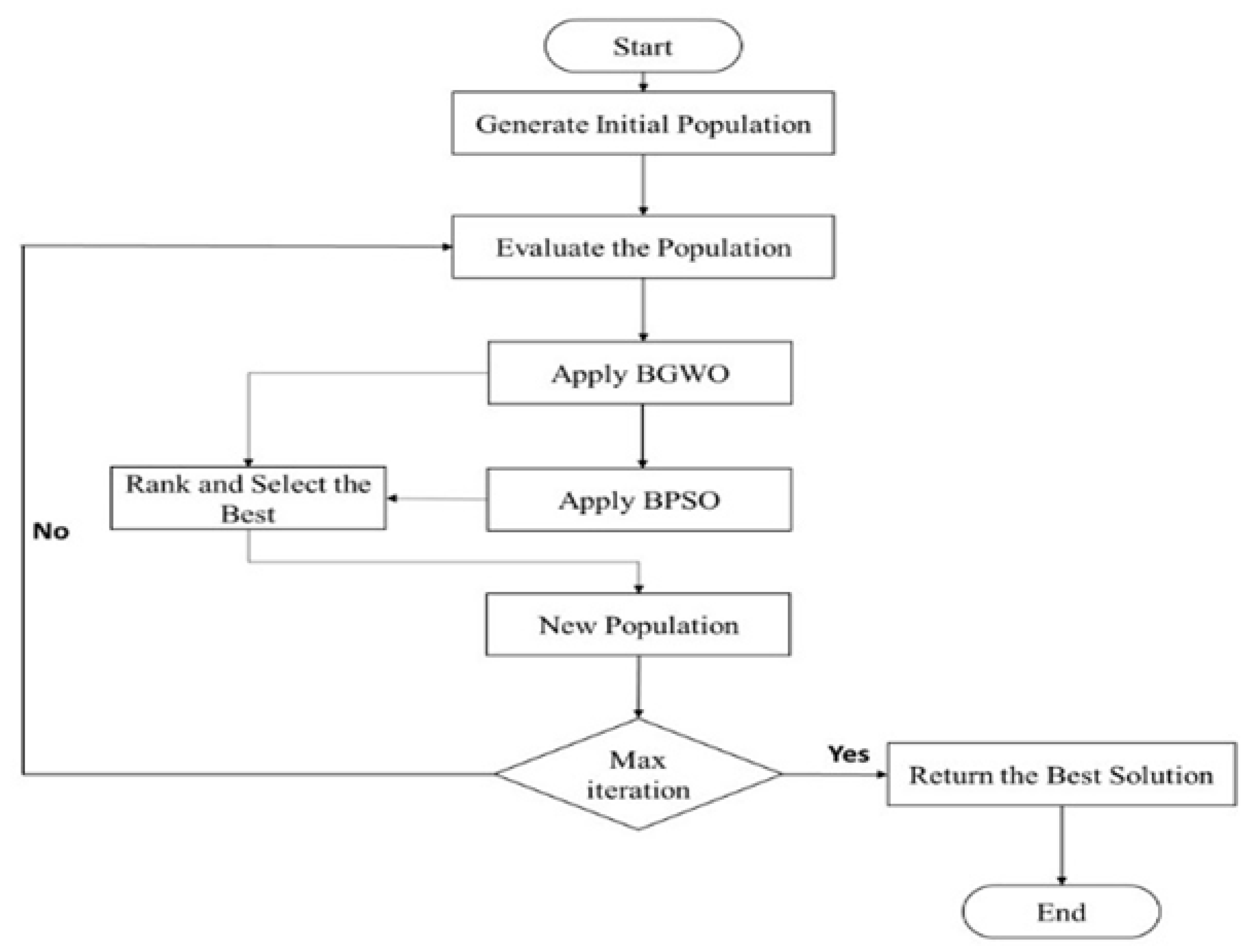
Some strong solutions may be omitted due to peer comparisons applied in IBGWO2. Therefore, IBGWO3 employs ranking to maintain the good solutions that might be lost due to this omission. The solutions, whether generated by GWO or PSO, are ranked based on their fitness values, and the fittest solutions are kept and used in the next iteration. These solutions may only be obtained from GWO, PSO, or both optimizers. Algorithm 2 presents the pseudo-code of IBGWO3, while
Figure 4 illustrates its flowchart. The same steps implemented in IBGWO2 are also implemented in IBGWO3, except for the steps in lines 19 and 20. In these lines, all solutions obtained by both GWO and PSO are ranked together based on their fitness values and the fittest solutions are retained for the next iteration.
| Algorithm 2: IBGWO3 |
1: Start
2: Set the maximum number of iterations T
3: Set the population size P
4: Initialize the individuals’ positions and velocities
5: Initialize the GWO parameters a, A, C
6: Initialize the PSO c1 and c2
7: t ← 1
8: While t < T do
9: p ← 1
10: For p < P do
11: Update the GWO positions like IBGWO2
12: End For
13: Save the GWO population
14: p ← 1
15: For p < P do
16: Update the PSO positions like IBGWO2
17: End For
18: Save the PSO population
19: Rank the GWO and PSO populations
20: Save the fittest solutions for the next iteration
21: t++
22: End While
23: Return the best solution
24: End |
- d.
IBGWO4
The IBGWO4 approach augments IBGWO3 with an additional step in which it ranks the solutions of three populations based on their fitness values to find the best solutions. Algorithm 3 lists the pseudocode of IBGWO4, while
Figure 5 illustrates its flowchart. The ranking is applied based on the solutions that are generated by both PSO and GWO, in addition to the initial population used by each iteration. The best solutions are kept as an initial population for the next iteration. Again, the same steps are implemented as those in IBGWO3 except for the steps in line 20. In this line, the ranking is performed for the three populations, i.e., the initial population, the GWO population, and the PSO population, and the best solutions are retained for the next iteration.
| Algorithm 3: IBGWO4 |
1: Start
2: Set the maximum number of iterations T
3: Set the population size P
4: Initialize the individuals’ positions and velocities
5: Initialize the GWO parameters a, A, C
6: Initialize the PSO c1 and c2
7: t ← 1
8: While t < T do
9: p ← 1
10: For p < P do
11: Update the GWO positions like IBGWO2
12: End For
13: Save the GWO population
14: p ← 1
15: For p < P do
16: Update the PSO positions like IBGWO2
17: End For
18: Save the PSO population
19: Rank initial, GWO, and PSO populations
20: Save the fittest solutions for the next iteration
21: t++
22: End While
23: Return the best solution
24: End |
5. Evaluation Metrics
The objective function, which is used to evaluate the different solutions, combines the classification accuracy and the number of selected features. The near-optimal solution is the one that exhibits the highest classification accuracy, i.e., the lowest classification error, and the least number of features. The fitness function that evaluates each obtained solution is computed as follows:
where ClassErr is the classification error provided by any classifier, such as K-Nearest Neighbor (KNN) [
71], which was used in this study; |q| is the number of selected features; and |Q| is the number of all features in the dataset. The parameter v is used to control the weights of the classification error and the feature subset length, respectively, when computing the fitness of the solution, where v ∈ [0, 1], as mentioned in [
41,
72].
The proposed approaches were evaluated based on a set of metrics, namely, average classification accuracy (ACA), average number of selected features (ASF), average fitness value (AFV), and average computational time (ACT). The mathematical formula of each of these metrics will be described in Equation (16), Equation (17), Equation (18), and Equation (19), respectively.
The ACA evaluates the classifier’s prediction ability using the group of features that is selected. It is defined by the following equation:
where R is the number of runs, S is the number of instances, and Pred
i and Act
i are the predictive and actual classes, respectively. The ASF evaluates how well each proposed approach performs in terms of the number of relevant features that are selected when tackling the FS issue. It is defined by the following equation:
where R is the number of runs, f is the number of selected features, and F is the total number of features in the dataset. The AFV illustrates the average fitness value obtained over a set of runs. AFV is defined by the following equation:
where R is the number of runs; Fit was previously defined in Equation (15). Finally, the ACT is calculated using the following equation, where Time is the total computational time of each run and R is the number of runs:
7. Simulation Results
A set of comparisons are introduced in this section to evaluate the performance of the proposed approaches. Firstly, the evaluation results of the proposed approaches based on the S-shaped TF are compared with the original BGWO and BPSO algorithms. Secondly, the results of the proposed approaches based on the V-shaped TF are compared with the original BGWO and BPSO algorithms. Finally, the comparisons of the best proposed approaches for S-shaped and V-shaped TFs are presented as follows. A comparative study was performed with eight state-of-the-art FS optimizers and another comparative study was performed with a recent hybrid FS optimizer that combined the BGWO and BPSO algorithms.
The classification accuracy of the proposed approaches was measured using the KNN classifier [
72]. KNN is one of the most widely used classifiers and is employed to evaluate and compare the performance of different feature selection algorithms [
12]. This is due to its simplicity, ease of implementation, and low computational complexity when compared with other classifiers. The authors would like to note that other common classifiers can also be employed but are deferred to a future extension of this work.
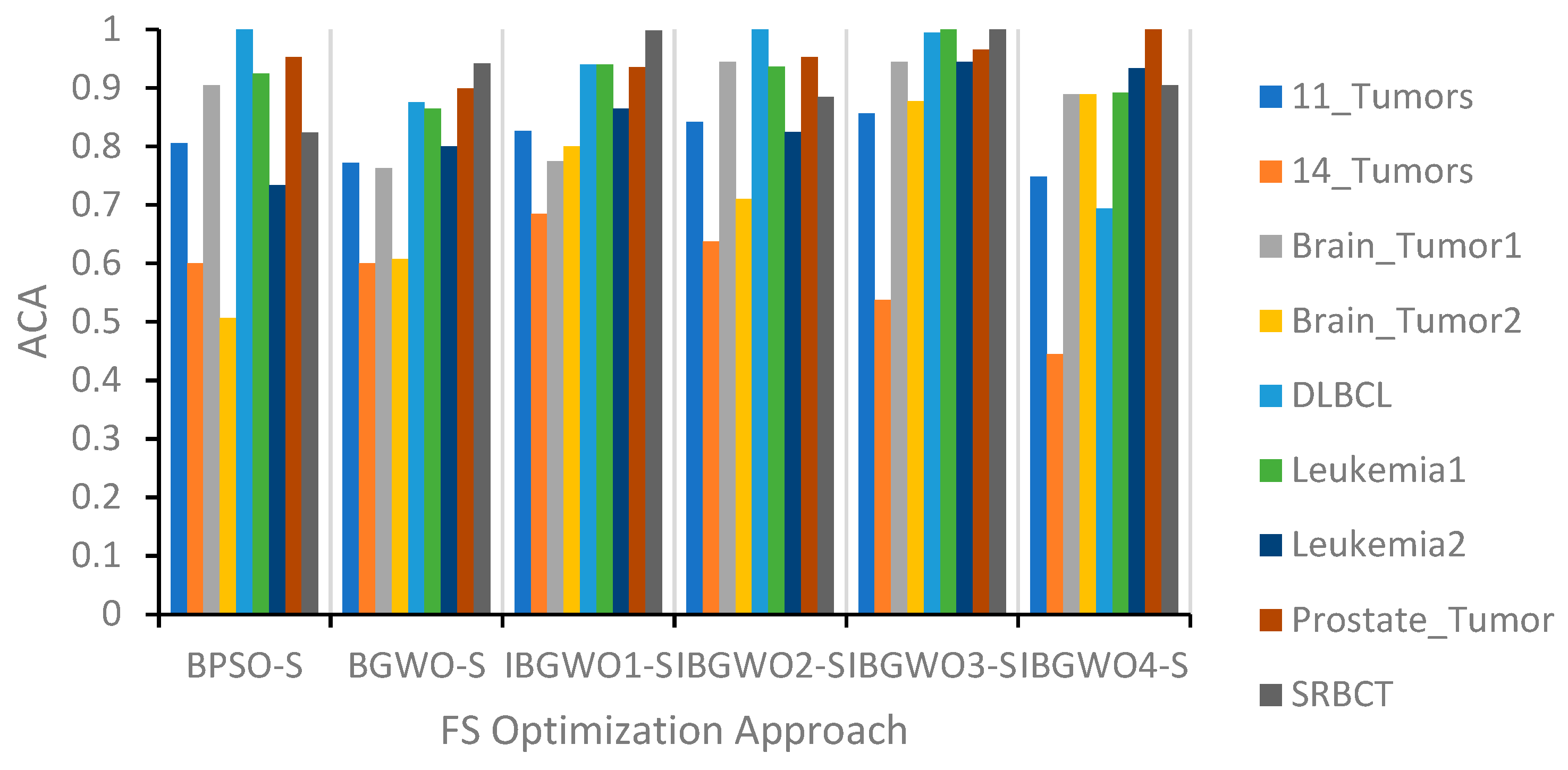
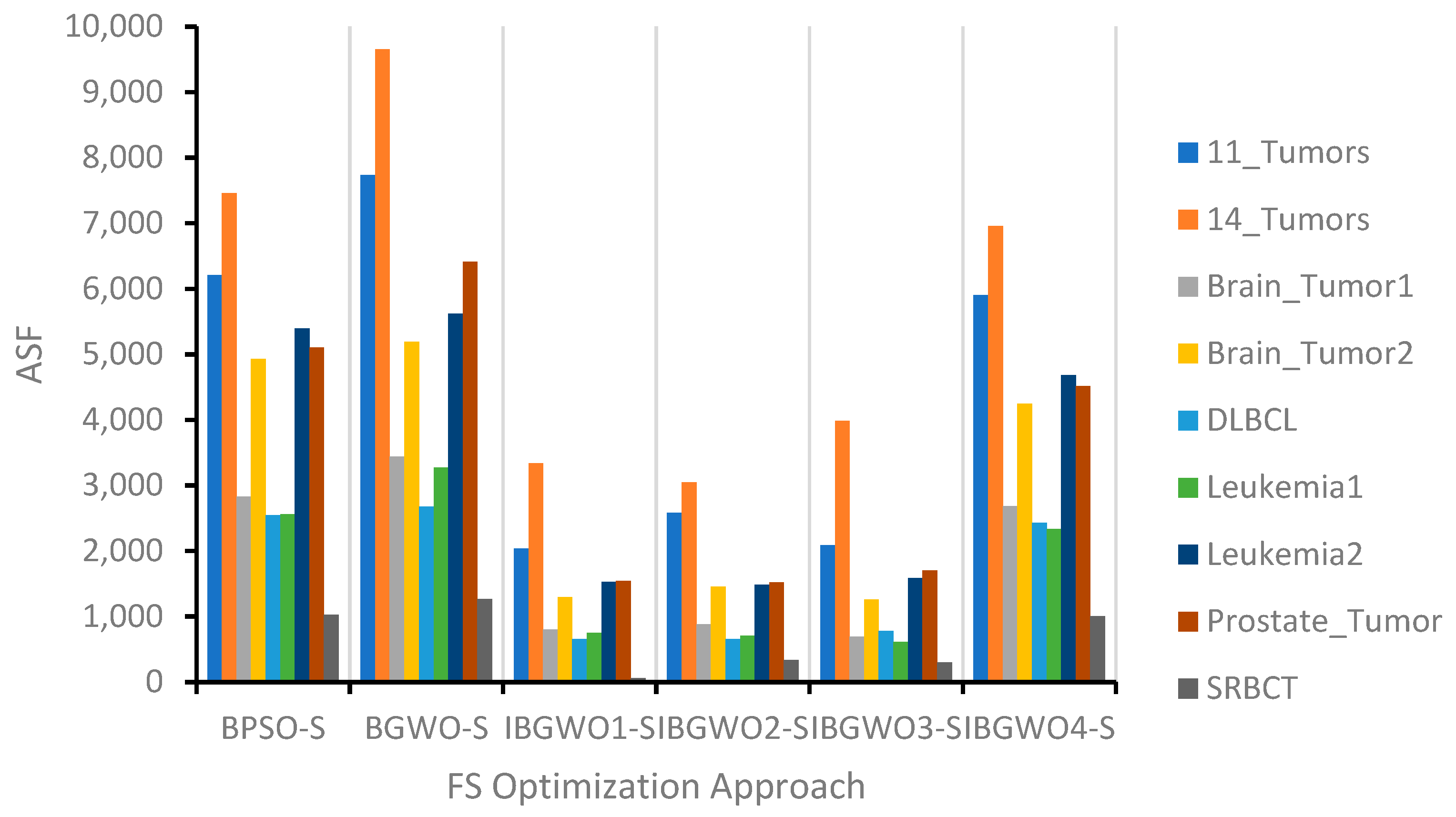
The proposed approaches based on the S-shaped TF were compared against the original BGWO and BPSO algorithms. These comparisons are illustrated in terms of ACA, ASF, and AFV, as shown in
Figure 6,
Figure 7 and
Figure 8, respectively.
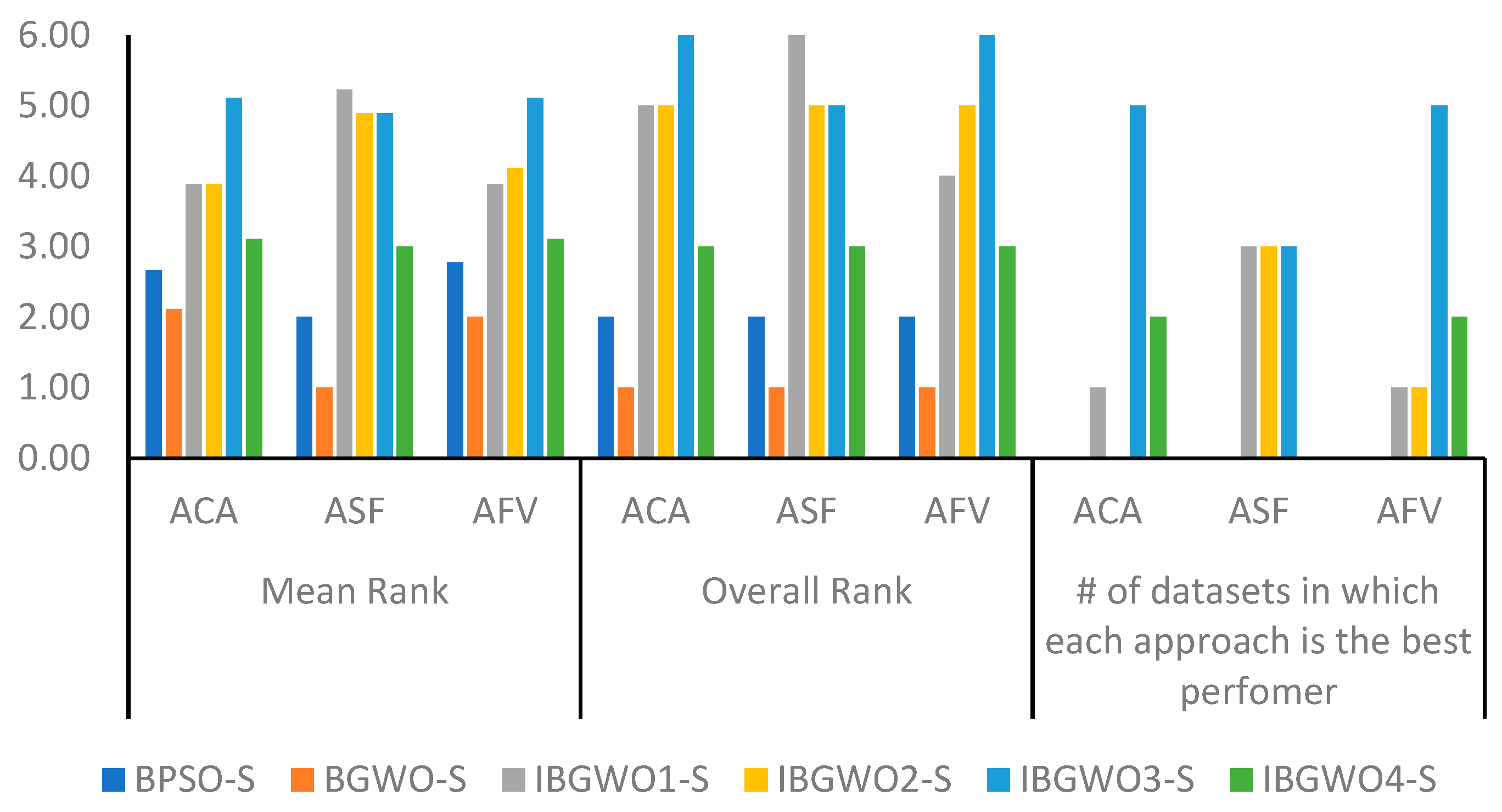
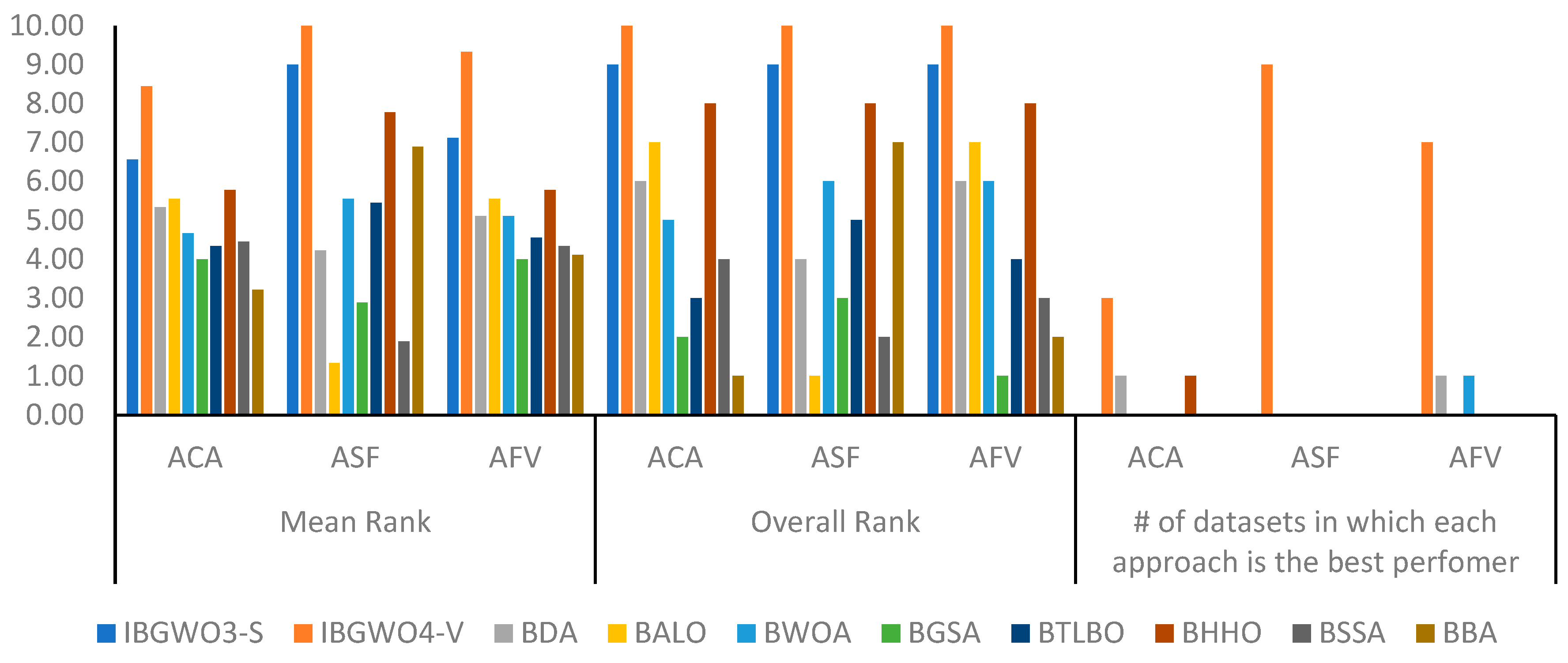
Figure 9 shows a statistical analysis of the proposed approaches based on the S-shaped TF in terms of the same three evaluation metrics. This figure shows the mean and overall ranks of each approach across all datasets under consideration. The rank is generally a number from 1 to 6 since there are six approaches compared against each other, where 6 indicates the highest-ranked approach. Additionally,
Figure 9 shows the number of datasets in which each approach obtained the best rank.
According to the ACA evaluation results shown in
Figure 6 and
Figure 9, IBGWO3-S exceeded other approaches in five datasets. IBGWO3-S achieved an average ACA value of 0.9 across all datasets. IBGWO4-S yielded the best performance in two datasets. It was expected that the IBGWO3-S and IBGWO4-S optimization approaches would result in the best solutions. The reason for this was that the IBGWO3-S approach took into consideration in each iteration the fittest of all populations that resulted from applying BGWO alone and from applying BGWO followed by BPSO. Also, IBGWO4-S added to this ranking process the initial population that resulted from the previous iteration. However, using the S-shaped TF was found to negatively affect the results of IBGWO4-S relative to the results of IBGWO3-S. In general, all proposed approaches were found to outperform the original BGWO-S and BPSO-S since the hybrid approaches combined the exploration and exploitation properties of both approaches.
Figure 7 shows that IBGWO1-S, IBGWO2-S, and IBGWO3-S achieved the best ASF results by selecting the fewest number of features in most of the datasets. As shown in
Figure 8, the mean and overall ranks show that IBGWO1-S, IBGWO2-S, and IBGWO3-S achieved the best ranks and outperformed other approaches in terms of selecting the most suitable features. IBGWO4-S was negatively affected by applying the S-shaped TF relative to the other three proposed approaches; however, it achieved better mean and overall ranks relative to the original BGWO-S and BPSO-S approaches.
Figure 8 and
Figure 9 summarize the findings in terms of AFV, which is a combination of the classification error and the number of selected features. Note that it is required to minimize the AFV value to improve the performance of the proposed optimizer. According to the results, IBGWO3-S achieved an average AFV value of 0.1 across all datasets. This optimizer provided the fittest outcomes when compared with all other optimizers, including the original BGWO-S and BPSO-S optimizers. This means that this approach was able to provide the most accurate balance between the minimum possible classification error and the minimum possible number of selected features in all datasets. Using the S-shaped TF negatively affected the usage of the IBGWO4-S optimizer approach in terms of the AFV metric.
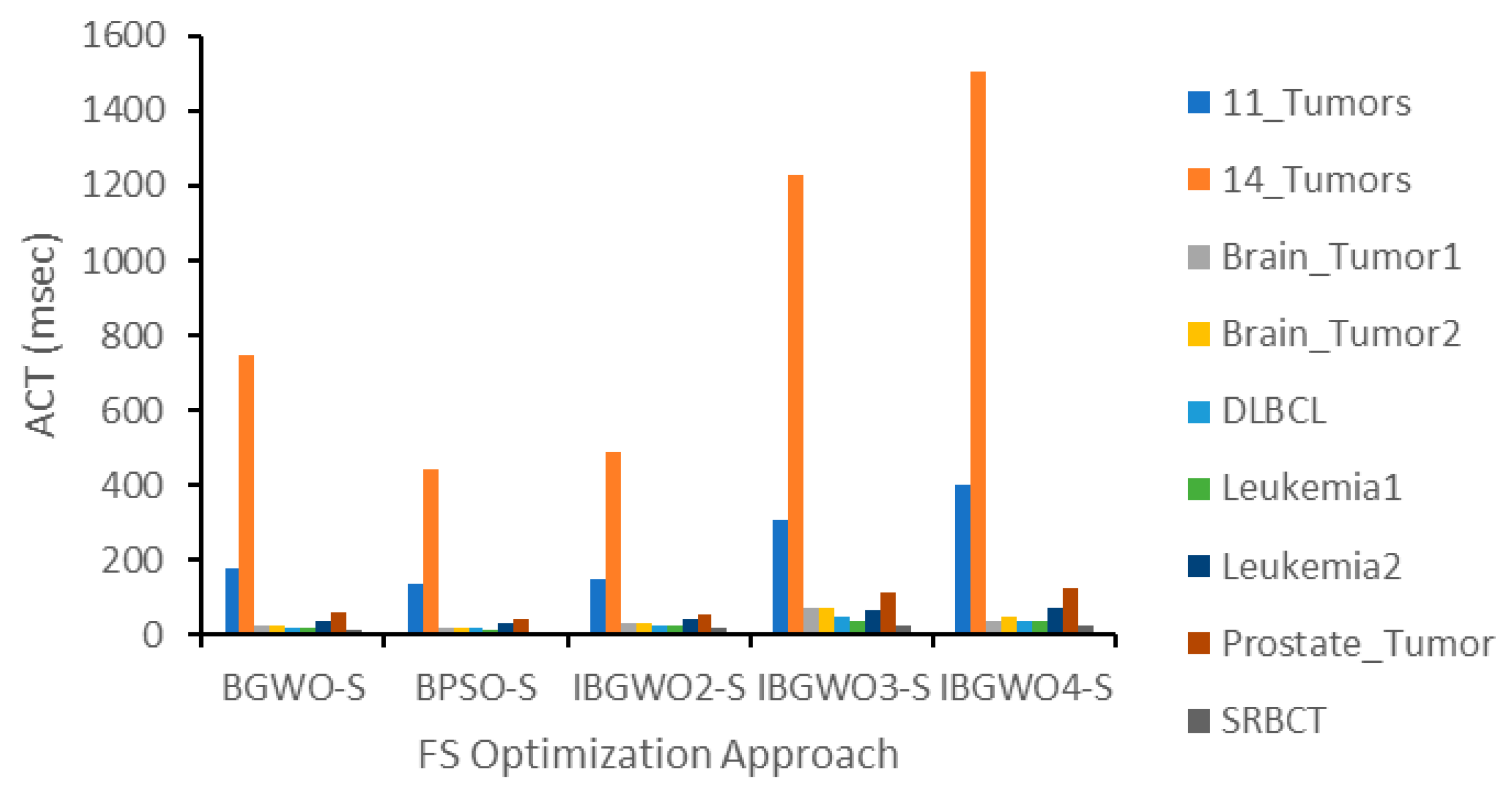
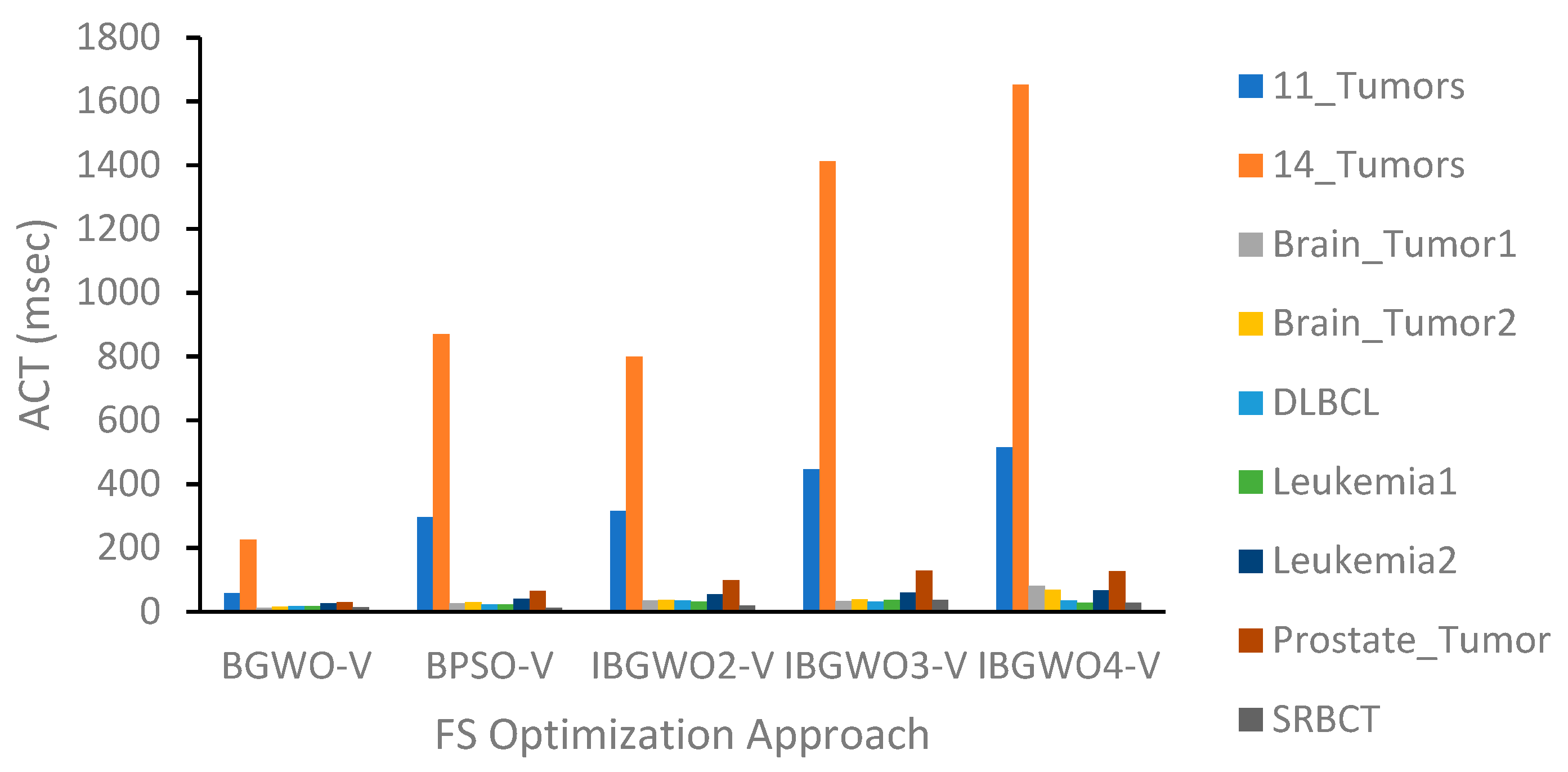
Figure 10 shows the evaluation results of the proposed FS optimizers based on the S-shaped TF in terms of the ACT. As expected, the figure shows that the most complicated approach, i.e., IBGWO4-S, had the most ACT, followed by IBGWO3-S and IBGWO2-S. The two latter approaches were less complex in the ranking process of the different solutions that were investigated in each iteration when compared to IBGWO4-S. This difference was more apparent for the 11_Tumers and 14_Tumers datasets than for other datasets. The reason for this was that, as shown previously in
Table 1, these two datasets contained the largest number of instances, features, and classes relative to other datasets. This normally increased the ACT of IBGWO4-S relative to the other two approaches. The original BPSO-S and BGWO-S had lower ACT than the three proposed approaches since the three proposed approaches were a hybrid of the former two approaches.
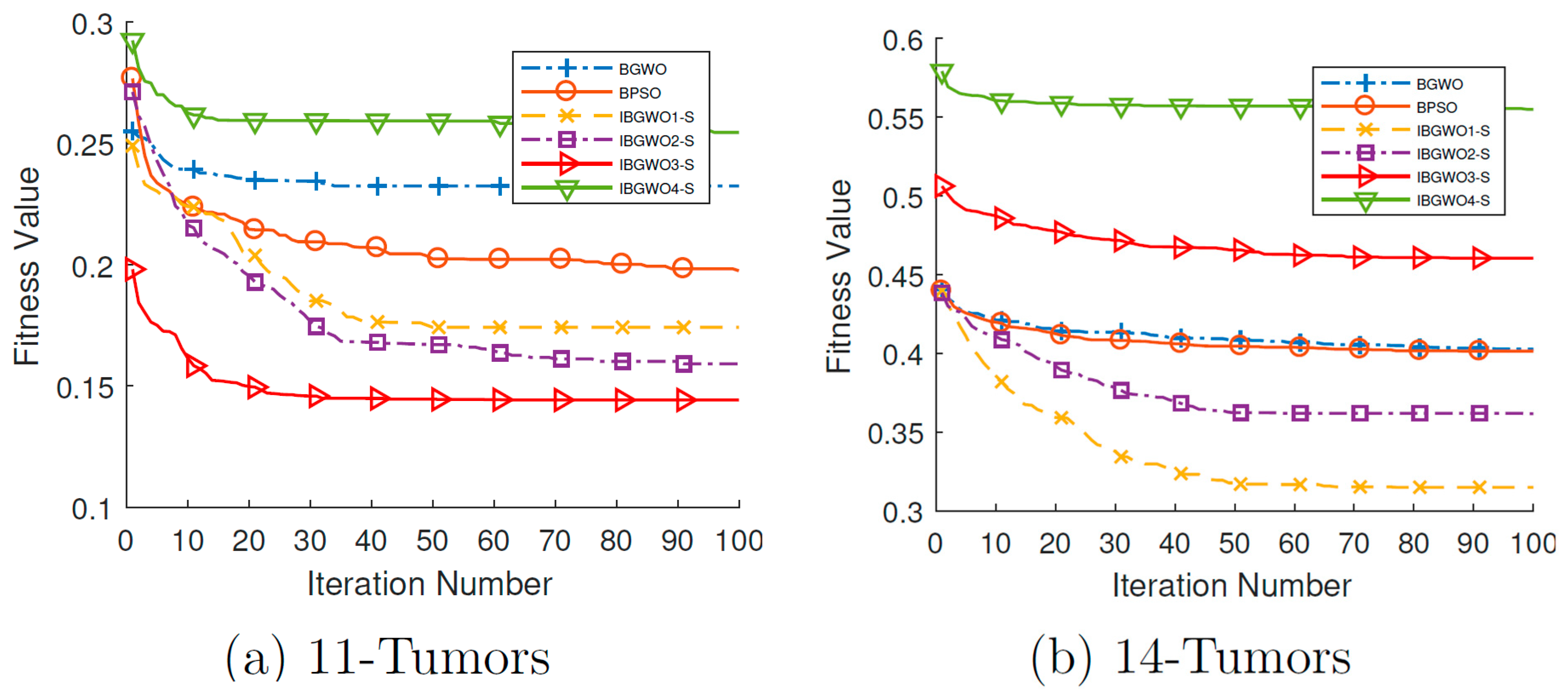
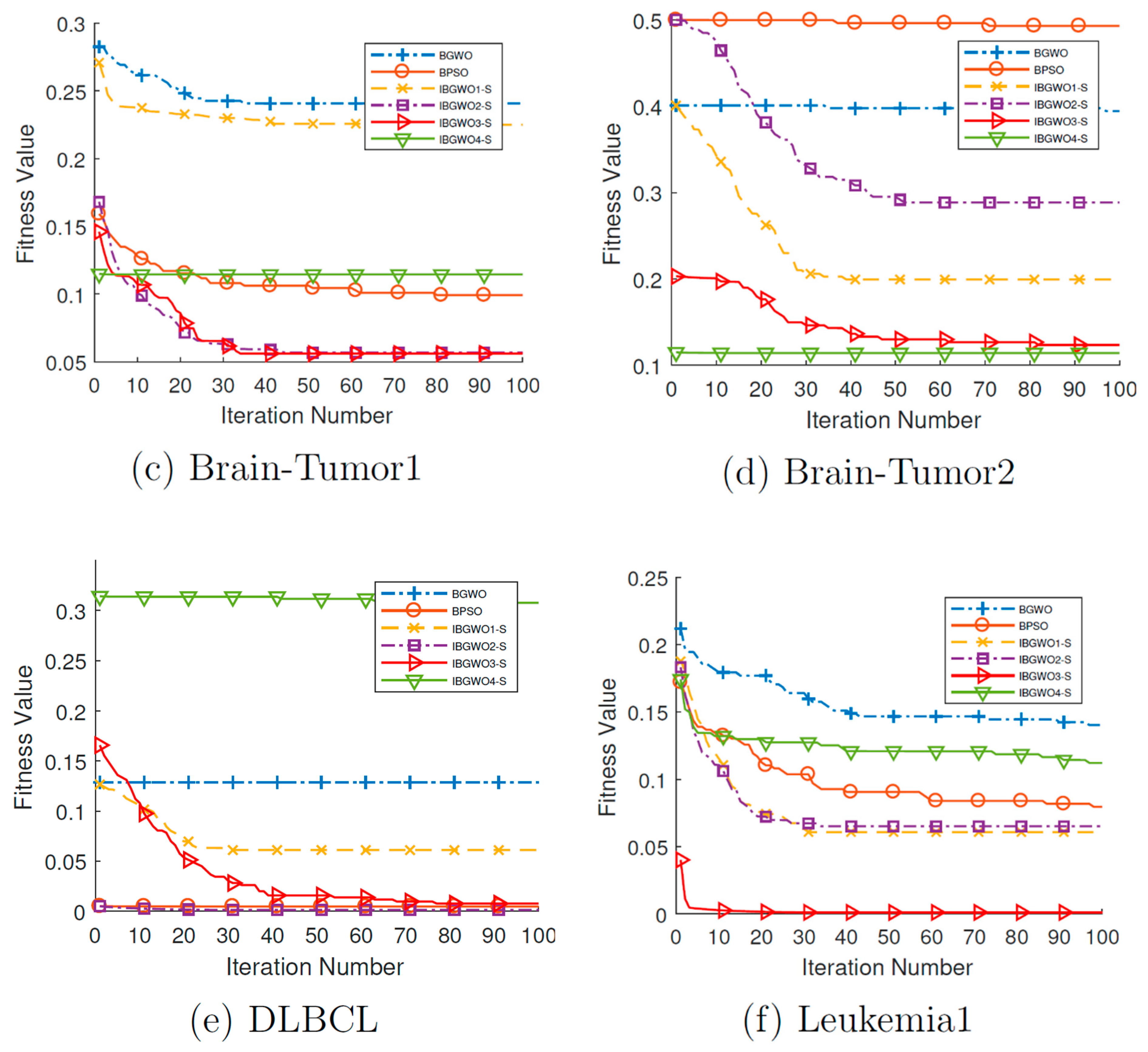
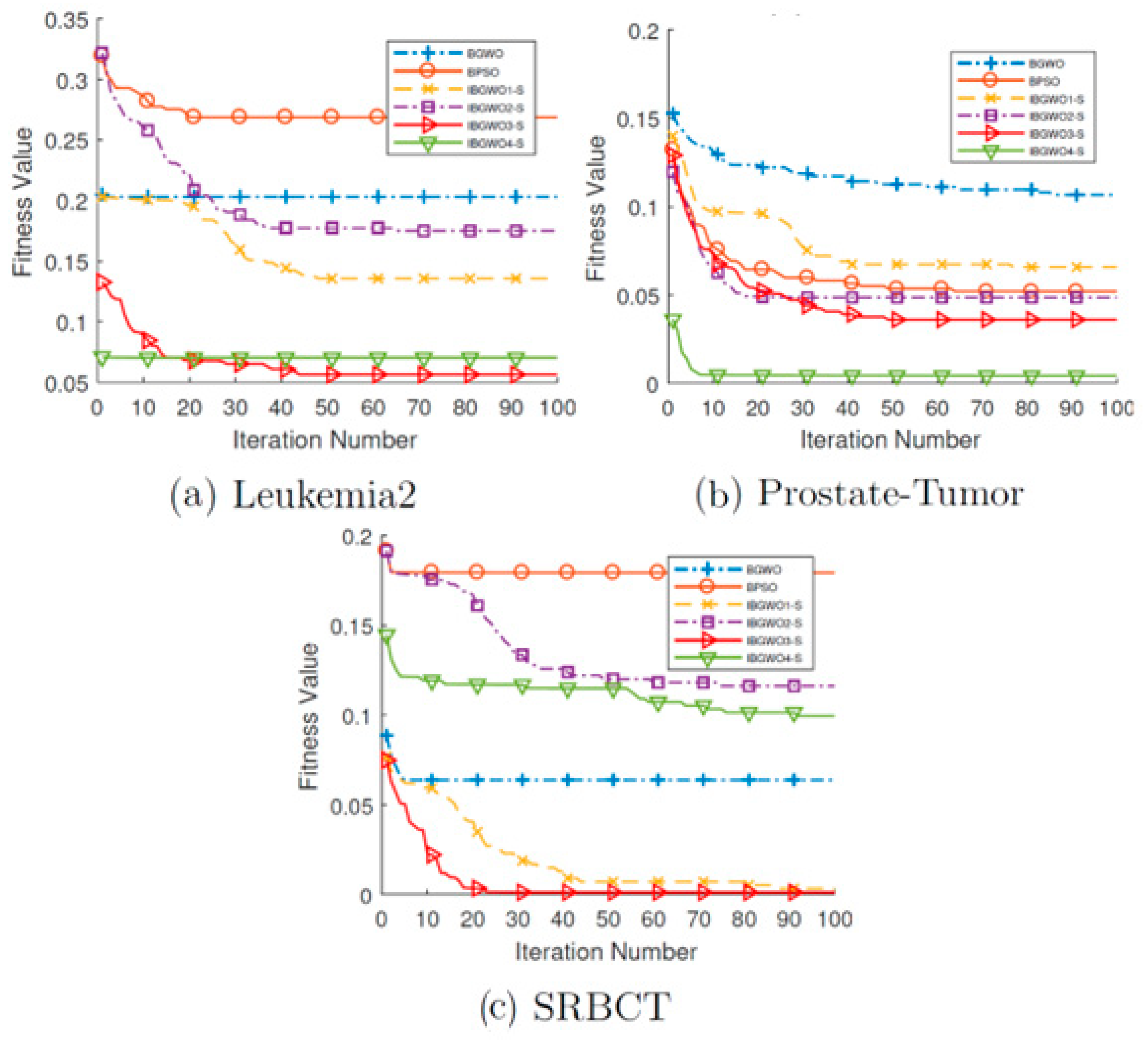
Figure 11 and
Figure 12 show the convergence curves for all FS optimizers based on the S-shaped TF over all iterations. IBGWO3-S had the best performance because other approaches converged early and then became stuck at the local optima. IBGWO3-S exhibited good behavior and obtained the lowest fitness values for most of the datasets. Since the fitness value is the ratio between the number of selected features to the overall features in addition to the classification error, as shown in Equation (15), the solution with the least ratio and the smallest error is the fittest. The curves of the fitness values clarify that IBGWO3-S was the best optimizer based on the S-shaped TF. This means that IBGWO3-S had a high tuning ability for local and global searches, which allowed it to achieve the global optimal solution. Moreover, it had a high ability to escape the area of local optima and search for the most promising area until it found the best global solution.
- b.
Evaluating the proposed approaches based on the V-shaped TF
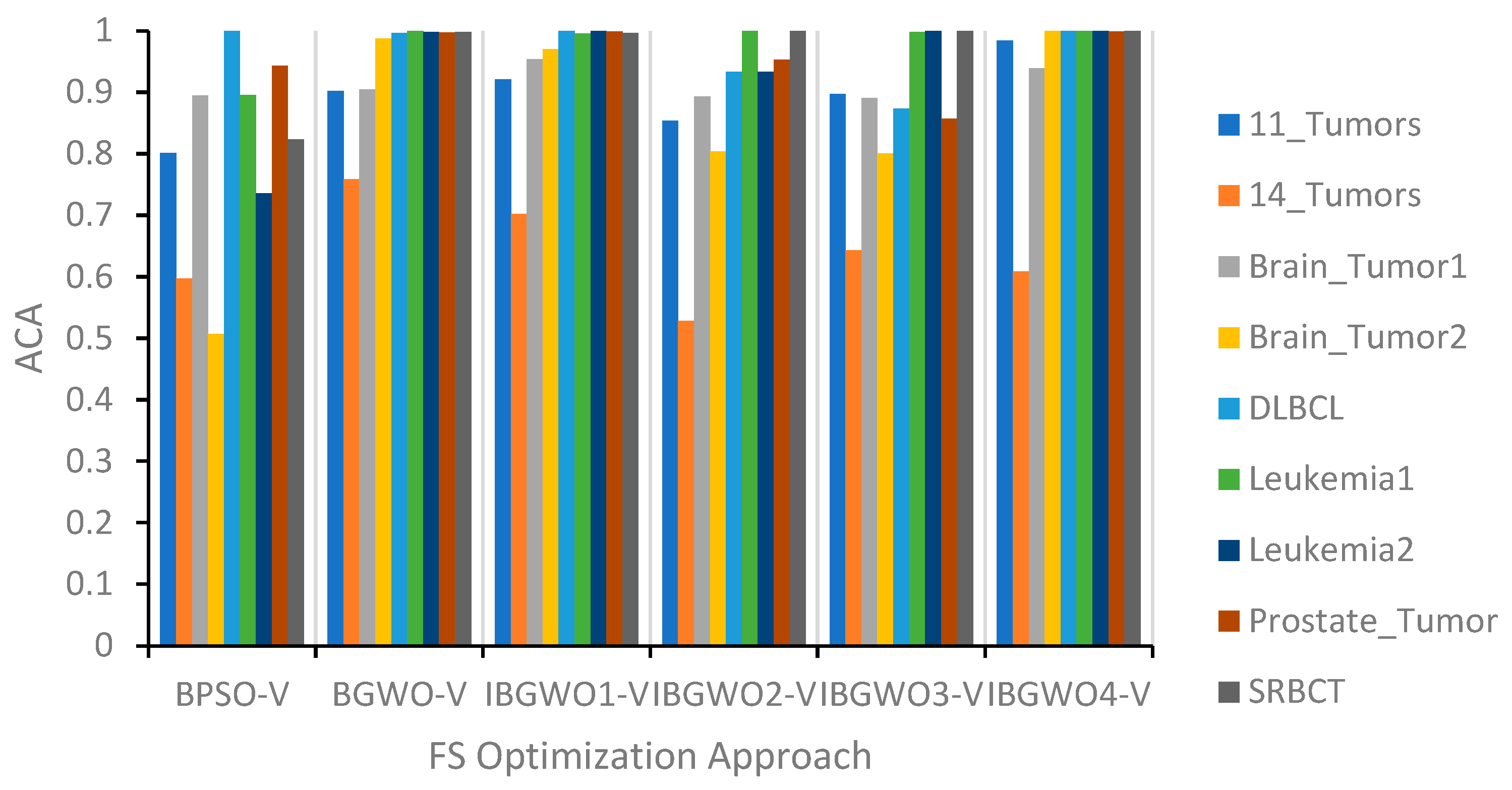
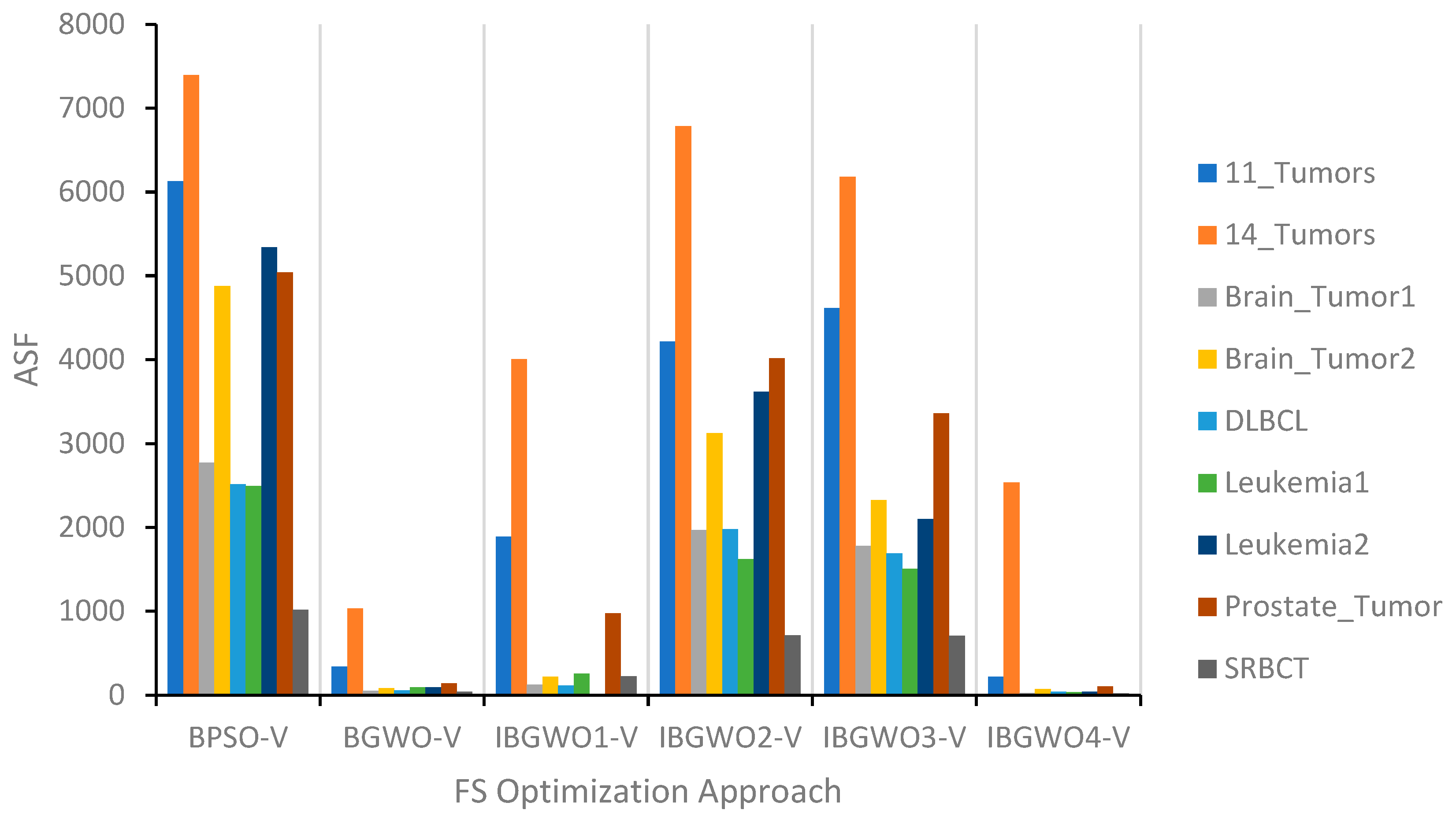
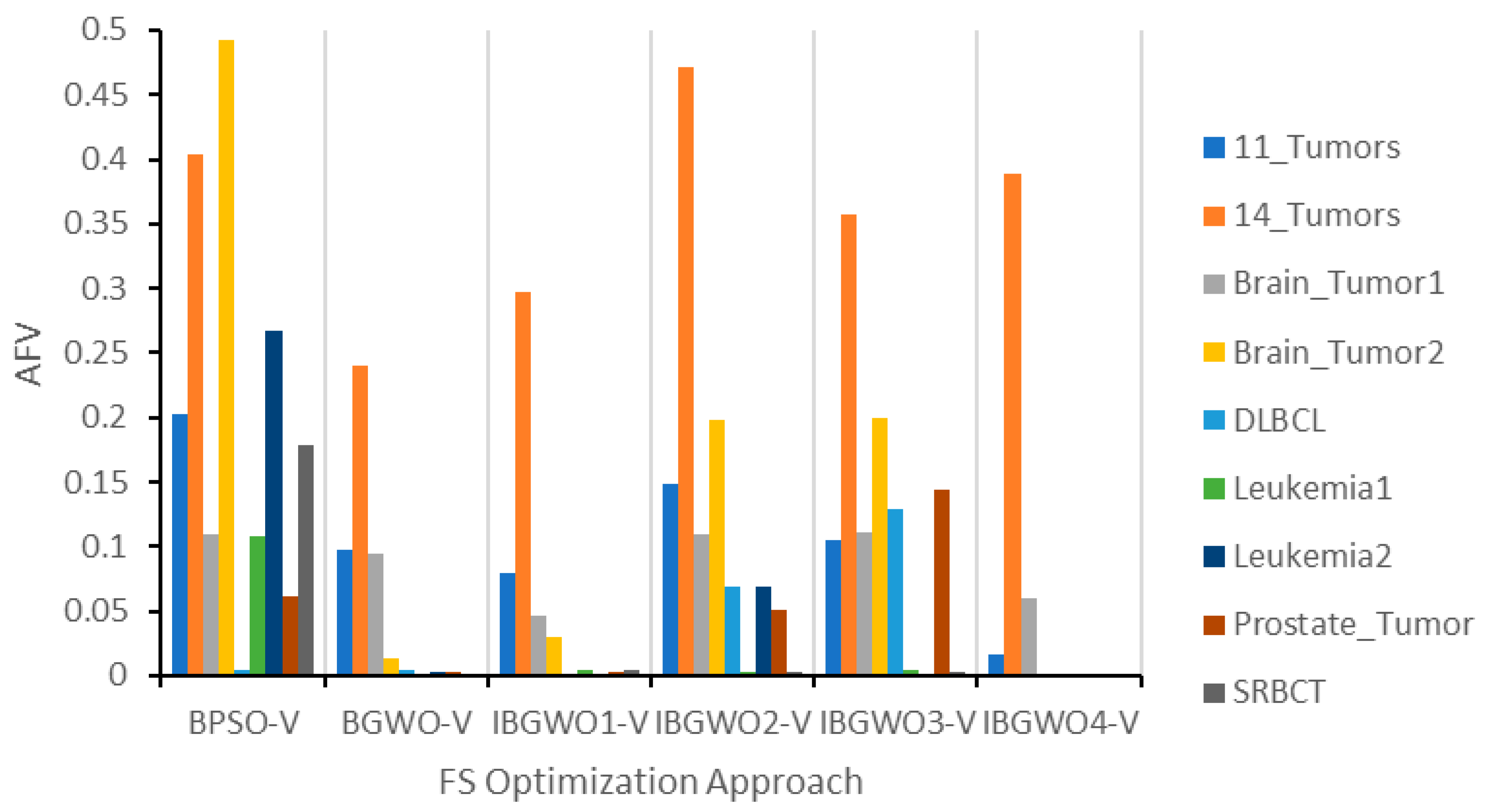
The proposed approaches based on the V-shaped TF were compared against the original BGWO and BPSO algorithms. These comparisons are illustrated in terms of ACA, ASF, and AFV, as shown in
Figure 13,
Figure 14 and
Figure 15, respectively.
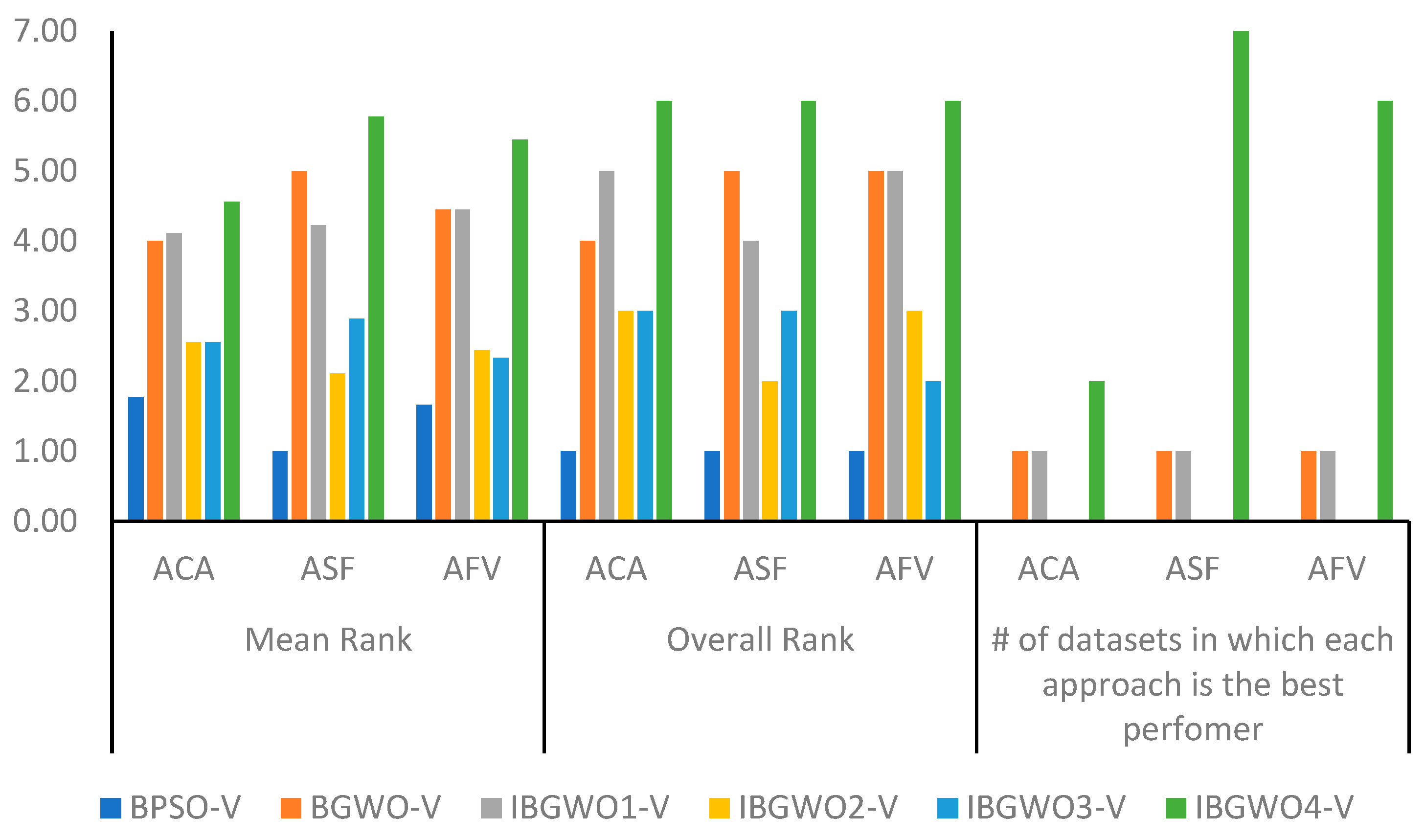
Figure 16 shows a statistical analysis of the proposed approaches based on the V-shaped TF in terms of the same three evaluation metrics.
As shown in
Figure 13 and
Figure 16, the ACA results show the superiority of IBGWO4-V compared with other approaches. It achieved the best ACA for six datasets, with five of them having an ACA equal to 1. IBGWO4-V achieved an average ACA value of 0.95 across all datasets. Moreover, IBGWO1-V obtained the best results for four datasets. In general, it was expected that IBGWO4-V would outperform other approaches since it considered in each iteration the ranking of the population that resulted from the previous iteration, the population that resulted from applying BGWO, and the population that resulted from both BGWO and BPSO. It was expected that IBGWO-2-V and IBGWO3-V would outperform IBGWO1-V; however, both were negatively affected by applying the V-shaped TF when compared with either BGWO-V or IBGWO4-V. This was not the case when using the S-shaped TF.
Figure 14 shows that IBGWO4-V achieved the best, i.e., lowest, ASF results when compared with other approaches. Also, BGWO-V and IBGWO1-V, respectively, obtained the best results after IBGWO4-V. The same reasons apply as described previously when discussing
Figure 13.
Figure 16 confirms the results obtained in
Figure 14 and
Figure 15. IBGWO4-V achieved an average AFV value of 0.05 across all datasets. This confirms that the IBGWO4-V had the best ability over all other proposed approaches to scan the search space and achieve the global optimal solution without getting stuck in local optima.
Figure 17 shows the evaluation results of the proposed FS optimizers based on the V-shaped TF in terms of the ACT. This figure confirms the results obtained previously in
Figure 10, which shows that using either S-shaped or V-shaped TFs did not affect the computational time of the proposed approaches.
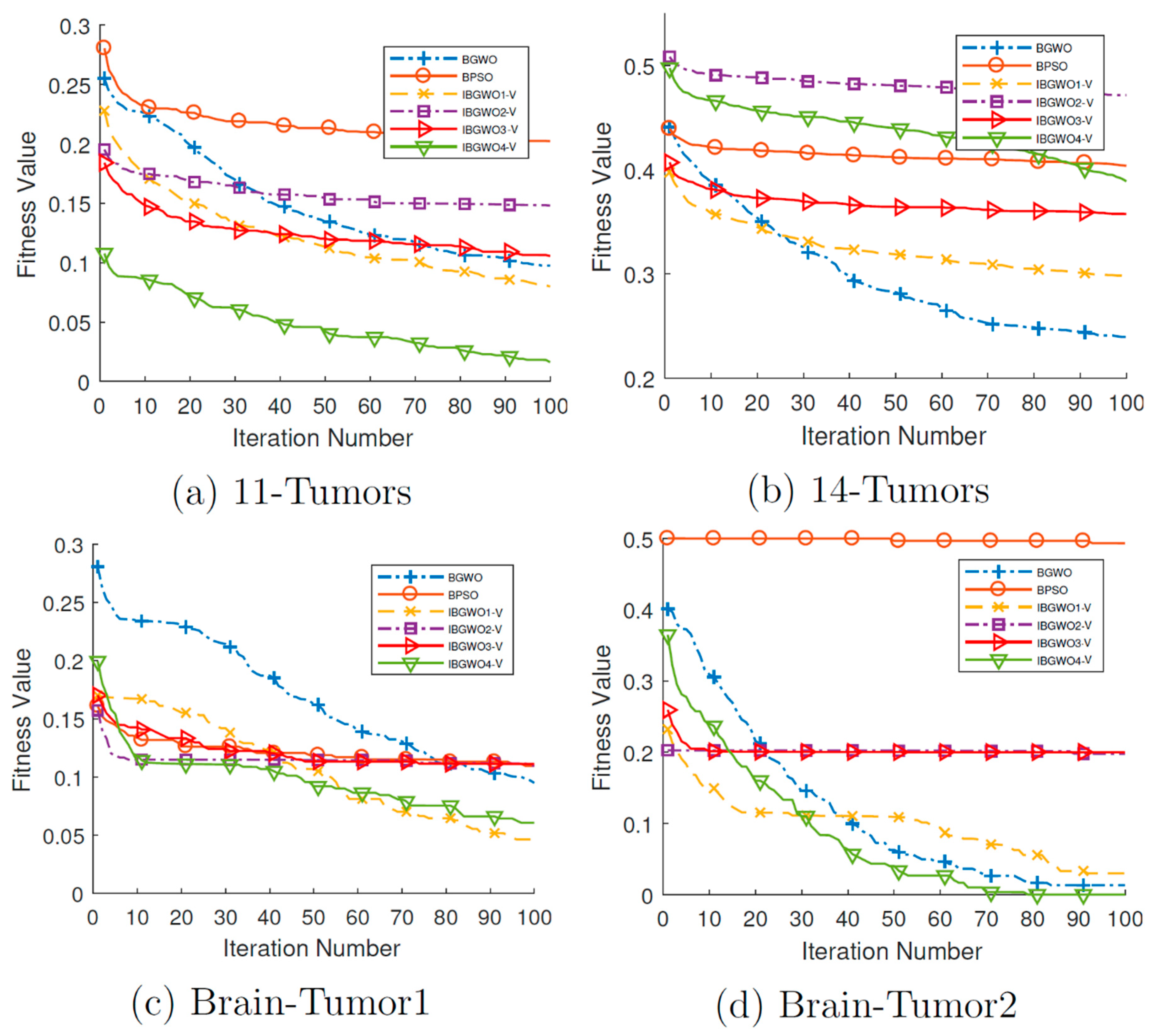
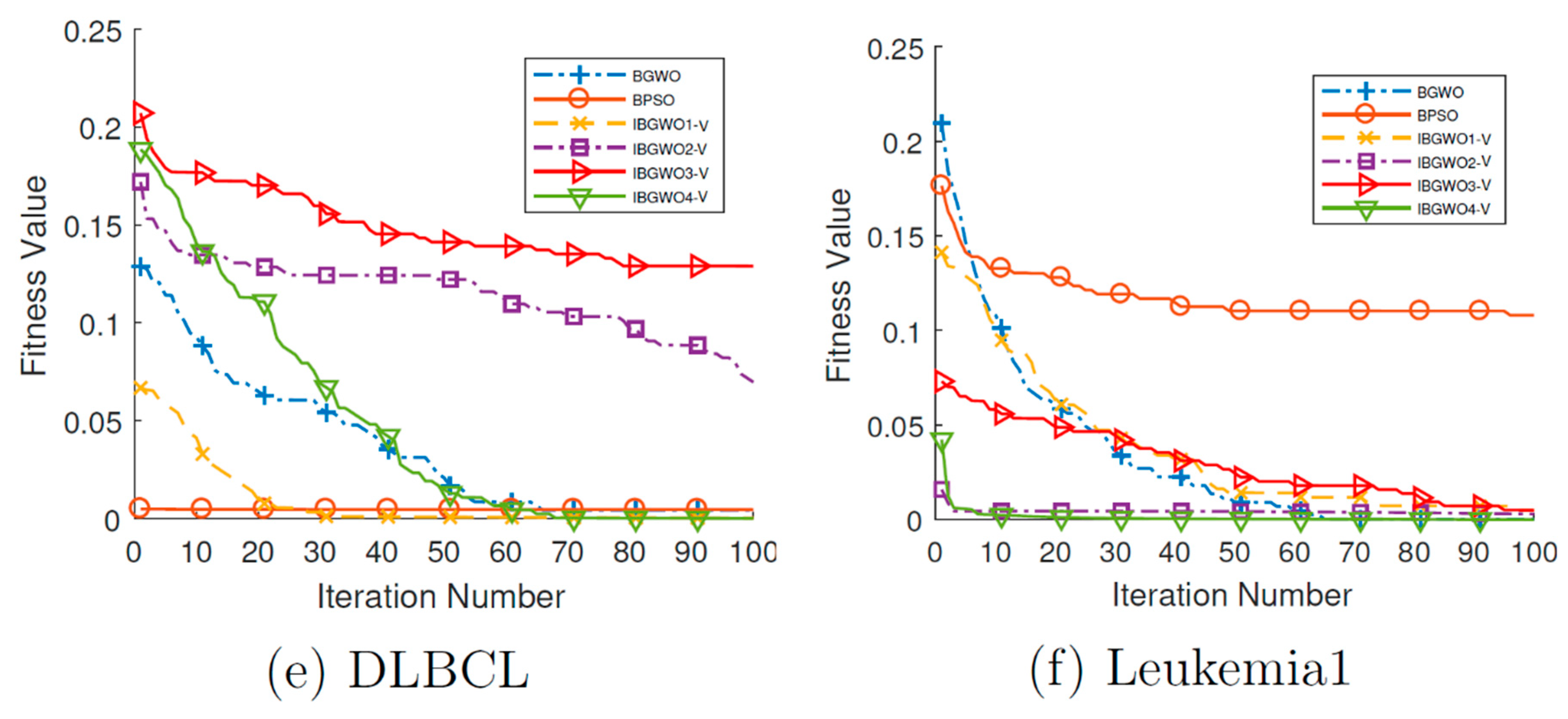
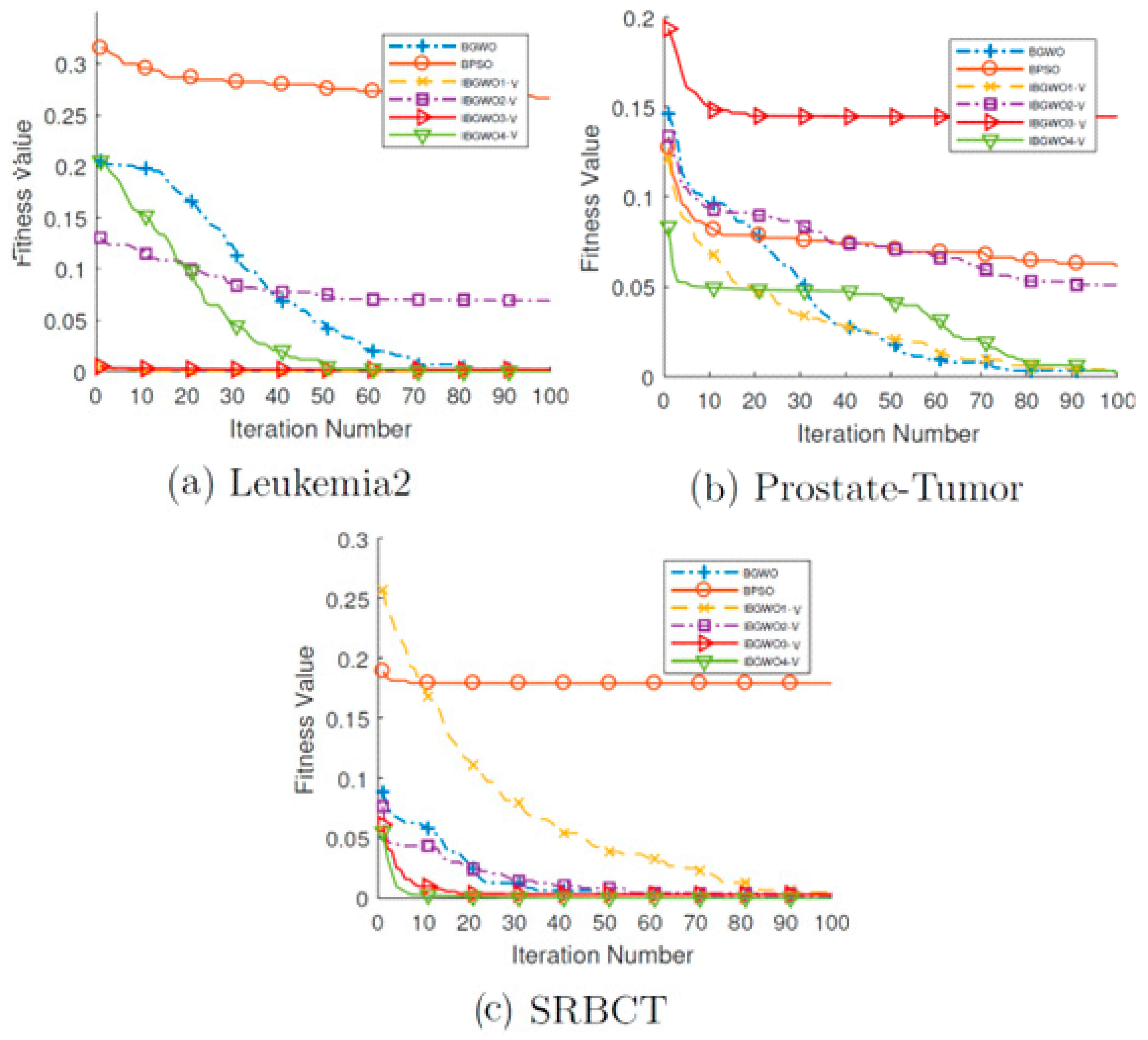
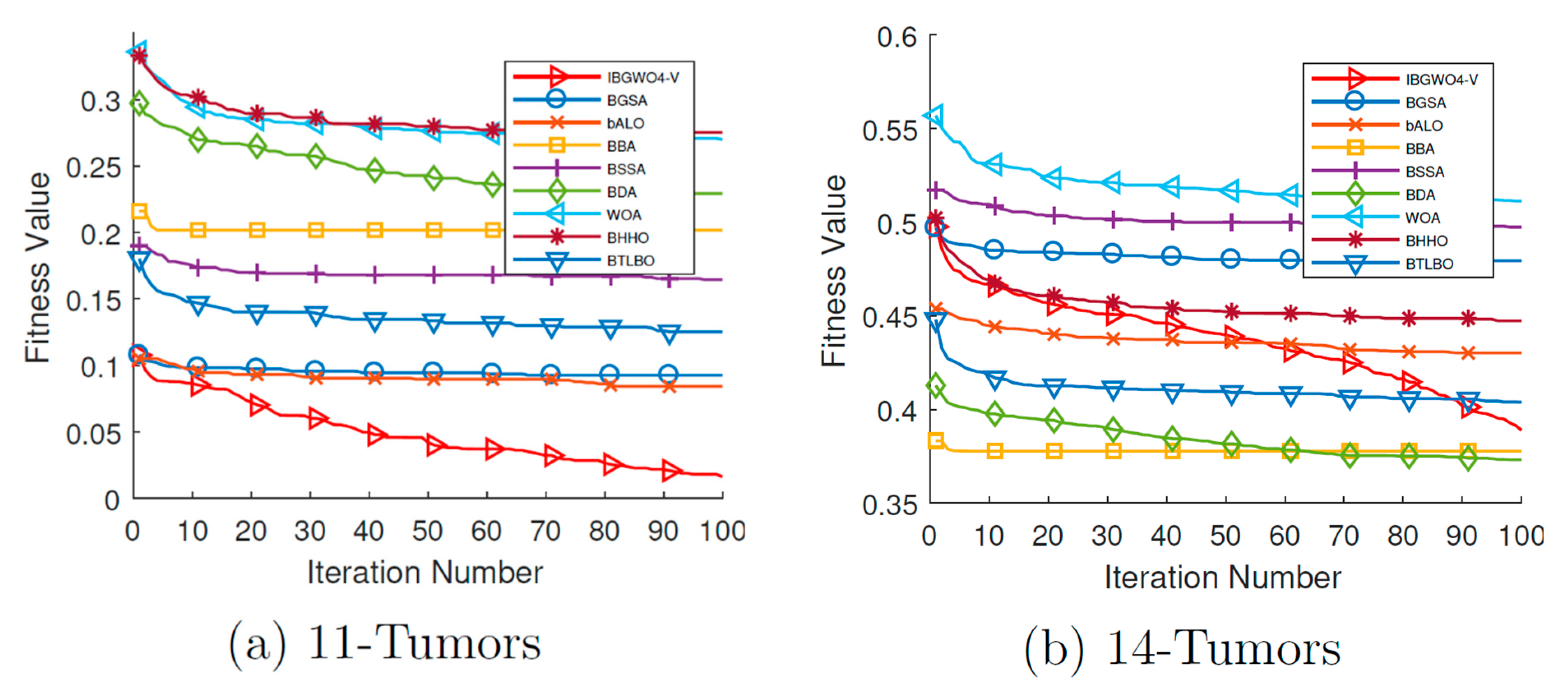
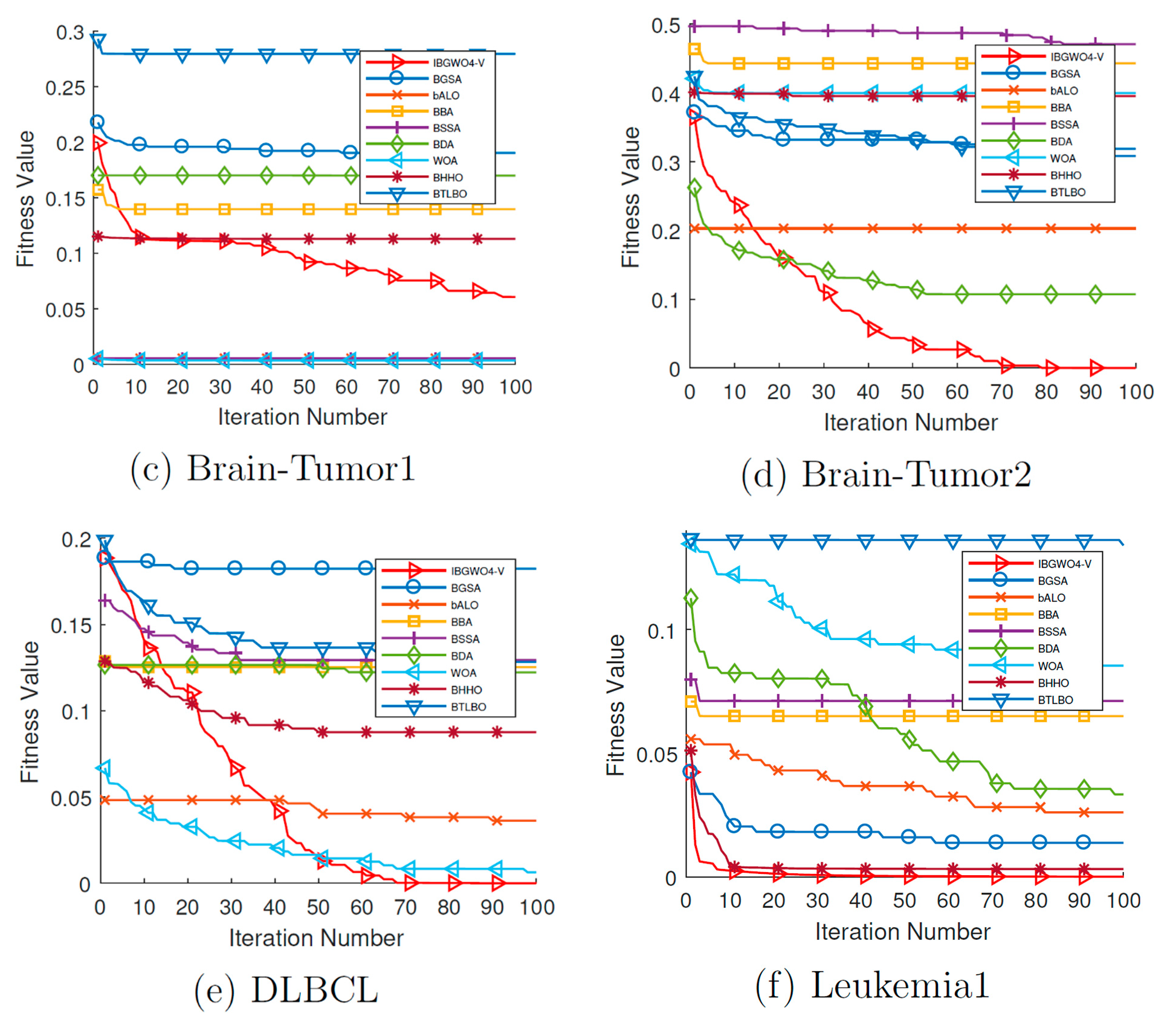
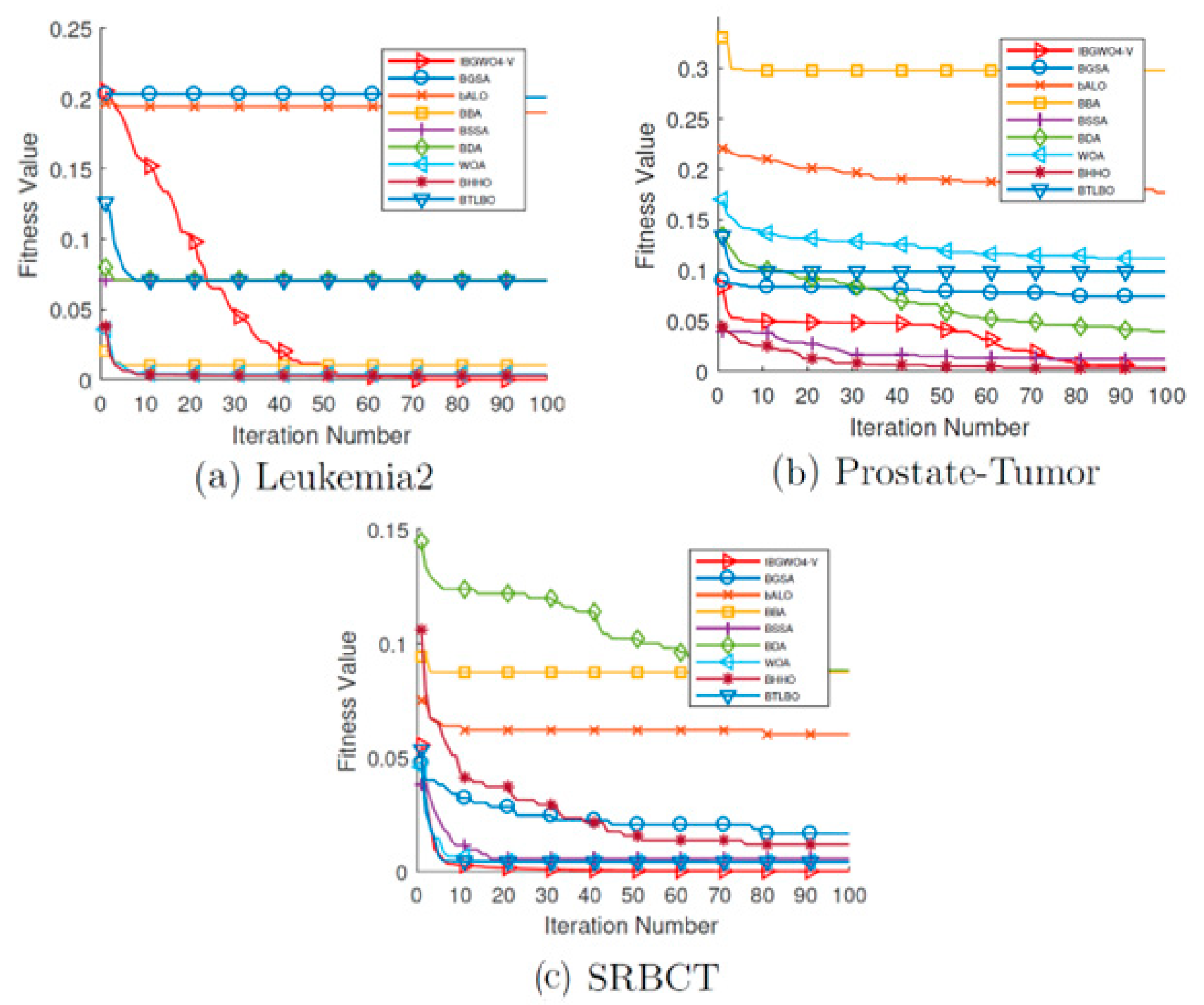
Figure 18 and
Figure 19 show the convergence curves for all FS optimizers based on the V-shaped TF over all iterations. The two figures show that, unlike many optimizers that get stuck at local optima in early iterations, IBGWO4-V could converge to the optimal solution. These curves show that IBGWO4-V explored the search space before exploiting the optimal solution.
In summary, the results shown in
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18 and
Figure 19 confirm the importance of selecting a suitable TF to increase the performance of the optimizers. Moreover, the good performance of the optimizer means a strong searching ability to avoid being stuck in a local optimum by having a good balance between global and local searching. Overall, IBGWO3-S and IBGWO4-V were the fittest optimizers based on S-shaped and V-shaped TFs, respectively.
- c.
Comparison with state-of-the-art metaheuristics
As confirmed in the previous two sections, IBGWO3-S and IBGWO4-V outperformed other approaches based on S-shaped and V-shaped TFs, respectively. This subsection presents the comparisons between these two approaches with eight state-of-the-art metaheuristic-based FS optimizers. The metaheuristics used in the comparisons were as follows: Binary Whale Optimization Algorithm (BWOA) [
31], Binary Dragonfly Algorithm (BDA) [
33], Binary Ant Lion Optimization (BALO) [
36,
38], Binary Gravitational Search Algorithm (BGSA) [
26], Binary Teaching–Learning-Based Optimization (BTLBO) [
27], Binary Harris Hawk Optimization (BHHO) [
32], Binary Bat Algorithm (BBA) [
77], and Binary Salp Swarm Algorithm (BSSA) [
78].
The work proposed in this paper was compared with the selected set of state-of-the-art feature selection optimizers since these optimizers were applied before to address our same research objective, which was to optimize the feature selection process. The next section will show the results of the comparison of our proposed approaches with one of the recent and advanced optimizers that combines binary PSO and binary GWO with a tournament selection strategy. The authors also plan to compare the proposed approaches with a set of advanced metaheuristic methods like the work proposed in [
51,
52,
58,
59] and other works that combine GWO with PSO. Such work can be compared with our approaches in a future extension of this work.
Figure 20 shows a statistical analysis of the comparison between IBGWO3-S and IBGWO4-V on one side and the eight selected state-of-the-art metaheuristic-based FS optimizers on the other side. This comparison was made in terms of the same three evaluation metrics, i.e., ACA, ASF, and AFV.
Figure 20 shows the mean and overall ranks of each approach across all datasets under consideration. The rank was generally a number from 1 to 10 since there were ten approaches compared against each other, where 10 means the highest-ranked approach. Additionally,
Figure 20 shows the number of datasets in which each approach obtained the best rank.
Figure 20 shows that IBGWO4-V achieved the best ACA results in nine datasets. The mean and overall rank values showed the superiority of IBGWO4-V over other optimizers, followed by IBGWO3-S. In terms of ASF, IBGWO4-V also outperformed other optimizers in all datasets. Additionally, the mean and overall rank ASF results showed that IBGWO4-V attained the best rank compared to other optimizers, followed by IBGWO3-S. In terms of AFV, the figure shows the superiority of IBGWO4-V in seven datasets. The mean and overall rank ASF results revealed that IBGWO4-V and IBGWO3-S also outperformed other optimizers. This confirms the potential of these two proposed approaches to jump out of the areas that contain the local optima and orient themselves towards the most promising area of relevant features.
Figure 21 and
Figure 22 show the convergence curves for all ten optimizers over all iterations. The two figures illustrate that IBGWO4-V outperformed other optimizers in order of fitness values. Convergence curves reveal the ability of this optimizer to avoid local optima and immature convergence. If an optimizer cannot make a stable trade-off between exploration and exploitation, then it will converge to local optima, which leads to immature convergence.
- d.
Comparison with a recent metaheuristic method
The best two proposed approaches, i.e., IBGWO3-S and IBGWO4-V, were compared with one of the recent metaheuristic FS optimizers that enhanced the performance of BGWO [
57]. This approach combined BPSO, BGWO, and tournament selection (TS) [
58] optimizers. This approach is named Hybrid Tournament Grey Wolf Particle Swarm (HTGWPS). A set of S-shaped and V-shaped binary transfer functions were used to develop different variants of this approach. The best two performing approaches were abbreviated in [
57] as HTGWPS-S1 and HTGWPS-V1. These two variants were compared with our two best-performing approaches, i.e., IBGWO3-S and IBGWO4-V.
Figure 23,
Figure 24,
Figure 25 and
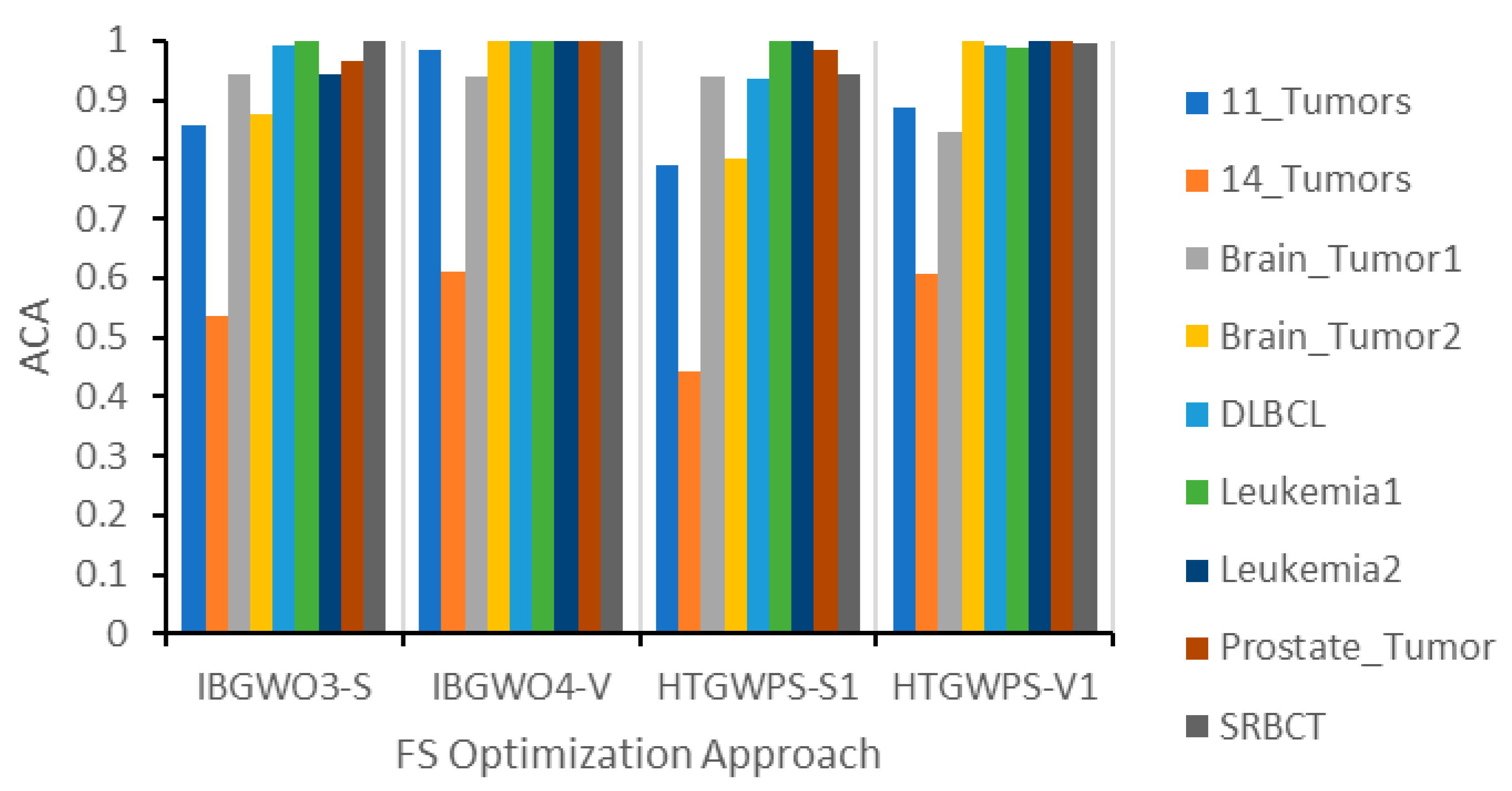
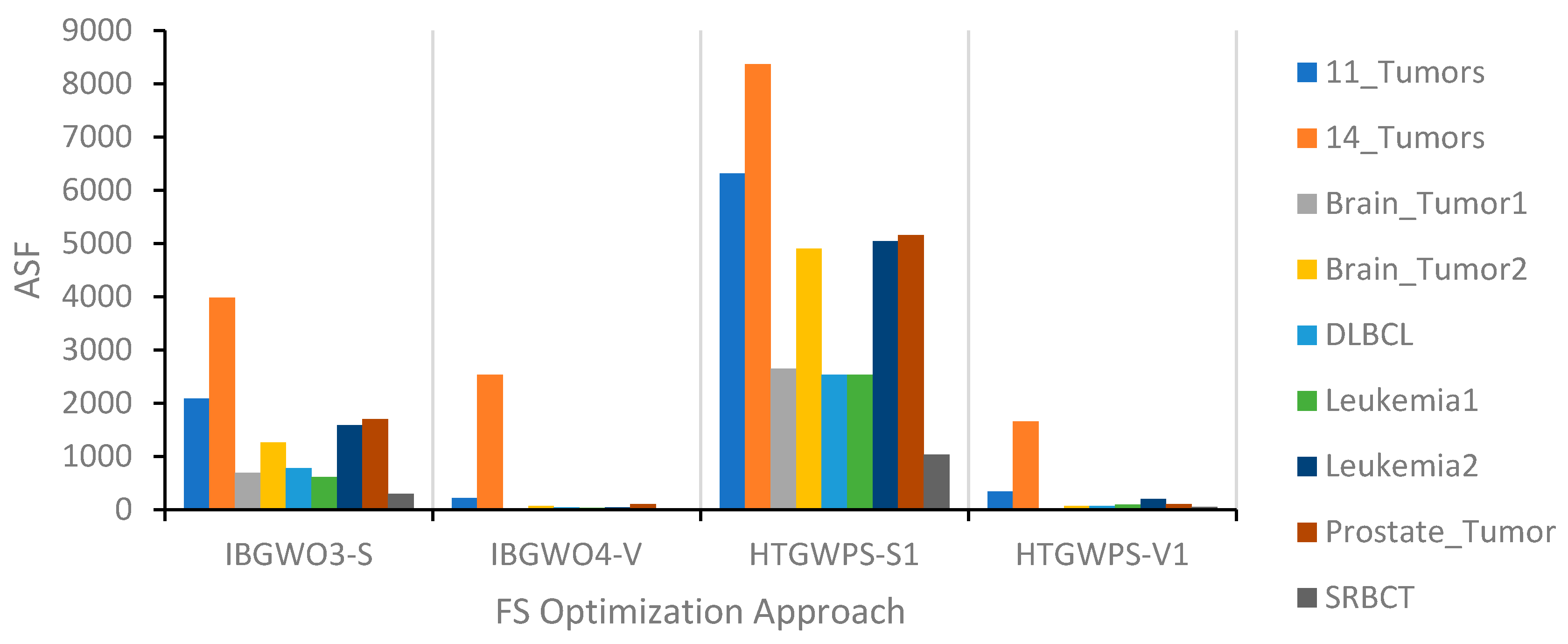
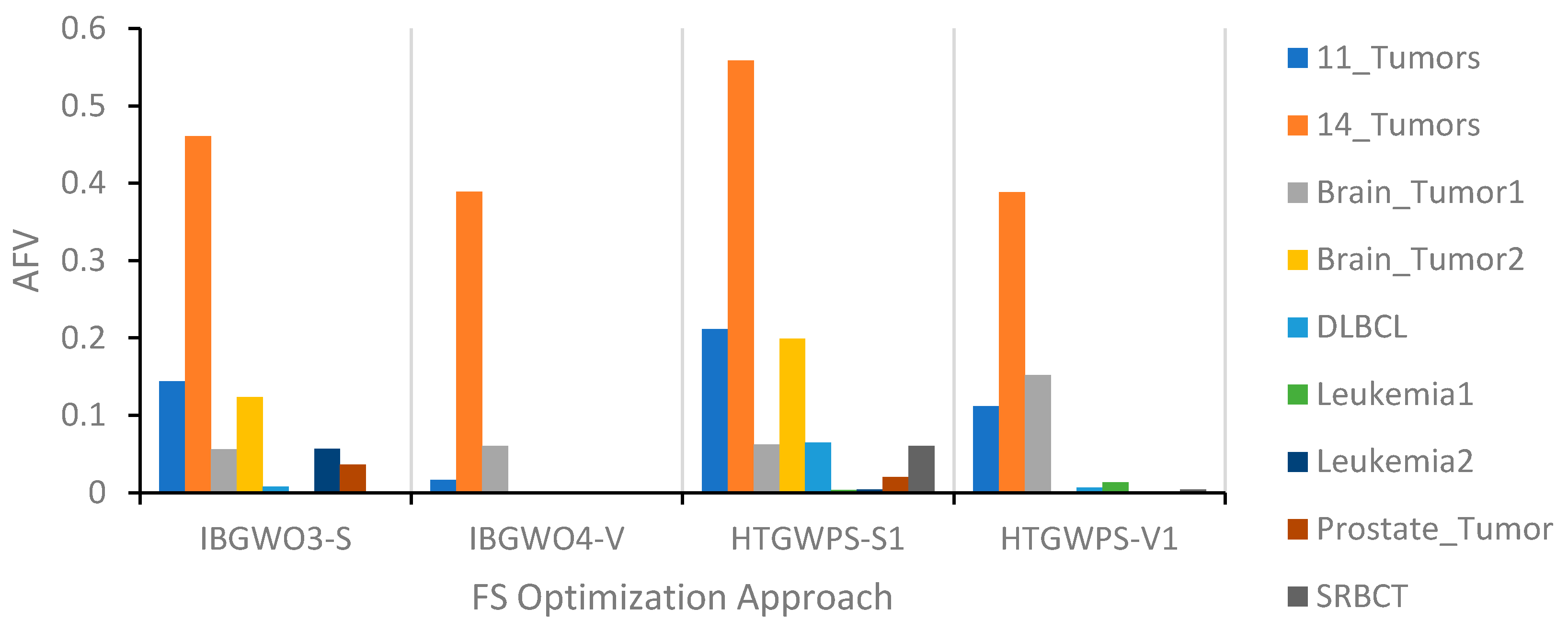
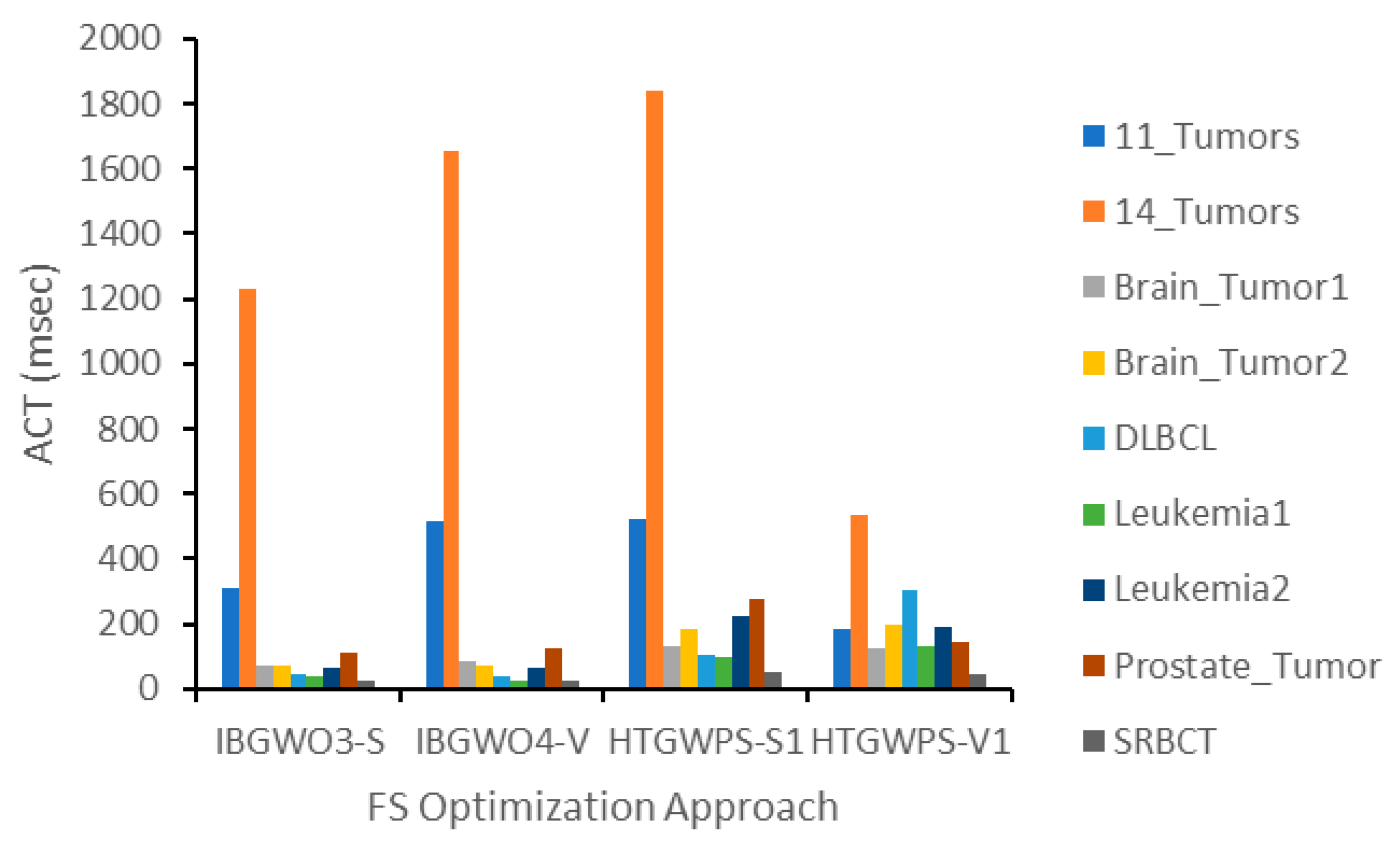
Figure 26 show the results of the comparisons of IBGWO3-S and IBGWO4-V with the two recent FS optimizers, i.e., HTGWPS-S1 and HTGWPS-V1, from the literature. The four figures show comparisons in terms of the four previously described evaluation metrics, i.e., ACA, ASF, AFV, and ACT, respectively.
Figure 23 shows that the proposed IBGWO3-S and IBGWO4-V optimizers achieved the highest ACA in three and seven datasets, respectively.
Figure 24 shows that IBGWO4-V achieved the lowest ASF in six datasets.
Figure 25 shows that IBGWO4-V achieved the lowest AFV in six datasets. Finally,
Figure 26 shows that IBGWO3-S and IBGWO4-V had the lowest ACT in three and four datasets, respectively. In general, IBGWO4 obtained better results than HTGWPS because the latter was based on selecting only one of three optimizers, i.e., BGWO, BPSO, or TS. On the contrary, IBGWO applied both BGWO and BPSO in each iteration with a ranking process among all solutions obtained from both optimizers. This enhanced the results obtained from IBGWO when compared with HTGWPS.
- e.
Computational complexity of the proposed approaches
In this section, the computational complexity of the proposed approaches is analyzed and presented.
Table 3 shows the computational complexity of the proposed approaches. The complexity was analyzed by computing the estimated total number of iterations for each approach. Moreover, a Big-O analysis in terms of the maximum number of iterations (T) and the population size (P) is presented. In general, all approaches passed through a set of iterations, i.e., T. In each iteration, two independent loops were run, where each loop counter was equal to P. In each iteration of IBGWO2, a P2P comparison was conducted between the two corresponding solutions produced by BGWO and BPSO. This comparison was not performed in IBGWO3 or IBGWO4. A ranking process, i.e., sorting, was applied at the end of each iteration in both IBGWO3 and IBGWO4 but not in IBGWO2. The complexity of this ranking process depended on the complexity of the applied sorting algorithm, which was a function in P. If the applied sorting algorithm had a linear or quadratic complexity, then it exhibited an O(P) or O(P
2) complexity, respectively. This led to total complexity for both IBGWO3 and IBGWO4 O(T*P) or O(T*P
2) depending on the complexity of the ranking process.
8. Discussion
In this section, the strong and weak points of each of the three proposed approaches are discussed. In general, hybrid metaheuristics are classified into two levels in terms of design issues: low-level and high-level [
23]. Low-level hybridization means that one optimizer is embedded inside another optimizer, while high-level hybridization means that one optimizer is performed after applying another optimizer. The three proposed approaches can be classified as high-level optimizers. In general, such hybridization adds more computational complexity, which is considered one of the limitations of such hybrid approaches.
In each iteration of IBGWO2, a P2P comparison was performed between each individual obtained from applying the BGWO optimizer and its corresponding individual obtained after applying BGWO and then BPSO. This P2P comparison was not applied collectively to all individuals in both populations. Therefore, the best solution among both populations could have been missed.
The previously mentioned limitation of IBGWO2 was overcome in IBGWO3 by applying the ranking process across all individuals in both populations obtained by BGWO and BGWO followed by BPSO. A further enhancement of IBGWO3 was achieved with IBGWO4. This enhancement considered the initial population obtained from every previous iteration in addition to the two populations obtained by BGWO and BGWO followed by BPSO. This clarified the reason why IBGWO4 generally provided better evaluation results than IBGWO3 and IBGWO2. However, the complexity of the ranking process increased when IBGWO4 or IBGWO3 was applied compared with IBGWO2.
Since a high-dimensional dataset was used in the evaluation of the three proposed approaches, the authors would like to discuss the suitability of each of the three approaches as the dimensionality of the dataset increased. As previously mentioned, IBGWO4 provided the best general performance, followed by IBGWO3 and IBGWO2, at the expense of computational complexity. Therefore, IBGWO4 can be used to provide the best classification accuracy with the least number of selected features for datasets with very high dimensionality of features. IBGWO4 will be suitable for this type of dataset provided that the computational complexity is not a concern or the target system is not time-constrained. However, if the computational complexity of analyzing this dataset type has priority over the classification accuracy and fitness values, IBGWO2 or IBGWO3 will be better to apply relative to IBGWO4. Selecting IBGWO2 or IBGWO3 will depend on the required classification accuracy and fitness values. IBGWO2 will provide the lowest classification accuracy and fitness values at the lowest computational complexity compared with the other two approaches.
An extensive numerical analysis needs to be implemented to provide insights into the relation between the performance of each of the three proposed approaches and the degree of dimensionality of the different datasets. This analysis will be implemented in a future extension of this work.
9. Conclusions and Future Directions
In this paper, three hybrid approaches were proposed to provide a solution to the FS optimization problem based on S2 and V2 binary TFs that were used to convert continuous solutions to binaries. In this work, the three hybrid approaches were proposed to enhance FS optimization by combining BGWO with BPSO. The objective of this combination was to resolve the GWO stuck-in-local-optima problem that can occur by leveraging the PSO-wide search space exploration ability on the solutions obtained by GWO.
A set of high-dimensional, small-instance medical datasets was utilized to evaluate the three proposed approaches. The datasets included multiclass, cancer-related human gene expression datasets. The evaluation experiments were performed to compare the three proposed approaches against the original BPSO and BPGWO, eight state-of-the-art FS optimizers, and, finally, one of the recent binary FS optimizers that combines BPSO with BGWO algorithms.
The evaluation results showed the superiority of IBGWO4-V compared with other investigated approaches in terms of a set of evaluation metrics, which were ACA, ASF, AFV, and ACT. The computational complexity of all proposed approaches was investigated and it was shown that the most complex approaches were IBGWO3 and IBGWO4. In summary, the results showed that IBGWO4-V is the most effective approach and provides the best balance between global and local searching techniques for FS optimization tasks. The results also confirmed the importance of selecting a suitable TF to increase the performance of the optimizers.
One of the salient limitations of the best-proposed approach, i.e., IBGWO4, is its computational complexity relative to the native BGWO, the native BGWO, and the other two proposed approaches, i.e., IBGWO2 and IBGWO3. When selecting one of the three proposed approaches, there should be a trade-off between the classification accuracy and fitness on one side and the computational complexity on the other side.
Future work will include a set of extensions as follows. Firstly, 10-fold cross-validation data splitting will be applied instead of the 80% training/20% testing data splitting approach. Secondly, the proposed algorithms will be further tested using unimodal functions, multi-modal functions, and fixed dimensional benchmark functions [
79]. This evaluation will provide a deeper analysis of the performance of the three proposed optimizers and show how these optimizers can overcome the issue of entrapment in local optima.
Thirdly, a numerical analysis that shows the relation between the performance of the three proposed approaches and the degree of dimensionality of the different datasets needs to be implemented in a future extension of this work. Fourthly, the authors plan to incorporate more advanced metaheuristic methods like the work proposed in [
51,
52,
58,
59] so that such work can be compared with the proposed approaches in a future extension of this work.
A fifth extension of this work will include utilizing the PSO’s searching mechanism to improve other SI methods, i.e., instead of GWO, which suffers from the problem of being stuck in local optimum solutions. Finally, the three proposed approaches can also be evaluated by using other common classifiers such as Support Vector Machines [
80] and Artificial Neural Networks [
81] to ensure that the proposed approaches maintain superiority and stability.