Balancing Privacy and Utility in Artificial Intelligence-Based Clinical Decision Support: Empirical Evaluation Using De-Identified Electronic Health Record Data

Abstract

The secondary use of electronic health records is essential for developing artificial intelligence-based clinical decision support systems. However, even after direct identifiers are removed, de-identified electronic health records remain vulnerable to re-identification, membership inference attacks, and model extraction attacks. This study examined the balance between privacy protection and model utility by evaluating de-identification strategies and differentially private learning in large-scale electronic health records. De-identified records from a tertiary medical center were analyzed and compared with three strategies—baseline generalization, enhanced generalization, and enhanced generalization with suppression—together with differentially private stochastic gradient descent. Privacy risks were assessed through k-anonymity distributions, membership inference attacks, and model extraction attacks. Model performance was evaluated using standard predictive metrics, and privacy budgets were estimated for differentially private stochastic gradient descent. Enhanced generalization with suppression consistently improved k-anonymity distributions by reducing small, high-risk classes. Membership inference attacks remained at the chance level under all conditions, indicating that patient participation could not be inferred. Model extraction attacks closely replicated victim model outputs under baseline training but were substantially curtailed once differentially private stochastic gradient descent was applied. Notably, privacy-preserving learning maintained clinically relevant performance while mitigating privacy risks. Combining suppression with differentially private stochastic gradient descent reduced re-identification risk and markedly limited model extraction while sustaining predictive accuracy. These findings provide empirical evidence that a privacy–utility balance is achievable in clinical applications.

1. Introduction

The secondary use of electronic health records (EHR) is essential for not only advancing precision medicine but also enabling multi-institutional research. Although large-scale cohort studies [1,2,3,4,5] and predictive modeling rely on secure and efficient data sharing, privacy protection remains a persistent challenge in clinical informatics. The COVID-19 pandemic underscored the value of rapid access to multi-institutional data for surveillance and predictive tool development, while simultaneously highlighting concerns about protecting individual patients from potential privacy breaches.

Even after direct identifiers such as names or patient numbers are removed, de-identified EHRs may still be vulnerable to advanced privacy threats. Quasi-identifiers—such as combinations of sex, age, and diagnosis—may enable re-identification when linked with external sources. Additionally, machine learning has introduced new risks. Membership inference attacks (MIA) [6,7,8,9,10,11] test whether an individual’s data were used in model training, whereas model extraction attacks (MEA) [12,13,14,15] attempt to replicate a deployed model through repeated queries. These threats raise concerns about the adequacy of conventional de-identification for the safe use of EHRs in clinical decision support systems (CDSS).

Although traditional approaches—including masking, suppression, k-anonymity, l-diversity, and t-closeness—reduce some risks, they often fall short against modern attack scenarios involving high-dimensional data. Differential privacy (DP) [16,17,18,19,20,21,22] provides rigorous mathematical protection but may degrade utility to the point of limiting clinical applicability. Prior studies have typically examined isolated threats, such as MIA, or relied on synthetic datasets; however, few have evaluated multiple attack vectors collectively or assessed how traditional de-identification and DP-based learning interact in real-world EHRs.

To address these research gaps, we developed an integrated privacy evaluation framework specifically designed for EHR data that covers three representative risks: membership inference, model extraction, and re-identification risk quantified through k-anonymity distributions. We applied it to a large EHR sample and compared three levels of de-identification—baseline generalization, enhanced generalization, and enhanced generalization with suppression—using differentially private stochastic gradient descent (DP-SGD) [23,24] as a privacy-preserving learning method. By combining conventional and modern privacy-preserving techniques, this study aimed to measure residual vulnerabilities, evaluate the protective value of suppression and DP-SGD, and quantify the resulting privacy–utility trade-offs. In doing so, it positions the work as an early empirical investigation of defense strategies on large-scale clinical EHR data, focusing on the study objectives rather than the outcomes.

2. Materials and Methods

2.1. Dataset

We modeled a multi-institutional use case based on EHRs collected at a single university-affiliated tertiary medical center. The dataset comprised 100,000 diagnosis records from January 2016 to December 2022, with 43 available variables, including age, sex, and diagnostic codes based on the Korean Standard Classification of Diseases (KCD), Eighth Edition and the International Classification of Diseases (ICD), Tenth Revision. Analyses were conducted with the approval of the institutional review board (IRB) of Wonju Severance Christian Hospital (IRB No. CR325065, Approval Date: 12 August 2025) under the supervision of an honest broker.

2.2. Data Processing and De-Identification

De-identification involved the following four steps: (1) removal of direct identifiers (e.g., patient numbers); (2) generalization of quasi-identifiers (QIs) (e.g., sex and diagnosis codes) to higher-level categories; (3) suppression of records with equivalence class size k < 5 to mitigate small-cell re-identification risk; and the (4) binning of continuous variables (e.g., age) to reduce disclosure while preserving distributional properties [25,26,27,28,29,30,31,32,33].

We compared three strategies that become progressively stronger:

Baseline generalization: Sex dichotomized as male/female; diagnosis codes generalized to three-character KCD-8/ICD-10 categories; age binned in 3-year intervals; geographic unit retained at its original level (not used as a QI).

Enhanced generalization: Relative to baseline, diagnosis codes collapsed to two-character chapters; age merged into 10-year bins; rare clinical-department codes grouped to reduce small equivalence classes.

Enhanced generalization with suppression: Enhanced generalization plus suppression of records with k < 5, shifting the overall distribution toward safer regions.

2.3. Data Analysis and Evaluation

All analyses were performed in Python 3.10 with standard scientific libraries. Details of the computational environment, including library versions and hardware specifications, are summarized in

Table 1. Experimental environment.

Parameter	Description
Programming language	Python 3.10
Core libraries	pandas 2.2.2; numpy 1.26.4; scikit-learn 1.5.1; statsmodels 0.14.2; XGBoost 2.0.3; Splink 3.10.0; recordlinkage 0.15
Differential privacy	PyTorch 2.4.0 with Rényi DP accountant; opacus (DP-SGD) 1.5.2
Parallelization	joblib (bootstrap resampling, repeated runs)
CPU	24-core Intel Xeon (Intel Corporation, Santa Clara, CA, USA)
GPU	NVIDIA RTX 5090 (24 GB memory) (NVIDIA Corporation, Santa Clara, CA, USA)
RAM	128 GB

.

Statistical comparisons were conducted using bootstrap resampling (1500 replicates) to estimate 95% confidence intervals. Model performance was assessed using the area under the receiver operating characteristic curve (AUROC), area under the precision–recall curve (AUPRC), accuracy, F1-score, and Brier score. Calibration was evaluated by expected calibration error (ECE) and reliability diagrams. MIAs and MEAs were implemented within the same framework to quantify privacy risks under baseline training and differential privacy conditions.

Differentially private stochastic gradient descent was applied to train victim models.

Table 2. Hyperparameters and runtime settings for DP-SGD training.

Parameter	Value	Description
Batch size (B)	256	Mini-batch size per iteration
Learning rate (η)	0.01	Initial step size for optimization
Clipping norm (C)	1.0	ℓ2 norm bound for per-sample gradients
Noise multiplier (σ)	1.1	Scale of Gaussian noise added to clipped gradients
Number of epochs (T)	150	Total training epochs
Privacy accountant	RDP	Used to compute (ε, δ) privacy guarantees
δ	1 × 10−5	Fixed delta parameter
Final ε	2.488	Reported privacy budget after training

Note. The reported privacy budget ε was averaged across 20 independent runs with different random seeds, and 95% confidence intervals were calculated. Rényi differential privacy (RDP) was used as the accountant method for computing the privacy budget.

summarizes the hyperparameters and runtime settings used to compute the reported privacy budget. To ensure robust estimation of both privacy and utility, the entire procedure was repeated for 20 independent runs with different random seeds, and mean values with 95% confidence intervals were reported.

2.4. Re-Identification Risk via k-Anonymity Distributions

Re-identification risk was assessed based on the distribution of equivalence class sizes formed by QI combinations. For the baseline analysis, we defined sex and the diagnosis code (SCIN_CD) as QIs. In addition, six QI sets were constructed by incorporating alternative combinations permitted under institutional policy, including admission month generalized to quarterly bins and main/secondary diagnosis flags. Each set was evaluated under enhanced generalization strategies, and procedures were specified to compute k-anonymity distributions and suppression rates to assess how variations in QI definitions may influence the estimation of re-identification risk. Table S1 reports detailed results: for each record, the equivalence class size k was computed and assigned to one of four bins (k = 1, 2–4, 5–9, ≥10), and distributions were summarized at both the class (number of classes per bin) and record (proportion of records per bin) levels.

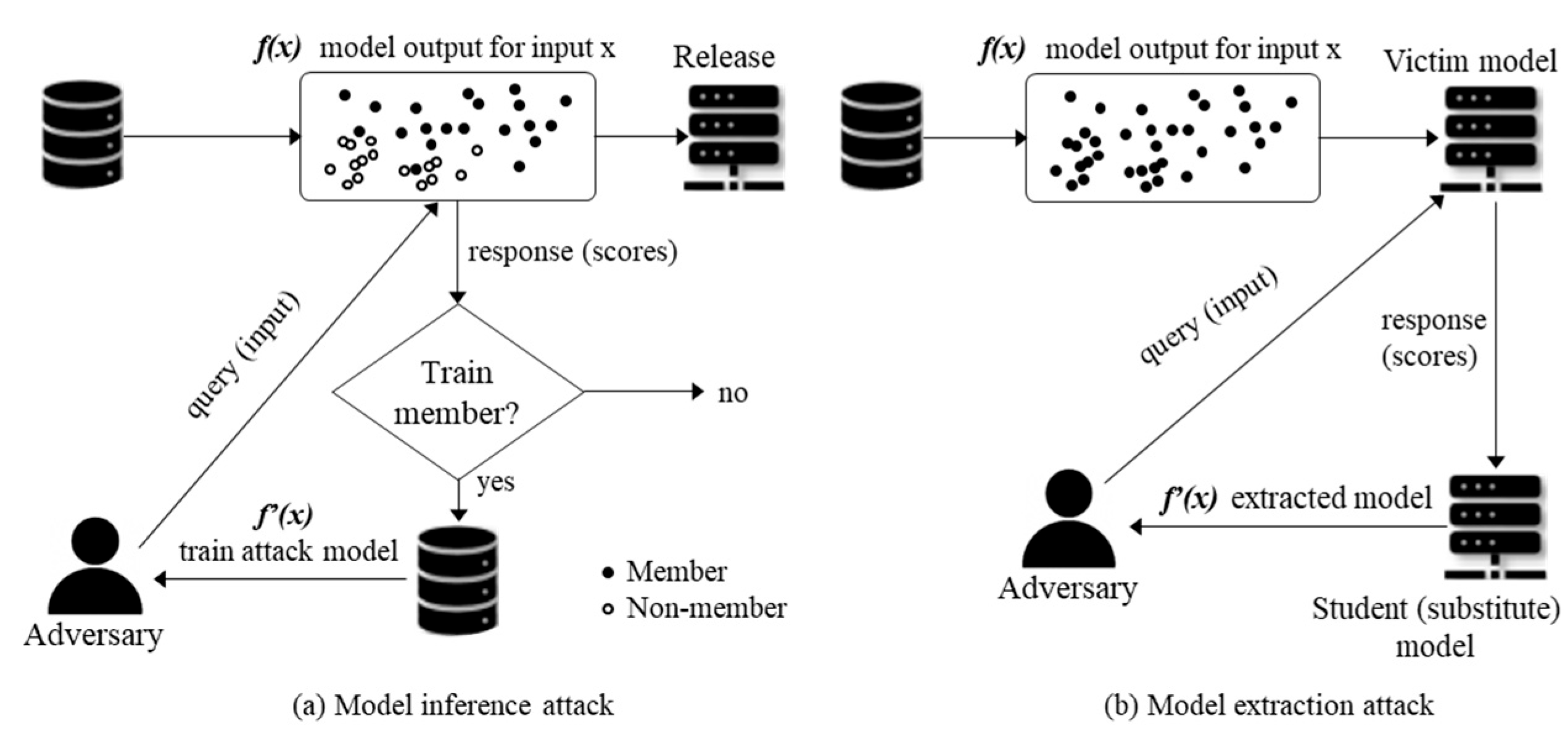
2.5. Membership Inference Attack (MIA)

MIAs evaluate whether an individual was included in model training (Figure 1a). We implemented three attacks: confidence (maximum predicted probability), entropy (entropy of the output distribution), and YeomLoss (per-sample loss). In addition, to reflect modern attack scenarios, we implemented a shadow-model MIA framework in which multiple shadow models were trained on disjoint data partitions and a logistic regression attack classifier was built using features such as confidence, margin, and cross-entropy loss. Each attack was repeated across 20 runs with different seeds. Data were split equally into training and test sets using patient-level grouping to prevent leakage. We reported the AUROC, accuracy, and attacker advantage. 95% confidence intervals (CIs) were estimated via patient-level block bootstrap (1500 replicates) using the bias-corrected and accelerated (BCa) method.

We conducted a subgroup-level screening based on the model confidence score. For each diagnostic label, we computed the AUROC and the attacker advantage, defined as the difference between true positive rate and false positive rate (TPR−FPR). Candidate labels were shortlisted when AUROC > 0.60 or advantage > 0.20. To avoid inflated estimates driven by repeated observations within the same patient, we then performed patient-level block bootstrap with 500 resamples on the selected labels and controlled multiplicity using the Benjamini–Hochberg procedure (q = 0.10). Significance was adjudicated by two criteria: (1) whether the 95% confidence interval exceeded 0.5 entirely and (2) whether the BH-adjusted q-value ≤ 0.10. Detailed subgroup outcomes are provided in Table S2, and threshold-sensitivity summaries appear in Table S3.

2.6. Model Extraction Attack (MEA)

In MEAs, a substitute student model is trained by querying the legitimately accessible target victim model (Figure 1b). We collected the victim’s probabilistic outputs and trained the student on these labels, before comparing model performance using AUROC, accuracy, F1-score, and Brier score, with 95% CIs from patient-level block bootstrap (1500 replicates) using BCa method.

2.7. Differential Privacy Stochastic Gradient Descent (DP-SGD)

This section details the training-level component of our privacy-preserving framework, which complements the data-level anonymization described earlier. Within this two-layered design, quasi-identifiers are first generalized and selectively suppressed to enforce structural privacy constraints at the dataset level (Section 2.2). Building on this foundation, DP-SGD is then applied to limit statistical leakage during model optimization. As summarized in Algorithm 1, the pipeline integrates suppression-based preprocessing, DP-SGD optimization, and RDP accounting into an end-to-end defense framework that ensures a verifiable (ε, δ) privacy guarantee for the overall training process.

Algorithm 1. Privacy-Preserving Training Pipeline

For clarity, the key training parameters are denoted as follows: b (mini-batch size), q = b/N (sampling rate), C (clipping threshold), σ (noise multiplier), η (learning rate), and E (number of training epochs). Input:  Raw dataset D with quasi-identifiers (QIs) and sensitive attributes (S); model fθ; parameters (b, q, C, σ, η, E)

Data Preprocessing (suppression stage):      Generalize QIs (e.g., age → 5-year bins, admission date → quarter)      Suppress records violating the k ≥ 5 criterion to obtain an anonymized dataset D′    Training (DP-SGD stage):      Iteratively sample mini-batches from D′        Clip per-sample gradients by C        Add Gaussian noise with multiplier σ        Update model parameters using learning rate η.    Privacy Accounting:      Track the cumulative privacy loss via RDP composition      Derive the overall (ε, δ) budget.

Output:  Final model parameters θ, resulting privacy budget (ε, δ), and metadata including (q, C, σ, b, η, E), random seeds, software versions, and hardware for reproducibility

2.7.1. Threat Model

The adopted threat model assumes an adversary attempting to infer the participation or sensitive attributes of individual records from model parameters or outputs. To mitigate such risks, the training procedure operates under record-level differential privacy, ensuring that each individual’s contribution to parameter updates remains statistically indistinguishable across neighboring datasets. This setting formally binds the cumulative privacy loss through RDP composition across training steps. The adversary’s inference capability is thereby bounded by (ε, δ)-differential privacy, providing a quantifiable measure of protection consistent with the framework’s overall privacy budget.

2.7.2. Mini-Batch Sampling and Per-Sample Gradient Computation

At each training step t, every record in the dataset of size N was independently selected with probability q using Poisson subsampling, forming a mini-batch Bₜ with expected size b ≈ qN. For model parameters θₜ and each data–label pair (xᵢ, yᵢ) in Bₜ, the per-sample gradient was computed as follows:

$$g_i^{(t)}=\nabla \theta \mathcal{l}(x_i,y_i,{\theta }_t).$$

(1)

2.7.3. Gradient Clipping

To prevent any single sample from disproportionately influencing model updates, per-sample gradient was bounded using ℓ₂-norm clipping. As shown in (2), each gradient $g_i^{(t)}$ was rescaled using the clipping threshold C, which limits the maximum allowable ℓ₂-norm:

$${\tilde{g}}_i^{(t)}=g_i^{(t)}\cdot \min \left(1,{\displaystyle \frac{C}{{‖g_i^{(t)}‖}_2}}\right).$$

(2)

If ${‖g_i^{(t)}‖}_2>C$, the gradient is projected onto the surface of the ℓ₂-ball of radius C; otherwise, it remains unchanged. This clipping bounds the sensitivity of each update and ensures consistent calibration of the Gaussian noise variance ${\sigma }^2{C}^2$. The choice of C determines the trade-off between privacy and stability—smaller values risk over-clipping, whereas larger ones require stronger noise to maintain privacy. We applied a uniform (flat) clipping norm across all layers for simplicity and reproducibility.

2.7.4. Noise Addition

To ensure differential privacy, Gaussian noise was added to the sum of the clipped gradients prior to averaging:

$${\tilde{g}}_t={\displaystyle \frac{1}{\left|B_t\right|}}{\displaystyle \sum _{i\in B_t}{\tilde{g}}_i^{(t)}}+\mathcal{N}(0,{\sigma }^2{C}^{2}I),$$

(3)

where σ is the noise multiplier, I is the identity matrix, and ${\tilde{g}}_t$ is the privatized gradient used for model updates.

2.7.5. Parameter Update

Model parameters were updated using the privatized gradient as follows:

$${\theta }_{t+1}={\theta }_t-\eta {\tilde{g}}_t,$$

(4)

where $\eta$ is the learning rate.

2.7.6. Privacy Accounting

Cumulative privacy loss during training was tracked using the subsampled Gaussian Rényi differential privacy accountant and converted to an (ε, δ) guarantee for the entire training run. Implementation was based on PyTorch 2.4.0 and Opacus 1.5.2, utilizing the RDPAccountant module [34,35,36,37,38,39]. The Poisson sampling probability was q = b/N, corresponding to q ≈ 256/99,839 ≈ 0.00256 for our dataset of N = 99,839 records. RDP orders α ∈ {1.25, 1.5, 2, 3, 4, 8, 16, 32, 64, 128, 256} were evaluated to compute ε(α), and δ was fixed at 1 × 10⁻⁵. The average ε and its 95% confidence interval were reported across 20 independent runs, yielding a final privacy budget of ε = 2.488 (95% CI: 2.322–2.721). This setting reflects a conservative privacy standard suitable for large-scale clinical EHR datasets. Key hyperparameters used in DP-SGD were as follows: batch size B = 256, learning rate η = 0.01, clipping norm C = 1.0, noise multiplier σ = 1.1, and training epochs T = 150. These settings are summarized in Table 1 and Table 2; the complete training configurations is provided in Table S5 to ensure reproducibility.

2.7.7. Design Choice and Implementation Details

We used a uniform clipping norm (C) across layers and a fixed noise multiplier (σ) throughout training to stabilize gradient variance and maintain consistent noise levels. Two complementary ablation experiments were conducted: (1) holding ε constant while varying C, tuning σ accordingly to maintain the target privacy budget, and (2) fixing C while varying σ to quantify its effect on the resulting (ε, δ).

3. Results

3.1. k-Anonymity Distributions

Figure 2 and

Table 3. Distribution of equivalence class sizes across de-identification strategies.

Interval	Baseline		Enhanced Generalization		Enhanced Generalization with Suppression
	ECs (n/%)	Recs (n/%)	ECs (n/%)	Recs (n/%)	ECs (n/%)	Recs (n/%)
k = 1	23/26.44%	23/0.36%	10/15.87%	10/0.16%	10/15.87%	10/0.16%
k = 2–4	24/27.59%	66/1.03%	15/23.81%	42/0.66%	15/23.81%	42/0.66%
k = 5–9	12/13.79%	79/1.24%	8/12.70%	57/0.89%	8/12.70%	56/0.88%
k ≥ 10	28/32.18%	6221/97.37%	30/47.62%	6280/98.29%	30/47.62%	6278/98.31%
suppressed	-	-	-	-	-	171/0.17%

Note. Values are presented as n/%. ECs = equivalence classes; Recs = records. For ECs, percentages are relative to the total number of equivalence classes under each method. For Recs, percentages are relative to the total number of records retained under each method (i.e., post-suppression totals where applicable), rather than the global cohort size. The analytic cohort comprised 99,839 records after excluding <0.01% with missing or invalid QI values.

summarize equivalence class distributions under the three de-identification strategies. The baseline strategy produced the lowest cumulative curve, reflecting a high proportion of small classes. Enhanced generalization shifted the curve upward. Combined generalization with suppression strategy produced the highest curve, indicating an overall increase in larger classes.

These results reveal that stronger de-identification strategies shift distributions toward safer regions, as summarized in Table 3. The baseline QI set (sex + SCIN_CD) achieved broad coverage at k ≥ 10 under the enhanced generalization strategy. In sensitivity analyses with additional QI sets, adding admission month (generalized to quarters) and diagnostic flags increased suppression to 56–66%; nevertheless, >40,000 training-eligible records were retained, and the k-anonymity distributions remained broadly consistent with the baseline (Table S1). At a stricter threshold of k ≥ 20, coverage decreased, but this was reported only as a sensitivity metric to illustrate the trade-off between stronger anonymity and data utility. These results indicate that even with elevated suppression, sufficient sample size was preserved for downstream modeling.

3.2. Baseline Evaluation

Before evaluating direct metric-based attacks, we validated the shadow-based MIA framework across 20 independent runs. As summarized in

Table 4. Shadow Model MIA (20 runs)—Summary Results.

Metric	Mean
Attack classifier AUROC	0.515 (95% CI: 0.514–0.516)
Threshold AUROC	0.504 (95% CI: 0.503–0.505)

Note. All 20 runs yielded AUROCs within ±0.02 of 0.5, and no run exceeded AUROC of 0.55, confirming chance-level attack performance despite the computational overhead.

, the attack classifier achieved a mean AUROC of 0.515 (95% CI: 0.514–0.516), while the threshold-based baseline yielded a mean AUROC of 0.504 (95% CI: 0.503–0.505). All runs remained within ±0.02 of 0.50, and no run exceeded an AUROC of 0.55, indicating that shadow-based MIAs consistently failed to infer membership. Overall, these results demonstrate that shadow-model MIAs remained at chance level and did not produce meaningful privacy leakage.

Table 5. Performance of membership inference attacks (chance-level results).

Attack Type	AUROC	Best Accuracy	Advantage
Confidence	0.503 (95% CI: 0.472–0.533)	0.527 (95% CI: 0.512–0.540)	0.027 (95% CI: 0.010–0.045)
Entropy	0.502 (95% CI: 0.472–0.533)	0.526 (95% CI: 0.511–0.541)	0.026 (95% CI: 0.009–0.044)
YeomLoss	0.503 (95% CI: 0.474–0.534)	0.529 (95% CI: 0.514–0.543)	0.030 (95% CI: 0.012–0.048)

Note. Results of three MIA methods (confidence, entropy, YeomLoss) under baseline training without DP-SGD. AUROC, accuracy, and attacker advantage remained near chance level, indicating that patient participation could not be reliably inferred.

presents MIA results under the baseline model using direct confidence-, entropy-, and loss-based attacks [40]. AUROC values were 0.503 (95% CI: 0.472–0.533), 0.502 (95% CI: 0.472–0.533), and 0.503 (95% CI: 0.474–0.534), respectively. The best accuracy ranged from 0.526 to 0.529, and the upper bound of attacker advantage was 0.030. These findings indicate that membership inference remained at chance level under baseline conditions. To address practical deployment concerns, we measured the computational overhead of shadow-based MIA and DP-SGD (Table S4). For shadow-based MIA, integrated wall-clock time was 37.570 s on GPU and 168.210 s on CPU, with corresponding peak memory usage of 2.8 GB GPU memory and 6.6–6.8 GB RAM. In comparison, DP-SGD training was lightweight, requiring only 1.030 s on GPU and 3.170 s on CPU per run, with modest CPU and memory utilization. These results confirm that shadow-based attacks remain computationally feasible even without GPU acceleration, whereas the overhead of DP-SGD was minimal across both devices.

At the distributional level, label-wise AUROC values centered near chance (median 0.511, interquartile range 0.059), with several tail candidates surpassing the screening thresholds (AUROC > 0.60 or advantage > 0.20)—predominantly among small-sample labels (≈ n = 20–40; Tables S2 and S3).

We further investigated rare diagnostic subgroups, as prior studies have suggested that sparsity can amplify privacy risks in membership inference attacks.

As summarized in

Table 6. Performance of model extraction attacks with bootstrap 95% CI (20 runs, n_boot = 1500).

Metric	Victim Model	Student Model
Correlation (prob.)	–	0.9999 (95% CI: 0.9998–1.0000)
MAE	–	0.0008 (95% CI: 0.0006–0.0011)
AUROC	0.975 (95% CI: 0.936–1.000)	0.9850 (95% CI: 0.9620–1.0000)
Accuracy	0.996 (95% CI: 0.991–0.999)	0.9960 (95% CI: 0.9910–0.9990)
F1-score	0.967 (95% CI: 0.945–0.981)	0.9680 (95% CI: 0.9470–0.9820)
Brier score	0.002 (95% CI: 0.002–0.003)	0.0020 (95% CI: 0.0016–0.0028)

Note. Values are reported with 95% bootstrap CIs (20 runs, n_boot = 1500). The student model, trained by querying victim outputs, achieved high correlation and low mean absolute error (MAE), demonstrating that victim predictions were closely replicated under baseline training. For the student model, values are presented to four decimal places to accurately represent very small differences from the victim model.

, the student model closely replicated the victim model’s probabilistic outputs. Predicted probabilities were highly correlated (r = 0.9999, 95% CI: 0.9998–1.0000), with mean absolute error of 0.0008 (95% CI: 0.0006–0.0011). AUROC was 0.975 (95% CI: 0.936–1.000) and 0.985 (95% CI: 0.962–1.000) for the victim and student models, respectively. The accuracy, F1-score, and Brier score were nearly identical across models.

3.3. Evaluation of DP-SGD in Clinical Models

3.3.1. MIAs with DP-SGD

Table 7. Membership inference attacks with DP-SGD.

Attack Type	AUROC	Best Accuracy	Advantage
Confidence	0.501 (95% CI: 0.480–0.523)	0.530 (95% CI: 0.506–0.568)	0.002 (95% CI: −0.000–0.012)
Entropy	0.501 (95% CI: 0.480–0.523)	0.530 (95% CI: 0.506–0.568)	0.002 (95% CI: 0.000–0.012)
YeomLoss	0.498 (95% CI: 0.477–0.520)	0.530 (95% CI: 0.505–0.568)	0.002 (95% CI: 0.000–0.010)

Note. Performance of Confidence, Entropy, and YeomLoss attacks against DP-SGD–trained models (20 runs, n_boot = 1500). All results were close to random guessing, confirming that DP-SGD mitigated membership inference risk. Advantage values (TPR–FPR) were approximately zero with confidence intervals overlapping zero, indicating that attackers could not systematically distinguish members from non-members.

summarizes MIA results with DP-SGD [41,42]. AUROC values for Confidence, Entropy, and YeomLoss attacks were 0.501 (95% CI: 0.480–0.523), 0.501 (95% CI: 0.480–0.523), and 0.498 (95% CI: 0.477–0.520), respectively. Best accuracy was 0.530 (95% CI: 0.505–0.568), and attacker advantage was 0.002. These results confirm that MIAs remained at chance level under DP-SGD.

3.3.2. MEAs with DP-SGD

Table 8. Model extraction attacks with DP-SGD.

Metric	Victim Model	Student Model	Victim–Student Agreement
AUROC	0.729 (95% CI: 0.654–0.785)	0.486 (95% CI: 0.382–0.646)	r = −0.008 (95% CI: −0.076–0.036)
Accuracy	0.950 (95% CI: 0.943–0.959)	0.950 (95% CI: 0.943–0.959)	MAE = 0.002 (95% CI: 0.001–0.005)
Brier score	0.050 (95% CI: 0.040–0.056)	0.050 (95% CI: 0.041–0.056)	–

Note. Victim models were trained with DP-SGD (C = 1.0, σ = 1.1, ε = 2.488, δ = 1 × 10⁻⁵), and student models queried their outputs. Reported AUROC, accuracy, Brier score, correlation, and MAE show that DP-SGD substantially curtailed replication of victim predictions while preserving acceptable accuracy.

shows MEA performance after DP-SGD [43]. The victim model maintained an AUROC of 0.729 (95% CI: 0.654–0.785), accuracy of 0.950 (95% CI: 0.943–0.959), and Brier score of 0.050 (95% CI: 0.040–0.056). By contrast, the student model achieved an AUROC of 0.486 (95% CI: 0.382–0.646), and the correlation with victim outputs was −0.008 (95% CI: −0.076–0.036). Mean absolute error increased slightly to 0.002 (95% CI: 0.001–0.005). Despite similar accuracy and Brier scores, the AUROC and correlation revealed that the student model did not replicate the victim model. Although victim–student agreement was assessed using correlation and MAE, the Brier scores were reported separately for each model because they reflect calibration performance within a single model rather than pairwise agreement.

As shown in Table 7, AUROC and accuracy decreased compared with Table 5. This reduction is primarily attributable to the stochastic noise introduced by DP-SGD, where gradient clipping and Gaussian perturbation are applied to each mini-batch update. These results indicate that DP-SGD reduced the replication of victim predictions by student models while maintaining accuracy at an acceptable level.

3.3.3. Privacy–Utility Metrics

With δ fixed at 1 × 10⁻⁵, the privacy budget estimated by the RDP accountant was ε ≈ 2.5 (95% CI 2.32–2.72). DP-SGD maintained stable test-set performance, demonstrating a practical privacy–utility balance as shown in

Table 9. Performance of DP-SGD: privacy and utility outcomes.

Category	Metric	Value	Interpretation
Privacy	δ	1 × 10−5 (fixed)	Preset privacy parameter
	ε	2.488 (95% CI 2.322–2.721)	Privacy budget (RDP accountant)
Utility	AUROC	0.729 (95% CI 0.654–0.785)	Discrimination ability
	Accuracy	0.950 (95% CI 0.943–0.959)	Classification performance
	log loss	0.293 (95% CI 0.228–0.347)	Calibration performance

Note. Results are averaged over 20 runs with 95% bootstrap CIs (n_boot = 1500). The privacy budget (ε ≈ 2.5, δ = 1 × 10⁻⁵) was computed using the RDP accountant. DP-SGD achieved this level of privacy while maintaining clinically acceptable AUROC and accuracy, demonstrating a practical privacy–utility balance.

.

4. Discussion

4.1. Principal Findings

In contrast to prior studies that primarily introduced privacy-preserving strategies such as federated learning, secure aggregation, and differential privacy [44,45,46], our work directly tested adversarial risks through empirical evaluation. Specifically, we examined re-identification, membership inference, and model extraction within a unified framework using real-world EHR data, thereby demonstrating how suppression and DP-SGD operate under practical conditions. By incorporating these attack scenarios, our study extends beyond the defensive focus of previous investigations and provides evidence that combined strategies can mitigate privacy risks without undermining clinical performance.

Screening suggested potential tail risks (AUROC > 0.60 or advantage > 0.20), however, conservative validation using patient-level block bootstrap (500 resamples) with the Benjamini–Hochberg procedure controlling the false-discovery rate (BH-FDR, q = 0.10) failed to substantiate these signals: no label had a 95% CI entirely above 0.5, and no label remained significant at q = 0.10. These findings collectively indicate that the apparent tail risks were inflated by small-sample volatility and within-patient dependence, rather than reflecting systematic leakage (Tables S2 and S3).

Enhanced generalization with suppression consistently shifted k-anonymity distributions toward safer regions. All membership inference attacks remained at chance level; thus, patient-level participation could not be reliably inferred. In contrast, MEAs replicated victim predictions—with near-perfect fidelity—under baseline training; however, this alignment was markedly reduced once DP-SGD was applied. Thus, these results demonstrate that conventional de-identification enhanced with suppression effectively mitigates re-identification risk, with DP-SGD playing a key role in limiting model extraction and preserving model integrity.

4.2. Interpretation

4.2.1. k-Anonymity

Suppressing rare QI combinations effectively reduced re-identification risk, demonstrating that modest record loss can substantially enhance data safety. This supports suppression as an essential complement to generalization when preparing datasets for secondary use, particularly in multi-institutional environments where linkage threats are amplified. Additional sensitivity analyses confirmed that our risk estimates were robust to variations in QI definitions permitted under institutional governance. Even when broader QI combinations such as admission month or diagnostic flags were considered, sufficient records remained to support downstream modeling (Table S1). At the stricter threshold of k ≥ 20, coverage was reduced, but this served only as a sensitivity metric to illustrate the trade-off between stronger anonymity and data utility.

4.2.2. Membership Inference Attacks

The negligible performance of MIAs indicates that models were not overfitted, reassuring clinicians that patient participation cannot be inferred even under modern shadow-based attacks. Although some rare subgroups produced unstable AUROC values, applying a stability filter that excluded labels with fewer than 20 samples confirmed that these extremes did not represent systematic leakage, consistent with prior reports on subgroup-specific privacy risks [47,48]. This criterion, detailed in Section 2.5, ensured consistency between subgroup analyses and the overall study design. Moreover, the measured overhead demonstrated that shadow-based MIAs are computationally lightweight, completing within seconds on GPUs and within minutes on CPUs, indicating that the risks examined in this study are not merely theoretical but practically realizable in hospital environments.

4.2.3. Model Extraction Attacks

Unlike MIAs, MEAs exposed a realistic deployment risk, as student models closely replicated victim predictions under baseline training. This vulnerability underscores the necessity of DP-SGD, not only for reducing replication but also for protecting the proprietary value of institutional CDSS models. In comparison with prior studies that reported limited empirical validation, our results provide concrete evidence that DP-SGD offers practical defense in hospital-scale clinical environments. For clinical settings, these results highlight that privacy-preserving training is critical not only to protect individuals but also to maintain the proprietary value of decision support models in practice.

4.2.4. Privacy–Utility Trade-Off

Crucially, these protections were achieved without eroding clinical usability. The models maintained stable predictive performance, supporting the feasibility of integrating DP-SGD into routine CDSS deployment. Thus, combining generalization with suppression at the data-sharing stage and DP-SGD during model training offers a practical strategy to balance privacy and utility, providing a foundation upon which to develop standardized guidelines in collaborative clinical research.

4.2.5. Defense with DP-SGD

DP-SGD functioned as the principal defense mechanism in this study. It substantially curtailed model extraction, safeguarding both patient privacy and institutional model assets. Moreover, this study provides one of the first empirical demonstrations of DP-SGD’s defensive effect using operational EHR datasets from clinical practice, thereby establishing its role as a practical safeguard rather than a purely theoretical construct. In line with this contribution, our findings are also consistent with prior studies on differential privacy, which have consistently reported that injecting calibrated noise into the training process leads to modest degradation in model performance [49,50]. In DP-SGD, gradient clipping limits the sensitivity of each update, and Gaussian noise is subsequently added to preserve (ε, δ)-differential privacy. Stronger privacy budgets (smaller ε) inevitably require higher noise variance, which increases optimization variance and reduces model utility [51]. Our results quantitatively demonstrate this privacy–utility balance on large-scale EHR data, showing that although AUROC was reduced as summarized in Table 8, the overall predictive performance remained within a clinically acceptable range. This suggests that meaningful privacy protection can be achieved without prohibitive loss of clinical utility.

4.3. Implications for CDSS and Data Sharing

First, enhanced generalization with suppression reduced re-identification risk and should be considered before data sharing. Second, although no incremental MIA risk was observed during model deployment, MEAs were evident under baseline training; thus, privacy-preserving learning approaches such as DP-SGD should be integrated as standard options. Third, because suppression may eliminate rare groups, suppression rates and complementary sensitivity analyses should be reported transparently. Overall, the combined use of generalization with suppression and DP-SGD can serve as a practical minimum standard for safeguarding privacy and model integrity in CDSSs. For clinicians, such safeguards will not only reduce legal liability but also ensure that decision support outputs remain reliable without compromising patient privacy. In clinical workflows, this dual protection can strengthen provider confidence and foster patient acceptance of artificial intelligence (AI)-based care. At the institutional level, this study provides an empirical basis for consensus guidelines, and facilitates safer data exchange in multi-institutional collaborations, which are critical for scaling CDSSs in real-world healthcare systems.

4.4. Strengths

This study has several notable strengths. First, it represents one of the few empirical investigations of privacy–utility trade-offs using large-scale, real-world, multi-year EHR data rather than synthetic or simulated datasets, thereby ensuring clinical applicability and relevance. Second, unlike prior studies that typically focused on a single attack vector, we simultaneously evaluated three representative privacy threats—membership inference, model extraction, and re-identification—within a unified framework. This comprehensive assessment provides a more realistic and holistic view of privacy risks in clinical AI models [52]. Third, we empirically demonstrated the effectiveness of DP-SGD in a clinical context, quantitatively showing its ability to mitigate attacks while maintaining clinically acceptable model performance. Fourth, we also uncovered structural vulnerabilities in rare diagnostic subgroups, providing novel empirical insight into subgroup-specific privacy risks that are increasingly recognized in the literature [52]. Thus, these contributions establish a novel empirical framework, positioning this study as a practical benchmark for developing standardized privacy guidelines in AI-based CDSS.

4.5. Limitations

First, k-anonymity alone does not capture all modern threats such as linkage or attribute inference; to overcome this limitation, complementary measures including l-diversity, t-closeness, and distribution-preserving transformations are needed. Second, the full privacy–utility curve across a broader range of ε values was not examined. Third, MEA threat models depended on specific assumptions about query budgets and output access, which may differ across operational environments. Fourth, although suppression and generalization can reduce the representation of rare groups, the resulting bias was not fully addressed in this study. Finally, this work relied on data from a single institution. In the current legal and regulatory environment, direct cross-hospital linkage of patient-level data is legally restricted, which prevented us from assessing heterogeneity across institutions where linkage risks and attack scenarios may differ. Accordingly, our findings should be interpreted as a comprehensive single-institution evaluation. Future studies should extend these analyses to collaborative settings through privacy-preserving approaches such as federated or distributed learning, which can enable collaborative validation without direct data sharing.

4.6. Future Work

Future research should extend the exploration of privacy–utility trade-offs across a broader range of ε values incorporating additional evaluation metrics—including calibration—to comprehensively capture clinical performance. Because linkage risks and attack scenarios may differ across institutions, future validation in broader collaborative environments is essential, and privacy-preserving approaches such as federated or distributed learning offer a feasible path for such collaborative evaluation. Greater attention should be paid to quantifying the loss of rare groups caused by suppression and to evaluate statistical correction methods such as inverse probability weighting, multiple imputation, or Bayesian modeling is warranted. Refining per-class evaluation methods to systematically capture subgroup privacy risks is also warranted. In particular, expanding shadow-based analyses with larger sample sizes, alternative attack architectures, and stability criteria will help clarify whether extreme values in rare classes represent statistical artifacts or actionable vulnerabilities. Additionally, attack scenarios should be expanded to include rare disease codes and multi-source linkage will enhance the realism of threat assessments. Finally, validating combined strategies such as federated learning with DP-SGD is critical to ensure reproducibility and support reliable multi-institutional research. Such advances will provide a stronger foundation for the safe and clinically meaningful deployment of AI-based CDSSs in real-world healthcare settings.

5. Conclusions

Enhanced generalization with suppression reduced re-identification risk, membership inference remained at a chance level, and model extraction was curtailed by DP-SGD. Overall, our findings provide an empirical benchmark for developing standardized privacy guidelines, demonstrating that defensive strategies can be operationalized without undermining clinical reliability. Although limited to a single institution, this study leveraged 100,000 multi-year diagnosis records, providing a foundation for cross-institutional validation. To our knowledge, this is among the first empirical studies to jointly evaluate multiple privacy risks and defenses on real-world EHR data, underscoring the novelty and practical contribution of our work. Moreover, they highlight the clinical and policy significance of integrating privacy-preserving strategies, thereby supporting reproducibility and enabling the safe deployment of AI-based CDSS to improve patient outcomes.