YOLO-Based Object and Keypoint Detection for Autonomous Traffic Cone Placement and Retrieval for Industrial Robots
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. YOLO-Based Models
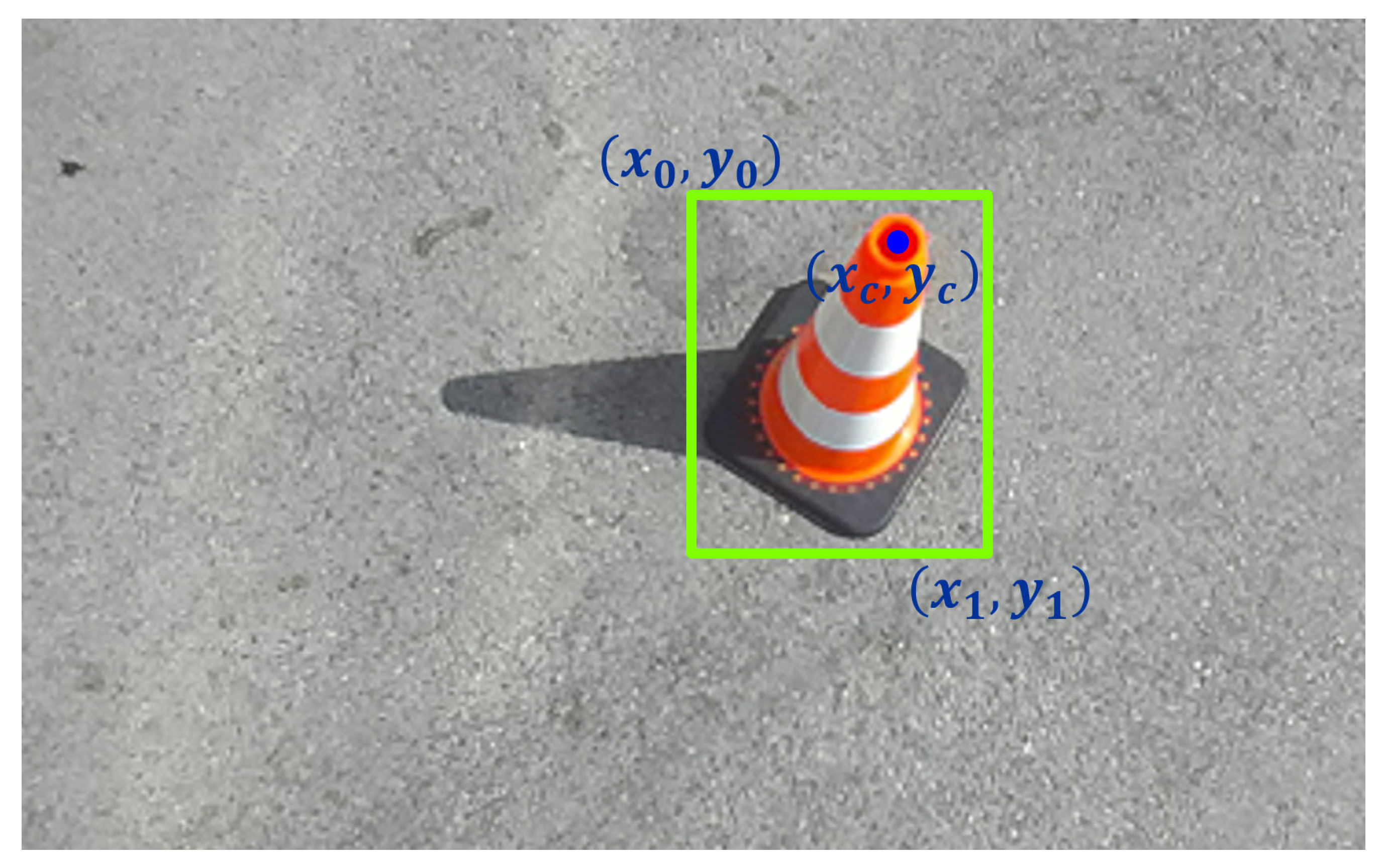
3.2. Dataset Collection and Annotation
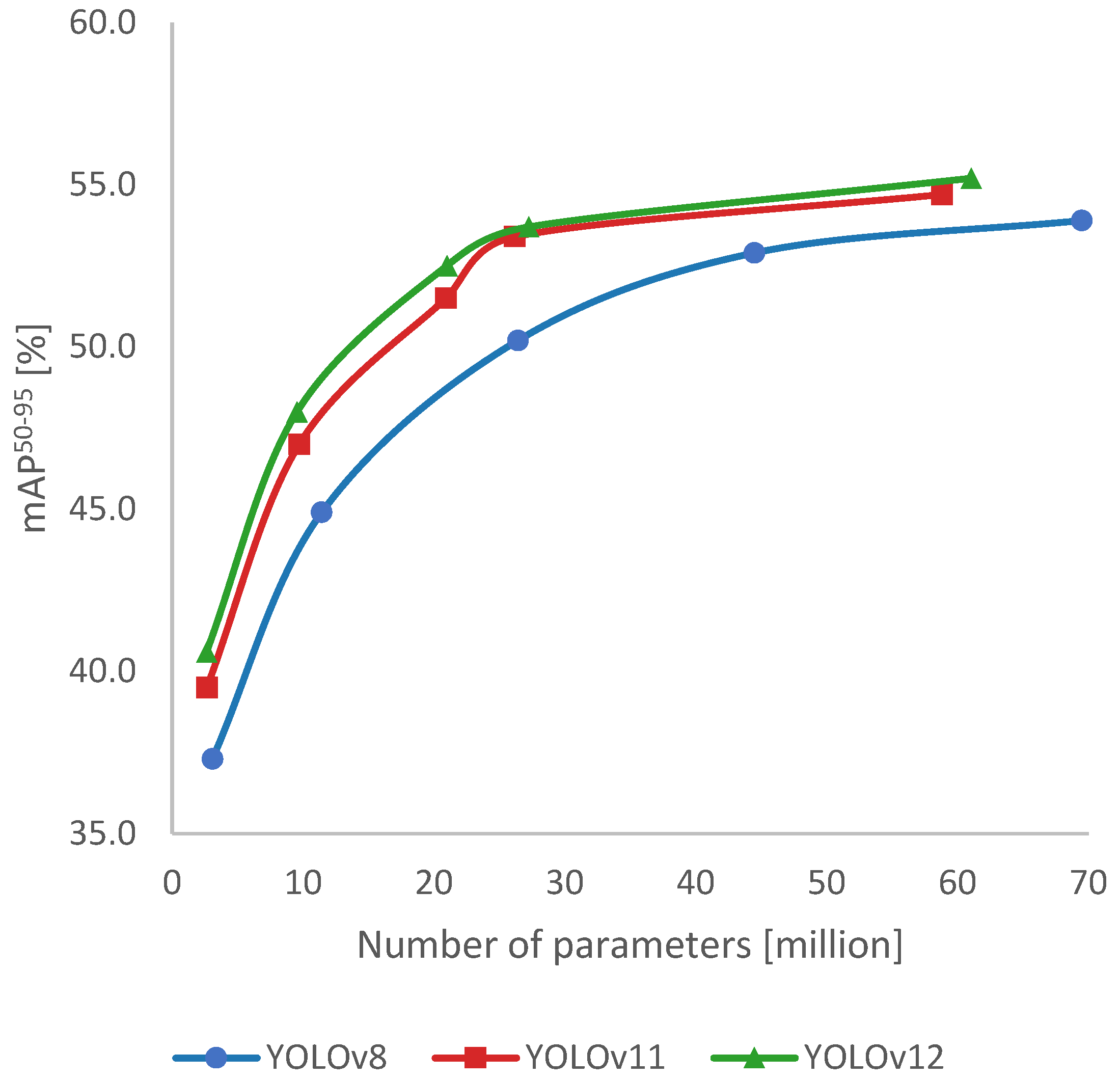
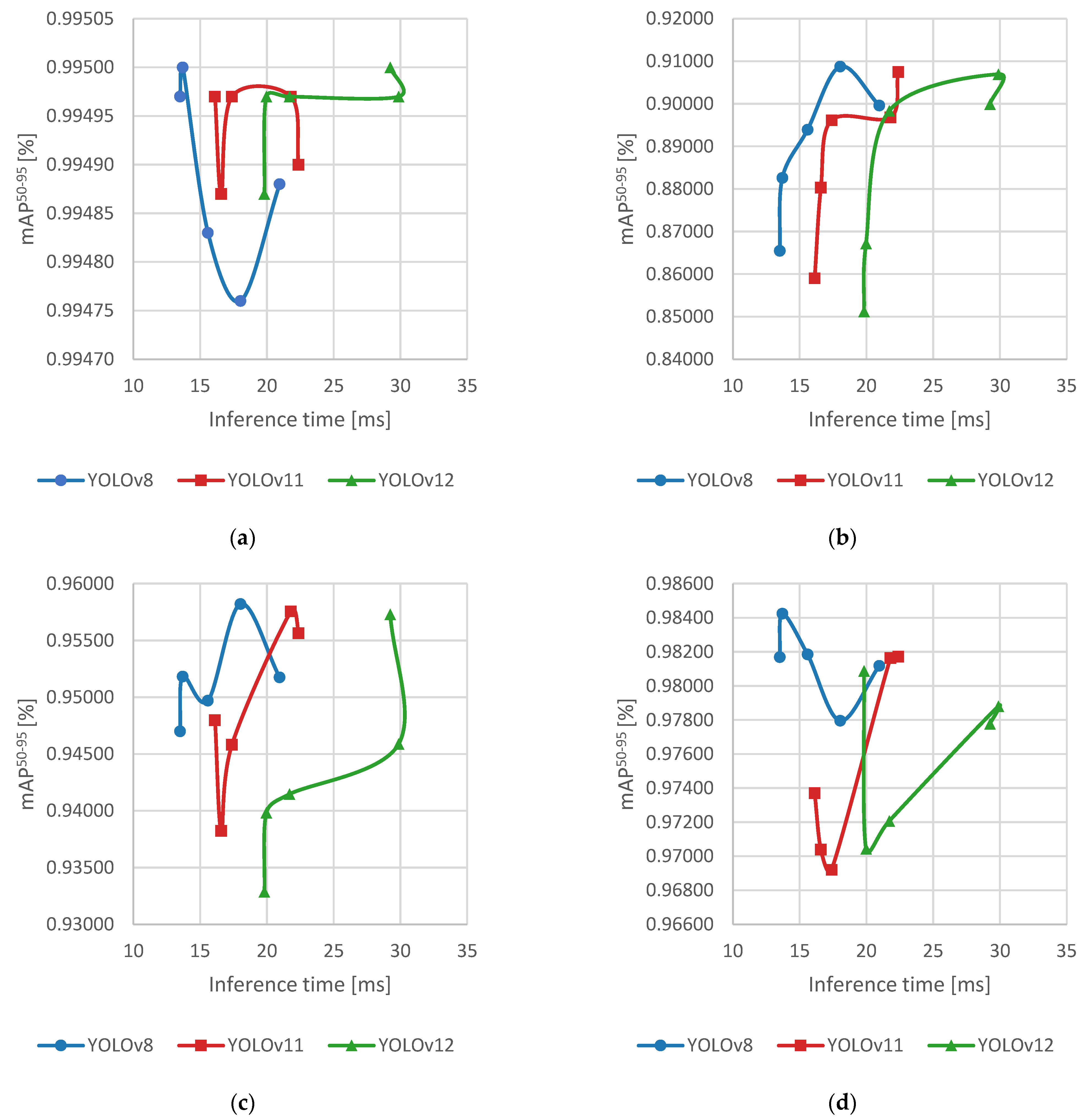
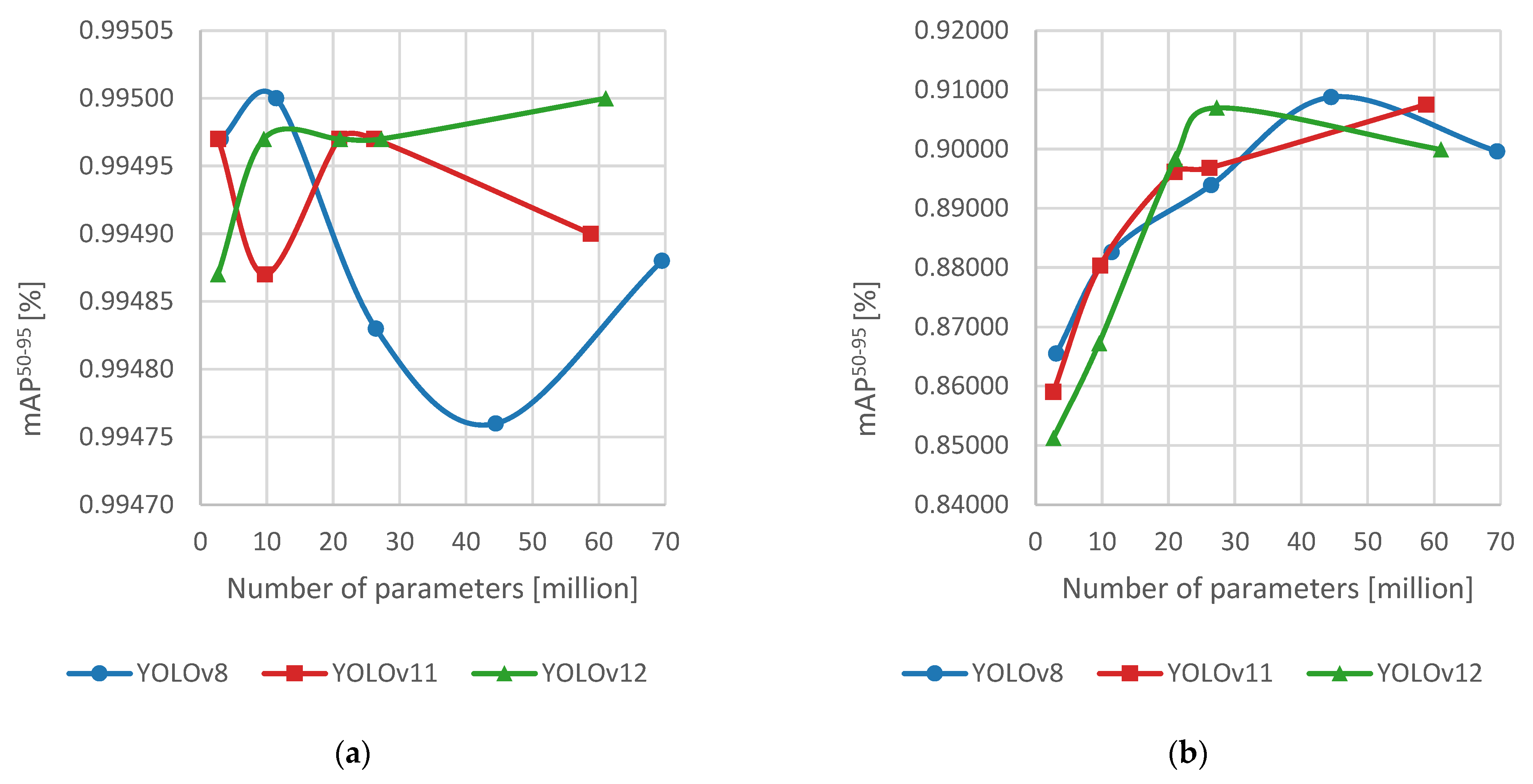
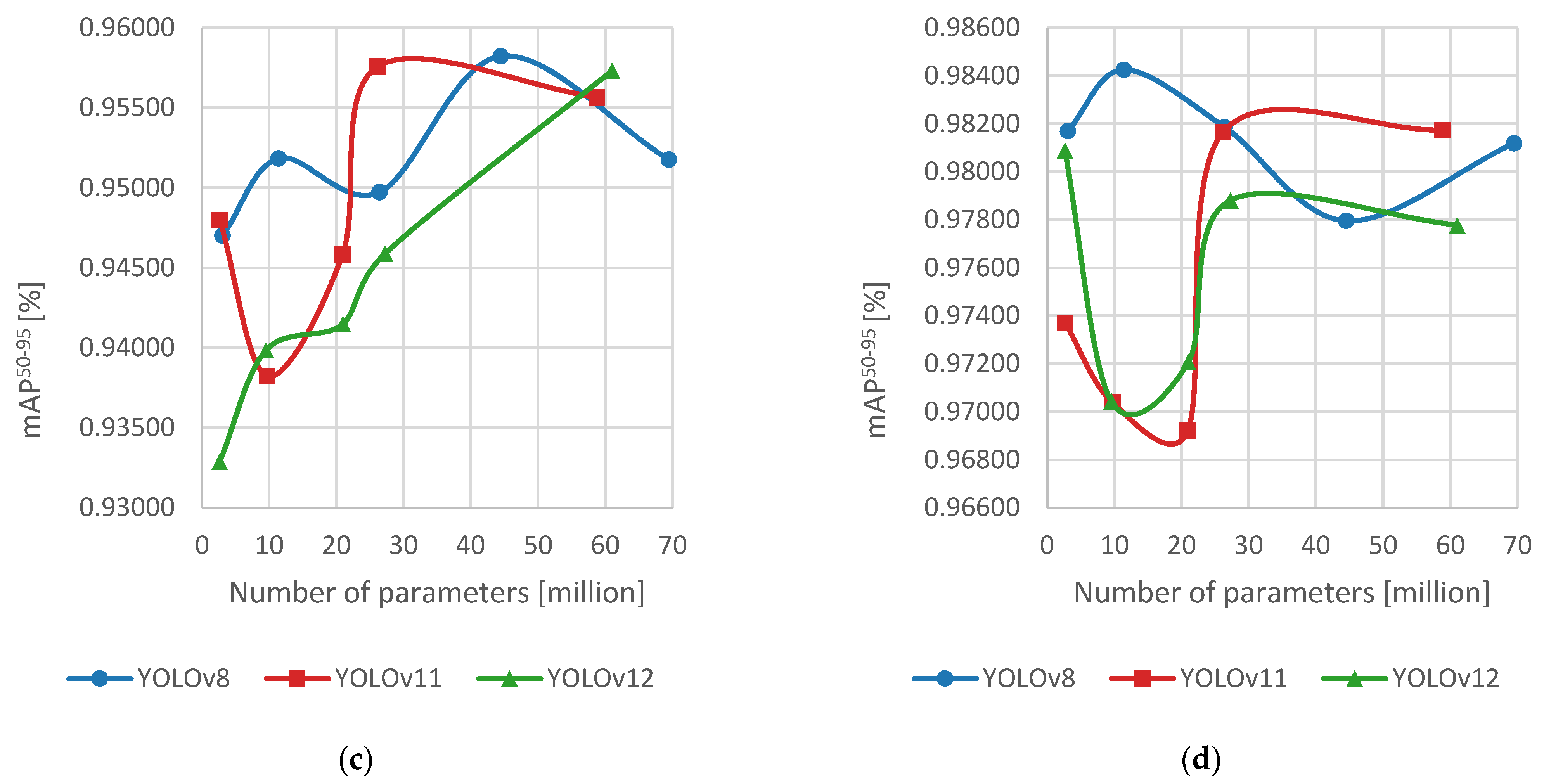
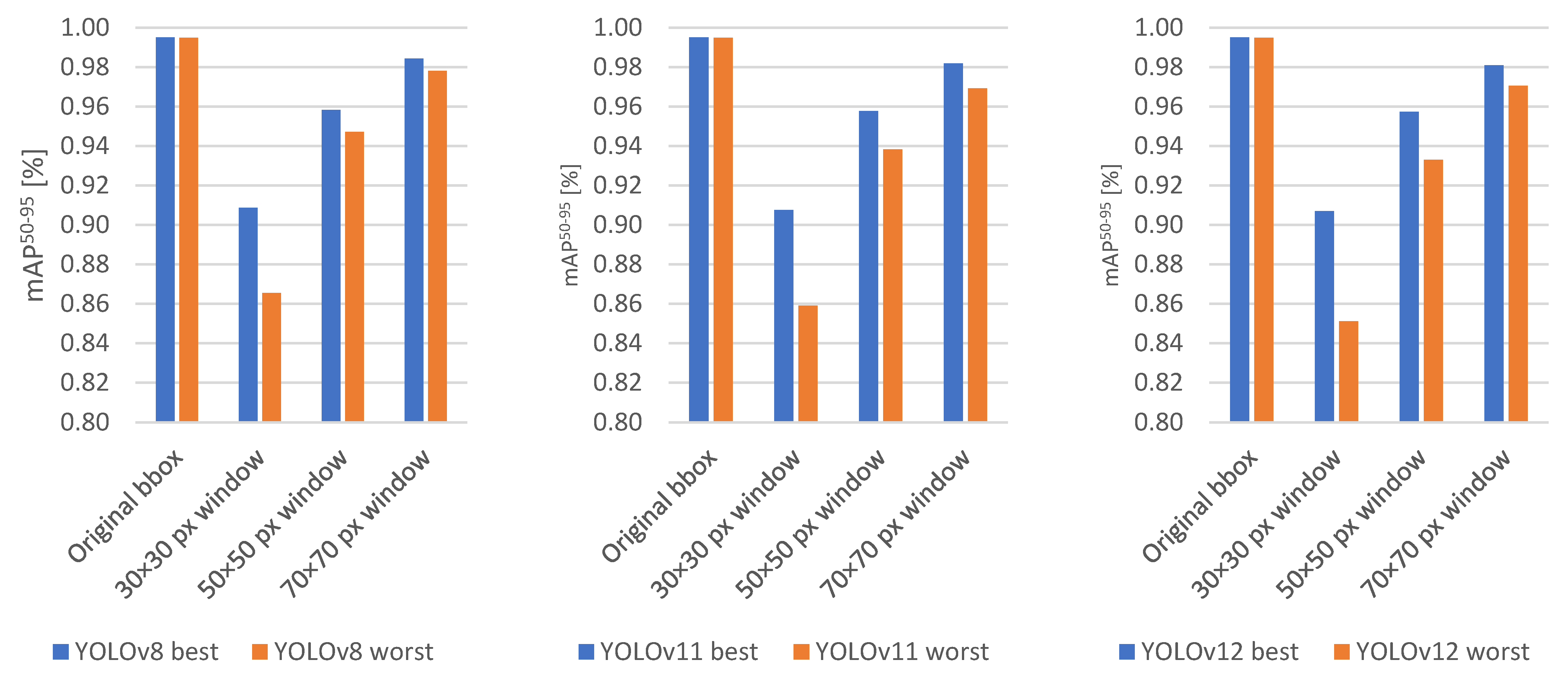
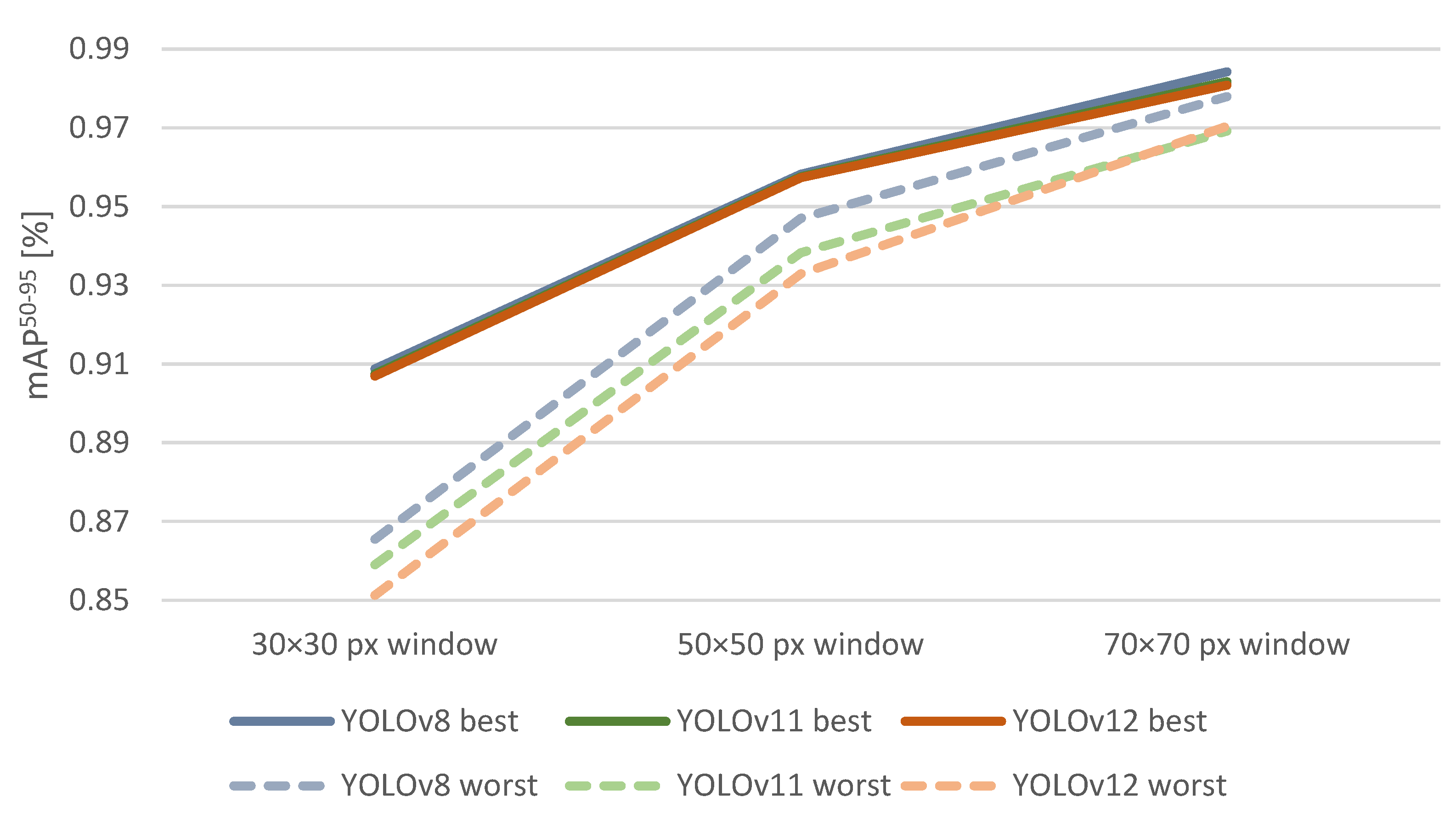
4. Results
5. Conclusions and Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alverhed, E.A.; Hellgren, S.; Isaksson, H.; Olsson, L.; Palmqvist, H.; Flodén, J. Autonomous Last-Mile Delivery Robots: A Literature Review. Eur. Transp. Res. Rev. 2024, 16, 4. [Google Scholar] [CrossRef]
- Shamout, M.; Ben-Abdallah, R.; Alshurideh, M.; Alzoubi, H.; Kurdi, B.A.; Hamadneh, S. A Conceptual Model for the Adoption of Autonomous Robots in Supply Chain and Logistics Industry. Uncertain Supply Chain. Manag. 2022, 10, 577–592. [Google Scholar] [CrossRef]
- Benčo, D.; Kubasáková, I.; Kubáňová, J.; Kalašová, A. Automated Robots in Logistics. Transp. Res. Procedia 2025, 87, 103–111. [Google Scholar] [CrossRef]
- Lackner, T.; Hermann, J.; Kuhn, C.; Palm, D. Review of Autonomous Mobile Robots in Intralogistics: State-of-the-Art, Limitations and Research Gaps. Procedia CIRP 2024, 130, 930–935. [Google Scholar] [CrossRef]
- Sodiya, E.O.; Umoga, U.J.; Amoo, O.O.; Atadoga, A. AI-Driven Warehouse Automation: A Comprehensive Review of Systems. GSC Adv. Res. Rev. 2024, 18, 272–282. [Google Scholar] [CrossRef]
- Choudhary, T. Autonomous Robots and AI in Warehousing: Improving Efficiency and Safety. Int. J. Inf. Technol. Manag. Inf. Syst. 2025, 16, 216–229. [Google Scholar] [CrossRef]
- Zeng, L.; Guo, S.; Wu, J.; Markert, B. Autonomous Mobile Construction Robots in Built Environment: A Comprehensive Review. Dev. Built Environ. 2024, 19, 100484. [Google Scholar] [CrossRef]
- Külz, J.; Terzer, M.; Magri, M.; Giusti, A.; Althoff, M. Holistic Construction Automation with Modular Robots: From High-Level Task Specification to Execution. IEEE Trans. Autom. Sci. Eng. 2025, 22, 16716–16727. [Google Scholar] [CrossRef]
- Jud, D.; Kerscher, S.; Wermelinger, M.; Jelavic, E.; Egli, P.; Leemann, P.; Hottiger, G.; Hutter, M. HEAP—The Autonomous Walking Excavator. Autom. Constr. 2021, 129, 103783. [Google Scholar] [CrossRef]
- Katsamenis, I.; Bimpas, M.; Protopapadakis, E.; Zafeiropoulos, C.; Kalogeras, D.; Doulamis, A.; Doulamis, N.; Martín-Portugués Montoliu, C.; Handanos, Y.; Schmidt, F.; et al. Robotic Maintenance of Road Infrastructures: The HERON Project. In Proceedings of the 15th International Conference on PErvasive Technologies Related to Assistive Environments, Corfu, Greece, 29 June–1 July 2022; ACM: New York, NY, USA, 2022; pp. 628–635. [Google Scholar]
- Bhardwaj, H.; Shaukat, N.; Barber, A.; Blight, A.; Jackson-Mills, G.; Pickering, A.; Yang, M.; Mohd Sharif, M.A.; Han, L.; Xin, S.; et al. Autonomous, Collaborative, and Confined Infrastructure Assessment with Purpose-Built Mega-Joey Robots. Robotics 2025, 14, 80. [Google Scholar] [CrossRef]
- Xu, Y.; Bao, R.; Zhang, L.; Wang, J.; Wang, S. Embodied Intelligence in RO/RO Logistic Terminal: Autonomous Intelligent Transportation Robot Architecture. Sci. China Inf. Sci. 2025, 68, 150210. [Google Scholar] [CrossRef]
- Dhall, A.; Dai, D.; Van Gool, L. Real-Time 3D Traffic Cone Detection for Autonomous Driving. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; IEEE: New York, NY, USA, 2019; pp. 494–501. [Google Scholar]
- Wang, F.; Dong, W.; Gao, Y.; Yan, X.; You, Z. The Full-Automatic Traffic Cone Placement and Retrieval System Based on Smart Manipulator. In Proceedings of the CICTP 2019, Nanjing, China, 2 July 2019; American Society of Civil Engineers: Nanjing, China, 2019; pp. 3442–3453. [Google Scholar]
- Wang, M.; Qu, D.; Wu, Z.; Li, A.; Wang, N.; Zhang, X. Application of Traffic Cone Target Detection Algorithm Based on Improved YOLOv5. Sensors 2024, 24, 7190. [Google Scholar] [CrossRef]
- Štibinger, P.; Broughton, G.; Majer, F.; Rozsypálek, Z.; Wang, A.; Jindal, K.; Zhou, A.; Thakur, D.; Loianno, G.; Krajník, T.; et al. Mobile Manipulator for Autonomous Localization, Grasping and Precise Placement of Construction Material in a Semi-Structured Environment. IEEE Robot. Autom. Lett. 2021, 6, 2595–2602. [Google Scholar] [CrossRef]
- Park, J.; Han, C.; Jun, M.B.G.; Yun, H. Autonomous Robotic Bin Picking Platform Generated From Human Demonstration and YOLOv5. J. Manuf. Sci. Eng. 2023, 145, 121006. [Google Scholar] [CrossRef]
- Hollósi, J.; Krecht, R.; Ballagi, Á. Development of Advanced Intelligent Robot Platform for Industrial Applications. ERCIM News 2025, 141, 40–41. [Google Scholar]
- Macenski, S.; Foote, T.; Gerkey, B.; Lalancette, C.; Woodall, W. Robot Operating System 2: Design, Architecture, and Uses in the Wild. Sci. Robot. 2022, 7. [Google Scholar] [CrossRef]
- Cao, Z.; Hidalgo, G.; Simon, T.; Wei, S.-E.; Sheikh, Y. OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 172–186. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep High-Resolution Representation Learning for Human Pose Estimation. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 5686–5696. [Google Scholar]
- Tekin, B.; Sinha, S.N.; Fua, P. Real-Time Seamless Single Shot 6D Object Pose Prediction. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: New York, NY, USA, 2018; pp. 292–301. [Google Scholar]
- Xiang, Y.; Schmidt, T.; Narayanan, V.; Fox, D. PoseCNN: A Convolutional Neural Network for 6D Object Pose Estimation in Cluttered Scenes. In Proceedings of the Robotics: Science and Systems XIV, Pittsburgh, PA, USA, 26 June 2018; Robotics: Science and Systems Foundation: Sydney, Australia, 2018. [Google Scholar]
- Hodan, T.; Barath, D.; Matas, J. EPOS: Estimating 6D Pose of Objects With Symmetries. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 11700–11709. [Google Scholar]
- Manuelli, L.; Gao, W.; Florence, P.; Tedrake, R. KPAM: KeyPoint Affordances for Category-Level Robotic Manipulation. In Robotics Research; Asfour, T., Yoshida, E., Park, J., Christensen, H., Khatib, O., Eds.; Springer International Publishing: Cham, Switzerland, 2022; Volume 20, pp. 132–157. [Google Scholar]
- Sundermeyer, M.; Marton, Z.-C.; Durner, M.; Triebel, R. Augmented Autoencoders: Implicit 3D Orientation Learning for 6D Object Detection. Int. J. Comput. Vis. 2020, 128, 714–729. [Google Scholar] [CrossRef]
- Wang, G.; Manhardt, F.; Shao, J.; Ji, X.; Navab, N.; Tombari, F. Self6D: Self-Supervised Monocular 6D Object Pose Estimation. In Computer Vision—ECCV 2020; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12346, pp. 108–125. [Google Scholar]
- Li, Z.; Hu, Y.; Salzmann, M.; Ji, X. SD-Pose: Semantic Decomposition for Cross-Domain 6D Object Pose Estimation. AAAI Conf. Artif. Intell. 2021, 35, 2020–2028. [Google Scholar] [CrossRef]
- Chen, X.; Ma, F.; Wu, Y.; Han, B.; Luo, L.; Biancardo, S.A. MFMDepth: MetaFormer-Based Monocular Metric Depth Estimation for Distance Measurement in Ports. Comput. Ind. Eng. 2025, 207, 111325. [Google Scholar] [CrossRef]
- Maji, D.; Nagori, S.; Mathew, M.; Poddar, D. YOLO-Pose: Enhancing YOLO for Multi Person Pose Estimation Using Object Keypoint Similarity Loss. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; IEEE: New York, NY, USA, 2022; pp. 2636–2645. [Google Scholar]
- McNally, W.; Vats, K.; Wong, A.; McPhee, J. Rethinking Keypoint Representations: Modeling Keypoints and Poses as Objects for Multi-Person Human Pose Estimation. In Computer Vision—ECCV 2022; Avidan, S., Brostow, G., Cissé, M., Farinella, G.M., Hassner, T., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2022; Volume 13666, pp. 37–54. [Google Scholar]
- Liu, W.; Di, N. RSCS6D: Keypoint Extraction-Based 6D Pose Estimation. Appl. Sci. 2025, 15, 6729. [Google Scholar] [CrossRef]
- Zhang, Q.; Xue, C.; Qin, J.; Duan, J.; Zhou, Y. 6D Pose Estimation of Industrial Parts Based on Point Cloud Geometric Information Prediction for Robotic Grasping. Entropy 2024, 26, 1022. [Google Scholar] [CrossRef]
- Alterani, A.B.; Costanzo, M.; De Simone, M.; Federico, S.; Natale, C. Experimental Comparison of Two 6D Pose Estimation Algorithms in Robotic Fruit-Picking Tasks. Robotics 2024, 13, 127. [Google Scholar] [CrossRef]
- Govi, E.; Sapienza, D.; Toscani, S.; Cotti, I.; Franchini, G.; Bertogna, M. Addressing Challenges in Industrial Pick and Place: A Deep Learning-Based 6 Degrees-of-Freedom Pose Estimation Solution. Comput. Ind. 2024, 161, 104130. [Google Scholar] [CrossRef]
- Lu, J.; Richter, F.; Yip, M.C. Pose Estimation for Robot Manipulators via Keypoint Optimization and Sim-to-Real Transfer. IEEE Robot. Autom. Lett. 2022, 7, 4622–4629. [Google Scholar] [CrossRef]
- Höfer, T.; Shamsafar, F.; Benbarka, N.; Zell, A. Object Detection And Autoencoder-Based 6d Pose Estimation For Highly Cluttered Bin Picking. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19 September 2021; IEEE: New York, NY, USA, 2021; pp. 704–708. [Google Scholar]
- Ali, M.L.; Zhang, Z. The YOLO Framework: A Comprehensive Review of Evolution, Applications, and Benchmarks in Object Detection. Computers 2024, 13, 336. [Google Scholar] [CrossRef]
- Murat, A.A.; Kiran, M.S. A Comprehensive Review on YOLO Versions for Object Detection. Eng. Sci. Technol. Int. J. 2025, 70, 102161. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Vairavasundaram, S. YOLO-Based Object Detection Models: A Review and Its Applications. Multimed. Tools Appl. 2024, 83, 83535–83574. [Google Scholar] [CrossRef]
- Terven, J.; Córdova-Esparza, D.-M.; Romero-González, J.-A. A Comprehensive Review of YOLO Architectures in Computer Vision: From YOLOv1 to YOLOv8 and YOLO-NAS. Mach. Learn. Knowl. Extr. 2023, 5, 1680–1716. [Google Scholar] [CrossRef]
- Cong, X.; Li, S.; Chen, F.; Liu, C.; Meng, Y. A Review of YOLO Object Detection Algorithms Based on Deep Learning. Front. Comput. Intell. Syst. 2023, 4, 17–20. [Google Scholar] [CrossRef]
- Jocher, G.; Chaurasia, A.; Qiu, J. Ultralytics YOLOv8. 2023. Available online: https://github.com/topics/yolov8 (accessed on 6 October 2025).
- Jocher, G.; Qiu, J. Ultralytics YOLO11. 2024. Available online: https://github.com/topics/yolo11 (accessed on 6 October 2025).
- Tian, Y.; Ye, Q.; Doermann, D. YOLOv12: Attention-Centric Real-Time Object Detectors. arXiv 2025, arXiv:2502.12524. [Google Scholar]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 8693, pp. 740–755. ISBN 9783319106014/9783319106021. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision Meets Robotics: The KITTI Dataset. Int. J. Robot. Res. 2013, 32, 1231–1237. [Google Scholar] [CrossRef]
- Yu, F.; Chen, H.; Wang, X.; Xian, W.; Chen, Y.; Liu, F.; Madhavan, V.; Darrell, T. BDD100K: A Diverse Driving Dataset for Heterogeneous Multitask Learning. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: New York, NY, USA, 2020; pp. 2633–2642. [Google Scholar]
- Soille, P. Morphological Image Analysis; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 9783642076961. [Google Scholar]
- Suzuki, S.; Be, K. Topological Structural Analysis of Digitized Binary Images by Border Following. Comput. Vis. Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Use of the Hough Transformation to Detect Lines and Curves in Pictures. Commun. ACM 1972, 15, 11–15. [Google Scholar] [CrossRef]
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the COMPSTAT’2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2010; pp. 177–186. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hollósi, J. YOLO-Based Object and Keypoint Detection for Autonomous Traffic Cone Placement and Retrieval for Industrial Robots. Appl. Sci. 2025, 15, 10845. https://doi.org/10.3390/app151910845
Hollósi J. YOLO-Based Object and Keypoint Detection for Autonomous Traffic Cone Placement and Retrieval for Industrial Robots. Applied Sciences. 2025; 15(19):10845. https://doi.org/10.3390/app151910845
Chicago/Turabian StyleHollósi, János. 2025. "YOLO-Based Object and Keypoint Detection for Autonomous Traffic Cone Placement and Retrieval for Industrial Robots" Applied Sciences 15, no. 19: 10845. https://doi.org/10.3390/app151910845
APA StyleHollósi, J. (2025). YOLO-Based Object and Keypoint Detection for Autonomous Traffic Cone Placement and Retrieval for Industrial Robots. Applied Sciences, 15(19), 10845. https://doi.org/10.3390/app151910845




