Contract-Graph Fusion and Cross-Graph Matching for Smart-Contract Vulnerability Detection
Abstract
1. Introduction
2. Related Works
3. Proposed Approach
3.1. Overview
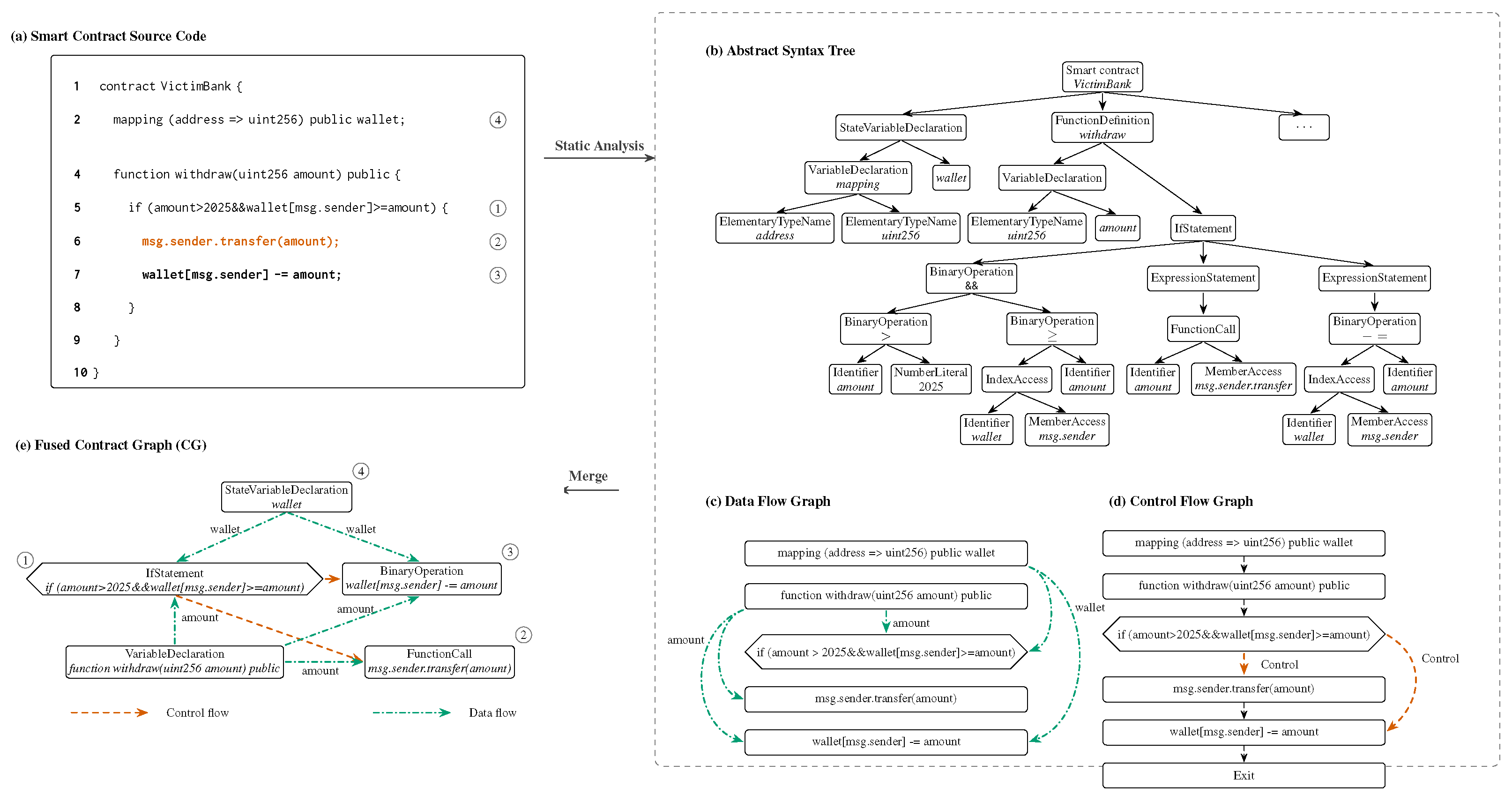
3.2. Contract-Graph Construction
| Algorithm 1 BuildContractGraph: extraction and fusion |
|
3.3. Pre-Training Phase
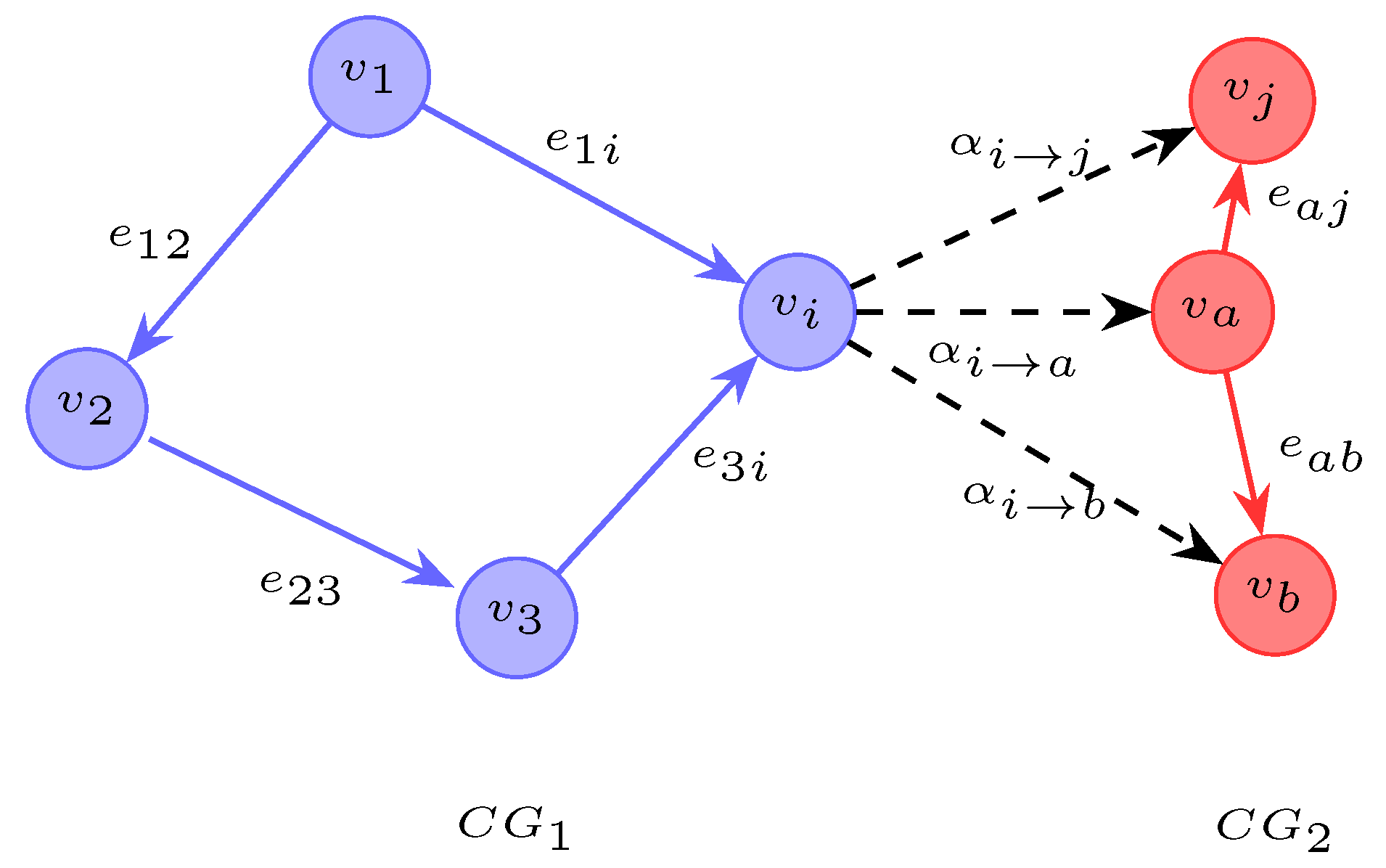
3.4. Cross-Graph Similarity with a Contract-Graph Matcher
3.5. Training and Detection
| Algorithm 2 TrainAndDetect: margin-based training and library-guided inference |
|
4. Empirical Evaluation
4.1. Datasets
4.2. Baselines and Setup
- (1)
- Static analysis and graphs. ASTs are extracted with solc-typed-ast [32]. CFG/DFG and def-use metadata come from Slither [31]. These artifacts are merged into contract-level graphs (Section 3.2) using NetworkX [34].
- (2)
- Encoder and matcher. GraphCodeBERT [33] is used (12 layers, hidden size 768, 12 heads, Adam). The contract-graph matcher uses embedded size 100, four hidden layers, learning rate , and test time threshold . Training occurs for 85 iterations (Section 3.4).
- (3)
- Baselines. For transparency and comparability, the baselines are organized into two families under a uniform evaluation interface-rule-based: sFuzz [35], SmartCheck [36], Osiris [37], Oyente [38], and Mythril [39]; and learning-based: LineVul [40], GCN [41], TMP [42], AME [43], Peculiar [44], CBGRU [45], and CGE [46]. All experiments follow the configurations specified in the original works.
- (4)
- Splits and protocol. A 60/20/20 train/validation/test split is used. The thresholds are chosen during validation and fixed during testing. Each experiment uses five random seeds; the means are reported.
- (5)
- Metrics. Precision, recall, and follow the standard definitions, which are not repeated here. For completeness, and Fowlkes–Mallows (FM) are reported as deterministic functions of .
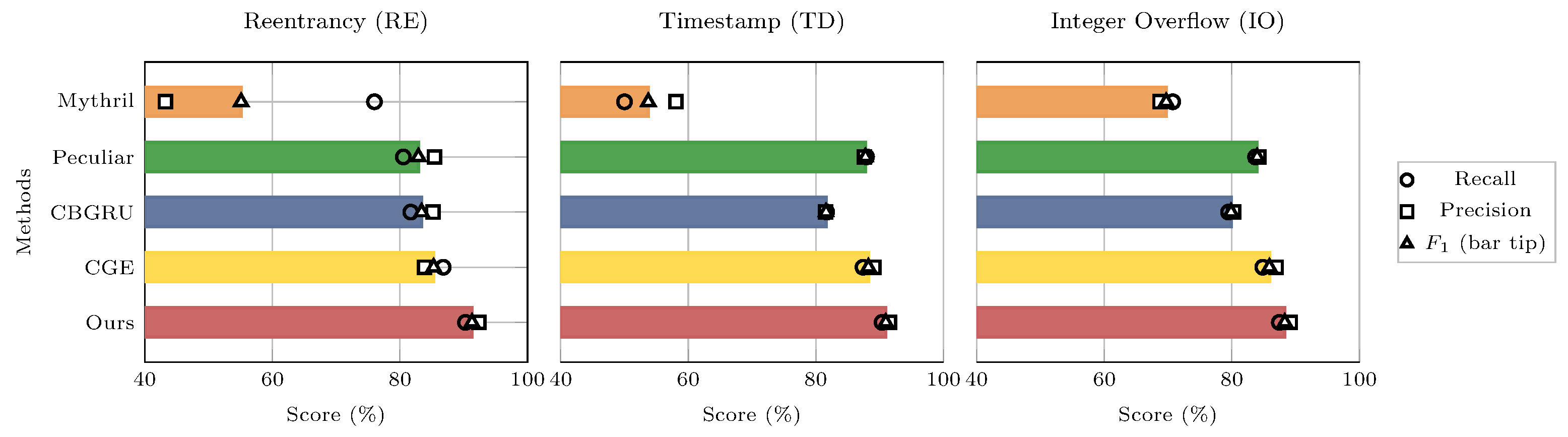
4.3. End-to-End Results
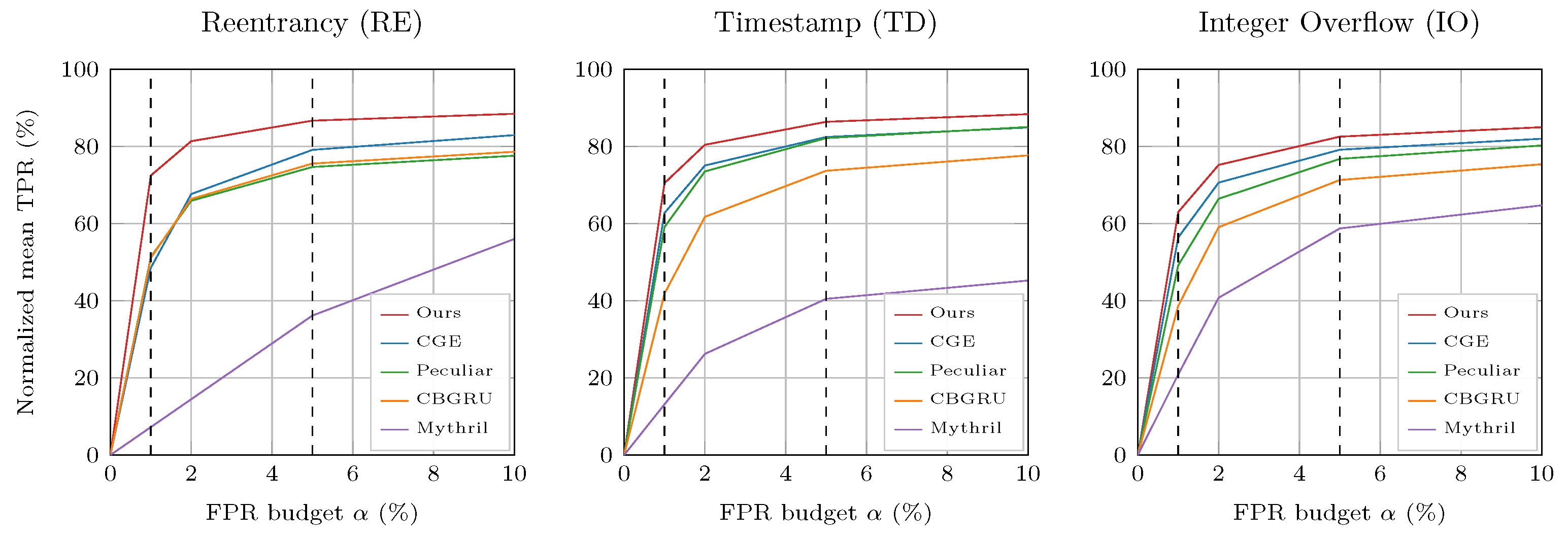
4.4. Low-FPR Sensitivity
4.5. Visual Diagnostics
4.6. Fusion and Ablations
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ivanov, N.; Li, C.; Yan, Q.; Sun, Z.; Cao, Z.; Luo, X. Security threat mitigation for smart contracts: A comprehensive survey. ACM Comput. Surv. 2023, 55, 326. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lin, C.C.; Liao, S.W. Unveiling vulnerabilities in DAO: A comprehensive security analysis and protective framework. In Proceedings of the 2023 IEEE International Conference on Blockchain (Blockchain 2023), Danzhou, China, 17–21 December 2023; pp. 151–158. [Google Scholar]
- Wu, H.; Yao, Q.; Liu, Z.; Huang, B.; Zhuang, Y.; Tang, H.; Liu, E. Blockchain for finance: A survey. IET Blockchain 2024, 4, 101–123. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Y.; Wu, J.; Li, Y.; Liu, X.; Zhou, J.; Zhang, Y. Survey of vulnerability detection and defense for Ethereum smart contracts. IEEE Trans. Netw. Sci. Eng. 2023, 10, 2419–2437. [Google Scholar]
- Qiu, F.; Liu, Z.; Hu, X.; Xia, X.; Chen, G.; Wang, X. Vulnerability Detection via Multiple-Graph-Based Code Representation. IEEE Trans. Softw. Eng. 2024, 50, 2178–2199. [Google Scholar] [CrossRef]
- Ding, H.; Liu, Y.; Piao, X.; Song, H.; Ji, Z. SmartGuard: An LLM-enhanced framework for smart contract vulnerability detection. Expert Syst. Appl. 2025, 269, 126479. [Google Scholar] [CrossRef]
- Luo, F.; Luo, R.; Chen, T.; Qiao, A.; He, Z.; Song, S.; Jiang, Y.; Li, S. SCVHunter: Smart Contract Vulnerability Detection Based on Heterogeneous Graph Attention Network. In Proceedings of the 2024 IEEE/ACM 46th International Conference on Software Engineering (ICSE 2024), Lisbon, Portugal, 14–20 April 2024; pp. 170:1–170:13. [Google Scholar]
- Chen, D.; Feng, L.; Fan, Y.; Shang, S.; Wei, Z. Smart contract vulnerability detection based on semantic graph and residual graph convolutional networks with edge attention. J. Syst. Softw. 2023, 202, 111705. [Google Scholar] [CrossRef]
- Wang, Y.; Le, H.; Gotmare, A.D.; Bui, N.D.; Li, J.; Hoi, S.C. CodeT5+: Open Code Large Language Models for Code Understanding and Generation. In Proceedings of the 2023 Association for Computational Linguistics Conference on Empirical Methods in Natural Language Processing (EMNLP 2023), Singapore, 6–10 December 2023; pp. 1069–1088. [Google Scholar]
- Durieux, T.; Ferreira, J.F.; Abreu, R.; Cruz, P. Empirical Review of Automated Analysis Tools on 47,587 Ethereum Smart Contracts. In Proceedings of the ACM/IEEE 42nd International Conference on Software Engineering, Seoul, Republic of Korea, 27 June–19 July 2020; pp. 530–541. [Google Scholar]
- Xiang, J.; Fu, L.; Ye, T.; Liu, P.; Le, H.; Zhu, L.; Wang, W. LuaTaint: A Static Analysis System for Web Configuration Interface Vulnerability of Internet of Things Device. IEEE Internet Things J. 2024, 12, 5970–5984. [Google Scholar] [CrossRef]
- Li, Y.; Ma, L.; Shen, L.; Lv, J.; Zhang, P. Open source software security vulnerability detection based on dynamic behavior features. PLoS ONE 2019, 14, E0221530. [Google Scholar] [CrossRef]
- Cai, J.; Li, B.; Zhang, J.; Sun, X.; Chen, B. Combine sliced joint graph with graph neural networks for smart contract vulnerability detection. J. Syst. Softw. 2023, 195, 111550. [Google Scholar] [CrossRef]
- Zhen, Z.; Zhao, X.; Zhang, J.; Wang, Y.; Chen, H. DA-GNN: A smart contract vulnerability detection method based on Dual Attention Graph Neural Network. Comput. Netw. 2024, 242, 110238. [Google Scholar] [CrossRef]
- Cao, S.; Sun, X.; Wu, X.; Lo, D.; Bo, L.; Li, B.; Liu, W. Coca: Improving and Explaining Graph Neural Network-Based Vulnerability Detection Systems. In Proceedings of the 2024 IEEE/ACM International Conference on Software Engineering (ICSE 2024), Lisbon, Portugal, 14–20 April 2024; pp. 155:1–155:13. [Google Scholar]
- Hussain, S.; Nadeem, M.; Baber, J.; Hamdi, M.; Rajab, A.; Al Reshan, M.S.; Shaikh, A. Vulnerability detection in Java source code using a quantum convolutional neural network with self-attentive pooling, deep sequence, and graph-based hybrid feature extraction. Sci. Rep. 2024, 14, 7406. [Google Scholar]
- Arp, D.; Quiring, E.; Pendlebury, F.; Warnecke, A.; Pierazzi, F.; Wressnegger, C.; Cavallaro, L.; Rieck, K. Pitfalls in Machine Learning for Computer Security. Commun. ACM 2024, 67, 104–112. [Google Scholar] [CrossRef]
- Guo, Y.; Bettaieb, S.; Casino, F. A comprehensive analysis on software vulnerability detection datasets: Trends, challenges, and road ahead. Int. J. Inf. Secur. 2024, 23, 3311–3327. [Google Scholar] [CrossRef]
- Wang, H.; Tang, Z.; Tan, S.H.; Wang, J.; Liu, Y.; Fang, H.; Xia, C.; Wang, Z. Combining structured static code information and dynamic symbolic traces for software vulnerability prediction. In Proceedings of the 46th International Conference on Software Engineering (ICSE 2024), Lisbon, Portugal, 14–20 April 2024. [Google Scholar]
- Jiao, T.; Xu, Z.; Qi, M.; Wen, S.; Xiang, Y.; Nan, G. A survey of Ethereum smart contract security: Attacks and detection. Distrib. Ledger Technol. Res. Pract. 2024, 3, 1–28. [Google Scholar] [CrossRef]
- Chu, H.; Zhang, P.; Dong, H.; Xiao, Y.; Ji, S.; Li, W. A survey on smart contract vulnerabilities: Data sources, detection and repair. Inf. Softw. Technol. 2023, 159, 107221. [Google Scholar] [CrossRef]
- Wei, Z.; Sun, J.; Zhang, Z.; Zhang, X.; Yang, X.; Zhu, L. Survey on quality assurance of smart contracts. ACM Comput. Surv. 2024, 57, 32. [Google Scholar] [CrossRef]
- Vidal, F.R.; Ivaki, N.; Laranjeiro, N. Vulnerability detection techniques for smart contracts: A systematic literature review. J. Syst. Softw. 2024, 217, 112160. [Google Scholar] [CrossRef]
- Wu, G.; Wang, H.; Lai, X.; Wang, M.; He, D.; Choo, K.-K.R. A comprehensive survey of smart contract security: State of the art and research directions. J. Netw. Comput. Appl. 2024, 226, 103882. [Google Scholar] [CrossRef]
- Sendner, C.; Petzi, L.; Stang, J.; Dmitrienko, A. Smarter Contracts: Detecting vulnerabilities in smart contracts with deep transfer learning (ESCORT). In Proceedings of the Network and Distributed System Security Symposium (NDSS 2023), San Diego, CA, USA, 27 February–3 March 2023; Internet Society: Reston, VA, USA, 2023; pp. 1–18. [Google Scholar]
- Ruaro, N.; Gritti, F.; McLaughlin, R.; Grishchenko, I.; Kruegel, C.; Vigna, G. Not your type! Detecting storage collision vulnerabilities in Ethereum smart contracts. In Proceedings of the Network and Distributed System Security Symposium (NDSS 2024), San Diego, CA, USA, 26 February–1 March 2024; Internet Society: Reston, VA, USA, 2024; pp. 1–16. [Google Scholar]
- Ferreira, J.F.; Durieux, T.; Maranhao, R. SmartBugs Wild Dataset: 47,398 Smart Contracts from Ethereum. Dataset. 2020. Available online: https://github.com/smartbugs/smartbugs-wild (accessed on 26 August 2025).
- Huang, Q.; Zeng, Z.; Shang, Y. An empirical study of integer overflow detection and false positive analysis in smart contracts. In Proceedings of the 8th ACM International Conference on Big Data and Internet of Things (BDIOT 2024), Macau, China, 14–16 September 2024; pp. 247–251. [Google Scholar]
- Ma, C.; Liu, S.; Xu, G. HGAT: Smart contract vulnerability detection method based on hierarchical graph attention network. J. Cloud Comput. 2023, 12, 93. [Google Scholar] [CrossRef]
- Xu, J.; Wang, T.; Lv, M.; Chen, T.; Zhu, T.; Ji, B. MVD-HG: Multigranularity smart contract vulnerability detection method based on heterogeneous graphs. Cybersecurity 2024, 7, 55. [Google Scholar] [CrossRef]
- Feist, J.; Grieco, G.; Groce, A. Slither: A static analysis framework for smart contracts. In Proceedings of the 2019 IEEE/ACM 2nd International Workshop on Emerging Trends in Software Engineering for Blockchain (WETSEB), Montreal, QC, Canada, 27 May 2019; pp. 8–15. [Google Scholar]
- Consensys. solc-typed-ast: A Typed Solidity AST Library, Version v18.1.4. GitHub Repository. 2024. Available online: https://github.com/ConsenSys/solc-typed-ast (accessed on 26 April 2024).
- Guo, H.; Yu, Y.; Li, X. ContractFuzzer: Fuzzing smart contracts for vulnerability detection. In Proceedings of the 2020 IEEE International Conference on Software Testing, Verification and Validation (ICST), Porto, Portugal, 24–28 October 2020; pp. 191–201. [Google Scholar]
- Hasan, M.; Kumar, N.; Majeed, A.; Ahmad, A.; Mukhtar, S. Protein–Protein Interaction Network Analysis Using NetworkX. In Protein–Protein Interactions: Methods and Protocols; Springer: Berlin/Heidelberg, Germany, 2023; pp. 457–467. [Google Scholar]
- Nguyen, T.D.; Pham, L.H.; Sun, J.; Lin, Y.; Minh, Q.T. sFuzz: An efficient adaptive fuzzer for Solidity smart contracts. In Proceedings of the 42nd ACM/IEEE International Conference on Software Engineering (ICSE 2020), Seoul, Republic of Korea, 27 June–19 July 2020; pp. 778–788. [Google Scholar]
- Tikhomirov, S.; Voskresenskaya, E.; Ivanitskiy, I.; Takhaviev, R.; Marchenko, E.; Alexandrov, Y. SmartCheck: Static analysis of Ethereum smart contracts. In Proceedings of the 1st International Workshop on Emerging Trends in Software Engineering for Blockchain (WETSEB), Goteburg, Sweden, 25 May 2018; pp. 9–16. [Google Scholar]
- Torres, C.F.; Schütte, J.; State, R. Osiris: Hunting for Integer Bugs in Ethereum Smart Contracts. In Proceedings of the 2018 Annual Computer Security Applications Conference (ACSAC 2018), San Juan, PR, USA, 3–7 December 2018; pp. 664–676. [Google Scholar]
- Luu, L.; Chu, D.-H.; Olickel, H.; Saxena, P.; Hobor, A. Making smart contracts smarter. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS), Vienna, Austria, 24–28 October 2016; pp. 254–269. [Google Scholar]
- Chee, C.Y.M.; Pal, S.; Pan, L.; Doss, R. An analysis of important factors affecting the success of blockchain smart contract security vulnerability scanning tools. In Proceedings of the 5th ACM International Symposium on Blockchain and Secure Critical Infrastructure (BSCI 2023), Melbourne, Australia, 10–14 July 2023; pp. 105–113. [Google Scholar]
- Fu, M.; Tantithamthavorn, C. LineVul: A transformer-based line-level vulnerability prediction. In Proceedings of the 19th International Conference on Mining Software Repositories (MSR 2022), Pittsburgh, PA, USA, 23–24 May 2022; pp. 608–620. [Google Scholar]
- Zhang, H.; Lu, G.; Zhan, M.; Zhang, B. Semi-Supervised Classification of Graph Convolutional Networks with Laplacian Rank Constraints. Neural Process. Lett. 2022, 54, 2645–2656. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, Z.; Qian, P.; Liu, Q.; Wang, X.; He, Q. Smart contract vulnerability detection using graph neural networks. In Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI 2020), Virtual, 11–17 July 2020; pp. 3283–3290. [Google Scholar]
- Liu, Z.; Xu, Q.; Chen, H.; Zhang, W. Hybrid analysis of integer overflow vulnerabilities in Ethereum smart contracts. Future Gener. Comput. Syst. 2021, 119, 91–100. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, Z.; Wang, S.; Lei, Y.; Lin, B.; Qin, Y.; Zhang, H.; Mao, X. Peculiar: Smart contract vulnerability detection based on crucial data flow graph and pre-training techniques. In Proceedings of the 32nd IEEE International Symposium on Software Reliability Engineering (ISSRE 2021), Wuhan, China, 25–28 October 2021; pp. 378–389. [Google Scholar]
- Zhang, R.; Wang, P.; Zhao, L. Machine learning-based detection of reentrancy vulnerabilities in smart contracts. Future Gener. Comput. Syst. 2022, 127, 362–373. [Google Scholar]
- He, L.; Zhao, X.; Wang, Y. GraphSA: Smart Contract Vulnerability Detection Combining Graph Neural Networks and Static Analysis. In Proceedings of the 26th European Conference on Artificial Intelligence ECAI 2023, Krakow, Poland, 30 September–4 October 2023; Frontiers in Artificial Intelligence and Applications. IOS Press: Amsterdam, The Netherlands, 2023; pp. 1026–1036. [Google Scholar]

| Methods | Reentrancy | Timestamp | Integer Overflow | Macro Avg | /FM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RE | TD | IO | |||||||||||||
| sFuzz | 13.99 | 10.71 | 12.13 | 28.05 | 24.73 | 26.29 | 25.66 | 27.70 | 26.64 | 22.57 | 21.05 | 21.69 | 13.18/12.24 | 27.32/26.34 | 26.04/26.66 |
| SmartCheck | 17.24 | 46.86 | 25.21 | 78.81 | 47.65 | 59.39 | 69.79 | 41.35 | 51.93 | 55.28 | 45.29 | 45.51 | 19.73/28.42 | 69.69/61.28 | 61.35/53.72 |
| Osiris | 62.82 | 39.91 | 48.81 | 53.65 | 59.85 | 56.58 | 61.33 | 41.79 | 49.71 | 59.27 | 47.18 | 51.70 | 56.35/50.07 | 54.79/56.67 | 56.09/50.63 |
| Oyente | 63.20 | 45.08 | 52.62 | 57.01 | 59.17 | 58.07 | 58.13 | 58.53 | 58.33 | 69.45 | 54.26 | 56.34 | 58.50/53.38 | 57.43/58.08 | 58.21/58.33 |
| Mythril | 76.00 | 43.22 | 55.10 | 50.00 | 58.05 | 53.73 | 70.73 | 68.73 | 69.72 | 65.58 | 56.67 | 59.52 | 65.99/57.31 | 51.43/53.87 | 70.32/69.72 |
| LineVul | 72.84 | 83.57 | 77.84 | 65.80 | 88.90 | 75.63 | 73.42 | 75.45 | 74.42 | 70.69 | 82.64 | 75.96 | 74.76/78.02 | 69.41/76.48 | 73.82/74.43 |
| GCN | 74.37 | 73.70 | 74.03 | 79.25 | 74.03 | 76.55 | 71.02 | 68.61 | 69.79 | 74.88 | 72.11 | 73.46 | 74.24/74.03 | 78.15/76.60 | 70.52/69.80 |
| TMP | 76.16 | 76.26 | 76.21 | 74.52 | 78.36 | 76.39 | 68.58 | 71.62 | 70.07 | 73.09 | 75.41 | 74.22 | 76.18/76.21 | 75.26/76.42 | 69.17/70.08 |
| AME | 79.71 | 81.31 | 80.50 | 82.24 | 80.98 | 81.61 | 69.48 | 71.75 | 70.60 | 77.14 | 78.01 | 77.57 | 80.02/80.51 | 81.98/81.61 | 69.92/70.61 |
| Peculiar | 80.53 | 85.39 | 82.89 | 87.94 | 87.60 | 87.77 | 83.72 | 84.23 | 83.97 | 84.06 | 85.74 | 84.88 | 81.46/82.92 | 87.87/87.77 | 83.82/83.97 |
| CBGRU | 81.70 | 85.16 | 83.39 | 81.68 | 81.51 | 81.59 | 79.48 | 80.29 | 79.88 | 80.95 | 82.32 | 81.62 | 82.37/83.41 | 81.65/81.59 | 79.64/79.88 |
| CGE | 86.78 | 83.83 | 85.28 | 87.39 | 89.09 | 88.23 | 84.86 | 86.95 | 85.89 | 86.34 | 86.62 | 86.47 | 86.17/85.29 | 87.72/88.24 | 85.27/85.90 |
| Proposed | 90.27 | 92.34 | 91.29 | 90.38 | 91.54 | 90.95 | 87.45 | 89.17 | 88.30 | 89.37 | 91.02 | 90.18 | 90.68/91.30 | 90.61/90.96 | 87.79/88.31 |
| Methods | Reentrancy | Timestamp | Integer Overflow | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | |
| AST only | 82.19 | 86.23 | 84.16 | 82.47 | 85.68 | 84.04 | 80.34 | 83.75 | 82.00 |
| CFG only | 83.45 | 86.78 | 85.08 | 83.19 | 85.27 | 84.22 | 81.27 | 83.53 | 82.39 |
| DFG only | 84.56 | 88.34 | 86.41 | 84.34 | 87.12 | 85.71 | 82.14 | 85.22 | 83.65 |
| Proposed (DFG only) | 84.56 | 88.34 | 86.41 | 84.34 | 87.12 | 85.71 | 82.14 | 85.22 | 83.65 |
| Proposed (no pre-trained encoder) | 80.58 | 85.12 | 82.78 | 81.22 | 85.89 | 83.49 | 79.34 | 83.62 | 81.42 |
| Proposed (no matcher) | 82.19 | 83.45 | 82.82 | 82.67 | 84.23 | 83.44 | 81.48 | 82.27 | 81.87 |
| Proposed (full) | 90.27 | 92.34 | 91.29 | 90.38 | 91.54 | 90.95 | 87.45 | 89.17 | 88.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, X.; Tan, Y.; Song, J.; Yang, F. Contract-Graph Fusion and Cross-Graph Matching for Smart-Contract Vulnerability Detection. Appl. Sci. 2025, 15, 10844. https://doi.org/10.3390/app151910844
Liang X, Tan Y, Song J, Yang F. Contract-Graph Fusion and Cross-Graph Matching for Smart-Contract Vulnerability Detection. Applied Sciences. 2025; 15(19):10844. https://doi.org/10.3390/app151910844
Chicago/Turabian StyleLiang, Xue, Yao Tan, Jun Song, and Fan Yang. 2025. "Contract-Graph Fusion and Cross-Graph Matching for Smart-Contract Vulnerability Detection" Applied Sciences 15, no. 19: 10844. https://doi.org/10.3390/app151910844
APA StyleLiang, X., Tan, Y., Song, J., & Yang, F. (2025). Contract-Graph Fusion and Cross-Graph Matching for Smart-Contract Vulnerability Detection. Applied Sciences, 15(19), 10844. https://doi.org/10.3390/app151910844






