Exploring Patterns in Quality Alerts via Random Forest and Multiple Correspondence Analysis

Featured Application

This study has practical applications in the monitoring and continuous improvement of quality management systems in manufacturing environments. Revealing patterns among product quality alerts through machine learning and multivariate analysis techniques leads to a deeper understanding of the origin and frequency of quality issues across machines, processes, and plant sections. The findings can guide preventive actions, efficient resource allocation, and targeted maintenance strategies, ultimately enhancing product consistency.

Abstract

This study presents a multivariate and machine learning-based approach to analyze quality alerts in an industrial manufacturing context. Based on data from recorded quality alerts, this research integrates exploratory data analysis, Multiple Correspondence Analysis (MCA), and Random Forest modeling to uncover hidden patterns among key categorical variables, including process, section, and priority. The analysis highlights structural associations and frequency distributions that differentiate alert behavior across various production units. Visualization tools such as heatmaps and bar charts are employed to provide actionable insights into the operational environment. The study has practical applications in the monitoring and continuous improvement of quality management systems in manufacturing environments. Identifying patterns in quality alerts through multivariate and machine learning techniques leads to a deeper understanding of the origin and frequency of quality issues across machines, processes, and plant sections. The findings can support preventive actions, efficient resource allocation, and targeted maintenance strategies, ultimately enhancing product consistency.

1. Introduction

In industrial manufacturing environments, ensuring consistent product quality requires timely identification and understanding of deviations in processes and systems. Quality alerts, which are records of nonconformities or anomalies detected during production, serve as key indicators of operational performance and process health. The increasing availability of production data has enabled the application of data-driven methods to extract actionable insights from such records. In this context, multivariate statistical techniques and machine learning approaches have proven effective for analyzing categorical variables and uncovering latent patterns that are not readily visible through traditional monitoring tools [1,2]. These methods facilitate deeper diagnostics of quality issues, supporting continuous improvement strategies within quality management systems [3]. Despite their potential, the integration of exploratory and predictive modeling in quality alert systems remains underexplored in many manufacturing sectors.

The concept of quality has evolved throughout human industrial activity. Mass production has enabled the promotion of standardization through process optimization, focusing on user consumption. However, the notion of quality also carries an economic perspective, often viewed in terms of cost and price. The implementation of quality management represents a challenge for organizations as it requires maintaining a workplace culture oriented toward continuous improvement. In this context, the product, the process, the user, and the concept of value are all essential to achieving organizational excellence [4,5]. Quality within organizations is a dynamic and multidimensional concept. It is not solely defined by technical criteria but also incorporates the perceptions of operational staff, which are key to determining its effectiveness [6,7]. Company indicators are essential tools for evaluating and managing quality. They allow for the quantitative measurement of performance across activities, support trend analysis, and help identify critical areas within processes. Moreover, they facilitate comparisons over time to evaluate the evolution of product quality [4]. The concept of performance indicators has roots in the philosophy of total quality, a strategic approach developed in the United States that reached full maturity through its application in Japan. The Japanese adaptation refined its implementation and emphasized the role of metrics in strategic decision-making and organizational sustainability [8]. The foundation of a quality management system rests on three pillars: planning, control, and improvement. Planning focuses on problem-solving through structured use of information; control involves performance assessment and corrective action; and improvement addresses root cause analysis and sustainable change [6,7,9]. In this framework, quality indicators are key tools to evaluate internal performance, ensure compliance, identify improvement areas, and enhance competitiveness [10]. Evaluating the quality process supports the development of corrective strategies, strengthens organizational learning, and guides responses to deviations from objectives [11,12]. Quality alerts, as internal notifications of product issues, allow organizations to reduce waste, enhance compliance, and support timely interventions [13,14].

In recent years, machine learning has emerged as a powerful tool for identifying patterns, classifying complex data, and supporting decision-making in industrial environments. Its ability to handle high-dimensional, heterogeneous datasets makes it particularly valuable for quality control systems that require predictive insights and adaptive responses. When applied appropriately, machine learning enables a shift from reactive to proactive quality management [12,15,16], enhancing operational efficiency and reducing variability across manufacturing processes.

To address these challenges, this study adopts a combined exploratory and predictive framework based on multivariate data analysis. Multiple Correspondence Analysis (MCA) enables the visualization of associations between key categorical variables, such as production processes, machine assignments, quality priorities, and organizational sections, offering insights into systemic relationships [17,18,19]. In parallel, machine learning techniques allow for the evaluation of variable importance and pattern extraction, contributing to a data-driven understanding of quality dynamics. Unlike traditional regression models that may be limited by assumptions of linearity and distribution, these approaches are well-suited to the complex, high-dimensional, and often categorical nature of industrial data [20]. Furthermore, visual tools such as heatmaps and bar charts enhance interpretability and communication with domain experts, bridging the gap between technical analysis and operational decision-making.

A hybrid methodology was employed, combining classical multivariate statistics with machine learning-based analysis to uncover structural patterns in industrial quality alerts. Machine learning techniques have become increasingly relevant in manufacturing research due to their capacity to manage high-dimensional data and reveal non-obvious relationships among variables [21,22]. These capabilities are especially beneficial for evaluating operational performance, classifying alerts, and identifying key process-related factors. In this context, the workflow integrated data preprocessing, visualization (bar plots and heatmaps), dimensionality reduction using Multiple Correspondence Analysis (MCA), and supervised learning models for variable selection and importance ranking.

This study seeks to analyze and model patterns of quality alerts within an industrial manufacturing setting through a multivariate, data-driven approach. The specific objectives are (i) to visualize the frequency and distribution of alerts and cases across production-related dimensions and to evaluate the relevance of key variables in understanding the intensity of alerts; (ii) to uncover structural associations among categorical variables linked to quality incidents; and (iii) to identify the most influential predictors of alert frequency, thereby enabling data-informed prioritization and supporting the implementation of early warning mechanisms in quality management systems.

The proposed methodology is applied to real-world operational data obtained from quality monitoring systems, encompassing both alert records and their corresponding case reports. The main categorical variables considered are process, section, and priority. In this context, process refers to the various stages or operations within the manufacturing workflow, particularly those related to metalworking activities. Section designates the specific areas of the production plant, such as assembly, delivery, or rolling, where these operations take place. Priority reflects the urgency or severity assigned to each quality alert, serving as a proxy for the potential impact on production continuity and product integrity.

2. Methods

The methodological framework adopted in this study integrates Multiple Correspondence Analysis (MCA) with Random Forest (RF) modeling to evaluate predictive relevance and validate variable importance. This combined approach offers both exploratory insight and predictive robustness and can be readily adapted to datasets from other companies or sectors that include categorical indicators.

2.1. Preliminaries

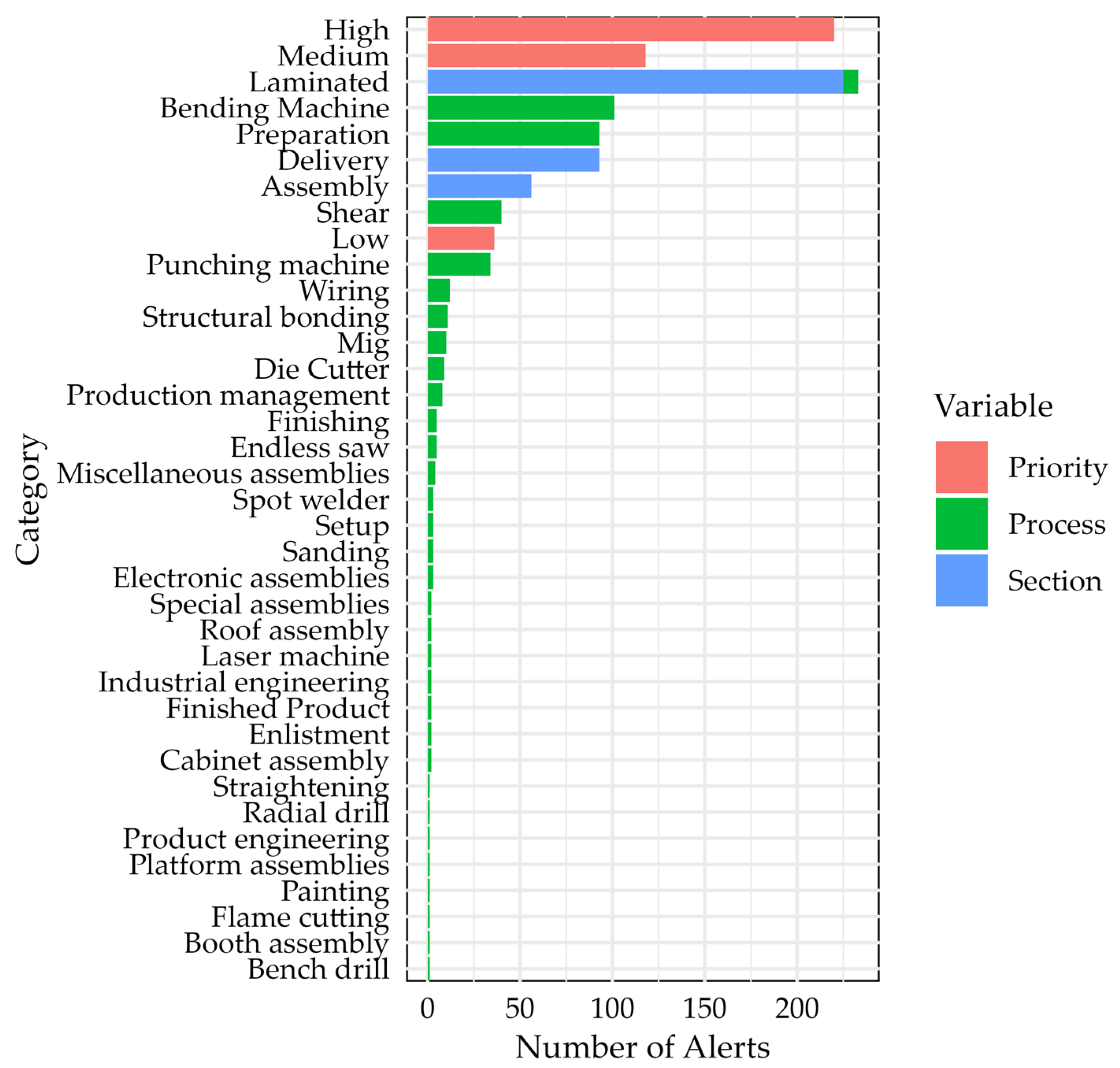
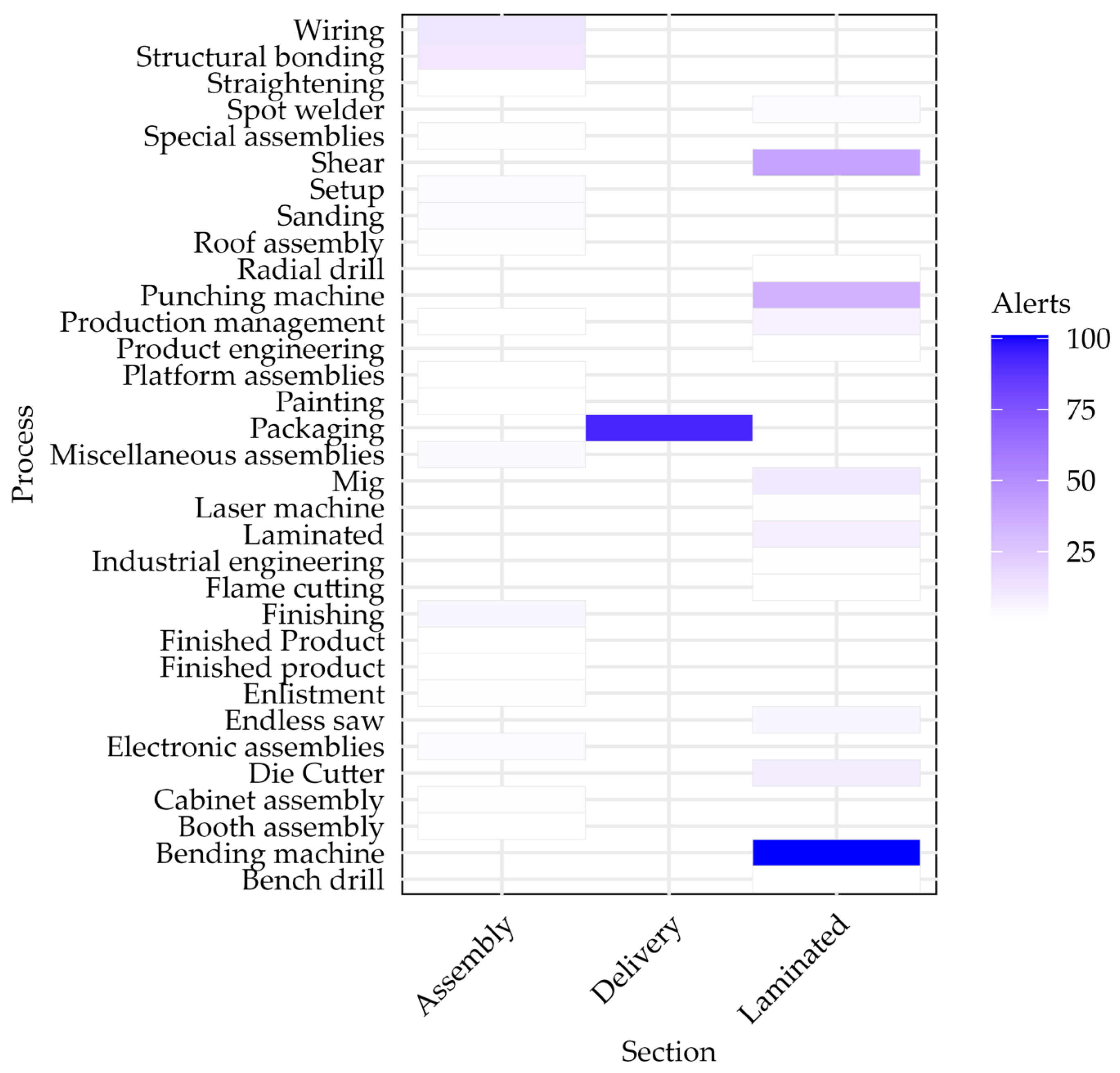
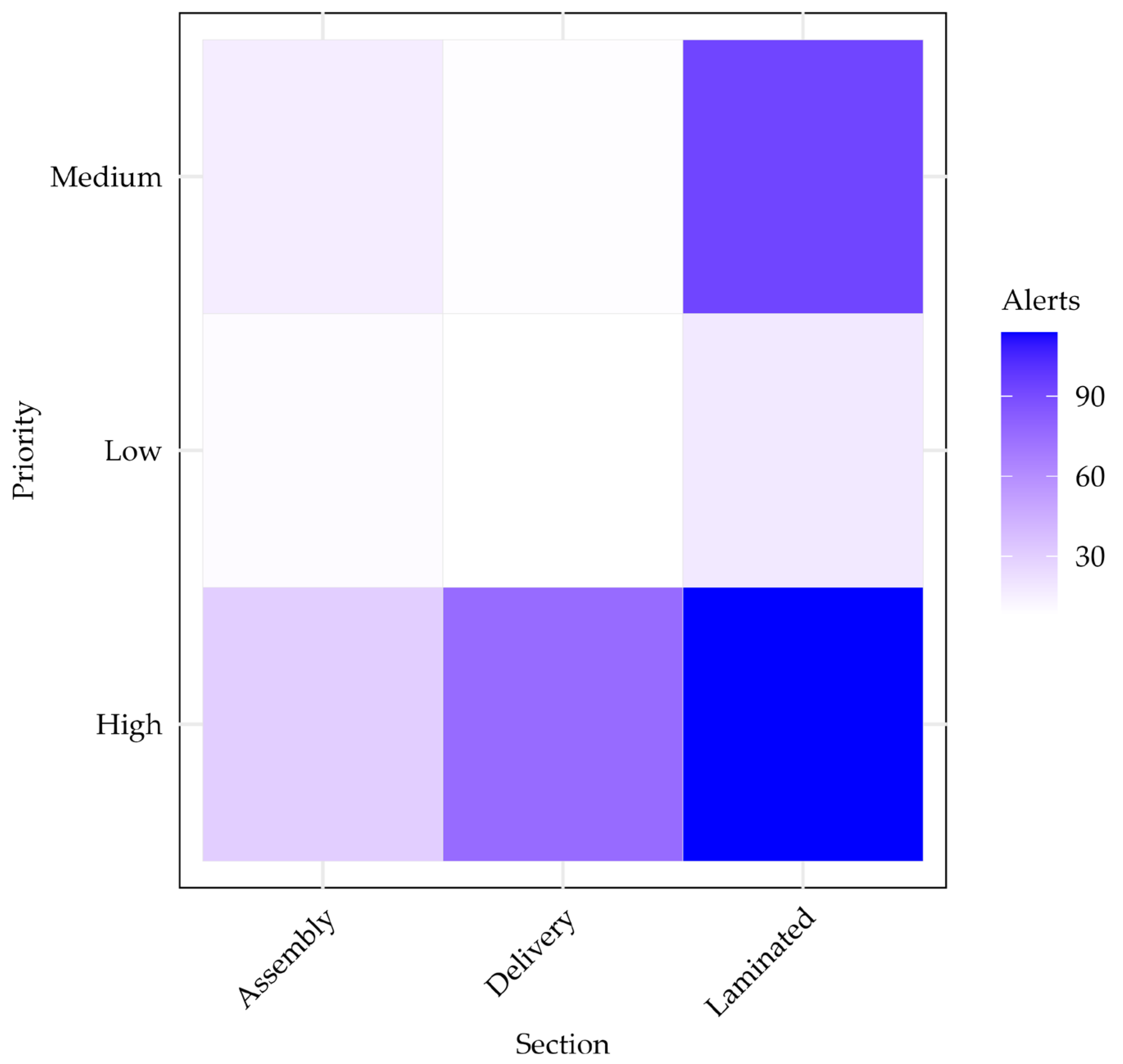
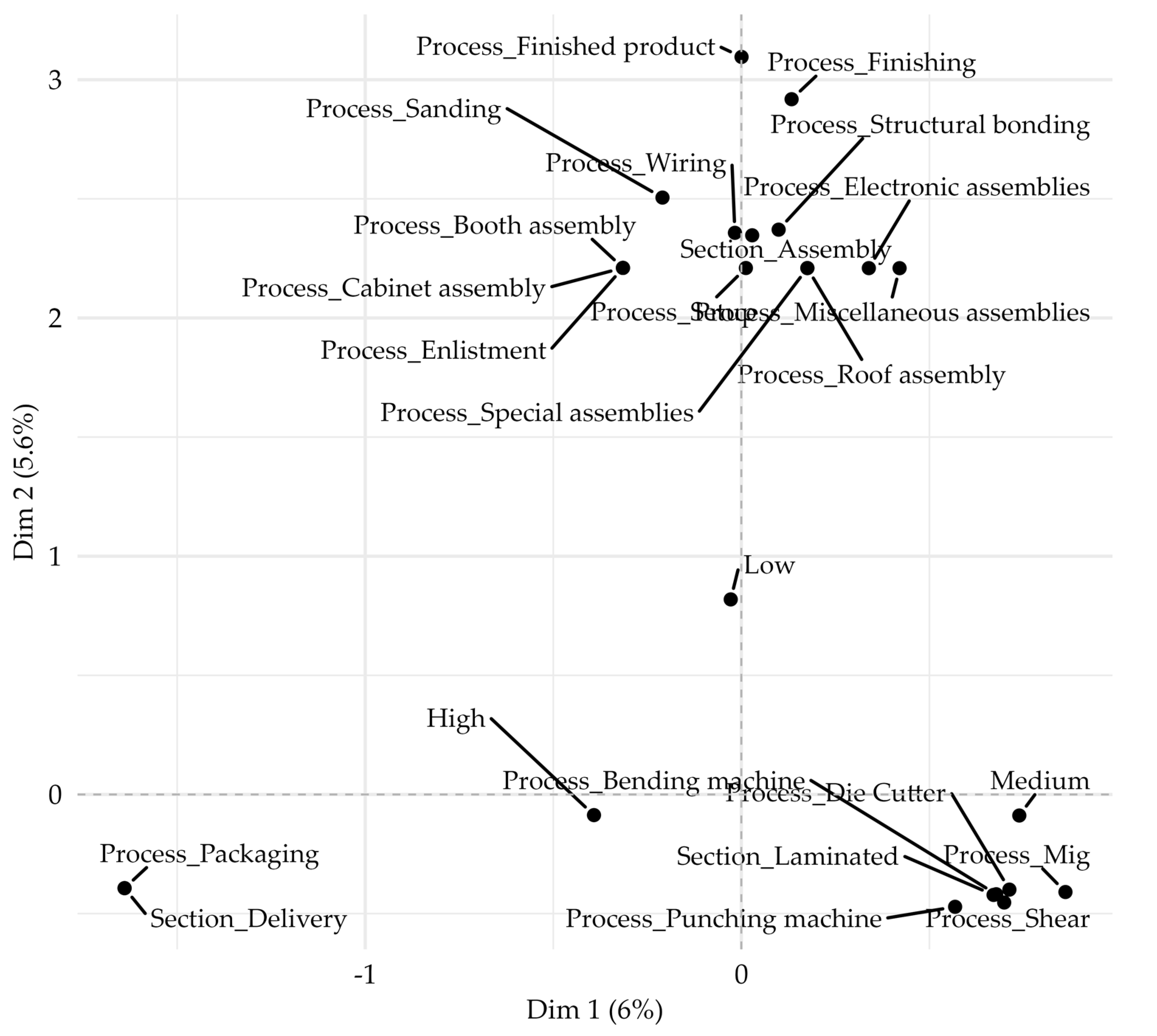
The Preliminaries Subsection lays the groundwork for this study by explaining the data structure, describing the core elements of MCA and Random Forest, and illustrating them with examples. It also connects the manufacturing context to the analytical framework through a conceptual diagram.

2.1.1. Conceptual Framework of the Production Line and Quality Notification Workflow

The data used in this study directly reflect manufacturing issues managed through the quality notification system. Figure 1 presents a conceptual diagram of the production line and the workflow of quality notifications.

These problems include the detection of anomalies in parts during production, such as representative defects, affected batches, and incidents tied to specific machines or critical production stages. The workflow described in the methodology—from anomaly detection by the supervisor, formal reporting by the quality engineer, review and registration in the Information System (IS), to follow-up and closure—ensures that each deviation is documented and categorized. In this way, notifications serve not only as a control mechanism but also as a structured input that enables analysis of recurrent deviations, prioritization of critical alerts, and a direct connection between the analytical results and industrial process management.

The diagram shows the main operational stages (cutting, welding, assembly, painting, and packaging), the points where alerts may arise, and the subsequent flow of notification, review, and closure in the information system. This representation connects the industrial context with the analytical framework, highlighting how raw production events are transformed into categorical variables (process, section, and priority) for statistical modeling.

2.1.2. MCA and Random Forest: Mathematical Foundations and Pseudocode

Multiple Correspondence Analysis (MCA) is an extension of Simple Correspondence Analysis (SCA) for more than two categorical variables. Its goal is to graphically represent the relationships between categories and observations in a low-dimensional space, preserving as much inertia as possible (variance in categorical data). The outmost basic concepts are as follows [18,23].

Let us suppose we have $n$ observations and J categorial variables with a total of m categories that are codified in a complete disjunctive matrix X of size n × m, with “ones” in the observed category and “zeros” in the rest of the entries.

• Frequency calculation. Let X be the complete disjunctive matrix of size n × m, where n is the number of observations and m is the number of categories. We define P as the relative frequency matrix. It holds that

  $$P={\displaystyle \frac{1}{n}}X,$$

  (1)
• Row and column profiles. Now, it is possible to obtain profiles of rows, $r$, and profiles of columns, $c$, as follows: $r_i={\sum }_j{P}_{ij}$ and $c_j={\sum }_i{P}_{ij}$. These $r_i$ and $c_j$ values will then be used as weights to centralize and normalize ${\chi }^2$ distances.
• Centering and scaling. Let r and c be the row and column profile vectors, respectively. Let $D_r$ be the diagonal matrix built from r, and let $D_c$ be the diagonal matrix built from c. Then, the standardized matrix Z is given by

  $$Z={D_r}^{-1/2}\left(P-r{c}^T\right){D_c}^{-1/2},$$

  (2)
• Singular Value Decomposition (SVD). Let Z be the standardized matrix defined in (2), while $U$ and $V$ are the left and right singular vector matrices, respectively, and $\mathsf{\Sigma }$ is the diagonal matrix of singular values. Its singular value decomposition is expressed as

  $$Z=U\mathsf{\Sigma }{V}^T,$$

  (3)

Let U and $\Sigma$ be the components obtained in decomposition (3). The row coordinates $F$ are

$$F={D_r}^{-1/2}U\mathsf{\Sigma },$$

(4)

and the column coordinates $G$ are

$$G={D_c}^{-1/2}V\mathsf{\Sigma },$$

(5)

Factor coordinates are obtained by projecting rows and columns onto the axes associated with the singular vectors. These are the points plotted in biplots/maps; proximities among categories (and observations) reflect their associations.

To operationalize these steps, the MCA workflow can be summarized as a sequence of transformations starting from the categorical dataset and ending with the factorial coordinates and explained inertia. The following pseudocode outlines the main stages of the procedure in a concise and reproducible manner:

Input: Categorical table with variables {Process, Section, Priority}

• Build complete disjunctive table X
• Compute relative frequencies P = X/n
• Obtain row (r) and column (c) profiles
• Construct standardized residual matrix Z
• Apply SVD: Z = U Λ V^T
• Project rows and columns onto factorial axes

Output: Factorial coordinates + percentages of inertia (Dim1, Dim2, …)

To further clarify the sequence of operations and highlight how categorical information is transformed into factorial coordinates, we provide a simple analytical example with a small dataset. This example illustrates each step of the MCA, from the construction of the disjunctive table to the interpretation of the resulting dimensions.

Consider three observations of two categorical variables:

Process = {Cutting, Welding};

Priority = {High, Low}.

The complete disjunctive structure is shown below:

Cutting	Welding	High	Low
1	0	1	0
0	1	0	1
1	0	0	1

Relative frequencies: $P={\displaystyle \frac{1}{3}}X$;

Profiles: r = (1/3, 1/3, 1/3)^T and c = (2/3, 1/3, 1/3, 2/3).

SVD of the standardized residuals Z produces two main dimensions that reveal the following associations:

Cutting is balanced between High and Low.

Welding is more strongly associated with Low.

This toy example illustrates how MCA maps categorical variables into a geometric space where proximities reflect the strength of associations among categories.

On the other hand, we present a brief review of the mathematics behind a Random Forest, which is basically an ensemble method constructed from numerous decision trees. In addition to the decision trees themselves, other concepts that make the Random Forest a suitable and essential alternative are bootstrap sampling, random selection, and ensemble voting [24].

1.

Decision Trees. The initial data space is split into regions (trees) by using criteria such as Gini or Enthropy. At each split, the algorithm selects the best variable and threshold by optimizing a criterion. Let t be a node in a decision tree and K be the number of classes. $p_{k|t}$ denotes the proportion of observations of class k at node t. The Gini index at node t is defined as

$$G\left(t\right)=1-{\sum }_{k=1}^K{\left(p_{k|t}\right)}^2\hspace{1em}with k=1,\dots ,K,$$

(6)

2.

Classification in Random Forests. Let B be the total number of trees in the forest, and let ${\widehat{C}}_b\left(x\right)$ be the class predicted by tree b for an observation x. The class predicted by the Random Forest Ĉ(x) is obtained by majority vote:

$$\widehat{C}\left(x\right)={\arg max}_k {\sum }_{b=1}^{B}I({\widehat{C}}_b\left(x\right)=k)\hspace{1em}with b=1,\dots ,B,$$

(7)

where the indicator function I(Ĉ_b(x) = k) equals 1 if the tree predicted class k, and 0 otherwise.

Prediction in regression with Random Forests. Let $T_b\left(x\right)$ be the prediction of tree b for observation x, and let B be the total number of trees in the forest. The final prediction $\widehat{f}(x)$ is calculated as the average of the individual predictions:

$$\widehat{f}(x)={\displaystyle \frac{1}{B}}{\sum }_{b=1}^B{T}_b\left(x\right)\hspace{1em}with b=1,\dots ,B,$$

(8)

3.

Random Feature Selection. At each split, only a random subset of predictors is considered. This decorrelates trees and prevents them from making the same mistakes.

4.

Importance of variables. The importance of a variable X_j is quantified by its average contribution to the reduction in node impurity across all decision nodes in which it is utilized within the forest.

The algorithm is conceptualized as an ensemble learning technique that constructs multiple decision trees using bootstrap samples of the training dataset and aggregates their outputs to generate robust predictions. The pseudocode below outlines the fundamental procedural steps, from data partitioning to ensemble prediction, in a clear and reproducible format.

Input: Dataset {Process, Priority} → Quality

1.

Choose number of trees T (e.g., T = 3)

2.

For each tree t in 1…T:

• Select bootstrap sample from dataset
• Build decision tree with randomly chosen variables for splitting

3.

For a new observation x:

• Each tree h_t(x) outputs a prediction
• Majority vote = final prediction

Output: Predicted class (High or Low quality)

Similarly to the step-by-step illustration of MCA using a small dataset, we now present a didactic example that demonstrates the functioning of a Random Forest model. Suppose we have a dataset in an array with two categorical variables and one binary label.

Process	Priority	Quality
Cutting	High	High
Welding	Low	Low
Cutting	Low	High

The Random Forest builds several decision trees. Each tree is trained with a bootstrap sample of the dataset and randomly selects variables at each split. Examples of simplified possible trees are as follows:

Tree 1:

Root: Priority

If High → High

If Low → Low

Tree 2:

Root: Process

If Cutting → High

If Welding → Low

Each new case is classified by majority vote of the trees:

(Process = Welding, Priority = Low)

Tree 1 → Low

Tree 2 → Low

Final prediction: Low quality

2.2. Data Sources

This study is based on a dataset extracted from a quality management system at a manufacturing company, which contains records of quality alerts. The quality alerts dataset includes categorical attributes such as process, section, machines, and priority. The dataset covers a continuous period of monthly operations and reflects a real industrial environment characterized by complex production workflows and multiple subprocesses.

The variables process, section, and priority represent the core dimensions of the alert system. Process refers to the type of operational workflow in which an alert is triggered; section identifies the organizational or physical area where the alert occurs; and priority indicates the assigned severity level (e.g., low, medium, or high). Although all three variables are categorical, they offer complementary perspectives: process reveals workflow-specific patterns, section situates alerts within the organizational structure, and priority reflects the relative criticality of the events.

During the data exploration phase, the variable machines was also examined. The analysis revealed a high degree of overlap between machines and process: over half of the records matched exactly, and most remaining differences were limited to variations in wording or granularity (e.g., packaging vs. preparation/packaging). To reduce redundancy and avoid collinearity, process was retained as a proxy variable, and machines was excluded. This ensured that each active variable contributed distinct, non-duplicated information to the Multiple Correspondence Analysis (MCA).

In MCA, all active categorical variables are treated with equal weight. To complement this structural analysis, a Random Forest model was applied as a robustness check. Within this framework, variable importance measures derived from the tree ensemble were used to assess the relative influence of each variable. This combined use of MCA for exploring structural associations and Random Forest for evaluating variable importance enhanced both the interpretive depth and practical relevance of the selected dimensions.

Finally, the dataset analyzed in this study corresponds to alerts collected over a five-year period. This time window was chosen to ensure that the data captured sufficient variability in operational conditions, processes, and organizational changes while avoiding excessive heterogeneity that might arise from including a longer historical period [25]. A period of five years provides a balance between robustness and representativeness: it is long enough to accumulate an adequate number of alerts (n = 374) and to reflect stable patterns across different contexts, but not so long as to dilute the analysis with outdated practices or obsolete process structures.

2.3. Data Preparation

During the data cleaning process, only records with missing values (NA) in the active categorical variables, process, section, and priority, were excluded. No imputation techniques were applied in order to preserve the integrity of the original information and avoid introducing artificial biases. Likewise, no transformations were performed that could alter the nature of the categories, as all variables were explicitly treated as factors. Although the database consists of reports collected at different points in time, the temporal variable was not included as an active factor in this exploratory multiple correspondence analysis. Prior to the analysis, we verified that the distribution of categories in the three variables remained stable throughout the observation period, and no anomalous concentrations were detected that significantly affected the results. Even if temporal trends were present, they would not affect the Multiple Correspondence Analysis (MCA), as the method is based on the structure of associations among categories independently of their chronological sequence. The final sample was constructed using complete and consistent records across the three variables of interest, ensuring that the resulting factorial structure reflects only the relationships among category levels, free from contamination by missing or inconsistent data. We consider this procedure to be a robust selection strategy that minimizes the risk of bias due to missing values or temporal fluctuations.

2.4. Exploratory Data Analysis

Descriptive statistics and frequency tables were generated using the package in R [26]. This provided an overview of distributions and missing data and supported the identification of dominant processes and sections contributing to alerts. Visual summaries such as bar charts and heatmaps were produced to detect operational patterns and guide subsequent analyses. The dplyr [27] package was used for data manipulation, and ggplot2 [28] was used for plotting the graphs. Additionally, the caret [29] package was employed for data partitioning and cross-validation in the Random Forest modeling.

2.5. Multivariate Analysis

To assess the adequacy of the correlation structure before applying Multiple Correspondence Analysis (MCA), the complete disjunctive table was constructed from the categorical variables process, section, and priority.

Multiple Correspondence Analysis (MCA) was applied to explore the structural associations among the categorical variables process, section, and priority. Conceptually, MCA extends correspondence analysis to more than two categorical variables, allowing the relationships among multiple categories to be represented in a low-dimensional factorial space [18,23,30]. This allows for interpretable mapping of categories where proximities indicate stronger associations.

On this binary matrix, the Kaiser–Meyer–Olkin (KMO) test was applied using the KMO() function from the Psych package in R [31] in order to verify the suitability of the data for factor reduction. Subsequently, MCA was performed using the MCA() function from the FactoMineR package [32], which is specifically designed for exploratory analysis of categorical data.

The visualization and extraction of MCA results were carried out using the Factoextra package [33], which provides tools for clear and interpretable graphical representation of multivariate analyses.

2.6. Random Forest Modeling

A predictive approach based on Random Forest modeling [34,35] was implemented to support the development of an early warning system for quality alerts. Historical data on process, section, and priority levels were used to train the model, which is capable of capturing complex nonlinear relationships and interactions among categorical variables. The Random Forest algorithm enabled the identification of high-risk configurations by estimating the expected number of alerts with reasonable accuracy. This predictive capability supports informed decision-making for preventive maintenance, quality control interventions, and resource prioritization within the manufacturing environment.

The Random Forest model was fitted as a regression ensemble [24], with process, section, and priority as predictors and Alert_Count as the response. Each tree was grown from a bootstrap sample of the training data; at each node, a random subset of predictors (mtry) was considered, and the split was selected by minimizing the residual sum of squares (RSS). Predictions for new data were obtained by averaging across all trees. Representative tree structures were extracted using the getTree() function from the randomForest package (with labelVar = TRUE), which reports the splitting variable, split criterion, child nodes, and terminal status. To enhance interpretability beyond individual trees, ensemble-level performance was evaluated using MAE and RMSE, complemented with variable importance measures and partial dependence plots (PDPs) for each predictor.

To evaluate the performance of the model, we employed the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE). These criteria were selected due to their widespread use in the applied literature and because they allow prediction errors to be interpreted in the same units as the response variable (Alert_Count). MAE provides a robust measure of the average absolute error, while RMSE penalizes extreme deviations more heavily, making it particularly sensitive to large errors. Other indicators, such as the Mean Error (ME) or the Residual Standard Error (RSE), are also valid; however, MAE and RMSE were prioritized for their ease of interpretation and their ability to transparently reflect the model’s accuracy in this context.

Additionally, in our Random Forest analysis, 80% of the dataset was used for training and 20% for validation. This approach allowed the model to be trained on the majority of the data while its performance was evaluated on an independent subset [36].

2.7. Ethical Statement

This study was approved by the Ethics Committee of Mitsubishi Electric de Colombia Ltd. (Bello, Colombia) on 23 December 2024 (Supplementary Materials). All procedures complied with the ethical standards of the institutional research committee and with the 1964 Helsinki Declaration and its later amendments. No personal or identifiable data were collected. The data used consisted solely of operational quality records. Written informed consent was obtained from internal personnel involved in the data provision process. The original manuscript was prepared in Spanish, and its translation into English was supported by generative artificial intelligence tools (GenAI) under human supervision to ensure accuracy and contextual fidelity.

3. Results

3.1. Exploratory Data Analysis

The analyzed datasets, comprising 374 alerts from 2020 to 2024, provide broad and comprehensive temporal coverage, with no duplicate records and minimal missing values. Common categorical variables such as process, machines, and section enable comparative operational analysis. The rolling section stands out as the most affected area, accounting for 60.2% of alerts and 61.4% of cases, suggesting that it is a critical point in the production chain. In terms of processes, packaging dominates alerts (24.9%), while punching machine leads the cases with a more evenly distributed frequency. Overall, the datasets offer valuable insights into operational patterns and temporal trends, facilitating the development of risk analyses and predictive models focused on critical areas. The distribution of quality alerts reveals critical patterns across various operational dimensions (see

Table 1. Summary of alerts by category.

Categorical Variables	Category	Alert_Count
Priority	High	220
	Low	36
	Medium	118
Process	Enlistment	2
	Bending machine	101
	Booth assembly	1
	Cabinet assembly	2
	Die cutter	9
	Electronic assemblies	2
	Endless saw	5
Machines	Enlistment/packing	4
	Assembly	26
	Bending machine	106
	Die cutter	10
	Drill	3
	Endless saw	5
	Flame cutting	1
	Laser machine	2
	MIG/spot welder	5
	Mig welder/spot	11
Section	Assembly	56
	Delivery	93
	Laminated	225

).

High-priority alerts dominate the dataset with 220 occurrences, indicating a substantial share of events with significant impact on product quality. In terms of process, bending machine reports the highest alert counts, suggesting recurring issues in mechanical operations. Machine-level data highlight bending machine and preparation/packaging as hotspots, together accounting for over 200 alerts. At the section level, laminated stands out with 225 alerts, pointing to possible systemic inefficiencies or control weaknesses. These findings provide valuable insights for prioritizing preventive measures, quality audits, and resource allocation strategies across manufacturing units.

The process variable is directly related to the machine variable, since each machine is designed to execute a specific stage of the production process. This direct correspondence justifies the use of the process as a representative variable as it encapsulates the operational functionality of the equipment involved. Figure 2 presents a stacked bar chart displaying the distribution of quality alerts classified by variable type: priority, process, and section.

Each bar corresponds to a specific category (e.g., high in priority, bending machine in process, or laminated in section) and is color-coded by dimension. This chart provides a global and comparative overview of where alerts are concentrated in the production system. It quickly highlights that the high-priority category and the laminated section are the most critical.

Figure 3 shows a heatmap relating processes to plant sections (assembly, delivery, and laminated). Unlike Figure 1, this visualization is two-dimensional and focuses on how alerts are distributed within the organizational structure of the plant. It allows the identification of localized patterns, such as high concentrations of alerts in preparation and bending machine within the delivery and laminated sections, respectively. It also shows that product engineering generates a significant number of alerts in delivery. Thus, Figure 3 not only quantifies but also spatially locates problem areas, helping to prioritize targeted interventions in critical processes and sections.

These visualizations allow for a detailed examination of how alerts are concentrated across different parts of the manufacturing system and reveal key patterns that can guide quality management interventions. This heatmap of process vs. section displays the number of alerts generated by each process within the three plant sections: assembly, delivery, and laminated.

Several notable patterns emerge: preparation and bending machine processes show high concentrations of alerts, specifically in the delivery and laminated sections, respectively. Product engineering also stands out in the delivery section, indicating a localized issue or bottleneck within this operational unit. Other processes like punching machine and shear also have moderate alert counts in the laminated section, suggesting that multiple stages within this area may contribute to quality deviations.

In contrast, many processes in the assembly section exhibit lower alert counts, reflecting a relatively stable or less problematic area.

Panel priority vs. section heatmap highlights how alerts of different priority levels are distributed across plant sections: high-priority alerts are the most prominent, especially in the laminated section, followed by delivery and assembly.

Figure 4 also uses a heatmap, but in this case, it relates alert priority (high, medium, and low) to plant sections.

Figure 4 complements the previous figure by showing not only the frequency of alerts but also their relative severity. Results indicate that the laminated section concentrates both the highest number of alerts and those of greatest severity (high priority). Medium-priority alerts are also concentrated in the laminated section, while low-priority alerts are more evenly distributed. Compared to Figure 3, this figure addresses a different question: rather than focusing on which processes generate alerts, it shows what level of criticality these alerts represent within each section.

The pattern represented in Figure 4 suggests that the laminated section is not only the most active in terms of alert volume but also in terms of severity. Medium-priority alerts also show higher values in the laminated section, though they are more evenly distributed than high-priority ones. Low-priority alerts are less concentrated overall but still appear more frequently in the laminated section.

The heatmaps collectively point to a systematic concentration of both frequent and high-priority alerts in the laminated section, with particular involvement of bending machines and related processes. Similarly, the delivery section shows vulnerability in preparation and product engineering activities. The assembly section, while not devoid of alerts, appears to experience lower severity and frequency.

3.2. Multiple Correspondence Analysis (MCA)

The overall KMO index obtained was 0.50, which corresponds to a marginal level of adequacy according to Kaiser’s criteria [37]. This result is consistent with what is expected in analyses with categorical variables since disjunctive coding generates numerous binary variables with limited correlations. Despite this level, MCA remains appropriate for this type of data, as its objective is to identify association patterns among categories rather than maximize explained variance.

Figure 5 presents a Multiple Correspondence Analysis (MCA) performed on a categorical dataset comprising key variables in the context of industrial quality management: priority, process, and section. All these variables are associated with quality alert records in a manufacturing environment. The purpose of the analysis is to visually represent the relationships among the categories of these qualitative variables by projecting them into a two-dimensional space defined by the first two principal dimensions (Dim1 and Dim2), which together explain approximately 11.6% of the total inertia (a measure analogous to variance in PCA). One of the most relevant aspects of Multiple Correspondence Analysis (MCA) is that the spatial proximity between categories suggests strong associations or co-occurrence patterns within the dataset. In the MCA plot, this is reflected by the proximity of Process_Preparation and Section_Delivery in the lower-left quadrant. This spatial alignment implies a structural link between preparation-related activities and the delivery section, potentially indicating that alerts in these areas share root causes or workflow dependencies. This cluster could represent a critical zone for operational review and targeted improvements.

In the lower-central area of the plot, Process_Punching machine, Process_Bending machine, and the high category of the priority variable are closely aligned. This grouping reinforces the hypothesis that these machine-intensive processes are associated with more severe quality alerts. Their spatial concentration suggests operational criticality in this segment of the production chain, meriting preventive maintenance and risk mitigation strategies. The central-right portion of the graph highlights the Section_Laminated category positioned near Process_Die Cutter, Process_Shear, and other mechanically intensive processes such as Process_Laser machine and Process_Bench drill. These associations point to a significant concentration of alerts in the laminated section, particularly tied to metal-cutting and shaping processes. This localized cluster suggests that certain process–section combinations may be especially prone to quality incidents.

In contrast, medium and low-priority levels are more dispersed across the MCA space. This spatial dispersion indicates a more heterogeneous distribution of alerts, lacking strong ties to specific processes or sections. This pattern implies that less critical events occur more broadly across the system and are likely associated with more variable, less centralized operational conditions.

Some categories, such as Process_Finished product, Process_Painting, and Process_Wiring, appear farther from the center of the plot. Their peripheral position suggests limited interaction or co-occurrence with other variables. Although these categories may contribute fewer alerts, their isolated behavior may still be of interest, especially if they represent specific workflows or isolated operational issues. From a practical standpoint, this MCA visualization offers a powerful tool for identifying patterns of co-occurrence, process–section dependencies, and potential areas of quality risk.

In Figure 6, 95% confidence ellipses were employed as a grouping method. This graphical choice is based on the fact that it allows for the simultaneous visualization of the central tendency of each group (through the centroid) and the variability of individuals around it. Unlike other delimitation methods, such as convex hulls or partitions generated by clustering algorithms, ellipses provide a more intuitive, statistically grounded, and interpretable representation within multivariate exploratory analysis. In this way, ellipses facilitate the identification of overlaps and differences between groups, thereby enhancing the clarity of result interpretation [23].

Figure 6 represents the individuals (observations) grouped according to combinations of two categorical variables: section (assembly, delivery, laminated) and priority (high, medium, low). Each point represents an observation in the dataset, and the ellipses indicate 95% confidence regions for each group, allowing for the visualization of internal dispersion and relative proximity between groups.

From a general perspective, there is a clear spatial differentiation among several groups. For instance, the combinations of laminated, medium and assembly, and medium sections are distinctly separated from the others, indicating that alerts in these categories exhibit unique behavior. Observations within these ellipses are homogeneous and share a common structure, suggesting consistent patterns in those operational contexts.

On the other hand, the groups delivery, low and assembly, and low appear relatively close in the upper-left quadrant, reflecting similarities in the structure of alerts when the priority is low in these sections. In contrast, assembly, high and delivery, and high show greater dispersion, suggesting more internal variability. That is, high-priority alerts in these sections do not follow a single or well-defined pattern.

In terms of the plot dimensions, Dim1 (6%) appears to discriminate primarily based on the alert priority level, while Dim2 (5.6%) adds further differentiation related to the operational section. Although the percentage of inertia explained by these two dimensions is moderate (11.6%), this is typical in analyses involving multiple qualitative variables.

More compact groups, such as those related to the laminated section, show consistent behaviors that could inform targeted interventions. Conversely, more dispersed groups, like assembly and high, may require more flexible strategies due to their heterogeneity.

3.3. Random Forest

The results obtained from the Random Forest model provide valuable insights into the predictive capacity and variable importance related to quality alerts. The Mean Absolute Error (MAE) was 5.26 and the Root Mean Square Error (RMSE) was 7.72, indicating a moderate deviation between the predicted and actual alert counts in the test set. The results of the 5-fold cross-validation (see

Table 2. Five-fold cross-validation.

Mtry	RMSE	R2	MAE
2	11.54	0.39	6.83
19	10.91	0.46	4.88
36	10.92	0.46	4.81

) show that the model achieved its best performance with mtry = 19, reaching a minimum RMSE of 10.91, an R² of 0.46, and an MAE of 4.88.

These metrics suggest that the model captures a significant amount of variance in the data.

Table 3. Importance of variables.

Variable	%IncMSE	IncNodePurity
Process	12.17	3842.38
Section	4.23	2058.30
Priority	3.78	376.39

highlights that the process variable is the most influential predictor (with a %IncMSE of 12.17 and a node purity of 3842.38), followed by section and priority, confirming that operational processes play a central role in explaining the frequency of quality alerts.

These findings support the usefulness of random forest as a predictive tool to identify high-alert areas and optimize quality control strategies.

A representative decision tree is presented in Supplementary Table S1, illustrating the sequence of splits, nodes, and terminal predictions. Supplementary Figure S1 presents variable importance in the Random Forest model. The %IncMSE metric shows the increase in prediction error when each variable is permuted, while IncNodePurity reflects its contribution to node purity. In both measures, process is the most influential variable, followed by section and priority. Additional trees, along with PDPs, are provided in the Supplementary Figures (Figures S2–S4) to make the internal logic of the model fully transparent.

Table 4. Representative decision tree extracted from Random Forest mode.

Left Daughter	Right Daughter	Split var	Split Point	Status	Prediction
2	3	Priority	2	−3	6.06
4	5	Section	4	−3	1.67
6	7	Section	5	−3	7.37
0	0		0	−1	1.50
0	0		0	−1	1.83
8	9	Section	1	−3	5.62
0	0		0	−1	76
10	11	Process	354,485,408	−3	2.19
12	13	Priority	3	−3	9.61
0	0		0	−1	1.2
0	0		0	−1	4.67
14	15	Process	8,585,740,287	−3	6.10
0	0		0	−1	14
16	17	Process	1,069,056	−3	2.12
0	0		0	−1	22
0	0		0	−1	1.4
0	0		0	−1	3.33

presents the structure of the first decision tree (k = 1) extracted from the Random Forest model. Each row corresponds to a node and reports the splitting variable (priority, section, or process), the split criterion, the left and right daughter nodes, the node status (internal or terminal), and the final prediction when the node is terminal.

For instance, the root node splits the records based on the variable priority; cases meeting the split condition are sent to node 2, while the others go to node 3. Further down, node 7 is terminal and predicts an average of 76 alerts, reflecting a group of observations with a high concentration of alerts. In contrast, node 4 is also terminal but yields a much smaller prediction (1.5 alerts on average). These results illustrate how the tree applies successive splits of categorical variables to generate differentiated predictions across subsets of the data. The values in the split point column are not actual data but internal base-10 encodings of a binary mask grouping the levels of categorical variables. This representation specifies which categories are assigned to each branch of the node in the tree.

4. Discussion

4.1. Exploratory Data Analysis

The findings provide a clear picture of the critical areas of the quality alert system in the manufacturing environment. The predominance of high-priority alerts (220 incidents) suggests that a large portion of the logged problems are not trivial but potentially disruptive events with significant consequences for product integrity. This concentration highlights the urgent need to investigate the root causes of these high-severity incidents and assess whether current detection, control, and mitigation protocols are sufficient.

At the section level, the rolled products area stands out with 225 alerts, suggesting deeper systemic inefficiencies or quality control failures. This consistently high alert rate may be due to operational complexity, greater product vulnerability, or insufficient process standardization. Together, these insights enable manufacturing leaders to prioritize quality audits, allocate resources more efficiently, and design preventive maintenance and quality control plans. Analytics supports a data-driven approach to operational improvement, driving both immediate corrective actions and long-term process optimization.

The stacked bar chart serves as a powerful tool for pinpointing critical points with the quality alert system. By visually aggregating alert counts across categories such as process, machines, and section, it allows decision-makers to easily detect areas with disproportionate frequencies of incidents, thus supporting the prioritization of corrective actions and resource allocation. This visualization reinforces the importance of adopting multivariate analytical approaches for industrial quality management as such methods enable the integration of complex categorical data into actionable insights [38]. In doing so, organizations can move toward a more data-driven and preventive quality control strategy, optimizing performance and reducing operational risks. These insights are essential for guiding preventive actions, optimizing maintenance schedules, and strengthening quality control procedures. Visualization tools such as heatmaps play a critical role in uncovering hidden hotspots and revealing interdependencies among variables. By highlighting spatial and categorical patterns, they support a more strategic, informed, and data-driven approach to quality management in manufacturing settings [39].

While traditional control charts define alerts based on sigma thresholds (e.g., ±2σ or ±3σ) [40], our methodology identifies atypical combinations of categorical variables (process, section, and priority) that are strongly associated with higher alert frequencies. In this sense, an “alert” is generated when the model predicts values that significantly deviate from the baseline distribution of alert counts in the data. These deviations act as early warning signals, analogous to sigma violations in control charts.

An important practical consideration is the potential occurrence of false alerts, a common limitation in machine learning applications for process monitoring and control. In the context of Random Forest, rare orb atypical events may occasionally be misclassified, leading to false positives, or underestimated, resulting in false negatives. Such cases highlight that the predictive model should not be interpreted as a fully automated detection mechanism but rather as a decision-support tool to complement existing quality control strategies. To enhance robustness, threshold adjustment, expert validation, and the integration of complementary approaches such as Statistical Process Control (SPC) charts [40] are recommended to verify model outputs and prevent unnecessary interventions. This perspective reinforces the applicability of the proposed methodology by acknowledging its limitations and situating it within a broader monitoring framework.

4.2. Multiple Correspondence Analysis (MCA)

The results obtained through Multiple Correspondence Analysis (MCA), as illustrated in Figure 4, reveal latent structures in the relationships among the categorical variables process, section, and priority, all of which are linked to the generation of quality alerts within a manufacturing environment. One of the key advantages of MCA is its ability to visually represent associations between qualitative categories by projecting them into a two-dimensional space, thereby facilitating the identification of co-occurrence patterns that would otherwise be difficult to detect [18,41].

The spatial proximity between Process_Preparation and Section_Delivery suggests a structural association between the initial stages of the production flow and the dispatch section. This pattern may reflect functional interdependencies driven by logistical workflows or inspection procedures that condition final product quality. Such findings are consistent with reported observations [41] which emphasize that MCA is effective in revealing “typical configurations” within categorical data, which are particularly useful in operational diagnostics.

Likewise, the clustering of Process_Bending Machine, Process_Punching Machine, and the high category of priority supports the hypothesis that machine-intensive operations are strongly associated with more severe alerts. This suggests that these processes may represent critical points in the production chain where failures have a higher impact on product integrity, aligning with studies that stress the importance of bottlenecks and their connection to quality degradation [38,42].

In the central-right portion of the MCA plot, Section_Laminated appears aligned with processes such as Process_Die Cutter, Process_Shear, and Process_Laser Machine, all associated with material cutting and shaping. This concentration indicates that the laminated area experiences a high incidence of alerts linked to mechanical operations, suggesting possible deficiencies in process control or technical conditions requiring targeted interventions.

In contrast, the medium and low-priority categories are more scattered throughout the MCA space. This dispersion suggests a more heterogeneous distribution of less critical events, with no clear association with specific processes or sections. Such variability is commonly observed in low-risk alerts, where a broader range of factors may contribute to alert generation [30]. Finally, peripheral categories such as Process_Painting and Process_Wiring show a more isolated behavior on the map. This may be attributed to their lower frequency or the specificity of their operational contexts. Although not primary hotspots, analyzing these processes individually may still yield valuable insights for targeted quality improvement.

The visualization presented in Figure 5, derived from Multiple Correspondence Analysis (MCA), provides key insights into how combinations of section and priority structure the distribution of quality alerts within the manufacturing process. The spatial grouping of observations into ellipses (representing 95% confidence regions) reveals both homogeneous and heterogeneous patterns across different operational contexts. For instance, the combinations of the laminated, medium and assembly, and medium sections are distinctly isolated in the MCA space, suggesting that quality alerts in these segments share unique and internally consistent characteristics. This points to stable operational behaviors in these areas, where alert types and conditions tend to follow repeated patterns. On the other hand, combinations such as delivery, low and assembly, and low cluster closely together in the upper-left quadrant, indicating structural similarities in low-priority alerts across these sections, a finding that can inform shared interventions or monitoring protocols [18,30,42].

Conversely, higher-priority alerts (e.g., assembly, high and delivery, and high) display greater internal dispersion, which suggests more diverse operational causes or inconsistent triggering conditions. These heterogeneous profiles may require adaptive quality strategies as alerts are not governed by a dominant cause or process. Although the first two dimensions explain only 11.6% of the total inertia, such variance is common in multidimensional categorical analyses and still provides actionable insights [18]. The first dimension (Dim1), which appears to separate alerts by priority level, and the second (Dim2), which captures section-based differences, together enable a richer interpretation of alert behavior. These findings emphasize the importance of considering the joint influence of multiple categorical factors and support the use of MCA as a powerful exploratory tool in quality management. By visualizing latent relationships between section and priority, this analysis facilitates the development of more targeted and predictive maintenance policies [30,38,41].

The first two dimensions of the Multiple Correspondence Analysis (MCA) explained 11.6% of the total inertia. Although this value may appear low, such percentages are typical in MCA applied to nominal variables, since the complete disjunctive coding generates a large number of binary indicators with weak correlations, thereby dispersing the variance across many dimensions [18,41]. The reliability of MCA results does not rely solely on the proportion of inertia explained by the leading dimensions, but rather on the interpretability and stability of association patterns as well as on the contributions and quality of representation of categories in the factorial space. In our study, the categories of process, section, and priority showed consistent and interpretable contributions, supporting the robustness of the conclusions despite the relatively low inertia percentage.

4.3. Random Forest

Based on the results, the performance of the Random Forest model demonstrates its effectiveness in modeling the frequency of quality alerts within an industrial context [35,43,44,45]. The obtained MAE (5.26) and RMSE (7.72) on the test dataset indicate a moderate but acceptable predictive error, suggesting that the model can generalize reasonably well to unseen data. The five-fold cross-validation (see Table 1) further supports the model’s stability, achieving optimal performance with an mtry value of 19, an RMSE of 10.91, and an R² of 0.46. These values indicate that nearly half of the variance in alert frequency is explained by the model, which is a meaningful outcome in operational environments where multiple unpredictable factors often influence quality incidents [46].

In terms of feature importance, the process variable stands out as the most influential predictor, followed by section and priority (see Table 2). The high %IncMSE and node purity associated with process indicate that the nature of specific manufacturing stages plays a decisive role in the generation of alerts. This aligns with previous findings suggesting that critical operational stages often concentrate higher risks of non-conformities and quality issues [47]. These results reinforce the utility of Random Forest not only for its predictive accuracy but also for its interpretability through variable importance measures. Consequently, this approach enables decision-makers to proactively identify high-risk areas, prioritize interventions, and allocate resources more effectively to enhance quality assurance strategies [48].

The coefficient of determination obtained in our model (R² = 0.46) indicates that approximately 53% of the variance remains unexplained. This outcome is not unexpected in models involving categorical variables, where explained variance is often lower compared to continuous data. Ordered and assessed categorical responses are subject to observer error, multidimensional influences, and structural constraints that inherently limit the proportion of variance explained [49,50]. Consequently, the value observed in this study should not be interpreted as a weakness of the model but rather as a reflection of the complexity of categorical data structures. The strength of the Random Forest approach lies precisely in its ability to capture association patterns and predictive structures even when a substantial proportion of variance remains formally unexplained.

From a methodological perspective, the use of a mixed approach brings clear advantages over applying single methods in isolation. Relying solely on Multiple Correspondence Analysis (MCA) would provide a structural understanding of the associations among categorical variables, but as an unsupervised technique, it does not assess predictive performance [18]. Conversely, logistic regression and related generalized linear models are standard tools for categorical data analysis and yield interpretable coefficients, yet they impose assumptions of linearity and independence that may not hold in complex industrial contexts [51]. By integrating MCA with Random Forests, our study benefits from both perspectives: MCA enhances interpretability by revealing the structural relationships among categories, while Random Forests contribute predictive robustness, capture nonlinear effects, and model higher-order interactions without strong distributional assumptions [24]. This integration ensures a more comprehensive analysis, combining explanatory clarity with predictive power.

5. Conclusions

The findings derived from Multiple Correspondence Analysis (MCA) and the Random Forest model offer a comprehensive, data-driven understanding of quality alerts in a manufacturing context. Identifying structural associations between key categorical variables (process, section, and priority), along with assessing the relative importance of each variable in predicting alert frequency, provides valuable insights into the factors impacting product quality. This methodological combination proves effective for extracting actionable knowledge from structured operational records, supporting informed quality management decisions.

The significance of this multidisciplinary approach lies in its ability to transform operational data into meaningful insights, which is a cornerstone in applied sciences. MCA and Random Forest have demonstrated their robustness in uncovering complex patterns within categorical data, making them valuable tools for industrial contexts where efficiency and quality are paramount.

Future studies may focus on incorporating temporal and sequential data to model the evolution of alerts over time, or on implementing more advanced methods such as neural networks or hybrid models that integrate qualitative and quantitative analyses. Additionally, applying this framework to other production settings and comparing results could help validate the model’s robustness and enhance its generalizability. Temporal information may reveal whether the associations observed between process, section, and priority are stable over time or whether they vary according to production cycles, seasonal demand, or external events (e.g., the pandemic). Such temporal dynamics could highlight periods of increased vulnerability, structural changes in processes, or shifts in alert severity distributions. Incorporating temporal trends in future research would therefore allow us to distinguish between persistent structural patterns and transient fluctuations, strengthening the robustness and applicability of the model for monitoring and decision-making.