Detecting the File Encryption Algorithms Using Artificial Intelligence

Abstract

In this paper, the authors analyze the applicability of artificial intelligence algorithms for classifying file encryption methods based on statistical features extracted from the binary content of files. The prepared datasets included both unencrypted files and files encrypted using selected cryptographic algorithms in Electronic Codebook (ECB) and Cipher Block Chaining (CBC) modes. These datasets were further diversified by varying the number of encryption keys and the sample sizes. Feature extraction focused solely on basic statistical parameters, excluding an analysis of file headers, keys, or internal structures. The study evaluated the performance of several models, including Random Forest, Bagging, Support Vector Machine, Naive Bayes, K-Nearest Neighbors, and AdaBoost. Among these, Random Forest and Bagging achieved the highest accuracy and demonstrated the most stable results. The classification performance was notably better in ECB mode, where no random initialization vector was used. In contrast, the increased randomness of data in CBC mode resulted in lower classification effectiveness, particularly as the number of encryption keys increased. This paper provides a comprehensive analysis of the classifiers’ performance across various encryption configurations and suggests potential directions for further experiments.

1. Introduction

Modern computer systems are used in nearly all aspects of everyday life. They can be found in both small, simple devices, such as smart vacuum cleaners, and large, complex systems like cars and airplanes. Their effectiveness largely depends on the ability to acquire, process, and store data that are essential for making decisions and performing tasks. While much of these data are non-sensitive and can be used without concerns, there is a significant amount that needs to be encrypted and protected to prevent unauthorized access.

Encrypted data traveling through a network is not a security problem unless they contain information that can be used to attack systems. One challenge is differentiating encrypted data from other types of binary data. Additionally, it is crucial to identify the encryption algorithm used to encode the data. This identification can serve as an important first step in detecting potential threats, especially in digital forensics or traffic seizure. Identifying a cryptographic algorithm can narrow subsequent cryptanalysis. In network monitoring, spotting weak or deprecated ciphers (e.g., Rivest Cipher 4 (RC4), Triple Data Encryption Algorithm (3DES)) or specific modes in flows leads to an increase in the security level. Also, detecting if the file is encrypted, compressed, or plain is used to prioritize the response [1]. Identifying the cryptographic algorithms used by a program in static or dynamic traces can aid in malware reverse-engineering [2].

Current algorithms for detecting encryption algorithms used for encrypting data can be divided into two main groups:

• Artificial intelligence-based;
• Using statistical analysis without the use of artificial intelligence.

In [3], the encrypted files were submitted to data-mining techniques such as Quinlan’s C4.5 decision tree algorithm implemented as J48 in WEKA, Functional Tree (FT), PART, Complement Naive Bayes, and Multilayer Perceptron classifiers. The percentage of identification for each of the algorithms was greater than a probabilistic bid.

In [4], the authors used the Hybrid Random Forest and Logistic Regression (HRFLR) model for training. In addition, two ensemble learning models, the Hybrid Gradient Boosting Decision Tree and Logistic Regression (HGBDTLR) model and the Hybrid K-Nearest Neighbors and Random Forest (HKNNRF) model, were used as controls to conduct controlled experiments.

In [5], the authors propose an approach using the decision tree generated by Quinlan’s decision tree generation algorithm (C4.5). A system that extracts eight features from a ciphertext and classifies the encryption algorithm using the C4.5 classifier is developed. The success rate of this proposed method is in the range of 70 to 75%.

Other papers are based on deep learning algorithms. Work [6] focuses on the construction of classifiers based on a residual neural network and feature engineering. The results show that the accuracy is generally over 90%. In [7], the authors use a deep learning framework, while in [8], the authors use a convolutional neural network.

Another approach is presented in [9], which demonstrates cryptographic algorithm identification methods using machine learning algorithms. The ciphertext classification challenge was performed using both image processing and natural language processing methods. For image processing purposes, convolutional neural networks (CNNs) were utilized, whereas text-CNN, transformers and bidirectional encoder representations from transformers (BERT) models were used as natural language processing tools.

While deep learning approaches such as CNNs and transformers have shown promising results in cryptographic algorithm identification (e.g., [8,10,11]), this study focuses on lightweight, feature-based classical machine learning models. This choice is motivated by the need for models with lower computational complexity that are suitable for deployment on resource-constrained devices and environments. This deliberate focus aligns with the practical applicability goals of the research.

In addition to methods utilizing artificial intelligence and machine learning algorithms, there are numerous examples of methods based on statistical data parameters. One of the factors used in detection is entropy. In [12], the accuracy of 53 distinct tests is verified for being able to differentiate between encrypted data and other file types. In [13], a modification of the statistical spectral test based on entropy analysis for identifying malicious programs that use encryption as a disguise has been described. The practical utilization of a method based on an entropy analysis is described in [14], where the authors propose a method to effectively detect ransomware for cloud services by estimating entropy. In [1], entropy analysis is enriched by a learning-based classifier to improve the accuracy of detection.

Some patented methods for detecting the encryption algorithm use more sophisticated methods, such as the compression ratio [15], byte distribution [16], or opcode frequency analysis [17].

In [18,19], the authors proposed the utilization of differential area analysis (DAA), which is a technique that analyzes file headers to differentiate compressed, regularly encrypted, and ransomware-encrypted files.

A summary of AI-based and non-AI-based encrypted file detection methods with their main attributes is presented in

Table 1. Comparison of AI-based and non-AI-based encrypted file detection methods.

Category	Example Techniques	Strengths/Limitations
AI-Based Methods	Machine learning classification (Support Vector Machine (SVM), Random Forest, Decision Trees) [3,4,5,20] Deep learning (CNN, Long Short-Term Memory (LSTM)) for byte sequence analysis [6,7,8] ML-based cryptographic detection in binaries [9]	High accuracy when trained on large, diverse datasets Can adapt to novel encryption schemes Requires significant labeled data and computational resources Potential overfitting to training data
Non-AI-Based Methods	Entropy measurement (Shannon entropy, spectral entropy) [1,12,13,14,21] Compression ratio tests [15] Byte distribution histograms [16] Opcode frequency analysis [17] Differential area analysis (DAA) [18,19]	Simple and fast to implement No need for training datasets May struggle to distinguish encryption from compression Vulnerable to evasion (e.g., partial encryption, crafted headers)

.

Table 1 presents a comparison between AI-based and non-AI-based methods for detecting encrypted files. The first column lists the method categories. The second column details example techniques within each category, such as machine learning classifiers (e.g., SVM, random forest) and deep learning approaches (e.g., CNN, LSTM) for AI-based methods, as well as statistical measures like entropy and compression tests for non-AI-based methods. The third column summarizes the main strengths and limitations of each category. AI-based methods generally achieve high accuracy on large, diverse datasets and can adapt to new encryption schemes but require significant computational resources and labeled data. Non-AI-based methods are simpler to implement and do not require training data but may struggle to distinguish encrypted data from compressed data and are more vulnerable to evasion techniques.

Although numerous approaches to detecting encryption algorithms have been proposed, many of them require large computational resources, extensive labeled datasets, or lack applicability in real-time forensic and network security scenarios. The scientific problem addressed in this work is the absence of lightweight and practical methods that can reliably identify encryption algorithms under constrained conditions. Therefore, the objective of this study is to develop a preliminary system for encryption algorithm identification that remains effective on resource-limited devices while enabling integration into automated traffic and file analysis solutions for digital forensics and network monitoring.

The selected file formats for generating datasets have been clearly confirmed as the most commonly used in internet communication by numerous studies and reports [22,23,24]. The dataset was created by randomly generating files in popular formats, which is an advantage over previous works based on materials available on the internet. In summary, a two-agent system is proposed in which random forest and bagging algorithms work together to improve classification accuracy. This work is not intended to be groundbreaking. Its primary goal was to demonstrate the possibility of detecting file encryption methods in systems with low computing power so that the process can be performed locally or in IoT systems on edge devices.

2. Materials and Methods

This section provides a detailed description of the methodology used to research the effectiveness of artificial intelligence algorithms in recognizing file encryption methods. The purpose of developing this research methodology was to ensure the repeatability of the experiment and to enable a reliable evaluation of the effectiveness of the selected machine learning algorithms. The research process consisted of the following stages:

• Selection of technology and test environment (Section 2.1);
• Preparation of datasets (Section 2.2);
• Selection of artificial intelligence algorithms (Section 2.3);
• Training and evaluation according to the established scheme (Section 2.4).

2.1. Selection of Technology and Test Environment

In order to conduct research on the effectiveness of recognizing (classifying) file encryption methods, Python version 3.9.6 was selected as the programming language. The entire research process was based on Python and its libraries. This language enabled the implementation of the part responsible for generating data, processing it, encrypting it using selected algorithms, and training artificial intelligence models. The venv mechanism, which is the standard system for creating virtual environments in Python, was used to isolate the runtime environment. This enabled easy library management, the elimination of conflicts between library versions, and ensured the repeatability of the results.

Six file types and their corresponding formats were selected for the experiments: image files—*.bmp, table files—*.csv, markup language files—*.html, source code files—*.py, text files—*.txt and sound files—*.wav. The main reason for choosing these file formats was the fact that they do not use lossy compression. This affected the quality and reliability of the results obtained in the experiments. The following Python libraries were used to create files in the selected formats:

• Faker (ver. 3.22.0)—generated realistic textual and numeric content for *.txt, *.csv, *.htm, and *.py files, enabling diversity in sample structure [25];
• Pillow (PIL, ver. 11.2.1)—created BMP images with customizable properties [26];
• Wave (standard module)—generated and manipulated uncompressed *.wav files [27];
• NumPy (ver. 2.0.2)—supported numeric encoding and the basic transformation of files content [28].

File encryption for research purposes was performed using the Python library—PyCryptodome (ver. 3.22.0). The following components from this library were used in this paper:

• Crypto_.Cipher—a module containing implementations of block ciphers in various encryption modes, e.g., Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), and Output Feedback (OFB), and stream ciphers [29];
• Crypto.Random.get_random_bytes())—a function used to generate pseudo-random byte strings used to create encryption keys and initialization vectors [30];
• Crypto.Util.Padding—Enabled block-aligned padding of input data [31].

The PyCryptodome library ARC4 is an implementation of the RC4 algorithm, which is in compliance with the documentation [32].

In order to extract features and perform statistical analysis of encrypted and unencrypted files, Python libraries were used that enable the manipulation of binary data and the performance of complex calculations. The following modules and libraries were used to perform these operations:

• NumPy—calculated metrics such as mean [33], variance [34], root mean square (RMS) [35], and byte-wise statistics [36,37,38];
• SciPy (ver. 1.13.1)—additional advanced calculations (e.g., skewness [39], kurtosis [40]);
• Collections.Counter—counting the frequency of bytes for histogram and entropy calculations [41];
• Math (standard module)—provided a logarithmic function for calculating entropy [42];
• Pandas (ver. 2.2.3)—organized extracted features into DataFrames, facilitating further manipulation and export to CSV for machine learning stages [43].

In order to conduct experiments to explore the effectiveness of artificial intelligence algorithms in recognizing file encryption methods, one of the most popular Python library—scikit-learn (ver. 1.6.1). It provides the necessary tools for data preparation, cross-validation, building artificial intelligence models, and evaluating their effectiveness such as the following:

• Sklearn.preprocessing—label encoding and feature normalization with LabelEncoder, MinMaxScaler, StandardScaler [44];
• Sklearn.model_selection—data splitting and k-fold cross-validation [45];
• Sklearn.metrics: comprehensive evaluation via accuracy, precision, recall, F1-score, log loss, and Area Under the Receiver Operating Characteristic Curve metrics [46];
• Sklearn.ensemble, sklearn.svm, sklearn.naive_bayes, sklearn.neighbors—these modules provided classes containing selected artificial intelligence algorithms [47,48,49,50].

To graphically represent the effectiveness of artificial intelligence models and visualize the statistical characteristics of encrypted and unencrypted datasets, two libraries were used: matplotlib (ver. 3.9.4) [51] and seaborn (ver. 0.13.2) [52].

A detailed description of the technology and test environment has been included deliberately so that the research can be presented in a way that allows it to be reproduced as accurately as possible. The aim of this section is to ensure complete transparency and enable the results to be replicated.

2.2. Preparation of Datasets

We chose not to use existing public datasets because they did not meet the requirements for the availability of files encrypted with different algorithms. The entire dataset was designed and generated independently, which ensured full control over its content and characteristics.

At the initial stage, a pilot test set consisting of 1000 text files (*.txt) was prepared, which were divided into five classes: encrypted with Advanced Encryption Standard (AES; 300 files), Data Encryption Standard (DES; 250 files), 3DES (200), RC4 (150) algorithms, and unencrypted files (100). All encryption was performed in ECB mode, with a single key per algorithm, which simplified the test environment and enabled preliminary verification of the effectiveness of the chosen methodology.

For the main experiment, files in six formats were created: *.txt (text), *.csv (tabular), *.html (markup), *.py (source code), *.bmp (lossless images) and *.wav (lossless audio files). The contents of the files corresponded to their type: text and code were generated automatically, images were created as homogeneous graphics, and *.wav files contained signals from several random waves.

For each format, samples ranging in size from 300 to 10,000 bytes were prepared for *.txt, *.csv, *.html, *.py and *.bmp, and from 10,000 to 500,000 bytes for *.wav, which is due to the characteristics of audio files. For each format, sets of 1000, 1800 and 3000 unique files were created for a total of 6000, 10,800 and 18,000 files, respectively.

The target files were encrypted with three block algorithms (AES, DES, 3DES) and one stream algorithm (RC4), using ECB and CBC modes (except for RC4). For each algorithm, three key variants were tested: a single key, three rotating keys, and six rotating keys. Some files were left unencrypted as a control sample. In this way, complete subsets of data were created for each combination of format, algorithm, mode, and number of keys.

Statistical features considered relevant based on the literature were extracted from each file (encrypted and unencrypted): byte entropy [53], byte mean [33], byte variance [34] and byte standard deviation [37], skewness [39], kurtosis [40], energy [38], RMS, and histogram of byte values in the range 0–255 [36]. The collected features and auxiliary data were then organized into DataFrame structures. Each row of the DataFrame represented a single file with all its extracted features and a class label (encryption algorithm or no encryption). The prepared datasets were saved in *.csv format, creating complete and easily accessible databases ready for the further analysis, training and evaluation of machine learning models.

In this paper, we decided to use only the basic statistical features mentioned above. This choice was a conscious and deliberate decision, based on solid foundations from the analyzed literature, which showed that properly selected basic statistical parameters effectively reflect the essential properties of encrypted and unencrypted data. These features are relatively easy to calculate, which allows for the creation of lightweight classification models based on them that are effective even with limited computational resources and smaller datasets. The literature shows that many of these parameters achieve encryption detection rates of over 90%, confirming their practical value in applications for detecting encrypted information [54]. Furthermore, limiting oneself to basic features allows for models with good overall interpretability and easy implementation, which is important in systems with limited hardware capabilities. Although more advanced techniques, such as n-gram analysis or the structural analysis of file headers, can potentially increase detection effectiveness in complex encryption modes, their implementation requires larger datasets and computing power. In the current study, based on examples from the literature and the specifics of the available resources, an approach was adopted that is optimal in terms of the balance between accuracy and computational complexity.

The datasets were intentionally designed in a simplified form to ensure full control over file characteristics and to minimize the need for additional transformations. This decision allowed for a transparent and reproducible experimental environment while reflecting the practical constraints of lightweight systems with limited computational resources.

Statistics and analyses from various sources show that the most popular formats for data exchange on the internet are text files, spreadsheets, HTML tags, BMP images, WAV sound files and source code [22,23,24]. Randomly generated files were used to prepare the test sets, rather than files downloaded from online resources, which distinguishes this approach from the works analyzed prior to the start of the research. In the final phase of the work, a two-agent system concept was developed based on two selected algorithms, increasing the reliability of classification. This work is not intended to be groundbreaking. Its primary goal was to demonstrate the possibility of detecting file encryption methods in systems with low computing power, allowing the process to be carried out locally or in IoT systems on edge devices.

Upon request, the authors will provide the prepared datasets, including the raw files and the extracted features, via GitHub repositories.

2.3. Selection of Artificial Intelligence Algorithms

To evaluate the effectiveness of classifying encryption algorithms based on statistical file characteristics, six different classifiers representing different machine learning paradigms were used: Random Forest [55], Support Vector Machine (SVM) [56], K-Nearest Neighbors (KNN) [57], Naive Bayes [58], AdaBoost (Adaptive Boosting) [59] and Bagging (Bootstrap Aggregating) [60].

The choice of algorithms was based on the results of previous research discussed in the earlier section—Introduction (Section 1). These models represent different machine learning paradigms and can be effectively run on resource-constrained systems, which supports the goal of this work, which is to develop lightweight and practical solutions.

2.4. Training and Evaluation According to the Established Scheme

The training data consisted of sets of features extracted from previously prepared sets of encrypted and unencrypted files. Before training columns with metadata (name, format) were removed, class labels were encoded numerically (LabelEncoder) and numerical features were scaled using MinMaxScaler [61], which improved the results obtained by the models (in a preliminary experiment, MinMaxScaler was compared with StandardScaler [62]—the former proved to be better; the choice of MinMaxScaler is explained later in this paper).

During the initial experiment (1000 text files), detailed tests were conducted to determine the impact of selected model parameters on classification quality. The following were analyzed, among other things:

• Random Forest: number of trees: {50, 100, 200}, maximum depth of trees: {none, 10, 20}, minimum samples to split a node: {2, 5}, minimum samples per leaf: {1, 2}, number of features considered at each split: {sqrt, log2, none};
• SVM: kernel function: {linear, rbf, polynomial, sigmoid}, regularization parameter C: {0.1, 1, 10}, gamma: {scale, auto}, degree (for polynomial kernel): {3, 4, 5}, independent term coef0 (for polynomial and sigmoid kernels): {0, 0.1, 1};
• Naive Bayes (GaussianNB): variance smoothing parameter: {$1\times {10}^{-9}$, $1\times {10}^{-8}$, $1\times {10}^{-7}$};
• k-Nearest Neighbors: number of neighbors: {3, 5, 7, 10}, weight function: {uniform, distance}, distance metric: {Euclidean, Manhattan, Minkowski};
• Bagging: number of base estimators: {10, 50, 100}, fraction of training samples per estimator: {0.5, 0.8, 1.0}, fraction of features per estimator: {0.5, 0.8, 1.0};
• AdaBoost: number of boosting iterations: {50, 100, 200}, learning rate: {0.01, 0.1, 1.0}.

For each model, a grid of selected parameter values was prepared. First, the models were run in their default configuration; then, the selected parameter was gradually modified, observing changes in the basic performance metrics (accuracy, precision, recall, F1-score, Area Under the Receiver Operating Characteristic Curve (AUC)). The same data-splitting strategy was used each time (StratifiedKFold—5 folds). The test results clearly showed that with a small and unbalanced set, no significant improvements were achieved when tuning the hyperparameters relative to the default settings. Sometimes, a slight deterioration in the stability of the models or excessive fitting to the selected training sample was even observed.

In the initial experiment on a set of 1000 files, five-fold cross-validation with class stratification (StratifiedKFold) was used to maintain the proportions of samples in each encryption class. The aim was to verify the stability of the results with an uneven distribution of classes.

The main experiment used classic, random five-fold cross-validation (KFold). The model training and testing process was similar: division into training/test sets, training, predictions, and calculation of metrics and their standard deviations (accuracy, precision, recall, F1-score, and where possible, log loss and AUC). The classification metrics results are calculated after each cross-validation iteration (fold) and then averaged (with standard deviation calculated) to obtain an overall assessment of the model on a given dataset. These steps are repeated for all 18 datasets for the main experiment, ensuring a comprehensive and comparable analysis of the algorithms’ effectiveness.

3. Results

This section presents the results of the research conducted for all datasets described in the previous section. For each of the sets, separate training and testing of artificial intelligence models was carried out. The experiments were divided into three stages:

• A preliminary experiment to select the optimal method (Section 3.1);
• Testing file encryption in Electronic Codebook mode (Section 3.2);
• Testing file encryption in Cipher Block Chaining mode (Section 3.3).

3.1. A Preliminary Experiment to Select the Optimal Method

A pilot experiment was conducted on 1000 generated *.txt text files, of which 300 were encrypted with AES, 250 were encrypted with DES, 200 were encrypted with 3DES, 150 were encrypted with RC4, and 100 were left unencrypted. All files were encrypted in ECB mode with each algorithm assigned a single key to simplify the research. After encrypting the file set according to the established proportions, it underwent a feature extraction process, which resulted in data ready for standardization using two scaling methods: MinMaxScaler and StandardScaler were compared. In addition, the impact of modifying artificial intelligence model parameters on the quality of results was examined.

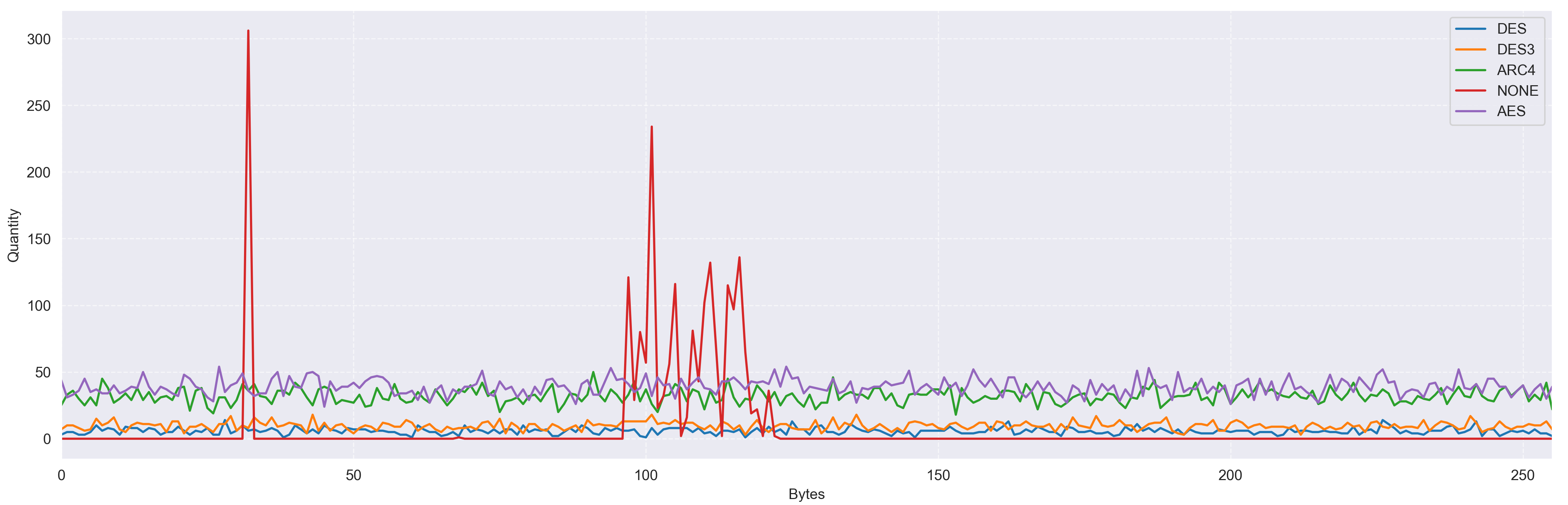
In order to illustrate the test dataset and the differences in byte distribution between encrypted and unencrypted files, a byte distribution histogram was prepared. Figure 1 clearly shows the deviation of the graph associated with unencrypted files (red color—‘NONE’)—the irregularity in the distribution of bytes. In the case of unencrypted data, the large number of peaks in specific byte ranges is very clearly visible. Significant jumps occur in the number of bytes with values close to 30 and in the range of 100–140, which may be related to the type of data and its structure—some ASCII characters appear much more frequently than others.

3.1.1. Choosing Data-Scaling Method

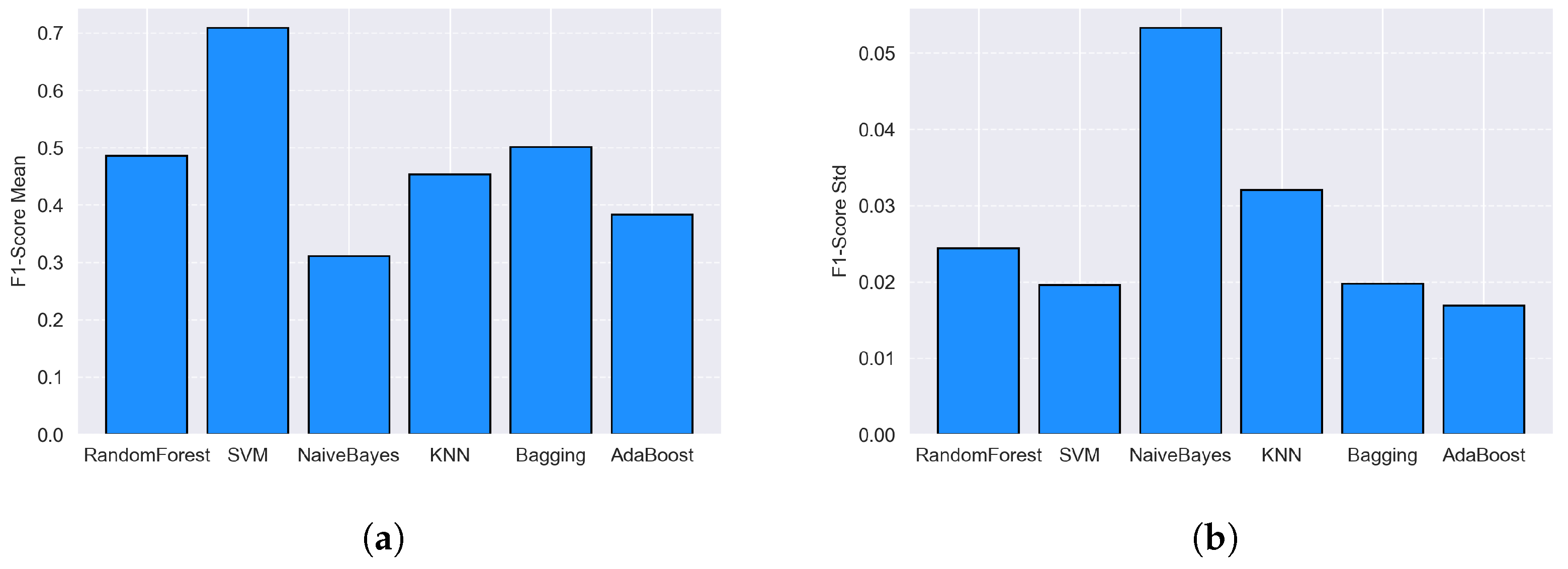
In a preliminary experiment, MinMaxScaler and StandardScaler were compared on a set of 1000 text files with F1-score as key performance metric. MinMaxScaler clearly provided the best results for the SVM model (F1-score increased from 0.669 to 0.709), while the other models showed slight or marginal differences: Bagging (F1-score remained unchanged at 0.501), Random Forest (slight decrease in F1-score from 0.489 to 0.486), AdaBoost (F1-score unchanged, 0.383, respectively), and k-NN achieved slightly better results with StandardScaler (F1-score for StandardScaler equal to 0.460, in the case of MinMaxScaler 0.454, respectively), and Naive Bayes remained the weakest (F1-score 0.310, respectively, in both cases). The advantage of SVM determined the choice of MinMaxScaler for further research.

These results are illustrated in Figure 2, which shows the average F1-score values for all algorithms in both scaling variants. The other quality measures (accuracy, precision, sensitivity, logarithmic loss, and AUC) confirmed the described trends and did not influence the decision on the choice of feature processing method.

3.1.2. The Impact of Changes in AI Models Parameters on Quality Results

The second stage of the preliminary experiment was to check the impact of tuning selected hyperparameters on the effectiveness of selected classifiers. For each model, a set of parameters with multiple values was defined, from which all possible combinations were generated using Cartesian products. Each configuration was trained five times using StratifiedKFold validation, and the averaged quality measure values were collected for further analysis.

The classification metric results presented in

Table 2. Changes in the values of artificial intelligence models quality metrics as a result of fine tuning their parameters.

Model	Accuracy	Precision	F1-Score
AdaBoost	+0.023	−0.090	−0.056
Bagging	−0.031	−0.031	−0.032
k-NN	+0.009	+0.007	+0.011
Naive Bayes	0.000	0.000	0.000
Random Forest	−0.010	−0.008	−0.013
SVM	−0.209	−0.268	−0.283

after parameters tuning show that in most cases, the effectiveness of the models decreased or remained unchanged compared to the default settings. We provide the following detail:

• For the AdaBoost model, a slight increase in accuracy was observed, but precision and F1-score deteriorated, suggesting an ambiguous effect of tuning;
• In the case of Bagging, there was a general decline in all metrics evaluated;
• The k-NN model achieved slight improvements in all key values;
• Naive Bayes remained unchanged in all metrics;
• In the Random Forest model, a slight decrease in accuracy and F1-score was observed;
• Although SVM achieved the best results in the experiment with standard settings, it showed a significant deterioration in key metrics after tuning.

Considering the observed decline or lack of improvement in effectiveness in most cases, it was decided to use classifiers with default parameters in further stages of the experiments.

The preliminary experiment was exploratory in nature—aimed at establishing a preliminary naive hypothesis and developing methods for feature processing and data scaling selection. It was conducted on an unbalanced dataset, as its main purpose was not to obtain final model evaluations but to prepare and optimize further research activities. This approach allowed for a reliable evaluation of scaling methods and model selection while laying the groundwork for extended analyses on larger, more balanced datasets in later stages of the research.

3.2. Testing File Encryption in Electronic Codebook Mode

This section presents the results of an experiment evaluating the effectiveness of artificial intelligence classifiers on data encrypted in Electronic Codebook mode. The analysis was conducted for three set sizes (6000, 10,800, and 18,000 files). For each data size, different numbers of keys per encryption algorithm were tested (1 key, 3 keys, and 6 keys). To assess the quality of classification, two of the six metrics that accurately reflect the behavior of the models were selected: accuracy and F1-score. They allow for a balanced assessment of classification effectiveness, taking into account both the correctness of assignments and the balance between precision and sensitivity. The results are presented taking into account the impact of these variables on the effectiveness of the selected models, which allows for an understanding of the role of data size and key diversity in the encryption task.

The choice of relatively small dataset sizes and their modest increments was intentional to demonstrate that even limited sample numbers reveal meaningful differences in classification performance. This approach highlights how slight increases in dataset size can impact model effectiveness, emphasizing the relevance of data quantity even in constrained experimental settings

The results obtained by individual machine learning models for each of the tested datasets are presented below.

Table 3. Random Forest—accuracy and F1-score depending on the number of samples and keys (ECB mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.761	0.760	0.700	0.700	0.659	0.660
10,800	0.774	0.772	0.721	0.721	0.683	0.683
18,000	0.783	0.781	0.722	0.722	0.693	0.694

shows that the Random Forest model demonstrated the highest classification effectiveness among all analysed algorithms. In each sample size, a systematic decrease in accuracy and F1-score was observed as the number of encryption keys increased. The best results—accuracy of 0.783 and F1-score of 0.781—were obtained for the largest sample (18,000 samples) and a single key. As the number of keys increased, the effectiveness gradually decreased, suggesting that the diversity of keys made it difficult for the model to distinguish between classes based on statistical features.

Table 4. Bagging—accuracy and F1-score depending on the number of samples and keys (ECB mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.741	0.739	0.689	0.689	0.656	0.656
10,800	0.762	0.761	0.711	0.711	0.679	0.679
18,000	0.774	0.772	0.717	0.716	0.685	0.686

shows that Bagging achieved results very similar to Random Forest but also showed a clear decrease in effectiveness as the number of keys increased. The highest accuracy (0.774) and F1-score (0.772) values were recorded for 18,000 samples and a single key. In each data size configuration, adding more keys lowered the quality indicators. This model, like Random Forest, performed better when the number of keys used was the smallest.

Table 5. SVM—accuracy and F1-score depending on the number of samples and keys (ECB mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.409	0.361	0.415	0.368	0.410	0.361
10,800	0.399	0.349	0.404	0.352	0.401	0.354
18,000	0.399	0.352	0.398	0.348	0.399	0.351

shows that Support Vector Machine was significantly less effective than ensemble models. Also in the case of SVM, increasing the number of keys in a given set resulted in a systematic decrease in accuracy and F1-score. While increasing the number of samples slightly improved the results, with greater key diversity, the model was unable to effectively learn repetitive patterns. Even with the largest possible set and 6 keys, SVM did not exceed 0.420 for both quality measures.

Table 6. k-NN—accuracy and F1-score depending on the number of samples and keys (ECB mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.547	0.541	0.514	0.508	0.511	0.507
10,800	0.557	0.549	0.540	0.536	0.517	0.512
18,000	0.578	0.570	0.532	0.524	0.518	0.510

shows that k-NN demonstrated moderately increasing effectiveness with an increase in the number of samples, but each time, a larger number of keys per algorithm worsened the accuracy and F1-score values obtained. The best results (up to 0.578 for accuracy) were still lower than in ensemble models. The results clearly indicate that k-NN is sensitive to the additional randomness introduced by the diversity of keys.

Table 7. AdaBoost—accuracy and F1-score depending on the number of samples and keys (ECB mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.499	0.476	0.458	0.392	0.452	0.383
10,800	0.500	0.455	0.438	0.384	0.466	0.424
18,000	0.506	0.570	0.468	0.409	0.466	0.424

demonstrates that AdaBoost improved its effectiveness as the number of samples increased, but a larger number of encryption keys resulted in a decrease in both accuracy and F1-score within a given set size. Even under the most favorable conditions (the largest number of samples, one key), the values did not match those of the Random Forest or Bagging models.

Table 8. Naive Bayes—accuracy and F1-score depending on the number of samples and keys (ECB mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.297	0.254	0.284	0.239	0.279	0.232
10,800	0.272	0.214	0.271	0.271	0.269	0.208
18,000	0.271	0.209	0.271	0.209	0.272	0.211

Note: Separate columns for accuracy and F1-score for each key variant.

reveals that Naive Bayes remained by far the weakest model in every combination of parameters. The number of keys had no significant impact on effectiveness—both accuracy and F1-score remained at a similar, low level (below 0.3). The low sensitivity of the model to the experiment parameters indicates that it is not suitable for this class of classification tasks.

3.3. Testing File Encryption in Cipher Block Chaining Mode

This section presents an analysis of the effectiveness of artificial intelligence classifiers on data encrypted using the Cipher Block Chaining mode. The research covered three set sizes: 6000, 10,800 and 18,000 files, as well as three variants regarding the number of keys used for encryption—one, three and six keys. Two key metrics were used to evaluate effectiveness: accuracy and F1-score, which allow for the simultaneous consideration of classification correctness and balance between the precision and sensitivity of models. The tables below illustrate the results obtained for each model and experiment configuration.

Table 9. Random Forest—accuracy and F1-score depending on the number of samples and keys (CBC mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.490	0.482	0.455	0.453	0.436	0.436
10,800	0.506	0.498	0.465	0.462	0.436	0.433
18,000	0.509	0.502	0.473	0.467	0.447	0.445

illustrates that the Random Forest classifier maintains a leading position in classification effectiveness for CBC-encrypted data. However, contrary to ECB mode, the achieved accuracy and F1-score values are overall lower, reflecting the increased complexity imposed by CBC’s block chaining. A clear trend emerges where accuracy and F1-score generally decrease with an increasing number of keys, indicating that higher key diversity complicates pattern recognition due to there being higher variance in the encrypted data.

Importantly, increasing the number of samples tends to improve results moderately with the largest dataset yielding the highest performance. Notably, though Random Forest typically performs best, in CBC mode, Bagging closely matches or slightly exceeds its results in some configurations, particularly for smaller key numbers and sample sizes, highlighting Bagging’s strong stability under these conditions.

As shown in

Table 10. Bagging—accuracy and F1-score depending on the number of samples and keys (CBC mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.471	0.461	0.464	0.463	0.442	0.440
10,800	0.498	0.490	0.468	0.464	0.447	0.444
18,000	0.503	0.496	0.477	0.471	0.452	0.449

, Bagging achieves classification quality very similar to Random Forest, often slightly outperforming it in CBC mode for specific cases. The metric values generally diminish as the number of keys increases, which is consistent with the expected effect of growing data heterogeneity. However, the fluctuations include some exceptions where, for example, the F1-score slightly increases with additional keys within given dataset sizes.

Table 11. SVM—accuracy and F1-score depending on the number of samples and keys (CBC mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.392	0.318	0.390	0.309	0.396	0.322
10,800	0.388	0.324	0.377	0.304	0.378	0.305
18,000	0.408	0.363	0.385	0.331	0.387	0.330

confirms that SVM models exhibit limited performance in CBC conditions compared to ensemble approaches. The classifier suffers from difficulties in effectively generalizing amidst the added complexity and dependencies introduced by CBC encryption. Although increasing the number of data samples provides modest improvements, the overall accuracy and F1-scores remain substantially below those of ensemble classifiers. Moreover, SVM’s response to rising key numbers is erratic rather than systematically decreasing, reflecting its sensitivity to noise and the intricate feature spaces created by CBC.

As per

Table 12. k-NN—accuracy and F1-score depending on the number of samples and keys (CBC mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.447	0.436	0.427	0.422	0.419	0.415
10,800	0.465	0.455	0.428	0.422	0.425	0.420
18,000	0.459	0.451	0.443	0.437	0.422	0.416

, k-NN shows moderate sensitivity to the number of keys: increasing keys tends to correlate with a reduction in both accuracy and F1-score, which is likely due to more diffuse clusters in the feature space caused by encryption diversity. Yet, this decline is partially mitigated by growing the dataset size, which improves metric values slightly. Despite these gains, k-NN results remain notably inferior to ensemble learners.

Table 13. AdaBoost—accuracy and F1-score depending on the number of samples and keys (CBC mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.444	0.406	0.415	0.359	0.401	0.316
10,800	0.431	0.388	0.415	0.352	0.412	0.337
18,000	0.427	0.353	0.433	0.378	0.411	0.331

shows that AdaBoost experiences improvements in classification metrics as the sample size grows, but similarly to other models, the accuracy and F1-score degrade with more keys being introduced. This reflects AdaBoost’s limited robustness against the increased complexity and noise stemming from higher key variability, especially under CBC encryption where inter-block dependencies further complicate the patterns.

Finally,

Table 14. Naive Bayes—accuracy and F1-score depending on the number of samples and keys (CBC mode).

Number of Samples	1 Key		3 Keys		6 Keys
	Accuracy	F1-Score	Accuracy	F1-Score	Accuracy	F1-Score
6000	0.366	0.313	0.366	0.314	0.371	0.322
10,800	0.372	0.307	0.375	0.310	0.368	0.302
18,000	0.296	0.260	0.376	0.315	0.372	0.306

clearly indicates that Naive Bayes performs poorest among the tested models. Its accuracy and F1-score values remain consistently low across all experimental settings, revealing a fundamental incapacity to capture complex statistical relationships in CBC-encrypted data.

The results of the experiments indicate similarities in the effectiveness trends of classifiers for data encrypted in CBC and ECB modes. However, CBC mode encryption is characterized by a significant decrease in effectiveness across almost all evaluation measures.

3.4. Comparison with Other Works

The results presented can only be compared to existing studies within a limited scope, typically by looking at the best results for similar datasets. The similarity between the datasets is determined based on their descriptions, which may differ significantly from more objective measures.

The two works, refs. [63,64], were selected for comparison. Selection was based mainly on similar datasets, experiments, and algorithms.

The work [63] presents the application of pattern classification methods to identify encryption algorithms based on the analysis of encrypted data. The research covered four block cipher algorithms: AES (128, 192, and 256-bit variants), DES (64 bits), IDEA (128 bits), and RC2 (42, 84, and 128 bits). All of the algorithms mentioned worked in ECB mode. The datasets consisted of 120, 240, and 400 encrypted files, and for each algorithm, the impact of the number of encryption keys used was also analyzed (the experiments were conducted with 1, 3, 5, and 30 unique keys for each algorithm, respectively). The input data consisted of various binary texts, and their processing was carried out at the byte histogram level (range of values from 0 to 255), which was generated in the MATLAB environment.

The results of the experiments showed a strong correlation between classification effectiveness and the number of keys used. For the variant based on one key per encryption algorithm, classification accuracy reached 100%. As the number of keys used increased, the classification effectiveness decreased significantly. Similarly, it was noted that the number of samples tested was also important—a larger number of files (400) contributed to an improvement in the classification quality achieved by the models.

The highest results were achieved by the Random Forest algorithm, which achieved 100% accuracy in the case of single-key encryption. As the number of keys increased, the accuracy dropped to around 55%. In turn, Instance-Based Learner achieved an accuracy of 25–30% in the most demanding data variants. As for the distinguishability of individual variants of the AES algorithm (128, 192, and 256 bits), it was not achieved. However, distinguishing AES from other algorithms was achieved. A similar problem (classification of variants) concerned the RC2 algorithm. All these results can be treated as similar to those described in this study.

In the work [64], the authors proposed a system for the automatic identification of encryption algorithms using artificial intelligence methods, in particular, the Random Forest algorithm.

The research used an extensive dataset containing ciphertexts generated by 39 different algorithms, including both symmetric (e.g., AES, DES, Blowfish) and asymmetric (RSA) algorithms in various modes of operation (CBC, CFB, CTR). Each encryption algorithm was represented by at least one million ciphertexts with data encrypted by 20 algorithms ultimately being used.

The results of the experiments showed very high classification accuracy, ranging from 90% to 95% depending on the pair of algorithms analyzed. Compared to the results presented in our work, with the highest accuracy of about 80%, the results in [64] are much better, reaching more than 95%.

4. Discussion

The unsuccessful hyperparameter tuning during the preliminary experiment, resulting in worse or unstable performance, likely stems from the small size of the pilot dataset, the high variance in the data, or particular properties of the feature space. Under these initial conditions, default parameters proved to be more stable and reliable for the experiments conducted.

Analyses of the results showed that ensemble models, such as Random Forest and Bagging, dominate in the classification of files encrypted in Electronic Codebook mode, significantly outperforming, e.g., the Support Vector Machine model. The Random Forest model achieved the highest metric values for the largest and most diverse dataset. With 18,000 samples and a single key, Random Forest achieved an accuracy of 0.783 and an F1-score of 0.781, while SVM, under identical conditions, reached an accuracy of 0.399 and an F1-score of 0.352. Bagging ranked just behind Random Forest (accuracy: 0.774, F1-score: 0.772). Thus, the difference between ensemble models and SVM is about 0.38 points in accuracy and 0.43 in F1-score, representing a practically significant advantage.

In addition, a systematic increase in the size of the dataset clearly had a positive effect on the classification performance of all models regardless of the number of keys. For example, Random Forest achieved an accuracy of 0.761 and an F1-score of 0.760 with the smallest set of 6000 samples and one key, while with the largest set of 18,000 samples, these values increased to 0.783 and 0.781. Similar patterns were seen in the Bagging model, where accuracy and F1-score values increased from 0.753 and 0.752 to 0.774 and 0.772 for the same set of configurations. This increase clearly indicates the key role of data abundance in building effective classifiers. For the other models, this effect was weak (k-NN, AdaBoost) or not present at all (SVM, Naive Bayes).

On the other hand, increasing the number of encryption keys did not bring the expected positive effects but rather had the opposite effect—it caused a gradual decrease in the effectiveness of the model for a given number of samples. For example, for Random Forest with 18,000 samples and 1 key, both accuracy and F1-score were around 0.783 and 0.781, while with 3 keys, they dropped to 0.722 and 0.722, and with 6 keys, they dropped to 0.693 and 0.694. These declines indicate that increasing key diversity increases data complexity, making it difficult for models to effectively recognize and generalize classification patterns. Similar trends were observed for Bagging and most other models, consistently reflecting a decrease in quality measures as the number of keys increased. This effect was particularly evident for the dominant models, but also present, to varying degrees, for SVM, k-NN, AdaBoost and Naive Bayes.

Among the other algorithms, SVM, k-Nearest Neighbors and AdaBoost showed stable, albeit significantly lower, results compared to ensemble models. Although all these models responded to an increase in the number of samples with an increase in effectiveness, their metrics still remained far from the best. For example, SVM achieved a maximum accuracy of approximately 0.399 and an F1-score of approximately 0.352 with the largest set and a single key. The k-NN model achieved an accuracy of approximately 0.578 and an F1-score of approximately 0.570 under the most favorable conditions, while AdaBoost fluctuated within similar ranges, but these values were still lower than the results of ensemble forests.

At the bottom of the classification effectiveness spectrum was Naive Bayes, which is a probabilistic classifier whose metrics did not exceed 0.3 for both accuracy and F1-score regardless of the size of the set or the number of keys. The low effectiveness of this model highlights the limitations of simple probabilistic approaches in classifying complex, encrypted data, where patterns can be highly blurred and variable.

In CBC, the ensemble methods, especially Bagging and Random Forest, remain the dominant tools in the classification of encrypted data. Bagging often slightly outperforms Random Forest, especially with fewer keys and an increasing number of samples. There are also a few noticeable cases where an increase in the number of keys causes a slight increase in metrics, which may indicate specific interactions between high key variability and the dynamics of ensemble models.

Single models such as SVM, k-NN, and AdaBoost perform significantly worse. Their effectiveness improves with increasing data, but they still lag significantly behind ensemble methods. In the case of SVM, there is no clear relationship between the number of keys and effectiveness, suggesting a lack of model stability in terms of changing encryption conditions. AdaBoost, on the other hand, although it improves with increasing dataset size, quickly loses effectiveness with increasing key diversity.

The k-NN model performs better than probabilistic models in the largest datasets, but it still lags behind ensemble methods. Naive Bayes ranks last, as its assumptions about feature independence prevent it from effectively detecting patterns in highly correlated and complex data encrypted in CBC mode.

The relatively poor performance of the Naive Bayes classifier can be attributed to its core assumption of feature independence, which is violated in encrypted data where statistical features exhibit strong correlations. This limitation hinders its ability to effectively capture complex patterns essential for classification.

Moreover, the observed decrease in classification performance in CBC mode, compared to ECB, is primarily due to the structural differences between these encryption modes. In ECB, each data block is encrypted independently, making it easier for models to identify patterns based on statistical features. Conversely, CBC employs chaining, where each block’s encryption depends on the previous ciphertext block, introducing dependencies and correlations between blocks. This inter-block linkage increases data complexity and dilutes the effectiveness of basic statistical features, posing significant challenges for classifiers.

These phenomena suggest that while ensemble methods remain robust across modes, especially in CBC, further research should explore advanced feature engineering techniques or alternative modeling approaches to better capture dependencies inherent in CBC-encrypted data.

In summary, CBC significantly hinders classification due to the links between blocks and increased data complexity. Ensemble methods, especially Bagging and Random Forest, are the most resistant to these challenges, but their effectiveness is lower than in ECB mode. Other classifiers show greater sensitivity to encryption parameters and lower overall effectiveness.

5. Conclusions

The presented paper proved that using artificial intelligence methods, it is possible to detect the used encryption algorithm. Using the Random Forest or Bagging algorithm gave acceptable results in almost all tests. Favorable results were particularly observed with the ECB encryption mode, where the absence of randomness introduced by the initialization vector enabled the models to recognize patterns in the files more effectively. In contrast, the CBC mode, which adds randomness through the use of an initialization vector (IV), made it significantly more challenging to identify the type of encryption. Additionally, the increasing number of encryption keys further complicated correct classification, leading all tested models to demonstrate decreased efficiency.

While this study focused on classical machine learning methods due to their relative simplicity and applicability on systems with limited computational resources, future work will emphasize the development and evaluation of advanced neural network architectures. Neural networks have demonstrated superior capability in capturing intricate and difficult-to-identify patterns in encrypted data, which can significantly enhance detection accuracy compared to traditional ML techniques.

The paper extracts a set of statistical features but does not analyze which features were most discriminative for the classification task. It is worth noting that prior studies in the literature have analyzed the effectiveness of individual features in distinguishing encrypted from unencrypted files. Based on these findings, it was assumed that similar feature effectiveness might apply to the identification of specific encryption algorithms. However, this assumption requires validation. Moreover, the primary goal of this study was not to assess the discriminative power of individual statistical features but rather to evaluate how machine learning algorithms perform in classifying encryption algorithms using the selected feature set. This insightful observation highlights an important direction for future work, which includes conducting detailed feature importance analyses and examining their impact on system performance, balancing accuracy with computational efficiency in resource-limited environments.

An important direction for future work is to conduct ablation studies to analyze the contribution of individual statistical features to the classification performance. Due to the large number of extracted features, such detailed analysis was beyond the scope of the current study and would require substantial additional effort. However, investigating which features have the most significant impact could lead to improved model efficiency and accuracy, guiding feature selection and model refinement in subsequent research.

Additionally, plans include investigating robust feature extraction methods resilient to the randomness introduced by cryptographic initialization vectors, expanding datasets, and incorporating a broader range of encryption algorithms. These steps aim to develop a comprehensive system for the automated recognition of encryption methods, improving practical applicability in computer forensics.

Future studies will focus on conducting hyperparameter tuning experiments on substantially larger datasets using more powerful computational resources. This will help clarify the relationship between feature characteristics and model performance, potentially improving classifier robustness and accuracy.

The research conducted primarily addressed the overall quality of the detection process without examining the influence of individual subprocesses on the final outcome. Future research will focus on this aspect, as it will help optimize the detection mechanism and reduce resource demands, such as processor and memory usage. Consequently, this will make it feasible to implement the proposed solution in Internet of Things (IoT) applications.

The selection of file types may exert a substantial influence on classification outcomes. In this study, file types frequently encountered in data transmission—specifically text, image, and audio files—were employed. The datasets comprised a heterogeneous mixture of these file types. Future work should examine the effect of file type separation on classification performance, as well as the impact of applying compression prior to and following encryption, to more rigorously evaluate the properties and robustness of the proposed method.

Confirmed research data and recommendations clearly indicate that the most commonly used data exchange strategies are based on formats such as *.txt, *.csv, *.html, *.bmp, *.wav, and text files with source code [22,23,24]. The datasets were created based on files with random content generated in these formats, which increases the reliability and objectivity of the experiment by eliminating dependence on ready-made files available on the web. Based on the results obtained and development plans, a two-agent system is proposed in which each agent uses an independent machine learning model—one Random Forest algorithm and the other Bagging. These models analyze data autonomously, generating separate classification decisions, and the final decision is made as a result of mutual support and combining their results, which increases the accuracy and resilience of the system to errors. This solution is particularly effective on devices with limited resources, such as IoT and edge computing systems. This work is not groundbreaking; its purpose is to demonstrate the possibility of effective file encryption method detection in systems with limited computing capabilities, enabling the process to be carried out locally or on edge devices.

It is possible to expand the research to include additional elements in the future. One key area for enhancement is increasing the file sizes used in the study. Furthermore, incorporating additional encryption algorithms and machine learning models would broaden the scope of analyses and better reflect real-world cases. The authors plan to concentrate on solutions that require fewer resources, especially in terms of CPU and memory. They aim to develop methods that can operate on machines without GPUs for neural network calculations. By executing neural network models, they seek to enhance the detection of hard-to-identify patterns in encrypted files, making it possible to implement these techniques on edge devices. The research conducted and planned could serve as an excellent starting point for creating a comprehensive system for automatically recognizing file encryption methods, ultimately providing valuable support for analytical activities in the field of computer forensics.