FPGA Spectral Clustering Receiver for Phase-Noise-Affected Channels

Abstract

This work extends our previous research on spectral clustering for mitigating nonlinear phase noise in optical communication systems by presenting the first complete FPGA implementation of the algorithm, including on-chip eigenvector computation with parallelization strategies. The implementation addresses the computational complexity challenges of spectral clustering through a heterogeneous CPU/FPGA co-design approach that partitions algorithmic stages between ARM processors and the FPGA fabric. While the achieved processing speeds of approximately 36 symbols per second do not yet meet the requirements for commercial optical transceivers, our hardware prototype demonstrates the feasibility and practical challenges of deploying advanced clustering algorithms on real-time hardware architectures. We detail the parallel Jacobi method for eigenvector computation, the Greedy K-means++ initialization strategy, and the comprehensive hardware mapping of all clustering stages. The system processes streaming m-QAM data through a windowed architecture and integrates a demapper to ensure label consistency, demonstrating improved bit error rate performance compared to K-means under severe phase noise conditions of −90 dBc/Hz at a 1 MHz offset. This implementation offers valuable insights into memory bandwidth limitations and resource utilization trade-offs, underscoring the crucial role of FPGAs as a bridge between algorithm development and high-speed optical system deployment.

1. Introduction

Optical communication systems face significant challenges due to nonlinear effects, particularly Kerr-induced phase noise [1,2], which severely distorts the constellation diagrams of high-order modulation formats such as m-QAM, increasing the difficulty of accurate symbol classification at the receiver [3,4]. While various digital signal processing techniques have been proposed to mitigate these impairments, including deep learning [5,6,7] and machine learning methods [8,9,10], their hardware implementation faces substantial scalability issues in real-time systems.

Spectral clustering is an unsupervised learning technique that transforms data into a new domain using the eigenvectors of a similarity graph constructed from the input data [11]. The transformation into spectral space often reveals cluster boundaries that are not linearly separable in the original domain [12], making it particularly suitable for identifying structures in distorted constellations affected by nonlinear phase noise. Spectral clustering enables dynamic adaptation to changing channel conditions without requiring labeled data or explicit channel models when applied to streaming m-QAM data [13]. However, the main challenge for real-time hardware deployment has been the computational complexity of the eigenvector decomposition stage.

In [14], the authors present a parallel implementation of the Jacobi algorithm for eigenanalysis, comparing its performance on CPUs, GPUs, and FPGAs. The research demonstrated that, despite using multi-threaded approaches, CPUs are not well-suited for this type of computation. The analysis concludes that FPGA implementations deliver the highest computational performance for matrix eigenanalysis using the Jacobi algorithm, though GPUs present a competitive alternative with easier development and better scalability.

To the best of our knowledge, Liu et al. [15] demonstrated the first application of spectral clustering for nonlinear phase noise compensation in 16-QAM systems using offline DSP. Building upon this foundation and our previous work [13] on the algorithm’s response to varying nonlinear phase noise and SNRs (5–20 dB) across 16/32/64-QAM constellations, this work presents the first hardware implementation of a spectral clustering-based demodulator for nonlinear phase noise mitigation.

We present a comprehensive System-on-Chip Field-Programmable Gate Array (SoC-FPGA) implementation of a spectral clustering receiver for m-QAM optical signals, encompassing all algorithmic stages, including affinity matrix construction, eigenvector and eigenvalue computation, and cluster assignment. The system supports real-time data stream processing [16] and includes an integrated demapper stage to resolve labeling ambiguities in windowed data. The core architecture is designed to handle the symbol flow in real time, overcoming the main hardware bottleneck by implementing a parallel Jacobi method for eigenvector computation.

The key contributions of this work include the first complete SoC-FPGA hardware implementation of a spectral clustering receiver for m-QAM signals affected by nonlinear phase noise, encompassing the on-chip computation of eigenvectors via a novel parallel Jacobi method with cyclic scheduling that reduces computational complexity. Additionally, the integration of a Greedy K-means++ initialization strategy enhances clustering stability under severe phase noise conditions. The proposed heterogeneous hardware/software co-design partitions tasks between the ARM CPU and the FPGA fabric to optimize resource utilization. While the processing speeds currently do not meet commercial requirements, the experimental results provide critical insights into memory bandwidth limitations as the fundamental bottleneck for real-time spectral clustering architectures on FPGA platforms. This work validates the robustness of spectral clustering compared to traditional K-means clustering in challenging noise environments and lays the groundwork for future architectural optimizations and scalability improvements.

The rest of this paper is organized as follows: Section 2 presents the spectral clustering algorithm and the parallelization strategies, emphasizing the new eigenvector computation stage and parallelization strategies. Section 3 describes the hardware/software co-design of the spectral clustering receiver. Section 4 discusses experimental results and performance analysis. Section 5 presents the discussion, and conclusions and future work are presented in Section 6.

2. Spectral Clustering Algorithm and Parallelization Strategies

The spectral clustering algorithm consists of two main stages implemented through our heterogeneous CPU/FPGA co-design approach. First, an affinity matrix A is constructed using a radial basis function (RBF) kernel and normalized with the diagonal matrix $D^{-{\displaystyle \frac{1}{2}}}$ to obtain the normalized Laplacian L. From L, the top k eigenvectors are computed and stacked into matrix X, which is row-normalized to form matrix Y. The second stage involves applying the K-means algorithm to the rows of the Y matrix, which represents the data transformed into spectral space.

In the particular case of QAM constellation analysis, the initialization of the centroids in K-means influences the quality of the final clustering [17,18]. The effect of centroid initialization on clustering performance was systematically evaluated using QAM constellation data affected by nonlinear phase noise, revealing that more sophisticated initialization methods help the algorithm find better groupings more reliably, leading to improved performance in challenging signal conditions.

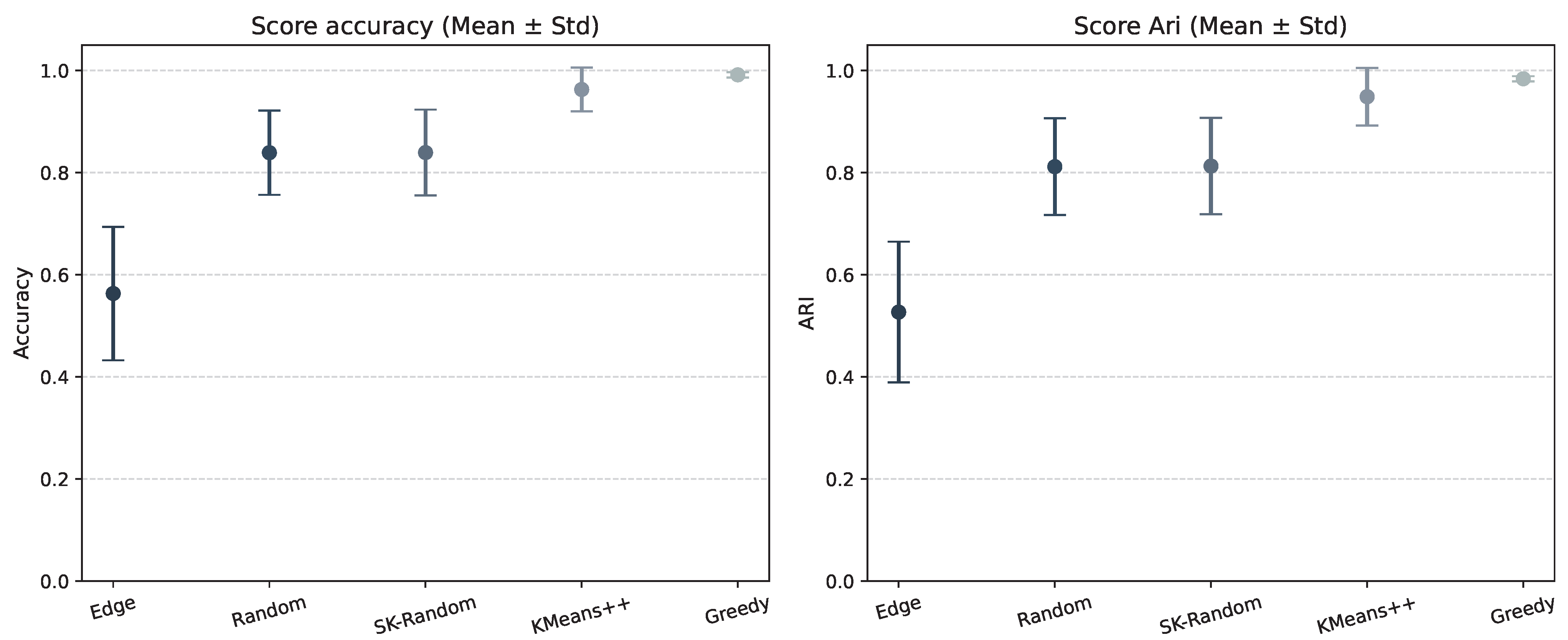
Figure 1 illustrates a comparison of the performance of different initialization methods applied to QAM constellation data. The Greedy K-means++ approach consistently achieves higher mean accuracy and lower variance compared to random, K-means++, and other strategies, indicating more robust and reliable clustering performance under severe phase noise conditions. Centroid initialization has a significant impact on the final clustering outcome, particularly in scenarios with substantial nonlinear distortions, which validates the adoption of Greedy K-means++ in hardware implementations, as it enhances the stability and quality of the spectral clustering receiver.

2.1. Greedy K-Means++ Initialization

Greedy K-means++ utilizes a proportional likelihood selection mechanism to choose new centroids, resulting in a better initial distribution that accelerates the algorithm’s convergence. Unlike the standard K-means++ algorithm (presented in Algorithm 1), which selects a single point as the next centroid at random based on probability, Greedy K-means++ evaluates multiple candidates and performs multiple trials at each sampling step, choosing the optimal centroid among the evaluated options. Greedy K-means++ is presented in Algorithm 2.

Algorithm 1 Standard K-means++ initialization

1: Input: A set of data points $X=\{x_1,x_2,\dots ,x_n\}$, number of clusters k. 2: Output: A set of k centroids $C=\{c_1,c_2,\dots ,c_k\}$.              ▹ Step 1: Choose the first centroid uniformly at random 3: Choose the first centroid $c_1$ from X uniformly at random. 4: $C\leftarrow \left\{c_1\right\}$.                    ▹ Step 2: Choose remaining $k-1$ centroids 5: for $j\leftarrow 2$ to k do 6:     Let D be an array of size n. 7:     for each point $x_i\in X$ do ▹ Find the squared distance to the nearest centroid in C 8:             $D\left[i\right]\leftarrow {min}_{c\in C}\left|\right|x_i-c{\left|\right|}^2$. 9:      end for              ▹ Choose the next centroid with weighted probability 10:     Choose the next centroid $c_j$ from X with a probability proportional to $D\left[i\right]$. 11:     i.e., pick $x_i$ with probability $P\left(x_i\right)={\displaystyle \frac{D\left[i\right]}{{\sum }_{l=1}^{n}D\left[l\right]}}$. 12:     $C\leftarrow C\cup \left\{c_j\right\}$. 13: end for 14: return C.

Algorithm 2 Greedy K-means++ initialization

1: Input: A set of data points $X=\{x_1,x_2,\dots ,x_n\}$, number of clusters k. 2: Output: A set of k centroids $C=\{c_1,c_2,\dots ,c_k\}$.                        ▹ Step 1: Initialize the first centroid 3: Choose the first centroid $c_1$ uniformly at random from X. 4: $C\leftarrow \left\{c_1\right\}$.                   ▹ Step 2: Calculate initial squared distances 5: Let D be an array of size n. 6: for each point $x_i\in X$ do 7:     $D\left[i\right]\leftarrow \left|\right|x_i-c_1{\left|\right|}^2$. 8: end for              ▹ Step 3: Iteratively select remaining $k-1$ centroids 9: for $j\leftarrow 2$ to k do 10:     $\mathrm{max\_gain}\leftarrow 0$. 11:     $\mathrm{next\_centroid}\leftarrow \mathrm{null}$. 12:     for each potential centroid $c^{\prime }\in X\setminus C$ do 13:           $\mathrm{current\_gain}\leftarrow 0$. 14:           for each point $x_i\in X$ do 15:                 $d_{old}\leftarrow D\left[i\right]$. 16:                 $d_{new}\leftarrow \left|\right|x_i-c^{\prime }{\left|\right|}^2$. 17:                 $\mathrm{current\_gain}\leftarrow \mathrm{current\_gain}+max(0,d_{old}-d_{new})$. 18:             end for 19:             if $\mathrm{current\_gain}>\mathrm{max\_gain}$ then 20:                 $\mathrm{max\_gain}\leftarrow \mathrm{current\_gain}$. 21:                 $\mathrm{next\_centroid}\leftarrow c^{\prime }$. 22:             end if 23:     end for 24:     $C\leftarrow C\cup \{\mathrm{next\_centroid}\}$.                      ▹ Update distances to the nearest centroid 25:     for each point $x_i\in X$ do 26:           $D\left[i\right]\leftarrow min(D\left[i\right],||x_i-\mathrm{next\_centroid}|{|}^2)$. 27:     end for 28: end for 29: return C.

Greedy K-means++ uses the following initialization procedure:

1.

Randomly select the first centroid.

2.

For each subsequent centroid, perform the following:

(a)

Instead of choosing a single point with probability proportional to $D{\left(x\right)}^2$, several random candidates are generated:

(b)

$$C=\{x_1,x_2,\dots ,x_{10}\}$$

(1)

(c)

For each candidate $x_c\in C$, compute the expected cost:

$$\mathrm{Cost}\left(x_c\right)=\sum _{x\in \mathrm{dataset}}\underset{c^{\prime }\in \mathrm{current}\mathrm{centroids}\cup \left\{x_c\right\}}{min}{\parallel x-c^{\prime }\parallel }^2$$

(2)

(d)

Select the candidate that minimizes the cost:

$$x_{\mathrm{next}}=arg\underset{x_c\in C}{min}\mathrm{Cost}\left(x_c\right)$$

(3)

3.

Repeat the process until K centroids are obtained.

2.2. Parallel Jacobi Method: Computation of Eigenvectors and Eigenvalues

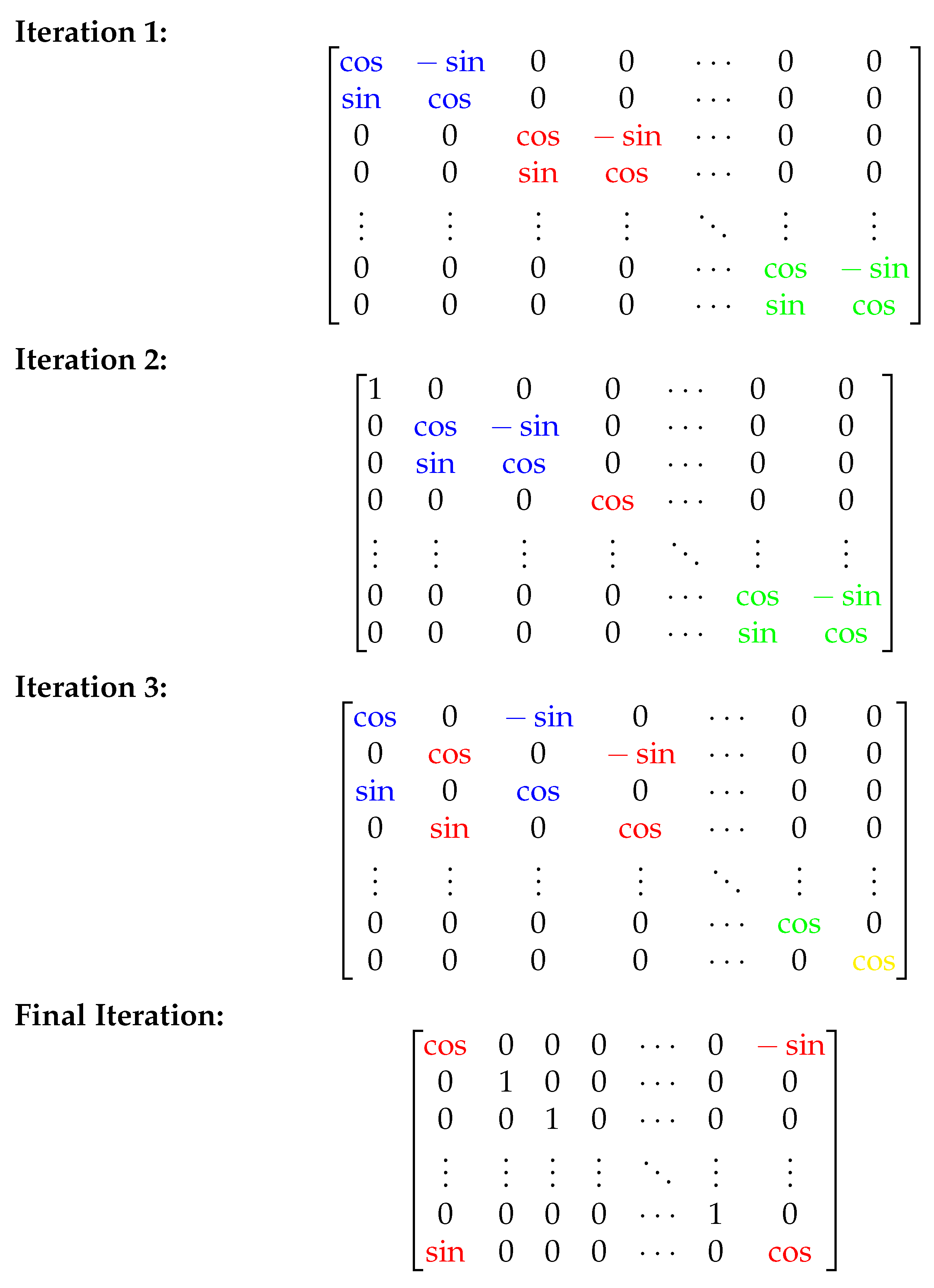
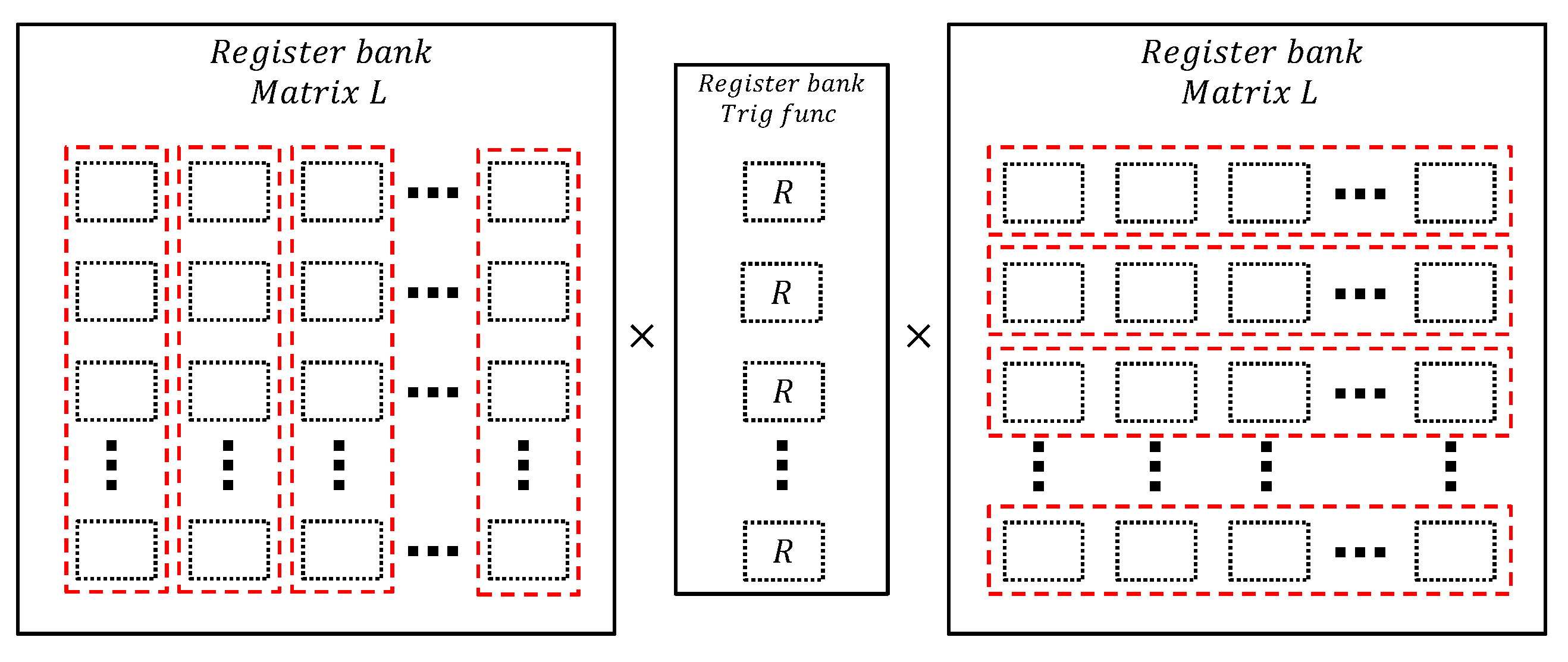
The eigenvector computation uses the Jacobi algorithm, which iteratively zeros the largest off-diagonal elements of a symmetric matrix via plane rotations. The classical Jacobi method requires $O\left(n^2\right)$ comparisons per iteration, making it computationally expensive for large matrices. To address this computational challenge, we implement the Cyclic-by-Row strategy, which traverses fixed pairs of rows and columns in each sweep, avoiding the search for the largest off-diagonal element and enabling more predictable hardware implementation.

This approach enables parallelization, since each Jacobi rotation only affects two rows and columns $(m,n)$, allowing multiple non-overlapping rotations to be performed simultaneously. The block-diagonal structure illustrated in Figure 2 demonstrates how multiple Jacobi rotations can be executed in parallel across different iterations, significantly accelerating convergence and making the algorithm suitable for FPGA hardware implementation. The parallel execution strategy reduces the overall computational latency while maintaining the numerical stability characteristics essential for accurate eigenvalue decomposition in optical communication systems.

3. Hardware/Software Co-Design of the Spectral Clustering Receiver

A hardware/software co-design approach for spectral clustering on a System-on-Chip FPGA enables designers to flexibly partition tasks between the CPU and FPGA, allowing each processing unit to handle operations best suited to its architectural strengths [19]. This collaborative development approach streamlines the design process, supports parallel development, and enables direct iteration and refinement of partitioning decisions on the reconfigurable platform [20]. The ability to rapidly reprogram the FPGA and profile system performance on chip provides valuable feedback, reduces development time, and increases system flexibility, making co-design especially advantageous for complex embedded applications in optical communications.

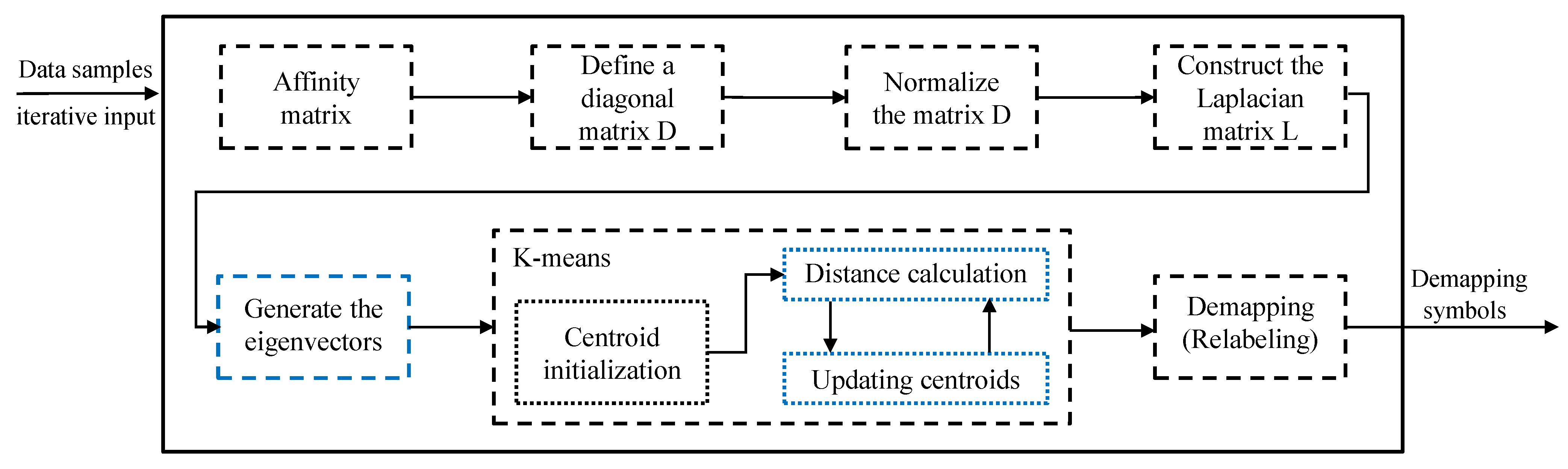
In our implementation, the spectral clustering pipeline is partitioned between the ARM CPU and the FPGA to utilize their respective strengths best. As shown in Figure 3, the ARM Cortex-A53 CPU is responsible for managing data samples, controlling iterative input, performing affinity matrix construction, defining and normalizing the diagonal matrix, constructing the Laplacian matrix, initializing centroids, and handling the final demapping and relabeling steps. The FPGA, in turn, is dedicated to accelerating the most computationally demanding stages, specifically generating the eigenvectors, calculating distances, and updating centroids during the K-means clustering process. This division of tasks allows for efficient resource utilization and demonstrates the potential for further scaling and optimization in real-time signal processing applications for next-generation optical systems [21].

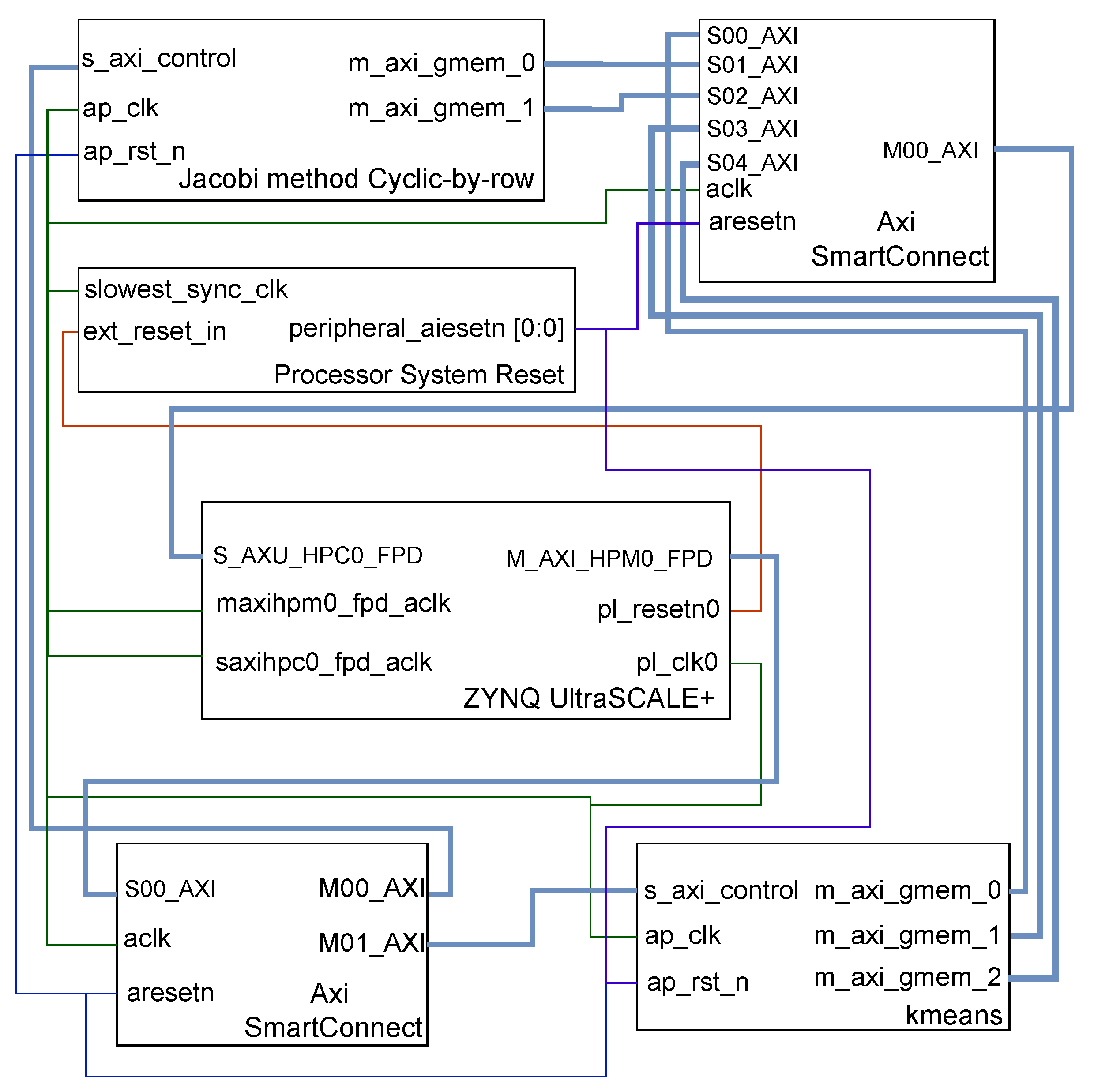
Figure 4 presents a detailed block diagram of the hardware/software co-design architecture implemented on a Zynq UltraScale FPGA platform. It shows the interconnection of key components via AXI interfaces and the flow of control and data signals across the system. At the center is the Zynq UltraScale MPSoC, integrating a processor system (PS) featuring an ARM Cortex-A53 and programmable logic (PL). The diagram highlights the AXI SmartConnect interconnects that facilitate high-bandwidth communication between the processor and programmable logic blocks. Key functional blocks include the hardware implementations of the parallel Jacobi method and the K-means clustering module. These are connected to the processor system through multiple master and slave AXI interfaces (denoted S00AXI, M00AXI, etc.), which support streaming data transfer and control signaling. The figure also shows memory controllers (m_axi_gmem0, m_axi_gmem1, and m_axi_gmem2) connected to dedicated memory banks accessed by computational units. Additionally, peripheral control signals, reset modules, clock domains, and AXI interconnect layers are depicted to illustrate system synchronization and resource management. Overall, the figure portrays a modular and scalable architecture where computationally heavy tasks are offloaded to FPGA logic, while the ARM processor handles coordination, initialization, and relabeling. The comprehensive AXI interconnect structure enables efficient communication and data streaming necessary for real-time spectral clustering.

The architecture operates in data streaming mode, processing incoming data samples without buffering the entire dataset, which is crucial for high-throughput optical communication systems where minimizing latency and resource utilization is essential. The design incorporates a dedicated demapping block that handles cluster labeling to ensure compatibility with m-QAM constellations, correcting inconsistencies arising from windowed processing in the streaming mode.

This section details the implementation’s modular structure, the internal data flow between components, and the strategies employed to optimize the design for FPGA resources.

3.1. Custom Processing Units

In previous work [22], the authors defined custom processing units (CuPUs) to implement complex functions or high-level digital signal processing (DSP) routines, going beyond the simple, clock-independent operations typically associated with processing elements (PEs) in hardware design. Unlike basic arithmetic operations, CuPUs represent complete routines that would require a finite state machine (FSM) and datapath in RTL. The term “custom” emphasizes that these units incorporate specific optimization directives specified by the authors. By executing independent operations, CuPUs enable parallel processing in hardware, supporting improved algorithm performance.

3.2. Parallel Jacobi Method CuPU

The parallel Jacobi rotations are mapped onto FPGA logic blocks, enabling simultaneous updates of matrix elements through the cyclic scheduling approach that ensures all off-diagonal elements are addressed efficiently. This implementation strategy, combined with pipelined arithmetic units for trigonometric operations, enables the practical computation of eigenvectors for moderate-size Laplacian matrices in real-time optical processing scenarios.

In the initial stage of the Jacobi method implementation, a dedicated register bank stores pre-computed values of sine and cosine functions within the range $[0,2\pi ]$, as well as arctangent function values in the range $[-1,1]$. With these pre-stored trigonometric values, matrix multiplications are performed only in positions where values directly affect the Laplacian matrix L, reducing computational overhead and memory access requirements. To enable parallel execution, a complete register bank partition contains the matrix L, and multiple non-overlapping rotation matrices R are defined, allowing simultaneous application of multiple rotations, as demonstrated in Figure 2, and the general scheme of the implementation of the Jacobi method on an FPGA is shown in Figure 5.

3.3. Euclidean Distance CuPU

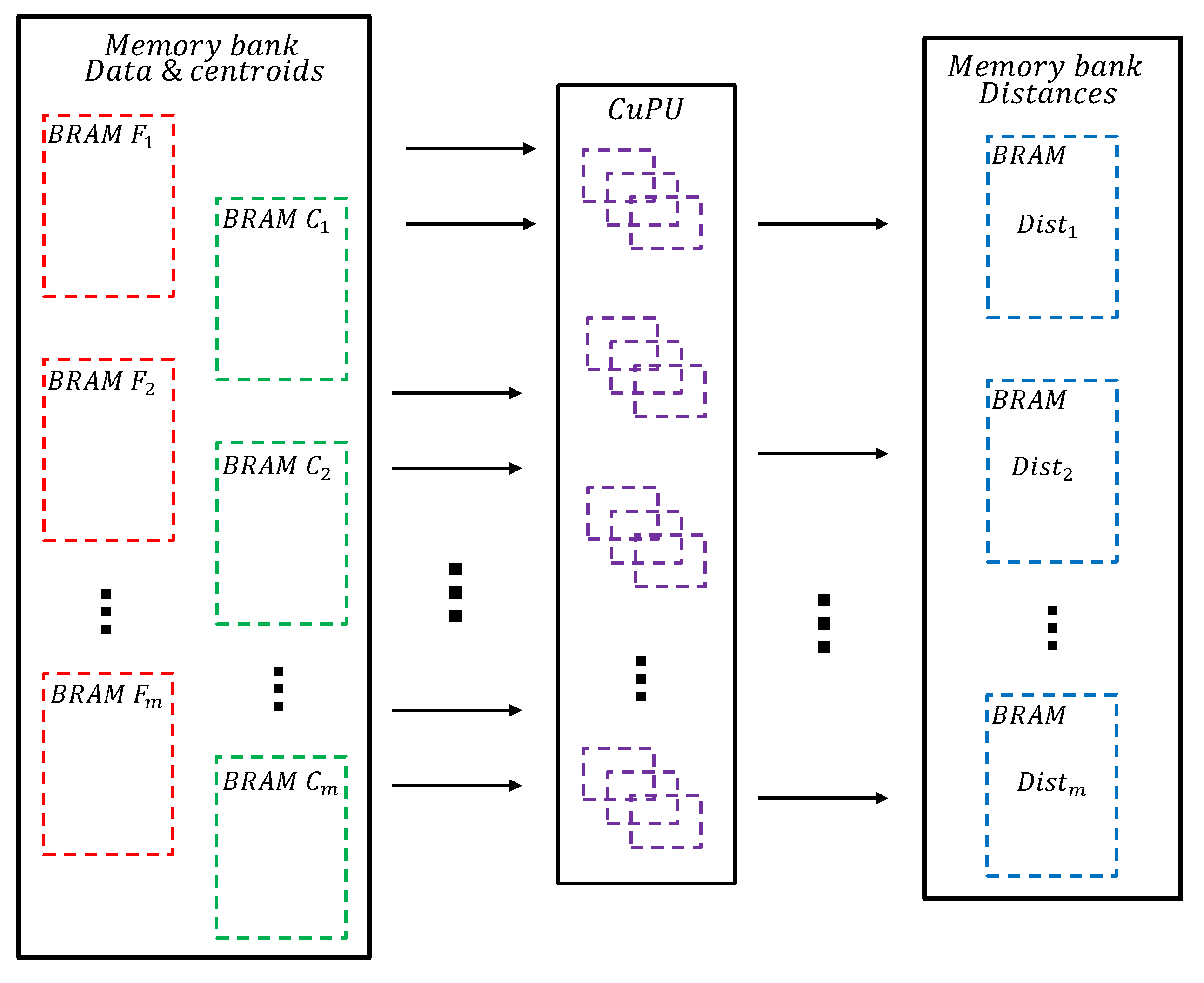
After initializing centroid positions on the CPU, the system proceeds to calculate Euclidean distances between each feature vector and the centroids, representing a fundamental step in the clustering process that enables the assignment of each data point to its nearest centroid.

The Euclidean distance for a point $x=(x_0,x_1)$ and a centroid $c=(c_0,c_1)$ is implemented using the standard formula:

$$\mathrm{distance}=\sqrt{{(x_0-c_0)}^2+{(x_1-c_1)}^2}$$

The Euclidean distance calculation CuPU loads data from dedicated memory banks, where each $BRAM{F}_m$ stores specific features of the data, and each $BRAM{C}_m$ stores the corresponding features of centroids. For example, in a 16-QAM constellation represented in eigenvector space where K-means is applied for data grouping, the implementation utilizes memory blocks $BRAM{F}_1$ through $BRAM{F}_{16}$, each containing 300 data points, while centroid blocks $BRAM{C}_1$ through $BRAM{C}_{16}$ each contain 16 values representing centroid characteristics.

The CuPU performs parallel calculation of Euclidean distances between data points and centroids, storing results in the dedicated distance memory bank, as illustrated in Figure 6.

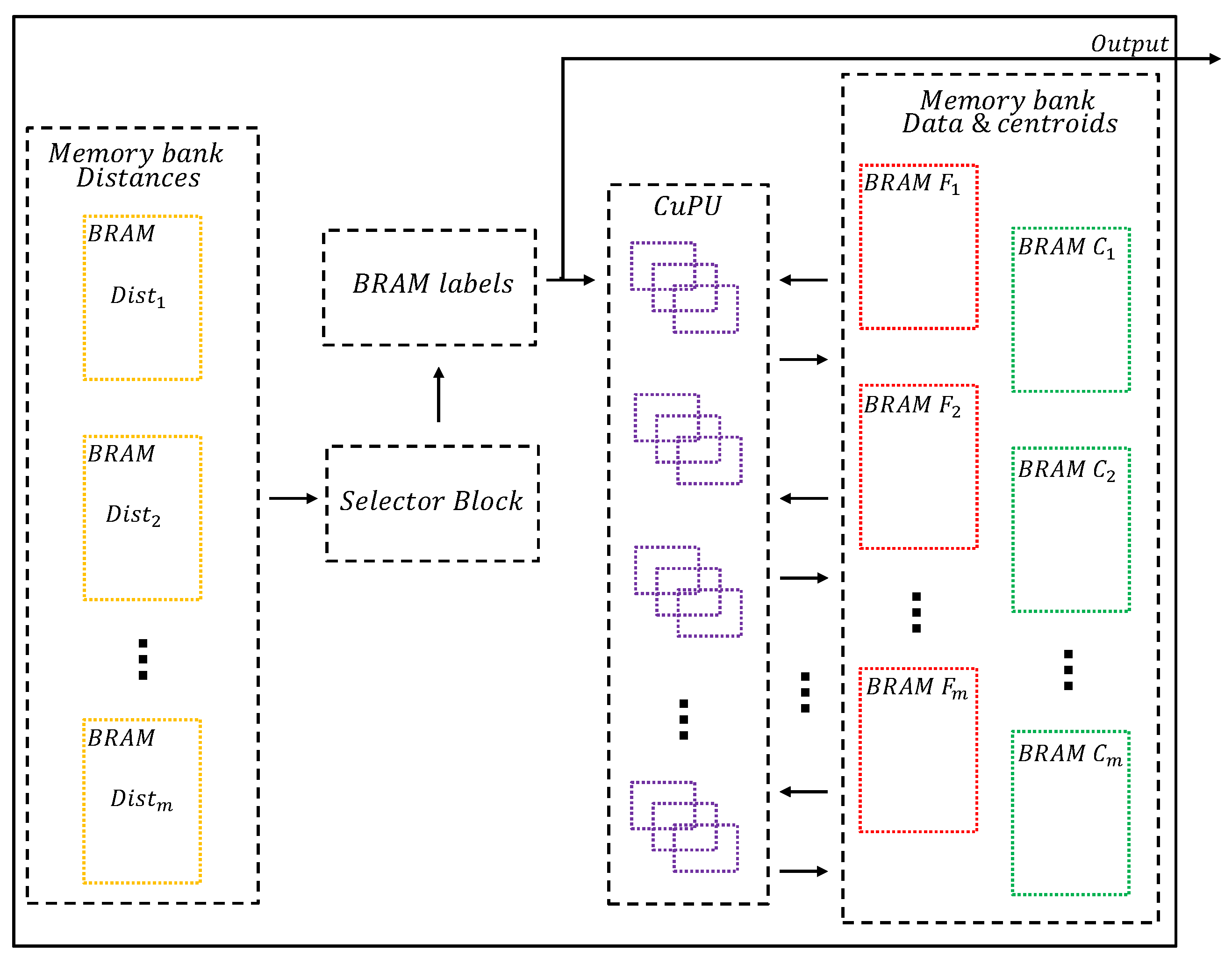
3.4. Centroid Update CuPU

Once labels are assigned based on minimum distance calculations to each centroid, the system enters the centroid update stage, where a selector block accesses corresponding memory addresses in each $BRAMDis{t}_m$ block and compares values to identify the minimum distance. The minimum value is assigned a label indicating which memory block contains the lowest distance, enabling proper cluster assignment. For example, during the first access cycle, the selector block examines the first memory address of each $BRAMDis{t}_m$ and identifies that the minimum value resides in $BRAMDis{t}_4$, consequently assigning label 4 and storing it in BRAM labels $BRAMlabels$.

The value corresponding to that position represents the characteristics of the first data point in the $BRAM{F}_m$ blocks and is utilized by the CuPU to calculate means and update centroids accordingly. In the given example, this value updates the centroid stored in $BRAM{C}_4$, with each label in $BRAMlabels$ being updated during each iteration as centroids are refined. After the iterative process, these labels represent the final data grouping, as demonstrated in the centroid update CuPU architecture shown in Figure 7.

4. Experimental Results

The hardware implementation was synthesized using Xilinx Vivado HLS 2023.1 (Advanced Micro Devices—AMD, Inc., Santa Clara, CA, USA) and targeted the MPSoC ZCU104 Evaluation Kit development board (Advanced Micro Devices—AMD, Inc., Santa Clara, CA, USA), which integrates a Zynq UltraScale+ MPSoC featuring both programmable logic and ARM Cortex-A53 cores operating at a 100 MHz clock frequency. The ZCU104 platform, featuring the XCZU7EV device with 504K system logic cells and 11 Mb of total block RAM (BRAM), represents a mid-range FPGA suitable for proof-of-concept development but inherently constrained for high-throughput applications compared to larger platforms.

The experimental evaluation reveals significant insights into the computational and resource requirements of implementing spectral clustering on reconfigurable hardware platforms. The parallel Jacobi implementation required 705,419,050 cycles (7.05 s at 100 MHz) to process a window of 255 symbols, yielding an effective throughput of approximately 36 symbols per second for 16-QAM modulation. Each symbol consists of two 32-bit floating point values to represent in-phase and quadrature, corresponding to 16,320 bits per second, see

Table 1. Time and resource table taken with a window size of 255. This is the largest window size that can be calculated in the ZCU104 board without exceeding the BRAM resources. The values were obtained from the design synthesis in Vivado.

Spectral Clustering	Latency (Cycles)	BRAM	DSP	FF	LUT
Parallel Jacobi method	705,419,050	122.5	58	11,083	13,178
K-means for spectral clustering	99,074	17.5	112	17,901	13,225
AXI Connect and others	Negligible	0	0	696	850
TOTAL	705,518,124	140	170	38,364	31,092

. While this performance is insufficient for commercial transceivers operating at multi-gigabit rates, it establishes a critical baseline for FPGA-based spectral clustering implementations and exposes fundamental system bottlenecks that limit scalability. To further illustrate the hardware acceleration effect, we compared the execution time of the complete spectral clustering algorithm processing a window of 255 symbols on both a non-parallel CPU (ARM-only) implementation and the heterogeneous ARM+FPGA implementation with parallel Jacobi eigenvector computation. Each timing measurement corresponds to 10 repetitions, accounting for system variability due to the operating system running on the ARM processor. The CPU implementation achieved a mean runtime of 81.89 with a standard deviation of 0.38 s, while the FPGA-accelerated implementation completed the task in 6.35 with a standard deviation of 0.01 s, yielding an approximate $13\times$ speedup. This significant reduction in processing time demonstrates the effectiveness of FPGA-based parallelization and hardware/software co-design in accelerating the computationally intensive spectral clustering algorithm for real-time optical communication applications.

Table 2. Comparison of execution times and speedup between the non-parallel CPU (ARM-only) implementation and the heterogeneous ARM + FPGA implementation of the spectral clustering algorithm processing a window of 255 symbols. The reported timings correspond to mean values over 10 repetitions, with the associated standard deviation representing measurement variability.

Architecture	Execution Time [s]	Speedup
ARM	81.890330 ± 0.378422	1
ARM + FPGA	6.354489 ± 0.013957	13

summarizes the comparison of computation times for spectral clustering and K-means.

The resource utilization analysis presented in Table 1 demonstrates that the implementation consumed 140 of 312 available BRAM blocks (44.8% utilization) on the ZCU104 platform, representing near-complete saturation of memory resources. The DSP slice utilization reached 170 out of 1728 available (9.8%), indicating that computational units were not the primary limiting factor in the system design. This resource distribution pattern highlights the memory-intensive nature of spectral clustering algorithms, where the construction and storage of the affinity matrix dominate system requirements rather than arithmetic computation capabilities. The K-means module was used in spectral clustering, processing 16 features, 16 centroids, and 255 data points after eigenvector computation. Additionally, the K-means algorithm is applied directly to the data as a baseline. For this reason, there are only two features (in-phase and quadrature), see

Table 3. Resources and latency summary for K-means module.

Module	Latency (Cycles)	BRAM	DSP	FF	LUT
K-means	96,077	9.3	14	4608	9216

.

Table 4. This table shows the times corresponding to the execution times of the spectral clustering modules that are executed on the PC, specifically on the ARM processor within the heterogeneous architecture on the ZCU104 board.

Process	Average Execution Time (μs)
Start to matrix L	18,821.8
Matrix X to centroid initialization	6204.5
Relabeling	188.2

presents the execution times for spectral clustering modules implemented on the ARM processor within the heterogeneous architecture, with the matrix L construction requiring 18,821.8 μs, representing a significant portion of the total processing time.

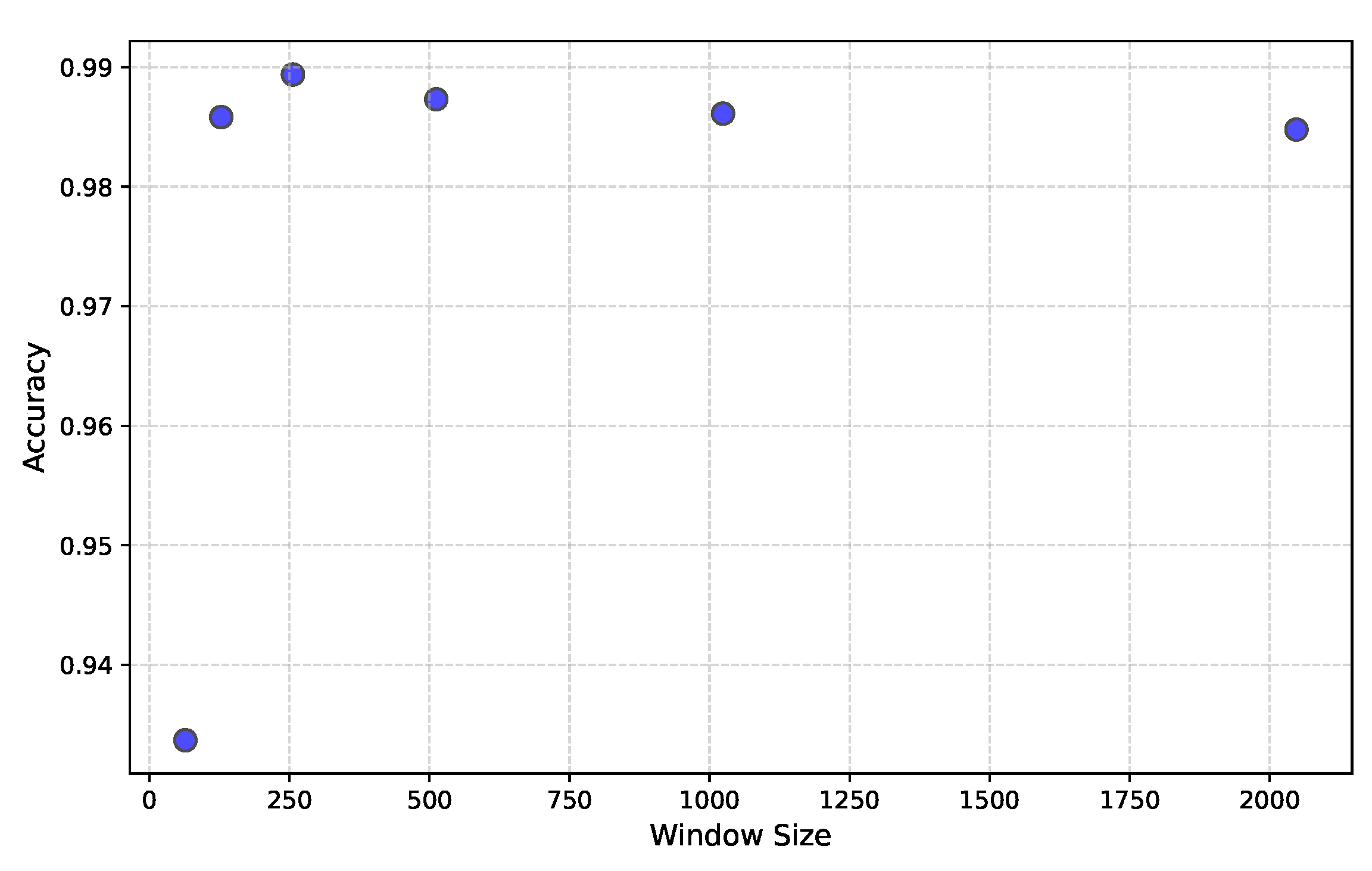
The relationship between window size and clustering accuracy, demonstrated in Figure 8, shows that performance stabilizes for window sizes of approximately 250 symbols or larger, validating the implementation’s design choice of 255 symbols as an optimal trade-off between accuracy and resource utilization given the BRAM constraints.

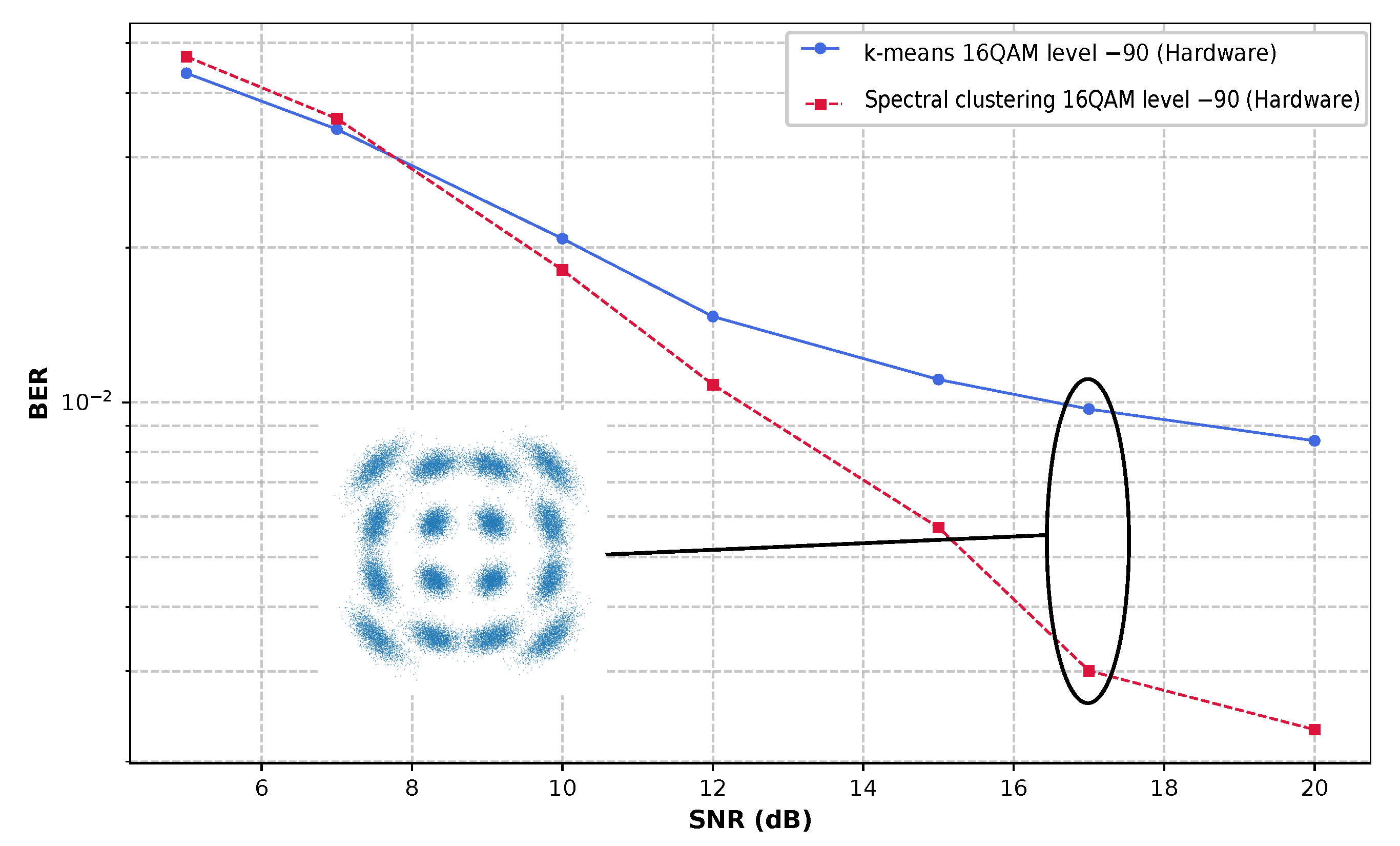
Under severe phase noise conditions (−90 dBc/Hz at a 1 MHz offset), as shown in Figure 9, the spectral clustering algorithm demonstrated superior bit error rate performance compared to K-means for 16-QAM signals, with the performance advantages becoming more pronounced as constellation complexity increased.

A comparative summary of the implemented methods is presented in

Table 5. Comparison of spectral clustering and K-means implementations.

Method	Accuracy	Latency	Resource Usage	Notes
Spectral clustering (this work)	High	High	High	Robust to nonlinear phase noise
K-means	Medium	Low	Low	Not robust under nonlinear phase noise

. Spectral clustering, as proposed in this work, achieves higher accuracy and demonstrates robustness against nonlinear phase noise, albeit at the cost of increased latency and resource usage due to the complexity of eigenvector decomposition and affinity matrix construction. In contrast, the FPGA-only K-means implementation offers lower latency and reduced resource consumption; however, its accuracy degrades significantly under severe noise conditions, thereby limiting its applicability in nonlinear optical channels. This comparison highlights the trade-off between computational complexity and noise robustness, underscoring the advantages of spectral clustering for advanced optical receiver architectures despite current hardware limitations.

5. Discussion

Our FPGA implementation reveals intrinsic constraints for spectral clustering on reconfigurable hardware platforms, where parallel processing capabilities must be carefully balanced against memory bandwidth limitations imposed by the target device architecture. The ZCU104 platform’s resource constraints, while suitable for algorithm validation and proof-of-concept development, expose fundamental challenges of implementing computationally intensive clustering algorithms in resource-constrained embedded environments.

The 7.05 s processing latency per window primarily stems from memory access patterns rather than computational complexity, as evidenced by the low DSP utilization (9.8%) compared to near-complete BRAM saturation (44.8%). This pattern aligns with recent research on FPGA-based matrix computations, which identifies memory bandwidth as the primary bottleneck rather than arithmetic capability in modern reconfigurable computing systems. The parallel Jacobi implementation, while reducing eigenanalysis complexity through spatial parallelization, still faces convergence challenges that scale with matrix dimensions and require an average of 22 iterations for acceptable numerical accuracy.

While recent implementations of machine learning-based nonlinearity compensation have achieved higher throughputs using GPU acceleration or specialized hardware for simpler clustering algorithms, our work demonstrates the feasibility of spectral clustering using heterogeneous CPU/FPGA co-design. Our implementation partitions the algorithm between ARM processors and the FPGA fabric, with the FPGA handling computationally intensive eigenanalysis through parallel Jacobi rotations while the CPU manages data flow and high-level control. This co-design strategy enables efficient resource utilization and provides a practical framework for implementing complex clustering algorithms in embedded optical systems.

The power efficiency characteristics of FPGA implementations, although not explicitly quantified in this work, typically demonstrate advantages over GPU-based alternatives for streaming DSP applications, particularly when algorithms can be spatially parallelized, as demonstrated in our Jacobi rotation scheme. This efficiency advantage becomes more significant in scenarios where sustained processing is required rather than burst computation, making FPGAs attractive for continuous optical signal processing applications.

The identified bottlenecks in memory bandwidth and eigenvalue computation convergence directly inform optimization priorities for future implementations targeting higher-throughput optical systems. Mixed-precision arithmetic could reduce resource overhead while maintaining clustering accuracy, particularly for eigenvalue computation stages where full precision may not be required throughout the entire algorithmic pipeline. The transition to larger FPGA platforms, such as the Virtex UltraScale+ family with integrated high-bandwidth memory, could alleviate memory constraints while providing significantly higher computational resources for more demanding applications.

6. Conclusions and Future Work

This work demonstrates the first complete SoC-FPGA hardware implementation of spectral clustering for optical communication receivers, including on-chip eigenvector and eigenvalue computation, using a parallel Jacobi method integrated within a heterogeneous CPU/FPGA co-design framework. Although the achieved processing speeds of approximately 36 symbols per second do not meet the requirements for commercial optical transceivers, our implementation validates the feasibility and exposes the practical challenges of deploying advanced clustering algorithms in real hardware systems.

The experimental results establish BRAM bandwidth as the fundamental limiter for windowed clustering architectures on FPGA platforms, with 44.8% memory utilization representing a critical constraint that affects both scalability and performance. Our implementation provides comprehensive insights into the memory–compute trade-offs inherent in spectral clustering algorithms, where the construction and storage of the affinity matrix dominate resource requirements rather than arithmetic operations. The superior performance of spectral clustering over K-means under severe phase noise conditions (−90 dBc/Hz at a 1 MHz offset) validates its potential for next-generation optical receivers despite current implementation constraints.

This work provides a valuable reference for future research and optimization in hardware-accelerated optical signal processing, highlighting the essential role of FPGAs as a bridge between algorithm development and the deployment of high-speed optical systems. The comprehensive characterization of performance bottlenecks and resource utilization patterns establishes a foundation for future optimization efforts, guiding the development of next-generation hardware architectures for intelligent optical receivers.

Future work should focus on architectural optimizations, including the use of mixed-precision arithmetic to reduce resource overhead, the exploration of advanced memory architectures to alleviate bandwidth constraints, and the investigation of hybrid algorithmic approaches that combine the strengths of spectral clustering with complementary techniques. The migration to application-specific integrated circuits (ASICs) or larger FPGA platforms with enhanced memory subsystems represents a promising pathway to overcome current throughput limitations while maintaining the algorithmic advantages demonstrated in this work. Additionally, integrating spectral clustering with emerging machine learning techniques could leverage complementary strengths for adaptive nonlinear compensation in next-generation optical communication systems.