Applications of Computational Mechanics Methods Combined with Machine Learning and Neural Networks: A Systematic Review (2015–2025)

Abstract

This review paper analyzes the recent applications of computational mechanics methods in combination with machine learning (ML) and neural network (NN) techniques, as found in the literature published between 2015 and 2024. We present how ML and NNs are enhancing traditional computational methods, such as the finite element method, enabling the solution of complex problems in material modeling, surrogate modeling, inverse analysis, and uncertainty quantification. We categorize current research by considering the specific computational mechanics tasks and the employed ML/NN architectures. Furthermore, we discuss the current challenges, development opportunities, and future directions of this dynamically evolving interdisciplinary field, highlighting the potential of data-driven approaches to transform the modeling and simulation of mechanical systems. The review has been updated to include pivotal publications from 2025, reflecting the rapid evolution of the field in multiscale modeling, data-driven mechanics, and physics-informed/operator learning. Accordingly, the timespan is now 2015–2025, with a focused inclusion of high-impact contributions from 2024 to 2025.

1. Introduction

In the last decade, computational mechanics has entered into an intensive dialog with machine learning and neural networks, and the aim of this synergy is not to replace well-established numerical tools, but to complement them, that is, to introduce physical knowledge into data models, accelerate costly computations, create surrogate models, and solve inverse problems under limited measurement information [1,2]. Recent reviews emphasize that combining physics-based and data-driven methods sets new standards of accuracy and computational efficiency, while also structuring engineering practices in the areas of material, flow, and structural modeling [3].

At the center of this shift are physics-informed approaches, in which physics-informed neural networks introduce initial-boundary equations directly into the loss function, enabling the solution of forward and inverse problems without full measurement fields [4,5]. In parallel, operator learning is developing, from Fourier operators FNO to DeepONet networks, which learn mappings between function spaces and create fast PDE surrogates, independent of mesh resolution [2,5]. For complex geometries and nonlinear couplings, graph neural networks are gaining importance, representing fields and conservation laws directly on mesh elements or point clouds, opening the way to multiple accelerations of fluid and solid mechanics simulations.

The integration of computational and data-driven methods brings particularly large benefits in constitutive modeling, multiscale modeling, uncertainty quantification, and inverse analysis. Data at the microstructural level can be compressed into deep material networks, which learn effective constitutive laws and transfer them to structural analyses at the macroscale [6]. In parallel, data-driven mechanics abandons explicit material laws in favor of direct work on datasets consistent with conservation principles, becoming a real alternative to classical FEM in material and structural tasks [3]. Advances in constitutive learning include enforcing polyconvexity and other thermodynamic conditions in neural models, and improving the stability and physical consistency of hyperelasticity descriptions [7]. At the same time, Bayesian methods for PINN, including B-PINN, enable reliable uncertainty estimation and robust identification of material parameters from noisy data, while cross-cutting UQ frameworks for scientific machine learning organize quality metrics, inference strategies, and comparative procedures needed in engineering practice [8,9].

Although physics-informed neural networks (PINNs) and operator learning methods such as the Fourier Neural Operator (FNO) and DeepONet have demonstrated strong capabilities in solving complex mechanics problems, several limitations have also been reported. These include sensitivity to the relative weighting of loss function terms, rigid dependence on hyperparameter tuning, and challenges in representing complex geometries or three-dimensional contact conditions. Recent studies suggest possible remedies, such as dynamic loss balancing, variational enforcement of boundary conditions, or domain decomposition strategies. While these techniques mitigate some of the difficulties, they highlight that the practical deployment of PINN and operator-learning approaches still require careful design and transparent reporting of model assumptions.

Surrogates and reduced-order models play an important role, replacing costly computations with fast approximations without losing key physical features. In fluid dynamics, convolutional networks and autoencoders have been shown to complement missing information and improve the resolution of turbulent fields, as well as create nonlinear reduced models for chaotic flows. Operator approaches FNO and DeepONet transfer this idea to the level of learning mappings between functions, combining generalizability with very high computational accelerations [2,5]. The common denominator is the ability to combine physical knowledge, data, and uncertainty estimation in a single workflow, which supports applications in design, diagnostics, and control [10].

Data-driven design is dynamically developing, including topology optimization, where generative models, such as GANs and diffusion models, shorten design time by quickly approximating material distributions and physical fields, as well as facilitating multi-criteria trade-offs, previously unattainable within reasonable computation time. From an application perspective, similar techniques are penetrating automotive engineering, for example, into lane detection and risk assessment of events, which further motivates the development of methods combining mechanics, computer vision, and uncertainty quantification [10].

Recent advances in data-driven computational mechanics have also highlighted the importance of targeted data enrichment. For example, adaptive sampling strategies have been proposed to systematically expand material databases in regions of high prediction error, thereby improving the robustness of surrogate models in both forward and inverse tasks [11]. Randomized solvers and adaptive error driven data augmentation now allow data-driven frameworks to escape local minima and deliver more stable convergence in large scale applications. These developments emphasize that the reliability of data-driven approaches depends not only on model architecture but also on the design and coverage of the underlying datasets [12].

In parallel, multiscale modeling has increasingly benefited from hybrid strategies coupling reduced-order bases with deep neural surrogates. Recent studies demonstrate that combining POD compression with transformer-based networks or convolutional encoders enables accurate stress–strain predictions at the macroscale while significantly reducing the computational burden of generating representative volume element (RVE) responses [13,14]. This offline and online separation, where the cost of database generation is balanced by notable speedups in macroscale simulations, illustrates how multiscale approaches are moving closer to real-time engineering design environments. At the same time, physics-informed neural networks (PINNs) and operator learning methods such as Fourier Neural Operators (FNOs) and DeepONets are gaining prominence [15].

This article organizes these achievements and focuses on publications from 2015 to 2024, with the compilation prepared based on a search in the Scopus database, followed by manual content qualification, and visualizations of concept co-occurrence carried out in the VOSviewer program. The categories of analysis and the assumptions for data selection correspond to the thematic scope of the Special Issue of Applied Sciences, which concerns intelligent systems and tools for optimal design in mechanical engineering, and to the keywords defined in the article project description, which constitutes our source file, together with query details, sample size, and classification rules.

This review has been prepared to organize the dynamically growing but still fragmented body of research at the intersection of computational mechanics and data-driven methods. In contrast to previous studies focusing on narrow topics, such as PINN alone, constitutive models, or surrogate methods, this article presents a coherent and multidimensional taxonomy of the entire field. It is based on five axes of analysis, namely categories of computational mechanics tasks, families of ML/NN methods, document types, research geography, and methodological approaches. The foundation is a clearly defined and reproducible query in the Scopus database, covering the TITLE–ABS–KEY fields, with precise domain and language constraints. The distinctive contribution of this work is the combination of thematic synthesis with quantitative analysis, including the use of statistical significance tests (χ²). This made it possible to separate lasting trends from random fluctuations and to indicate where an actual change in research profile occurred (for example, a shift in emphasis toward deterministic methods and material modeling), and where the field structure remained stable.

After the Introduction, Section 2 presents the methodological framework, including the study design, the query applied in the Scopus database, qualification criteria and the publication selection process, the adopted classification scheme, as well as the principles of data extraction and the bibliometric tools used. Section 3, entitled State of the Art, is divided into four parts. The first part (Section 3.1) discusses computational mechanics and modeling methods, presenting six main task categories and their application in solving differential equations, constitutive modeling, inverse analysis, and surrogate model construction. The second part (Section 3.2) concerns machine learning and neural network methods, characterizing three basic families of approaches and their role as tools for approximating physical phenomena, uncertainty quantification, and inverse design. The third part (Section 3.3) focuses on future directions of development, pointing out, among others, the importance of differentiable solvers, models with physical guarantees, as well as the standardization of validation and uncertainty quantification procedures. The fourth part (Section 3.4) summarizes the findings so far. Section 4 presents a statistical picture of the research field, showing quantitative results and significance tests regarding the distributions of thematic categories, document types, and geography publication. Section 5 contains the discussion, which combines qualitative and quantitative conclusions, as well as addressing limitations and practical implications of the results. The article concludes with Section 6, which presents final conclusions, formulating synthetic recommendations regarding further research and implementation opportunities. Such a content structure guides the reader logically from the discussion of methods and data, through quantitative and statistical analyses, to practical conclusions, ensuring consistency of narrative and clarity of the entire presentation of results.

To reflect the ongoing acceleration of research, the corpus and discussion now include 2025 contributions, particularly on multiscale FE²/UMAT–NN couplings, data-driven computational mechanics, and PINN/operator learning (e.g., recent Comput. Methods Appl. Mech. Eng. articles). This update strengthens both the state-of-the-art synthesis and the forward-looking recommendations.

2. Materials and Methods

Section 2 organizes the methodological framework of the review and guides the reader from the overall research concept to the details of data acquisition, selection, and processing. First, the study design and data source are presented, together with the rationale for choosing Scopus as the sole controlled repository, as well as the specification of temporal, linguistic, and disciplinary scope. Next, the search strategy is outlined, including the full query applied to the title, abstract, and keyword fields, along with imposed restrictions and filters. Subsequent sections describe the inclusion and exclusion criteria and the two-stage selection procedure with reference to the PRISMA scheme, ensuring transparency and replicability of the process. A consistent classification scheme was also introduced, covering computational mechanics categories and ML and NN method classes, and additionally the authors’ affiliation countries, document types, and methodological approaches. The chapter further explains the principles of field extraction from records, the set of comparative measures used, and the bibliometric tools, including term density maps and co-occurrence networks prepared in VOSviewer, with appropriate figure captions and reference to the tool’s source publication. These methodological frames comply with the requirements of the Special Issue of Applied Sciences devoted to intelligent systems and tools for optimal design in mechanical engineering.

In Section 2, a complete and reproducible methodological framework was built, ranging from query design to classification and visualization, which made it possible to form a coherent corpus of publications and prepare the ground for substantive and quantitative analyses in the subsequent parts of the study. The sources and search parameters were defined, clear inclusion and exclusion criteria established, selection documented in the PRISMA scheme, a five-dimensional classification framework introduced, the set of extraction fields and comparative measures determined, and bibliometric tools described together with their limitations. Thanks to this chapter, the subsequent narrative is based on a transparent process and comparable data, which strengthens the credibility of the conclusions of the entire article.

2.1. Research Design and Data Sources

The study was designed as a systematic review with a bibliometric analysis component, aimed at identifying and synthesizing applications of machine learning and neural network methods in combination with computational mechanics methods, particularly in the areas of material modeling, surrogate models, inverse analysis, and uncertainty. The only controlled data source was the Scopus database, the search was conducted in the combined fields of title, abstract, and keywords, and the scope was limited to the years 2015–2024, the English language, and the subject areas Computer Science and Engineering, which ensures metadata consistency and reproducibility of the procedure. In the first step, a query defined around the phrase Computational Mechanics in connection with Machine Learning or Neural Networks returned 109 records, then after applying a keyword filter for AI method classes, 101 publications were obtained, and after removing three out-of-scope items, the final corpus comprised 98 papers, which were subjected to further analysis. These data comes from the working file accompanying the article, including the full Scopus query and a description of the constraints, which makes it possible to faithfully reproduce the search.

The selection procedure was designed in two stages: First, topical relevance was assessed based on metadata and abstracts, then the full text was analyzed in the case of included or ambiguous items, while in parallel a consistent classification scheme was prepared. Each publication was assigned across five interdependent dimensions: to a category from the group Computational Mechanics Methods and Modeling, namely Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, Inverse Analysis; to an AI method class, namely Core Neural Networks, Deep Neural Networks, General Machine Learning; to the country of authors’ affiliation based on Scopus data; to the document type, namely Conference Paper, Article, Other; and to the methodological approach, namely Experiment, Literature Analysis, Case Study, Conceptual, determined on the basis of content. This structure enables cross-sectional comparisons and mapping of the research landscape from the perspective of computational mechanics tasks and algorithmic classes.

To ensure transparency and reproducibility, a complete set of materials, including the exact wording of the query with filters, the list of 98 records with metadata (namely authors, affiliations, DOI identifiers, and keywords), and input files for bibliometric visualizations, was archived in the open Zenodo repository under the DOI: https://doi.org/10.5281/zenodo.17116232. To generate term density and keyword co-occurrence maps, the VOSviewer software (version 1.6.20) was used, with each visualization accompanied by the recommended caption indicating the tool’s origin and citing the source publication of VOSviewer. This structured design meets MDPI requirements for methodological transparency, facilitates replication of the search and classification, and provides the basis for a reliable synthesis of results in the subsequent sections of the article.

2.2. Search Strategy

The search strategy was based exclusively on the Scopus database in order to ensure high metadata quality, consistent filtering, and full reproducibility. The results were limited to English-language publications in the subject areas of Computer Science and Engineering, within the years 2015–2024, and the search was conducted jointly in the Title, Abstract, and Keyword fields. This procedure was defined to match the scope of the review, which combines computational mechanics with machine learning and neural network methods.

The search was carried out in two steps. The first step identified literature on computational mechanics in connection with AI in a broad sense, while the second step refined the list using keywords for ML and NN method classes. The following query was applied to the TITLE, ABS, and KEY fields, covering the timespan, language, and two Scopus subject areas, together with a list of keywords describing computational mechanics tasks and methods:

„TITLE-ABS-KEY(“Computational Mechanics” AND (“Machine Learning” OR “Neural Networks”)) AND PUBYEAR > 2014 AND PUBYEAR < 2025 AND (LIMIT-TO (SUBJAREA,”COMP”) OR LIMIT-TO (SUBJAREA,”ENGI”)) AND (LIMIT-TO (LANGUAGE,”English”)) AND (LIMIT-TO (EXACTKEYWORD,”Finite Element Method”) OR LIMIT-TO (EXACTKEYWORD,”Inverse Problems”) OR LIMIT-TO (EXACTKEYWORD,”Surrogate Modeling”) OR LIMIT-TO (EXACTKEYWORD,”Constitutive Models”) OR LIMIT-TO (EXACTKEYWORD,”Uncertainty Analysis”) OR LIMIT-TO (EXACTKEYWORD,”Stochastic Systems”) OR LIMIT-TO (EXACTKEYWORD,”Elastoplasticity”) OR LIMIT-TO (EXACTKEYWORD,”Elasticity”) OR LIMIT-TO (EXACTKEYWORD,”Surrogate Model”) OR LIMIT-TO (EXACTKEYWORD,”Plasticity”) OR LIMIT-TO (EXACTKEYWORD,”Multiscale Modeling”) OR LIMIT-TO (EXACTKEYWORD,”Mesh Generation”) OR LIMIT-TO (EXACTKEYWORD,”Finite Element Analyse”) OR LIMIT-TO (EXACTKEYWORD,”Constitutive Modeling”) OR LIMIT-TO (EXACTKEYWORD,”Stochastic Models”) OR LIMIT-TO (EXACTKEYWORD,”Stress Analysis”) OR LIMIT-TO (EXACTKEYWORD,”Degrees Of Freedom (mechanics)”) OR LIMIT-TO (EXACTKEYWORD,”Boundary Value Problems”))”.

Next, a refining keyword filter has been added for the ML and NN methods:

„AND (LIMIT-TO (EXACTKEYWORD,”Machine Learning”) OR LIMIT-TO (EXACTKEYWORD,”Neural Networks”) OR LIMIT-TO (EXACTKEYWORD,”Neural-networks”) OR LIMIT-TO (EXACTKEYWORD,”Deep Learning”) OR LIMIT-TO (EXACTKEYWORD,”Learning Systems”) OR LIMIT-TO (EXACTKEYWORD,”Deep Neural Networks”) OR LIMIT-TO (EXACTKEYWORD,”Artificial Neural Network”) OR LIMIT-TO (EXACTKEYWORD,”Recurrent Neural Networks”) OR LIMIT-TO (EXACTKEYWORD,”Convolutional Neural Network”) OR LIMIT-TO (EXACTKEYWORD,”Convolutional Neural Networks”))”.

In the first step, 109 records were obtained, after applying the second filter, 101 records remained, and after manual verification, three out-of-scope items were removed, resulting in a final corpus of 98 publications selected for extraction and classification. The full wording of the queries, the lists of keywords, and the counts at the stages of identification, screening, and qualification are available in the Zenodo repository, which strengthens the transparency and reproducibility of the research procedure.

The process of data collection and preparation is illustrated in Figure 1, the diagram has a vertical layout with four sequentially connected blocks and arrows, without color coding.

The top block presents the full Scopus query together with year, subject area, and language restrictions. The next block shows the narrowing through computational mechanics keywords, followed by the block presenting the ML and NN method filter, and beneath it the information on the size of the final corpus, 98 articles. The lower part of the diagram organizes the classification framework used in the subsequent analysis, namely the computational mechanics tasks, that is, Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, and Inverse Analysis; the AI method classes, that is, Core Neural Networks, Deep Neural Networks, and General Machine Learning, as well as categories based on Scopus metadata, authors’ affiliation countries, document types, and the manually determined research methodology; Experiment, Literature Analysis, Case Study, and Conceptual. Thus, the figure provides a concise, black-and-white guide to the query and classification principles applied in this review.

The articles qualified for analysis were described and compiled in the form of working files, which, together with metadata and input files for visualization, were archived in the open Zenodo repository. The repository contains Excel files including the responses to the Scopus queries, with complete metadata (titles, authors, affiliations, DOIs, keywords), as well as the input files used in the bibliometric analyses. Full texts of the articles are not provided there, as they are available online through Scopus and other publisher repositories. This dataset ensures transparency, durability, and reproducibility of the results, and enables reuse of the corpus in future updates. The literature selected for analysis covers references [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112]. This corresponds to a corpus of 98 publications that met the established substantive and formal criteria, identified through the Scopus search query, a two-stage screening procedure, and keyword normalization.

While the TITLE–ABS–KEY filter ensured high precision of the query, such a strict strategy may also exclude relevant contributions that use alternative terminology. To reduce this bias, we constructed a normalization vocabulary. For example, operator learning is also referred to as neural operators, graph neural networks are also termed GNN, GCN or MGN, and finite element analysis is often used interchangeably with finite element method. Nevertheless, a small number of false negatives were identified. For instance, papers describing neural operator surrogates without explicitly using the phrase operator learning, or studies on graph message-passing networks without the exact term graph neural networks, were not captured by the automatic query. We therefore complemented the Scopus search with targeted manual screening of references in leading review articles and high-impact journals. This procedure increases recall while keeping transparency about the possible bias introduced by strict keyword matching.

2.3. Rationale for the Review, Purpose of the Study and Problems of the Study

Previous studies at the intersection of computational mechanics and data-driven methods are fragmented, often focusing on single tasks or algorithm classes, and rarely covering the full spectrum of problems, that is, numerical methods, material modeling, multiscale modeling, surrogate models, stochastic methods and uncertainty, and inverse analysis, in combination with the three families of approaches, that is, machine learning, core neural networks, deep neural networks. There is a lack of a coherent taxonomy that integrates these axes with unified quality and computational cost metrics, as well as a lack of transparent criteria for literature selection and explicit rules for terminology normalization. This review fills these gaps, being based on a clearly defined Scopus query covering the years 2015–2024, the English language, and the subject areas Computer Science and Engineering, with a final corpus of 98 publications after manual scope verification. Five interdependent classification dimensions were adopted, namely computational mechanics tasks, AI method classes, country of authors’ affiliation, document type, and methodology, which enables cross-sectional comparisons and identification of thematic and methodological gaps.

The review distinguishes itself from earlier work in three respects. First, it presents a comprehensive cross-section of applications, linking initial–boundary value problems, constitutive models, and multiscale issues with specific classes of learning architectures, which allows algorithmic solutions to be related to physical requirements and computational constraints. Second, it introduces a bibliometric layer based on explicit metadata and VOSviewer visualizations, which enables quantitative assessment of field dynamics, term co-occurrence, as well as the geographic and document-type distribution. Third, it ensures full reproducibility, providing the exact wording of the query, inclusion and exclusion criteria, the classification structure, and the compiled records deposited together with input files for visualization, which meets editorial transparency requirements and facilitates future updates.

The main objective of the review is to provide synthetic ordering and critical assessment of applications of machine learning and neural networks in computational mechanics, with mapping of tasks against data types, modes of embedding physical knowledge, and computational costs, as well as identification of research priorities relevant to engineering practice, including reliability, scalability, and reproducibility. The study poses the following research questions:

• What classes of problems in computational mechanics dominate the literature, and what integration patterns with data-driven methods are most frequently applied, that is, physics-informed loss functions, operator learning, graph networks, and in which configurations they yield the greatest qualitative benefits.
• What data types, geometry and mesh representations, and boundary condition and validation schemes are reported in the analyzed works, and which combinations provide the best compromise between accuracy and computational cost.
• To what extent do publications account for uncertainty quantification, verification and validation, and report computational costs, for example, accelerations relative to reference solvers and hardware requirements, and what conclusions follow for engineering practice.
• Whether, in the years 2015–2024, there was a significant growth trend in the number of publications across the six computational mechanics categories, and what the cumulative growth rate was over the entire period.
• Whether the structure of methods changes over time, that is, whether the share of works using deep neural networks increases compared to core neural networks and classical machine learning, and whether the observed changes are statistically significant.
• How the distribution of document types and authors’ affiliation countries evolves in the studied period, and whether the share of journal articles increases relative to conference papers, and whether geographic concentration intensifies, with an assessment of the significance of these trends.

The first three questions are substantive in nature, allowing identification of dominant tasks in computational mechanics, revealing thematic gaps, and assessing the readiness of methods for operation in engineering environments, with reliable uncertainty information and the possibility of integration into design and maintenance processes. The remaining three questions are statistical, measuring the popularity of the topic and the dynamics of the research field, including analyses of annual trends, cumulative growth rates, and significance tests of changes in method shares and publication forms. This set of problems structures the practical and quantitative objectives of the review, enabling coherent analysis and unambiguous interpretation of results in the subsequent sections.

The outcome of the substantive component will be an organized taxonomy of tasks and methods, cross-tables of method by task, and evidence cards for representative case studies, which will compile data types, modes of embedding physical knowledge, quality metrics, and computational costs. The quantitative layer will provide VOSviewer maps of term density and co-occurrence, distributions by document type and country of affiliation, as well as conclusions from significance tests, which will allow linking the dynamics of field development with methodological directions and application areas.

The practical value of the review lies in formulating recommendations for designing workflows in computational mechanics, selecting algorithm classes for task types, curating datasets, and reporting uncertainty and computational costs. The reproducibility layer, that is, the explicit search query, classification scheme, and openly available corpus, facilitates updates in subsequent years, supports comparability across research teams, and promotes the transfer of methods into engineering practice.

2.4. Eligibility Criteria

The literature selection was designed to be transparent and reproducible, and a two-stage screening was applied; first, titles, abstracts, and keywords were assessed, then full texts were analyzed in borderline cases. The construction of the criteria refers to good reporting practices for reviews in MDPI, including the way selection stages and justifications are presented in the PRISMA style, while strictly reflecting the query parameters adopted in this study, the years 2015–2024, the English language, the subject areas Computer Science and Engineering, the combined search of the Title, Abstract, Keywords fields, and keyword filters describing computational mechanics tasks and AI method classes. The final corpus after manual verification comprises 98 publications, in accordance with the compilation in the working file.

Works were included for analysis if they simultaneously met substantive and formal conditions. A direct connection to computational mechanics was required in at least one of the six categories, Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, Inverse Analysis; and in the use of data methods, Machine Learning, Core Neural Networks, Deep Neural Networks, which had to follow from the metadata or the content. Publications in English published in the years 2015–2024 were accepted and classified in Scopus under the subject areas Computer Science or Engineering. Journal articles, conference papers, and items marked as Other, for example, book chapters and review articles, were included if they presented a coherent methodological contribution or synthesized results in a way that allowed unambiguous classification. Access to the full text and a complete set of basic metadata, title, authors, affiliations, DOI identifier, keywords, was required.

Works not meeting any of the conditions were excluded from the corpus. Publications without an ML or NN component were eliminated, as were publications without a direct connection to computational mechanics issues, items outside the accepted years, language, and subject areas, incomplete records, and duplicates identified on the basis of DOI or title. Materials of a non-technical nature were rejected if they did not explicitly contain a component of computational or data methods in the context of equations, constitutive models, or multiscale analyses, as well as works with inadequate reporting, without a description of data, without quality metrics, or without information enabling the assessment to be reproduced. In cases where the full text did not allow assignment to any category, the item was marked as out-of-scope.

The decision chain corresponds to the stages of the Scopus query. After applying the query and filters, 109 records were obtained, refining the keyword list for ML and NN methods yielded 101 publications, and manual verification of scope compliance resulted in the exclusion of three items outside the thematic scope, which set the final count at 98. Justifications for inclusion and exclusion decisions were documented, and multiple assignments of the same item to several classification categories were allowed, which reflects the multidimensionality of the subject. Consistency of the procedure with MDPI good practices and the adopted protocol ensures comparability and reproducibility of the selection in subsequent updates of the review.

2.5. Selection Procedure and Screening

Screening was conducted in two stages, first, titles, abstracts, and keywords were assessed, then full texts of included or ambiguous items were analyzed. Before the actual screening, a short calibration was carried out on a random sample of records, the aim being to harmonize the interpretation of criteria and the terminology related to computational mechanics and data methods. Two reviewers conducted the assessment independently; decisions were recorded in a form with three possible outcomes, include, exclude, and unclear, and discrepancies were resolved by consensus, and, if necessary, with the involvement of a third person. For transparency, each decision was assigned a reason code, among others, the lack of an ML or NN component, outside the scope of computational mechanics, inadequate document type, incomplete metadata, lack of assessable method, which later made it possible to compile exclusion categories in the outcome report.

In the title and abstract screening, a minimal set of decision questions was applied, namely whether the work directly concerned computational mechanics in one of the six categories, Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, Inverse Analysis, and whether it used data methods understood as machine learning, core neural networks, or deep neural networks. If the answer was positive, the publication was directed to full-text screening, if negative, it was excluded, if ambiguous, it was marked as unclear and also directed to full-text screening. At this stage, multiple assignments of topics and methods was allowed, reflecting the complexity of tasks, and terminological inconsistencies were reduced by normalizing keywords to a reference list, for example, merging neural networks and neural-networks into one class, unifying finite element analyze to finite element method, merging convolutional neural network and convolutional neural networks.

Deduplication was technically confirmed on the basis of DOI identifiers and titles, and borderline cases of sibling publications, that is conference and journal versions of the same work, were resolved in favor of the version more complete methodologically. Full-text assessment served to verify whether the publication met all substantive and formal criteria, in particular, whether it actually contained a data-method component applied in the context of computational mechanics, whether it reported input data and metrics appropriate to the task, and whether the method description allowed unambiguous classification. For review and conceptual articles, a coherent taxonomy or methodological conclusion referring to the defined axes was required. Lack of access to the full text, incomplete metadata, or inconsistencies between title, keywords, and content resulted in exclusion with the assignment of the appropriate reason code. All decisions at this stage were recorded in a selection log, and disputed classifications were corrected by consensus.

The flow of records between stages together with the number of items at each step is presented in the PRISMA diagram, Figure 2. The methodology followed the PRISMA 2020 guidelines, with the completed checklist provided in the Supplementary Materials [113]. The diagram covers identification, screening, eligibility assessment, and final inclusion.

At the screening stage, all 109 records were assessed, refining the keyword list for ML and NN methods resulted in 101 items forwarded to full-text assessment, with no work lost at the full-text retrieval stage. At the eligibility stage, the full texts of 101 publications were analyzed, three were excluded for substantive reasons, and ultimately 98 works were included, which formed the review corpus. Stage indicators confirm the effectiveness of the procedure, retention after screening was 92.7%, full-text exclusions accounted for 3.0% of the reports analyzed, and the proportion of publications included relative to the number of records identified was 89.9%. The dominant cause of exclusions at the initial stage, that is the refinement of the keyword list, confirms that thematic narrowing was carried out at the metadata level before content assessment, which ensures a technically homogeneous corpus for further classification and quantitative analyses.

2.6. Classification Scheme

The classification scheme was built on five parallel dimensions, which ensures consistent coding of content and allows for comparability of results in subsequent analyses. Each document may receive more than one label within a given dimension if this follows from its scope or metadata, and variant or synonymous terms were normalized to reference lists, which reduces indexing artifacts and facilitates cross-sectional comparisons.

The first dimension covers areas of computational mechanics. Six groups were distinguished that organize the most frequently occurring tasks: Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, Inverse Analysis. These groups were assigned corresponding descriptors, including Finite Element Method, Boundary Value Problems, Mesh Generation, Degrees of Freedom, Constitutive Models, Plasticity, Elasticity, Elastoplasticity, Stress Analysis, Surrogate Modeling, Stochastic Systems, Uncertainty Analysis, and Inverse Problems.

The second dimension concerns data methods. Three overarching categories were applied, reflecting the level of complexity of approaches: General Machine Learning, Core Neural Networks, Deep Neural Networks. The first group included, among others, Machine Learning, machine learning, and Learning Systems; the second group included Neural Networks, neural-networks, and Artificial Neural Network; the third group included Deep Learning, Deep Neural Networks, Convolutional Neural Network, Convolutional Neural Networks, and Recurrent Neural Networks. Differences in spelling and lexical variants were merged into parent classes, which enables comparisons between publications.

The third dimension reflects the geography of output based on authors’ affiliations. The set applied includes Australia, Austria, Canada, China, France, Germany, Greece, India, Luxembourg, United Kingdom, United States, and Others, with all appropriate labels assigned to co-authored publications, which allows for the analysis of international collaboration.

The fourth dimension organizes document types in line with Scopus classification. Article, Conference Paper, and the group Other were included, the latter comprising, among others, review articles and book chapters, provided they met substantive and formal criteria.

The fifth dimension describes the methodological approach, determined on the basis of content and authors’ declarations. Four categories were applied, Experiment, Literature Analysis, Case Study, and Conceptual, which facilitates the assessment of solution maturity and methodological rigor.

This five-dimensional structure enables the construction of cross-tables, for example, data method by mechanics category, the analysis of distributions by document type and authors’ affiliation countries, as well as unambiguous interpretation of bibliometric results in subsequent chapters.

The term density map in Figure 3 shows central clusters around the terms’ finite element method, neural-networks, machine-learning, and deep learning, as well as medium-density fields related to surrogate modeling, inverse problems, boundary value problems, and uncertainty analysis. Yellow indicates the highest density, that is, the topics most frequently co-occurring in the corpus. Lexical pairs of the same meaning, such as machine learning and machine-learning or neural networks and neural-networks, were merged in the quantitative analysis, although they may appear as separate spots in the density visualization, which does not distort the overall picture of the dominance of core concepts of mechanics and learning methods.

To ensure reproducibility of the five-dimensional classification, explicit labeling rules and conflict resolution procedures were defined. Each record could receive multiple labels within a given dimension, but a single primary label was always assigned when needed for cross tabulation.

• Mechanical problem. The label was chosen based on the stated research objective in the title and abstract. When a paper addressed multiple tasks, the primary label corresponded to the problem driving the evaluation protocol or the main result. For example, if a study built a surrogate to estimate parameters, the primary label was Inverse Analysis, while Surrogate Methods was recorded as secondary.
• Data class. A distinction was made between simulated and experimental data. The primary label was determined by the dominant source, defined as more than 50% of the dataset used for training and evaluation. If both sources were comparable, the label Dual was assigned and explicitly reported in figure captions.
• Country. The country label was derived from the first author affiliation. In multinational collaborations, a multi country flag was added. If the first author listed several affiliations, the first institutional country was used.
• Document type. The assigned label reflected the publication venue, that is journal article, conference proceedings, preprint or review. If a preprint was later published in a journal, the label journal article was used, and the preprint was listed as secondary.
• Methodology. The label reflected the central computational approach. If two approaches were combined, the primary label was the method governing the training objective or inference at deployment. For example, when a graph-based model enforced physics through a penalty, graph neural networks was primary and physics informed was secondary. When boundary conditions were imposed as hard constraints that dominated feasibility, Physics informed became primary.

Conflict resolution followed a clear precedence: (i) task intent over tool choice, (ii) data source over data format, (iii) venue type over manuscript stage. Borderline cases were adjudicated by two independent reviewers and disagreements resolved by discussion. A random 10% sample was re-labeled after two weeks to assess consistency, yielding agreement above 0.9 in terms of Cohen’s kappa.

Examples of specific assignments include a study titled Surrogate Modeling for Parameter Identification in Elastography with synthetic training data and limited experimental validation was labeled primarily as Inverse Analysis, Simulated with Surrogate Methods, Experimental as secondary; a paper on mesh-independent field prediction with PINNs on CT derived geometries based on clinical scans only was labeled Forward Modeling, Experimental, Physics informed; and a conference contribution on Operator Learning for Turbulent Flow Reconstruction fine-tuning DeepONet on DNS snapshots was labeled Forward Modeling, Simulated, Operator learning, Conference.

Cross tabulations in Section 4 are computed using primary labels, while secondary labels are used in sensitivity analyses presented in the Zenodo repository.

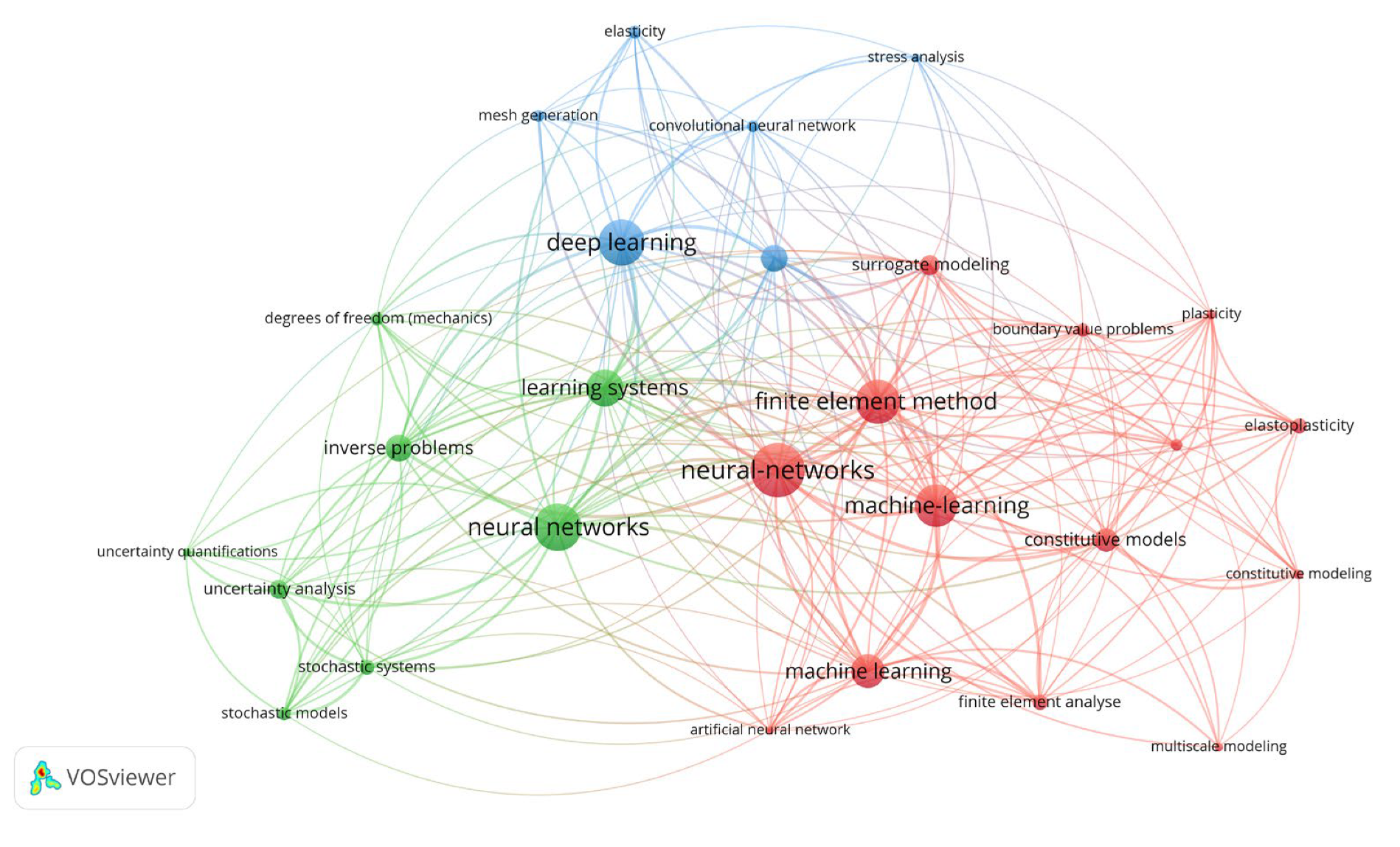
The term co-occurrence network in Figure 4 structures the conceptual space into three distinct clusters. The red cluster brings together machine-learning, finite element method, boundary value problems, and constitutive models, which reflects works combining classical mechanics tasks with ML methods. The green cluster includes neural networks, inverse problems, uncertainty analysis, and stochastic systems, indicating a line of research linking networks with inverse analysis and uncertainty. The blue cluster centers on deep learning and convolutional neural network, accompanied by terms such as mesh generation and elasticity, which confirms the broad applications of deep networks, particularly convolutional ones. The thickness of the edges between nodes illustrates the strength of co-occurrences, with especially visible links between the finite element method and machine-learning, as well as between inverse problems and neural networks.

2.7. Data Extraction and Benchmarks

From each publication, a standardized set of fields was extracted to ensure a comparable characterization of the studies and their results. The computational mechanics task was recorded, that is, Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, Inverse Analysis, together with the corresponding descriptors, among others Finite Element Method, Boundary Value Problems, Constitutive Models, Surrogate Modeling, Uncertainty Analysis, Inverse Problems. In addition, the data method class was recorded, that is, General Machine Learning, Core Neural Networks, Deep Neural Networks, with normalization of lexical variants, for example, Machine learning and Learning Systems to Machine Learning, Neural-networks to Neural Networks, Convolutional Neural Network and Convolutional Neural Networks to Deep Neural Networks. For clarity, the document type, the country of authors’ affiliation, and the methodological approach, Experiment, Literature Analysis, Case Study, Conceptual, were also included in accordance with the classification rules described in the working materials. This set was supplemented with technical fields, such as the type of equations and boundary conditions represented, geometry and mesh representation, dataset size and splitting, description of the architecture and loss function components, as well as information on computational costs and elements of reproducibility, code and data availability, and DOI identifiers.

Comparative measures were selected to reflect the nature of the tasks. For continuous fields and differential equations, L2 errors, MAE, MSE, and energy consistency indicators were included; for surrogate models, accelerations relative to reference solvers, as well as training and inference times were recorded; for inverse analyses and material identification, parameter errors and credibility measures were reported; and in some works, calibration metrics and uncertainty interval widths were also noted. The results were normalized to the most frequently reported metrics within each task class and compiled in comparative tables, with interpretive commentary linking algorithmic quality to computational costs and resource constraints.

The bibliometric layer was implemented using VOSviewer version 1.6.20, and density maps of terms and co-occurrence networks of keywords were prepared to identify thematic clusters and central nodes. Each visualization was accompanied by the recommended caption.

The synthesis of results was carried out along two lines. First, thematic synthesis within the six categories of computational mechanics and three classes of data methods, which allows linking specific tasks with model types and methods of embedding physical knowledge, among others boundary conditions in the loss function, energy constraints, operator learning. Second, quantitative aggregation covering geographic distribution, document types, and methodological approaches, with the possibility of constructing cross-tables, for example, data method by mechanics category, as well as analyzing popularity trends within the corpus.

The description of the procedure remains consistent with transparency guidelines, the Scopus query with filters, the inclusion and exclusion criteria, definitions of classification categories, and the full list of 98 publications with metadata are prepared for release in the Zenodo repository. In this way, the subsection integrates extraction, comparative measures, bibliometrics, and synthesis, which ensures reproducibility of conclusions and enables updating of the review in subsequent editions.

2.8. Limitations

The scope of the review is defined by a single source, the Scopus database, the English language, and the years 2015–2024, as well as a restriction on the areas of Computer Science and Engineering. This choice guarantees consistent metadata and uniform selection criteria, while introducing the risk of omitting publications indexed exclusively in other databases and works in other languages. Indexing delays must also be taken into account, which may result in underestimation of the newest items at the end of the study period.

Further limitation arises from the construction of the search query. EXACTKEYWORD descriptors were used for both the terminology of computational mechanics, for example, Finite Element Method, Surrogate Modeling, Inverse Problems, and data methods, for example, Machine Learning, Neural Networks, Convolutional Neural Network, which increases precision, but may remove works that use less common synonyms or a different naming convention. This risk was mitigated by jointly searching the Title, Abstract, and Keywords fields and by normalizing lexical variants, nevertheless individual false negatives cannot be ruled out, nor, conversely, borderline items classified into the corpus.

The selection procedure included independent double screening and consensus decisions. Despite these safeguards, classification along five dimensions, that is, computational mechanics category, data method class, country of affiliation, document type, methodology, contains an element of expert judgment. Subjectivity concerns in particular multi-topic cases and publications with concise descriptions of data and metrics, therefore a normalization glossary was used, and decision justifications were recorded, nonetheless isolated ambiguities may remain.

A significant barrier to comparisons is the heterogeneity of tasks and metrics. The analyzed works concern different equations and boundary conditions, diverse representations of geometry and meshes, and differing validation protocols. Authors use different error measures, for example, L2, MAE, MSE, and energy indicators, and in surrogate models, they report computational speedups under different hardware configurations. Common benchmarks and consistent descriptions of computational costs are rare, thus there is no basis for a formal meta-analysis of effects, and comparative conclusions are descriptive in nature.

The bibliometric layer is based on keyword co-occurrence analysis and VOSviewer visualizations. The maps are descriptive, they reflect the structure of indexing and term frequency, not the quality of methods or strength of evidence. Results depend on the threshold for including terms, the rules for merging synonyms, and the choice of clustering algorithm; therefore, interpretations of clusters and concept centrality should be related to the substantive context of the review and not treated as causal indicators.

At the external level, publication and selection bias must be considered. Positive results dominate in technical literature, reports of failures and negative outcomes are rare, which may inflate expected performance measures. The review does not include gray literature and preprints outside Scopus, for example, industrial reports and internal materials, which often contain information on deployments and operational constraints.

The generalizability of the conclusions is limited by environmental and computational differences. Applications of ML and NN in computational mechanics depend on data size and quality, mesh resolution, hardware configuration, for example, GPU, and adopted simplifications, for example, 2D instead of 3D. Many studies rely on synthetic data or limited experiments, and results under industrial conditions may differ from those presented in articles. Some publications do not report prediction uncertainty or full computational costs, which hinders the assessment of risk and scalability.

The above limitations do not invalidate the conclusions of the review, but they delineate the boundaries of their applicability. In subsequent iterations, the query is planned to be extended to additional databases, including IEEE Xplore and Web of Science, in consideration of selected languages other than English, refinement of the synonym glossary, and reporting of the classification agreement coefficient. It is recommended to promote open benchmarks, standardized evaluation protocols, and transparent reporting of computational costs and uncertainty, which will enable more rigorous comparisons in future work.

The literature coverage extends through 2025; due to indexing latency in Scopus, some very recent items may not yet be captured at the time of querying. This limitation was mitigated by targeted manual screening of references and the inclusion of 2025 publications identified through journal websites and cross citations.

3. State of the Art

Section 3 constitutes the core of the study and is divided into four complementary subsections. Section 3.1 presents the main currents of contemporary computational mechanics, grouped into six thematic categories: Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, and Inverse Analysis. Their role is discussed in solving problems governed by differential equations, in constitutive modeling, in inverse analysis, and in the development of surrogate models. Section 3.2 focuses on the three main classes of data-driven methods: General Machine Learning, Core Neural Networks, and Deep Neural Networks. Their applications are presented as tools supporting material modeling, approximation of complex physical phenomena, uncertainty quantification, and inverse design. Section 3.3 outlines future directions of development and synthesizes conclusions from the two preceding subsections, highlighting key avenues for further research, such as the advancement of differentiable solvers, models with physical guarantees, and the standardization of validation and uncertainty quantification procedures. The chapter concludes with Section 3.4, which summarizes the key observations and formulates practical implications for the further development of computational mechanics and data-driven methods.

3.1. Computational Mechanics Methods and Modeling

The starting point of contemporary computational mechanics is the tight coupling of boundary equation discretization with the approximation of physical fields and, increasingly, with machine learning. Mature approaches, from classical FEM to meshfree and variational methods, are now being enriched with neural networks, which either replace selected stages of computation, or enter the solver as “components” of numerical methods. This methodological shift is well illustrated by works in which the network becomes part of the method, from the Neural Element Method (NEM), in which neurons construct shape functions and stiffness matrices, creating a bridge between ANN and weak formulations and W2 [16], to integrated I FENN frameworks, where a PINN maps the nonlocal response directly into the definition of element stiffness and its derivatives, in order to drive the nonlinear solver to convergence at a cost comparable to local damage models [17]. Against this backdrop, meshfree EFG formulations with MLS approximation are developing in parallel, here combined with HSDT9 and a lightweight network for instantaneous prediction of FGM plate deflections, which shows a measurable gain in time and accuracy relative to FEM [18]. In the opposite direction are concepts in which FEM integrates an NN as an exchangeable solver component, and the FEMIN frameworks aggressively replace parts of the mesh with a neural model to accelerate crash simulations without loss of fidelity [19]. Yet another line is represented by HiDeNN FEM, where the network takes over the role of constructing shape functions and r-adaptivity, boosting accuracy and suppressing “hourglass” modes in nonlinear 2D/3D problems [20]. Finally, the differentiable, GPU-accelerated JAX FEM solver opens an “off the shelf” path to inverse design, because sensitivities here are a by-product of automatic differentiation [21]. These trends: element as network, network as element, solver as differentiable graph, create a common language of next-generation computational methods.

A special place is occupied by physics-informed networks, PINNs, and related energy methods. In elastodynamics, PINNs with mixed outputs, displacements and stresses, and enforced satisfaction of I/BCs break through the known difficulties of classical PINNs, especially for complex boundary conditions [22]. The “meshless + PINN” formulation shows that deep collocation can reliably reproduce the response of elastic, hyperelastic, and plastic materials without generating FEM-labeled data [23]. In optimization applications, the deep energy method, DEM, serves both for solving the forward problem and for formulating a fully self-supervised topology optimization framework, where sensitivities arise directly from the DEM displacement field, thus a second “inverse” network becomes unnecessary [24]. On the other hand, PINNTO replaces finite element analysis in the SIMP topology optimization loop with a private, energy-based PINN, thanks to which design can proceed without labeled data [25]. In elliptic BVPs, it has been shown that loss-function modifications enable convolutional networks to act as FEM surrogates, with accuracies comparable to Galerkin discretizations [26], and variational PINNs at the same time provide more precise identification of material parameters, also for heterogeneous distributions [27].

Today, constitutive modeling is a key arena where physics and data meet. Instead of directly predicting stress, the SPD-NN architecture learns the Cholesky factor of the tangent stiffness, which weakly enforces energy convexity, temporal consistency, and Hill’s criterion, and in practice stabilizes FEM computations with history-dependent materials [28]. The “training with constraints” approach improves hyperelasticity learning by imposing energy conservation, normalization, and material symmetries, which increases solver convergence stability [29]. In classes of models that guarantee polyconvexity from the outset, neural ODEs introduce monotonic derivatives of the energy with respect to invariants, which ensures the existence of minima and successfully transfers to experimental skin data [30]. Deep long-memory networks reproduce viscoplasticity with memory of rate and temperature, satisfying path consistency conditions and capturing history effects in solders [31]. When scale effects are nonlocal, CNN hybrids can learn nonlocal closures without explicitly known submodels, thanks to the convolutional structure that follows from the formal solution of the transport PDE [32]. In geotechnics, a tensorial, physics-encoded formulation respects stress invariants and porosity, maintaining the requirements of isotropic hypoplasticity and readiness for integration in BVP solvers [33]. In turn, geometric DL, graphs, and Sobolev training learn anisotropic hyperelasticity from microstructures, taking care of the smoothness of the energy functional and the correctness of its derivatives [34], and graph embeddings allow interpretable internal variables for multiscale plasticity [35]. In soft materials, conditional networks, CondNN, compactly parameterize the influence of rate, temperature, and filler on full constitutive curves of elastomers [36], and RNN-based descriptions are also integrated into gradient damage frameworks, avoiding localization [37]. A synthetic comparison of “model-free” and “model-based” approaches for computational homogenization explains when constitutive NNs underperform or outperform DDCM with distance minimization or entropy maximization, and how pre- and post-processing costs differ [38].

Beyond the material laws themselves, flows of information across scales are important. Fully connected networks trained on RVE data of fibrous materials can reproduce energy derivatives with respect to invariants and be plugged in as UMATs in FEM, linking the micro-network with the macro-simulation without painful on-the-fly coupling [39]. CNNs with PCA predict complete stress–strain curves of composites, also beyond the elastic limit, enabling high-throughput design with limited data [40]. In classical FE2, a “data-driven” mechanics with adaptive sampling controlled by a DNN has been proposed, which significantly reduces offline cost while maintaining the quality of the macro response [13]. Meta-modeling games with DRL automate the selection of hyperparameters and the “law architecture” for NN-based elastoplasticity in a multiscale approach [41]. A broader perspective on the roles of ML in multiscale modeling, from homogenization to materials design, is outlined by cross-sectional reviews [42,43]. In elastoplastic composites, combining computational homogenization with ANN makes it possible to build DDCM databases more cheaply, yet with high fidelity in 3D tasks [44].

In parallel, an ecosystem of surrogate methods that accelerate analysis is maturing. U-Mesh, a U-Net-type architecture, approximates the nonlinear force–displacement mapping in hyperelasticity and works across many geometries and mesh topologies, with small errors relative to POD [45]. CNNs trained on FEM data solve torsion for arbitrary cross-sections, bypassing laborious discretization [46], and Bayesian operator learning, VB-DeepONet, adds credible a posteriori uncertainties and better generalization than deterministic DeepONet [47]. In fluid–structure interaction, networks take over the role of one of the sub-solvers, shortening cosimulation time without loss of accuracy [48], and in MEMS, NN surrogates enable efficient Bayesian calibration with MCMC despite the cost of FEA [49]. In the domain of general shapes, a multiresolution network interpolated to mesh nodes predicts scalar fields, stresses, temperature, on arbitrary input meshes, R² close to 0.9–0.99, which makes it a realistic alternative to FEM in design loops [50]. Moreover, a cGAN transferred from image processing allows near real-time emulation of FEM responses, deflections, stresses, with 5–10% error after only 200 training epochs [51]. They are supported by “Sobolev training” techniques with residual weighting, which insert partial derivatives into the loss function, reducing generalization error in linear and nonlinear mechanics [52], and meshfree NIM hybrids that integrate variational formulations with differentiable programming [53]. Even an apparently “minor” component, such as Gaussian quadrature, can be learned and adapted to the element and material, which translates into savings in stiffness matrix integration [54].

The new paradigm does not avoid uncertainty; on the contrary, it models and exploits it. An experimental–numerical program for C40/50–C50/60 concretes combines tests with ANN-based identification of fracture parameters, in order to directly propose stochastic parameter models [55]. For FGM shells, SVM provides a fast substitute for Monte Carlo in analyzing temperature effects on natural frequencies, with verification against classical MCS [56]. ROMES frameworks and related error models learn regressions of residual indicators to predict the error of approximate solutions, which provides quality control for nonlinear parametric equations [57]. Nonparametric probabilistic learning by Soize–Farhat makes it possible to model model-form uncertainty and identify hyperparameters through a statistical inverse problem, and then accelerate it with a predictor–corrector scheme [58]. When probability distributions are lacking, interval networks, DINNs, propagate interval uncertainties through cascades of models, providing credible prediction ranges [59]. In laminated composites, ANNs faithfully reproduce first-ply failure statistics directly against Monte Carlo [60], and in forecasting fatigue crack growth, a selected NN architecture can operate in real-time with uncertain inputs [61]. In computational turbulence, an elegant, frame-independent representation of stress tensor perturbations by unit quaternions has been proposed, which is crucial for UQ and ML in RANS modeling [62]. Synthetic geotechnical reviews emphasize that input selection and data representation determine AI effectiveness under high material uncertainty [63].

Inverse problems are the natural culmination of this trend. Galerkin graph networks with a piecewise polynomial basis strictly impose boundary conditions and assimilate sparse data, solving forward and inverse tasks in a unified manner on unstructured meshes [64]. In heat conduction and convection, combining simulation and deep networks allows boundary conditions to be recovered in strongly nonlinear problems from only a few temperature measurements [65]. In geophysics, deep networks for borehole resistivity inversion require carefully designed loss functions and error control to ensure real-time stability [66], while alternative migration, learning, and cost-functional methods reveal the positions of cracks in brittle media [67]. Differentiable approaches, such as JAX FEM, turn full 3D FEA into a component of gradient programming, which automates inverse and topology design [21,68]. At material scales, from hierarchical wrinkling to the thermal conductivity of composites, surrogate models and parameter-space planning enable inversion on a minute time scale instead of multi-day searches [69], and stable determination of liquid metal microfoam with a prescribed thermal conductivity [70]. In 3D/4D printing, reviews clearly indicate that ML is becoming a primary tool for inverse design of mechanical properties and active shape [71].

All the above threads also intertwine at the level of theoretical and methodological foundations. BINNs propose a boundary-integral formulation with networks that naturally embed boundary conditions and reduce problem dimensionality [72]. For PINNs, a priori error estimates have been derived, combining Rademacher analysis with Galerkin least squares, which form a basis for convergence theory [73]. Reviews of deep learning in mechanics synthesize five roles of DL, substitution, enhancement, discretizations as networks, generativity, and RL, organizing the dynamic landscape of methods [74], while other surveys contain the “classics and the state of the art,” from LSTMs to transformers and hyper-reduction [75]. In structural practice, deep and physics-informed networks can in places replace FEA in accurately reproducing stress and strain fields, although PINNs show greater generalization capacity [76], and qualitative inference from networks trained on FEM data can meaningfully support structural assessment [77]. In topology optimization, DNNs significantly accelerate sensitivity analysis by mapping the sensitivity field from a reduced mesh back to a fine mesh [78].

Finally, it is worth noting the rapidly developing “games on data.” Data-driven games between the “stress player” and the “strain player” provide nonparametric, unsupervised effective laws that reduce to classical displacement-driven boundary problems [79]. In turn, a non-cooperative meta-modeling game uses two competing AIs for automatic calibration, validation, and even falsification of constitutive laws, through experiment design and adversarial attacks, in order to realistically describe the range of model applicability [80]. At the very foundations of fracture micromechanics, diffusion–transformer models are emerging that generalize beyond atomistic databases, predicting crack initiation and dynamics [81]. Complementing this panorama is a reflection on the role of LLMs in applied mechanics, not only as assistive tools, but as potential interfaces for exploring mechanical knowledge and designing computations [82].

The article [83] provides an overview of advances in computational mechanics and numerical simulations, including CFDs, gas dynamics, multiscale modeling, and classical discretization tools. The paper [84] presents the use of artificial neural networks to identify the parameters of poroelastic models, combining the ANN approach with asymptotic homogenization and finite element method to characterize materials with differentiated porosity and Poisson ratio of the solid matrix. The paper [85] presents a solution to the statistical inverse problem in multiscale computational mechanics using an artificial neural network, combining probabilistic modeling with uncertainty analysis and identification of parameters of heterogeneous materials. The paper [86] presents an adaptive surrogate model based on the local radial point interpolation method (LRPIM) and directional sampling technique for probabilistic analysis of the turbine disk, demonstrating improvements in computational accuracy and efficiency compared to classical response surface models, Kriging, and neural networks. The article [87] provides an overview of surrogate modeling techniques used in structural reliability problems, including ANN, kriging, and polynomial chaos in combination with LHS and Monte Carlo simulation, with a focus on reducing computational costs in uncertainty analyses. The paper [88] proposes a hybrid approach to describe the elastic–plastic behavior of open-cell ceramic foams, combining a homogenized material model with interpolation of FEM simulation results using neural networks, which significantly reduced the computational effort. The paper [89] presents a method of stochastic neural network-assisted structural mechanics, in which the phase angles of the spectral representation are used as inputs, and the network, trained on a small subset of Monte Carlo samples, accelerates uncertainty calculations regardless of the size of the FEM model.

Within Category Group 1, a coherent architecture of methods is taking shape, (i) hybrid discretizations, elements and meshes as networks, and networks in the solver, (ii) PINNs and energy methods carrying BCs and ICs and physical conditions in the loss function, (iii) constitutive NNs with structures enforcing thermodynamics and convexity, (iv) multiscale models integrating ANN and UMAT and FE2 data-driven approaches, (v) surrogates and operator learning with UQ and credibility, and (vi) inversion based on differentiable simulation. The most urgent tasks include formal error estimates and convergence criteria, especially for 3D PINNs, standardization of surrogate model credibility with an uncertainty measure, and scaling to geometries and meshes of arbitrary topology without loss of computational stability. These directions are already outlined in the cited works, and their further integration foreshadows the next generation of computational methods that will “converse” equally well with physical equations and with data.

To conclude the analysis of methods in Section 3.1, a summary has been prepared in

Table 1. Summary of Section 3.1.

Category	Theme (What Is Addressed)	Data and Sensors	Research Task	Models and Techniques	Metrics and Implementation Requirements	Example Key Refs [n]
Computational Methods	Physics-guided neural solvers and hybrid FEM–NN pipelines to accelerate/replace classical FE steps (static, dynamic, TO)	Computed fields (FEM/PDE states), BC/IC specifications; occasional sparse field samples	Forward solution of PDEs; elastic/elasto-dynamic analysis; topology optimization; solver acceleration	PINN and variational/Energy PINN (DEM); meshfree deep collocation; FEM–NN integration (I-FENN, FEMIN); PINNTO for TO; hybrid training for elliptic PDEs; Incremental Neural CDE for time dependence	L2/MSE on PDE residuals; energy functionals; strict/penalized BC/IC; numerical stability in FE coupling; guaranteed convergence in TO loops; runtime speedups vs. FEM	[16,18,24,26,34,36,55,90]
Material Modeling	Data-driven constitutive laws with physics-aware constraints for stability/consistency	FE/RVE fields; stress–strain trajectories; microstructure-derived descriptors	Learn constitutive responses (hyperelasticity, plasticity, path dependence) for FE	SPD-NN (predict tangential stiffness); constrained NN training (thermodynamic consistency, symmetries); RVE→macro surrogates	Energy convexity/policonvexity surrogates; Hill’s criterion; stable FE updates; MAE/MSE on stresses; robustness to noise/small data	[17,83,84,91]
Multiscale Modeling	Efficient FE2/homogenization with learned surrogates and database construction	Micro–macro paired datasets (RVE simulations); microstructure images/graphs	Bridge micro to macro; reduce online FE2 cost	Data-driven FE2; curated micro–macro databases; RVE-trained NNs embedded in UMAT/solvers	Macro accuracy vs. RVE ground truth; offline/online cost split; generalization across geometries	[45,83,91]
Surrogate Methods	Fast surrogates for elliptic/solid mechanics and FE workflows	FEM snapshots; synthetic PDE solutions	Replace expensive FE steps; rapid what-if studies	Surrogate-based PINN/CNN; DEM; meshless DCM; hybrid MGA-MSGD training; PINNTO	ROM-style speedups; fidelity to FE baselines; stability under domain/BC changes	[24,34,55,87,90]
Stochastic Methods and Uncertainty	Credible predictions via error modeling and UQ without overfitting	FEM runs, residual indicators; experimental data for calibration	Error modeling, Bayesian/interval UQ; efficient UQ for MEMS	ML error models for nonlinear systems; probabilistic learning for model-form error; interval deep learning; NN surrogates for Bayesian inverse UQ	Error bounds (posterior intervals); calibration/validation splits; epistemic vs. aleatory separation; tractable UQ cost	[19,38,39,92]
Inverse Analysis	Recover parameters/fields from sparse data with physics constraints	Sparse sensors (DIC, strains), partial boundary/initial data; FE priors	Material/property identification; design-from-response (TO, PINN-inverse)	PINN with mixed outputs; physics-informed GNN Galerkin; PINNTO for topology; hybrid (PDE-guided) training	Physical feasibility (BCs, constitutive admissibility); stability under sparse/noisy observations	[16,36,93]

, which organizes the discussed threads into the subcategories Computational Methods, Material Modeling, Multiscale Modeling, Surrogate Methods, Stochastic Methods and Uncertainty, and Inverse Analysis, presenting for each group the leading theme, data types and sensors, for example, computational or FEM fields, DIC, strain gauges, microstructure images, the research task, the models and techniques used, including PINNs or variational PINNs, operator learning, FNO or DeepONet, GNNs, meshfree methods, ROMs or surrogates, and the metrics and implementation requirements, L2 or MAE or MSE, energy measures, enforcement of BCs and ICs, numerical stability, thermodynamic consistency, speedups relative to FEM, together with references [n]. The summary serves as a map of concepts and methods, unifies terminology throughout the chapter, enables comparison of data ranges and algorithms, and provides an assessment of operational readiness, runtime, and approaches to uncertainty, which closes the methodological part and prepares the basis for the synthetic conclusions in Section 3.3.

The data in

Table 2. Quantitative snapshot for Section 3.1.

Paper [Ref]	Task and Setting	Accuracy Metric (as Reported)	Reported Speedup or Time Reduction	Notes
IM-CNN on arbitrary meshes [50]	Scalar field prediction on arbitrary meshes and shapes	R2 ≈ 0.91 for von Mises stress, R2 ≈ 0.99 for temperature	Not reported	Multiresolution IM-CNN interpolated to mesh nodes; realistic alternative for design loops.
cGAN surrogate for FEM responses [51]	Near real-time emulation of deflections and stresses	≈5–10% field error after ~200 training epochs	Near real-time emulation, numeric speedup not reported	Approach transferred from image processing to FEM response fields.
JAX-FEM differentiable solver [21]	Differentiable 3D FEM for inverse design at ~7.7 million DOFs	Not applicable	≈10× speedup vs. baseline	GPU-accelerated solver exposes gradients for automated inverse design.
EFG–ANN hybrid for FGM plates [18]	Meshless EFG assisted by a lightweight ANN, static analysis	Not explicitly quantified	≈99.94% time reduction vs. EFG	Reported large runtime savings on the benchmark case.
CNN + PCA for composites [40]	Prediction of full stress–strain curves beyond elasticity	Mean error < 10% on a limited configuration set	Not reported	Highlights data efficiency for material curve prediction.
ML inverse design of wrinkle microstructures [68]	Inverse design over ~1,000,000 options	Design objective, not a PDE norm	>10 days → <1 min exploration time	Strong compression of design search space.

show that IM-CNN models operating on arbitrary meshes achieve high field accuracy (R² approximately 0.9 to 0.99), generative cGAN emulators maintain about 5 to 10 percent error with near real-time inference, and differentiable solvers such as JAX-FEM deliver roughly a tenfold speedup at very large numbers of degrees of freedom. EFG-ANN hybrids can reduce computational time by up to about 99.94 percent in specific configurations, CNN plus PCA methods for composites keep mean errors below 10 percent, and machine-learning-based inverse design shortens the exploration of million-scale design spaces from more than ten days to under one minute. Taken together, this confirms that different classes of methods occupy distinct points on the accuracy–cost–robustness trade-off, which we revisit in the synthesis in Section 3.3.

Reporting is standardized by explicitly distinguishing the offline cost of generating micromodel databases from the online cost at the macroscale. For multiscale pipelines, the offline profile states the database cardinality, approximate data size and generation time, and the sampling strategy used to cover the material state space. The online profile states the macro mesh size in elements, the accuracy tolerance relative to the reference model, the typical per-step runtime in milliseconds, and the wall-clock speedup at matched accuracy tolerance together with any observed accuracy loss. In practice, UMAT–NN couplings trade a substantial offline investment for stable macro-level solves, data-driven FE² with adaptive sampling reduces both offline and online burdens by focusing queries in high-value regions of the state space, and deep material networks integrated at the macro level provide large online gains once a suitable database has been curated. Across the studies discussed here, reported speedups range from several times to tens or even hundreds of times at comparable accuracy, which is critical for design loops and parametric studies.

Cross-family transfer beyond the training distribution is made explicit by adopting a protocol in which models are trained on one family of shapes or meshes and evaluated on a distinct family, and stress tests are performed at loads between 1.2 and 1.5 times the training envelope. Performance is assessed by standard field errors and by physics-residual monitors that quantify departures from equilibrium or energy balance. Within this protocol, IM-CNN-style surrogates tend to transfer well when boundary conditions and loading patterns remain compatible, whereas residuals can increase when topological differences or mesh-quality gaps are pronounced. U-Mesh-style surrogates offer fast inference across diverse discretizations but benefit from explicit domain control to maintain physical plausibility under extrapolative loads. Reporting both error and residual indicators helps define safe operating ranges for deployment.

Inverse settings require robustness to be documented with respect to additive noise and sensor sparsity. A practical protocol perturbs observations with one to five percent Gaussian noise and reduces sensor density by factors of ten and twenty, while tracking the error in both parameters and reconstructed fields. Accuracy typically degrades more with sensor sparsity than with mild noise, which suggests that penalization alone is insufficient. Effective stabilization combines Sobolev or Tikhonov regularization with physics barriers and, where possible, hard or variational enforcement of boundary conditions. Bayesian or ensemble-based operator learning provides calibrated uncertainty that supports decision making when data are scarce. Reports therefore include the exact noise levels, sensor density and layout, the chosen regularization, and the resulting confidence measures alongside point estimates.

3.2. Machine Learning and Neural Networks

In this chapter I show how machine learning methods, from classical shallow networks to deep architectures with embedded physical knowledge, are increasingly interwoven with computational mechanics, as approximators of constitutive laws, as fast solvers of differential equations, and as tools for inverse design and uncertainty quantification.

First, it is useful to capture the idea of the “network as a finite element,” which builds a bridge between ANNs and classical discretizations. The author of the Neural Element Method demonstrated that neurons can be used to construct shape functions and then employed in weak and weakened weak formulations, which provides an explicit link between ANNs and FEM or S-FEM, numerical demonstrations confirmed the feasibility of the approach and opened the way to new loss functions with desirable convexity in machine learning [16]. In a similar spirit, HiDeNN FEM ties hierarchical DNNs to nonlinear FEM, introducing differentiation blocks, r-adaptivity, and material derivatives, which in 2D and 3D significantly reduces element distortions and increases accuracy, the perspective is smooth integration with any existing solver [20]. A bolder move is to replace parts of the mesh directly with a network and plug it into the FEM code, the FEMIN platform for crash simulations proposes a temporal TgMLP and an LSTM variant as state predictors, showing that fidelity can be preserved while computation time is reduced, the next steps are generalization to multi-material brittle–plastic scenarios [19]. In turn, I-FENN integrates a PINN into the definition of element stiffness in order to “carry” local strain into a nonlocal response and to build the Jacobian matrix or residual vector, mesh independence was obtained at the cost of a local damage model, which suggests further development toward other forms of nonlocality [17].

The second axis concerns deep networks trained on energy or with physical information. In computational elastodynamics, authors of label-free PINNs proposed mixed outputs, displacement plus stress, and enforced I or BCs within a composite architecture, which improved accuracy and trainability without labeled data, a natural continuation is scaling to multiphysics wave problems and contact [22]. The deep energy method showed that by training on an energy functional one can solve 3D hyperelasticity and viscoelasticity in a meshless manner and obtain on-demand responses after training, further work includes stable couplings in thermomechanics and frictional contact [94]. In a similar vein, Meshless Deep Collocation combines DL with collocation for linear, hyperelastic, and plastic materials, dispensing entirely with meshes and external data; directions for development include low-regularity boundary conditions and large deformations with anisotropy [23]. At the interface of boundary value problems and ANNs, BINNs have appeared, in which the unknowns are reduced to the boundary and residuals of integral equations are minimized, the method naturally enforces boundary conditions and is suitable for unbounded domains, which encourages work on dynamic boundary-integral equations [72]. In elliptic problems, it has been shown that an appropriately modified loss function, together with CNN architectures, in PINN models can approximate BVP solutions comparable to FEM, it will be interesting to test behavior for strongly heterogeneous coefficients [26,93]. Physics-informed graph neural Galerkin connects GCNs with a variational formulation and a piecewise polynomial basis, which facilitates enforcement of boundary conditions, operation on unstructured meshes, and unifies forward and inverse problem solving, development of this line includes nonlinear materials and contact [64]. In topology optimization two studies, DEM-TO and PINNTO, showed that costly FEA can be replaced, respectively, by DEM and by a PINN, yielding designs comparable to SIMP and approximating sensitivities without an auxiliary network, the future lies in manufacturing constraints and multi-objective settings [24,25].

The third thread is learning constitutive laws with guarantees of stability and interpretability. Constraint-based learning for hyperelasticity imposes energy conservation, normalization, and material symmetries, which stabilizes convergence and improves noise robustness; the next steps are systematic enforcement of piecewise polyconvexity [29]. Polyconvex Neural ODE constructs monotonic approximations of energy derivatives with respect to invariants and guarantees polyconvexity, demonstrating advantages over phenomenological models on skin data, a promising direction is anisotropic formulations with memory [30]. The SPD-NN architecture does not learn stresses directly, but the Cholesky factor of the tangent stiffness matrix, which implies positive definiteness, the second law of work, and temporal consistency, the method appears promising for embedding in contact solvers [28]. A comparison of architectures for inelasticity, black box versus “weak physics” and “strong physics,” confirmed that explicit enforcement of thermodynamic principles yields better generalization, standardized tests for complex loadings are needed [95]. Learning nonlocal constitutive relations via convolutional “neighborhood-to-point” mappings reproduces the formal structure of transport equation solutions and allows a submodel to be “discovered” without data from that scale, which naturally encourages applications in turbulence and variable-order closures [32]. Geometric DL for anisotropic hyperelasticity uses weighted microstructure graphs and Sobolev training to obtain smooth energy functionals and accurate predictions of stresses and fracture in polycrystals, future work should correlate graph descriptors with 3DXRD observations [34]. This is complemented by graph embeddings for multiscale plasticity, by which the evolution of plastic strains is predicted in a low-dimensional, interpretable feature space, further work includes coupling with damage [35]. In geotechnics, physically encoded “tensor” networks operate on stress invariants and soil state parameters, strictly enforcing the laws of isotropic hypoplasticity, a promising step is to move to anisotropy and load history [33]. Conceptually, scientific ML for coarse-grained models proposes combining manifold learning, GENERIC canonical formulations, and data regression, a natural path is the automatic selection of internal variables [91]. On the application side, a fully connected NN trained on discrete fiber network, RVE, data and embedded as a UMAT reproduces energies and stresses of biopolymer gels with a convex functional and symmetric Hessian, which directly encourages hybrid data, experiment plus RVE [39].

History-dependent materials require memory representations. LSTM architectures faithfully reproduce viscoplasticity with history effects of strain and temperature on numerical data from Anand’s law, which suggests applications to solder materials under realistic thermal profiles [31]. To overcome RNN sensitivity to increment size, incremental Neural Controlled Differential Equations, INCDE, were proposed and their stability and convergence were demonstrated for J2 and Drucker–Prager plasticity, also under FEM conditions and cyclic loading, the next step is contact and poroelastic couplings [96]. A generalization of this idea, dedicated to data generation and architecture, showed how to train RNN models for path-dependent materials so as to preserve consistency under variable increments in a Newton solver, which makes the method practical for boundary value problems [97].

The link between microstructure and field prediction is of particular importance. The combination of PCA with CNNs made it possible to predict entire stress–strain curves of composites beyond elasticity with a mean error below 10 percent on a limited set of configurations, it is worth extending this to phase heterogeneity and degradation [40]. A new IM-CNN architecture interpolates feature maps to nodes of arbitrary meshes and achieves R² ≈ 0.91 for von Mises stress and 0.99 for temperature, which suggests usefulness in shape optimization with arbitrary topology [50]. From a generative perspective, a progressive transformer–diffusion model learned mechanisms of atomistic fracture in brittle materials and generalized beyond the training geometry, providing a tool for rapid scanning of microstructure designs for fracture resistance [81]. At the validation level, deep learning recovered fiber orientation distributions in platelet composites from thermal, DIC, measurements, and predictions agreed with microscopy, future work should target full-field 3D reconstructions [98]. In biomedicine, a simple ANN predicted critical displacements and stresses in the proximal femur for different geometries and loads, indicating the potential of clinical decision support in implant personalization [99]. Additionally, an efficient method for building DDCM databases for composites, homogenization of RVEs, ANN, data augmentation, reduces the cost of generating the “material genome” without loss of accuracy, the next step involves materials with buckling and degradation [44].

Where networks become solvers for inverse design, we obtain a genuine computational gain. The JAX FEM library showed that a differentiable, GPU-accelerated 3D solver enables automatic inverse design without hand-derived sensitivities, achieving about a tenfold speedup for problems with 7.7 million DOFs, a natural continuation is full integration with PINNs and ROMs [21]. In conduction and convection, the authors built a base of synthetic solutions to train networks that performed inversion of boundary conditions from a few measurements; subsequent studies should include noisy measurements and real geometry [65]. In hierarchical wrinkle micropatterns, ML replaced iterative, costly FEM in inverse design and reduced exploration of a million options from more than ten days to less than one minute, and extensions include process constraints and multiphysics [69]. A forward-looking review of the role of ML in 3D or 4D printing design organizes the landscape of inverse problems from structural properties to active shape change, experimental validation standards are urgently needed [71].

Every data-driven model requires assessment of credibility and uncertainty. Machine learning error models, ROMES, build statistical corrections to approximate solutions of nonlinear systems by combining feature regression, for example, from residuals, with a noise model, the direction is consistency with adaptive sampling [57]. VB-DeepONet introduces a Bayesian approach to operator learning, reducing overfitting and providing predictive uncertainty, which is directly useful in risk-aware optimization [47]. A credibility study for a DNN surrogate of a NACA0012 airfoil showed how to conduct verification and validation, VVUQ, for ML surrogates in CFD, the next step is out-of-distribution scenarios [90]. In MEMS, combining an ANN surrogate with MCMC enabled fast UQ and calibration of manufacturing parameters based on voltage responses, similar frameworks are suitable for photonic sensors and microactuators [49]. When probabilistic information is scarce, interval deep learning operates on input intervals, propagating uncertainty without distributional assumptions; a promising direction is interval–probabilistic hybrids [59].

Domain applications show a wide spectrum of integration. In fluid–structure interaction, surrogates integrated into KratosMultiphysics shortened runtime without significant loss of accuracy, both in weak and strong coupling, further work includes stability under large deformations and unsteady flows [48]. A geotechnical review documents the dominance of ANNs, 35 percent, and RF or SVM in mechanical property tasks and highlights the need for physics-guided and adaptive methods on multiscale data, PINNs, and invariant-encoding networks appear central here [63]. Analyses of FGM under temperature showed that SVM can effectively accelerate the analysis of natural frequencies under thermal uncertainty, material degradation should be included [56]. In laminated composites, ANNs reproduce stochastic first-ply failure comparably to Monte Carlo, which suggests applications in reliability-based design [60]. In predicting fatigue crack growth, networks achieved very low MSE and stable generalization with small sample sizes, edge GPU implementations in SHM monitoring are conceivable [61]. In SHM of a composite wing, multifidelity frameworks combine ANNs with low-fidelity correction, reducing the number of high-fidelity FEA points, extensions include environmental uncertainties and aging [100]. For FE², it has been shown that DNNs guide adaptive sampling of the “material genome” database, which radically lowers offline cost, the next step is coupled fields and failure [13]. Alongside this, there has been an uncommon use of GANs to “image” FEM inputs and outputs provided near real-time predictions with 5–10 percent errors, and an interesting direction in coupling with constraint mechanics [51]. Finally, deep learning can even design numerics, networks that fit the number of Gauss quadrature points and optimize the cost of assembling stiffness matrices, thus, validation on higher-order elements will be useful [54].

Let us finish with a meta view. Reviews systematize the field as five categories of DL in mechanics: substitution, enhancement, discretizations as networks, generative, and RL, revealing where ML truly accelerates FEA and where it still lags, indicating that numerical stability and boundary condition imposition are key [74]. A broad review combines classics and recent advances, PINNs, LSTMs, transformers, with limitations and training practices, which provides a good risk map for high-stakes engineering [75]. From the standpoint of data theory and verification, “data-driven games” formulate the identification of an effective law as a non-cooperative game between stress and strain, thus, multiphysics versions with process constraints are appealing [79,80]. “Meta-modeling games” with RL automate both the construction of a friction–separation law and its calibration, validation, and falsification in an antagonistic setting; the direction is collaboration with laboratories on “adversarial experiments” [68].

The paper [101] proposes a hybrid learning strategy MGA, MSGD for physically informed neural networks to approximate solutions to linear elliptic partial differential equations, with a focus on PINN-type loss function construction and training optimization. The paper [92] evaluates the usefulness of shallow neural networks for stress updates in computational solid mechanics by integrating them with the FEM solver and comparing them with conventional schemes for elastic, nonlinearly elastic, and elastic–plastic materials. The article [102] provides an overview of the applications of physical knowledge neural networks (PINNs) in computational solids mechanics, discussing numerical frameworks, architectures, and algorithms, as well as their use in constitutive modeling, reverse analysis, and damage forecasting of materials and structures. The paper [103] presents a data augmentation technique for a regression surrogate model in civil engineering, using convolutional neural networks to predict loads in collision scenarios and analyzing the impact of the number of training sets and t-SNE classification methods on prediction accuracy. The paper [104] proposed a component-based machine learning paradigm for discovering velocity-dependent and pressure-sensitive plasticity models, in which material law learning was divided into sequential programs involving elasticity, initial flow, and amplification laws, and trained neural networks were tested on simulation, experimental, and homogenization data.

The paper [105] presents the use of recursive neural networks with dimensionality reduction and decomposition techniques as surrogate models in multiscale computation, enabling the recovery of the evolution of microstructure state variables in the localization step and significantly accelerating computations thanks to the implementation of GPUs. The paper [106] presents the construction of a substitute model for predicting the strength of crushed elements using machine learning methods and deep networks, based on data from dynamic elastic–plastic analysis and an adaptive structural evaluation method. The paper [107] presents a comparison of different neural network architectures in constitutive modeling of elastic–plastic materials, indicating the effectiveness of history-based approaches and internal variables in the reproduction of material models. The article [108] provides an overview of the latest developments in multiscale modeling based on machine learning, with a focus on simulation, homogenization of composites, defect modeling and materials design, highlighting the potential of ML methods in improving the efficiency and accuracy of computations.

The article [109] presents a comprehensive overview of machine learning-based modeling in structural engineering, covering computational mechanics, SHM, design and fabrication, stress and failure analysis, and materials modeling and design, indicating the role of ML methods in increasing computational efficiency. The paper [110] presents a neural network-based framework for constitutive modeling of inelastic materials, with a general stress update procedure based on RNN, construction-free training strategies, and a thermodynamic coherence verification criterion, compared to GRU and LSTM architectures. The paper [111] presents variational PINNs with domain decomposition, CV PINNs in which residues on subdomains are numerically integrated, and test functions embedded in convolutional filters, which increases parallelism and accuracy and allows for effective reversal problems, such as identifying uneven damage. The paper [112] proposed an improved PINN for 3D hyperflexibility, combining residues in the strong form with potential energy in a multicomponent loss function with adaptive weighting, meshfree approach, and label-free learning, which enables rapid determination of responses for different boundary conditions.

In summary, networks trained on data and physics have permeated three layers of computational mechanics, (i) solver “cores,” PINNs, DEM, BINNs, GCNs, (ii) constitutive laws, from SPD-NN and neural ODEs to RNNs or NCDEs, and (iii) engineering tools, inverse design, UQ, SHM. The most urgent research perspectives are, formal guarantees of stability and convergence in multiphysics couplings, especially under low-regularity boundary conditions, hierarchical UQ, Bayesian or interval, with “certificates” of trust, standardized VVUQ test suites, and differentiable “simulation ↔ learning” pipelines operating in the loop in design and experimental environments. Both constructive efforts, for example, JAX FEM [21], and methodological ones, for example, VB-DeepONet [47], point in this direction, and their integration promises a new wave of “learning-in-the-solver” tools for responsible and scalable design.

To conclude the analysis of methods in Section 3.2, a summary has been prepared in

Table 3. Summary of Section 3.2.

Class	Theme (What Is Addressed)	Data and Sensors	Research Task	Architectures and Techniques	Metrics and Implementation Requirements	Example Key Refs [n]
General Machine Learning	Overviews and foundations for DL/ML in computational mechanics; differentiable simulation; operator learning with UQ	Experimental datasets, numerical fields, simulation logs	Survey, taxonomy, and differentiable/mechanistic ML toolchains	Reviews; differentiable FEM (JAX-FEM); operator learning with VB-DeepONet for UQ	Clarity on compute/training budgets; calibration and generalization; uncertainty calibration	[19,32,69,70,77]
Core Neural Networks	Feed-forward/CNN/RNN baselines for constitutive laws and path-dependent behavior; physics-aware training	Time series (stress–strain), FE fields, microstructures	Constitutive modeling; stress/field prediction on meshes	FFNN/CNN; RNN/LSTM; Sobolev-training and residual weighting; RNN frameworks for inelasticity	Accuracy (MAE/MSE/R2); thermodynamic consistency; stability in FE loops; training with scarce/noisy data	[25,29,42,103,112]
Deep Neural Networks	Advanced/structured DL: geometric DL on graphs, transformers/diffusion, boundary-integral NNs, inverse design	Images/graphs of microstructure, sensor/field images, PDE boundary data	Multiscale inference; fracture dynamics; boundary-only learning; inverse microstructure design	Geometric DL (GNN) for anisotropy and plasticity; transformer-diffusion for fracture; BINN (boundary-integral NN); CNN/IM-CNN on arbitrary meshes; ML-assisted inverse design; data augmentation for composites	Accuracy vs. FE/FFT baselines; mesh/geometry generalization; training time vs. inference speed	[30,48,67,95]

, which organizes the discussed threads into the classes General Machine Learning, Core Neural Networks, and Deep Neural Networks. For each group, it presents the leading theme, data, and sensor types, for example, experimental datasets, numerical fields, image or sensor data, the research task, the architectures and techniques employed, including classical ML, CNN or RNN or LSTM, operator learning, FNO or DeepONet, and graph models, as well as metrics and requirements, accuracy, uncertainty calibration, UQ, training and inference time, computational demands, together with references. The summary serves as a concept and method map, standardizes terminology within data categories, facilitates comparison of algorithms, and provides an assessment of operational maturity and approaches to uncertainty, closing the methodological layer and forming the basis for the synthesis of conclusions in Section 3.3.

3.3. Future Directions of Development

The consolidation of findings from Section 3.1 and Section 3.2 suggests the convergence of two hitherto parallel currents, classical computational mechanics methods and machine learning or neural networks. The coming years will therefore bring not only faster computations and better approximations, but above all the co-design of solvers and data models under the rigor of physical equations, uncertainty, and the need for inverse design. This requires both improved, differentiable solvers, and “physics-embodied” network architectures together with credible validation procedures. The outline of such an agenda emerges from the compiled source literature on which Section 3.1 and Section 3.2 are based.

The first axis of development is differentiable, co-designed solvers, differentiable simulation, in which the neural network is part of the elementary computation step rather than an external add-on. Integration of networks into stiffness matrices and tangent procedures, as demonstrated in I-FENN, reduces the cost of nonlocal damage models without losing mesh independence [17]. In turn, FEMIN replaces selected parts of a FEM solver’s mesh with NN modules, accelerating crash simulations while preserving fidelity of dynamics [19]. In the same spirit, HiDeNN FEM systematizes approximation through hierarchical NNs and r-adaptivity, which strengthens convergence in 2D and 3D [20]. The differentiable JAX FEM natively exposes derivatives, making optimization and inverse design first-class citizens of the solver [21]. Hybrid, meshfree NIM closes this line by fusing meshfree techniques with differentiable programming in a single, physically anchored framework [53].

The second axis concerns network-based, yet theory-consistent material models. The SPD-NN architecture enforces positive definiteness of tangents and satisfies energy and second-order criteria, which stabilizes coupling with FEM even under load history [60]. The neural ODE concept reinforces this consistency by guaranteeing polyconvexity of the strain energy at the model construction stage [30]. Constraint-based learning and physical regularization, as in hyperelasticity with enforced symmetries and normalization, improve stability and convergence under small, noisy datasets [29]. Geometric deep learning allows the topology of microstructures to be embedded into energy functionals and plasticity, which opens interpretable micro–macro “bridges” [34]. Energy-based formulations, DEM, indicate that minimizing energy with NNs can replace the FEM stage within the optimization loop, while remaining consistent with variational principles [94].

The third axis addresses history-dependent models formulated so as to converge in nonlinear solvers. LSTMs have demonstrated the ability to reproduce viscoplasticity with thermal and rate memory faithfully [31]. The new family of models, INCDE, Neural Controlled Differential Equations, ensures continuity and stability of elastoplastic predictions under variable integration steps, which is essential for iterative FEM [97]. At the same time, practical implementation issues of RNNs in solvers are alleviated through modified data generation and increment-aware architectures [96,97]. In the multiscale localization step, dimensionality reduction and decomposition into several RNNs enable recovery of microstructural states, not only macro responses [105].

The fourth axis encompasses multiscale behavior and nonlocality. Learning nonlocal constitutive relations, inspired by formal solutions of transport equations, provides interpretable convolutional structures for closure models [32]. On the other hand, coarse-graining paths and data-driven constitutive models guided by thermodynamic assumptions, GENERIC, yield safe generalizations when faithful RVE–macro coupling is impractical [91]. FE² frameworks based on DDCM and adaptive data augmentation show how to build “material genomes” offline efficiently for fast macroscale solutions [13].

The fifth axis is operator learning and graph-based formulations. Galerkin graph PINNs develop discrete, variational PINNs that rigorously enforce boundary conditions and operate on unstructured meshes [64]. Bayesian operator learning, such as VB-DeepONet, adds uncertainty calibration and resistance to overfitting, a foundation for engineering decision making [47].

The sixth axis concerns next-generation PINNs. Variational residual formulations enable more convergent enforcement of equations and the fusion of BCs or ICs with data in a single objective [27]. Boundary-integral networks, BINNs, transfer unknowns to the boundary and naturally respect boundary conditions in complex geometries [72]. Meshless, collocation, and energy-based approaches show that PINNs or DEM can be self-sufficient 3D solvers, especially where meshing is a barrier [112]. In elastodynamics, composite DNNs with enforced BCs confirm that PINNs can operate without labeled data also in dynamics [22].

The seventh axis, crucial from an implementation perspective, is credibility, uncertainty, and error control. Work on rigorous credibility evidence for surrogate models, for example, flow around NACA0012, show how to report confidence bounds, and where models fail [90]. Learning error models for reduced, approximate solutions of nonlinear systems provides corrections and measures of epistemic uncertainty that can be attached to predictions [57]. Probabilistic learning and predictor–corrector schemes in UQ reduce the cost of identifying hyperparameters of reduced models [58]. Using NNs as surrogates within full Bayesian inversion pipelines, for example, MEMS, enables scalable MCMC, making manufacturing parameter uncertainties realistic [49]. When input distributions are unavailable, interval deep learning provides credible inference ranges and can be integrated into model cascades [59].

The eighth axis is the economics of data, from augmentation to reference repositories. The reviewed studies show that sensible augmentation, for example, synthetic trajectories for RNNs and enrichment of “sparse” composite data, can radically improve generalization and reduce the cost of high-fidelity simulations [93]. Augmentation and training set selection techniques for surrogates, including t-SNE-based approaches, allow efficient use of small datasets [103]. Database construction frameworks combining homogenization and ANNs propose a low-cost way to create broad σ–ε maps for DDCM, including in 3D [44].

The ninth axis is end-to-end inverse design and topology optimization. PINNTO removes the need for FEA in the TO loop by solving elasticity directly with an energy-based network and producing designs comparable to SIMP [25]. DEM allows sensitivities to be computed without auxiliary inverse networks by exploiting self-adjointness of compliance [24]. Differentiable FEM, JAX FEM, opens the way to automated 3D inverse design workflows [21]. ML approaches to inversion in heat conduction and to the fabrication of wrinkle microstructures show that inverse design can be “unlocked” even where classical iterations are impractical [65,69]. Additive manufacturing in 3D or 4D is becoming a natural proving ground for such algorithms, with a growing role for ML in shaping active responses [71].

The tenth axis is real-time simulation and digital twins. U-Mesh with a U-Net offers instantaneous displacement fields in hyperelasticity and approximates FEM solutions at a fraction of the cost, which is essential for interactive applications and control [45]. Predicting scalar fields without being “tied” to a single mesh enables surrogates to transfer across arbitrary geometries and discretization densities [50]. In fluid–structure interaction, replacing one subsystem with an NN surrogate shortens simulation time while maintaining quality, paving the way for FSI digital twins [48]. In structural health monitoring, multifidelity frameworks combine FEM with a fast ML corrector, reducing the number of expensive high-fidelity points needed for diagnosis [100].

The eleventh axis reveals generative models and large language models in applied mechanics. Diffusion transformers can capture fracture dynamics at the atomistic level and suggest material design inspirations beyond the training data [81]. Representing FEM inputs and outputs as images and using cGANs proposes a new language for coupling simulation and surrogates, close to computer vision tools [51]. Finally, LLMs, although they require critical validation, have the potential to automate analysis, summarize findings, and generate experimental code, but only within verifiable workflows [82].

The twelfth cross-cutting axis is standardization of validation, adversarial tests, and data games. Meta-modeling games with reinforcement learning, both for model construction and falsification, force architectures to “pass exams” on difficult, contradictory scenarios and improve the credibility of data-driven paradigms [73]. Data-driven games formalize the tension between mechanical consistency, equilibrium and compatibility, and proximity to material data, without a parametric model wrapper [79]. In parallel, a priori error estimation frameworks for shallow PINNs are being developed, which brings the PINN environment closer to the mature FEM standards of error analysis [73].

The common denominator of these axes is connectivity. The methods of Section 3.1, FEM, BVPs, homogenization, multiscale modeling, UQ, and Section 3.2, NNs, DNNs, operator learning, cease to compete and begin to interpenetrate, the NN becomes a shape function, a material law, or a sensitivity block, while the solver becomes a differentiable backbone that imposes physics and learns jointly with the data. With all this, rigor cannot be relinquished, in subsequent studies, we should require explicit mechanisms for ensuring stability, as in SPD-NN [28], and thermodynamic guarantees, as in polyconvex formulations [30], and the reporting of uncertainty and credibility, as in surrogate assessment programs and error models [57,90]. This should be supported by open datasets and code, for example, public PINN or I-FENN code [17], and multiscale benchmarks, for example, RVE to UMAT to FEM, [39], and procedures for adversarial tests [80].

In summary, the development perspective is not “replacing FEM with NNs,” but a new generation of hybrid, credible tools that combine equation discretization, operator learning, and statistical thinking about error and uncertainty. In this vision, the designer, the experimentalist, and the algorithm operate within a single, differentiable loop, from observation, through identification, to inverse design, in full accordance with the laws of mechanics and with transparent quantification of ignorance.

3.4. Summary

This work presents a coherent panorama of how two orders, classical computational mechanics, Section 3.1, and machine learning methods, Section 3.2, are converging toward a common equilibrium point. On the “physics first” side, the core remains PDE discretizations, FEM or EFG or BEM, meshfree, variational, and Galerkin methods, which ensure physical correctness, numerical stability, and transparent error control. On the “data first” side, deep architectures are increasingly mature, CNNs, RNNs or LSTMs, Neural or Controlled ODEs, operator learning, as are PINN or DEM classes and FEM–NN hybrids that inject physical knowledge into the loss function, the architecture, or the training procedure. Against this backdrop, the answers to the three research questions arise not from ad hoc “tricks,” but from an emerging integrative logic, the choice of learning algorithm and representation should be queued with respect to the PDE form, geometry, and data availability, credibility mechanisms, UQ, V and V, error control, should be linked directly to where the model “touches” physics, boundary conditions, governing laws, material properties, and to computational costs reported in an auditable manner. Three themes dominate the review, (i) forward and inverse problems governed by PDEs, elliptic or hyperbolic, elastostatics, elastodynamics, conduction, FSI, (ii) constitutive modeling, hyperelasticity, viscoelasticity, plasticity, damage, nonlocality, (iii) multiscale computing and topology optimization. For (i), “physics informed” frameworks perform best, from classical PINNs and energy variants, DEM, to variational and graph formulations, graph Galerkin, which couple representation learning with the imposition of BCs or ICs and equation residuals in strong or weak form, enabling both forward solves and parameter inversion under sparse observations.

In particular, Galerkin graph formulations handle irregular geometries and unstructured meshes effectively, and variational formulations improve trainability and BC enforcement without tedious penalty tuning. Operator learning, for example, DeepONet and its Bayesian variants, yields the greatest benefits when generalization is required across families of input fields or excitations and domains, rather than “reconstructing” a single task. For (ii), the advantage lies with architectures that enforce thermodynamic consistency and nonlinear analysis requirements, polyconvexity, SPD tangents, monotonicity of energy derivatives, polyconvex Neural ODEs, SPD NNs, and various forms of Sobolev and physics-constrained learning led to stable stress updates in FEM solvers. Path-dependent material responses are most reliably captured by continuous sequential models, Neural or Controlled ODEs, and carefully trained RNNs or LSTMs, provided consistency is maintained with respect to the incremental step and integration in a Newton scheme. In (iii), FEM–NN hybrids, I-FENN, HiDeNN FEM, FEMIN, accelerate solvers by embedding networks in shape functions or tangent matrices, while differentiable simulation tools, for example, JAX FEM, facilitate coupling learning with inverse design and gradient automation. Where throughput matters, CNN or U-Net surrogates and mesh-interpolating networks outperform classical ROMs in on-the-fly displacement or stress field prediction, provided the extrapolation range is tightly controlled. These observations are consistent with a broad portion of the analyzed literature and domain examples, from label-free elastodynamics to poroelastic parameter inversion, FSI, NDT, and topology optimization.

It should be noted that datasets are typically hybrid, high-fidelity synthetics, FEM or FFT, RVEs, are complemented by measurements, for example, DIC, triaxial tests, experimental characterizations. Favorable representation patterns include images and feature maps, U-Net, cGAN, where rapid field prediction over families of similar domains is key, graphs or meshes and operator mappings when geometry, topology, and loads must vary, and learned shape functions or meshfree collocation where pointwise compliance with the PDE is to be tightly controlled. Enforcing boundary conditions and physics proves decisive; moving from “soft” penalties to weak or variational formulations, or to composite networks that satisfy BCs a priori substantially lowers data requirements and improves training stability. On the validation side, the best results come from cross-domain tests over geometry, loading regimes, and mesh densities, not only train or test splits, and from verification against an independent solver, for example, FEM as “gold standard,” or experiment. Data bottlenecks are alleviated by augmentation methods, classical and physics-guided, selective completion of DDCM bases, and hybrid training algorithms that balance hypothesis-space exploration with computational cost. Consequently, the best accuracy–cost compromise is usually achieved by combining physics-encoded learning, PINN or DEM or variational, a representation aligned with the problem discretization, graph or mesh or meshfree, and cross-domain validation, domain, BC, loading.

In addition, the share of studies reporting uncertainty and credibility is growing, but practice is not yet uniform. Strong examples include Bayesian operator learning, VB-DeepONet, and error models for ROMs and approximate solutions, which learn mappings from error indicators to solution errors and allow predictive quality to be extrapolated. Interval and probabilistic approaches show how to handle nonprobabilistic uncertainty and model-form uncertainty. In parallel, credibility assessment frameworks for surrogate predictors in CFD or aerospace applications are emerging, which is particularly important for operational decisions. On the cost side, two mature paths are observed, (i) integrating NNs inside solvers, FEMIN, I-FENN, HiDeNN FEM, (ii) differentiable FEM solvers, JAX FEM.

Both paths provide objective speedup metrics and GPU scaling. Domain studies report time reductions in two to three orders of magnitude, for example, a reduction relative to EFG of about 99.94 percent in an EFG–ANN setting, and there is more frequent reporting of hardware configurations and the release of code and data, which promotes replication. However, unified V and V protocols for data-driven models, and, in particular, a standard for reporting the computing budget, training or inference time, memory or energy use, are still lacking. The practical conclusion is the necessity to tie each result to, a, an a posteriori test against a solver or experiment, b, quantification of predictive uncertainty, and c, an explicit cost profile.

Synthesis and implications for practice. The analysis indicates that the greatest qualitative benefits arise when physics regulates learning, energy functional, PDE residuals, variational loading of the loss, and the architecture respects the problem structure, graphs, SPD or polyconvex networks, Neural or Controlled DEs for load history. Operator learning is preferred when generalization is required in function space, varying BCs or loads, materials, geometries, CNN or IM-CNN surrogates when the goal is ultra-fast field prediction over families of shapes, PINNs or DEM when labels are lacking or when parameter inversion under sparse data are being solved. FEM–NN hybrids are optimal when modular interchangeability and compatibility with FEM infrastructure are important, and differentiable solvers facilitate coupling with design and UQ. Regardless of choice, V and V plus UQ plus costs must be co-equal outcomes, not add-ons.

In light of the above, the work answers the posed questions, first, it identifies the dominant classes of tasks, PDE-governed forward or inverse, constitutive, multiscale or TO, and indicates in which configurations PINNs or DEM, operator learning, and graph networks deliver the greatest qualitative gains. Second, it organizes data types, geometry or mesh representations, and BC enforcement methods, showing that the strongest accuracy–cost compromise is obtained by coupling weak or variational formulations with discretization-aligned representations and cross-domain validation. Third, it shows that although UQ and V practices are increasingly common, with specific theoretical frameworks and tools emerging, such as Bayesian or operator learning, error models, interval analyses, the standard for reporting costs requires further harmonization; in practice, the rule should be that, without UQ or V and an explicit cost, there is no credibility. Taken together, the results trace a clear path for implementing data-driven methods in computational mechanics, physics as the primary regulator, architecture aligned with geometry, validation against solver or experiment, a clear computing budget, and mandatory uncertainty quantification. This approach allows simulation time to be reduced by orders of magnitude while maintaining, and controlling, quality, which makes it useful in safety-critical engineering applications.

It should also be emphasized that the combination of Section 3.1 and Section 3.2 is not a simple sum of methods, but a coherent methodology; we chose the learning scheme not because it is “new,” but because it best fits the specific PDE, data, and validation goals. In this sense, computational mechanics and machine learning do not compete, but co-create a new computational practice, which is transparent, reproducible, and economical.

4. Statistical Overview

The growing interest in the applications of computational methods and artificial intelligence in computational mechanics is confirmed by the entire analyzed corpus. In the years 2015–2019, eight publications were identified, while in 2020–2024, as many as 90 were identified, which gives a total of 98 items and translates into 8.16 percent and 91.84 percent of the entire corpus, respectively. In the second sub-period, the number of works is therefore nearly 11.25 times higher, an increase in +82 publications. The numbers and shares are presented in

Table 4. Publications by year in all categories.

Name	2015–2019	2020–2024	All Years	Share [%]
Total	8	90	98	100.0
Document Type
Conference Paper	1	18	19	19.39
Journal Article	7	67	74	75.51
Other	0	5	5	5.1
Computational Mechanics Methods and Modeling
Computational Methods	1	41	42	42.86
Material Modeling	1	34	35	35.71
Stochastic Methods and Uncertainty	6	12	18	18.37
Surrogate Methods	1	13	14	14.29
Inverse Analysis	1	17	18	18.37
Multiscale Modeling	0	8	8	8.16
Machine Learning and Neural Networks
General Machine Learning	3	50	53	54.08
Core Neural Networks	5	52	57	58.16
Deep Neural Networks	1	44	45	45.92
Research Methodology
Experiment	5	68	73	74.49
Literature Analysis	3	27	30	30.61
Conceptual	6	68	74	75.51

.

Within the classes of artificial intelligence methods, network-based approaches maintain a very strong position, while “classical” machine learning has become increasingly widespread. Across the entire period, Core Neural Networks appear in 57 papers (58.16 percent), General Machine Learning in 53 (54.08 percent), and Deep Neural Networks in 45 (45.92 percent). The temporal distribution shows a clear strengthening of deep approaches, in 2015–2019, Deep Neural Networks were present in one out of eight publications (12.50 percent), whereas in 2020–2024, they were present in 44 out of 90 publications (48.89 percent). Core Neural Networks remain dominant, from five of eight (62.50 percent) to 52 of 90 (57.78 percent), while General Machine Learning increases in frequency from three of eight (37.50 percent) to 50 of 90 (55.56 percent). These data indicate a gradual shift toward neural networks, especially deep ones, while at the same time maintaining, and even expanding, the use of ML methods as a whole. In Figure 5, the distribution of AI method classes in the corpus is presented: General Machine Learning, Core Neural Networks, and Deep Neural Networks, for 2015–2019 and 2020–2024.

Among document types, journal articles are dominant. Across the entire set, Journal Articles account for 74 out of 98 items (75.51 percent), conference papers for 19 out of 98 (19.39 percent), and the category Other covers 5 out of 98 (5.10 percent). The dynamics between sub-periods confirm the maturity of the publication stream, in 2015–2019, articles accounted for seven out of eight (87.50 percent) and one out of eight conferences 12.50 percent), in 2020–2024 articles were 67 out of 90 (74.44 percent), conferences 18 out of 90 (20.00 percent), while the share of the category Other appears only in the second sub-period with 5 out of 90 (5.56 percent). This distribution suggests that research results are increasingly taking the mature form of journal articles, although the growing share of conferences also indicates rapid expansion of the thematic field. In Figure 6, the structure of document types in the corpus is presented: Journal Article, Conference Paper, and Other, for 2015–2019 and 2020–2024.

In the area of methods and modeling in computational mechanics, a clear shift can be observed from early stochastic profiling toward deterministic methods and material modeling. Across the entire set, Computational Methods dominate with 42 out of 98 (42.86 percent), followed by Material Modeling with 35 out of 98 (35.71 percent). Next are Inverse Analysis with 18 out of 98 (18.37 percent) and Stochastic Methods and Uncertainty with 18 out of 98 (18.37 percent), then Surrogate Methods with 14 out of 98 (14.29 percent), and finally Multiscale Modeling with 8 out of 98 (8.16 percent). The split into periods highlights the differences even more clearly; in 2015–2019, the emphasis was mainly on Stochastic Methods and Uncertainty, 6 out of 8, 75.00 percent, while Computational Methods, Material Modeling, Surrogate Methods, and Inverse Analysis each appeared in only one out of eight (12.50 percent), and Multiscale Modeling was absent. In 2020–2024, a strong reorientation takes place, Computational Methods with 41 out of 90 (45.56 percent) and Material Modeling with 34 out of 90 (37.78 percent) become dominant, Inverse Analysis with 17 out of 90 (18.89 percent) and Surrogate Methods with 13 out of 90 (14.44 percent) grow, while Stochastic Methods drop proportionally to 12 out of 90 (13.33 percent), and Multiscale Modeling appears visibly with 8 out of 90 (8.89 percent). This distribution indicates the maturation of deterministic analysis tools and the development of material modeling and surrogate methods, accompanied by a reduced emphasis on uncertainty as a central research axis. In Figure 7, the categories within Computational Mechanics Methods and Modeling are presented: Computational Methods, Material Modeling, Stochastic Methods and Uncertainty, Surrogate Methods, Inverse Analysis, and Multiscale Modeling, for 2015–2019 and 2020–2024.

In methodological approaches, conceptual and empirical studies prevail. Across the entire period, Conceptual accounts for 74 out of 98 publications (75.51 percent), and Experiment for 73 out of 98 (74.49 percent), while Literature Analysis has a smaller share with 30 out of 98 (30.61 percent). Over time, the dominance of experiments becomes consolidated, in 2015–2019 Experiment represented five out of eight (62.50 percent), and in 2020–2024, as many as 68 out of 90 (75.56 percent). At the same time, Literature Analysis decreases in share from three out of eight (37.50 percent) to 27 out of 90 (30.00 percent), whereas Conceptual maintains a very high and stable level, from six out of eight (75.00 percent) to 68 out of 90 (75.56 percent). This picture confirms the transition from field exploration to intensive data-driven and validation-oriented research, while maintaining a strong conceptual component that defines the framework for further methodological development. In Figure 8, the methodological approaches in the corpus are presented: Experiment, Literature Analysis, and Conceptual, for 2015–2019 and 2020–2024.

Next, χ² independence tests were performed to verify whether the distributional differences between the two sub-periods are statistically significant (α = 0.05). For Document Type, the result was χ²(2) = 0.82, p = 0.66, which does not provide grounds for rejecting the hypothesis of independence, the observed increase in the share of conference publications does not significantly alter the overall pattern dominated by journal articles. In the group Computational Mechanics Methods and Modeling, the value χ²(5) = 20.98, p < 0.001, indicates a significant structural change between the periods and statistically confirms the previously described reorientation from stochastic approaches toward deterministic methods and material modeling, with the parallel emergence of surrogate and multiscale methods. For Machine Learning and Neural Networks, χ²(2) = 1.98, p = 0.37, and for Research Methodology, χ²(2) = 0.30, p = 0.86; in both cases no significant differences in distributions between 2015 and 2019 and 2020 and 2024 are found, meaning that the trends observed in the descriptions, such as the growth of deep network applications or the higher share of experimental studies, represent developmental directions, but with the current sample size they do not translate into statistically confirmed structural change. Overall, only in the area of methods and modeling in computational mechanics do we observe a statistically significant transformation of the research profile, in the other groups the structure remains stable.

The geographical structure of publications confirms that the surge in the number of works after 2019 had a broad character, encompassing many centers, while maintaining a clear leadership of the United States. In 2015–2019, eight publications were recorded, and in 2020–2024 as many as 90, giving a total of 98 items. The numbers and shares are presented in

Table 5. Publications by year in countries.

Country	2015–2019	2020–2024	All Years	Share [%]
All countries	8	90	98	100.0
United States	4	40	44	44.9
Germany	0	13	13	13.27
China	1	11	12	12.24
United Kingdom	1	8	9	9.18
France	1	6	7	7.14
India	0	5	5	5.1
Australia	0	4	4	4.08
Austria	1	2	3	3.06
Canada	1	2	3	3.06
Luxembourg	0	3	3	3.06
Greece	1	1	2	2.04
Other	1	12	13	13.27

. Across the entire period, the largest number of works comes from the United States, 44 publications, 44.90 percent of all entries in the “All years” column, followed by Germany with 13 (13.27 percent) and China with 12 (12.24 percent). The next group includes the United Kingdom, 9, 9.18 percent, and France, 7, 7.14 percent, followed by India, 5, 5.10 percent, Australia, 4, 4.08 percent, Austria, Canada, and Luxembourg, 3 each, 3.06 percent, and Greece, 2, 2.04 percent. The category Other encompasses the long tail of countries with smaller contributions, 13 publications, 13.27 percent.

The temporal distribution shows both the consolidation of the leader and a clear geographical diversification after 2019. In 2015–2019, half of the works came from the USA (four out of eight, 50.00 percent), and single articles from China, the United Kingdom, France, Austria, Canada, and Greece (one out of eight each, 12.50 percent), while Germany, India, Australia, and Luxembourg were not represented. In 2020–2024, the picture expands, the USA remains dominant (40 out of 90, 44.44 percent), while Germany (13 out of 90, 14.44 percent) and China (11 out of 90, 12.22 percent) join as the strongest centers outside the USA. The United Kingdom (8 out of 90, 8.89 percent) and France (6 out of 90, 6.67 percent) show stable contributions, while India (5 out of 90, 5.56 percent) and Australia (4 out of 90, 4.44 percent) become clearly visible. Importantly, smaller centers as well, for example, Luxembourg, with 3 out of 90 (3.33 percent), and the category Other with 12 out of 90 (13.33 percent), signal a broadening of the activity map. In terms of increments, the largest growth is observed in the USA (+36), Germany (+13), China (+10), the United Kingdom (+7), France (+5), India (+5), and Australia (+4) compared to the first sub-period. Overall, the leadership of the USA was maintained, but the leader’s relative share declined (from 50.00 percent to 44.44 percent), which is a typical signal of the maturation and internationalization of the research stream. In Figure 9, the distribution of publications by country is presented: United States, Germany, China, United Kingdom, France, India, Australia, Austria, Canada, Luxembourg, Greece, and Other, for 2015–2019 and 2020–2024.

For the purpose of assessing changes in geographical structure, a χ² independence test was conducted for the distribution of countries between sub-periods. The result χ²(11) = 10.87, p = 0.45 does not allow rejection of the independence hypothesis, which means that despite the strong increase in the number of publications, the proportions between countries did not change significantly in statistical terms. In other words, the post-2019 expansion was broadly distributed, with growth occurring in many countries in parallel, without a fundamental reshuffling of the hierarchy, the USA remained the leader, while Germany and China joined most strongly.

The links of computational methods with artificial intelligence families and methodological approaches show how the computational basis of analyses is being built. Computational Mechanics Methods and Modeling with the groups Machine Learning and Neural Networks and Research Methodology are presented in

Table 6. Publications by Computational Mechanics Methods and Modeling in other categories.

Name	Computational Methods	Material Modeling	Stochastic Methods and Uncertainty	Surrogate Methods	Inverse Analysis	Multiscale Modeling	Total
Total	42	35	18	14	18	8	98
Machine Learning and Neural Networks
General Machine Learning	24	17	9	9	9	6	53
Core Neural Networks	29	19	11	7	11	3	57
Deep Neural Networks	20	19	5	11	7	2	45
Research Methodology
Experiment	33	28	12	12	14	4	73
Literature Analysis	11	13	7	2	3	6	30
Conceptual	35	27	11	11	15	3	74

.

In the relationship between computational methods and artificial intelligence families, the strongest node is the pairing of Core Neural Networks with Computational Methods. A total of 29 co-occurrences were recorded, which represents 29.59 percent of the entire corpus, 69.05 percent of all publications with the Computational Methods label, and 50.88 percent of works tagged as Core Neural Networks. The second pole is the pair General Machine Learning and Computational Methods, 24 co-occurrences, that is 24.49 percent of the corpus, 57.14 percent in the Computational Methods column, 45.28 percent in the General Machine Learning row. The third most frequent connection is Deep Neural Networks with Computational Methods, 20 co-occurrences, 20.41 percent of the corpus, 47.62 percent in the column, 44.44 percent in the Deep Neural Networks row.

In the area of Material Modeling, a comparable embedding is observed in deep networks and in “core” networks, with 19 co-occurrences each, which corresponds to 54.29 percent of the entire Material Modeling column, 42.22 percent of all publications tagged as Deep Neural Networks, and 33.33 percent of those tagged as Core Neural Networks. An important complement is provided by Surrogate Methods, which in 78.57 percent of cases co-occur with Deep Neural Networks, 11 out of 14, which corresponds to 11.22 percent of the entire corpus and 24.44 percent of all works tagged as Deep Neural Networks. In Multiscale Modeling, the strongest link is with General Machine Learning, 6 out of 8 co-occurrences, 75.00 percent of the column, 11.32 percent in the General Machine Learning row, while the link with neural networks is weaker.

Looking from the AI families’ perspective, the distribution of emphases is similar. In General Machine Learning, Computational Methods dominate, 24 out of 53, 45.28 percent, followed by Material Modeling, 17 out of 53, 32.08 percent, while Stochastic Methods and Uncertainty, Surrogate Methods, and Inverse Analysis each record nine co-occurrences, 16.98 percent in the row. In Core Neural Networks, half of the records are linked with Computational Methods, 29 out of 57, 50.88 percent, and one third with Material Modeling, 19 out of 57, 33.33 percent. In Deep Neural Networks, the two main pillars are Computational Methods, 20 out of 45, 44.44 percent, and Material Modeling, 19 out of 45, 42.22 percent, with a marked complement from Surrogate Methods, 11 out of 45, 24.44 percent.

This indicates that the computational core, consisting of deterministic methods and material modeling, serves as a common platform for all AI families, while surrogate methods are particularly often used together with deep networks. The heat map of AI family co-occurrences with Computational Mechanics Methods and Modeling categories is presented in Figure 10.

In the links between computational methods and methodological approaches, conceptual and experimental studies prevail. In the Computational Methods column, the share of conceptual publications is 83.33 percent (35 out of 42), and experimental 78.57 percent (33 out of 42). In Material Modeling, the distribution is similar, 77.14 percent of works are conceptual (27 out of 35) and 80.00 percent experimental (28 out of 35). In Inverse Analysis, conceptual approaches also dominate with 83.33 percent (15 out of 18) and experimental with 77.78 percent (14 out of 18). In Surrogate Methods, experiments account for 85.71 percent (12 out of 14) and conceptual approaches 78.57 percent (11 out of 14). In Stochastic Methods and Uncertainty, experiments constitute 66.67 percent (12 out of 18) and conceptual approaches 61.11 percent (11 out of 18). A different picture is seen in Multiscale Modeling, where literature reviews account for the largest share, 75.00 percent (6 out of 8), which suggests an earlier phase of knowledge consolidation in this segment.

The row-wise methodological analysis confirms the concentration of research on two computational pillars. In Experiment, almost half of co-occurrences concern Computational Methods (33 out of 73, 45.21 percent), and more than one third Material Modeling (28 out of 73, 38.36 percent), while Inverse Analysis remains relevant (14 out of 73, 19.18 percent) as well as Stochastic and Surrogate with 16.44 percent each (12 out of 73 in both columns). In Literature Analysis, the most significant roles are played by Material Modeling (13 out of 30, 43.33 percent) and Computational Methods (11 out of 30, 36.67 percent), with an elevated share of Multiscale Modeling (6 out of 30, 20.00 percent). In Conceptual, Computational Methods again prevail (35 out of 74, 47.30 percent) together with Material Modeling (27 out of 74, 36.49 percent), while Inverse Analysis remains an important complement (15 out of 74, 20.27 percent). The heat map of methodological approaches co-occurring with Computational Mechanics Methods and Modeling categories is presented in Figure 11.

Statistical tests confirm that the observed differences are practical rather than structural. For the Machine Learning and Neural Networks block, the χ² value was 6.55 with 10 degrees of freedom and p = 0.77. For the Research Methodology block, the χ² value was 12.48 with 10 degrees of freedom and p = 0.25. In both cases there are no grounds to reject the independence hypothesis, which means that the distributions of co-occurrences between AI families and between methodological approaches and computational method categories do not differ significantly in statistical terms. We interpret the result as a stable computational core supporting all AI families and most types of research; however, clear application emphases that it does not lead to statistically confirmed structural reshuffling.

It should be noted that in the entire period 2015–2024, we observed a very strong increase in publication activity. The number of works increased from 8 in 2015–2019 to 90 in 2020–2024, a total increase of 82 publications, or +1025 percent relative to the baseline. Expressed as a compound annual growth rate (CAGR) between the two five-year sub-periods, the growth rate was about 62.3 percent per year. Across the six categories of computational mechanics, the trend is consistent; Computational Methods grew from 1 to 41 (CAGR ≈ 110 percent per year), Material Modeling from 1 to 34 (≈102 percent per year), Inverse Analysis from 1 to 17 (≈76 percent per year), Surrogate Methods from 1 to 13 (≈67 percent per year), and Stochastic Methods and Uncertainty from 6 to 12 (≈14.9 percent per year). Multiscale Modeling appears only in the second sub-period, from zero to eight, which should be treated as the entry of a new topic rather than growth measurable by CAGR. The change in distribution across these six categories is statistically significant, χ² = 20.98, df = 5, p < 0.001, which confirms the transition from an early emphasis on stochastic methods toward deterministic methods and material modeling, with increasing use of surrogate methods and the emergence of multiscale threads. The question concerning the existence of a growth trend and its scale should therefore be considered positively resolved and statistically confirmed.

As for the structure of AI methods, the share of deep neural networks increased from 12.5 percent (1/8) in 2015–2019 to 48.9 percent (44/90) in 2020–2024, while core neural networks maintained a high share, 62.5 percent to 57.8 percent, and general machine learning increased from 37.5 percent to 55.6 percent. Despite this clear rise in the importance of deep networks, no statistically significant change was found in the distribution between the three AI families, χ² = 1.98, df = 2, p = 0.37. This means that the observed growth of DNNs is a clear application trend, but with the current sample size and co-labeling, it does not translate into a statistically confirmed reshaping of shares. Co-occurrence analyses further indicate that all AI families most often combine with the pair Computational Methods and Material Modeling, and deep networks relatively more often co-occur with surrogate methods, these differences are interpretively clear, but statistically inconclusive. The question concerning changes in AI methods should therefore be considered partially resolved, the direction of change is clear, but its statistical significance is not confirmed.

In the distribution of document types, journal articles remain dominant, 75.5 percent of the entire set, 74.4 percent in 2020–2024, with a smaller but growing share of conference papers, from 12.5 percent to 20.0 percent, and the appearance of the “Other” category in the second sub-period, 5.6 percent. The χ² test does not confirm a significant change in the structure of document types over time, χ² = 0.82, df = 2, p = 0.66, which indicates a stable dominance of the journal form with moderate expansion of communication channels through conferences. In the geographical dimension, the United States maintains the leading position, 44.9 percent of all publications, and after 2019 strong German and Chinese centers joined, with a clear broadening of the map of participating countries. At the same time, no statistically significant reshuffling of the country distribution between sub-periods was recorded, χ² = 10.87, df = 11, p = 0.45. In practice, this means with internationalization without increased concentration, the US share declines slightly, from 50.0 percent to 44.4 percent, and the “long tail” of countries grows, but these changes are not large enough to be considered structural. The question concerning changes in document types and affiliation geography has therefore been resolved descriptively, the directions of change are clear, but there is no evidence of statistical significance.

In summary, the first research question receives an affirmative, statistically supported answer, there is very strong growth and a significant transformation within computational mechanics categories. The second question has a conditional answer, the share of deep neural networks is clearly increasing, but without confirmation of a significant structural change relative to core neural networks and classical machine learning. The third question has been resolved in descriptive terms, the dominance of journal articles and the geographical distribution of leading centers remain structurally stable, while the observed shifts toward internationalization and the moderate increase in the role of conferences are not statistically significant. Overall, the picture indicates a mature, rapidly growing research stream in which there is a significant change in the profile of computational mechanics methods, while publication channels and affiliation geography remain structurally stable.

5. Discussion

This discussion has been structured from two complementary analytical perspectives. First, a thematic comparison was carried out, focusing on the characteristics and dominant directions of integration between computational mechanics methods and machine learning or neural networks. Next, a statistical comparison was conducted, covering the dynamics of publication counts, distributions of document types, thematic categories, algorithmic classes, and geographical affiliations. The final part discusses the limitations of the study and their implications for engineering practice and future research. The basis of the discussion is a uniform corpus of 98 publications from 2015 to 2024, identified and classified according to the adopted research procedure, which included Scopus search, bibliometric visualizations with VOSviewer, and application of a five-dimensional classification scheme.

Thematically, the strongest thread remains the integration of PDE-governed methods with learning, where physics acts as the “regulator” of the model. Physics-informed neural networks, PINNs, embed boundary, and initial conditions and conservation laws directly into the loss function, enabling both forward and inverse tasks under label scarcity [16], and a synthetic overview of physics-informed approaches across problem classes is given in [55]. Where generality “across functions” is key, different BCs, excitations, material parameters, operator learning (FNO, DeepONet) gains the advantage, building mesh-independent surrogates that generalize entire families of equations [26,93]. Graph neural networks, GNNs, naturally handle complex geometries and unstructured meshes, which is crucial in flows, FSI, and deformable solids [18,64]. In material modeling, there is a visible transition from black-box approximators to architectures with physical guarantees, deep material networks trained on microstructures support transfer of knowledge to the macro-level [24], data-driven computational mechanics, DDCM, eliminates parametric laws in favor of datasets consistent with conservation principles [17], and polyconvex networks and constructions ensuring positive definiteness of tangents stabilize FEM simulations and respect thermodynamic requirements [83,101]. In fluid dynamics, ML methods serve as surrogates and tools for reconstruction of missing information [45,91], but in safety-critical engineering tasks UQ frameworks become indispensable, from Bayesian PINNs to cross-cutting surveys of uncertainty in scientific ML [22,39]. The thematic picture is completed by the growing role of design applications, in topology optimization generative models, GANs and diffusion, shorten exploration time but require coupling with physical constraints to avoid “attractive but unphysical” solutions [35,36], while in parallel vehicle-oriented applications add further emphasis on speed and credibility [90]. Bibliometric maps with VOSviewer confirm the centrality of finite element method, machine learning or neural networks, and the rising visibility of surrogate modeling and inverse problems [69].

The qualitative picture correlates well with the quantitative data. In 2015–2019, eight publications were identified, while in 2020–2024 as many as 90, giving a total of 98, which represents an ~11.25-fold increase (+82 publications) after 2019. The structure of document types remains stable, journal articles dominate (74/98, 75.51 percent), and the growth in the share of conference papers is not statistically significant, χ²(2) = 0.82, p = 0.66. The most pronounced change concerns computational mechanics categories, from an early emphasis on Stochastic Methods and Uncertainty (6/8) the field has shifted toward Computational Methods (41/90 in 2020–2024) and Material Modeling (34/90), confirmed by χ²(5) = 20.98, p < 0.001. In AI method classes, the role of deep networks has grown (from 12.5 percent to 48.89 percent of publications), though at the given sample size the change is not significant, χ²(2) = 1.98, p = 0.37. Methodologically, a “dual” profile persists, conceptual and experimental works dominate in parallel, respectively, 74/98 and 73/98, with no significant differences between sub-periods, χ²(2) = 0.30, p = 0.86. Geographically, the USA remains the leader (44/98, 44.90 percent), with marked increases in Germany (13/98) and China (12/98), but the lack of significant distributional change, χ²(11) = 10.87, p = 0.45, suggests global diffusion of methods after 2019. These numbers support the conclusion that the community is shifting from “stochastic profiling” toward deterministic, physics-encoded methods and mature surrogates for design and inversion.

Taken together, the two dimensions indicate three consistent vectors. First, physics-informed and operator-learning frameworks dominate today, combining BC or IC and law compliance with cross-domain generality and computational gain [55,64,93]. Second, in constitutive modeling, priority is given to architectures with built-in guarantees, polyconvexity, SPD tangents, thermodynamic consistency, solutions that genuinely “cooperate” with the FEM solver [17,24,83,101]. Third, surrogates plus UQ are becoming the standard for engineering decisions; reviews and Bayesian work show that without uncertainty calibration it is difficult to speak of credible application in practice [38,45,92]. In parallel, generative methods accelerate design exploration but require strict coupling with physics and transparent reporting of computational costs [35,36]. This picture is consistent with bibliometric maps and the directional changes in thematic category shares [69].

The discussion must be framed by the limitations of the review and of the literature itself. First, the scope of sources was limited to Scopus, the English language, and the years 2015–2024, with additional EXACTKEYWORD filters, which improves reproducibility but risks omitting works outside the index or under different terminology conventions. Second, heterogeneity of tasks, different PDEs, geometry or mesh representations, metrics, L2, MAE, MSE, energy measures, and cost reporting, training or inference time, hardware, prevents formal meta-analysis of effects, hence cautious, descriptive comparisons, consistent with V and V or UQ recommendations in scientific ML [22]. Third, multi-label classification, one publication may belong to several categories, violates independence assumptions in χ² tests, so significance results should be treated as indicative rather than definitive. Fourth, practices for reporting uncertainty and model extrapolation limits remain inconsistent, especially in generative architectures, where strict coupling with physical constraints and credibility protocols is needed [36,39,41].

From an engineering practice perspective, the above findings yield concrete recommendations. In PDE tasks, it is advisable to prefer energy or variational formulations and explicit BC or IC enforcement, PINN or variational PINN, and where generalization “across functions” is required, to employ operator learning, FNO or DeepONet, preferably in Bayesian versions when decisions are risk laden. In nonlinear and history-dependent materials, the advantage lies with models providing guarantees, polyconvexity, SPD, which maintain stability in the solver. Surrogates should be combined with UQ and an explicit computational budget, time, energy, memory, and results validated against the “gold standard,” FEM or experiment, as well as cross-domain tests. Finally, V and V standardization, common benchmarks, and reporting protocols are needed, exactly as long encouraged by cross-cutting and methodological studies.

In conclusion, both numerical data and thematic review lead to a consistent finding of a mature symbiosis between computational mechanics and ML or NN methods, physics should regulate learning, operator perspectives provide generality, and credibility requires UQ and transparent computational costs. In this arrangement, “new” methods do not replace FEM and classical discretizations, but rather enrich them with fast, generalizable, and auditable components, which in many applications translates into order-of-magnitude speedups while maintaining, and controlling, quality.

6. Conclusions

Across the entire time horizon, we observe a clear and strong upward trend in the number of publications. The volume increased from eight items in 2015–2019 to 90 in 2020–2024, which means a rise of 82 papers and a 1,025 percent increase relative to the baseline. The compound annual growth rate of publications, calculated between the two five-year sub-periods, was about 62.3 percent per year. The dynamics are consistent across the six categories of computational mechanics, and the independence test confirms a significant change in the distribution of shares between categories. In numerical terms, Computational Methods grew from 1 to 41 items, Material Modeling from 1 to 34, Inverse Analysis from 1 to 17, Surrogate Methods from 1 to 13, and Stochastic Methods and Uncertainty from 6 to 12. Multiscale Modeling appears only in the second sub-period as an emerging strand. The χ² result of 20.98 with five degrees of freedom and p less than 0.001 confirms that a genuine thematic transformation has taken place within the six categories, a shift from an early emphasis on stochastic approaches toward deterministic methods and material modeling, alongside increasing use of surrogate models and the emergence of a multiscale thread. The fourth problem is therefore resolved positively, with statistical confirmation of the scale of growth and the significance of the change in the research profile.

In the structure of artificial intelligence methods, the importance of deep neural networks is clearly increasing. The share of deep neural networks rose from 12.5 percent in the first sub-period to 48.9 percent in the second, while core neural networks maintained a high presence, and classical machine learning increased in frequency. However, the independence test does not confirm a significant structural change among the three families of approaches, the χ² value of 1.98 with two degrees of freedom and p equal to 0.37 indicates that the observed shifts represent a developmental direction rather than a statistically decisive reshuffling of shares. The fifth problem is therefore assessed as partially resolved. In practical terms, the importance of deep networks is growing, and they are particularly often combined with surrogate methods, yet with the adopted multi-labeling and available sample size there is no structural change confirmed by the test.

In document types, the stable dominance of journal articles persists. In the entire corpus they account for three quarters of publications, and in 2020–2024 for nearly three quarters of all items. The share of conference publications grows moderately, and the category Other appears only in the second sub-period. The χ² of 0.82 with two degrees of freedom and p equal to 0.66 does not confirm a significant change in the structure of document types. In the geographical dimension, the United States remains the leader for the entire period, after 2019 Germany and China join markedly, and the activity map expands to additional countries. Here, too, no significant reshuffling of the distribution is visible, the χ² of 10.87 with 11 degrees of freedom and p equal to 0.45 indicates internationalization without increased concentration. The sixth problem is thus resolved descriptively, pointing to structural stability of publication channels and broad geographical diffusion, but without a statistically significant reallocation of shares among countries and document types.

In response to the first problem, concerning dominant task classes and patterns of integration with data methods, three areas form the core of applications. First, PDE-governed tasks, where the greatest qualitative gains come from direct embedding of physics into learning via energy functionals, equation residuals, or variational formulations. Such approaches reduce the need for labels, facilitate enforcement of boundary conditions, and improve generalization capacity. Second, work on constitutive models, in which priority is given to architectures that guarantee thermodynamic and numerical consistency, that is, polyconvex strain energy, positive definiteness of tangents, and smoothness of functionals. These solutions cooperate much better with finite element solvers and mitigate convergence issues. Third, operator and graph configurations, that is, operator learning for generalization across families of conditions and geometries, and graph networks for unstructured meshes, which deliver substantial computational gains and facilitate model transfer between tasks. From the co-occurrence summary, it follows that all families of data methods most often pair with the duo Computational Methods and Material Modeling, and deep networks co-occur with surrogate methods at an above-average rate. The practical conclusion is clear. The greatest qualitative and computational benefits come from coupling learning with physical regularization at the level of the objective function or architecture, and, secondly, from using representations aligned with the geometry and discretization of the problem.

The second problem concerns data types, geometry and mesh representations, and the imposition of boundary conditions and validation. The best accuracy–cost compromise is achieved where high-fidelity synthetic data, for example, finite element reference solutions or homogenization samples, are combined with experimental data in a coherent validation procedure. Graph and mesh representations ensure correct transfer of models between geometries and discretization densities. Image-based representations and field maps are useful for rapid predictions over families of similar domains, provided the model’s operating range remains clearly defined. Direct enforcement of boundary conditions and governing laws through weak and variational formulations proves crucial for stability and data economy, and validation practice should go beyond the train–test split to include cross-domain tests, that is, with new geometries, conditions, and mesh resolutions. The synthetic result of this section is that accuracy and computational cost are most favorable when representation and learning are designed to match the structure of the task, rather than the other way around.

The third problem concerns uncertainty quantification, verification and validation, and reporting of computational costs. The analyzed literature increasingly introduces uncertainty frameworks, in particular Bayesian approaches in operator learning and error models for reduced and surrogate methods. At the same time, reporting practices remain heterogeneous. Many works lack a full computational cost profile, that is, training and inference time, hardware configuration, memory and energy usage, as well as explicit out-of-distribution tests. For this reason, we recommend minimum credibility rules. Each result should be compared to a reference solver or experiment, and predictive uncertainty should be estimated by probabilistic methods, or at least by interval methods, together with an unambiguous statement of the computational budget. Such rules move data-driven models from demonstration to tools ready for engineering applications.

In light of the entire body of evidence, the answers to the six questions are unambiguous. The dominant task classes and clear patterns of integration with data methods have been identified, which deliver the greatest qualitative benefits, especially when physics regulates learning and representation respects geometry and discretization. The combinations of data types, representations, and boundary-condition enforcement that best balance accuracy and cost have been indicated, and validation recommendations have been formulated. The maturity of uncertainty and cost-reporting practices has been assessed, with indications of where standards are necessary. The existence of a very strong growth trend and a significant transformation within the six categories of computational mechanics have been confirmed. A directional increase in the importance of deep networks has been shown, without confirmation of a structural change in method families. Finally, structural stability of document types and affiliation geography has been demonstrated alongside growing diffusion of the topic.

Actionable checklist for authors and reviewers. Validation: include cross-domain tests that vary geometry, load and mesh, and report an independent FE or experimental baseline. Costs: report offline and online compute, GPU hours and CPU hours, and memory footprint. Uncertainty quantification: provide interval or Bayesian uncertainty and explicit error models. Reproducibility: release code and data or at least a minimal reproducible bundle. Submissions that do not address costs and uncertainty quantification should be treated as demonstrations rather than deployable tools, and any claims of operational readiness ought to be qualified accordingly.

On this basis, we formulate final conclusions and a work program for the future. First, in initial–boundary value problems, energy and variational formulations and explicit enforcement of conditions are preferred, and where generalization across families of conditions, geometries, and parameters is required, operator learning is most appropriate, preferably in versions with uncertainty calibration. Second, in material modeling, priority remains with architectures that provide physical guarantees, since these ensure stability and consistency when coupled with solvers. Third, surrogates and operator learning should be combined with uncertainty quantification procedures and an explicit cost profile, and results should be verified on geometries and conditions outside the training set. Fourth, reporting practice should be standardized. Open benchmarks, standardized V and V protocols, and clear guidelines for reporting the computational budget, including training and inference time and hardware configuration, are needed. Fifth, differentiable solvers and co-design of algorithms with physics are key, which will facilitate inverse design, optimization, and sensitivity analysis within a single, coherent computational loop. Sixth, subsequent editions of the review should broaden the bibliographic and linguistic basis, document classification agreement, and consistently deposit code and data to strengthen reproducibility and comparability across centers.

In summary, computational mechanics and data methods today form a mature symbiosis. The thematic transformation within the six categories is statistically significant and drives a transition toward deterministic methods, material modeling, and surrogates. The role of deep networks is growing in practice, though without confirmation of a structural change in method families. Publication channels and affiliation geography remain structurally stable, alongside parallel internationalization. Most importantly, credibility rigor must be implemented. Only in combination with unambiguous enforcement of physics, consistent validation, and transparently reported computational costs will new hybrid tools fully unlock their potential in the design and operation of mechanical systems.

In the future, the review is planned to be extended to include literature from other bibliographic databases, including IEEE Xplore, Web of Science, and, where possible, Google Scholar. Including additional sources will capture a fuller picture of the research landscape, especially since some publications in mechanical, materials, or transportation engineering may be indexed selectively only in certain repositories. Extending the base to literature in other languages, as well as selected gray literature and industrial reports, will further strengthen the credibility of the synthesis. This will allow subsequent versions of the article to better reflect the global development of the field and ensure comparability across research centers worldwide. Emphasizing this direction is important, since the growing dynamics of integrating computational mechanics with machine learning and neural networks are not limited to English-language publications indexed in Scopus. A broader approach, encompassing diverse databases, will not only answer the research questions more fully, but also provide a more balanced picture of the evolution of methods, reporting practices, and application directions.