Domain-Oriented Hierarchical Topology Optimisation—An Approach for Heterogeneous Materials †
Abstract
1. Introduction
2. Hierarchical Formulation in Linear Elasticity
3. Subdomain Multiscale Topology Optimisation
4. Numerical Modelling
4.1. Hierarchical Models
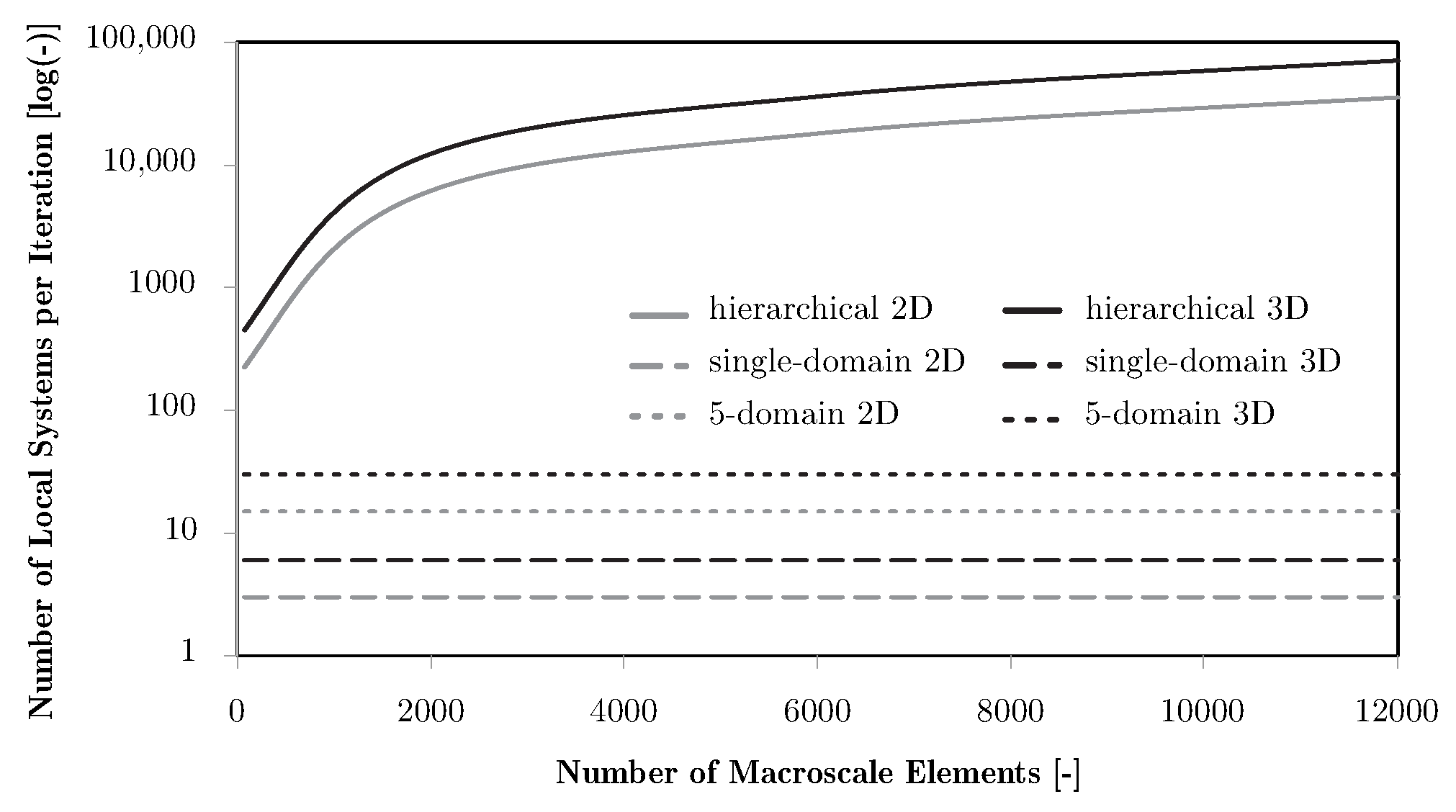
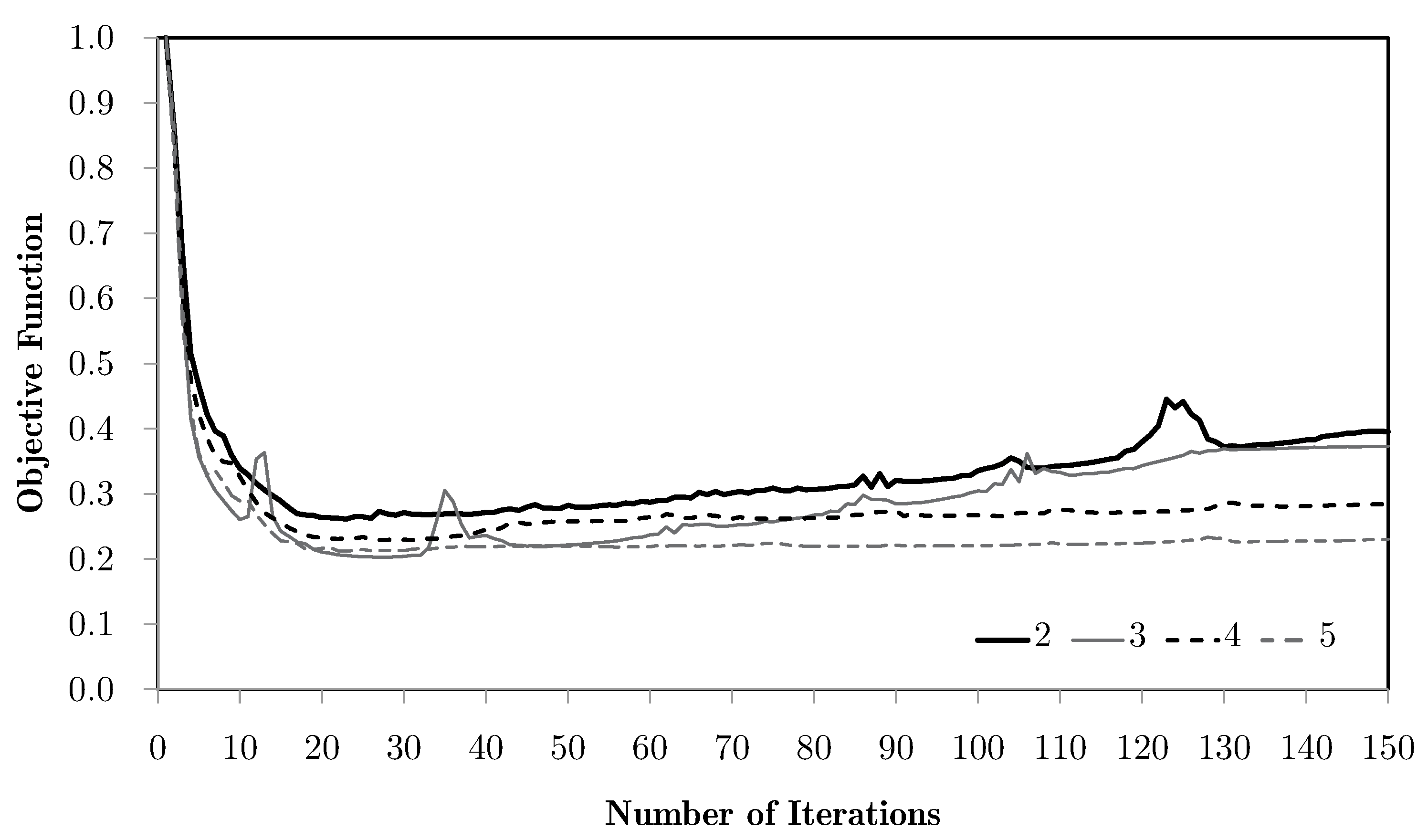
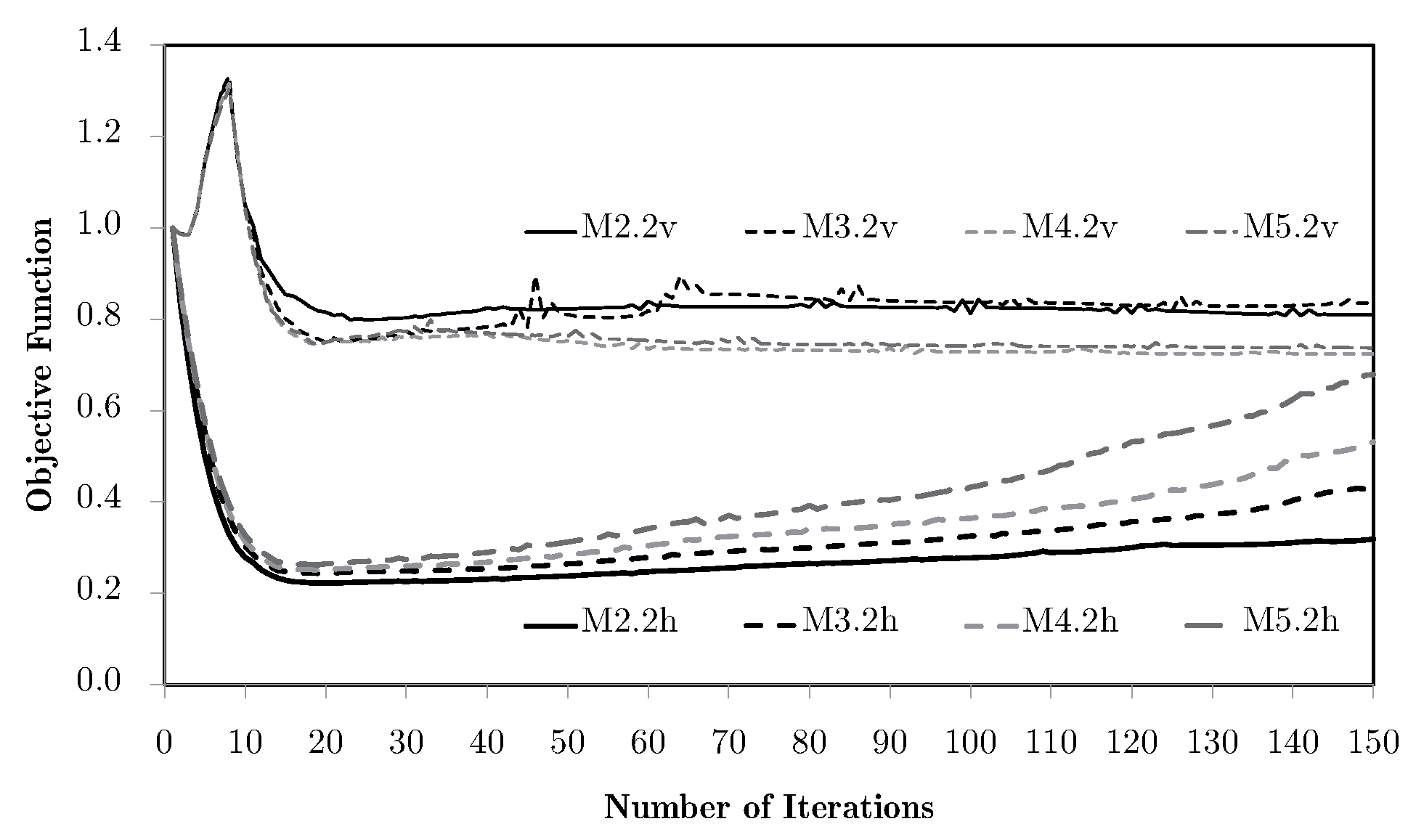
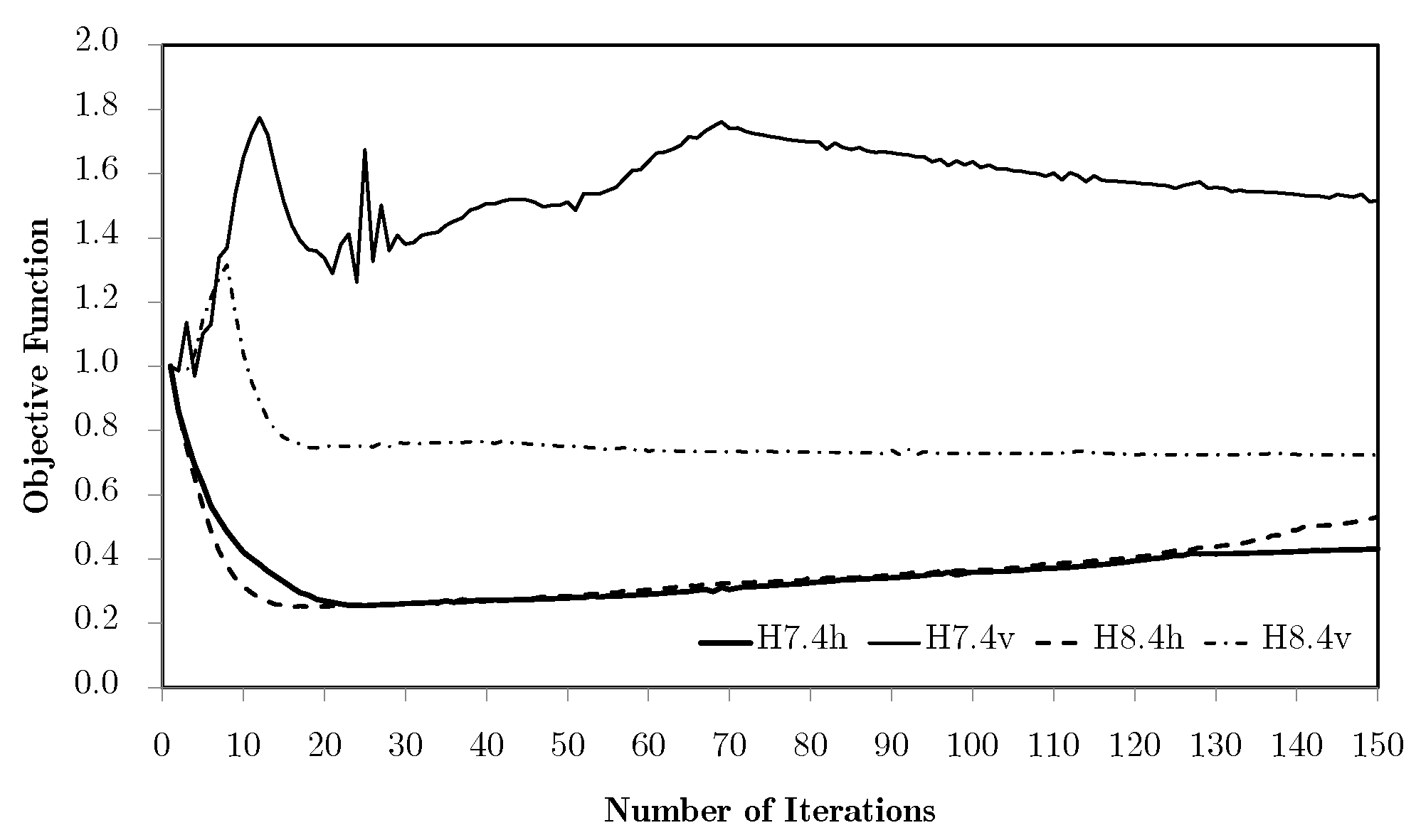
4.2. Multiscale Optimisation Algorithms
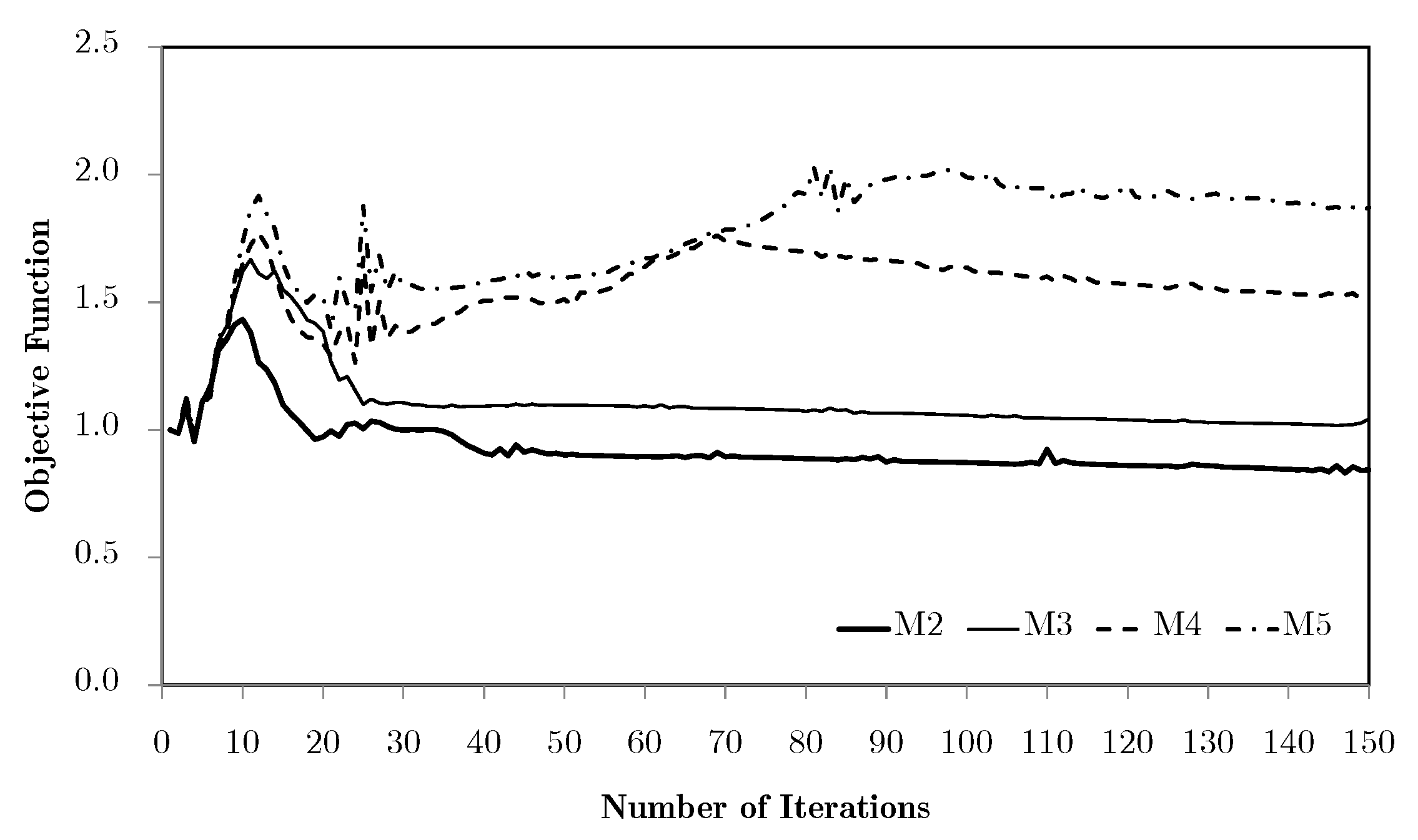
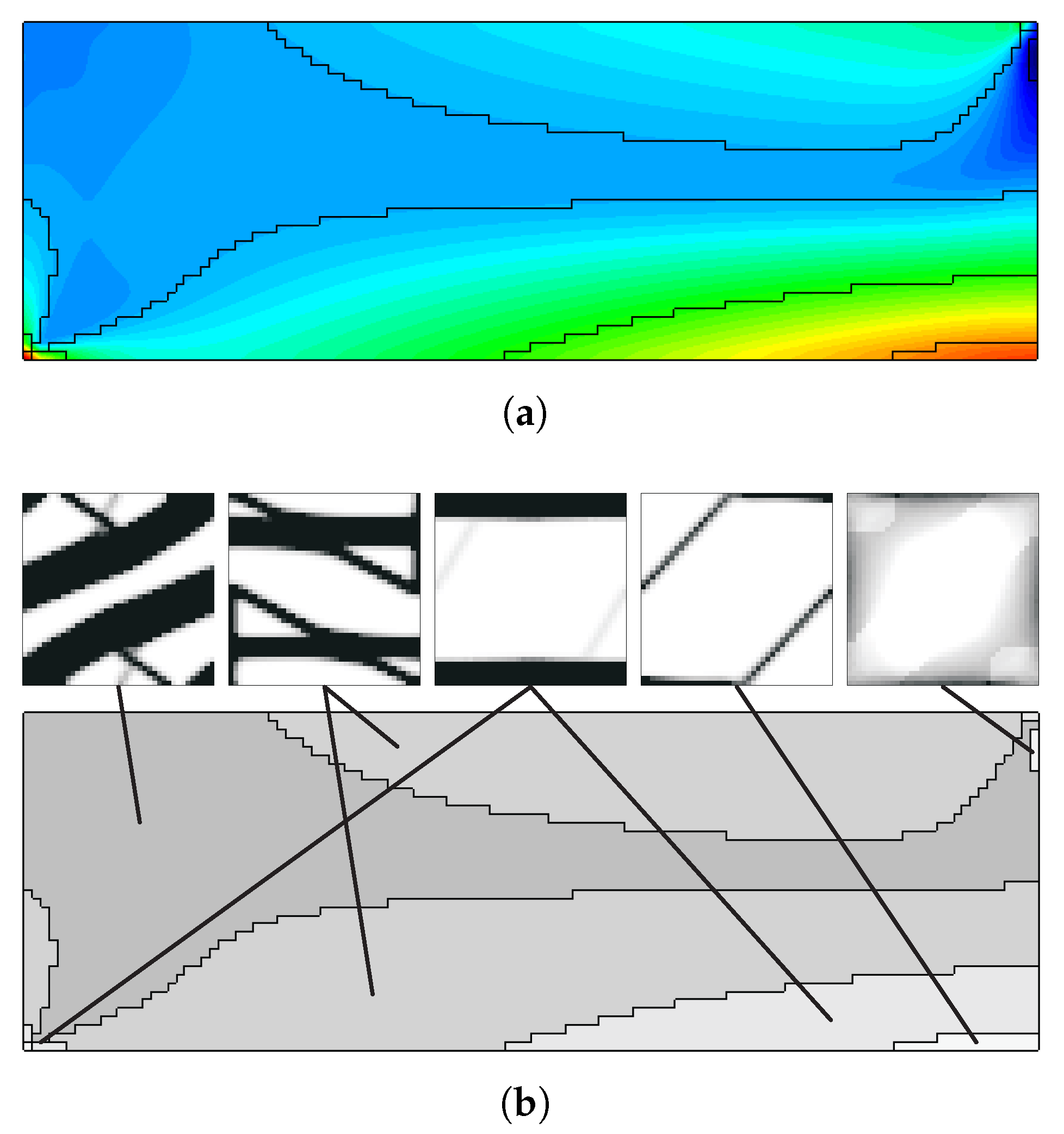
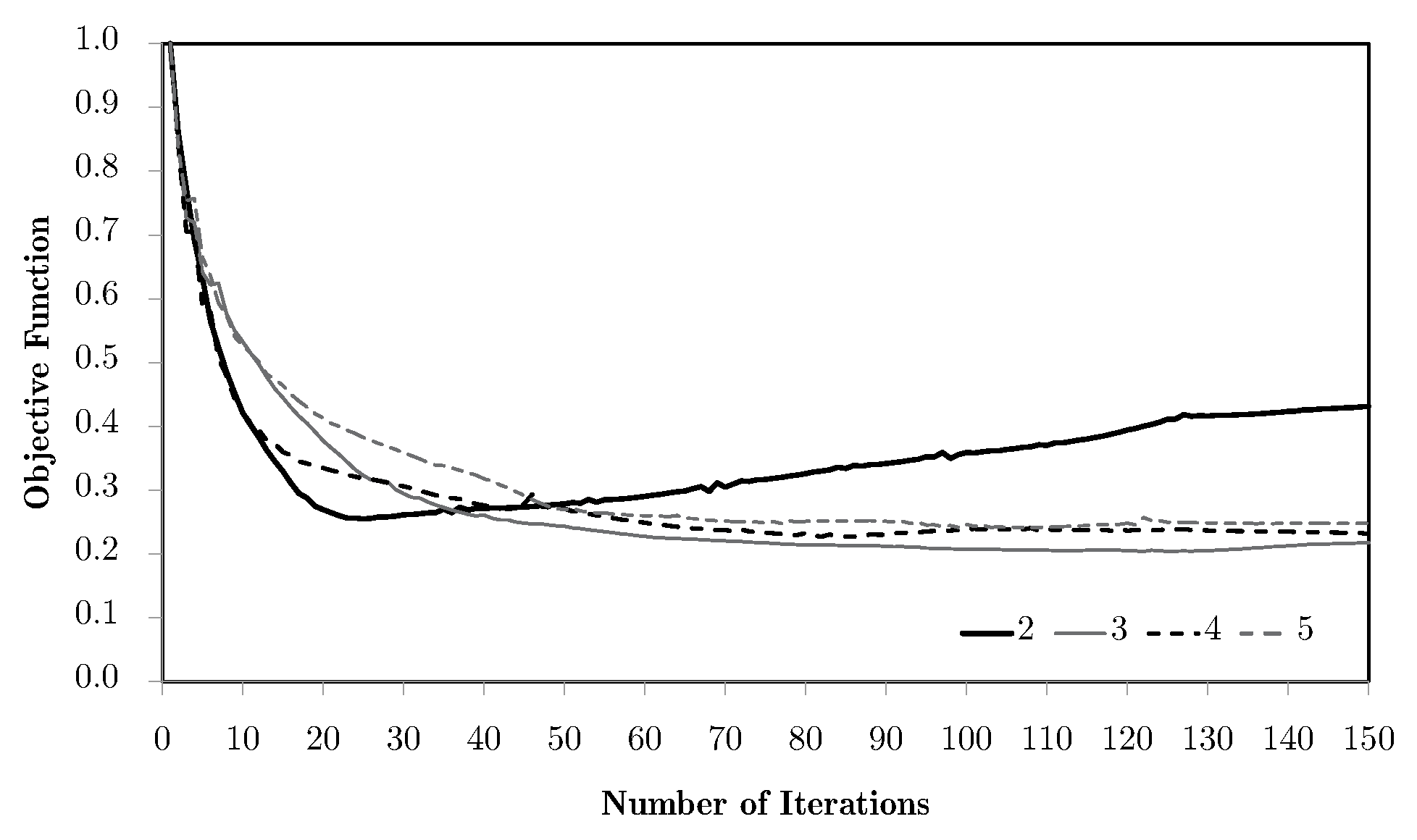
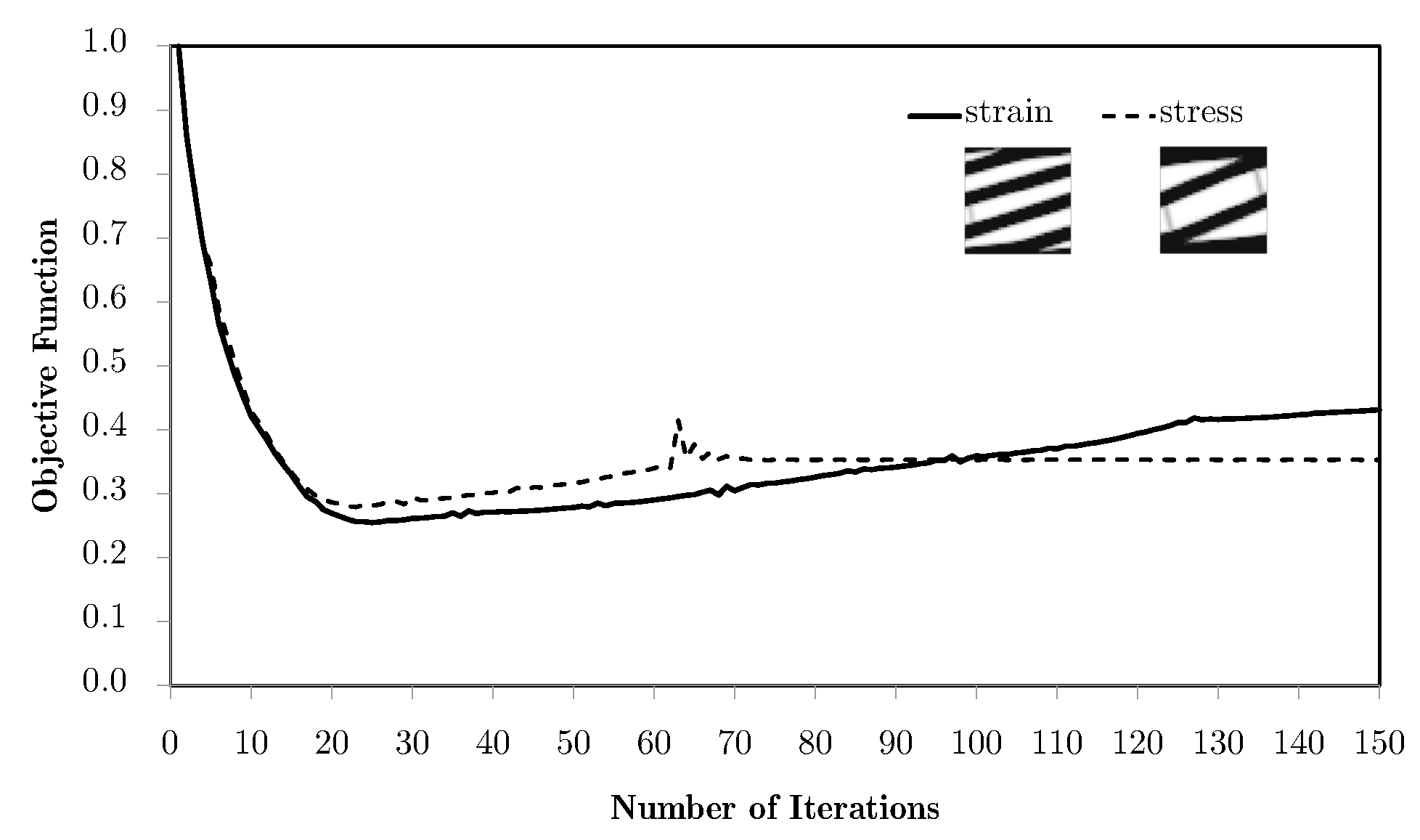
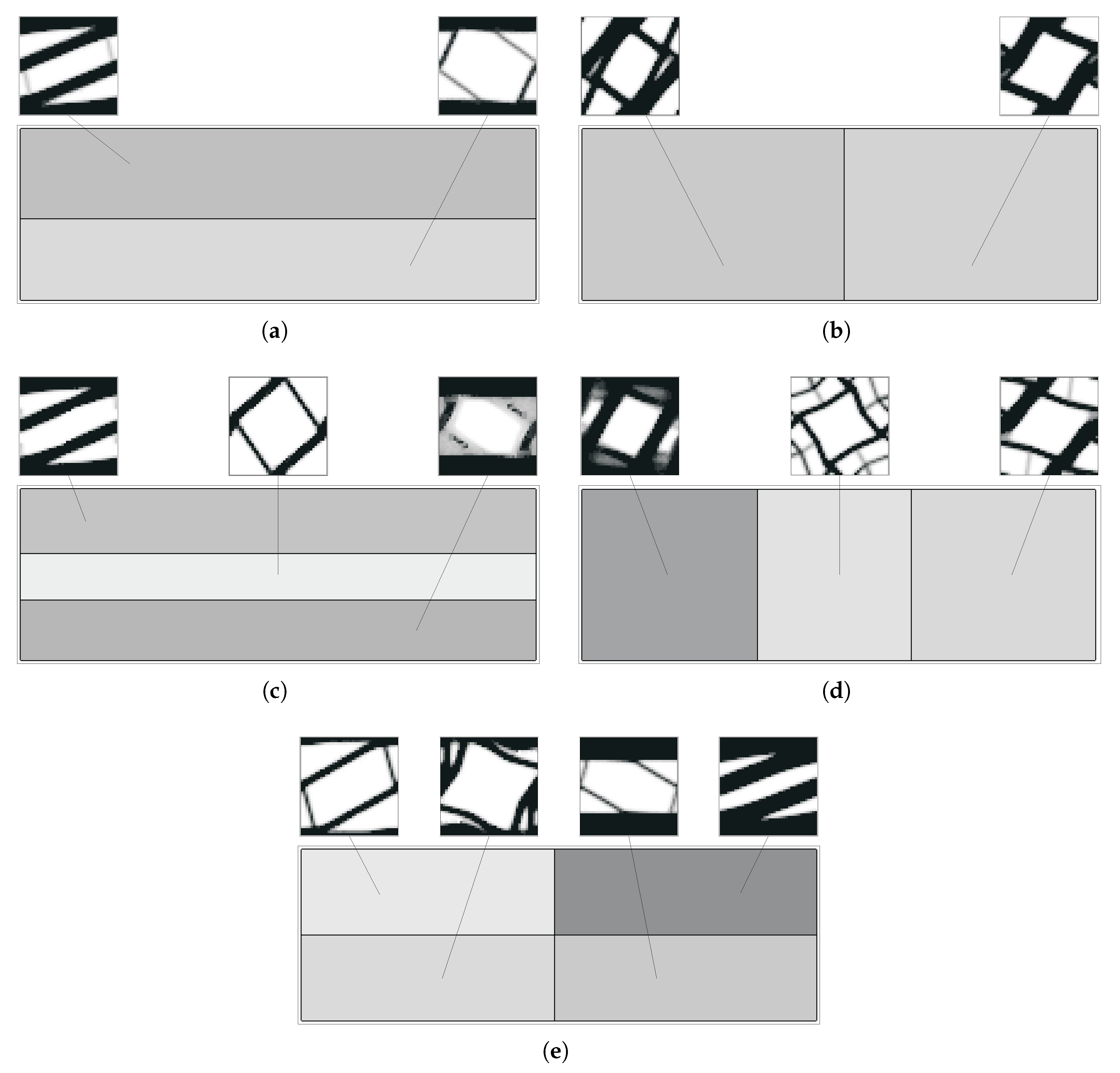
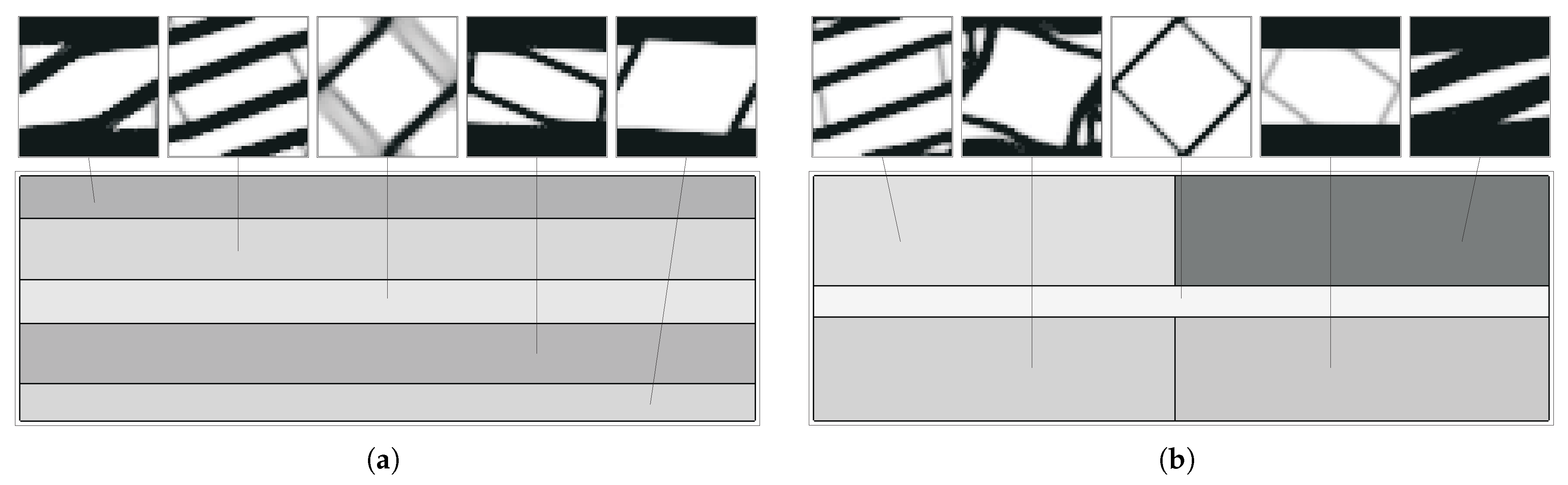
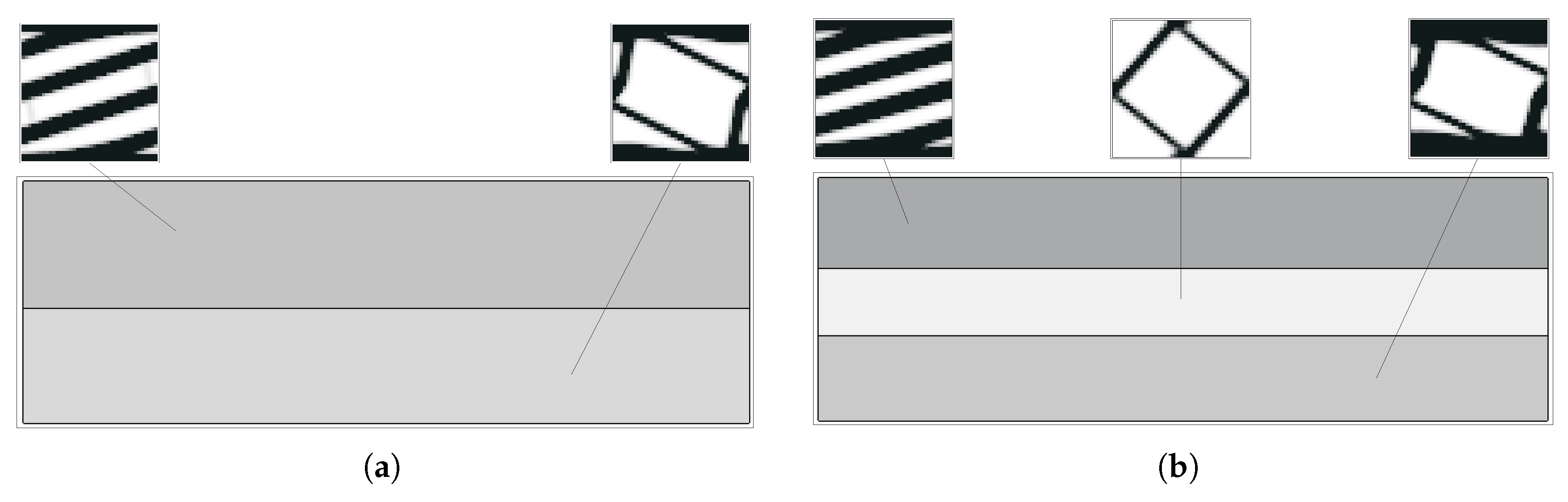
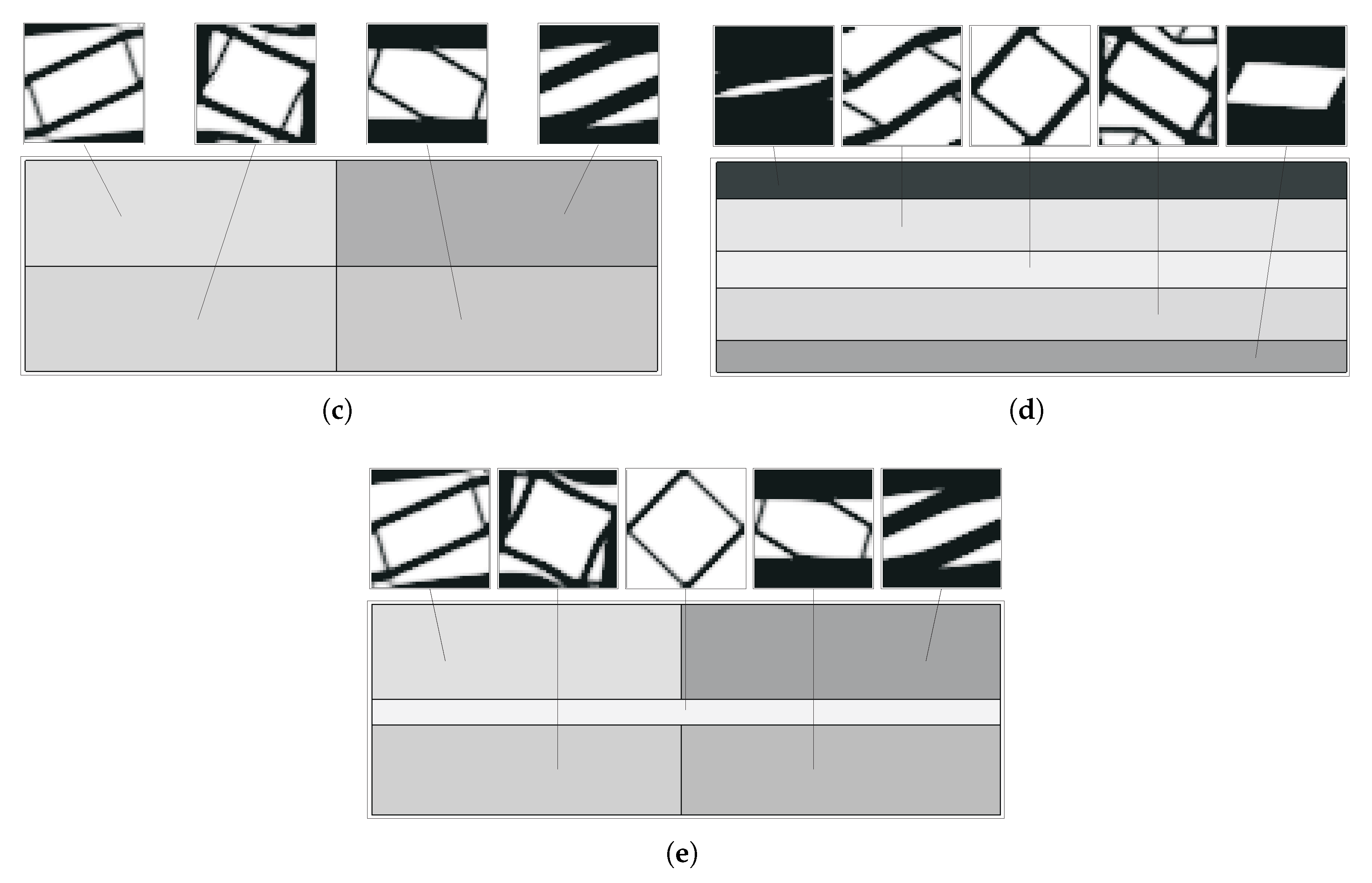
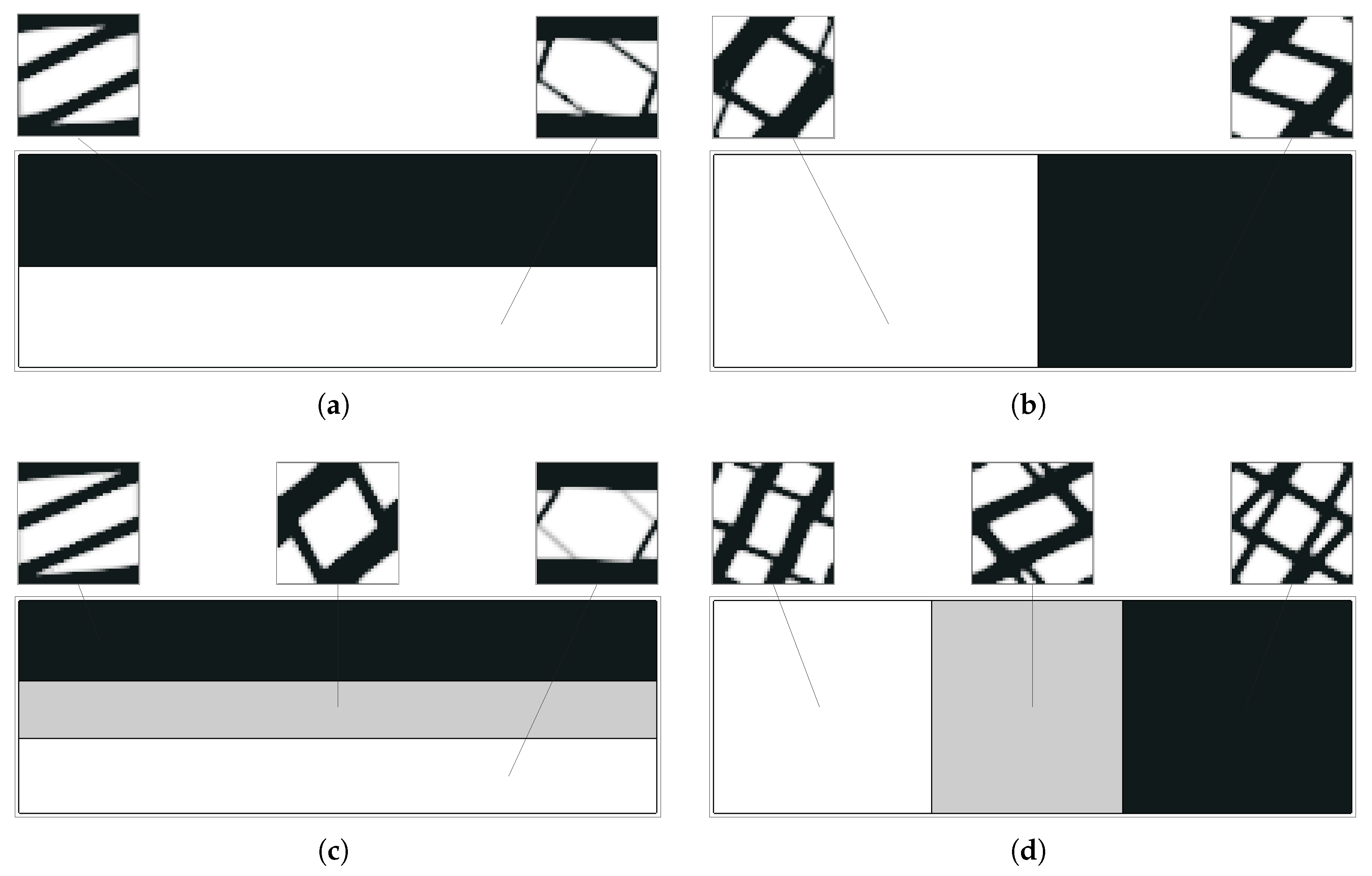
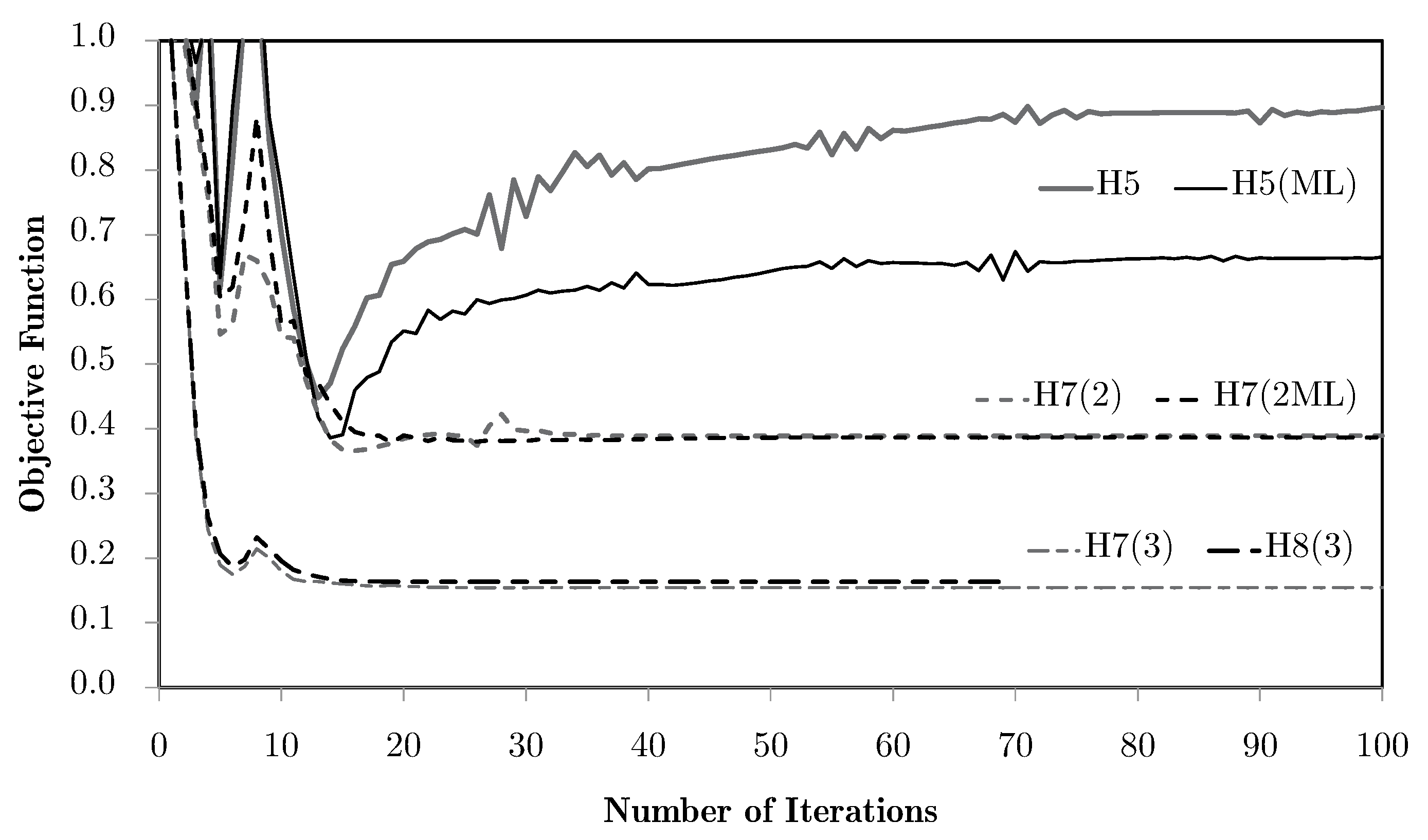
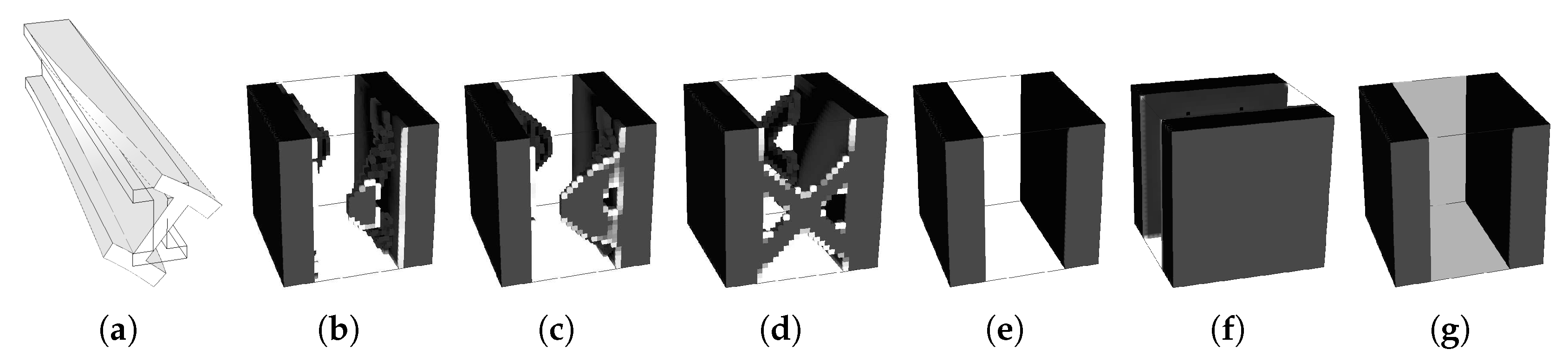
5. Multiscale Optimisation Results
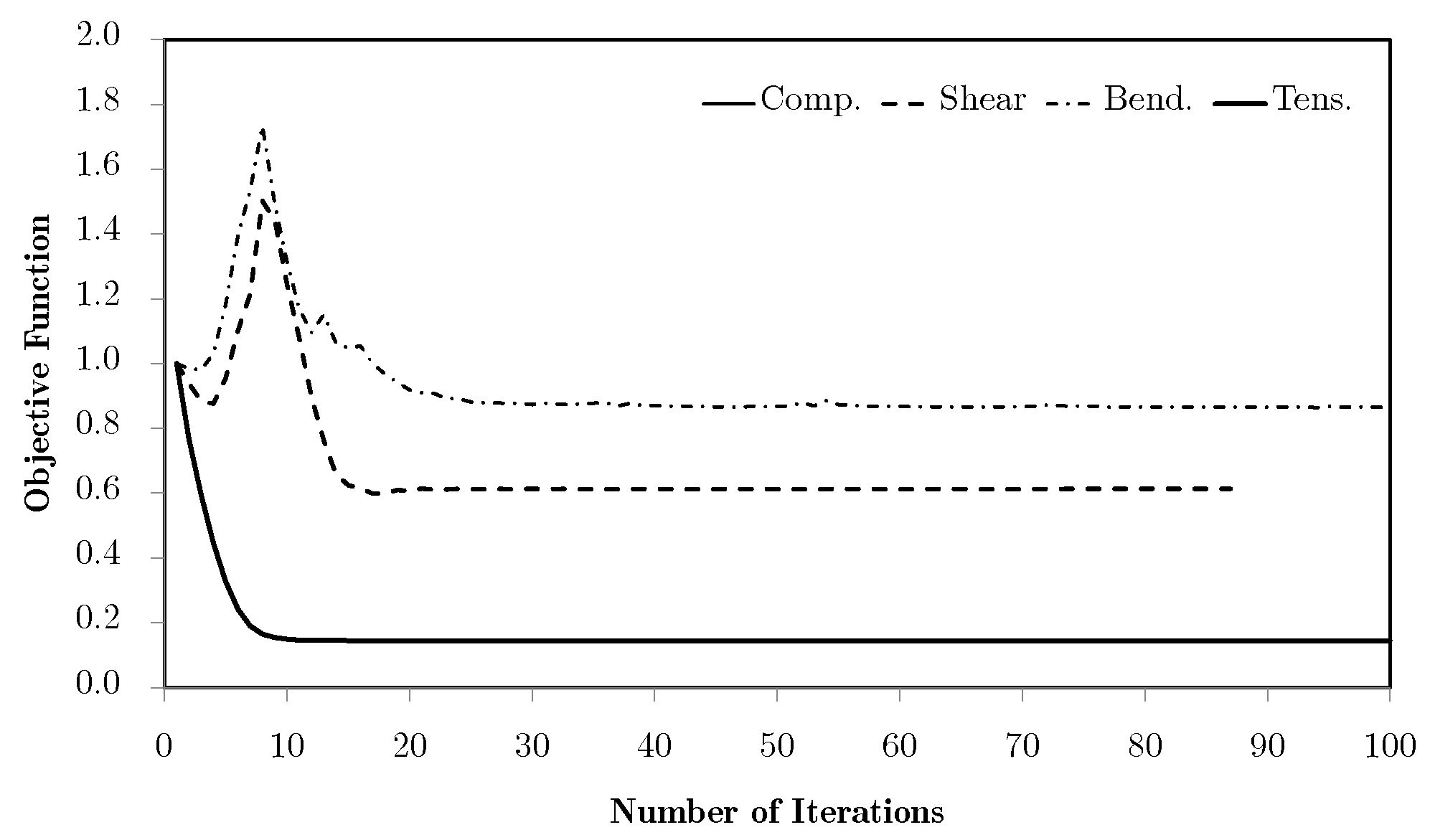
5.1. Single Domain Approach
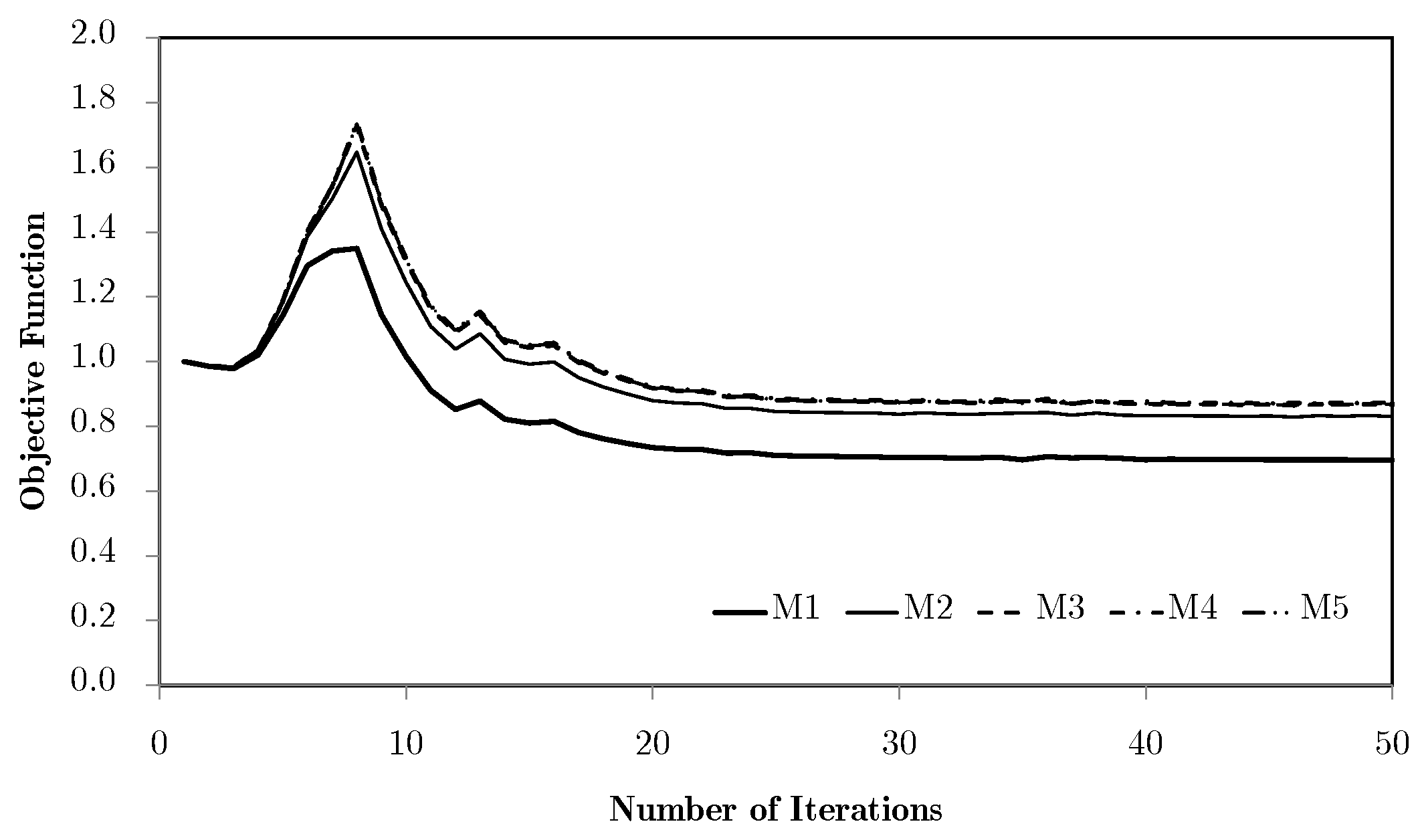
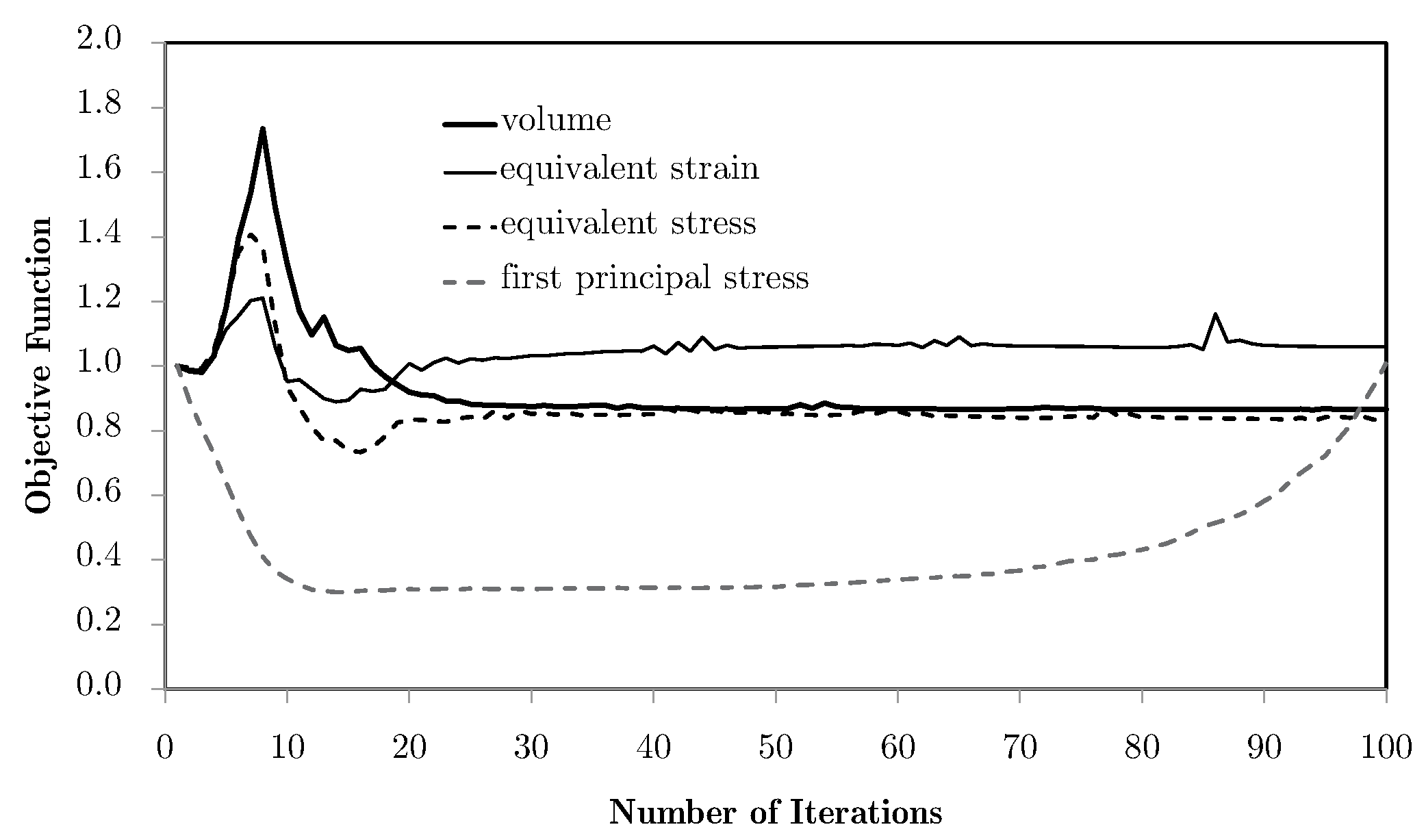
5.2. Subdomain Multiscale Optimisation
6. Final Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CONLIN | CONvex LINearisation method |
| HEA | Asymptotic Expansion Homogenisation |
| MMA | Method of Moving Asymptotes |
| SIMP | Solid Isotropic Material with Penalisation |
References
- Bendsøe, M.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Rodrigues, H.; Fernandes, P. A material based model for topology optimization of thermoelastic structures. Int. J. Numer. Methods Eng. 1995, 38, 1951–1965. [Google Scholar] [CrossRef]
- Diaz, A.; Lipton, R. Optimal material layout for 3D elastic structures. Struct. Multidiscip. Optim. 1997, 13, 60–64. [Google Scholar] [CrossRef]
- Theocaris, P.; Stavroulakis, G. Multilevel optimal design of composite structures including materials with negative Poisson’s ratio. Struct. Multidiscip. Optim. 1998, 15, 8–15. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. Homogenization and Structural Topology Optimization: Theory, Practice, and Software; Springer: London, UK, 1999. [Google Scholar]
- Theocaris, P.; Stavroulakis, G. Optimal material design in composites: An iterative approach based on homogenized cells. Comput. Methods Appl. Mech. Eng. 1999, 169, 31–42. [Google Scholar] [CrossRef]
- Allaire, G. Shape Optimization by the Homogenization Method; Applied Mathematical Sciences; Springer: New York, NY, USA, 2002; Volume 164. [Google Scholar]
- Rodrigues, H.; Guedes, J.; Bendsøe, M. Hierarchical optimization of material and structure. Struct. Multidiscip. Optim. 2002, 24, 1–10. [Google Scholar] [CrossRef]
- Bendsøe, M.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Guedes, J.; Lubrano, E.; Rodrigues, H.; Turteltaub, S. Hierarchical optimization of material and structure for thermal transient problems. In IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials—Solid Mechanics and Its Applications; Bendsøe, M.P., Olhoff, N., Sigmund, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 137, pp. 527–536. [Google Scholar]
- Rodrigues, H. Topology optimization of structures: Applications in the simulation and design of cellular materials. In Computational Methods in Engineering & Science: Proceedings of Enhancement and Promotion of Computational Methods in Engineering and Science X, Sanya, China, 21–23 August 2006; Yao, Z.H., Yuan, M.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Coelho, P.; Fernandes, P.; Cardoso, J.; Guedes, J.; Rodrigues, H. Hierarchical topology optimisation of structures subjected to constraints on material design. In Proceedings of the EngOpt2008—International Conference on Engineering Optimisation, Rio de Janeiro, Brazil, 1–5 June 2008. [Google Scholar]
- Coelho, P.; Fernandes, P.; Guedes, J.; Rodrigues, H. A hierarchical model for concurrent material and topology optimisation of three-dimensional structures. Struct. Multidiscip. Optim. 2008, 35, 107–115. [Google Scholar] [CrossRef]
- Gu, X.; He, S.; Dong, Y.; Song, T. An improved ordered SIMP approach for multiscale concurrent topology optimization with multiple microstructures. Compos. Struct. 2022, 287, 115363. [Google Scholar] [CrossRef]
- Gao, J.; Wen, Z.; Zhai, X.; Chen, F.; Kang, H. Concurrent topology optimization of multiscalecomposites with differentiable microstructures. Comput. Methods Appl. Mech. Eng. 2024, 431, 117271. [Google Scholar] [CrossRef]
- Dias-de-Oliveira, J. Topology Optimisation Methodologies for Structural Analysis. Ph.D. Thesis, Universidade de Aveiro, Aveiro, Portugal, 2013. (In Portuguese). [Google Scholar]
- Dias-de-Oliveira, J.; Pinho-da-Cruz, J.; Teixeira-Dias, F. Domain-oriented multiscale optimization for composite materials. In Proceedings of the ESAFORM 25, 28th International ESAFORM Conference on Material Forming, Paestum, Italy, 7–9 May 2025; pp. 486–495. [Google Scholar]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Fleury, C.; Braibant, V. Structural optimization: A new dual method using mixed variables. Int. J. Numer. Methods Eng. 1986, 23, 409–428. [Google Scholar] [CrossRef]
- Fleury, C. CONLIN: An efficient dual optimizer based on convex approximation concepts. Struct. Multidiscip. Optim. 1989, 1, 81–89. [Google Scholar] [CrossRef]
- Sigmund, O.; Petersson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Rozvany, G.; Zhou, M.; Birker, T. Generalized shape optimization without homogenization. Struct. Multidiscip. Optim. 1992, 4, 250–252. [Google Scholar] [CrossRef]
- Bendsøe, M.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Sigmund, O. Morphology-based black and white filters for topology optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef]
- Coelho, P. Modelos Hierárquicos para a Análise e Síntese de Estruturas e Materiais com Aplicações à Remodelação Óssea. Ph.D. Thesis, Universidade Nova de Lisboa, Lisbon, Portugal, 2009. (In Portuguese). [Google Scholar]
- Bendsøe, M. Optimization of Structural Topology, Shape, and Material; Springer: Berlin, Germany, 1995. [Google Scholar]
- Guedes, J.; Kikuchi, N. Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods. Comput. Methods Appl. Mech. Eng. 1990, 83, 143–198. [Google Scholar] [CrossRef]
- Pinho-da-Cruz, J.; Oliveira, J.; Teixeira-Dias, F. Asymptotic homogenisation in linear elasticity. Part I: Mathematical formulation and finite element modelling. Comput. Mater. Sci. 2009, 45, 1073–1080. [Google Scholar] [CrossRef]
- Oliveira, J.; Pinho-da-Cruz, J.; Teixeira-Dias, F. Asymptotic homogenisation in linear elasticity. Part II: Finite element procedures and multiscale applications. Comput. Mater. Sci. 2009, 45, 1081–1096. [Google Scholar] [CrossRef]
- de Kruijf, N.; Zhou, S.; Li, Q.; Mai, Y. Topological design of structures and composite materials with multiobjectives. Int. J. Solids Struct. 2007, 44, 7092–7109. [Google Scholar] [CrossRef]
- Cherkaev, A.; Krog, L.; Küçük, I. Stable optimal design of two-dimensional elastic structures. Control Cybern. 1998, 27, 265–282. [Google Scholar]
- Rodrigues, H.; Jacobs, C.; Guedes, J.; Bendsøe, M. Global and local material optimization models applied to anisotropic bone adaptation. In IUTAM Symposium on Synthesis in Bio Solid Mechanics—Solid Mechanics and Its Applications; Pedersen, P., Bendsøe, M.P., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; Volume 69, pp. 209–220. [Google Scholar]
- Coelho, P.; Fernandes, P.; Rodrigues, H. Numerical modeling of bone tissue adaptationt—A hierarchical approach for bone apparent density and trabecular structure. J. Biomech. 2009, 42, 830–837. [Google Scholar] [CrossRef] [PubMed]
- Rozvany, G. Exact analytical solutions for some popular benchmark problems in topology optimization. Struct. Multidiscip. Optim. 1998, 15, 42–48. [Google Scholar] [CrossRef]




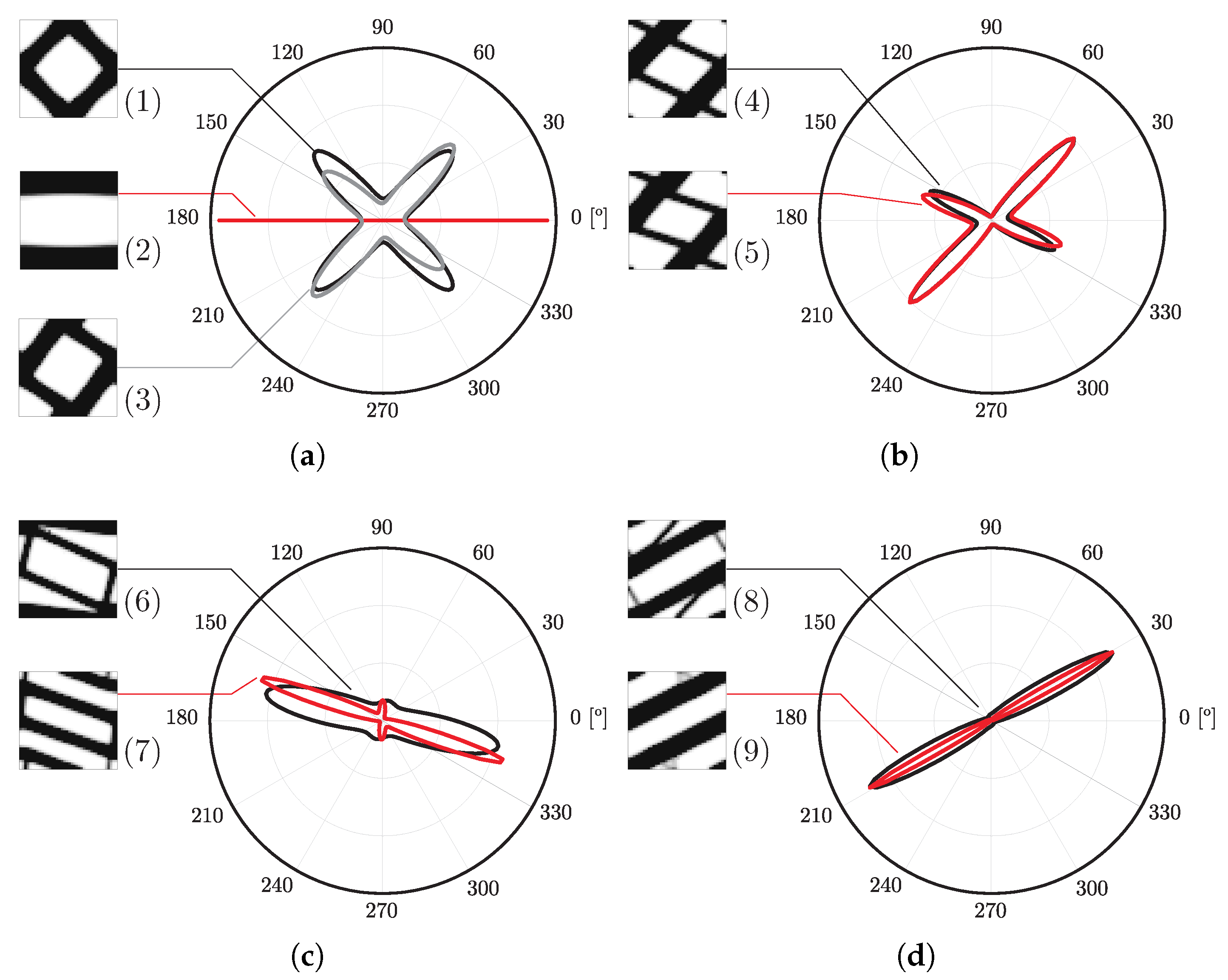
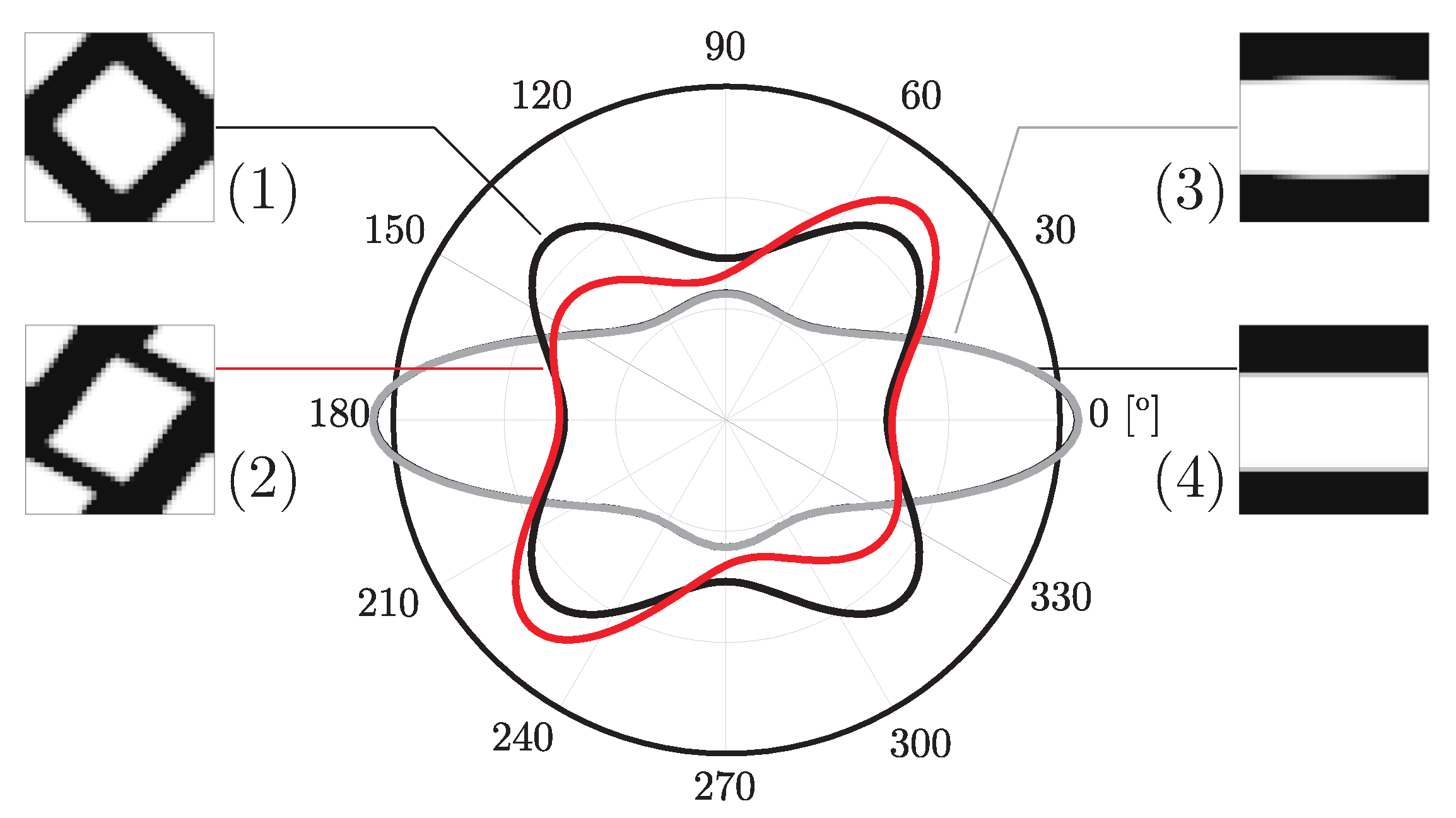
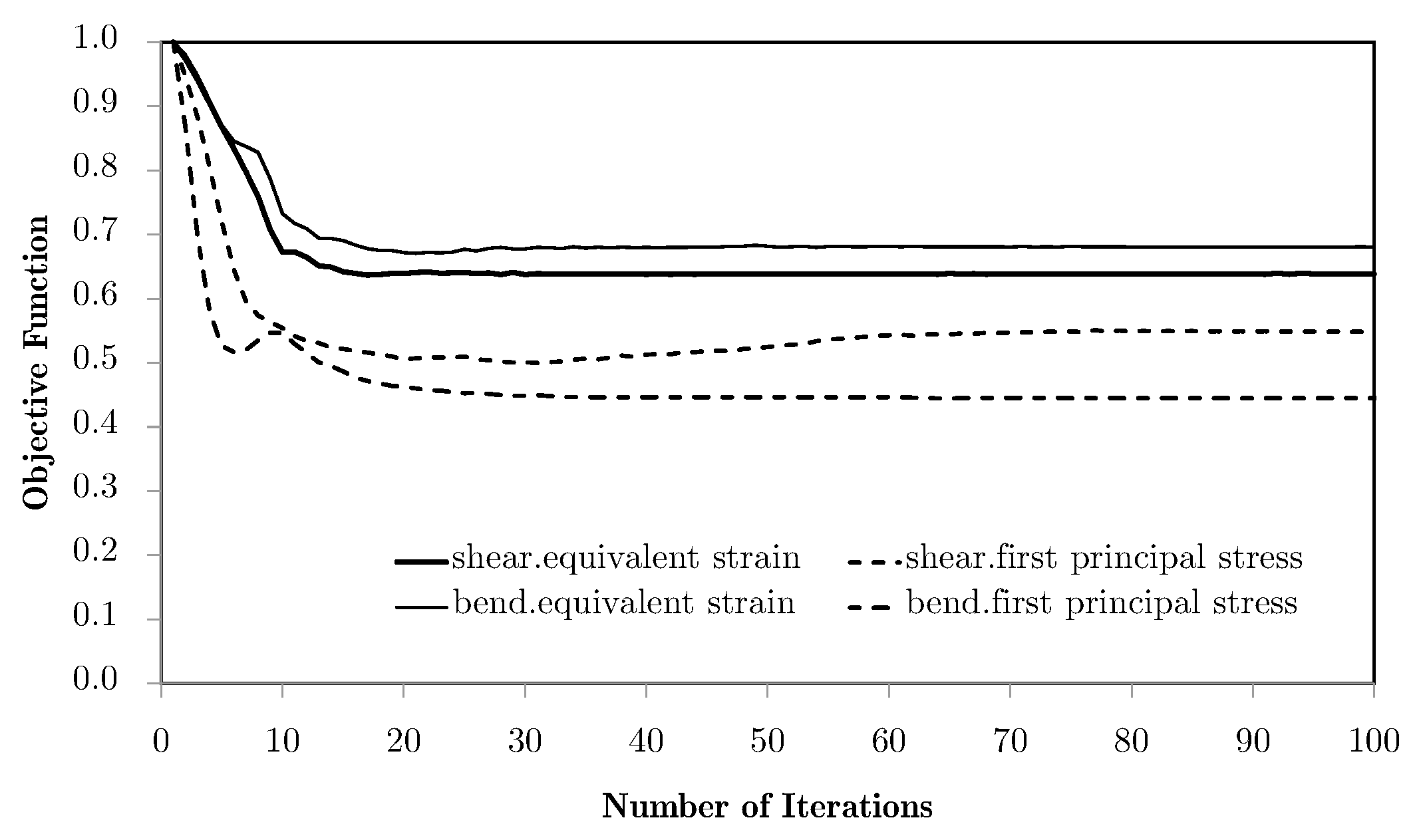





| Strategy | Description | Application | Performance |
|---|---|---|---|
| H1 | Hierarchical: optimisation acts only on microscale densities; macroscale densities are dependent. | Full hierarchical (type I, micro-driven). | High accuracy, very costly. |
| H2 | Inverse homogenisation: the isolated local problem solved for imposed macroscopic fields. | Design of unit-cell materials with target effective properties. | Efficient, but not linked to a global structure. |
| H3 | Hierarchical: simultaneous optimisation of macro- and microscale densities. | Full hierarchical (type II, concurrent macro–micro). | High accuracy, very costly. |
| H4 | Single-domain: optimisation at microscale only, macroscale density fixed to the global volume fraction. | One representative unit-cell optimised for the whole structure. | Very efficient; equivalent to H1 with one local problem. |
| H5 | Single-domain: independent macro- and micro-updates; equivalent to H3 but reduced to one local problem. | Same as H4, used for comparative studies and benchmarking. | Same results as H4 in practice. |
| H6 | Decoupled: macrostructure optimised as a SIMP problem; microscale solved independently. | Structural optimisation with a single global optimal cellular/composite material. | Yields discrete macro- and microstructures. |
| H7 | Subdomain-based: each macro subdomain has its own microscale problem, with both scales updated. | H3-based, regional tailoring of composite structures. | Balances detail and cost; dependent on subdomain definition. |
| H8 | Subdomain-based: constant macro density equal to the global constraint; only microscale updated. | Similar to H7, but a simpler global problem. | More stable and efficient than H7, with slightly less flexibility. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dias-de-Oliveira, J.; Pinho-da-Cruz, J.; Teixeira-Dias, F. Domain-Oriented Hierarchical Topology Optimisation—An Approach for Heterogeneous Materials. Appl. Sci. 2025, 15, 10201. https://doi.org/10.3390/app151810201
Dias-de-Oliveira J, Pinho-da-Cruz J, Teixeira-Dias F. Domain-Oriented Hierarchical Topology Optimisation—An Approach for Heterogeneous Materials. Applied Sciences. 2025; 15(18):10201. https://doi.org/10.3390/app151810201
Chicago/Turabian StyleDias-de-Oliveira, João, Joaquim Pinho-da-Cruz, and Filipe Teixeira-Dias. 2025. "Domain-Oriented Hierarchical Topology Optimisation—An Approach for Heterogeneous Materials" Applied Sciences 15, no. 18: 10201. https://doi.org/10.3390/app151810201
APA StyleDias-de-Oliveira, J., Pinho-da-Cruz, J., & Teixeira-Dias, F. (2025). Domain-Oriented Hierarchical Topology Optimisation—An Approach for Heterogeneous Materials. Applied Sciences, 15(18), 10201. https://doi.org/10.3390/app151810201








