Enhancing Machinery-Aided Composting Through Multiobjective Optimization

Abstract

This study focuses on optimizing the composting process through advanced multiobjective optimization techniques, aiming to minimize both operational costs and CO₂ emissions by efficiently allocating tasks to specialized machinery. It introduces three novel multiobjective models that uniquely integrate cost minimization, CO₂ emission reduction, and maximized waste processing, addressing a critical gap in sustainable composting. The first model prioritizes cost reduction, providing a foundational framework for optimizing resource allocation. Building on this, the second model integrates environmental considerations, balancing cost minimization with the reduction of CO₂ emissions to achieve a sustainable trade-off. The third model takes a broader approach by maximizing the volume of organic waste processed within a workday while simultaneously minimizing emissions. These models incorporate real-world constraints, such as machinery capacity, operational work hours, and required rest periods for compost piles. The findings underscore the potential of multiobjective optimization to tackle complex industrial challenges. This research offers a practical and sustainable solution that harmonizes economic efficiency with environmental stewardship, demonstrating its applicability to processes as intricate as composting.

1. Introduction

The efficient management of organic waste represents one of the foremost global challenges at present, as a substantial fraction of this material continues to be deposited in landfills, where improper treatment can endanger both the environment and human health [1]. In response, composting has emerged as an innovative and essential solution to mitigate the adverse impacts of this important issue. This eco-friendly and cost-efficient practice transforms organic waste into valuable organic fertilizer [2]. Various composting methods have been developed to optimize this process. For example, aerobic composting creates waste piles that are systematically aerated through regular turning to ensure uniformity and temperature control. Key factors influencing the success of aerobic composting include the use of composting machinery, turning capacity (TC), composting cycles, and the management of compost piles. A comprehensive analysis of these critical components is presented below.

Composting Machines. Aerobic composting requires specialized machinery. These machines are pulled by tractors. Therefore, the use of diesel is necessary in this process. In this work, we are going to classify the composting machines into three types, according to the pile width that can be handled by each machine. This classification is presented in

Table 1. Classification of each machine based on their specifications.

Name	Pile Width (m)	Required Power (m3/h)
Type I	2.5	300 (70 HP)
Type II	3.0	500 (80 HP)
Type III	3.5	700 (95 HP)

. For more technical information about these machines, please consult [3].

Compost Piles. Within the composting by turning process, a surface is made up of waste piles created in parallel, separated by a given space e. Each pile is removed by a machine that is anchored to a tractor that passes through space e. These waste piles are turned once every two days.

Turning Capacity. Turning capacity indicates the amount of waste that a machine can process in a given time interval; it is defined as $TC={\displaystyle \frac{volume}{time}}$.

Composting cycles. The duration necessary for the biodegradation of a given organic waste is referred to as the composting cycle.

As mentioned above, composting plays a crucial role in mitigating the negative impacts of this global challenge. In this study, we revisit the methodology from [4,5] and introduce new strategies for modeling the composting problem. The main contributions can be summarized as follows:

• Three innovative multiobjective optimization models for the composting process are introduced.
• The first model focuses on minimizing the overall cost of the composting process while ensuring an efficient allocation of available machinery. The most notable feature of this model is that it directly reduces machine maintenance costs by ensuring a balanced use of all available machines.
• The second model builds upon the first, aiming to not only reduce costs but also maintain CO₂ emissions at minimal levels. This model stands out by aligning itself with global sustainability goals by seeking a reduction in CO₂ emissions.
• The third model prioritizes minimizing CO₂ emissions while simultaneously maximizing the capacity for processing organic waste. The impact of this proposal is the robustness of the model, which allows its adaptation to large-scale composting facilities.

The remainder of this work is organized as follows: Section 2 presents the background. The composting problem, the proposed models, implementation details, and numerical experimentation can be found in Section 3. Finally, concluding comments are presented in Section 4.

Related Work

In recent years, various optimization methods have been applied to enhance the composting process. These methods include both mathematical and artificial intelligence-based approaches [6]. Achieving optimization in the composting process requires detailed knowledge of the process. From a statistical perspective, modeling involves collecting and analyzing experimental data. For instance, the Taguchi method, a statistical design approach, entails conducting controlled experiments to gather data, analyzing the results, and gaining insights into the process behavior to optimize it [7]. In [8], the authors used central composite design and response surface methodology to optimize floral waste composting, showing that the experimental data could be described using second-order polynomial equations. Using ANOVA, the authors in [9] identified three process variables that significantly impacted wheat straw composting. In [10], ANNs were employed to model the conversion of leachate into compost. Linear programming was applied in [11] to minimize the total system cost for waste and energy management, while in [12], a mixed Integer Linear Programming approach was used to optimize various aspects of the composting process, such as determining the optimal processing network for a waste-to-energy system. A review of proposed optimization models in this field can be found in [13].

2. Materials and Methods

2.1. Multiobjective Optimization Problem

Consider the Multiobjective Optimization Problem (MOP) that can be expressed as follows:

$$\begin{array}{cccc}\underset{\mathit{x}\in \Omega }{min}& & \mathit{F}\left(\mathit{x}\right)& \\ s.t.& & \mathit{x}\in \Omega .\end{array}$$

(1)

where $\mathit{F}\left(\mathit{x}\right)$ consists of k objective functions that often conflict with one another, and $\Omega$ is the decision space. The optimality of a MOP is defined using the concept of Pareto dominance: let $\mathit{v},\mathit{w}\in {\mathbb{R}}^k$, then $\mathit{v}$ is less or equal than $\mathit{w}$ ($\mathit{v}{\le }_p\mathit{w}$), if $v_i\le w_i$ for all $i\in \{1,\dots ,k\}$; the relation ${<}_p$ is defined analogously. A vector $\mathit{y}\in \Omega$ is dominated by a vector $\mathit{x}\in \Omega$ ($\mathit{x}\prec \mathit{y}$) with respect to (1) if $\mathit{F}\left(\mathit{x}\right){\le }_p\mathit{F}\left(\mathit{y}\right)$ and $\mathit{F}\left(\mathit{x}\right)\ne \mathit{F}\left(\mathit{y}\right)$, else $\mathit{y}$ is called non-dominated by $\mathit{x}$. In case $\mathit{F}\left(\mathit{x}\right){<}_p\mathit{F}\left(\mathit{y}\right)$ the relation is called strong Pareto dominance. A point ${\mathit{x}}^{\ast }$ is Pareto optimal to (1) if there is no $\mathit{y}\in \Omega$ which dominates $\mathit{x}$. The set of all the Pareto optimal points $P_{\Omega }$ is called the Pareto set, and its image $\mathit{F}\left(P_{\Omega }\right)$ is called the efficient set or Pareto front.

2.2. Generalized Assignment Problem

The Generalized Assignment Problem (GAP) is a problem that seeks to assign a set of tasks to a set of agents, where each task requires a certain amount of resources and each agent has a limited capacity to provide those resources, the main objective is to assign all tasks to agents in such a way that the total cost is minimized.

The GAP may be formulated as an Integer Linear Programming (ILP) model with binary variables. Let n be the number of tasks to be assigned to m agents and define $N=\{1,2,\dots ,n\}$ and $M=\{1,2,\dots ,m\}$. The ILP model is defined as follows:

$$\begin{array}{ccc}min& {\displaystyle \sum _{i=1}^m\sum _{j=1}^n{c}_{ij}{x}_{ij}}& \\ s.t.& \sum _{j=1}^n{r}_j{x}_{ij}\le b_i,& \forall i\in M\\ & \sum _{i=1}^m{x}_{ij}=1,& \forall j\in N,\\ & x_{ij}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{task}j\mathrm{is}\mathrm{assigned}\mathrm{to}\mathrm{agent}i\hfill \\ 0,\hfill & \mathrm{if}\mathrm{not}.\hfill \end{array}\right.& \forall i\in M,j\in N,\end{array}$$

(2)

where, $c_{ij}$ is the cost of task j being assigned to agent i, $r_j$ is the amount of resource required for task j by the agent, and $b_i$ is the resource units available to agent i.

Different approaches can be used when solving a GAP. In [14], a conventional branch and bound technique is used. In [15], another possible method for solving GAP is used. It involves minimizing gaps in unit-duration task scheduling through a greedy approach that iterates until the optimal solution is found. Meanwhile, an experimental investigation into solving the GAP using Genetic Algorithm (GA) and Simulated Annealing is presented in [16]. While in [17], the authors solved the GAP via Differential Evolution (DE). In [18], Discrete Differential Evolution was proposed to solve the multiobjective GAP, simultaneously optimizing cost, time, and profit. Similarly, in [19], the Fuzzy Programming Technique was applied to a multi-index GAP, incorporating both linear and nonlinear membership functions. In [20], a multiobjective genetic algorithm was employed to solve the constrained assignment problem, which generalizes various assignment problems. Furthermore, in [21], an algorithm was developed to obtain Pareto-optimal solutions for a biobjective GAP with linear and nonlinear objectives, focusing on minimizing cost and time.

On the other hand, recent studies have explored various optimization and artificial intelligence techniques to improve waste management systems, primarily focusing on prediction, resource allocation, and environmental impact mitigation. For instance, ref. [22] integrated machine learning models such as Support Vector Machines, Random Forest, and Extreme Gradient Boosting with optimization techniques to forecast waste generation and improve economic and environmental efficiency. Similarly, ref. [23] investigated several machine learning algorithms, demonstrating that Random Forest achieved the highest accuracy for predicting operational parameters such as the time required to empty recycling containers. In contrast, ref. [24] proposed a hybrid algorithm combining metaheuristics with simulation to address stochastic demands and multi-depot cooperation in waste collection routing. Their results highlighted the benefits of considering uncertainty and inter-depot collaboration in logistics optimization.

In [25], the authors address the challenges of solving high-dimensional multimodal Multiobjective Optimization Problems, where achieving convergence to the Pareto front while maintaining solution diversity is particularly difficult. Their main contribution lies in the development of an approach capable of effectively exploring complex, high-dimensional landscapes that resemble real-world problems, while balancing convergence and diversity—an aspect that is critical for practical engineering optimization. In [26], a novel hybrid optimization–simulation framework is proposed to support decision-making in smart and sustainable manufacturing environments. Experimental results demonstrate that the approach produces schedules that achieve a better trade-off between energy efficiency and productivity, which is highly relevant in industrial contexts where both energy consumption and time efficiency must be considered to ensure sustainable production. Lian, Gu, and Jiao in [27] propose a new PSO algorithm which is specifically designed to maximize profit by minimizing tardiness and due-date penalties in job scheduling. Its computational modeling highlights potential applications in manufacturing automation and production systems. Ye and colleagues in [28] integrate learning-based guidance into multiobjective optimization through a method that dynamically improves search strategies as optimization progresses, adapting to problem structures and solution landscapes. Finally, in [29], the authors address the disassembly line balancing problem (DLBP), a crucial challenge in remanufacturing and recycling industries, where product disassembly must be both efficient and mindful of worker-related factors. Wei and collaborators propose a multiobjective discrete harmony search optimizer (MODHSO) that simultaneously enhances disassembly efficiency, balances workloads, and incorporates human factor considerations.

2.3. Proposed Models

In the following, we explain how the composting by turning problem was modeled using different approaches. We briefly mentioned the considered assumptions, and finally, the mathematical model in each case is presented. The modeling of the problem was carried out under specific assumptions regarding the composting process, which are summarized as follows:

• Each compost pile must undergo exactly three processing operations per cycle, with each cycle lasting six days.
• Following each processing operation, the compost pile is required to remain at rest for one day.
• The working schedule consists of 8 h shifts, of which H hours are considered fully productive.
• A compost pile cannot be processed simultaneously by more than one machine.
• The uniformity of compost piles is not considered.

Based on the data presented in Table 1, and by setting $H=6$ as the number of fully productive hours, this value is set according to the data provided by a composting company. The maximum daily processing capacity of each machine is provided in

Table 2. Maximum processing capacity per day for each type of machine.

Name	Maximum Volume (m3)
Type I	$V_{max\_I}=(300{\mathrm{m}}^3/\mathrm{h})\left(6\mathrm{h}\right)=1800{\mathrm{m}}^3$
Type II	$V_{max\_II}=(500{\mathrm{m}}^3/\mathrm{h})\left(6\mathrm{h}\right)=3000{\mathrm{m}}^3$
Type III	$V_{max\_III}=(700{\mathrm{m}}^3/\mathrm{h})\left(6\mathrm{h}\right)=4200{\mathrm{m}}^3$

. Consequently, the maximum processable volume per day, considering $n_1$ Type I machines, $n_2$ Type II machines, and $n_3$ Type III machines, is given by the following:

$$V_{\max }=n_1\times V_{max\_I}+n_2\times V_{max\_II}+n_3\times V_{max\_III}.$$

(3)

If the volume exceeds $V_{\max }$, then the problem would have no feasible solutions and, therefore, would be unsolvable. It is worth mentioning that the feasibility of the solutions does not depend on the number of piles that need to be processed but on the daily maximum volume. Thus, there can be n number of compost piles such that the sum of the volumes to be processed per day is less than or equal to $V_{\max }$.

2.3.1. Model 1: Multiobjective Generalized Assignment Problem Approach (MOGAP)

This model is a natural extension of the one proposed in [5]. The objective of this study is to minimize the overall cost of composting n piles of organic waste by utilizing m available machines, while ensuring a balanced allocation across the different machine types. In [5], an important result was obtained when we aimed to compost a small volume of organic waste, that is, we have a reduced number of piles. The best allocation scheme was to let the most economical machine, in terms of diesel consumption, carry out the entire composting process. Recall that, by directly minimizing diesel usage, the overall cost of the composting process was also reduced, as the monetary cost was considered as the product of diesel price and liters consumed, with the price being variable and independent of the process itself. This was not the best scenario, at least from a management point of view, since we are not using all the available machines, and the most used machine shows greater wear, thus accelerating the need for maintenance, which has a direct impact on administrative expenses.

Let $c_{ij}$ denote the cost, measured in liters of diesel, associated with processing pile j using machine i, $t_{ij}$ represent the time required by machine i to process pile j; and $x_{ijk}$ indicate the assignment of pile j to machine i on day k. Note that $x_{ijk}=1$ if pile j is assigned to machine i on day k and $x_{ijk}=0$ otherwise. Let $K=\{1,2,\dots ,6\}$ be the number of workdays, $N=\{1,2,\dots ,n\}$ denote the set of piles, and $M=\{1,2,\dots ,m\}$ the set of available machines. Then, the following model is defined:

$$\begin{array}{cccc}min\hfill & & \sum _{i=1}^2\sum _{i=1}^m\sum _{j=1}^n{c}_{ij}{x}_{ijk},\hfill & \\ max\hfill & & \underset{i\in M}{max}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij1}\right\}-\underset{i\in M}{min}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij1}\right\}\hfill & \\ \hfill & & +\underset{i\in M}{max}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij2}\right\}-\underset{i\in M}{min}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij2}\right\},\hfill & \\ s.t.\hfill & & \sum _{j=1}^n{t}_{ij}{x}_{ij1}\le H\hfill & \forall i\in M,\hfill \\ \hfill & & \sum _{j=1}^n{t}_{ij}{x}_{ij2}\le H\hfill & \forall i\in M,\hfill \\ \hfill & & \sum _{i=1}^m{x}_{ij1}+2\sum _{i=1}^m{x}_{ij2}+\sum _{i=1}^m{x}_{ij3}=2\hfill & \forall j\in N,\hfill & \\ \hfill & & \sum _{i=1}^m{x}_{ij3}+2\sum _{i=1}^m{x}_{ij4}+\sum _{i=1}^m{x}_{ij5}=2\hfill & \forall j\in N,\hfill & \\ \hfill & & \sum _{i=1}^m{x}_{ij5}+\sum _{i=1}^m{x}_{ij6}=1\hfill & \forall j\in N.\hfill \end{array}$$

(4)

Remark

Given the assumptions that each pile must be composted three times per cycle and that six days constitute a composting cycle, the model described above can be simplified to optimize only the first two days, since the assumption of a one-day rest period directly affects the process. Note that if pile j is turned on the first day, it must remain at rest on the second day, which implies that it will be turned on again on the third day, and so on. This provides a significant advantage by reducing the number of variables and, consequently, the computational cost. With this consideration, the reduced model is defined as follows:

$$\begin{array}{cccc}min\hfill & & \sum _{i=1}^2\sum _{i=1}^m\sum _{j=1}^n{c}_{ij}{x}_{ijk},\hfill & \\ max\hfill & & \underset{i\in M}{max}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij1}\right\}-\underset{i\in M}{min}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij1}\right\}\hfill & \\ \hfill & & +\underset{i\in M}{max}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij2}\right\}-\underset{i\in M}{min}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij2}\right\},\hfill & \\ s.t.\hfill & & \sum _{j=1}^n{t}_{ij}{x}_{ij1}\le H\hfill & \forall i\in M,\hfill \\ \hfill & & \sum _{j=1}^n{t}_{ij}{x}_{ij2}\le H\hfill & \forall i\in M,\hfill \\ \hfill & & \sum _{i=1}^m{x}_{ij1}+\sum _{i=1}^m{x}_{ij2}=1\hfill & \forall j\in N.\hfill \end{array}$$

(5)

2.3.2. Model 2: Constrained Multiobjective Generalized Assignment Approach (CMOGAP)

Aerobic composting of organic waste can impact the environment due to the pollutants emitted by the machinery used in the process. Although composting itself is environmentally friendly, the use of machinery, often powered by fossil fuels, can contribute to the release of carbon dioxide (CO₂), nitrogen oxides (NO_x), and particulate matter into the atmosphere. These emissions contribute to air pollution and the greenhouse effect, counteracting some of the environmental benefits of composting. Furthermore, if machines are not properly maintained, they can leak oil or other harmful substances into the soil or water, further damaging ecosystems. Therefore, the previous model is not sufficient to help the environment. That is why a modification is proposed through a restriction that seeks to keep CO₂ at low emission levels.

Now, consider the variables and sets defined in Section 2.3.1 and let $\mu$ be the constant representing the CO₂ emissions per liter of diesel, with a value of $2.62{\displaystyle \frac{kgC{O}_2}{l}}$ as reported in [30]. Then we define the following model:

$$\begin{array}{cccc}min\hfill & & \mu \left(\sum _{i=1}^2\sum _{i=1}^m\sum _{j=1}^n{c}_{ij}{x}_{ijk}\right),\hfill & \\ max\hfill & & \underset{i\in M}{max}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij1}\right\}-\underset{i\in M}{min}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij1}\right\}\hfill & \\ \hfill & & +\underset{i\in M}{max}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij2}\right\}-\underset{i\in M}{min}\left\{\sum _{j\in N}{c}_{ij}{x}_{ij2}\right\},\hfill & \\ s.t.\hfill & & \sum _{j=1}^n{t}_{ij}{x}_{ij1}\le H\hfill & \forall i\in M,\hfill \\ \hfill & & \sum _{j=1}^n{t}_{ij}{x}_{ij2}\le H\hfill & \forall i\in M,\hfill \\ \hfill & & \sum _{i=1}^m{x}_{ij1}+\sum _{i=1}^m{x}_{ij2}=1\hfill & \forall j\in N,\hfill \\ \hfill & & w_1\sum _{k=1}^2\sum _{j=1}^n{t}_{1j}{x}_{1jk}+\dots +w_m\sum _{k=1}^2\sum _{j=1}^n{t}_{mj}{x}_{mjk}\le \theta .\hfill \end{array}$$

(6)

Here, the first objective function aims to minimize the kilograms of CO₂ emitted during the composting process. The second objective function is the equilibrium function, which prevents the overloading of any single machine. In other words, this objective function aims to ensure that the assignment of compost piles is well-distributed across all machines. The first and second constraints relate to the limitations of fully productive working hours, while the third constraint is related to the assumptions regarding the number of times a pile must be turned and the day of rest required after turning. Lastly, the final constraint aims to regulate the cost associated with the maintenance of the different machines. In this section, $w_i$ is a weighting factor for the maintenance cost of the i-th machine, considering the different types of available machines. It is calculated as follows:

$$w_i={\displaystyle \frac{p_i}{p_1+\dots +p_m}}i\in \{1,2,...,m\},$$

(7)

where $p_i$ represents the power of the i-th machine. Furthermore, $\theta$ denotes the average maintenance cost, considering the weights and volume to be processed. The numerical experimentation of the CMOGAP approach is presented in the following section.

2.3.3. Model 3: Multiobjective Optimization Problem Approach (MOP)

In this model, we aim to maximize the volume of organic waste that can be processed during a workday while minimizing the $C{O}_2$ emissions caused by the machinery used.

$$\begin{array}{cccc}max\hfill & & \sum _{i=1}^m{x}_i,\hfill & \\ min\hfill & & \mu \sum _{i=1}^m{\displaystyle \frac{C{D}_i}{C{V}_i}}{x}_i,\hfill & \\ s.t.\hfill & & {\displaystyle \frac{1}{C{V}_i}}{x}_i\le 6\hfill & \forall i\in \{1,2.\dots ,m\}.\hfill \end{array}$$

(8)

where $\mu$ is the constant indicating the kilograms of CO₂ emitted by 1 liter of diesel, the value of $\mu$ is $2.62{\displaystyle \frac{kgC{O}_2}{l}}$, $C{V}_i$ is the turning capacity of the i-th machine, and $C{D}_i$ corresponds to diesel consumption of the i-th machine. Remember that 8 h work days are considered, with 6 h being fully productive, thus $H=6$.

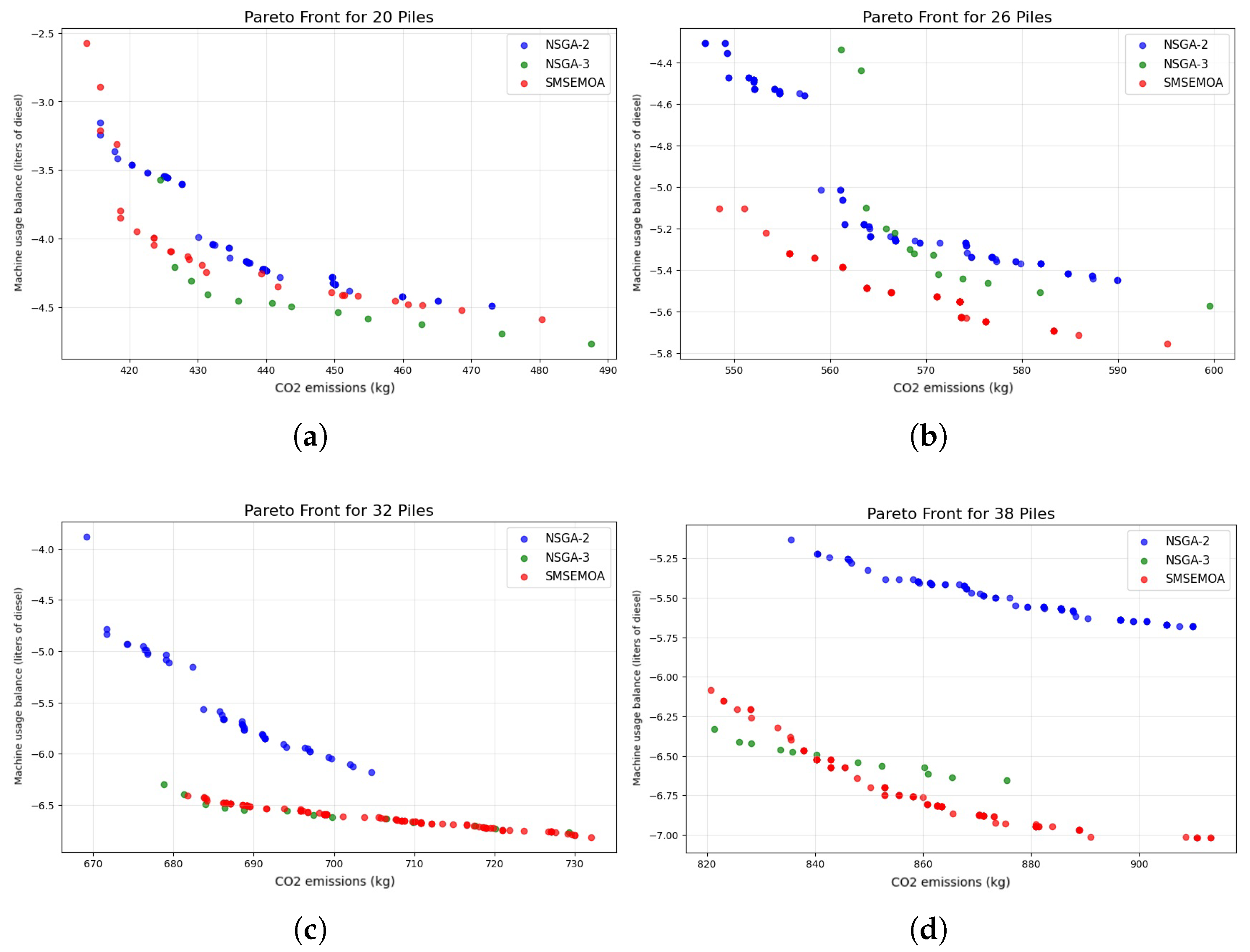
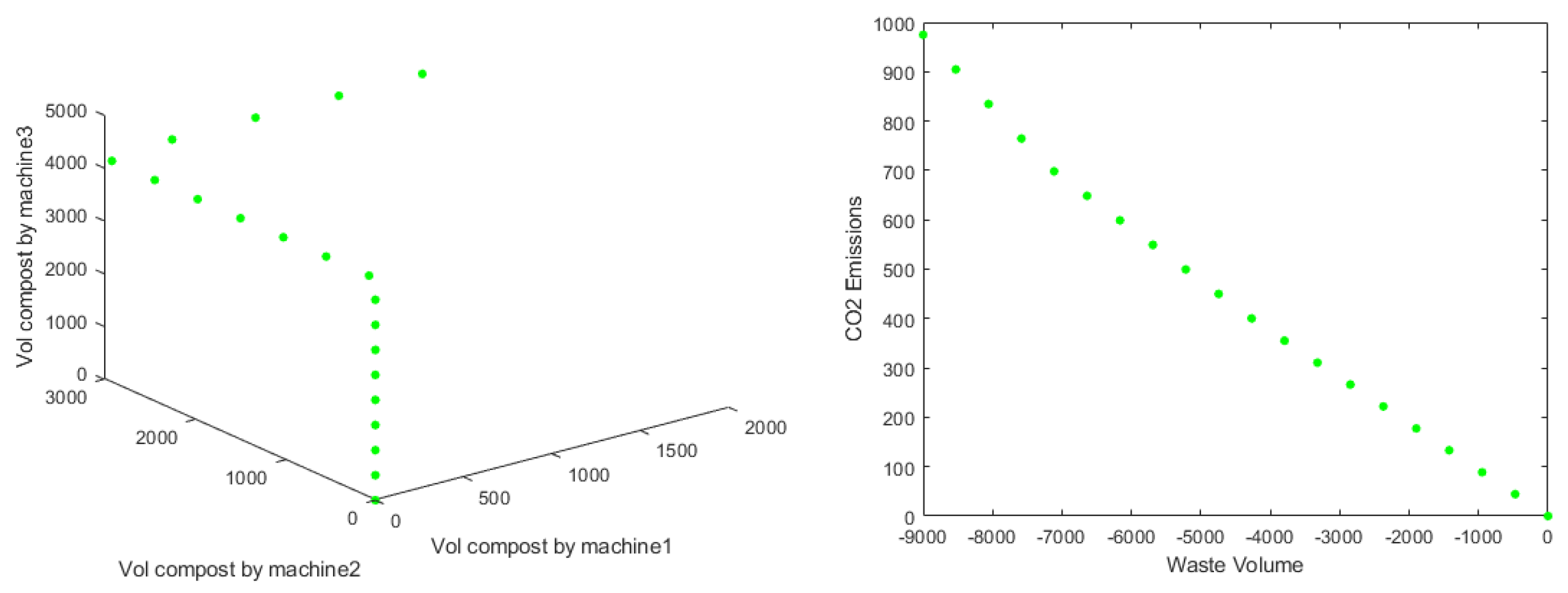
3. Results

3.1. Solving Model 1

To carry out the numerical experimentation of this model, The Pymoo 0.6.1.3 [31] platform was used. Two distinct experiments were designed to assess the performance of the proposed model. In the first experiment, only three machines—one of each type—were considered, while the number of piles increased. In the second experiment, the number of piles was fixed, and different numbers of machines were considered. To address both problems, three algorithms were considered: SMS-EMOA, NSGA-II, and NSGA-III. The following parameters were considered: population size $N=100$, probability of crossover $p_c=0.9$, and probability of mutation $p_m=1$. We defined the stopping criteria using the maximum number of function evaluations ($feva{l}_{max}=$ 50,000).

First, the selected algorithms were tested on Model 1, considering a range from $n=20$ to $n=44$ piles, increasing by 2 piles per case, in each experiment, with $m=3$ machines (one of each type). The experiment started with 20 piles, as a smaller number leads to identical results for all three algorithms. This occurred because, in configurations with fewer piles, the problem was less complex. For the second experiment, we tested Model 1 considering $n=60$ piles and a total of $m=5$ machines. Each case finds a different number of machines of each type. To measure the performance of each algorithm, the hypervolume indicator (HV) was employed [32]. This indicator is a popular metric used in multiobjective optimization to evaluate the performance of different algorithms. It measures the volume of the objective space dominated by a given set of solutions. A larger hypervolume indicates a better distribution of solutions in the objective space, which is desirable in optimization problems. The results obtained from 30 independent runs are presented in

Table 3. Numerical results considering Model 1 (MOGAP Approach).

First Scenario
# Piles	SMS-EMOA HV	NSGA-II HV	NSGA-III HV
20	0.6893	0.8077	0.7612
std.	0.1188	0.0513	0.0977
22	0.5879	0.7304	0.7099
std.	0.0946	0.0522	0.0653
24	0.4812	0.6411	0.6112
std.	0.1643	0.0538	0.0706
26	0.5430	0.7917	0.7355
std.	0.2108	0.0938	0.0967
28	0.5658	0.7148	0.6843
std.	0.1478	0.0855	0.0753
30	0.4381	0.6270	0.5917
std.	0.1708	0.0718	0.0851
32	0.5145	0.7598	0.5675
std.	0.2800	0.2071	0.1037
34	0.4950	0.7008	0.5788
std.	0.1593	0.0545	0.1048
36	0.4899	0.6509	0.5692
std.	0.1712	0.6824	0.0988
38	0.5509	0.6954	0.5747
std.	0.1417	0.0811	0.0687
40	0.5295	0.6876	0.6017
std.	0.1416	0.0614	0.1217
42	0.5087	0.6913	0.6252
std.	0.2148	0.1106	0.1410
44	0.5039	0.6821	0.6959
std.	0.2188	0.1115	0.1188
Second Scenario
Cases	SMS-EMOA HV	NSGA-II HV	NSGA-III HV
1	0.4066	0.4704	0.1970
std.	0.2751	0.2963	0.2405
2	0.4896	0.4838	0.3351
std.	0.2190	0.2477	0.2256
3	0.4762	0.5439	0.2632
std.	0.2128	0.1613	0.2233

.

Table 3 shows the results of both scenarios for the HV indicator obtained by the three different algorithms. In the first scenario, as the number of piles increased, the HV values tended to decrease across all three algorithms (SMS-EMOA, NSGA-II, and NSGA-III), which is expected as the problem becomes more complex with more piles, making it harder to achieve high HV values. Among the algorithms, NSGA-II consistently achieved the highest HV, followed by NSGA-III, while SMS-EMOA yielded the lowest HV values. This outcome may seem counterintuitive, given that SMS-EMOA directly optimizes the hypervolume indicator; however, its selection mechanism prioritizes maintaining a well-distributed Pareto front, which can lead to a trade-off between diversity and convergence. In contrast, NSGA-II, based on non-dominated sorting and crowding distance, balances exploration and exploitation more effectively, allowing it to reach better regions of the Pareto front in this problem. In the second scenario, the HV values did not exhibit a clear decreasing trend, but NSGA-II continued to outperform the other algorithms, followed by NSGA-III, while SMS-EMOA maintained the lowest values. The standard deviations remained relatively low across most cases, indicating stable results, although they slightly increased as the complexity of the problem grew, particularly in the first scenario.

In this model, where, in addition to cost minimization, our objective was to achieve a balanced distribution of machine usage to prevent overloading a single unit, we observed that in Scenario 1, as the number of stacks increased, the HV decreased. This is due to the significant increase in the number of variables. However, we noticed that the standard deviation values showed only minor variations, which suggests that we could expect stability in the results. We can observe that in all cases, NSGA-II was superior to the other algorithms, suggesting that it is more effective in this type of problem.

Figure 1 shows the Pareto fronts obtained for different pile configurations. For 20 piles, all three algorithms (NSGA-II, NSGA-III, and SMS-EMOA) yield similar performance, with overlapping solutions. As the number of piles increases, NSGA-II consistently dominates the other methods, achieving better convergence towards the Pareto front.

3.2. Solving Model 2

As in the previous model, the numerical experimentation of Model 2 (CMOGAP approach) was carried out under two scenarios. In the first scenario, only one machine of each type was considered while the number of piles to be composted increased. In the second scenario, the volume of organic waste was fixed, while the number of machines of each type was varied. The same experimental setting was used. The results obtained are presented in

Table 4. Numerical results considering Model 2 (CMOGAP approach).

First Scenario
Piles	SMS-EMOA	NSGA-II	NSGA-III
20	0.7979	0.6539	0.7593
std	0.0701	0.1715	0.1075
22	0.7528	0.5746	0.6947
std	0.0702	0.1422	0.0857
24	0.6407	0.5039	0.6488
std	0.0695	0.1483	0.0737
26	0.7765	0.5369	0.7291
std	0.0982	0.2264	0.1120
28	0.7452	0.6027	0.6725
std	0.0543	0.1194	0.0791
30	0.6212	0.4296	0.6095
std	0.0751	0.1757	0.0819
32	0.7581	0.5521	0.6921
std	0.1072	0.1903	0.1095
34	0.7280	0.5134	0.6908
std	0.0803	0.1775	0.0892
36	0.6578	0.5066	0.6283
std	0.0768	0.1637	0.0717
38	0.7164	0.5368	0.6845
std	0.0853	0.1485	0.1012
40	0.6661	0.5433	0.6559
std	0.0809	0.1317	0.0775
42	0.6847	0.4822	0.6473
std	0.0868	0.2525	0.1130
44	0.6959	0.6821	0.5039
std	0.1188	0.1115	0.2188
Second Scenario
Cases	SMS-EMOA	NSGA-II	NSGA-III
1	0.4263	0.4327	0.3402
std	0.3099	0.3264	0.2830
2	0.5123	0.4273	0.3458
std	0.2663	0.2413	0.2657
3	0.5096	0.5299	0.3588
std	0.1558	0.1853	0.2301

.

Table 4 shows the results of both scenarios for the HV obtained by the three algorithms for Model 2 (CMOGAP approach). The results indicate that, in the first scenario, as the number of piles increased, the HV values tended to decrease across all three algorithms (SMS-EMOA, NSGA-II, and NSGA-III), which aligns with the expectation that increasing the number of piles makes the problem more complex, leading to lower-quality solutions in terms of HV. Unlike the results of Model 1, where NSGA-II exhibited the highest HV values, SMS-EMOA now outperformed the other two algorithms in most cases. This shift in performance can be attributed to the nature of SMS-EMOA’s hypervolume-based selection mechanism, which, despite its inherent computational complexity, became advantageous as the difficulty of the problem increased. As the number of piles grew, maintaining a well-spread Pareto front became increasingly challenging, and SMS-EMOA, by directly optimizing the hypervolume metric, was better suited to handle this difficulty, resulting in improved HV values compared to NSGA-II and NSGA-III. In the second scenario, where the cases were considered instead of a continuous increase in piles, the HV values exhibited less variation, and NSGA-II and SMS-EMOA achieved comparable performance, while NSGA-III generally yielded lower HV values. The standard deviations remained relatively stable, indicating consistent algorithmic behavior across different settings. In Figure 2 we can observe that the Pareto front with greater efficiency was SMS-EMOA as the number of piles increased.

3.3. Solving Model 3

To carry out the numerical experimentation of this model, it is worth noting that we dealt with a linear MOP with only one constraint. Therefore, a classic approach could be considered to solve the proposed model. We used the NBI method, considering 20 initial points. Figure 3 shows the results. It is observed that NBI computed the edges of the cube generated by the defined functions. To clarify the meaning of this cube, note that the only way to achieve zero CO₂ emissions is by not using any machine at all—that is, the solution $(0,0,0)$. Since our goal is to increase the volume of organic waste processed, we must first use the machine with the best efficiency ratio $(C{D}_i/C{V}_i)$ until it reaches its maximum allowed capacity, defined by the constraint ${\displaystyle \frac{1}{C{V}_i}}{x}_i\le 6$. This corresponds to the vertical line from $(0,0,0)$ to $(0,0,400)$ in the cube. At that point, we activate the second most efficient machine, which operates until it also reaches its maximum capacity. This stage is represented by the line from $(0,0,400)$ to $(0,3000,4000)$.

Finally, to achieve the maximum total volume, we must progressively use the least efficient machine. This is represented by the line from $(0,3000,4000)$ to $(2000,3000,4000)$.

4. Discussion and Conclusions

In this study, we successfully developed three different models to address the complex optimization problem of composting. These models were designed to solve a complex problem that considers not only the financial cost of composting operations but also the environmental impact, specifically the CO₂ emissions generated by specialized machinery used in the process. By applying real-world data, the models proved to be both practical and effective, achieving the main goals of minimizing cost and reducing emissions. The results clearly demonstrate that our approach can significantly improve the sustainability of composting systems, promoting environmental conservation and more efficient use of resources.

The usefulness of these models lies in their ability to support decision-making in real composting operations. They offer a reliable framework for balancing economic and environmental priorities, making them highly relevant for industries and policymakers focused on sustainable waste management.

It is important to acknowledge certain limitations of the present study. In particular, the models rely on the assumption of uniform diesel consumption across different machines, although in practice this may vary depending on factors such as machine type, age, or maintenance status. Moreover, other environmental impacts beyond CO₂ emissions, such as ${\mathrm{NO}}_x$ or particulate matter, were not considered. Addressing these aspects could provide a more comprehensive assessment of the environmental footprint of the composting process.

Looking ahead, future research could enhance these models by incorporating additional variables, such as different types of compostable materials and their specific effects on CO₂ emissions. There is also strong potential in exploring hybrid optimization methods, such as combining genetic algorithms with other advanced techniques, to further improve performance. In particular, hybrid approaches such as combining NSGA-II with Differential Evolution strategies or integrating particle swarm optimization with local search methods could be investigated to improve convergence and solution diversity. Furthermore, validating the models with real operational data from composting facilities, as well as benchmark datasets, would strengthen their reliability and applicability. Expanding the scope of the study to cover a wider range of practical scenarios would help validate the models across different contexts, increasing their adaptability and real-world impact. Moreover, examining the social and economic outcomes of optimized composting strategies could provide valuable insights into their role in promoting sustainability at a broader level. Overall, this work lays a solid foundation for developing more efficient, eco-friendly composting systems with long-term benefits for both the environment and society.