Nighttime Reactive Power Optimization for Large-Scale PV Plants: Minimizing Compensation Equipment Investment

Abstract

The increasing integration of photovoltaic (PV) power systems poses challenges for nighttime voltage regulation because long high-voltage (HV) and ultra-high-voltage (UHV) underground cables generate capacitive reactive power that elevates the grid voltage. Conventional compensators based on passive inductors and capacitors are bulky, costly, and inflexible, rendering them unsuitable for substation use. This study proposes an optimization-based strategy that leverages the existing inverter infrastructure of PV plants to provide nighttime reactive power compensation without additional hardware. A genetic algorithm (GA) determines the optimal number and spatial deployment of inverters to minimize line losses. Field validation at a 120 MW PV plant with 1292 inverters shows that the strategy reduces reverse reactive power from 0.84 MVAr to 0.00214 MVAr and line losses from 1.8235 kW to 0.386 kW using only 55 inverters, achieving near-zero additional capital expenditure (CAPEX). This method enhances the voltage stability and system efficiency while reducing the investment and maintenance costs.

1. Introduction

The rapid development and transformation of green energy have significantly changed energy structure and usage [1,2]. Recently, utility-scale PV systems have been deployed in remote regions to meet growing energy demands. When PV power plants do not operate at night, reactive power is generated, which causes instability in network voltage. Insufficient reactive power causes the voltage to drop, whereas excessive reactive power increases the system voltage to excessively high levels. To stabilize the network voltage, reactive power must be controlled by considering the network power demand.

Various voltage-regulation devices, such as constant power controllers, voltage regulators, and energy-storage devices, have been employed to compensate for reactive power in PV power plants. In addition to these devices, a continuous power control method has been employed to reduce the power output of power plants [3]. Energy-storage devices are also employed to suppress network voltage fluctuations and reactive power generation; however, they incur additional investment costs [4]. Static and dynamic virtual compensation methods have been developed to enhance network voltage stability. However, large-scale applications are necessary but also require considerable investment [5]. According to ref. [6], when the penetration level of a PV systems reaches approximately 30% of the local load, it becomes difficult to maintain the voltage within acceptable limits without implementing reactive power control via inverters. This threshold is consistent with the voltage-regulation requirements specified in IEEE Std 1547™-2018 [7], which mandates that distributed energy resources (DERs) must provide voltage support functions to ensure grid stability. This finding underscores the importance of inverter-based voltage regulation in environments with high PV penetration. Although traditional reactive power compensation devices such as capacitor banks are still widely used, their large physical footprint and complex installation render them unsuitable for deployment in existing substations. In contrast, utilizing existing PV plant inverters to provide nighttime reactive power support offers a more flexible and cost-effective alternative.

During the power generation process, inverters inherently generate reactive power; thus, PV power plants must participate in reactive power compensation during the active generation. However, when reactive power support is mandated during non-generating periods, it is necessary to consider how to economically dispatch inverters within PV plants to stabilize the voltage without incurring additional installation costs.

The concept of utilizing photovoltaic systems as static synchronous compensators, commonly referred to as PV-STATCOMs, has been introduced in recent years to enhance voltage stability and provide reactive power support during both the generating and non-generating periods [8]. Moreover, earlier studies demonstrated the capability of PV inverters to perform local power factor correction, further confirming their potential for reactive support [9].

In large-scale PV power plants, the number of inverters typically exceeds several thousand, and the length of high-voltage (HV) and ultra-high-voltage (UHV) underground cables spans several tens of kilometers. The reactive power generated by these systems is predominantly capacitive. However, the reactive power capacity of PV inverters is constrained by the impedance of their transmission lines [10,11]. Therefore, when dispatching inverters for reactive power support, it is essential to consider strategies to simultaneously minimize line losses. This constitutes one of the primary objectives of this study.

Significant progress has been made in nighttime reactive power compensation for PV systems. Huque et al. investigated the feasibility of utilizing PV inverters to provide reactive power during the nighttime to reduce grid operating costs. This method has economic and technical advantages [12]. In addition, Minai et al. proposed a reactive power optimization strategy for power systems using a GA, specifically targeting systems such as PV power plants. The method effectively improved the bus voltage profiles and ensured compliance with voltage standards [13]. However, these studies primarily focused on theoretical analysis and simulation-based validation and lacked field-test data from large-scale PV plants. Further research is required to evaluate the effectiveness and reliability of these methods for real-world applications.

Table 1. Comparative summary of research results on nighttime reactive power control in PV systems.

Study	Method Used	Field Implementation	Plant Scale	Optimization Target	Key Result
Alenius et al. [11]	Nighttime PV-STATCOM (fixed control)	No	Simulated (medium-scale)	Improve voltage profile	Reduced overvoltage during nighttime
Rezende et al. [12]	GA-based optimization	No	Simulated	Bus voltage deviation minimization	Improved voltage compliance
This Study	GA optimization (real field)	Yes	120 MW/1292 inverters	Reactive power dispatch and line loss minimization	Reduced Q feedback from 0.84 MVAr to 0.00214 MVAr; line loss from 1.8235 kW to 0.386 kW

compares the practicality of nighttime reactive power control between this study and the previous literature, while

Table 2. Comparison of nighttime reactive power compensation approaches.

Item	SVC (Static Var Compensator)	SVG/STATCOM	Proposed PV-STATCOM (Using Existing Inverters)
Main equipment	Reactors + controllable capacitors/reactors + thyristor valves	Power electronic modules (IGBTs, DC capacitor, control system)	Existing PV inverters (only control logic adjustment required)
Additional CAPEX (Capital Expenditure)	High (dedicated devices required)	Very high (equipment + DC capacitor + transformer)	Almost zero (no extra hardware required)
Space requirement	Medium (installed at substations/plant site)	High (floor area + cooling system)	None (utilizes existing inverters)
HV switchgear/civil work	Additional HV breakers and bus extensions required	Additional HV breakers and cooling facilities required	Not required
O&M cost	Medium (maintenance of reactors/capacitors)	High (lifetime of power electronics/cooling system)	Very low (integrated with PV inverter maintenance)
Response speed	Medium (ms–s)	Fast (ms level)	Fast (comparable to STATCOM)
Typical applications	Voltage support in transmission/substations	Dynamic voltage control in large grids	Nighttime reactive power support in large PV plants
Investment effectiveness	High investment, long payback	Very expensive, difficult to recover	Near-zero investment, maximizing utilization of existing assets

details the control methods and investment benefits relative to traditional reactive power compensators.

To address this issue, a GA was adopted in this study to optimize the reactive power output of a PV power plant and determine a dispatch strategy for inverter-based reactive power compensation. The GA offers excellent performance in solving large-scale optimization problems. It requires only a well-defined objective function without the need for gradient information and is capable of handling both discrete and continuous variables simultaneously. The GA provides high adaptability, given that this study involves a mixed-variable optimization problem to determine the number of inverters to activate (integer variables) and their reactive power outputs (continuous variables). To verify the effectiveness of the proposed method, a field test was conducted on a large-scale photovoltaic (PV) power plant with an installation capacity of 120 MW.

2. Inverter-Based Reactive Power Control

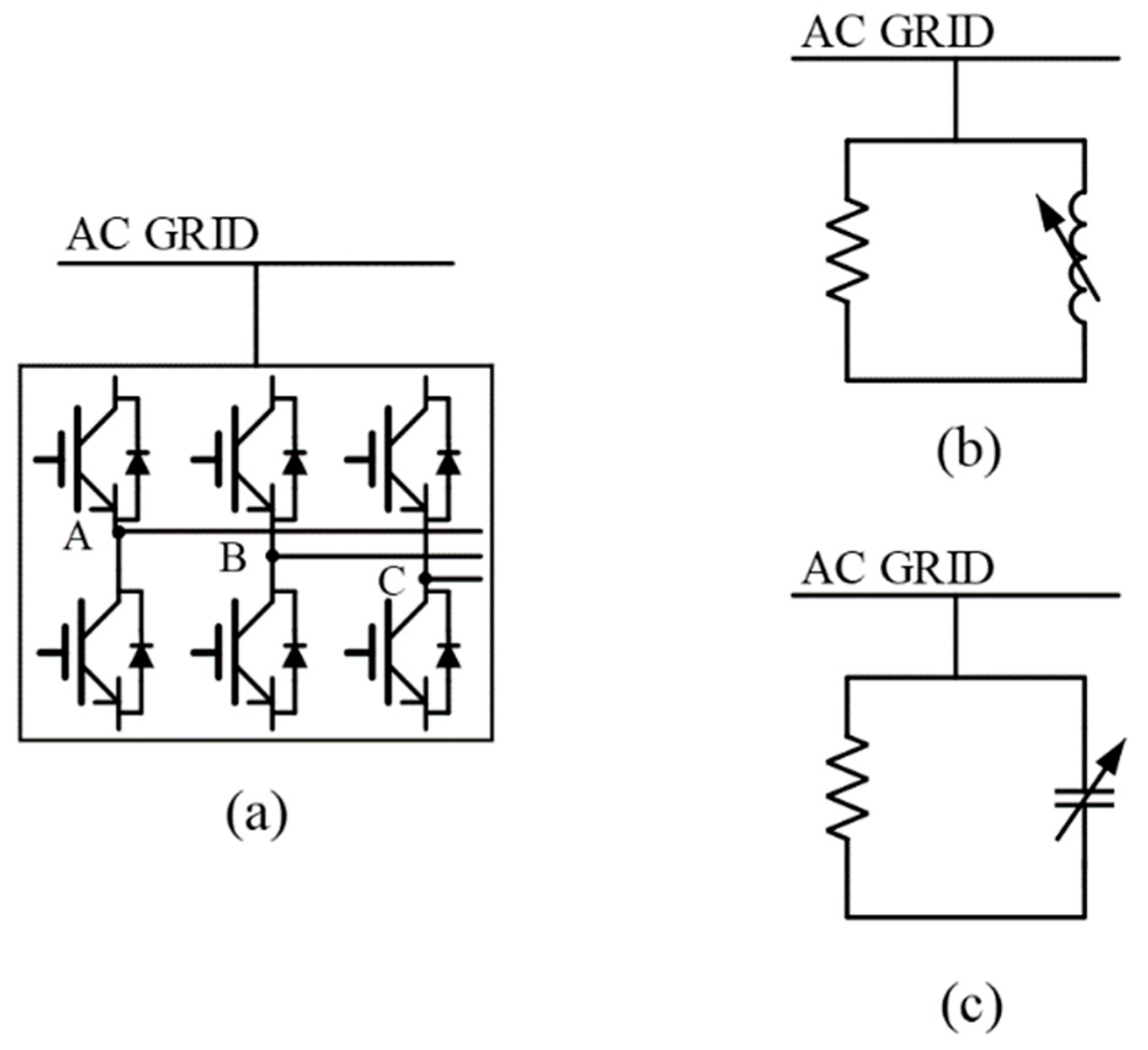
The inverter converts the direct current (DC) supplied by the solar panels into alternating current (AC) for the power output. At night, the inverter’s nighttime reactive power compensation mode is activated. In this mode, inverters in the PV power plant remain connected to the utility grid on the AC side throughout the night and consume only a small amount of energy from the grid to power their internal components. This allows the inverters to inject purely reactive power into the grid for voltage support. Figure 1 illustrates the circuit of the inverter operating in nighttime mode.

Reactive power compensation is critical in power systems for regulating the voltage levels, improving the power factor, and enhancing the overall system operating efficiency. Although reactive power compensation does not directly supply active power to the system, it plays a vital role in maintaining voltage stability and enabling the effective transmission of active power. Inverters compensate for the reactive power by leveraging their internal power electronic components and advanced control technologies. These technologies allow inverters to flexibly adjust the phase angle of the current, thereby enabling the absorption or injection of reactive power, as needed. The inverter process to compensate for the reactive power is described as follows:

2.1. Operating Principle of the Inverter

The inverter primarily converts DC into AC. However, it can also control the phase angle, voltage magnitude, and frequency of AC output. The inverter can control the injection or absorption of reactive power by adjusting the phase angle between the output voltage and the current.

2.2. Phase Angle Control Mechanism

In AC power systems, the total power consists of active and reactive components. The phase angle between the voltage and current determines the power distribution ratio. The reactive power corresponds to the orthogonal component and can be dynamically compensated for by controlling the phase angle of the current. The inverter regulates the reactive power via the following mechanism:

• When the output current lags behind the voltage (phase angle close to +90°), the inverter behaves as an inductive load and absorbs reactive power, thereby suppressing the overvoltage conditions.
• When the output current leads to a voltage (phase angle close to −90°), the inverter behaves as a capacitive load and injects reactive power, supporting low-voltage scenarios.

2.3. d-q Axis Decoupled Control Strategy

In this study, a standard d-q axis current control method was adopted. During nighttime operation, under the condition $I_d=0$ reactive power output is regulated by adjusting the $I_q$ component. The corresponding reactive power expression is given as

$$Q_i={\displaystyle \frac{3}{2}}{V}_i·I_{q,i}$$

(1)

$$\left|Q_i\right|\le Q_{max}=\sqrt{S_{rated}^2-P_i^2}$$

(2)

where

Q_i 

Reactive power output of inverter $i$.

V_i 

Output voltage magnitude of inverter $i$.

I_q,i 

q-axis current component.

Q_max 

Maximum reactive power capability.

S_rated 

Rated apparent power of the inverter.

P_i 

Active power output of inverter $i$.

Since $P_i=0$ during nighttime, the maximum available reactive power becomes

$$Q_{max}=S_{rated}$$

(3)

2.4. Dispatch Logic and Constraint Modeling

The inverter can dynamically adjust its reactive power output in response to grid conditions such as voltage fluctuations or load variations. These adjustments are typically driven by voltage monitoring and control algorithms that leverage the fast-response capabilities of the inverter. This dynamic reactive power compensation plays a critical role in maintaining the grid stability. In the GA optimization framework, the dispatch decision variable is defined as a binary vector.

$$b=[b_1,b_2,b_3\cdots ,b_n]; b_i\in \left\{\mathrm{0,1}\right\}$$

(4)

where $b_i=1$ indicates that inverter $i$ is activated to participate in reactive power dispatch. The algorithm determines the activation of each inverter based on the following criteria:

• The total reactive power requirement derived from voltage sensitivity analysis;
• Line loss minimization based on the distance to the substation and cable impedance;
• The reactive power limit $Q_i$ of each inverter, as defined by manufacturer specifications.

2.5. Nighttime Operating Modes of Inverters

Various high-voltage underground cables of different sizes are used in large-scale photovoltaic (PV) power plants. At night, the PV plants stop generating active power. Although the reactive power absorbed by distribution transformers is usually minimal, it may still cause slight voltage deviations. The equation for the capacitive reactive power with respect to the line voltage and cable length is

$$Q_c=V^2·\omega ·c^{\prime }·L$$

(5)

where

Q_c 

Capacitive reactive power (kVAR).

V 

Line voltage (kV).

ω 

Angular frequency ($2\pi f)$.

c′ 

Cable capacitance per unit length (F/km).

L 

Cable length (km).

The 22.8 and 161 kV underground cables provide reactive power to the system. The influx of a large amount of reactive power during nighttime increases the system voltage, thereby affecting power quality. In severe cases, it triggers the operation of the overvoltage protection relays. To mitigate this issue, the selected inverters are switched to night-time reactive power absorption mode. However, when implementing this mode, it is necessary to consider the associated line losses and the impact of distribution transformers.

3. GA for Reactive Power Optimization

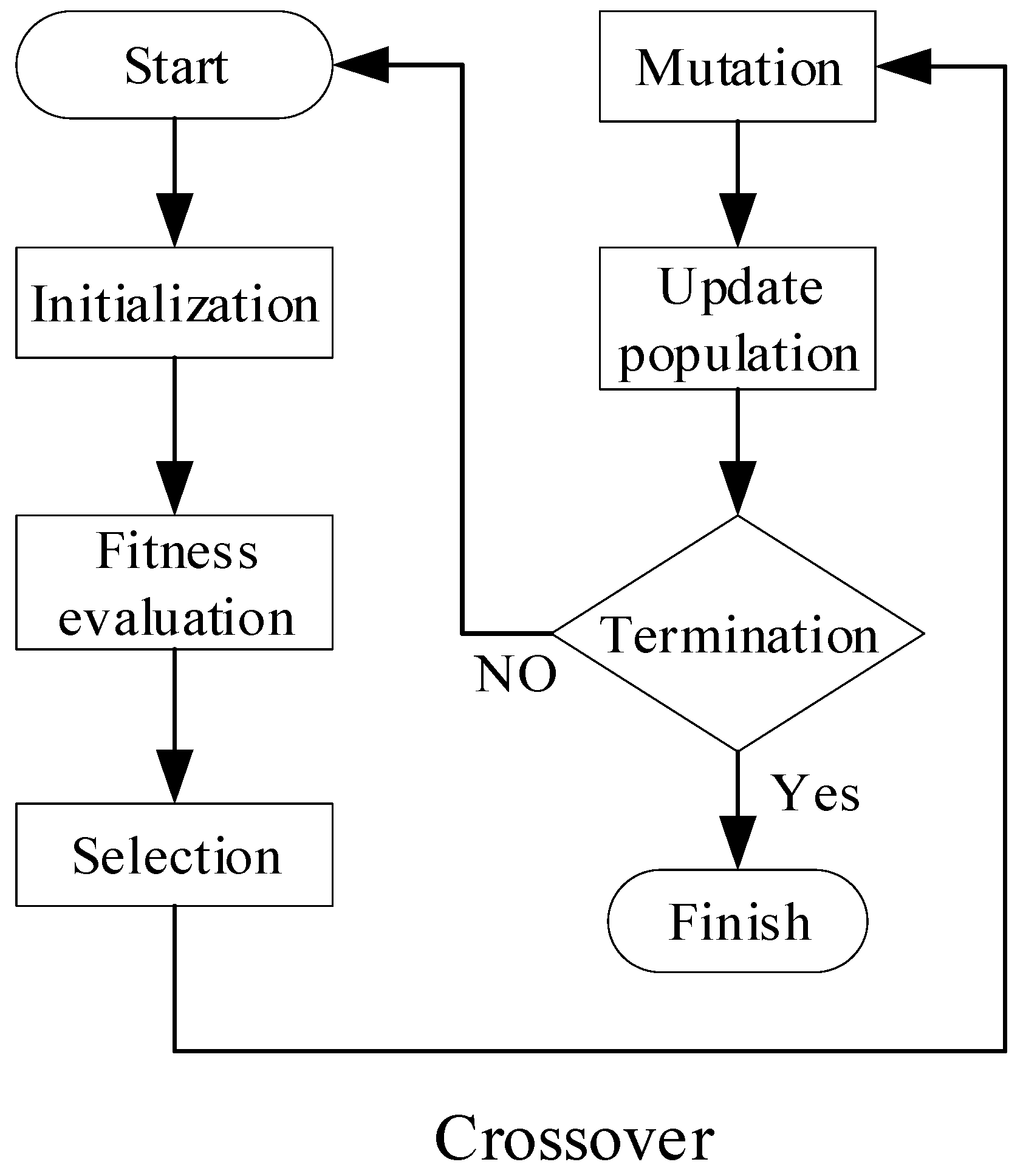
The GA is a learning algorithm that imitates biological processes. During the natural evolution of organisms, a group of individuals forms a generation (population) that reproduces individuals who can adapt to the environment and survive with a higher probability.

The GA process is illustrated in Figure 2 and consists of the following steps.

• The total reactive power requirement is first obtained via voltage sensitivity analysis;
• Fitness Evaluation: The fitness of each candidate solution is calculated based on the objective function and constraint conditions.
• Selection: Based on the fitness value, a subset of better candidate solutions is selected as the parent candidates for the next generation.
• Crossover: The selected parent candidates are combined to generate new candidate solutions.
• Mutation: Some candidate solutions are randomly modified to increase the diversity of solutions.
• Population Update: The old population is replaced with new candidate solutions, and the process is repeated.
• Termination Condition: The genetic algorithm terminates when a predefined stopping criterion is met (e.g., the maximum number of iterations or an adequately optimal solution is found).

In this study, we determined the optimal number of inverters to be dispatched and identified the specific regions in which the inverters were involved in reactive power compensation. To achieve this, we defined the objective function as follows:

$$F_1=\left|Q_{+}-Q_{Line}^{DTR}-Q_{-}\right|$$

(6)

$${F_2=(Line}_{loss})$$

(7)

$$Min({\omega }_1{F}_1+{\omega }_2{F}_2)$$

(8)

Constraints were defined as

$$Q_{-}=\sum _{i=1}^n{Q}_i$$

(9)

where

Q₊ 

Reactive power supplied by underground cables.

$Q_{Line}^{DTR}$

Reactive power absorbed by underground cables and distribution transformers during nighttime operation.

Q₋ 

Total reactive power absorbed by inverters during nighttime operation.

Line_loss 

$\sum _{j=1}^{m}3I_j^2{R}_j$. The line losses resulting from the participation of multi-task inverters.

n 

Number of inverters participating in reactive power compensation.

ω₁,ω₂ 

Weights (${\omega }_1=0.5, {\omega }_2=0.5$ in this study).

Q_i 

Amount of reactive power compensated for by inverter i.

F₁,F₂ 

Dimensionless (non-dimensionalized) objectives. $F_1$ was normalized with respect to the maximum nighttime reverse reactive power (2.8 MVAr), and $F_2$ was normalized with respect to the maximum line loss (2 kW). This non-dimensionalization removes the physical units, ensuring that both objectives are directly comparable.

The line loss base value of 2 kW corresponds to the maximum nighttime line loss (1.8235 kW) obtained from a random dispatch of 68 inverters (without optimization), along with a small safety margin.

In this study, the genetic algorithm (GA) was selected as the primary optimization method owing to the following advantages:

• The total reactive power requirement derived from voltage sensitivity analysis.
  The GA utilizes a population-based parallel search combined with stochastic mutation mechanisms, which enables it to effectively escape local optima. This characteristic makes it particularly well suited for addressing nonlinear and high-dimensional optimization problems, such as the complex combinatorial scheduling of inverter quantities and the spatial deployment considered in this research.
• Compatibility with mixed-variable problems.
  The GA requires only the evaluation of the objective function and does not rely on gradient information, allowing it to handle both discrete and continuous variables. This is especially advantageous for current applications that involve joint optimization of discrete inverter activation decisions and continuous reactive power outputs.
• The high degree of parallelizability.
  The independent evaluation of each chromosome in the population enables efficient parallel computation, making the GA particularly applicable to large-scale systems, such as the 1292-inverter PV plant studied in this work.

Moreover, although machine learning techniques, such as reinforcement learning and deep neural networks, have demonstrated strong performance in real-time control and highly uncertain environments, they typically require extensive offline training with large volumes of historical data. Because this study focuses on the static dispatch problem, such methods are not considered suitable.

4. Field Experiments and Results

A field experiment was conducted at a fully constructed and operational 120 MW photovoltaic (PV) power plant. The plant consists of 24 step-up substation units, and a two-stage voltage transformation process is adopted, where the inverter output voltage is boosted from 0.38 kV to 161 kV. The internal distribution system includes feeders and branch cables extending over 3 km, and the maximum capacity of the distribution transformers is 6500 kVA. In this study, a GA was employed to determine the optimal number and spatial allocation of inverters to be activated during nighttime operation with the aim of absorbing the reactive power backfeed into the grid while simultaneously minimizing line losses.

4.1. Parameter Settings

This study was conducted in a large-scale PV power plant equipped with 1292 inverters. A GA was applied to determine the optimal placement of inverters for reactive power compensation and to calculate the number of inverters that needed to be activated at night to offset the reactive power backfeed into the grid. The optimization process was implemented using MATLAB’s built-in GA function. The corresponding parameter settings are as follows:

• Initial population range: During the nighttime operation, the PV plant injected 2.8 MVAr of reactive power into the grid. Each inverter has a rated output of approximately 50 kVAr, corresponding to 56 inverters. The initial population range was set between 30 and 65 to ensure sufficient search diversity while accommodating possible variations in the inverter output during operation and to avoid excessively large initial values that could hinder the convergence of the algorithm.
• Population size: The population size was set to 1000 to avoid falling into local optima, provide a broader search space, and increase the probability of finding the global optimum;
• Crossover fraction: Since the locations of inverters to be activated in nighttime reactive power compensation were not easily identified, the crossover fraction of 0.9 was chosen to accelerate convergence and quickly identify the optimal solution;
• Mutation rate: The mutation step size was adaptively adjusted according to the population performance and constraint conditions, ensuring that the mutated individuals remain within the feasible solution space.
• Fitness evaluation: The fitness value of each candidate solution was calculated using the objective function. A lower fitness value indicates a better solution; therefore, it was calculated to determine the minimum number of inverters and minimize the line losses.
• Constraint tolerance: To solve problems involving nonlinear constraints, the allowable tolerance was set to 1 × 10⁻⁵.
• Maximum generation: Because the objective function is nonlinear, the maximum generation value was defined as 400 to ensure sufficient exploration time for identifying the optimal solution.

The selection of the above parameter values was based on preliminary tests, which balanced solution accuracy and computational efficiency. The optimization results also demonstrated robustness to small variations in parameter settings, indicating that the proposed method does not overly depend on specific parameter choices. Therefore, the GA performance is not overly sensitive to parameter tuning, ensuring the reliability of the optimization results.

4.2. Power Plant Equipment and Nighttime Reverse Reactive Power Output

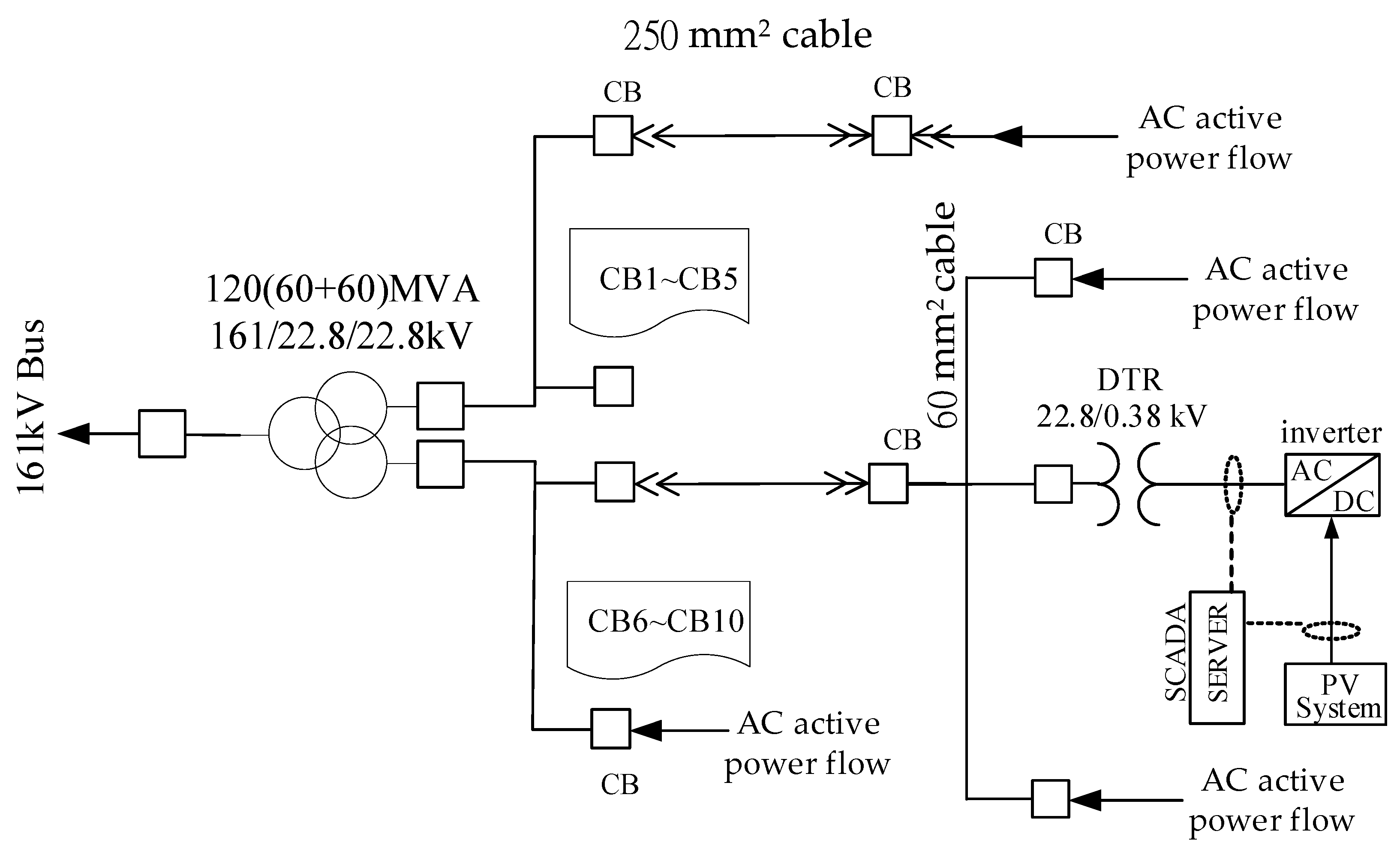
Figure 3 shows a single-line diagram of the monitored large-scale PV power plant. As shown, all the critical nodes from the DC side to the AC side are equipped with SCADA systems to enable real-time monitoring and data logging. The ultra-high-voltage underground cables used in the PV plant were rated 161 kV × 2000 mm², whereas the medium-voltage underground cables were rated 25 kV × 250 mm² and 25 kV × 60 mm². The plant is equipped with 24 step-up substation units, which are primarily used to boost the inverter output voltage from 0.38 kV to 22.8 kV. The impedance values of the associated equipment and distribution transformers (DTRs) are listed in

Table 3. Impedance characteristics of transformers and cables.

DTR. NO.	Breaker ID	S (kVA)	Transformer Impedance (PU%)	250 mm2 XLPE Cable Length (km)	250 mm2 Cable Resistance (Ω/km)	250 mm2 Cable Reactance (Ω/km)	60 mm2 XLPE Cable Length (km)	60 mm2 Cable Resistance (Ω/km)	60 mm2 Cable Reactance (Ω/km)	Overall Line Resistance (Ω)	Overall Line Reactance (Ω)
1	1A01-S1	6500	8	0.358	0.02585	0.0173	0.234	0.0709	0.0135	0.0967	0.0308
2	1A01-S3	4500	6	0.358	0.02585	0.0173	0.191	0.0579	0.0110	0.0837	0.0283
3	1A01-S7	5000	6	0.358	0.02585	0.0173	0.386	0.1170	0.0223	0.1428	0.0395
4	1A02-S1	5500	7	0.613	0.04426	0.0296	0.088	0.0267	0.0051	0.0709	0.0347
5	1A02-S3	3000	6	0.613	0.04426	0.0296	0.06	0.0182	0.0035	0.0624	0.0330
6	1A02-S7	4500	6	0.613	0.04426	0.0296	0.453	0.1373	0.0261	0.1815	0.0557
7	1A03-S1	6500	8	0.565	0.04079	0.0273	0.136	0.0412	0.0078	0.0820	0.0351
8	1A03-S3	6500	8	0.565	0.04079	0.0273	0.22	0.0667	0.0127	0.1075	0.0400
9	1A03-S7	6500	8	0.565	0.04079	0.0273	0.368	0.1115	0.0212	0.1523	0.0485
10	1A04-S1	6500	8	1.861	0.13436	0.0898	0.241	0.0730	0.0139	0.2074	0.1037
11	1A04-S3	6500	8	1.861	0.13436	0.0898	0.178	0.0539	0.0103	0.1883	0.1001
12	1A04-S7	5500	7	1.861	0.13436	0.0898	0.4	0.1212	0.0231	0.2556	0.1129
13	1B01-S1	4500	6	2.104	0.15191	0.1015	1.061	0.3215	0.0612	0.4734	0.1627
14	1B01-S3	5000	6	2.104	0.15191	0.1015	1.226	0.3715	0.0707	0.5234	0.1722
15	1B01-S5	4500	6	2.104	0.15191	0.1015	0.294	0.0891	0.0170	0.2410	0.1185
16	1B01-S7	5500	7	2.104	0.15191	0.1015	0.141	0.0427	0.0081	0.1946	0.1097
17	1B02-S1	5000	6	3.228	0.23306	0.1558	0.218	0.0661	0.0126	0.2991	0.1683
18	1B02-S3	5000	6	3.228	0.23306	0.1558	0.087	0.0264	0.0050	0.2594	0.1608
19	1B02-S7	6500	8	3.228	0.23306	0.1558	0.302	0.0915	0.0174	0.3246	0.1732
20	1B03-S1	5000	6	2.347	0.16945	0.1133	0.142	0.0430	0.0082	0.2125	0.1214
21	1B03-S3	4500	6	2.347	0.16945	0.1133	0.123	0.0373	0.0071	0.2067	0.1203
22	1B03-S7	4500	6	2.347	0.16945	0.1133	0.24	0.0727	0.0138	0.2422	0.1271
23	1B04-S1	4500	6	2.832	0.20447	0.1367	0.18	0.0545	0.0104	0.2590	0.1470
24	1B04-S3	6500	8	2.832	0.20447	0.1367	0.248	0.0751	0.0143	0.2796	0.1510

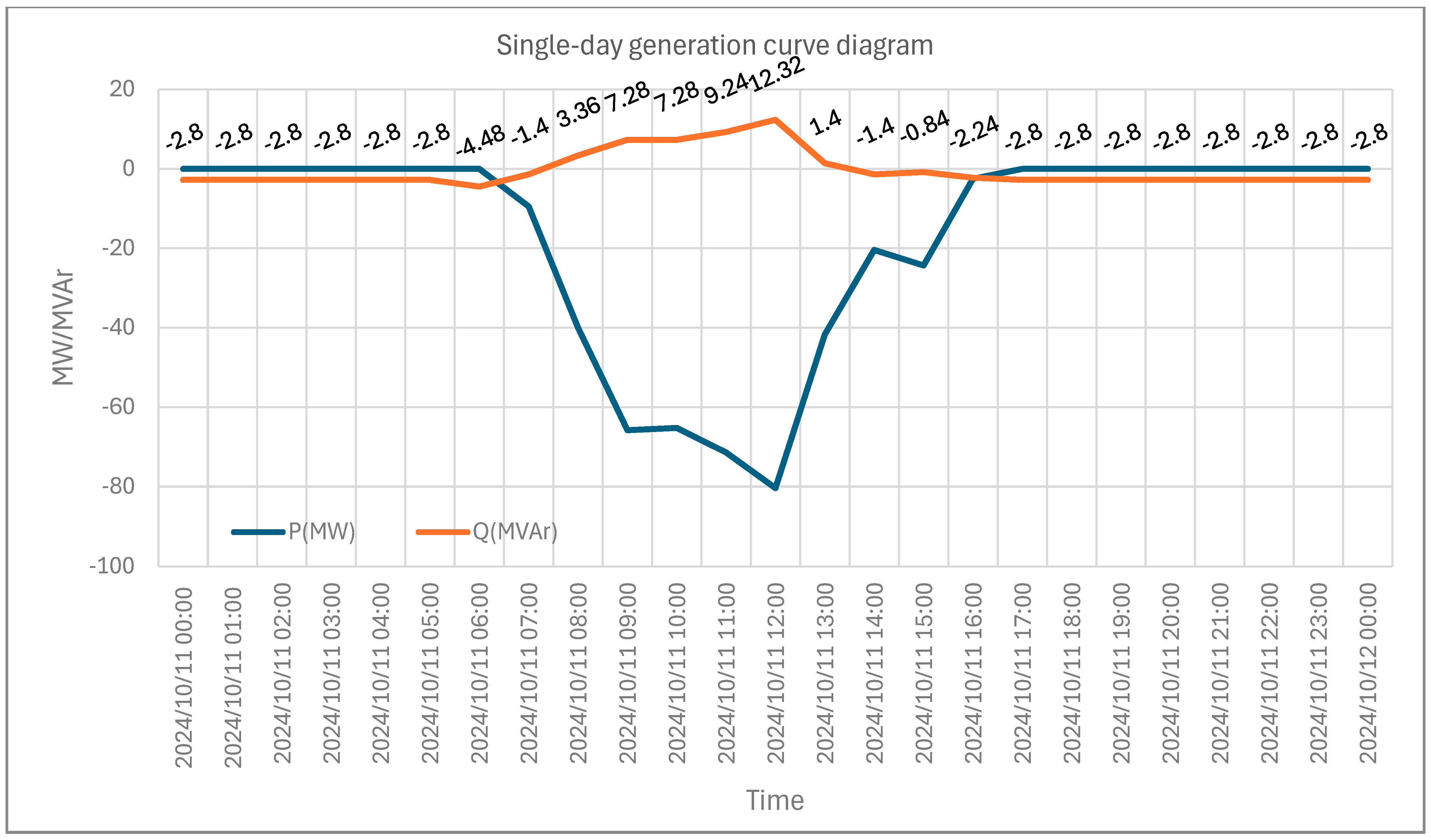
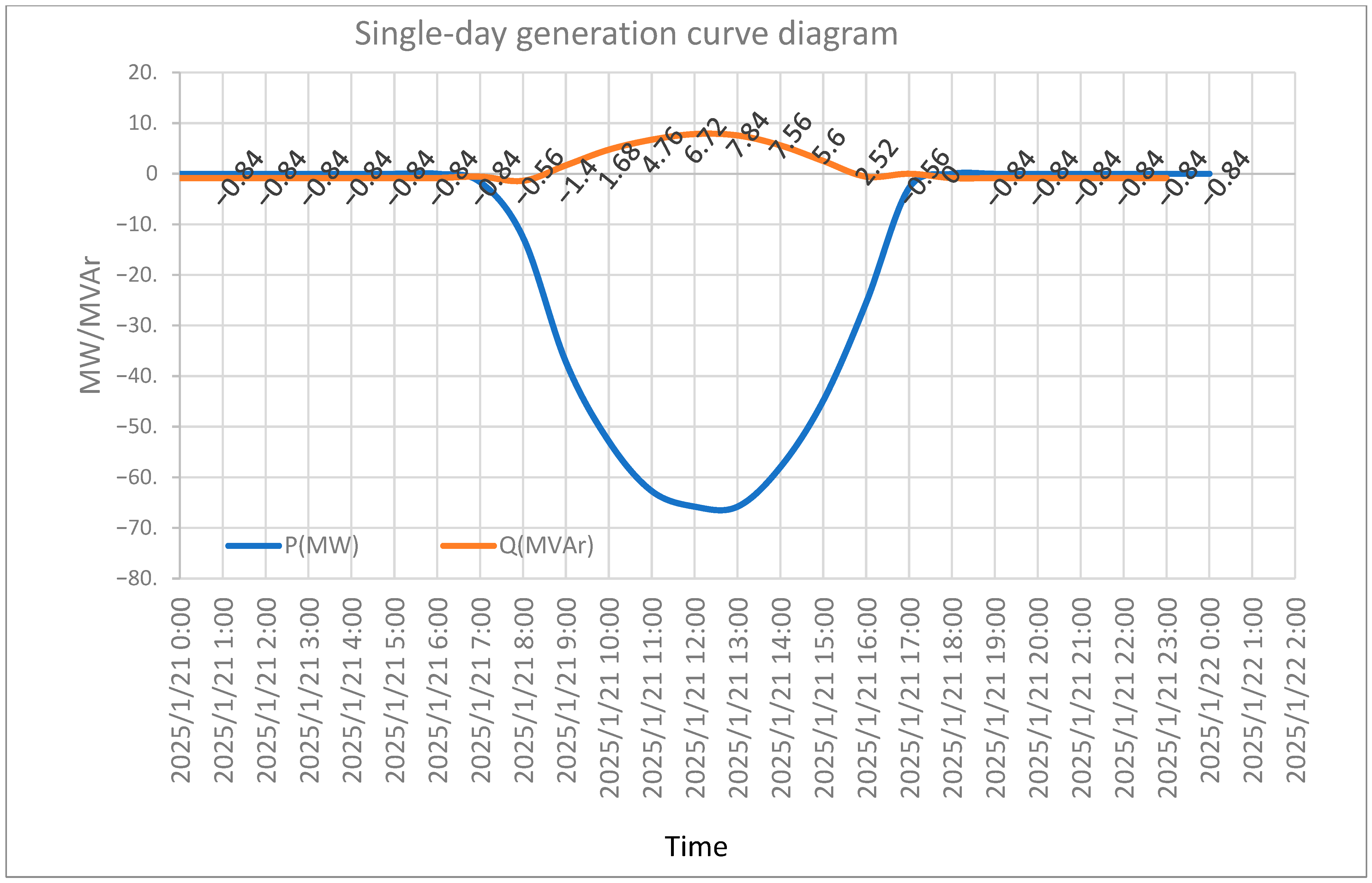
. Figure 4 shows the active and reactive power outputs of the PV power plant at the point of common coupling (PCC). All the data presented in the figure were obtained from the regional power dispatch center of the Taiwan Power Company. The symbol “—” indicates power flowing into the grid. During the non-generating period (from 18:00 to 6:00), the PV plant injected 2.8 MVAr of reactive power into the grid, which either violated the grid code requirements or raised concerns regarding the triggering of overvoltage protection mechanisms.

4.3. Field Measurement Analysis and Discussion

We compared the results obtained by randomly selecting the inverter locations with those optimized using the GA. Figure 5 shows the results during the non-generating period (18:00 to 06:00), where 68 inverters were randomly activated at DTR No. 7 in night-time reactive power absorption mode. The system was injected with an excessive 0.84 MVAr of reactive power (causing a shift from capacitive to inductive behavior), and line losses amounted to 1.8235 kW.

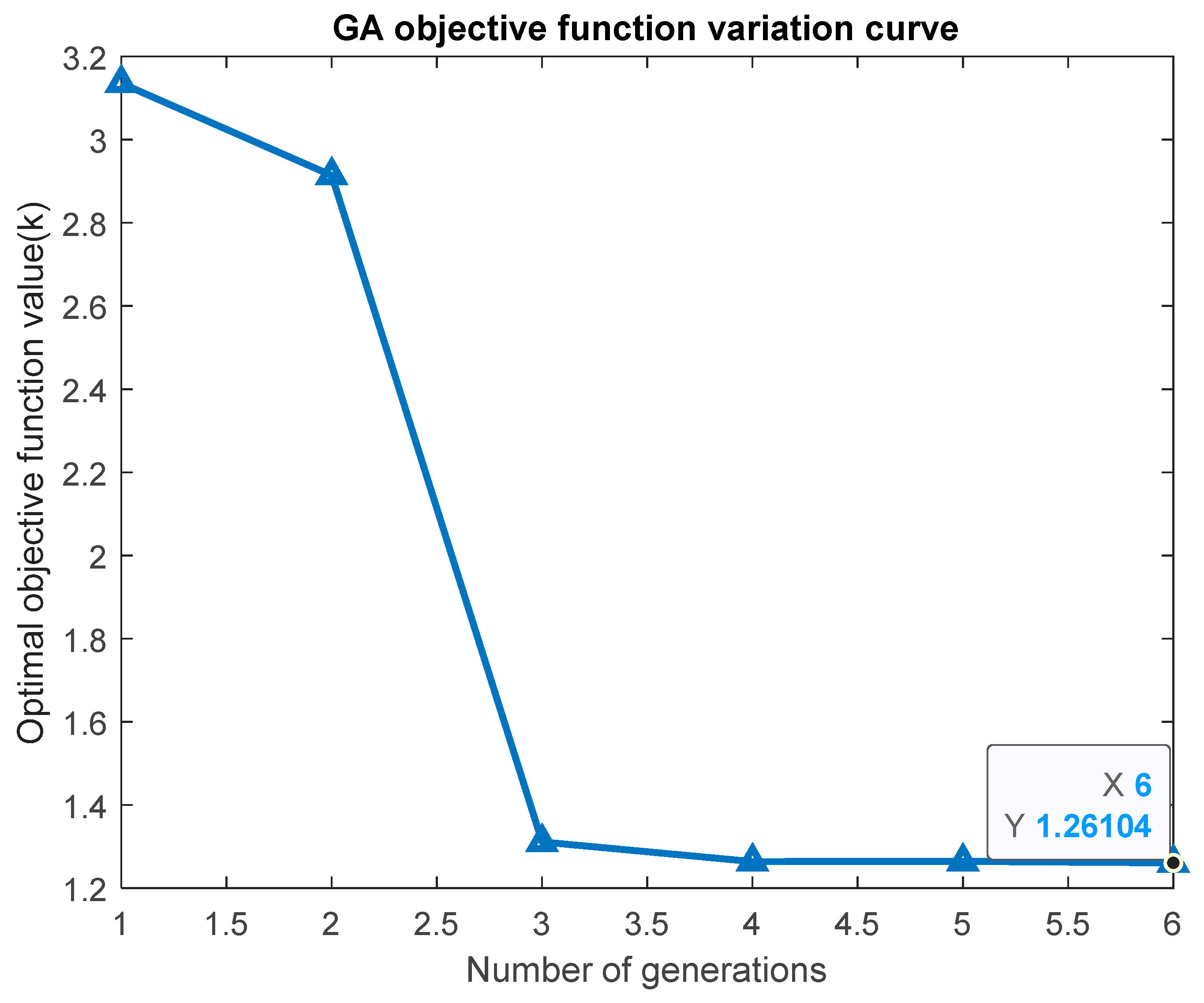
As shown in Figure 6, the GA reached convergence by the sixth generation, demonstrating that the optimization process was both stable and efficient. Therefore, the subsequent results were obtained using the solutions after convergence, ensuring the reliability of the inverter allocation strategy. The objective function value is 1.26104 k, which is significantly lower than that of the single inverter when the constraint tolerance is set to 0.00001. To enhance the convergence accuracy, the maximum number of generations was increased to 400, and the population size was set to 1000. Figure 7 illustrates the optimal number and locations of inverters determined by the GA: 11 inverters at DTR No. 2, 14 at DTR No. 4, and 30 at DTR No. 5, for a total of 55 inverters.

The GA selected DTRs Nos. 2, 4, and 5 as the optimal inverter groups, which is consistent with the electrical characteristics of the system. These transformers are relatively close to the PCC and have smaller line impedances; therefore, the reactive power injected at these points directly supports the bus voltage and reduces unnecessary reactive flows along the feeders, thereby lowering the line losses. Because the compensation efficiency is higher at these locations, fewer inverters must be activated to meet the nighttime reactive power requirements. This explains why the GA converged to these specific DTRs rather than to other locations. The reactive power backfeed to the grid at the point of interconnection was reduced to the ideal value of 0.00214 MVAr (Figure 8).

5. Discussion

This paper proposes a genetic algorithm (GA)-based inverter dispatch method for nighttime reactive power compensation in large-scale photovoltaic (PV) plants. Compared with the existing approaches, several scenarios require further discussion.

5.1. Comparison with Literature

Unlike previous studies [12,13], which mostly relied on theoretical or simulation analyses, this study validated the GA-based inverter dispatch method using real operational data from a 120 MW PV plant, thereby offering greater practical applicability. In addition to improving the voltage profiles, this study simultaneously incorporated the minimization of the nighttime reactive power backfeed and line losses, thereby providing a more comprehensive optimization strategy. It is worth emphasizing that the proposed method has already been field-tested and successfully implemented in a fully operational 120 MW PV power plant, which clearly distinguishes this work from purely simulation-based studies.

5.2. Comparison with Conventional SVC and STATCOM Solutions

According to an analysis by Thunder Said Energy (2022) [14], with the increasing penetration of renewable energy, the market demand for SVCs and STATCOMs could grow up to thirty-fold, with typical costs of approximately 100–150 USD/kVAR. This underscores the significant investment burden of traditional flexible AC transmission system (FACTS) equipment, in sharp contrast to the PV-STATCOM approach proposed in this study, which utilizes existing PV inverters. Although conventional SVCs and STATCOMs can effectively provide reactive power support, they require substantial capital investment, dedicated equipment, and sufficient installation space. As shown in Table 2, the proposed inverter dispatch method achieves an equivalent reactive power compensation capability with virtually no additional investment because it directly leverages the existing PV inverter infrastructure. This result demonstrates the clear advantages in terms of cost-effectiveness and operational simplicity, making it particularly suitable for large-scale PV plants.

5.3. Practical Considerations and Limitations

Although the proposed method has been validated with field data and is shown to be effective, its performance may still be influenced by the grid structure and inverter control capabilities. For example, in scenarios in which inverters do not support nighttime reactive power absorption, conventional SVCs or STATCOMs may still need to be implemented. Additionally, the proposed method has several advantages. The maintenance and safety risks are much lower compared with SVCs/STATCOMs installed at high or extra-high voltage levels because all reactive power compensation is carried out at the low-voltage side of the PV plant. Moreover, failures in SVCs or STATCOMs may trigger busbar differential protection (87B), potentially leading to a complete plant shutdown and substantial economic losses.

Overall, the GA-based optimization framework proposed in this study can effectively reduce the nighttime reactive power backfeed at the PCC and minimize line losses with virtually no additional investment, while demonstrating high adaptability in real-world PV plant operation.

6. Conclusions

Conventional reactive power compensators are constructed using passive components, such as inductors and capacitors, which are typically large and require substantial installation space. These devices are generally installed on the high-voltage or ultra-high-voltage sides of a system, necessitating the use of additional circuit-breakers. Limited available space is a significant challenge for installation in shared booster stations that are already in operation. Furthermore, traditional reactive power compensators often suffer from overcompensation or undercompensation, which makes it difficult to achieve precise reactive power control.

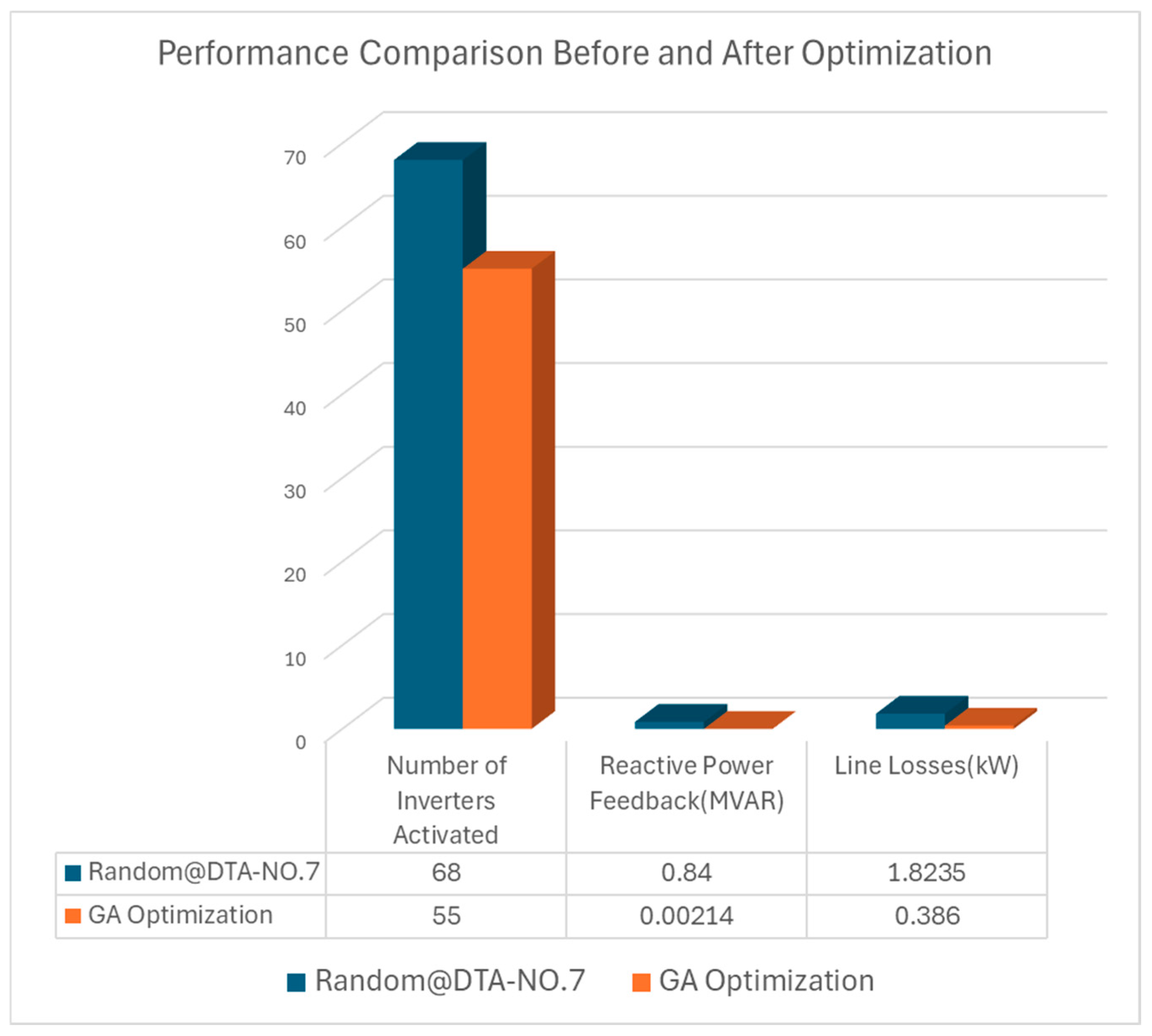
In this study, a GA was applied to determine the optimal number and placement of the inverters. A total of 55 inverters were activated in the nighttime reactive power compensation mode at the PV power plant where the experiment was conducted. Using this approach, the reactive power backfeed into the grid was significantly reduced to 0.00214 MVAr, and the line losses decreased from 1.8235 kW to 0.386 kW. A comparison of the system performance before and after optimization is shown in Figure 9.

The developed method was successfully implemented in a fully operational, large-scale PV power plant. The results demonstrated that the GA-based method effectively reduced the number of inverters required and minimized the line losses, thereby significantly lowering the operation and maintenance costs of the PV power plant while extending the service life of the inverters. The proposed strategy demonstrates strong applicability to the existing PV infrastructure and offers a cost-effective solution for reactive power control.

Future research will focus on integrating machine learning with inverter anomaly detection. In terms of machine learning, a Digital Twin (DT) framework can be employed to enable the real-time monitoring and dispatch of inverters, thereby realizing an economic dispatch model. For anomaly detection, techniques such as Principal Component Analysis (PCA) and one-class Support Vector Machines (OCSVMs) can be applied to identify inverters with reduced generation efficiency. Subsequently, multi-objective optimization methods may be employed to further enhance the overall system performance and power generation efficiency.