An NETD-Based Optimization Model for the Operating Range of a Staring Infrared System

Abstract

Operating range is an important indicator for determining the detection capability of an infrared search and track (IRST) system. To address the deficiencies of a traditional range model, such as excessive parameters and calculations, a noise-equivalent temperature difference (NETD)-based range optimization model for staring IRST systems is derived, offering a new solution method. Compared with traditional range models, the proposed model uses fewer parameters, fully considers the spectral radiation characteristics of the object and background and separately fits the integral part into a function related only to the range, which simplifies calculation and improves accuracy. The proposed operating range model is applied to a flying object for sample calculation, and the accuracy of the model is verified by field experiments.

1. Introduction

Infrared search and tracking (IRST) systems, as an example of passive detection technology, have significant applications in both military and civilian fields. They possess advantages such as strong concealment and excellent anti-interference capabilities, making them particularly suitable for modern battlefield environments. In IRST systems based on infrared focal plane imaging, several metrics are used to evaluate system performance, including specific detectivity (D*) [1], noise-equivalent temperature difference (NETD) [2,3,4], minimum resolvable temperature difference (MRTD) [5], and minimum detectable temperature difference (MDTD) [6]. Among these, D* and NETD are related only to the infrared system’s intrinsic characteristics, while MRTD and MDTD are observer-dependent and thus have a certain degree of subjectivity.

Operating range is one of the most critical factors determining system performance and is also the main metric for evaluating an infrared system’s performance [7,8]; therefore, deriving the infrared system range equation using D* and NETD offers good general applicability.

Since IRST system specifications typically provide the NETD but not the specific detectivity, it is not possible to directly utilize the specific detectivity-based operating range model for calculations. Therefore, a more convenient and effective method is to derive the NETD-based operating range model and use the NETD as a known parameter to calculate the operating range of an IRST system.

A large number of in-depth studies have been conducted on range models for infrared systems. The most classic range model equation was proposed by R. D. Hadson [9] in 1969; it is derived from D* and is simple to compute, but it does not account for the spectral radiative characteristics of the target, background, and atmospheric transmittance and is only applicable to point detectors, among its other limitations. The authors of [10] comprehensively considered the effects of background radiation and image blurring of the target and derived a range equation applicable to infrared focal plane detector systems, but this did not take into account the spectral radiative characteristics of the target, background, and atmospheric transmittance. The authors of [11] approximated the background spectral radiance using blackbody radiation laws, but still calculated the target using total band radiative intensity, ignoring the spectral radiative characteristics of the target and atmospheric transmittance. In [12], traditional calculation methods based on constant or average atmospheric transmittance were replaced with a method that divides the spectrum into equal intervals, taking into account the effect of irregular variations in atmospheric transmittance caused by spectrally selective atmospheric absorption on the effective range; however, this study was based on a point detector and did not consider the case of a staring detector. In 2021, Driggers et al. [13] introduced the pulse visibility coefficient into the range equation of infrared systems and analyzed the effects of factors such as jitter and noise on the effective range, but they did not take into account dispersion and other effects caused by the short-term random errors of the tracking system. The authors of [14] considered dispersion caused by short-term random errors on the basis of the previous work; their improved range-to-target model is relatively complete. Therefore, in the current paper, we select the model from Reference [14] for further improvement, obtaining an infrared system range equation based on NETD.

At present, there are three methods based on deriving the range equation. The derivation concept for the first method involves substituting the expression of the NETD into the $D*$-based range model of the IRST system to replace $D*$, finally obtaining the expression for the operating range. This method depends on the accuracy of the range expression based on D* itself; if the expression based on D* has large errors, it will greatly affect the accuracy of the infrared system range model based on NETD. The derivation concept for the second method is as follows: since the instantaneous field of view (FOV) of the IRST system is larger than the open angle of the object, the provided NETD should be corrected for the FOV, and the operating range should be calculated via the inverse square law of the FOV. For point detectors, the second method has smaller errors. However, for staring detectors, the operating range is determined by the pixel with the maximum response on the focal plane. Owing to the small size of a single pixel, the diffusion spot generated by the image of a point object could be larger than one pixel because of the effects of diffraction, aberration, and jitter. Therefore, using the second method could cause certain errors. Moreover, the relationship between atmospheric transmittance and wavelength is not considered in the derivation process of the second method. The third method uses the NETD to calculate the F-number of the system and then calculates the operating range based on the F-number. The solution process of the third method is complicated, and the number of response pixels on the focal plane is considered only when calculating the integration time, which is still not the same as the actual situation.

To address these deficiencies, this paper proposes an optimization model for the operating range of infrared systems based on NETD. First, the NETD expression based on the staring IRST system is derived. Then, the expression for the operating range is derived, and a normalization processing method is given for the solution. The solution process improves calculation accuracy by combining theoretical calculated values and actual measured values. Finally, a range model is used to carry out sample calculations on a flying object to validate the reliability of the range model, and the influence of NETD and focal length on the operating range is analyzed. The proposed model offers a reference for evaluating and analyzing the performance of IRST systems and the factors related to the operating range of the system.

2. Derivation of NETD Expression

NETD is defined as the temperature difference between the object and background at which the signal-to-noise ratio (SNR) for the system output is 1. This represents the minimum signal level from the observed target that infrared detector can detect [15]. In recent decades, J.M Lioyd [16], R.D.Hadson [9], Charles M. Hanson [17], Wu Xiaoping [18], Chen Rujun [19] and other scholars have proposed expressions for the NETD from different perspectives. These expressions are constructed based on the thermal detector or the focal plane detector, corresponding to different IRST systems. To fully consider influencing factors such as atmospheric transmittance and ensure the subsequently derived range equation is applicable to a staring IRST system, it is necessary to first derive the NETD expression.

The NETD is measured according to the method in Figure 1; therefore, the expression of the NETD could be derived based on Figure 1.

Spectral radiant power of the object received at the focal plane $P(\lambda )$ is given as follows:

$$P(\lambda )=E(\lambda )\cdot A_0\cdot {\tau }_0(\lambda )$$

(1)

where $E(\lambda )$ is the spectral irradiance, $A_0$ is the area of the entrance pupil of the optical system, and ${\tau }_0(\lambda )$ is the transmittance of the optical system.

The test blackbody is the Lambertian radiation source, and the inverse square distance law gives $E(\lambda )={\displaystyle \frac{J(\lambda ){\tau }_{\alpha }(\lambda ,R)}{R^2}}$ [20], where $J(\lambda )$ is the object spectral radiance intensity, ${\tau }_{\alpha }(\lambda ,R)$ is the atmospheric transmittance, and R is the distance from the test blackbody to the system. When measuring the NETD, the blackbody is very close to the focal plane; therefore, the atmospheric transmittance is negligible. The transmittance of the optical system can be approximately considered a constant, ${\tau }_0$.

Substituting into the equation gives

$$P(\lambda )={\displaystyle \frac{J(\lambda ){\tau }_0}{R^2}}\cdot A_0$$

(2)

$J(\lambda )={\alpha }^{\prime }{\beta }^{\prime }{R}^{2}L(\lambda )$, where ${\alpha }^{\prime }{\beta }^{\prime }$ indicates that the solid angle is subtended by the optical system with respect to the edge of the object, $L(\lambda )$ represents the spectral radiance of the object, and $A_0$ is the effective light transmission area of the optical system.

Substituting this into Equation (2) gives

$$P(\lambda )={\alpha }^{\prime }{\beta }^{\prime }L(\lambda ){\tau }_0{A}_0$$

(3)

For the staring IRST system, the focal plane is composed of N pixels. In the field measurement of the NETD, the image of the test blackbody on the focal plane accounts for approximately half of the focal plane, so the energy received by a single pixel is $2/N$ of the total energy received by the system. Since the radiation power difference between the object and the background causes the detector to respond, Equation (3) can be rewritten as follows:

$$\Delta P(\lambda )={\displaystyle \frac{2A_0\Delta L(\lambda ){\tau }_0{\alpha }^{\prime }{\beta }^{\prime }}{N}}$$

(4)

where $\Delta P(\lambda )$ is the spectral radiance power difference between the object and the background, and $\Delta L(\lambda )$ is the spectral radiance brightness difference between the object and the background.

When the temperature difference is not large, the difference can be written in differential form. Because temperature is not the only variable that affects the spectral radiance, it is written in the form of partial derivatives:

$$\Delta P(\lambda )=2A_0{\displaystyle \frac{\partial L(\lambda )}{N\cdot \partial T}}{\tau }_0{\alpha }^{\prime }{\beta }^{\prime }dT$$

(5)

The responsivity of the detector $\mathrm{R}$ [9,16] is calculated as follows:

$$\mathrm{R}={\displaystyle \frac{U_{n}D*}{{(A_d\Delta f)}^{\frac{1}{2}}}}$$

(6)

where $U_n$ is the noise RMS voltage of the detector, $A_d$ is the area of a single pixel, $\Delta f$ is the noise-equivalent bandwidth of the detector, and $D*$ is the specific detectivity. Therefore, the signal voltage generated by the detector $U_s$ is calculated as follows:

$$\begin{array}{cc}{U}_s& =\mathrm{R}{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\Delta P(\lambda )d\lambda }\hfill \\ & ={\displaystyle \frac{2U_{n}D*A_0{\tau }_0{\alpha }^{\prime }{\beta }^{\prime }}{N\cdot {(A_d\Delta f)}^{\frac{1}{2}}}}{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda dT}\hfill \end{array}$$

(7)

The SNR of the detection system is obtained as follows:

$${\displaystyle \frac{U_s}{U_n}}={\displaystyle \frac{2A_{0}D*{\tau }_0{\alpha }^{\prime }{\beta }^{\prime }}{N\cdot {(A_d\Delta f)}^{\frac{1}{2}}}}{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda dT}$$

(8)

According to the definition of the NETD, the temperature difference determined at the SNR = 1 is the NETD; therefore, Equation (8) can be changed to the following:

$${\displaystyle \frac{2A_{0}D*{\tau }_0{\alpha }^{\prime }{\beta }^{\prime }}{N\cdot {(A_d\Delta f)}^{\frac{1}{2}}}}{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda dT}=1$$

(9)

Therefore, the NETD is as follows:

$$NETD=dT={\displaystyle \frac{N\cdot {(A_d\Delta f)}^{\frac{1}{2}}}{2A_{0}D*{\tau }_0{\alpha }^{\prime }{\beta }^{\prime }{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda }}}$$

(10)

$A_0={\displaystyle \frac{\pi D_0^2}{4}}$, where $A_0$ is the effective light transmission area of the optical system and $D_0$ is the entrance pupil diameter of the optical system. Substituting this into Equation (10) gives

$$NETD={\displaystyle \frac{2N\cdot {(A_d\Delta f)}^{\frac{1}{2}}}{\pi D_0^{2}D*{\tau }_0{\alpha }^{\prime }{\beta }^{\prime }{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda }}}$$

(11)

As shown in Figure 1, the solid angle subtended by the optical system with respect to the edge of the object is equal to the solid angle spanned by the image formed on the focal plane. Since the image of the test blackbody on the focal plane accounts for approximately half of the focal plane, the open angle of the object to the system is as follows:

$${\alpha }^{\prime }{\beta }^{\prime }={\displaystyle \frac{N{A}_d}{2f^2}}$$

(12)

Substituting Equation (12) into Equation (11) gives

$$NETD={\displaystyle \frac{4f^2{(\Delta f)}^{\frac{1}{2}}}{\pi D_0^{2}D*{\tau }_0{A}_d^{\frac{1}{2}}\cdot {\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda }}}$$

(13)

Equation (13) is the NETD expression for the staring IRST system.

From the derivation above, it can be seen that the NETD expression is based on the following two assumptions:

(1)

The temperature difference between the object and the background is very small, and the background is uniform. Therefore, $∆$T can be approximated as dT, simplifying the calculation.

(2)

The specific detectivity D* is independent of other parameters related to NETD expression. Therefore, D* can be taken out of the integral as a constant term to simplify the calculation.

This indicates that NETD reflects an infrared search and track system’s performance in measuring small temperature differences and extended targets.

From reference [15], the magnitude of the infrared system NETD reflects the system’s noise characteristics; NETD can also be analyzed and derived from the perspective of system noise. Because staring infrared focal plane detectors exhibit charge-trap responses and have certain memory effects, detector noise can be analyzed and treated using fractional-order derivatives [21].

3. NETD-Based Operating Range Equation of the Staring IRST System

The NETD expression derived above takes into account the factors of distant small targets and atmospheric transmittance; below we further derive the infrared system range equation based on NETD.

3.1. Derivation of the Operating Range Equation

The derivation of the traditional effective range model is based on the assumption of uniform energy distribution: it is assumed that the target radiation falling on the focal plane is entirely received by the target pixels and that each responding pixel receives exactly the same target radiation. Therefore, the target radiation received by a single target pixel is 1/n of the total target radiation; thus, multiplying the single-detector infrared system range model by 1/n yields the staring IRST system range model. However, when the target is at a distance beyond the effective range of the rangefinder, it can be regarded as a point target; its image on the focal plane is a blur spot whose size is determined by diffraction and aberrations [22]. The scattering spot may be located at the center of a pixel or in the inactive area between pixels, thereby affecting the efficiency with which the target’s radiation is received by the pixel. The derivation in reference [14] explains the impact of speckle via the pulse visibility factor (PVF) and describes the effect of short-term random tracking errors by the number of pixels the target occupies in the focal plane.

From Ref. [14], the available range model of an IRST system based on D* is as follows:

$$R^2={\displaystyle \frac{\pi D_0^{2}D*{\tau }_0\delta }{4n\sqrt{A_d\cdot \Delta f}\cdot R_{SN}}}\cdot {\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}[J_t(\lambda )-N_b(\lambda )\cdot A]\cdot P_V(\lambda )\cdot {\tau }_{\alpha }(\lambda ,R)d\lambda }$$

(14)

where $J_t$ is the object radiation intensity; $L_b$ is the background radiance; ${\tau }_a(\lambda ,R)$ is the atmospheric transmittance; $\Delta f$ is the effective noise bandwidth; $R_{SN}$ is the SNR of the IRST system; $\delta$ is the signal processing factor; D* is the specific detectability; A is the effective radiation area of the object; n is the number of pixels occupied by the object on the focal plane; and $P_V$ represents the pulse visibility factor (PVF) (for its definition, please refer to Ref. [23]).

Simultaneously treating Equations (13) and (14) gives the NETD-based operating range equation of the staring IRST system:

$$R^2={\displaystyle \frac{f^2\delta }{NETD\cdot A_d\cdot n\cdot R_{SN}}}\cdot {\displaystyle \frac{{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}[J_t(\lambda )-L_b(\lambda )\cdot A]\cdot P_V(\lambda )\cdot {\tau }_{\alpha }(\lambda ,R)d\lambda }}{{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda }}}$$

(15)

A comparison of Equations (14) and (15) reveals that the NETD-based operating range equation of the staring IRST system requires fewer parameters, and only NETD, $f$ $\delta$, $A_d$, and $R_{SN}$ are related to the IRST system, while D* $D_0$ ${\tau }_0(\lambda )$ and other parameters are eliminated. The infrared system range expression shown in Equation (14) requires parameters such as the optical system’s entrance aperture diameter and the optical system transmittance, all of which must be measured separately, making it inconvenient to use.

From Equation (15), the detection sensitivity of the infrared system is measured by NETD; if the temperature difference between the target and the background is smaller than the NETD value, the target signal will be treated as background noise and discarded, and in that case, no effective range exists. With the target radiance and background radiance unchanged, the operating range R is uniquely determined by the NETD, which indicates that, at this distance, the optical power emitted by the target reaching the detector equals the optical power from the test body corresponding to the NETD temperature difference, and the system can just discern the target. Therefore, the value of R determines the maximum effective range of the infrared system for a given target and background.

3.2. Calculation of the Test Blackbody Radiance

The radiance of the test blackbody satisfies Planck’s law; therefore,

$${\displaystyle \frac{\partial L(\lambda )}{\partial T}}={\displaystyle \frac{\partial }{\partial T}}\left({\displaystyle \frac{c_1}{\pi {\lambda }^5(e^{\frac{c_2}{\lambda T}}-1)}}\right)={\displaystyle \frac{e^{\frac{c_2}{\lambda T}}{c}_1{c}_2}{\pi {\lambda }^6{T}^2{\left(e^{\frac{c_2}{\lambda T}}-1\right)}^2}}={\displaystyle \frac{c_2{e}^{\frac{c_2}{\lambda T}}\cdot L(\lambda )}{\lambda T^2\left(e^{\frac{c_2}{\lambda T}}-1\right)}}$$

(16)

where $c_1$ is the first radiation constant, $c_1=2\pi h{c}^2=3.7415\times {10}^8(\mathrm{W}\cdot {\mathsf{\mu }\mathrm{m}}^4{/\mathrm{m}}^2)$, and $c_2$ is the second radiation constant, $c_2=hc/k=1.43879\times {10}^4(\mathsf{\mu }\mathrm{m}\cdot \mathrm{k})$. Equation (16) cannot be directly integrated and must be simplified. Owing to the small temperature difference between the measured blackbody and the ambient temperature, $e^{{\displaystyle \frac{c_2}{\lambda T}}}$ is very large, so $e^{{\displaystyle \frac{c_2}{\lambda T}}}$ is approximately equal with $\left(e^{{\displaystyle \frac{c_2}{\lambda T}}}-1\right)$, and Equation (16) can be reduced to

$${\displaystyle \frac{\partial L(\lambda )}{\partial T}}={\displaystyle \frac{c_2\cdot L(\lambda )}{\lambda T^2}}$$

(17)

Thus,

$${\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{\partial L(\lambda )}{\partial T}d\lambda }={\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}\frac{c_2\cdot L(\lambda )}{\lambda T^2}d\lambda }\approx {\displaystyle \frac{c_2}{{\lambda }_1{T}^2}}\cdot {\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}L(\lambda )d\lambda }$$

(18)

From Equation (18), the integral can be conveniently calculated by knowing the temperature of the test blackbody.

3.3. Solution Method for the Operating Range Model

Section 3.2 presents the calculation method for the radiance of the test blackbody in the 3–5 μm band, which is used in the range equation of the IRST system. However, there is also an integral with respect to the wavelength in Equation (15) (denoted as $U(R)$), as shown in Equation (19), which is more difficult to solve directly.

$$U(R)={\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}[J_t(\lambda )-L_b(\lambda )\cdot A]\cdot P_V(\lambda )\cdot {\tau }_{\alpha }(\lambda ,R)d\lambda }$$

(19)

3.3.1. Calculation of Object Spectral Radiation Characteristics

In the industrial temperature range (typically below 2000 K), the emissivity of many materials varies little within the infrared band and can be approximated as a constant [24]. Therefore, such targets can be treated approximately as gray bodies, and the Planck formula can be used to approximate the target’s spectral radiance. In this case, the target spectral radiance $J_t(\lambda )$ is obtained as follows:

$$J_t(\lambda )={\displaystyle \frac{\epsilon A{c}_1}{\pi {\lambda }^5(e^{\frac{c_2}{\lambda T_t}}-1)}}$$

(20)

where $\epsilon$ is the emissivity, $A$ is the effective radiation area of the object, and $T_t$ is the object surface temperature.

Flying objects, such as aircraft and rockets, have three radiation characteristics: skin radiation, nozzle radiation, and tail flame radiation [14]. The three types of radiation intensities need to be calculated separately and then summed to obtain the object’s overall radiation intensity. Notably, because the main radiation of this type of flying object includes the nozzle radiation and tail flame radiation, the radiation intensity of the object observed from different directions is quite different. The skin radiation and nozzle radiation can be approximately calculated via Equation (20), whereas the calculation of the tail flame radiation is more complicated, and simulations can be performed with the models developed in Refs. [25,26,27].

3.3.2. Calculation of Background and Atmospheric Transmittance

The background radiance and atmospheric transmittance are related to the site environment. Taking clear-sky ground conditions as an example, background radiation is composed mainly of solar radiation, atmospheric radiation, and surface object radiation, as shown in Figure 2.

During the daytime and at wavelengths less than 4 μm, the IR radiation of surface objects is related to the reflectance of sunlight and the materials that constitute the surface objects. When the wavelength is longer than 4 μm, the IR radiation of surface objects mainly comes from their own thermal radiation. The thermal radiation of surface objects is related to their temperature and emissivity, and most surface objects have a higher emissivity [20]. Because the sky temperature varies with height, the calculation of atmospheric IR radiation is more complicated, and layering theory is currently used [28].

Atmospheric transmittance is an important environmental parameter for calculating the operating range of an IRST system. Many factors affect the atmospheric transmittance, and the calculation is relatively complicated. At present, radiative transfer models, such as DISORT (DIScrete Ordinate Radiative Transfer), ARTS (Atmospheric Radiative Transfer Simulator), LOWTRAN (LOW-resolution atmospheric TRANsmittance model), and MODTRAN (MODerateresolution atmospheric TRANsmission), are primarily used to calculate atmospheric transmittance [29,30].

In this study, MODTRAN software was used to calculate background radiance and atmospheric transmittance. MODTRAN uses wavenumbers to characterize electromagnetic waves, and the unit is cm⁻¹. When the mid-wave IR band is selected for calculation, the wavenumber corresponding to 3–5 μm is in the range of 2000–3333 cm⁻¹. The MODTRAN calculation step size is 1 cm⁻¹, the calculation accuracy is high, and MODTRAN can precisely characterize the spectral characteristics of atmospheric transmittance and background radiation. The atmospheric transmittance data obtained by the MODTRAN software are saved in a .txt file and can also be exported as an Excel file. The model atmospheric parameters, aerosol parameters, and geometric path parameters are input to calculate the background spectral radiance.

3.3.3. Normalization Method

It is difficult to solve Equation (19) directly. Additionally, based on the method described in Section 3.3.1 and the theoretical calculation performed by MODTRAN software, results often have certain errors. In this paper, we use the normalization method. First, the object radiation intensity obtained from the theoretical calculations $J_t(\lambda )$ and the background radiance $L_b(\lambda )$ are normalized to obtain the normalized object radiation intensity $J_t^{*}(\lambda )$ and the normalized background radiance $L_b^{*}(\lambda )$, respectively. Equation (21) shows the mathematical expression of normalization processing:

$$\begin{array}{l}{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{J}_t(\lambda )d\lambda }=J_t{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{J}_t^{*}(\lambda )d\lambda }\\ {\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{L}_b(\lambda )d\lambda }=L_b{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{L}_b^{*}(\lambda )d\lambda }\end{array}$$

(21)

The value of $J_t$ is the reading of the infrared radiometer; it is different from the overall spectral radiative characteristics because the radiometer performs an integrated measurement over the entire mid-wave infrared range (3–5 μm), reflecting the overall radiative intensity within the mid-wave band. By multiplying by the normalized spectral radiant intensity computed using Planck’s law, the target’s spectral radiant intensity is obtained, allowing the target’s spectral characteristics to be reconstructed. The value of $L_b$ uses the actual measurements from the all-sky background radiometer and likewise requires restoring the spectral characteristics of the background based on the normalized spectral radiance. $J_t$ and $L_b$ are substituted back into the integral part, different R values are set for separate calculations, and finally an expression is fit for the integral part. This processing method aims to quantify the proportion of target radiation intensity and background radiation brightness under different wavelengths to their actual radiation intensity or brightness, while taking into account both theoretical calculations and actual measurement results, improving the accuracy of the calculation.

Substituting this into Equation (19) gives the following:

$$U(R)=J_t{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{J}_t^{*}(\lambda )\cdot P_v\cdot {\tau }_{\alpha }(\lambda ,R)d\lambda }-A\cdot L_b{\displaystyle {\int }_{{\lambda }_1}^{{\lambda }_2}{L}_b^{*}(\lambda )\cdot P_v\cdot {\tau }_{\alpha }(\lambda ,R)d\lambda }$$

(22)

Considering that the results calculated by MODTRAN are all discrete points with a step size of 1 cm⁻¹, the ${\lambda }_1\sim {\lambda }_2$ interval is divided into n equal parts with $\Delta \lambda ={\lambda }_{i+1}-{\lambda }_i$ as the step, and the integral is changed to the following summation:

$$U(R)=J_t{\displaystyle \sum _{i=0}^{n-1}{J}_t^{*}({\lambda }_i)\cdot P_V({\lambda }_i)\cdot {\tau }_{\alpha }({\lambda }_i,R)\cdot \Delta \lambda }-A\cdot L_b{\displaystyle \sum _{i=0}^{n-1}{L}_b^{*}({\lambda }_i)\cdot P_V({\lambda }_i)\cdot {\tau }_{\alpha }({\lambda }_i,R)\cdot \Delta \lambda }$$

(23)

where $J_t^{*}({\lambda }_i)$ represents the normalized spectral radiance intensity of object at wavelength ${\lambda }_i$; $L_b^{*}({\lambda }_i)$ represents the normalized background spectral radiance at wavelength ${\lambda }_i$; ${\tau }_{\alpha }({\lambda }_i,R)$ is the atmospheric spectral transmittance at wavelength ${\lambda }_i$; and $P_V({\lambda }_i)$ is the PVF at wavelength ${\lambda }_i$.

From Equation (23), $U(R)$ is composed of two terms. The first term is written as $U_t(R)$, and the second term is written as $U_b(R)$:

$$\begin{array}{l}{U}_t(R)={\displaystyle \sum _{i=0}^{n-1}{J}_t^{*}({\lambda }_i)\cdot P_V({\lambda }_i)\cdot {\tau }_{\alpha }({\lambda }_i,R)\cdot \Delta \lambda }\\ U_b(R)={\displaystyle \sum _{i=0}^{n-1}{L}_b^{*}({\lambda }_i)\cdot P_V({\lambda }_i)\cdot {\tau }_{\alpha }({\lambda }_i,R)\cdot \Delta \lambda }\end{array}$$

(24)

Substituting these into Equation (23) gives

$$U(R)=J_t\cdot U_t(R)-A\cdot L_b\cdot U_b(R)$$

(25)

By substituting the measured and calculated quantities into Equation (24) and setting different values of R, the corresponding $U_t(R)$ and $U_b(R)$ values can be calculated. The relationship curves of $U_t(R)$ and $U_b(R)$ with R are plotted, the analytical expressions of $U_t(R)$ and $U_b(R)$ with R are obtained by fitting, and substituting the expressions into Equation (25) gives the analytical expression of $U(R)$ for R. Substituting the analytical expression into Equation (15) gives the operating range equation without integration, thus reducing the computational complexity.

4. Action Distance Model Example Calculation

4.1. IRST System Parameters

A staring IRST system is used for example validation. Some parameters of the IRST system are presented in

Table 1. Parameters for the IRST system.

Name	Value
NA	0.25
$R_{SN}$	7.65 (the minimum value)
d	15 μm
$\delta$	0.25
${\tau }_0$	0.7
NETD	25 mK
D0	90 mm
$d_{cc}$	15 μm

, where NA is the numerical aperture of the optical system, N is the number of arrays, d is the pixel size, and $d_{cc}$ is the pixel spacing.

From Table 1, the F-number and focal length of the optical system are as follows:

$$F^{\#}={\displaystyle \frac{1}{2NA}}=2$$

(26)

$$f=F^{\#}\cdot D_0=180 \mathrm{mm}$$

(27)

The area of a single pixel $A_d$ is as follows:

$$A_d=15 \mathsf{\mu }\mathrm{m}\times 15 \mathsf{\mu }\mathrm{m}=2.25\times {10}^{-10} {\mathrm{m}}^2$$

(28)

The focal plane fill factor FF is as follows:

$$FF={\left({\displaystyle \frac{d}{d_{cc}}}\right)}^2=100\%$$

(29)

According to Ref. [13], when the FF is 100%, the fitted expression of the focal plane average PVF is as follows:

$$P_V(\lambda )=0.0335+0.9665e^{-0.887\left({\displaystyle \frac{F\lambda }{d_{cc}}}\right)}$$

(30)

When the operating range of the IRST system is evaluated, the object is considered a point object, and its open angle to the optical system is less than one pixel, so the object linearity is not considered. The minimum number of pixels that can cause the system to respond is 9, so n = 9.

For the reference standard of the NETD test on an IRST system [31], the 308K blackbody was chosen to test the NETD in this study, and the radiance of the test blackbody could be calculated via Equation (18).

4.2. Field Experiment Process

A helium balloon with a small carbon furnace was used as an object for measurement. Since the radiation of a small carbon furnace in the 3–5 μm band is much greater than that of a helium balloon, the test object is a small carbon furnace with a temperature of 623 K and an effective radiation area of approximately 0.1 m² and can be treated as a gray body with an approximate emissivity of 0.9. The object flight height is 180 m.

The test was conducted at 2:00 pm on 1 October 2024. The visibility of the atmosphere was 10 km, the relative humidity was 80%, there were no clouds or rain, and the ambient temperature was 23 °C. The solar zenith angle was 47.36°, and the azimuth angle was 222°.

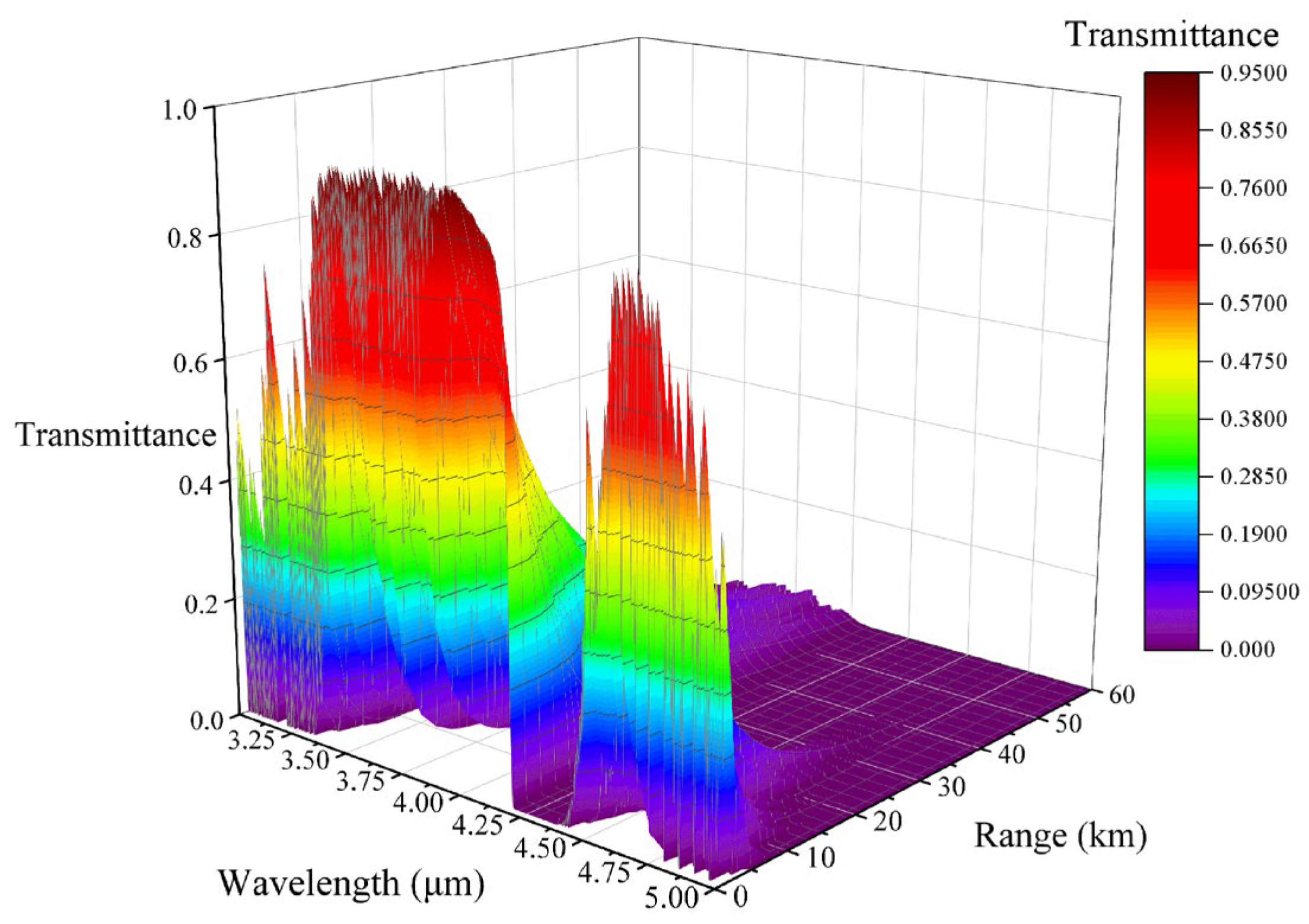
MODTRAN was used to calculate the atmospheric spectral transmittance in the 3–5 μm band at different distances. The distance was set from 10 km to 100 km, with a step size of 2 km. The MODTRAN input parameters are shown in

Table 2. MODTRAN parameter settings (atmospheric transmittance).

Input Parameters	Values of Parameters
Calculation Option	MODTRAN
Model Atmosphere	Mid-latitude Summer
Type of Atmospheric Path	Slant Path
Mode of Execution	Transmittance
Water Column	6000 atm-cm
CO2 Mixing Ratio	420 ppmv
Aerosol Model Used	Rural − VIS = 23 km
Surface Meteorological Range (VIS)	10 km
Ground Altitude Above Sea Level	0.037 km
Use Cloud/Rain Aerosol Extensions	No Clouds or Rain
Observer Height	2 m
Final Height	180 m

.

The calculation result is shown in Figure 3:

MODTRAN software exhibits discernible deviations between calculated atmospheric transmittance and actual environmental conditions. Primarily, the model employs standardized atmospheric profiles by default, whereas real-world vertical distributions of atmospheric constituents (such as CO₂, O₃, and CH₄) are significantly influenced by monsoon dynamics and anthropogenic activities. Secondly, the model’s computation of aerosol and cloud scattering relies on the “spherical particle assumption,” yet most actual aerosol particles and cloud hydrometeors are non-spherical, leading to inaccuracies in scattering coefficient calculations. Furthermore, the computational results of MODTRAN are highly dependent on input parameters, where errors in these parameters propagate through the system, thereby amplifying the discrepancy between MODTRAN’s outputs and actual measurements. Where feasible, employing daily vertical profiles from radiosonde stations to replace standard profiles, alongside measured aerosol optical depth (AOD) and particle size distributions from ground-based sun photometers instead of default aerosol types, can enhance the alignment of MODTRAN simulations with empirical conditions.

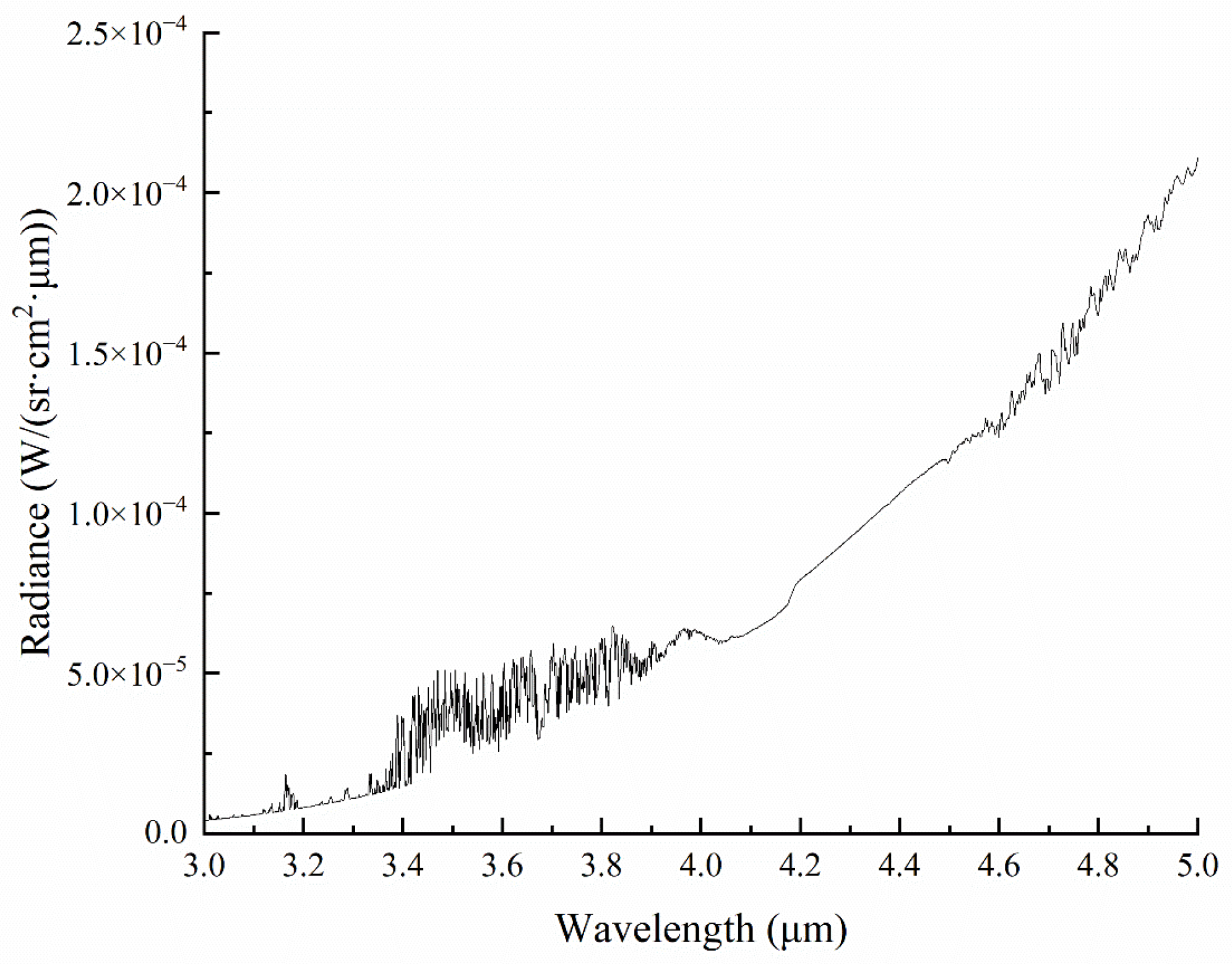
Under the same environmental conditions, the background spectral radiance was calculated via MODTRAN. The input parameters of MODTRAN are shown in

Table 3. MODTRAN parameter settings (radiance).

Input Parameters	Values of Parameters
Calculation Option	MODTRAN
Model Atmosphere	Mid-latitude Summer
Type of Atmospheric Path	Slant Path to Space or Ground
Mode of Execution	Radiance with Scattering
Water Column	6000 atm-cm
CO2 Mixing Ratio	420 ppmv
Temperature at First Boundary	298 K
Aerosol Model Used	Rural − VIS = 23 km
Surface Meteorological Range (VIS)	10 km
Ground Altitude Above Sea Level	0.037 km
Use Cloud/Rain Aerosol Extensions	No Clouds or Rain
Observer Height	2 m
Zenith Angle	83.11°
Day of Year	275
Extraterrestrial Source	Sun
Sun Zenith Angle	42.64°

.

The calculation result is shown in Figure 4:

From Figure 4, it can be seen that the background spectral radiance in the mid-wave band generally increases with increasing wavelength, but there is an oscillatory waveform at 3.4–3.9 μm, which emerges because the main absorbers in the atmosphere are water vapor (H₂O), carbon dioxide (CO₂), and ozone (O₃). These molecules, because of their vibrational–rotational energy level structures, strongly absorb or emit infrared radiation from the surface, the sun, and the molecules themselves at specific wavelengths, creating a series of characteristic absorption and emission lines. Water vapor molecules exhibit significant absorption bands near 3.2 μm and 3.7 μm [32], while carbon dioxide molecules and ozone molecules contribute less to the absorption in the 3.4–3.9 μm band [33,34]. Therefore, introducing normalized spectral radiance into the calculations can fully account for the effects of water vapor molecules in the 3.4–3.9 µm range, improving calculation accuracy.

The infrared radiometer measured the target radiance as 1.953 W·sr⁻¹. A mobile platform was set up, with the infrared system placed at the center of the platform and two automatic sun and sky photometers positioned on either side of the infrared system, the photometer optical heads oriented the same as the infrared detector. The sky background radiance measurements in the midwave range are obtained from the two photometers on the PC and the average is taken as the final result. The automatic sun and sky photometers measured the background radiance near the target as 1.57 ${\mathrm{W}/(\mathrm{m}}^2\cdot \mathrm{Sr})$. The initial horizontal distance between the mobile platform and the hot-air balloon launch site was 15 km. When the target rose to the predetermined altitude, the platform was moved in the direction away from the hot-air balloon until the infrared system could no longer just detect the target.

The experiment used the Hi-Target iRTK5 intelligent RTK system for auxiliary distance measurements. This system performs distance measurement based on GPS differential methods and supports multiple satellite navigation systems including BDS, GPS, GLONASS, and GALILEO, with positioning accuracy within 4 cm. During the experiment, the iRTK5 receiver 1 was fixed on top of the infrared system to ensure the receiver was stable and did not wobble; the iRTK5 receiver 2 was fixed inside the hot-air balloon gondola to ensure the receiver’s measurement reference was as close to the carbon furnace as possible. The data sampling interval was set to 0.1 s, recording 10 sets of three-dimensional coordinate data per second, and measurements were taken continuously 20 times to obtain the position information of receivers 1 and 2, which was then converted into distance values between receivers 1 and 2.

The experimental results are shown in the table below.

The experimental measured values average approximately 15,647.731 m. As shown in

Table 4. Measurement results of RTK system.

Test Count	Test Distance/m	Test Count	Test Distance/m
1	15,647.656	11	15,647.746
2	15,647.672	12	15,647.753
3	15,647.681	13	15,647.748
4	15,647.678	14	15,647.767
5	15,647.682	15	15,647.774
6	15,647.690	16	15,647.772
7	15,647.694	17	15,647.779
8	15,647.693	18	15,647.785
9	15,647.738	19	15,647.786
10	15,647.728	20	15,647.804

, the measured distance fluctuates after the decimal point, but the overall trend is a slight increase in distance with the number of tests. This is because the hot air balloon swings slightly under the influence of air currents and moves slightly farther within 2 s.

4.3. Solving and Analysis of Effective Range

The following solution is derived based on the optimized range model presented in this paper.

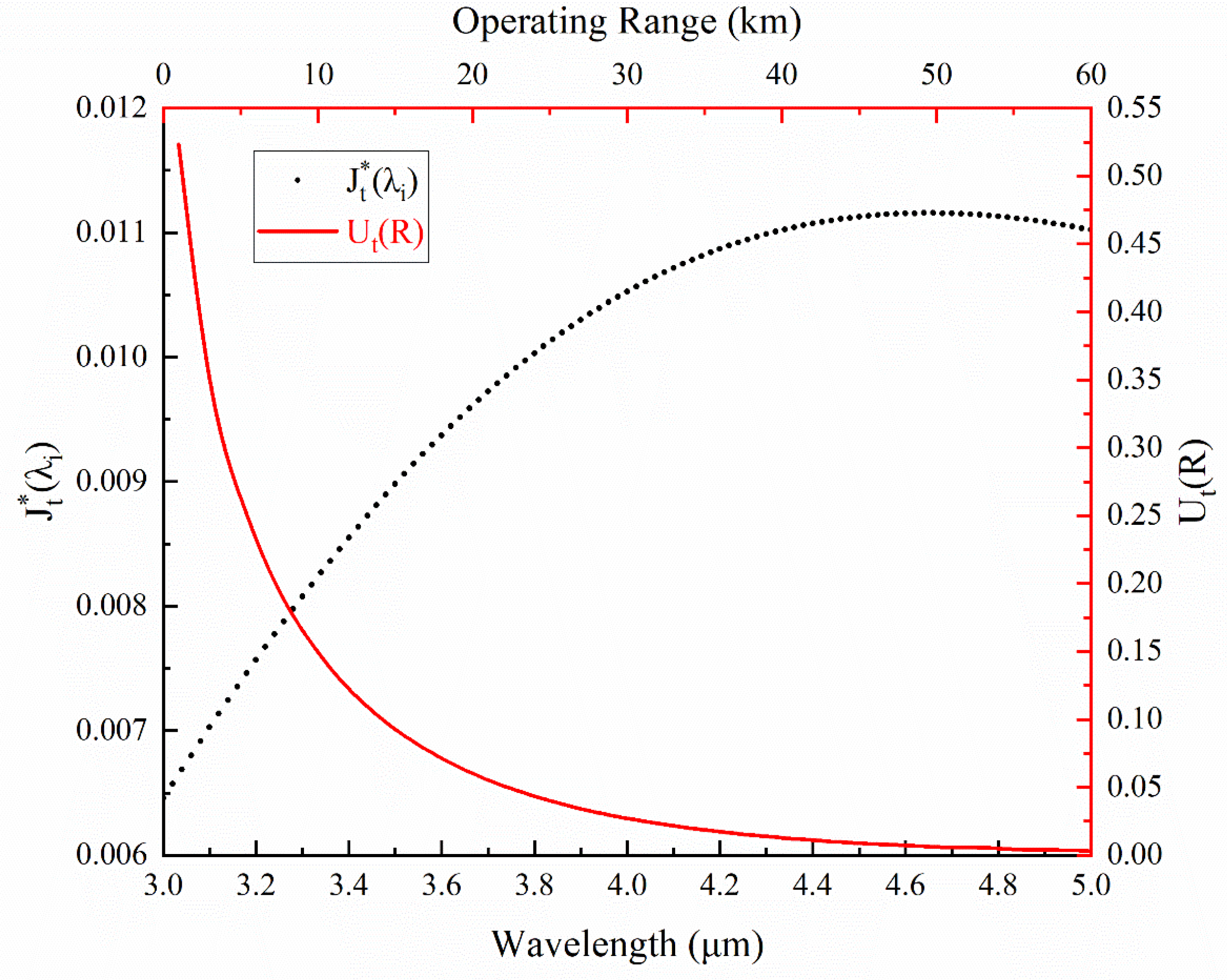
Using Equation (20), the spectral radiance of the small carbon furnace $J_t(\lambda )$ can be obtained; after normalization and discretization with a step size of 0.02 μm, the relationship of $J_t^{*}({\lambda }_i)$ with the wavelength can be obtained. After substituting $J_t^{*}({\lambda }_i)$, Equation (30), and the atmospheric transmittance into Equation (24), the relationship of $U_t(R)$ with range can be obtained. The fitting result of the discretized $J_t^{*}({\lambda }_i)$ and $U_t(R)$ is shown in Figure 5.

$U_t(R)$ after fitting is obtained as follows:

$$U_t(R)=0.3277e^{-0.3996R}+0.3292e^{-0.08368R}$$

(31)

Similarly, after normalizing the background spectral radiance calculated by MODTRAN and discretizing it with a step size of 0.02 μm, the relationship of $L_b^{*}({\lambda }_i)$ with the wavelength can be obtained. After substituting $L_b^{*}({\lambda }_i)$, Equation (30), and the atmospheric transmittance are into Equation (24), the relationship of $U_b(R)$ with range can be obtained. The fitting result of the discretized $L_b^{*}({\lambda }_i)$ and $U_b(R)$ is shown in Figure 6.

$U_b(R)$ after fitting is obtained as follows:

$$U_b(R)=0.403e^{-0.434R}+0.2196e^{-0.09258R}$$

(32)

Substituting Equations (31) and (32) and other parameters into Equation (25) gives the following:

$$\begin{array}{cc}\hfill U(R)& =0.6400e^{-0.3996R}+0.6429e^{-0.08368R}\hfill \\ & -0.0633e^{-0.434R}-0.0345e^{-0.09258R}\hfill \end{array}$$

(33)

Equation (33) is the fitting function of $U(R)$.

After substituting Equation (33) into (15) and each parameter of the IRST system, the iterative calculations were performed via MATLAB, R2024a and the operating range of the IR search system was obtained as R = 16.3596 km.

In comparison with the measurement results of the field experiment in Section 4.2, the relative error of the IR operating range measured by the method in this paper is 4.55%. There are still some errors between the theoretical calculation results and the actual measurements, which are caused by the approximation of the object radiation and the fact that the actual atmospheric conditions are far more complicated than the simulation results. Consequently, more accurate measurements of actual conditions can be obtained, thereby reducing errors.

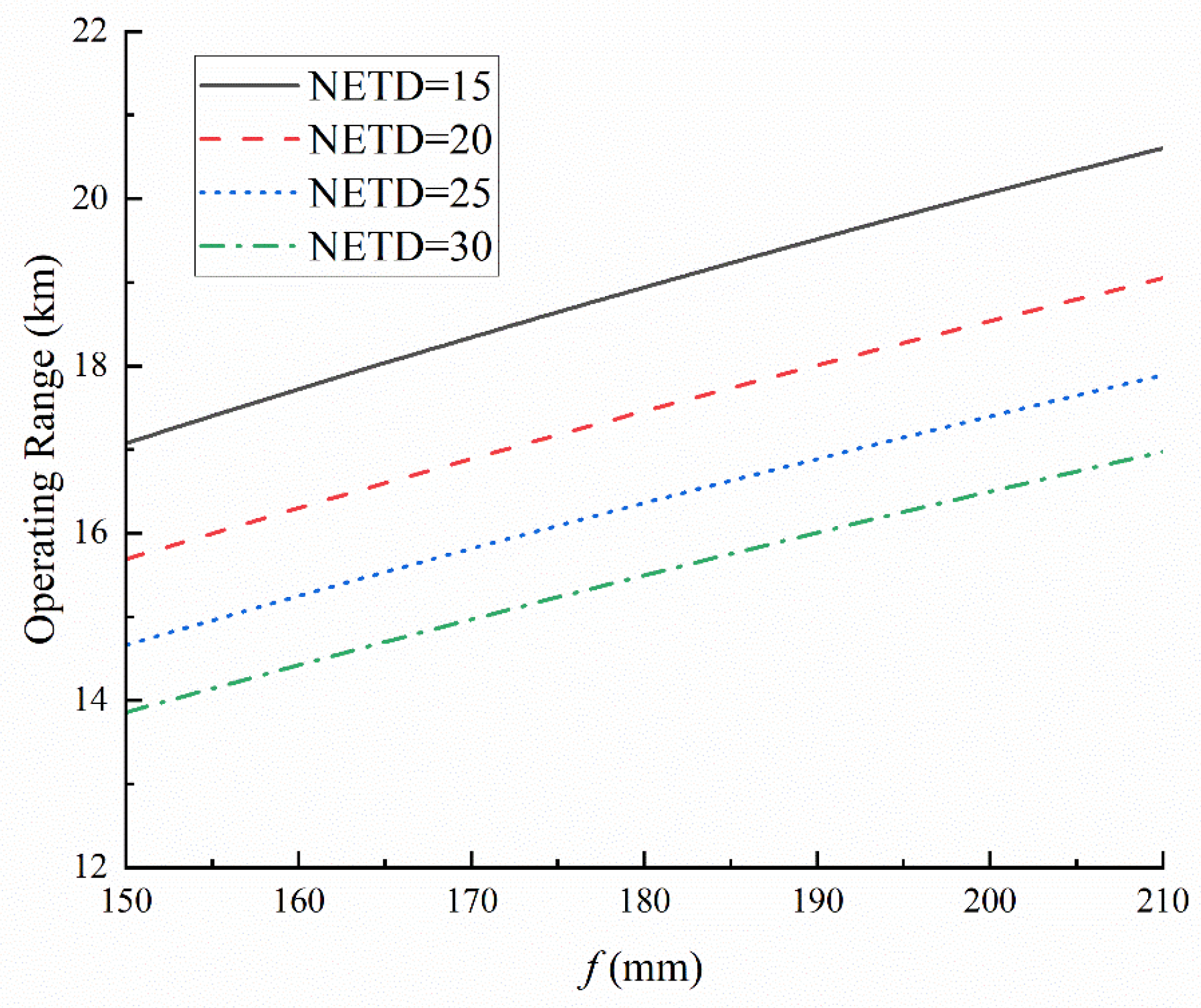
The operating range model established in this paper shows that NETD and focal length $f$ are important parameters affecting the operating range. Using the example calculation results without changing other conditions, the relationships between the operating range and NETD and focal length $f$ are shown in Figure 7.

Figure 7 shows that, within the focal length of 150–210 mm, the operating range has an approximately linear relationship with the focal length, and the operating range increases with increasing focal length. Moreover, changes in NETD also have significant effects on the operating range. The smaller the NETD is, the larger the operating range, and the increasing speed is larger. Since the F-number of the optical system of the IR detector is generally between 1 and 4, limited by the aperture of the optical system, the focal length cannot be excessively increased to improve the operating range. The NETD can be reduced by reducing the operating temperature of the detector, thus effectively improving the range [35]. At present, for some mid-wave and long-wave detectors, the NETD has decreased to below 10 mK [36,37], and the detection performance has greatly improved.

5. Conclusions

In this paper, we establish an NETD-based optimization model for a staring IRST system. First, the NETD expression for the staring IRST system is rederived. Based on the NETD expression, the expression of the operating range is derived, and the calculation method of each part is analyzed. Finally, the operating range model is used to carry out example calculations to verify the reliability of the model. Moreover, the effects of the NETD and the focal length of the optical system on the operating range are analyzed. The calculation results show that the operating range increases with increasing focal length and increases with decreasing NETD. This paper provides the following conclusions:

(1)

Compared with the traditional IRST system range model, the NETD-based IRST system range model requires fewer parameters, and there are corresponding national standards for the measurement conditions of NETD, making the calculation more convenient.

(2)

Theoretically calculated object spectral radiation intensity and background spectral radiance fully consider the spectral radiation characteristics of the object and background, but there is a certain deviation between the theoretically calculated and the actual values; the actual measurement accuracy is relatively high, but the measured values often do not reflect the overall spectral radiation characteristics. The theoretical calculation values are normalized and used as the weight of the actual measurement values to obtain new spectral radiation characteristics of the object and background. The proposed method considers the advantages of both theoretical calculations and actual measurements and is more in line with the actual situation.

(3)

The NETD has an important effect on the operating range. Reducing NETD can improve the performance of the detector and increase the operating range of the system.

IRST systems are widely used in object identification and reconnaissance. The NETD-based range model of the staring IRST system is more convenient for estimating the range of the various commonly used staring systems, so the performance can be better evaluated. In the field of IRST system performance evaluation, the NETD-based operating range model proposed in this study can be directly applied to the preliminary design phase of new staring infrared search and track systems. By inputting system parameters and environmental conditions, it enables rapid assessment of the operational range under various design schemes, thereby guiding detector selection and signal processing algorithm design. Furthermore, this model provides performance boundaries for infrared subsystems within multi-sensor systems equipped with infrared channels—such as shipborne electro-optical systems—facilitating the formulation of fusion strategies.

The limitations of the optimized model for operating range in this paper are mainly as follows: First, the operating range model shows that the operating range of the IRST system is strongly affected by the object and site environment. Therefore, the efficiency evaluation and system optimization of the IRST system must be performed in consideration of the specific application scenarios of the IRST system. Second, model results are highly dependent on the calculation accuracy of atmospheric radiative transfer software such as MODTRAN. Under complex meteorological conditions (e.g., haze, dust storms, turbulence), existing atmospheric models may exhibit significant errors and need to be corrected using on-site measured data. Third, the model approximates targets as graybodies and uses a fixed emissivity. In reality, the surface temperature distribution of flight targets (such as aircraft and missiles) is nonuniform, and the nozzle and exhaust plume radiation exhibit strong directionality and time variability, which can cause increased prediction errors in close-range or highly dynamic scenarios. Fourth, the model for operating range assumes the radiative properties of the target and background remain constant over the integration time, but when the target maneuvers at high speed or the scene changes drastically (for example, cloud cover), this assumption introduces errors and a dynamic correction mechanism must be introduced. Future research can proceed in the following directions: further optimize the spectral radiance model for diverse complex targets to improve the accuracy of calculating target spectral radiance intensity, and combine deep learning techniques to enhance the model’s adaptability and computational efficiency.