Novel Imaging Devices: Coding Masks and Varifocal Systems

Abstract

To design novel imaging devices, we use masks coded with numerical sequences. These masks work in conjunction with varifocal systems that implement zero-throw tunable magnification. Some masks control field depth, even when the size of the pupil aperture remains fixed. Pairs of vortex masks are used to implement tunable phase radial profiles, like axicons and lenses. The autocorrelation properties of the Barker sequences are applied to the generation of narrow passband windows on the OTF. For this application, we apply Barker matrices in rectangular coordinates. A similar procedure, but now in polar coordinates, is useful for sensing in-plane rotations. We implement geometrical transformations by using zero-throw, tunable, anamorphic magnifications.

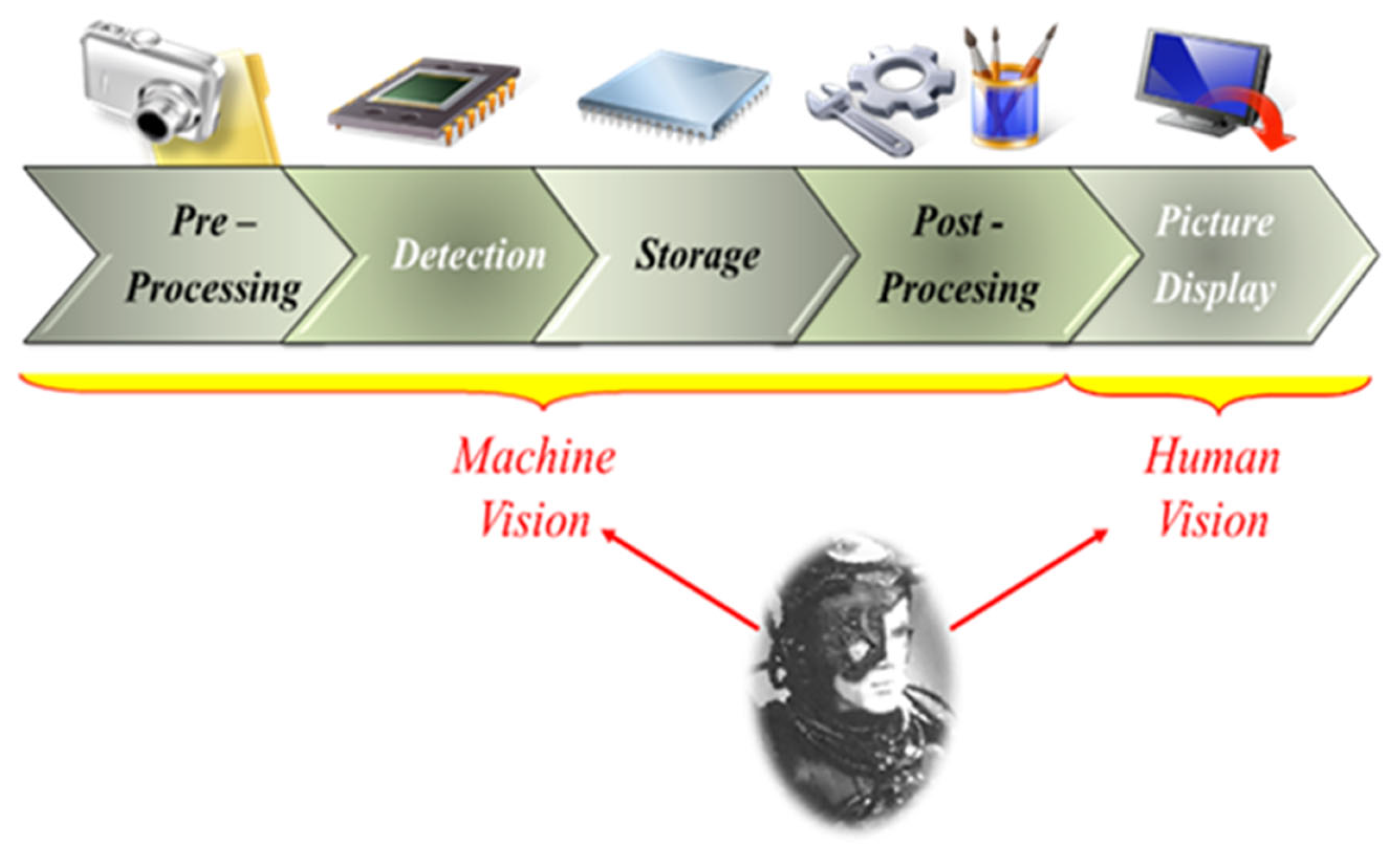
1. Introduction

For several applications in image science, it is important to gather pictures with high resolution and an extended depth of field. It is commonly assumed that these two goals are incompatible. For controlling the depth of field of an optical system, the simplest and most commonly used technique consists of reducing the size of the pupil aperture. Of course, this simple solution reduces light-gathering power and decreases the resolution of the optical system. To avoid this dilemma, here, we control field depth in terms of the OTF [1,2,3,4].

To extend the depth of field with fixed-pupil apertures, one can use annular apertures [5,6,7]. This technique has been extrapolated to the use of apertures that are coded with gray-level transmittance masks, which have an annular profile over the whole pupil aperture [8].

By taking into account the image quality chain, as in Figure 1, some of us have suggested a different approach. In a previous proposal, we considered gathering high-quality 3-D images in a single snapshot. To this end, we employ a two-stage process. In the first stage, the optical system employs a mask (in generic terms, an apodizer) that reduces the impact of focus error [9]. In other words, the optical system performs a pre-processing operation. By reducing the influence of focus errors, the pre-processing masks collect images with the same quality and all the planes contained in the 3-D image. The same image quality means that the OTF does not have zero values even when one changes the focus error coefficient. This property has a drawback. The recorded images have a reduction in signal modulation, and hence, the recorded picture is not necessarily suitable for human visualization. However, a single snapshot can be used to compensate for the reduction in signal modulation. For this latter task, it is desirable to use a simple, digital post-processing algorithm.

To achieve our intended aim, it is convenient to recognize that in the optical system, the mask must generate a modulation transfer function (MTF) with the two following characteristics: (a) In the absence of noise, the MTF should be different from zero within its passband of the optical system. (b) In the presence of noise, the values of the MTF should be equal to or greater than a given threshold value for surpassing the variations in white noise [10].

In parallel to these developments, we note the need for having optical systems with tunable magnification. Typically, one associates variable magnifications with the use of zoom systems, or with the use of varifocal lenses. According to Plummer, Baker, and van Tassell [11], it was Kitajima [12] who filled the first patent of varifocal lenses. Kitajima’s proposal was improved with the innovations of Lohmann [13,14,15,16] and of Alvarez [17,18]. In the last decade, several technological developments have been achieved for implementing lenses with tunable optical power [19,20,21,22,23,24,25,26,27,28]. Then, as a natural step, we incorporate the use of varifocals systems for proposing novel optical devices.

Our current aim is to propose new optical systems that incorporate masks coded with numerical sequences. The masks can work in conjunction with varifocal systems [29,30]. In this publication, we discuss optical systems with tunable magnification at zero-throw [31,32].

In Section 2, we discuss optical methods for extending the depth of field. We emphasize a generalized version of the Lohmann–Alvarez technique for controlling the optical path difference in transparent masks. This generalization allows us to propose optical devices that govern field depth while preserving the same full pupil aperture. In Section 3, we exploit the autocorrelation properties of the Barker sequences [33] in rectangular coordinates for generating narrow pass windows on the OTF. In Section 4, we apply the Barker sequences, in polar coordinates, for proposing an optical sensor for in-plane rotations [34]. In Section 5, we consider the use of zero-throw tunable anamorphic magnifications for performing geometrical transformations [35,36,37]. And in Section 6, we summarize our contribution.

2. Reassessments

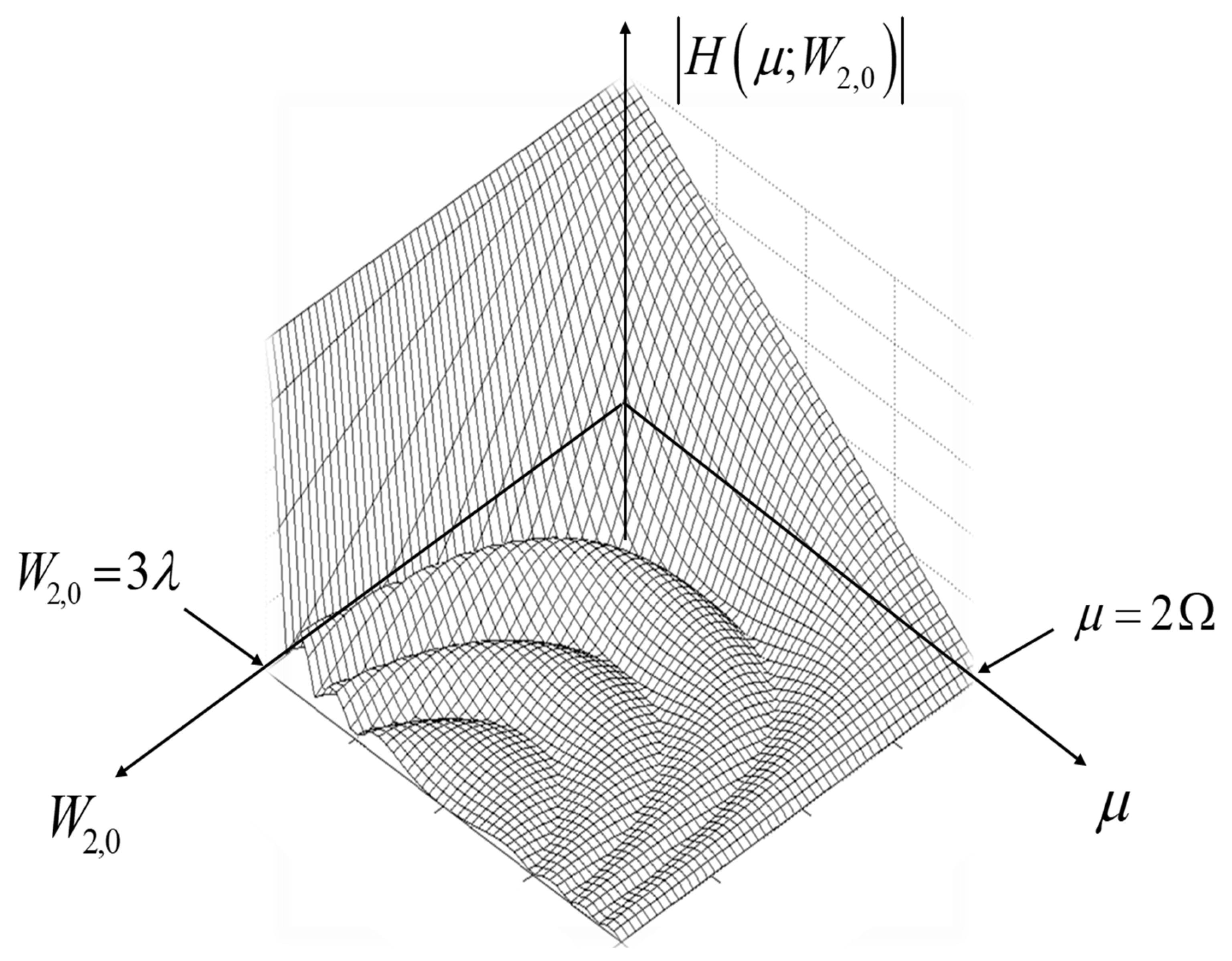
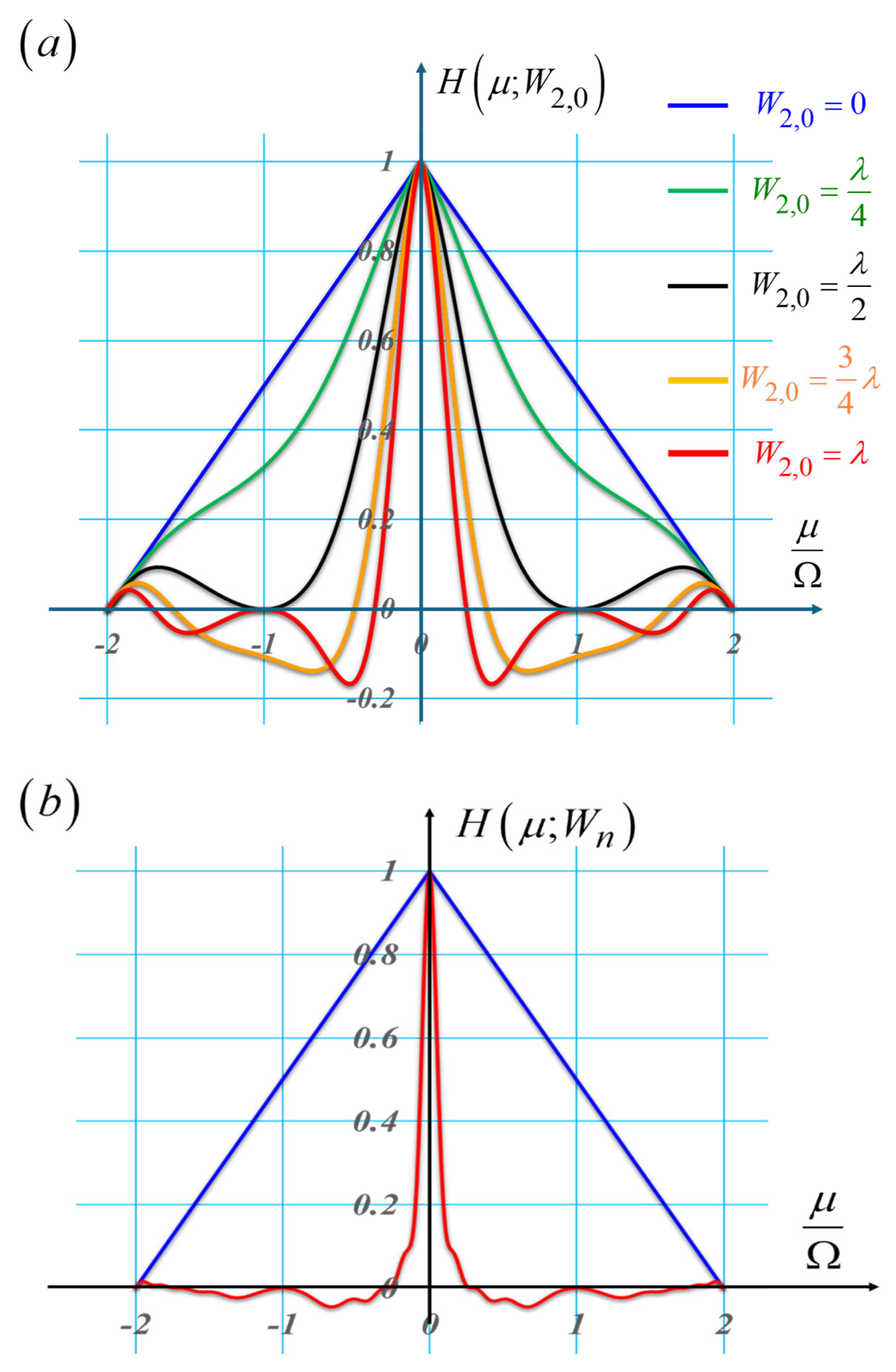
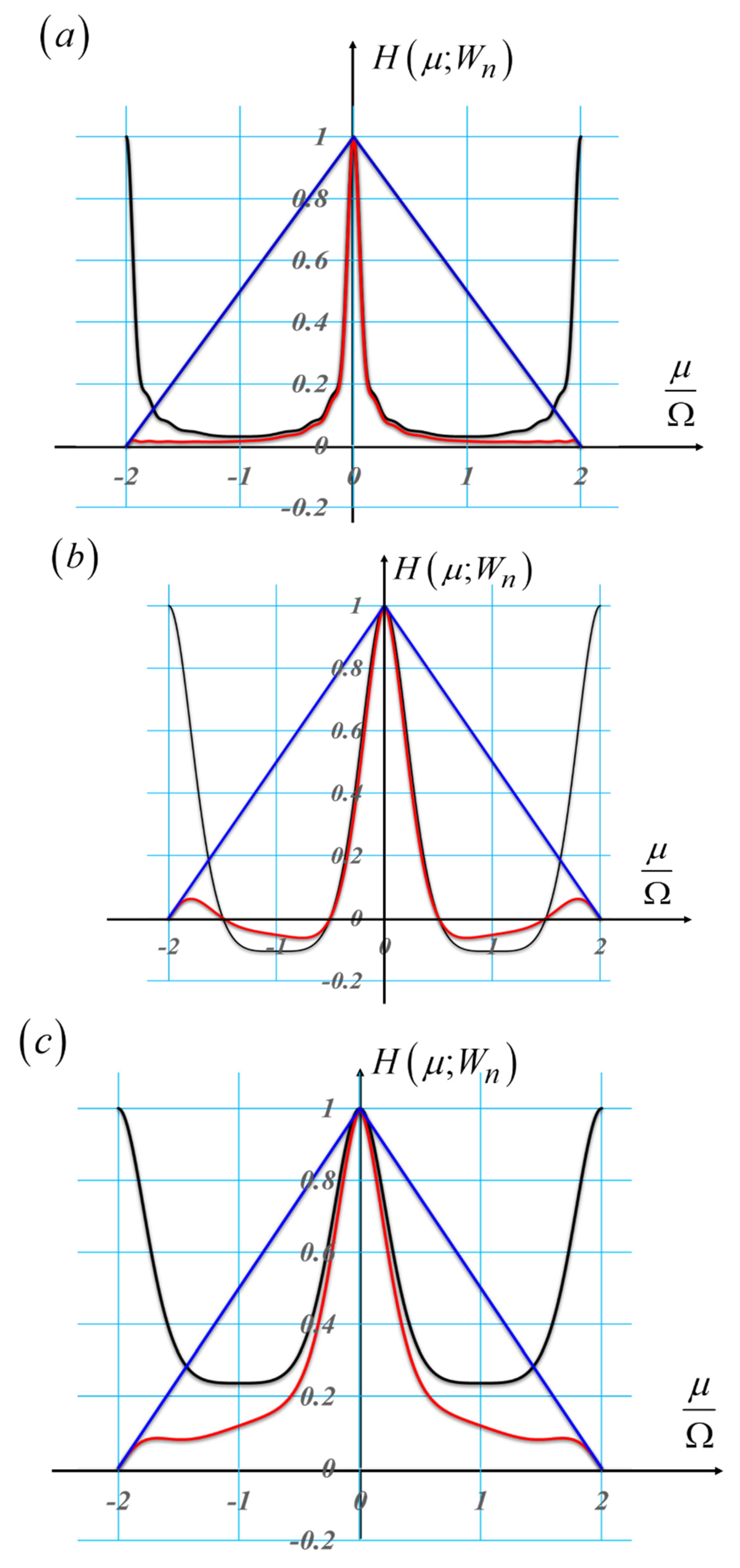
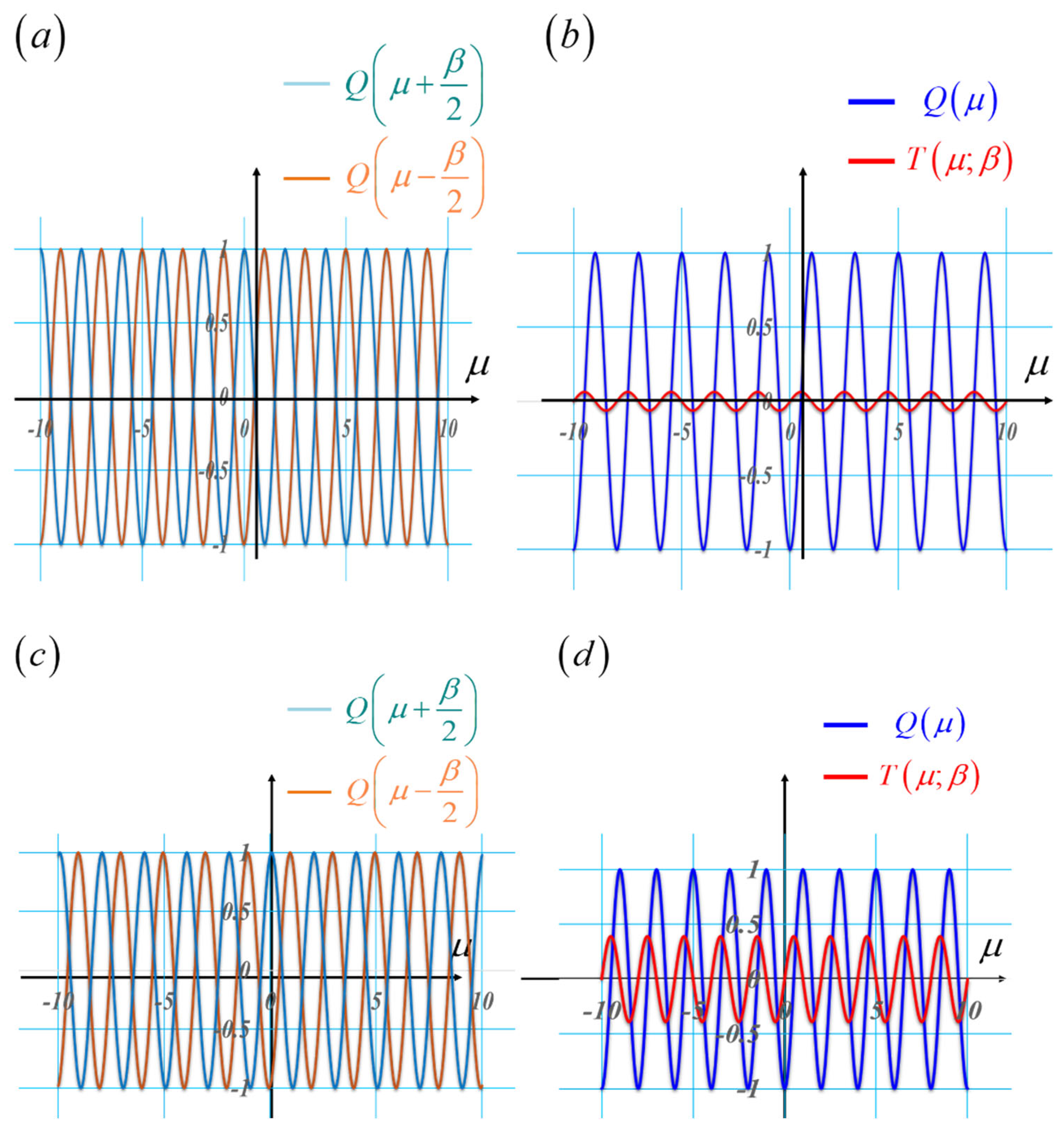
2.1. Multiple Snapshots: An Average OTF

This approach was advanced by Haeusler, who proposed to record (on the same photographic plate) several out-of-focus images of the same object. In this manner, one can generate an averaged OTF, which alleviates the impact of focus errors [38].

For avoiding errors due to misalignments and to magnification variations, one of us proposed an alternative method. As depicted in Figure 2, for this technique, the detection plane remains fixed, while one records a finite number of snapshots. At each snapshot, the optical system varies the focus error coefficient. This technique overcomes the limitations imposed by the detector dynamic range [39]. In what follows, we discuss a simple model for the latter technique.

For a 1-D imaging process, the out-of-focus OTF reads

$$H\left(\mu ;W_{2,0}\right)=H_0\left(\mu \right)\mathrm{sinc}\left(8\left({\displaystyle \frac{W_{2,0}}{\lambda }}\right)\left(1-\left|{\displaystyle \frac{\mu }{2\Omega }}\right|\right)\left({\displaystyle \frac{\mu }{2\Omega }}\right)\right).$$

(1)

In Equation (1), we denote the spatial frequency with the Greek letter |µ|. At the edge of the pupil aperture, the cutoff spatial frequency is Ω. As is common in scalar diffraction, the wavelength is denoted as λ. The in-focus OTF is

$$H_0\left(\mu \right)=\left(1-\left|{\displaystyle \frac{\mu }{2\Omega }}\right|\right)rect\left({\displaystyle \frac{\mu }{4\Omega }}\right).$$

(2)

In Figure 3, we show 3-D graphs of the OTF in Equation (1).

Next, we consider that one records several snapshots, say N. At each snapshot, one changes the optical power of the field lens, then one can alter the focus error coefficient. That is, at n-fold snapshot, the focus error coefficient is W_2,0 = W_n, where W_n can be either a deterministic value, or a random real number. We define the average OTF as

$$〈H\left(\mu \right)〉={\displaystyle \sum _{\begin{array}{l} \\ n=1\end{array}}^{\begin{array}{l}N\\ \end{array}}}{p}_{n}H\left(\mu ;W_{2,0}=W_n\right).$$

(3)

In Equation (3), we include a weighting factor, p_n, which one can incorporate digitally at each snapshot. The weighting factors can be arbitrarily selected. And if there are positive real numbers, with values less than unity, the weighting factors can be thought of as probability values taken from density function. By substituting Equation (1) in Equation (3), we obtain

$$〈H\left(\mu \right)〉=H_0\left(\mu \right){\displaystyle \sum _{\begin{array}{l} \\ n=1\end{array}}^{\begin{array}{l}N\\ \end{array}}}{p}_n\mathrm{sinc}\left(8\left({\displaystyle \frac{W_n}{\lambda }}\right)\left(1-\left|{\displaystyle \frac{\mu }{2\Omega }}\right|\right){\displaystyle \frac{\mu }{\Omega }}\right).$$

(4)

From Equation (4), we note that the average OTF can resemble the in-focus OTF. In Figure 4 and Figure 5, we show a numerical simulation that shows the impact of the second factor in Equation (4).

In Figure 4, we plot the variations inflicted on the OTF as one increases the value of the focus error coefficient. In Figure 4a, the blue curve is the in-focus OTF, which is plotted as a visual reference to the other curves. In Figure 4b, we show again the in-focus OTF in blue. The curve in red is the average OTF.

In Figure 5, in blue, we show the in-focus OTF. In red, we depict the average OTF. For visualizing the influence of the second factor in Equation (4), we include the variations in this factor as function of the spatial frequency. The curves in black depict the random variations that are associated with the second factor in Equation (4). In Figure 5a, the second factor has only positive values. In Figure 5b, the curve in black shows that the second factor can have negative values. And in Figure 5c, the curve in black has distinctive positive values. These graphical results illustrate the randomness of the second factor in Equation (4).

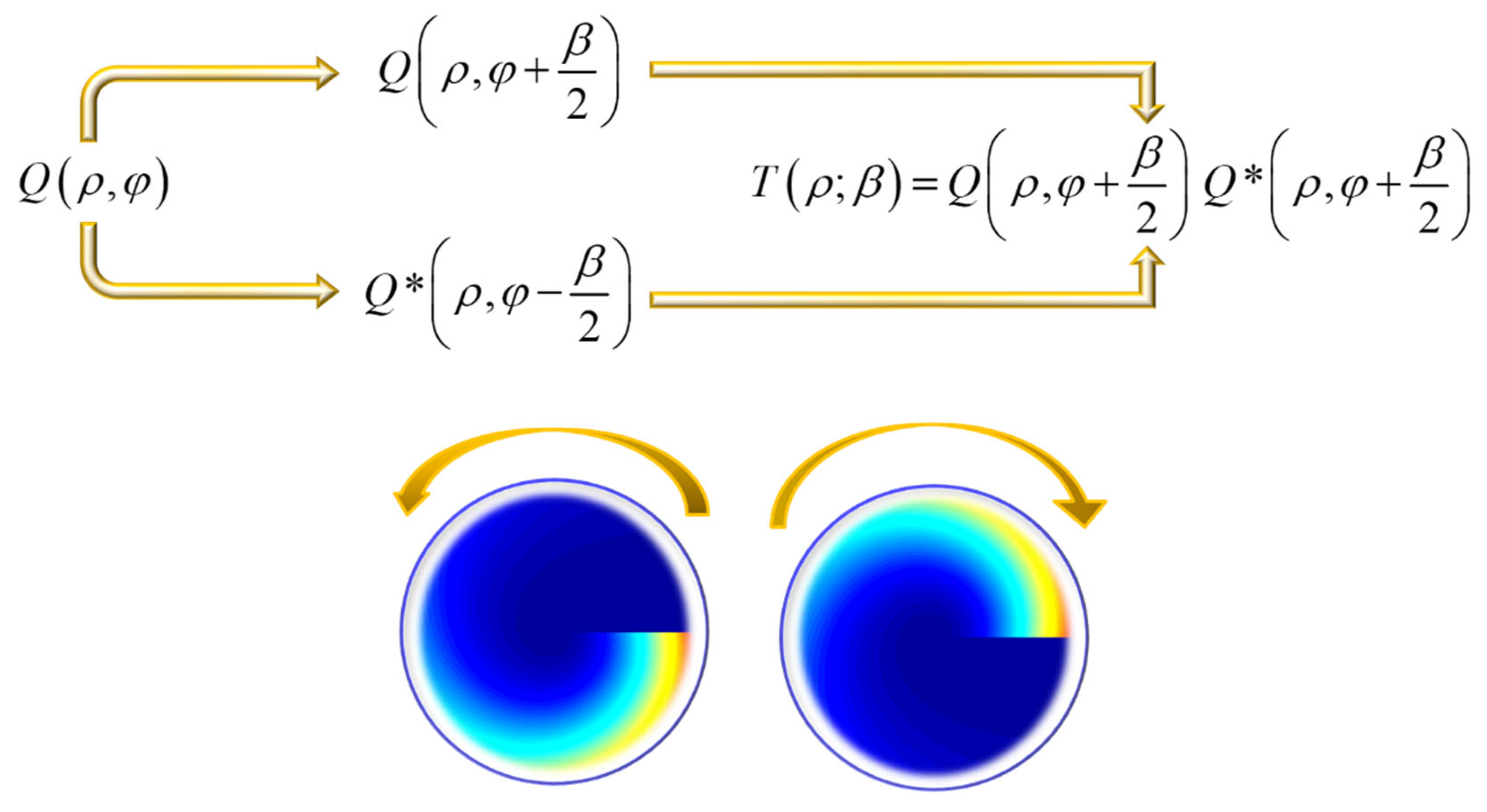
2.2. Single Snapshot: A Useful Similarity

Searching for useful tools for describing the imaging process, in terms of scalar diffraction, Papoulis [40], Guigay [41] and Goodman [42] propose the use of the ambiguity function in optics. Some of us noted that there is indeed a mathematical similarity between the expression for the out-of-focus OTF and the expression for evaluating the ambiguity function. That is, the integral for evaluating the out-of-focus OTF reads

$$H\left(\mu ;W_{2,0}\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}Q(\nu +{\displaystyle \frac{\mu }{2}})Q*(\nu -{\displaystyle \frac{\mu }{2}})\exp \{\mathrm{i}2\pi \left({\displaystyle \frac{W_{2,0}\mu }{\lambda {\Omega }^2}}\right)\nu \}d\nu .$$

(5)

$$\chi \left(t,\nu \right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}Q(\eta +{\displaystyle \frac{\nu }{2}})Q*(\eta -{\displaystyle \frac{\nu }{2}})\exp \left(\mathrm{i}2\pi t\nu \right)d\eta .$$

(6)

This analogy was applied for linking the visualization of the ambiguity function with a nonconventional display of the out-of-focus OTF [43]. To this end, as shown in Figure 6, we recognize the following relationships

$$\nu \to \mu ;t\to y=\left({\displaystyle \frac{2W_{2,0}}{\lambda {\Omega }^2}}\right)\mu .$$

(7)

In Equation (7), we change the temporal frequency ν by the spatial frequency µ, and the temporal variation, t, into a spatial variation, y. And then, we recognize that the spatial variation is related linearly with the spatial frequency µ. The slope of the linear relationship is proportional to the focus error coefficient W_2,0. For obtaining a value of the MTF, with focus error, one traces a straight line through the origin with slope 2 W_2,0/(λ Ω²). Next, we find the intersection of this inclined line with a vertical line located at µ = σ. The point (σ, 2W_2,0/(λ Ω²)) visually indicates the out-of-focus MTF H(σ, W_2,0). Hence, one can argue that the modulus of the ambiguity function is a highly redundant picture since it contains all the defocused MTFs.

The picture in Figure 6a visually indicates that the ambiguity function of a clear pupil aperture changes substantially with an in-plane rotation. Meanwhile, the picture in Figure 6b changes slowly with an in-plain rotation. Of course, this heuristic description should be part of a 3-D display of the MTFs as in Figure 7.

The results in Figure 7 were obtained with masks that can change their optical path difference [44]. In what follows we indicate how it is possible to modify the optical path difference. The above description has been considered by several other authors, who have pointed out the strengths and the limitations of our initial proposal [45,46,47,48,49,50,51,52].

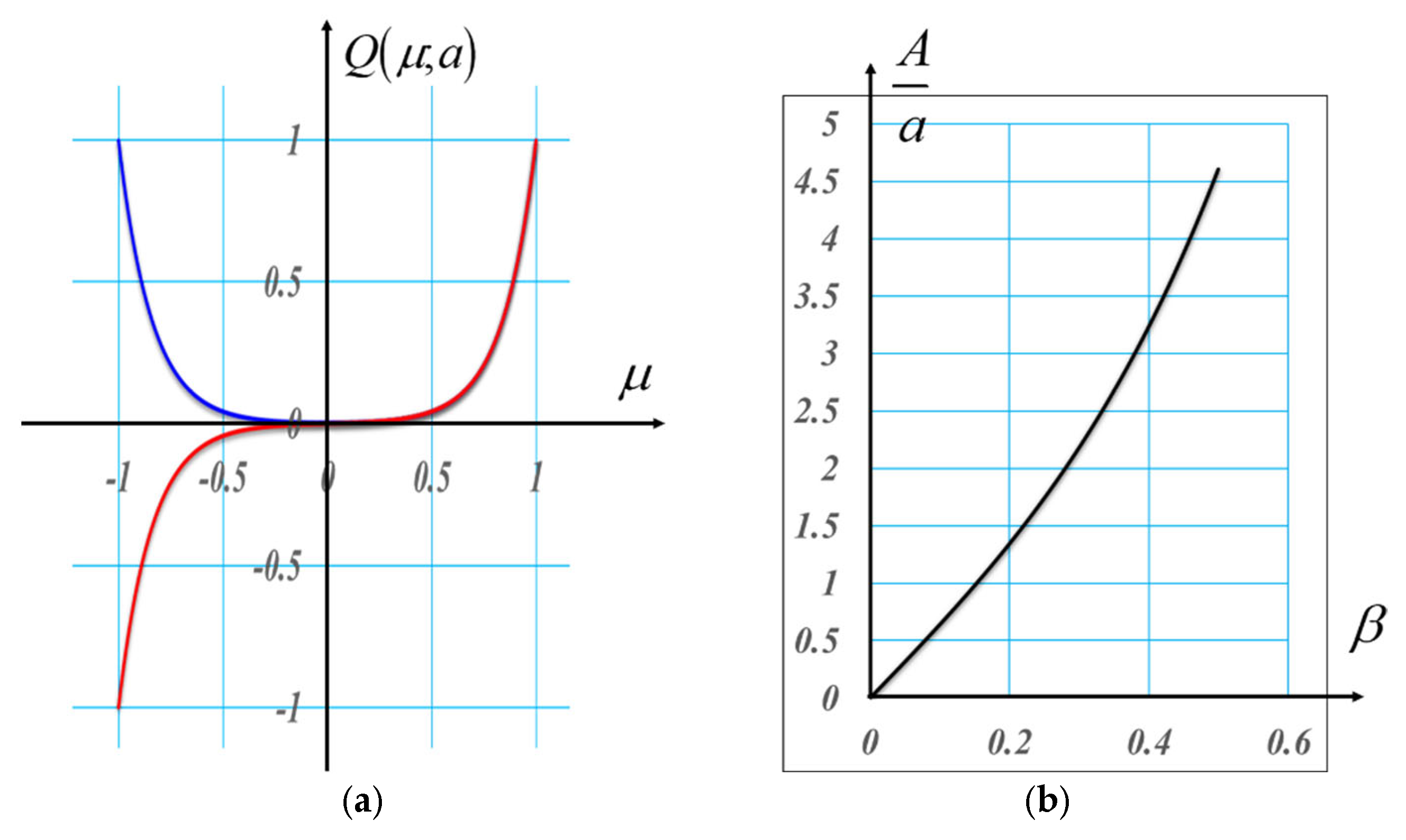
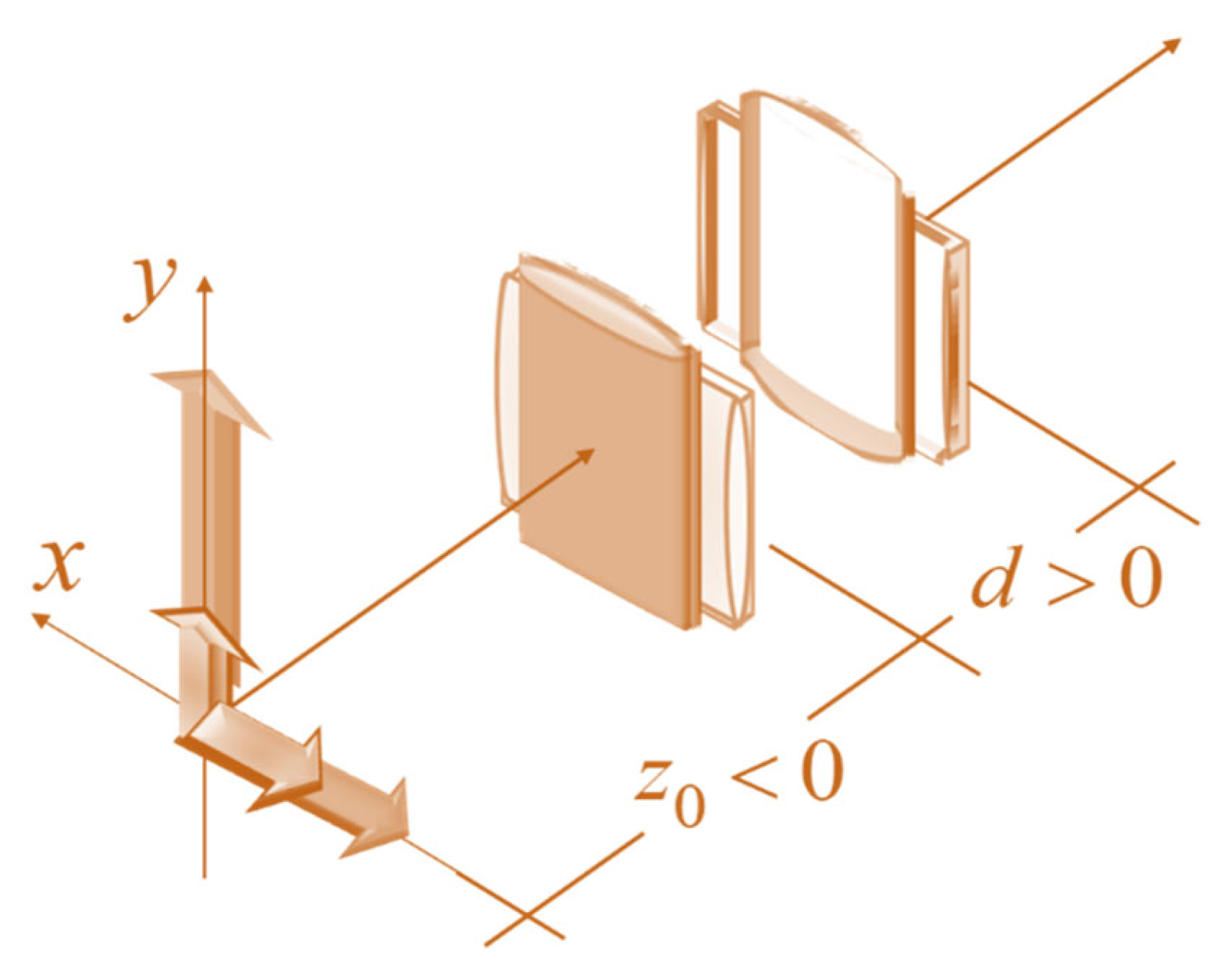
2.3. Generalized Lohmann–Alvarez Pairs

In remarkable contributions, Lohmann and Alvarez proposed the use of two phase conjugated, cubic phase masks for implementing a varifocal lens. In mathematical terms, their procedure reads as follows

$$Q\left(\mu \right)=\exp \left[-i2\pi \left({\displaystyle \frac{a}{\lambda }}\right){\left({\displaystyle \frac{\mu }{\Omega }}\right)}^3\right]rect\left({\displaystyle \frac{\mu }{2\Omega }}\right).$$

(8)

In Equation (8), we follow the same notation as in Equation (1). But now, the lower-case letter “a” denotes the optical path difference (in units of λ) of the cubic phase mask. If one uses a pair of phase conjugate masks that are laterally shifted, say, by the spatial frequency β, then the complex amplitude transmittance is

$$T\left(\mu ;\beta \right)=Q\left(\mu +{\displaystyle \frac{\beta }{2}}\right)Q*\left(\mu -{\displaystyle \frac{\beta }{2}}\right).$$

(9)

By substituting Equation (8) in Equation (9), one obtains

$$T\left(\mu ;\beta \right)=\exp \left[-i2\pi \left({\displaystyle \frac{a}{\lambda }}\right){\left({\displaystyle \frac{\beta }{2\Omega }}\right)}^3\right]\exp \left[-i2\pi \left({\displaystyle \frac{3a\beta }{\lambda \Omega }}\right){\left({\displaystyle \frac{\mu }{\Omega }}\right)}^2\right]rect\left({\displaystyle \frac{\mu +\frac{\beta }{2}}{2\Omega }}\right)rect\left({\displaystyle \frac{\mu -\frac{\beta }{2}}{2\Omega }}\right).$$

(10)

From Equation (10), we observe that the second term has a quadratic phase variation that can be thought of as the complex amplitude transmittance of lens. As the optical path difference changes with the lateral shift beta, then the lens has variable focal length. It is relevant to note that the mathematical steps for going from Equations (8)–(10) can be associated with the procedure used in the calculus of differences [53]. Therefore, as a working hypothesis, we want to explore other possibilities. As depicted in Figure 8, we show the steps for obtaining a generalized version of Lohmann–Alvarez technique.

We discuss two cases. In the first case, we describe a technique for controlling the diffraction efficiency of a sinusoidal phase grating [54]. In the second case, we discuss a similar technique for tuning the optical path difference of a mask that extends the depth of field [55]. And consequently, it opens the possibility of governing the depth of field, at full pupil apertures. For the first case, we consider the complex amplitude transmittance

$$Q\left(\mu \right)=\exp \left[-i2\pi \left({\displaystyle \frac{a}{\lambda }}\right)\cos \left(2\pi {\displaystyle \frac{\mu }{\eta }}\right)\right].$$

(11)

In Equation (11), the Greek letter η denotes the period of the phase grating if one uses spatial frequencies. That is η = d/λ f. Now, if one uses a phase conjugate pair, the complex amplitude reads,

$$T\left(\mu ;\beta \right)=Q\left(\mu +{\displaystyle \frac{\beta }{2}}\right)Q*\left(\mu -{\displaystyle \frac{\beta }{2}}\right).$$

(12)

By substituting Equation (11) in Equation (12), we have that

$$T\left(\mu ;\beta \right)=\exp \left[i2\pi \left({\displaystyle \frac{A}{\lambda }}\right)\sin \left(2\pi {\displaystyle \frac{\mu }{\eta }}\right)\right].$$

(13)

In Equation (13), the new optical path difference is expressed as an amplification equation

$$A=a\sin \left(\pi {\displaystyle \frac{\beta }{\eta }}\right).$$

(14)

It is clear from Equation (14), and from Figure 9, that one can control the amplification associated with the amplitude of the sinusoidal phase variation by a lateral displacement of the elements forming the phase conjugate pair.

For the sake of completeness in our current discussion, in Figure 10, we show some steps associated with the proposed procedure.

For the second case in the above proposed generalization, we consider the use of a pair of masks, which have hyperbolic phase variations. In this case, for the initial mask, the complex amplitude transmittance reads

$$Q\left(\mu ;a\right)=\exp \left[i2\pi \left({\displaystyle \frac{a}{\lambda }}\right)\cosh \left(2\pi {\displaystyle \frac{\mu }{\Omega }}\right)\right].$$

(15)

We use Equation (15) for setting a pair. The elements of the pair are laterally shifted by the spatial frequency β. Then, the complex amplitude distribution is

$$T\left(\mu ;\beta \right)=Q\left(\mu +{\displaystyle \frac{\beta }{2}};a\right)Q*\left(\mu -{\displaystyle \frac{\beta }{2}};a\right).$$

(16)

By substituting Equation (15) in Equation (16), we obtain

$$T\left(\mu ;\beta \right)=\exp \left[i2\pi \left({\displaystyle \frac{A}{\lambda }}\right)\sinh \left(2\pi {\displaystyle \frac{\mu }{\Omega }}\right)\right].$$

(17)

In Equation (17), the upper-case letter A denotes the amplification obtained by using the pair. That is,

$$A=a\sinh \left(\pi {\displaystyle \frac{\beta }{\Omega }}\right).$$

(18)

At the left-hand side of Figure 11, we plot the phase profiles of the hyperbolic masks under discussion. In blue, the variations are associated with the even function of a hyperbolic cosine. In red, the variations are associated with the odd function of a hyperbolic cosine. At the right-hand side of Figure 11, we plot the amplification ratio as a function of the lateral displacement β.

For the sake of completeness in our current discussion, in Figure 12, we show some steps associated with the proposed procedure.

We discuss now the MTFs associated with the use of the masks with hyperbolic phase profiles, which can tune the optical path difference by a lateral shift between the masks. In Figure 13a, as reference, we show the impact of focus errors on the MTF of a clear pupil aperture. The focus error coefficient varies from W_2,0 = 0 to W_2,0 = 3λ, in steps of λ. In Figure 13b, we show the impact of focus errors on the MTF of a mask with that uses a pair hyperbolic phase profile, as in Equation (17). Again, the focus error coefficient varies from W_2,0 = 0 to W_2,0 = 3λ, in steps of λ.

It is apparent from Figure 13b that the MTFs are practically the same, for variations in the focus error coefficient in the range |W_2,0| < 3λ, provided that the amplitude of the hyperbolic variations has an optical path difference a = 17λ. Hence, one can tune the depth of field by laterally shifting the elements of the hyperbolic pair. In next section, we show that the above results can be translated to the control of the optical path difference, but now in polar coordinates.

2.4. A Vortex (Helical) Pair

In Figure 14, we show the steps for obtaining an angular version of the Lohmann–Alvarez technique. Instead of a lateral displacement between the members of the pair, now we consider that the elements are in-plane rotated by an angle β.

For this application, we consider that the initial mask has a vortex complex amplitude transmittance

$$Q\left(\rho ,\phi \right)=\exp \left[i2\pi \left({\displaystyle \frac{a}{\lambda }}\right)R\left(\rho \right)\left({\displaystyle \frac{\phi }{2\pi }}\right)\right].$$

(19)

Next, we form a pair by placing together one element and its complex conjugate element. The forming elements are in-plane rotated by an angle β. In mathematical terms,

$$T\left(\rho ;\beta \right)=Q\left(\rho ,\phi +{\displaystyle \frac{\beta }{2}}\right)Q*\left(\rho ,\phi +{\displaystyle \frac{\beta }{2}}\right).$$

(20)

By substituting Equation (19) in Equation (20), we obtain the overall complex amplitude transmittance

$$T\left(\rho ;\beta \right)=\exp \left[i2\pi \left({\displaystyle \frac{a\beta }{\lambda \pi }}\right)R\left(\rho \right)\right].$$

(21)

It is clear from Equation (21) that by selecting a linear phase variation, R(ρ) = (ρ/Ω,) we can control the optical path difference of an axicon. Furthermore, by selecting a quadratic phase variation, R(ρ) = (ρ/Ω)², we can govern the optical path difference of a lens. Trivially, the same procedure applies for higher-order terms. And in this manner, we can control the magnitude of the aberration coefficients of a given wavefront.

In Figure 15, we exhibit a pictorial that displays the results in Equations (13), (17) and (21). The pictorial summarizes our goal for extending the Lohmann–Alvarez technique of using pairs of masks for controlling the optical path difference.

In the next section, we focus our attention on the use of masks that are coded with the Barker sequences.

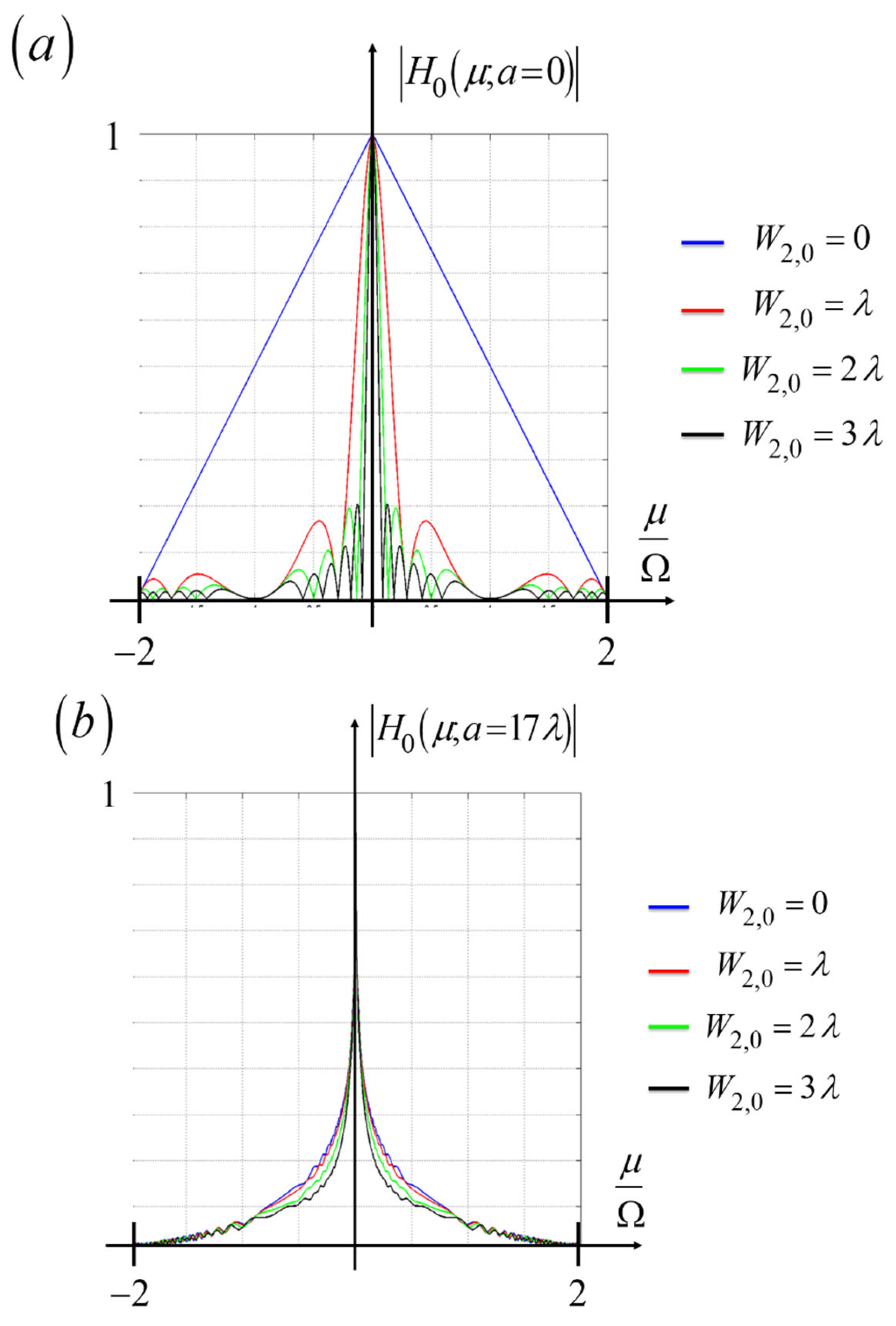
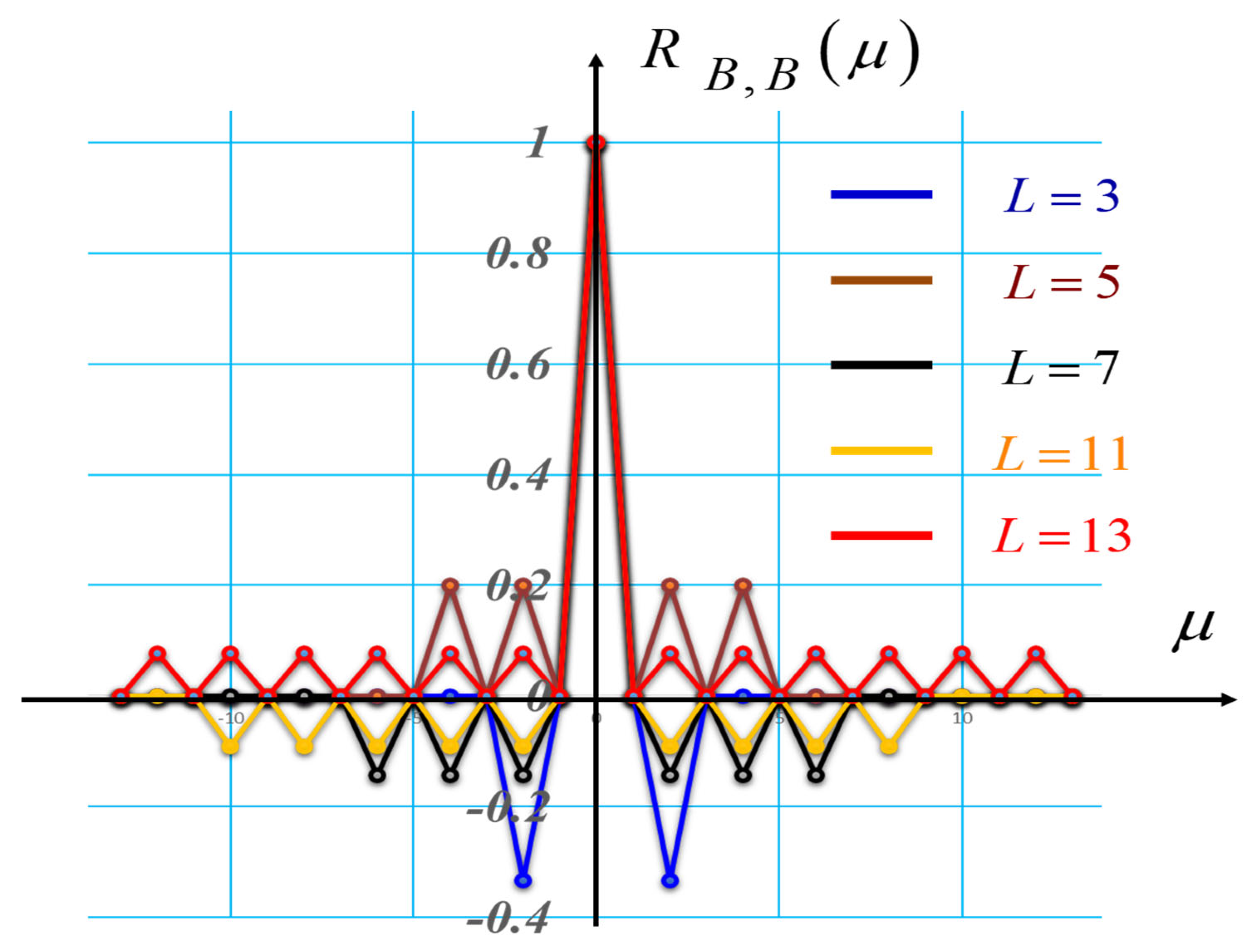
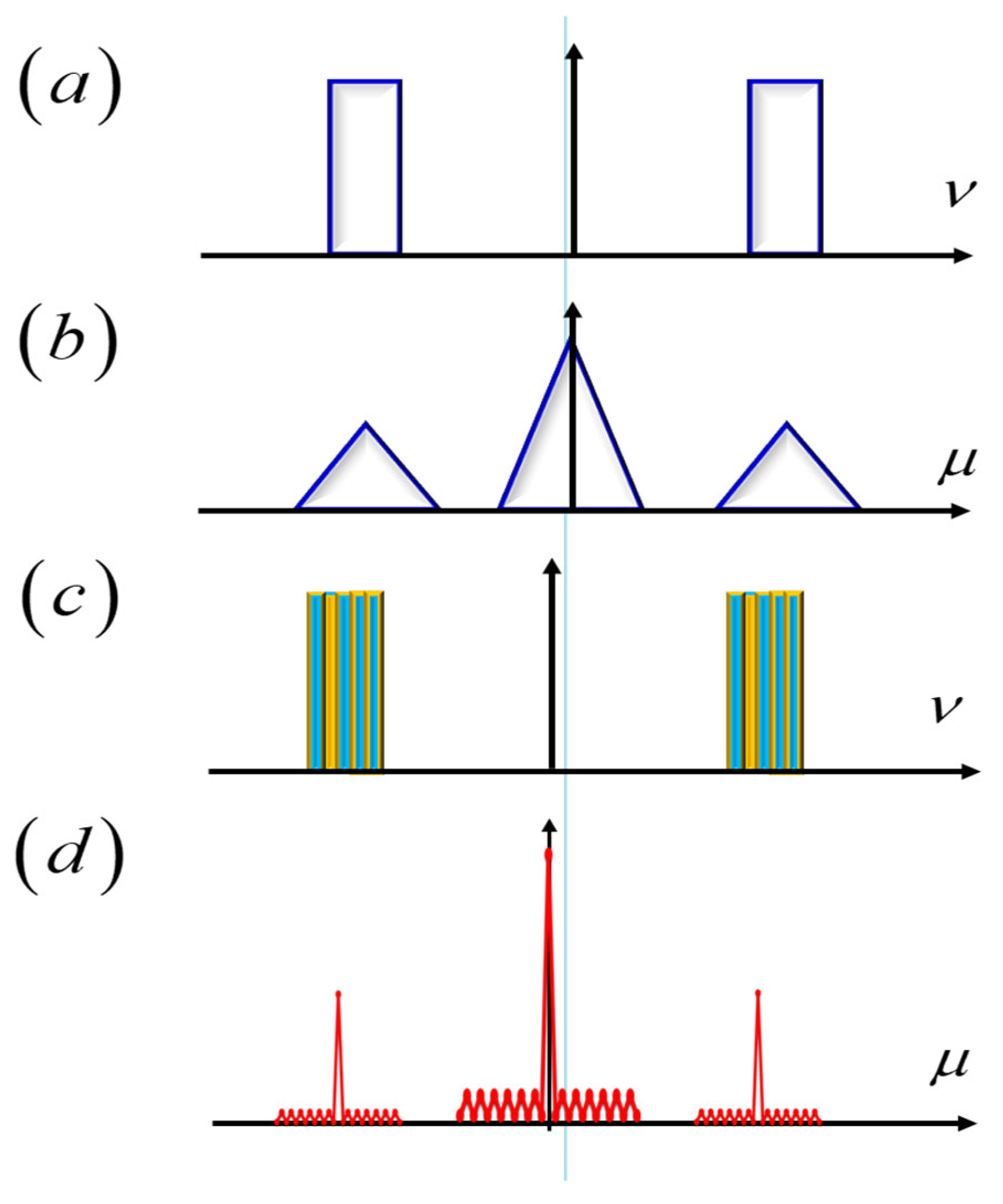
3. Rectangular Barker Matrices

In this application, we employ masks that are coded with the Barker sequences, which are listed in

Table 1. We list some of the Barker sequences that are employed in our current discussion.

Length	Barker Sequence
L = 3	{1,1,−1}
5	{1,1,1,−1,1}
7	{1,1,1,−1,−1,1,−1}
11	{1,1,1,−1,−1,−1,1,−1,−1}
13	{1,1,1,1,1,−1,−1,1,1,−1,1,−1,1}

.

A remarkable feature of the Barker sequences are their autocorrelations, which consist of a distinctive, narrow central peak. As depicted in Figure 16, around the main peak, there are secondary peaks with low amplitude. Now, the OTF is the autocorrelation of the pupil function. If the pupil is coded with a Barker sequence, then the associated OTF inherits the autocorrelation characteristics of Barker sequences.

It is known that two narrow slits can be suitably employed for obtaining windows on the OTF in Moiré photography [56,57,58,59]. Now, the OTF is the autocorrelation of the pupil function. Hence, as depicted in Figure 17, if the pupil is coded with a Barker sequence, then the associated OTF inherits the autocorrelation characteristics of Barker sequences. And in this manner, we generate narrow windows on the OTF.

In Figure 18, we illustrate the coding of the pupil aperture with a pair of Barker masks, in substitution of the narrow slits. For implementing this idea in two dimensions, it is necessary to extend the concept of coded sequences in matrix format.

In Figure 19, we show the Barker matrices of order n X n, when n = 3, 5, 7, 11, and 13.

In the above application, the extension to the Barker matrices is performed in rectangular coordinates. It is also possible to define the Barker matrices in polar coordinates, as we discuss next.

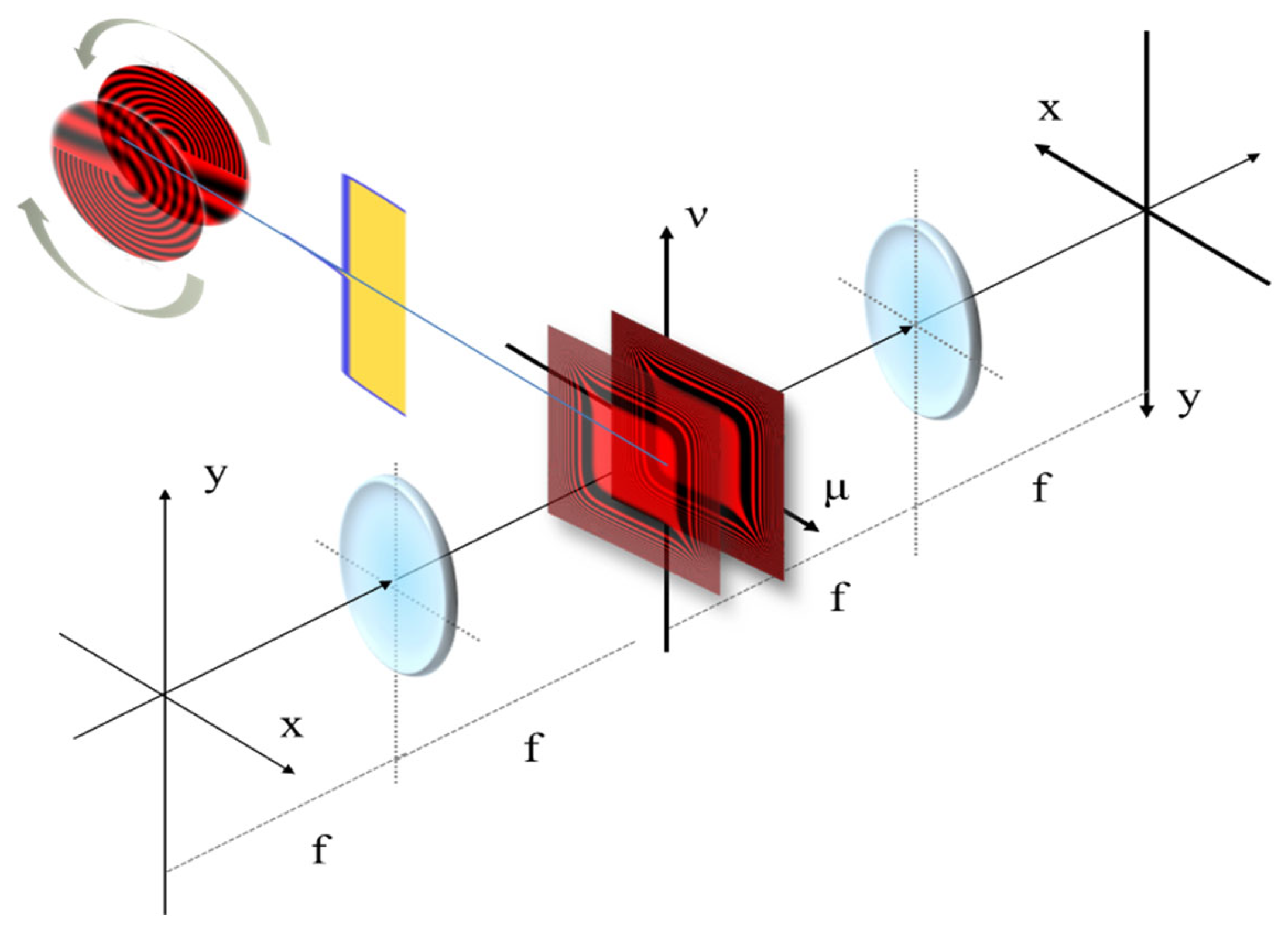
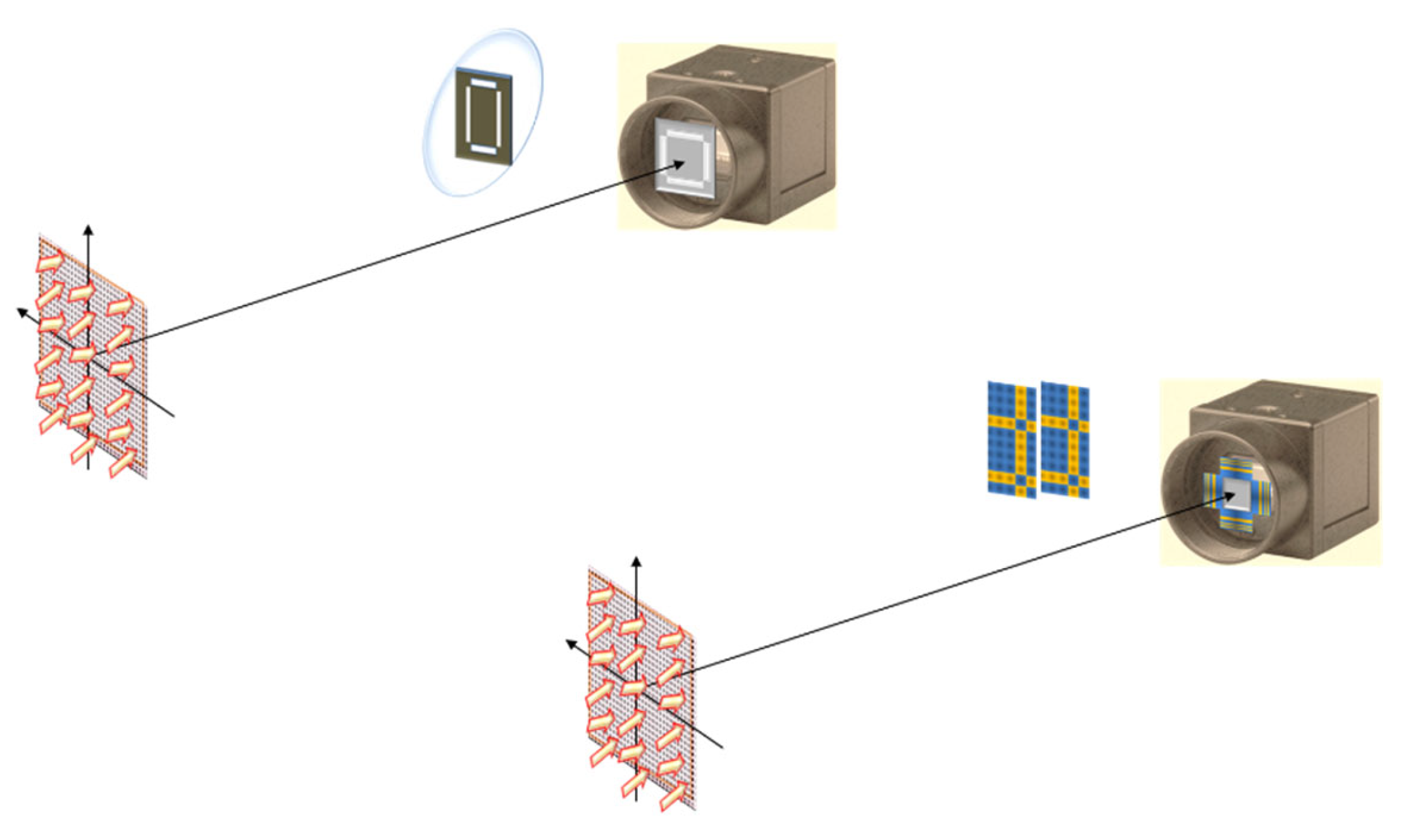
4. Rotational Sensor: Radial Barker Matrices

In Figure 20, we show the scheme for obtaining spokes that are coded angularly with the Barker sequences. At the left-hand side of Figure 20, we depict the angular coding of the Barker sequence of length L = 13. For some applications, it may be necessary to have more than 13 radial slits. If this is the case, at the right-hand side of Figure 20, we show a mask that contains 169 radial slits. In this latter case, the code is a direct product of the Barker sequence of length 13; as is discussed in [60].

The above-described masks were employed for setting a sensor of in-plane rotations. For this application, the optical setup is shown in Figure 21.

We note that the coding scheme in Figure 20 and Figure 21 is restricted to angular variations. So, the following question arises. Is it possible to implement the coding in radial and angular variations? The answer to the question is yes. In Figure 22, we show masks that code the previous Barker matrices but now are in polar coordinates. In fact, for that mask in Figure 22, the radial variation is quadratic as is common in zone plates. Therefore, the masks in Figure 22 are zone plates that are coded with the Barker sequences.

As part of our current scope, in the following section, we include the use of varifocal systems, which can work in conjunction with the already discussed masks.

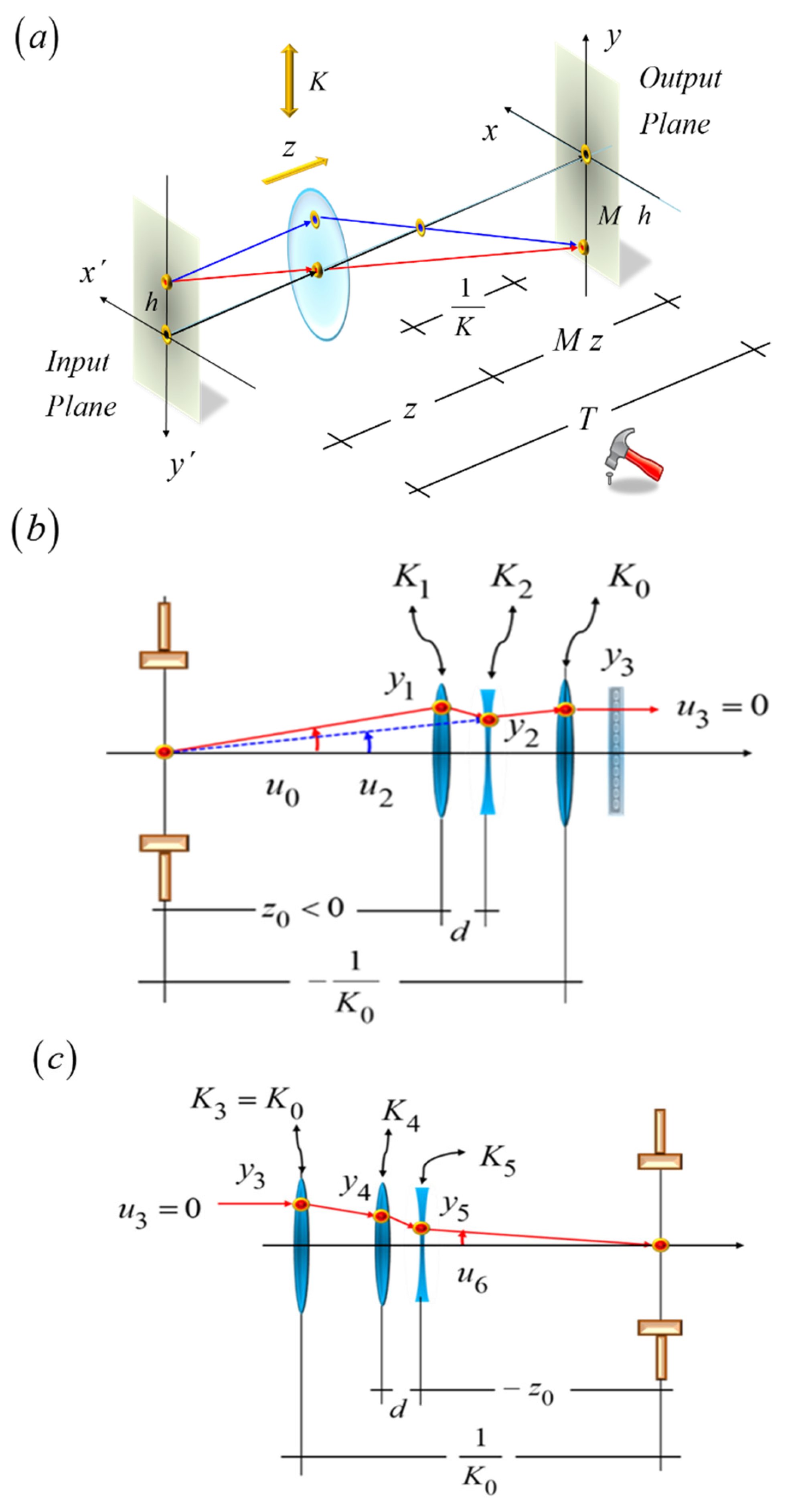
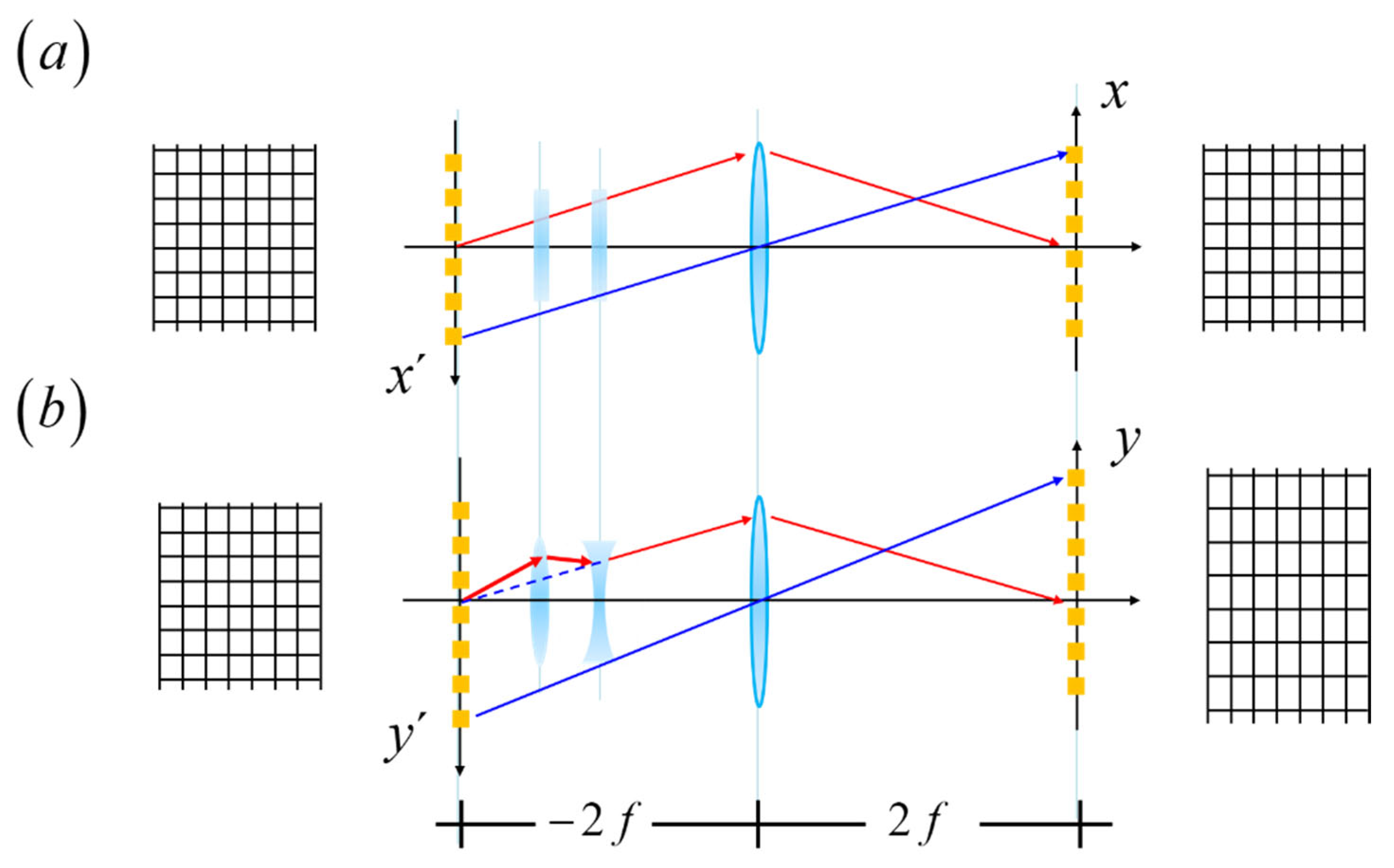
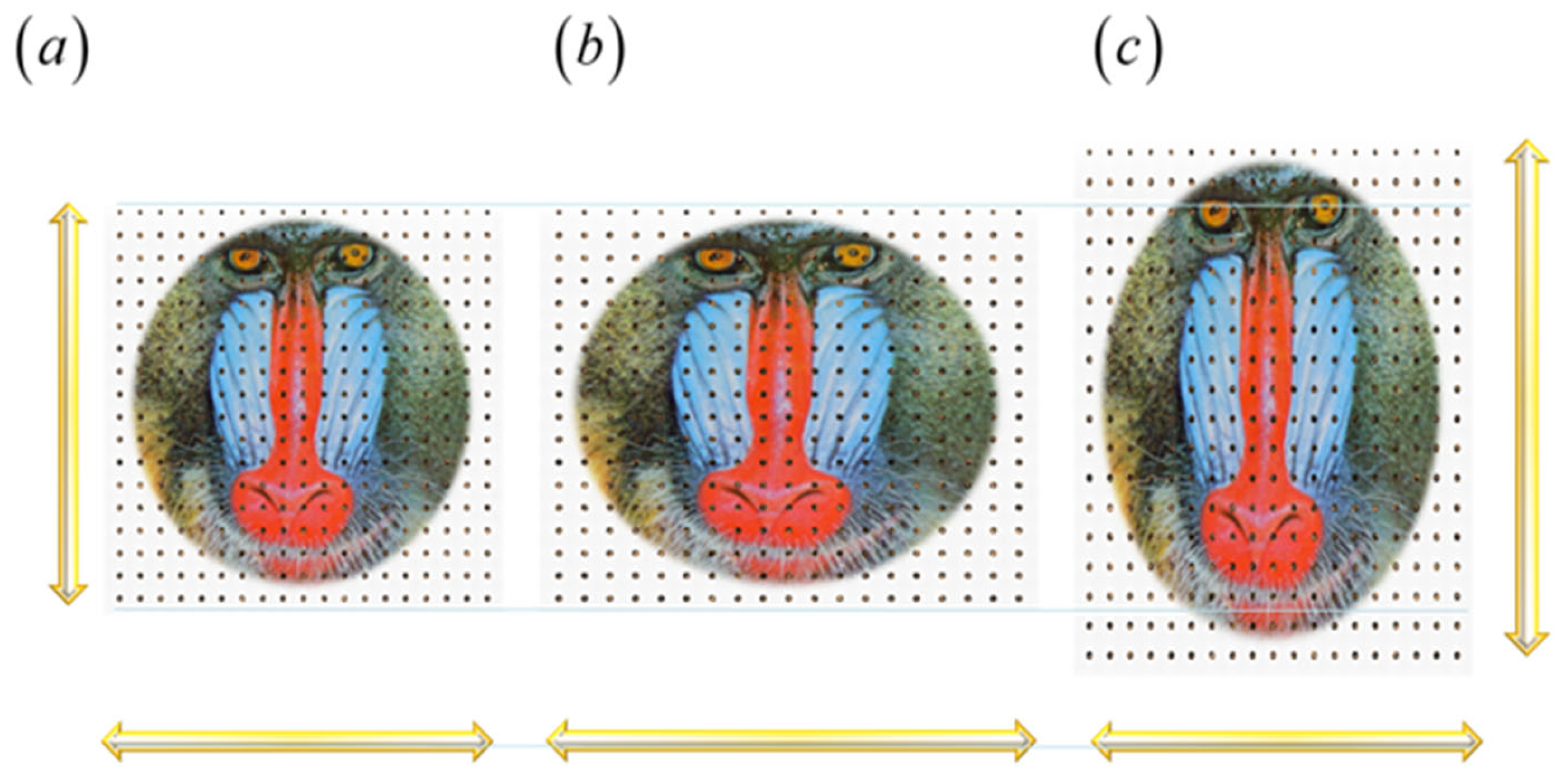
5. Tunable Anamorphic Magnifications

In Figure 23, we show an optical setup that generates variable magnification between conjugate planes, which are separated by a fixed distance, T, known as the throw.

From Figure 23, we observe that it is necessary to employ at least two varifocal lenses for achieving tunable magnifications, while preserving the axial positions of the conjugate planes. In Figure 23a, we indicate the need to perform two actions for implementing tunable magnifications with fixed throw, T. As the optical power of the lens changes, one needs to move the varifocal lens along the optical axis.

In Figure 23b, we show the use of two varifocals for implementing tunable magnification of the input picture, while preserving the image at the input plane. The varifocal system is a zero-throw device. In Figure 23c, we employ an initial collimating lens, which has fixed optical power. At its back focal plane, we can implement an angular tunable magnification by using two varifocal lenses. In this manner, this device is a Barlow lens that preserves the location of the initial back focal plane, while tuning the angular magnification [58].

Furthermore, we have noted that optical system in Figure 23b can be used to generate tunable anamorphic magnifications [59]. To this end, we substitute the varifocal spherical lenses by varifocal cylindrical lenses as is depicted in Figure 24.

A nonconventional application of the tunable anamorphic magnification is the production of geometrical transformations, which were pioneered by Bryngdahl. For illustrating this application, we show the optical setup in Figure 25.

In Figure 26, we show some numerical simulations of the proposed geometrical transformations. In Figure 26a, the image of a baboon has the same magnification along the x-axis and the y-axis. In Figure 26b, the absolute value of the magnification along the x-axis is higher than that along the y-axis. And in Figure 26c, the absolute value of the magnification along the x-axis is smaller than the absolute value of the magnification along the y-axis.

At this stage, except for anamorphic spectacles for visual inspection and for geometrical transformations, we do not have any other applications for the use of tunable, anamorphic magnifications. Further discussions are needed for understanding the impact of wave aberrations in anamorphic systems with tunable magnification [61].

6. Conclusions

We have applied some numerical sequences for coding masks, which are used in conjunction with varifocal systems for designing novel imaging devices. Specifically, we have exploited the concept of average OTF for extending the depth of field of an optical system. Furthermore, we have extended the Lohmann–Alvarez technique (in rectangular coordinates) field depth, while preserving the size of the pupil aperture. For this application, we have discussed the use of the calculus of differences in the design of devices with governable optical path differences.

We have noted that there is an analogy between the Lohmann–Alvarez technique rectangular coordinates, and the use of a pair of vortex lenses in polar coordinates. We have exploited this analogy for designing optical pairs of vortex masks, which can generate tunable phase radial profiles, like axicons and lenses.

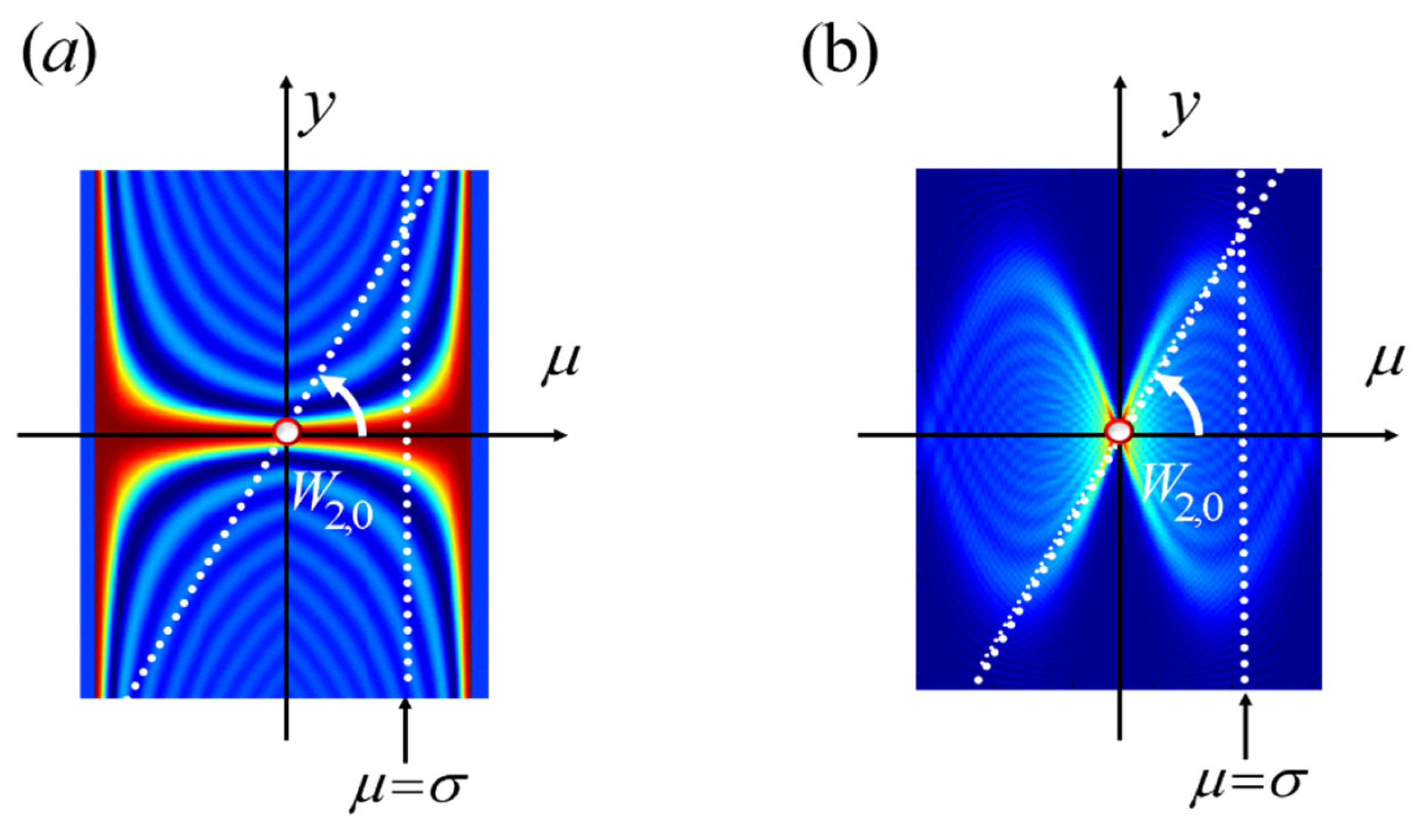
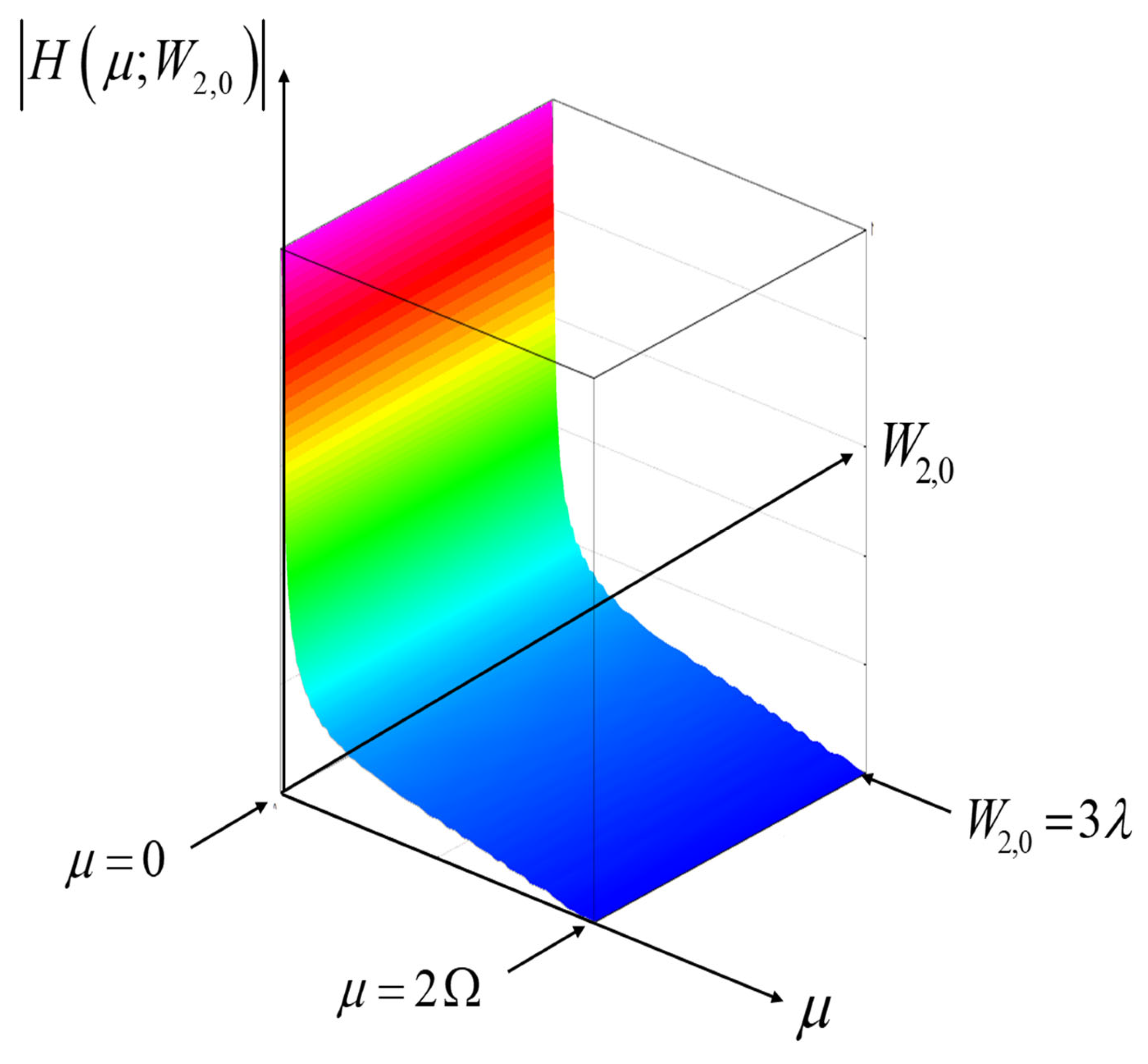
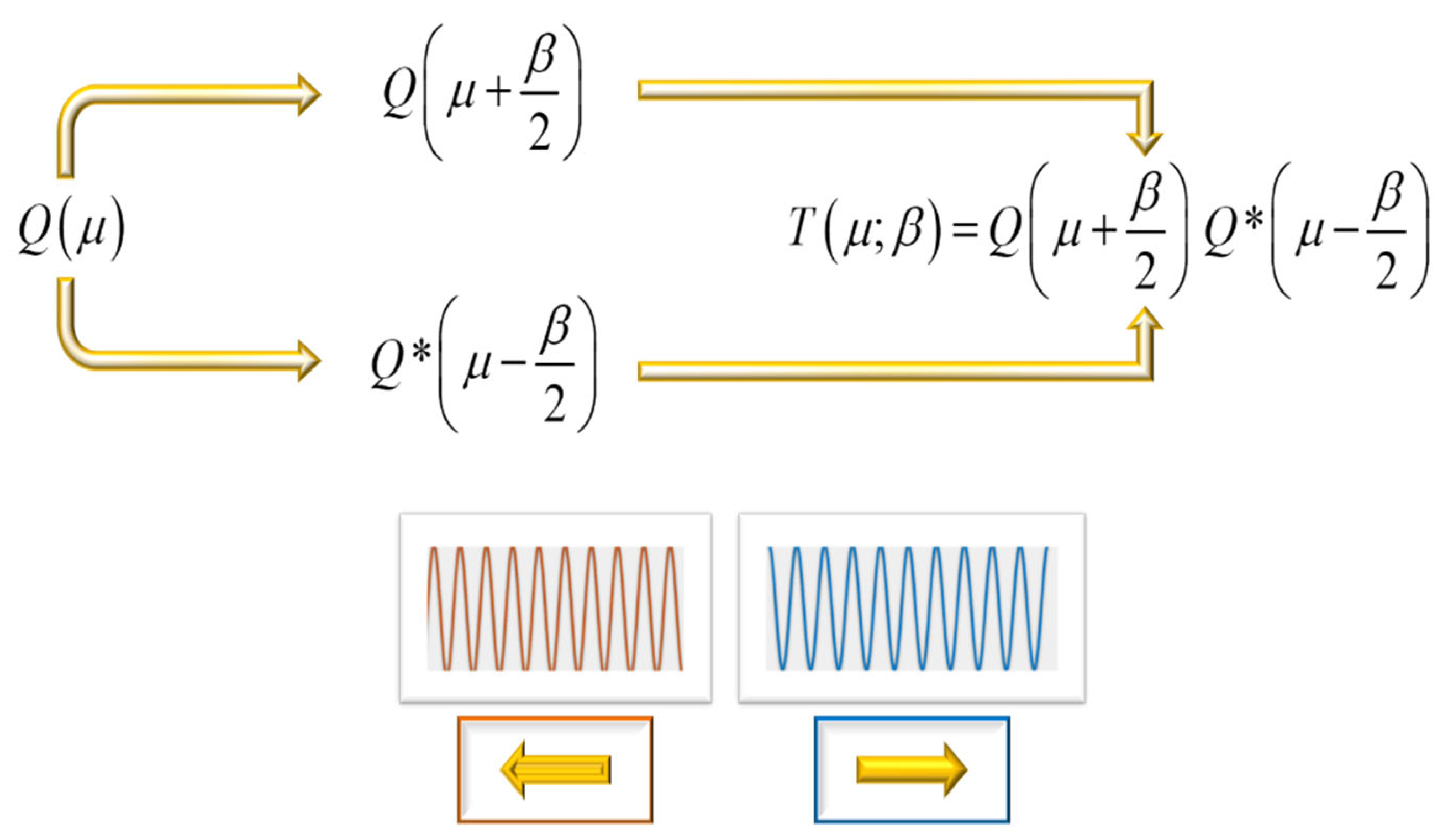
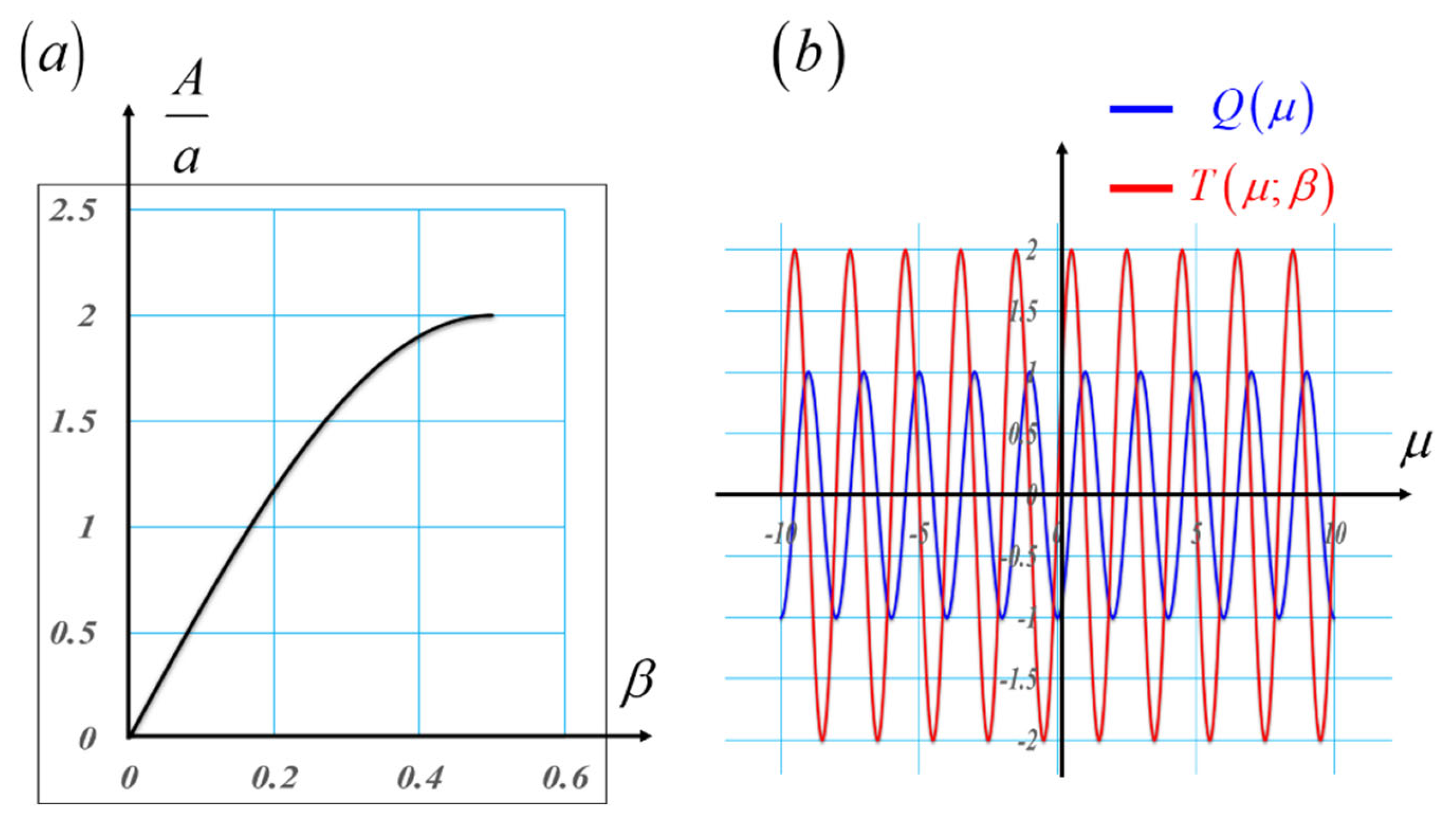
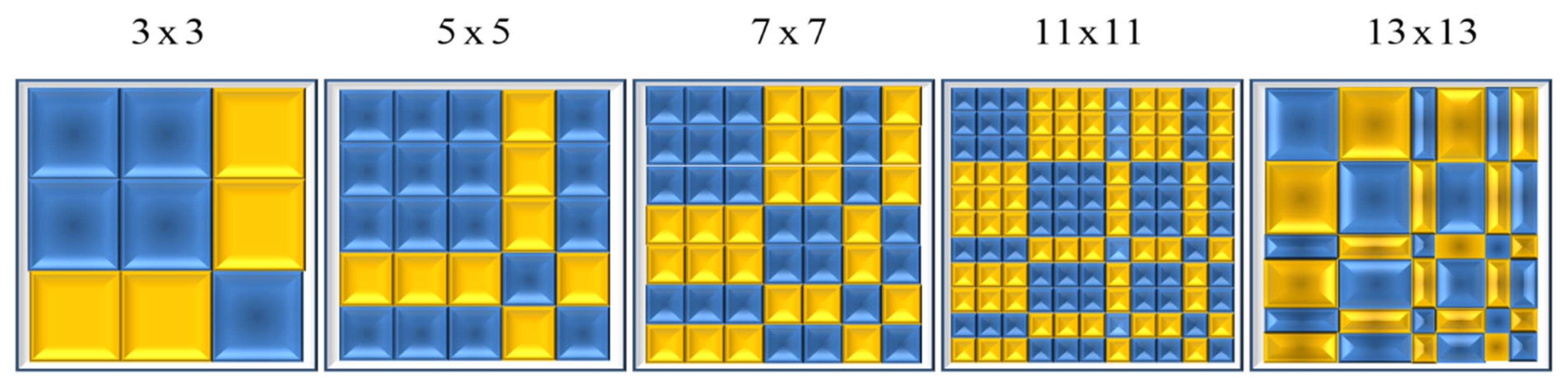
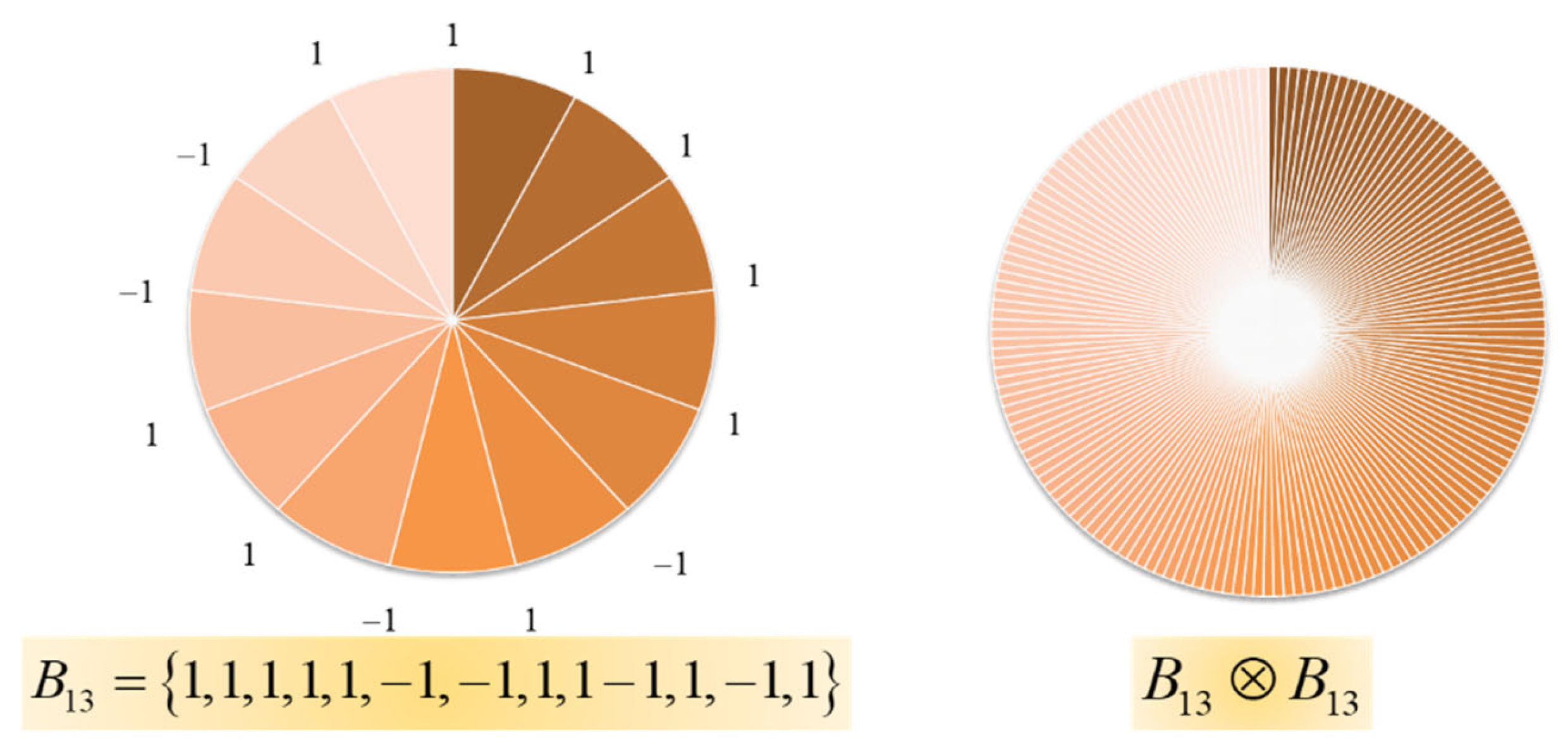
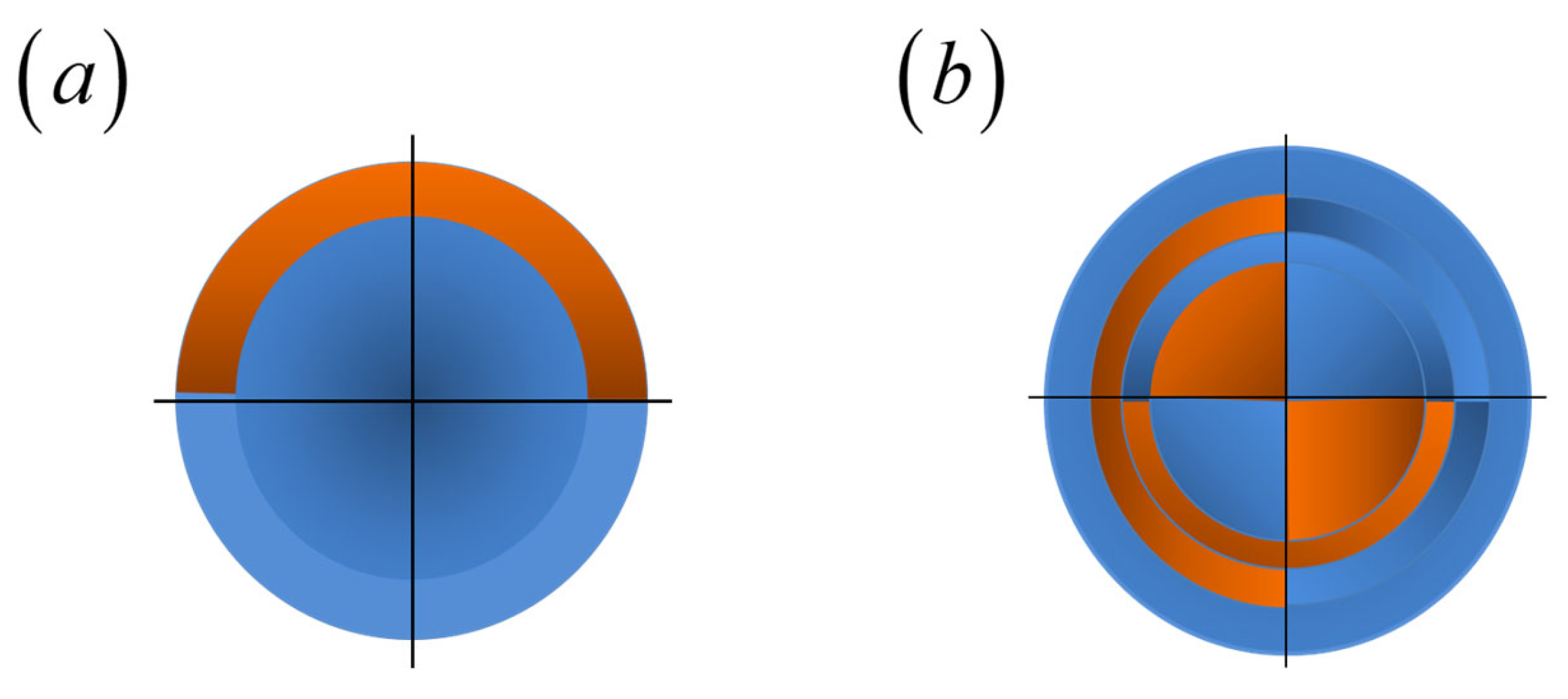
We have exploited the autocorrelation properties of the Barker sequences for generating narrow passband windows, on the OTF. For applications in 2-D Moiré photography, we discussed the use of rectangular masks, which are denoted as the Barker matrices.

A similar procedure, but now in polar coordinates, is useful for designing novel zone plates, here denoted as Barker zone plates, for sensing angular shifts.

We have explored the use of optical systems that generate tunable magnification at zero-throw, for describing anamorphic tunable magnifications, which are of interest in optical processors that produce geometrical transformations.