Variation in Seismic Wave Velocities at Shallow Depth and the Masking of Nonlinear Soil Behavior Based on the ARGONET (Cephalonia, Greece) Vertical Array Data
Abstract
1. Introduction
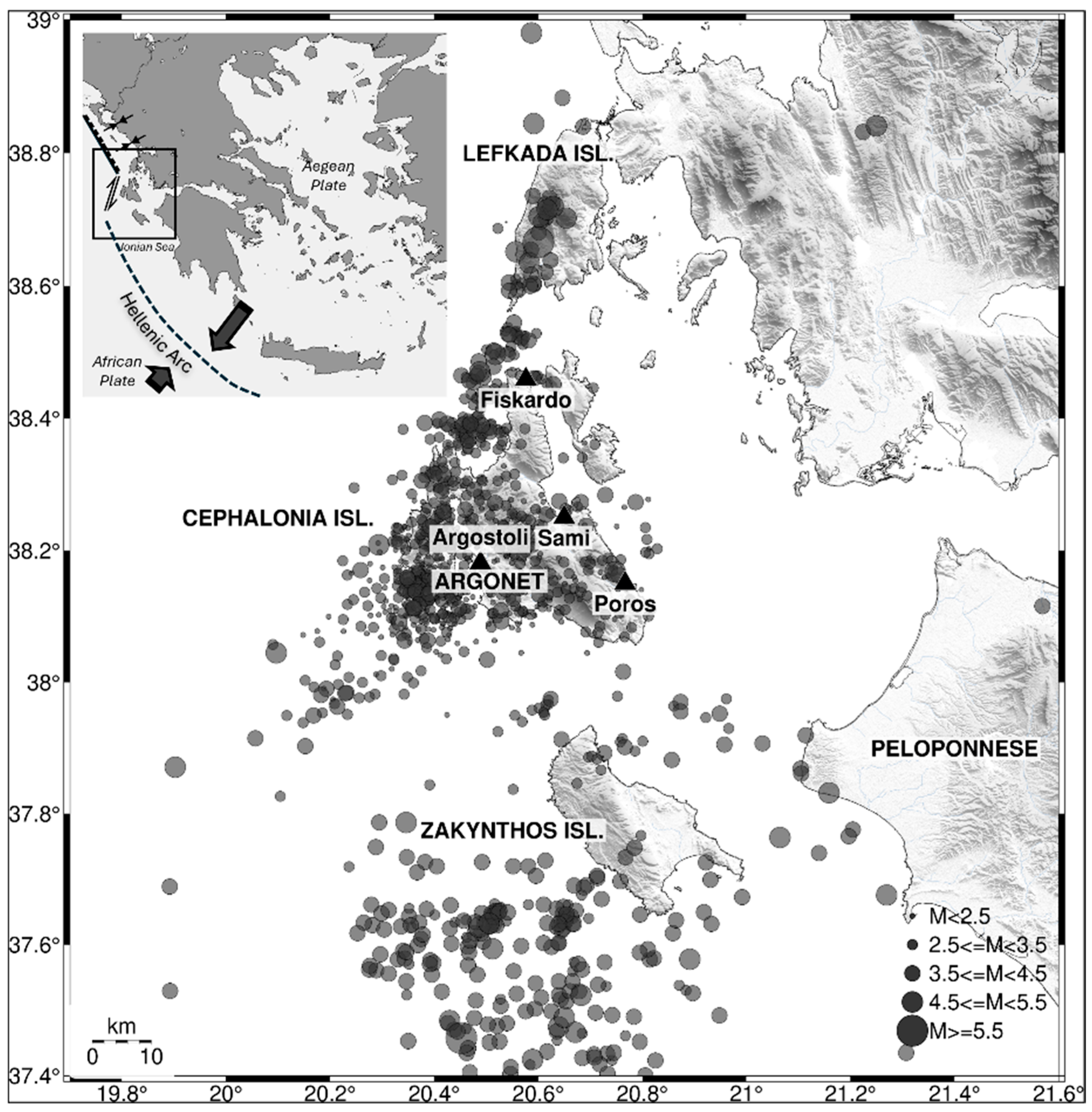
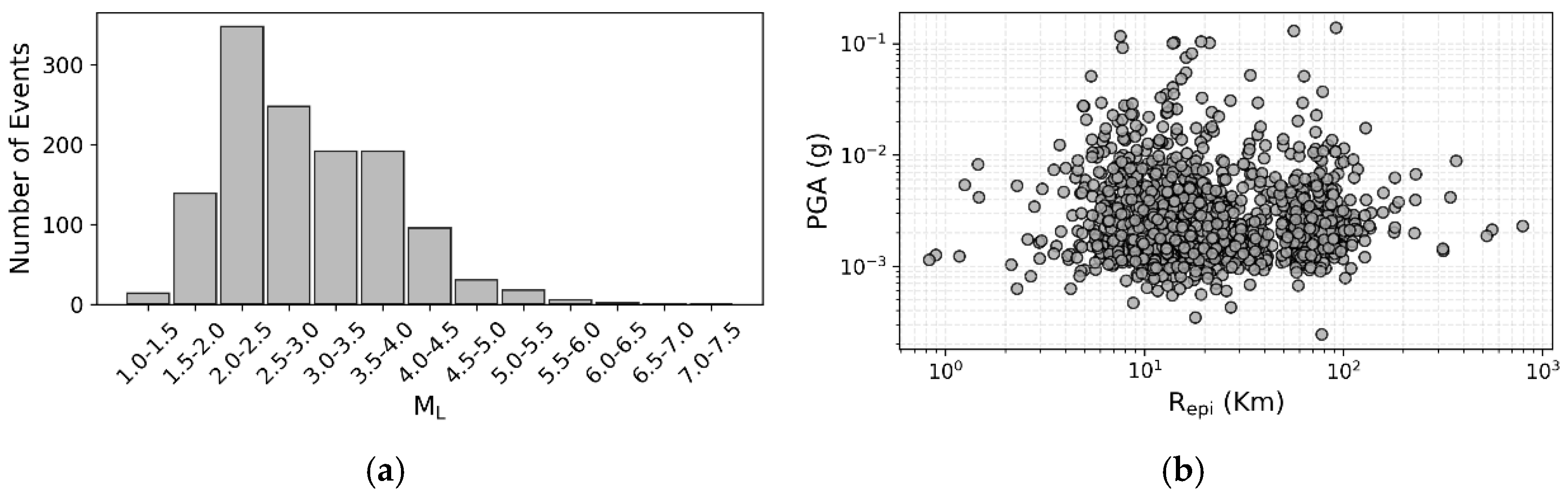
2. Data
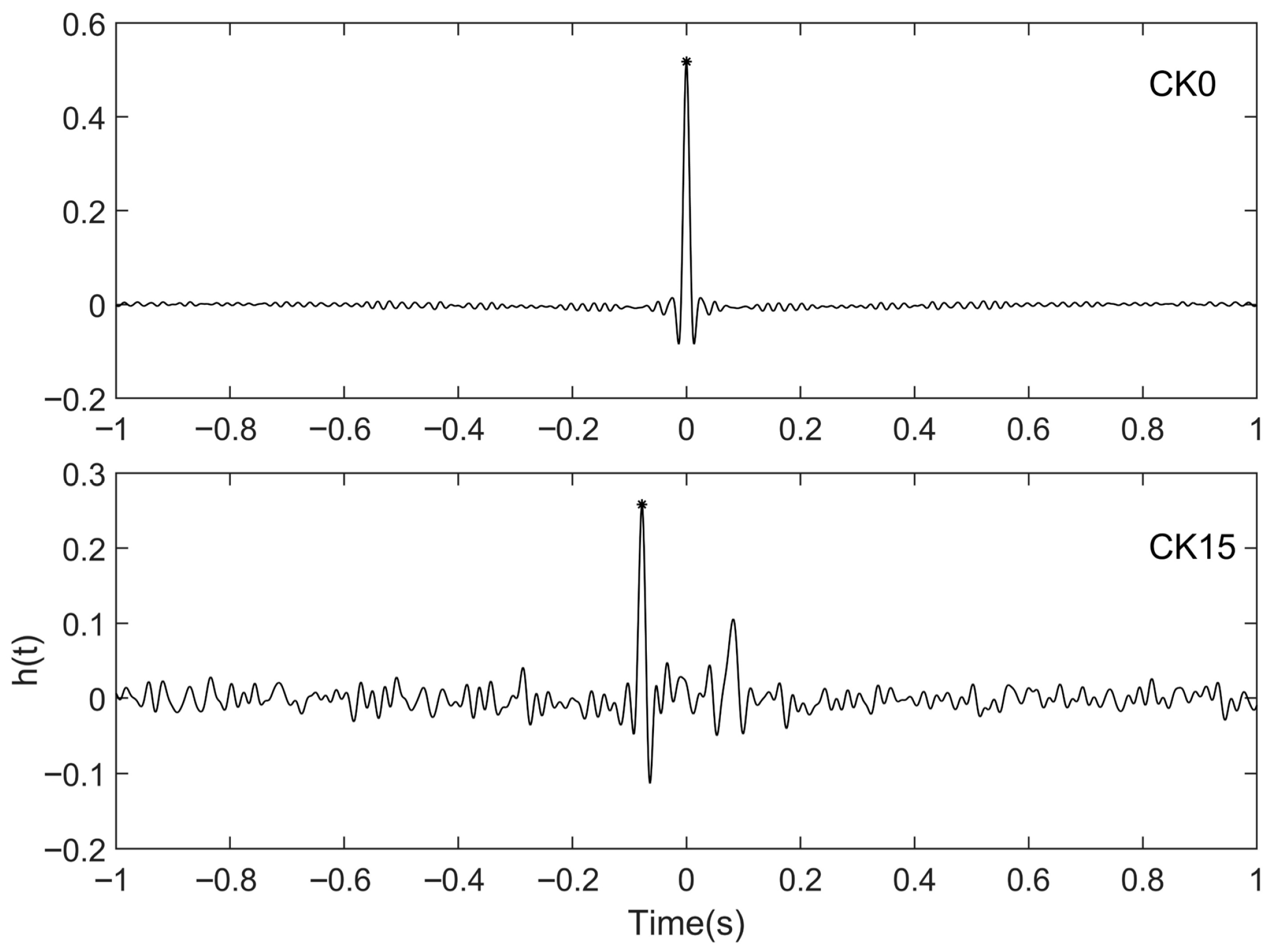
3. Interferometry by Deconvolution
4. Interferometry Results
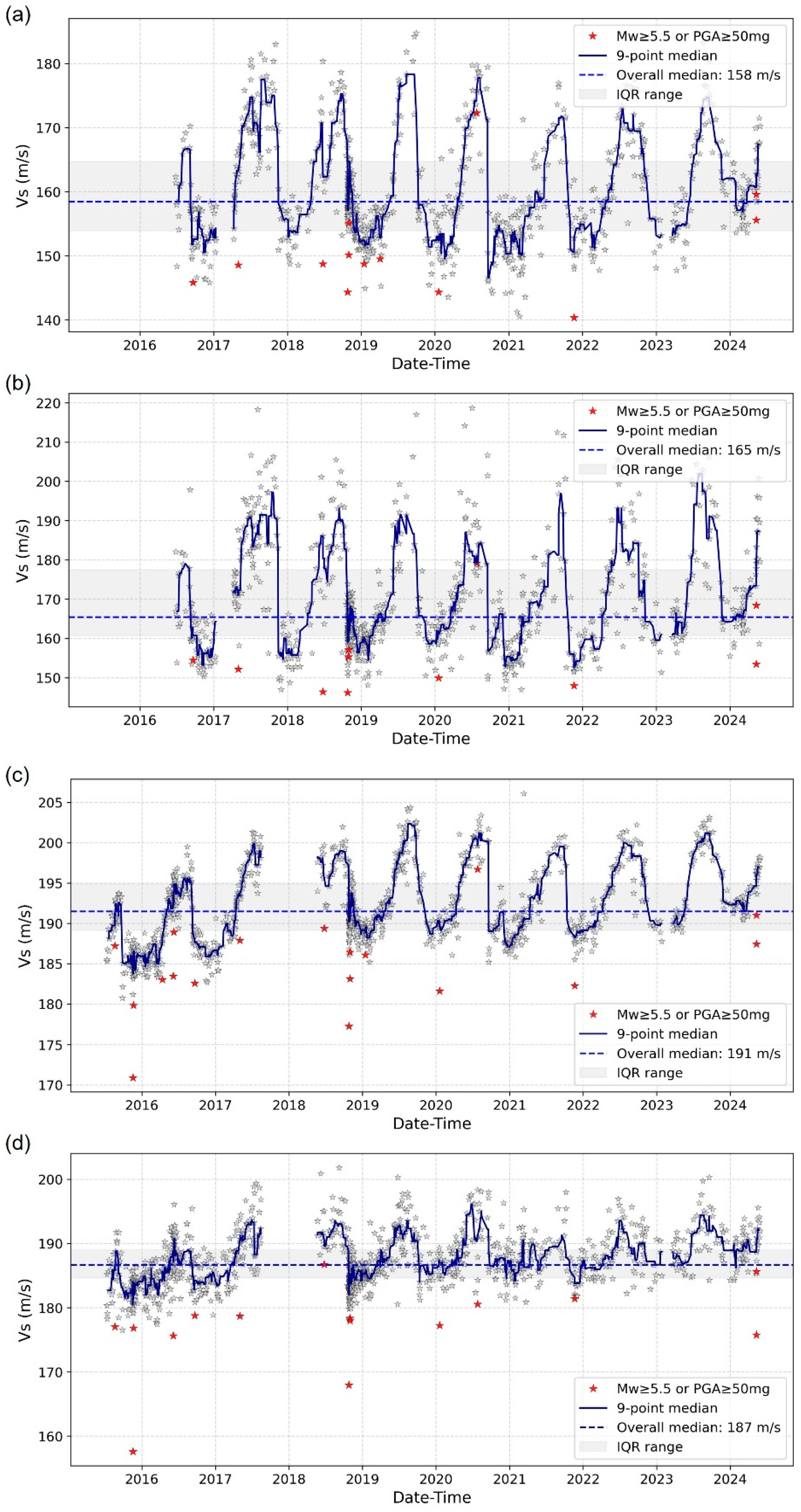
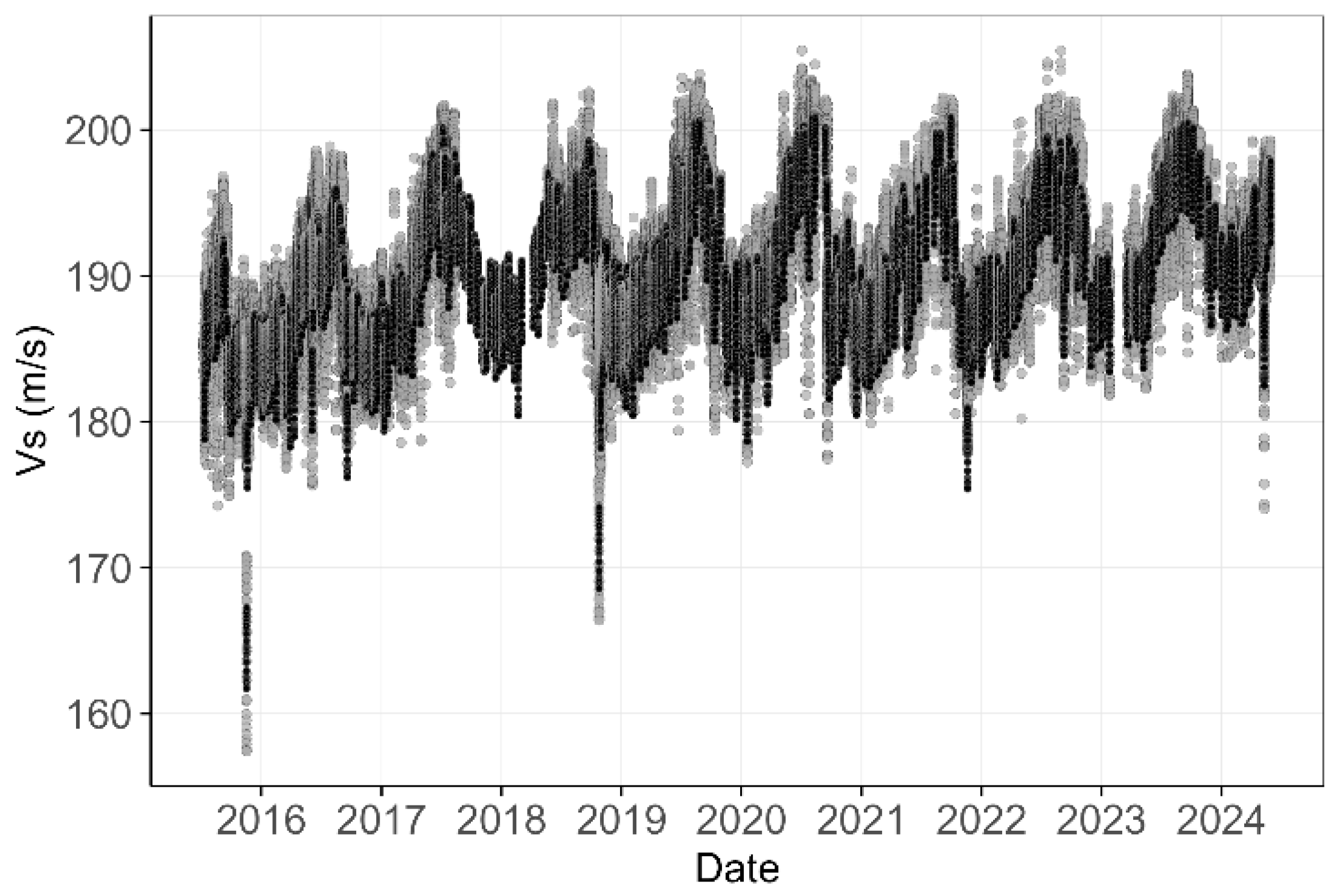
4.1. Temporal Variation of
4.2. Indication for Nonlinear Soil Behavior from
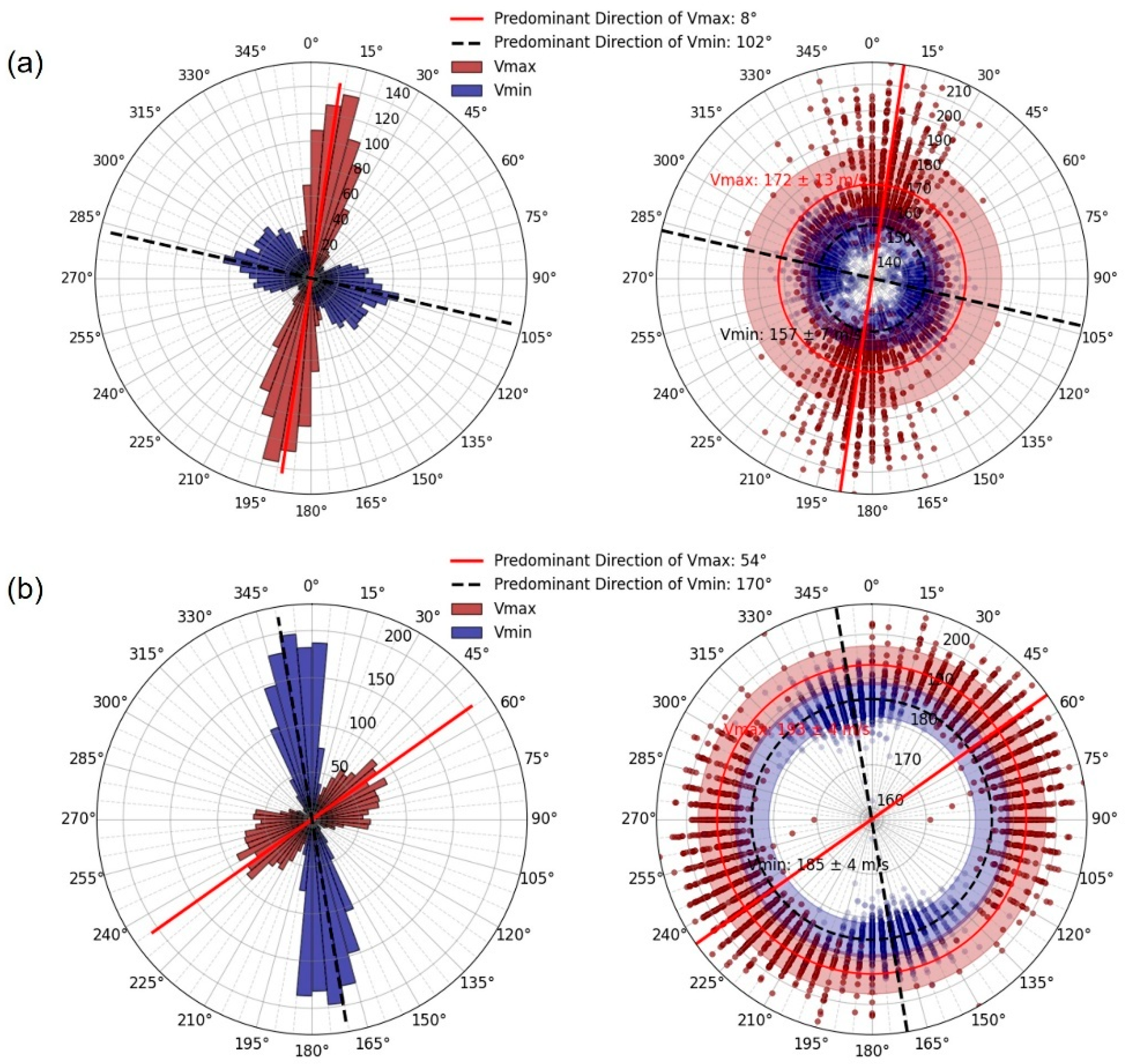
4.3. Azimuthal Variation of
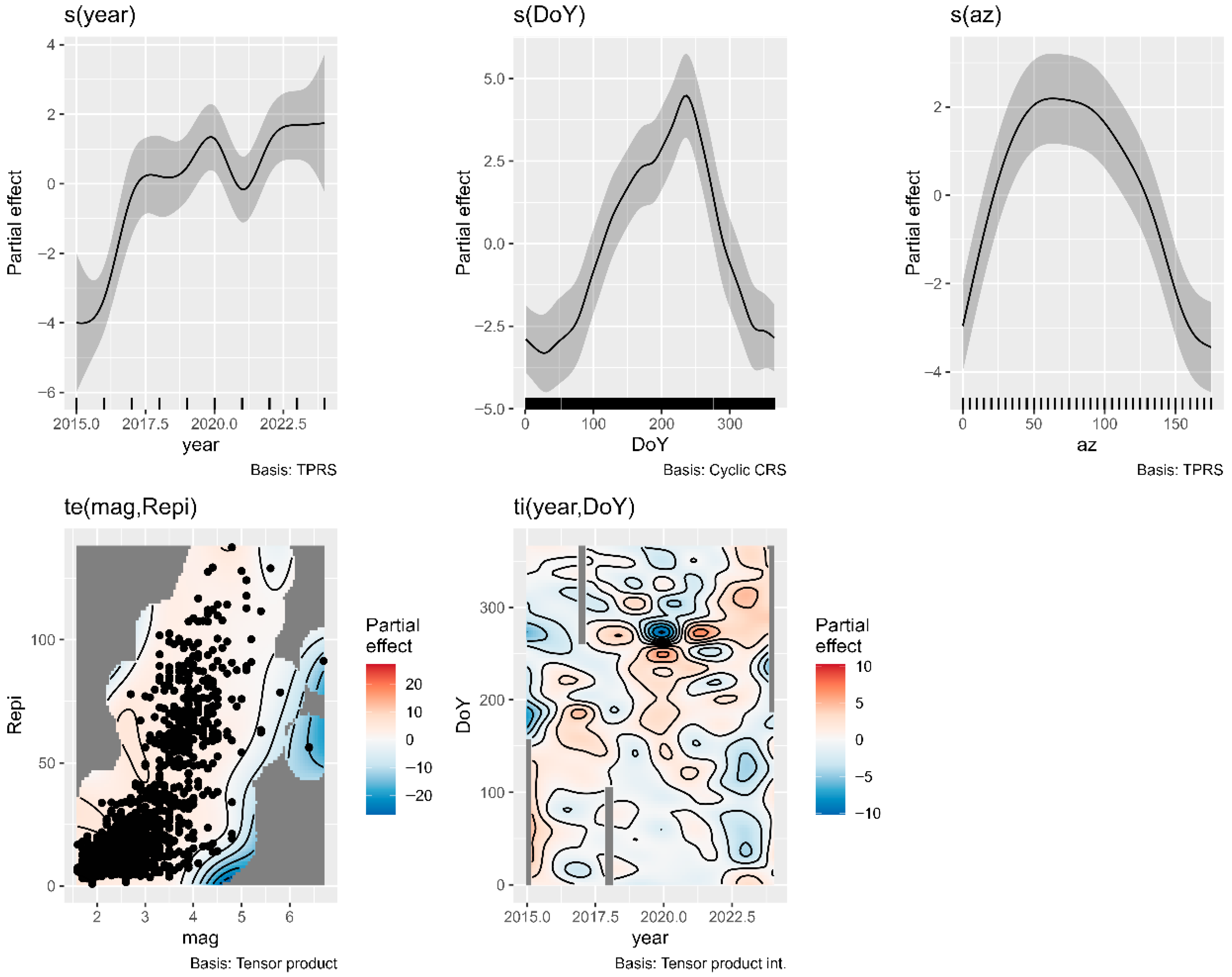
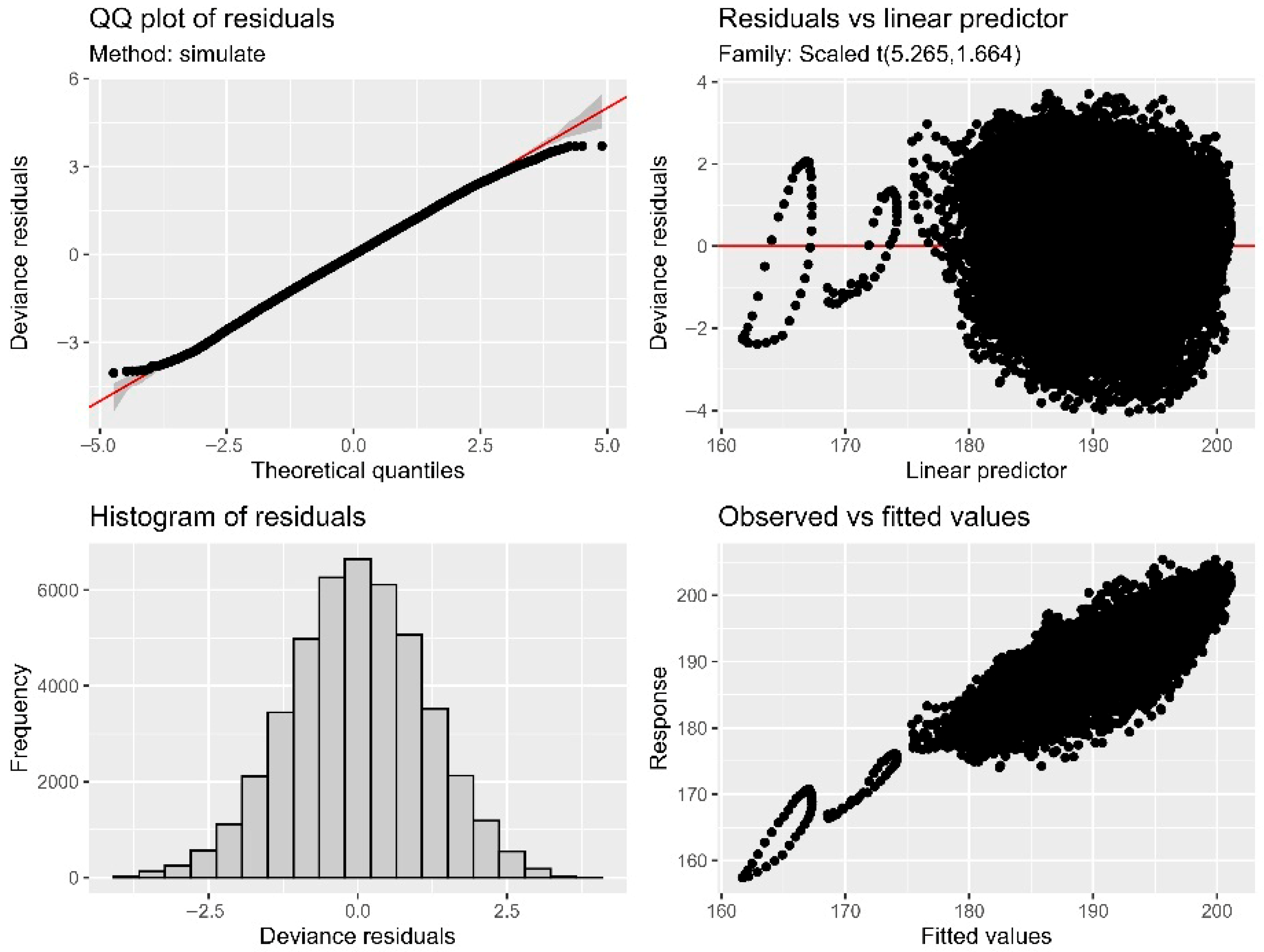
5. Disentangling the Various Partial Effects on Through a Generalized Additive Model
6. Implications for the Masking of Reduction Due to Nonlinear Soil Behavior
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PGA | Peak Ground Acceleration |
| GAM | Generalized Additive Model |
| IQR | Interquartile Range |
| CRS | Cubic Regression Splines |
| TPRS | Thin Plate Regression Splines |
References
- Mehta, K.; Snieder, R.; Graizer, V. Downhole receiver function: A case study. Bull. Seismol. Soc. Am. 2007, 97, 1396–1403. [Google Scholar] [CrossRef]
- Nakata, N.; Snieder, R. Near-surface weakening in Japan after the 2011 Tohoku-Oki earthquake. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Nakata, N.; Snieder, R. Estimating near-surface shear wave velocities in Japan by applying seismic interferometry to KiK-net data. J. Geophys. Res. 2012, 117, B01308. [Google Scholar] [CrossRef]
- Chandra, J.; Guéguen, P.; Steidl, J.H.; Bonilla, L.F. In Situ Assessment of the G-γ Curve for Characterizing the Nonlinear Response of Soil: Application to the Garner Valley Downhole Array and the Wildlife Liquefaction Array. Bull. Seism. Soc. Am. 2015, 105, 993–1010. [Google Scholar] [CrossRef]
- Guéguen, P. Predicting nonlinear site response using spectral acceleration VS PGV/VS30: A case history using the Volvi-Test site. Pure Appl. Geophys. 2016, 173, 2047–2063. [Google Scholar] [CrossRef]
- Roumelioti, Z.; Hollender, F.; Guéguen, P. Rainfall-Induced Variation of Seismic Waves Velocity in Soil and Implications for Soil Response: What the ARGONET (Cephalonia, Greece) Vertical Array Data Reveal. Bull. Seism. Soc. Am. 2020, 110, 441–451. [Google Scholar] [CrossRef]
- Qin, L.; Steidl, J.H.; Qiu, H.; Nakata, N.; Ben-Zion, Y. Monitoring seasonal shear wave velocity changes in the top 6 m at Garner Valley in southern California with borehole data. Geophys. Res. Lett. 2022, 49, e2022GL101189. [Google Scholar] [CrossRef]
- Rubin, A.M. Using Repeating Earthquakes to Correct High-Precision Earthquake Catalogs for Time-Dependent Station Delays. Bull. Seism. Soc. Am. 2002, 92, 1647–1659. [Google Scholar] [CrossRef]
- Paoletti, V. Remarks on factors influencing shear wave velocities and their role in evaluating susceptibilities to earthquake-triggered slope instability: Case study. Nat. Hazards Earth Syst. Sci. 2012, 12, 2147–2158. [Google Scholar] [CrossRef]
- Sens-Schönfelder, C.; Wegler, U. Passive image interferometry and seasonal variations of seismic velocities at Merapi volcano, Indonesia. Geophys. Res. Lett. 2006, 33, L21302. [Google Scholar] [CrossRef]
- Larose, E.; Bontemps, N.; Lacroix, P.; Taipe, E. Landslide monitoring in southern Peru: SEG Geoscientists without borders® project. Proc. SEG Tech. Program Expand. Abstr. 2017, 5322–5326. [Google Scholar] [CrossRef]
- Wang, Q.-Y.; Brenguier, F.; Campillo, M.; Lecointre, A.; Takeda, T.; Aoki, Y. Seasonal crustal seismic velocity changes throughout Japan. J. Geophys. Res. Res. Solid Earth 2017, 122, 7987–8002. [Google Scholar] [CrossRef]
- Clements, T.; Denolle, M.A. Tracking groundwater levels using the ambient seismic field. Geophys. Res. Lett. 2018, 45, 6459–6465. [Google Scholar] [CrossRef]
- Miao, Y.; Shi, Y.; Wang, S.Y. Temporal change of near surface shear wave velocity associated with rainfall in Northeast Honshu, Japan. Earth Planets Space 2018, 70, 204. [Google Scholar]
- Wen, K.-L. Non-linear soil response in ground motions. Earthq. Eng. Struct. Dyn. 1994, 26, 599–608. [Google Scholar]
- Sato, K.; Kokusho, T.; Matsumoto, M.; Yamada, E. Nonlinear seismic response and soil property during strong motion. Soils Found. 1996, 36, 41–52. [Google Scholar] [CrossRef] [PubMed]
- Sawazaki, K.; Sato, H.; Nakahara, H.; Nishimura, T. Temporal change in site response caused by earthquake strong motion as revealed from coda spectral ratio measurement. Geophys. Res. Lett. 2006, 33, L21303. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, S.Y.; Cheng, K.; Miao, Y. In situ characterization of nonlinear soil behavior of vertical ground motion using KiK-net data. Bull. Earthq. Eng. 2020, 18, 4605–4627. [Google Scholar] [CrossRef]
- Rubinstein, J.L.; Beroza, G.G. Evidence for widespread nonlinear strong ground motion in Mw 6.9 Loma Prieta Earthquake. Bull. Seism. Soc. Am. 2004, 94, 1595–1608. [Google Scholar] [CrossRef]
- Rubinstein, J.L.; Beroza, G.G. Depth constraints on nonlinear strong ground motion from the 2004 Parkfield earthquake. Geophys. Res. Lett. 2005, 32, L14313. [Google Scholar] [CrossRef]
- Sawazaki, K.; Sato, H.; Nakahara, H.; Nishimura, T. Time-Lapse Changes of Seismic Velocity in the Shallow Ground Caused by Strong Ground Motion Shock of the 2000 Western-Tottori Earthquake, Japan, as Revealed from Coda Deconvolution Analysis. Bull. Seism. Soc. Am. 2009, 99, 352–366. [Google Scholar] [CrossRef]
- Peng, Z.; Ben-Zion, Y. Temporal changes of shallow seismic velocity around the Karadere-Duzce branch of the North Anatolian Fault and strong ground motion. Pure Appl. Geophys. 2006, 163, 567–599. [Google Scholar] [CrossRef]
- Takagi, R.; Okada, T. Temporal change in shear velocity and polarization anisotropy related to the 2011 M9.0 Tohoku-Oki earthquake examined using KiK-net vertical array data. Geophys. Res. Lett. 2012, 39, L09310. [Google Scholar] [CrossRef]
- Sawazaki, K.; Snieder, R. Time-lapse changes of P- and S-wave velocities and shear wave splitting in the first year after the 2011 Tohoku earthquake, Japan: Shallow subsurface. Geophys. J. Int. 2013, 193, 238–251. [Google Scholar] [CrossRef]
- Wang, H.Y.; Jiang, W.P.; Wang, S.Y.; Miao, Y. In situ assessment of soil dynamic parameters for characterizing nonlinear seismic site response using KiK-net vertical array data. Bull. Earthq. Eng. 2019, 17, 2331–2360. [Google Scholar] [CrossRef]
- Régnier, J. Non-linear soil response at strong motion observation sites with a focus on borehole array. In Proceedings of the 6th IASPEI/IAEE International Symposium: Effects of Surface Geology on Seismic Motion, Kyoto, Japan, 30 August–1 September 2021. [Google Scholar]
- Grendas, I.; Roumelioti, Z.; Theodoulidis, N.; Hollender, F. Ground-Motion Dependency on Seasonal Variations: Observations at the ARGONET Array, Cephalonia, Greece. Bull. Seism. Soc. Am. 2025, 115, 1801–1817. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Gutenberg, B. Effects of ground on earthquake motion. Bull. Seismol. Soc. Am. 1957, 47, 221–250. [Google Scholar] [CrossRef]
- Wiggins, J.J.H. Effect of site conditions on earthquake intensity. J. Struct. Div. 1964, 90, 279–314. [Google Scholar] [CrossRef]
- Borcherdt, R.D. Effects of local geology on ground motion near San Francisco Bay. Bull. Seismol. Soc. Am. 1970, 60, 29–61. [Google Scholar]
- Bard, P.-Y.; Bouchon, M. The Two-Dimensional Resonance of Sediment-Filled Valleys. Bull. Seism. Soc. Am. 1985, 75, 519–541. [Google Scholar] [CrossRef]
- Tucker, B.E.; King, J.L. Dependence of sediment-filled valley response on input amplitude and valley properties. Bull. Seism. Soc. Am. 1984, 74, 153–165. [Google Scholar] [CrossRef]
- Bard, P.Y. Effects of surface geology on ground motion: Recent results and remaining issues. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1994; pp. 305–323. [Google Scholar]
- Anderson, J.G.; Lee, Y.; Zeng, Y.; Day, S. Control of strong motion by the upper 30 meters. Bull. Seism. Soc. Am. 1996, 86, 1749–1759. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology, 2nd ed.; University Science Books: Sausalito, CA, USA, 2002. [Google Scholar]
- Kristek, J.; Moczo, P.; Bard, P.Y.; Hollender, F.; Stripajová, S. Computation of amplification factor of earthquake ground motion for a local sedimentary structure. Bull. Earthq. Eng. 2018, 16, 2451–2475. [Google Scholar] [CrossRef]
- Gan, B.-L.; Zhang, D.-M.; Huang, Z.-K.; Zheng, F.-Y.; Zhu, R.; Zhang, W. Ontology-driven knowledge graph for decision-making in resilience enhancement of underground structures: Framework and application. Tunn. Undergr. Space Technol. 2025, 163, 106739. [Google Scholar] [CrossRef]
- Theodoulidis, N.; Hollender, F.; Mariscal, A.; Moiriat, D.; Bard, P.Y.; Konidaris, A.; Cushing, M.; Konstantinidou, K.; Roumelioti, Z. The ARGONET (Greece) Seismic Observatory: An Accelerometric Vertical Array and Its Data. Seism. Res. Lett. 2018, 89, 1555–1565. [Google Scholar] [CrossRef]
- KF Network, Institute of Engineering Seismology Earthquake Engineering, Atomic Energy and Alternative Energies Commission, University of Patras, & Ionian University. ARGONET, a Vertical Accelerometric Array Implemented on the Island of Kefalonia in Greece [Data set]. 2015, International Federation of Digital Seismograph Networks. Available online: https://doi.org/10.7914/3my7-3148 (accessed on 29 July 2025).
- Clayton, R.W.; Wiggins, R.A. Source shape estimation and deconvolution of teleseismic bodywaves. Geophys. J. R. Astron. Soc. 1976, 47, 151–177. [Google Scholar] [CrossRef]
- Riga, E.; Hollender, F.; Roumelioti, Z.; Bard, P.Y.; Pitilakis, K. Assessing the applicability of deconvolution of borehole records for determining near-surface shear wave attenuation. Bull. Seism. Soc. Am. 2019, 109, 621–635. [Google Scholar] [CrossRef]
- Roumelioti, Z.; Hollender, F. Seasonal Variation of VS at Shallow Depth and Nonlinear Behavior of Soil Based on the ARGONET Vertical Array Data. Tech. Ann. 2024, 1. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models. Statist. Sci. 1986, 1, 297–310. [Google Scholar] [CrossRef]
- Wood, S.N. mgcv: Mixed GAM Computation Vehicle with Automatic Smoothness Estimation, R Package Vvrsion 1.9-3. 2025. Available online: https://cran.r-project.org/web/packages/mgcv/index.html (accessed on 28 September 2025).
- Saltogianni, V.; Moschas, F.; Stiros, S. The 2014 Cephalonia Earthquakes: Finite Fault Modeling, Fault Segmentation, Shear and Thrusting at the NW Aegean Arc (Greece). Pure Appl. Geophys. 2018, 175, 4145–4164. [Google Scholar] [CrossRef]
- Pham, H.Q.; Fredlund, D.G.; Lee Barbour, S. A study of hysteresis models for soil-water characteristic curves. Can. Geotech. J. 2005, 42, 1548–1568. [Google Scholar] [CrossRef]
- James, S.R.; Knox, H.A.; Abbott, R.E.; Screaton, E.J. Improved moving window cross-spectral analysis for resolving large temporal seismic velocity changes in permafrost. Geophys. Res. Lett. 2017, 44, 4018–4026. [Google Scholar] [CrossRef]
- Voisin, C.; Guzmán, M.A.R.; Réfloch, A.; Taruselli, M.; Garambois, S. Groundwater Monitoring with Passive Seismic Interferometry. J. Water Resour. Prot. 2017, 09, 1414–1427. [Google Scholar] [CrossRef]
- Illien, L.; Andermann, C.; Sens-Schönfelder, C.; Cook, K.L.; Baidya, K.P.; Adhikari, L.B.; Hovius, N. Subsurface Moisture Regulates Himalayan Groundwater Storage and Discharge. AGU Adv. 2021, 2, e2021AV000398. [Google Scholar] [CrossRef]
- Mao, S.; Lecointre, A.; van der Hilst, R.D.; Campillo, M. Space-time monitoring of groundwater fluctuations with passive seismic interferometry. Nat. Commun. 2022, 13, 4643. [Google Scholar] [CrossRef]
- Delouche, E.; Stehly, L. Seasonal Seismic Velocity Variations Measured Using Seismic Noise Autocorrelations to Monitor the Dynamic of Aquifers in Greece. J. Geophys. Res. Solid Earth 2023, 128, e2023JB026759. [Google Scholar] [CrossRef]
- Shen, Z.; Yang, Y.; Fu, X.; Adams, K.H.; Biondi, E.; Zhan, Z. Fiber-optic seismic sensing of vadose zone soil moisture dynamics. Nat. Commun. 2024, 15, 6432. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Karagiannidis, A.; Dafis, S.; Kalimeris, A.; Kotroni, V. Ianos—A hurricane in the Mediterranean. Bull. Am. Meteorol. Soc. 2022, 103, E1621–E1636. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service ERA5-Land Hourly Data from 1950 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2024. Available online: https://doi.org/10.24381/cds.e2161bac (accessed on 1 October 2024).
- Muñoz Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications, Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Simpson, G.L. gratia: Graceful ggplot-Based Graphics and Other Functions for GAMs Fitted Using mgcv, [R package] Version 0.11.1. 2023. Available online: https://cran.r-project.org/web/packages/gratia/index.html (accessed on 28 September 2025).
- Beyreuther, M.; Barsch, R.; Krischer, L.; Megies, T.; Behr, Y.; Wassermann, J. ObsPy: A Python toolbox for seismology. Seism. Res. Lett. 2010, 81, 530–533. [Google Scholar] [CrossRef]
- MathWorks. MATLAB, Version R2022a; MathWorks: Natick, MA, USA, 2022.
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools version 6. Geochem. Geophys. Geosystems 2019, 20, 5556–5564. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roumelioti, Z.; Hollender, F.; Theodoulidis, N.; Grendas, I. Variation in Seismic Wave Velocities at Shallow Depth and the Masking of Nonlinear Soil Behavior Based on the ARGONET (Cephalonia, Greece) Vertical Array Data. Appl. Sci. 2025, 15, 10727. https://doi.org/10.3390/app151910727
Roumelioti Z, Hollender F, Theodoulidis N, Grendas I. Variation in Seismic Wave Velocities at Shallow Depth and the Masking of Nonlinear Soil Behavior Based on the ARGONET (Cephalonia, Greece) Vertical Array Data. Applied Sciences. 2025; 15(19):10727. https://doi.org/10.3390/app151910727
Chicago/Turabian StyleRoumelioti, Zafeiria, Fabrice Hollender, Nikolaos Theodoulidis, and Ioannis Grendas. 2025. "Variation in Seismic Wave Velocities at Shallow Depth and the Masking of Nonlinear Soil Behavior Based on the ARGONET (Cephalonia, Greece) Vertical Array Data" Applied Sciences 15, no. 19: 10727. https://doi.org/10.3390/app151910727
APA StyleRoumelioti, Z., Hollender, F., Theodoulidis, N., & Grendas, I. (2025). Variation in Seismic Wave Velocities at Shallow Depth and the Masking of Nonlinear Soil Behavior Based on the ARGONET (Cephalonia, Greece) Vertical Array Data. Applied Sciences, 15(19), 10727. https://doi.org/10.3390/app151910727





