A Collaborative Swarm-Differential Evolution Algorithm for Multi-Objective Multi-Robot Task Assignment

Abstract

Multi-Robot Task Assignment (MRTA) is a critical and inherently multi-objective problem in diverse real-world applications, demanding the simultaneous optimization of conflicting objectives such as minimizing total travel distance and balancing robot workload. Existing multi-objective evolutionary algorithms (MOEAs) often struggle with slow convergence and insufficient diversity when tackling the combinatorial complexity of large-scale MRTA instances. This paper introduces the Collaborative Swarm-Differential Evolution (CSDE) algorithm, a novel MOEA designed to overcome these limitations. CSDE’s core innovation lies in its deep, operator-level fusion of Differential Evolution’s (DE) robust global exploration capabilities with Particle Swarm Optimization’s (PSO) swift local exploitation prowess. This is achieved through a unique fused velocity update mechanism, enabling particles to dynamically benefit from their personal experience, collective swarm intelligence, and population diversity-driven knowledge transfer. Comprehensive experiments on various MRTA scenarios demonstrate that CSDE consistently achieves superior performance in terms of convergence, solution diversity, and Pareto front quality, significantly outperforming standard multi-objective algorithms like Multi-Objective Particle Swarm Optimization (MOPSO), Multi-Objective Differential Evolution (MODE), and Multi-Objective Genetic Algorithm (MOGA). This study highlights CSDE’s substantial contribution to the MRTA field and its potential for more effective and efficient multi-robot system deployment.

1. Introduction

The burgeoning field of multi-robot systems (MRS) has profoundly reshaped our approach to complex operational challenges across diverse domains, spanning from automated warehousing and precision agriculture to intricate space exploration and disaster response [1]. Central to the effective deployment and coordination of these systems is the Multi-Robot Task Assignment (MRTA) problem [2]. This foundational challenge involves optimally allocating a set of available tasks to a team of robots, aiming to achieve system-wide objectives while adhering to various operational constraints. The inherent complexity of MRTA problems stems from their combinatorial nature: as the number of robots and tasks increases, the potential assignment permutations grow exponentially, rendering exhaustive search methods computationally intractable for real-world scenarios [3]. For instance, the exact assignment of N tasks to K robots, without considering sequencing, already involves $K^N$ possibilities. For a problem size of $K=4$ and $N=50$, a simple exhaustive search would need to evaluate $4^{50}\approx 1.27\times {10}^{30}$ assignments. This number is computationally prohibitive and provides a strong quantitative rationale for the transition to meta-heuristic solutions. Furthermore, practical MRTA applications frequently demand the simultaneous optimization of multiple, often conflicting, objectives, such as minimizing total travel distance for the entire fleet, maximizing task completion rates, and ensuring an equitable distribution of workload among robots [4]. Balancing these competing objectives adds another layer of significant challenge, pushing the boundaries of traditional optimization paradigms.

Current methodologies for tackling the MRTA problem typically fall into two broad categories: exact methods and heuristic/meta-heuristic approaches. While exact methods, such as integer linear programming or constraint programming, can guarantee optimal solutions for smaller instances, their prohibitive computational cost makes them impractical for large-scale or dynamic environments. Consequently, meta-heuristic algorithms, including Particle Swarm Optimization (PSO) [5], Differential Evolution (DE) [6], Genetic Algorithms (GAs) [7], and Ant Colony Optimization (ACO) [8], have emerged as popular alternatives due to their ability to find near-optimal solutions within reasonable computational time. However, these individual meta-heuristics often exhibit specific limitations. For instance, PSO is known for its rapid convergence but can be prone to premature convergence into local optima, particularly in high-dimensional and multimodal landscapes. Conversely, DE excels in global exploration and possesses robust local optima avoidance capabilities due to its differential mutation strategy, but it can sometimes suffer from slower convergence speeds. The limitations of these isolated optimization paradigms—namely, the trade-off between exploration and exploitation and their propensity to become trapped in sub-optimal solutions—underscore a critical need for more sophisticated and robust problem-solving mechanisms in the context of multi-objective MRTA [9].

Driven by the imperative to overcome the inherent limitations of standalone meta-heuristics, this study explores a novel approach centered on knowledge transfer between DE and PSO paradigms. Our core motivation stems from the observation that while individual algorithms possess unique strengths, a synergistic integration could harness these advantages to create a more powerful and adaptable search strategy. By enabling the dynamic exchange of search experience and strategic guidance, a combined framework can enhance both the breadth of exploration across the solution landscape and the speed and precision of convergence towards the Pareto optimal front. This concept of collaborative intelligence, where different algorithmic philosophies inform and enhance one another, forms the bedrock of our research. It aims to develop a system that not only efficiently locates high-quality solutions but also maintains a diverse set of trade-off solutions, crucial for practical decision-making in multi-objective scenarios.

In response to these challenges and drawing upon the potential of synergistic algorithmic integration, this paper introduces the Collaborative Swarm-Differential Evolution (CSDE) algorithm, a novel multi-objective evolutionary algorithm (MOEA) specifically designed for the complexities of the Multi-Robot Task Assignment (MRTA) problem. Our primary innovation lies in the operator-level fusion of DE’s robust global exploration capabilities with PSO’s swift local exploitation prowess. This deep integration is realized through a fused velocity update mechanism that dynamically assimilates individual experiential knowledge, collective collaborative knowledge from an external archive, and population diversity exploration knowledge derived from differential perturbations. Beyond this core knowledge transfer mechanism, CSDE incorporates a sophisticated multi-objective Pareto front maintenance strategy, employing non-dominated sorting and crowding distance assignment to ensure both convergence and diversity of the discovered solutions. Furthermore, the algorithm is bolstered by a self-adaptive parameter management scheme, which dynamically tunes critical algorithmic parameters such as inertia weight and learning factors, thereby optimizing the balance between exploration and exploitation throughout the evolutionary process. These synergistic contributions enable CSDE to efficiently navigate the complex multi-objective landscape of the MRTA problem, yielding a comprehensive and well-distributed set of Pareto optimal solutions.

The remainder of this paper is structured as follows. Section 2 provides a comprehensive overview of related work in multi-robot task assignment and multi-objective evolutionary algorithms (MOEAs). Section 3 formally defines the MRTA problem, detailing its mathematical formulation, objective functions, and constraints. Section 4 presents the proposed CSDE algorithm in detail, elaborating on its architecture, the fused velocity update mechanism, multi-objective Pareto front maintenance strategies, and self-adaptive parameter management. Section 5 describes the experimental setup and presents the empirical results, comparing CSDE’s performance against state-of-the-art algorithms, including Multi-Objective Particle Swarm Optimization (MOPSO), Multi-Objective Differential Evolution (MODE), and Multi-Objective Genetic Algorithm (MOGA). Finally, Section 6 concludes the paper and outlines directions for future research.

2. Related Work

Before delving into the specifics of our proposed methodology, it is crucial to establish a robust foundation by reviewing the existing landscape of relevant research. This section first provides a comprehensive overview of the MRTA problem, clarifying its complexities and the various approaches employed for its resolution. Subsequently, we will explore the fundamental principles of MOO, which are indispensable for addressing the multifaceted nature of real-world MRTA scenarios. Finally, we will examine prevalent hybrid and collaborative meta-heuristic strategies, laying the groundwork for understanding the inspiration and unique contributions of our CSDE algorithm.

2.1. Multi-Robot Task Assignment Problem

The MRTA problem represents a cornerstone challenge in the field of MRS, directly influencing their operational efficacy across a myriad of applications, ranging from automated manufacturing and logistics to critical missions such as exploration, search and rescue, and environmental monitoring. Fundamentally, MRTA involves the judicious allocation of a set of tasks to a team of available robots, with the overarching goal of optimizing system-wide objectives while adhering to specific operational and environmental constraints. The inherent complexity of MRTA problems necessitates a clear classification to delineate problem scope and applicable solution methodologies. Common categorizations include:

1.

Single-task robots vs. multi-task robots: distinguishing whether each robot can execute only one task at a time or is capable of performing multiple tasks sequentially or concurrently.

2.

Single-robot tasks vs. multi-robot tasks: classifying if a task requires the attention of only one robot or if it demands coordinated effort from multiple robots.

3.

Instantaneous vs. time-extended tasks: differentiating between tasks that are completed at a single point in time and those requiring sustained effort over a duration.

4.

Online vs. offline assignment: determining if tasks are assigned dynamically as they arrive (online) or if all tasks are known beforehand and assigned in a pre-computation phase (offline). Our current study focuses on an offline MRTA scenario. This format assumes that all tasks are known in advance, which is a foundational problem type for many real-world applications, such as automated warehousing and preplanned surveillance missions. By addressing the problem in a static, offline setting, we can rigorously evaluate the core performance of our algorithm—its convergence, diversity, and solution quality—without the complexities of dynamic changes. This approach allows for a controlled and precise analysis of the algorithm’s fundamental strengths.

5.

Single-objective vs. multi-objective optimization: identifying whether the problem aims to optimize a single performance metric (e.g., total distance) or multiple, often conflicting, objectives (e.g., total distance, task load balance, completion time). The MRTA variant addressed in this paper explicitly falls under multi-objective optimization, demanding the concurrent optimization of total travel distance and task load imbalance.

The combinatorial explosion inherent in most MRTA variants, particularly those involving routing components like the Traveling Salesperson Problem (TSP) for task sequencing, renders them NP-hard. This computational intractability implies that as the number of robots (K) and tasks (N) increases, the search space grows exponentially, making exhaustive enumeration infeasible for practical problem sizes. For instance, the exact assignment of N tasks to K robots, without considering sequencing, already involves $K^N$ possibilities. When routing is factored in, the complexity escalates further.

The choice to focus on an offline setting in this paper is strategic. It provides a controlled and reproducible environment to rigorously benchmark the core capabilities of our proposed CSDE algorithm in a multi-objective context, isolating its performance from the complexities of dynamic and real-time task arrival. However, the superior convergence and diversity performance of CSDE, as demonstrated in our experiments, make its core optimization engine an ideal candidate for integration into replanning frameworks for dynamic or online MRTA. In such systems, CSDE could be used to rapidly re-optimize task allocations whenever new information or tasks become available.

2.2. Multi-Objective Optimization (MOO)

Many real-world optimization problems, including complex engineering design, economic planning, and, critically, MRTA, are inherently characterized by the need to simultaneously optimize multiple, often conflicting, objectives. This class of problems falls under the domain of MOO, also known as multi-criteria optimization or Pareto optimization. Unlike single-objective problems where the goal is to find a unique global optimum, MOO seeks to identify a set of compromise solutions that represent the best possible trade-offs among the competing objectives [10]. Formally, a multi-objective minimization problem with M objectives and D decision variables can be expressed as

$$\begin{array}{c}\hfill \underset{\mathbf{x}}{min}\mathbf{F}\left(\mathbf{x}\right)=\left[\begin{array}{c}{f}_1\left(\mathbf{x}\right)\\ f_2\left(\mathbf{x}\right)\\ ⋮\\ f_M\left(\mathbf{x}\right)\end{array}\right]\\ \hfill \mathrm{subject}\mathrm{to}\mathbf{x}\in \mathrm{\Omega }\end{array}$$

(1)

where $\mathbf{x}=[x_1,x_2,\dots ,x_D]$ is the decision vector, $\mathrm{\Omega }$ is the feasible decision space, and $f_j\left(\mathbf{x}\right)$ represents the j-th objective function. The vector $\mathbf{F}\left(\mathbf{x}\right)$ maps a decision vector from the decision space $\mathrm{\Omega }$ to the objective space $\mathcal{Z}$.

The fundamental concept in MOO is that of dominance. For two solutions, ${\mathbf{x}}_A$ and ${\mathbf{x}}_B$, in the decision space: ${\mathbf{x}}_A$ is said to dominate ${\mathbf{x}}_B$ (denoted as ${\mathbf{x}}_A\prec {\mathbf{x}}_B$) if and only if ${\mathbf{x}}_A$ is no worse than ${\mathbf{x}}_B$ on all objectives, and ${\mathbf{x}}_A$ is strictly better than ${\mathbf{x}}_B$ on at least one objective.

Mathematically, for a minimization problem, this means

$$\begin{array}{cc}\hfill f_j\left({\mathbf{x}}_A\right)\le f_j\left({\mathbf{x}}_B\right),& \mathrm{for}\mathrm{all}j\in \{1,\dots ,M\},\hfill \\ \hfill f_k\left({\mathbf{x}}_A\right)<f_k\left({\mathbf{x}}_B\right),& \mathrm{for}\mathrm{at}\mathrm{least}\mathrm{one}k\in \{1,\dots ,M\}.\hfill \end{array}$$

(2)

If neither ${\mathbf{x}}_A$ dominates ${\mathbf{x}}_B$ nor ${\mathbf{x}}_B$ dominates ${\mathbf{x}}_A$, they are said to be non-dominated with respect to each other.

The ultimate goal in MOO is to find the Pareto-optimal set (PS), which comprises all solutions in the decision space that are not dominated by any other feasible solution. The mapping of these Pareto-optimal solutions into the objective space forms the Pareto Front (PF). Since, in most practical problems, it is computationally intractable to find all Pareto-optimal solutions, the objective of MOEAs is to find a good approximation of the true Pareto Front. A “good approximation” implies two key characteristics: convergence, meaning the solutions generated are as close as possible to the true Pareto Front, and diversity, meaning the solutions are uniformly spread across the Pareto Front, representing a wide range of trade-offs.

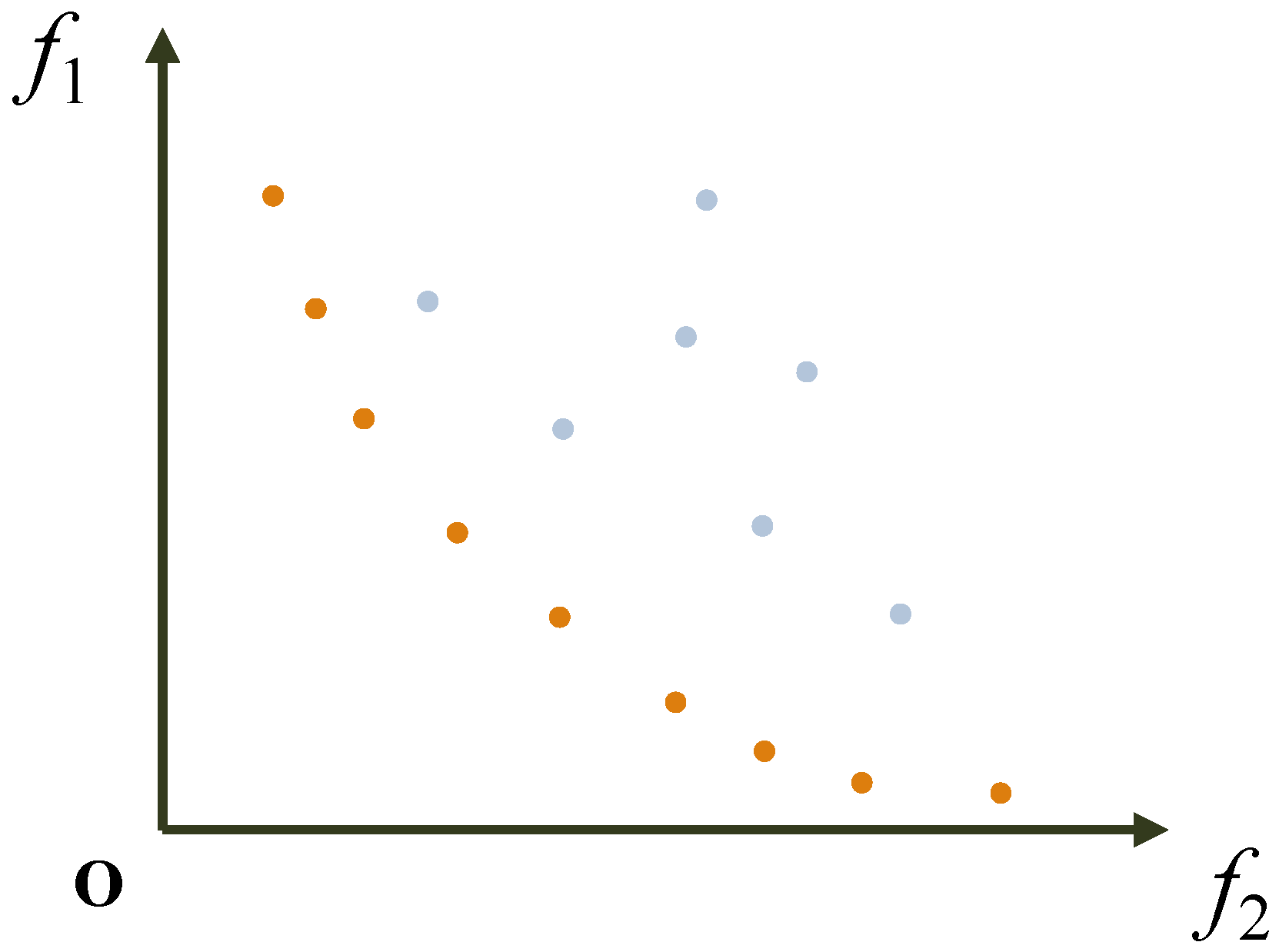
Figure 1 depicts the dominance relationship among solutions in a two-dimensional objective space. The orange points represent the first non-dominated front, which are mutually non-dominated and are not dominated by any light blue point. Conversely, the light blue points constitute the second non-dominated front, being dominated by the orange points. In MOO, the objective of the algorithm is to find and maintain a set of non-dominated solutions, such as those represented by the orange points, to approximate the true Pareto front.

The multi-objective nature of the MRTA problem, specifically the conflict between minimizing total travel distance ($f_1\left(X\right)$) and minimizing task load imbalance ($f_2\left(X\right)$), gives rise to a classic trade-off relationship. A solution that achieves an extremely low total travel distance often does so by assigning a disproportionately large number of tasks to a few nearby robots, thereby increasing the workload imbalance. Conversely, a solution with a perfectly balanced workload might require robots to traverse longer distances to reach tasks, leading to a higher total travel distance. This inherent conflict means that no single solution can optimize both objectives simultaneously, and the optimal results are not a single point but a set of non-dominated solutions forming the Pareto front. This front represents the full spectrum of trade-off solutions, from those that prioritize efficiency (low travel distance) to those that prioritize fairness (low load imbalance).

The complexity of this trade-off, especially in large-scale, high-dimensional search spaces, presents significant challenges for standard MOEAs. While methods like MOPSO are effective for rapid convergence, their strong reliance on a global best can sometimes lead to premature convergence to a narrow region of the Pareto front, failing to discover the full diversity of trade-off solutions. Similarly, MODE, despite its robust global exploration capabilities, can exhibit slower convergence rates during the exploitation phase, potentially resulting in a Pareto front that is not sufficiently close to the true optimal front. Our proposed CSDE algorithm is explicitly designed to overcome these limitations by synergistically combining the complementary strengths of these paradigms.

Over the past decades, several prominent MOEAs have emerged to address the dual challenges of convergence and diversity in complex optimization problems. NSGA-II [11], a highly influential MOEA, pioneered the use of non-dominated sorting to efficiently classify solutions into “fronts”, and crowding distance assignment to promote diversity within these fronts. These core mechanisms, widely adopted in subsequent MOEAs (including the one proposed in this paper), collectively drive populations towards the PF while ensuring a broad and uniform distribution of solutions. Building on single-objective principles, MOPSO [12] adapts PSO’s velocity and position updates for multi-objective scenarios, commonly employing an external archive to guide the swarm’s movement towards non-dominated regions. While MOPSO often converges quickly, it can sometimes suffer from premature convergence or insufficient diversity. Conversely, MODE [13] applies DE’s powerful differential mutation and recombination operators, offering robust global exploration and strong local optima avoidance. However, MODE variants can exhibit slower convergence during the exploitation phase when fine-tuning solutions.

These foundational MOEAs have significantly advanced multi-objective problem-solving. Yet, achieving an optimal balance between rapid convergence and comprehensive diversity remains a critical challenge, particularly for intricate problems like MRTA. This ongoing pursuit motivates the development of more advanced, often hybridized, optimization strategies to push the boundaries of performance.

2.3. Related Research

The Multi-Robot Task Allocation problem is a critical area of research in robotics, addressing how to efficiently assign tasks to a team of robots to achieve mission objectives. Various approaches have been explored, ranging from evolutionary algorithms and market-based strategies to game theory and constrained optimization.

2.3.1. Evolutionary Algorithms and Optimization for MRTA

Evolutionary Algorithms (EAs), owing to their global search capabilities, have been widely applied to MRTA problems with notable success. Miloradović et al. [14] transformed MRTA into an extended Traveling Salesman Problem (TSP), combining mixed-integer linear programming with a genetic mission planner to enhance efficiency through local optimization. Kong et al. [15] integrated greedy search with an improved Particle Swarm Optimization (PSO) to search for optimal task-robot combinations. Huang et al. [16] proposed a niching immune optimization algorithm based on softmax regression, utilizing population pre-judgment to reduce evaluation time and accelerate computation. Nedjah et al. [17] designed a stochastic distributed algorithm to optimize communication for large-scale robot swarm allocation. Li et al. [18] integrated a high-reward mechanism, benefit distribution, and historical task information, proposing a stable quantum PSO to speed up the search. Beyond traditional EAs, researchers have explored more specialized optimization techniques. Gautam et al. [19] proposed a distributed algorithm for balanced multi-robot task allocation by computing a traveling salesman tour using a distributed genetic algorithm and partitioning it among robots via an auction algorithm, demonstrating superior load balancing and minimized travel distance. Yang et al. [20] introduced a multi-objective evolutionary algorithm with a maximin fitness function and a one-by-one update scheme for multi-robot scheduling in intelligent warehouses, effectively balancing energy consumption and outperforming existing algorithms. Nekovář et al. [21] tackled power transmission line inspection using UAVs by formulating the problem as a Multi-tour Set Traveling Salesman Problem (MS-TSP), solved with Integer Linear Programming (ILP) for optimal solutions and a Greedy Randomized Adaptive Search Procedure (GRASP) heuristic for faster, near-optimal results. While these methods have demonstrated excellent performance in improving efficiency, most primarily focus on finding a single optimal solution, often neglecting the crucial aspect of diversity maintenance in multi-objective contexts.

In response to the limitations of individual meta-heuristics, a prominent research direction has been the hybridization of different paradigms to leverage their complementary strengths. Among these, the hybridization of DE and PSO has proven particularly effective in creating powerful optimizers that achieve a better balance between exploration and exploitation. These hybrid algorithms, often termed DEPSOs, have been extensively reviewed and categorized based on factors such as the relationship between parent optimizers (e.g., collaboration, embedding, assistance), the hybridization level, and the type of information transferred. A wide range of DEPSO variants exists in the literature, demonstrating diverse design ideas to improve performance for specific problems. For example, some approaches, like DEPSO-ZX, use DE to perturb the personal best positions of particles to prevent stagnation. Others, such as PSO with differentially perturbed velocity (DEPSO-DKC) [22], embed DE’s differential mutation into PSO’s velocity update to enhance population diversity.

Unlike these existing methods, our proposed CSDE algorithm introduces a deep, operator-level fusion. This is achieved through a unique fused velocity update mechanism that synergistically combines a particle’s personal best experience, the collective knowledge from a global archive, and a diversity-driven differential perturbation term from DE. This fundamental difference in design allows CSDE to dynamically balance exploration and exploitation in a more integrated and powerful manner than traditional methods. This is evidenced by our experimental results, where CSDE consistently achieves superior performance in terms of convergence, solution diversity, and overall Pareto front quality, especially for multi-objective problems where maintaining a comprehensive set of trade-off solutions is critical.

2.3.2. Market-Based and Auction Mechanisms

Market-based approaches and auction mechanisms have emerged as a robust paradigm for dynamic and distributed MRTA, particularly in environments with unreliable communication or changing task requirements. Ferri et al. [23] proposed the Periodic Auctions Distributed Algorithm (PADA), a market-based framework for autonomous underwater surveillance networks, enabling dynamic task reallocation through periodic auctions. Wang and Sheng [24] introduced a multi-robot task allocation algorithm based on an anxiety model and a modified Contract Network Protocol (CNP), incorporating trust, familiarity, and capability parameters to enhance efficiency and robustness. Karmani et al. [25] presented the Market-based Approach with Look-ahead Agents (MALA) for large-scale multi-agent task reallocation, where agents use a modified Universal Traveling Salesman Problem (U-TSP) to negotiate and optimize assignments, demonstrating scalability and reduced complexity. Further advancements in auction-based methods include the work by Madhyastha et al. [26], who proposed a distributed approach for scheduling autonomous vehicle fleets using agent-based procurement auctions, significantly improving passenger waiting times and fuel efficiency. Trigui et al. [27] developed two distributed market-based algorithms, DMB and IDMB, with IDMB showing near-optimal solutions and outperforming centralized methods by enabling task swapping. Khamis et al. [28] investigated market-based approaches for complex task allocation in mobile surveillance systems, comparing centralized and hierarchical strategies and highlighting the effectiveness of hierarchical dynamic tree allocation for large-scale scenarios. Liu et al. [29] introduced the Constraint-based Approach (CoBA) for multi-robot coordination, leveraging a market-based approach with an AND/OR task tree and indirect bidding to handle temporal and communication constraints in complex environments like disaster response. For robust and decentralized task allocation, Choi et al. [30] proposed the consensus-based decentralized auction algorithm (CBAA) and its extension, the consensus-based bundle algorithm (CBBA), for autonomous vehicle fleets. These algorithms combine auction-based selection with consensus-based conflict resolution, guaranteeing conflict-free assignments even with inconsistent information. Building on this, Chen et al. [31] extended consensus-based auction algorithms with a cluster-first strategy and dynamic grouping for multi-robot systems with critical time constraints, enhancing solution quality and robustness in unstable communication environments. Sujit and Beard [32] proposed a distributed sequential auction scheme for UAVs with limited sensor and communication ranges, ensuring efficient task allocation through neighbor-based target validation and sequential auctions. Zhang et al. [33] introduced an efficient Stochastic Clustering Auction (SCA) for heterogeneous robotic teams, which uses a modified Swendsen–Wang method to allow stochastic transfers and swaps of task clusters, improving global cost. Basile et al. [34] explored auction-based mechanisms for Smart Logistic Systems (SLSs), evaluating different auction types and demonstrating a methodology for tuning auction-based algorithms to optimize performance.

2.3.3. Advanced Coordination and Scheduling Strategies

Emerging technologies and theoretical frameworks continue to inject vitality into MRTA research, offering more sophisticated coordination and scheduling solutions. Zheng and Wang [35] developed a distributed parallel framework that decomposes tasks into sub-task automata, enhancing allocation efficiency. Dai et al. [36] integrated a backpropagation neural network with a GA to optimize execution speed. Otte et al. [37] employed an auction algorithm to address scenarios with impaired communication, introducing a valuation function to enhance robustness. Bai et al. [38] proposed a reliability allocation method for degradation processes, integrating factor evaluation hierarchical analysis with T–S fuzzy fault tree analysis, adaptable for multi-fault systems. Beyond these, game theory provides a powerful lens for analyzing cooperation in MRTA. Martín et al. [39] proposed a cooperative game theory-based algorithm for MRTA, utilizing the Shapley value to cluster robots and tasks, demonstrating improved computational efficiency and allocation cost for large-scale problems compared with genetic algorithms. Reis et al. [40] proposed an axiomatic framework based on Social Choice Theory to analyze the MRTA problem, using Arrow’s Impossibility Theorem to study task allocation mechanisms under different preference profiles and robot capabilities. Addressing specific practical challenges, Aljalaud et al. [41] proposed a multi-UAV task allocation algorithm inspired by the area-restricted search (ARS) behavior of animal foraging, significantly reducing rescue time in search and rescue missions. For industrial applications, De Ryck et al. [42] proposed a decentralized task allocation algorithm for Automated Guided Vehicle (AGV) systems that integrates routing constraints into the auction process, reducing congestion and improving routing efficiency. Ham and Park [22] presented a comprehensive study on human–robot task allocation and scheduling inspired by the Boeing 777 Fully Autonomous Upright Build (FAUB) project, formulating the problem as a flexible job shop scheduling problem and demonstrating the computational efficiency of constraint programming for optimal schedules.

2.3.4. Challenges and Future Directions

From the analysis of these diverse research streams, a critical gap emerges in the state-of-the-art for multi-objective MRTA. While evolutionary algorithms offer powerful global search capabilities, they often face an inherent trade-off between convergence speed and solution diversity, a limitation that is particularly acute for standalone meta-heuristics like PSO or DE. Market-based and advanced coordination methods are excellent for specific practical constraints but typically do not generate a comprehensive set of Pareto optimal trade-off solutions, which is essential for informed decision-making in multi-objective problems. Our proposed CSDE algorithm is designed to bridge this gap. By achieving an operator-level fusion of DE’s robust global exploration and PSO’s swift local exploitation, CSDE offers a single, coherent framework that can overcome the limitations of individual paradigms, providing a more effective and efficient solution for complex multi-objective MRTA problems.

In industrial practice, robots often require charging or task switching after completion, leading to dynamic resource availability. This necessitates algorithms that can generate a diverse set of high-quality solutions to support flexible decision-making. However, existing methods frequently fall short in maintaining diversity and computational efficiency in complex scenarios, particularly facing bottlenecks in generating multimodal solutions. For instance, the Single Task, Single Robot, Task Allocation (ST-SR-TA) mode often requires balancing long-term sequencing with dynamic adjustments, where traditional EAs frequently struggle due to their inherent randomness or parameter dependencies. Designing efficient algorithms capable of adapting to MRTA’s multimodal characteristics, especially in multi-objective contexts where a range of trade-offs is desired, thus becomes a key research imperative. Against this background, this study proposes the CSDE framework, which, through continuous encoding and a novel fused velocity update mechanism that synergistically combines DE for global exploration and PSO for local exploitation, aims to significantly optimize both solution diversity and computational efficiency. This research provides a practical and robust solution for complex multi-objective MRTA problems, addressing the aforementioned limitations of existing methods.

3. Problem Formulation

The MRTA problem is a cornerstone in multi-robot systems research, focusing on the optimal allocation of a set of tasks to a team of robots. In this study, we specifically address an MRTA scenario comprising N independent tasks that must be precisely assigned to K robots. Each robot initiates its operation from a designated depot, undertakes its allocated tasks, and subsequently returns to its originating depot upon completion. The inherent complexity of this problem stems from its combinatorial nature and the necessity to concurrently optimize multiple, often conflicting, objectives to achieve a truly effective and efficient task distribution.

The foundational elements of this MRTA problem are explicitly defined to establish a clear framework for optimization. We consider a finite set of depots, $D=\{d_1,d_2,\dots ,d_K\}$, where each $d_k$ not only represents a unique geographical location but also serves as the operational base for a robot, marking its departure and return points. Concurrently, a collection of tasks, $T=\{t_1,t_2,\dots ,t_N\}$, represents distinct points in the environment that require service. A fundamental constraint dictates that each task $t_j$ must be executed exactly once by precisely one robot.

A comprehensive distance matrix, $M_{ij}$, quantifies the shortest path distance between any two nodes, i and j, within the problem domain, encompassing both depots and task locations. This matrix is pre-computed to facilitate efficient path calculation and inter-node navigation. This pre-computation, executed before the optimization process begins, significantly enhances computational efficiency for subsequent fitness evaluations. For the purpose of applying evolutionary algorithms, the MRTA problem is encoded into a structured representation suitable for continuous optimization. A prospective task assignment solution is therefore represented as a real-valued decision vector $X=[x_1,x_2,\dots ,x_N]$, where the dimensionality of the vector directly corresponds to the total number of tasks. Each element $x_j$ within this vector is associated with the j-th task and is constrained to fall within the continuous interval $[0,K)$. The transformation from this continuous encoding to a discrete task assignment is straightforward: task $t_j$ is definitively decoded and assigned to depot $d_k$, where $k=\lfloor x_j\rfloor +1$. This deterministic mapping ensures that every task is uniquely and unambiguously linked to a specific operating depot. Moreover, once tasks are assigned to a particular depot, their precise execution sequence is subsequently optimized by the internal path planning module. This sequencing typically involves solving a TSP variant for the tasks assigned to that specific robot, thereby minimizing the intra-depot travel distance and contributing to the overall path efficiency. To achieve this, the internal path planning module employs a heuristic approach, where the 2-opt algorithm is utilized to determine a near-optimal tour for each robot’s assigned tasks. By reducing the individual travel distance, this method provides an efficient solution to the NP-hard TSP sub-problem, which in turn plays a crucial role in ensuring the overall computational performance of the algorithm.

The problem, in its essence, is cast as a multi-objective optimization problem, requiring the simultaneous improvement of two critical, often conflicting, objectives. The first objective, minimizing total travel distance ($f_1\left(X\right)$), aims to reduce the cumulative distance traversed by all robots as they execute their allocated tasks. For any given assignment solution X, which is first rigorously decoded, the set of tasks $T_k$ assigned to each depot $d_k$ is identified. The path planning module then computes $D_k$, representing the shortest path distance for robot k to cover its assigned tasks in $T_k$ and return to $d_k$. The aggregate total travel distance is simply the summation of these individual robot distances:

$$f_1\left(X\right)=\sum _{k=1}^K{D}_k$$

(3)

It is important to note that if a depot is not assigned any tasks, its corresponding $D_k$ is considered zero, reflecting no travel overhead. Complementing the efficiency objective is the second objective, minimizing task load imbalance ($f_2\left(X\right)$). This objective addresses the crucial need for an equitable distribution of tasks among the robotic fleet. An imbalanced workload can lead to operational inefficiencies, with some robots being overutilized while others remain idle, ultimately impacting system throughput and overall robustness. To quantify this imbalance, we utilize the variance of the number of tasks assigned to each depot:

$$f_2\left(X\right)={\displaystyle \frac{1}{K}}\sum _{k=1}^K\left(\right|T_k{|-\overline{N})}^2$$

(4)

where $|T_k|$ denotes the cardinality of the task set assigned to depot $d_k$, and $\overline{N}=N/K$ is the average number of tasks per robot. A lower variance directly correlates with a more balanced and desirable task distribution across the robotic team.

In addition to these objectives, the MRTA problem is subject to several fundamental constraints that ensure the feasibility and validity of any proposed solution. Foremost among these is the unique task assignment constraint: every task must be assigned to exactly one robot. This ensures that no task is overlooked or redundantly performed. Furthermore, the valid robot traversal constraint stipulates that each robot must commence its operational route from its designated depot, successfully complete all its assigned tasks, and conclude its route by returning to the very same depot. These constraints collectively define the boundaries of the feasible solution space.

Synthesizing these elements, the multi-robot task assignment problem is formally expressed as a bi-objective optimization problem:

$$\begin{array}{c}\hfill \mathrm{Minimize}:F\left(X\right)=(f_1\left(X\right),f_2\left(X\right))\end{array}$$

(5)

$$\begin{array}{c}\hfill \mathrm{Subject}\mathrm{to}:\forall j\in \{1,\dots ,N\},x_j\in [0,K)\end{array}$$

(6)

$$\begin{array}{c}\hfill \forall t_j\in T,\exists d_k\in D\mathrm{s}.\mathrm{t}.t_j\mathrm{is}\mathrm{assigned}\mathrm{to}{d}_k.\end{array}$$

(7)

This comprehensive formulation precisely delineates the mathematical structure of the MRTA problem being addressed, providing a solid foundation for the subsequent development and analysis of the CSDE algorithm.

4. Collaborative Swarm-Differential Evolution (CSDE)

The CSDE algorithm represents a novel knowledge-transfer-based multi-objective evolutionary algorithm specifically engineered for the complexities of the MRTA problem. Its innovation lies in the strategic integration of the robust global exploration capabilities inherent in DE with the swift local exploitation prowess characteristic of PSO. This integration transcends a mere concatenation of operators; it constitutes a profound, operator-level fusion designed to facilitate dynamic and effective knowledge transfer between these distinct optimization paradigms. This synergistic collaboration ultimately enhances the algorithm’s capacity to thoroughly explore the solution space and converge efficiently towards a well-distributed Pareto front. CSDE’s operational efficacy is rooted in its unique algorithmic architecture, its core knowledge transfer mechanism, sophisticated multi-objective decision-making, and adaptive parameter tuning. These components are elaborated in the subsequent sections, followed by the overall algorithm flow.

4.1. Encoding and Decoding for MRTA

To effectively apply the CSDE algorithm to the discrete MRTA problem, a robust and intuitive encoding and decoding mechanism is indispensable. This mechanism translates the continuous real-valued decision variables of the evolutionary algorithm into a valid and interpretable task assignment plan for the robots. Each individual (particle) within the CSDE population maintains a position vector ($X_i$), a real-valued array of length N, where N is the total number of tasks. Each element $x_j$ in this vector corresponds to the j-th task and holds a continuous value within the range $[0,K)$, where K is the number of robots (or depots).

The decoding process then translates these continuous values into discrete task assignments. For each task $t_j$, its corresponding value $x_j$ in the position vector is used to determine which of the K robots it is assigned to. Specifically, task $t_j$ is assigned to robot $d_k$, where the robot index k is derived using the floor function and a simple offset:

$$k=\lfloor x_j\rfloor +1$$

(8)

This formula ensures that any floating-point value within $[0,1)$ maps to robot 1, $[1,2)$ maps to Robot 2, and so on, up to $[K-1,K)$ mapping to robot K. This deterministic mapping guarantees that every task is uniquely assigned to a single robot, satisfying a fundamental constraint of the MRTA problem. Once tasks are assigned to a specific robot, their execution sequence is then optimized by an internal path planning module, which typically solves a TSP variant for the tasks allocated to that robot to minimize its travel distance.

Consider an illustrative example with $N=5$ tasks and $K=3$ robots. As depicted in Figure 2, a hypothetical position vector for an individual is $X=[0.8,2.1,1.5,0.3,2.9]$; applying the decoding formula results in the following task assignments: Robot 1: Tasks $\{t_1,t_4\}$, Robot 2: Task $\left\{t_3\right\}$, Robot 3: Tasks $\{t_2,t_5\}$. After this assignment, the path planning module would then determine the optimal sequence for Robot 1 to visit $t_1$ and $t_4$, for Robot 2 to visit $t_3$, and for Robot 3 to visit $t_2$ and $t_5$, minimizing their respective travel distances. This encoding scheme effectively maps the continuous optimization space of CSDE to the discrete assignment decisions of the MRTA problem, facilitating the algorithm’s search for optimal multi-objective solutions.

4.2. Fused Velocity Update Mechanism: Operator-Level Knowledge Transfer

The innovative core of CSDE resides in its Fused Velocity Update Mechanism, serving as the primary conduit for operator-level knowledge transfer between the DE and PSO paradigms. This sophisticated mechanism enables each individual (particle) to dynamically assimilate diverse forms of optimization knowledge, derived from its own historical experience, the collective intelligence of the swarm, and the inherent diversity within the population. We distinctly conceptualize three pivotal knowledge sources integrated within CSDE:

1.

Individual experiential knowledge: Intrinsically tied to the individual best position ($pbes{t}_i$) of each particle. This personal historical record guides a particle’s current movement towards previously discovered promising regions of the search space, representing its accumulated success.

2.

Collective collaborative knowledge: Derived directly from the External Archive, a dynamic repository of the collective non-dominated solutions accumulated by the entire population. From this archive, a “global best” particle position ($gbest$) is stochastically selected for each particle, serving as a powerful societal beacon that directs the particle towards the most successful collective achievements uncovered by the swarm.

3.

Population diversity exploration knowledge: A unique form of wisdom directly transferred from the DE paradigm. It manifests as a differential perturbation term, ingeniously derived from the vector difference between two distinct, randomly selected individuals from the current population. This component introduces a potent exploratory force, enabling particles to leverage the intrinsic variance within the population to escape local optima and robustly probe novel, unsearched regions of the landscape.

These distinct knowledge forms are synergistically combined within the CSDE fused velocity update formula:

$$\begin{array}{c}\hfill V_{new,i}=w·V_{old,i}+c_1·r_1·(pbes{t}_i-X_i)\\ \hfill +c_2·r_2·(gbest-X_i)+F_{DE}·r_3·(X_{ra}-X_{rb})\end{array}$$

(9)

Each term within this comprehensive formula plays a vital role in facilitating this intricate knowledge transfer. The inertial term ($w·V_{old,i}$), governed by the inertia weight w, embodies the particle’s memory and its propensity to maintain its previous trajectory, thereby reflecting the persistence of its self-acquired experience. The cognitive learning term ($c_1·r_1·(pbes{t}_i-X_i)$), influenced by the cognitive learning factor $c_1$ and a random number $r_1\in [0,1]$, precisely guides the particle towards its individual best position, symbolizing the crucial assimilation of personal experiential knowledge. Complementing this, the social learning term ($c_2·r_2·(gbest-X_i)$), driven by the social learning factor $c_2$ and a random number $r_2\in [0,1]$, pulls the particle towards a collective non-dominated solution sampled from the External Archive, representing the potent influence of collective collaborative knowledge. Most significantly, the differential perturbation term ($F_{DE}·r_3·(X_{ra}-X_{rb})$) serves as the direct channel for transferring DE’s formidable exploratory power. Here, $F_{DE}$ is a DE-specific scaling factor, $r_3$ is a random number in $[0,1]$, and $X_{ra}$ and $X_{rb}$ are two distinct, randomly chosen individuals from the current population. This term injects a dynamic, diversity-driven force by leveraging the difference vector between two other individuals. This intrinsic mechanism proactively promotes escaping local optima and facilitates the robust exploration of novel regions, acting as a direct transfer of population diversity knowledge. This deep, synergistic fusion enables a powerful transfer of knowledge across paradigms: DE’s diversity-enhancing capabilities are intrinsically woven into PSO’s rapid convergence mechanism, while PSO’s guided search (through personal and global bests) accelerates the overall optimization process of the DE-infused particles. This bidirectional influence cultivates an exceptionally robust search strategy that effectively balances global exploration and local exploitation throughout the entire optimization process.

4.3. Multi-Objective Pareto Front Maintenance: Diversity and Convergence Mechanisms

To effectively navigate the complex multi-objective search space inherent in MRTA problems and ensure convergence towards a well-distributed Pareto front, CSDE incorporates a sophisticated Multi-Objective Pareto Front Maintenance strategy. This strategy rigorously evaluates solutions based on their multi-objective performance and employs advanced mechanisms to select and preserve the most promising individuals across generations. The two primary objective functions, $f_1\left(X\right)$ (total travel distance) and $f_2\left(X\right)$ (task load imbalance), dictate the fitness landscape for each individual. The evaluation process systematically decodes each individual’s position vector, utilizes a dedicated path planning module for precise distance calculation (which judiciously employs internal caching mechanisms to optimize repeated calculations for identical task sequences), and computes the variance in task distribution.

Central to this maintenance strategy are two interconnected mechanisms: non-dominated sorting and crowding distance assignment. These mechanisms are applied to both the current population of individuals and the External Archive, which diligently stores the best non-dominated solutions discovered throughout the evolutionary process. Non-dominated sorting is the initial, fundamental step in ranking individuals based on their objective values. Furthermore, within each non-dominated front, crowding distance is meticulously computed to ensure the essential diversity of the solutions.

To ensure the External Archive remains a high-quality, non-dominated, and well-distributed repository of solutions, a rigorous, multi-step maintenance protocol is executed at the end of each generation. First, the non-dominated solutions from the current population are identified and aggregated with all existing solutions in the External Archive. This combined pool is then subjected to a new round of non-dominated sorting. All solutions that have become dominated by a newly discovered solution are pruned from the set. If the size of the remaining non-dominated set exceeds the predefined maximum archive size, a diversity-based thinning mechanism is activated. The crowding distance is calculated for all solutions within the oversized non-dominated set. Solutions with the smallest crowding distance—indicating that they are in the most crowded regions of the objective space—are progressively removed until the archive size is reduced to its predefined limit. This ensures the preservation of solutions that contribute most to the diversity of the approximated Pareto front and is crucial for the algorithm’s stability and ability to reproduce high-quality results.

For each individual $X_i$ on a specific front, its crowding distance $C{D}_i$ serves as a quantitative measure of the density of other solutions surrounding it in the objective space. A larger crowding distance value signifies that the individual is situated in a less crowded region, making it a valuable contributor to maintaining a broad and uniform distribution across the approximated Pareto front. The crowding distance for an individual $X_i$ on a given front is rigorously calculated by summing the normalized absolute differences in objective values of its two nearest neighbors along each objective axis. Specifically, for an individual $X_i$:

$$\begin{array}{c}\hfill C{D}_i=\sum _{m=1}^M{\displaystyle \frac{f_m\left(X_{i+1}^{\left(m\right)}\right)-f_m\left(X_{i-1}^{\left(m\right)}\right)}{f_m^{max}-f_m^{min}}}\end{array}$$

(10)

Here, $f_m\left(X_{i+1}^{\left(m\right)}\right)$ and $f_m\left(X_{i-1}^{\left(m\right)}\right)$ represent the objective values of the $(i+1)$-th and $(i-1)$-th solutions, respectively, in the list of individuals sorted according to the m-th objective for that specific front. Solutions positioned at the extreme ends of the objective range within a front are conventionally assigned an infinite crowding distance to guarantee their preservation. This dual-criteria selection strategy—prioritizing individuals based on their non-dominated rank first, then by their crowding distance—is fundamental to CSDE. It ensures that the algorithm simultaneously promotes rapid convergence towards the true Pareto front while diligently maintaining a broad and uniformly distributed set of solutions along its trajectory.

4.4. Self-Adaptive Parameter Management

To further enhance the algorithm’s adaptability and performance across diverse and dynamic problem instances, CSDE incorporates a sophisticated Self-Adaptive Parameter Management strategy. This mechanism allows key algorithmic parameters to evolve or adjust dynamically throughout the optimization process, rather than remaining static. This adaptive capability is crucial for ensuring that CSDE can optimally balance exploration (searching new regions) and exploitation (refining existing solutions) by dynamically tuning the influence of each knowledge source to maximize search efficiency and solution quality throughout the evolutionary cycle.

Specifically, the inertia weight (w), which modulates the influence of a particle’s previous velocity, is dynamically adjusted through a linear decay mechanism over the course of generations. This strategic reduction allows for a greater emphasis on global exploration in the early stages of the search, transitioning towards finer local exploitation as the evolutionary process progresses. The formula for the linear decay of w is given by:

$$\begin{array}{c}\hfill w=w_{start}-(w_{start}-w_{end})·{\displaystyle \frac{gen}{MaxGenerations}}\end{array}$$

(11)

Here, $w_{start}$ denotes the initial inertia weight, $w_{end}$ represents the final inertia weight, $gen$ signifies the current generation number, and $MaxGenerations$ is the total number of generations the algorithm is set to run.

Similarly, the learning factors ($c_1$ for cognitive learning and $c_2$ for social learning), which respectively dictate the pull towards individual best solutions and collective best solutions, are also subject to adaptive schemes. A commonly employed and effective strategy involves varying $c_1$ and $c_2$ inversely. This means that as the influence of individual learning ($c_1$) decreases, the emphasis on group collaboration ($c_2$) proportionally increases. This promotes individual exploration in the initial phases, gradually transitioning towards more collaborative exploitation as the search matures. Such adaptive rules can be expressed as

$$\begin{array}{c}\hfill c_1=c_{1,start}-(c_{1,start}-c_{1,end})·{\displaystyle \frac{gen}{MaxGenerations}}\end{array}$$

(12)

$$\begin{array}{c}\hfill c_2=c_{2,start}+(c_{2,end}-c_{2,start})·{\displaystyle \frac{gen}{MaxGenerations}}\end{array}$$

(13)

Furthermore, the differential evolution scaling factor ($F_{DE}$), which is critical for controlling the intensity of the differential perturbation and thus the exploratory power derived from DE, can also be dynamically adjusted. While a constant $F_{DE}$ is a common choice, more advanced adaptive strategies can be employed. For instance, $F_{DE}$ could be adapted based on metrics such as the population’s diversity or the observed convergence stagnation of the algorithm. This ensures that a strong exploratory pressure is maintained when needed (e.g., in stagnant regions) and gradually reduced when more precise exploitation becomes advantageous. A possible non-linear decay rule to achieve this could be

$$\begin{array}{c}\hfill F_{DE}\left(gen\right)=F_{DE,min}+(F_{DE,max}-F_{DE,min})\end{array}$$

(14)

$$\begin{array}{c}\hfill ·cos\left({\displaystyle \frac{\pi }{2}}·{\displaystyle \frac{gen}{MaxGenerations}}\right)\end{array}$$

(15)

This particular non-linear decay rule ensures a high exploratory impact in early stages and a gradual, controlled reduction as the search refines. This comprehensive adaptive management of these pivotal parameters collectively ensures that CSDE dynamically tunes the influence of each knowledge source, contributing significantly to its overall robust and efficient performance in navigating complex multi-objective landscapes.

5. Experiments

This section details the comprehensive experimental evaluation conducted to assess the performance of the proposed CSDE algorithm. Our primary objective is to rigorously demonstrate CSDE’s effectiveness in solving multi-objective MRTA problems. Specifically, this evaluation aims to highlight CSDE’s superiority in terms of solution convergence, diversity, and overall Pareto front quality when compared against established MOEAs, using Inverted Generational Distance (IGD) and Hypervolume (HV) as key performance indicators. The experiments provide empirical evidence supporting the benefits of CSDE’s knowledge-transfer mechanisms and robust capabilities across various problem complexities.

5.1. Simulation Environment and Map Generation

All experiments were meticulously conducted within a custom-built simulation environment, engineered to model real-world MRTA scenarios with granular control over problem complexity. This environment facilitates the generation of diverse and challenging test instances. The foundational map structure is a grid-based representation, with each cell categorized as either traversable or obstructed.

The map generation strategy creates heterogeneous environments reflecting varied MRTA challenges. As shown in Figure 3, we start with a base $50\times 50$ grid map, initialized as fully traversable. Obstacles are then introduced to achieve a predetermined obstacle ratio of $0.3$ through a sophisticated growth mechanism: Obstacle clusters are initiated from random seed points and expanded outwards using a Breadth-First Search (BFS)-like methodology. Each cluster has a random size (typically 5 to 25 cells), and merging with pre-existing, distinct obstacle clusters is prevented. This growth adheres to 4-directional (Manhattan) connectivity. A local smoothing filter is applied for a minimal number of iterations (e.g., two) to refine obstacle shapes and remove isolated cells, without creating connections between inherently disjoint obstacle blocks. To further augment topological complexity, a distinct “digit-shaped” obstacle (1 to 9) can be optionally embedded at the map’s center. For this experimental suite, nine distinct map instances were systematically generated, each embedding a different digit from 1 to 9.

Upon obstacle generation, a fixed number of robots ($K=4$) and tasks ($N=50$ or 100) are randomly distributed across the traversable areas. A crucial post-placement verification ensures all tasks are reachable from at least one depot, and vice versa. Depot locations are strategically selected from traversable cells, maintaining a minimum Manhattan distance constraint (typically a quarter of the map’s maximum dimension) to ensure dispersion. For each map, a distance matrix is meticulously pre-computed, quantifying the shortest path distance between every possible pair of depot and task locations using an efficient shortest-path algorithm (e.g., A* or Dijkstra’s). This pre-computation is paramount for rapid and efficient objective function evaluation.

5.2. Experimental Setup

To guarantee impartiality, robustness, and replicability, all evaluated algorithms were subjected to identical, rigorous experimental conditions. Each algorithm’s performance was assessed through 30 independent runs per problem instance.

Algorithmic parameters for CSDE and its comparative counterparts were meticulously configured for a fair comparison. The population size ($N_{pop}$) was uniformly 100, and the maximum number of generations ($MaxGenerations$) was fixed at 500. The External Archive Size ($MaxArchiveSize$) was set to 150 (1.5 times the population size).

For the proposed CSDE algorithm, its search behavior was meticulously governed by a set of dynamically adapted and fixed parameters. The inertia weight (w) was configured to linearly decrease from an initial value of $w_{start}=0.9$ to a final value of $w_{end}=0.4$ over the course of generations, enabling a smooth transition from global exploration to local exploitation. Concurrently, the cognitive learning factor ($c_1$) for personal best attraction linearly decreased from $c_{1,start}=2.5$ to $c_{1,end}=0.5$, while the social learning factor ($c_2$) for collective best attraction linearly increased from $c_{2,start}=0.5$ to $c_{2,end}=2.5$. This inverse adaptive scheme for $c_1$ and $c_2$ strategically balances individual learning with swarm collaboration throughout the optimization process. Furthermore, the DE scaling factor ($F_{DE}$) was dynamically adjusted using a cosine adaptation rule, varying typically from a minimum of 0.4 to a maximum of 0.9, ensuring a flexible perturbation intensity. The crossover rate ($CR$) for the DE components was consistently set to 0.9.

To rigorously evaluate CSDE’s performance, it was systematically benchmarked against two prominent MOEAs: MOPSO and MODE. For standard MOPSO, the inertia weight followed a linear decrease from 0.9 to 0.4, with the cognitive and social learning factors fixed at $c_1=2.0$ and $c_2=2.0$, respectively. Standard MODE employed a fixed scaling factor $F=0.5$ and a crossover rate $CR=0.9$. For the MOGA, the population size was set to 100, the crossover rate was 0.8, and the mutation rate was 0.1. Crucially, all comparative algorithms, including CSDE, utilized identical underlying multi-objective maintenance mechanisms, specifically non-dominated sorting and crowding distance calculation, and adhered to the exact same encoding and decoding strategies as detailed previously. This meticulous consistency in shared components ensures that any observed performance differences can be directly attributed to the distinct evolutionary operators and parameter adaptation schemes of the respective algorithms.

To provide a comprehensive quantitative assessment, IGD and HV were employed as multi-objective performance indicators. A lower IGD value signifies superior performance, indicating both closer proximity to the true Pareto front and a better spread of solutions. A higher HV value signifies superior overall performance, encompassing both robust convergence and broad diversity.

5.3. Performance Analysis and Comparative Study

This section offers a comprehensive analysis of the proposed CSDE algorithm’s performance in the MRTA problem, benchmarked against comparative algorithms including PSO, GA, and DE. The analysis primarily focuses on IGD (lower is better) and HV (higher is better) metrics.

The results of 50-task scenarios are shown in

Table 1. Comparison of methods on different maps (IGD and HV metrics).

Map	CSDE		MOPSO		MOGA		MODE
	IGD	HV	IGD	HV	IGD	HV	IGD	HV
Map 1	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$8.11\times {10}^4$	$1.11\times {10}^2$	$4.85\times {10}^4$	$2.85\times {10}^2$	$3.01\times {10}^4$	$1.71\times {10}^2$	$\mathbf{5.32}\times {\mathbf{10}}^{\mathbf{4}}$
Map 2	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{9.72}\times {\mathbf{10}}^{\mathbf{4}}$	$7.03\times {10}^1$	$6.49\times {10}^4$	$1.85\times {10}^2$	$6.13\times {10}^4$	$9.23\times {10}^1$	$8.34\times {10}^4$
Map 3	$\mathbf{4.95}\times {\mathbf{10}}^{-\mathbf{1}}$	$9.26\times {10}^4$	$7.72\times {10}^1$	$6.10\times {10}^4$	$2.20\times {10}^2$	$5.83\times {10}^4$	$1.08\times {10}^2$	$\mathbf{8.57}\times {\mathbf{10}}^{\mathbf{4}}$
Map 4	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{9.79}\times {\mathbf{10}}^{\mathbf{4}}$	$1.12\times {10}^2$	$5.86\times {10}^4$	$2.74\times {10}^2$	$4.25\times {10}^4$	$1.80\times {10}^2$	$6.59\times {10}^4$
Map 5	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{1.16}\times {\mathbf{10}}^{\mathbf{5}}$	$5.78\times {10}^1$	$8.62\times {10}^4$	$1.13\times {10}^2$	$8.03\times {10}^4$	$1.26\times {10}^2$	$8.07\times {10}^4$
Map 6	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{1.05}\times {\mathbf{10}}^{\mathbf{5}}$	$1.10\times {10}^2$	$6.25\times {10}^4$	$2.98\times {10}^2$	$5.82\times {10}^4$	$2.54\times {10}^2$	$6.28\times {10}^4$
Map 7	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{9.10}\times {\mathbf{10}}^{\mathbf{4}}$	$9.26\times {10}^1$	$6.19\times {10}^4$	$1.77\times {10}^2$	$5.66\times {10}^4$	$1.11\times {10}^2$	$7.40\times {10}^4$
Map 8	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{1.54}\times {\mathbf{10}}^{\mathbf{5}}$	$1.18\times {10}^2$	$1.10\times {10}^5$	$1.98\times {10}^2$	$9.21\times {10}^4$	$1.54\times {10}^2$	$1.03\times {10}^5$
Map 9	$2.54\times {10}^0$	$\mathbf{7.81}\times {\mathbf{10}}^{\mathbf{4}}$	$1.04\times {10}^2$	$4.08\times {10}^4$	$\mathbf{8.08}\times {\mathbf{10}}^{\mathbf{1}}$	$5.40\times {10}^4$	$6.91\times {10}^1$	$5.87\times {10}^4$

. CSDE consistently demonstrated remarkable performance, largely surpassing the comparative algorithms. As detailed in Table 1, CSDE achieved an IGD value of 0.0 (or values extremely close to 0.0, indicating negligible deviation) across most maps (1, 2, 4, 5, 6, 7, 8). This exceptional result signifies not only precise convergence to the reference Pareto front but also the maintenance of excellent solution diversity, indicating that CSDE is capable of finding a comprehensive and high-quality set of trade-off solutions. CSDE’s HV performance was equally impressive, securing the highest HV values on the majority of maps (Maps 2, 4, 5, 6, 7, and 8). This robustifies CSDE’s leading position, indicating its superior capability to provide well-distributed and high-quality solutions for the MRTA problem in these scenarios. Notably, on Maps 1, 3, and 9, the MODE algorithm slightly outperformed CSDE in terms of HV, suggesting that for certain map configurations, the pure DE approach might find a slightly larger dominated area. However, CSDE still maintained significantly lower IGD values on these maps, especially on Map 1, where its IGD was $0.00\times {10}^0$ compared with MODE’s $1.71\times {10}^2$, highlighting its superior convergence.

As task complexity increased to 100-task scenarios, as presented in

Table 2. Comparison of methods on different maps (IGD and HV metrics).

Map	CSDE		MOPSO		MOGA		MODE
	IGD	HV	IGD	HV	IGD	HV	IGD	HV
Map 1	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{6.17}\times {\mathbf{10}}^{\mathbf{5}}$	$2.71\times {10}^2$	$4.71\times {10}^5$	$5.83\times {10}^2$	$2.02\times {10}^5$	$2.10\times {10}^2$	$4.58\times {10}^5$
Map 2	$1.06\times {10}^2$	$7.15\times {10}^5$	$\mathbf{1.45}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{6.51}\times {\mathbf{10}}^{\mathbf{5}}$	$5.77\times {10}^2$	$1.69\times {10}^5$	$5.68\times {10}^2$	$5.29\times {10}^5$
Map 3	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{5.80}\times {\mathbf{10}}^{\mathbf{5}}$	$2.69\times {10}^2$	$4.03\times {10}^5$	$4.86\times {10}^2$	$2.28\times {10}^5$	$2.56\times {10}^2$	$3.90\times {10}^5$
Map 4	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{7.50}\times {\mathbf{10}}^{\mathbf{5}}$	$2.24\times {10}^2$	$5.73\times {10}^5$	$5.90\times {10}^2$	$2.48\times {10}^5$	$2.28\times {10}^2$	$5.78\times {10}^5$
Map 5	$3.29\times {10}^2$	$\mathbf{3.38}\times {\mathbf{10}}^{\mathbf{5}}$	$\mathbf{1.10}\times {\mathbf{10}}^{\mathbf{1}}$	$2.80\times {10}^5$	$7.70\times {10}^2$	$8.81\times {10}^4$	$6.41\times {10}^2$	$2.34\times {10}^5$
Map 6	$1.08\times {10}^2$	$\mathbf{5.68}\times {\mathbf{10}}^{\mathbf{5}}$	$\mathbf{2.09}\times {\mathbf{10}}^{\mathbf{1}}$	$4.55\times {10}^5$	$7.08\times {10}^2$	$1.69\times {10}^5$	$6.45\times {10}^2$	$4.07\times {10}^5$
Map 7	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{6.61}\times {\mathbf{10}}^{\mathbf{5}}$	$1.60\times {10}^2$	$4.98\times {10}^5$	$8.25\times {10}^2$	$1.76\times {10}^5$	$5.80\times {10}^2$	$4.88\times {10}^5$
Map 8	$3.98\times {10}^2$	$\mathbf{8.31}\times {\mathbf{10}}^{\mathbf{5}}$	$\mathbf{9.04}\times {\mathbf{10}}^{\mathbf{0}}$	$7.51\times {10}^5$	$6.63\times {10}^2$	$2.42\times {10}^5$	$6.24\times {10}^2$	$6.95\times {10}^5$
Map 9	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{5.55}\times {\mathbf{10}}^{\mathbf{5}}$	$2.12\times {10}^2$	$4.01\times {10}^5$	$6.13\times {10}^2$	$1.15\times {10}^5$	$2.42\times {10}^2$	$3.93\times {10}^5$

, CSDE maintained robust competitiveness and demonstrated significant scalability. It consistently optimized its IGD value to 0.0 on Maps 1, 3, 4, 7, and 9, further confirming its excellent ability to converge accurately to the Pareto front even for larger problem instances. Correspondingly, CSDE also achieved the highest HV values on Maps 1, 3, 4, 7, and 9, solidifying its standing as one of the most outstanding algorithms for larger-scale MRTA problems. However, in these more complex 100-task scenarios, MOPSO exhibited notably superior performance on specific map configurations: it achieved the lowest IGD values on Maps 2, 5, 6, and 8, and the highest HV values on Map 2 and Map 8. This indicates that while CSDE generally excels, MOPSO’s strong local exploitation capabilities might offer distinct advantages in terms of convergence for certain extremely complex or topologically unique environments within the 100-task set.

This intriguing observation points to a potential nuance in the CSDE algorithm’s search behavior. We hypothesize that in these specific scenarios, the search landscape might contain a few exceptionally promising, yet geographically compact, regions. In such cases, MOPSO’s aggressive and singular focus on local exploitation, driven by its rapid convergence towards the best solutions, allows it to quickly “drill down” into these areas and find high-quality solutions faster than CSDE. This suggests that while CSDE’s DE-driven exploration is vital for avoiding local optima and maintaining diversity, its influence might, in rare cases, slow down the fine-tuning process in landscapes that are better suited for rapid exploitation.

Overall, CSDE exhibits exceptional comprehensive performance in solving the MRTA problem across varying complexities, significantly outperforming the conventional MOGA and MODE algorithms, and generally surpassing MOPSO in most evaluated cases. CSDE’s frequent attainment of IGD values near zero and its consistent leadership in HV scores strongly affirm its robust advantages in terms of Pareto front convergence accuracy, solution set diversity, and overall quality. This superior performance is primarily attributed to CSDE’s meticulously designed operator-level knowledge transfer mechanism, its effective elitist preservation strategy via the External Archive, and the inherent powerful global exploration and local exploitation capabilities derived from the intelligent fusion of DE and PSO paradigms, complemented by adaptive parameter management. While CSDE demonstrates substantial advantages, MOPSO’s superior performance in certain 100-task scenarios suggests areas for further optimization in CSDE’s adaptability for extremely complex or topologically unique environments. Future research will focus on enhancing CSDE’s generalizability and robustness for large-scale, high-complexity MRTA problems.

5.4. Analysis of Ablation Study Results

To precisely quantify the contribution of each core component within the proposed CSDE algorithm, a comprehensive ablation study was conducted. This involved systematically evaluating CSDE against two reduced versions: CSDE-NoDE, where the DE component was entirely removed, and CSDE-NoPSO, which operated without the PSO component. This rigorous analysis, presented in

Table 3. Comparison of CSDE variants on different maps (IGD and HV metrics).

Map	CSDE		CSDE-NoDE		CSDE-NoPSO
	IGD	HV	IGD	HV	IGD	HV
Map 1	$\mathbf{2.66}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{5.32}\times {\mathbf{10}}^{\mathbf{4}}$	$3.02\times {10}^2$	$1.73\times {10}^4$	$4.07\times {10}^1$	$5.62\times {10}^4$
Map 2	$\mathbf{2.39}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{4.73}\times {\mathbf{10}}^{\mathbf{4}}$	$1.74\times {10}^2$	$1.25\times {10}^4$	$7.32\times {10}^1$	$3.29\times {10}^4$
Map 3	$\mathbf{2.10}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{4.38}\times {\mathbf{10}}^{\mathbf{4}}$	$2.13\times {10}^2$	$1.28\times {10}^4$	$4.85\times {10}^1$	$4.23\times {10}^4$
Map 4	$\mathbf{5.71}\times {\mathbf{10}}^{-\mathbf{1}}$	$\mathbf{4.75}\times {\mathbf{10}}^{\mathbf{4}}$	$2.40\times {10}^2$	$1.95\times {10}^4$	$1.11\times {10}^2$	$3.80\times {10}^4$
Map 5	$\mathbf{3.15}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{5.44}\times {\mathbf{10}}^{\mathbf{4}}$	$1.98\times {10}^2$	$1.86\times {10}^4$	$4.92\times {10}^1$	$4.94\times {10}^4$
Map 6	$\mathbf{1.44}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{5.36}\times {\mathbf{10}}^{\mathbf{4}}$	$2.50\times {10}^2$	$1.23\times {10}^4$	$7.29\times {10}^1$	$4.71\times {10}^4$
Map 7	$\mathbf{1.09}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{3.63}\times {\mathbf{10}}^{\mathbf{4}}$	$1.53\times {10}^2$	$1.01\times {10}^4$	$7.15\times {10}^1$	$2.31\times {10}^4$
Map 8	$\mathbf{1.45}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{2.14}\times {\mathbf{10}}^{\mathbf{4}}$	$1.62\times {10}^2$	$6.83\times {10}^3$	$2.30\times {10}^1$	$2.21\times {10}^4$
Map 9	$\mathbf{8.31}\times {\mathbf{10}}^{-\mathbf{1}}$	$\mathbf{4.60}\times {\mathbf{10}}^{\mathbf{4}}$	$2.48\times {10}^2$	$1.23\times {10}^4$	$1.15\times {10}^2$	$4.32\times {10}^4$

(for 50-task scenarios) and

Table 4. Comparison of CSDE variants on different maps (IGD and HV metrics).

Map	CSDE		CSDE-NoDE		CSDE-NoPSO
	IGD	HV	IGD	HV	IGD	HV
Map 1	$\mathbf{4.18}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{7.08}\times {\mathbf{10}}^{\mathbf{4}}$	$2.47\times {10}^2$	$2.54\times {10}^4$	$1.01\times {10}^2$	$6.76\times {10}^4$
Map 2	$\mathbf{7.56}\times {\mathbf{10}}^{\mathbf{1}}$	$1.34\times {10}^5$	$1.84\times {10}^2$	$8.88\times {10}^4$	$7.22\times {10}^1$	$\mathbf{1.72}\times {\mathbf{10}}^{\mathbf{5}}$
Map 3	$\mathbf{1.95}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{1.76}\times {\mathbf{10}}^{\mathbf{5}}$	$3.31\times {10}^2$	$5.33\times {10}^4$	$1.54\times {10}^2$	$1.48\times {10}^5$
Map 4	$\mathbf{2.12}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{2.13}\times {\mathbf{10}}^{\mathbf{5}}$	$3.61\times {10}^2$	$6.57\times {10}^4$	$2.16\times {10}^2$	$1.89\times {10}^5$
Map 5	$1.03\times {10}^2$	$9.58\times {10}^4$	$1.39\times {10}^2$	$7.58\times {10}^4$	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{1.26}\times {\mathbf{10}}^{\mathbf{5}}$
Map 6	$\mathbf{6.56}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{2.28}\times {\mathbf{10}}^{\mathbf{5}}$	$3.33\times {10}^2$	$7.97\times {10}^4$	$1.58\times {10}^2$	$2.20\times {10}^5$
Map 7	$\mathbf{2.01}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{2.91}\times {\mathbf{10}}^{\mathbf{5}}$	$6.43\times {10}^2$	$9.63\times {10}^4$	$5.39\times {10}^2$	$2.46\times {10}^5$
Map 8	$9.45\times {10}^1$	$6.95\times {10}^4$	$2.78\times {10}^2$	$2.67\times {10}^4$	$\mathbf{0.00}\times {\mathbf{10}}^{\mathbf{0}}$	$\mathbf{9.72}\times {\mathbf{10}}^{\mathbf{4}}$
Map 9	$\mathbf{1.09}\times {\mathbf{10}}^{\mathbf{1}}$	$\mathbf{2.01}\times {\mathbf{10}}^{\mathbf{5}}$	$3.84\times {10}^2$	$7.76\times {10}^4$	$2.53\times {10}^2$	$1.94\times {10}^5$

(for 100-task scenarios), unequivocally demonstrates that both the DE and PSO components are critical and indispensable for CSDE’s superior performance in solving the MRTA problem, highlighting their profound synergy.

Similarly, the removal of the PSO component (CSDE-NoPSO) also results in a noticeable performance drop compared with the full CSDE algorithm. While CSDE-NoPSO generally performs better than CSDE-NoDE (as its IGD values are lower and HV values are higher than CSDE-NoDE across most instances), its performance consistently lags behind the complete CSDE algorithm in the majority of cases. For example, in 50-task scenarios, CSDE consistently outperforms CSDE-NoPSO in terms of both IGD and HV on almost all maps (e.g., on Map 4, CSDE’s IGD is $5.71\times {10}^{-1}$ vs. CSDE-NoPSO’s $1.11\times {10}^2$; HV is $4.75\times {10}^4$ vs. $3.80\times {10}^4$). This indicates that the PSO component is crucial for enhancing convergence speed and fine-tuning local search by effectively guiding the population towards promising regions based on individual and collective best experiences, thus refining the discovered solutions and improving the overall quality of the approximated Pareto front.

It is worth noting a few isolated instances, particularly in the more complex 100-task scenarios, where CSDE-NoPSO exhibits surprisingly competitive or even superior performance. Specifically, for Maps 2, 5, and 8 in the 100-task scenario (Table 4), CSDE-NoPSO achieves lower IGD values (including an IGD of 0.0 on Maps 5 and 8) and higher HV values than the full CSDE. This intriguing observation suggests that in certain highly complex or topologically unique environments, the guiding influence of the PSO’s local exploitation might, counter-intuitively, hinder the DE’s global exploration by pulling individuals too quickly towards sub-optimal regions. In such challenging landscapes, a more unconstrained global search (primarily driven by DE without strong PSO guidance) might prove more effective in discovering the true Pareto front. However, these are exceptions, and across the overwhelming majority of test cases, the full CSDE significantly outperforms its ablated counterparts.

To clarify the selection, Maps 2, 5, and 8 were not chosen arbitrarily but because they consistently showed these anomalous results. As can be seen in Figure 3, the depots in these maps are mainly located near the edges and adjacent to obstacle clusters, while the traversable regions are fragmented with relatively narrow passages. Such structures make it harder for robots to enter or leave task areas. When combined with the scattered distribution of tasks, these conditions create a rugged and multimodal fitness landscape, where local exploitation (PSO) can lead to premature convergence. This explains why DE-driven global exploration in CSDE-NoPSO occasionally achieved better performance on these specific instances.

This phenomenon can be attributed to the inherent characteristics of the DE and PSO paradigms. In rugged or multimodal search spaces, PSO’s strong reliance on local and global best solutions can lead to premature convergence, causing the search to become trapped in suboptimal regions. In contrast, DE’s differential mutation operator provides a more robust, diversity-driven global exploration. For the specific map instances where CSDE-NoPSO performed better, the problem landscape likely favored an unconstrained global search over guided exploitation. The DE component in CSDE-NoPSO was able to effectively escape local optima and maintain a more comprehensive exploration of the search space, ultimately yielding a higher quality solution set.

In conclusion, this ablation study unequivocally confirms that both the DE and PSO components play distinct yet profoundly complementary roles within the CSDE algorithm. The DE component provides crucial global exploration and diversity maintenance, preventing premature convergence by enabling robust search across the solution space. Concurrently, the PSO component offers powerful local exploitation and guided convergence, ensuring thorough refinement of promising regions and accelerating the approach towards the Pareto front. Their synergistic interaction enables CSDE to effectively navigate the multi-objective optimization landscape of MRTA, leading to its superior and robust performance in achieving low IGD and high HV. The findings strongly validate CSDE’s core design principle: the integrated strength of these two meta-heuristics is greater than the sum of their individual parts, making them both essential for achieving state-of-the-art results and robust problem-solving capabilities across diverse MRTA challenges.

5.5. Replanning Under Dynamic Changes

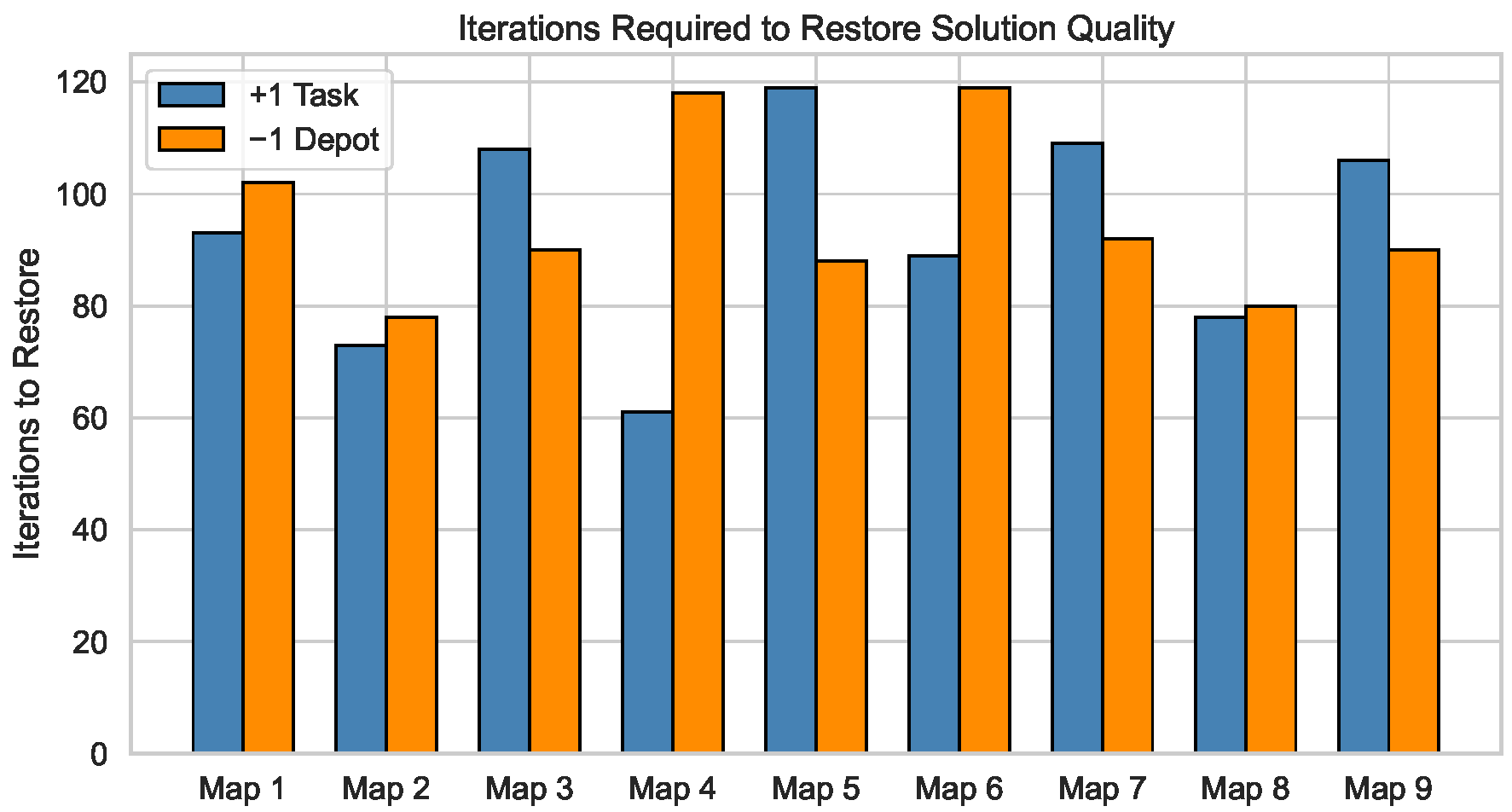
To assess CSDE’s ability to adapt online, we evaluate two dynamic scenarios on all nine benchmark maps: (i) the arrival of one new task ($+1$ task) and (ii) the loss of one robot ($-1$ depot). For each scenario and map, we measure the number of iterations required for CSDE to restore solution quality to within 2% of the baseline (static) performance. Concretely, letting $f_{\mathrm{base}}^{\star }$ denote the best baseline objective (total distance; lower is better) and $f_t$ the best-so-far objective at iteration t, we declare restoration at the smallest t such that

$${\displaystyle \frac{f_t-f_{\mathrm{base}}^{\star }}{f_{\mathrm{base}}^{\star }}}\le 0.02.$$

The aggregated results are shown in Figure 4, indicating that CSDE typically restores solution quality within ∼70–120 iterations across maps, providing a quantitative measure of responsiveness under dynamic changes.

To complement this overview, Figure 5 plots detailed convergence histories for all nine maps, each showing the baseline, $+1$ task, and $-1$ depot trajectories of the best objective value over iterations. As an illustrative case, on Map 1, the addition of one task initially degrades solution quality, but CSDE recovers to near-baseline within $\approx 93$ iterations; removing one depot induces a larger drop yet CSDE regains stability after $\approx 102$ iterations. Other maps exhibit comparable patterns, with recovery speed influenced by obstacle density and task dispersion: more fragmented traversable regions (e.g., Map 5) tend toward the upper end of the 70–120 range, while simpler layouts (e.g., Map 2) recover faster.

Together, these results confirm CSDE’s robustness (consistent recovery to high-quality solutions) and efficiency (fast restoration within a limited number of iterations) under dynamic task arrivals and resource reductions, supporting its suitability for practical multi-robot systems requiring frequent replanning.

5.6. Comparison of Parameter Adaptation Schemes

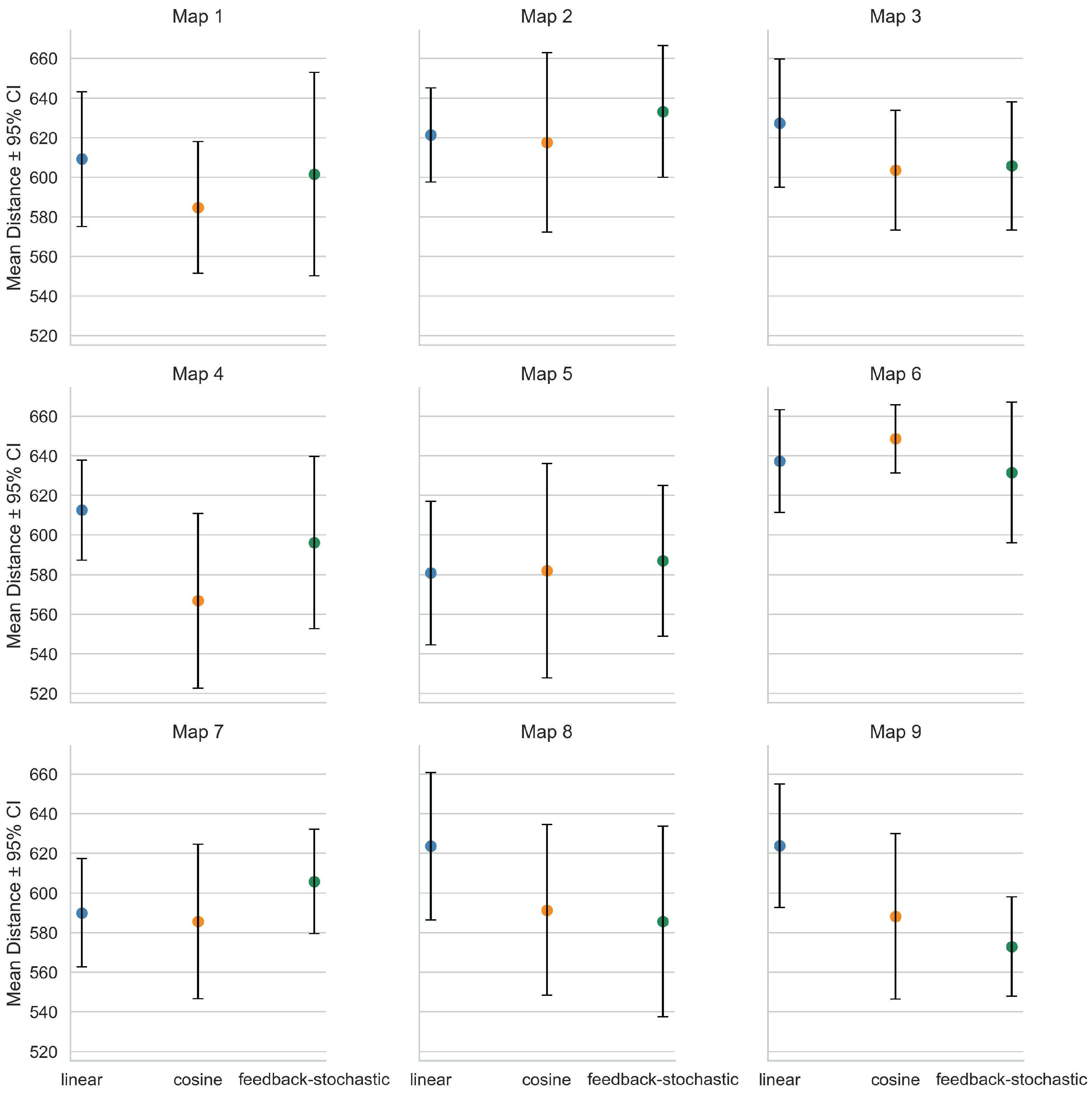
We further examine how parameter adaptation affects CSDE by comparing three schemes: linear decay, cosine-based adjustment, and feedback-stochastic adaptation. Each scheme is executed 10 times per map on all nine maps; we report the mean total distance (lower is better) with 95% confidence intervals (CI).

Figure 6 summarizes cross-map trends: The cosine scheme frequently attains the lowest mean distance (notably on Maps 1, 3, and 4); the feedback-stochastic scheme is competitive on several maps but exhibits higher variance, reflecting its adaptive yet stochastic nature; the linear scheme is stable but generally slightly inferior. To make per-map differences more legible, given the small absolute gaps (typically 20–40 units around ∼600), Figure 7 employs point plots with 95% CI instead of bars, which better reveal subtle yet consistent advantages while preserving uncertainty visualization. Overall, cosine-based adaptation offers the most balanced trade-off between convergence speed and solution quality, while feedback-stochastic can be advantageous in specific instances at the cost of higher variability.

5.7. Pareto Front Visualizations

This section presents a compelling visual representation of the Pareto fronts generated by the CSDE algorithm and its comparative counterparts, serving as a crucial complement to the quantitative results detailed in Section 5.3. These plots, depicting the trade-off between the two primary objectives (total travel distance on the x-axis and task load imbalance on the y-axis), reinforce the findings regarding IGD and HV. For minimization problems, a well-performing algorithm, characterized by low IGD and high HV, is expected to exhibit a Pareto front that is both close to the ideal point (the origin, representing minimum values for both objectives) and widely spread, effectively covering the entire trade-off surface.

Visual inspection of the generated Pareto front plots, as exemplified in Figure 8 for the 100-task scenarios, clearly corroborates the superior performance of our proposed CSDE algorithm. On numerous maps, CSDE’s Pareto front (represented by blue points) consistently appears closest to the ideal point (the origin of the plot), demonstrating its excellent convergence. This visual proximity directly reflects the consistently low IGD values achieved by CSDE, as presented in Table 2. Furthermore, CSDE’s fronts are often observed to be remarkably well-distributed and widely spread along the trade-off curve, effectively covering a broad range of optimal compromises between the Total Travel Distance and Task Load Imbalance objectives. This comprehensive coverage across the objective space is a direct visual representation of the high HV values secured by CSDE, confirming its ability to provide a diverse set of high-quality solutions.

In sharp contrast, the Pareto fronts generated by the comparative algorithms, particularly MOGA (green points) and often MODE (red points), generally appear significantly further away from the origin and frequently exhibit less uniform distribution, noticeable gaps, or a more clustered appearance along their respective fronts. MOPSO (orange points) often shows better performance than MOGA and MODE, but CSDE generally maintains a clear advantage in proximity to the origin and front coverage. This visual disparity aligns perfectly with their quantitatively higher IGD values and lower HV values presented in Section 5.3. These visual differences underscore that CSDE not only excels in numerical performance metrics but also produces visually appealing, well-converged, and highly effective Pareto fronts that offer a rich set of practical trade-off solutions, thereby confirming its overall robustness and efficiency in solving the complex MRTA problem.

6. Conclusions

This paper successfully introduced the CSDE algorithm, a novel multi-objective evolutionary algorithm specifically engineered for the intricate MRTA problem. Our work addressed the critical need for a more robust and efficient optimizer by proposing an innovative operator-level fusion of DE’s powerful global exploration capabilities with PSO’s efficient local exploitation mechanisms. This deep integration, uniquely facilitated by a fused velocity update mechanism, enabled CSDE to dynamically leverage both individual and collective knowledge while effectively enhancing and maintaining population diversity throughout the optimization process.

Through comprehensive experiments conducted on diverse MRTA instances, CSDE consistently demonstrated superior performance when benchmarked against state-of-the-art multi-objective evolutionary algorithms, including MOPSO, MODE, and MOGA. Achieving frequent IGD values near zero and consistently leading in HV scores, CSDE proved its exceptional ability to converge accurately to the true Pareto front and provide a well-distributed set of high-quality trade-off solutions for the MRTA problem. Furthermore, a rigorous ablation study unequivocally confirmed that both the DE and PSO components are indispensable and contribute synergistically to CSDE’s overall effectiveness, validating the efficacy of their integrated design.

Despite its significant advantages, CSDE’s performance on certain complex map configurations suggests avenues for further refinement. Future research will primarily focus on enhancing CSDE’s robustness and generalizability for large-scale and dynamic MRTA problems. Specifically, we will explore adapting our current problem formulation, which simplifies task load balancing by not considering task weights or costs, to more practical scenarios. Additionally, we will investigate the algorithm’s scalability with an increasing number of robots or tasks, analyzing its computational complexity and addressing potential bottlenecks in the path-planning module. The core strengths of CSDE, including its robust exploration and swift exploitation, position it as an ideal candidate for a dynamic scheduling module in online scenarios where events such as robot failures or new task arrivals necessitate rapid replanning. This research will also involve exploring more refined adaptive parameter tuning mechanisms and more sophisticated fusion mechanisms with other meta-heuristic components to further improve local optima avoidance and overall search efficiency. In particular, the investigation of adaptive parameter control will be an important future direction, as the current use of predefined decay rules, while effective, may limit flexibility in highly dynamic environments.